Solar radiation estimation on a tilted surface using sky models in the Afar region of Ethiopia

The aim of this study is to estimate solar radiation on an inclined surface using sky models. Two anisotropic (direction dependent) and two isotropic (independent of direction) sky models were used for 12.11°N (latitude) and 40.63°E (longitude) in the Afar region of Ethiopia. The sky model outputs were compared to sample statistical test data from the Ethiopian Meteorological Institute and found to exceed expectations in all cases. We found that the Hay and Davies model predicted the highest incident solar radiation throughout the year. Finally, the model that we propose for estimation of solar radiation events on a tilted surface is the Liu and Jordan (LJ) isotropic model, which has the fewest statistical errors out of all the models evaluated in this study and shows good agreement with the estimated data.

1 Introduction

Solar radiation data constitute the most important source of information for estimating the average incident radiation, which is needed for appropriate design and assessment of solar energy conversion devices (Sabziparvar, 2008). Photovoltaic (PV) sources play critical roles in meeting the growing need for clean energy in Ethiopia because they are environmentally friendly and renewable (Khaled et al., 2024). Different types of solar radiation data provide various advantages in the design and development of solar energy systems (Jakhrani et al., 2012, 2013). Daily records are often easy to acquire and can be used to estimate hourly radiation in affluent countries. Access to more detailed solar radiation data is critical when building and evaluating solar-based conversion devices. However, PV power generation is extremely sensitive to variations in solar irradiation as well as other local environmental conditions, such as temperature, sunshine time, and solar geometry, whereas electrical power production can be achieved relatively easily (Mawloud et al., 2024a). Most developing countries, including Ethiopia, lack fundamental statistics on solar radiation for substantial surfaces owing to inadequate infrastructure (Li et al., 2008; Dazhi and Chris, 2020), because of which the necessary measurement equipment and techniques are often beyond means. Hence, methodologies for calculating solar radiation must be developed using more readily available meteorological data (El-Sebaii et al., 2010a). For decades, several models have been used to approximate the amount of solar radiation incident on horizontal surfaces around the world using various climatic characteristics, such as wind speed, humidity, maximum and minimum ambient temperatures, and cloud cover (El-Sebaii and Trabea, 2003).

Solar radiation assessments are often difficult owing to multiple influencing elements, such as meteorological, climatic, and radiometric factors (Mawloud et al., 2024b). Wu et al. (2007a) and Wu et al. (2007b) used air temperature, total precipitation, sunshine hours, and metrological data from the Nanchang station in China from 1994 to 2005 to anticipate the daily global solar radiation. Furthermore, simple approaches for accurately estimating the monthly average of daily solar radiation on a horizontal surface have been developed for locations like Turkiye (Bulut and Buyukalaca, 2007). Researchers have also used satellite data to create a model for calculating the monthly average hourly global radiation in tropical regions with high aerosol loads; this method was used to construct hourly maps of solar radiation at a specified site (Janjai et al., 2009). It is important to determine the beam and diffuse components of the total incident radiation on a horizontal surface. Once these factors are calculated, they can be used on inclined surfaces to assess the short- and long-term efficiencies of solar devices, such as PV modules and inclined flat-plate collectors.

Several studies (Solanki, 2011; Solanki and Sangani, 2008) have offered empirical correlations to help calculate the monthly average daily diffuse radiation on a horizontal surface; here, the horizontal diffuse radiation was determined using the clearness index (k_T), ratio of monthly averages of the daily hours to maximum possible number of daily hours of bright sunshine (S/S_O), ratio of monthly averages of the daily diffuse radiation to global solar radiation (H_D/H_G), and ratio of the monthly averages of the daily diffuse radiation to extraterrestrial horizontal solar radiation (H_D/H_O) (Dazhi and Chris, 2020; Solanki, 2011). Solanki and Sangani (2008) proposed a new method for forecasting the monthly average value of the daily beam radiation on a horizontal surface (H_B) using the elevation angle constant (ε) at a certain location and time. Moreover, Ozan and Tuncay (2009) used an artificial neural network and satellite data to estimate the monthly mean daily average values of the horizontal direct and diffuse radiation components. Meteorological stations regularly monitor the global and diffuse radiation energies from the sun on horizontal surfaces, but solar radiation representations are rarely available for inclined surfaces. To determine the size of such an inclined system and predict its long-term performance, the solar radiation incident on inclined surfaces must be evaluated by comparing the solar radiation intensities acquired from level surfaces with those acquired from inclined surfaces of interest. In this regard, it is well established that latitude and day of the year influence the ideal inclination in the northern hemisphere.

The optimal tilt angle is larger during winter (latitude+15) and smaller during summer (latitude−15). Several studies in the literature offer varied recommendations for the ideal tilt based solely on latitude (Sudhakar et al., 2013). The collectors operate better when facing true north as they can receive sunlight maximally over a longer period of time. To maximize the total energy gathered over a 12-month period, the collector plates are frequently tilted at variable angles pointing northward, ranging from 0 to 40° (Al-Ghezi et al., 2022; Yousif et al., 2019; John et al., 2020).

Three components of radiation are incident on a tilted exposed surface, namely, diffuse radiation, radiation with bending, and radiation reflected off the ground. The simple geometric relationships between horizontal and tilted surfaces can be used to calculate the beam radiation exposure of a tilted surface. An isotropic model and a simple method can be used to estimate the ground reflections with a high degree of accuracy. For the diffuse component, there are no simple relationships as diffuse radiation lacks a specified angle of incidence upon a horizontal surface. Diffuse radiation measured on a level surface is often compared to that on a tilted surface using various sky models; these models can be broadly classified as isotropic or anisotropic.

The following are the primary goals of this study:

• Estimating the monthly average values of the global, diffuse, and beam solar radiations on horizontal surfaces in the Afar region of Ethiopia using empirical methods.

• Estimating the total solar radiation incident on a tilted surface at 12.11°N, which is the latitude of the Afar region, using empirical models.

• Comparing the estimated data with each model using statistical metrics, such as mean absolute percentage error (MAPE), mean bias error (MBE), t-statistic, root mean-squared error (RMSE), and normalized RMSE.

2 Materials and methods

2.1 Study location

The present study was conducted in the Afar region of northeastern Ethiopia between the latitudes of 12.11°N and 40.65°E. As shown in Figure 1, the altitudes in this region range from 116 to 1500 m below sea level and have an average barometric pressure of 97 kPa (Federal Democratic Republic of Ethiopia Central Statistical Agency, 2014). The meteorological station located in the Afar region experiences a subtropical steppe climate and is located 404 m (1325.46 feet) above sea level (Natei et al., 2022; Abdusalam et al., 2014).

Figure 1

Figure 1. Study location showing the map of Ethiopia and the Afar region (MDPI, 2025).

The following are some brief details about the Afar region:

• Temperatures are consistently hot on average.

• The average annual temperature ranges from 30°C to 40°C.

• January, February, March, April, and December are dry months.

• March, April, May, June, and July are the warmest months, with temperatures often exceeding 40°C.

December is the coolest month, while August is the wettest month (Natei et al., 2022; Abdusalam et al., 2014).

2.2 Solar radiation on a horizontal surface

The following parameters should be considered when estimating the solar radiation incident on a tilted surface: declination (δ); latitude (∅); angle of incidence (θ); surface azimuth angle (γ); hour angle (ω); day of the year (N); global, beam, diffuse, and reflected solar radiations; orientation toward the equator; tilt angle (β); sky clearness (k_T); cloudiness index (k_d).

The monthly average daily solar radiation on a horizontal surface (H_O) is given by the empirical formula in Equation 1:

${\mathrm{H}}_{\mathrm{o}}=\frac{24}{\mathbf{\pi }}\times I_{sc}\left[1+0.033\cos \frac{360N}{365}\right]\left[\cos \varnothing \cos \delta \sin {\omega }_s+\frac{\pi {\omega }_s}{180}\sin \varnothing \sin \delta \right]\text{kWh}/m^2\text{day}(1)$

where N is the day of the year, ω_s is the sunshine hour angle for the mean day of the month (degrees), $\varphi$ is the latitude angle (degrees), δ is the declination angle (degrees); and $I_{sc}$ is the solar constant, which is equal to 1367 kW/m².

Cooper’s model (Khai et al., 2014) shown in Equation 2 provides a mathematical representation of the declination angle:

$\delta =23.34\sin \frac{360}{365}\left(284+N\right),(2)$

where N represents the day of the year beginning in January, as shown in Table 1. According to Solanki (2011), the sunshine hour angle (ω_s) for a location depends on the solar declination angle and latitude as follows:

${\omega }_s={\cos }^{-1}\left(-\tan \delta \tan \varnothing \right).(3)$

Table 1

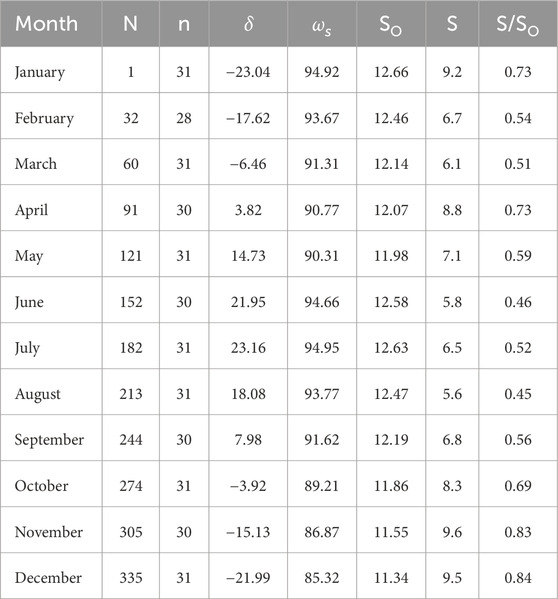
Table 1. Input parameters for the estimation of monthly average daily global solar radiation in Afar region for estimation of solar radiation, S_o = 2${\omega }_s$/15 (a = 1.03, b = 0.371).

The monthly average daily global solar radiation on a horizontal surface (H_G) is given by the Angstrom equation (Ismial et al., 2024):

$\frac{{\mathrm{H}}_{\mathrm{G}}}{{\mathrm{H}}_{\mathrm{O}}}=\mathrm{a}+\mathrm{b}\left(\frac{\mathrm{S}}{{\mathrm{S}}_{\mathrm{o}}}\right),(4)$

where S is the monthly average daily hours of bright sunshine and S_O is the monthly average value of the maximum possible daily hours of bright sunshine, which is given by Equation 5:

${\omega }_s=\frac{15}{2}{S}_O⟺S_o=\frac{2}{15}{\omega }_{S.}(5)$

In Equation 4, a and b are empirical constants known as the angstrom constants and are obtained from curve fitting data: the values of these constants for Ethiopian cities in the Afar region are a = 1.03 and b = 0.371 (Federal Democratic Republic of Ethiopia Central Statistical Agency, 2014). Natei et al. (2022) Natel examined the radiation data for fifteen Ethiopia cities, and proposed the following equation for the estimation of diffused radiation t:

$\mathrm{a}=-0.110+0.235\cos \mathrm{\varphi }+0.323\left(\frac{\mathrm{S}}{{\mathrm{S}}_{\mathrm{o}}}\right),(6)$

$\mathrm{b}=1.449-0.553\cos \mathrm{\varphi }-0.694\left(\frac{\mathrm{S}}{{\mathrm{S}}_{\mathrm{o}}}\right),(7)$

where $\varphi ={12.11}^o$ for the Afar region, using the value of S from EMI record data and that of S_o from Equation 5. Figure 2a shows the variation of declination angle throughout the year 2017 in the Afar region. The angle formed between the equator and a line drawn from the center of the earth to the center of the sun is considered as the solar declination. The average solar declination angle is zero; this angle is positive in the summer (from April to September) and negative in the winter (from January to March and October to December). In the northern hemisphere, the declination reaches the maximum value of 23.45° during summer solstice and minimum value of −23.45° during winter solstice, as shown in Figure 2a. Figure 2b shows the monthly input parameters measured by the EMI using the monthly average daily hours of bright sunshine (S) and maximum monthly average daily hours of bright sunshine (S_o). For the Afar region, Natei et al. (2022) used the available radiation data to estimate the diffuse radiation as in Equation 8:

$\frac{{\overline{\mathrm{H}}}_{\mathrm{D}}}{{\overline{\mathrm{H}}}_{\mathrm{G}}}=1.03-0.371\left(\frac{\mathrm{S}}{{\mathrm{S}}_{\mathrm{o}}}\right).(8)$

Figure 2

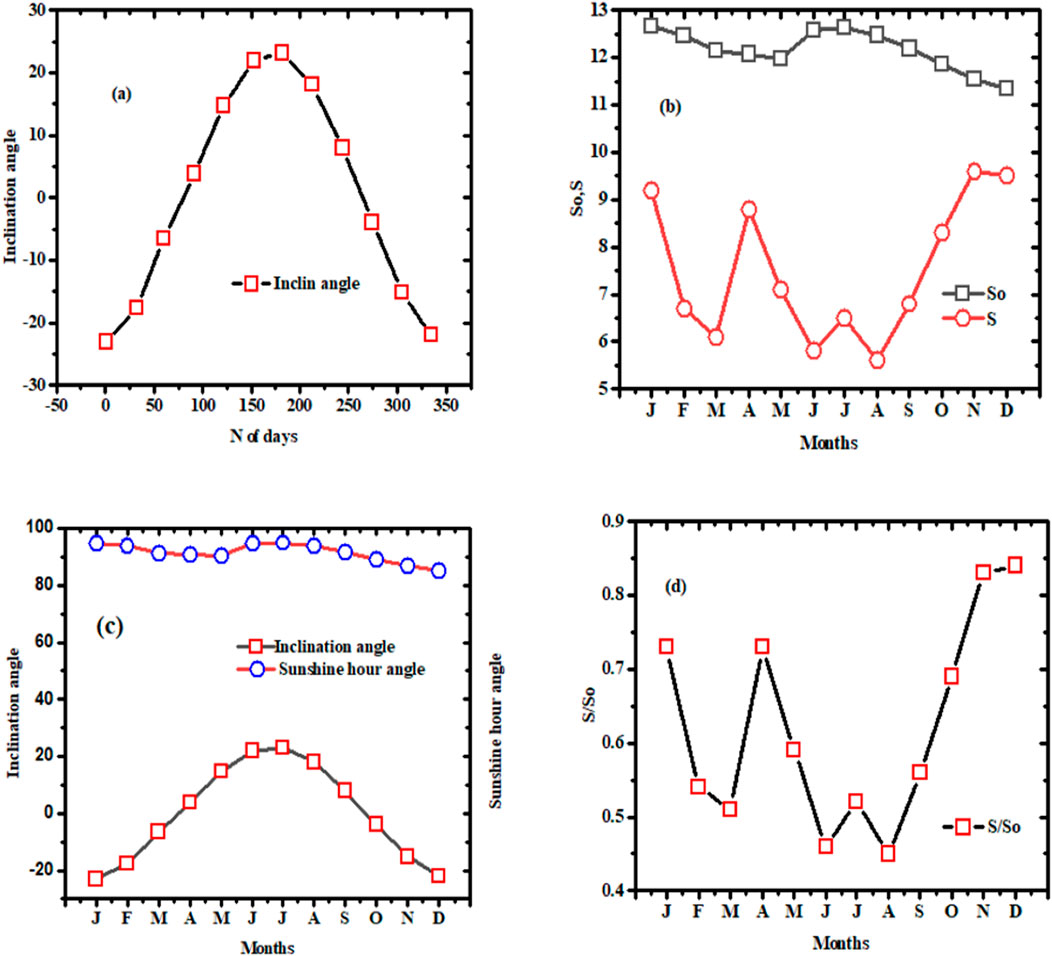
Figure 2. (a) Declination angle with respect to the days of the year 2017. (b) Monthly S_o and S values, (c) sunshine and declination angles, and (d) ratio of S/S_o for the Afar region.

Figure 2c shows the declination angle and sunshine hour angle for the Afar region; the graphs describe the dependence of the sunshine hour angle ${\omega }_s$ on the solar declination angle and latitude for a specific location. Figure 2d shows the graph for the ratio $\mathrm{S}/{\mathrm{S}}_{\mathrm{O}}$ for the Afar region, as documented in Table 1. The monthly average beam radiation on a horizontal surface (Equation 9) is usually estimated by subtracting the diffuse radiation from the global solar radiation on a horizontal surface (Equation 10):

${\mathrm{H}}_{\mathrm{B}}={\mathrm{H}}_{\mathrm{G}}-{\mathrm{H}}_{\mathrm{D}}.(\mathrm{\hspace{0.17em}9})$

This means that the global radiation is the sum of the diffuse and beam radiation components.

${\mathrm{H}}_{\mathrm{G}}={\mathrm{H}}_{\mathrm{B}}+{\mathrm{H}}_{\mathrm{D}}(\mathrm{\hspace{0.17em}10})$

2.3 Solar radiation on a tilted surface

A total of three components, namely diffuse irradiation from the sky, radiation reflected onto a tilted surface from the surrounding surfaces, and direct or beam radiation from the sun, comprise the direct solar radiation incident on a tilted surface. Thus, the total incident solar radiation on a tilted surface (H_T) can be expressed as Equation 11 below:

${\mathrm{H}}_{\mathrm{T}}={\mathrm{H}}_{\mathrm{B}}+{\mathrm{H}}_{\mathrm{R}}+{\mathrm{H}}_{\mathrm{D}},(11)$

where H_B is the incident beam radiation, H_R is the radiation reflected from the ground, H_D is the diffuse radiation incident on a tilted surface, and H_T is the monthly total daily incident solar radiation.

The beam radiation incident on a tilted surface is given by Equation 12:

${\overline{\mathrm{H}}}_{\text{TB}}={\overline{\mathrm{H}}}_{\mathrm{B}}{\overline{\mathrm{R}}}_{\mathrm{B}}={\overline{\mathrm{R}}}_{\mathrm{B}}\left({\overline{\mathrm{H}}}_{\mathrm{G}}-{\overline{\mathrm{H}}}_{\mathrm{D}}\right).(12)$

Based on the assumption that the total radiation incident on a horizontal surface is equal to the sum of the diffuse radiation and monthly average daily beam radiation, we can estimate that $\left({\overline{\mathrm{H}}}_{\mathrm{B}}={\overline{\mathrm{H}}}_{\mathrm{G}}-{\overline{\mathrm{H}}}_{\mathrm{D}}\right)$. Meanwhile, the beam radiation is the ratio of mean daily beam radiation incident on the tilted surface to that on the horizontal surface. Thus, R_B is a function of the atmospheric transmittance, which is given as ${\overline{\mathrm{R}}}_{\mathrm{B}}={\mathrm{H}}_{\text{TB}}/{\mathrm{H}}_{\mathrm{B}}$, and can be found using Equation 13 for surfaces in the northern hemisphere that slope toward the equator (the most advantageous azimuth angle is γ = 0 for the PV module collector) (Frank et al., 2018).

Thus, the value of ${\overline{\mathrm{R}}}_{\mathrm{B}}$ is computed as

${\overline{\mathrm{R}}}_{\mathrm{B}}=\frac{\cos \mathrm{\theta }}{\cos {\mathrm{\theta }}_{\mathrm{z}}}=\frac{\sin \mathrm{\delta }\sin \left(\varnothing -\mathrm{\beta }\right)+\cos \mathrm{\delta }\cos \left(\varnothing -\mathrm{\beta }\right)}{\sin \mathrm{\delta }\sin \varnothing +\cos \mathrm{\delta }\cos \varnothing \cos \mathrm{\omega }},(13)$

where ω is the hour angle, δ is the declination angle, ∅ is the latitude, and β is the surface inclination angle (all measured in terms of degrees).

The portion of the solar radiation that reaches the Earth’s surface and is reflected by buildings, trees, terrain, and other boundary-intercepting objects is known as ground-reflected radiation. This radiation is reflected from surfaces that are exposed to the sky (Khaled et al., 2024). There is a view factor (R_r) between the ground and slope from the horizontal to a tilted surface, as given by Equation 14:

${\mathrm{R}}_{\mathrm{r}}=\frac{1-\cos \mathrm{\beta }}{2}.(14)$

Considering isotropic reflection of the beam and diffuse radiation from the ground with a diffuse reflectance of ρ for the total solar radiation, the reflected radiation (H_TR) from the surroundings to the surface is given by Equation 15:

${\mathrm{H}}_{\text{TR}}=\mathrm{\rho }{\mathrm{H}}_{\mathrm{G}}\left(\frac{1-\cos \mathrm{\beta }}{2}\right),(\mathrm{\hspace{0.17em}15})$

where β is the slope of the tilted surface, and ρ is the ground reflectance constant that varies based on the surroundings of the tilted surface. According to Muneer (2004), the commonly used values for ground reflectance are ρ = 0.2 for hot and humid tropical locations, ρ = 0.5 for dry tropical locations, and ρ = 0.9 for snow-covered terrain.

Diffuse radiation (H_TD) is the component of total solar radiation that results when atmospheric scattering produces a shift in the direction of solar radiation (Frank et al., 2018). The direction of diffuse radiation is variable and may be difficult to identify as it is often determined by the highly variable conditions of air purity and cloudiness. Diffuse radiation consists of three components, namely the isotropic, circumsolar, and horizon brightening parts. The isotropic diffuse radiation component is evenly received across the entire sky dome. The circumsolar diffuse component is received from further dispersion of solar radiation and is concentrated in the section of the sky around the sun (Muneer, 2004). The component responsible for horizon brightening is concentrated close to the horizon and is most noticeable when the sky is clear (Ianhui et al., 2024).

In general, the diffuse component of radiation incident on an inclined surface is composed of the isotropic, circumsolar, and horizon brightening factors, which are given by Equations 16–18:

${\mathrm{H}}_{\text{TD}}={\mathrm{H}}_{\mathrm{D},\text{iso}}{\mathrm{F}}_{\mathrm{c}-\mathrm{s}}+{\mathrm{H}}_{\mathrm{D},\text{cs}}{\overline{\mathrm{R}}}_{\mathrm{B}}+{\mathrm{H}}_{\mathrm{D},\text{hs}}{\mathrm{F}}_{\mathrm{c}-\text{hz}},(16)$

${\mathrm{F}}_{\mathrm{c}-\mathrm{s}}=\frac{1+\cos \mathrm{\beta }}{2},(17)$

${\mathrm{H}}_{\mathrm{T}}={\overline{\mathrm{H}}}_{\mathrm{B}}{\overline{\mathrm{R}}}_{\mathrm{B}}+\mathrm{\rho }{\mathrm{H}}_{\mathrm{G}}\left(\frac{1-\cos \mathrm{\beta }}{2}\right)+{\mathrm{H}}_{\mathrm{D},\text{iso}}\left(\frac{1+\cos \mathrm{\beta }}{2}\right)+{\mathrm{H}}_{\mathrm{D},\text{cs}}{\overline{\mathrm{R}}}_{\mathrm{B}}+{\mathrm{H}}_{\mathrm{D},\text{hs}}{\mathrm{F}}_{\mathrm{c}-\text{hz}}.(18)$

2.4 Sky models for diffuse radiation

Two broad categories of sky models have been used to estimate diffuse radiation on a tilted surface, namely, anisotropic and isotropic models (Widen, 2009; Robinson and Stone, 2004; Yufei et al., 2023; Carlos et al., 2020; Evseev and Kudish, 2009; Kambezidis, 2021). To determine a suitable sky model for the Afar region, four empirical models were selected and assessed in this study. Two of these models were investigated; these were anisotropic models, namely, the Hay and Davies (HD) and Reindl et al. (RE) models (Giovanni et al., 2016; Przemyslaw et al., 2016), and the other two were isotropic models, namely, the Liu and Jordan (LJ) and Koronakis (KO) models (Sethi et al., 2013; Erdélyi et al., 2014). According to the HD model, diffuse solar radiation only contributes in an isotropic and circumsolar manner and has no effect on horizon brightening.

The total radiation on a tilted surface based on this model is given by Equation 19:

${\overline{\mathrm{H}}}_{\mathrm{T}}=\left({\mathrm{H}}_{\mathrm{B}}+{\overline{\mathrm{H}}}_{\mathrm{D}}\mathrm{A}\right){\overline{\mathrm{R}}}_{\mathrm{B}}+{\overline{\mathrm{H}}}_{\mathrm{G}}\mathrm{\rho }\left(\frac{1-\cos \mathrm{\beta }}{2}\right)+{\overline{\mathrm{H}}}_{\mathrm{D}}\left(\frac{1+\cos \mathrm{\beta }}{2}\right)\left(1-\frac{{\overline{\mathrm{H}}}_{\mathrm{B}}}{{\overline{\mathrm{H}}}_{\mathrm{O}}}\right)+\frac{{\overline{\mathrm{H}}}_{\mathrm{B}}}{{\overline{\mathrm{H}}}_{\mathrm{O}}}{\overline{\mathrm{R}}}_{\mathrm{B}},(19)$

where A is the anisotropy index that is a function of the atmospheric transmittance for beam radiation and is given by Equation 20:

$\mathrm{A}=\frac{{\overline{\mathrm{H}}}_{\mathrm{B}}}{{\overline{\mathrm{H}}}_{\mathrm{o}}}.(20)$

While the diffuse components that are directly facing the sun are presumed to be circumsolar, those that reach the remaining parts of the sky dome are considered to be isotropic. The anisotropy index was proposed by Hay and Davies and is used to weight these components, which helps determine how much of the diffuse radiation can be classified as circumsolar, while the remaining is presumed to be isotropic radiation. A horizon brightening factor was included in the RE model along with the isotropic diffuse and circumsolar radiation components. The same fractions of the solar beam and reflected radiation components were considered by Liu and Jordan as well as other investigators. In addition, a modulating factor $f=\sqrt{\frac{{\overline{H}}_B}{{\overline{H}}_G}}$ was included to weight the horizon brightening factor ${\sin }^3\left(\frac{\beta }{2}\right)$. This model takes into account three diffuse component fractions, namely, ${\overline{\mathrm{H}}}_{\mathrm{T}\mathrm{D},\text{iso}}$, ${\overline{\mathrm{H}}}_{\mathrm{T}\mathrm{D},\text{hz}}$, and ${\overline{\mathrm{H}}}_{\mathrm{T}\mathrm{D},\text{cs}}$, as given in Equation 21:

${\overline{\mathrm{H}}}_{\mathrm{T}}=\left({\overline{\mathrm{H}}}_{\mathrm{B}}+{\overline{\mathrm{H}}}_{\mathrm{D}}\mathrm{A}\right){\overline{\mathrm{R}}}_{\mathrm{B}}+{\overline{\mathrm{H}}}_{\mathrm{G}}\mathrm{\rho }\left(\frac{1-\cos \mathrm{\beta }}{2}\right)+{\overline{\mathrm{H}}}_{\mathrm{D}}\left\{\left(1-\mathrm{A}\right)\times \frac{1+\cos \mathrm{\beta }}{2}\right\}\left[1+\sqrt{\frac{{\overline{\mathrm{H}}}_{\mathrm{B}}}{{\overline{\mathrm{H}}}_{\mathrm{G}}}}{\sin }^3\left(\frac{\mathrm{{\rm B}}}{2}\right)\right]+\mathrm{A}{\overline{\mathrm{R}}}_{\mathrm{B}}.(21)$

The LJ model states that there are three components to solar radiation incident on a tilted surface, namely the beam radiation, reflected radiation from the ground, and diffuse radiation. Although the circumsolar and horizon brightening components are believed to be zero, the diffuse radiation component is simply considered to be isotropic (Equation 22). Hence, the overall formula for computing the total radiation on a tilted surface is proposed as the sum of the beam, earth-reflected, and isotropic diffuse radiation components.

${\overline{\mathrm{H}}}_{\text{TD}}={\overline{\mathrm{H}}}_{\mathrm{D}}\left(\frac{1+\cos \mathrm{\beta }}{2}\right)(\mathrm{\hspace{0.17em}22})$

Thus, $H_T$ is given by Equation 23 as follows:

${\overline{\mathrm{H}}}_{\mathrm{T}}={\overline{\mathrm{H}}}_{\mathrm{B}}{\overline{\mathrm{R}}}_{\mathrm{B}}+{\overline{\mathrm{H}}}_{\mathrm{G}}\mathrm{\rho }\left(\frac{1-\cos \mathrm{\beta }}{2}\right)+{\overline{\mathrm{H}}}_{\mathrm{D}}\left(\frac{1+\cos \mathrm{\beta }}{2}\right).(23)$

Koronakis proposed that the slope value of β = 90° accounts for about 66.7% of the diffuse solar radiation of the entire sky dome and modified the premise of the isotropic circumsolar diffuse radiation as Equation 24.

${\mathrm{F}}_{c-s}=\frac{2+\cos \mathrm{\beta }}{3}(24)$

Thus, the total incident radiation on a tilted surface is given by Equation 25:

${\overline{\mathrm{H}}}_{\mathrm{T}}={\overline{\mathrm{H}}}_{\mathrm{B}}{\overline{\mathrm{R}}}_{\mathrm{B}}+{\overline{\mathrm{H}}}_{\mathrm{G}}\mathrm{\rho }\left(\frac{1-\cos \mathrm{\beta }}{2}\right)+{\overline{\mathrm{H}}}_{\mathrm{D}}\left(\frac{2+\cos \mathrm{\beta }}{3}\right).(25)$

2.5 Methods of model evaluation

This study compares data from the Ethiopian Meteorological Institute with skewed global solar radiation data for climate conditions in the Afar region and predicted global solar radiation data. The statistical analysis conducted using five statistical tests, namely, the MAPE (in %) (Equation 26), MBE (in kWh/m²·day) (Equation 27), RMSE (in kWh/m²·day) (Equation 28), normalized root mean-squared error (NRMSE) (Equation 29), and t-statistic (Equation 30).

$\text{MAPE}=\frac{1}{\mathrm{n}}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}\frac{\left(\mathrm{H}-{\mathrm{H}}_{\mathrm{P}}\right)}{\mathrm{H}}\times 100\%(26)$

$\text{MBE}=\frac{1}{\mathrm{n}}\sum \left({\mathrm{H}}_{\text{Pi}}-{\mathrm{H}}_{\mathrm{i}}\right)(27)$

$\text{RMSE}=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\left({\mathrm{H}}_{\text{Pi}}-{\mathrm{H}}_{\mathrm{i}}\right)}^2}(28)$

$\text{NRMSE}=\frac{1}{{\mathrm{H}}_{\max }-{\mathrm{H}}_{\min }}\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\left({\mathrm{H}}_{\text{Pi}}-{\mathrm{H}}_{\mathrm{i}}\right)}^2}(29)$

$\mathrm{t}-\text{stat}=\sqrt{\frac{\left(\mathrm{n}-1\right){\text{MBE}}^2}{{\text{RMSE}}^2-{\text{MBE}}^2}}(30)$

Here, H_i are the true or actual values, H_Pi are the predicted values, and n is the total number of observations. The optimal value of the MAPE is zero; additionally, the MBE should ideally be zero, but a low value is desirable (Ashraf et al., 2024).

3 Results and discussion

3.1 Regression constant for the Afar region

The input parameters for estimating solar radiation values on horizontal and tilted surfaces are shown in Table 1. According to Cooper’s model (Khai et al., 2014), the declination angle (δ) ranges from −23.04° (January solstice) to +23.16° (June solstice). On the two annual equinoxes (March and September), the declination angle is zero. The sunrise and sunset hour angles vary depending on the latitude; however, they are both similar owing to symmetry. The average sunshine hour angle (ω_s) in the Afar region is roughly 94.92° in January, 94.16° in June, and 94.95° in July, which provide an accurate estimate of the solar radiation. Table 1 shows that throughout the year, the percentage of sunshine duration (S/S_o) is approximately 62% ± 21%, with the highest values of 83% and 84% being recorded in November and December, respectively. With these values, the regression constants for the Afar region are derived from the Angstrom equations as a = 1.03 and b = 0.371.

3.2 Solar radiation on a horizontal surface

To estimate the extraterrestrial solar radiation on a daily basis (H_o) shown in Figure 3, we used the input parameters like declination angle, sunlight hour angle, and day length; thus, the maximum H_o of 8.58 kWh/m²·day was observed in January, while the minimum H_o of 7.45 kWh/m²·day was estimated in October. Then, we estimated the global solar radiation (H_G) on a monthly average daily basis for a horizontal surface using the regression constants for the Afar region. According to Figure 3 (Table 2), the estimated values of H_G are 5.83 kWh/m²·D in March and 6.71 kWh/m²·D in June. It is generally suggested to use the LJ dispersed solar radiation model to anticipate daily diffuse radiation values at various locations around the world. However, Mohammad et al. (2019) and Chikh et al. (2012) presented modified equations under different conditions.

Figure 3

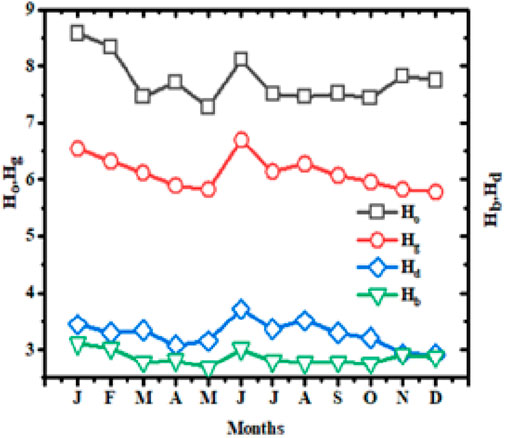
Figure 3. Variation of the monthly average daily solar radiation values (Ho, H_G, H_B, and H_D) on a horizontal surface in Afar region.

Table 2

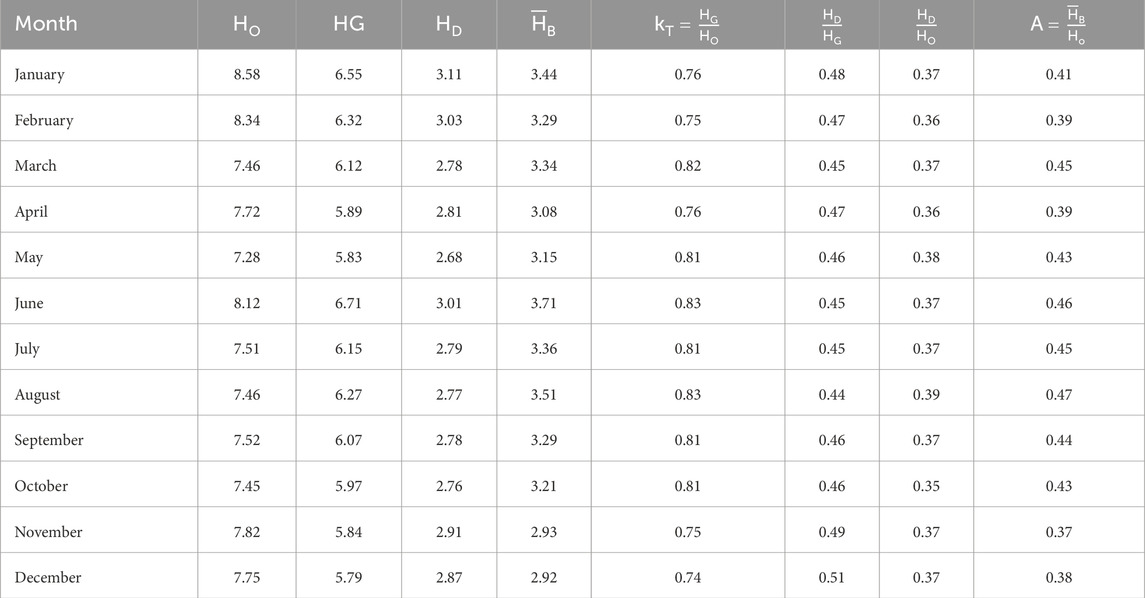
Table 2. Variation of monthly average values of daily solar radiation (H_O, H_G, H_D, H_B, and H_GM) on a horizontal surface in Afar region (H_O in kWh/m²·day).

There are no available scientific reports about Ethiopia’s Afar region from the alternative model perspective. The estimated results show that the amount of H_D is 2.85 kWh/m²·D or 42.1% of the total global solar radiation. From the perspective of application, the availability of such a large amount of average monthly solar radiation in the Afar region is excellent, as shown in Figure 3. Typically, the monthly average beam radiation on a horizontal surface is calculated by deducting the dispersed solar radiation from the global solar radiation on the surface. As shown in Figure 3, we note that the average beam radiation is 3.26 kWh/m²·D or 53.2% of the total global solar radiation.

3.3 Sky conditions in the Afar region

The fraction of extraterrestrial radiation that reaches the Earth’s surface as global solar radiation is used to calculate the clearness index, which is a measure of the atmospheric transparency. This indicates how clear the sky is to a certain extent, and is given as ${\mathrm{k}}_{\mathrm{T}}={\mathrm{H}}_{\mathrm{G}}/{\mathrm{H}}_{\mathrm{O}}$. It is encouraging to observe that the sky over the Afar region is very clear almost throughout the year (${\mathrm{k}}_{\mathrm{T}}$ > 0.74), as derived from the predicted values of H_O and H_G.

Figure 4 illustrates transmission through the atmosphere $k_T$ together with the diffuse and global radiation values. The minimum values of ${\mathrm{k}}_{\mathrm{T}}$ were 0.74 in December, 0.75 in February and November, and 0.76 in January and April, while the maximum values were 0.83 in June and August. In the Afar region, the sky is typically clear for PV applications that require solar radiation all around the year. The empirical coefficients for the Afar region are shown in Figure 4 in terms of H_D/H_O, H_D/H_G, and k_T.

Figure 4

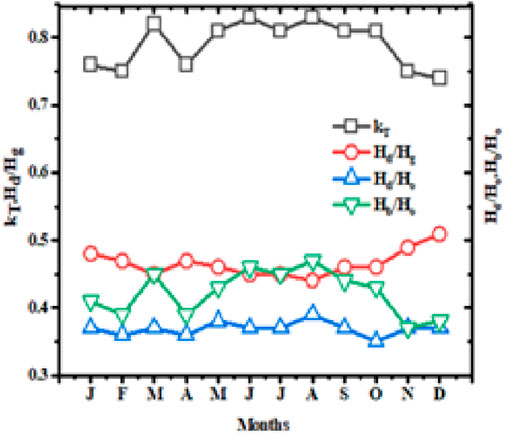
Figure 4. Monthly variation of the clearness index k_T = H_G/H_O as well as ratios H_D/H_O and H_D/H_G in Afar region.

3.4 Variation of solar radiation on a tilted surface

A comparison between two anisotropic models, namely the HD and RE models, as well as two isotropic models, namely the LJ and KO models, revealed that both model categories generated almost identical results. As shown in Figure 5, the KO and LJ models produce somewhat lower values than the RE model. The circumsolar components in the diffuse radiation portion were the reason for this finding with respect to the RE model. The HD model showed the highest estimated value outputs of all the models; here, a modulating factor was used to weight the term for horizon brightening, and each of the diffuse components were considered separately. Of all the isotropic and anisotropic models, the LJ model showed the lowest estimated outcome. This was because of the optimization of the slope; all models anticipated more incident solar energy on a tilted surface than on a horizontal surface.

Figure 5

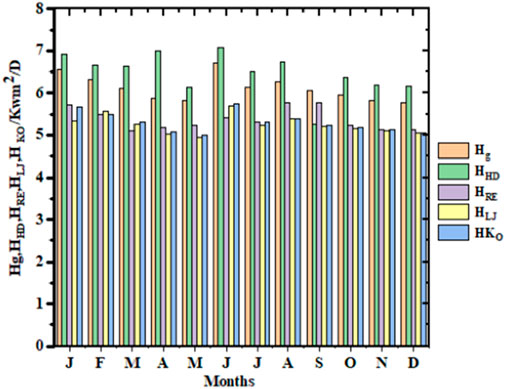
Figure 5. Comparison of predictions obtained using different models with the measured monthly average daily solar radiation on a tilted surface in Afar region.

3.5 Statistical analysis of the models

The statistical analysis results of the solar radiation sky models are shown in Figures 6–9. After estimating the horizontal surface data using the four different models, the global component of solar radiation on the tilted surface was calculated and compared with measured data for the tilted surface. We used a value of 0.2 for the ground reflectance in these calculations. Figure 6 shows that the HD model has a MAPE ranging from −0.82% to −2.52%, while the LJ model has a MAPE range of −2.31% to −3.14%, the KO model has a MAPE of −2.32% to −2.89%, and the RE model has a MAPE of −1.87% to −2.85%. This confirms that the error of the KO model is between those of the HD and LJ models.

Figure 6

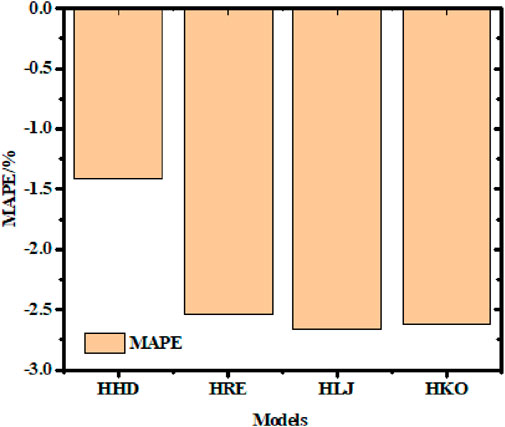
Figure 6. Mean absolute percentage error (MAPE) values obtained using different models. HD: Hay and Davies model; RE: Reindl et al.’s model; LJ: Liu and Jordan model; KO: Koronakis model.

Figure 7

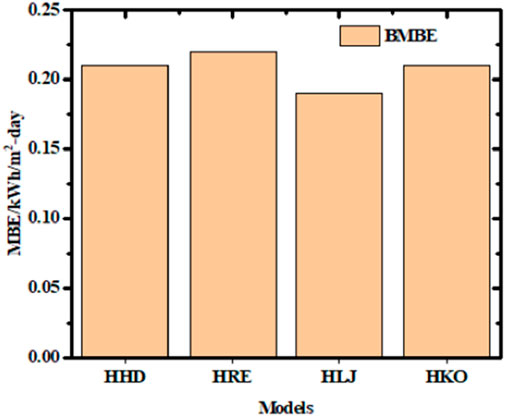
Figure 7. Mean bias error (MBE) values obtained for different models. HD: Hay and Davies model; RE: Reindl et al.’s model; LJ: Liu and Jordan model; KO: Koronakis model.

Figure 8

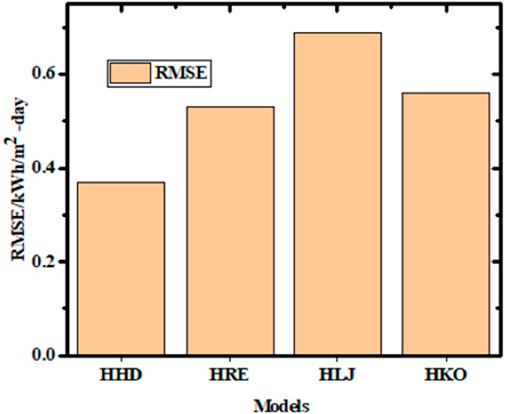
Figure 8. Root mean-squared error (RMSE) values obtained for different models. HD: Hay and Davies model; RE: Reindl et al.’s model; LJ: Liu and Jordan model; KO: Koronakis model.

Figure 9

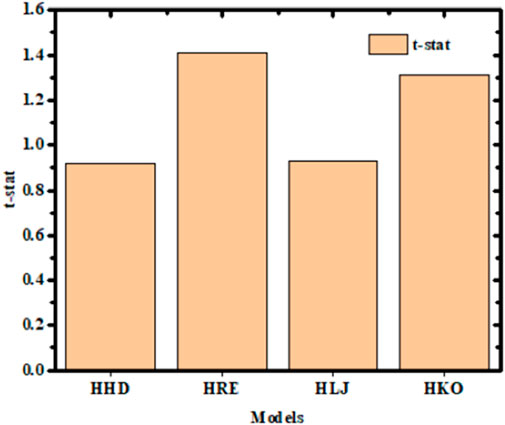
Figure 9. T-statistic values obtained for the different models. HD: Hay and Davies model; RE: Reindl et al.’s model; LJ: Liu and Jordan model; KO: Koronakis model.

The MBE allows term-by-term comparison of the actual variations between the estimated and measured values to provide insights into the long-term results of the models. In other words, it serves as a gauge for the mean departure between the anticipated values and satellite record data. Figure 7 shows that the HD model had minimum and maximum MBE values of 0.061 and 0.136 kWh/m²·day, the KO model had values of 0.17 and 0.24 kWh/m²·day, the LJ model showed values of 0.12 and 0.26 kWh/m²·day, and RE model yielded values of 0.25 and 0.14 kWh/m²·day, respectively.

The short-term performances of the models are indicated by the RMSE values. A smaller RMSE value indicates better model performance. Nonetheless, a few sizeable errors in the total can cause the RMSE to increase noticeably. The ideal RMSE value is zero; however, it is generally always positive. Figure 8 illustrates that the LJ model produced the highest RMSE values ranging from 0.48 to 0.94 kWh/m²·day, with an annual average of 0.69 kWh/m²·day. In contrast, the HD model generated low RMSE values ranging from 0.21 to 0.48 kWh/m²·day, with an annual average of 0.37 kWh/m²·day. The KO and RE models showed average RMSE values of 0.53 and 0.69 kWh/m²·day, respectively. The MBE values for the RE and HD models were 0.89 and 0.77 kWh/m²·day, respectively. Given that a low MBE value (with broad scatter around the line of perfect estimation) can coexist with a high RMSE value, it is clear that the MAPE, MBE, and RMSE may not be adequate markers of model performance. Conversely, it is feasible to have a large MBE value along with a comparatively low RMSE value.

Although these statistical indicators offer a sensible approach for comparing the models, they are unable to determine with certainty if a model estimate is statistically significant, that is, whether the estimates are noticeably different from the measured values. In addition to enabling model comparison, the t-statistic indicator shows whether a model’s estimates are statistically significant at a given degree of confidence (Ashraf et al., 2024). According to some works (Badescu, 2002; Marwal et al., 2012; Inci and Hasan, 2002), the t-statistic produces more dependable and illuminating results when used with the RMSE and MBE. The model performance is considered to be better when the t-statistic value is smaller. As seen in Figure 9, the t-statistic values of the HD, LJ, KO, and RE models were estimated to be 0.92, 0.93, 1.31, and 1.41, respectively. These findings show that isotropic models have lower t-stat values than anisotropic models.

As seen in Figure 10, the NRMSE values of the HD, LJ, KO, and RE models were estimated as 0.21, 0.63, 1.84, and 0.8, respectively. These findings show that isotropic models have lower NRMSE values than anisotropic ones. Such similarities between the models are expected considering that the latter type of models use solar radiation. Models with greater performances will thus be given more weight during the averaging stage. In the case of the strongest-performing unit model, the NRMSE is comparable to that of a unit model with far better performance.

Figure 10

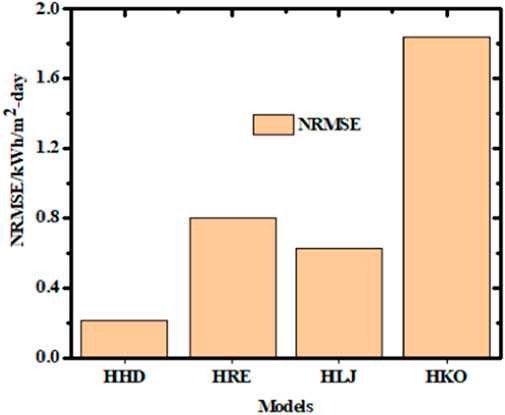
Figure 10. Normalized RMSE values for the different models. HD: Hay and Davies model; RE: Reindl et al.’s model; LJ: Liu and Jordan model; KO: Koronakis model.

A comparison of the estimated incident solar radiation on a tilted surface (H_T) and radiation values from NASA data (H_NASA) is presented in Table 3. H_NASA and H_T are estimated from models with similar patterns, so the highest recorded H_NASA value is 6.48 kWh/m²·day in March and the lowest value is 5.51 kWh/m²·day in January. H_NASA records show higher radiation values compared to H_RE, H_LJ, and H_KO estimates, as shown in Figure 11, while H_HD is higher than H_NASA for the Afar region.

Table 3

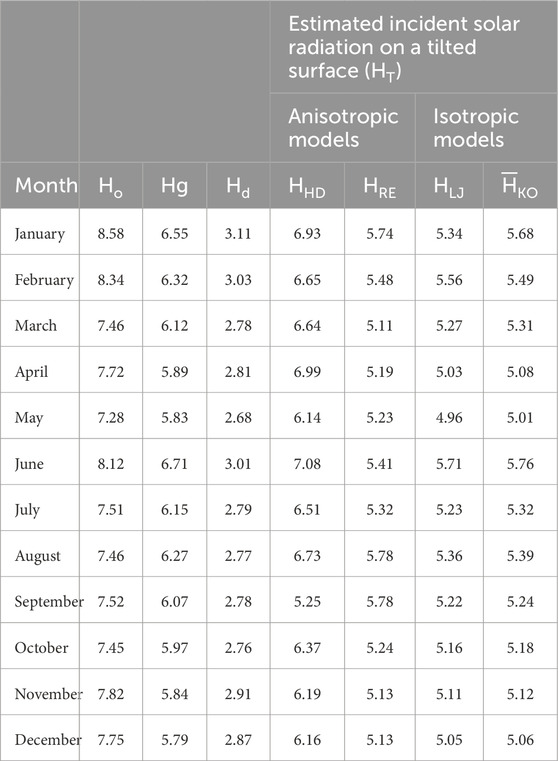
Table 3. Estimated monthly average values of daily incident solar radiation (kWh/m²·day) on a tilted surface in Afar region using different models (R_B = 0.75).

Figure 11

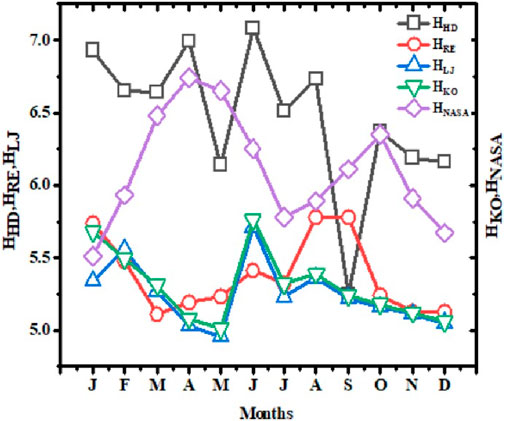
Figure 11. Comparison of estimated solar radiation values from this study with the H_NASA recorded data.

4 Conclusion

Solar radiation values were estimated for horizontal and tilted surfaces in the Afar region located in the northern part of Ethiopia using various input parameters like the inclination angle, daylight hours, and day length. A comparative investigation was also conducted using four different sky models at a tilt angle of 12.21° for the Afar region. Based on the findings, the following conclusions are drawn:

1. Estimates for the Afar region indicate that the mean values of the anticipated horizontal solar radiation (Ho), global solar radiation (H_G), and diffuse solar radiation (H_D) on a horizontal surface are 7.75, 6.12, and 2.86 kWh/m²·day, respectively.

2. The HD model predicted the highest average solar energy irradiation on a tilted surface (6.47 kWh/m²·day), followed by the RE model (4.89 kWh/m²·day), LJ model (5.25 kWh/m²·day), and KO model (5.31 kWh/m²·day).

3. Most isotropic models predicted sufficient solar radiation availability throughout the year and higher results for the duration of August to February when the weather conditions were favorable.

4. Based on the anisotropic models, the worst month is May for both the HD model (6.14 kWh/m²·day) and RE model (5.11 kWh/m²·day). However, for the same month of May, the isotropic models predict values of 4.96 kWh/m²·day (LJ model) and 5.01 kWh/m²·day (KO model).

5. The statistical analysis results showed that among the four models, the least MAPE was −1.41%, MBE was 0.19 kWh/m²·day, RMSE was 0.37 kWh/m²·day, and t-stat was 0.92 kWh/m²·day.

6. The present study is an initial research effort for the Afar region on estimating solar radiation incident on a tilted surface using isotropic and anisotropic sky models.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors without undue reservation.

Author contributions

AA: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Resources, Supervision, Writing–original draft, Writing–review and editing. TA: Conceptualization, Writing–review and editing. BD: Validation, Writing–review and editing.

Funding

The authors declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The authors wish to thank the Ethiopia National Agency of Meteorological Service, Addis Ababa, for providing the data to complete this work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdusalam, D., Usman, M., and Bala, K. (2014). Insolation levels using temperature model forSustainable application of photovoltaic technology in some selected locations of Nigeria. J. Energy Technol. Pollut. 4 (1), 19–28. doi:10.1175/WCAS-D-13-00068.1

CrossRef Full Text | Google Scholar

Ahmad, M. J., and Tiwari, G. N. (2009). Optimization of tilted angle for solar collector to receive maximum radiation. Open Renew. Energy J. 2, 19–26. doi:10.1080/01430750.2009.9675788

CrossRef Full Text | Google Scholar

Al-Ghezi, M. K. S., Mahmoud, B. K., Alnasser, T. M. A., and Chaichan, M. T. (2022). A comparative study of regression models and meteorological parameters to estimate the global solar radiation on a horizontal surface for Baghdad city, Iraq. Int. J. Renew. Energy Dev. 11 (1), 71–81. doi:10.14710/ijred.2022.38493

CrossRef Full Text | Google Scholar

Ali, E. G., Ümit, A., Hüseyin, B., Alper, E., and Gökhan, Y. (2023). A state of art review on estimation of solar radiation with various models. Heliyon 21 (2). doi:10.1016/j.heliyon.2023.e13167

CrossRef Full Text | Google Scholar

Ashraf, F., Abdulhaleem, H. L., Hosny, M. H., and Harry, D. K. (2024). Status of solar-energy adoption in GCC, Yemen, Iraq, and Jordan: challenges and carbon-footprint analysis. Clean Technol. 6 (2), 700–731. doi:10.3390/cleantechnol6020036

CrossRef Full Text | Google Scholar

Badescu model (2002). 3D isotropic approximation for solar diffuse irradiance on tilted surfaces. Renew. Energy 26 (2), 221–233. doi:10.1016/s0960-1481(01)00123-9

CrossRef Full Text | Google Scholar

Bulut, H., and Buyukalaca, O. (2007). Simple model for the generation of daily global solar radiation data in Turkey. Appl. Energy 84, 510 477–491. doi:10.1016/j.apenergy.2006.10.003

CrossRef Full Text | Google Scholar

Carlos, T., Ana, M., Gracia, A., Giorgio, B., Jose, A., and Antonio, U. (2020). Evaluation of solar radiation transposition models for passive energy management and building integrated photovoltaics. Energies 13 (3), 702. doi:10.3390/en13030702

CrossRef Full Text | Google Scholar

Chikh, C. M., Mahrane, A., and Haddadi, M. (2012). Modeling the diffuse part of the global solar radiation in Algeria. Energy 18, 1068–1075. doi:10.1016/j.egypro.2012.05.121

CrossRef Full Text | Google Scholar

Dazhi, Y., and Chris, G. (2020). Ensemble model output statistics for the separation of direct and diffuse components from 1-min global irradiance. Sol. Energy 208, 591–603. doi:10.1016/j.solener.2020.05.082

CrossRef Full Text | Google Scholar

El-Sebaii, A., Al-Hazmi, F. S., Al-Ghamdi, A. A., and Yaghmour, S. J. (2010a). Global, direct and diffuse solar radiation on horizontal and tilted surfaces in Jeddah, Saudi Arabia. Appl. Energy 87, 568–576. doi:10.1016/j.apenergy.2009.06.032

CrossRef Full Text | Google Scholar

El-Sebaii, A. A., Al-Hazmi, F. S., Al-Ghamdi, A. A., and Yaghmour, S. J. (2010b). Global, direct and diffuse solar radiation on horizontal and tilted surfaces in Jeddah, Saudi Arabia. Appl. Energy 87, 568–576. doi:10.1016/j.apenergy.2009.06.032

CrossRef Full Text | Google Scholar

El-Sebaii, A. A., and Trabea, A. A. (2003). Estimation of horizontal diffuse solar radiation in Egypt. Energy Convers. manage. 44, 2471–2482. doi:10.1016/S0196-8904(03)00004-9

CrossRef Full Text | Google Scholar

Erdélyi, R., Yimin, W., Weisi, G., and Giuseppe, C. (2014). Three-dimensional SOlar RAdiation Model (SORAM) and its application to 3-D urban planning. Sol. Energy 101, 63–67. doi:10.1016/j.solener.2013.12.023

CrossRef Full Text | Google Scholar

Evseev, E. G., and Kudish, A. I. (2009). The assessment of different models to predict the global solarradiation on a surface tilted to the south Solar. Energy 83 (3), 377–388doi. doi:10.1016/j.solener.2008.08.010

CrossRef Full Text | Google Scholar

Federal Democratic Republic of Ethiopia Central Statistical Agency (2014). Population projection of Ethiopia for all regions at wereda level from 2014 – 2017. Available online at: http://www.statsethiopia.gov.et.

Google Scholar

Frank, K., Charles, F. K., and Jana, B. M. (2018). Principles of sustainable energy systems. Third Edition. CRC Pres: Boca Raton.

Google Scholar

Giovanni, P., Alessandro, P., Paolo, B., Andrea, G., and Ardeshir, M., (2016). Solar irradiance modelling and uncertainty on building hourly profiles of heating and cooling energy needs. Conference: IV High Performance Buildings Conference at PurdueAt: West Lafayette, Indiana, U.S, 11-14, 3359.

Google Scholar

Ianhui, B., Xiaowei, W., Erhan, A., Xuemei, Z., and Xuemei, Z. (2024). Global solar radiation and its interactions with atmospheric substances and their effects on air temperature change in ankara province. Climate 12 (3), 35. doi:10.3390/cli12030035

CrossRef Full Text | Google Scholar

Inci, T. T., and Hasan, T. (2002). Global solar radiation over Turkey: comparison of predicted and measured Data. Renew. Energy 25 (1), 55–67. doi:10.1016/s0960-1481(00)00197-x

CrossRef Full Text | Google Scholar

Ismial, A., Faith, Y., Ahmet, P., Sema, S., Asir, G., Galip, O., et al. (2024). A new approach to estimation solar radiation. Arsel 14, 3. doi:10.20508/ijrer.v14i3.14913.g8909

CrossRef Full Text | Google Scholar

Jakhrani, A. Q., Othman, A. K., Rigit, A. R. H., Samo, S. R., and Kamboh, S. A. (2012). Estimation of incident solar radiation on tilted surface by different empirical models. Int. J.Sci. Res. Publ. 2 (12), 1–6.

Google Scholar

Jakhrani, A. Q., Samo, S. R., Rigit, A. R. H., and Kamboh, S. A. (2013). Selection of models for calculation of incident solar radiation on tilted surface. World Appl. Sci. J. 22 (9), 1334–1343. doi:10.1016/j.compeleceng.2024.109411

CrossRef Full Text | Google Scholar

Janjai, S., Pankaew, P., and Laksanaboonsong, J. (2009). A model for calculating hourly global solar radiation from satellite data in the tropics. Appl. Energy 86, 1450–1457. doi:10.1016/j.apenergy.2009.02.005

CrossRef Full Text | Google Scholar

John, A. D., Beckman, W. A., and Blair, N. (2020). Solar engineering of thermal processes. Photovoltaics Wind 25. doi:10.1002/9781119540328

CrossRef Full Text | Google Scholar

Kambezidis, H. D. (2021). The solar radiation climate of Greece. Climate 9, 183. doi:10.3390/cli9120183

CrossRef Full Text | Google Scholar

Khai, M. N., Nor, M. A., Othman, I., Mohd, Z., and Abidin, Ab. K. (2014). Assessment of Solar radiation on diversly oriented surfaces and optimum tilts for solar absorber in Malaysia tropical latitude. Int. J. Energy Eng. 5, 75. doi:10.1007/s40095-014-0075-7

CrossRef Full Text | Google Scholar

Khaled, F., Maw, loud G., Sarra, M., Abderahmane, B., and Tayeb, B. (2024). A novel learning approach for short-term photovoltaic power forecasting - a review and case studies. Eng. Appl. Artif. Intell. 133, 108502. doi:10.1016/j.engappai.2024.108502

CrossRef Full Text | Google Scholar

Li, D. H. W., Lam, T. N. T., and Chu, V. W. C. (2008). Relationship between the total solar radiation on tilted surfaces and the sunshine hours in Hong Kong. Sol. Energy 82 (12), 1220–1228. doi:10.1016/j.solener.2008.06.002

CrossRef Full Text | Google Scholar

Marwal, V. K., Punia, R. C., Sengar, N., and Dashora, P. (2012). Indian J. Sci. Technol. 5, 0974–6846. doi:10.17485/ijst/2016/v9i44/92041

CrossRef Full Text | Google Scholar

Mawloud, G., Fezzani, A., Mohamed, Z., Rabehi, A., Ferkous, K., Bailek, N., et al. (2024a). An analysis of case studies for advancing photovoltaic power forecasting through multi-scale fusion techniques. Sci. Rep. 14, 6653. doi:10.1038/s41598-024-57398-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Mawloud, G., Toufik, A., Abdelfetah, B., Samir, H., and Nadjem, B. (2024b). Enhancing direct Normal solar Irradiation forecasting for heliostat field applications through a novel hybrid model. Energy Convers. Manag. 304 (15), 118189. doi:10.1016/j.enconman.2024.118189

CrossRef Full Text | Google Scholar

MDPI (2025). MDPI. Available online at: https://www.mdpi.com/land/land-06-00082/article_deploy/html/images/land-06-00082-g001.png.

Google Scholar

Mohammad, S. A., Basharat, J., Md, A. A., and Evangelos, B. (2019). Generalized models for estimation of global solar radiation based on sunshine duration and detailed comparison with the existing: a case study for India. Sustain. Energy Technol. Assessments 31, 179–198DOI. doi:10.1016/j.seta.2018.12.009

CrossRef Full Text | Google Scholar

Muneer, T. (2004). Solar radiation and day light models. Oxford: Elsevier.

Google Scholar

Natei, E. B., Abreham, B. A., Ashenafi, A. A., Chernet, A. G., Girum, A. T., and Yedilfana, S. M. (2022). Estimation of Global solar radiation using sunshine-based models in Ethiopia, Benti et al. Cogent Eng. 9. doi:10.1080/23311916.2022.211420053

CrossRef Full Text | Google Scholar

Noorian, M., Moradi, I., and Kamali, G. A. (2008). Evaluation of 12 models to estimate hourly diffuse irradiation on inclined surfaces. Renew. Energy33 33, 1406–1412. doi:10.1016/j.renene.2007.06.027

CrossRef Full Text | Google Scholar

Ozan, S., and Tuncay, K. (2009). Estimation of solar radiation over Turkey using artificial neural network and satellite data. Appl. Energy 518 (86), 1222–1228. doi:10.1016/j.apenergy.2008.06.003

CrossRef Full Text | Google Scholar

Przemyslaw, S., Rafał, S., and Krzysztof, O. (2016). Methodology to estimate variations in solar radiation reaching densely forested slopes in mountainous terrain. Int. J. Biometeorology 60 (12), 1983–1994. doi:10.1007/s00484-016-1185-0

CrossRef Full Text | Google Scholar

Robinson, D., and Stone, A. (2004). Solar radiation modelling in the urban context. Sol. Energy 77 (3), 295–309. doi:10.1016/j.solener.2004.05.010

CrossRef Full Text | Google Scholar

Sabziparvar, A. A. (2008). A simple formula for estimating global solar radiation in central arid deserts of Iran. Renew. Energy 33, 1002–1010. doi:10.1016/j.renene.2007.06.015

CrossRef Full Text | Google Scholar

Sethi, V. P., Sumathy, K., and Pal, D. S. (2013). Optimum inclination angles of booster mirrors and solar RADIATION availability on the horizontal and inclined box type solar cooker. J. Power Energy Eng. 5, 1–26. doi:10.4236/jpee.2013.15008

CrossRef Full Text | Google Scholar

Solanki, C. S. (2011). Solar photo voltaic fundamental, technologies and applications. second edn. New Delhi: PHI Learning Pvt. Ltd., 301. Available online at: https://www.scirp.org/reference/referencespapers?Referenceid=1336889.

Google Scholar

Solanki, C. S., and Sangani, C. S. (2008). Estimation of monthly averaged direct normal solar radiation using elevation angle for any location. Sol. Energy Mater. Sol. Cells 92, 38–44. doi:10.1016/j.solmat.2007.08.006

CrossRef Full Text | Google Scholar

Sudhakar, K., Srivastava, T., Satpathy, G., and Premalatha, M. (2013). Modelling and estimation of photosynthetically active incident radiation based on global irradiance in Indian latitudes. Int. J. Energy Env. Engg. 4 (21), 21–28. doi:10.1186/2251-6832-4-21

CrossRef Full Text | Google Scholar

Widen, J. (2009). “Distributed photovoltaic in the Swedish energy system,” in Model development and simulation. Uppsala, Sweden: Uppsala University Sweden, 1–89. Available online at: https://www.osti.gov/etdeweb/servlets/purl/964469.

Google Scholar

Wu, G., Liu, Y., and Wang, T. (2007b). Methods and strategy for modeling daily global solar radiation with measured meteorological data— a case study in Nanchang station, China. Energy Convers. manage. 48, 2447–2452. doi:10.1016/j.enconman.2007.04.011

CrossRef Full Text | Google Scholar

Wu, J., Zhang, M., and Lin, W. (2007a). A case study of a frontal system simulated by a climate model: clouds and radiation. J.Geophysics Res. 112, D12201. doi:10.1029/2006jd008238

CrossRef Full Text | Google Scholar

Yousif, J. H., Al-Balushi, H. A., Kazem, H. A., and Chaichan, M. T. (2019). Analysis and forecasting of weather conditions in Oman for renewable energy applications. Case Stud. Therm. Eng. 13, 100355. doi:10.1016/j.csite.2018.11.006

CrossRef Full Text | Google Scholar

Yufei, Z., Arno, S., and SolarGAN, C. W. (2023). SolarGAN: synthetic annual solar irradiance time series on urban building facades via Deep Generative Networks. Energy AI 12, 100223. doi:10.1016/j.egyai.2022.100223

CrossRef Full Text | Google Scholar

Nomenclature

$\mathit{\gamma }$ Azimuth angle (degree)

$\mathit{\beta }$ Tilt angle (degree)

$\mathit{\theta }$ Angle of incidence (degree)

$\mathit{\epsilon }$ Elevation angle (degree)

$\mathit{\omega }$ Hour angle (degree)

$\mathbf{\Phi }$ Latitude angle (degree)

${\mathit{\theta }}_{\mathit{z}}$ Zenith angle (degree)

${\mathit{\omega }}_{\mathit{s}}$ Sunset hour angle for the mean day of the month (degree)

a, b Angstrom constants (for Afar region: a = 1.021, b = 0.371)

A Anisotropy index

f Modulating factor

F_c-s View factor for circumsolar diffuse radiation

F_c-hz View factor for horizon brightening solar diffuse radiation

H_B Monthly average daily beam radiation on horizontal surface (kWh/m²·day)

H_D Monthly average daily diffuse radiation (kWh/m²·day)

H_T Total incident solar radiation on tilted surface (kWh/m²·day)

H_TB Beam radiation on tilted surface (kWh/m²·day)

H_TD Diffuse radiation on tilted surface (kWh/m²·day)

H_TR Ground reflection radiation on tilted surface (kWh/m²·day)

H_O Monthly average daily extraterrestrial solar radiation (kWh/m²·day)

I_SC Solar constant (1.367 kW/m²)

N Day of the year

H_G Monthly average daily global solar radiation (kWh/m²·day)

k_T Monthly average clearness index

MAPE Mean absolute percentage error (%)

MBE Mean bias error (kWh/m²·day)

RMSE Root mean-squared error (kWh/m²·day)

t-stat t-statistic value

HD Hay and Davies model

LJ Liu and Jordan model

KO Koronakis model

RE Reindl et al. model

EMI Ethiopia Meteorological Institute

S Monthly average daily hours of bright sunshine (h)

S_o Monthly average of the maximum possible daily hours (day length) of bright sunshine