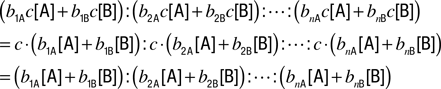Understanding the neural computations underlying object recognition is important for understanding the function of any sensory system. Generally speaking, each sensory system extracts specific features of the total impinging sensory information while ignoring others. One strategy for filtering sensory information is to use an encoding mechanism that is invariant to the irrelevant features. For example, the visual system uses spatial opponent circuits to create perceptual invariance to illumination, allowing the surface properties of visual objects to be identified despite changes in incident lighting (
Palmer, 1999
).
Many vertebrate species use chemosensation as the chief means of extracting ecologically-significant information from the environment, including the identity, age and health of conspecifics (
Beauchamp and Yamazaki, 2003
;
Boehm and Zufall, 2006
), the presence of predators (
Takahashi et al., 2005
), and the availability of energetic and nutritional resources (
Hao et al., 2005
;
Reinhard et al., 2004
). Like object recognition in the visual system, odor-based recognition is likely to involve computations that produce invariance to certain kinds of chemical information.
A fundamental form of perceptual invariance in chemosensation is concentration invariance, the ability of an organism to recognize the same odor at different concentrations. Changes in concentration result in a change in the number (and sometimes pattern) of olfactory glomeruli activated by an odor (
Johnson and Leon, 2000
;
Ma and Shepherd, 2000
;
Malnic et al., 1999
;
Rubin and Katz, 1999
;
Sachse and Galizia, 2003
;
Wachowiak and Cohen, 2001
), raising the question of how such different patterns of glomerular activation lead to similar olfactory percepts (
Arctander, 1969
;
Cleland et al., 2007
;
Krone et al., 2001
). Several physiological models have been proposed (
Cleland et al., 2007
;
Hopfield, 1999
), but there is little behavioral data on the perceptual phenomena these mechanisms need to explain. It is apparent that odors retain their perceptual character over some range of concentrations, with changes in perceptual character over concentration being an exception rather than a rule (
Arctander, 1969
). However, to our knowledge no psychophysical experiments have specifically characterized the phenomenon of concentration invariance.
We performed psychophysical experiments on rats with the aim of obtaining insight into underlying neural mechanisms of odor identification. The subjects were trained on a binary odor mixture discrimination (
Uchida and Mainen, 2003
) and then tested with randomly-rewarded probe trials of different concentration. The results show that rats classify mixtures according to the molar ratios of components and that this strategy allows them to achieve concentration invariance over at least a tenfold concentration range, even enabling them to generalize to concentrations that they have not been trained on. We propose a simple opponent-circuit model to account for these observations. We suggest that this mechanism might underlie concentration-invariant odor recognition not only for binary mixtures but also for monomolecular odorants and more complex mixture odors.
All procedures were carried out in accordance with National Institute of Health standards as approved by the Cold Spring Harbor Laboratory Institutional Animal Care Use Committee. Eleven male Long-Evans hooded rats (around 200 g at the start of training) were tested in a two-alternative odor discrimination task using water restriction for motivation. The experimental apparatus and training procedures were the same as those described previously (
Uchida and Mainen, 2003
) except where noted. Performance was monitored and delivery of odors and water reinforcement were controlled using computer data acquisition hardware (National Instruments, Austin, TX, USA) and custom software written in MATLAB (Mathworks, Natick, MA, USA).
Odor Delivery and Definitions of Odor Concentrations
Odors were delivered using a custom-made olfactometer. Binary odor mixtures in various proportions at various absolute concentrations were delivered in pseudorandom order. The mixture ratios and absolute concentrations were produced by differential air flow dilution using a pair of mass flow controllers (Aalborg Instruments and Controls, Organgeburg, NY, USA). Saturated vapor was obtained by flowing air at flow rates of 0 100 ml/min through a liquid odorant loaded freshly on each session in a disposable syringe filter (glass microfiber, 2.7 μm pore size, #6823 1327 Whatman). The flow rate of each odor is represented by
fA or
fB which is normalized such that “100” corresponds to 60 ml/min. The odor streams were mixed with a clean air adjusted to produce a constant final flow rate of 1,000 ml/min. The odorants used are caproic acid, 1-hexanol, S(+)-2-octanol and R(−)-2-octanol. Caproic acid was further diluted 1:10 in mineral oil. These odors were chosen based on the previous imaging and behavioral studies (
Uchida and Mainen, 2003
;
Uchida et al., 2000
). Odor concentrations were chosen to roughly match perceived intensity in humans. These concentrations did not cause obvious biases in categorization behavior for 50/50 binary odor mixtures in odor discrimination task. The linearity of concentration dilution was verified using a gas chromatograph (Hewlett-Packard 6890) with flame ionization detector.
Odor Discrimination Task
Experiments were conducted in a box with three conical ports on one wall, the central one being used for odor sampling and the other two for response. Infrared emitter-detector pairs served to detect entry and exit of the snout from the port. Rats initiated trials by a nose entry into the odor sampling port, which triggered the delivery of an odor lasting up to 1 s. Reward was available for correct choices for up to 2 s after the rat left the odor sampling port. A minimum interval of 4 s from the response to the start of the next valid trial was imposed.
Rats were initially shaped to sample an odor stimulus at the central odor port in order to obtain water reward at the left or right reward port (
Uchida and Mainen, 2003
). This shaping took about 5–6 days. Rats were then trained to discriminate pure odor pairs (denoted “A” and “B”; with flow rates
fA =
fB =
k) where
k is the sum of the flow rates for odor A and B. The total flow rate used during training is designated
k = 100 and corresponds to 60 ml/min diluted by clean air to produce the final flow rate of 1,000 ml/min, as described above. Following training to criterion (90% accuracy, in 1–4 sessions, ∼200 trials/session), binary odor mixtures in different proportions (
k = 100;
fA/
fB = 95/5, 80/20, 68/32, 56/44, 44/56, 32/68, 20/80, 5/95) were gradually introduced over several sessions (6–8 sessions), and rats were rewarded for choosing the side associated with the dominant component. After reaching asymptotic performance, testing began using interleaved probe stimuli with the same ratios but different absolute concentrations (e.g.,
k = 50). Probe stimuli were diluted by reducing the air flow of the carrier stream (for twofold dilution) or by diluting the odorants in mineral oil (tenfold dilution). Probe trials comprised less than 20% of total trials and responses to probes were randomly rewarded (at a probability of 0.5) at both response ports. Each rat was tested in 6.7 ± 3.6 (mean ± SD) sessions containing a sum of 238 ± 126 and 1216 ± 478 trials for probe and trained stimuli, respectively.
Data Analysis
A maximum likelihood procedure was used to fit performance as a function of the stimulus using a logistic function
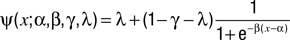
where α corresponds to the bias (or indifference point), β is the slope, γ is the upper bound and λ is the lower bound (
Wichmann and Hill, 2001
). We tested which of several different independent variables (
x) predicted rats’ performance the best: absolute concentration of one odor mixture component (
x =
fA;
x =
fB), the ratio of two components (
x =
fA/
fB) and the difference of two components (
x =
fA –
fB). We first fit a logistic psychometric function (Equation 1) to left/right choice behavior on training stimuli using one of the independent variables, and then calculated the likelihood of obtaining the performance for the probe stimuli given the fitted logistic function based on a Bernoulli processes. For example,
L(
x =
fA/
fB) =
P (data for probes|psychometric function fitted for training stimuli using
x =
fA/
fB as a predictor). Then pair-wise comparisons of the goodness of these fits were made using log likelihood ratios. For example, to compare
x =
fA/
fB to
x =
fA we computed the log-likelihood ratio, log [
L(
x =
fA/
fB)/
L(
x =
fA)]. The statistical significance of log-likelihood ratios were estimated using a resampling (bootstrap) method whereby the probability of obtaining a negative log-likelihood by chance was estimated and compared to the actual calculated log-likelihood. Significance was considered
p < 0.05.
Error bars in performance functions (Figures
1
B, C,
2
B, C and
3
B, C) show ±1 SEM calculated using the binomial model,
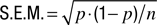
.
Combinatorial Ratio Coding Model
Following
Hopfield (1999)
, consider receptor “coverage” defined by
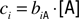
for receptor
i, [A] is the molar concentration of a ligand A, and
biA is the binding constant of this receptor to A. When two odors, A and B, are present, coverage of this receptor can be approximated by the sum of the two coverages,
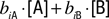
. Under this assumption the ratio of receptor coverages across receptors 1, 2, …
n is
When total concentration is changed by the factor of c, without changing ratio of [A] and [B], the ratio of receptor coverages becomes
Thus, the ratio of receptor coverages is invariant to dilution of odorants.
We performed psychophysical experiments on rats using a binary odor mixture discrimination task (
Uchida and Mainen, 2003
) (Figure
1
). Subjects were first trained on binary mixtures of two odorants (“A” and “B”) delivered in eight different ratios (Figure
1
A) produced by independently varying the flow rates of odor streams
fA and
fB in a carrier stream of fixed rate (see Materials and methods section). In the first experiment, two alternative responses (left vs. right nose poke) were differentially rewarded according on which of the two mixture components had the higher concentration. These training procedures left open a variety of strategies for subjects to solve the problem. In particular, correct responses to the training stimuli could be obtained by ignoring one component and responding according to whether the other component had a high or low concentration. Alternatively, responses could be based on both components.
Figure 1. Odor mixture discrimination by rats respects the ratio of mixture components. (A) Stimuli were binary mixtures of two odorants (A, caproic acid; B, 1-hexanol) whose magnitudes, fA and fB, were varied by air flow dilution (100 = 60 ml/min of saturated vapor diluted in 1,000 ml/min clean air, see Materials and methods section). Training stimuli (black filled circles) were rewarded according to the dominant component. The reward boundary is indicated by the magenta diamond. Note that training stimuli were chosen such that fA + fB = 100. Test stimuli (red circles) were randomly rewarded (p = 0.5). Note that test stimuli were chosen to have fA + fB = 50. Note that training and test stimuli were chosen with the same component ratios (as indicated by the gray lines). The yellow line (fA/fB = 1) represents stimulus classification based on ratio of two mixture components. The green line (fA = 50) represents a classification boundary based on one component (A). Note that yellow and green lines both correctly classify the training stimuli but result in different classifications of the test stimuli. (B) Performance of one rat on training odors (black filled circles) and probes (red circles). The abscissa is the ratio of the odor mixture components, fA/fB and the ordinate is the fraction of choices for the port associated with odor A. A sigmoid function was fitted to the choices of the rat on training stimuli (see Materials and methods section) using the odor mixture ratio as the independent variable. Error bars show ±1 SEM (see Materials and methods section). Some training data points are not visible because they are hidden behind the corresponding test data points. Note that the sigmoid also fits the test stimuli even they were not used in the fitting procedure. (C) The same data as (B) plotted using the magnitude of odor A (fA) as the independent variable. The fit is also performed using the magnitude of component A as the independent variable. Note that the fitted function does not accurately predict the probe responses. (D) Experiment with 1/10 dilution probe stimuli. Training stimuli (black filled circles) had fA + fB = 100. Test stimuli (red circles) were chosen such that fA + fB = 10. Note that in this experiment, dilution was achieved by liquid rather than air dilution. (E) Performance of one rat on training odors (black filled circles) and 1/10 dilution probes (red circles). The independent variable is the ratio fA/fB. (F) Choices of one rat on training and 1/10 dilution probe stimuli. The independent variable is the single component fA.
To test what kind of chemical information subjects based their decisions, subjects were tested by interleaving probe stimuli at 1/2 the training concentration (i.e., 50% of the flow rate; Figure
1
A, red circles). Probe trials were randomly rewarded so that subjects received no feedback as to a “correct” strategy and comprised <20% of trials to discourage rats from learning the lower reward rate associated with these stimuli. We analyzed the data by plotting choice functions using different independent variables corresponding to different types of extracted information. When the ratio
fA/
fB was used as the independent variable, responses to the probe stimuli fell on the same line as the training stimuli (Figure
1
B). That is, the fraction of left vs. right choices to a given probe could be accurately predicted by the performance with a training stimulus of the same component ratios. In contrast, when a single component was the independent variable, responses to the probe stimuli no longer match the line fitted to the training data (
fA, Figure
1
C;
fB not shown). This result supports the idea that when encountering mixture stimuli rats naturally tend to base their decisions on information extracted about the ratio of mixture components.
Across the population, a similar pattern was obtained, with left/right choices on probe trials being closely predicted by choices on training stimuli of the same mixture ratio. We quantified these results by testing how well a sigmoid function fit to the training stimuli predicted choices on the probe stimuli (see Materials and methods section). For 4 out of 4 rats tested using 1-hexanol vs. caproic acid and 3 out of 4 rats tested with R(+)-2-octanol vs. S(−)-2-octanol, choices on probe stimuli (twofold diluted) were significantly better fit when the mixture ratio as opposed to either single component was used as the independent variable (criterion
p < 0.05 for each subject, bootstrap test). To examine whether these results would generalize to a wider concentration range, we tested an additional set of rats with more diluted probe stimuli (tenfold dilution in mineral oil, 1-hexanol vs. caproic acid) (Figure
1
D). In this condition, rats continued to generalize according to mixture ratio (Figure
1
E and F). Although choice functions were less exactly matched by the predictions based on the training set, possibly because the difference in intensity between probe and test stimuli was more salient, 3 out of 3 subjects tested showed a better fit with a ratio-based function than a function of either component (
p < 0.05 for each subject, bootstrap test).
Concentration-invariant odor classification based on extraction of ratio information could explain how rats could generalize from training stimuli to probe stimuli at concentrations they have not experienced. However, while training odors were delivered at a fixed concentration in the odor stream, it is possible that subjects were inadvertently exposed to diluted concentrations of the training stimuli outside the direct odor stream. Therefore, we ran additional subjects using probe stimuli with higher rather than lower concentration than the training stimuli (Figure
2
A). Since subjects would have no way to experience concentrations higher than the source, generalization in this case could not arise from inadvertent training with diluted odors. In this experiment, choices on higher-concentration probe stimuli (1.5-fold) were also closely predicted using the ratios of components as the independent variable (Figure
2
B) and not well using either single component (Figure
2
C). This difference was significant in 3 out of 3 rats tested (criterion
p < 0.05, bootstrap test). This result suggests that generalization across concentrations may be based on an intrinsic computation rather than requiring experience with different concentrations.
Figure 2. Odor mixture discrimination by component ratio generalizes to higher concentration probe stimuli. (A) Training stimuli (black filled circles) had
fA +
fB = 100. Test stimuli (red circles) were chosen such that
fA +
fB = 150. The training reward boundary is indicated by the magenta diamond. See
Figure 1
A for details.
(B) Choices of one rat on training stimuli and test stimuli with higher concentration. The independent variable is the ratio
fA/fB. Some training data points are not visible because they are hidden behind the corresponding test data points.
(C) Choices of one rat on training and test stimuli. The independent variable is the single component
fA.
The preceding experiments show that the ratio of mixture components is a good predictor of choice behavior. But could a similar choice pattern also be obtained by a different computation such as the difference of mixture components? Choices based on the ratio of mixture components correspond to a discrimination boundary of
fA/
fB =
r, indicated by the yellow line in Figures
1
A, D,
2
A and
3A
. When mixture components have equal intensity and the training category boundary is half way between the two components, the ratio discrimination boundary,
fA/
fB = 1, is equivalent to one based on the difference of mixture components,
fA −
fB = 0 (yellow line in Figure
1
A) and could therefore yield a similar pattern of behavior. However, this is a very special case. In general, if the mixture components have unequal intensity or the training category boundary is shifted toward one component, the boundaries diverge and the two discrimination strategies will yield very different choice patterns. Therefore, to better distinguish behavior based on ratios vs. differences of chemical components, in the next experiment, rats were trained with a shifted category boundary, i.e.,
fA/
fB = 3 (Figure
3
A), where the ratio boundary (yellow line) and difference boundary (blue line) were well separated. When tested in these conditions, subjects’ behavior was significantly better predicted by a ratio computation,
fA/
fB, than the difference
fA −
fB (Figure
3
B and C) (2 out of 2 rats at twofold dilution; 1 out of 2 rats at tenfold dilution; criterion of
p < 0.05, bootstrap test).
Figure 3. Odor mixture discrimination boundary is not necessarily orthogonal to the training set. (A) Training stimuli (
fA +
fB = 100; black filled circles) and lower concentration test stimuli (
fA +
fB = 50; red circles). The training reward boundary is indicated by the magenta diamond. Note that the boundary shifted in this experiment to
fA = 3·
fB. The yellow line indicates the classification boundary for a ratio computation (
fA/fB = 3) while the blue line indicates the classification boundary orthogonal to the training stimulus set (
y =
fA −
fB =
c). See also
Figure 1
A for details of legend.
(B) Performance of one rat on training and test stimuli with a shifted training reward boundary. The independent variable is the ratio of mixture components
fA/fB.
(C) The same data as in (B) but where the independent variable is the difference of mixture components,
fA −
fB.
Ecologically important information is conveyed by the identities of chemical species present in the environment. Mammalian olfaction is based on a large array of different receptor types with relatively broad and partially overlapping chemical sensitivities. This allows a wide range of odorants to be encoded by activation of specific combinations of receptor types (
Malnic et al., 1999
). However, in such a combinatorial code, patterns of receptor activation will reflect not only the identity of odorants present but also their concentrations (
Johnson and Leon, 2000
;
Kajiya et al., 2001
;
Ma and Shepherd, 2000
;
Malnic et al., 1999
;
Rubin and Katz, 1999
;
Sachse and Galizia, 2003
;
Wachowiak and Cohen, 2001
). While concentration can be important for guiding behavior, for the purpose of odor recognition, concentration is often irrelevant. By what means can the nervous system deduce odorant identity independent of concentration when the two variables are intertwined at the level of receptor activity?
A possible solution to concentration-invariant odor recognition is suggested by the fact that the molar ratios of components in a chemical mixture remain constant even if the absolute concentration of the mixture is altered. If the nervous system could encode information about the relative ratios of chemical species rather than the intensities of individual species, then it could naturally achieve odor recognition that was invariant to dilution through bulk flow and mixing due to air currents which could be expected to dominate in a typical terrestrial environment. In the present report, we tested this idea by training rats to perform a binary odor mixture categorization at a given concentration and probing to see how their behavior generalized to higher and lower concentrations. We found that rats’ spontaneous (unreinforced) choices on the test stimuli precisely obeyed the ratio of mixture components in the training set, suggesting that they are in fact extracting such ratio information. Interestingly, recognition through chemical ratios also appears to characterize pheromonal communication in moths (
Baker et al., 1976
;
Lanier et al., 1980
;
Tóth et al., 1992
) and beetles (
Lanier et al., 1980
), suggesting that such a strategy may be a general one for chemical sensing.
What algorithms might the olfactory system use to encode chemical ratios? One plausible algorithm calls for logarithmic receptor encoding followed by subtraction of signals from different receptors (
Brody and Hopfield, 2003
). This algorithm yields an exact ratio code by the property that log (A/B) = log (A) − log (B). Although it is not clear whether receptor activation functions are well-approximated by a log function, a difference of power law concentration functions, A
X − B
Y, where the exponents
X and
Y are <1, can also approximate a log ratio. Such power law concentration response functions are consistent with the nature of olfactory intensity scaling (e.g.,
Cain, 1969
). It has also been proposed that a concentration invariant code could be obtained by subtraction and normalization, as in: (A − B)/(A + B) (
Cleland et al., 2007
). Although our experiments involved binary mixtures, the same algorithms could readily be generalized to monomolecular odors as long as a single chemical species activates multiple receptors, which is typically the case at all but near-threshold concentrations. Application to more complex natural odors comprising multiple chemical components is similarly straightforward. Comparisons across multiple pairs (or larger sets) of receptor types could create highly specific concentration-invariant representations (see Materials and methods section). We suggest the term “combinatorial ratio code” to describe such an odor coding strategy.
The subtractive operations required by ratio coding algorithms could be implemented by opponent interactions analogous to those prominent in visual processing (
Shepherd, 1994
). Such interactions occur at the level of olfactory bulb mitral cells both through inhibitory interneurons in the glomerular layer and at the granule cell layer. An alternative source for subtractive operations would be feedforward or feedback inhibition in the olfactory cortex. Studies in locust suggest that concentration-invariant odor identity information is embedded in population activity patterns in the antennal lobe projection neurons (considered equivalent to mitral/tufted cells in vertebrates) (
Stopfer et al., 2003
). But whereas concentration response profiles of single neurons in the antennal lobe are relatively complex, single neurons in a downstream area, the mushroom body, respond in a more concentration-invariant manner. Electrophysiological recordings from neurons in the olfactory bulb and cortex during psychophysical experiments similar to the ones described here will be useful to understanding how concentration invariant representations are constructed in the mammalian olfactory system.
Circuit-based mechanisms for concentration invariant odor identity coding depend on analog (rather than binary) receptor responses. The range of concentration-invariance for such mechanisms would be limited by the dynamic range of receptor concentration-response functions. It is important to note that the range of concentrations tested in the present experiments was limited to tenfold, while the dynamic range of identifiable odors can span a much larger range, sometimes over several orders of magnitude (
Krone et al., 2001
). Olfactory receptor neuron dynamic ranges are on average about tenfold (
Rospars et al., 2003
), but glomerular signals may have dynamic ranges up to 2–3 orders of magnitude (
Meister and Bonhoeffer, 2001
;
Rubin and Katz, 1999
;
Wachowiak and Cohen, 2001
;
Wachowiak et al., 2002
). Whereas odors are generally thought to retain their perceptual character over a range of concentrations (
Arctander, 1969
), larger concentration changes (e.g., 100-fold) yield changes in perceptual properties for some odors (
Gross-Isseroff and Lancet, 1988
;
Laing et al., 2003
) but not others (
Krone et al., 2001
). If invariant recognition was indeed based on circuit-based ratio coding, perceptual breakpoints for specific odors would be expected to vary depending on dynamic ranges of the receptor types involved in their transduction. This is a prediction that could be assayed using psychophysical testing.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
We thank Mitsuko Uchida, Stephanie Edger and Eugenia Friedman for assistance with behavioral experiments, members of Mainen laboratory and Adil Khan for discussion and comments on the manuscript. Supported by the National Institute on Deafness and Other Communication Disorders (DC006104), Searle Scholars Program, Packard Foundation and Burroughs Wellcome Fund (Z. F. M.) and a fellowship from the Japan Society for the Promotion of Science and the Cold Spring Harbor Laboratory Association (N.U.).
Arctander, S. (1969). Perfume and Flavor Chemicals (Aroma Chemicals). Las Vegas, NV, Steffen’s Arctander’s Publications.
Baker, T. C., Carde, R. T., and Roelofs, W. L. (1976). Behavioral responses of male
Argyrotaenia velutinana (Lepidoptera: Tortricidae) to components of its sex pheromone.
J. Chem. Ecol. 2, 333–352.
Beauchamp, G. K., and Yamazaki, K. (2003). Chemical signalling in mice.
Biochem. Soc. Trans. 31, 147–151.
Boehm, T., and Zufall, F. (2006). MHC peptides and the sensory evaluation of genotype.
Trends Neurosci. 29, 100–107.
Brody, C. D., and Hopfield, J. J. (2003). Simple networks for spike-timing-based computation, with application to olfactory processing. Neuron 37, 843–852.
Cain, W. S. (1969). Odor intensity after self-adaptation and cross-adaptation.
Percept. Psychophys. 7, 271–275.
Cleland, T. A., Johnson, B. A., Leon, M., and Linster, C. (2007). Relational representation in the olfactory system.
Proc. Natl. Acad. Sci. U.S.A. 104, 1953–1958.
Gross-Isseroff, R., and Lancet, D. (1988). Concentration-dependent changes of perceived odor quality.
Chem. Senses 13, 191–204.
Hao, S., Sharp, J. W., Ross-Inta, C. M., McDaniel, B. J., Anthony, T. G., Wek, R. C., Cavener, D. R., McGrath, B. C., Rudell, J. B., Koehnle, T. J., and Gietzen, D. W. (2005). Uncharged tRNA and sensing of amino acid deficiency in mammalian piriform cortex.
Science 307, 1776–1778.
Hopfield, J. J. (1999). Odor space and olfactory processing: collective algorithms and neural implementation.
Proc. Natl. Acad. Sci. U.S.A. 96, 12506–12511.
Johnson, B. A., and Leon, M. (2000). Modular representations of odorants in the glomerular layer of the rat olfactory bulb and the effects of stimulus concentration.
J. Comp. Neurol. 422, 496–509.
Kajiya, K., Inaki, K., Tanaka, M., Haga, T., Kataoka, H., and Touhara, K. (2001). Molecular bases of odor discrimination: reconstitution of olfactory receptors that recognize overlapping sets of odorants.
J. Neurosci. 21, 6018–6025.
Krone, D., Mannel, M., Pauli, E., and Hummel, T. (2001). Qualitative and quantitative olfactometric evaluation of different concentrations of ethanol peppermint oil solutions.
Phytother. Res. 15, 135–138.
Laing, D. G., Legha, P. K., Jinks, A. L., and Hutchinson, I. (2003). Relationship between molecular structure, concentration and odor qualities of oxygenated aliphatic molecules.
Chem. Senses 28, 57–69.
Lanier, G. N., Classon, A., Stewart, T., Piston, J. J., and Silverstein, R. M. (1980). Ips pini: the basis for interpopulational differences in pheromone biology.
J. Chem. Ecol. 6, 677–687.
Ma, M., and Shepherd, G. M. (2000). Functional mosaic organization of mouse olfactory receptor neurons.
Proc. Natl. Acad. Sci. U.S.A. 97, 12869–12874.
Malnic, B., Hirono, J., Sato, T., and Buck, L. B. (1999). Combinatorial receptor codes for odors.
Cell 96, 713–723.
Meister, M., and Bonhoeffer, T. (2001). Tuning and topography in an odor map on the rat olfactory bulb.
J. Neurosci. 21, 1351–1360.
Palmer, S. E. (1999). Vision Science: Photons to Phenomenology. Cambridge, The MIT Press.
Reinhard, J., Srinivasan, M. V., and Zhang, S. (2004). Olfaction: scent-triggered navigation in honeybees.
Nature 427, 411.
Rospars, J. P., Lansky, P., Duchamp, A., and Duchamp-Viret, P. (2003). Relation between stimulus and response in frog olfactory receptor neurons in vivo.
Eur. J. Neurosci. 18, 1135–1154.
Rubin, B. D., and Katz, L. C. (1999). Optical imaging of odorant representations in the mammalian olfactory bulb.
Neuron 23, 499–511.
Sachse, S., and Galizia, C. G. (2003). The coding of odour-intensity in the honeybee antennal lobe: local computation optimizes odour representation.
Eur. J. Neurosci. 18, 2119–2132.
Shepherd, G. M. (1994). Discrimination of molecular signals by the olfactory receptor neuron.
Neuron 13, 771–790.
Stopfer, M., Jayaraman, V., and Laurent, G. (2003). Intensity versus identity coding in an olfactory system.
Neuron 39, 991–1004.
Takahashi, L. K., Nakashima, B. R., Hong, H., and Watanabe, K. (2005). The smell of danger: a behavioral and neural analysis of predator odor-induced fear.
Neurosci. Biobehav. Rev. 29, 1157–1167.
Tóth, M., Löfstedt, C., Blair, B. W., Cabello, T., Farag, A. I., Hansson, B. S., Kovalev, B. G., Maini, S., Nesterov, E. A., Pajor, I., Sazanov, A. P., Shamshev, I. V., Subchev, M., and Szöcs, G. (1992). Attraction of male turnip moths Agrotis segetum (Lepidoptera: Noctuidae) to sex pheromone components and their mixtures at 11 sites in Europe, Asia, and Africa.
J. Chem. Ecol. 18, 1337–1347.
Uchida, N., and Mainen, Z. F. (2003). Speed and accuracy of olfactory discrimination in the rat.
Nat. Neurosci. 6, 1224–1229.
Uchida, N., Takahashi, Y. K., Tanifuji, M., and Mori, K. (2000). Odor maps in the mammalian olfactory bulb: domain organization and odorant structural features.
Nat. Neurosci. 3, 1035–1043.
Wachowiak, M., and Cohen, L. B. (2001). Representation of odorants by receptor neuron input to the mouse olfactory bulb.
Neuron 32, 723–735.
Wachowiak, M., Cohen, L. B., and Zochowski, M. R. (2002). Distributed and concentration-invariant spatial representations of odorants by receptor neuron input to the turtle olfactory bulb.
J. Neurophysiol. 87, 1035–1045.
Wichmann, F. A., and Hill, N. J. (2001). The psychometric function: I. Fitting, sampling, and goodness of fit.
Percept. Psychophys. 63, 1293–1313.