
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Virol. , 15 July 2022
Sec. Viral Diversification and Evolution
Volume 2 - 2022 | https://doi.org/10.3389/fviro.2022.929851
This article is part of the Research Topic Insights in Viral Diversification and Evolution: 2021 View all 5 articles
Cooperation is a main driver of biological complexity at all levels. In the viral world, gene sharing among viral genomes, complementation between genomes or interactions within quasispecies are frequently observed. In this contribution, we explore the effects of flexible associations between fully fledged viruses and subviral entities, such as virus satellites, in viral dynamics and, in particular, in stable viral coexistence. We devise a mathematical model to compare different situations of competition between two viruses and to quantify how the association with a satellite qualitatively modifies dynamical equilibria. The relevant parameter is the invasion fitness of each virus or of the virus-satellite tandem, which in the model depends on the transmission rate of viruses and on their effect on host survival. In a virus-virus competition, one of the viruses becomes eventually extinct, recasting the competitive exclusion law of ecology. However, an association with a satellite might change the outcome of the competition in two ways, either to favor the less competitive virus (regardless of whether it is the helper virus or not) or to allow for the stable coexistence of the two viruses and the satellite. The virus-satellite association differs from other mechanisms proposed in ecology to date to enhance species coexistence. We hypothesize that such an association constitutes a parsimonious evolutionary pathway towards more stable cooperative associations, such as bipartite viral forms, a collaborative association unique to viruses.
There are many instances in the Virosphere of associations of viruses with kin or with subviral entities (1). The involved agents propagate independently, and engage in transient associations that can be contingent or necessary regarding successful completion of the replication cycle. Virus satellites, for instance, are subviral particles that require the assistance of a specific helper virus for its replication and/or encapsidation (2), see Figure 1. Their association with the helper virus is therefore necessary for the satellite, but contingent in principle for the virus (though some viruses also require the satellite for encapsidation). Bipartite viruses, in turn, have their genome fragmented into two pieces that encapsidate separately but are essential in the viral cycle, so their mutual cooperation is necessary (8, 9).
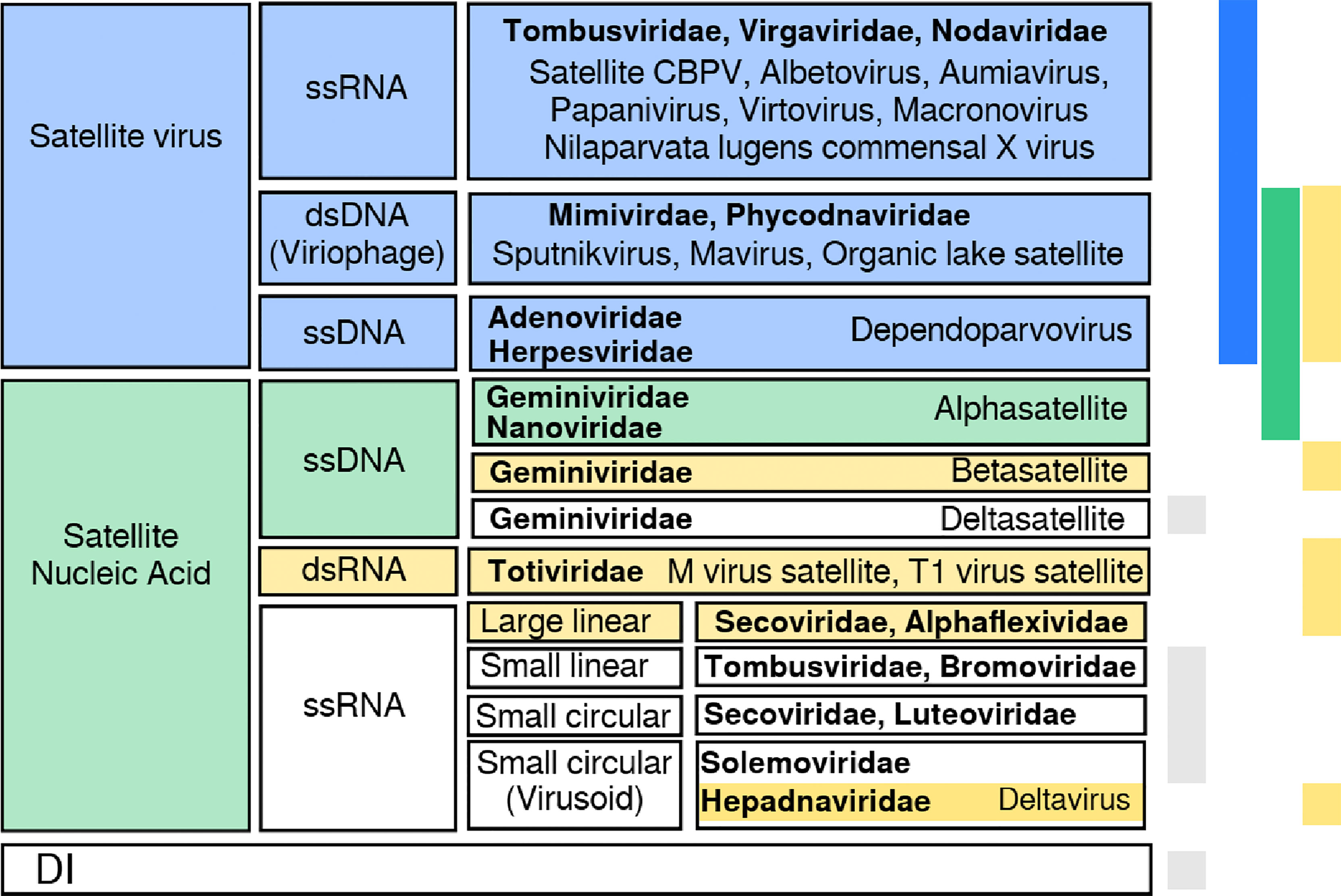
Figure 1 Summary of classes of satellite viruses. There is no straightforward classification of satellites, although distinguishable groups come to light when looking at the genetic material, helper virus family, host, or coded proteins. Here we show a possible classification into two groups, depending on whether they code for a capsid protein (satellite viruses) or not (satellite nucleic acid). Satellite viruses comprise plant satellites with jelly roll capsid proteins, dependoparvovirus and viriophages (3, 4). Satellite nucleic acids include α/β-satellites and Seconviridae satellites coding for a replicase or a replication helper protein; M virus satellite expresses a toxin and HDV codes for an antigen. This group includes non-coding —circular— ssDNAs (5) and RNAs with a compact folded structure with ribozyme activity (6, 7). Colors on the right bars show the protein each satellite codes for: capsid (blue), replicase (green), other (yellow). Grey stands for no coded protein. Helper virus families are shown in bold font; DI stands for defective interfering genomes (e.g., coated like defective interfering particles or uncoated).
Virus-satellite associations are ubiquitous in plants, and less frequent in other hosts. Examples infecting animals are the Hepatitis δ virus (HDV) (10), the genus Dependoparvovirus (4, 11) that infects vertebrates, and virus-satellite associations that have bees (12) and planthoppers (13) as hosts. There are also two cases of dsRNA satellites associated to the Totiviridae family that infect unicellular eukaryotes (14, 15). In several cases, co-infection of animal hosts with the corresponding satellite results in an attenuation of viral symptoms (13, 16, 17).
Infections by multiple viruses and a variety of subviral entities are common in wild plants (18), opening up a high potential for mutual interaction. It has been observed that unrelated viruses within these mixtures do not seem to compete, but rather to cooperate, a fact that might explain their ubiquity (19). Co-infection of a host with subviral particles usually modifies the pathogenicity of the helper virus (18, 20). The spectrum of phenotypic modifications elicited in plants through such interactions is actually remarkably broad. Some viral species within the Tombusviridae family, for instance, take part in associations that include a variety of satellites coding for the capsid protein (21). In vitro, Tombusviruses spontaneously generate defective interfering particles (DIPs) that systematically lessen the symptoms of the infection by interfering with the replication process (22). However, co-infections with heterologous viruses, e.g. that of Potyvirus with Tombusvirus species as machlomovirus of maize chlorotic mottle, often increase the virulence of Tombusvirus (23), as it also happens in other Potyvirus co-infections with heterologous viruses (24). In Bromoviruses, virus-satellite associations can both attenuate or enhance the pathogenicity of the phenotype (25). Geminiviridae is the family with the largest number of virus-satellite associations, often modifying the virulence and host-range of the virus (26). Overall, while short-lived interactions may just involve an increase or decrease in viral accumulation levels (a common effect in infections where DIPs or satellites have spontaneously emerged), long-term interactions correlate with a variety of changes in transmission (27), host range (28), or cell tropism. Sustained interactions are in all likelihood a prerequisite to eventually develop a necessary, mutual interdependence between any two contingently interacting elements.
From an ecological perspective, phenotypic changes caused by transient associations with other viral and subviral agents affect viral dynamics, change viral epidemiology (29), and redefine the overall ecological role of the association (30–32), as compared to infections caused by a single virus. As such, they have to be subject to strong selection, since they may play a main role in virus survival by varying the cost that infection impinges on the host, changing adaptive strategies or, as we show in this contribution, qualitatively modifying the outcome of competition for hosts with co-circulating viral species. An integration of quantitative epidemiology at various levels, including in-host evolution and diverse adaptive strategies, is essential to better understand molecular associations and their ecological effects (33).
Previous modeling studies have addressed the effect of co-infection by viruses and subviral particles unable to replicate on their own. Specific models have addressed the evolution of virulence in Cucumber mosaic virus over two hosts (34) and have shown that highly virulent phenotypes occur in mixed infections, in agreement with field observations. Dynamics of virus-DIPs have been also formally studied based on results of in vitro observations, revealing that dynamics in virus cultures can be oscillatory (35) but also intrinsically unpredictable under very general conditions (36); among others, DIPs can cause the extinction of the parental virus (37). General models exploring properties of virus-satellite associations have often focused on conditions for coexistence of the partners, showing that coexistence can be favored under structured demes (38) but is in general difficult under metapopulation dynamics (39). A general result for infections within a single host states that beneficial co-infection suffices to allow for the stable coexistence of different variants (19). Still, the variety of models, and therefore mechanisms, identified for the stable coexistence of heterologous viral associations is reduced, probably as a result of our limited knowledge of the intricacies of such associations in nature, and to the small number of cases described (20). The state-of-the-art is similar in the case of necessary associations, such as in multipartite viruses, where specific mechanisms that may counteract the deleterious effects of independent propagation are still unclear (40, 41).
Empirical observations strongly support that multiple viral species can co-infect the same host, and be simultaneously present in a given environment. However, the conditions under which stable coexistence is possible are unclear. In ecology, the search for mechanisms that allow for species coexistence (42) has a long tradition that goes back to an early empirical observation (43), later summarized in the competitive exclusion principle: two species feeding on the same resource cannot stably coexist in the long run (44). In this work, we address the question of which conditions allow the stable persistence, in a fixed ecological environment with a single host, of different viral species. Based on observations as those described above, we explore the hypothesis that associations between helper viruses and satellite-like particles that modify the phenotype of the infection can function as a possible stabilizing mechanism, thus enhancing viral diversity. We present a simple model of virus-satellite association and evaluate its effects in the asymptotic stability of the ensemble when two monopartite viruses and a satellite that uses one of them as helper virus co-circulate in a host population. In an instance of the competitive exclusion principle, stable co-circulation of two monopartite viruses is not possible in that scenario, since one of the species unavoidably invades the host population in finite time. Our main result, in contrast, is that the virus-satellite association changes the possible stable equilibria and, in particular, promotes the long-term stable coexistence of both viruses and the satellite in a host population when, as most natural associations do, the satellite modulates the viral phenotype. The precise entities that can stably coexist are determined by the type of association (commensal, mutualistic, or parasitic), with no analogous mechanism in ecological models.
We address the epidemic propagation of viruses in a well-mixed host population through a set of differential equations representing the amount of susceptible hosts, H, of hosts infected by a virus, X, of hosts infected by the helper virus, Y, and of hosts simultaneously infected by the helper virus and the satellite, S (see Figure 2). Capital letters, therefore, describe the abundance of hosts in each of four states: susceptible H or infected hosts in the infected states X,Y, and S; where needed, we will use lower-case letters to refer to virus x, helper virus y, and satellite s. The model, therefore, does not explicitly consider free viral populations. In our models, infections are persistent and there is no class of recovered hosts. This is the rule for plant viruses, but not necessarily so for animal viruses. Therefore, and although we generically speak of hosts all through the paper, our scenarios better apply to plant-infecting viruses and, as it has been defined, to any system where infections are persistent. Finally, note that we refer to competition for hosts in all instances, not to within-host competition.
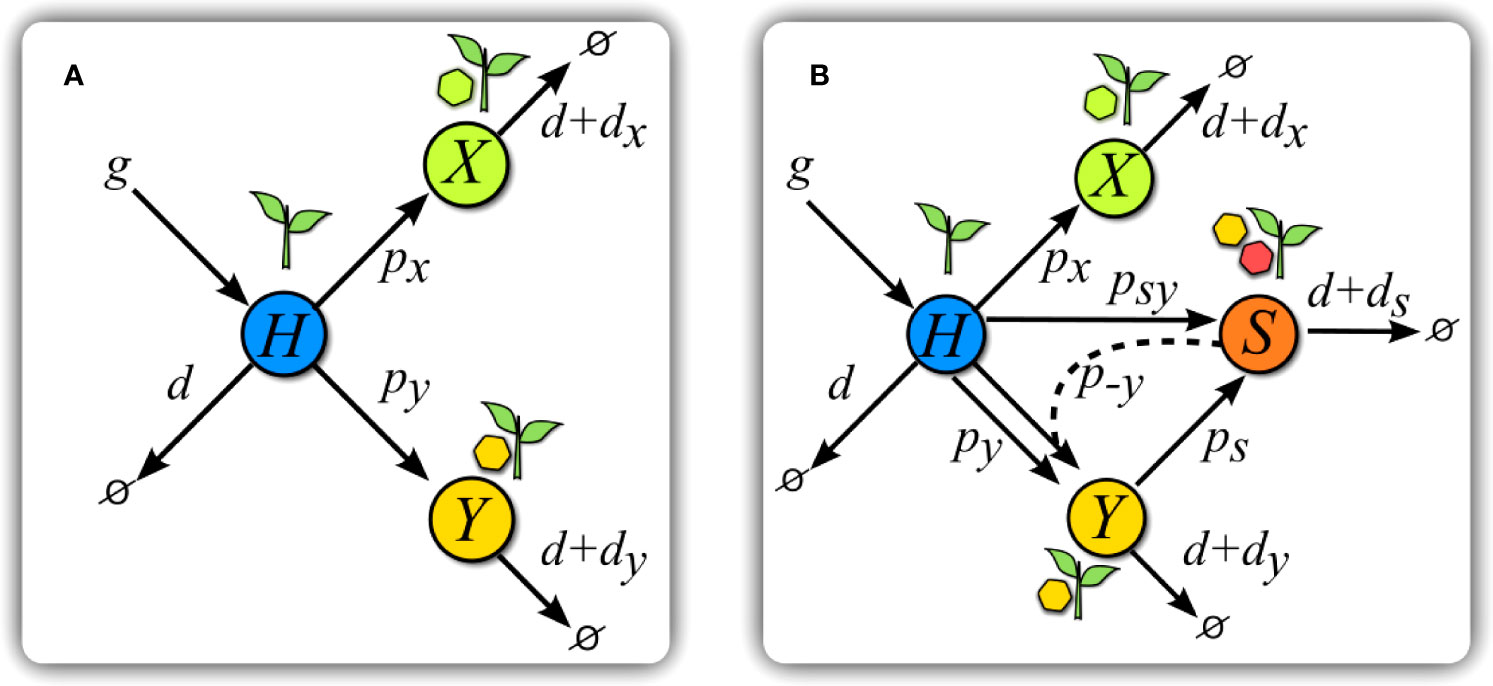
Figure 2 Scheme of models. (A) Scheme of Model V. Healthy hosts H are seeded at a constant rate g and die with basal rate d. Transitions to infected states happen at rates px and py for each virus. Infected hosts X and Y suffer from an increase di, $i= x, y$, in basal mortality. (B) Scheme of Model S. The introduction of a satellite with y as helper virus adds new transitions with respect to (A). Hosts in class Y can get infected at a rate ps by a satellite upon contact with hosts in class S. Hosts in this latter class are simultaneously infected by virus y and its satellite, and have an increase ds in their mortality rate. Infection of H plants by the helper virus and the satellite simultaneously occurs at a rate psy upon contact with class S. A co-infected plant S can also infect H plants only with virus y at a rate p−y . The color code is maintained all through the paper.
We keep the model intendedly simple so as to derive general principles arising from competition for hosts between the association of a helper virus and a satellite and a second monopartite virus. We do so to emphasize that relevant ecological dynamics do depend on the success of a specific strategy in front of alternative others. In order to highlight the main processes involved in such competition, we have made some simplifying assumptions. For instance, we assume super infection exclusion between the two viruses, such that hosts cannot be simultaneously infected by the two monopartite viruses. This is a convenient simplification to obtain exact results; as a consequence, coexistence in the context of our model means “ecological coexistence”, in the sense that the two viral strains and the satellite stably co-circulate in the host population under conditions that will be made explicit later. A second simplification is that of a mean-field approximation [common in paradigmatic epidemic models (45)], where the dynamics are described through differential equations and space is not explicitly modeled, therefore assuming that hosts interact homogeneously through averaged values.
The general dynamics of the process are as follows. Healthy hosts appear at a constant rate g and decay or die at a natural rate d. The amount of healthy, susceptible hosts at time t is H(t) and that of hosts infected by either virus is X(t) and Y(t). If no confusion arises, we will obviate the explicit dependence on t. Contacts between susceptible and infected hosts cause infection of susceptible hosts at rates px and py, respectively, that stand for the transmission rates of either virus. Infection by x or y increases the death rate of the host in amounts dx and dy. This scenario corresponds to a simple situation where two fully competent viruses compete for hosts (see Figure 2A), and is described by the following equations:
In the absence of viruses (X=0, Y=0), the abundance of hosts stabilizes at H* = g/d, as obtained by solving dH/dt = 0. Therefore, Eq. (1) entails a maximum carrying capacity of hosts in the absence of parasites. From now on, and given its relevance in determining the existence and stability of the various solutions, as it will be shown, the quantity d/g will be called host turnover.
It is a consequence of the symmetry between eqs. (2) and (3) that one of the viruses always displaces the other —with rare marginal exceptions, as later shown. Alternatively, for a small enough host replacement, both viruses become extinct: infected hosts die before new susceptible hosts are available to maintain the epidemic.
In the former scenario of competition between two viruses, we are now introducing a possible association with a satellite that can only multiply in presence of its helper virus. Due to the symmetry between the equations describing the dynamics of each virus, Eqs. (2) and (3), the choice of the helper virus does not affect the results, so we selected virus y without loss of generality. Class S, corresponding to hosts infected by the tandem y - s, is affected by an increase ds in mortality.
Due to the dependence of the satellite on its helper virus for replication, s can only be transmitted (to classes H or Y) through contacts with class S, either to healthy hosts, at rate psy, or to hosts already infected with y, at rate ps. In agreement with our superinfection exclusion, hosts in class X cannot be infected by classes Y or S. Finally, hosts in class S can also transmit only the helper virus under contacts with class H, this process occurring at rate p−y . A scheme of the interactions of this model can be seen in Figure 2B, and the set of equations considering all of the previous processes reads:
Note that, if we set S(t = 0) = 0 as an initial condition, this system is in practice equivalent to Model V. This nonetheless, the formal inclusion of the satellite modifies the study of the fixed points and stability of the system, as we show in the Supplementary Information.
The satellite non-trivially breaks the symmetry between the dynamics of hosts in classes X and Y, and therefore between the two corresponding viruses. As we will show through analytical and computational analyses, the satellite can benefit or impair its helper virus (thus impairing or benefiting virus x), or can promote the stable coexistence of all parts.
In order to clarify the effects of the introduction of a satellite in the outcome of competition between two monopartite viruses infecting the same host (model S), we begin by analyzing the stable solutions of the dynamics in the absence of the satellite (model V). All parameters in the models (death and transmission rates and host growth) are positive defined. The results obtained for model V are not conceptually new, but serve to properly compare the dynamics of the more complex model S with a baseline situation. Fixed points of the dynamics are the solutions to , where (model V) or (model S). The values of the variables satisfying the fixed point equations are denoted H*, X*, Y* and S* in the following. These values have to be equal to or larger than zero for the solution to have biological meaning: this results into conditions for existence and non-negativity that the model parameters have to fulfill. The study of stability of the solutions has been carried out using standard methodology of dynamical systems, as detailed in the Supplementary Information. Stability of the solutions also yields conditions on formal relationships that the model parameters have to satisfy. In the next two sections we summarize the solutions of models V and S and their stability properties, together with their ecological interpretation.
Depending on model parameters, model V has four different and positive solutions, three of them stable and one quasi-stable: i) none of the viruses are able to invade the population of hosts and both get extinct; ii) and iii) one of the two viruses stably coexists with the host and the other virus becomes extinct; iv) the two viruses coexist quasistably in the population. These four solutions map on three main extended regions in the space of parameters.
An important quantity arising in the formal analysis of the model is the ratio between the transmission rate of a virus, pi, and its overall effect on host death rate, d + di, where i = x, y. This ratio is an instance of the invasion fitness Fi =pi /( d+di ) of each virus, and determines which strategy is uninvadable (46). The ratio d/g is a measure of the replacement of healthy hosts. Smaller d/g means shorter times are needed for the appearance of susceptible healthy hosts. Note that, as in compartmental models for epidemic propagation, epidemic thresholds are defined as those conditions that permit the propagation of an incipient epidemic. Epidemic thresholds can be calculated by imposing that changes in the amount of infected hosts are positive when most of the population is susceptible, that is, dX/dt>0 when H* =g/d−ε, X* =ε, and similarly for dY/dt. This yields
where and are the epidemic thresholds for each of the two viruses, and infection propagation can only be sustained when and/or . Still, the condition that the two thresholds are larger than 1 does not suffice to guarantee that both viruses are simultaneously present in the population. It is the relationship between the two epidemic thresholds (or, equivalently, between the corresponding invasion fitnesses) that determines their persistence.
Invasion fitness Fi and host turnover d/g are the two main quantities determining the relevant equilibria of the system. A summary of such solutions and their stability is reported in Table 1 (see Supplementary Material for further details). Figure 3 shows a representative example of the localization in parameter space of the four possible solutions for model V. In that particular example, we have fixed d = 0.05, dy = 0.25, py = 0.1, and px = 0.1 and explored the {g, dx} plane. Changes in parameter values shift the boundaries between different solutions but do not cause qualitative changes. We observe large regions where both viruses become extinct or where either x or y coexist with the host.
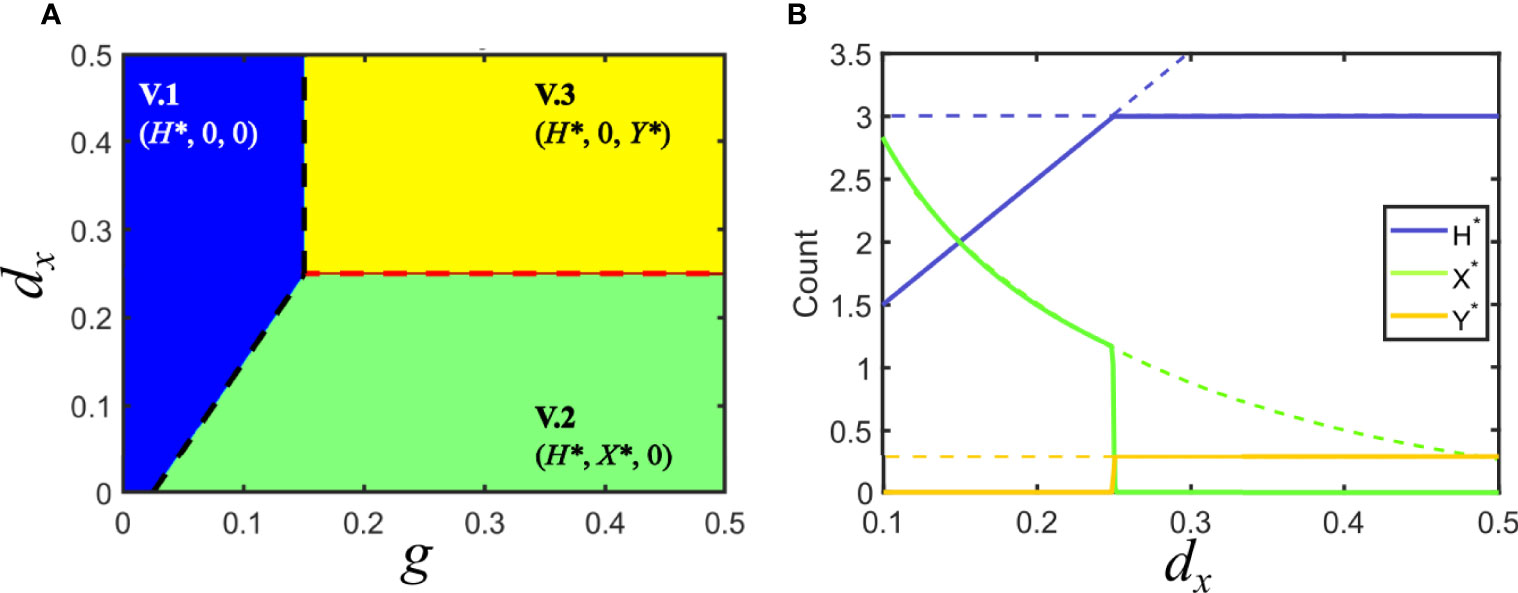
Figure 3 Solutions for Model V in parameter space. (A) Phase space of solutions in the plane of the variables host growth (g) and increase in host death rate due to infection by virus x (dx). The different solutions are indicated by the legend, here and elsewhere. In the blue region, none of the viruses can invade the population of hosts, d/g > Fi, i = x,y. The black dashed line indicates the boundary where d/g = Fi . Green and yellow regions correspond to solutions that satisfy Fx > Fy and Fy > Fx, respectively, where one of the viruses invades the population of hosts and displaces the other. The red dashed line corresponds to the marginal coexistence solution. (B) Bifurcation diagram for a cross section of the phase space in A corresponding to g = 0.5. Lines indicate the amount of each class at the fixed point, as shown in the legend. Dashed lines represent unstable solutions that are continued by solid lines corresponding to stable solutions. Green and yellow regions in A correspond to dx < 0.25 and dx > 0.25. Vertical lines show the degenerate solution of coexistence of the two viruses for dx = 0.25. Note that the values of H* and Y* become independent of dx in the region where y is the invading virus (and thus x becomes extinct). Parameters used: d = 0.05, px = 0.1, py = 0.1, dy = 0.25.
If host turnover is larger than invasion fitness for both viruses (solution V.1), both viral populations become extinct. This region corresponds to the blue area in Figure 3A, and describes a solution where the rate of appearance of new susceptible hosts is slower than the time needed by any of the viruses to invade the population: in absence of sufficient susceptible hosts, any parasite becomes extinct. From the viewpoint of epidemic propagation, solution V.1 occurs when parameters are such that the epidemic thresholds have not been crossed. No epidemic is possible below threshold: note that the conditions to be above the epidemic threshold are consistent with those obtained when calculating the existence and stability of solution V.1 (see Table 1).
This situation holds whenever the invasion fitness of the two viruses is different and at least one of them is higher than host turnover: Fi > Fj and Fi > d/g for at least one i, j∈ {x,y} . The solution is symmetric under the exchange i⇒j . These situations correspond to solutions V.2 and V.3, represented as green and yellow regions in Figure 3A. The abundances of susceptible and infected hosts depends on all model parameters. These symmetric solutions are a particular instance of the competitive exclusion principle, where there is no stable coexistence of two species (the two viruses) competing for the same resource (the host).
The temporal incidence [proportional to our variable X(t)] of the mosaic-inducing viruses Cucumber mosaic virus, Watermelon mosaic virus-2, Papaya ringspot virus watermelon strain and Zucchini yellow mosaic virus was monitored for three years (47). The growth rate estimated for the four viruses was highly variable, and spanned about two orders of magnitude. The final amount of susceptible, non-infected hosts (proportional to H*) was found to vary between about 5 and 97% (47). A quantification of independent parameter values in the model requires the estimation of additional variables from data, such as the dynamics of the total number of hosts or the mortality rate of infected hosts (48). This nonetheless, the range of values estimated for H* already points at a broad range of variation for invasion fitness (see solution V.2 in Table 1).
This is a marginal solution sitting at the boundary separating the two solutions where one of the viruses invades and the other becomes extinct. Coexistence only occurs when the two viruses have identical invasion fitness, and both are higher than host turnover, Fy = Fx > d/g. This condition maps to a single line in parameter space. Further, since the equilibrium values of X* and Y* are degenerated, a second condition establishes that none of them be zero (in which case the solution would correspond to cases V.2 or V.3). This means that, at this boundary, the amount of hosts infected by x or y is not unique, as illustrated by the vertical line in Figure 3B, where the amounts of X and Y appear superimposed. The degeneration of the solution is also reflected in its analytical form V.4, since Y* is given as a function of X* (see Table 1 and Supplementary Information).
It is not to be expected that any natural system strictly meets the conditions for coexistence here derived. In the example in Figure 3, any minor inaccuracy in the value of dx would kick the system out of coexistence and cause the extinction of one of the viruses. In general, arbitrary changes in dx, dy, px or py would cause the system to depart from the (quasi)stable solution. In more realistic situations, stochasticity, noise, or heterogeneity of any kind would push the system away from this marginal solution and into one of the extended regions where either one or both viruses become extinct. Therefore, co-circulating different viral species are, in general, not to be found in a host population under the conditions of model V even if both epidemic thresholds and are larger than 1, due to competitive exclusion.
The introduction of the satellite breaks the symmetry of equations describing the dynamics of the two viruses. In this new situation, it is not straightforward to predict which of the viruses or associations is going to succeed in invading the host population. A variety of outcomes is possible depending on the new parameters.
We first extend our definition of invasion fitness to the virus-satellite association,
where for convenience we define pc =psy +p−y (with dc =dsy =ds ). Note that, since the likelihood of independent transmission is larger than joint transmission, Fc > Fsy.
The system of equations (4-7) has seven different fixed point solutions (for all parameters taking positive values), summarized in Table 2. Four of them coincide with the solutions for model V, namely: extinction of the two viruses (S.1), invasion of virus x (S.2) or virus y (S.3) and (marginal) coexistence of hosts with viruses x and y (S.4). Three new solutions appear where the satellite co-circulates with one or two of the viruses. The first of them (S.5) corresponds to the extinction of virus x and the stable coexistence of the tandem virus y-satellite with the host. In two more solutions (embraced under S.6) the three agents (virus x, virus y and satellite) stably co-circulate in the population of hosts. In the following, we examine in detail solutions S.5 and S.6 to discuss how the introduction of the satellite modifies the different equilibria depending on the phenotypic effects of its association with the helper virus.
If the satellite behaves as a commensal parasite, co-infection with its helper virus does neither modify the regions of different equilibria nor their stability. Formally, this occurs when Fc = Fy. Figure 4 depicts the regions for the different equilibria and shows that the region corresponding to solution V.3 is now split into two subregions embracing solutions S.3 and S.5: in the former, the satellite becomes extinct; in the latter, it co-circulates with virus y.
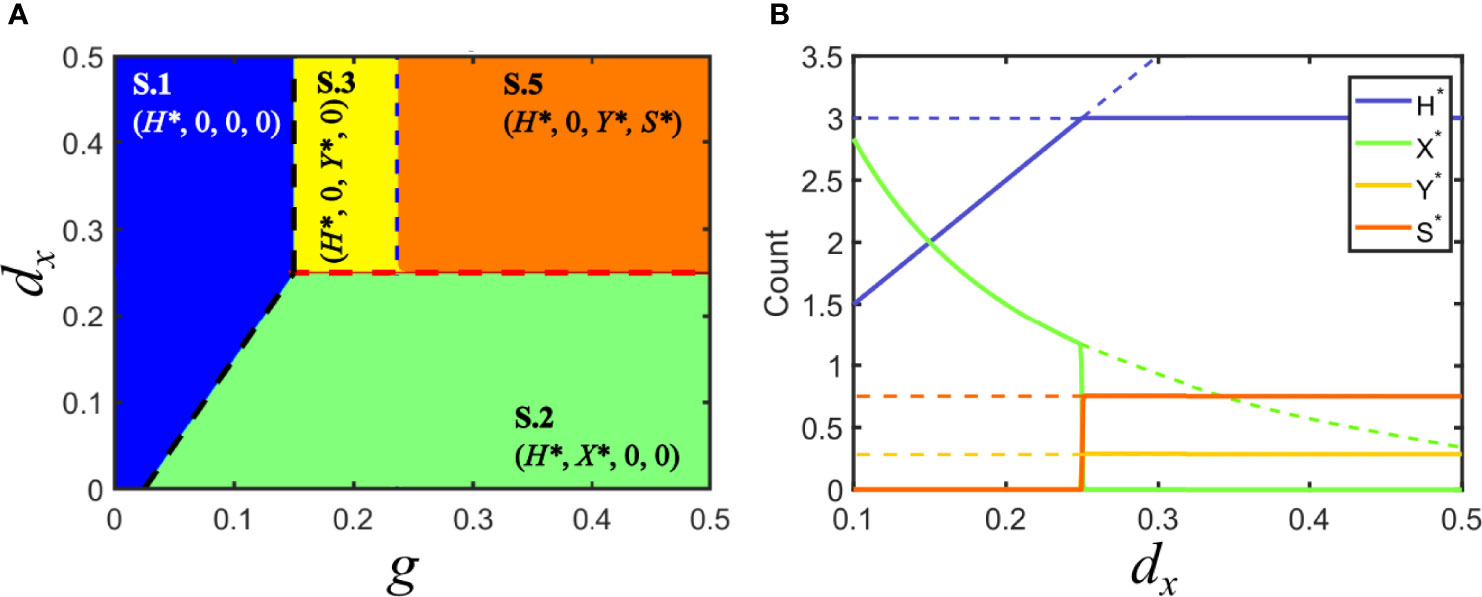
Figure 4 Solutions for model S in parameter space: commensal satellite. (A) Phase space of solutions in the plane {g,dx} for a commensal satellite (Fc = Fy). The description of regions corresponding to solutions S.1 (in blue, viruses cannot infect hosts), S.2 (in green, virus x invades and virus y becomes extinct) and S.3 (in yellow, virus y invades and virus x becomes extinct) are analogous to those described for Model V. In the new orange region, the satellite stably coexists with its helper virus, S.5. Red and black dashed lines are as in Figure 3. The blue dashed line signals the boundary separating the regions with and without co-circulating satellite. Note that the absence of virus y prevents the stable circulation of the satellite (below dx = 0.25). (B) Bifurcation diagram of a cross section of A, for g = 0.5. As above, lines stand for the amount of each class at equilibrium. Dashed lines correspond to unstable solutions, while solid lines correspond to stable solutions. Solutions collide with the degenerated solution S.4 at d = 0.05, px = 0.1, py = 0.1, dy = 0.25, ps = 0.8, psy = 0.04, ds = 0.3, p−y = 0.0766.
Invasion of virus y without the satellite (S.3) holds when Fy ( 1−γ )>Fsy , where γ=( g/( d+dy )−d/py )ps /( d+ds ) . This condition is shown as a vertical, blue dashed line in Figure 4. As the invasion fitness F of the virus-satellite association increases, it becomes harder for the helper virus to survive on its own until, eventually, solution S.5 becomes stable and substitutes S.3: in S.5, Y* ≠0 and, simultaneously, S* ≠0 . In general, this means that satellites are persistent in helper virus populations, but the virus still infects a subpopulation of hosts in the absence of the satellite. There are few examples where the interaction between a virus and a satellite does not seem to affect the phenotype of the helper virus. This is the case of the larger ssRNA satellites associated with nepoviruses, which in most cases do not modify the multiplication rate or the symptoms caused by the helper virus alone (49). Since there is coexistence of helper virus and satellite, the dynamics of that system could be described by our solution S.5.
The size of the region spanned by solution S.5 depends on the ability of virus y to infect susceptible hosts alone when jumping from joint virus-satellite infections. Therefore, it progressively narrows if p−y decreases. A successful strategy from the viewpoint of the satellite, therefore, could be to evolve towards associations that make the y-virus more dependent on s for transmission, progressively selecting increases in ps that could eventually turn p−y negligible. That is, the association would evolve from commensal to mutualistic.
Consider the situation in model V where Fx > Fy , with Fx > d/g (solution V.2): virus y is at a disadvantage and therefore unable to invade the population of hosts. In that situation, cooperation with a satellite can prevent its extinction if the satellite provides a sufficiently high increase in invasion fitness to its association with y. This occurs when the invasion fitness of the virus-satellite association is slightly larger than Fx. A region of parameters that was previously occupied only by solution S.2 becomes now bistable, such that depending on the initial conditions it can lead to the elimination of y (and the concomitant disappearance of the satellite), or to the extinction of x in favor of the virus-satellite association (solution S.5), see Figure 5.
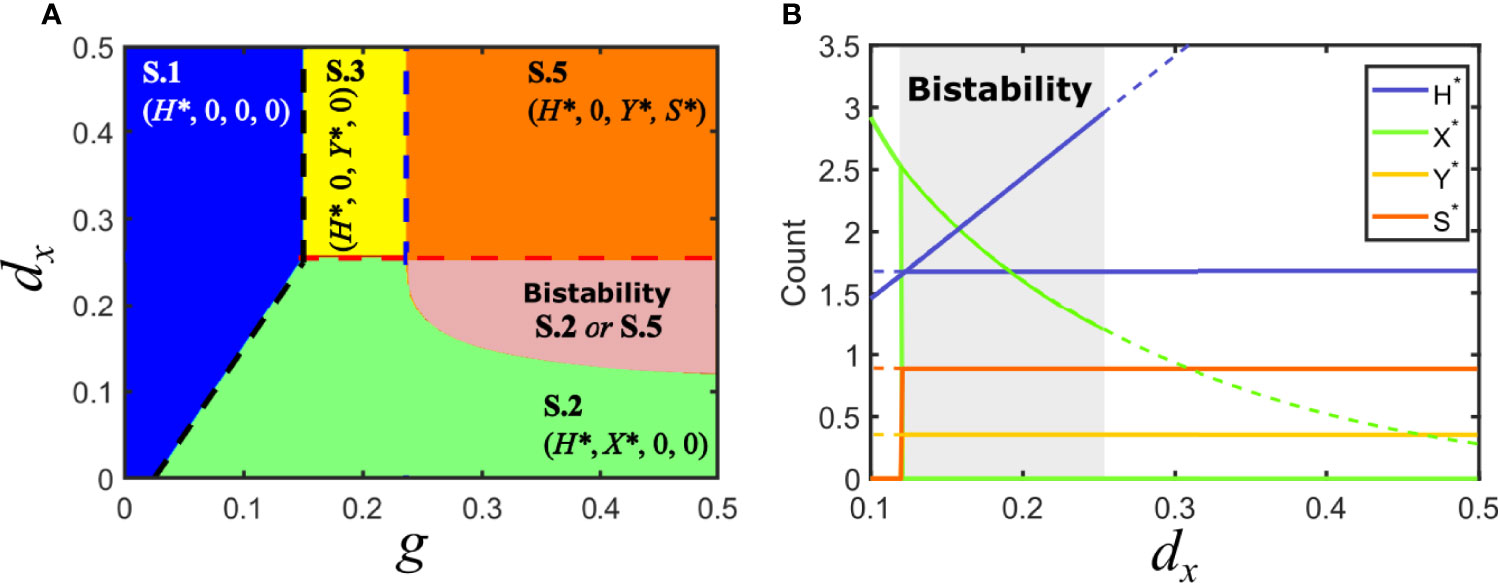
Figure 5 Solutions for model S in parameter space: mutualistic satellite. (A) Phase space of solutions in the plane {g, dx} for a mutualistic satellite. Here, Fc > Fy. Some of the previous equilibrium solutions are maintained, as long as the inequalities that define them remain unchanged. However, a region of bistability appears, where solutions S.2 and S.5 are possible for the same parameters, depending on the initial conditions. (B) Bifurcation diagram of a cross section of A, for g = 0.5. As above, lines stand for the amount of each class at equilibrium. Dashed lines correspond to unstable solutions, while solid lines correspond to stable solutions. A region of bistability for 0.12 < dx <0.25 is shown in gray. A bifurcation where two solutions appear occurs at dx = 0.12 ; solutions collide with the degenerated solution S.4 and stability is modified at dx = 0.25. Note that we have represented simultaneously the two possible solutions in this plot, but only one of them occurs for given initial conditions, either S.2 or S.5. The values of H*, Y* and S* do not depend on dx for S.5. Parameters used: d=0.05, px =0.1, py =0.1, dy =0.25, ps =0.8, psy =0.04, ds =0.3, p−y =0.2.
At the boundary that separates the region of bistability (where both S.2 and S.5 are possible) from solution S.2 as a unique solution, the values of H* for each solution coincide and equal H*=(d+dx)/px, as Figure 5B shows. By using the explicit expression for H* obtained for S.5 (see Supplementary Information) one can obtain an implicit analytical expression for the lower bistability boundary.
Mutualistic associations between helper viruses and satellites have been documented in natural systems. For example, there is a three-party system formed by Groundnut rosette virus (GRV), Groundnut rosette assistor virus (GRAV) and Groundnut rosette satellite (GRsat). GRV does not code for a capsid protein and is transmitted in GRAV particles, but only under the presence of GRsat. While GRV and GRAV are transmitted by the aphid Apis craccivora with an efficiency of about 60% (both in infections of GRAV alone and in mixed infections with GRV and GRAV), the satellite GRsat is essential for transmission, and found in all GRV-infected plants (50). In this case, therefore, the presence of the satellite is essential for transmission of the helper virus. A second example is that of Beet necrotic yellow vein virus, a multipartite virus composed of five positive-stranded RNAs. The efficiency of transmission by the soil plasmodiophorid Polymyxa betae in infections with RNA1 and RNA2 is 37%; however, in presence of RNA4, considered a satellite, the efficiency reaches 100% (51). Panicum mosaic virus (PMV) is essential for the replication of Satellite panicum mosaic virus (SPMV), but not for its encapsidation, since SPMV codes for its own capsid. The presence of SPMV in infections with PMV increases the titer of the helper virus and contributes to systemic invasion of the infected plant, since the latter depends on the interaction between SPMV’s capsid protein and PMV (52).
From an evolutionary viewpoint, satellites that confer their helper virus an increase in invasion fitness may be a low-cost solution to guarantee rapid adaptation to new hosts, since such an adaptive strategy, in principle, does not require adaptive mutations. The three cases just discussed (GRV, BNYVV and PMV) could be examples of such an adaptive process.
In some cases, mutualistic associations seem to have further evolved to necessary association between the parts, as in the bipartite virus formed by Pea enation mosaic virus 1 (PEMV1) and Pea enation mosaic virus 2 (PEMV2): PEMV1 provides a capsid required for PEMV2 transmission, while PEMV2 provides a movement protein required for systemic movement of PEMV within the infected plant (53).
Consider now the situation in model V where Fx > Fy , with Fx > d/g (solution V.3): virus x is at a disadvantage and virus y has invaded the host population. An association of y with a parasitic satellite can be a burden to the helper virus and diminish its relative advantage while, at the same time, it could potentially benefit x, the virus that was initially eliminated in the competition between the two monopartite viruses. It turns out that the association with a satellite under the conditions above does not necessarily entail, in contrast to previous equilibria, the elimination of either x or the y-satellite tandem. Actually, if the invasion fitness of the association virus y-satellite is such that Fc <Fx <Fy , then virus x can simultaneously coexist with virus y and the satellite in regions where it became extinct when the satellite was absent. The conditions above correspond to the relevant solution embraced under S.6, that we label S.6.a, see Supplementary Information. There is a second degenerate solution that requires Fc <Fx <Fy (solution S.6.b) that has no biological relevance, in the same sense as discussed above for other degenerate solutions.
Figure 6 illustrates the parameter space for the case of a parasitic satellite and shows the appearance of an extended region of coexistence. The boundary limiting the coexistence region can be analytically calculated by noting that, at that boundary, the values of X* for solutions S.5 and S.6.a coincide and are equal to zero. See Supplementary Information for an explicit expression of the latter solution.
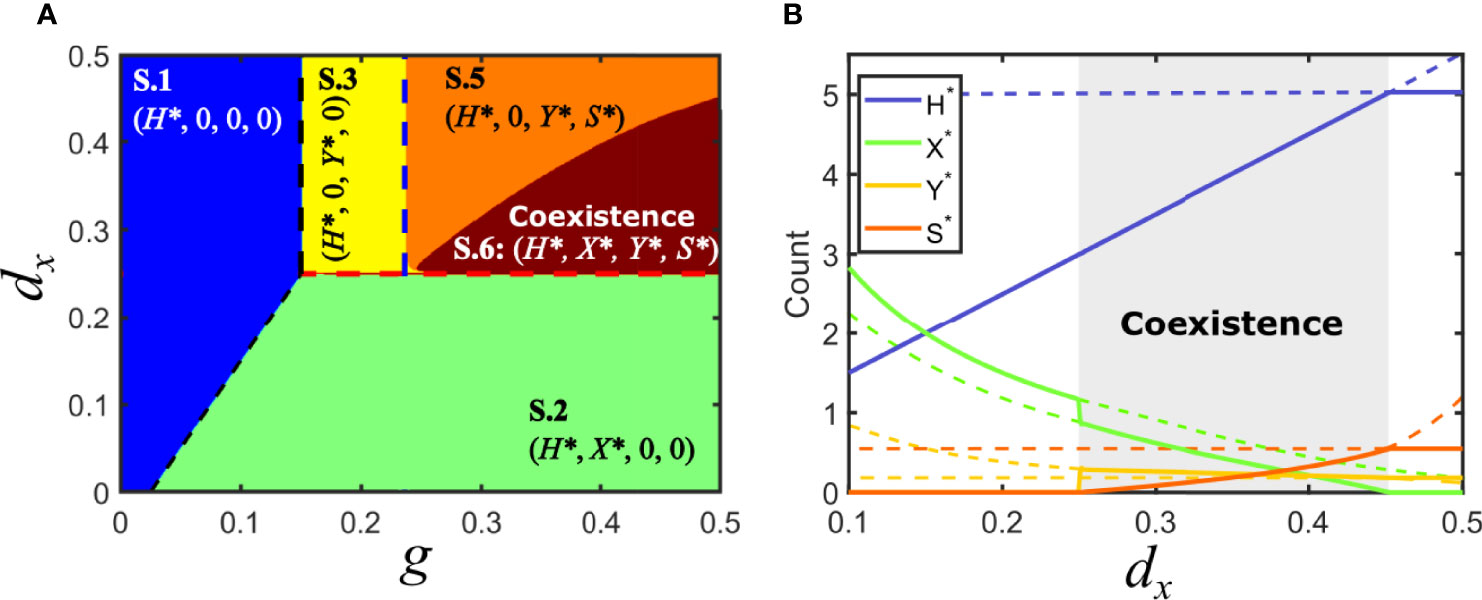
Figure 6 Solutions for model S in parameter space: parasitic satellite. (A) Phase space of solutions in the plane {g,dx} for a parasitic satellite in the particular case Fc < Fy. A region of coexistence occupies part of the area where the virus y-satellite eliminated virus x if the satellite was commensal or mutualistic. (B) Bifurcation diagram of a cross-section of A, for g = 0.5. A region of co-existence of all the populations is shown in gray for 0.25 < dx <0.4529 , corresponding to solution S.6. Solutions collide with the degenerated solution S.4 at dx = 0.25; a bifurcation occurs at dx = 0.4529A zoom of the region of coexistence for variables X*, Y* and S* can be found in the Supplementary Information. Parameters used d=0.05, px =0.1, py =0.1, dy =0.25, ps =0.8, psy =0.04, ds =0.3, p−y =0.016.
As of now, field data do not allow the identification of situations where it is the association with a satellite that permits the stable coexistence of multiple viral species. However, there are empirical examples of parasitic associations where the satellite is detrimental for one or more phenotypic traits of the helper virus. Cucumber mosaic virus satellite (CMV RNAsat), for example, diminishes the accumulation of Cucumber mosaic virus (CMV) in tomato plants and negatively affects its transmission by aphids (54). Field studies indeed show that transmission of the satellite requires a sufficient efficiency of transmission of the helper virus: when the incidence of plants infected with CMV reaches 90%, almost 80% of these are simultaneously infected with CMV RNAsat; however, mixed infections decrease to 50% for a fraction of plants infected with CMV around 65% (54). Independent experimental studies of CMV transmission support the field observation by showing that the efficiency of transmission of CMV in absence of the satellite reaches 86%, while this figure decreases to 65% in presence of the satellite (55).
Some studies have shown that the level of satellite abundance in virus-satellite associations is highly variable, with up to 100% in the mutualistic association of PMV with its satellite or in some regions for mixed infections of helper virus population and Rice yellow mottle virus satRNA (56) to very low, as in Cucumber mosaic virus satRNA (57). These observations are compatible with solutions S.5 and S.6.a, where the level of co-infected hosts in class S depends on several different model parameters. In particular, it grows when the rate of joint y-s transmission, ps increases, and vice versa, reaching 100% in situations where, in the context of our model, both the replication and the propagation of y become fully dependent on the presence of s.
The case of coexistence is an interesting and ecologically relevant situation where the association with a parasitic satellite is only partly detrimental for virus y, while it actually benefits both virus x and the diversity of circulating viral species (and subviral entities).
We have introduced a simple epidemic model to analyze stable states in a system formed by two fully fledged viruses and an associated satellite. This model contains the minimum set of players with symmetric (between the two viruses) and asymmetric interactions (between a virus and a satellite) of different nature (commensal, parasitic or mutualistic) able to display a range of ecological equilibria when competing for a common host.
Our main qualitative result is that stable coexistence of all players is possible in extended regions of parameter space, thus paving the way to the emergence of highly diverse viral ecologies, where multiple interactions between viruses may take place. Though biological and epidemiological outcomes of interactions among co-infecting viruses seem to be hardly predictable (32), long-lived loose interactions as those arising between the agents in our model create favorable circumstances for the emergence of a viral social life (58, 59) and the concomitant appearance of game-like strategies (60), for evolution towards more permanent associations, or to promote recombination between dissimilar viral and subviral particles (27, 61). Recombination, for example, has led to the emergence of new species, both in DNA viruses as begomoviruses (62), and in RNA viruses, as is the case of Watermelon mosaic virus, which arose through recombination of two legume-infecting viruses (63).
Our results only refer to long-time equilibria (i.e. to stable coexistence in a mathematical sense), and therefore do not apply to transient coexistence. In natural systems, the time needed for one viral species to cause the elimination of a second one (corresponding, for example, to solutions V.2 or V.3) can be so large that transient co-circulation of various viral species could be the most common situation: this transient coexistence should not be mistaken by solution V.4, which strictly refers to stable, long-term coexistence. A detailed analysis of how long it takes to attain ecological equilibrium and a quantification of typical evolutionary times for the emergence of new viral species infecting a given host would be needed, among others, to discriminate between transient and actual coexistence. Such an analysis is out of the scope of the present contribution, but it is important to keep in mind that, due to the long times involved in ecological dynamics, natural systems can be out-of-equilibrium most of the time.
In the light of our results, it is worth discussing the major assumption we have made, that is superinfection exclusion. Our second assumption, the use of a deterministic description of the dynamics, mostly affects the stability of marginal solutions (i.e., those solutions demanding a precise coincidence of certain parameters). The incorporation of stochasticity of any kind (in the form of space, which entails probabilistic contagion, finite populations, heterogeneous contacts, noise or any form of disorder), as it would occur in any natural system, turn solutions V.4, S.4, and S.6.b irrelevant, since they become unstable under any minor modification of most parameter values.
Assuming superinfection exclusion is useful to obtain exact analytical results, and therefore to gain insight into major ecological effects of virus-satellite associations. If this simplification is lifted, further interaction terms between viruses x and y, between x and the satellite, or even among the three entities, and new equations accounting for different states with various combinations of co-infecting entities have to be considered. Both the number of equations involved and their complexity would increase, preventing the achievement of exact expressions for equilibria and their stability, and therefore masking the interpretation of generic results. Let us however be more explicit about this point and sketch how the relaxation of that assumption could affect the results here obtained. The simplest scenario corresponds to commensal co-infection, in which case the qualitative results here presented remain unchanged: propagation of different entities in the host population could be independently analyzed, and the state of each individual host at a given time would be the product of probabilities of being infected with any of the viruses or sets of partners considered in the model. If co-infection causes changes in phenotype, however, the nature of the different equilibria might change, but one can argue that such changes would be qualitatively analogous to these explored here.
When equations describing the dynamics of additional infected classes are included in the model, the actual challenge is to characterize the new conditions under which coexistence occurs, since these could take much more involved mathematical expressions. Still, the mechanisms underlying coexistence, in particular, would not differ from the ones identified in this study as long as interaction terms take mathematical forms analogous to those considered here, that is, if interactions occur in pairs. This is not a limiting assumption, since all general contagion processes involve only pair contacts, regardless of whether multiple particles of various types are transmitted through the contact. We therefore conclude that the basic model explored in this work contains essential mechanisms for coexistence resulting from asymmetrical interactions among the involved partners, and its results can be conceptually extrapolated to scenarios with a larger number of players.
The problem of identifying coexistence conditions and the involved partners also admits a complementary viewpoint. Instead of considering an enlarged dynamical system with many interacting viral and subviral entities, and struggle to identify the conditions ensuring coexistence, we could take a more pragmatic approach and ask which is the subset of viruses and subviral agents able to coexist when pooled from a large ensemble of viruses and subviral particles that infect a given host. This subset would be, by definition, an ensemble fulfilling the conditions for coexistence in that host, and it could vary from host to host. From this viewpoint, the result of evolving towards regions of coexistence —should this be a situation under selection— is equivalent to drawing the subset of viral species and subviral entities able to coexist at a given time. This latter scenario conceptually agrees with common observations of multiple viral species (and possible subviral particles) persistently co-infecting the same host, especially in plants.
The problem of species diversity has a counterpart in ecology, where coexistence among species was deemed difficult due to the competitive exclusion principle (44). The search for mechanisms that permit species coexistence has a long tradition in ecology (42), and several models have considered the persistence of two competing prey species as a result of predation in situations where one of the preys would otherwise become extinct (64). There are, however, important differences between predator-mediated prey coexistence and satellite-mediated viral coexistence, as introduced in our work. The main novelty of our approach relies on the mechanism we are proposing: fixed points with positive population density become asymptotically stable as a result of the association between helper viruses and satellites. Virus-satellite interactions are conceptually and formally different from prey-predator interactions, as implemented in ecological models. Though coexistence at the fixed point of the dynamics in mean-field models can hold if species are not identical (65), ecological models have more often explored persistence of populations without fixed-point coexistence (66, 67), diffusion-mediated coexistence, thus requiring explicit space (68), or long-term persistence sustained by frequency-dependent selection (69).
The equilibrium solutions and the overall scenarios we have found in our models find their counterpart in natural situations, and do share some of their difficulties. While co-infection by multiple viral species or strains is common, detection and identification of involved parties and the nature of their interactions present major problems in etiological and epidemiological studies (33). In our modelling approach, we can just describe regions of parameter space where coexistence is or is not possible, but only a quantification of interactions and parameters can allow for a more specific identification of partners and their relationships.
All examples of satellite viruses summarized in Figure 1 represent necessary, asymmetric associations that have likely evolved from more loose interactions between helper viruses and satellites. In a parsimonious evolutionary scenario, it is sensible to assume that a monopartite virus coding for all functions needed to complete the viral cycle modified at some point its genome through the association with a satellite coding for genes providing new or different functions, either improving its packaging efficiency or its transmissibility, or modifying its infecting phenotype. A colonization of a new host where the genes provided by the satellite were instrumental could have also been a plausible evolutionary pathway, followed by the elimination of the old, now useless, equivalent gene in the viral genome. This sort of reasoning agrees with hypotheses relating high viral diversity to advantages at early phases of host colonization (70), where loose associations could quickly modify the viral phenotype without the need of incorporating genetic changes (9)
Coexistence of viral and subviral agents in a single host may act as well as a stepping stone towards mutually dependent necessary associations, as bipartite viral forms. Symmetric associations characterized by mandatory complementation between the parties could arise through different evolutionary pathways. They could evolve from asymmetric associations, as these described in the previous paragraph, when the survival of the helper virus becomes more dependent on the satellite. Also, they could be generated de novo through associations between complementary, defective particles. Finally, fully fledged viruses of dissimilar origin could produce a new phenotype and, eventually, streamline their genomes to minimize functional redundancy, in a sort of viral Black Queen association (71). The three pathways above could eventually yield what is usually described as a bipartite virus. Further particles could be added to the system through similar processes, causing in a parsimonious way the emergence of multipartite viral forms.
The computational code required to generate all the results in this study is publicly available at https://github.com/aluciasanz/satcompet.git.
AL-S, JA and SM participated in the overall conception and design of the study; SM designed the models; AL-S implemented the models and performed the simulations; AL-S and JA carried out the analytical calculations. AF and FG-A made substantial contributions to the discussion and interpretation of the results. AL and SM wrote the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
Grant PID2020-113284GB-C21 (SM) funded by MCIN/AEI/10.13039/501100011033; grant RTI2018-094302-B-I00 (AF, FG-A) funded by MINECO. The Spanish MICINN has also funded the “Severo Ochoa” Centers of Excellence to CNB, SVP-2014-068581 (AL-S), SEV 2017-0712 (AL-S, JA, SM) and to CBGP, SEV 2016-0672 (AF, FG-A). JA received support from the Spanish State Research Agency (AEI) through project MDM-2017-0737 Unidad de Excelencia “María de Maeztu”—Centro de Astrobiología (CSIC-INTA). AL-S is funded by the Centers for Disease Control and Prevention (grant 75D30121P10600) and the Army Research Office (grant W911NF1910384).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fviro.2022.929851/full#supplementary-material
1. Elena SF, Bernet GP, Carrasco JL. The Games Plant Viruses Play. Curr Opin Virol (2014) 8:62–7. doi: 10.1016/j.coviro.2014.07.003
2. Kassanis B. Properties and Behaviour of a Virus Depending for its Multiplication on Another. J Gen Microbiol (1962) 27:477–88. doi: 10.1099/00221287-27-3-477
3. Krupovic M, Cvirkaite-Krupovic V. Towards a More Comprehensive Classification of Satellite Viruses. NRM (2012) 234. doi: 10.1038/nrmicro2676-c4
4. Krupovic M, Kuhn JH, Fisher MG. A Classification System for Virophages and Satellite Virus. Arch Virol (2016) 161:233–47. doi: 10.1007/s00705-015-2622-9
5. Stanley J, Saunders K, MS P, Wong SM. Novel Defective Interfering Dnas Associated With Ageratum Yellow Vein Geminivirus Infection of Ageratum Conyzoides. Virology (1997) 239:87–96. doi: 10.1006/viro.1997.8856
6. Hadidi A, Flores R, Randles JW, Palukaitis P. Viroids and Satellites. 1st ed. Oxford UK:Elsevier Science (2017).
7. Roossinck MJ, Sleat D, Palukaitis P. Satellite RNAs of Plant Viruses: Structures and Biological Effects. Microbiol Revs. (1992) 56:256–79. doi: 10.1128/mr.56.2.265-279.1992
8. Sicard A, Michalakis Y, Gutiérrez S, Blanc S. The Strange Lifestyle of Multipartite Viruses. PLos Path. (2016) 12:e1005819. doi: 10.1371/journal.ppat.1005819
9. Lucía-Sanz A, Manrubia S. Multipartite Viruses: Adaptive Trick or Evolutionary Treat? NPJ Syst Biol Appl (2017) 3:34. doi: 10.1038/s41540-017-0035-y
10. Makino S, Chang MF, Shieh CK, Kamahora T, Vannier DM, Govindarajan S, et al. Molecular Cloning and Sequencing of a Human Hepatitis Delta (δ) Virus RNA. Nature (1987) 329:343–6. doi: 10.1038/329343a0
11. Cotmore SF, Agbandje-McKenna M, Chiorini JA, Mukha DV, Pinteland DJ, Qiu J, et al. The Family Parvoviridae. Arch Virol (2014) 159:1239–47. doi: 10.1007/s00705-013-1914-1
12. Ribière M, Olivier V, Blanchard P. Chronic Bee Paralysis: A Disease and a Virus Like No Other? J Invert. Pathol (2010) 103:S120–S131. doi: 10.1016/j.jip.2009.06.013
13. Nakashima N, Kawahara N, Omura T, Noda H. Characterization of a Novel Satellite Virus and a Strain of Himetobi P Virus (Dicistroviridae) From the Brown Planthopper, Nilaparvata Lugens. J Invert. Pathol (2006) 91:53–6. doi: 10.1016/j.jip.2005.10.001
14. Khoshnan A, Alderete JF. Characterization of Double-Stranded RNA Satellites Associated With the Trichomonas Vaginalis Virus. J Virol (1995) 69:6892–97. doi: 10.1128/jvi.69.11.6892-6897.1995
15. Schmitt MJ, Breining F. The Viral Killer System in Yeast: From Molecular Biology to Application. FEMS Microbiol Rev (2002) 26:257–75. doi: 10.1111/j.1574-6976.2002.tb00614.x
16. King AM, Adams MJ, Carstens EB, Lefkowitz EJ eds. The Subviral Agents. San Diego: Elsevier (2012) p. 1211–1219.
17. Yau S, Lauro FM, DeMaere MZ, Brown MV, Thomas T, Raftery MJ, et al. Virophage Control of Antarctic Algal Host–Virus Dynamics. Proc Natl Acad Sci USA (2011) 108:6163–8. doi: 10.1073/pnas.1018221108
18. Roossinck MJ. Symbiosis Versus Competition in Plant Virus Evolution. Nat Revs. Microbiol (2005) 3:917–24. doi: 10.1038/nrmicro1285
19. Leeks A, Segredo-Otero EA, Sanjuán R, West SA. Beneficial Coinfection can Promote Within-Host Viral Diversity. Virus Evol (2018) 4:vey028–8. doi: 10.1093/ve/vey028
20. García-Arenal F, Fraile A. Chapter 56 - Origin and Evolution of Satellites. In: Hadidi A, Flores R, Randles JW, Palukaitis P, editors. Viroids and Satellites. Boston: Academic Press (2017). p. 605–14. doi: 10.1016/B978-0-12-801498-1.00056-5
21. Syller J. Molecular and Biological Features of Umbraviruses, the Unusual Plant Viruses Lacking Genetic Information for a Capsid Protein. Physiol Mol Plant Pathol (2003) 63:35–46. doi: 10.1016/j.pmpp.2003.08.004
22. Havelda Z, Hornyik C, Válóczi A, Burgyán J. Defective Interfering RNA Hinders the Activity of a Tombusvirus-Encoded Posttranscriptional Gene Silencing Suppressor. J Virol (2005) 79:450–457. doi: 10.1128/JVI.79.1.450-457.2005
23. Scheets K. Maize Chlorotic Mottle Machlomovirus and Wheat Streak Mosaic Rymovirus Concentrations Increase in the Synergistic Disease Corn Lethal Necrosis. Virology (1998) 242:28–38. doi: 10.1006/viro.1997.8989
24. Pruss G, Ge X, Shi XM, Carrington JC, Bowman Vance V. Plant Viral Synergism: The Potyviral Genome Encodes a Broad-Range Pathogenicity Enhancer That Transactivates Replication of Heterologous Viruses. Plant Cell (1997) 9:859–68. doi: 10.1105/tpc.9.6.859
25. Palukaitis P, Roossinck MJ. Spontaneous Change of a Benign Satellite RNA of Cucumber Mosaic Virus to a Pathogenic Variant. Nat Biotechnol (1996) 14:1264–8. doi: 10.1038/nbt1096-1264
26. Nawaz-ul-Rehman MS, Fauquet CM. Evolution of Geminiviruses and Their Satellites. FEBS Lett (2009) 583:1825–32. doi: 10.1016/j.febslet.2009.05.045
27. Elena S. Evolutionary Constraints on Emergence of Plant RNA Viruses. Recent Adv Plant Virol (2011), 283–300. doi: 10.21775/9781910190357
28. McLeish M, Fraile A, García-Arenal F. Evolution of Plant–Virus Interactions: Host Range and Virus Emergence. Curr Opin Virol (2019) 34:50–5. doi: 10.1016/j.coviro.2018.12.003
29. Alcaide C, Rabadán MP, Moreno-Pérez MG, Gómez P. Chapter Five - Implications of Mixed Viral Infections on Plant Disease Ecology and Evolution. In: Kielian M, Mettenleiter TC, Roossinck MJ, editors. Advances in Virus Research, San Diego, USA:Academic Press (2020). 106:145–69.
30. Betancourt M, Fraile A, García-Arenal F. Cucumber Mosaic Virus Satellite RNAs That Induce Similar Symptoms in Melon Plants Show Large Differences in Fitness. J Gen Virol (2011) 92:1930–8. doi: 10.1099/vir.0.032359-0
31. McLeish M, Sacristán S, Fraile A, García-Arenal F. Coinfection Organizes Epidemiological Networks of Viruses and Hosts and Reveals Hubs of Transmission. Phytopathology (2019) 109:1003–10. doi: 10.1094/Phyto-08-18-0293-R
32. Syller J. Chapter 30 - Interspecific and Intraspecific Interactions Among Plant Viruses in Mixed Infections. In: Awasthi L, editor. Applied Plant Virology. San Diego,:Academic Press (2020). p. 437–53.
33. Jeger MJ. The Epidemiology of Plant Virus Disease: Towards a New Synthesis. Plants (2020) 9:1768. doi: 10.3390/plants9121768
34. Betancourt M, Escriu F, Fraile A, García-Arenal F. Virulence Evolution of a Generalist Plant Virus in a Heterogeneous Host System. Evol. Appl (2013) 6:875–90. doi: 10.1111/eva.12073
35. Frank SA. Within-Host Spatial Dynamics of Viruses and Defective Interfering Particles. J Theor Biol (2000) 206:279–90. doi: 10.1006/jtbi.2000.2120
36. Kirkwood TBL, Bangham CR. Cycles, Chaos, and Evolution in Virus Cultures: A Model of Defective Interfering Particles. Proc Natl Acad Sci USA (1994) 91:8685–89. doi: 10.1073/pnas.91.18.8685
37. Grande-Pérez A, Lázaro E, Domingo E, Manrubia SC. Suppression of Viral Infectivity Through Lethal Defection. Proc Natl Acad Sci USA (2005) 102:4448–52. doi: 10.1073/pnas.0408871102
38. Szathmáry E. Viral Sex, Levels of Selection, and the Origin of Life. J Theor Biol (1992) 159:99–109. doi: 10.1016/S0022-5193(05)80770-2
39. Nee S. Mutualism, Parasitism and Competition in the Evolution of Coviruses. Phil. Trans R Soc Lond B. (2000) 355:1607–13. doi: 10.1098/rstb.2000.0722
40. Lucía-Sanz A, Aguirre J, Manrubia S. Theoretical Approaches to Disclosing the Emergence and Adaptive Advantages of Multipartite Viruses. Curr Opin Virol (2018) 33:89–95. doi: 10.1016/j.coviro.2018.07.018
41. Zwart MP, Blanc S, Johnson M, Manrubia S, Michalakis Y, Sofonea MT. Unresolved Advantages of Multipartitism in Spatially Structured Environments. Virus Evol (2021) 7:Veab004. doi: 10.1093/ve/veab004
42. Tokeshi M. Species Coexistence. In: Ecological and Evolutionary Perspectives. Wiley-Blackwell (2009). p. 468.
43. Gause GF. Experimental Studies on the Struggle for Existence : I. Mixed Population of Two Species of Yeast. J Exp Biol (1932) 9:389–402. doi: 10.1242/jeb.9.4.389
44. Hardin G. The Competitive Exclusion Principle. Science (1960) 131:1292–7. doi: 10.1126/science.131.3409.1292
45. Hethcote HW. The Mathematics of Infectious Diseases. SIAM. Rev (2000) 42:599–653. doi: 10.1137/S0036144500371907
46. Lehmann L, Mullon C, Akçay E, Van Cleve J. Invasion Fitness, Inclusive Fitness, and Reproductive Numbers in Heterogeneous Populations. Evolution (2016) 70:1689–702. doi: 10.1111/evo.12980
47. Alonso-Prados J, Luis-Arteaga M, Alvarez J, Moriones E, Batlle A, Laviña A, et al. Epidemics of Aphid-Transmitted Viruses in Melon Crops in Spain. Eur J Plant Pathol (2003) 109:129–38. doi: 10.1023/A:1022598417979
48. Escriu F, Fraile A, García-Arenal F. The Evolution of Virulence in a Plant Virus. Evolution (2003) 57:755–65. doi: 10.1111/j.0014-3820.2003.tb00287.x
49. Palukaitis P, Rezaian A, García-Arenal F. Satellite Nucleic Acids and Viruses. In: Mahy BW, Van Regenmortel MH, editors. Encyclopedia of Virology (Third Edition). Oxford: Academic Press (2008). p. 526–35.
50. Murant AF. Dependence of Groundnut Rosette Virus on its Satellite Rna as Well as on Groundnut Rosette Assistor Luteovirus for Transmission by Aphis Craccivora. J Gen Virol (1990) 71:2163–66. doi: 10.1099/0022-1317-71-9-2163
51. Tamada T, Abe H. Evidence That Beet Necrotic Yellow Vein Virus Rna-4 is Essential for Efficient Transmission by the Fungus Polymyxa Betae. J Gen Virol (1989) 70:3391–8. doi: 10.1099/0022-1317-70-12-3391
52. Omarov RT, Qi D, Karen-Beth SG. The Capsid Protein of Satellite Panicum Mosaic Virus Contributes to Systemic Invasion and Interacts With its Helper Virus. J Virol (2005) 79:9756–64. doi: 10.1128/JVI.79.15.9756-9764.2005
53. Doumayrou J, Sheber M, Bonning BC, Miller WA. Role of Pea Enation Mosaic Virus Coat Protein in the Host Plant and Aphid Vector. Viruses (2016) 8:312. doi: 10.3390/v8110312
54. Escriu F, Fraile A, García-Arenal F. Evolution of Virulence in Natural Populations of the Satellite Rna of Cucumber Mosaic Virus. Phytopathology (2000) 90:480–5. doi: 10.1094/PHYTO.2000.90.5.480
55. Escriu F, Perry KL, García-Arenal F. Transmissibility of Cucumber Mosaic Virus by Aphis Gossypii Correlates With Viral Accumulation and is Affected by the Presence of its Satellite Rna. Phytopathology (2000) 90:1068–72. doi: 10.1094/PHYTO.2000.90.10.1068
56. Pinel A, Abubakar Z, Traore O, Konaté G, Fargette D. Molecular Epidemiology of the Rna Satellite of Rice Yellow Mottle Virus in Africa. Arch Virol (2003) 148:1721–33. doi: 10.1007/s00705-003-0138-1
57. Palukaitis P, García-Arenal F. Cucumoviruses. Adv Virus Res (2003) 62:241–323. doi: 10.1016/S0065-3527(03)62005-1
58. Díaz-Muñoz SL, Sanjuán R, West S. Sociovirology: Conflict, Cooperation, and Communication Among Viruses. Cell Host Microbe (2017) 22:437–41. doi: 10.1016/j.chom.2017.09.012
59. Sanjuán R. The Social Life of Viruses. Annu Rev Virol (2021) 8:183–99. doi: 10.1146/annurev-virology-091919-071712
60. Leeks A, West SA, Ghoul M. The Evolution of Cheating in Viruses. Nat Commun (2021) 12:6928. doi: 10.1038/s41467-021-27293-6
61. García-Arenal F, Fraile A, Malpica J. Variation and Evolution of Plant Virus Populations. Int Microbiol (2003) 6:225–32. doi: 10.1007/s10123-003-0142-z
62. Chakraborty S, Vanitharani R, Chattopadhyay B, Fauquet CM. Supervirulent Pseudorecombination and Asymmetric Synergism Between Genomic Components of Two Distinct Species of Begomovirus Associated With Severe Tomato Leaf Curl Disease in India. J Gen Virol (2008) 89:818–28. doi: 10.1099/vir.0.82873-0
63. Desbiez C, Joannon B, Wipf-Scheibel C, Chandeysson C, Lecoq H. Recombination in Natural Populations of Watermelon Mosaic Virus: New Agronomic Threat or Damp Squib? J Gen Virol (2011) 92:1939–48. doi: 10.1099/vir.0.031401-0
64. May RM. Stability and Complexity in Model Ecosystems. Princeton: Princeton University Press (1974).
65. Bastolla U, Lässig M, Manrubia SC, Valleriani A. Biodiversity in Model Ecosystems, I: Coexistence Conditions for Competing Species. J Theor Biol (2005) 235:521–30. doi: 10.1016/j.jtbi.2005.02.005
66. Hutson V, Vickers G. A Criterion for Permanent Coexistence of Species, With an Application to a Two-Prey One-Predator System. Math Biosci (1983) 63:253–69. doi: 10.1016/0025-5564(82)90042-6
67. Abrams PA. Is Predator-Mediated Coexistence Possible in Unstable Systems? Ecology (1999) 80:608–21. doi: 10.1890/0012-9658(1999)080[0608:ipmcpi]2.0.co;2
68. Mimura M, Kan-on Y. Predation-Mediated Coexistence and Segregation Structures. In: Nishida T, Mimura M, Fujii H, editors. Patterns and Waves, North Hollandf - Amsterdam:Elsevier (1986). 18:129–55. doi: 10.1016/S0168-2024(08)70130-9
69. Ishii Y, Shimada M. Learning Predator Promotes Coexistence of Prey Species in Host-Parasitoid Systems. Proc Natl Acad Sci (2012) 109:5116–20. doi: 10.1073/pnas.1115133109
70. Gonzalez-Jara P, Fraile A, Canto T, García-Arenal F. The Multiplicity of Infection of a Plant Virus Varies During Colonization of Its Eukaryotic Host. J Virol (2009) 83:7487–94. doi: 10.1128/JVI.00636-09
Keywords: viral dynamics model, subviral agents, cooperation, ecological competition, viral coexistence
Citation: Lucia-Sanz A, Aguirre J, Fraile A, García-Arenal F and Manrubia S (2022) Defective Subviral Particles Modify Ecological Equilibria and Enhance Viral Coexistence. Front.Virol. 2:929851. doi: 10.3389/fviro.2022.929851
Received: 27 April 2022; Accepted: 26 May 2022;
Published: 15 July 2022.
Edited by:
Rafael Sanjuán, University of Valencia, SpainReviewed by:
Asher Leeks, Yale University, United StatesCopyright © 2022 Lucia-Sanz, Aguirre, Fraile, García-Arenal and Manrubia. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Susanna Manrubia, c21hbnJ1YmlhQGNuYi5jc2ljLmVz
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.