Phase and thermodynamics-informed predictive model for laser beam additive manufacturing of a multi-principal element alloy

The complex solidification cycles experienced by multi-principal element alloys (MPEAs) during laser-based additive manufacturing (LBAM) often lead to structural defects that affect the build quality. The underlying thermal processes and phase transformations are a function of the process parameters employed. With a moving Gaussian heat source to mimic LBAM and leveraging material thermodynamics guidelines from CALculation of PHAse Diagrams (CALPHAD), we estimate the temperature-dependent thermal properties, phase fractions, and melt pool geometry using an experimentally validated computational fluid dynamics model. The results substantiate that the peak temperatures are inversely correlated to the scan speeds, and the melt pool dimensions can assist in the predictive selection of process parameters such as hatch distance and layer thickness. A relatively low cooling rate recorded during the process is ascribed to the preheating of the substrate to ensure printability of the alloy.

The promising material properties of multi-principal element alloys (MPEAs) have intrigued the research community over the past decade, especially with regard to engineering and processing stable solid solutions that are able to withstand harsh environments (Rickman et al., 2019; Roy et al., 2020; Roy et al., 2021a; Roy et al., 2021b; Khakurel et al., 2021; Roy and Balasubramanian, 2021; Sreeramagiri et al., 2021). Alloy design challenges are typically addressed by computation and data-enabled techniques, while material-scale validation of the predicted properties has been generally realized through arc melting and thin film synthesis (Joress et al., 2020; Roy et al., 2020). Metal additive manufacturing (AM) has emerged as a viable solution for alloy discovery and synthesis, fostering rapid assessment of the predicted design space (Sreeramagiri et al., 2020). However, challenges associated with the complicated thermal history, cooling mechanisms, and complex solidification phenomena must be overcome to realize the potential of metal AM (Rahman et al., 2019). Additionally, component fabrication continues to remain a challenge when porting process parameters across AM platforms and underscores the importance of understanding thermally induced artifacts such as residual stresses. These artifacts are primarily caused by the processing parameters, viz., laser power, scan speed, hatch distance, and powder flow rate, that influence the quality of the manufactured specimen. Thus, scrutiny of the effects of AM parameters on the thermal history during processing can enable an effective control for component fabrication. We note that in the literature, researchers have employed the linear volume-of-fluid (VOF) model to simulate phase change behavior that may be displaced from the transformations observed in multi-principal elements and complex alloys. We believe that our work is one of the first efforts in correlating material phase evolution and melt pool dynamics by incorporating thermodynamic data from the Scheil solidification curves, contributing to a relatively more accurate replication of the physical process.

Processing parameters employed in metal AM influence thermophysical properties and material behavior, such as conductivity, specific heat, and melt pool dynamics. For instance, the size of the melt pool is directly proportional to the power of the laser beam (LB) under a constant scanning speed. Therefore, information about the thermal history during processing is vital to characterize the quality of the components synthesized by an LBAM process. Experimental techniques to characterize in situ the thermal profiles, microstructures, phase evolution, and residual stresses include synchrotron-based high-energy X-ray diffraction (HEXRD), neutron diffraction, pyrometers, and thermal cameras (Hu et al., 2019; Zhang et al., 2020). Nonetheless, the intensive time and resource demands associated with these techniques necessitate the use of computational tools, such as computational fluid dynamics (CFD) and finite element (FE) method, to gain quantitative insights into the thermal history, melt pool dynamics, heat transfer, fluid flow, and, consequently, the residual stresses during laser processing of metallic alloys (Lankalapalli et al., 1996; Choi et al., 2005; Qi et al., 2006; Moraitis and Labeas, 2008; Wang et al., 2008; Roberts et al., 2009; Liu et al., 2010; Wen and Shin, 2010; Wang et al., 2011; Cho et al., 2012; Michopoulos et al., 2018; Rahman et al., 2019).

The higher fidelity of emerging 3D models has contributed to robust predictions of temperature distributions, shape of the melt pool, keyhole formations, etc., in as-built AM parts. The related literature is centered around employing linear functions of solidus and liquidus temperatures to predict the phase change from solid to liquid for the metal/alloy deposits. Critically, linear functions may not yield accurate results for MPEAs, given the complexities in the material composition and microstructure. A phase diagram (CALculation of PHAse Diagrams (CALPHAD))-guided novel 3D CFD model, proposed herein, can aid in understanding the variation of thermophysical properties during LBAM of an AlCoCrFeNi MPEA. This model leverages material thermodynamics using CALPHAD/Scheil simulations to precisely calculate the phase transformation as a function of temperature and predict the resultant thermal properties.

The commercial Ansys Fluent 21.0 package is adopted to simulate the LBAM synthesis of an AlCoCrFeNi MPEA over a domain of size 5 mm × 5 mm × 5 mm coated with a 0.07-mm layer of the alloy powder, as illustrated in Figures 1A, B. The geometry is discretized using finer elements encompassing the powder and gradually increasing the element size away from the deposit toward the bottom of the substrate. The simulation does not model a specific build plate material, but rather, a constant wall temperature of 1000 K is applied as the boundary condition at the base of the manufactured MPEA specimen. The simulation assumes a chemically inert environment, while the heat transfer coefficient is determined using the Nusselt analogy. Discretizing the powder with finer elements augments accurate predictions of the thermal phenomena near the laser-irradiated zones. In contrast, the use of coarser elements far from the deposit enhances computational efficiency with minimal loss in precision. The finite volume method is employed to numerically solve the energy and momentum conservation equations with the second-order upwind scheme; the technical specifications are listed in Table 1. To mimic laser melting and solidification, the entire top surface of the powder bed is scanned by a moving heat source (laser beam) of 80 μm diameter with 200 W power. Four representative scenarios are examined with varied laser scan speeds, viz., 333 mm/s, 500 mm/s, 700 mm/s, and 1,000 mm/s, to interrogate the effect of speed on the melt pool geometry. While parameters associated with the surrounding environment, powder morphology, etc., can contribute to the alloy processing, we consider them invariant for the purpose of this study. Because earlier reports on this MPEA suggest a high cracking susceptibility during LBAM, the substrate is preheated to 1000 K to eliminate such artifacts in modeling (Karlsson et al., 2019).

FIGURE 1

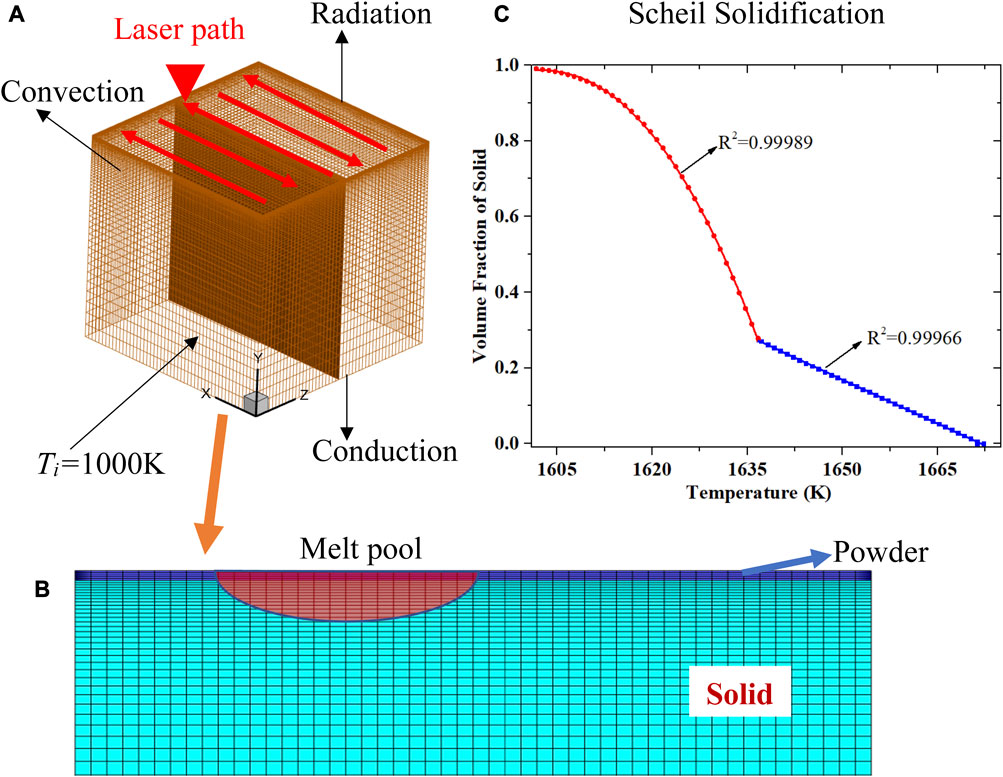
FIGURE 1. (A) Computational domain representing the 3D AlCoCrFeNi MPEA with laser-beam rastering in the x and z directions to deposit a layer of the alloy powder. (B) Magnified cross-sectional representation of the mid-plane in (A) illustrating the refined mesh constituted of smaller elements for powder particles together with coarser elements for solid particles, employed to increase computing efficiency. The point irradiated by the laser beam indicates a phase change to liquid, forming the melt pool. (C) The user-defined Scheil cooling curve obtained from Thermo-Calc is utilized to impose the boundary conditions on the solid/liquid volume fractions as a function of temperature to accurately predict the phase transformations.

TABLE 1

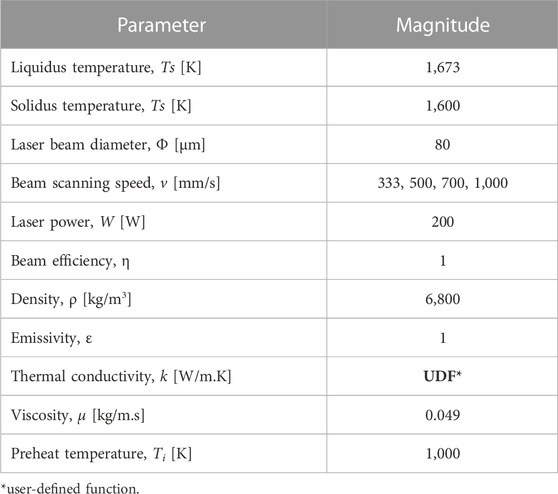
TABLE 1. Processing parameters considered in the CFD model to simulate LBAM synthesis of AlCoCrFeNi MPEA.

A Gaussian distribution function is selected to model the intensity of the laser beam along the radial direction, assuming a retarding intensity with an increasing penetration depth along the Y direction. Equation 1 describes the Gaussian volumetric heat source of the laser beam (Liu et al., 2010; Rahman et al., 2019) that is incorporated as a source term ($\dot{Q}$) into the collective energy conservation equation along with the speed [v_s (m/s)] of the laser beam (Eq. 4). Additionally, the overall model complexity is attributed to the simultaneous solution of the continuity and momentum conservation equations.

${\dot{Q}}_{\left(x,y,z\right)}=\eta \frac{H_S\times I_y}{S},(1)$

where $\dot{Q}$ is the heat source [W/m³], $\eta$ is the laser efficiency, $H_S$ is the Gaussian heat source, $I_y$ is the penetration function, and $S$ is the penetration depth [m].

${\mathrm{I}}_{\mathrm{y}}=\frac{1}{0.75}\left(-2.25{\left(\frac{\mathrm{y}}{\mathrm{S}}\right)}^2+1.5\left(\frac{\mathrm{y}}{\mathrm{S}}\right)+0.75\right),(2)$

${\mathrm{H}}_{\mathrm{S}}=\frac{2\mathrm{W}}{\mathrm{\pi }{\mathrm{\Phi }}_{\mathrm{E}}^2}\exp \left\{-\frac{2\left[{\left(\mathrm{x}-{v_s.\mathrm{t}-\mathrm{x}}_{\mathrm{s}}\right)}^2+{\left(\mathrm{z}-{\mathrm{z}}_{\mathrm{s}}\right)}^2\right]}{{\mathrm{\Phi }}_{\mathrm{E}}^2}\right\},(3)$

where $W$ is the laser power [W], ${\mathrm{\Phi }}_{\mathrm{E}}^2$ is the laser beam diameter (m), t is time (s), x is the direction along the x-axis, z is the direction along the z-axis, x_s is the starting point in the x-direction, and z_s is the starting point in the z-direction. Likewise, the collective energy conservation equation with v_s [m/s] being the speed of the laser beam reduces to

$\frac{\partial T}{\partial t}+v_s\frac{\partial T}{\partial x_i}=\nabla \left(\frac{k\left(T\right)}{\rho c_p\left(T\right)}\nabla T\right)+\frac{\dot{Q}}{\rho c_p\left(T\right)}+\frac{g_{y}w}{c_p\left(T\right)}+\frac{\mu }{\rho c_p\left(T\right)}{\Phi }_V,(4)$

where T is the temperature (K), t is time (s), x_i is the direction along the x-axis, c_p is the specific heat (J/kg.K), g_y is the gravitational force along the y direction (9.81 m/s²), and ${\Phi }_V$ is the viscous dissipation term.

Figure 1C displays the Scheil solidification curve obtained from the Thermo-Calc High-Entropy Alloy (HEA) database (Andersson et al., 2002). Scheil simulations assume an infinite diffusion in liquid and no diffusion in the solid phase to evaluate the liquid/solid phase fractions at a given temperature. The prediction suggests that on cooling the alloy, nucleation initiates at ∼1673 K (identified at 0.1% solid fraction from Scheil simulation) with the formation of BCC_B2 followed by a secondary BCC_B2#2 precipitation at ∼1635 K. This result is documented in the literature that suggests the formation of an ordered B2 matrix with disordered BCC precipitates in Al_xCoCrFeNi MPEA when the mole fraction of Al, x > 0.8 (Sreeramagiri and Balasubramanian, 2022). Consequently, the phase constitution of the MPEA is considered to be liquid at temperature (T) > 1673 K and solid at T < 1600 K, with the co-existence of both phases between this temperature range. Importantly, this information from Scheil simulations is replicated by linear and polynomial functions (Eqs 5 and 6) by identifying the best fits to embed the phase fractions as user-defined functions (UDFs) and predict the volume fraction of any constituent [solid (f_S)] phase as a function of temperature, herein obtained from the computational toolkit.

${\mathrm{F}\mathrm{o}\mathrm{r}\left(1600\mathrm{K}<T\le 1636.73\mathrm{K}\right),f}_S=12.95558-0.00775\times T,(5)$

${\mathrm{F}\mathrm{o}\mathrm{r}\left(1636.73\mathrm{K}<T\le 1673\mathrm{K}\right),f}_S=11416.32936-22.18327\times T+0.01435\times T^2-3.09044\times {10}^{-6}\times T^3.(6)$

A grid independence examination is performed to probe the effect of mesh size on the accuracy of the CFD predictions, with one low and two high-density meshes to evaluate the resultant (peak) temperatures, as displayed in Figure 2A. A mesh containing 137,500 cells and 420,500 faces, which suitably estimates the highest recorded peak temperature for a beam speed of 333 mm/s, is employed for all the analyses on the AlCoCrFeNi MPEA (Figure 1A). The model is validated by prior experimental measurements (Jamshidinia et al., 2013) of a Ti–6Al–4V alloy processed by varying the beam scan speeds at 100, 300, and 500 mm/s. Simulations on Ti–6Al–4V using the aforementioned models and the properties reported in the literature (Yang et al., 2021) reveal the corresponding melt pool widths for three different beam speeds 100, 300, and 500 mm/s to be 0.7645, 0.718, and 0.662 mm, in agreement with experiments, as shown in Figure 2B. The invariant input conditions considered together with the four different scan speeds, viz., 333 mm/s, 500 mm/s, 700 mm/s, and 1,000 mm/s, are listed in Table 1.

FIGURE 2

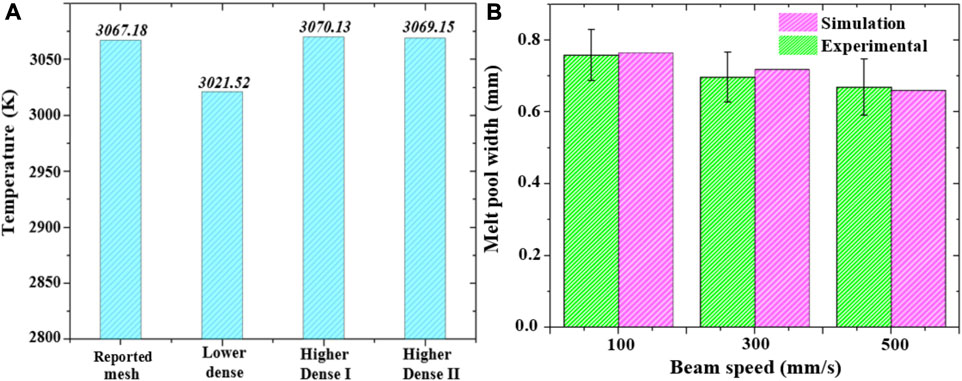
FIGURE 2. (A) The grid independence study on three different mesh sizes for AlCoCrFeNi MPEA suggests that a higher density mesh yields accurate results, which we choose for further analyses. (B) The melt pool widths for different beam scanning speeds, as predicted from the simulations for Ti-6Al-4V, when compared against experimental reports, validate the accuracy of the model (Jamshidinia et al., 2013).

Figure 3 elucidates the effect of scan speed on the temperature and enthalpy profiles resulting from laser irradiation on the top surface (for X-Z plane at Y = 5.07 mm) over an orthogonal section of the X-Y plane at Z = 2.5 mm. Note that the UDFs are integrated to predict the solid/liquid phases as a function of the temperature at any spatial location and at a given time instant. The computational results suggest that the melt assumes a notably high temperature of ∼3,067.18 K at a scanning speed of 333 mm/s (Figure 3A). The predictions assert that the maximum temperature experienced by the alloy melt varies almost linearly as a function of scan speed, with the lowest peak temperature of ∼1769.8 K occurring at the highest speed of 1,000 mm/s, a marked difference of ∼60% across the scan speed limits imposed on this CFD model. CALPHAD results corroborate that the AlCoCrFeNi MPEA induces a liquid phase upon heating (melting temperature) at 1673 K, which is close to the peak temperature at 1,000 mm/s. The contribution of superheating effects due to rapid heating (Sreeramagiri et al., 2021) in LBAM can result in an upward shift in the melting point, producing an improper melting of all the powder at this peak temperature. In consequence, the alloy fabricated at 1,000 mm/s using 200 W realizes defects, such as lack of fusion and un/under-melted powder, causing unanticipated failures in the fabricated part. Thus, a scan speed of <1,000 mm/s for the specified laser power and geometry can ensure complete melting and manufacture of potentially high-quality specimens.

FIGURE 3

FIGURE 3. (A) The cross-sectional and (B) mid-plane temperature contours during laser melting reveal the effect of speed on the peak temperature experienced during LBAM of AlCoCrFeNi MPEA. The slowest beam produces the highest peak temperature as well as the widest and longest melt pool. The variable “time” merely indicates the time instant of the simulation when the snapshot of the molten pool at the mid-plane is recorded.

The geometric dimensions of the melt pool, that is, its width and depth, provide insights into the probable defects, such as balling, and assist in tuning the laser power to achieve a continuous melt pool. In particular, the laser power and the scan speed define the stability and size of the melt pool. These two aspects of the melt pool underline the geometry and, consequently, the balling in L-PBF (Hussain et al., 2020; Hussain et al., 2022). One can select the layer height during deposition based on the depth of the melt pool and the hatch distance based on the width. In addition to the dependence of the peak temperature and enthalpy on the scanning speed displayed in Figure 4A, we present the variations in depth, width, and length of the melt pool as a function of the scan speed in Figure 4B. The predictions substantiate that an oval-shaped melt pool develops on the X-Y plane, with the depth and width decreasing with increasing scan speeds. The deepest (0.185 mm) melt pool and the longest tail (1.01 mm) are noted at 333 mm/s. Furthermore, at that scan speed (333 mm/s), the melt pool is the widest, which is attributed to the prolonged exposure and relatively higher thermal energy input. Catechizing Figure 4B yields a linear relationship between the scan speed and width/depth/length of the melt pool. This correlation can be leveraged to predict the width and depth of the melt pool and preferentially select the hatch distance and the layer height for a specific scan speed and a given laser power. Additionally, a tailing effect is evident due to heat trapping in the solidified region, in concurrence with the literature.

FIGURE 4

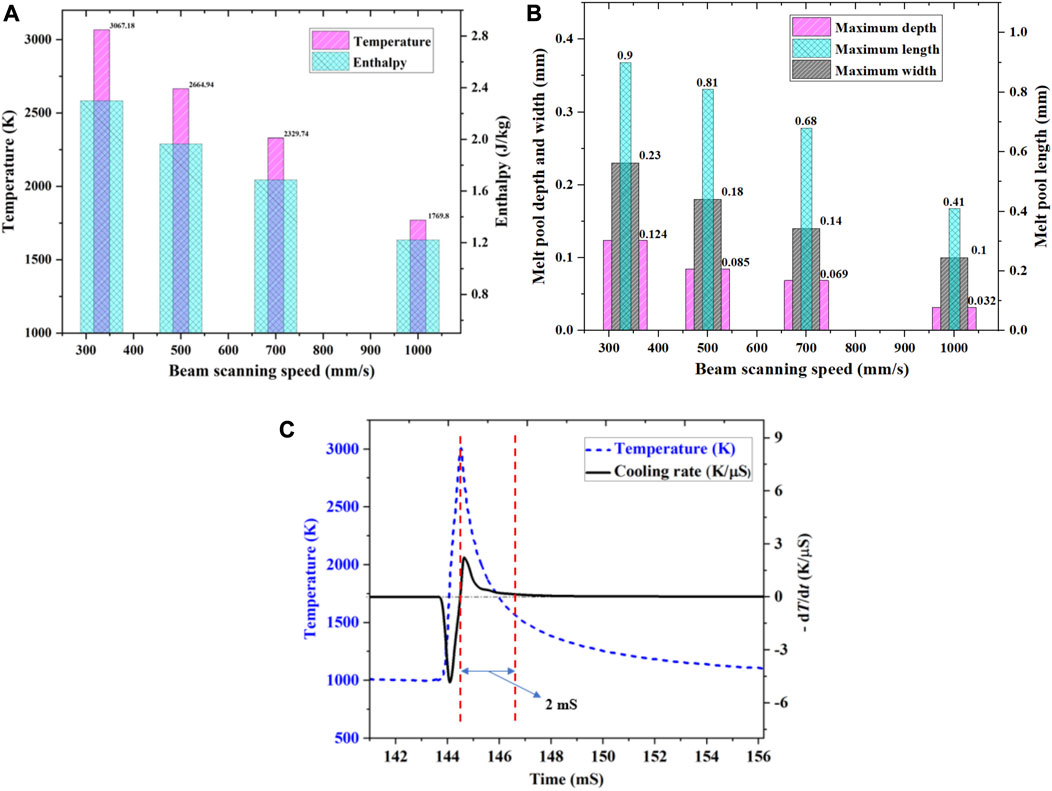
FIGURE 4. The variation with the increasing laser beam scanning speed (mm/s) of (A) the peak temperature and enthalpy and (B) the maximum width, depth, and length of the melt pool (mm) indicate that these thermal and geometric properties vary linearly with the scan speed. The peak temperatures imply that a speed of 1,000 mm/s will produce under/un-melted powder in the deposit as it is in the neighborhood of the melting point of the MPEA. The results also provide insights into the selection of hatch distance and layer thickness for a specified laser power during processing. (C) Prediction of the cooling rate (CR) at a point on the top surface at a beam scanning speed of 333 mm/s. The temperature distribution suggests that the MPEA transitions from melt to solid in 0.002 s with a cooling rate of ∼7 × 10⁵ K/s for improved fabricability. A relatively low cooling rate is realized as a consequence of preheating the substrate in the simulations. The solidus temperature is considered to evaluate the CR because, post-solidification, the role of the CR is of less significance.

The cooling rates (CRs) that the MPEAs are subjected to during synthesis drive the lattice distortions, resulting in significant variations in the structural properties (Roy et al., 2021b; Sreeramagiri et al., 2021). Literature on AlCoCrFeNi MPEAs suggests that a relatively higher cooling rate stimulates severe lattice distortion, which improves the elastic modulus at the expense of ductility (Roy et al., 2021b; Sreeramagiri et al., 2021). Figure 4C reproduces the variation of temperature at the mid-point on the laser-irradiated surface, recorded immediately before melting and after solidification, as a function of time for 333 mm/s scan speed. The computations account for temperatures up to 1600 K, the solidus temperature of the alloy per the Scheil simulations, as the CR during solidification suggests reasons for most of the aforementioned artifacts. On the other hand, the CR post-solidification has minimal influence on the microstructure, as B2/BCC are the primary phases in this alloy, and no additional phase precipitates in the solid when cooling, specifically at such high cooling rates. Furthermore, the effects of post-solidification heating and cooling cycles on the microstructures are significant when processing a multi-layer deposit and are beyond the scope of this study. Evaluation of CRs under these conditions implies that the MPEA cools from melt to solid (∼3067 K–1600 K) in 0.002 s with a CR of 7 × 10⁵ K/s (Roy et al., 2021b; Sreeramagiri et al., 2021). A relatively lower order is noted for the CR from the simulations as compared to the actual CRs experienced in LBAM (∼10⁶ K/s) because of the preheating of the substrate at ∼1000 K and the lower scan speed considered. Preheating the substrate results in a relatively improved fabricability of the MPEA using powder bed fusion (PBF)-based LBAM.

In summary, the LBAM synthesis of AlCoCrFeNi MPEA is mimicked using a CFD model to investigate the effects of process parameters on key thermal properties, such as peak temperatures, melt pool widths, and cooling rates. A Gaussian moving laser is used as a heat source, and the thermal variations in the model are defined by UDFs. The latter embed information on solid/liquid phase fraction as a function of temperature into the simulations. The phase transformation data are obtained from materials thermodynamics, viz., CALPHAD/Scheil simulations, to accurately predict the solid/liquid phase fraction at any given location and time. The results corroborate that for a specified laser power, the scan speed employed during LBAM drives the peak temperatures recorded in the melt pool; for the synthesis of AlCoCrFeNi MPEA, the highest peak temperature of 3067 K is realized at the lowest scan speed of 333 mm/s. The peak temperatures are found to decrease linearly with increasing scan speeds. Additionally, the melt pool width and depth, as predicted from the model, can assist in the selective implementation of process parameters, such as hatch distance and layer thickness, during processing. Lastly, quantifying the peak temperatures in congruence with the solidus temperatures indicates a cooling rate of ∼7 × 10⁵ K/s. We attribute the relatively low cooling rate in a PBF platform to the preheated substrate, which is required for good fabricability of the multicomponent alloy.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

CD: formal analysis, investigation, methodology, visualization, and writing—original draft. PS: formal analysis, investigation, visualization, and writing—review and editing. GB: conceptualization, funding acquisition, project administration, resources, supervision, and writing—review and editing. All authors contributed to the article and approved the submitted version.

Funding

The simulations were performed on the Lehigh University LTS computing cluster, Hawk, acquired through the National Science Foundation (NSF) award OAC-2019035. The research was supported by the NSF award # CMMI-1944040.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Andersson, J. O., Helander, T., Höglund, L., Shi, P., and Sundman, B. (2002). Thermo-Calc and DICTRA, computational tools for materials science. Calphad 26, 273–312. doi:10.1016/s0364-5916(02)00037-8

CrossRef Full Text | Google Scholar

Cho, W. I., Na, S. J., Thomy, C., and Vollertsen, F. (2012). Numerical simulation of molten pool dynamics in high power disk laser welding. J. Mater. Process. Technol. 212, 262–275. doi:10.1016/j.jmatprotec.2011.09.011

CrossRef Full Text | Google Scholar

Choi, J., Han, L., and Hua, Y. (2005). Modeling and experiments of laser cladding with droplet injection. J. Heat Transf. 127, 978–986. doi:10.1115/1.2005273

CrossRef Full Text | Google Scholar

Hu, X., Nycz, A., Lee, Y., Shassere, B., Simunovic, S., Noakes, M., et al. (2019). Towards an integrated experimental and computational framework for large-scale metal additive manufacturing. Mater. Sci. Eng. 761, 138057. doi:10.1016/j.msea.2019.138057

CrossRef Full Text | Google Scholar

Hussain, S., Alagha, A. N., and Zaki, W. (2022). Imperfections Formation in thin layers of NiTi triply periodic minimal surface lattices fabricated using laser powder bed fusion. Materials 15 (2022), 7950. doi:10.3390/ma15227950

PubMed Abstract | CrossRef Full Text | Google Scholar

Hussain, S., Alagha, A. N., and Zaki, W. (2020). “Volume 3: advanced materials: design, processing, characterization and applications,” in Proceedings of the ASME 2022 International Mechanical Engineering Congress and Exposition: advances in Aerospace Technology, Columbus, Ohio, USA, October 30-November 3, 2022 (ASME).

Google Scholar

Jamshidinia, M., Kong, F., and Kovacevic, R. (2013). Numerical modeling of heat distribution in the electron beam Melting® of Ti-6Al-4V. J. Manuf. Sci. Eng. Trans. ASME 135, 061010. doi:10.1115/1.4025746

CrossRef Full Text | Google Scholar

Joress, H., Decost, B. L., Sarker, S., Braun, T. M., Jilani, S., Smith, R., et al. (2020). A high-throughput structural and electrochemical study of metallic glass formation in Ni–Ti–Al. ACS Comb. Sci. 22, 330–338. doi:10.1021/acscombsci.9b00215

PubMed Abstract | CrossRef Full Text | Google Scholar

Karlsson, D., Marshal, A., Johansson, F., Schuisky, M., Sahlberg, M., Schneider, J. M., et al. (2019). Elemental segregation in an AlCoCrFeNi high-entropy alloy – a comparison between selective laser melting and induction melting. J. Alloys Compd. 784, 195–203. doi:10.1016/j.jallcom.2018.12.267

CrossRef Full Text | Google Scholar

Khakurel, H., Taufique, M. F. N., Roy, A., Balasubramanian, G., Ouyang, G., Cui, J., et al. (2021). Machine learning assisted prediction of the Young’s modulus of compositionally complex alloys. Sci. Rep. 11, 1–10. doi:10.1038/s41598-021-96507-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Lankalapalli, K. N., Tu, J. F., and Gartner, M. (1996). A model for estimating penetration depth of laser welding processes. J. Phys. D 29, 1831–1841. doi:10.1088/0022-3727/29/7/018

CrossRef Full Text | Google Scholar

Liu, C., Wu, B., and Zhang, J. X. (2010). Numerical investigation of residual stress in thick titanium alloy plate joined with electron beam welding. Metallurgical Mater. Trans. B 41, 1129–1138. doi:10.1007/s11663-010-9408-y

CrossRef Full Text | Google Scholar

Michopoulos, J. G., Iliopoulos, A. P., Steuben, J. C., Birnbaum, A. J., and Lambrakos, S. G. (2018). On the multiphysics modeling challenges for metal additive manufacturing processes. Addit. Manuf. 22, 784–799. doi:10.1016/j.addma.2018.06.019

CrossRef Full Text | Google Scholar

Moraitis, G. A., and Labeas, G. N. (2008). Residual stress and distortion calculation of laser beam welding for aluminum lap joints. J. Mater. Process. Technol. 198, 260–269. doi:10.1016/j.jmatprotec.2007.07.013

CrossRef Full Text | Google Scholar

Qi, H., Mazumder, J., and Ki, H. (2006). Numerical simulation of heat transfer and fluid flow in coaxial laser cladding process for direct metal deposition. J. Appl. Phys. 100, 024903. doi:10.1063/1.2209807

CrossRef Full Text | Google Scholar

Rahman, M. S., Schilling, P. J., Herrington, P. D., and Chakravarty, U. K. (2019). Thermofluid properties of Ti-6Al-4V melt pool in powder-bed electron beam additive manufacturing. J. Eng. Mater. Technol. Trans. ASME 141, 041006. doi:10.1115/1.4043342

CrossRef Full Text | Google Scholar

Rickman, J. M., Chan, H. M., Harmer, M. P., Smeltzer, J. A., Marvel, C. J., Roy, A., et al. (2019). Materials informatics for the screening of multi-principal elements and high-entropy alloys. Nat. Commun. 10, 1–10. doi:10.1038/s41467-019-10533-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Roberts, I. A., Wang, C. J., Esterlein, R., Stanford, M., and Mynors, D. J. (2009). A three-dimensional finite element analysis of the temperature field during laser melting of metal powders in additive layer manufacturing. Int. J. Mach. Tools Manuf. 49, 916–923. doi:10.1016/j.ijmachtools.2009.07.004

CrossRef Full Text | Google Scholar

Roy, A., Babuska, T., Krick, B., and Balasubramanian, G. (2020). Machine learned feature identification for predicting phase and Young's modulus of low-medium- and high-entropy alloys. Scr. Mater. 185, 152–158. doi:10.1016/j.scriptamat.2020.04.016

CrossRef Full Text | Google Scholar

Roy, A., and Balasubramanian, G. (2021). Predictive descriptors in machine learning and data-enabled explorations of high-entropy alloys. Comput. Mater. Sci. 193, 110381. doi:10.1016/j.commatsci.2021.110381

CrossRef Full Text | Google Scholar

Roy, A., Munshi, J., and Balasubramanian, G. (2021a). Low energy atomic traps sluggardize the diffusion in compositionally complex refractory alloys. Intermet. (Barking) 131, 107106. doi:10.1016/j.intermet.2021.107106

CrossRef Full Text | Google Scholar

Roy, A., Sreeramagiri, P., Babuska, T., Krick, B., Ray, P. K., and Balasubramanian, G. (2021b). Lattice distortion as an estimator of solid solution strengthening in high-entropy alloys. Mater. Charact. 172, 110877. doi:10.1016/j.matchar.2021.110877

CrossRef Full Text | Google Scholar

Sreeramagiri, P., and Balasubramanian, G. (2022). Directed energy deposition of multi-principal element alloys. Front. Mater. 9, 825276. doi:10.3389/fmats.2022.825276

CrossRef Full Text | Google Scholar

Sreeramagiri, P., Bhagavatam, A., Ramakrishnan, A., Alrehaili, H., and Dinda, G. P. (2020). Design and development of a high-performance Ni-based superalloy WSU 150 for additive manufacturing. J. Mater. Sci. Technol. 47, 20–28. doi:10.1016/j.jmst.2020.01.041

CrossRef Full Text | Google Scholar

Sreeramagiri, P., Roy, A., and Balasubramanian, G. (2021). Effect of cooling rate on the phase formation of AlCoCrFeNi high-entropy alloy. J. Phase Equilibria Diffusion 42, 772–780. doi:10.1007/s11669-021-00918-5

CrossRef Full Text | Google Scholar

Wang, L., Felicelli, S., Gooroochurn, Y., Wang, P. T., and Horstemeyer, M. F. (2008). Optimization of the LENS® process for steady molten pool size. Mater. Sci. Eng. 474, 148–156. doi:10.1016/j.msea.2007.04.119

CrossRef Full Text | Google Scholar

Wang, R., Lei, Y., and Shi, Y. (2011). Numerical simulation of transient temperature field during laser keyhole welding of 304 stainless steel sheet. Opt. Laser Technol. 43, 870–873. doi:10.1016/j.optlastec.2010.10.007

CrossRef Full Text | Google Scholar

Wen, S., and Shin, Y. C. (2010). Modeling of transport phenomena during the coaxial laser direct deposition process. J. Appl. Phys. 108, 044908. doi:10.1063/1.3474655

CrossRef Full Text | Google Scholar

Yang, X., Barrett, R. A., Tong, M., Harrison, N. M., and Leen, S. B. (2021). Towards a process-structure model for Ti-6Al-4V during additive manufacturing. J. Manuf. Process. 61, 428–439. doi:10.1016/j.jmapro.2020.11.033

CrossRef Full Text | Google Scholar

Zhang, F., Chen, L., and Bhattacharyya, D. (2020). In situ synchrotron and neutron characterization of additively manufactured alloys. JOM 73, 174–176. doi:10.1007/s11837-020-04489-7

CrossRef Full Text | Google Scholar