Deep Heating of a Snowpack by Solar Radiation

The observed gradual change in the Earth’s climate most noticeably affects the snow cover and ice sheets in the polar regions, especially during the long polar summer, when solar radiation leads to considerable increase in temperature and partial melting at some distance from the snow or ice surface. This effect, which in the polar regions is more pronounced in the snow cover, deserves serious attention as an important geophysical problem. In this article, for the first time, a theoretical analysis is made of the conditions under which the absorption of directional radiation penetrating a weakly absorbing scattering medium has a maximum at some distance from the illuminated surface. It is shown that the maximum absorption of radiation inside an optically thick medium exists only at illumination angles less than 60° from the normal. An analytical solution was obtained that gives both the magnitude of this maximum absorption and its depth below the illuminated surface. Calculations of solar radiation transfer and heat propagation in the snow layer are also performed. Various experimental data on the ice absorption index in the visible range are taken into account when determining the optical properties of snow. To calculate the transient temperature profile in the snow layer, the heat conduction equation with volumetric absorption of radiation is solved. The boundary conditions take into account the variation of solar irradiation, convective heat transfer, and radiative cooling of snow in the infrared transparency window of the cloudless atmosphere. The calculations show that the radiative cooling should be taken into account even during the polar summer.

Introduction

In recent years, there has been a marked melting of snow and ice in the polar and circumpolar regions, which is a significant factor in overall climate change (Barry and Hall-McKim 2018; Kokhanovsky and Tomasi 2020). One of the problems deserving special attention is the solar heating and even melting of snow at a depth below the surface of the snow cover. This effect was probably first discussed by Brandt and Warren (1993) and the term “solid-state greenhouse” was suggested for this phenomenon which was discussed also by Liston and Winther (2005). The physical explanation for this effect, typical of a long polar summer, is based on the interaction of two factors. First of all, it is the very weak absorption of visible radiation by the ice particles that form the snow. Therefore, a part of the visible solar radiation is absorbed several centimeters from the surface of the snow cover (Kokhanovsky, 2021a; 2021b). The absorption maximum turns out to be at some distance from the surface, and a special attention is paid to this issue in the article. Second, due to the low thermal conductivity of snow, much of this heat does not escape to the surface. This heat is continuously transferred by heat conduction to a considerable depth, where it accumulates and can even lead to snow melting away from the surface, which is usually cooled by convective heat transfer to the cold air above snow, as well as by radiative cooling in the infrared transparency window of the cloudless atmosphere.

Let us first consider the conditions under which the absorption maximum of the shortwave external radiation is located at some distance from the surface of the scattering medium illuminated by the directional radiation. To solve this problem, we can use the approach for arbitrary oblique illumination proposed in (Dombrovsky and Randrianalisoa 2018) and used in (Dombrovsky et al., 2019) to calculate the radiative transfer in a layer of snow. The computational results obtained by Dombrovsky et al. (2019) make clear the role of convective cooling or heating of snow, mid-infrared radiative cooling of snow surface, and continuous heating of deep snow layers due to heat conduction. Some numerical results for the effect of a sloping snow surface on solar heating of snow were also obtained.

In the layer of isotropic snow, the general radiative transfer equation (RTE) is as follows (Dombrovsky and Baillis 2010; Howell et al., 2021; Modest and Mazumder 2021):

$\mathbf{\Omega }\nabla I_{\lambda }\left(\mathit{r},\mathbf{\Omega }\right)+{\beta }_{\lambda }\left(\mathit{r}\right)I_{\lambda }\left(\mathit{r},\mathbf{\Omega }\right)=\frac{{\sigma }_{\lambda }\left(\mathit{r}\right)}{4\pi }\underset{\left(4\pi \right)}{{\displaystyle \int }}{I}_{\lambda }\left(\mathit{r},\mathbf{\Omega }\prime \right) {\Phi }_{\lambda }\left(\mathit{r},\mathbf{\Omega }\mathit{\prime }\times \mathbf{\Omega }\right) d\mathbf{\Omega }\mathit{\prime }(1)$

where $I_{\lambda }$ is the spectral radiation intensity at point $\mathit{r}$ in direction $\mathbf{\Omega }$, ${\beta }_{\lambda }={\alpha }_{\lambda }+{\sigma }_{\lambda }$ is the extinction coefficient, ${\alpha }_{\lambda }$ and ${\sigma }_{\lambda }$ are the coefficients of absorption and scattering, respectively, and ${\Phi }_{\lambda }$ is the scattering phase function. The thermal radiation of snow in the middle-infrared is responsible for the so-called radiative cooling. Obviously, this radiation is not contained in Eq. 1. It should be taken into account only in the boundary condition of the energy equation.

The weak absorption of short-wave radiation in an optically thick layer of snow leads to the strong multiple light scattering. As a result, it is sufficient to use the simplest transport model for the single scattering (Dombrovsky 2012):

${\Phi }_{\lambda }\left(\mathit{r},{\mu }_0\right)=\left(1-{\overline{\mu }}_{\lambda }\left(\mathit{r}\right)\right)+2{\overline{\mu }}_{\lambda }\left(\mathit{r}\right)\delta \left(1-{\mu }_0\right)(2)$

where ${\mu }_0=\mathbf{\Omega }\mathit{\prime }\times \mathbf{\Omega }$ is the cosine of the angle of scattering, $\delta$ is the Dirac delta-function, and ${\overline{\mu }}_{\lambda }$ is the asymmetry factor of scattering:

${\overline{\mu }}_{\lambda }\left(\mathit{r}\right)=\frac{1}{2}\underset{-1}{\overset{1}{{\displaystyle \int }}}{\mu }_0 {\Phi }_{\lambda }\left(\mathit{r},{\mu }_0\right)d{\mu }_0(3)$

Of course, the normalization condition $\frac{1}{2}\underset{-1}{\overset{1}{{\displaystyle \int }}}{\Phi }_{\lambda }\left({\mu }_0\right) d{\mu }_0=1$ is satisfied by function (2). The transport model proved to be sufficiently accurate for many problems of radiative transfer in weakly absorbing and strongly scattering media (Dombrovsky and Baillis 2010; Dombrovsky and Lipiński 2010). Interestingly, the computational results obtained using the transport model are normally very close to those obtained with the more complex Henyey–Greenstein analytical model (Dombrovsky et al., 2011a; Dombrovsky et al., 2013). This statement is also correct in the case under study.

The transport form of the RTE, which follows from Eqs 1–3, is similar to that for a hypothetical isotropic scattering (Dombrovsky 2012; Dombrovsky 2019):

$\mathbf{\Omega }\nabla I_{\lambda }\left(\mathit{r},\mathbf{\Omega }\right)+{\beta }_{\lambda }^{\mathrm{tr}}{I}_{\lambda }\left(\mathit{r},\mathbf{\Omega }\right)=\frac{{\sigma }_{\lambda }^{\mathrm{t}\mathrm{r}}}{4\pi }{G}_{\lambda }\left(\mathit{r}\right),G_{\lambda }\left(\mathit{r}\right)=\underset{\left(4\mathrm{\pi }\right)}{{\displaystyle \int }}{I}_{\lambda }\left(\mathit{r},\mathbf{\Omega }\right) \mathrm{d}\mathbf{\Omega }(4)$

where $G_{\lambda }$ is the irradiance and the modified coefficients are:

${\sigma }_{\lambda }^{\mathrm{t}\mathrm{r}}={\sigma }_{\lambda }\left(1-{\overline{\mu }}_{\lambda }\right),{\beta }_{\lambda }^{\mathrm{t}\mathrm{r}}={\alpha }_{\lambda }+{\sigma }_{\lambda }^{\mathrm{t}\mathrm{r}}={\beta }_{\lambda }-{\sigma }_{\lambda }{\overline{\mu }}_{\lambda }(5)$

Consider a semi-infinite plane-parallel layer of a scattering medium, such as snow, illuminated directly by solar radiation. In the case of oblique incidence, the radiation field in the medium is three-dimensional. Fortunately, the 3D problem can be radically simplified. Let us note that the irradiance field in snow at illumination at the same angle relative to the normal to the surface, but at different azimuthal angle differs only in the rotation relative to the normal. As a result, the irradiance field is the same as in the case of uniform radiation along a conical surface. This cone with a vertical axis is formed by solar rays with the same zenith angle. Hence, we can solve the equivalent axisymmetric problem as it was done by Dombrovsky et al. (2011b), Dombrovsky and Randrianalisoa (2018) and Dombrovsky et al. (2019). The axial symmetry allows us to integrate the RTE over the azimuthal angle:

$\mu \frac{\partial I_{\lambda ,i}}{\partial z}+{\beta }_{\lambda }^{\mathrm{t}\mathrm{r}}{I}_{\lambda ,i}=\frac{{\sigma }_{\lambda }^{\mathrm{t}\mathrm{r}}}{2}{G}_{\lambda ,i},G_{\lambda ,i}\left(z\right)=\underset{-1}{\overset{1}{{\displaystyle \int }}}{I}_{\lambda ,i}\left(z,\mu \right) d\mu ,\mu =\cos \theta ,z>0(\mathrm{6a})$

$I_{\lambda ,i}\left(0,\mu \right)=I_{\lambda }^{\mathrm{sol}}\left({\mu }_i\right) \delta \left({\mu }_i-\mu \right),I_{\lambda ,i}\left(\infty ,-\mu \right)=0,\mu ,{\mu }_i>0(\mathrm{6b})$

where ${\mu }_i=\cos {\theta }_i$, ${\theta }_i$ is the incidence angle, $I_{\lambda }^{sol}$ is the solar radiation intensity. The diffuse radiation from the sky is relatively small, and it is neglected in boundary conditions (6b).

It is important that the radiative transfer equation is linear. This allows us to separately consider the contribution of direct radiation from the Sun and radiation scattered by the atmosphere. For the direct irradiation we have:

$\mu \frac{\partial I_{\lambda ,i}}{\partial {\tau }_{\lambda }^{\mathrm{t}\mathrm{r}}}+I_{\lambda ,i}=\frac{{\omega }_{\lambda }^{\mathrm{t}\mathrm{r}}}{2}{G}_{\lambda ,i},G_{\lambda ,i}\left({\tau }_{\lambda }^{\mathrm{t}\mathrm{r}}\right)=\underset{-1}{\overset{1}{{\displaystyle \int }}}{I}_{\lambda ,i}\left({\tau }_{\lambda }^{\mathrm{t}\mathrm{r}},\mu \right) \mathrm{d}\mu (\mathrm{7a})$

$I_{\lambda ,i}\left(0,\mu \right)=I_{\lambda }^{\mathrm{sol}}\left({\mu }_i\right)\delta \left({\mu }_i-\mu \right),I_{\lambda ,i}\left(\infty ,-\mu \right)=0,\mu ,{\mu }_i>0(\mathrm{7b})$

where ${\tau }_{\lambda }^{\mathrm{t}\mathrm{r}}\left(z\right)=\underset{0}{\overset{z}{{\displaystyle \int }}}{\beta }_{\lambda }^{\mathrm{t}\mathrm{r}}\left(z\right) dz$ is the dimensionless optical coordinate, ${\omega }_{\lambda }^{\mathrm{t}\mathrm{r}}\left(z\right)={\sigma }_{\lambda }^{\mathrm{t}\mathrm{r}}\left(z\right)/{\beta }_{\lambda }^{\mathrm{t}\mathrm{r}}\left(z\right)$ is the transport albedo. As usual, the total values of radiation intensity and irradiance are:

$I_{\lambda ,i}\left({\tau }_{\lambda }^{\mathrm{t}\mathrm{r}},\mu \right)=J_{\lambda ,i}\left({\tau }_{\lambda }^{\mathrm{t}\mathrm{r}},\mu \right)+I_{\lambda }^{sol}\left({\mu }_i\right)E_{\lambda ,i}\delta \left(\mu -{\mu }_i\right),E_{\lambda ,i}=\exp \left(-{\tau }_{\lambda }^{\mathrm{t}\mathrm{r}}/{\mu }_i\right)(8)$

$G_{\lambda ,i}\left({\tau }_{\lambda }^{\mathrm{t}\mathrm{r}}\right)=G_{\lambda ,i}^{\mathrm{d}\mathrm{i}\mathrm{f}}\left({\tau }_{\lambda }^{\mathrm{t}\mathrm{r}}\right)+I_{\lambda }^{\mathrm{s}\mathrm{o}\mathrm{l}}\left({\mu }_i\right)E_{\lambda ,i},G_{\lambda ,i}^{\mathrm{d}\mathrm{i}\mathrm{f}}=\underset{-1}{\overset{1}{{\displaystyle \int }}}{J}_{\lambda ,i} d\mu (9)$

The radiative transfer problem for the diffuse radiation component can be written as:

$\mu \frac{\partial J_{\lambda ,i}}{\partial {\tau }_{\lambda }^{\mathrm{t}\mathrm{r}}}+J_{\lambda ,i}=\frac{{\omega }_{\lambda }^{\mathrm{t}\mathrm{r}}}{2}\left(G_{\lambda ,i}^{\mathrm{d}\mathrm{i}\mathrm{f}}+I_{\lambda }^{\mathrm{s}\mathrm{o}\mathrm{l}}\left({\mu }_i\right)E_{\lambda ,i}\right)(\mathrm{10a})$

$J_{\lambda ,i}\left(0,\mu \right)=J_{\lambda ,i}\left(\infty ,-\mu \right)=0,\mu >0(\mathrm{10b})$

This problem can be further simplified because the source function in Eq. 10a is independent of $\mu$ and the two-flux (Schwarzschild–Schuster) model is applicable. The detailed analysis of this model in (Dombrovsky and Baillis 2010) showed its sufficiently high accuracy. For the considered problem of radiative transfer in a snowpack this approach was proved to be also applicable (Dombrovsky et al., 2019). The two-flux method is based on the following approximation of the diffuse radiation intensity:

$J_{\lambda ,i}\left({\tau }_{\lambda }^{\mathrm{t}\mathrm{r}},\mu \right)=\{\begin{array}{l}{J}_{\lambda ,i}^{-}\left({\tau }_{\lambda }^{\mathrm{t}\mathrm{r}}\right) \mathrm{when} -1<\mu <0\\ J_{\lambda ,i}^{+}\left({\tau }_{\lambda }^{\mathrm{t}\mathrm{r}}\right) \mathrm{when} 0<\mu <1\end{array}(11)$

Integrating Eq. 10a, one can obtain the boundary-value problem for the irradiance $G_{\lambda ,i}^{dif}=J_{\lambda ,i}^{-}+J_{\lambda ,i}^{+}$ (Dombrovsky and Baillis 2010). It the case of vertically homogeneous snow, one can obtain the analytical solution:

$G_{\lambda ,i}^{\mathrm{d}\mathrm{i}\mathrm{f}}=\frac{4{\omega }_{\lambda }^{\mathrm{t}\mathrm{r}}}{{\xi }_{\lambda }^2-1/{\mu }_i^2}\left(E_{\lambda ,i}-\frac{2+1/{\mu }_i}{2+{\xi }_{\lambda }}{E}_{\lambda }^{\mathrm{d}\mathrm{i}\mathrm{f}}\right)I_{\lambda }^{\mathrm{s}\mathrm{o}\mathrm{l}}\left({\mu }_i\right)(\mathrm{12a})$

$E_{\lambda }^{\mathrm{d}\mathrm{i}\mathrm{f}}=\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\xi }_{\lambda }{\tau }_{\lambda }^{\mathrm{t}\mathrm{r}}\right),{\xi }_{\lambda }=2\sqrt{1-{\omega }_{\lambda }^{\mathrm{t}\mathrm{r}}}\ne 1/{\mu }_i(\mathrm{12b})$

where ${\mu }_i$ is a parameter. There are two different exponential functions in Eq. 12a: $E_{\lambda ,i}$ is related to the not-scattered collimated radiation, whereas $E_{\lambda }^{dif}$ corresponds to the diffuse radiation. It is not difficult to see that the depth of propagation of collimated radiation is smaller than that of the diffuse one when ${\omega }_{\lambda }^{\mathrm{t}\mathrm{r}}>0.75$. This makes clear the evolution of the radiation field with the depth. After entering a strongly scattering medium, the directional solar radiation in the vicinity of snow surface is converted into diffuse (but not isotropic) radiation. Due to multiple scattering, absorption of diffuse radiation is enhanced in a medium with a very small absorption coefficient. As a result of this absorption, the radiation flux decreases, and with it the absorbed power of radiation also decreases. The absorbed radiation power is determined using the calculated irradiance profiles for direct solar radiation:

$P\left(z\right)=\underset{{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}}{\overset{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{{\displaystyle \int }}}p\left(\lambda ,z\right)\mathrm{d}\lambda ,p\left(\lambda ,z\right)={\alpha }_{\lambda }{G}_{\lambda ,i}\left(z\right)(13)$

where ${\lambda }_{\min }$ and ${\lambda }_{\max }$ are the boundaries of the main wavelength range that contributes to the radiative transfer in the layer.

Absorption Maximum in a Scattering Medium

In the case of an optically thick homogeneous medium layer, the position of the maximum (along the optical coordinate ${\tau }_{\lambda }^{\mathrm{t}\mathrm{r}}$) of the spectral component of the absorbed radiation energy, $p\left(\lambda ,{\tau }_{\lambda }^{\mathrm{t}\mathrm{r}}\right)$, inside the layer is determined from the condition $\frac{d{\overline{G}}_{\lambda ,i}}{d{\tau }_{\lambda }^{\mathrm{t}\mathrm{r}}}=0$, where

${\overline{G}}_{\lambda ,i}\left({\tau }_{\lambda }^{\mathrm{t}\mathrm{r}}\right)=E_{\lambda ,i}+\frac{4{\omega }_{\lambda }^{\mathrm{t}\mathrm{r}}}{{\xi }_{\lambda }^2-1/{\mu }_i^2}\left(E_{\lambda ,i}-\frac{2+1/{\mu }_i}{2+{\xi }_{\lambda }}{E}_{\lambda }^{\mathrm{d}\mathrm{i}\mathrm{f}}\right)(14)$

It the case of a strongly scattering medium, it follows that the maximum of the absorbed radiation power occurs at:

${\tau }_{\lambda ,\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{t}\mathrm{r}}={\mu }_i\ln \left(\frac{2{\mu }_i-1}{{\xi }_{\lambda }\left(2-{\xi }_{\lambda }\right)}\right)\text{when}{\xi }_{\lambda }\ll 1/{\mu }_i(15)$

The value ${\omega }_{\lambda }^{\mathrm{t}\mathrm{r}}$ was excluded using the formula $4{\omega }_{\lambda }^{\mathrm{t}\mathrm{r}}=4-{\xi }_{\lambda }^2$. Equation 15 makes sense only when ${\mu }_i>0.5\left({\theta }_i<60°\right),$ but this restriction suits us fine. The formal use of this equation may give zero or negative values of ${\tau }_{\lambda ,max}^{\mathrm{t}\mathrm{r}}$. The latter means that there is no maximum of absorbed power inside the medium layer at the angle of incidence less than $60°$ (e.g., at the Sun in the zenith). The condition of ${\tau }_{\lambda ,max}^{\mathrm{t}\mathrm{r}}=0$ gives the boundary of the region of $\left({\omega }_{\lambda }^{\mathrm{t}\mathrm{r}},{\mu }_i\right)$ where the maximum of the absorbed radiation power exists at some distance under the irradiated surface of the medium layer. This boundary can be obtained analytically as a solution for the second-order algebraic equation:

${\xi }_{\lambda }^2-2{\xi }_{\lambda }-\left(2{\mu }_i-1\right)=0(16)$

The resulting solution is as follows:

${\xi }_{\lambda }=1-\sqrt{2\left(1-{\mu }_i\right)}(17)$

Obviously, the deepest penetration of the collimated radiation into the medium takes place at the normal incidence $\left({\mu }_i=1\right)$ when Eq. 17 gives ${\xi }_{\lambda }=1$ and ${\omega }_{\lambda }^{\mathrm{t}\mathrm{r}}=0.75$. The large boundary value of transport albedo shows that the internal maximum of absorption takes place for highly-scattering media only. The results of calculations in the most interesting range of $0\le {\theta }_i\le 45°$ are presented in Figure 1, where the curve ${\omega }_{\lambda }^{\mathrm{t}\mathrm{r}}\left({\theta }_i\right)$ separates the regions corresponding to the absorption maximum directly at the surface of the illuminated medium and below this surface. Interestingly, the absorption maximum can occur only at a distance from the irradiated surface when the angle of incidence is less than 60^o even the case of a weakly scattering medium.

Figure 1

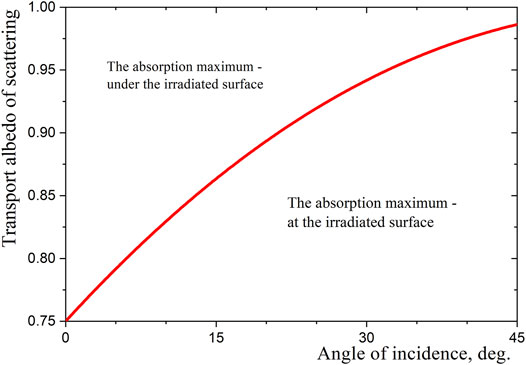
Figure 1. Predominant surface or internal absorption of collimated radiation (regions below and above the line).

It is also interesting to calculate the ratio of the maximum local absorption of radiation to that on the surface of the medium illuminated along the normal:

${\overline{p}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left({\omega }_{\lambda }^{\mathrm{t}\mathrm{r}}\right)=\frac{\left(1+\zeta \right)\left(2+{\xi }_{\lambda }\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\tau }_{\lambda ,\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{t}\mathrm{r}}\right)-3\zeta \mathrm{e}\mathrm{x}\mathrm{p}\left(-{\xi }_{\lambda }{\tau }_{\lambda ,\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{t}\mathrm{r}}\right)}{2+{\xi }_{\lambda }-\zeta \left(1-{\xi }_{\lambda }\right)},\zeta =4{\omega }_{\lambda }^{\mathrm{t}\mathrm{r}}/\left({\xi }_{\lambda }^2-1\right)(18)$

where ${\tau }_{\lambda ,max}^{\mathrm{t}\mathrm{r}}$ is determined by Eq. 15. The increase at the optical depth ${\tau }_{\lambda ,max}^{\mathrm{t}\mathrm{r}}$ where the absorption maximum is located, as well as the relative value of ${\overline{p}}_{max}$ of this maximum for media with high values of the transport albedo of single scattering ${\omega }_{\lambda }^{\mathrm{t}\mathrm{r}}$ is shown in Figure 2. It can be seen that the effect of deep absorption of radiation is most pronounced for media with ${\omega }_{\lambda }^{\mathrm{t}\mathrm{r}}>0.99$. For example, when ${\omega }_{\lambda }^{\mathrm{t}\mathrm{r}}=0.999$9, the absorption maximum is at the optical depth ${\tau }_{\lambda ,max}^{\mathrm{t}\mathrm{r}}=3.23$ and its relative value ${\overline{p}}_{max}=1.85$. This seemingly exotic situation takes place for pure snow in the visible part of the solar spectrum. Against this background, the application of Bouguer’s law in some publications on radiation propagation in scattering and weakly absorbing media looks especially inappropriate.

Figure 2

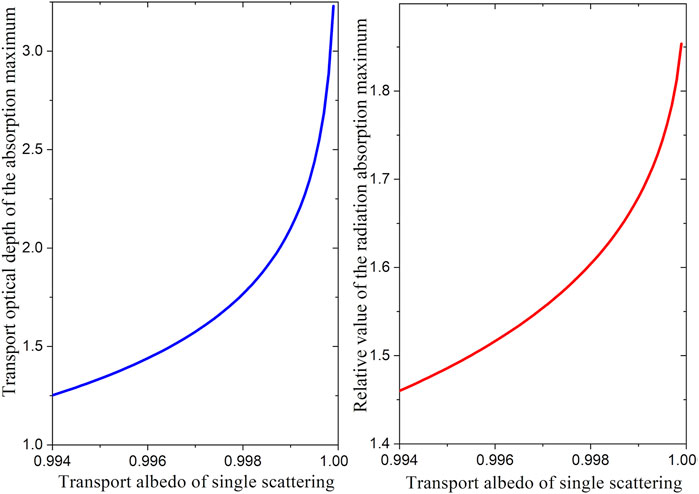
Figure 2. Location and magnitude of maximum absorption of directional radiation in scattering and weakly absorbing medium.

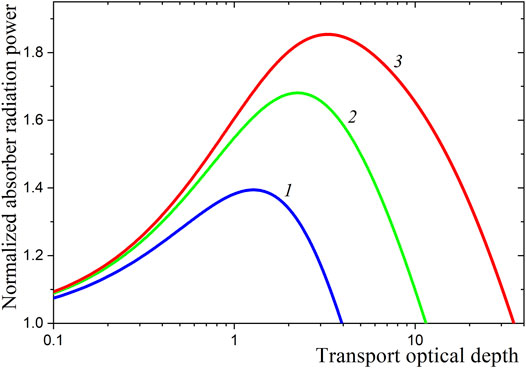
Figure 3 shows several profiles of the absorption of external radiation in highly scattering media illuminated along the normal. The absorption of radiation is large at optical depths much greater than the depth of the absorption maximum. For example, at ${\omega }_{\lambda }^{\mathrm{t}\mathrm{r}}=\mathrm{0,9999}$ even at ${\tau }_{\lambda }^{\mathrm{t}\mathrm{r}}=30$ the absorbed power of radiation is higher than near the illuminated surface.

Figure 3

Figure 3. Profiles of radiation absorption at normal incidence: 1 – ${\omega }_{\lambda }^{tr}=0.99$, 2 – $0.999$, 3 – $0.9999$.

Spectral Optical Properties OF Snow

To calculate the absorption of solar radiation in snowpack, one needs the spectral local optical properties of snow. These properties, in turn, can be determined only with the known spectral optical constants of ice as the only substance for pure snow. The optical constants are considered as real and imaginary parts of the complex index of refraction, $m\left(\lambda \right)=n\left(\lambda \right)-i\kappa \left(\lambda \right)$, where $n$ is the index of refraction and $\kappa$ is the index of absorption. The optical constants of ice obtained by Warren and Brandt (2008) are plotted in Figure 4. The presented wavelength range is wider than that required to solve the problem of radiative heating and includes the near-ultraviolet spectral range considered in (Dombrovsky et al., 2022). Note that the measurements by Picard et al. (2016) showed larger values of $\kappa$ in the wavelength range of $0.39<\lambda <0.6$ µm than those obtained by Warren and Brandt (2008) (see Figure 4). In this paper, for the first time, we compare the calculated data on the transfer of shortwave radiation in the snow layer for the different dependences of $\kappa \left(\lambda \right)$ in the visible.

Figure 4

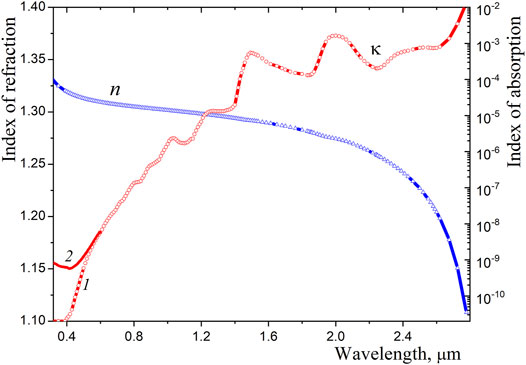
Figure 4. Spectral optical constants of pure ice. Two sets of data for the index of absorption are plotted: 1 – Warren and Brandt (2008), 2 – Picard et al. (2016).

The transition from very small values of the absorption index in the visible range to its large values in the near-infrared determines quite different optical properties of ice and snow in these spectral ranges. In particular, the high value of snow albedo in the visible range is a result of high transparency of pure ice. Note that even very small impurities such as aerosol particles may strongly affect the albedo of snow (Kokhanovsky, 2021c). In this regard, one can recommend the following recent papers: Kokhanovsky et al. (2018), He and Flanner (2020), Kokhanovsky (2021a), Pu et al. (2021). Note that the optical properties of snow polluted with atmospheric dust or soot particles (He et al., 2018; Dombrovsky and Kokhanovsky 2020a; Shi et al., 2021) do not depend on the choice between the absorption data for pure snow in the short-wave range. However, in this paper, we consider only pure snow, for which this choice may matter.

Modeling of the optical properties of various scattering media is often based on classical Mie theory (Bohren and Huffman 1998). However, in many cases one can use the geometric optics (GO), which works well for large particles, as well as some combined methods (Bi et al., 2011; Lindqvist et al., 2018; Kokhanovsky, 2021c). Such a possibility is important for ice grains of complex shape (Libois et al., 2013; Liou and Yang 2016; Ishimoto et al., 2018). Interestingly, in some cases reliable results can be obtained from physically sound approximate solutions (Kokhanovsky 2021b).

Dombrovsky et al. (2019) have considered the spherical ice grains of different size instead of nonspherical ice particles in random orientation. It was assumed that the complex shape of the ice grains has little effect on solar heating of the snowpack. The different sizes of ice grains were treated as those corresponding to different snow morphology. It was shown that the monodisperse model can be used instead of the detailed calculations for polydisperse grains. Therefore, we restrict ourselves to the calculation results for the case of monodispersed spheres with $a=100$ µm. A comparison with the Mie theory in (Dombrovsky et al., 2019) showed that the GO approximation is very accurate and one can use a relatively simple analytical solution derived in the early paper by Kokhanovsky and Zege (1995). In some cases, it is convenient to use the simplest analytical approximations for the main optical properties of weakly absorbing spherical particles suggested in (Dombrovsky 2002) and in the recent paper by Kokhanovsky (2021b). In particular, following (Dombrovsky et al., 2019) we use simpler relations in the region of weakest absorption, where a formal application of a more general solution yields erroneous results.

For calculations of radiation transport in the transport approximation we need only two dimensionless characteristics of absorption and scattering of light by individual particles: the absorption efficiency factor, $Q_a$, and the transport efficiency factor of scattering, $Q_s^{\mathrm{t}\mathrm{r}}=Q_s\times \left(1-\overline{\mu }\right),$ where $\overline{\mu }$ is the asymmetry factor of scattering. Note that the values of $Q_a$ and $Q_s$ are introduced as absorption or scattering cross sections divided by $\pi a^2$, where $a$ is the particle radius (Bohren and Huffman 1998). We consider also the transport efficiency factor of extinction, $Q_{\mathrm{t}\mathrm{r}}=Q_a+Q_s^{\mathrm{t}\mathrm{r}}$, and transport albedo, ${\omega }_{\mathrm{t}\mathrm{r}}=Q_s^{\mathrm{t}\mathrm{r}}/Q_{\mathrm{t}\mathrm{r}}$. It is known that these characteristics depend not only on optical constants but also on the dimensionless diffraction parameter $x=2\pi a/\lambda$.

Calculations show that light scattering significantly dominates over absorption in the visible range (Figure 5). This leads to the reflection of most of the shortwave solar radiation from the snow. At the same time, the remaining part of the solar radiation is scattered in a snowpack (Kokhanovsky 2021b; 2021c). As a result, visible light contributes significantly to heating the deep layers of snow, while infrared radiation from the Sun is absorbed in a relatively thin surface layer.

Figure 5

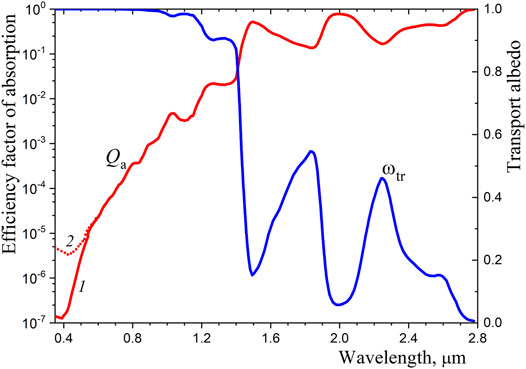
Figure 5. Efficiency factor of absorption and transport albedo of ice grain. Calculations using different data for the ice absorption index in the visible range: 1 – Warren and Brandt (2008), 2 – Picard et al. (2016).

Note that the hypothesis of independent scattering by single ice grains in snow is true (Mishchenko 2018). It is really the case because of a high porosity of snow and large sizes of ice grains. Therefore, the optical properties of snow can be calculated as follows (Dombrovsky and Baillis 2010):

$\left\{{\alpha }_{\lambda },{\sigma }_{\lambda }^{\mathrm{t}\mathrm{r}},{\beta }_{\lambda }^{\mathrm{t}\mathrm{r}}\right\}=0.75f_v\left\{Q_a,Q_{\mathrm{s}}^{\mathrm{t}\mathrm{r}},Q_{\mathrm{t}\mathrm{r}}\right\}/a(19)$

The transport albedo of scattering for snow coincides with the same value for a single ice grain: ${\omega }_{\lambda }^{\mathrm{t}\mathrm{r}}={\omega }_{\mathrm{t}\mathrm{r}}$. Returning to Figure 5, we note that the calculated value of the snow albedo in the short-wave region is very close to unity for both the absorption data (Warren and Brandt 2008) and the data (Picard et al., 2016). For example, at wavelength $\lambda =0.4$ µm in the first case we have ${\omega }_{\lambda }^{\mathrm{t}\mathrm{r}}=1.4\times {10}^{-5}$ and in the second case – $1-{\omega }_{\lambda }^{\mathrm{t}\mathrm{r}}=2.9\times {10}^{-5}$. This means that regardless of the initial absorption data, we are dealing with a deep and strong absorption maximum for the visible radiation.

Absorption of Solar Radiation in Snowpack

In this section, we limit ourselves to calculating the absorption of direct solar radiation, neglecting the relatively small contribution of radiation scattered by the atmosphere. The vertical profile of the normalized absorbed power is illustrated in Figure 6 for the normal incidence separately for the visible and near-infrared spectral ranges. It is not necessary to consider the real spectrum of solar radiation that has passed through the atmosphere in order to make a qualitative estimate. Instead, we will use the Planck spectrum at temperature $T_{sol}=6000\text{K}$. It is interesting to calculate separately the contributions of the visible and the near-infrared ranges to the absorbed power of radiation:

$\overline{P}\left(z\right)={\overline{P}}_{\mathrm{v}\mathrm{i}\mathrm{s}}\left(z\right)+{\overline{P}}_{\mathrm{n}\mathrm{i}\mathrm{r}}\left(z\right),{\overline{P}}_{\mathrm{v}\mathrm{i}\mathrm{s},\mathrm{n}\mathrm{i}\mathrm{r}}=P_{\mathrm{v}\mathrm{i}\mathrm{s},\mathrm{n}\mathrm{i}\mathrm{r}}/\underset{{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}}{\overset{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{{\displaystyle \int }}}{I}_b\left(T_{\mathrm{sol}},\lambda \right) \mathrm{d}\lambda (20)$

where ${\lambda }_{min}=0.4$ µm and ${\lambda }_{max}=2.8$ µm and $P_{vis,ni\mathrm{r}}$ is calculated using Eq. 13 for the spectral ranges 0.4–0.78 and 0.78–2.8 µm, respectively. Of course, one can use more accurate values for the conventional solar temperature and the boundaries of the visible and near-infrared ranges as it was recommended in the monograph by Kokhanovsky (2021c). However, it is not important for the presented estimations. According to (Dombrovsky et al., 2019), we introduce the normalized coordinates $f_{\text{v}}z$ and $\overline{P}/f_{\text{v}}$ in Figure 6A, where $f_v$ is the volume fraction of ice is a snow layer.

Figure 6

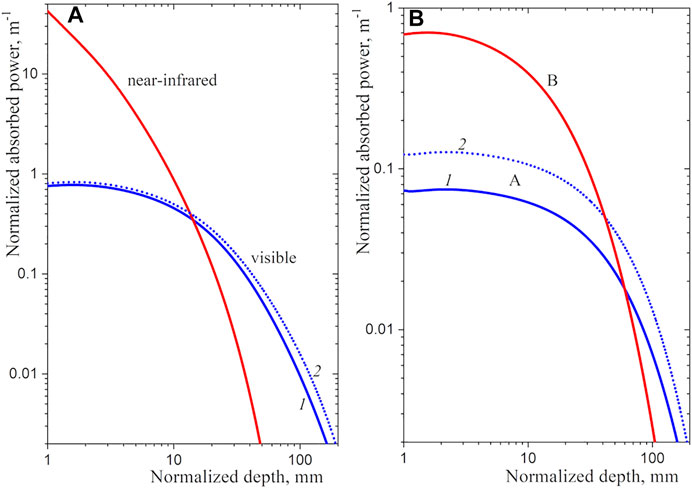
Figure 6. Contributions of different spectral ranges to the absorbed radiation power. Calculations using different data for the ice absorption index in the visible subrange A: 1 – Warren and Brandt (2008), 2 – Picard et al. (2016) are performed. Spectral ranges are as follows: left panel - visible (0.4–0.78 micron), near-infrared (0.78–2.8 micron); right panel - (A) (0.4–0.6 micron), (B) (0.6–0.78 micron).

As one might expect, infrared radiation is absorbed mostly in a thin surface layer, while visible light is absorbed almost uniformly in a relatively thick layer. The result is in good agreement with the work of Munneke et al. (2009), which discusses the deep penetration of shortwave solar radiation and its role in the thermal balance of the snow cover.

For better clarity, Figure 6B shows similar dependences for the two parts of the visible spectrum: $0.4<\lambda <0.6$ µm (A) and $0.6<\lambda <0.78$ µm (B). In the calculations for the sub-range A, different data on the ice absorption index are used, which give similar dependences of the absorbed power on depth, differing slightly only in the absolute value. As we have already discussed, the position and relative magnitude of the absorption maximum are the same for the two variants of the ice absorption index in the visible range. The calculations using the data by Picard et al. (2016) give a slightly greater absorption of the shortwave radiation.

Of course, knowing the local value of the absorbed radiation power is not enough to calculate the snow temperature. The next step in solving the problem requires the transient energy equation with appropriate initial and boundary conditions. The wide-range spectral dependence of $\kappa \left(\lambda \right)$ as given by Warren and Brandt (2008) will be used in these calculations.

Transient Heat Transfer Model

Consider now the 1D problem of heat transfer. As in (Dombrovsky and Kokhanovsky 2021), we will not consider such processes as ice sublimation and water vapor diffusion in the snow layer, which may be of interest for studying the changing microstructure of snow. The problem statement for the transient temperature field, $T\left(\mathrm{t},z\right),$ in a layer of snow is:

$\rho c\frac{\partial T}{\partial \mathrm{t}}=\frac{\partial }{\partial z}\left(k\frac{\partial T}{\partial z}\right)+P,t>\mathrm{0,0}<z<d_{\mathrm{t}\mathrm{h}}(\mathrm{21a})$

$T\left(0,z\right)=T_0\left(z\right)(\mathrm{21b})$

$z=0,-k\frac{\partial T}{\partial z}=h \left(T_{\mathrm{a}\mathrm{i}\mathrm{r}}-T\right)-\epsilon \pi \underset{{\lambda }_{\mathrm{w}1}}{\overset{{\lambda }_{\mathrm{w}2}}{{\displaystyle \int }}}{I}_b\left(T,\lambda \right) \mathrm{d}\lambda z=d_{\mathrm{t}\mathrm{h}},\frac{\partial T}{\partial z}=0(\mathrm{21c})$

where $z$ is the coordinate measured from the irradiated surface, $\rho$, $c$, and $k$ are the density, the specific heat capacity, and the thermal conductivity of snow or ice, $T_{ai\mathrm{r}}\left(\mathrm{t}\right)$ is the temperature of ambient air (outside the thermal boundary layer), and $h\left(\mathrm{t}\right)$ is the convective heat transfer coefficient. The adiabatic condition at the boundary $z=d_{\mathrm{t}h}>>d$ means that we neglect heat transfer at $z>d_{\mathrm{t}h}$. Of course, the value of $d_{\mathrm{t}h}$ increases with time and should be estimated using additional calculations. The heat transfer coefficient is determined by a wind speed. The last term in the right-hand side of the boundary condition at $z=0$ is the mid-infrared radiative cooling due to thermal radiation of snowpack or ice sheet in the atmospheric transparency window of ${\lambda }_{w1}<\lambda <{\lambda }_{w2}$ (${\lambda }_{w1}=8$ µm, ${\lambda }_{w2}=13$ µm) (Hossain and Gu 2016). The radiative cooling is limited during the night time when it is not compensated by solar mid-infrared radiation. Therefore, the coefficient $\epsilon$ varies from zero in the day time to the unity at night. The absorbed radiation power, $P\left(z\right)$, at arbitrary conditions of solar illumination should be recalculated during the combined problem solution.

The latent heat of ice melting was accounted for by an equivalent increase in the heat capacity in a narrow temperature range near the melting temperature. This technique was successfully used in (Dombrovsky et al., 2009; Dombrovsky et al. 2015; Dombrovsky et al. 2019). It is interesting that the three cited papers considered completely different problems: the first of them dealt with the solidification of core melt droplets in a severe nuclear reactor accident, the second one with the freezing and thawing of biological tissues in cryosurgery, and the third one with the melting of freezing snow under periodic solar heating.

In numerical calculations, an implicit finite-difference scheme of the second order of approximation was used. Note that the model should be generalized in the case of significant snow melt or rain over snow, as water penetrates through the snow and solidifies at a greater depth.

Analysis of Solar Heating of a Snowpack

We used the algorithm and input data from (Dombrovsky et al., 2019) to calculate the solar heating of snow. Because of the considerable uncertainty in the snow thermal conductivity (Arenson et al., 2015), there may be a systematic error. At the same time, changes in solar illumination conditions over time in the summer solstice and the local altitude of 70^o were calculated accurately and the light scattered by cloudless atmosphere was taken into account as it was done by Dombrovsky et al. (2019).

As an example, we consider the case of windless weather, when the heat transfer coefficient can be assumed to be $h=6$ W/(m² K) (Defraeye et al., 2011; Mirsadeghi et al., 2013). The temperature profiles in a snowpack calculated for the conventional first day of solar irradiation at $T_0=T_{ai\mathrm{r}}\left(0\right)=-10$°C are presented in Figure 7.

Figure 7

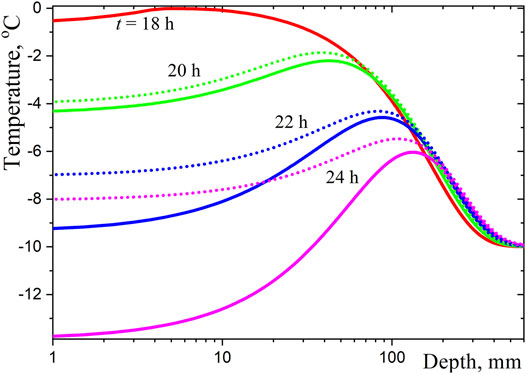
Figure 7. Typical profiles of temperature in snowpack in the evening: Solid lines—complete calculations, dotted lines—without radiative cooling.

The calculations showed that the melting temperature is reached at noon near the surface (it is not shown in the figure) and temperature maximum is shifted to the depth about 5 mm at 6 p.m. due to convective cooling (see Figure 7). Further moving of the temperature maximum to the larger depth is accompanied by cooling of the surface layer of the snow cover. Convective cooling predominates in the evening hours, and radiative cooling is strongly manifested closer to midnight. Obviously, radiative cooling under cloudless skies should be taken into account during the period of weak solar irradiation.

Following (Dombrovsky et al., 2019), similar calculations can be made for solar heating of snow, for example, over 3 days. However, the calculation of snow cover heating over many days and, even more so, over a long polar summer is associated with serious difficulties and requires the development of a special physical model. This task is beyond the scope of the present study. A simple physical estimate using the Fourier number for snow shows that it takes about 10 years for snow to warm to a depth of 100 m. Note that the heating time is directly proportional to the square of the depth and the solar heat “stored” at depth during the summer continues to spread deep into the depths even during the polar winter.

Of course, the real process is more complicated and is not reduced to simple heat conduction. It is interesting to discuss briefly the main stages of the process for the case of a very thick snow layer. Most likely, at a not very deep depth, the snow will begin to melt. The resulting water will flow down between the snow particles. This flow is very slow because of the high hydraulic resistance of the dispersed medium with small pores and water will freeze at a slightly deeper depth, where the snow temperature is noticeably lower. This is how the ice layer will start to form, probably with gas bubbles scattering the radiation (Dombrovsky and Kokhanovsky 2020b). Solar heating in several years increases the thickness of the ice layer. Over many years, conditions may develop in which ice melting will lead to the formation of a gas cavity and a lake under the ice sheet. It is possible that deep solar heating is one of the reasons (along with ice melting under pressure and geothermal heat) for the formation of some of the many discovered lakes under the Greenland and Antarctic ice sheets.

Conclusion

A theoretical analysis of the conditions under which the absorption of collimated radiation penetrating into a weakly absorbing scattering medium has a maximum at a considerable distance from the illuminated surface was presented for the first time. It is shown that the maximum absorption of radiation inside an optically thick medium exists only at illumination angles less than 60° from the normal. Both the depth at which the local absorption of solar radiation is maximum and the magnitude of this maximum are greatest at illumination along the normal. The greatest optical depth of the maximum location (by transport attenuation coefficient) is 3.23. In this case, the maximum local power of absorbed radiation energy is 85% higher than that at the illuminated surface of the medium. The obtained approximate analytical solution is general and applicable to various scattering media.

The possibility of deep heating of the pure snow cover by solar radiation during the polar summer is confirmed by calculations based on a general physical model, which is not limited to determining the solution for the absorbed radiation power. The transient problem of combined heat transfer was solved taking into account the change in the zenith angle of the Sun with time as well as the heat conduction in snow and both convective and radiative cooling of the snow surface.

The obtained numerical solution can be used for studies of the propagation of heat into the depth of the snowpack. It was shown that the computational results are not very sensitive to the choice between the published data for the absorption index of pure ice in the visible range. It is interesting that by the evening of the first sunny day, the snow temperature at a depth of 4 mm becomes about 2° higher than on the surface, and by midnight this temperature difference can reach 6°, while the zone of maximum heating shifts to a depth of about 12 cm. This process continues during the long polar summer, leading to heating and possible melting of snow at a considerable depth.

The calculations have shown that the radiative cooling of snow in the transparency window of the cloudless atmosphere should be taken into account during periods of relatively low solar illumination, even during the polar summer.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

LD and AK contributed to conception and design of the study. LD made the calculations and wrote the draft manuscript. Both authors contributed to manuscript revision, read, and approved the submitted version.

Conflict of Interest

Author AAK is employed by Brockman Consult.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

A. A. Kokhanovsky, and C. Tomasi (Editors) (2020). Physics and Chemistry of the Arctic Atmosphere (Cham (Switzerland): Springer Nature).

Google Scholar

Arenson, L. U., Colgan, W., and Marshall, H. P. Physical, thermal, and Mechanical Properties of Snow, Ice, and Permafrost. Ch. 2 in “Snow and Ice-Related Hazards, Risk and Disasters”, 35–75. New York: Academic Press (2015). doi:10.1016/B978-0-12-394849-6.00002-0

CrossRef Full Text | Google Scholar

Barry, R. G., and Hall-McKim, E. A. (2018). Polar Environments and Global Change. Cambridge (UK): Cambridge University Press.

Google Scholar

Bi, L., Yang, P., Kattawar, G. W., Hu, Y., and Baum, B. A. (2011). Scattering and Absorption of Light by Ice Particles: Solution by a New Physical-Geometric Optics Hybrid Method. J. Quantitative Spectrosc. Radiative Transfer 112 (9), 1492–1508. doi:10.1016/j.jqsrt.2011.02.015

CrossRef Full Text | Google Scholar

Bohren, C. F., and Huffman, D. R. (1998). Absorption and Scattering of Light by Small Particles. New York: Wiley.

Google Scholar

Brandt, R. E., and Warren, S. G. (1993). Solar-heating Rates and Temperature Profiles in Antarctic Snow and Ice. J. Glaciol. 39 (131), 99–110. doi:10.1017/s0022143000015756

CrossRef Full Text | Google Scholar

Defraeye, T., Blocken, B., and Carmeliet, J. (2011). Convective Heat Transfer Coefficients for Exterior Building Surfaces: Existing Correlations and CFD Modelling. Energ. Convers. Manage. 52 (1), 512–522. doi:10.1016/j.enconman.2010.07.026

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., and Baillis, D. (2010). Thermal Radiation in Disperse Systems: An Engineering Approach. New York: Begell House.

Google Scholar

Dombrovsky, L. A., Davydov, M. V., and Kudinov, P. (2009). Thermal Radiation Modeling in Numerical Simulation of Melt-Coolant Interaction. Comput. Therm. Scien 1 (1), 1–35. doi:10.1615/ComputThermalScien.v1.i1.10

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., and Kokhanovsky, A. A. (2020a). Light Absorption by Polluted Snow Cover: Internal versus External Mixture of Soot. J. Quantitative Spectrosc. Radiative Transfer 242, 106799. doi:10.1016/j.jqsrt.2019.106799

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., Kokhanovsky, A. A., and Randrianalisoa, J. H. (2019). On Snowpack Heating by Solar Radiation: A Computational Model. J. Quantitative Spectrosc. Radiative Transfer 227, 72–85. doi:10.1016/j.jqsrt.2019.02.004

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., and Kokhanovsky, A. A. (2020b). Solar Heating of Ice Sheets Containing Gas Bubbles. J. Quantitative Spectrosc. Radiative Transfer 250, 106991. doi:10.1016/j.jqsrt.2020.106991

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., and Kokhanovsky, A. A. (2021). “Solar Heating of the Cryosphere: Snow and Ice Sheets,” in Springer Series in Light Scattering. Editor A. Kokhanovsky (Cham (Switzerland): Springer Nature), 6, 53–109. doi:10.1007/978-3-030-71254-9_2

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., Nenarokomova, N. B., Tsiganov, D. I., and Zeigarnik, Y. A. (2015). Modeling of Repeating Freezing of Biological Tissues and Analysis of Possible Microwave Monitoring of Local Regions of Thawing. Int. J. Heat Mass Transfer 89, 894–902. doi:10.1016/j.ijheatmasstransfer.2015.05.117

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., and Randrianalisoa, J. H. (2018). Directional Reflectance of Optically Dense Planetary Atmosphere Illuminated by Solar Light: An Approximate Solution and its Verification. J. Quantitative Spectrosc. Radiative Transfer 208, 78–85. doi:10.1016/j.jqsrt.2018.01.016

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., Randrianalisoa, J. H., Lipiński, W., and Baillis, D. (2011a). Approximate Analytical Solution to normal Emittance of Semi-transparent Layer of an Absorbing, Scattering, and Refracting Medium. J. Quantitative Spectrosc. Radiative Transfer 112 (12), 1987–1994. doi:10.1016/j.jqsrt.2011.04.008

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., Randrianalisoa, J., Lipiński, W., and Timchenko, V. (2013). Simplified Approaches to Radiative Transfer Simulations in Laser-Induced Hyperthermia of Superficial Tumors. Comput. Therm. Scien 5 (6), 521–530. doi:10.1615/ComputThermalScien.2013008157

CrossRef Full Text | Google Scholar

Dombrovsky, L. A. (2019). “Scattering of Radiation and Simple Approaches to Radiative Transfer in Thermal Engineering and Biomedical Applications,” in Springer Series in Light Scattering. Editor A. Kokhanovsky (Cham (Switzerland): Springer Nature), 4, 71–127. doi:10.1007/978-3-030-20587-4_2

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., Solovjov, V. P., and Webb, B. W. (2011b). Attenuation of Solar Radiation by a Water Mist from the Ultraviolet to the Infrared Range. J. Quantitative Spectrosc. Radiative Transfer 112 (7), 1182–1190. doi:10.1016/j.jqsrt.2010.08.018

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., Solovjov, V. P., and Webb, B. W. (2022). Effect of Ground-Based Environmental Conditions on the Level of Dangerous Ultraviolet Solar Radiation. J. Quantitative Spectrosc. Radiative Transfer 279, 108048. doi:10.1016/j.jqsrt.2021.108048

CrossRef Full Text | Google Scholar

Dombrovsky, L. A. (2002). Spectral Model of Absorption and Scattering of thermal Radiation by Droplets of Diesel Fuel. High Temper 40 (2), 242–248. doi:10.1023/A:1015207307857

CrossRef Full Text | Google Scholar

Dombrovsky, L. A. (2012). The Use of Transport Approximation and Diffusion-Based Models in Radiative Transfer Calculations. Comput. Therm. Scien 4 (4), 297–315. doi:10.1615/ComputThermalScien.2012005050

CrossRef Full Text | Google Scholar

He, C., and Flanner, M. (2020). “Snow Albedo and Radiative Transfer: Theory, Modeling, and Parameterization,” in Springer Series in Light Scattering. Editor A. Kokhanovsky (Cham (Switzerland): Springer Nature), 5, 67–133. doi:10.1007/978-3-030-38696-2_3

CrossRef Full Text | Google Scholar

He, C., Liou, K. N., Takano, Y., Yang, P., Qi, L., and Chen, F. (2018). Impact of Grain Shape and Multiple Black Carbon Internal Mixing on Snow Albedo: Parameterization and Radiative Effect Analysis. J. Geophys. Res. Atmos. 123 (2), 1253–1268. doi:10.1002/2017JD027752

CrossRef Full Text | Google Scholar

Hossain, M. M., and Gu, M. (2016). Radiative Cooling: Principles, Progress, and Potentials. Adv. Sci. 3 (7), 1500360. doi:10.1002/advs.201500360

PubMed Abstract | CrossRef Full Text | Google Scholar

Howell, J. R., Mengüç, M. P., Daun, K., and Siegel, R. (2021). Thermal Radiation Heat Transfer. 7th Edition. New York: CRC Press.

Google Scholar

Ishimoto, H., Adachi, S., Yamaguchi, S., Tanikawa, T., Aoki, T., and Masuda, K. (2018). Snow Particles Extracted from X-ray Computed Microtomography Imagery and Their Single-Scattering Properties. J. Quantitative Spectrosc. Radiative Transfer 209, 113–128. doi:10.1016/j.jqsrt.2018.01.021

CrossRef Full Text | Google Scholar

Kokhanovsky, A. A. (2021a). Snow Optics. Cham (Switzerland): Springer Nature.

Google Scholar

Kokhanovsky, A. A. (2021b). Light Penetration in Snow Layers. J. Quantitative Spectrosc. Radiative Transfer 278, 108040. doi:10.1016/j.jqsrt.2021.108040

CrossRef Full Text | Google Scholar

Kokhanovsky, A. A. (2021c). The Broadband Albedo of Snow. Front. Environ. Sci. 9, 757575. doi:10.3389/fenvs.2021.757575

CrossRef Full Text | Google Scholar

Kokhanovsky, A. A., and Zege, E. P. (1995). Local Optical Parameters of Spherical Polydispersions: Simple Approximations. Appl. Opt. 34 (24), 5513–5519. doi:10.1364/AO.34.005513

PubMed Abstract | CrossRef Full Text | Google Scholar

Kokhanovsky, A., Lamare, M., Di Mauro, B., Picard, G., Arnaud, L., Dumont, M., et al. (2018). On the Reflectance Spectroscopy of Snow. The Cryosphere 12 (7), 2371–2382. doi:10.5194/tc-12-2371-2018

CrossRef Full Text | Google Scholar

Kuipers Munneke, P., van den Broeke, M. R., Reijmer, C. H., Helsen, M. M., Boot, W., Schneebeli, M., et al. (2009). The Role of Radiation Penetration in the Energy Budget of the Snowpack at Summit, Greenland. The Cryosphere 3 (2), 155–165. doi:10.5194/tc-3-155-2009

CrossRef Full Text | Google Scholar

Libois, Q., Picard, G., France, J. L., Arnaud, L., Dumont, M., Carmagnola, C. M., et al. (2013). Influence of Grain Shape on Light Penetration in Snow. The Cryosphere 7 (6), 1803–1818. doi:10.5194/tc-7-1803-2013

CrossRef Full Text | Google Scholar

Lindqvist, H., Martikainen, J., Räbinä, J., Penttilä, A., and Muinonen, K. (2018). Ray Optics for Absorbing Particles with Application to Ice Crystals at Near-Infrared Wavelengths. J. Quantitative Spectrosc. Radiative Transfer 217, 329–337. doi:10.1016/j.jqsrt.2018.06.005

CrossRef Full Text | Google Scholar

Liou, K.-N., and Yang, P. (2016). Light Scattering by Ice Crystals: Fundamentals and Applications. Cambridge: Cambridge University Press. doi:10.1017/CBO9781139030052

CrossRef Full Text | Google Scholar

Lipiński, W., and Dombrovsky, L. A. (2010). A Combined P1 and Monte Carlo Model for Multidimensional Radiative Transfer Problems in Scattering Media. Comput. Therm. Scien 2 (6), 549–560. doi:10.1615/ComputThermalScien.v2.i6.60

CrossRef Full Text | Google Scholar

Liston, G. E., and Winther, J.-G. (2005). Antarctic Surface and Subsurface Snow and Ice Melt Fluxes. J. Clim. 18 (10), 1469–1481. doi:10.1175/JCLI3344.1

CrossRef Full Text | Google Scholar

Mirsadeghi, M., Cóstola, D., Blocken, B., and Hensen, J. L. M. (2013). Review of External Convective Heat Transfer Coefficient Models in Building Energy Simulation Programs: Implementation and Uncertainty. Appl. Therm. Eng. 56 (1-2), 134–151. doi:10.1016/j.applthermaleng.2013.03.003

CrossRef Full Text | Google Scholar

Mishchenko, M. I. (2018). "Independent" and "dependent" Scattering by Particles in a Multi-Particle Group. OSA Continuum 1 (1), 243–260. doi:10.1364/OSAC.1.000243

CrossRef Full Text | Google Scholar

Modest, M. F., and Mazumder, S. (2021). Radiative Heat Transfer. 4th Edition. New York: Academic Press.

Google Scholar

Picard, G., Libois, Q., and Arnaud, L. (2016). Refinement of the Ice Absorption Spectrum in the Visible Using Radiance Profile Measurements in Antarctic Snow. The Cryosphere 10 (6), 2655–2672. doi:10.5194/tc-10-2655-2016

CrossRef Full Text | Google Scholar

Pu, W., Shi, T., Cui, J., Chen, Y., Zhou, Y., and Wang, X. (2021). Enhancement of Snow Albedo Reduction and Radiative Forcing Due to Coated Black Carbon in Snow. The Cryosphere 15 (5), 2255–2272. doi:10.5194/tc-15-2255-2021

CrossRef Full Text | Google Scholar

Shi, T., Cui, J., Chen, Y., Zhou, Y., Pu, W., Xu, X., et al. (2021). Enhanced Light Absorption and Reduced Snow Albedo Due to Internally Mixed mineral Dust in Grains of Snow. Atmos. Chem. Phys. 21 (8), 6035–6051. doi:10.5194/acp-21-6035-2021

CrossRef Full Text | Google Scholar

Warren, S. G., and Brandt, R. E. (2008). Optical Constants of Ice from the Ultraviolet to the Microwave: A Revised Compilation. J. Geophys. Res. 113 (D14), D14220. doi:10.1029/2007JD009744

CrossRef Full Text | Google Scholar

Nomenclature

$a$ radius of ice grain, µm

$c$ specific heat capacity, J/(kg K)

$d$ thickness, m

$E$ exponential function

$f_v$ volume fraction

$G$ spectral irradiance, W/(m² µm)

$h$ heat transfer coefficient, W/(m² K)

$I$ spectral radiation intensity, W/(m² µm)

$J$ diffuse radiation intensity, W/(m² µm)

$k$ thermal conductivity, W/(m K)

$m$ complex index of refraction

$n$ index of refraction

$P$ absorbed radiative power, W/m³

$p$ spectral radiative power, W/(m³ µm)

$Q$ efficiency factor

$T$ temperature, K or °C

$\mathrm{t}$ time, h

$x$ diffraction parameter

$z$ coordinate, m

Greek Symbols

$\alpha$ absorption coefficient, m⁻¹

$\beta$ extinction coefficient, m⁻¹

$\delta$ Dirac delta and declination of the Sun, rad

$\epsilon$ coefficient in Eq. 21c

$\zeta$ coefficient introduced by Eq. 18

$\theta$ zenith angle, rad

$\kappa$ index of absorption

$\lambda$ radiation wavelength, µm

$\mu$ cosine of an angle

$\overline{\mu }$ asymmetry factor of scattering

$\xi$ parameter introduced by Eq. 12b

ρ density, kg/m³

$\sigma$ scattering coefficient, m⁻¹

$\tau$ optical thickness

$\Phi$ scattering phase function

$\omega$ single scattering albedo

Subscripts and Superscripts

0 initial value

a radius of ice grain, µm absorption

air air

b blackbody

c critical

nir near-infrared

s scattering

sky sky

sol solar

surf surface

th thermal

tr transport

vis visible range

w spectral window

λ spectral