Laser-Induced Thermal Treatment of Superficial Human Tumors: An Advanced Heating Strategy and Non-Arrhenius Law for Living Tissues

The most interesting, but insufficiently known results obtained by the author in modeling laser-induced hyperthermia of human tumors are discussed. It is important that the traditional equation for the local bio-heat transfer does not work in superficial layers of the body. It is shown also that the classical Arrhenius law is not applicable to living tissues because of the tissue regeneration due to oxygen supplied by the arterial blood. The latter is one of the main reasons of the suggested strategy of laser heating of tumors in the therapeutic window of semitransparency when the tumor asphyxiation is considered as one of important weapons against the cancer. The other advantages of this advanced strategy of a soft thermal treatment (in few of sessions), which is painless for patients, are discussed as well. Some features of modeling various heat transfer modes are also considered. The best choice between the simplest differential models for the radiative transfer calculations is dependent of the particular problem statement. The known finite-difference or finite element algorithms can be preferable in solving transient heat transfer problems. As a rule, it depends on the shape of the computational region. It is expected that this paper will help the colleagues to overcome some typical weaknesses of computational modeling of infrared photothermal treatment of superficial tumors.

Introduction

Hyperthermia or thermal therapy, most likely, is the oldest method of treating superficial human tumors (there is documentary evidence of the use of this method in ancient Egypt around 3000 BC). With the invention of modern lasers, this method, sometimes used in combination with chemotherapy and ionizing radiation therapy (van der Zee, 2002; Camerin et al., 2005; Datta et al., 2015; Mallory et al., 2016; Peeken et al., 2017), has been fundamentally improved and continues to be successfully applied in medical practice. The essence of local tumor hyperthermia is that cancer cells are destroyed even with slight (up to 42–44°C), but prolonged overheating, while under similar and even stronger thermal conditions the healthy cells can be self-regenerated (Yarmolenko et al., 2011; Spichka et al., 2019).

The intensive development of modern technologies has led to the use of gold and composite nanoparticles in laser hyperthermia (mainly for the treatment of superficial tumors) (Huang and El-Sayed, 2010; Chatterjee et al., 2011; Bayazitoglu et al., 2013; Jague et al., 2014; Abadeer and Murphy, 2016; Kaur et al., 2016; Bucharskaya et al., 2018; Dykman and Khlebtsov, 2019; Vines et al., 2019). The implementation of such particles into biological tissues leads to a significant increase in the local absorption coefficient in one or another part of the therapeutic semitransparency window, which covers the wavelength range from about 0.6 to 1.4 μm (Cheong et al., 1990; Duck, 1990; Mobley and Vo-Dinh, 2003; Tuchin, 2007; Bashkatov et al., 2011; Jacques, 2013) and allows one to act on tissues at a certain depth under the irradiated body surface.

The possibility of using short-pulse lasers has led to the development of alternative methods of laser-induced treatment and to new difficulties in modeling processes in biological tissues, especially when nanoparticles are embedded in tissues (Jaunich et al., 2008; Muthukumaran and Mishra, 2008; Liu and Hsu, 2008; Bhuvaneswari and Wu, 2009; Ruan et al., 2010; Mishra et al., 2012; Zhang et al., 2013; Browmik et al., 2014; Randrianalisoa et al., 2014; Yakovlev et al., 2019). At the same time, a number of methodological issues that arise even with the use of continuous-wave lasers and without nanoparticles remain insufficiently clarified. As a result, even in recent publications there are physical errors in the formulation of the heat transfer problem and also not reasonable choice of the method for calculating the radiative transfer. Moreover, the kinetic models of thermal tissue injury ignore the continuous regeneration of living tissue due to oxygen supplied by erythrocytes of the arterial blood. These disadvantages not only may lead to significant errors in the calculations, but also do not make it possible to choose the right strategy for combating superficial cancerous tumors.

In this regard, the author considers the objective of the present work in a well-grounded and understandable presentation of key physical issues using the example of the most technically simple model of laser-induced hyperthermia.

Transport Approximation and Differential Models

The radiative transfer in biological tissues has the following features that are important for the rational choice of an appropriate method for solving the problem:

1 In the therapeutic window of semitransparency, the scattering of radiation by numerous structural elements of each biological cell with size comparable with the radiation wavelength is much greater than the absorption of radiation (e.g. Mobley and Vo-Dinh, 2003).

2 To calculate the temperature of biological tissue, it is necessary to know the power field of the radiation absorbed in the medium, while the angular distribution of the radiation intensity does not matter.

The first of these circumstances means that the incident radiation undergoes multiple scattering. In problems of this type, the details of the phase function of single scattering are not important, and the simplest transport approximation is quite sufficient. According to this approximation, the scattering function is replaced by a sum of the isotropic component and the term describing the peak of forward scattering. In this case, the general radiative transfer equation (Howell et al., 2021; Modest and Mazumder, 2021) is greatly simplified and has the same form as that for the hypothetical isotropic scattering. The transport approximation, first proposed for problems of neutron transport (Davison, 1957; Pomraning, 1965; Sanchez and McCormick, 1982), is widely used for radiative heat transfer in scattering media by (Dombrovsky, 1996a, Dombrovsky, 1996b, Dombrovsky, 2012, Dombrovsky, 2016, Dombrovsky, 2019) and by Dombrovsky and Baillis (2010), as well as for radiative transfer in biological tissues (Tuchin, 2007; Kienle et al., 2007; Sandell and Zhu, 2011; Jacques, 2013; Dombrovsky et al., 2011, Dombrovsky et al., 2012, Dombrovsky et al., 2013, Dombrovsky et al., 2015, Eisel et al., 2018). Note that researchers dealing with the optical properties of biological tissues talk about equivalent isotropic scattering and use the term “reduced scattering coefficient” instead of the “transport scattering coefficient”. It seems appropriate to recall also several recent publications on various problems of thermal engineering, geophysics, and aerospace engineering (Dombrovsky et al., 2016; Dombrovsky et al., 2017; Dombrovsky et al., 2018; Dombrovsky et al., 2019; Dombrovsky et al., 2020; Krainova et al., 2017; Dombrovsky and Randrianalisoa, 2018), a fairly accurate solution of which was obtained using the transport approximation.

Due to the linearity of the radiative transfer equation, the traditional technique can be used: the radiation intensity at each point of the medium is presented as a sum of the diffuse component and the directional incident radiation, which is exponentially attenuated in the medium (Sobolev, 1975). As a result, it is sufficient to focus on more complex problem for the diffuse radiation.

The second feature of the problem being solved suggests a possibility of a simple description of the angular dependence of the diffuse component of the radiation field. It is known that this approach leads to one of the simplest differential approximations: either to the known P₁-approximation, or to the modified two-flux approximation taking into account the effect of total internal reflection at the body surface (Dombrovsky et al., 2006). In both cases, the calculation of the power field of the radiation absorbed in the medium is reduced to solving a boundary value problem for an ordinary differential equation of the second order. The choice between the named differential approximations is determined by the dimension of the problem and the type of boundary conditions (Dombrovsky et al., 2012, 2015). Comparison with exact numerical calculations for a typical problem of laser hyperthermia (Dombrovsky et al., 2013) showed that the modified two-flux method gives rather accurate results when solving one-dimensional problems. At the same time, the classical diffusion approximation (P₁), which ignores the discontinuity in the angular dependence of the radiation intensity on the irradiated surface, is more universal, since it is applicable for computational regions of complex shapes. As for the relatively large error of P₁ near the body surface, this disadvantage turns out to be insignificant, for example, when cooling the surface, which is recommended for the promising peripheral heating of the tumor (Dombrovsky et al., 2012).

Transient Heat Transfer Model

The simplest and frequently used description of heat transfer in the human body is based on the so-called bioheat equation proposed in the early work by Pennes (1948). It was assumed that the arterial blood temperature, $T_b$, is uniform throughout the tissue while the venous blood temperature is equal to the local tissue temperature $T_t$. The resulting transient energy equation is as follows:

${\left(\rho c\right)}_t\frac{\partial T_t}{\partial t}=\mathit{\nabla }\left(k_t\mathit{\nabla }{T}_t\right)+{\rho }_b{c}_b{\omega }_b\left(T_b-T_t\right)+W_{\mathrm{m}}(1)$

where the second term on the right-hand side is responsible for the heat transfer due to arterial blood perfusion of rate ${\omega }_b$, and the last term $W_m$ is the metabolic heat generation within the tissue. Approximate Eq. 1 contains obvious physical contradictions. It is assumed that heat transfer from arterial blood does not depend on the diameter of the blood vessels, whereas in many parts of the body there are only thinner vessels and capillaries. This equation does not take into account the cooling of arterial blood. This can be applicable only to estimate the volumetric heat transfer in internal organs containing large vessels of arterial blood.

A more general model for heat transfer in human tissues should be based on two coupled energy equations for the tissue and arterial blood with the spatial and time variation of the arterial blood temperature (Khaled and Vafai, 2003; Nakayama and Kuwahara, 2008). The models of this type have been considered in early paper by Xuan and Roetzel (1997) and also in more recent publications (Dombrovsky et al., 2012; He and Liu, 2017; Wang et al., 2018; Andreozzi et al., 2019; Dutta and Kundu, 2019).

In this paper, we consider only superficial tumors. This simplifies significantly the calculations of heat transfer. There are several layers of biological tissue at the surface of the body: a thin epidermis that does not contain blood vessels, dermis (sometimes subdivided into several layers) and a fat layer with a small number of capillaries. The fat layer is followed by the muscle layer with more arteries. Superficial tumors, as a rule, are concentrated in the dermis, can penetrate into the fat layer, but do not reach the muscle layer. According to (Dombrovsky et al., 2012), the difference between the temperature of tissue and arterial blood in the fat layer and epidermis is negligible and heat is transferred from the muscle layer to the body surface mainly by conduction.

Obviously, there is no need in a separate energy equation for blood in the human skin, and the heat transfer during hyperthermia can be calculated using the following simple equation:

${\left(\rho c\right)}_t\frac{\partial T_t}{\partial t}=\mathit{\nabla }\left(k_t\mathit{\nabla }{T}_t\right)+W_{\mathrm{m}}+W_{\mathrm{r}\mathrm{a}\mathrm{d}}(2)$

where the last term is the absorbed radiation power.

Eq. 2 seems too simple to suggest an original tumor heating method. Fortunately, this is not the case, and the author’s experience in calculating the transient temperature fields in structures of complex shapes made it possible to suggest an interesting way of uniformly heating the tumor. This is the so-called indirect heating strategy.

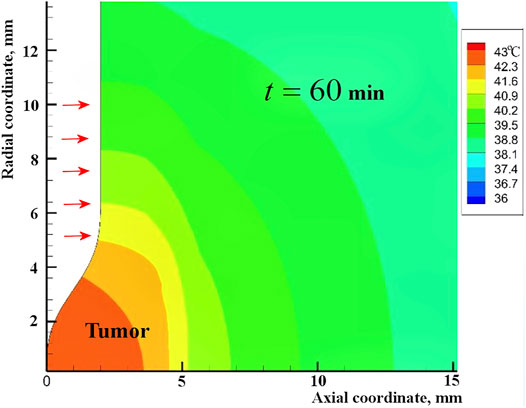
It is known that direct laser heating of a superficial tumor can lead to an undesirable protective reaction of the body with an increase in local perfusion. Periodic heating of only the annular region around the tumor using a scanning laser beam proposed by Dombrovsky et al. (2012) radically changes the strategy of hyperthermia. During the long pauses between heating periods, heat is transferred to the tumor by conduction. In this case, the tumor is heated uniformly from several sides (Figure 1). The human thermal regulation system is not designed to receive an additional heat from the body volume (not from the body surface), and such heating should not cause a significant increase in perfusion. Heating of healthy tissue around a tumor can be enhanced by introducing gold nanoparticles into the illuminated area, but embedding the nanoparticles into biological tissues is related with serious additional difficulties, instead of which it is sufficient to increase the power of incident laser radiation.

FIGURE 1

FIGURE 1. A typical temperature field in the case of a periodic peripheral laser heating.

When calculating both the field of the absorbed radiation power and transient axisymmetric temperature field in the tumor and surrounding healthy tissues, it is possible to use the universal finite element method, which is more convenient for computational regions of complex shape (Chen, 2011; Zienkiewicz et al., 2013), as was done in (Dombrovsky et al., 2012).

Sometimes, it is possible to use a simpler and more economical finite-difference method. In the heat conduction part of the problem, the implicit scheme of the second order of approximation with splitting the spatial differential operator into two parts and alternately integrating the equation at each time step along a set of grid lines in the axial and radial directions is preferable (Dombrovsky et al., 2015).

It is known that when using the finite element method, the problem is reduced to solving a system of algebraic equations with a matrix in which nonzero elements form a rather wide band along the diagonal of the matrix. The width of the band depends on a particular procedure for numbering the nodes of the finite element model. When using a finite-difference algorithm with splitting the problem into alternating heat propagation in orthogonal directions, the width of a similar band of nonzero matrix elements is equal to three. Therefore, the calculations by the program using the finite-difference method turns are much faster. In the numerical solution of transient axisymmetric problems with equally detailed discretization of the computational region and the same time steps, according to the author’s experience, the finite-difference solution is about six times faster than when using the finite element method. I am talking about my home codes, which differed only in the numerical solution of the problem.

It is important to note that the use of peripheral heating of the tumor can be accompanied by water cooling of the irradiated body surface, where most of heat receptors are located. One can find some details about the cutaneous temperature receptors and the pain related with the heating the body surface in (Spray, 1986; Lorenz et al., 2002; Kobayashi, 2015). The water cooling the body surface makes the suggested strategy almost painless and allows longer sessions with detailed control of the process parameters.

Heating the normal human tissue around the tumor is relatively low due to significant radial spreading of heat (see Figure 1). At the same time, this heating is extremely important because the red blood cells of arterial blood lose a part of the oxygen they carry (Collins et al., 2015). Moreover, a favorable factor is the possible destruction of some overheated capillaries at the border of the tumor due to the release of gases in the heated blood. As a result, the oxygen regeneration of tumor tissue decreases. In fact, the peripheral heating is accompanied by asphyxiation of the tumor with its partial or complete necrosis. The latter is an important part of the recommended heating strategy.

It goes without saying that the suggested method of laser-induced hyperthermia of superficial tumors does not exclude alternative approaches, such as that proposed in the recent study by Yin et al. (2020).

Non-Arrhenius Kinetics of Thermal Damage

In many publications on the modeling of hyperthermia, the kinetics of thermal degradation of tumor tissue is described by the classical Arrhenius equation, which can be written as follows (Dewey, 2009):

$\frac{\partial \xi }{\partial t}=\left(1-\xi \right)A\exp \left(-\frac{E}{RT}\right)\xi \left(0\right)=0(3)$

where $\xi$ is the degree of thermal destruction, $E$ is the activation energy, and the initial condition means a conventional beginning of the process. The values of $A$ and $E$ should be determined experimentally.

The Arrhenius’s law correctly describes the known physical phenomenon: the exponential intensification of thermal destruction with increasing temperature. Nevertheless, when trying to apply this law to living human tissue, it becomes obvious that the above formulation cannot be immediately employed. It is enough to compare the state of, for example, a piece of meat left in a warm room with air temperature about 37°C (outside the fridge), and the state of the muscle tissue of a living person. In no case can one ignore the continuous process of regeneration of human tissues due to arterial blood flow, which supplies the cells of the body with oxygen. Of course, the last statement is true for tumor tissues.

An attempt to take into account the regeneration of living tissues when describing their possible damage during hyperthermia by modification of Eq. 3 was undertaken in (Dombrovsky and Timchenko, 2015) (see also (Dombrovsky, 2019):

$\begin{array}{l}\frac{\partial {\xi }_i}{\partial t}=\left(1-{\xi }_i\right)A_{i}exp\left(-\frac{E_i}{RT}\right)-B_i{\xi }_i{\omega }_b\\ {\xi }_i\left(0\right)=0i=1,\mathrm{...},6\end{array}(4)$

where $i\le 5$ are the numbers of skin layers, $i=6$ corresponds to the tumor tissue, and $B_{\text{i}}$ are the dimensionless coefficients. It was assumed in that $B_{\text{i}}=B_{\text{h}}\gg 1$ for all the healthy tissues, whereas $B_6=0$ (for the totally destroyed regeneration of the tumor tissue). The last assumption is supported by experimental data for very high sensitivity of red blood cells to the overheating expected at the periphery of the tumor (Gershfeld and Murayama, 1988; Fasano et al., 2010). It should be noted that when using the traditional Eq. 3, which does not take into account the regeneration of living biological tissues, the formal solution gives an incorrect result with noticeable thermal damage to these tissues already within several tens of minutes of thermal therapy. At the same time, the use of the kinetic model (4) gives a qualitatively correct result, indicating damage only to the tumor, which does not receive oxygen-rich arterial blood during the recommended peripheral heating (Dombrovsky, 2019).

Strictly speaking, the loss of oxygen by erythrocytes during heating of arterial blood as it approaches the heated tumor can also be described by the Arrhenius law with some values of the activation energy and the coefficient before the exponent.

The loss of oxygen by erythrocytes of arterial blood heated at the periphery of the tumor can be significant only for superficial tumors, which are approached by relatively thin blood vessels and capillaries. In this case, the average velocity of blood flow is small and the time of its heating is sufficient for a significant decrease in the oxygen content in erythrocytes.

It is important to remind that the present work is not related to tumors far from the surface of the body, in places where there are significantly larger arteries. The relatively rapid flow of blood through the large arteries makes it impossible any thermal degradation of erythrocytes. The discussed strategy of indirect/peripheral heating of such tumors is also not expected to be applicable.

In addition, with the slow thermal treatment of the tumor, more detailed kinetic models should consider multi-stage conversions in tumor cells (Feng and Fuentes, 2011; Pearce, 2013; Crapse et al., 2021). This means that a complete Arrhenius equation includes several exponential terms responsible for these stages of the process. Such a complete description of the kinetics of thermal damage of tumor tissues is not associated with additional mathematical difficulties. However, there are no reliable data in the literature for the parameters of the detailed kinetic models applicable for various tumors. Therefore, currently, as a rule, simpler models are used and multi-stage kinetic models are beyond the scope of the present paper.

Conclusion

A discussion of physical and computational modeling of heat transfer in laser-induced hyperthermia of superficial human tumors is presented, including differential models for radiative transfer, various approaches to the analysis of transient heat transfer, and possible modifications of traditional kinetic models of thermal degradation of tumors.

In radiative transfer modeling, the transport approximation and differential models are recommended for the diffuse component of the radiation field which contributes a lot to the absorbed radiation power. The heat transfer in a multilayer skin can be approximately calculated using the transient energy equation taking into account mainly two modes of heat transfer: the ordinary heat conduction and volumetric heat generation due to the absorbed external radiation. In kinetics of the tumor degradation, it is shown that a partial regeneration of normal human tissues at the periphery of the tumor due to oxygen supplied with the arterial blood should not be ignored.

When modeling radiative transfer, it is recommended to use the transport approximation for the scattering phase function and one of the differential models for the diffuse component of the radiation field, which makes the main contribution to the absorption of laser radiation. Heat transfer in a multilayer human skin can be calculated using the transient energy equation, which takes into account two main effects: ordinary heat conduction and volumetric heat due to the absorbed radiation power. In the kinetics of tumor damage, it has been shown that one should not ignore the partial self-regeneration of normal tissues at the tumor periphery due to oxygen supplied with arterial blood.

The motivation and advantages of the previously suggested painless procedure of a peripheral/indirect periodic heating of the tumor with a focus on the tumor asphyxiation are clarified in detail. It is expected that this discussion will be instructive for alternative procedures developed by other researchers as well.

The author hopes that this paper will be useful for young and not so experienced researchers to overcome some typical weaknesses of computational modeling the photothermal treatment of superficial tumors.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

I would like to express my sincere gratitude to Victoria Timchenko for her cooperation and support during my several short-term visits to the University of New South Wales (Sydney) in the period from 2011 to 2015, when most of the theoretical researches were carried out. I am also grateful to Jaona Randrianalisoa and Wojciech Lipiński for their contribution to particular joint studies cited in the paper.

References

Abadeer, N. S., and Murphy, C. J. (2016). Recent Progress in Cancer Thermal Therapy Using Gold Nanoparticles. J. Phys. Chem. C. 120 (9), 4691–4716. doi:10.1021/acs.jpcc.5b11232

CrossRef Full Text | Google Scholar

Andreozzi, A., Brunese, L., Iasiello, M., Tucci, C., and Vanoli, G. P. (2019). Modeling Heat Transfer in Tumors: A Review of Thermal Therapies. Ann. Biomed. Eng. 47, 676–693. doi:10.1007/s10439-018-02177-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Bashkatov, A. N., Genina, E. A., and Tuchin, V. V. (2011). Optical Properties of Skin, Subcutaneous and Muscle Tissues: a Review. J. Innov. Opt. Health Sci. 4 (1), 9–38. doi:10.1142/s1793545811001319

CrossRef Full Text | Google Scholar

Bayazitoglu, Y., Kheradmand, S., and Tullius, T. K. (2013). An Overview of Nanoparticle Assisted Laser Therapy. Int. J. Heat Mass Transfer. 67, 469–486. doi:10.1016/j.ijheatmasstransfer.2013.08.018

CrossRef Full Text | Google Scholar

Bhowmik, A., Repaka, R., Mishra, S. C., and Mitra, K. (2014). Analysis of Radiative Signals From Normal and Malignant Human Skins Subjected to a Short-Pulse Laser. Int. J. Heat Mass Transfer. 68, 278–294. doi:10.1016/j.ijheatmasstransfer.2013.09.032

CrossRef Full Text | Google Scholar

Bhuvaneswari, M., and Wu, C.-Y. (2009). Differential Approximations for Transient Radiative Transfer in Refractive Planar Media With Pulse Irradiation. J. Quantitative Spectrosc. Radiative Transfer. 110 (6-7), 389–401. doi:10.1016/j.jqsrt.2009.01.001

CrossRef Full Text | Google Scholar

Bucharskaya, A. B., Maslyakova, G. N., Chekhonatskaya, M. L., Terentyuk, G. S., Navolokin, N. A., Khlebtsov, B. N., et al. (2018). Plasmonic Photothermal Therapy: Approaches to Advanced Strategy. Lasers Surg. Med. 50 (10), 1025–1033. doi:10.1002/lsm.23001

PubMed Abstract | CrossRef Full Text | Google Scholar

Camerin, M., Rello, S., Villanueva, A., Ping, X., Kenney, M. E., Rodgers, M. A. J., et al. (2005). Photothermal Sensitisation as a Novel Therapeutic Approach for Tumours: Studies at the Cellular and Animal Level. Eur. J. Cancer. 41 (6), 1203–1212. doi:10.1016/j.ejca.2005.02.021

CrossRef Full Text | Google Scholar

Chatterjee, D. K., Diagaradjane, P., and Krishnan, S. (2011). Nanoparticle-Mediated Hyperthermia in Cancer Therapy. Ther. Deliv. 2 (8), 1001–1014. doi:10.4155/tde.11.72

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Z. (2011). The Finite Element Method: Its Fundamentals and Applications in Engineering. Singapore: World Sci. Publ.

Google Scholar

Cheong, W. F., Prahl, S. A., and Welch, A. J. (1990). A Review of the Optical Properties of Biological Tissues. IEEE J. Quan. Electron. 26 (12), 2166–2185. doi:10.1109/3.64354

CrossRef Full Text | Google Scholar

Collins, J.-A., Rudenski, A., Gibson, J., Howard, L., and O’Driscoll, R. (2015). Relating Oxygen Partial Pressure, Saturation and Content: the Haemoglobin-Oxygen Dissociation Curve. Breathe. 11 (3), 194–201. doi:10.1183/20734735.001415

PubMed Abstract | CrossRef Full Text | Google Scholar

Crapse, J., Pappireddi, N., Gupta, M., Shvartsman, S. Y., Wieschaus, E., and Wühr, M. (2021). Evaluating the Arrhenius Equation for Developmental Processes. Mol. Syst. Biol. 17 (8), e9895. doi:10.15252/msb.20209895

PubMed Abstract | CrossRef Full Text | Google Scholar

Datta, N. R., Ordóñez, S. G., Gaipl, U. S., Paulides, M. M., Crezee, H., Gellermann, J., et al. (2015). Local Hyperthermia Combined With Radiotherapy And-/or Chemotherapy: Recent Advances and Promises for the Future. Cancer Treat. Rev. 41 (9), 742–753. doi:10.1016/j.ctrv.2015.05.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Davison, B. (1957). Neutron Transport Theory. London: Oxford University Press.

Google Scholar

Dewey, W. C. (2009). Arrhenius Relationships From the Molecule and Cell to the Clinic. Int. J. Hyperthermia. 25 (1), 3–20. doi:10.1080/02656730902747919

CrossRef Full Text | Google Scholar

Dombrovsky, L. A. (1996a). Approximate Methods for Calculating Radiation Heat Transfer in Dispersed Systems. Therm. Eng. 43 (3), 235–243.

Google Scholar

Dombrovsky, L. A. (1996b). Radiation Heat Transfer in Disperse Systems. New York: Begell House.

Google Scholar

Dombrovsky, L. A., and Baillis, D. (2010). Thermal Radiation in Disperse Systems: An Engineering Approach. New York: Begell House.

Google Scholar

Dombrovsky, L. A., Timchenko, V., Jackson, M., and Yeoh, G. H. (2011). A Combined Transient thermal Model for Laser Hyperthermia of Tumors With Embedded Gold Nanoshells. Int. J. Heat Mass. Transfer. 54 (25-26), 5459–5469. doi:10.1016/j.ijheatmasstransfer.2011.07.045

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., and Timchenko, V. M. (2015). Laser Induced Hyperthermia of Superficial Tumors: Computational Models for Radiative Transfer, Combined Heat Transfer, and Degradation of Biological Tissues. Therm. Proc Eng. 7 (1), 24–36. (in Russian).

Google Scholar

Dombrovsky, L. A. (2012). The Use of Transport Approximation and Diffusion-Based Models in Radiative Transfer Calculations. Comput. Therm. Scien 4 (4), 297–315. doi:10.1615/computthermalscien.2012005050

CrossRef Full Text | Google Scholar

Dombrovsky, L. A. (2016). A New Method to Retrieve Spectral Absorption Coefficient of Highly-Scattering and Weakly-Absorbing Materials. J. Quantitative Spectrosc. Radiative Transfer 172, 75–82. doi:10.1016/j.jqsrt.2015.07.025

CrossRef Full Text | Google Scholar

Dombrovsky, L. A. (2019). “Scattering of Radiation and Simple Approaches to Radiative Transfer in Thermal Engineering and Biomedical Applications,” in Springer Series in Light Scattering. Editor A. Kokhanovsky (Cham (Switzerland): Springer Nature), 4, 71–127. doi:10.1007/978-3-030-20587-4_2

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., Dembele, S., Wen, J. X., and Sikic, I. (2018). Two-Step Method for Radiative Transfer Calculations in a Developing Pool Fire at the Initial Stage of its Suppression by a Water spray. Int. J. Heat Mass Transfer. 127, 717–726. doi:10.1016/j.ijheatmasstransfer.2018.07.095

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., Kokhanovsky, A. A., and Randrianalisoa, J. H. (2019). On Snowpack Heating by Solar Radiation: A Computational Model. J. Quantitative Spectrosc. Radiative Transfer. 227, 72–85. doi:10.1016/j.jqsrt.2019.02.004

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., Levashov, V. Y., Kryukov, A. P., Dembele, S., and Wen, J. X. (2020). A Comparative Analysis of Shielding of thermal Radiation of Fires Using Mist Curtains Containing Droplets of Pure Water or Sea Water. Int. J. Therm. Sci. 152, 106299. doi:10.1016/j.ijthermalsci.2020.106299

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., and Randrianalisoa, J. H. (2018). Directional Reflectance of Optically Dense Planetary Atmosphere Illuminated by Solar Light: An Approximate Solution and its Verification. J. Quantitative Spectrosc. Radiative Transfer. 208, 78–85. doi:10.1016/j.jqsrt.2018.01.016

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., Randrianalisoa, J., Lipinski, W., and Timchenko, V. (2013). Simplified Approaches to Radiative Transfer Simulations in Laser-Induced Hyperthermia of Superficial Tumors. Comput. Therm. Scien. 5 (6), 521–530. doi:10.1615/computthermalscien.2013008157

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., Reviznikov, D. L., Kryukov, A. P., and Levashov, V. Y. (2017). Self-Generated Clouds of Micron-Sized Particles as a Promising Way of a Solar Probe Shielding From Intense Thermal Radiation of the Sun. J. Quantitative Spectrosc. Radiative Transfer. 200, 234–243. doi:10.1016/j.jqsrt.2017.06.025

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., Reviznikov, D. L., and Sposobin, A. V. (2016). Radiative Heat Transfer From Supersonic Flow With Suspended Particles to a blunt Body. Int. J. Heat Mass Transfer. 93, 853–861. doi:10.1016/j.ijheatmasstransfer.2015.10.072

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., Timchenko, V., and Jackson, M. (2012). Indirect Heating Strategy for Laser Induced Hyperthermia: An Advanced thermal Model. Int. J. Heat Mass Transfer 55 (17-18), 4688–4700. doi:10.1016/j.ijheatmasstransfer.2012.04.029

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., Timchenko, V., Pathak, C., Piazena, H., Müller, W., and Jackson, M. (2015). Radiative Heating of Superficial Human Tissues with the Use of Water-Filtered Infrared-A Radiation: A Computational Modeling. Int. J. Heat Mass Transfer 85, 311–320. doi:10.1016/j.ijheatmasstransfer.2015.01.133

CrossRef Full Text | Google Scholar

Dombrovsky, L., Randrianalisoa, J., and Baillis, D. (2006). Modified Two-Flux Approximation for Identification of Radiative Properties of Absorbing and Scattering media from Directional-Hemispherical Measurements. J. Opt. Soc. Am. A. 23 (1), 91–98. doi:10.1364/josaa.23.000091

CrossRef Full Text | Google Scholar

Duck, F. A. (1990). Physical Properties of Tissue: A Comprehensive Reference Book. San Diego: Academic Press.

Google Scholar

Dutta, J., and Kundu, B. (2019). Exact Analysis Based on BDLTNE Approach for THermal Behaviour in Living Tissues during Regional Hyperthermia Therapy. Acta Mech. 230, 2853–2871. doi:10.1007/s00707-019-02427-6

CrossRef Full Text | Google Scholar

Dykman, L. A., and Khlebtsov, N. G. (2019). Gold Nanoparticles in Chemo-, Immuno-, and Combined Therapy: Review [Invited]. Biomed. Opt. Express. 10 (7), 3152. doi:10.1364/boe.10.003152

PubMed Abstract | CrossRef Full Text | Google Scholar

Eisel, M., Ströbl, S., Pongratz, T., Stepp, H., Rühm, A., and Sroka, R. (2018). Investigation of Optical Properties of Dissected and Homogenized Biological Tissue. J. Biomed. Opt. 23 (9)–9. doi:10.1117/1.JBO.23.9.091418

CrossRef Full Text | Google Scholar

Fasano, A., Hömberg, D., and Naumov, D. (2010). On a Mathematical Model for Laser-Induced Thermotherapy. Appl. Math. Model. 34 (12), 3831–3840. doi:10.1016/j.apm.2010.03.023

CrossRef Full Text | Google Scholar

Feng, Y., and Fuentes, D. (2011). Model-Based Planning and Real-Time Predictive Control for Laser-Induced Thermal Therapy. Int. J. Hyperthermia. 27 (8), 751–761. doi:10.3109/02656736.2011.611962

CrossRef Full Text | Google Scholar

Gershfeld, N. L., and Murayama, M. (1988). Thermal Instability of Red Blood Cell Membrane Bilayers: Temperature Dependence of Hemolysis. J. Membrain Biol. 101, 67–72. doi:10.1007/bf01872821

CrossRef Full Text | Google Scholar

He, Z.-Z., and Liu, J. (2017). A Coupled Continuum-Discrete Bioheat Transfer Model for Vascularized Tissue. Int. J. Heat Mass Transfer. 107, 544–556. doi:10.1016/j.ijheatmasstransfer.2016.11.053

CrossRef Full Text | Google Scholar

Howell, J. R., Mengüç, M. P., Daun, K., and Siegel, R. (2021). Thermal Radiation Heat Transfer. Seventh Edition. New York: CRC Press.

Google Scholar

Huang, X., and El-Sayed, M. A. (2010). Gold Nanoparticles: Optical Properties and Implementations in Cancer Diagnosis and Photothermal Therapy. J. Adv. Res. 1 (1), 13–28. doi:10.1016/j.jare.2010.02.002

CrossRef Full Text | Google Scholar

Jacques, S. L. (2013). Optical Properties of Biological Tissues: a Review. Phys. Med. Biol. 58 (11), R37–R61. doi:10.1088/0031-9155/58/11/r37

PubMed Abstract | CrossRef Full Text | Google Scholar

Jague, D., Maestro, L. M., del Rosal, B., Haro-Gonzalez, P., Benayas, A., Plaza, J. L., et al. (2014). Nanoparticles for Photothermal Therapies. Nanoscale. 16 (6), 9494–9530. doi:10.1039/C4NR00708E

CrossRef Full Text | Google Scholar

Jaunich, M. K., Raye, S., Kim, K., Mitra, K., and Guo, Z. (2008). Bio-Heat Transfer Analysis during Short Pulse Irradiation of Tissues. Int. J. Heat Mass. Transfer. 51 (23-24), 5511–5521. doi:10.1016/j.ijheatmasstransfer.2008.04.033

CrossRef Full Text | Google Scholar

Kaur, P., Aliru, M. L., Chadha, A. S., Asea, A., and Krishnan, S. (2016). Hyperthermia Using Nanoparticles - Promises and Pitfalls. Int. J. Hyperthermia. 32 (1), 76–88. doi:10.3109/02656736.2015.1120889

CrossRef Full Text | Google Scholar

Khaled, A.-R. A., and Vafai, K. (2003). The Role of Porous Media in Modeling Flow and Heat Transfer in Biological Tissues. Int. J. Heat Mass Transfer. 46 (26), 4989–5003. doi:10.1016/s0017-9310(03)00301-6

CrossRef Full Text | Google Scholar

Kienle, A., Wetzel, C., Bassi, A., Comelli, D., Taroni, P., and Pifferi, A. (2007). Determination of the Optical Properties of Anisotropic Biological Media Using an Isotropic Diffusion Model. J. Biomed. Opt. 12 (1), 014026. doi:10.1117/1.2709864

CrossRef Full Text | Google Scholar

Kobayashi, S. (2015). Temperature Receptors in Cutaneous Nerve Endings Are Thermostat Molecules That Induce Thermoregulatory Behaviors against thermal Load. Temperature. 2 (3), 346–351. doi:10.1080/23328940.2015.1039190

PubMed Abstract | CrossRef Full Text | Google Scholar

Krainova, I. V., Dombrovsky, L. A., Nenarokomov, A. V., Budnik, S. A., Titov, D. M., and Alifanov, O. M. (2017). A Generalized Analytical Model for Radiative Transfer in Vacuum thermal Insulation of Space Vehicles. J. Quantitative Spectrosc. Radiative Transfer. 197, 166–172. doi:10.1016/j.jqsrt.2017.01.039

CrossRef Full Text | Google Scholar

Liu, L. H., and Hsu, P.-f. (2008). Time Shift and Superposition Method for Solving Transient Radiative Transfer Equation. J. Quantitative Spectrosc. Radiative Transfer. 109 (7), 1297–1308. doi:10.1016/j.jqsrt.2007.10.005

CrossRef Full Text | Google Scholar

Lorenz, J., Cross, D. J., Minoshima, S., Morrow, T. J., Paulson, P. E., and Casey, K. L. (2002). A Unique Representation of Heat Allodynia in the Human Brain. Neuron. 35 (2), 383–393. doi:10.1016/s0896-6273(02)00767-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Mallory, M., Gogineni, E., Jones, G. C., Greer, L., and Simone, C. B. (2016). Therapeutic Hyperthermia: The Old, the New, and the Upcoming. Crit. Rev. Oncology/Hematology. 97, 56–64. doi:10.1016/j.critrevonc.2015.08.003

CrossRef Full Text | Google Scholar

Mishra, S. C., Muthukumaran, R., and Maruyama, S. (2012). Comparison of the Thermal Effects of the Transport of a Short-Pulsed Laser and Multi-Pulse Laser through a Participating Medium. Int. J. Heat Mass. Transfer. 55 (21-22), 5583–5596. doi:10.1016/j.ijheatmasstransfer.2012.05.047

CrossRef Full Text | Google Scholar

Mobley, J., and Vo-Dinh, T. (2003). “Optical Properties of Tissue,” in Biomedical Photonics Handbook. Editor T. Vo-Dinh (Boca Raton (FL): CRC Press), 2–1. doi:10.1201/9780203008997.sec1

CrossRef Full Text | Google Scholar

Modest, M. F., and Mazumder, S. (2021). Radiative Heat Transfer. Fourth Edition. New York: Academic Press.

Google Scholar

Muthukumaran, R., and Mishra, S. C. (2008). Transient Response of a Planar Participating Medium Subjected to a Train of Short-Pulse Radiation. Int. J. Heat Mass Transfer. 51 (9-10), 2418–2432. doi:10.1016/j.ijheatmasstransfer.2007.08.035

CrossRef Full Text | Google Scholar

Nakayama, A., and Kuwahara, F. (2008). A General Bioheat Transfer Model Based on the Theory of Porous media. Int. J. Heat Mass. Transfer. 51 (11-12), 3190–3199. doi:10.1016/j.ijheatmasstransfer.2007.05.030

CrossRef Full Text | Google Scholar

Pearce, J. A. (2013). Comparative Analysis of Mathematical Models of Cell Death and Thermal Damage Processes. Int. J. Hyperthermia. 29 (4), 262–280. doi:10.3109/02656736.2013.786140

CrossRef Full Text | Google Scholar

Peeken, J. C., Vaupel, P., and Combs, S. E. (2017). Integrating Hyperthermia Into Modern Radiation Oncology: What Evidence Is Necessary? Front. Oncol. 7, 132. doi:10.3389/fonc.2017.00132

PubMed Abstract | CrossRef Full Text | Google Scholar

Pennes, H. H. (1948). Analysis of Tissue and Arterial Blood Temperatures in the Resting Human Forearm. J. Appl. Physiol. 1 (2), 93–122. doi:10.1152/jappl.1948.1.2.93

CrossRef Full Text | Google Scholar

Pomraning, G. C. (1965). A Flexible Numerical Approach to Linear Transport Problems. Trans. Amer Nucl. Soc. 8, 488–489.

Google Scholar

Randrianalisoa, J. H., Dombrovsky, L. A., Lipiński, W., and Timchenko, V. (2014). Effects of Short-Pulsed Laser Radiation on Transient Heating of Superficial Human Tissues. Int. J. Heat Mass Transfer. 78, 488–497. doi:10.1016/j.ijheatmasstransfer.2014.07.011

CrossRef Full Text | Google Scholar

Ruan, L. M., Wang, S. G., Qi, H., and Wang, D. L. (2010). Analysis of the Characteristics of Time-Resolved Signals for Transient Radiative Transfer in Scattering Participating Media. J. Quantitative Spectrosc. Radiative Transfer. 111 (16), 2405–2414. doi:10.1016/j.jqsrt.2010.06.019

CrossRef Full Text | Google Scholar

Sanchez, R., and McCormick, N. J. (1982). A Review of Neutron Transport Approximations. Nucl. Sci. Eng. 80 (4), 481–535. doi:10.13182/NSE80-04-481

CrossRef Full Text | Google Scholar

Sandell, J. L., and Zhu, T. C. (2011). A Review of In-Vivo Optical Properties of Human Tissues and its Impact on PDT. J. Biophoton. 4 (11-12), 773–787. doi:10.1002/jbio.201100062

CrossRef Full Text | Google Scholar

Sobolev, V. V. (1975). Light Scattering in Planetary Atmospheres. In International Series of Monographs in Natural Philosophy, 76. New York: Pergamon Press.

Google Scholar

Spichka, A., Butnaru, D., Bezrukov, E. A., Sukhavov, R. B., Atala, A., Burdukovskii, V., et al. (2019). Skin Tissue Regeneration for Burn Injury. Stem Cell Res Ther. 10, 94. doi:10.1186/s13287-019-1203-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Spray, D. C. (1986). Cutaneous Temperature Receptors. Annu. Rev. Physiol. 48, 625–638. doi:10.1146/annurev.ph.48.030186.003205

PubMed Abstract | CrossRef Full Text | Google Scholar

Tuchin, V. V. (2007). Tissue Optics: Light Scattering Methods and Instruments for Medical Diagnosis. Second Edition. Bellingham (WA): SPIE Press, PM166.

Google Scholar

van der Zee, J. (2002). Heating the Patient: a Promising Approach? Ann. Oncol. 13 (8), 1173–1184. doi:10.1093/annonc/mdf280

PubMed Abstract | CrossRef Full Text | Google Scholar

Vines, J. B., Yoon, J.-H., Ryu, N.-E., Lim, D.-J., and Park, H. (2019). Gold Nanoparticles for Photothermal Cancer Therapy. Front. Chem. 7, 167. doi:10.3389/fchem.2019.00167

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, S.-L., Qi, H., Ren, Y.-T., Chen, Q., and Ruan, L.-M. (2018). Optimal Temperature Control of Tissue Embedded With Gold Nanoparticles for Enhanced thermal Therapy Based on Two-Energy Equation Model. J. Therm. Biol. 74, 264–274. doi:10.1016/j.jtherbio.2018.04.011

CrossRef Full Text | Google Scholar

Xuan, Y., and Roetzel, W. (1997). Bioheat Equation of the Human Thermal System. Chem. Eng. Technol. 20 (4), 268–276. doi:10.1002/ceat.270200407

CrossRef Full Text | Google Scholar

Yakovlev, E., Shandybina, G., and Shamova, A. (2019). Modelling of the Heat Accumulation Process During Short and Ultrashort Pulsed Laser Irradiation of Bone Tissue. Biomed. Opt. Express. 10 (6), 3030–3040. doi:10.1364/BOE.10.003030

PubMed Abstract | CrossRef Full Text | Google Scholar

Yarmolenko, P. S., Moon, E. J., Landon, C., Manzoor, A., Hochman, D. W., Viglianti, B. L., et al. (2011). Thresholds for Thermal Damage to Normal Tissues: an Update. Int. J. Hyperthermia. 27 (4), 320–343. doi:10.3109/02656736.2010.534527

CrossRef Full Text | Google Scholar

Yin, Y., Ren, Y., Li, H., and Qi, H. (2020). Characteristic Analysis of Light and Heat Transfer in Photothermal Therapy Using Multiple-Light-Source Heating Strategy. Int. J. Therm. Sci. 158, 106533. doi:10.1016/j.ijthermalsci.2020.106533

CrossRef Full Text | Google Scholar

Zhang, Y., Yi, H., and Tan, H. (2013). One-dimensional Transient Radiative Transfer by Lattice Boltzmann Method. Opt. Express. 21 (21), 24532–24539. doi:10.1364/OE.21.024532

PubMed Abstract | CrossRef Full Text | Google Scholar

Zienkiewicz, O. C., Taylor, R. L., and Zhu, J. Z. (2013). The Finite Element Method: Its Basis and Fundamentals. Seventh Edition. New York: Elsevier.

Google Scholar

Nomenclature

A coefficient in the Arrhenius equation, s⁻¹

B coefficient in Eq. 4, dimensionless

c specific heat capacity, J/(kg K)

E activation energy, J/mol

k thermal conductivity, W/(m K)

W volumetric power, W/m³

Greek symbols

ξ degree of tissue degradation, dimensionless

ρ density of tissue, kg/m³

ω rate of blood perfusion, s⁻¹

Subscripts and superscripts

b Arterial blood

h healthy

m metabolic

rad radiative

t human tissue