
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Syst. Biol., 12 January 2023
Sec. Translational Systems Biology and In Silico Trials
Volume 2 - 2022 | https://doi.org/10.3389/fsysb.2022.1063308
This article is part of the Research TopicUse of Quantitative Systems Pharmacology Pipelines to Bridge in Vitro and in Vivo Results in Drug DiscoveryView all 5 articles
 Meghna Verma1*†
Meghna Verma1*† Louis Gall2†
Louis Gall2† Jacopo Biasetti3†
Jacopo Biasetti3† Giovanni Y. Di Veroli2†
Giovanni Y. Di Veroli2† Cesar Pichardo-Almarza2†
Cesar Pichardo-Almarza2† Megan A. Gibbs4†
Megan A. Gibbs4† Holly Kimko4*†
Holly Kimko4*†Quantitative systems pharmacology (QSP) modeling has become an increasingly popular approach impacting our understanding of disease mechanisms and helping predict patients’ treatment responses to facilitate study design or development go/no-go decisions. In this paper, we highlight the notable contributions and opportunities that QSP approaches are to offer during the drug development process by sharing three examples that have facilitated internal decisions. The barriers to successful applications and the factors that facilitate the success of the modeling approach is discussed.
Since its advent as an approach described in the NIH white paper from 2011 (Peter et al., 2011), quantitative systems pharmacology (QSP) modeling has gained popularity in drug development. While the scope of QSP modeling needs further clarification (Bradshaw et al., 2019), it includes an attempt to quantitatively unravel the complex mechanisms and interactions between physiology and drugs (including investigational drugs) to predict responses given a drug intervention. Systems biology-based models describe biological pathways and their regulatory networks at molecular, cellular, tissue, and organ system levels to further the understanding of biological processes (Loewe and Hillston, 2008). Pharmacokinetic-pharmacodynamic (PKPD) modeling aims towards understanding pharmacological responses by quantifying the relationship between observed drug exposure and its observed non-clinical or clinical endpoints, often linking exposure to one endpoint whilst QSP models are used to capture multiple longitudinal biomarker measurements simultaneously in disease platform models. PKPD modeling is considered a top-down approach such that it is driven by already-observed data, whereas systems biology-based modeling is a bottom-up approach in that it starts from the fundamental understanding of biological knowledge such as molecular or cellular signaling pathways to predict the behavior of biological systems (Figure 1). In this context, quantitative systems pharmacology modeling can be considered as a balanced platform of bottom-up and top-down modeling approaches, which allows integration of biological knowledge available a priori and observed data obtained posteriori to help drug development decisions in a science-informed and practical way.
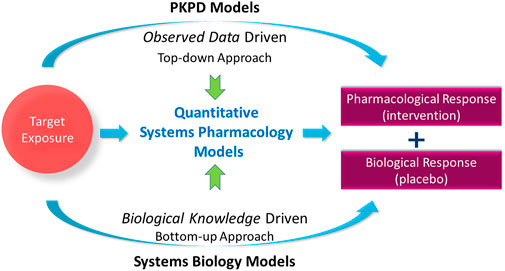
FIGURE 1. Quantitative systems pharmacology models balance the models to predict the pharmacological response via observed data-driven pharmacokinetic-pharmacodynamic (PKPD) models and biological knowledge-driven systems biology models.
The availability of quantitative longitudinal data from non-clinical research has led to the increased use of these models in the internal decision-making process in pharmaceutical companies. QSP models are developed at various biological scales ranging from cellular, molecular, tissue, organ, patient, and/or population levels, thereby highlighting the use of these models in delineating various multiscale mechanisms of pharmacological responses (Nijsen et al., 2018). These models have been used to determine the affinity required to engage a target; aid the target validation and lead discovery stage; predict and monitor drug response by identifying appropriate biomarkers; and predict toxicity effects in various organs. QSP models are frequently used for dosage regimen decisions for first-in-human studies by utilizing a wide range of non-clinical data and published competitor’s clinical data. In addition, the models allow cost-effective assessment to help understand target engagement for efficacy and safety risks for optimization of clinical study designs. Furthermore, the QSP modeling approach can be also taken to efficiently expedite development for an alternate drug indication during life cycle management process wherein the drug targets different diseases or patient populations via the same or similar mechanism of action. There are several publications that emphasize the emerging potential of QSP applications for pharmaceutical research in improving drug development decision-making (Leil and Bertz, 2014; Ramanujan et al., 2016; Bloomingdale et al., 2017; Clausznitzer et al., 2018; Bradshaw et al., 2019; Aghamiri et al., 2022).
The availability of biological knowledge and data from the preclinical stage allows development of QSP models, but the sparsity and limited granularity of observed data still constrains their predictive capability. Nevertheless, employment of these models at the stage, where clinical data is yet to be collected, has the potential to predict clinical responses to make an impact in the decisions of dosage regimen, subject enrollment criteria, sampling/monitoring times, biomarker-adaptive clinical trial design, rescue drug intervention strategy, etc. The QSP approach has been used in various therapeutic areas: a PubMed search with keywords “quantitative systems pharmacology” AND therapeutic areas listed as “autoimmune”, “cardiovascular”, “infection”, “metabolism”, “neuroscience” or “oncology” yielded the following metabolic QSP models amount to the highest number of models with a total of 112 cases; next is oncology with 45; cardiovascular models, 21; neuroscience, nine; infection, 10; and autoimmune disease, 4, over the last decade (as of December 2022).
QSP model applications in the clinical stage include further addressing the biological mechanism of action of a therapeutic agent; identifying biomarkers to predict clinical success; or understanding disease pathology (Knöchel et al., 2022), which provide a way to address clinical development decisions such as biomarker interpretation, study subject enrollment stratification, or competitive landscape evaluation (Ramanujan et al., 2016). An example of a successful application of QSP models from a clinician’s point of view may include offering insights on dosage individualization, based on their biomarker levels, to improve the probability of success of the treatment. Precision medicine will be better achieved by providing appropriate diagnostic tools: these technologies can help clinicians quantify multiple relevant biomarkers to subgroup patients in their susceptibility to a disease, prognosis, or likelihood of responding to a drug, and a QSP approach can guide the decisions on which biomarker(s) is the most informative.
Figure 2 is a schematic showing potential impact of systems modeling in the drug development pipeline. In this paper, we highlight the impact of QSP modeling via three case study applications that answered specific questions in early drug development. We show how various modeling approaches such as agent-based modeling (ABM); hybrid modeling with ordinary differential equations (ODE), partial differential equations (PDE), and ABM; and non-linear mixed-effects modeling with ODE are routinely used to influence the internal decision-making processes at various drug development stages at AstraZeneca. Case 1 shows how an agent-based modeling approach can be used in the context of gastrointestinal safety assessment (predictions of chemotherapy-induced diarrhea); Case 2 shows a hybrid model in the context of cardiovascular diseases guiding study dosage regimen decisions in human ventricular progenitor therapy development and Case 3 show how a systems modeling approach was used in oncology for the characterization of the interplay of longitudinal biomarkers given little available data. The mathematical details (code and impact) of these case studies will be discussed in separate stand-alone papers.
Chemotherapy-induced diarrhea presents a constant challenge for the development of safe and tolerable drugs. It is among the primary reasons for treatment interruption during drug development and clinical trials: the incidence of chemotherapy-induced diarrhea has been estimated to be as high as 80% (McQuade et al., 2016). For a given chemotherapeutic compound, this toxicity can be mitigated by carefully selecting a dose and a dosing regimen before a first-in-human study, and these should be decided through non-clinical experiments and fit-for-purpose mathematical modeling and simulations. Traditionally, non-clinical toxicity studies involve animal experiments, but gastrointestinal toxicity does not always translate between species: some dosages can be tolerated in animals but are devastating to humans, and vice versa (Peters et al., 2020).
We can surmount the interspecies difference by working with human cells, usually in the form of enteroids/organoids/organ-on-a-chip systems, but this approach is not without its own caveats. In vivo crypts and organoids show marked differences, and though great progress has been made to make these systems replicate in vivo crypts as closely as possible, the results are not immediately translatable (Peters et al., 2020). These differences include, but are not limited to, a lack of a supporting mesenchyme layer (with signaling cells of its own, which are involved in extensively studied injury-recovery feedback mechanisms), zonation/compartmentalization differences due to the different geometries, and mechanical/physical differences that are relevant to cellular proliferation and mobility (caused by the different geometries and surrounding environments). Therefore, a dictionary is required to translate the in vitro data into clinical adverse effect prediction observed in real patients, for which a QSP model is a suitable choice.
In pursuit of this dictionary, we developed an agent-based model that simulated the interactions of individual cells (the agents) interacting in the geometry of the crypt. The model incorporates all the major cell types and multiple clinically relevant signaling mechanisms. It replicates the geometry, physical and mechanical forces and cell zonation of in vivo crypts and demonstrates many experimentally observed phenotypes. With the assumption that the mechanistic action of a drug is the same in organoids and real crypts, we used this agent-based model to transfer the experimentally observed effects in human-derived organoids into predictions of chemotherapy-induced diarrhea in real patients. The model can be viewed as an in silico organ that, by replicating multiple aspects of human biology, can be used in the drug-discovery pipeline to make safety and toxicity predictions, circumventing the need for animal studies, and/or test biological hypotheses to gain mechanistic insight.
The intestinal crypt is particularly amenable to an agent-based modelling approach (see (Meineke et al., 2001) (Pitt-Francis et al., 2009) (Buske et al., 2011) for a selection of historic applications of agent-based modelling to the intestinal crypt). The compartmentalization of the cells in the crypt, and the inner workings of signaling mechanisms that cause this, are well studied, with bountiful single-cell data (including signaling knockouts (Riccio et al., 2008), ablations of single types of cells (Tan et al., 2021), and more (Liu et al., 2019)) with spatial and temporal resolution. Indeed, building an agent-based model of the gastrointestinal crypt is not a new concept, but our new model contains an unprecedented number of sub-systems (internal protein networks and intercellular signaling mechanisms), allowing it to recreate many clinically relevant phenotypes, recovering from a variety of injuries in experimentally verified fashion.
For the development of the model, we focused on three key tenets (in roughly ascending order of importance): computational speed/efficiency, modularity, and a focus on emergent behavior. Computational speed has long plagued agent-based modelling and is a topic of great interest. The simulation of all the agents can be computationally intensive and hence time consuming (Bonabeau, 2002), but in our current model, a full virtual drug exposure with all analytics obtained from the model can be calculated within minutes on a standard consumer laptop. In a pharmacological setting, this is a vital feature: a quick, efficient model allows many more trial simulations for greater accuracy in results, increasing flexibility in testing hypotheses and vastly improving ease of use.
The ABM is comprised of multiple sub-systems, such as those describing intercellular signaling, the cell’s DNA integrity, the cell cycle proteins, etc., which are mathematical models in their own right. Each individual piece of the model was chosen according to current knowledge, but this can, and will, change over time: because of this, the sub-systems of the model are modular such that each sub-system is easily replaceable without a full-scale reparameterization of the model. This also allows us to expand the model to introduce new pathways and modalities that may be required for better understanding of a drug’s action.
We focused on five signaling mechanisms that have been experimentally demonstrated to be vital for the correct functioning of the intestinal epithelium (to-be-published work by Louis Gall et al., “An agent-based model of the mouse small intestinal epithelium enables the prediction of the spatiotemporal dynamics of drug-induced events at multiple scales”). Briefly, these are the following signaling mechanisms: Wnt, Notch, BMP, ZNRF3/RNF43 and Hippo-YAP mediated contact inhibition, which are all dynamically and continuously simulated in the model, to maintain homeostasis and drive the model back to homeostasis following injury. Based on these signals, the cells follow rules which determine whether the cell should proliferate or differentiate, and if so what type of cell to become. In total, we considered seven types of cells (stem cells, absorptive progenitors, secretory progenitors, Paneth cells, enterocytes, enteroendocrine and goblet cells) that form over 99% of the intestinal epithelium (Haber et al., 2017).
Cellular proliferation in the model is governed by internal cell cycles simulated in each cell, represented by a previously published mathematical model (Csikász-Nagy, 2009) with an additional set of equations describing the cell’s DNA and RNA content. The cell cycle proteins, along with the DNA and RNA levels, are used to govern cellular proliferation: rising and falling cyclin levels thereby determining a cell’s progression through the division cycle, and the integrity of DNA is checked at cell cycle checkpoints. The model can be viewed as a collection of individually simple rules that combine to produce the complex emergent behaviors and phenotypes exhibited by the crypt-villus complex. The net result of the myriad internal and inter-cellular protein networks is a model that is driven constantly towards the homeostatic state, capable of responding to and recovering from injury and insult in a realistic manner. Here, it should be stressed that we can still verify the model outputs with comparison to experimental data, making the model quantitative.
All these sub-systems can be individually perturbed to simulate the effects of drugs. The workflow of the model is shown in Figure 3. We first coupled a PK model for the concentration of a drug to the sub-cellular systems of the ABM, fitting the effects of the drug on single cells according to the data obtained from organoid experiments. We then simulate this drug-cell interaction in every cell of the ABM, allowing us to replicate the propagation of this drug-induced injury from the single-cell level to the entire epithelial tissue. We then extrapolate this epithelial injury, which manifests as a reduction cells in the villus compartment or a reduction of cells of a particular type (e.g., goblet cell loss), to predict the probability of adverse outcomes. For example, as presented in Figure 3, we associate the risk of diarrhea to the severity and duration of epithelial cell loss in the villus. This is the main translational step, wherein we used the model to translate non-clinical experiments on organoids to robust clinical predictions of gastrointestinal toxicity in real patients.
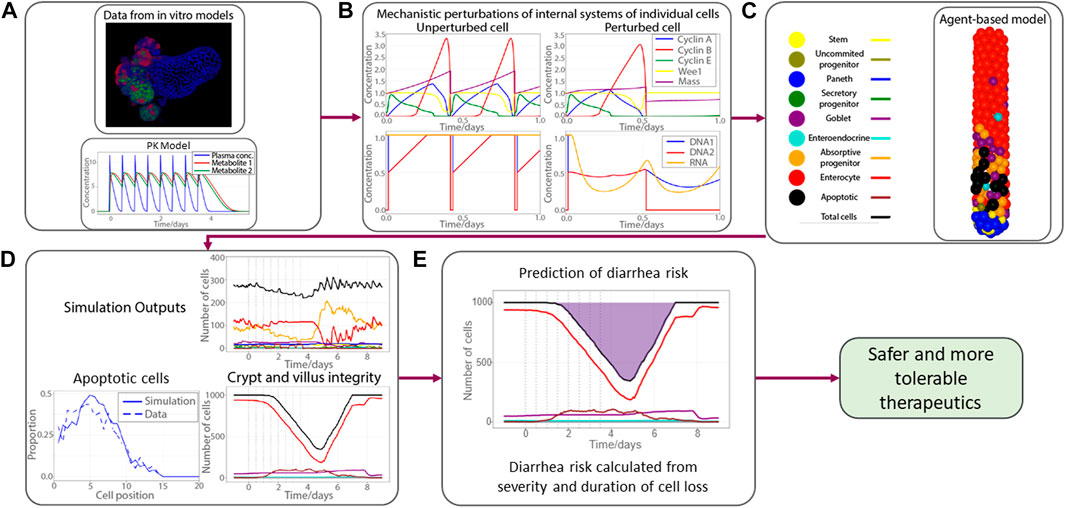
FIGURE 3. Workflow of the gastrointestinal agent-based model. (A) Mechanistic knowledge and drug effect gathered from organoid experiments, PK model for a fictitious drug; (B) four subplots show key cell cycle proteins (top panel) and DNA and RNA integrity (bottom panel) for no therapy-induced perturbation (left panel) and perturbation (right panel); (C) demonstrative picture of an ABM simulation of the crypt subject to drug injury with apoptotic cells shown in black; (D) proportion of apoptotic cells at each cell position (left bottom panel); number of cells (same color codes as in (C))in crypt (top right panel) and villus (bottom right panel); (E) pictorial demonstration of calculation of diarrhea risk, derived from duration and severity of epithelial cell loss, shaded region represents the period the number of cells on epithelium is below the homeostatic amount. Pharmacokinetics (PK); Agent based model (ABM); Deoxyribonucleic acid (DNA); Ribonucleic acid (RNA).
We built an agent-based model with multiple clinically relevant signaling pathways and internal protein interaction networks. The core ABM can be viewed as a platform, which was designed to be readily expandable, eliminating the need for the redevelopment and parameterization of entirely new, bespoke models for each drug. Rather than a collection of equations calibrated to explain known data, we have constructed an in silico crypt structure which can be used for hypothesis generation and the prediction of the toxicity and safety risks of a drug. Our agent-based modelling was possible for the gastrointestinal crypt because of the abundance of suitable data in the intestinal epithelium, which can be difficult to obtain (in terms of time and money, and experimental techniques needed to isolate and analyze the relevant biological systems). The necessary information includes temporal and spatial data (with a resolution of the scale of individual cells), knowledge of the types, location and lineages of a single cell and a clear understanding of the multiple signaling networks that influence cell differentiation and zonation.
In summary, this modeling approach facilitates the translation from experiments on human cells to real-world predictions of gastrointestinal toxicity such as therapy-induced diarrhea. This model may be further used for understanding of pathology to develop a new drug related to intestinal cell structure (e.g., inflammatory bowel disease). We expect that this approach will save time and money by reducing/removing the need for animal experiments, and thereby expediting the development of safer and/or more efficacious drugs for patients.
Myocardial infarction, the occlusion of a coronary artery and the subsequent damage of myocardial tissue, can result in the death of up to one billion cardiomyocytes. The lost cardiomyocytes cannot be regained due to the limited regenerative potential of the adult mammalian heart (Frangogiannis, 2015). A promising therapeutic approach under development is the endovascular delivery of human ventricular progenitor (HVP) cells to the infarcted region of the heart with the goal of generating new cardiac myocytes that can be assembled into a three-dimensional functional ventricular heart tissue (Poch et al., 2022). Such an approach has the potential of providing a safe and efficacious therapy leading to full cardiac functional recovery for patients suffering from heart failure with reduced ejection fraction (Foo et al., 2021).
Myocardial regeneration is based on a complex interplay of cells and molecular pathways spanning several temporal and spatial scales. This therapeutic intervention interacts with the three-phased cellular responses that follow a myocardial infarction: the inflammatory, proliferative, and maturation phases (Humeres and Frangogiannis, 2019a). Predicting the time-dependent response of the treated tissue, to maximize therapeutic potential, is a daunting task, which a reliable computational model may facilitate by testing multiple therapeutic scenarios in silico. Furthermore, the safety and efficacy of this therapeutic intervention should, ideally, be assessed by reflecting individual patient’s specific variables such as the location of the HVP injection, the number of injections, and the number of cells per injection.
To model such a complex series of biological events, an ABM framework was chosen, with ABMs falling within the broad category of QSP models by integrating several scales from molecular pathways to organ behavior. ABMs allow the tissue and organ level behavior to naturally emerge from the simulated cellular level while also allowing the integration of intracellular pathways and tissue level chemical kinetics within their framework (Metzcar et al., 2019). The developed computational model is a combination of ordinary differential equations (ODEs) describing key intracellular pathways governing cellular proliferation and differentiation; partial differential equations (PDEs) describing tissue level chemical kinetics; and an overarching ABM framework describing the cellular dynamics and connecting the various scales together.
Given the complexity of this multifaceted biological response, the most relevant biological mechanisms had to be selected to develop a computationally reasonable model accounting for the sequela of events between the initial myocardial insult and the HVP-driven myocardial remodeling. As part of this selection process, every biological event deemed important enough to be included in the model went through an evaluation stage where different degrees of simplification were applied: for example, (i) the complex post-infarct chemokine field was modeled as a single representative chemotactic agent (Rouillard and Holmes, 2014), (ii) key cell types such as host cardiac myocytes, fibroblasts, donor HVPs, and endothelial cells were considered in the parsimonious model, and (iii) two temporal phases were defined - (a) the initial acute remodeling phase and (b) the subsequent HVP delivery and its remodeling phase. An HVP modeling and simulation workflow is shown in Figure 4A.
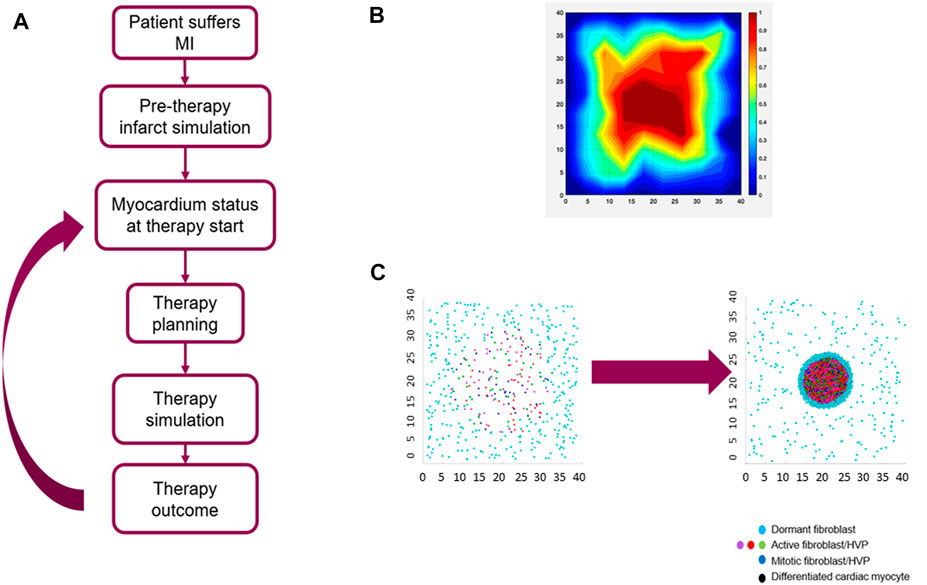
FIGURE 4. Agent-Based Model (ABM) of myocardial infarction (MI) and human ventricular progenitor (HVP) therapy. (A) clinical HVP therapy modeling and simulation workflow; (B) collagen area fraction predicted by the ABM at the end of the acute remodeling phase of myocardial infarction; (C) simulation example of HVP proliferation and differentiation: initial stage before HVP injection where only host fibroblasts are present (left) and final stage after HVP injection where a mixture of host fibroblasts and HVPs are present (right). Size of the simulated domain (shown in mm) is 4 × 4 cm.
A region of damaged myocardial tissue, characterized by the release of a representative inflammatory cytokine, is defined at the start of the simulation within a larger area of healthy myocardium, in turn characterized by an anti-inflammatory phenotype. The representative cytokine field represents the combined effect of transforming growth factor-β (TGF-β), fibroblast growth factors (FGFs), interleukin-1β, tumor necrosis factor alpha (TNF-α) and the other cytokines released during the initial inflammatory phase. Host fibroblasts, dispersed throughout the entire cardiac tissue, are modeled to react by migrating towards the injury site following the cytokine gradient. After reaching the infarcted myocardial region, these fibroblasts are modeled to secrete new collagen. At each timestep the fibroblasts’ position and the cytokine field are updated, the latter is described by a diffusion-reaction PDE. This remodeling phase is assumed to last for up to 14 days (Humeres and Frangogiannis, 2019b). In addition to migrating toward the injury site and secreting new collagen, host fibroblasts switch between an active, pro-inflammatory phenotype and a dormant one depending on the strength of the local cytokine field: the local cytokine field is evaluated for each fibroblast and, if above a threshold, the fibroblast is considered active. Fibroblasts proliferate and become apoptotic after they reach a maximum number of proliferating events. The collagen area fraction at the end of acute remodeling phase is shown in Figure 4B.
The model accounts for the time delay between infarction and HVP cell injection in selected locations inside and around the infarcted tissue. The delivered HVPs mature over time and differentiate into cardiac myocytes replacing the damaged tissue. The new cardiomyocytes, by replacing non-contractile tissue, lead to an improvement in the ejection fraction, the primary metric for therapy evaluation. An example of simulation results of HPV proliferation and differentiation is shown in Figure 4C.
In summary, a computational model of heart regeneration following HVP cell injection has been developed to help identify optimal delivery settings, on a patient-specific basis, for therapy-planning via outcome prediction. The model is used to evaluate the safety and efficacy of the therapy at the in vivo preclinical stage, with the goal of employing it for clinical translation. In vivo preclinical trials are expensive and time-consuming, with a parameter space that is difficult to be fully investigated, with a caveat that the results might be sparse and therefore difficult to interpret. QSP models such as one presented here are, therefore, a promising avenue to support experimental work. Given the complexity of the underlying biological mechanisms and the multiple temporal and spatial scales involved, the ABM framework has provided us with the ability to connect different temporal and spatial scales seamlessly. Furthermore, this approach can be also used to predict the effect of pharmacological therapies (e.g., anti-arrhythmic drugs) and evaluate their effect on the overall cell therapy outcomes, which prepares for the mitigation of adverse events that might arise under specific therapeutic conditions. The model has its set of challenges that include computationally and biologically complex mechanisms: (i) multiple spatial and timescales that lead to computational challenges to accommodate the time scales of fast intracellular kinetics vs days/months of infarct remodeling at the tissue/organ level and (ii) intricacies of the complex network of cytokines regulating inflammation. Despite these challenges, this modeling approach facilitates answering therapy development questions like dose, injection site, and number of injection sites as monotherapy or in combination with other pharmacological interventions.
Immuno-oncology (IO) is an essential part of the cancer therapeutic arsenal for a variety of cancer types and stages. Tumors use checkpoint proteins [e.g., the cytotoxic T lymphocyte-associated molecule-4 and programmed cell death receptor-1 (PD1)] that suppress immune system responses to evade detection, and therapeutic interventions based on checkpoint inhibitions have proven to be successful. However, there are still a lot of patients who require different effective therapy (Haslam and Prasad, 2019), and limiting regulatory T cells may be therapeutically effective (anti-Treg) by directly reducing Treg activities, leading to indirect augmentation of the function of effector T cells (Teff).
QSP modeling approach was taken to answer if targeting Treg enhances the efficacy of a checkpoint inhibitor (anti-PD1). Mice experiments directly answer the question by observing tumor size changes, but they do not provide insights on longitudinal changes in biomarkers due to the difficulty in sampling. With such a limitation of data scarcity, QSP modeling was expected to help elucidate the mechanistic interplay of anti-PD1 and anti-Treg on Treg and Teff longitudinal changes.
Instead of a full representation of the immune system with all its components in the model, our systems modelling strategy focused on specific components that characterize the major pathways while maintaining connections among measurable biomarkers. In this case study, the underlying dynamics are represented via two components of the immune system: i) an immuno-response component via cytotoxic effector T cells (Teff), which attack tumor cells and ii) an immuno-suppressive component via Treg and PD1/PDL1 (Programmed cell death-1/-ligand 1), which control immune evasion mechanisms. These two components are modelled to modulate the tumor growth that is assumed to continue if uninhibited.
The diagram in Figure 5A shows the model representation where the tumor grows and sheds antigens that stimulate Treg and Teff; Teff drive tumor killing; Treg downregulate the activity of Teff; PDL1 binding to Teff downregulates Teff; and the PDL1 level is increased by Teff. The QSP model was built using collected longitudinal data of tumor size kinetics, Treg (measured via a biomarker called Forkhead box P3: FOXP3) and Teff (associated with a biomarker called granzyme B: GzmB). The pharmacological treatments studied include an anti-Treg drug, a PD1 antibody (anti-PD1) drug, and their combination. The inter-individual variability was addressed using non-linear mixed effects modeling (Kosinsky et al., 2018) by allowing the stimulation of the immune cells and the initial inoculum size vary among mice.
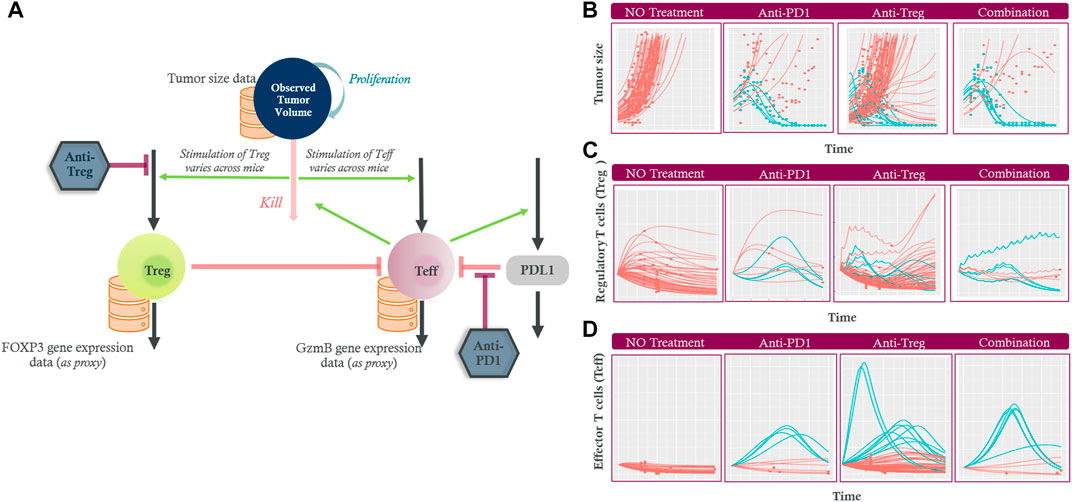
FIGURE 5. (A) The diagram shows the tumor growing (“proliferation”) and being eliminated (“kill”) by effector T cells (Teff). Increased tumor death is assumed to stimulate Teff and regulatory T cells (Treg) via antigen shedding leading to various stimulation. Teff upregulate PDL1 (green arrow) while their own activity is downregulated by Treg cells (left orange inhibition line) and the PDL1 (right orange inhibition line). The inhibition by anti-Treg and anti-PD1 treatment are also indicated (maroon inhibition line). Longitudinal experimental data (orange databases) for tumor size, Treg and Teff data were used to calibrate the model. The model captured the heterogeneity in (B) Tumor size, (C) Treg, and (D) Teff changes over time in non-treated (first column), anti-PD1 (second column), anti-Treg (third column) and the combination (fourth column) treated mice. The tumor size, Treg and Teff profiles for mice classed as responders are shown in blue while non-responders are shown in red (several Treg profiles after anti-Treg treatments are hidden beneath the red decreasing non-responder profiles). Regulatory T cells (Treg); Effector T cells (Teff); Programmed cell death ligand 1 (PDL1); Granzyme B (GzmB); Forkhead box P3 (FOXP3) protein.
Figure 5B shows that the model captured the heterogeneity in tumor growth in the absence of any treatment. Administration of an anti-PD1 drug or an anti-Treg drug at a projected therapeutic dose resulted in tumor growth inhibition in some of the studied mice. The combination of the treatments led to slightly more responders compared to those of anti-PD1 only, although the number of studied mice was small (responders: non-responders = 6:4 vs. 4:6). The time-course effects on Treg (Figure 5C) and Teff (Figure 5D) by the two monotherapies and their combination were predicted, given the limited measured data: since the final biopsy sample was obtained upon animal sacrifice at the end of the experiment, Treg and Teff data were available at one time point from each non-responder mouse, whereas the responder could not provide any measurable data due to no tumor biopsy that can be taken.
The modeling approach provided insights into plausible longitudinal changes of Teff and Treg despite limited measured data. In non-responders with an anti-PD1 drug only, the Teff activity did not change or decreased (Figure 5D) whereas the level of Treg initially increases in most cases prior to a plateau or decrease (Figure 5C). The initial increase in Treg is likely due to the uncontrolled tumor growth and its subsequent antigen shedding that stimulated the Treg activity. In contrast, the responders were predicted to have a delayed Treg build-up while a sustained rapid increase of Teff was observed. Both cell types subsequently decreased upon the tumor disappearing in the responders.
With the anti-Treg, Treg activity was depressed in most cases in accordance with the treatment’s mechanism of action (several blue responder Treg profiles after anti-Treg treatments are hidden beneath the red non-responder profiles in Figure 5C). The dosing intervals of anti-Treg (short half-life) were reflected as fluctuations in the predicted Treg level. The Treg activity increased once the treatment was terminated in the non-responder. Although the Treg profiles showed high inter-individual variability even in the no-treatment cohort, the responders were always predicted to have robust increase in Teff, suggesting that Teff is a better predictive marker for the response compared to Treg. In other words, while Treg are the therapy target, the response is mainly driven by the intrinsic capability of each mouse’s Teff that are stimulated by the tumor. The Teff activity is masked by Treg in the absence of treatment, and when an anti-Treg weakens the Treg’s inhibition effect on Teff, the increased Teff activity becomes apparent. The combination of these drugs leads to a synergistic process where simultaneous modulation of Treg and Teff activity resulted in an enhanced response, although several mice did not respond even in the combination.
This case study demonstrates that the longitudinal interplay of tumor inhibition, Treg and Teff could be deciphered using the modeling approach despite no or limited measured biomarker data. Although the immune response mechanisms used in the model were grossly simplified, the model could capture the observed main patterns in the response and provide an understanding of the complex dynamics associated with the response. Considering the hypothesis that anti-Treg treatment as a combination with anti-PD1 would provide additional treatment effects, longitudinal Treg profiles may have been regarded more directly relevant for drug development decisions. However, this case study indicates longitudinal Treg profiles have high inter-individual variability, and the Teff profiles may better predict pharmacological responses.
In summary, we developed a minimalistic description of immune and immune-suppression activity by reflecting the observed two longitudinal biomarkers of each study subject simultaneously, although there are several other mathematical IO modeling approaches (Sancho-Araiz et al., 2021). This approach ensured that the link to the two targets under-consideration (PD1 receptor and Treg cells) is explicit and the predictions could be interpreted with a simple mechanism given the available limited data. Moreover, in our approach we also captured the pre-clinical variability in response through the non-linear mixed effect approach, which is not often done within QSP applications.
This paper demonstrates the role of QSP modeling efforts in AstraZeneca’s drug development program via case studies, which were selected to cover a wide range of mathematical modeling methods including agent-based modeling, partial differential equation modeling, and ordinary differential equation modeling. Other applications of systems modeling at AstraZeneca include evaluation of new target pathways; optimization of compound physicochemical properties; characterization of efficacy and toxicity mechanisms of action; recommendation of treatment posology of monotherapies and combination therapies by balancing efficacy and toxicity; and guidance of study subject stratification strategies based on clinical responder features. Particularly, quantitative systems modeling plays a critical role in predicting clinical hematological toxicity risks by translating preclinical data obtained from micro-physiological systems (MPS), which use human hematopoietic stem cells and progenitor cells in the bone marrow (Pin et al., 2021). The analysis of MPS data is routinely performed to simulate clinical outcomes under various dosage regimens for mono- and combination-therapies to recommend the optimal dosage regimen to be studied in clinical trials.
Given our understanding of the crucial role that QSP plays, some challenges exist in the path towards achieving the goals set for QSP models. The major challenge is the limitation in data to support complex biological and pharmacological systems. Inconsistent, imbalanced, missing and/or limited data in various datasets can affect the prediction accuracy of these models (Cheng et al., 2022). Fortunately, project experimentalists are willing to conduct studies to generate essential data if such studies are both feasible to conduct and considered valuable for better clinical prediction via modeling. However, complex assay development and inherently complex physiological systems result into scarcity of relevant multi-scale data. These challenges may lead to modeling bias with incorrect assumptions, which requires systems modelers to develop computationally efficient methods to check the model performance (e.g., multi-parameter model diagnostic profiling (Fey et al., 2015)). Another notable challenge is the accessibility of models with standardized annotation. To meet the accelerated timelines of projects that require model-derived insights, available models in the public domain can be adopted to answer compound-specific questions thereby eliminating the need to build a model from scratch. However, often times, these models can fail to run or fail to reproduce published outcomes (Kirouac et al., 2019). The external sharing of QSP models via markup languages and open-source code will help enhance the reusability, and collaborative development of these models (Fleisher et al., 2017). This is particularly important if QSP models are to be accepted as a part of regulatory submissions because, from a regulatory perspective, this transparency will improve the admissibility of these models.
As tremendous time and effort is required to develop these complex models, early engagement between modelers and the project team is necessary. Due to the inherent nature of the QSP model framework being multiscale; being computationally complex; and requiring extensive data from non-clinical as well as clinical space, early-stage planning and involvement of QSP modelers in the project team are inevitable. The development and success of these models are dependent on i) the quality, amount, and type of data available from non-clinical to clinical research and ii) the interdisciplinary collaboration among translational scientists, quantitative modelers (who understand pharmacology and systems biology), and clinicians. Especially, rapid advancement in new drug modalities such as cell therapy, gene therapy, bis-specific engagers, antisense nucleotides to name a few (that accompany a plethora of hypotheses and missing information in addition to observed data) requires input from various expertise to help integrate the available knowledge. This further emphasizes the need for collaboration and makes it inevitable to have continuing conversation, engagement among the modeler, project team, and regulatory agencies regarding model use, model credibility assessment, verification, and decision risk.
There is a steady rise in both QSP-related publications and submissions to the US Food Drug Administration (FDA) (Zineh, 2019), but the inclusion of QSP models in regulatory documents is still at its early stages. In 2014, the US FDA evaluated an alternate dosing regimen in the treatment of hypoparathyroidism, which was possible using an open-source QSP model (Peterson and Riggs, 2010). Based on the quantitative evaluation of the model, the FDA asked for optimization of the dosing regimen to address safety concerns for hypercalciuria. It is therefore important for QSP models to be transparent, reproducible and be extended beyond the research space to have an impact in drug development. A consortium-based article by the UK QSP network group (created in 2015) outlined the recommendations and provided a checklist of best practices for QSP models that can enhance the quality, reproducibility, and further applicability of QSP models (Cucurull-Sanchez et al., 2019). Gadkar et al. highlighted the important components of the QSP modeling process crucial for success, which includes the identification of impactful questions, understanding of time constraints and agreement on feasible modeling goals as crucial parts of project initiation (Gadkar et al., 2016). FDA scientists discussed model calibration, validation, and performance of a few published QSP models and proposed a list of questions to be addressed for the QSP model assessment to establish common expectations (Bai et al., 2019).
The systems modeling approaches have been useful for company’s discussions thereby facilitating go/no-go decisions or study design decisions. While the potential of QSP modeling approaches need more clinical verification, the future iterations of these models with clinical data from various stages can especially aid in reducing the Phase I concerns on safety, assisting in repositioning Phase II efficacy ‘failures’, and/or assisting in patient increase responder rates by proposing study subject stratification strategy (few listed in Figure 2). It is important to note that as clinical development is expensive compared to non-clinical and early development, tailoring each step of drug development with earlier quantitative pharmacological understanding of a drug candidate can aid overall financial savings. With the recent advancement in biomarker assay methods, novel non-clinical experiment systems, and high computing power, in addition to an interest in model-informed drug development by academia, regulatory agencies, and pharmaceutical companies, we anticipate more successful use cases of QSP modeling integrated in drug development and regulatory decisions.
All authors, MV, LG, JB, GVD, CPA, MG and HK contributed towards writing the manuscript.
All authors were employed by AstraZeneca while the manuscript was written. The work was supported by AstraZeneca.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Aghamiri, S. S., Amin, R., and Helikar, T. (2022). Recent applications of quantitative systems pharmacology and machine learning models across diseases. J. Pharmacokinet. pharmacodynamics 49 (1), 19–37. doi:10.1007/s10928-021-09790-9
Bai, J. P. F., Earp, J. C., and Pillai, V. C. (2019). Translational quantitative systems pharmacology in drug development: From current landscape to good practices. AAPS J. 21 (4), 72. doi:10.1208/s12248-019-0339-5
Bloomingdale, P., Housand, C., Apgar, J. F., Millard, B. L., Mager, D. E., Burke, J. M., et al. (2017). Quantitative systems toxicology. Curr. Opin. Toxicol. 4, 79–87. doi:10.1016/j.cotox.2017.07.003
Bonabeau, E., Agent-based modeling: Methods and techniques for simulating human systems. Proc. Natl. Acad. Sci. U. S. A., 2002;99:7280–7287. doi:10.1073/pnas.082080899
Bradshaw, E. L., Spilker, M. E., Zang, R., Bansal, L., He, H., Jones, R. D. O., et al. (2019). Applications of quantitative systems pharmacology in model-informed drug discovery: Perspective on impact and opportunities. CPT Pharmacometrics Syst. Pharmacol. 8 (11), 777–791. doi:10.1002/psp4.12463
Buske, P., Galle, J., Barker, N., Aust, G., Clevers, H., and Mjpcb, Loeffler (2011). A comprehensive model of the spatio-temporal stem cell and tissue organisation in the intestinal crypt. PLoS Comput. Biol. 7 (1), e1001045. doi:10.1371/journal.pcbi.1001045
Cheng, L., Qiu, Y., Schmidt, B. J., and Wei, G-W. (2022). Review of applications and challenges of quantitative systems pharmacology modeling and machine learning for heart failure. J. Pharmacokinet. pharmacodynamics 49 (1), 39–50. doi:10.1007/s10928-021-09785-6
Clausznitzer, D., Pichardo-Almarza, C., Relo, A. L., van Bergeijk, J., van der Kam, E., Laplanche, L., et al. (2018). Quantitative systems pharmacology model for alzheimer disease indicates targeting sphingolipid dysregulation as potential treatment option. CPT Pharmacometrics Syst. Pharmacol. 7 (11), 759–770. doi:10.1002/psp4.12351
Csikász-Nagy, A. (2009). Computational systems biology of the cell cycle. Briefings Bioinforma. 10 (4), 424–434. doi:10.1093/bib/bbp005
Cucurull-Sanchez, L., Chappell, M. J., Chelliah, V., Amy Cheung, S. Y., Derks, G., Penney, M., et al. (2019). Best practices to maximize the use and reuse of quantitative and systems pharmacology models: Recommendations from the United Kingdom quantitative and systems pharmacology network. CPT Pharmacometrics Syst. Pharmacol. 8 (5), 259–272. doi:10.1002/psp4.12381
Fey, D., Halasz, M., Dreidax, D., Kennedy, S. P., Hastings, J. F., Rauch, N., et al. (2015). Signaling pathway models as biomarkers: Patient-specific simulations of JNK activity predict the survival of neuroblastoma patients. Sci. Signal. 8 (408), ra130. doi:10.1126/scisignal.aab0990
Fleisher, B., Brown, A. N., and Ait-Oudhia, S. (2017). Application of pharmacometrics and quantitative systems pharmacology to cancer therapy: The example of luminal a breast cancer. Pharmacol. Res. 124, 20–33. doi:10.1016/j.phrs.2017.07.015
Foo, K. S., Lehtinen, M. L., Leung, C. Y., Lian, X., Xu, J., Keung, W., et al. (2021). Human ISL1(+) ventricular progenitors self-assemble into an in vivo functional heart patch and preserve cardiac function post infarction. Mol. Ther. J. Am. Soc. Gene Ther. 29 (1), 409. doi:10.1016/j.ymthe.2020.11.015
Frangogiannis, N. G. (2015). Pathophysiology of myocardial infarction. Compr. Physiol. 5 (4), 1841–1875. doi:10.1002/cphy.c150006
Gadkar, K., Kirouac, D. C., Mager, D. E., van der Graaf, P. H., and Ramanujan, S. (2016). A six-stage workflow for robust application of systems pharmacology. CPT Pharmacometrics Syst. Pharmacol. 5 (5), 235–249. doi:10.1002/psp4.12071
Haber, A. L., Biton, M., Rogel, N., Herbst, R. H., Shekhar, K., Smillie, C., et al. (2017). A single-cell survey of the small intestinal epithelium. Nature 551 (7680), 333–339. doi:10.1038/nature24489
Haslam, A., and Prasad, V. J. Jno (2019). Estimation of the percentage of US patients with cancer who are eligible for and respond to checkpoint inhibitor immunotherapy drugs. JAMA Netw. Open 2 (5), e192535–e. doi:10.1001/jamanetworkopen.2019.2535
Humeres, C., and Frangogiannis, N. G. (2019). Fibroblasts in the infarcted, remodeling, and failing heart. JACC Basic Transl. Sci. 4 (3), 449–467. doi:10.1016/j.jacbts.2019.02.006
Humeres, C., and Frangogiannis, N. G. (2019). Fibroblasts in the infarcted, remodeling, and failing heart. JACC Basic Transl. Sci. 4 (3), 449–467. doi:10.1016/j.jacbts.2019.02.006
Kirouac, D., Cicali, B., and Schmidt, S. (2019). Reproducibility of quantitative systems pharmacology models: Current challenges and future opportunities. CPT Pharmacometrics Syst. Pharmacol. 8, 205–210. doi:10.1002/psp4.12390
Knöchel, J., Nilsson, C., Carlsson, B., Wernevik, L., Hofherr, A., Gennemark, P., et al. (2022). A case-study of model-informed drug development of a novel PCSK9 anti sense oligonucleotide. Part 1: First time in man to phase II. CPT: pharmacometrics & systems pharmacology 11 (12), 1569–1577. doi:10.1002/psp4
Kosinsky, Y., Dovedi, S. J., Peskov, K., Voronova, V., Chu, L., Tomkinson, H., et al. (2018). Radiation and PD-(L)1 treatment combinations: Immune response and dose optimization via a predictive systems model. J. Immunother. cancer 6 (1), 17. doi:10.1186/s40425-018-0327-9
Leil, T. A., and Bertz, R. (2014). Quantitative Systems Pharmacology can reduce attrition and improve productivity in pharmaceutical research and development. Front. Pharmacol. 5, 247. doi:10.3389/fphar.2014.00247
Liu, L., Guo, Y., Zheng, J., Lu, Y., Shen, Y., Huang, C., et al. (2019). Paneth cell ablation increases the small intestinal injury during acute necrotizing pancreatitis in rats. Mol. Med. Rep. 20 (1), 473–484. doi:10.3892/mmr.2019.10274
Loewe, L., and Hillston, J. (2008). Computational models in systems biology. Genome Biol. 9 (12), 328. doi:10.1186/gb-2008-9-12-328
McQuade, R. M., Stojanovska, V., Abalo, R., Bornstein, J. C., and Nurgali, K. (2016). Chemotherapy-induced constipation and diarrhea: Pathophysiology, current and emerging treatments. Curr. Emerg. Treat. 7, 414. doi:10.3389/fphar.2016.00414
Meineke, F. A., Potten, C. S., and Loeffler, M. (2001). Cell migration and organization in the intestinal crypt using a lattice-free model. Cell Prolif. 34 (4), 253–266. doi:10.1046/j.0960-7722.2001.00216.x
Metzcar, J., Wang, Y., Heiland, R., and Macklin, P. (2019). A review of cell-based computational modeling in cancer biology. JCO Clin. cancer Inf. 3, 1–13. doi:10.1200/cci.18.00069
Nijsen, M. J. M. A., Wu, F., Bansal, L., Bradshaw-Pierce, E., Chan, J. R., Liederer, B. M., et al. (2018). Preclinical QSP modeling in the pharmaceutical industry: An IQ consortium survey examining the current landscape. CPT Pharmacometrics Syst. Pharmacol. 7 (3), 135–146. doi:10.1002/psp4.12282
Peter, K., Altman, Russ B., KimBrouwer, L. R., Califano, Andrea, David, Z., D'Argenio, , et al. (2011). Brian shoichet JLS, shankar subramaniam, piet van der Graaf and paolo vicini quantitative and systems pharmacology in the post-genomic era: New approaches to discovering drugs and understanding therapeutic mechanisms NIH white paper. Bethesda: NIH. Group QW. Report No.
Peters, M. F., Choy, A. L., Pin, C., Leishman, D. J., Moisan, A., Ewart, L., et al. (2020). Developing in vitro assays to transform gastrointestinal safety assessment: Potential for microphysiological systems. Lab a chip 20 (7), 1177–1190. doi:10.1039/c9lc01107b
Peterson, M. C., and Riggs, M. M. J. B. (2010). A physiologically based mathematical model of integrated calcium homeostasis and bone remodeling. Bone 46 (1), 49–63. doi:10.1016/j.bone.2009.08.053
Pin, C., Collins, T., Gibbs, M., and Kimko, H. (2021). Systems modeling to quantify safety risks in early drug development: Using bifurcation analysis and agent-based modeling as examples. AAPS J. 23 (4), 77. doi:10.1208/s12248-021-00580-2
Pitt-Francis, J., Pathmanathan, P., Bernabeu, M. O., Bordas, R., Cooper, J., Fletcher, A. G., et al. Chaste: A test-driven approach to software development for biological modelling. 2009;180(12):2452–2471. doi:10.1016/j.cpc.2009.07.019
Poch, C. M., Foo, K. S., De Angelis, M. T., Jennbacken, K., Santamaria, G., Bähr, A., et al. (2022). Migratory and anti-fibrotic programmes define the regenerative potential of human cardiac progenitors. Nat. Cell Biol. 24 (5), 659–671. doi:10.1038/s41556-022-00899-8
Ramanujan, S., Gadkar, K., and Kadambi, A. (2016). Quantitative systems pharmacology: Applications and adoption in drug development. Systems pharmacology and pharmacodynamics. New York City: Springer.
Riccio, O., van Gijn, M. E., Bezdek, A. C., Pellegrinet, L., van Es, J. H., Zimber-Strobl, U., et al. (2008). Loss of intestinal crypt progenitor cells owing to inactivation of both Notch1 and Notch2 is accompanied by derepression of CDK inhibitors p27Kip1 and p57Kip2. EMBO Rep. 9 (4), 377–383. doi:10.1038/embor.2008.7
Rouillard, A. D., and Holmes, J. W. (2014). Coupled agent-based and finite-element models for predicting scar structure following myocardial infarction. Prog. biophysics Mol. Biol. 115 (2-3), 235–243. doi:10.1016/j.pbiomolbio.2014.06.010
Sancho-Araiz, A., Mangas-Sanjuan, V., and Trocóniz, I. F. (2021). The role of mathematical models in immuno-oncology: Challenges and future perspectives. Pharmaceutics 13 (7), 1016. doi:10.3390/pharmaceutics13071016
Tan, S. H., Phuah, P., Tan, L. T., Yada, S., Goh, J., Tomaz, L. B., et al. (2021). A constant pool of Lgr5+ intestinal stem cells is required for intestinal homeostasis. Cell Rep. 34 (4), 108633. doi:10.1016/j.celrep.2020.108633
Keywords: Quantitative systems pharmacology, systems modeling, model informed drug development, quantitative systems toxicology, Computational modeling
Citation: Verma M, Gall L, Biasetti J, Di Veroli GY, Pichardo-Almarza C, Gibbs MA and Kimko H (2023) Quantitative systems modeling approaches towards model-informed drug development: Perspective through case studies. Front. Syst. Biol. 2:1063308. doi: 10.3389/fsysb.2022.1063308
Received: 06 October 2022; Accepted: 21 December 2022;
Published: 12 January 2023.
Edited by:
Federico Reali, Fondazione The Microsoft Research - University of Trento Centre for Computational and Systems Biology, ItalyReviewed by:
Saroja Ramanujan, Development Sciences, Genentech, United StatesCopyright © 2023 Verma, Gall, Biasetti, Di Veroli, Pichardo-Almarza, Gibbs and Kimko. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Meghna Verma, bWVnaG5hLnZlcm1hQGFzdHJhemVuZWNhLmNvbQ==; Holly Kimko, aG9sbHkua2lta29AYXN0cmF6ZW5lY2EuY29t
†ORCID: Meghna Verma, orcid.org/0000-0002-7776-0433; Louis Gall, orcid.org/0000-0002-1805-2357; Jacopo Biasetti, orcid.org/0000-0001-7180-7889; Giovanni Di Veroli, orcid.org/0000-0002-5251-8181; Cesar Pichardo-Almarza, orcid.org/0000-0002-8283-6068; Megan Gibbs, orcid.org/0000-0002-7258-8187; Holly Kimko, orcid.org/0000-0003-1456-4862
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.