- Laboratory of Systems and Synthetic Biology, Wageningen University & Research, Wageningen, Netherlands
Introduction
This editorial inaugurates the section Data and Model Integration of the new Frontiers in Systems Biology. In what follows, I will present a general discussion of topics in data and model integration which I hope will illustrate the challenging and exciting research opportunities that lay ahead in computational Systems Biology.
“Without data you’re just another person with an opinion”. (W. E. Deming, 1900-1993).
The Two Worlds of Systems Biology
In Systems Biology two approaches can be distinguished when investigating a biological system, be it a cell or a complete organism: the bottom up and top-down approaches (Figure 1A).
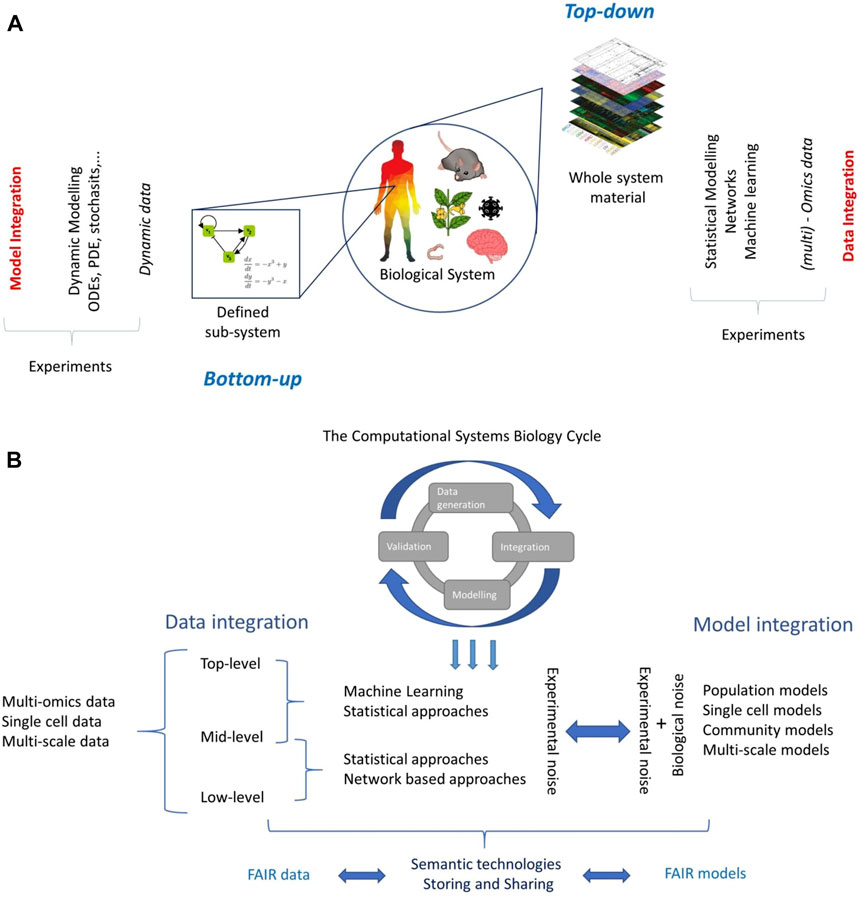
FIGURE 1. (A) The two worlds of Systems Biology. Partially adapted from (Chang, Creighton et al., 2013). (B) Overview of data and model integration in the Systems Biology context.
The bottom-up approach, or inductive approach (Oltvai and Barabási 2002), begins from a detailed understanding of a particular biological or biochemical mechanism (or combination thereof) such as a pathway, a chemical reaction, or a gene regulatory network which constitutes a subset of a larger and more complex system (Figure 1A). The aim is to create a mathematical model that can reproduce experimental data (Torres and Santos 2015); such models are usually based on (systems of) differential equations, and data collected is dynamic in time, but many other approaches are possible (ElKalaawy and Wassal 2015).
The top-down approach, or deductive approach (Oltvai and Barabási 2002), aims to gain insights on the whole biological system using system-wide data acquired using high-throughput experimental techniques, often at different omics levels (Haas, Zelezniak et al., 2017). Information is extracted by applying statistical modelling, data reduction techniques, and machine learning tools often in combination with network inference and analysis (Ideker and Krogan 2012; Rosato, Tenori et al., 2018).
These models are phenomenological in nature but serve to uncover new insights into the biological system under study (Bruggeman, Hornberg et al., 2007). The goal is to characterize the interactions among the many molecular constituents of the system (genes, proteins, metabolites) to describe comprehensibly the interactions among the molecular constituents of the system (genes, proteins, metabolites, etc.), possibly across different conditions (Ideker and Krogan 2012; Rosato, Tenori et al., 2018), to understand how these parts interact and how these interactions shape the system-wide behavior.
The two approaches should be combined in an iterative and virtuous cycle, with the top-down approach generating hypotheses to be tested experimentally in the laboratory. Experiments should confirm or disprove the hypotheses and generate or suggest new experiments that will inform a new set of data in an iterative manner: Ideally, the two worlds of Systems Biology should feed each other information until a model is produced that is able to reproduce the behavior of the systems under investigation (Kitano, 2002a; Kitano, 2002b).
As a matter of fact, the two worlds do not communicate, or communicate sporadically and with great difficulty, and work as separate strategies; paradoxically, it is the advancement of both experimental and computational techniques, with their increasing refinement and complexity, that drives the bottom-up and top-down approaches further apart, entrenching systems biology in silos based on distinct disciplines and methods (Vodovotz 2021).
Integration is thus the overall grand challenge in Systems Biology and the Frontiers in Systems Biology is therefore dedicated to the concept of integration across disciplines, across modelling scales, across datasets, and across computational methodologies (Vodovotz 2021).
Data and Model Integration plays and will play an even greater role in modern biological science and solicits significant theoretical and applied advances in different areas of research, from classical statistic, to machine, to semantic technologies.
The Challenge Ahead: Data Integration Requires Different Approaches and Computational Tools
The advent of high-throughput omics technology and experimental platforms has enabled the quick and cost-effective measurement of a biological system at different levels, from transcriptome to epigenome (Haas, Zelezniak et al., 2017; Krassowski, Das et al., 2020). This has led to an era where data is abundantly available but tools to analyze it efficiently are missing or not optimal (Marx 2013).
Data integration (fusion) aims to combine data from multiple experimental platforms/omics levels to obtain more information about a system than could be obtained by considering a single type of data (Haas, Zelezniak et al., 2017; Krassowski, Das et al., 2020) (Figure 1B). A typical example is to combine gene expression profiles with protein or metabolite abundance profiles. How to better combine data is an open problem and the solutions are often devised on an ad-hoc basis.
Since data fusion is common in many fields of research, different taxonomies have been proposed to describe different approaches that can be classified according to one of the following criteria (Castanedo 2013): 1) Relationships between the data platforms, 2) Input data abstraction, 3) Input and output data abstraction levels, 4) the JDL (Joint Directors of Laboratories) data fusion framework (White 1987; Steinberg, Bowman et al., 1998), and 5) Type of architecture.
In Systems Biology, as well in analytical chemistry (Smolinska, Engel et al., 2019), the categorization of the data integration process is based on the abstraction level at which the data are fused (criterion 2). Under this taxonomy, three abstraction levels are distinguished, namely, low-, mid-, and high-level data fusion (Roussel, Bellon-Maurel et al., 2003).
Low-level data integration consists of the concatenation of two or more data sets (matrices) containing different measurements acquired on the same objects; such a concatenated matrix is then used for data analysis. This way of proceeding often results in data sets containing far more variables than observations which challenges the use of classical multivariate tools. Mid-level data integration attempts to resolve this problem by first performing dimensionality reduction followed by a low-level integration. Finally, the top-level data integration pertains the combination of the results obtained from the analyses performed on the different data matrices.
All these steps are challenging in themselves and impact on how efficiently we can use different data types to inform Systems Biology investigation of an organism.
The data integration problem at the low- and mid-level is usually attacked by means of statistical approaches: a great deal of work has been made, especially in the chemometrics community, mostly deploying statistical approaches, often with the goal of extracting the information that is common or unique to the different types of data (Hanafi and Kiers 2006; Acar, Lawaetz et al., 2013; Acar et al., 2014; van der Kloet, Sebastián-León et al., 2016) with methods like DISCO or DISCO-SCA (Van Deun, Van Mechelen et al., 2012).
While metabolomics has enjoyed an almost symbiotic relationship with chemometrics and benefited from it (Rosato, Tenori et al., 2018), these methods and their use have not propagated to the other disciplines that inform the top-down world of Systems Biology, like transcriptomics, proteomics, and other omics levels. In this respect the challenge is dual faced: from one side, the necessity of developing tools that can deal with the ever-increasing amount of data of different natures, on the other side, the necessity of making these methods available and understandable to practitioners, overcoming the major bottleneck responsible for the current siloed nature of Systems Biology.
I am of the opinion that data integration will benefit greatly from network science, especially for what concerns the analysis of network multiplexes (Kivelä, Arenas et al., 2014). While monolayer networks, such as those built from metabolite correlations or gene (co-)expression profiles describe associations between one type of molecular feature or information, a multilayer network connects nodes exiting in different layers, thus describing the inter-relationships and interaction across different levels of a system. This approach is fully consistent with the representation of a biological system as a set of interconnected networks, operating at different time and spatial scales.
Inferring the topology of interaction networks from data obtained from different omics level will play a bigger role in Systems Biology, with both synchronous (in a step-by-step fashion, two omics at a time) and asynchronous (all data concurrently) integration (Hawe, Theis et al., 2019) with possible use of prior biological knowledge in the inference process, not dissimilar to what was proposed for the analysis of omics data sets (Ramakrishnan, Vogel et al., 2009; Namkung, Raska et al., 2011; Reshetova, Smilde et al., 2014; Cambiaghi, Ferrario et al., 2017).
The challenge is now how to cross-link the statistical and network-based approaches and make them a tool in the toolbox of the system biologist. This will call for a stronger interaction between different communities of theoretical and applied statisticians, bioinformaticians, and chemometricians.
The Challenge Ahead: Tackling Data Heterogeneity
Taking into account the heterogeneity of the data that recent technological development has allowed access to will become a fundamental step. Metagenomics and metaproteomics, together with data from complex microbial communities (microbiome), are becoming more common, along with single cell measurements: DNA, RNA, protein, methylated DNA, or open chromatin nucleosome positioning can be simultaneously measured on the same cell. This data presents a complex structure, a large degree of sparsity, and an often unknown underlying experimental error structure. Proper data integration and analysis will be possible only through the characterization of experimental noise and its inclusion in all steps of data analysis and modelling.
The Challenge Ahead: Model Integration
The creation of a mathematical model to understand, predict, control, or design a biological system is a core theme in Systems Biology and it lays at the center of the bottom-up world (Torres and Santos 2015) (Figure 1A). Biological systems are dynamic in nature, and many biological processes, like enzyme-catalyzed reactions (Michaelis and Menten 1913), the action potentials in neurons (Hodgkin and Huxley 1952), the prey-predator interaction of species (Lotka 1920; Volterra 1926), and epidemic dynamics (Ross 1915; MacDonald, Cuellar et al., 1968), have been traditionally formulated as (systems of) nonlinear ordinary differential equations (ODEs). However, different approaches exists, based on partial differential equations, Bayesian equations, stochastic modelling, Petri nets, agent-based modelling, etc. [see (ElKalaawy and Wassal 2015) for a review].
All these approaches (Figure 1B) come with different limitations and challenges: Formulating an ODE model for a particular biological process may be simple, but the structural identification and estimation of the model parameters (which actually contain the information describing the system) are a critical challenge.
While model identification and estimation has relied on numerical methods (Moles, Mendes et al., 2003; Chis, Banga et al., 2011), the last few years have seen the emergence of the use of machine learning techniques, such as neural networks (Raissi, Perdikaris et al., 2019; Yazdani, Lu et al., 2020), to solve estimation problems or the proposal of new approaches which augment scientific models with machine-learnable structures to achieve scientifically-based learning (Rackauckas, Ma et al., 2020). We can anticipate that machine learning and deep learning will play a pivotal role in the model identification and estimation, and novel approaches will be devised to address more complex scenarios such those described through stochastic modelling.
Answering relevant biological questions and the modeling of an organism, however, implies going from the study of isolated mechanisms to the study of the interaction of such mechanisms. This naturally leads to the problem of model integration which touches different scales, both temporal and spatial (for which Frontiers is Systems Biology has a dedicated section: See Multiscale Mechanistic Modeling section https://www.frontiersin.org/journals/systems-biology/sections/multiscale-mechanistic-modeling#about).
However, even the integration at a single level poses tremendous challenges. For instance, the advent of single cell measurement opens the possibility, at least in principle, to create models that are cell-specific. Developing algorithms and tools or conceptual frameworks for integrating such models to understand the emerging behavior of cells communities (Bak-Maier and Stojkovic 2005; Aguirre de Cárcer 2020), tissues (Machado, Duque et al., 2015) and, ultimately, organisms is thus necessary. Stochastics modelling (Wilkinson 2009; Wilkinson 2018) at the cell level will be certainly central to this task, but it comes with its own challenges, among them the problem of distinguishing between interesting biological variability and experimental variability, which is, in itself, sometimes ambiguous (Hsu and Moses 2021).
The Challenge Ahead: Noise as Trait d’Union Between Data and Model Integration
Noise permeates biology at all levels (Monod 1971); as far back as 1940, Max Delbruck recognized that fluctuations in small populations of enzyme molecules could affect cell physiology (Delbrück 1940). Since then, a great deal of effort and interest has been put into understanding how biological noise shapes the behavior of biological systems (Simpson, Cox et al., 2009; Tsimring 2014; Diambra and Santillán 2019; Eling, Morgan et al., 2019; Prado Casanova 2020).
However, it should be remembered that the experimental noise ultimately affects the level of accuracy with which a system, no matter how big or small, can be described and characterized. From this standpoint, the characterization of the experimental noise is the fil rouge connecting data and model integration (Figure 1B). Characterization of experimental noise is a formidable task and will call for the input of both theoretical and experimental communities with a concerted effort of multidisciplinary expertise, in a truly Systems Biology spirit to understand data generation mechanisms, to arrive at effective integration of data and models.
The Challenge Ahead: Sharing and Dissemination of Data and Models
A discussion about data and model integration cannot stray from touching a practical yet fundamental aspect: the storing and sharing of data and models. Successful data and model integration rests on the assumption that data and models are curated [not enough emphasis can be put on the curation step and its implications (Lyngdoh 2013; Freitas and Curry 2016)], openly shared, and findable without restriction. For this, I strongly advocate for FAIR (Findable, Accessible, Interoperable, and Reusable) (Wilkinson, Dumontier et al., 2016) data and models (https://www.go-fair.org/fair-principles/) (Figure 1B).
Many funding organizations, like the European Commission, have in now in place policies and mandates that require FAIR data and Open Access to publications and research data (Collins, Genova et al., 2018) or, like the American NIH (Health 2018) (https://datascience.nih.gov/nih-strategic-plan-data-science) and most recently the UNESCO (https://en.unesco.org/science-sustainable-future/open-science/recommendation), indicate FAIR guidelines to open science and data as a guiding principle.
Although most researchers recognize the importance of sharing research data (and models), most of them had never shared or reused research data (Y. Zhu, 2020).
Many communities that are an integral part of the system biology family have proposed data standard and reporting guidelines (Transcriptomics (Brazma, Hingamp et al., 2001); Proteomics (Taylor, Paton et al., 2007); Metabolomics (Fiehn, Robertson et al., 2007); (Figure 1B) but only the genomics community has a long standing precedent for data sharing and open science, which dates back to the Bermuda Principles of 1996 (Cook-Deegan & McGuire, 2017). Why this happened is difficult to say: Gene expression profiling as we know today became popular in the second half of the 90’s (Schena et al., 1995, 1996) and the community immediately recognized the importance of making transcriptomics data widely available. The GEO database was created in 2000 (Clough & Barrett, 2016). Since then, the deposition of transcriptomics profiles to the GEO database become a de facto prerequisite for publication.
Here, in the Data and Model integration section, we aim to foster a systems biology community that is truly FAIR and Open, inviting contributors to store and share data, models, protocols, and publications relating to systems biology research projects through platforms like FAIR-DOM (Wolstencroft, Krebs et al., 2016) (http://www.fair-dom.org) and relevant databases.
This implies that we should see an integrative systems biology relying on the exploitation of semantic web technologies for data integration and sharing (Figure 1B). The idea of a semantic systems biology system dates back to the early 2000s (Jenssen and Hovig 2002) but it is due to initiative such as SEEK (Wolstencroft, Owen et al., 2011) and FAIR-DOM (Wolstencroft, Krebs et al., 2016) that it has reached a larger audience and is now ready to be embraced by the whole community.
Concluding Remarks
The Data and Model Integration section of Frontiers in Systems Biology aims to become a forum for the dissemination, sharing, and discussion of results addressing the theoretical and practical problems originating from the need to integrate data and data resources, algorithms, models, and frameworks. The section welcomes multi- and cross-disciplinary research, spanning from statistics to network science, from data and computer science to data analysis, from semantic approaches to experimental works, aiming to achieve better understanding of the mechanisms underlying the generation of the diverse types of data used in systems biology investigations.
“Data! Data Data! I can’t make bricks without clay!” (A Conan Doyle, 1859-1930).
Author Contributions
ES is the sole author, having conceived, written, and edited this manuscript.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Acar, E., Papalexakis, E. E., Gürdeniz, G., Rasmussen, M. A., Lawaetz, A. J., Nilsson, M., et al. (2014). Structure-Revealing Data Fusion. BMC bioinformatics 15 (1), 239. doi:10.1186/1471-2105-15-239
Acar, E., Lawaetz, A. J., Rasmussen, M. A., and Bro, R. (2013). Structure-revealing Data Fusion Model with Applications in Metabolomics. Citeseer: EMBC.
Aguirre de Cárcer, D. (2020). Experimental and Computational Approaches to Unravel Microbial Community Assembly. Comput. Struct. Biotechnol. J. 18, 4071–4081. doi:10.1016/j.csbj.2020.11.031
Bak-Maier, M., and Stojkovic, A. (2005). Complex Cell Behaviors in Development: Recent Progress and Emerging Challenges. Genome Biol. 6 (7), 331. doi:10.1186/gb-2005-6-7-331
Brazma, A., Hingamp, P., Quackenbush, J., Sherlock, G., Spellman, P., Stoeckert, C., et al. (2001). Minimum Information about a Microarray experiment (MIAME)-toward Standards for Microarray Data. Nat. Genet. 29 (4), 365–371. doi:10.1038/ng1201-365
Bruggeman, F. J., Hornberg, J. J., Boogerd, F. C., Westerhoff, H. V., Baginsky, S., and Fernie, A. R. (2007). Introduction to Systems Biology. Plant Systems Biology Basel, Birkhäuser Basel, 1–19.
Cambiaghi, A., Ferrario, M., and Masseroli, M. (2017). Analysis of Metabolomic Data: Tools, Current Strategies and Future Challenges for Omics Data Integration. Brief Bioinform 18 (3), 498–510. doi:10.1093/bib/bbw031
Castanedo, F. (2013). A Review of Data Fusion Techniques. scientific World J. 2013. doi:10.1155/2013/704504
Chang, K., Weinstein, J. N., Collisson, E. A., Mills, G. B., Shaw, K. R., Ozenberger, B. A., et al. (2013). The Cancer Genome Atlas Pan-Cancer Analysis Project. Nat. Genet. 45 (10), 1113–1120. doi:10.1038/ng.2764
Chis, O.-T., Banga, J. R., and Balsa-Canto, E. (2011). Structural Identifiability of Systems Biology Models: a Critical Comparison of Methods. PloS one 6 (11), e27755. doi:10.1371/journal.pone.0027755
Collins, S., Genova, F., Harrower, N., Hodson, S., Jones, S., Laaksonen, L., et al. (2018). Turning FAIR into Reality: Final Report and Action Plan from the European Commission Expert Group on FAIR Data. Luxembourg: Publications Office of the European Union.
Delbrück, M. (1940). Statistical Fluctuations in Autocatalytic Reactions. J. Chem. Phys. 8 (1), 120–124. doi:10.1063/1.1750549
Diambra, L., and Santillán, M. (2019). Editorial: Emergent Effects of Noise in Biology: From Gene Expression to Cell Motility. Front. Phys. 7 (83). doi:10.3389/fphy.2019.00083
Eling, N., Morgan, M. D., and Marioni, J. C. (2019). Challenges in Measuring and Understanding Biological Noise. Nat. Rev. Genet. 20 (9), 536–548. doi:10.1038/s41576-019-0130-6
ElKalaawy, N., and Wassal, A. (2015). Methodologies for the Modeling and Simulation of Biochemical Networks, Illustrated for Signal Transduction Pathways: A Primer. Biosystems 129, 1–18. doi:10.1016/j.biosystems.2015.01.008
Fiehn, O., Robertson, D., Griffin, J., van der Werf, M., Nikolau, B., Morrison, N., et al. (2007). The Metabolomics Standards Initiative (MSI). Metabolomics 3 (3), 175–178. doi:10.1007/s11306-007-0070-6
Haas, R., Zelezniak, A., Iacovacci, J., Kamrad, S., Townsend, S., and Ralser, M. (2017). Designing and Interpreting 'multi-Omic' Experiments that May Change Our Understanding of Biology. Curr. Opin. Syst. Biol. 6, 37–45. doi:10.1016/j.coisb.2017.08.009
Hanafi, M., and Kiers, H. A. L. (2006). Analysis of K Sets of Data, with Differential Emphasis on Agreement between and within Sets. Comput. Stat. Data Anal. 51 (3), 1491–1508. doi:10.1016/j.csda.2006.04.020
Hawe, J. S., Theis, F. J., and Heinig, M. (2019). Inferring Interaction Networks from Multi-Omics Data. Front. Genet. 10 (535), 535. doi:10.3389/fgene.2019.00535
Hodgkin, A. L., and Huxley, A. F. (1952). A Quantitative Description of Membrane Current and its Application to Conduction and Excitation in Nerve. J. Physiol. 117 (4), 500–544. doi:10.1113/jphysiol.1952.sp004764
Hsu, I. S., and Moses, A. M. (2021). Stochastic Models for Single‐cell Data: Current Challenges and the Way Forward. FEBS J. 11. doi:10.1111/febs.15760
Ideker, T., and Krogan, N. J. (2012). Differential Network Biology. Mol. Syst. Biol. 8 (1), 565. doi:10.1038/msb.2011.99
Jenssen, T.-K., and Hovig, E. (2002). The Semantic Web and Biology. Drug Discov. Today 7 (19), 992. doi:10.1016/s1359-6446(02)02458-3
Kitano, H. (2002a). Computational Systems Biology. Nature 420 (6912), 206–210. doi:10.1038/nature01254
Kitano, H. (2002b). Systems Biology: A Brief Overview. Science 295 (5560), 1662–1664. doi:10.1126/science.1069492
Kivelä, M., Arenas, A., Barthelemy, M., Gleeson, J. P., Moreno, Y., and Porter, M. A. (2014). Multilayer Networks. J. Complex Networks 2 (3), 203–271. doi:10.1093/comnet/cnu016
Krassowski, M., Das, V., Sahu, S. K., and Misra, B. B. (20201598). State of the Field in Multi-Omics Research: From Computational Needs to Data Mining and Sharing. Front. Genet. 11, 610798. doi:10.3389/fgene.2020.610798
Lotka, A. J. (1920). Analytical Note on Certain Rhythmic Relations in Organic Systems. Proc. Natl. Acad. Sci. USA 6 (7), 410–415. doi:10.1073/pnas.6.7.410
Lyngdoh, A., Baker, D., and Evans, W. (2013). “What We Leave behind: the Future of Data Curation,” in Trends, Discovery, and People in the Digital Age (Oxford, England: Chandos Publishing), 153–165. doi:10.1016/b978-1-84334-723-1.50010-3
MacDonald, G., Cuellar, C. B., and Foll, C. V. (1968). The Dynamics of Malaria. Bull. World Health Organ. 38 (5), 743–755.
Machado, P. F., Duque, J., Étienne, J., Martinez-Arias, A., Blanchard, G. B., and Gorfinkiel, N. (2015). Emergent Material Properties of Developing Epithelial Tissues. BMC Biol. 13 (1), 98. doi:10.1186/s12915-015-0200-y
Moles, C. G., Mendes, P., and Banga, J. R. (2003). Parameter Estimation in Biochemical Pathways: a Comparison of Global Optimization Methods. Genome Res. 13 (11), 2467–2474. doi:10.1101/gr.1262503
Monod, J. (1971). Chance and Necessity: an Essay on the Natural Philosophy of Modern Biology. Tech. Cult. 13 (4), 662. doi:10.2307/3102860
Namkung, J., Raska, P., Kang, J., Liu, Y., Lu, Q., and Zhu, X. (2011). Analysis of Exome Sequences with and without Incorporating Prior Biological Knowledge. Genet. Epidemiol. 35 (S1), S48–S55. doi:10.1002/gepi.20649
Oltvai, Z. N., and Barabási, A.-L. (2002). Life's Complexity Pyramid. Science 298 (5594), 763–764. doi:10.1126/science.1078563
Prado Casanova, M. (2020). Noise and Synthetic Biology: How to Deal with Stochasticity. NanoEthics 14 (1), 113–122. doi:10.1007/s11569-020-00366-4
Rackauckas, C., Ma, Y., Martensen, J., Warner, C., Zubov, K., Supekar, R., et al. (2020). Universal Differential Equations for Scientific Machine Learning. arXiv preprint arXiv:2001.04385.
Raissi, M., Perdikaris, P., and Karniadakis, G. E. (2019). Physics-informed Neural Networks: A Deep Learning Framework for Solving Forward and Inverse Problems Involving Nonlinear Partial Differential Equations. J. Comput. Phys. 378, 686–707. doi:10.1016/j.jcp.2018.10.045
Ramakrishnan, S. R., Vogel, C., Kwon, T., Penalva, L. O., Marcotte, E. M., and Miranker, D. P. (2009). Mining Gene Functional Networks to Improve Mass-Spectrometry-Based Protein Identification. Bioinformatics 25 (22), 2955–2961. doi:10.1093/bioinformatics/btp461
Reshetova, P., Smilde, A. K., van Kampen, A. H., and Westerhuis, J. A. (2014). Use of Prior Knowledge for the Analysis of High-Throughput Transcriptomics and Metabolomics Data. BMC Syst. Biol. 8 Suppl 2 (2), S2–S11. doi:10.1186/1752-0509-8-S2-S2
Rosato, A., Tenori, L., Cascante, M., De Atauri Carulla, P. R., Martins dos Santos, V. A. P., and Saccenti, E. (2018). From Correlation to Causation: Analysis of Metabolomics Data Using Systems Biology Approaches. Metabolomics 14 (4), 37. doi:10.1007/s11306-018-1335-y
Ross, R. (1915). Some A Priori Pathometric Equations. Bmj 1 (2830), 546–547. doi:10.1136/bmj.1.2830.546
Roussel, S., Bellon-Maurel, V., Roger, J.-M., and Grenier, P. (2003). Fusion of Aroma, FT-IR and UV Sensor Data Based on the Bayesian Inference. Application to the Discrimination of white Grape Varieties. Chemometrics Intell. Lab. Syst. 65 (2), 209–219. doi:10.1016/s0169-7439(02)00111-9
Simpson, M. L., Cox, C. D., Allen, M. S., McCollum, J. M., Dar, R. D., Karig, D. K., et al. (2009). Noise in Biological Circuits. WIREs Nanomed Nanobiotechnol 1 (2), 214–225. doi:10.1002/wnan.22
Smolinska, A., Engel, J., Szymanska, E., Buydens, L., Blanchet, L., and Cocchi, M. (2019). “General Framing of Low-, Mid-, and High-Level Data Fusion with Examples in the Life Sciences,” in Data Handling in Science and Technology (Elsevier), 31, 51–79. doi:10.1016/b978-0-444-63984-4.00003-x
Steinberg, A. N., Bowman, L., and White, F. E. (1998). Revisions to the JDL Data Fusion Model. Quebec: The Joint NATO/IRIS Conference.
Taylor, C. F., Paton, N. W., Lilley, K. S., Binz, P.-A., Julian, R. K., Jones, A. R., et al. (2007). The Minimum Information about a Proteomics experiment (MIAPE). Nat. Biotechnol. 25 (8), 887–893. doi:10.1038/nbt1329
Torres, N. V., and Santos, G. (2015). The (Mathematical) Modeling Process in Biosciences. Front. Genet. 6 (354), 354. doi:10.3389/fgene.2015.00354
Tsimring, L. S. (2014). Noise in Biology. Rep. Prog. Phys. 77 (2), 026601. doi:10.1088/0034-4885/77/2/026601
van der Kloet, F. M., Sebastián-León, P., Conesa, A., Smilde, A. K., and Westerhuis, J. A. (2016). Separating Common from Distinctive Variation. BMC bioinformatics 17 Suppl 5 (5), 195–286. doi:10.1186/s12859-016-1037-2
Van Deun, K., Van Mechelen, I., Thorrez, L., Schouteden, M., De Moor, B., Van Der Werf, M. J., et al. (2012). DISCO-SCA and Properly Applied GSVD as Swinging Methods to Find Common and Distinctive Processes. PloS one 7 (5), e37840. doi:10.1371/journal.pone.0037840
Vodovotz, Y. (2021). Integrating Mindsets and Toolsets at the Frontier of Systems Biology. Front. Syst. Biol. 1 (1). doi:10.3389/fsysb.2021.745692
Volterra, V. (1926). "Variazioni e fluttuazioni del numero d'individui in specie animali conviventi."
White, F. E. (1987). Data Fusion Lexicon, Joint Directors of Laboratories, Technical Panel for C3, Data Fusion Sub-panel. San Diego: Naval Ocean Systems Center.
Wilkinson, D. J. (2009). Stochastic Modelling for Quantitative Description of Heterogeneous Biological Systems. Nat. Rev. Genet. 10 (2), 122–133. doi:10.1038/nrg2509
Wilkinson, M. D., Dumontier, M., Aalbersberg, I. J., Appleton, G., Axton, M., Baak, A., et al. (2016). The FAIR Guiding Principles for Scientific Data Management and Stewardship. Sci. Data 3, 160018. doi:10.1038/sdata.2016.18
Wolstencroft, K., Krebs, O., Snoep, J. L., Stanford, N. J., Bacall, F., Golebiewski, M., et al. (2016). FAIRDOMHub: a Repository and Collaboration Environment for Sharing Systems Biology Research. Nucleic Acids Res. 45 (D1), D404–D407. doi:10.1093/nar/gkw1032
Wolstencroft, K., Owen, S., du Preez, F., Krebs, O., Mueller, W., Goble, C., et al. (2011). The SEEK. Methods Enzymol. 500, 629–655. doi:10.1016/b978-0-12-385118-5.00029-3
Keywords: data fusion, data heterogeneity, data sharing, FAIR principles, measurement noise, networks, model sharing, semantic web approaches
Citation: Saccenti E (2021) Specialty Grand Challenge: Data and Model Integration in Systems Biology. Front. Syst. Biol. 1:800894. doi: 10.3389/fsysb.2021.800894
Received: 24 October 2021; Accepted: 02 November 2021;
Published: 03 December 2021.
Edited and Reviewed by:
Yoram Vodovotz, University of Pittsburgh, United StatesCopyright © 2021 Saccenti. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Edoardo Saccenti, ZWRvYXJkby5zYWNjZW50aUB3dXIubmw=
 Edoardo Saccenti
Edoardo Saccenti