- 1Center for Space Physics, Boston University, Boston, MA, United States
- 2Earth Systems Research Center, University of New Hampshire, Durham, NH, United States
- 3Space Weather Laboratory, NASA Goddard Space Flight Center, Greenbelt, MD, United States
- 4Department of Physics, The Catholic University of America, Washington DC, MD, United States
- 5College of Science, George Mason University, Fairfax, VA, United States
- 6School of Physics and Astronomy, College of Science and Engineering, University of Minnesota, Minneapolis, MN, United States
- 7Department of Atmospheric and Oceanic Sciences, University of California Los Angeles, Los Angeles, CA, United States
We analyze the properties of relativistic (>700 keV) electron precipitation (REP) events measured by the low-Earth-orbit (LEO) POES/MetOp constellation of spacecraft from 2012 through 2023. Leveraging the different profiles of REP observed at LEO, we associate each event with its possible driver: waves or field line curvature scattering (FLCS). While waves typically precipitate electrons in a localized radial region within the outer radiation belt, FLCS drives energy-dependent precipitation at the edge of the belt. Wave-driven REP is detected at any MLT sector and L shell, with FLCS-driven REP occurring only over the nightside–a region where field line stretching is frequent. Wave-driven REP is broader in radial extent on the dayside and accompanied by proton precipitation over 03–23 MLT, either isolated or without a clear energy-dependent pattern, possibly implying that electromagnetic ion cyclotron (EMIC) waves are the primary driver. Across midnight, both wave-driven and FLCS-driven REP occur poleward of the proton isotropic boundary. On average, waves precipitate a higher flux of >700 keV electrons than FLCS. Both contribute to energy deposition into the atmosphere, estimated of a few MW. REP is more associated with substorm activity than storms, with FLCS-driven REP and wave-driven REP at low L shells occurring most often during strong activity (SML* < −600 nT). A preliminary analysis of the Solar Wind (SW) properties before the observed REP indicates a more sustained (∼5 h) dayside reconnection for FLCS-driven REP than for wave-driven REP (∼3 h). The magnetosphere appears more compressed during wave-driven REP, while FLCS-driven REP is associated with a faster SW of lower density. These findings are useful not only to quantify the contribution of >700 keV precipitation to the atmosphere but also to shed light on the typical properties of wave-driven vs FLCS-driven precipitation which can be assimilated into physics-based and/or predictive radiation belt models. In addition, the dataset of ∼9,400 REP events is made available to the community to enable future work.
1 Introduction
Energetic (>10 s keV) electrons trapped in the Earth’s outer radiation belt undergo various processes including acceleration, transport, and loss (Li and Hudson, 2019; Reeves et al., 2003). We primarily focus on the loss of relativistic (>700 keV) electrons into the atmosphere (i.e., relativistic electron precipitation, REP), attributed to pitch-angle scattering either due to plasma waves or field line curvature. Both mechanisms violate the conservation of adiabatic invariants (Schulz and Lanzerotti, 1974), resulting in a change in electron pitch-angle and the subsequent precipitation into Earth’s atmosphere. The growing consensus that the precipitation of radiation belt electrons possibly affects atmospheric ionization and chemistry (Capannolo et al., 2024a; Chapman-Smith et al., 2023; Duderstadt et al., 2021; Fytterer et al., 2015; Khazanov et al., 2018; 2021; Meraner and Schmidt, 2018; Mironova et al., 2015; Pettit et al., 2021; Randall et al., 2005; 2015; Robinson et al., 1987; Sinnhuber et al., 2012; Yu et al., 2018) highlights the need for a comprehensive characterization of this phenomenon in terms of location, flux, input power and geomagnetic activity, to accurately quantify contribution of REP in atmospheric models (Matthes et al., 2017; van de Kamp et al., 2016).
Among the various plasma waves observed in Earth’s magnetosphere, chorus, hiss, and electromagnetic ion cyclotron (EMIC) waves are known to cause precipitation (Thorne, 2010). Extensive observational, theoretical, and numerical studies have revealed that EMIC waves are often the primary driver of high-energy precipitation (e.g., Blum et al., 2024; Capannolo et al., 2019; Hendry et al., 2016; Yahnin et al., 2016; 2017). As a low-Earth-orbit (LEO) satellite passes through the precipitation region, it observes an enhanced precipitating electron flux, typically corresponding to the radial scale of the equatorial wave driver and the favorable conditions of wave-particle scattering (see Section 2.2 for the description of an example of wave-driven REP; Figure 1A).
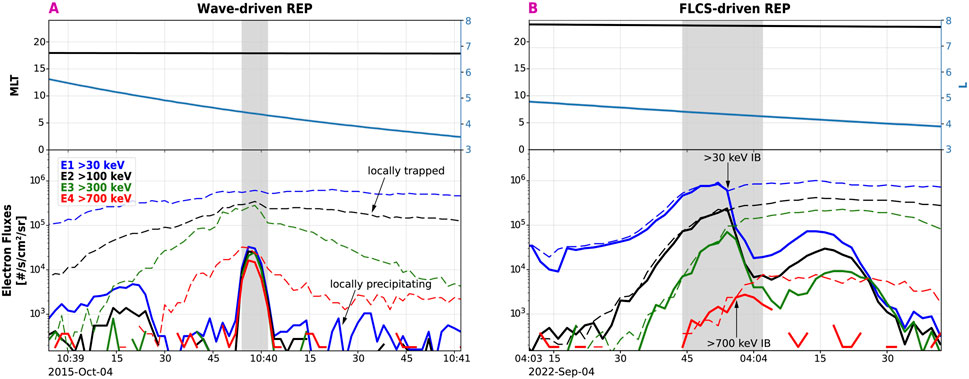
Figure 1. Examples of a wave-driven event (A) and FLCS-driven event (B). Top panels show the MLT (black) and L-shell (blue). Lower panels show the electron fluxes observed by POES, color-coded in energy. Dashed lines indicate the 90° telescope measurements (i.e., locally trapped electrons) and solid lines indicate the 0° telescope measurements (i.e., locally precipitating electrons). REP identified by the DL classifier is highlighted in gray. In panel B, we indicate the isotropic boundary (IB): the IB for >30 keV occurs at a slightly higher L shell than that for >700 keV electrons.
Field line curvature is associated with the precipitation of both protons and electrons: as field lines stretch away from the Earth, their curvature radius decreases, becoming comparable to the particle gyroradius (typically by a factor of ∼8; e.g., Büchner and Zelenyi, 1989; Dubyagin et al., 2018; 2021; Sergeev et al., 1983; 1993), leading to particle loss (field line curvature scattering, FLCS). This process is often observed near the nightside current sheet thus also referred to as current sheet scattering (CSS). Satellites at low altitudes detect FLCS-driven precipitation as an energy-dependent precipitation profile, with high-energy particles precipitating at lower L shells than low-energy particles (see Section 2.2 for the description of an example of FLCS-driven REP; Figure 1B). When the precipitating flux is approximately equal to the trapped flux, the pitch-angle distribution is isotropic, and the precipitation is observed at LEO. This border defines the isotropy boundary (IB) and its location varies depending on the species and energy (e.g., Capannolo et al., 2022a; Ganushkina et al., 2005; Sivadas et al., 2019; Wilkins et al., 2023; Zou et al., 2024). Due to the larger Larmor radius of protons, the proton IB is located at lower latitudes than the electron IB. Additionally, high-energy proton/electron IB is located at lower latitudes than low-energy proton/electron IB.
So far, studies have revealed that REP occurs at any magnetic local time (MLT), although it is more common from pre-dusk to post-midnight (Carson et al., 2012; Chen et al., 2023; Comess et al., 2013; Gasque et al., 2021; Hendry et al., 2016; Qin et al., 2024; Smith et al., 2016; Shekhar et al., 2017; 2018). However, there are still open questions about whether the observed REP was associated with waves, FLCS, or a combination of both. Understanding the drivers of REP is key for characterizing the typically expected contribution to the atmosphere from waves or FLCS and shedding light on loss processes in the outer belt.
In this work, we leverage the spatial trends of the REP electron flux observed at LEO by the POES (Polar Orbiting Environmental Satellites) and MetOp (Meteorological Operational) constellation to distinguish the associated driver: wave-driven REP occurs within the belt with a rather radially isolated profile, while FLCS-driven REP occurs at the outer edge of the belt and is accompanied by lower energy electron precipitation at higher L shells. These distinct features have been used in previous work to attempt to associate drivers with the precipitation observed at LEO; however, the focus has so far been limited to a short period (Yahnin et al., 2016; 2017; Wilkins et al., 2023) or a specific local time sector (Capannolo et al., 2022a). Here, we extend the analysis to all the POES/MetOp available 2-s data, covering the period from 2012 through 2023 with the aid of the deep learning-based classifier we developed in the past (Capannolo et al., 2022b). We describe the POES/MetOp data and methodology employed in Section 2 and illustrate the typical properties of wave-driven vs FLCS-driven REP in Section 3 (occurrence rate, location, flux, precipitation intensity, radial scales, and power into the atmosphere). We also investigate the REP association with proton precipitation and geomagnetic activity in Sections 4 and 5, respectively. Section 6 illustrates the solar wind (SW) trends preceding the observed precipitation. Together with our analysis, we release the dataset of REP events, categorized by the driver, to enable future studies in the community.
2 Data and methodology
To analyze the properties of the relativistic electron precipitation, we built a dataset of REP events observed at LEO, separated by drivers. We used data from the POES (Polar Orbiting Environmental Satellites) and MetOp (Meteorological Operational) satellite constellation (described in section 2.1) and the classifier we developed in Capannolo et al. (2022b), based on deep learning (DL). The methodology for collecting REP events is described in section 2.2.
2.1 POES/MetOp constellation
The POES/MetOp satellites (POES hereafter) cover all L shells and several MLT sectors by orbiting with high inclination (∼98.7°) at ∼800–850 km of altitude, with periods of ∼100 min (e.g., Evans and Greer, 2004; Rodger et al., 2010) and providing data at a 2-s cadence. The Medium Energy Proton and Electron Detector (MEPED) onboard each satellite monitors electron and proton fluxes at several energy ranges and two look-directions (0° telescope pointed at zenith and 90° telescope orthogonal to it; 30° of full aperture). With this configuration and a loss cone angle of ∼60° at LEO, when POES crosses mid-to-high latitudes, MEPED allows probing of the outer radiation belt population, both deep into the loss cone (locally precipitating population) and just outside it (locally trapped and mirroring particles) (e.g., Nesse Tyssøy et al., 2016). When intense precipitation is observed in POES/MetOp data, the 0° flux approaches the 90° flux. In other words, given a certain flux of the mirroring population, the portion of the precipitating population is comparable to the trapped one, such that the ratio R = 0°/90° (i.e., precipitation intensity or efficiency) approaches a value of ∼1. When R = 1, precipitation is isotropic, and the loss cone is full. Recent work by Selesnick et al. (2020) demonstrated that the 0° telescope sometimes detects trapped particles when diffusion is weak; however, such ambiguity does not apply to our work as we only consider time intervals of rather intense and distinct precipitation.
The nominal integral electron channels measure electrons at >30 keV (E1), >100 keV (E2), and >300 keV (E3), with the addition of a virtual electron channel that measures electrons at >700 keV (E4) from the P5 (2.5–6.9 MeV) and P6 (>6.9 MeV) proton channels (details in Green, 2013; Yando et al., 2011). Several past studies relied on the combination of these channels or the virtual E4 channel itself to identify relativistic electron precipitation (Capannolo et al., 2019; 2022a; Carson et al., 2012; Chen et al., 2023; Gasque et al., 2021; Qin et al., 2018; Shekhar et al., 2017; 2018; Yahnin et al., 2016; 2017). We also use the differential proton channels onboard MEPED (P1: 30–80 keV, P2: 80–250 keV, P3: 250–800 keV) to investigate the concurrent proton precipitation during the REP events.
It is worth mentioning a few caveats about POES data. In this work, we use the IGRF (International Geomagnetic Reference Field) magnetic field model, which is readily available in POES data. With another more sophisticated magnetic field model, the nightside L shell values would be slightly higher than those reported here. POES is known to have a rather high noise floor level (Nesse Tyssøy et al., 2016) and thus is not that sensitive to low flux values. As a result, our dataset might likely be biased to REP events with moderately high fluxes compared with other REP events observed with more sensitive instruments (e.g., ELFIN, FIREBIRD-II, etc.).
2.2 REP event dataset: Selection and classification of events
Figure 1 illustrates two examples of a typical REP: wave-driven in panel A and FLCS-driven in panel B. For a wave-driven REP (Figure 1A), the precipitating >700 keV electron flux (red solid line) is enhanced well within the outer belt, marked by the locally trapped >700 keV electron flux (red dashed line). For a FLCS-driven REP (Figure 1B), as L shell increases (from right to left), the first population reaching isotropy (i.e., similar precipitating and trapped flux) is the most energetic one (>700 keV, red); this is then followed by the >300 keV electron IB (green), the >100 keV electron IB (black), and finally the >30 keV electron IB. As a result, the classic signature of a FLCS-driven REP shows high-energy precipitation at lower L than low-energy precipitation, which instead occurs at higher L shells. This is a direct consequence of the electron gyroradius being energy-dependent. High-energy electrons have a larger gyroradius, thus are scattered by field lines with a larger curvature radius (i.e., farther away from Earth), but low-energy electrons, given their smaller gyroradius, require a smaller curvature radius (i.e., closer to Earth) to be scattered.
Capannolo et al. (2022b) developed a classifier of REP events based on the long short-term memory (LSTM; Hochreiter and Schmidhuber, 1997) deep learning architecture. This tool identifies REP and classifies it into either wave-driven or FLCS-driven REP. Although the performance is suitable for identifying and classifying events between wave and FLCS drivers (F1 ∼ 0.95), false positives or misclassified events are still possible. To use this classifier for scientific research, we post-process the model outputs to ensure events are properly classified. The post-processing routine is as follows:
1. Shift by 3 data points for each event (to improve centering the event boundaries around the event and account for the observed LSTM delay; see details in Capannolo et al., 2022b)
2. Merge wave-driven events if separated by only 5 data points
3. Discard unphysical events defined as a) maximum E4 0° count rate is less than 2 counts/s (discard precipitating fluxes at noise level), b) E4 90° has missing values within the event boundaries, and c) E4 0° flux is higher than E1, E2, E3 to avoid possible penetration outside the primary 0° telescope aperture (e.g., Evans and Greer, 2004; Shekhar et al., 2017; Gasque et al., 2021).
Note that none of the identified events occur within the South Atlantic Anomaly. Given that the classifier is based on machine learning, which is intrinsically probabilistic, the event boundaries represent regions of highly likelihood for precipitation, rather than precisely identifying flux enhancements using specific thresholds, as done in previous studies (e.g., Capannolo et al., 2022a; Carson et al., 2012; Gasque et al., 2021). Following the post-processing, we visually inspected each event identified and classified by the model (∼10,000 wave-driven, ∼12,000 FLCS-driven; see Supplementary Table S1 in Supplementary Material) and discarded any non-ideal REP event. An ideal wave-driven event resembles the one shown in Figure 1A, while FLCS-driven events are similar to that in Figure 1B. Specifically, a wave-driven event occurs a) within the outer belt (90° flux is relatively high both at lower and higher L shells than the 0° flux localized enhancement), b) isolated in L shell, and c) without energy-dependent precipitation at E1, E2 or E3. A FLCS-driven REP event is ideal if a) it occurs at the outer edge of the outer belt, b) precipitation is isotropic at all energies within the event boundaries, c) no additional precipitation is occurring during the energy dispersion profile (this could indicate additional waves/mechanisms), and d) no E1, E2, E3 0° flux fluctuations are occurring at L shells higher than the outer event boundary (considering the first ∼5 data points following the event boundary; this ensures the FLCS-driven isotropy is relatively in a steady state). Events categorized as one but belonging to two different classes (waves vs FLCS) are also excluded, but a wave-driven event near an FLCS-driven event (if clearly distinct) is included in the dataset if each event adheres to the aforementioned rules of the respective category. Examples of excluded events are shown in Supplementary Figure S1 in the Supplementary Material. We adopted a system of flags to distinguish between events to keep (flag = 0), discard (flag = 1), events to merge (flag = 2), misclassified events (flag = 3), and events to merge that have been misclassified (flag = 23). Supplementary Table S1 in SM illustrates how many events per flag we found and provides the model performance after our visual filter. The dataset is available in the repository by Capannolo and Staff (2024b).
Table 1 shows the number of wave-driven and FLCS-driven REP events identified, listed by year. There is a much larger number of wave-driven events (∼7,400) than FLCS events (∼2,000), although the model originally identified a similar number of REP in the two categories. We found that most wave-driven events (∼73%) are truly ideal, while FLCS-driven REP tends to be rather complex and does not often adhere to our definition of an “ideal FLCS-driven REP event” (only 16% of FLCS events are included). This finding is not surprising since the tail region is highly dynamic and overlapping mechanisms can be at play (field line scattering, excitation of waves, injections, etc.). We preferred to discard a large number of events in this category, including only those truly driven by FLCS. This approach allows us to study the properties of REP specifically driven by FLCS without the influence of other competing processes. Like any statistical dataset, this one is not necessarily a complete dataset of all REP events occurring from 2012 through 2023, as it relies on the deep learning classifier described in Capannolo et al. (2022b) and adheres to the criteria described above.

Table 1. Number of wave-driven (blue) and FLCS-driven (orange) REP events, listed by year and summed together (black).
2.3 Geomagnetic indices and solar wind data
We primarily focus on the westward auroral electrojet (AL) index. AL has been widely used to investigate substorm activity and we expect wave-driven or FLCS-driven REP to occur in association with substorms (i.e., during tail stretching and injections). We use the 1-min SML (maximum westward auroral electrojet) and SMR (symmetric ring current intensity) indices, which are the SuperMAG equivalents to the auroral index AL and the high-resolution ring current index Sym-H, respectively (Gjerloev, 2012; Newell and Gjerloev, 2011). We calculate SML* (SMR*) as the minimum SML (SMR) index over 3 h preceding the REP UT. While SML provides an instantaneous measurement of the westward auroral electrojet, SML* is useful to highlight if a substorm was occurring in the 3-h window before the observed REP. Similarly, SMR* provides insights on a storm occurring in the previous 3 h. The OMNI dataset provides 1-min resolution solar wind (SW) data.
3 Properties of REP
We used the event dataset to analyze the L-MLT distribution of REP and its occurrence rate given the number of POES passes (section 3.1). Then, we evaluate the average flux distribution and the precipitation efficiency (Section 3.2). We also investigated the radial extent of precipitation (Section 3.3) and estimated the input power of precipitation into the atmosphere (Section 3.4).
3.1 Occurrence rate and L-MLT distribution
The top row of Figure 2 shows the distribution in L-MLT bins (1 L by 1 MLT) of the total number of events (A), the wave-driven events (B), and the FLCS-driven events (C) in a logarithmic color scale. Most events are found in the 18–24 MLT sector, with a peak around ∼21 MLT and primarily focused between 4 and 6 L shells. The panels in the lower row show the occurrence rate of the REP events, calculated as the number of events found in each bin and divided by the number of POES passes in the same bin. The overall trends remain, though these plots highlight that REP events are observed only occasionally by POES data. Considering the total number of REP events and the cumulative days from 2012 through 2023, we find that the POES constellation crosses a region of precipitation at least twice a day (on average).
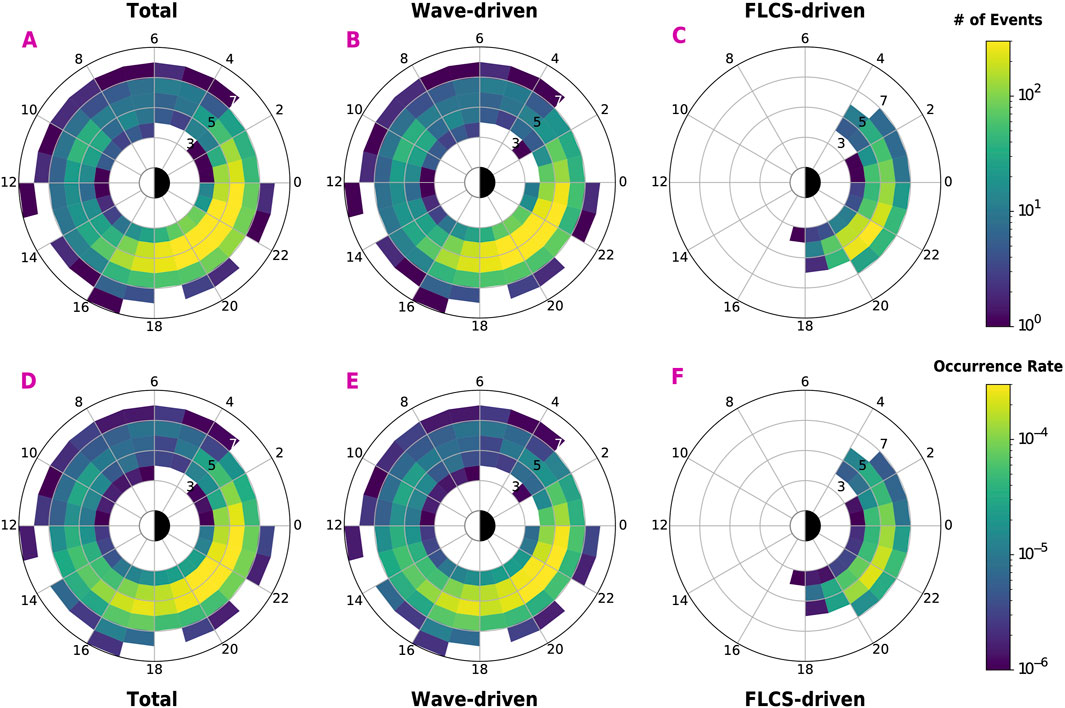
Figure 2. Distribution of the REP event number (top panels) and occurrence rates (bottom panels) for all events (A, D), wave-driven events (B, E) and FLCS-driven events (C, F). Color bars are on a logarithmic scale. Bin sizes are 1 L and 1 MLT.
Wave-driven precipitation occurs at any MLT sector, though is observed more frequently over ∼15–02 MLT, peaking in the heart of the outer belt at 4–6 L shells. This result agrees with previous literature both from POES data as well as other LEO satellites and is often attributed to EMIC wave scattering (e.g., Angelopoulos et al., 2023; Blum et al., 2015; Capannolo et al., 2021; 2023; Gasque et al., 2021). Wave-driven precipitation over 02–14 MLT has also been associated with EMIC waves (e.g., Blum et al., 2024; Hendry et al., 2016; Qin et al., 2018); however, this causal relationship seems to be less strong than that in the post-noon to post-midnight sectors. We do not explore this possible association in this work, though we speculate in section 4 on its simultaneous occurrence with proton precipitation–a proxy of EMIC wave activity. FLCS-driven precipitation only occurs on the night side, where field lines are indeed likely undergoing stretching. The FLCS occurrence rate peaks at pre-midnight (∼21–22 MLT) and at 5–6 L shells, in overall agreement with previous work linking field line curvature scattering with electron precipitation (e.g., Capannolo et al., 2022a; Comess et al., 2013; Smith et al., 2016; Yahnin et al., 2016; 2017; Wilkins et al., 2023). The FLCS-driven occurrence rates are lower than the wave-driven ones given the lower number of purely FLCS-driven events than the wave-driven ones (see Section 2.2 for details), rather than a true indication of FLCS occurring less frequently than wave-driven precipitation. Supplementary Figure S2 in the SM illustrates the distribution of events as a function of latitude and longitude, both in geographic and geomagnetic coordinates.
3.2 Relativistic electron flux and precipitation intensity
Figure 3 illustrates the distribution of average electron fluxes and the precipitation intensity (top row for wave-driven and bottom row for FLCS-driven). The average electron flux is calculated by averaging the E4 90° and 0° fluxes for each event and then sorting them into L-MLT bins and calculating the average values. The trapped flux (panels A and D) decreases as a function of L shell and is constant over MLT except for a slight enhancement over 6–10 MLT (Supplementary Figure S3 in SM), reproducing an expected trend for energetic electrons (Qin et al., 2024; Meredith et al., 2016; Allison et al., 2017). The precipitating flux (panels B and E) follows a similar trend in L shell without a clear MLT variation (Supplementary Figure S4 in SM). The fluxes for wave-driven events are overall higher than those during FLCS-driven events. Such a finding is expected as wave-driven REP typically occurs within the outer belt, while FLCS-driven precipitation occurs at the outer boundary of the belt, where the flux is already decreasing.
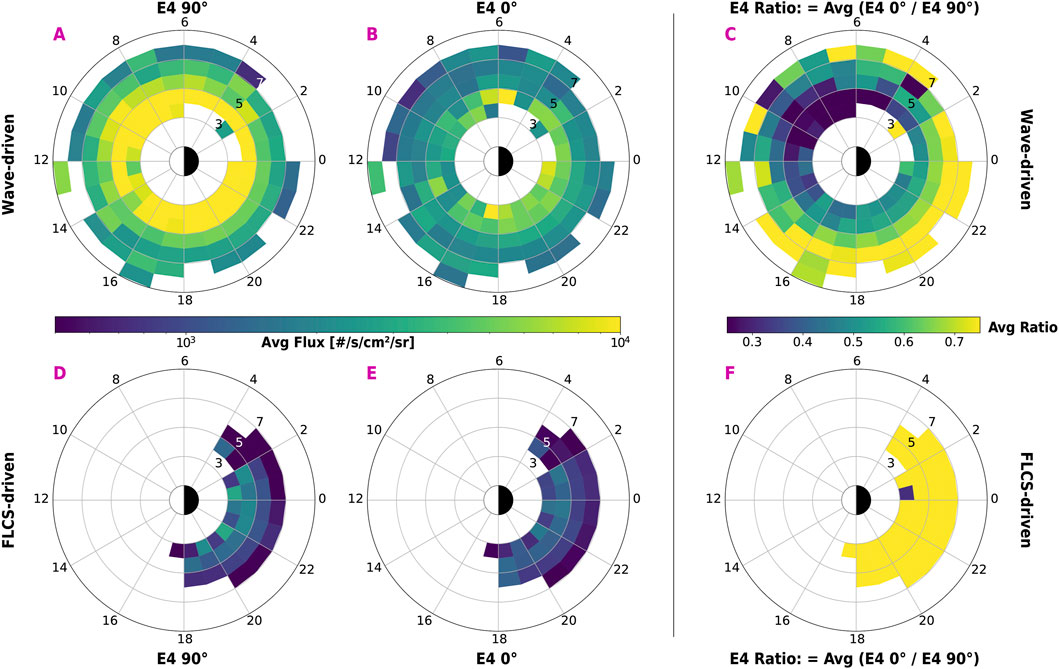
Figure 3. Relativistic (>700 keV) electron flux and precipitation intensity for wave-driven events (top row) and FLCS-driven events (lower row). Electron flux for the 90° (trapped, (A, D)) and 0° (precipitating, (B, E)) telescopes averaged (binned) in each bin from the averaged fluxes within each event boundaries. The upper and lower panels share the same logarithmic color scale. Precipitation intensity (C, F) calculated from the ratio 0°/90° for each event and averaged in each bin. The upper and lower panels share the same color scale.
Panels C and F illustrate the precipitation efficiency or intensity (e.g., Capannolo et al., 2019; Qin et al., 2024), calculated as the ratio of the precipitating flux over the locally trapped flux (fluxes are averaged within the event boundaries) for each event and binned in L-MLT. This ratio estimates how many electrons are precipitating (i.e., deep into the loss cone) compared to those locally mirroring (i.e., outside the loss cone), thus not contributing to the local precipitation. Previous studies also show how this value can be linked to diffusion coefficients, wave properties, and minimum resonant energy (Angelopoulos et al., 2023; Li et al., 2013; Longley et al., 2022); however, these calculations are left as future work. Given the isotropic nature of the FLCS-driven REP, the ratio is high throughout the region where FLCS events are found. Similar to FLCS-driven intensity, wave-driven REP is more efficient as a function of L but presents a minimum over ∼6–12 MLT and ∼3–6 L (Supplementary Figure S5 in SM). The trend in L shell is consistent with previous results from ELFIN observations described by Qin et al. (2024) and is probably due to the steeper L shell slope of the trapped flux compared to the precipitating flux.
An interesting feature of wave-driven REP is that its efficiency drops in the dawn-to-noon MLT sector. Although precipitation in this sector does not occur frequently (Figure 2E), it is nevertheless observed albeit with weaker intensity. This suggests that the dawn-to-noon waves are not particularly efficient at scattering >700 keV electrons. On the contrary, the ratio stays consistently higher elsewhere. The precipitation from noon to post-dusk has often been associated with EMIC waves (e.g., Blum et al., 2015; Capannolo et al., 2021; 2023; Hendry et al., 2016; Li et al., 2014; Rodger et al., 2015): the wave-electron resonant conditions are indeed favorable in these regions of high plasma density and low magnetic field, typically when the minimum resonant energy can be low enough to be detected by the >700 keV POES integral channel (Jordanova et al., 2008; Meredith et al., 2003; Silin et al., 2011; Summers and Thorne, 2003; Qin et al., 2020; Woodger et al., 2018). This would also explain why the efficiency is lower over the dawn-to-noon MLT sector: here, the resonant condition for EMIC-driven precipitation typically occurs at several MeV rather than the preferential sub-MeV and ∼MeV energies detected by POES. In this region, other waves, such as hiss and chorus waves are present, and we cannot exclude their contribution (e.g., Blum et al., 2015; Ma et al., 2021; Reidy et al., 2021; Shumko et al., 2021; Kandar et al., 2023). Identifying the specific wave driver of this precipitation requires further investigations. Precipitation across midnight has also been associated with EMIC waves (Blum et al., 2024; Capannolo et al., 2022a; Comess et al., 2013; Yahnin et al., 2016; 2017; Smith et al., 2016); however, here, both waves and FLCS contribute to precipitation, with the FLCS-driven efficiency being higher than the wave-driven one.
3.3 Radial extent
The DL-based classifier (mentioned in Section 2.2) identifies the boundaries of each REP event, typically characterized by intense precipitation. Here, we calculate the radial extent ΔL and ΔMLAT (magnetic latitude) associated with each event. ΔL estimates the approximate equatorial region in the radial direction where waves or FLCS are efficient at scattering electrons, while ΔMLAT provides the latitudinal extent at low altitudes. To avoid bias in the analysis, we also rule out a small percentage of events that span only a single data point (
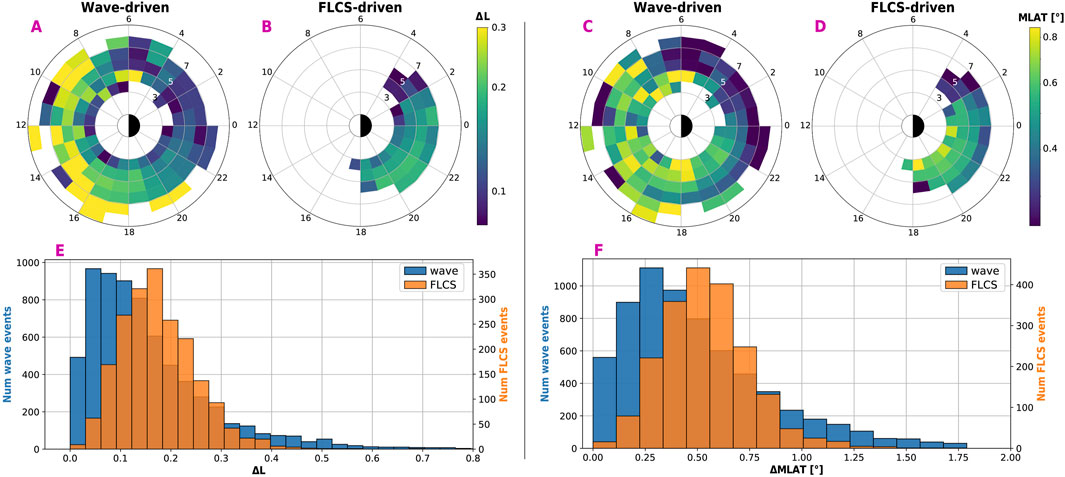
Figure 4. Radial extent of REP (left: ΔL, right: ΔMLAT), binned in L-MLT (top) and shown as a histogram (bottom, blue for wave-driven, orange for FLCS-driven).
There is a clear asymmetry between dayside and nightside for wave-driven REP, with REP being broader on the dayside than the nightside, as evident in both radial and latitudinal scales (see Supplementary Figures S6, S7 in SM for more details). Again, this could be an indicator that waves or the scattering regions are more extended on the dayside, possibly a consequence of different generation mechanisms (magnetotail injections vs solar wind fluctuations). Several case studies leveraged multi-point observations and found that dayside EMIC waves triggered by solar wind structures could be more extended in both MLT and L shell (e.g., Blum et al., 2016; 2021; Engebretson et al., 2015; 2018; Usanova et al., 2008; Yan et al., 2023a; 2023b; Yu et al., 2017), while nightside waves are generally more localized, often occurring during substorm activity (e.g., Blum et al., 2015; Capannolo et al., 2019; Clilverd et al., 2015; Jun et al., 2019a; Jun et al., 2019b). This was also statistically confirmed by Blum et al. (2017) through measurements by Van Allen Probes. They found that dayside EMIC waves are more spatially extended than nightside EMIC waves, which instead tend to persist longer. Furthermore, Figures 4A, C reveal a minor asymmetry pre/post-midnight for wave-driven REP. As previously found in Capannolo et al. (2022a), post-midnight REP is more localized than pre-midnight REP, possibly suggesting that the waves or the conditions favorable for electron scattering vary in radial scale across midnight. Contrary to the day/night asymmetry, the variation across midnight has yet to be explained.
Finally, we want to emphasize that we only consider the spatial scale of single REP events as identified by a single POES pass across the precipitation region. There are several indications that REP occurs in patches, covering multiple MLT sectors, likely reproducing the L-MLT extent of its associate driver. For example, previous case studies show several satellite passes or balloon observations associated with EMIC wave activity, spread over a few MLT sectors (e.g., Capannolo et al., 2021; Shekhar et al., 2020; Woodger et al., 2018), demonstrating that the entire region of REP is certainly broader than that observed by a single POES pass. Similarly, when the magnetotail stretches away from Earth, we expect that a few MLT sectors will be affected by FLCS, likely delineating a nightside REP that extends in longitude (Wilkins et al., 2023; Zou et al., 2024; Sivadas et al., 2019). Accurately quantifying the realistic extent over MLT (not only in the radial/latitudinal direction) is a key step in estimating the true energy input into the atmosphere, which we aim to explore in future studies. In the next section, however, we present a first approximation.
3.4 Estimate of the relativistic electron power input into the atmosphere
As discussed in the introduction, REP can impact the atmospheric chemistry and possibly the radiative balance. Its effects heavily depend on the energy input into the atmospheric system, defined not only by the energy flux but also the precipitation spatial extent (in latitude and longitude), as well as its duration. As a first comparison, Figure 5 illustrates the contribution to the atmosphere due to waves (top) or FLCS (bottom). The first column shows the fraction of precipitating flux depending on the associated driver compared to the total precipitating flux. Waves dominate the precipitation over the FLCS, contributing to at least 70% of the average precipitating flux in regions overlapping with FLCS-driven REP.
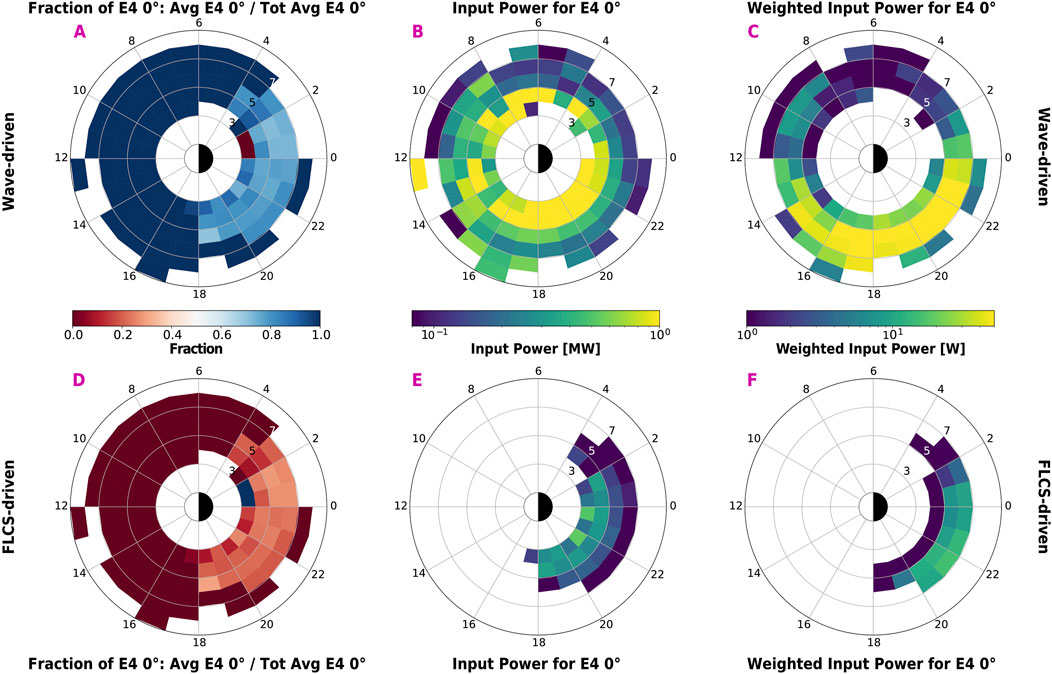
Figure 5. Comparison of input contribution for wave-driven (top row) and FLCS-driven (bottom row) REP. Panels (A, D): fraction of the total precipitating >700 keV electron flux attributed to one driver, calculated as the ratio between the average > 700 keV electron flux (in each bin) for one driver and the total average >700 keV electron flux (in each bin) for both drivers. Panels (B, E): input power expressed in Mega Watts. Panels (C, F): input power weighted by the occurrence rates in Figure 2 in Watts.
Out of the factors that quantify the REP energy input (flux, size, duration), we can estimate the >700 keV input power (a combination of energy flux and spatial extent) assuming a) the 0° electron flux is constant throughout the loss cone, b) the center energy for the >700 keV channel is ∼879 keV (Peck et al., 2015), c) the latitudinal extent of REP is calculated as the difference between the minimum and maximum magnetic latitude in each bin, and d) the longitudinal extent is assumed ∼1 MLT (bin size of the dial plots). The power is calculated as the >700 keV precipitating electron flux multiplied by the center energy, the solid angle factor for a loss cone of ∼58° (2π[cos (0°)-cos (58°)] ∼ 2.96 sr) and the spherical area covered by the latitude (as in c) above) and longitude (1 MLT) extent of the REP (in each bin). The results are in Figures 5B, E, highlighting that the input power for wave-driven REP is systematically higher than FLCS-driven REP, mostly due to the higher energy flux during wave-driven precipitation. Panels C and F illustrate the input power weighted by the occurrence rate of REP in Figures 2E, F. Energy deposition most often occurs at L > 5 in the pre-midnight region for FLCS-driven REP and from post-noon to midnight for wave-driven REP (peaking over 5–7 L), with a smaller contribution at 9–11 MLT.
Assuming an EMIC-driven precipitation region of 1° in magnetic latitude and 3–12 MLT azimuthal extent (Blum et al., 2017; 2020; Clausen et al., 2011; Engebretson et al., 2015; Hendry et al., 2020; Kim et al., 2016a; Mann et al., 2014), Capannolo et al. (2024a) estimated, from a small sample of EMIC-driven precipitation events observed by ELFIN (Capannolo et al., 2023), an average hemispheric contribution of a few to 10s of MW, with an energy flux in the loss cone of ∼3.3 × 10−2 erg/cm2/s (63 keV–2.8 MeV electron energies), primarily deposited in the mesosphere. Wilkins et al. (2023) estimated an average energy flux varying from ∼0.1–0.6 × 10−2 erg/cm2/s and a contribution of ∼10 MW for FLCS-driven >50 keV precipitation (area defined by 1° latitudinal extent and 18–06 MLT) using ELFIN. For the present dataset, the average energy flux in the loss cone is ∼1.33 × 10−2 erg/cm2/s for a wave-driven REP and ∼0.4 × 10−2 erg/cm2/s for a FLCS-driven REP, with an average latitudinal extent of ∼0.5° (calculated as point c) above), providing an average input power of 0.66 MW and 0.19 MW (considering 1 MLT of azimuthal scale), respectively. For wave-driven REP, assuming an azimuthal extent of 3–12 MLT, the input power is ∼2–8 MW. For FLCS-driven REP, assuming an azimuthal extent of 2–10 MLT (the highest boundary given the distribution of events in Figure 2, third column), the power is ∼0.4–2 MW. These estimates are comparable to those from previous results (Capannolo et al., 2024a; Wilkins et al., 2023) albeit smaller given a more localized radial extent and POES higher orbit (∼847 km on average) compared to ELFIN’s (∼450 km), resulting in a smaller loss cone (∼58° vs ∼66°) thus energy flux. Furthermore, these estimates only include the electron flux >700 keV and, due to the high noise level affecting POES, the electron fluxes above a few MeV are likely underestimated. Finally, the 0° telescope only probes deep into the loss cone over a field of view of 30°, underestimating the total loss cone flux.
From a power standpoint, wave-driven REP is clearly dumping more energy into the atmospheric system; however, providing only the input power is not yet enough to quantify the total energy input as atmospheric effects of REP significantly depend on the duration of such phenomenon. Once more light is shed on how sustained wave-driven vs FLCS-driven REP is, one can finalize the entire energy input into the atmosphere and perform modeling to quantify the associated effects (e.g., Duderstadt et al., 2021). In addition, while wave-driven REP mostly occurs at >700 keV possibly accompanied by 100 s keV electrons if driven by EMIC waves (Capannolo et al., 2021; 2023; Hendry et al., 2017), FLCS drives precipitation across all energies, down to 10 s keV, thus affecting a broader range of altitudes, from the E region and below.
4 Proton precipitation during REP
As mentioned, proton precipitation can also occur during REP and, just as for REP, we can attribute it to FLCS or waves depending on its precipitation profile. Isolated 10s–100 s keV proton precipitation is driven by EMIC waves and thus can be used as a proxy for EMIC wave activity (see Capannolo et al., 2023 and references therein). Proton precipitation with an energy-dependent profile is instead associated with FLCS. Figure 6 displays the Superposed Epoch Analysis (SEA) results for the median electron and proton flux during REP events, assuming the 0-epoch at the minimum L shell of each event (vertical dashed line). The x-axis shows the number of seconds from the 0-epoch and the L shell increases from left to right. Panels A, C, and D are relative to wave-driven events, separated into 23–03, 15–23, and 03–15 MLT sectors. Panel B illustrates the SEA for FLCS events. The top subplots show the proton flux observations in three energy channels (P1: 30–80 keV, P2: 80–250 keV, P3: 250–800 keV), while the lower panels show the electron flux, dashed lines for the trapped populations and solid lines for the precipitating populations. First, the median profile of the wave-driven and FLCS-driven REP nicely reproduces the characteristics of isolated vs energy-dependent REP, as described in Section 1. Note that electron channels are affected by proton contamination when proton precipitation is occurring (which is the case for most REP events; Yando et al., 2011; Rodger et al., 2010), thus the <700 keV electron fluxes are not necessarily reliable unless further data processing is considered (not a focus of this work). This is particularly evident in panel B where, before the main FLCS-driven event, an apparent FLCS-driven precipitation is observed in the 0° telescope for the E1, E2, and E3 channels: this is clear evidence of proton contamination due to the FLCS observed in the proton channels.
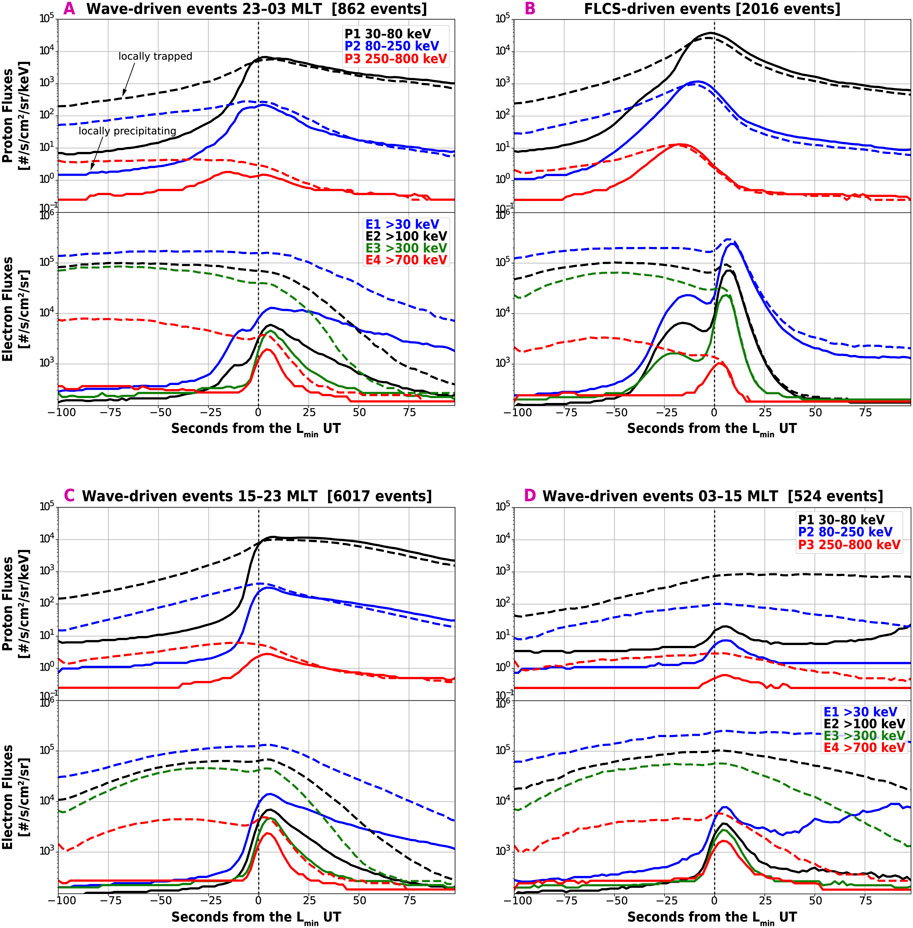
Figure 6. Superposed epoch analysis (SEA) for proton and electron fluxes during wave-driven REP (panels (A, C, D)) and FLCS-driven REP (panel (B)). Moving averages of median proton and electron fluxes are shown at different energies (legend in panel (A)). Wave-driven REP is separated into three MLT sectors: 23–03 MLT (night, (A), 15–23 MLT (dusk, (C), and 03–15 MLT (day, (D). The vertical line indicates the epoch 0 and the inner boundary (Lmin) of each event.
FLCS-driven REP (Figure 6B) occurs at higher L shells (i.e., latitudes, poleward) than the isotropic boundary of protons, also demarcated by an energy-dependent precipitation profile. Such a feature is expected, considering that protons have larger gyroradii than electrons and thus can be scattered by field lines with larger curvature radius (i.e., closer to Earth; e.g., Dubyagin et al., 2018; 2021; Ganushkina et al., 2005). This is also the case for wave-driven REP observed across midnight (∼23–03 MLT). Wave-driven REP at dawn-to-post noon, instead, shows weak isolated proton precipitation occurring simultaneously with electron precipitation, indicating that EMIC waves are likely driving this precipitation, at least in a statistical sense. Most wave-driven REP (15–23 MLT) occur together with proton precipitation occurring simultaneously at all proton energies, without resembling a FLCS or an isolated profile. This is the result of proton precipitation triggered at all energies (possibly an indicator of EMIC waves) at the lower L shell boundary, followed by isotropic proton precipitation likely driven by FLCS. After inspecting these events, we indeed find that some occur past the proton isotropic boundary, some occur during isolated proton precipitation (thus associated with EMIC waves), and some show isolated proton precipitation soon followed by a proton FLCS. Note that although we show some evidence that REP is driven by EMIC waves, especially over 03–23 MLT, we refrain from drawing any strong conclusions on the type of wave driver, as we have not comprehensively analyzed the in-situ wave data in conjunction with the observed REP.
Figure 7 illustrates the proton precipitation efficiency (ratio R = 0°/90°) in an L-MLT plot. Panels A–C indicate proton precipitation efficiency during wave-driven REP for the P1, P2, and P3 channels, respectively. Panel D shows the proton precipitation intensity at the P1 channel 30–80 keV (P2 and P3 display similar trends, not shown). While proton precipitation is intense at any L and MLT during FLCS-driven REP (see paragraph above for explanation), the intensity for wave-driven REP is highest from 13 to 3 MLT, an area that coincides with protons either precipitated by waves or FLCS. The overall efficiency is also slightly weakening as proton energy increases. Proton precipitation is instead weakest over 03–13 MLT, although sporadically moderate/high in some L-MLT bins. This agrees with what was observed in the SEA of wave-driven REP over 03–15 MLT: an overall weak and isolated proton precipitation.
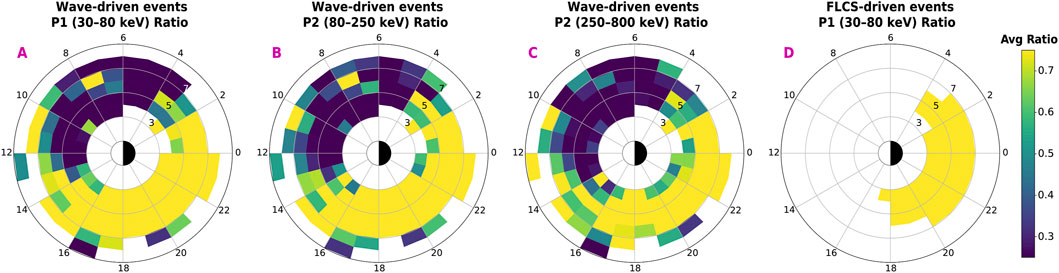
Figure 7. Proton precipitation intensity (ratio R = 0°/90°) during wave-driven REP (panels (A–C)) and FLCS-driven REP (panel (D)). The ratio is averaged in each bin from the ratio 0°/90° for each event. Ratios for the P1 (30–80 keV), P2 (80–250 keV), P3 (250–800 keV) channels are shown for wave-driven REP. Only the ratio for P1 is shown for FLCS-driven REP (P2 and P3 show a similar distribution).
5 Geomagnetic activity associated with REP
We explore the relationship between REP events and substorm activity indicated by the SML* index (please see Section 2.3 for details; Gjerloev, 2012; Newell and Gjerloev, 2011). We expect that both wave-driven and FLCS-driven REP are associated with substorm activity, given that waves are excited by magnetotail injections and field line stretching is more favorable during substorm onsets (e.g., Li et al., 2008; 2009; Remya et al., 2018; 2020; Sivadas et al., 2019). The left-hand side of Figure 8 presents the occurrence rate in L-MLT bins of the wave-driven events sorted by weak (SML* > −400 nT), moderate (−600 nT < SML* < −400 nT), and strong (SML* < −600 nT) activity (top row: wave-driven REP; lower row: FLCS-driven REP). Periods of weak activity are more frequent than intense activity, as indicated by the total number of POES passes per bin in the lower right in each dial plot. Supplementary Figure S8 in the SM shows the distribution of the events rather than the occurrence rate. Wave-driven REP occurs most commonly when SML* > −400 nT (∼3,400 events; Supplementary Figure S8), including dawnside events which are rarer during stronger activity; however, the occurrence rate of REP is maximized during strong activity and observed at L < 7 until L ∼ 3 (Figure 8C). The bulk of the wave-driven REP extends from dusk towards post-midnight during weak activity and seems to broaden towards the dayside as substorm activity is enhanced with most wave-driven REP occurring from post-noon to post-midnight, as also noted by Chen et al. (2023). The wave-driven REP events in the ∼9–11 MLT seem to persist at any substorm intensity (Supplementary Figure S8), with an increasing occurrence rate with SML* as for the rest of REP. Pre-dawn precipitation is instead primarily detected during weak substorms. It is challenging to isolate the source of the pre-dawn to pre-noon precipitation as this could also be related to other mechanisms of wave excitation, such as solar wind pressure pulses (Kim et al., 2016; Park et al., 2016; Saikin et al., 2016; Usanova et al., 2012). FLCS-driven events are observed most during strong substorms, spanning all L shells, which is reasonable given that magnetic field line stretching is enhanced with substorm intensity. The next column in Figure 8 depicts the SML* for each event averaged in L-MLT bins for wave-driven events (D) and FLCS-driven events (H). We notice an inverse relationship between SML* and L: the precipitation at lower L shells for both event types is associated with stronger substorm activity (see also Supplementary Figure S9). Most intense substorms drive more intense injections that can reach lower L shells and enhance waves there, possibly driving wave-driven REP. Simultaneously, during intense substorms, field line stretching is significantly enhanced, decreasing the curvature radius of the field lines even at lower L shells. As a result, FLCS-driven REP is observable closer to Earth during strong substorm activity. Wave-driven REP over ∼10–22 MLT sector coincides with periods of strongest substorms (reaching ∼−1,000 nT), especially at low L shell. This suggests a heightened rate of wave excitation in the region during strong substorms driving REP. Previous studies have shown a link between periods of increased substorm activity and an enhancement of EMIC wave presence (e.g., Chen et al., 2020; Saikin et al., 2016) in the late pre-noon to the early pre-midnight region, which could explain the association of wave-driven REP with strong substorm intensity.
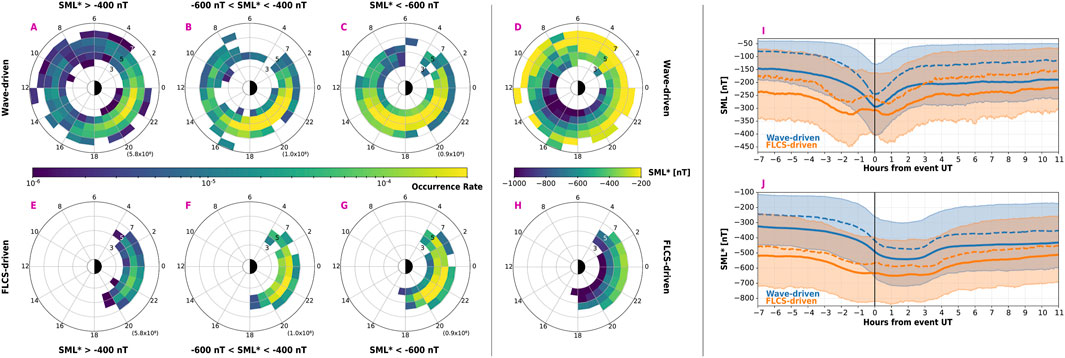
Figure 8. Association of REP with geomagnetic activity. Left-hand side: occurrence rate of the wave-driven (panels (A–C)) and CSS-driven (panels (E–G)) REP events sorted by weak (left), moderate (middle), and strong (right) activity quantified with the SML* index. Numbers in the lower right indicate the total number of POES passes. Panels (D, H) geomagnetic activity intensity for each event averaged in each bin. Panels (I, J) superposed epoch analysis (SEA) for the SML and SML* index (blue for wave-driven and orange for FLCS-driven). The vertical line indicates epoch 0 corresponding to the UT of each event. Solid lines indicate the averages, dashed lines indicate the medians and the shaded regions are demarcated by the lower (25th) and upper (75th) quartiles.
Figures 8I, J illustrate the SEA results for the SML and SML* indices. Wave-driven events are indicated in blue, and FLCS-driven events are indicated in orange. The reference point (0-epoch) is taken as the UT of the observed REP, and the mean (solid line), median (dashed line), and lower and upper quartiles (lower and upper boundary of the shaded area) are calculated. During both wave-driven and FLCS-driven events, there is an indication of substorm activity (negative SML, further decreasing towards the 0-epoch). While wave-driven events possibly occur during a single substorm (one minimum in Figure 8I), perturbing the magnetosphere for ∼3 h (Figure 8J), FLCS-driven REP is probably driven by a more complex scenario. In fact, the SML SEA reveals two possible minima, suggesting that multiple substorms might be occurring, which merge into a ∼4 h sustained minimum when the SML* is considered. Figure 8J also shows that the substorm activity is stronger (∼-650 nT) for FLCS-driven REP compared to wave-driven REP, suggesting that a more intense stretching is required to drive FLCS-driven REP, while wave-driven REP can occur during slightly weaker substorms (∼-550 nT). This agrees with previous results from Capannolo et al. (2022a). Furthermore, the geomagnetic activity associated with wave-driven REP seems slightly shorter (by ∼1 h) than that attributed to FLCS-driven REP. Note that in a SEA, selecting a 0-epoch that characterizes the beginning of the analyzed phenomenon is essential, otherwise missed alignments of events might obscure sharper signatures (i.e., an abrupt SML drop associated with substorms). Here, a simple choice was to use the UT of the observed REP; however, the real UT start of the precipitation is unknown and we can only rely on POES observations crossing the precipitation region at some point. It might be interesting to instead align the SEA by the onset of the specific substorm driving the REP. We plan to explore the association between REP and substorm in the future, as well as understand whether specific substorm phases are more favorable for wave-driven REP or FLCS-driven REP.
From a preliminary analysis of the SuperMAG SMR index (i.e., equivalent to Sym-H; Gjerloev, 2012; Newell and Gjerloev, 2011), the events occur during non-storm times (SMR* ≳ −30 nT) or at most moderate-to-weak (SML* ≳ −100 nT) storm activity (see Supplementary Figure S10 in the SM), indicating that REP might be triggered more often by substorms than storms. During large-scale geomagnetic activity (as is the case for storms), magnetopause shadowing is often a competing mechanism with particle precipitation; therefore, a lack of storm-time REP observations might be attributed to electrons being lost to the magnetopause, rather than being precipitated by waves or field line stretching (e.g., Li et al., 2024; Lyu et al., 2022; 2024; Staples et al., 2022; Shprits et al., 2006; Turner et al., 2012; Tu et al., 2019; Yu et al., 2013). These preliminary results are far from conclusive, and more analyses are needed to shed light on the occurrence of REP during substorms vs storms. In particular, it might be insightful to analyze the occurrence of EMIC wave-driven REP during storm or non-storm times (Remya et al., 2023), inside or outside the plasmapause (Jun et al., 2019b), with or without magnetotail injections (Jun et al., 2019a), and also explore the association of the observed REP during dropout or non-dropout events (Nnadih et al., 2023).
6 Solar wind trends before REP
The SW is the driver of most magnetospheric processes, including geomagnetic storms and substorms and radiation belt dynamics. A variety of research has been conducted on the relationship between SW, radiation belts, waves, and geomagnetic activity (e.g., Benacquista et al., 2018; Kilpua et al., 2015; 2019; Marchezi et al., 2022; Roosnovo et al., 2024; Reeves et al., 2003; 2011; Salice et al., 2023; Turner et al., 2019; Yan et al., 2023a; 2023b). However, a comprehensive understanding is still incomplete, often because there are several mechanisms at play at different timescales and L-MLT locations between a SW fluctuation, a possible storm or substorm, and the resulting REP. Here, we conduct a preliminary analysis to investigate the SW conditions associated with wave-driven and FLCS-driven REP to see if there is any significant difference between the SW associated with these types of precipitation. We perform a superposed epoch analysis on the interplanetary magnetic field amplitude (IMF) and its z-component (Bz), the flow speed (V), the density, and the pressure. As in Figures 8I, J, the 0-epoch corresponds to the UT of the observed REP. Figure 9 shows the SEA for wave-driven (blue) and FLCS-driven (orange) events. The IMF is almost constant for FLCS-driven REP and increasing for wave-driven REP. A signature of dayside magnetic reconnection (negative Bz) is likely for both wave-driven and FLCS-driven REP. The key difference is that, during wave-driven REP, Bz has a sharper decrease starting from ∼3 h before REP, while Bz is progressively increasing in magnitude for FLCS-driven REP over a ∼5 h window. Additionally, Bz is in magnitude slightly higher for FLCS events compared to wave ones; however, the minimum Bz is approximately comparable. This could indicate that FLCS-driven REP occurs when the magnetic reconnection is sustained for a longer time (and marginally more intense) compared with wave-driven REP. Note that the 0-epoch is again marked by the UT when POES observed REP rather than the true start time of the precipitation. As mentioned above, this could misalign the SW time series, possibly obscuring clearer patterns in the data (i.e., sharp enhancements or dropouts of a SW variable).
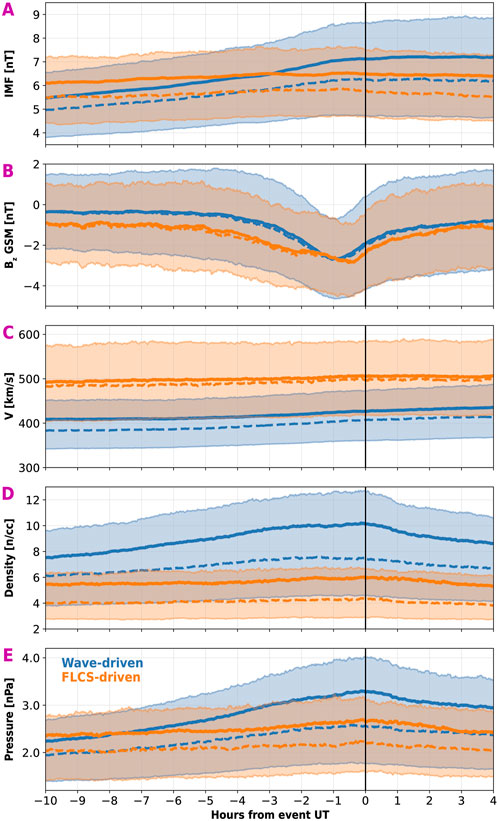
Figure 9. Superposed epoch analysis (SEA, moving averages) for SW parameters [(A): magnetic field amplitude IMF, (B): its z-component Bz, (C): flow speed, (D): density, and (E): pressure] associated with wave-driven REP (blue) and FLCS-driven REP (orange). The vertical line indicates the epoch 0 corresponding to the UT of each event. Solid lines indicate the averages, dashed lines indicate the medians, and the shaded regions are demarcated by the lower (25th) and upper (75th) quartiles.
Wave-driven REP is associated with a slower and denser SW than FLCS-driven REP. SW prior to FLCS-driven REP seems to remain overall constant in speed, density, and pressure, while SW associated with wave-driven REP is stronger towards the observed REP UT. This might suggest that while FLCS-driven REP occurs during steady SW and more stretched (i.e., faster SW) magnetotail conditions (e.g., Axford, 1964; Song et al., 1999), wave-driven REP is associated with a SW that enhances the dayside magnetospheric compression. This is partly in agreement with previous studies associating EMIC waves (the possible driver of wave-driven REP) with SW characterized by higher density and pressure (Clausen et al., 2011; Chen et al., 2020; Upadhyay et al., 2022). A more detailed analysis is needed to fully understand which specific SW conditions drive different types of REPs, and we plan to perform this in the future. The scenario is indeed complex since SW can trigger storms and substorms, which in turn can drive wave-driven and/or FLCS-driven REP. At the same time, SW pressure pulses can also excite dayside EMIC waves, and thus possibly lead to wave-driven REP. It will be interesting to investigate whether different locations of REP events are driven by specific SW conditions or if there are common patterns in SW data revealing known structures, such as coronal mass ejections or high-speed streamers. Shedding light on the structures that most favorably drive REP will certainly be insightful for space weather prediction models.
7 Summary & conclusion
The profile of relativistic electron precipitation (REP) along a LEO satellite pass is a tell-tale signature of its associated driver: waves typically drive a rather isolated precipitation within the outer belt, while FLCS drives relativistic electron precipitation at lower L shells accompanied by low-energy precipitation at higher L shells, exhibiting an energy-dependent pattern. In this work, we leverage these features and analyze the characteristics of wave-driven REP and FLCS-driven REP using the POES/MetOp constellation from 2012 through 2023. Our findings are summarized as follows:
1. REP is observed on localized radial scales (<0.3 L, <1° MLAT), occurring over 3–8 L shells, at any MLT sector, with the highest occurrence between 4 and 6 L shells and pre-midnight.
2. Wave-driven REP is most often observed over ∼15–02 MLT, more spatially extended on the dayside. REP is most intense at higher L shells and weakest over 6–12 MLT and ∼3–6 L. REP across midnight (23–03 MLT) is accompanied by proton precipitation driven by FLCS, REP over 03–15 MLT occurs together with isolated proton precipitation, possibly suggesting EMIC waves as the wave driver. Over 15–23 MLT (where wave-driven REP is most common), proton precipitation is strong and exhibits an enhancement without energy dependence, followed by isotropic proton precipitation–a possible result of EMIC waves and/or proton FLCS.
3. FLCS-driven REP occurs on the night side (18–04 MLT), is strong in intensity, and is typically more radially extended than nightside wave-driven precipitation. REP occurs poleward of the proton isotropic boundary, as expected.
4. Wave-driven and FLCS-driven REP both deposit energy into the atmosphere, with wave-driven REP dominating given its higher >700 keV energy flux. The average wave-driven input power into the atmosphere is ∼0.66 MW compared to ∼0.19 MW due to FLCS, over 1 MLT and 0.5 L shell. More realistic azimuthal scales for precipitation provide ∼2–8 MW for wave-driven REP (3–12 MLT) and ∼0.4–2 MW for FLCS-driven REP (2–10 MLT).
5. REP typically occurs during substorm activity rather than storms, with low-L shell REP observed during strongest substorms (SML* < −800 nT on average). Wave-driven REP over ∼10–21 MLT is associated with intense substorms, while is observed during weaker substorms (SML* > −400 nT) elsewhere.
6. Preliminary analysis of SW conditions associated with REP shows that FLCS-driven REP is on average occurring during a sustained (∼5 h) dayside reconnection and a steady SW with an average speed of ∼500 km/s and average pressure of ∼2.4 nPa, while wave-driven REP is typically occurring during a shorter (∼3 h) dayside reconnection accompanied by a compressed magnetosphere with pressure increasing to ∼3.2 nPa.
These findings agree with previous results focused on studying REP (e.g., Capannolo et al., 2021; 2022a; 2023; Chen et al., 2023; Gasque et al., 2021; Shekhar et al., 2017; Yahnin et al., 2016; 2017; Wilkins et al., 2023) and highlight some interesting features that could be further analyzed to shed light on the precipitation drivers (e.g., weak wave-driven REP over 6–12 MLT, broader dayside wave-driven REP than nightside REP, asymmetry of FLCS-driven REP across midnight, asymmetry of wave-driven REP in radial extent across midnight). The specific wave type associated with REP (EMIC, chorus, hiss) remains poorly constrained although there is evidence that EMIC waves might be the primary wave driver. Conjunction or correlation studies between REP and in-situ wave activity could enhance our knowledge of this process. In addition to understanding more about the REP properties and drivers, efforts should also be dedicated to carefully disentangling the relationship between REP and SW, REP and substorms as well as REP and storms. The chain of processes starting from the SW fluctuation and triggering storm/substorm activity, enhancing wave excitation, and scattering relativistic electrons into the atmosphere is rather complex, but its understanding is key to improving predictive models of the magnetospheric system.
Finally, it is crucial to comprehensively describe the energy deposition into the atmospheric system. In particular, quantifying the duration of the wave-driven vs FLCS-driven REP and modeling the resulting atmospheric chemistry and dynamics are key to comparing their respective effects on the atmosphere. Although wave-driven REP seems to be playing a major role (i.e., higher occurrence rate, higher electron flux), FLCS-driven precipitation probably occurs at any time (i.e., it defines the outer belt boundary; Sivadas et al., 2019) and thus, at net, could deposit more energy into the atmosphere than the wave-driven REP. The quantification of the regional extent of REP precipitation is as important as describing its temporal duration. Some work suggests that REP occurs in patches extending a few MLT sectors (e.g., Capannolo et al., 2019; 2021; Shekhar et al., 2020), possibly as wide as the azimuthal extent of waves and magnetic field stretching. Furthermore, while wave-driven REP is potentially accompanied by some lower energy electron precipitation, FLCS always drives efficient (i.e., isotropic) precipitation for electrons from 10 s keV and above, thus influencing the atmospheric chemistry over a broader range of altitudes (∼50–100 km) compared to the ionization due to wave-driven REP primarily impacting the mesosphere (Capannolo et al., 2024a).
In conclusion, we invite the community to leverage the database of REP events available at https://doi.org/10.5281/zenodo.13144517 for statistical work, simulations, or modeling, as it provides a reliable set of clear precipitation observations from POES satellites, thus far not yet available to the public.
Data availability statement
The datasets presented in this study can be found in the online repository at: https://doi.org/10.5281/zenodo.13144517. Average properties of the events are also available there, binned by L-MLT, as the figures in this work. Please reach out to L. Capannolo at bHVpc2FjYXBAYnUuZWR1 if you are interested in using the dataset. Original POES/MetOp data at 2-second resolution is available here: https://www.ncei.noaa.gov/data/poes-metop-space-environment-monitor/access/l1b/v01r00/. SuperMAG data is available here: https://supermag.jhuapl.edu/info/. OMNI data is available at https://spdf.gsfc.nasa.gov/pub/data/omni/omni_cdaweb/. The DL classifier is available at the GitHub repository https://github.com/luisacap/REPs_classifier_codes_for_paper.git: the code to run the classifier on a 2-second POES/MetOp data is paper_load_model_poes_predictions_2023update.py, which uses the model saved in the REPs_classifier_model folder, the LSTM_scaler.joblib and a set of functions in paper_library_2023update.py.
Author contributions
LC: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Visualization, Writing–original draft, Writing–review and editing. AS: Data curation, Formal Analysis, Resources, Software, Visualization, Writing–review and editing. WL: Conceptualization, Investigation, Methodology, Supervision, Visualization, Writing–review and editing. KD: Conceptualization, Investigation, Supervision, Writing–review and editing. NS: Conceptualization, Investigation, Visualization, Writing–review and editing. JP: Investigation, Writing–review and editing. SE: Investigation, Writing–review and editing. MQ: Investigation, Writing–review and editing. X-CS: Investigation, Writing–review and editing. QM: Investigation, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. LC, AS, and WL acknowledge the NSF (grants AGS 2247265, AGS 2401265, AGS-2402179) and NASA (grants 80NSSC23K1054, 80NSSC20K1270, 80NSSC20K0704, and 80NSSC21K1312) for making this research possible. XS acknowledges the NSF grant AGS-2247774 and NASA grants 80NSSC24K0239 and 80NSSC24K0266. QM acknowledges the NASA grants 80NSSC20K0196 and 80NSSC24K0572, and NSF grant AGS-2225445.
Acknowledgments
The authors thankfully acknowledge the NSF and NASA agencies for making this research possible. The authors also gratefully acknowledge the SuperMAG collaborators (https://supermag.jhuapl.edu/info/?page=acknowledgement) for making the geomagnetic indices available. We acknowledge the Python libraries PySPEDAS, PyTplot, Matplotlib, Pandas, Numpy, Xarray, Joblib, TensorFlow.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2024.1495008/full#supplementary-material
References
Allison, H. J., Horne, R. B., Glauert, S. A., and Del Zanna, G. (2017). The magnetic local time distribution of energetic electrons in the radiation belt region. J. Geophys. Res. Space Phys. 122, 8108–8123. doi:10.1002/2017JA024084
Angelopoulos, V., Zhang, X. J., Artemyev, A. V., Mourenas, D., Tsai, E., Wilkins, C., et al. (2023). Energetic electron precipitation driven by electromagnetic ion cyclotron waves from ELFIN’s low altitude perspective. Space Sci. Rev. 219 (5), 37. doi:10.1007/s11214-023-00984-w
Axford, W. (1964). Viscous interaction between the solar wind and the Earth’s magnetosphere. Planet. Space Sci. 12 (1), 45–53. doi:10.1016/0032-0633(64)90067-4
Benacquista, R., Boscher, D., Rochel, S., and Maget, V. (2018). Variations of the electron fluxes in the terrestrial radiation belts due to the impact of corotating interaction regions and interplanetary coronal mass ejections. J. Geophys. Res. Space Phys. 123, 1191–1199. doi:10.1002/2017JA024796
Blum, L., Li, X., and Denton, M. (2015). Rapid MeV electron precipitation as observed by SAMPEX/HILT during high-speed stream-driven storms. J. Geophys. Res. Space Phys. 120, 3783–3794. doi:10.1002/2014JA020633
Blum, L. W., Agapitov, O., Bonnell, J. W., Kletzing, C., and Wygant, J. (2016). Emic wave spatial and coherence scales as determined from multipoint van allen probe measurements. Geophys. Res. Lett. 43, 4799–4807. doi:10.1002/2016GL068799
Blum, L. W., Bonnell, J. W., Agapitov, O., Paulson, K., and Kletzing, C. (2017). EMIC wave scale size in the inner magnetosphere: observations from the dual Van Allen Probes. Geophys. Res. Lett. 44 (3), 1227–1233. doi:10.1002/2016GL072316
Blum, L. W., Bruno, A., Capannolo, L., Ma, Q., Kataoka, R., Torii, S., et al. (2024). On the spatial and temporal evolution of EMIC wave-driven relativistic electron precipitation: magnetically conjugate observations from the Van Allen Probes and CALET. Geophys. Res. Lett. 51, e2023GL107087. doi:10.1029/2023GL107087
Blum, L. W., Halford, A., Millan, R., Bonnell, J. W., Goldstein, J., Usanova, M., et al. (2015b). Observations of coincident EMIC wave activity and duskside energetic electron precipitation on 18-19 January 2013. Geophys. Res. Lett. 42, 5727–5735. doi:10.1002/2015GL065245
Blum, L. W., Koval, A., Richardson, I. G., Wilson, L. B., Malaspina, D., Greeley, A., et al. (2021). Prompt response of the dayside magnetosphere to discrete structures within the sheath region of a coronal mass ejection. Geophys. Res. Lett. 48, e2021GL092700. doi:10.1029/2021GL092700
Blum, L. W., Remya, B., Denton, M. H., and Schiller, Q. (2020). Persistent EMIC wave activity across the nightside inner magnetosphere. Geophys. Res. Lett. 47 (6), e2020GL087009. doi:10.1029/2020GL087009
Büchner, J., and Zelenyi, L. M. (1989). Regular and chaotic charged particle motion in magnetotaillike field reversals: 1. Basic theory of trapped motion. J. Geophys. Res. 94 (A9), 11821–11842. doi:10.1029/JA094iA09p11821
Capannolo, L., Li, W., and Huang, S. (2022b). Identification and classification of relativistic electron precipitation at earth using supervised deep learning. Front. Astron. Space Sci. 9, 858990. doi:10.3389/fspas.2022.858990
Capannolo, L., Li, W., Ma, Q., Qin, M., Shen, X.-C., Angelopoulos, V., et al. (2023). Electron precipitation observed by ELFIN using proton precipitation as a proxy for electromagnetic ion cyclotron (EMIC) waves. Geophys. Res. Lett. 50, 21. doi:10.1029/2023GL103519
Capannolo, L., Li, W., Ma, Q., Shen, X.-C., Zhang, X.-J., Redmon, R. J., et al. (2019). Energetic electron precipitation: multievent analysis of its spatial extent during EMIC wave activity. J. Geophys. Res. Space Phys. 124, 2466–2483. doi:10.1029/2018JA026291
Capannolo, L., Li, W., Millan, R., Smith, D., Sivadas, N., Sample, J., et al. (2022a). Relativistic elec-tron precipitation near midnight: drivers, distribution, and properties. J. Geophys. Res. Space Phys. 127, e2021JA030111. doi:10.1029/2021ja030111
Capannolo, L., Li, W., Spence, H., Johnson, A. T., Shumko, M., Sample, J., et al. (2021). Energetic electron precipitation observed by FIREBIRD-II potentially driven by EMIC waves: location, extent, and energy range from a multievent analysis. Geophys. Res. Lett. 48 (5), e2020GL091564. doi:10.1029/2020GL091564
Capannolo, L., Marshall, R., Li, W., Berland, G., Duderstadt, K., Sivadas, N., et al. (2024a). Unraveling the atmospheric energy input and ionization due to EMIC-driven electron precipitation from ELFIN observations. AGU Adv. 5, e2023AV001096. doi:10.1029/2023AV001096
Capannolo, L., and Staff, A. (2024b). Relativistic Precipitation Events (driven by waves or field line scattering) from POES 2-second data. Zenodo. doi:10.5281/zenodo.13144517
Carson, B. R., Rodger, C. J., and Clilverd, M. A. (2012). POES satellite observations of EMIC-wave driven relativistic electron precipitation during 1998–2010. J. Geophys. Res. 118, 232–243. doi:10.1029/2012JA017998
Chapman-Smith, K., Seppälä, A., Rodger, C. J., Hendy, A., and Forsyth, C. (2023). Observed loss of polar mesospheric ozone following substorm-driven electron precipitation. Geophys. Res. Lett. 50, e2023GL104860. doi:10.1029/2023GL104860
Chen, H., Gao, X., Lu, Q., and Tsurutani, B. T. (2023). Global distribution of relativistic electron precipitation and the dependences on substorm injection and solar wind ram pressure: long-term POES observations. J. Geophys. Res. Space Phys. 128, e2023JA031566. doi:10.1029/2023JA031566
Chen, H., Gao, X., Lu, Q., Tsurutani, B. T., and Wang, S. (2020). Statistical evidence for EMIC wave excitation driven by substorm injection and enhanced solar wind pressure in the Earth's magnetosphere: two different EMIC wave sources. Geophys. Res. Lett. 47, e2020GL090275. doi:10.1029/2020GL090275
Clausen, L. B. N., Baker, J. B. H., Ruohoniemi, J. M., and Singer, H. J. (2011). EMIC waves observed at geosynchronous orbit during solar minimum: statistics and excitation. J. Geophys. Res. 116 (A10), A10205. doi:10.1029/2011JA016823
Clilverd, M. A., Duthie, R., Hardman, R., Hendry, A. T., Rodger, C. J., Raita, T., et al. (2015). Electron precipitation from EMIC waves: a case study from 31 May 2013. J. Geophys. Res. Space Phys. 120, 3618–3631. doi:10.1002/2015JA021090
Comess, M. D., Smith, D. M., Selesnick, R. S., Millan, R. M., and Sample, J. G. (2013). Duskside relativistic electron precipitation as measured by SAMPEX: a statistical survey. J. Geophys. Res. Space Phys. 118, 5050–5058. doi:10.1002/jgra.50481
Dubyagin, S., Apatenkov, S., Gordeev, E., Ganushkina, N., and Zheng, Y. (2021). Conditions of loss cone filling by scattering on the curved field lines for 30 keV protons during geomagnetic storm as inferred from numerical trajectory tracing. J. Geophys. Res. Space Phys. 126, e2020JA028490. doi:10.1029/2020JA028490
Dubyagin, S., Ganushkina, N. Y., and Sergeev, V. A. (2018). Formation of 30 keV proton isotropic boundaries during geomagnetic storms. J. Geophys. Res. Space Phys. 123, 3436–3459. doi:10.1002/2017JA024587
Duderstadt, K. A., Huang, C.-L., Spence, H. E., Smith, S., Blake, J. B., Crew, A. B., et al. (2021). Estimating the impacts of radiation belt electrons on atmospheric chemistry using FIREBIRD II and Van Allen Probes observations. J. Geophys. Res. Atmos. 126 (7), e2020JD033098. doi:10.1029/2020JD033098
Engebretson, M. J., Posch, J. L., Capman, N. S. S., Campuzano, N. G., Bělik, P., Allen, R. C., et al. (2018). MMS, Van Allen Probes, GOES 13, and ground-based magnetometer observations of EMIC wave events before, during, and after a modest interplanetary shock. J. Geophys. Res. Space Phys. 123, 8331–8357. doi:10.1029/2018JA025984
Engebretson, M. J., Posch, J. L., Wygant, J. R., Kletzing, C. A., Lessard, M. R., Huang, C., et al. (2015). Van Allen probes, NOAA, GOES, and ground observations of an intense EMIC wave event extending over 12 h in magnetic local time. J. Geophys. Res. Space Phys. 120 (7), 5465–5488. doi:10.1002/2015JA021227
Evans, D. S., and Greer, M. S. (2004). Polar orbiting environmental satellite space environment monitor–2 instrument descriptions and archive data documentation, NOAA tech. Mem. 1.4. Boulder, Colorado: Space Environ. Lab.
Fytterer, T., Mlynczak, M. G., Nieder, H., Pérot, K., Sinnhuber, M., Stiller, G., et al. (2015). Energetic particle induced intra-seasonal variability of ozone inside the Antarctic polar vortex observed in satellite data. Atmos. Chem. Phys. 15, 3327–3338. doi:10.5194/acp-15-3327-2015
Ganushkina, N. Y., Pulkkinen, T. I., Kubyshkina, M. V., Sergeev, V. A., Lvova, E. A., Yahnina, T. A., et al. (2005). Proton isotropy boundaries as measured on mid- and low-altitude satellites. Ann. Geophys. 23, 1839–1847. doi:10.5194/angeo-23-1839-2005
Gasque, C. L., Millan, R. M., and Shekhar, S. (2021). Statistically determining the spatial extent of relativistic electron precipitation events using 2-s polar-orbiting satellite data. J. Geophys. Res. Space Phys. 126, 4. doi:10.1029/2020JA028675
Gjerloev, J. W. (2012). The SuperMAG data processing technique. J. Geophys. Res. 117, A09213. doi:10.1029/2012JA017683
Green, J. C. (2013). MEPED telescope data processing algorithm theoretical basis document. Natl. Oceanic and Atmos. Admin. National Geophysical Data Center. Available at: https://www.ngdc.noaa.gov/stp/satellite/poes/docs/NGDC/MEPED%20telescope%20processing%20ATBD_V1.pdf.
Hendry, A. T., Rodger, C. J., and Clilverd, M. A. (2017). Evidence of sub-MeV EMIC-driven electron precipitation. Geophys. Res. Lett. 44, 1210–1218. doi:10.1002/2016GL071807
Hendry, A. T., Rodger, C. J., Clilverd, M. A., Engebretson, M. J., Mann, I. R., Lessard, M. R., et al. (2016). Confirmation of EMIC wave-driven relativistic electron precipitation. J. Geophys. Res. Space Phys. 121, 5366–5383. doi:10.1002/2015JA022224
Hendry, A. T., Santolik, O., Miyoshi, Y., Matsuoka, A., Rodger, C. J., Clilverd, M. A., et al. (2020). A multi-instrument approach to determining the source-region extent of EEP-driving EMIC waves. Geophys. Res. Lett. 47 (7), e2019GL086599. doi:10.1029/2019GL086599
Hochreiter, S., and Schmidhuber, J. (1997). Long short-term memory. Neural comput. 9 (8), 1735–1780. doi:10.1162/neco.1997.9.8.1735
Jordanova, V. K., Albert, J., and Miyoshi, Y. (2008). Relativistic electron precipitation by EMIC waves from self-consistent global simulations. J. Geophys. Res. 113 (A3), A00A10. doi:10.1029/2008JA013239
Jun, C.-W., Yue, C., Bortnik, J., Lyons, L. R., Nishimura, Y. T., and Kletzing, C. A. (2019b). EMIC wave properties associated with and without injections in the inner magnetosphere. J. Geophys. Res. Space Phys. 124, 2029–2045. doi:10.1029/2018JA026279
Jun, C.-W., Yue, C., Bortnik, J., Lyons, L. R., Nishimura, Y. T., Kletzing, C. A., et al. (2019a). A statistical study of EMIC waves associated with and without energetic particle injection from the magnetotail. J. Geophys. Res. Space Phys. 124, 433–450. doi:10.1029/2018JA025886
Kandar, H., Blum, L., Shumko, M., Chen, L., and Shue, J.-H. (2023). The repetition period of MeV electron microbursts as measured by SAMPEX/HILT. Geophys. Res. Lett. 50, e2023GL104663. doi:10.1029/2023GL104663
Khazanov, G. V., Robinson, R. M., Zesta, E., Sibeck, D. G., Chu, M., and Grubbs, G. A. (2018). Impact of precipitating electrons and magnetosphere-ionosphere coupling processes on ionospheric conductance. Space weather. 16, 829–837. doi:10.1029/2018SW001837
Khazanov, G. V., Sibeck, D. G., and Chu, M. (2021). “Magnetosphere–ionosphere coupling of precipitating electrons and ionospheric conductance,” in Magnetospheres in the solar system. Editors R. Maggiolo, N. André, H. Hasegawa, D. T. Welling, Y. Zhang, and L. J. Paxton doi:10.1002/9781119815624.ch16
Kilpua, E. K. J., Hietala, H., Turner, D. L., Koskinen, H. E. J., Pulkkinen, T. I., Rodriguez, J. V., et al. (2015). Unraveling the drivers of the storm time radiation belt response. Geophys. Res. Lett. 42, 3076–3084. doi:10.1002/2015GL063542
Kilpua, E. K. J., Turner, D. L., Jaynes, A., Hietala, H., Koskinen, H. E. J., Osmane, A., et al. (2019). Outer Van Allen radiation belt response to interacting interplanetary coronal mass ejections. J. Geophys. Res. Space Phys. 124, 1927–1947. doi:10.1029/2018JA026238
Kim, G.-J., Kim, K.-H., Lee, D.-H., Kwon, H.-J., and Park, J.-S. (2016b). Occurrence of EMIC waves and plasmaspheric plasmas derived from THEMIS observations in the outer magnetosphere: revisit. J. Geophys. Res. Space Phys. 121, 9443–9458. doi:10.1002/2016JA023108
Kim, K.-H., Shiokawa, K., Mann, I. R., Park, J.-S., Kwon, H.-J., Hyun, K., et al. (2016a). Longitudinal frequency variation of long-lasting EMIC Pc1-Pc2 waves localized in the inner magnetosphere. Geophys. Res. Lett. 43 (3), 1039–1046. doi:10.1002/2015GL067536
Li, W., and Hudson, M. K. (2019). Earth's van allen radiation belts: from discovery to the van allen probes era. J. Geophys. Res. Space Phys. 124, 8319–8351. doi:10.1029/2018JA025940
Li, W., Ni, B., Thorne, R. M., Bortnik, J., Green, J. C., Kletzing, C. A., et al. (2013). Constructing the global distribution of chorus wave intensity using measurements of electrons by the POES satellites and waves by the Van Allen Probes. Geophys. Res. Lett. 40, 4526–4532. doi:10.1002/grl.50920
Li, W., Thorne, R. M., Angelopoulos, V., Bonnell, J. W., McFadden, J. P., Carlson, C. W., et al. (2009). Evaluation of whistler-mode chorus intensification on the nightside during an injection event observed on the THEMIS spacecraft. J. Geophys. Res. 114, A00C14. doi:10.1029/2008JA013554
Li, W., Thorne, R. M., Meredith, N. P., Horne, R. B., Bortnik, J., Shprits, Y. Y., et al. (2008). Evaluation of whistler mode chorus amplification during an injection event observed on CRRES. J. Geophys. Res. 113, A09210. doi:10.1029/2008JA013129
Li, Z., Millan, R. M., Hudson, M. K., Woodger, L. A., Smith, D. M., Chen, Y., et al. (2014). Investigation of EMIC wave scattering as the cause for the BARREL 17 January 2013 relativistic electron precipitation event: a quantitative comparison of simulation with observations. Geophys. Res. Lett. 41, 8722–8729. doi:10.1002/2014GL062273
Li, Z.-G., Tu, W., Selesnick, R., and Huang, J. (2024). Modeling the contribution of precipitation loss to a radiation belt electron dropout observed by Van Allen Probes. J. Geophys. Res. Space Phys. 129, e2023JA032171. doi:10.1029/2023JA032171
Longley, W. J., Chan, A. A., Jaynes Allison, N., Elkington, S. R., Pettit, J. M., Ross Johnathan, P. J., et al. (2022). Using MEPED observations to infer plasma density and chorus intensity in the radiation belts. Front. Astron. Space Sci. Sec. Space Phys. 9. doi:10.3389/fspas.2022.1063329
Lyu, X., Ma, Q., Tu, W., Li, W., and Capannolo, L. (2022). Modeling the simultaneous dropout of energetic electrons and protons by EMIC wave scattering. Geophys. Res. Lett. 49, e2022GL101041. doi:10.1029/2022GL101041
Lyu, X., Tu, W., Huang, J., Ma, Q., and Li, Z.-G. (2024). Modeling the simultaneous dropout of energetic electrons and protons by magnetopause shadowing. Geophys. Res. Lett. 51, e2023GL106681. doi:10.1029/2023GL106681
Ma, Q., Li, W., Zhang, X.-J., Bortnik, J., Shen, X.-C., Connor, H. K., et al. (2021). Global survey of electron precipitation due to hiss waves in the Earth’s plasmasphere and plumes. J. Geophys. Res. Space Phys. 126, e2021JA029644. doi:10.1029/2021JA029644
Mann, I. R., Usanova, M. E., Murphy, K., Robertson, M. T., Milling, D. K., Kale, A., et al. (2014). Spatial localization and ducting of EMIC waves: van Allen Probes and ground-based observations. Geophys. Res. Lett. 41 (3), 785–792. doi:10.1002/2013GL058581
Marchezi, J. P., Dai, L., Alves, L. R., Da Silva, L. A., Sibeck, D. G., Lago, A. D., et al. (2022). Electron flux variability and ultra-low frequency wave activity in the outer radiation belt under the influence of interplanetary coronal mass ejections and High-Speed solar wind streams: a statistical analysis from the Van Allen Probes era. J. Geophys. Res. Space Phys. 127, e2021JA029887. doi:10.1029/2021JA029887
Matthes, K., Funke, B., Andersson, M. E., Barnard, L., Beer, J., Charbonneau, P., et al. (2017). Solar forcing for CMIP6 (v3.2). Geosci. Model Dev. 10, 2247–2302. doi:10.5194/gmd-10-2247-2017
Meraner, K., and Schmidt, H. (2018). Climate impact of idealized winter polar mesospheric and stratospheric ozone losses as caused by energetic particle precipitation. Atmos. Chem. Phys. 18, 1079–1089. doi:10.5194/acp-18-1079-2018
Meredith, N. P., Horne, R. B., Isles, J. D., and Green, J. C. (2016). Extreme energetic electron fluxes in low Earth orbit: analysis of POES E > 30, E > 100, and E > 300 keV electrons. Space weather. 14, 136–150. doi:10.1002/2015SW001348
Meredith, N. P., Thorne, R. M., Horne, R. B., Summers, D., Fraser, B. J., and Anderson, R. R. (2003). Statistical analysis of relativistic electron energies for cyclotron resonance with EMIC waves observed on CRRES. J. Geophys. Res. 108 (A6), 1250. doi:10.1029/2002ja009700
Mironova, I. A., Aplin, K. L., Arnold, F., Bazilevskaya, G. A., Harrison, R. G., Krivolutsky, A. A., et al. (2015). Energetic particle influence on the earth's atmosphere. Space Sci. Rev. 194, 1–96. doi:10.1007/s11214-015-0185-4
Nesse Tyssøy, H., Sandanger, M. I., Ødegaard, L.-K. G., Stadsnes, J., Aasnes, A., and Zawedde, A. E. (2016). Energetic electron precipitation into the middle atmosphere—constructing the loss cone fluxes from MEPED POES. J. Geophys. Res. Space Phys. 121, 5693–5707. doi:10.1002/2016JA022752
Newell, P. T., and Gjerloev, J. W. (2011). Evaluation of SuperMAG auroral electrojet indices as indicators of substorms and auroral power. J. Geophys. Res. 116, A12211. doi:10.1029/2011JA016779
Nnadih, S., Blum, L., Xiang, Z., Tu, W., Lyu, X., Usanova, M. E., et al. (2023). Contrasting storm-time radiation belt events with and without dropouts—the importance of CME shocks. J. Geophys. Res. Space Phys. 128, e2023JA031293. doi:10.1029/2023JA031293
Park, J.-S., Kim, K.-H., Shiokawa, K., Lee, D.-H., Lee, E., Kwon, H.-J., et al. (2016). EMIC waves observed at geosynchronous orbit under quiet geomagnetic conditions (Kp ≤ 1). J. Geophys. Res. Space Phys. 121, 1377–1390. doi:10.1002/2015JA021968
Peck, E. D., Randall, C. E., Green, J. C., Rodriguez, J. V., and Rodger, C. J. (2015). POES MEPED differential flux retrievals and electron channel contamination correction. J. Geophys. Res. Space Phys. 120, 4596–4612. doi:10.1002/2014JA020817
Pettit, J. M., Randall, C. E., Peck, E. D., and Harvey, V. L. (2021). A new MEPED-based precipitating electron data set. J. Geophys. Res. Space Phys. 126 (12), e2021JA029667. doi:10.1029/2021JA029667
Qin, M., Hudson, M., Millan, R., Woodger, L., and Shekhar, S. (2018). Statistical investigation of the efficiency of EMIC waves in precipitating relativistic electrons. J. Geophys. Res. Space Phys. 123, 6223–6230. doi:10.1029/2018JA025419
Qin, M., Hudson, M., Millan, R., Woodger, L., and Shen, X. (2020). Statistical dependence of EMIC wave scattering on wave and plasma parameters. J. Geophys. Res. Space Phys. 125 (4), e2020JA027772. doi:10.1029/2020JA027772
Qin, M., Li, W., Shen, X.-C., Angelopoulos, V., Selesnick, R., Capannolo, L., et al. (2024). Global survey of energetic electron precipitation at low Earth orbit observed by ELFIN. Geophys. Res. Lett. 51, e2023GL105134. doi:10.1029/2023GL105134
Randall, C. E., Harvey, V. L., Holt, L. A., Marsh, D. R., Kinnison, D., Funke, B., et al. (2015). Simulation of energetic particle precipitation effects during the 2003–2004 Arctic winter. J. Geophys. Res. Space Phys. 120 (6), 5035–5048. doi:10.1002/2015JA021196
Randall, C. E., Harvey, V. L., Manney, G. L., Orsolini, Y., Codrescu, M., Sioris, C., et al. (2005). Stratospheric effects of energetic particle precipitation in 2003–2004. Geophys. Res. Lett. 32 (5), L05802. doi:10.1029/2004GL022003
Reeves, G. D., McAdams, K. L., Friedel, R. H. W., and O'Brien, T. P. (2003). Acceleration and loss of relativistic electrons during geomagnetic storms. Geophys. Res. Lett. 30 (10), 1529. doi:10.1029/2002GL016513
Reeves, G. D., Morley, S. K., Friedel, R. H. W., Henderson, M. G., Cayton, T. E., Cunningham, G., et al. (2011). On the relationship between relativistic electron flux and solar wind velocity: paulikas and Blake revisited. J. Geophys. Res. 116, A02213. doi:10.1029/2010JA015735
Reidy, J. A., Horne, R. B., Glauert, S. A., Clilverd, M. A., Meredith, N. P., Woodfield, E. E., et al. (2021). Comparing electron precipitation fluxes calculated from pitch angle diffusion coefficients to LEO satellite observations. J. Geophys. Res. Space Phys. 126, e2020JA028410. doi:10.1029/2020JA028410
Remya, B., Halford, A. J., Sibeck, D. G., Murphy, K. R., and Fok, M.-C. (2023). Understanding quiet and storm time EMIC waves—van Allen Probes results. J. Geophys. Res. Space Phys. 128, e2023JA031712. doi:10.1029/2023JA031712
Remya, B., Sibeck, D. G., Halford, A. J., Murphy, K. R., Reeves, G. D., Singer, H. J., et al. (2018). Ion injection triggered EMIC waves in the Earth's magnetosphere. J. Geophys. Res. Space Phys. 123, 4921–4938. doi:10.1029/2018JA025354
Remya, B., Sibeck, D. G., Ruohoniemi, J. M., Kunduri, B., Halford, A. J., Reeves, G. D., et al. (2020). Association between EMIC wave occurrence and enhanced convection periods during ion injections. Geophys. Res. Lett. 47–3. doi:10.1029/2019GL085676
Robinson, R. M., Vondrak, R. R., Miller, K., Dabbs, T., and Hardy, D. (1987). On calculating ionospheric conductances from the flux and energy of precipitating electrons. J. Geophys. Res. 92 (A3), 2565–2569. doi:10.1029/JA092iA03p02565
Rodger, C. J., Clilverd, M. A., Green, J. C., and Lam, M. M. (2010). Use of POES SEM-2 observations to examine radiation belt dynamics and energetic electron precipitation into the atmosphere. J. Geophys. Res. 115, A04202. doi:10.1029/2008JA014023
Rodger, C. J., Hendry, A. T., Clilverd, M. A., Kletzing, C. A., Brundell, J. B., and Reeves, G. D. (2015). High-resolution in situ observations of electron precipitation-causing EMIC waves. Geophys. Res. Lett. 42, 9633–9641. doi:10.1002/2015GL066581
Roosnovo, A., Artemyev, A. V., Zhang, X.-J., Angelopoulos, V., Ma, Q., Grimmich, N., et al. (2024). Relativistic electron precipitation events driven by solar wind impact on the Earth's magnetosphere. J. Geophys. Res. Space Phys. 129, e2023JA032257. doi:10.1029/2023JA032257
Saikin, A. A., Zhang, J.-C., Smith, C. W., Spence, H. E., Torbert, R. B., and Kletzing, C. A. (2016). The dependence on geomagnetic conditions and solar wind dynamic pressure of the spatial distributions of EMIC waves observed by the Van Allen Probes. J. Geophys. Res. Space Phys. 121, 4362–4377. doi:10.1002/2016JA022523
Salice, J. A., Nesse, H., Babu, E. M., Smith-Johnsen, C., and Richardson, I. G. (2023). Exploring the predictability of the high-energy tail of MEE precipitation based on solar wind properties. J. Geophys. Res. Space Phys. 128, e2022JA031194. doi:10.1029/2022JA031194
Schulz, M., and Lanzerotti, L. J. (1974). Particle diffusion in the radiation belts. New York: Springer.
Selesnick, R. S., Tu, W., Yando, K. B., Millan, R. M., and Redmon, R. J. (2020). POES/MEPED angular response functions and the precipitating radiation belt electron flux. J. Geophys. Res. Space Phys. 125, e2020JA028240. doi:10.1029/2020JA028240
Sergeev, V. A., Malkov, M., and Mursula, K. (1993). Testing the isotropic boundary algorithm method to evaluate the magnetic field configuration in the tail. J. Geophys. Res. 98 (A5), 7609–7620. doi:10.1029/92JA02587
Sergeev, V. A., Sazhina, E. M., Tsyganenko, N. A., Lundblad, J. Å., and Søraas, F. (1983). Pitch-angle scattering of energetic protons in the magnetotail current sheet as the dominant source of their isotropic precipitation into the nightside ionosphere. Planet. Space Sci. 31, 1147–1155. doi:10.1016/0032-0633(83)90103-4
Shekhar, S., Millan, R., and Smith, D. (2017). A statistical study of the spatial extent of relativistic electron precipitation with polar orbiting environmental satellites. J. Geophys. Res. Space Phys. 122 (11), 274–311. doi:10.1002/2017JA024716
Shekhar, S., Millan, R. M., and Hudson, M. K. (2018). A statistical study of spatial variation of relativistic electron precipitation energy spectra with polar operational environmental satellites. J. Geophys. Res. Space Phys. 123, 3349–3359. doi:10.1002/2017ja025041
Shekhar, S., Millan, R. M., Woodger, L. A., and Qin, M. (2020). Quantification of the atmospheric relativistic electron precipitation on 17 January 2013. J. Geophys. Res. Space Phys. 125, e2020JA028014. doi:10.1029/2020JA028014
Shprits, Y. Y., Thorne, R. M., Friedel, R., Reeves, G. D., Fennell, J., Baker, D. N., et al. (2006). Outward radial diffusion driven by losses at magnetopause. J. Geophys. Res. 111, A11214. doi:10.1029/2006JA011657
Shumko, M., Blum, L. W., and Crew, A. B. (2021). Duration of individual relativistic electron microbursts: a probe into their scattering mechanism. Geophys. Res. Lett. 48, e2021GL093879. doi:10.1029/2021GL093879
Silin, I., Mann, I. R., Sydora, R. D., Summers, D., and Mace, R. L. (2011). Warm plasma effects on electromagnetic ion cyclotron wave MeV electron interactions in the magnetosphere. J. Geophys. Res. 116 (A5), A05215. doi:10.1029/2010JA016398
Sinnhuber, M., Nieder, H., and Wieters, N. (2012). Energetic particle precipitation and the chemistry of the mesosphere/lower thermosphere. Surv. Geophys. 33 (6), 1281–1334. doi:10.1007/s10712-012-9201-3
Sivadas, N., Semeter, J., Nishimura, Y. T., and Mrak, S. (2019). Optical signatures of the outer radiation belt boundary. Geophys. Res. Lett. 46, 8588–8596. doi:10.1029/2019GL083908
Smith, D. M., Casavant, E. P., Comess, M. D., Liang, X., Bowers, G. S., Selesnick, R. S., et al. (2016). The causes of the hardest electron precipitation events seen with SAMPEX. J. Geophys. Res. Space Phys. 121, 8600–8613. doi:10.1002/2016JA022346
Song, P., DeZeeuw, D. L., Gombosi, T. I., Groth, C. P. T., and Powell, K. G. (1999). A numerical study of solar wind—magnetosphere interaction for northward interplanetary magnetic field. J. Geophys. Res. 104 (A12), 28361–28378. doi:10.1029/1999JA900378
Staples, F. A., Kellerman, A., Murphy, K. R., Rae, I. J., Sandhu, J. K., and Forsyth, C. (2022). Resolving magnetopause shadowing using multimission measurements of phase space density. J. Geophys. Res. Space Phys. 127 (2), e2021JA029298. doi:10.1029/2021ja029298
Summers, D., and Thorne, R. M. (2003). Relativistic electron pitch-angle scattering by electromagnetic ion cyclotron waves during geomagnetic storms. J. Geophys. Res. 108 (A4), 1143. doi:10.1029/2002JA009489
Thorne, R. M. (2010). Radiation belt dynamics: the importance of wave-particle interactions. Geophys. Res. Lett. 37 (22), L22107. doi:10.1029/2010GL044990
Tu, W., Xiang, Z., and Morley, S. K. (2019). Modeling the magnetopause shadowing loss during the June 2015 dropout event. Geophys. Res. Lett. 46, 9388–9396. doi:10.1029/2019GL084419
Turner, D., Shprits, Y., Hartinger, M., and Angelopoulos, V. (2012). Explaining sudden losses of outer radiation belt electrons during geomagnetic storms. Nat. Phys. 8 (3), 208–212. doi:10.1038/nphys2185
Turner, D. L., Kilpua, E. K. J., Hietala, H., Claudepierre, S. G., O'Brien, T. P., Fennell, J. F., et al. (2019). The response of Earth's electron radiation belts to geomagnetic storms: statistics from the Van Allen Probes era including effects from different storm drivers. J. Geophys. Res. Space Phys. 124, 1013–1034. doi:10.1029/2018JA026066
Upadhyay, A., Kakad, B., Kakad, A., and Rawat, R. (2022). Effect of solar wind pressure and substorm linked particle injection on local time distribution of electromagnetic ion cyclotron waves. Front. Astron. Space Sci. 9. doi:10.3389/fspas.2022.866023
Usanova, M. E., Mann, I. R., Bortnik, J., Shao, L., and Angelopoulos, V. (2012). THEMIS observations of electromagnetic ion cyclotron wave occurrence: dependence on AE, SYMH, and solar wind dynamic pressure. J. Geophys. Res. 117, A10218. doi:10.1029/2012JA018049
Usanova, M. E., Mann, I. R., Rae, I. J., Kale, Z. C., Angelopoulos, V., Bonnell, J. W., et al. (2008). Multi-point observations of magnetospheric compression-related EMIC Pc1 waves by THEMIS and CARISMA. Geophys. Res. Lett. 35, L17S25. doi:10.1029/2008GL034458
van de Kamp, M., Seppälä, A., Clilverd, M. A., Rodger, C. J., Verronen, P. T., and Whittaker, I. C. (2016). A model providing long-term data sets of energetic electron precipitation during geomag-netic storms. J. Geophys. Res. Atmos. 121 (20), 2015JD024212. doi:10.1002/2015jd024212
Wilkins, C., Angelopoulos, V., Runov, A., Artemyev, A., Zhang, X.-J., Liu, J., et al. (2023). Statistical characteristics of the electron isotropy boundary. J. Geophys. Res. Space Phys. 128, e2023JA031774. doi:10.1029/2023JA031774
Woodger, L. A., Millan, R. M., Li, Z., and Sample, J. G. (2018). Impact of background magnetic field for EMIC wave-driven electron precipitation. J. Geophys. Res. Space Phys. 123 (10), 8518–8532. doi:10.1029/2018JA025315
Yahnin, A. G., Yahnina, T. A., Raita, T., and Manninen, J. (2017). Ground pulsation magnetometer observations conjugated with relativistic electron precipitation. J. Geophys. Res. Space Phys. 122, 9169–9182. doi:10.1002/2017JA024249
Yahnin, A. G., Yahnina, T. A., Semenova, N. V., Gvozdevsky, B. B., and Pashin, A. B. (2016). Relativistic electron precipitation as seen by NOAA POES. J. Geophys. Res. Space Phys. 121, 8286–8299. doi:10.1002/2016JA022765
Yan, Y., Yue, C., Ma, Q., Zhou, X.-Z., Zong, Q.-G., Fu, H., et al. (2023b). Prompt appearance of large-amplitude EMIC waves induced by solar wind dynamic pressure enhancement and the subsequent relativistic electron precipitation. J. Geophys. Res. Space Phys. 128, e2023JA031399. doi:10.1029/2023JA031399
Yan, Y., Yue, C., Yin, Z.-F., Zhou, X.-Z., Zong, Q.-G., and Li, J.-H. (2023a). Amplitude-dependent properties and excitation mechanisms of EMIC waves in the Earth's inner magnetosphere. J. Geophys. Res. Space Phys. 128, e2023JA031451. doi:10.1029/2023JA031451
Yando, K., Millan, R. M., Green, J. C., and Evans, D. S. (2011). A Monte Carlo simulation of the NOAA POES medium energy proton and Electron detector instrument. J. Geophys. Res. 116, A10231. doi:10.1029/2011JA016671
Yu, X., Yuan, Z., Huang, S., Wang, D., Li, H., Qiao, Z., et al. (2017). EMIC waves covering wide L shells: MMS and Van Allen Probes observations. J. Geophys. Res. Space Phys. 122, 7387–7395. doi:10.1002/2017JA023982
Yu, Y., Jordanova, V. K., McGranaghan, R. M., and Solomon, S. C. (2018). Self-consistent modeling of electron precipitation and responses in the ionosphere: application to low-altitude energization during substorms. Geophys. Res. Lett. 45, 6371–6381. doi:10.1029/2018GL078828
Yu, Y., Koller, J., and Morley, S. (2013). Quantifying the effect of magnetopause shadowing on electron radiation belt dropouts. Ann. Geophys. 31 (11), 1929–1939. Copernicus Publications. doi:10.5194/angeo-31-1929-2013
Keywords: radiation belts, electron precipitation, field line curvature scattering, wave-particle interactions, atmospheric energy input, precipitating electron flux, electron loss, EMIC waves
Citation: Capannolo L, Staff A, Li W, Duderstadt K, Sivadas N, Pettit J, Elliot S, Qin M, Shen X-C and Ma Q (2024) Properties of relativistic electron precipitation: a comparative analysis of wave-induced and field line curvature scattering processes. Front. Astron. Space Sci. 11:1495008. doi: 10.3389/fspas.2024.1495008
Received: 11 September 2024; Accepted: 22 October 2024;
Published: 08 November 2024.
Edited by:
Mirko Piersanti, University of L’Aquila, ItalyReviewed by:
Emma E. Woodfield, British Antarctic Survey (BAS), United KingdomGiulia D’Angelo, Institute for Space Astrophysics and Planetology (INAF), Italy
Copyright © 2024 Capannolo, Staff, Li, Duderstadt, Sivadas, Pettit, Elliot, Qin, Shen and Ma. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Luisa Capannolo, bHVpc2FjYXBAYnUuZWR1
 Luisa Capannolo
Luisa Capannolo Andrew Staff
Andrew Staff Wen Li
Wen Li Katharine Duderstadt2
Katharine Duderstadt2 Nithin Sivadas
Nithin Sivadas Sadie Elliot
Sadie Elliot Murong Qin
Murong Qin Xiao-Chen Shen
Xiao-Chen Shen Qianli Ma
Qianli Ma