- Geophysical Department, Porter School of the Environment and Earth Sciences, Tel Aviv University, Tel Aviv, Israel
Space weather prediction is a central focus of solar-terrestrial studies, with forecasts of geomagnetic storms deemed critical due to their significant practical implications. We have gathered facts that highlight the effects of geomagnetic storms on electric power systems and satellites. Recent studies indicate that geomagnetic storms of moderate intensity are statistically associated with larger spike amplitudes of telluric currents potentially leading to power outages compared to those caused by major storms. This underscores the importance of building reliable forecasts for all geomagnetic storms, especially given that solar cycles 20–24 saw less than 1% of storms classified as severe or extreme. A major challenge in current prediction models, even those utilizing advanced machine learning techniques, is the decline in accuracy for forecast lead times beyond 3 h, limiting the ability to mitigate infrastructure damage effectively. In this work, we provide a concise overview of geomagnetic storm statistics, describe key forecasting methods, recent advancements, and discuss the challenges in achieving accurate and timely storm predictions.
1 Introduction
A prediction of geomagnetic storms has significant implications for modern society, especially as our reliance on space and terrestrial technology grows. These intense geomagnetic field disturbances are associated with severe space weather events, solar cosmic rays and energetic particles damaging sensitive satellite equipment, creating disruptions of radiowave propagation and connection to satellites, inducing telluric currents that lead to power system transformer saturation and excessive heating in all elongated wired systems, and causing negative biological effects (e.g., Pulkkinen et al., 2005; Khabarova and Dimitrova, 2009; Lakhina and Tsurutani, 2016; Malandraki and Crosby, 2018; Daglis et al., 2021; Buzulukova and Tsurutani, 2022; Khabarova et al., 2024).
Prediction of geomagnetic storms involves understanding a complex interplay of solar phenomena and their interaction with the Earth’s magnetosphere. The challenge lies in estimating initial properties of potentially geoeffective streams, such as fast Interplanetary Coronal Mass Ejections (ICMEs) and Stream Interaction Regions (SIRs) or longer-lived Corotating Interaction regions (CIRs) surrounding high-speed flows from coronal holes, tracing their evolution during propagation, and finding dependencies that allow giving an alert in a reasonable time (Joselyn, 1995; Vennerstroem, 2001; Siscoe and Schwenn, 2006; Tsurutani et al., 2006; Zhang et al., 2007; Kay et al., 2017; Luhmann et al., 2022; Mursula et al., 2022). A scheme of the key solar-terrestrial couplings linking the solar activity, flows and streams in the heliosphere and their effects on the Earth is given by Daglis et al. (2021).
Besides the purely academic significance of understanding solar-terrestrial couplings, it is crucial to comprehend the mechanisms of how the solar wind impacts Earth’s magnetosphere to predict the risks geomagnetic storms pose to power grid systems and space technology. This understanding aims to forecast all geomagnetic storms, not just the severe ones, with lead times ranging from hours to days, allowing society to prepare and mitigate potential damage, which is a complex challenge that remains unresolved (see Srivastava et al., 2021 and references therein). This mini-review highlights the practical importance of geomagnetic storm forecasting, consolidates findings from various studies to identify current challenges in improving predictions, and proposes potential solutions to advance the field.
2 Practical importance of predicting geomagnetic storms
The potential harms of geomagnetic storms are frequently highlighted in space physics literature as a justification for in-depth research on solar and space plasma processes. However, there are relatively few practical studies addressing the direct consequences of space weather impacts on terrestrial infrastructure or proposing mitigation measures. While solar activity does not directly affect the Earth or humans, several key indirect impacts of space weather must be considered (see Lakhina and Tsurutani, 2016; Buzulukova and Tsurutani, 2022, and references therein). Solar flares emit X-rays and cosmic rays that disrupt radio waves and GPS signals, making the dayside ionosphere particularly vulnerable (e.g., Daglis et al., 2021; Buzás et al., 2023). High-speed solar wind streams with a strong southward-directed IMF trigger geomagnetic storms, inducing electric fields that disrupt power grids (Molinski, 2002; Sorokin et al., 2023). These streams also accelerate charged particles locally and re-accelerate solar energetic particles, which collectively bombard Earth’s magnetosphere, causing auroras, particle precipitation, and thermosphere heating (Zank et al., 2015; Malandraki and Crosby, 2018; Daglis et al., 2019; Daglis et al., 2021; Reames, 2021; Khabarova et al., 2021). Particle enhancements can occur even without geomagnetic storms. Additionally, varying geomagnetic fields and cosmic rays affect biological systems, especially in high-latitude regions and the South Atlantic Anomaly area, though the exact mechanisms remain unclear (Tchijevsky, 1938; Khabarova and Dimitrova, 2009; Dimitrova and Babayev, 2018; Khabarova et al., 2024). See details in Supplementary Material S1.
Among risks listed above, Geomagnetically Induced Currents (GICs) represent the biggest space-weather relater problem pushing the governments over the world seeking for the scientific community’s help since telluric GICs can severely impact power grids during geomagnetic storms (e.g., Daglis et al., 2021; Boutsi et al., 2023; Calabia et al., 2023; Evans et al., 2024; Souza et al., 2024). An analysis of related risks have been carried out in several developed countries (e.g., Hines et al., 2008; Persons and Rusco, 2018; Lucas et al., 2020; Ryu et al., 2020; Gritsutenko et al., 2023). It shows that some of measures preventing blackouts, such as a targeted disconnection of high-voltage transmission lines, can only be achieved if they are based on correct and timely predictions of geomagnetic storms. Recently, (Mac Manus et al., 2022; Mac Manus et al., 2023) simulated GIC levels across New Zealand’s network transformers under various extreme storm scenarios, finding up to 35% of transformers at risk. More details can be found in the Supplementary Material S1.
Figure 1 illustrates potential connections between power outages and space weather by comparing the annual number of major blackouts in the United States with sunspot numbers and the Kp index over two solar cycles. Hines et al., 2008 suggest that smaller-scale events, under 400 MW, occur irregularly but increase in frequency over time. In contrast, the most common larger events, in the 400–999 MW range (derived from Figure 3 of Hines et al., 2008), smoothly wave, showing two peaks between 1984 and 2006, as depicted in Figure 1A.
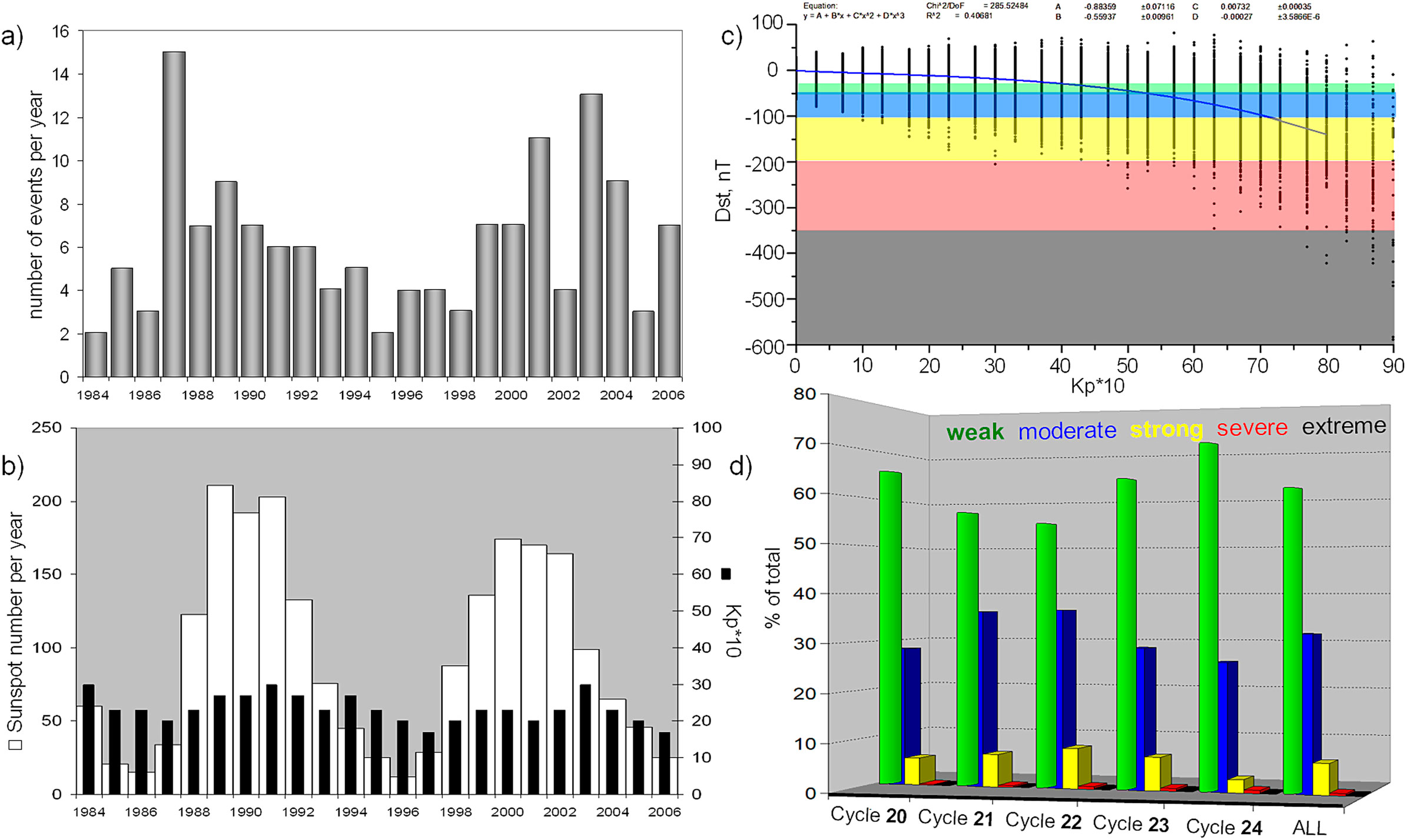
Figure 1. Electric power system failures modulated by solar activity and statistical properties of geomagnetic storms. (A) Number of large blackouts per year in the United States with the event size (amount of electricity taken off) of 400–999 MW. Data are provided by Hines et al. (2008). (B) Sunspot number per year (white) and Kp⋅10 (black), OMNI2 database data. (C) Dst index vs. Kp⋅10. OMNI2 hourly data for 1964–2023. (D) Percentage of storms of the certain intensity for cycles 20–24 and for all cycles in total (ALL). Data are taken from Abe et al. (2023). The Kp and Dst datasets can be found in the NASA’s Space Physics Data Facility – OMNI web data repository: https://omniweb.gsfc.nasa.gov/ow.html, and WDC Kyoto: https://wdc.kugi.kyoto-u.ac.jp/dst_provisional/. Storm intensity categories are based on Dst values and indicated by colors in (C, D). Weak intensity is marked by green, moderate—by blue, strong is yellow, severe is red, and extreme is black. Although there is significant variation in Dst values relative to Kp, an approximate correspondence between the level of geomagnetic field disturbances characterized by Dst can be found for Kp values greater than 4 (see https://www.swpc.noaa.gov/noaa-scales-explanation). Kp = 4 is typically considered to indicate a disturbed geomagnetic field or a weak geomagnetic storm. Kp = 5 corresponds to a weak or minor storm, Kp = 6 indicates a moderate storm, Kp = 7 signifies a strong storm, Kp = 8 represents a severe storm, and Kp = 9 denotes an extreme storm.
The fluctuation in large blackout numbers follows variations of the sunspot numbers and the Kp index recorded in the OMNI2 database for the same period. Geomagnetic activity, indicated by the Kp index in Figure 1B, does not perfectly align with the solar cycle reflected in the sunspot number because it is influenced by both geoeffective ICMEs and SIRs/CIRs (e.g., Boroyev et al., 2020). The latter peak from the declining phase of solar activity through the solar minimum, as shown by Mursula et al. (2022). Consequently, the Kp profile is smoother and slightly shifted to the right compared to the solar cycle peak marked by sunspot numbers. Blackouts may be linked to the solar cycle both directly, via the damaging effects of GICs, and indirectly, through changes in the atmosphere and weather events or even human factors.
It is important to note that the highest GIC amplitudes do not always match the strongest geomagnetic activity (Ngwira et al., 2015; Dimmock et al., 2020; Gritsutenko et al., 2023). The sudden GIC spikes resulting in dramatic changes in the power grid are related to the time derivative of the ground horizontal magnetic field. Significant GIC jump excitations, potentially leading to power system failures, occur not only during the main storm phase but are also related to magnetospheric-ionospheric sudden impulses or sudden storm commencements prior geomagnetic storms caused by sharp changes in the solar wind dynamic pressure, VLF-ULF pulsations in the geomagnetic field, and even intensification of substorms. Gritsutenko et al. (2023) show that the peak of the excitement of GIC spikes is statistically associated with Kp ranging from 4 to 6, not with the maximal Kp values. This finding aligns with the results of the recent analysis of the most intense storms with Dst < −150 nT observed during solar cycle 24 in the Mediterranean region (Boutsi et al., 2023).
A similar effect can be observed in the analysis of satellite losses and malfunctions (Baker, 2001; Cilden-Guler et al., 2021). While severe geomagnetic storms are known to damage satellites, such as disrupting their trajectories, as recently noted during the extreme Gannon geomagnetic storm in May 2024 (Parker and Linares, 2024) — moderate storms also pose significant risks. The primary threat comes from energetic “killer” electrons with energies ranging from 0.5 to 5 MeV at geostationary orbit. These electrons are linked to the arrival of geoeffective ICMEs and SIRs, which are nonlinearly associated with the geomagnetic activity level and may peak before or after the geomagnetic storm maximum (see Baker, 2001; Wrenn, 2009; Daglis et al., 2019; Miteva et al., 2023, and references therein).
Information about satellite malfunctions or losses is often proprietary and not publicly available, complicating research into the physical factors affecting sensitive satellite equipment. However, some general data is accessible in the literature. For instance, NASA reported that an ICME caused the loss of 38 commercial satellites in February 2022 (https://svs.gsfc.nasa.gov/5193/). A moderate geomagnetic storm with a Dst minimum of −66 nT on 3 February 2022 coincided with the launch of Starlink satellites, leading to such significant losses (Miteva et al., 2023; Baruah et al., 2024).
As Solar Cycle 25 peaks, the risk to Earth-orbiting satellites and spacecraft operating in the solar wind increases. For instance, the ACE and DSCOVR L1 spacecraft malfunctioned after the severe geomagnetic storm of 24 March 2004, failing to provide critical solar wind density data for 2 weeks, which halted related forecasts. This highlights the urgent need for the scientific community to prioritize methods for predicting all geomagnetic storms, from weak to extreme, rather than focusing only on intense events, which remains a challenge despite the growing number of prediction models.
3 Geomagnetic storm prediction: geomagnetic storm intensity classifications, general approaches, solutions and problems
3.1 Classifications
Space weather prediction models commonly rely on two key geomagnetic activity indices: Kp and Dst (Wintoft and Wik, 2018; Chakraborty and Morley, 2020; Matzka et al., 2021; Xu et al., 2020; Park et al., 2021; Wang J. et al., 2023; Zhang et al., 2023; Sierra-Porta et al., 2024). See https://kp.gfz-potsdam.de/en/and https://wdc.kugi.kyoto-u.ac.jp/index.html and Supplementary Material S1 for details.
Kp and Dst indices, which characterize geomagnetic activity at different geomagnetic latitudes and are calculated differently, do not have a direct correspondence which complicates a comparison of the results of prognostic techniques using different indices (Borovsky and Shprits, 2017). Figure 1C displays the relationship between Dst and Kp⋅10, fitted with a cubic polynomial (with coefficient values provided above the panel). The categorization of Dst, from weak to extreme storm intensity, is represented in different colors.
Figure 1D shows that the occurrence rate of geomagnetic storms of varying intensities is inversely related to the color proportions representing storm intensity in Figure 1C. Based on statistics from Abe et al. (2023), which we used to calculate the percentage of storms by intensity, weak storms constitute 61% of all storms observed during solar cycles 20–24 (labeled as “ALL” in Figure 1D). Moderate storms account for 32%, strong storms – 6.4%, severe storms – 0.45%, and extreme storms — just 0.12%. Over these five solar cycles, the occurrence of moderate and strong storms shows an anticorrelation with the rate of weak storms, with a correlation coefficient of −0.9. Although the number of cycles is too small to draw definitive conclusions, if this trend continues in solar cycle 25, it could offer insights for predicting the probability of moderate and strong storms in future cycles. Figure 1D illustrates the importance of forecasting all geomagnetic storms because the majority of storms are weak and moderate.
3.2 General approaches
Geomagnetic storm forecasting relies on understanding solar wind-magnetosphere interactions. The Earth’s magnetosphere reacts to any solar wind variations (Borovsky, 2023), but storms occur when magnetic reconnection is triggered by specific solar wind conditions, particularly when the IMF is southward and the solar wind speed is high, known as the “VBz paradigm” (Lakhina and Tsurutani, 2016). These conditions typically arise from high-speed ICMEs or SIRs surrounding fast solar wind flows from coronal holes (Vennerstroem, 2001; Siscoe and Schwenn, 2006; Tsurutani et al., 2006; Zhang et al., 2007; Cid et al., 2014; Kim et al., 2014; Kay et al., 2017; Daglis et al., 2021; Echer and Gonzalez, 2022; Luhmann et al., 2022; Mursula et al., 2022).
The accuracy of predictions depends on the timescale considered, as well as the quality of the input data and models used. In terms of the alert time, the geomagnetic storm prognoses are divided into three categories: long-term, mid-term, and short-term. Long-term predictions from 3 days to a week based on estimations of the development of active processes and coronal hole dynamics at the Sun are rarely used since they are accurate for predicting the likelihood of a geomagnetically active period but cannot correctly forecast the exact timing or intensity of individual storms.
Mid-term forecasts aim to predict storms up to several days in advance. Some of them are based on the expert estimation of the direction of CMEs or the occurrence of low-latitude coronal holes, and some of them use modeling. They can be given in the simple verbal alert ways sometimes complemented with the Kp level forecast or in the probabilistic form, when a certain probability is given next to the certain intensity of the geomagnetic storm (e.g., https://spaceweather.com/ and https://www.swpc.noaa.gov/products/3-day-forecast).
Some empirical techniques use MHD or semi-empirical models to estimate V and Bz at the Earth’s orbit. The models rely on the solar magnetic field data and recalculate the corresponding IMF and plasma parameters from the source surface to the Earth (see Pizzo et al., 2011; Reiss et al., 2016; https://www.swpc.noaa.gov/products/wsa-enlil-solar-wind-prediction) or use interplanetary scintillation data (Jackson et al., 1998; https://ips.ucsd.edu). More details can be found in Supplementary Material S1.
There are also models employing the L1 spacecraft data. These are usually the same models as used for short-term predictions but with larger leading times. Mid-term predictions based on the empirical models aim to extend the forecasting horizon from 1 h to 3 h and beyond, yet challenges arise due to the diminishing relevance of data as the time frame increases (Shprits et al., 2019; Nair et al., 2023; Xu et al., 2023; Wang C et al., 2023). Achieving reliable forecasts beyond 3 h has proven to be complex and, as of now, is thought to reach a practical limit (Pulkkinen et al., 2022).
Short-term predictions focus on forecasting geomagnetic storms minutes or hours before they occur, primarily using data from L1 spacecraft and geomagnetic indices (see Shprits et al., 2019; Nair et al., 2023; Wang C et al., 2023; Wang J et al., 2023 and references therein). They are reliable for determining if a storm will happen within a specific timeframe based on the propagation time of the geoeffective stream or flow from L1 to the magnetosphere. Such forecasts not only provide probabilistic predictions but also compare predicted Dst and Kp indices with real-time geomagnetic activity indices (e.g., https://lasp.colorado.edu/space_weather/dsttemerin/dsttemerin.html, https://swx-trec.com/dst/, https://spaceweather.ru/content/extended-geomagnetic-storm-forecast; http://eng.sepc.ac.cn/dstModel.php).
3.3 Solutions
Methodologies of the geomagnetic storm prediction based on the knowledge of solar-terrestrial couplings have traditionally ranged from MHD-based models, like ENLIL, to empirical models, using primarily V and the IMF Bz (see Joselyn, 1995; Luo et al., 2017 and references therein). Predictions are sometimes based on other known physical principles, such as pre-storm variations in the X-ray, cosmic ray and energetic particle fluxes associated with the arrival of geoeffective streams (e.g., Chakraborty and Morley, 2020; Wang C et al., 2023; Belov et al., 2024). Another approach involves the similarity technique, where models assess the resemblance between the current situation and past geomagnetic storms (e.g., Xu et al., 2023). There are also hybrid models and models that differentiate between ICMEs and SIRs as drivers of geomagnetic storms (e.g., Kim et al., 2014; Park et al., 2021). In recent years, many models have incorporated machine learning (ML) techniques.
ML methods for predicting geomagnetic storms represent a significant shift towards data-driven approaches in geomagnetic storm prediction, which increasingly leverage advanced ML algorithms to improve forecast accuracy and adaptability (e.g., Gruet et al., 2018; Pulkkinen et al., 2022; Conde et al., 2023; Hu et al., 2023; Wang J et al., 2023; Zhang et al., 2023; Xu et al., 2023). These algorithms utilize vast datasets related to solar activity and geomagnetic indicators to anticipate storm events, adapting various techniques to enhance predictive accuracy.
A recent competition, the “MagNet: Model the Geomagnetic Field” challenge, organized by the National Oceanic and Atmospheric Administration and the University of Colorado, attracted 1,197 models competing to predict real-time Dst values using a shared dataset (Nair et al., 2023). The winning model, a bidirectional Long Short-Term Memory (LSTM)-Gated Recurrent Unit (GRU) with three Flattening Layers and three Dense Layers, utilized the parameters shown in Figure 2A. The data were grouped into 1-h intervals, with the mean and standard deviation calculated for each feature. The model used normalized data from the 128 h preceding the prediction time.
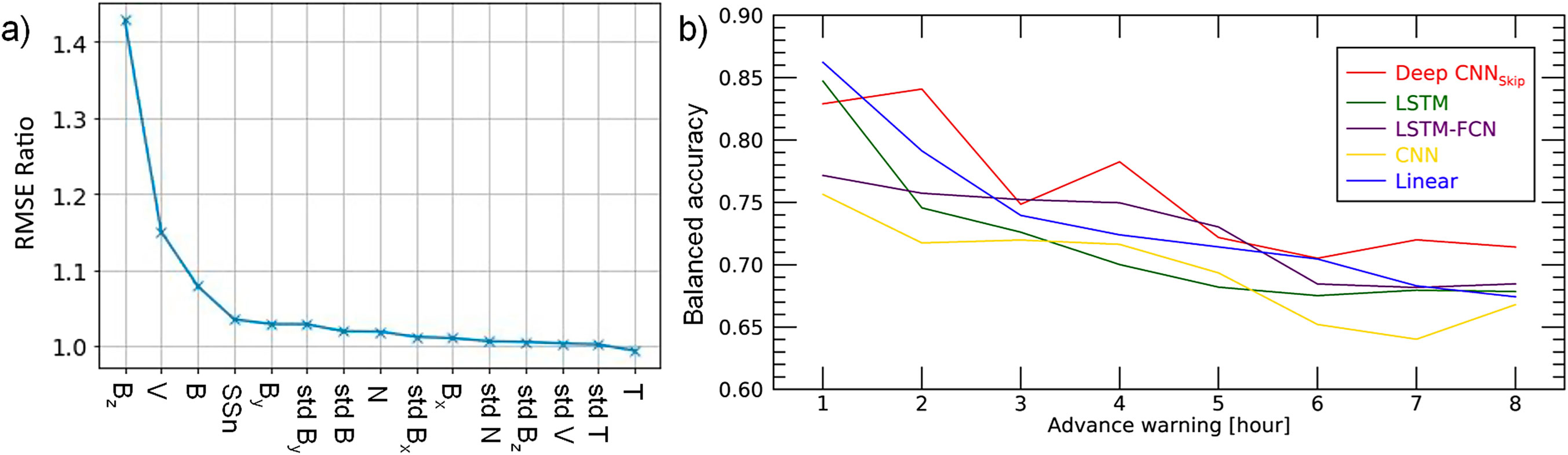
Figure 2. Examples of characteristics of machine learning models predicting geomagnetic storms. (A) Ratio of the root-mean-square for each feature (parameter) to IMF Bz, the main predictive feature. Blue curve characterizes the importance of parameters on which the model is based. Bx, By, and Bz are three IMF components (GSM). V, N, and T are the solar wind speed, density and temperature, respectively. “Std” means standard deviation. Adapted from Nair et al. (2023) under the terms of the Creative Commons CC BY license. (B) Balanced accuracy for the five most effective neural network architectures (represented by different colored lines as indicated in the legend) shown for multi-hour advance warnings of geomagnetic storms with SYM-H< −50 nT. Adapted from Telloni et al. (2023) under Copyright 2024 IOP Publishing, CC: Daniele Telloni and authors.
Figure 2A shows the permutation feature importance for the winning model, where RMSE (root-mean-square error) represents the error between observed and predicted Dst values. The x-axis lists the model’s input parameters, and the y-axis shows the ratio of the RMSE for each feature compared to the most important one (see more information in Supplementary Material S1). This technique assesses the impact of each input feature. Upon forecasting of indices such as Dst or SYM-H, the model inputs (e.g., V, Bz, and B, and other parameters) are tested for their importance. The method starts by measuring the model’s baseline performance using RMSE. At the next step, each feature is shuffled (permuted) one by one, breaking its link to the target variable, and the model’s performance is recalculated. The larger the performance drop occurs after a feature is shuffled, the more important that feature is. Balanced accuracy representing the average of recall values is another useful metric, particularly valuable when dealing with imbalanced datasets (e.g., Cristoforetti et al., 2022), which is a common issue in geomagnetic storm forecasting since severe storms are much rarer than quiet periods (see Supplementary Material S1).
As one can see in Figure 2A, the model easily finds the VBz dominance in the ability to predict Dst, to which it adds the parameters known as secondary-important features in empirical modeling, namely, total IMF (B), the smoothed sunspot numbers (SSn), and IMF By component, with the tail of less-important parameters that still improve the quality of predictions: standard deviations of the most important parameters that can characterize the level of turbulence of the solar wind as well as the solar wind density (N), the radial IMF component Bx, the temperature (T), and their standard deviations.
3.4 Problems
The main challenge in space weather forecasting is that even well-known hazards associated with geomagnetic storms are poorly predicted, with most techniques providing reliable alerts only 60 min in advance, leaving insufficient time for implementing space weather countermeasures. The five models compared in Figure 2B, adapted from Telloni et al. (2023), utilize V, Bz, B, T, N, and the SYM-H index — an analogue of hourly Dst with one-minute resolution. The correlation matrix between the parameters and SYM-H and performance metrics values are given, respectively, in Figure 1 and Tables 3, 4 of Telloni et al. (2023). As illustrated in Figure 2B, the prediction accuracy tends to decline as the forecast lead time increases. This issue is corroborated by numerous studies using various models and input parameters (e.g., Shprits et al., 2019; Xu et al., 2020; Nair et al., 2023; Wang C et al., 2023; Xu et al., 2023), which similarly find that extending the forecast lead time compromises prediction accuracy. The solar wind conditions measured at L1 have both linear and near-linear links with the state of the magnetosphere and, subsequently, with geomagnetic indices at different timescales. For lower advance warning hours, linear models outperform deep CNNs because the relationship between solar wind parameters and geomagnetic storms is near-linear in the short term. As a result, linear models capture the direct connection effectively with fewer parameters. On the other hand, the magnetospheric response to changes in solar wind conditions at longer timescales involves more complex interactions and delayed effects, which require sophisticated models capable of capturing complex patterns and temporal dependencies. As a result, deep CNNs perform better for longer advance warning periods, which is important for mid-term forecasts (e.g., see Siciliano et al., 2021 and references therein). The performance difference reflects the models’ differing abilities to handle simpler vs. more complex relationships, though data quality and training can still impact the exact magnitude of improvement.
One can also find the geomagnetic storm forecast accuracy of NOAA mid-term prognoses (24 h in advance) www.swpc.noaa.gov/sites/default/files/images/u30/SWPC%20GPRA%20Metric%20Description.pdf and https://www.swpc.noaa.gov/content/geomagnetic-activity-forecast-verification, which remains at the probabilistic ∼50% level. Note that G1 storm in the NOAA classification corresponds to Kp = 5. Alternative techniques, such as remote sensing of the solar wind or MHD large-scale modeling are useful to understand the propagation of streams in the interplanetary medium in general, but they are often wrong or give a 12-h-delay in predictions of the increase in the speed or density of the solar wind (e.g., Jian et al., 2011).
Another major issue in geomagnetic storm prediction is the lack of open-access platforms for real-time data and difficulty in comparing different models, as many do not provide historical data or rely on different indices. Additionally, significant storms are rare, making up less than 1% of the data, which creates challenges for ML models that struggle with imbalanced datasets, often overlooking rare events. Incomplete datasets, such as the OMNI dataset with 20% missing data, further complicate training, leading to variable predictions. Traditional model-based methods, often paired with ML, assume Gaussian noise, but real spacecraft data deviate from this, reducing reliability. These challenges show that we are still in the early stages of achieving reliable geomagnetic storm forecasts.
4 Discussion
The ultimate goal of predicting geomagnetic storms is to provide a sufficient warning time for these events, which is critical for mitigating potential damages to satellites, power grids, and communication infrastructures. To address these challenges, various methodologies are explored, including the use of ensemble models that combine multiple predictive algorithms to enhance the accuracy of predictions. Meanwhile, the biggest problem of the current geomagnetic storm forecasts is the low accuracy of mid-term predictions with the advance time from 3 h to 3 days.
Short-term geomagnetic storm forecasts are highly accurate, primarily due to the time lag between detecting an approaching geoeffective stream by spacecraft at L1 and its actual impact on the Earth’s magnetosphere. This allows us to take advantage of the fact that solar wind conditions signaling the onset of a storm are observable about an hour in advance. There is the assumption that the magnetosphere responds almost instantly to changes in solar wind, with the influx of energy mainly depending on VBz. Consequently, most mid-term forecasts rely on the same approach as short-term ones, monitoring the solar wind speed and the IMF strength and direction measured at L1 as primary model inputs. Efforts to enhance these predictions, including models combining solar source data with L1 observations, continue to follow this paradigm, focusing on the same solar wind parameters.
The core problem with current storm prediction methods is that they are very effective for short-term forecasts but almost useless for mid-term ones. This is because predicting what is going to happen requires analyzing events leading up to the phenomenon under study, i.e., to the geomagnetic storm in our case — not just studying solar wind conditions once the storm has already started but looking for precursors. Another major flaw in the dominant approach is the assumption that all geomagnetic storms, regardless of their cause or intensity, are driven by the same key solar wind parameters.
In these terms, future studies of pre-storm conditions applied to the geomagnetic storm prognosis seem to be the way to solve the problems discussed above. The pre-storm variations in the X-ray (Chakraborty and Morley, 2020), energetic particle flux (Ameri and Valtonen, 2019; http://tromos.space.noa.gr/aspecs/#home), the cosmic ray intensity (Wang C et al., 2023), ULF variations, and enhancements in the solar wind plasma parameters (Khabarova, 2007; Khabarova and Yermolaev, 2008; Balasis et al., 2024; Santoso et al., 2024) may increase the accuracy of mid-term predictions, especially being combined with those distinguishing between different storm sources (e.g., Park et al., 2021).
Given that around 90% of storms during solar cycles 20–24 were weak to moderate, focusing on predicting all storms — not just extreme events — is critical, as these moderate storms statistically cause greater power grid disruptions. The fact that recent satellite issues occurred during a moderate storm further emphasizes the need for reliable forecasts as solar cycle 25 peaks. AI advancements, combined with real-time models like SWX-TREC (https://swx-trec.com/geoelectric/), may improve mitigating storm impacts, while creation of regional space weather centers like the recently opened Chinese Meridian Project (https://www.meridianproject.ac.cn/en/) and Tel Aviv University Space Weather Center (https://www.spaceweather.sites.tau.ac.il/) can help integrate scientific research into operational forecasting, improving preparedness for space weather. Future directions should include both studies of pre-storm conditions in the solar wind and exploring more sophisticated ML algorithms to automate feature selection processes, thereby improving prediction accuracy for geomagnetic storm events.
Author contributions
OK: Conceptualization, Formal Analysis, Investigation, Methodology, Visualization, Writing–original draft, Writing–review and editing. CP: Conceptualization, Project administration, Supervision, Writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The authors thank the International Office at Tel Aviv University for partial funding.
Acknowledgments
This study was carried out as a part of the activity of the Space Weather Center of the Tel Aviv University (https://www.spaceweather.sites.tau.ac.il/). Olga Khabarova thanks the Center for Absorption in Science, Ministry of Immigration and Absorption, State of Israel for the support.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2024.1493917/full#supplementary-material
References
Abe, O. E., Fakomiti, M. O., Igboama, W. N., Akinola, O. O., Ogunmodimu, O., and Migoya-Orué, Y. O. (2023). Statistical analysis of the occurrence rate of geomagnetic storms during solar cycles 20–24. Adv. Space Res. 71 (5), 2240–2251. doi:10.1016/j.asr.2022.10.033
Ameri, Dh., and Valtonen, E. (2019). Potential role of energetic particle observations in geomagnetic storm forecasting. Adv. Space Res. 64 (3), 801–813. doi:10.1016/j.asr.2019.05.012
Baker, D. N. (2001). “Satellite anomalies due to space storms,” in Space storms and space weather hazards. NATO science series. Editor I. A. Daglis (Dordrecht: Springer), 38, 285–311. doi:10.1007/978-94-010-0983-6_11
Balasis, G., De Santis, A., Papadimitriou, C., Boutsi, A. Z., Cianchini, G., Giannakis, O., et al. (2024). Swarm investigation of ultra-low-frequency (ULF) pulsation and plasma irregularity signatures potentially associated with geophysical activity. Remote Sens. 16, 3506. doi:10.3390/rs16183506
Baruah, Y., Roy, S., Sinha, S., Palmerio, E., Pal, S., Oliveira, D. M., et al. (2024). The loss of Starlink satellites in February 2022: how moderate geomagnetic storms can adversely affect assets in low-earth orbit. Space weather 22, e2023SW003716. doi:10.1029/2023SW003716
Belov, A. V., Belova, E. A., Shlyk, N. S., Abunina, M. A., Abunin, A. A., and Belov, S. M. (2024). Forbush effects and geomagnetic storms. Geomagn. Aeron. 64, 289–301. doi:10.1134/S0016793224600097
Borovsky, J. E. (2023). Further investigation of the effect of upstream solar-wind fluctuations on solar-wind/magnetosphere coupling: is the effect real? Front. Astron. Space Sci. 9 (id), 433. doi:10.3389/fspas.2022.975135
Borovsky, J. E., and Shprits, Y. Y. (2017). Is the Dst index sufficient to define all geospace storms? J. Geoph. Res. 122 (11), 11543–11547. doi:10.1002/2017ja024679
Boroyev, R. N., Vasiliev, M. S., and Baishev, D. G. (2020). The relationship between geomagnetic indices and the interplanetary medium parameters in magnetic storm main phases during CIR and ICME events. J. Atmosph. Sol-Terr. Phys. 204, 105290. doi:10.1016/j.jastp.2020.105290
Boutsi, A. Z., Balasis, G., Dimitrakoudis, S., Daglis, I. A., Tsinganos, K., Papadimitriou, C., et al. (2023). Investigation of the geomagnetically induced current index levels in the Mediterranean region during the strongest magnetic storms of solar cycle 24. Space weather 21, e2022SW003122. doi:10.1029/2022SW003122
Buzás, A., Kouba, D., Mielich, J., Burešová, D., Mošna, Z., Koucká Knížová, P., et al. (2023). Investigating the effect of large solar flares on the ionosphere based on novel Digisonde data comparing three different methods. Front. Astron. Space Sci. 10, 1201625. doi:10.3389/fspas.2023.1201625
Buzulukova, N., and Tsurutani, B. (2022). Space weather: from solar origins to risks and hazards evolving in time. Front. Astron. Space Sci. 9, 1017103. doi:10.3389/fspas.2022.1017103
Calabia, A., Lu, G., and Bolaji, O. S. (2023). Editorial: advances on upper atmosphere characterization for geodetic space weather research and applications. Front. Astron. Space Sci. 10, 1211582. doi:10.3389/fspas.2023.1211582
Chakraborty, S., and Morley, S. K. (2020). Probabilistic prediction of geomagnetic storms and thepindex. J. Space Weather Space Clim. 10, 36. doi:10.1051/swsc/2020037
Cid, C., Palacios, J., Saiz, E., Guerrero, A., and Cerrato, Y. (2014). On extreme geomagnetic storms. J. Space Weather Space Clim. 4, A28. doi:10.1051/swsc/2014026
Cilden-Guler, D., Kaymaz, Z., and Hajiyev, Ch. (2021). Geomagnetic disturbance effects on satellite attitude estimation. Acta Astronaut. 180, 701–712. doi:10.1016/j.actaastro.2020.12.044
Conde, D., Castillo, F. L., Escobar, C., García, C., García, J. E., Sanz, V., et al. (2023). Forecasting geomagnetic storm disturbances and their uncertainties using deep learning. Space weather 21, e2023SW003474. doi:10.1029/2023SW003474
Cristoforetti, M., Battiston, R., Gobbi, A., Iuppa, R., and Piersanti, M. (2022). Prominence of the training data preparation in geomagnetic storm prediction using deep neural networks. Sci. Rep. 12, 7631. doi:10.1038/s41598-022-11721-8
Daglis, I. A., Chang, L. C., Dasso, S., Gopalswamy, N., Khabarova, O. V., Kilpua, E., et al. (2021). Predictability of variable solar–terrestrial coupling. Ann. Geophys. 39, 1013–1035. doi:10.5194/angeo-39-1013-2021
Daglis, I. A., Katsavrias, C., and Georgiou, M. (2019). From solar sneezing to killer electrons: outer radiation belt response to solar eruptions. Philosophical Trans. Ser. A, Math. Phys. Eng. sci 377 (2148), 20180097. doi:10.1098/rsta.2018.0097
Dimitrova, S., and Babayev, E. (2018). “Space weather effects on human health,” in Variability of the Sun and sun-like stars: from asteroseismology to space weather. Editors J. P. Rozelot, and E. S. Babayev (Les Ulis, France: EDP Sciences), 177–186. doi:10.1051/978-2-7598-2196-9.c012
Dimmock, A. P., Rosenqvist, L., Welling, D. T., Viljanen, A., Honkonen, I., Boynton, R. J., et al. (2020). On the regional variability of dB/dt and its significance to GIC. Space weather 18, e2020SW002497. doi:10.1029/2020SW002497
Echer, E., and Gonzalez, W. D. (2022). Relation between Dst* and interplanetary parameters during single-step geomagnetic storms. Adv. Space Res. 70 (10), 2830–2841. doi:10.1016/j.asr.2022.07.031
Evans, J. S., Correira, J., Lumpe, J. D., Eastes, R. W., Gan, Q., Laskar, F. I., et al. (2024). GOLD observations of the thermospheric response to the 10–12 May 2024 Gannon superstorm. Geophys. Res. Lett. 51, e2024GL110506. doi:10.1029/2024GL110506
Gritsutenko, S., Korovkin, N., Sakharov, Y., and Sokolova, O. (2023). Assessment of geomagnetically induced currents impact on power grid modelling. Magnetism 3, 135–147. doi:10.3390/magnetism3020011
Gruet, M. A., Chandorkar, M., Sicard, A., and Camporeale, E. (2018). Multiple-hour-ahead forecast of the Dst index using a combination of long short-term memory neural network and Gaussian process. Space weather 16, 1882–1896. doi:10.1029/2018SW001898
Hines, P., Apt, J., and Talukdar, S. (2008). “Trends in the history of large blackouts in the United States,” in 2008 IEEE power and energy society general meeting - conversion and delivery of electrical energy in the 21st century (Pittsburgh, PA, USA), 1–8. doi:10.1109/PES.2008.4596715
Hu, A., Camporeale, E., and Swiger, B. (2023). Multi-hour-ahead Dst index prediction using multi-fidelity boosted neural networks. Space weather 21, e2022SW003286. doi:10.1029/2022SW003286
Jackson, B. V., Hick, P. L., Kojima, M., and Yokobe, A. (1998). Heliospheric tomography using interplanetary scintillation observations: 1. Combined Nagoya and Cambridge data. J. Geophys. Res. 103 (A6), 12049–12067. doi:10.1029/97JA02528
Jian, L. K., Russell, C. T., Luhmann, J. G., MacNeice, P. J., Odstrcil, D., Riley, P., et al. (2011). Comparison of observations at ACE and Ulysses with Enlil model results: stream interaction regions during Carrington rotations 2016–2018. Sol. Phys. 273 (1), 179–203. doi:10.1007/s11207-011-9858-7
Joselyn, J. A. (1995). Geomagnetic activity forecasting: the state of the art. Rev. Geophys. 33 (3), 383–401. doi:10.1029/95RG01304
Kay, C., Gopalswamy, N., Reinard, A., and Opher, M. (2017). Predicting the magnetic field of earth-impacting CMEs. Astrophys. J. 835, 117. doi:10.3847/1538-4357/835/2/117
Khabarova, O., and Dimitrova, S. (2009). On the nature of people’s reaction to space weather and meteorological weather changes. Sun Geosph. 4 (2), 60–71. Available at: http://www.shao.az/SG/v4n2/SG_v4_No2_2009-p-60-71.pdf.
Khabarova, O., Malandraki, O., Malova, H., Kislov, R., Greco, A., Bruno, R., et al. (2021). Current sheets, plasmoids and flux ropes in the heliosphere. Part I. 2-D or not 2-D? General and observational aspects. Space Sci. Rev. 217, 38. doi:10.1007/s11214-021-00814-x
Khabarova, O., Pinaev, S. K., Chakov, V. V., Chizhov, A. Y., and Pinaeva, O. G. (2024). Trends in childhood leukemia incidence in urban countries and their relation to environmental factors, including space weather. Front. Public Health 12, 1295643. doi:10.3389/fpubh.2024.1295643
Khabarova, O. V. (2007). Current problems of magnetic storm prediction and possible ways of their solving. Sun Geosph. 2 (1), 33–38. Available at: http://sg.shao.az/v2n1/SG_v2_No1_2007-pp-33-38.pdf.
Khabarova, O. V., and Yermolaev, Yu.I. (2008). Solar wind parameters' behavior before and after magnetic storms. J. Atm Sol. Terr. Phys. 70 (2-4), 384–390. doi:10.1016/j.jastp.2007.08.024
Kim, R.-S., Moon, Y.-J., Gopalswamy, N., Park, Y.-D., and Kim, Y.-H. (2014). Two-step forecast of geomagnetic storm using coronal mass ejection and solar wind condition. Space weather 12 (4), 246–256. doi:10.1002/2014SW001033
Lakhina, G. S., and Tsurutani, B. T. (2016). Geomagnetic storms: historical perspective to modern view. Geosci. Lett. 3, 5. doi:10.1186/s40562-016-0037-4
Lucas, G., Love, J. J., Kelbert, A., Bedrosian, P. A., and Rigler, E. J. (2020). A 100-year geoelectric hazard analysis for the U.S. high-voltage power grid. Space weather 18, e2019SW002329. doi:10.1029/2019SW002329
Luhmann, J. G., Li, Y., Lee, C. O., Jian, L. K., Arge, C. N., and Riley, P. (2022). Solar cycle variability in coronal holes and their effects on solar wind sources. Space weather 20, e2022SW003110. doi:10.1029/2022SW003110
Luo, B., Liu, S., and Gong, J. (2017). Two empirical models for short-term forecast of Kp. Space weather 15 (3), 503–516. doi:10.1002/2016SW001585
Mac Manus, D. H., Rodger, C. J., Dalzell, M., Renton, A., Richardson, G. S., Petersen, T., et al. (2022). Geomagnetically induced current Modeling in New Zealand: extreme Storm analysis using multiple disturbance scenarios and industry provided hazard magnitudes. Space weather 20, 12. doi:10.1029/2022SW003320
Mac Manus, D. H., Rodger, C. J., Renton, A., Ronald, J., Harper, D., Taylor, C., et al. (2023). Geomagnetically induced current mitigation in New Zealand: operational mitigation method development with industry input. Space weather 21, e2023SW003533. doi:10.1029/2023SW003533
Malandraki, O. E., and Crosby, N. B. (2018). “Solar energetic particles and space weather: science and applications,” in Solar particle radiation storms forecasting and analysis. Astrophysics and space science library. Editors O. Malandraki, and N. Crosby (Cham: Springer), 444, 1–26. doi:10.1007/978-3-319-60051-2_1
Matzka, J., Stolle, C., Yamazaki, Y., Bronkalla, O., and Morschhauser, A. (2021). The geomagnetic Kp index and derived indices of geomagnetic activity. Space weather 19, e2020SW002641. doi:10.1029/2020SW002641
Miteva, R., Samwel, S. W., and Tkatchova, S. (2023). Space weather effects on satellites. Astronomy 2, 165–179. doi:10.3390/astronomy2030012
Molinski, T. S. (2002). Why utilities respect geomagnetically induced currents. J. Atmosph. Sol-Ter. Phys. 64, 1765–1778. doi:10.1016/S1364-6826(02)00126-8
Mursula, K., Qvick, T., Holappa, L., and Asikainen, T. (2022). Magnetic storms during the space age: occurrence and relation to varying solar activity. J. Geophys. Res. 27, e2022JA030830. doi:10.1029/2022JA030830
Nair, M., Redmon, R., Young, L.-Y., Chulliat, A., Trotta, B., Chung, C., et al. (2023). MagNet—a data-science competition to predict disturbance storm-time index (Dst) from solar wind data. Space weather 21, e2023SW003514. doi:10.1029/2023SW003514
Ngwira, C. M., Pulkkinen, A. A., Bernabeu, E., Viljanen, A., and Crowley, G. (2015). Characteristics of extreme geoelectric fields and their possible causes: localized peak enhancements. Geophys. Res. Lett. 42, 6916–6921. doi:10.1002/2015GL065061
Park, W., Lee, J., Kim, K. C., Lee, J., Park, K., Miyashita, Y., et al. (2021). Operational Dst index prediction model based on combination of artificial neural network and empirical model. J. Space Weather Space Clim. 11, 38. doi:10.1051/swsc/2021021
Parker, W. E., and Linares, R. (2024). Satellite drag analysis during the may 2024 Gannon geomagnetic storm. J. Spacecr. Rockets 61, 1412–1416. doi:10.2514/1.A36164
Persons, T. M., and Rusco, F. (2018). “Technology assessment. Critical infrastructure protection,” in Protecting the electric grid from geomagnetic disturbances (United States Senate: United States Government Accountability Office Report to the Committee on Homeland Security and Governmental Affairs). Available at: https://www.gao.gov/products/gao-19-98.
Pizzo, V., Millward, G., Parsons, A., Biesecker, D., Hill, S., and Odstrcil, D. (2011). Wang-sheeley-arge–enlil cone model transitions to operations. Space weather 9, S03004. doi:10.1029/2011SW000663
Pulkkinen, A., Lindahl, S., Viljanen, A., and Pirjola, R. (2005). Geomagnetic storm of 29-31 October 2003: geomagnetically induced currents and their relation to problems in the Swedish high-voltage power transmission system. Space weather 3 (8). doi:10.1029/2004SW000123
Pulkkinen, T. I., Brenner, A., Al Shidi, Q., and Toth, G. (2022). Statistics of geomagnetic storms: global simulations perspective. Front. Astron. Space Sci. 9, 972150. doi:10.3389/fspas.2022.972150
Reames, D. V. (2021). Solar energetic particles, 2nd ed.; open access. Cham, Switzerland: Springer Nature. doi:10.1007/978-3-030-66402-2
Reiss, M. A., Temmer, M., Veronig, A. M., Nikolic, L., Vennerstrom, S., Schöngassner, F., et al. (2016). Verification of high-speed solar wind stream forecasts using operational solar wind models. Space weather 14 (7), 495–510. doi:10.1002/2016SW001390
Ryu, M., Nagarajan, H., and Bent, R. (2020). Algorithms for mitigating the effect of uncertain geomagnetic disturbances in electric grids. Electr. Power Syst. Res. 189, 106790–107796. doi:10.1016/j.epsr.2020.106790
Santoso, A., Sismanto, S., Priyatikanto, Rh., Hartantyo, E., and Martiningrum, D. R. (2024). The intensity of the geomagnetic storms associated with imf and solar wind parameters during solar cycle 24. Earth Planet. Phys. doi:10.26464/epp2024069
Shprits, Y. Y., Vasile, R., and Zhelavskaya, I. S. (2019). Nowcasting and predicting the Kp index using historical values and real-time observations. Space weather 17, 1219–1229. doi:10.1029/2018SW002141
Siciliano, F., Consolini, G., Tozzi, R., Gentili, M., Giannattasio, F., and De Michelis, P. (2021). Forecasting SYM-H index: a comparison between long short-term memory and convolutional neural networks. Space weather 19, e2020SW002589. doi:10.1029/2020SW002589
Sierra-Porta, D., Petro-Ramos, J. D., Ruiz-Morales, D. J., Herrera-Acevedo, D. D., García-Teheran, A. F., and Tarazona Alvarado, M. (2024). Machine learning models for predicting geomagnetic storms across five solar cycles using Dst index and heliospheric variables. Adv. Space Res. 74 (8), 3483–3495. doi:10.1016/j.asr.2024.08.031
Siscoe, G., and Schwenn, R. (2006). CME disturbance forecasting. Space Sci. Rev. 123, 453–470. doi:10.1007/s11214-006-9024-y
Sorokin, V., Yaschenko, A., Mushkarev, G., and Novikov, V. (2023). Telluric currents generated by solar flare radiation: physical model and numerical estimations. Atmosphere 14 (3), 458. doi:10.3390/atmos14030458
Souza, J. R., Dandenault, P., Santos, A. M., Riccobono, J., Migliozzi, M. A., Kapali, S., et al. (2024). Impacts of storm electric fields and traveling atmospheric disturbances over the Americas during 23–24 April 2023 geomagnetic storm: experimental analysis. J. Geophys. Res. 129, e2024JA032698. doi:10.1029/2024JA032698
Srivastava, N., Mierla, M., and Zhang, J. (2021). Editorial: space weather prediction: challenges and prospects. Front. Astron. Space Sci. 8, 818878. doi:10.3389/fspas.2021.818878
Tchijevsky, A. L. (1938). Les epidémies et les perturbations electromagnétiques du milieu extérieur. Paris, France: Hippocrate. Available at: https://search.worldcat.org/formats-editions/14724886.
Telloni, D., Lo Schiavo, M., Magli, E., Fineschi, S., Guastavino, S., Nicolini, G., et al. (2023). Prediction capability of geomagnetic events from solar wind data using neural networks. Astrophys. J. 952, 111. doi:10.3847/1538-4357/acdeea
Tsurutani, B. T., Gonzalez, W. D., Gonzalez, A. L. C., Guarnieri, F. L., Gopalswamy, N., Grande, M., et al. (2006). Corotating solar wind streams and recurrent geomagnetic activity: a review. J. Geophys. Res. 111, A7. doi:10.1029/2005JA011273
Vennerstroem, S. (2001). Interplanetary sources of magnetic storms: a statistical study. J. Geophys. Res. 106 (A12), 29175–29184. doi:10.1029/2001JA000004
Wang, C., Ye, Q., He, F., Chen, B., and Zhang, X. (2023). A new method for predicting non-recurrent geomagnetic storms. Space weather 21, e2023SW003522. doi:10.1029/2023SW003522
Wang, J., Luo, B., Liu, S., and Shi, L. (2023). A machine learning-based model for the next 3-day geomagnetic index (Kp) forecast. Front. Astron. Space Sci. 10, 1082737. doi:10.3389/fspas.2023.1082737
Wintoft, P., and Wik, M. (2018). Evaluation of Kp and Dst predictions using ACE and DSCOVR solar wind data. Space weather 16, 1972–1983. doi:10.1029/2018SW001994
Wrenn, G. L. (2009). Chronology of ‘killer’ electrons: solar cycles 22 and 23. J. Atmosph. Sol.-Terr. Phys. 71 (10–11), 1210–1218. doi:10.1016/j.jastp.2008.08.002
Xu, S., Huang, S., Yuan, Z., Deng, X., and Jiang, K. (2020). Prediction of the Dst index with bagging ensemble-learning algorithm. Astrophys. J. Suppl. Ser. 248, 14. doi:10.3847/1538-4365/ab880e
Xu, W., Zhu, Y. M., Zhu, L., Lu, J., Wei, G., Wang, M., et al. (2023). A class of Bayesian machine learning model for forecasting Dst during intense geomagnetic storms. Adv. Space Res. 72 (9), 3882–3889. doi:10.1016/j.asr.2023.07.009
Zank, G. P., Hunana, P., Mostafavi, P., Roux, J. A. L., Li, G., Webb, G. M., et al. (2015). Diffusive shock acceleration and reconnection acceleration processes. Astrophys. J. 814 (1), 137. doi:10.1088/0004-637X/814/2/137
Zhang, J., Feng, Y., Zhang, J., and Li, Y. (2023). The short time prediction of the Dst index based on the long-short time memory and empirical mode decomposition–long-short time memory models. Appl. Sci. 13, 11824. doi:10.3390/app132111824
Keywords: space weather, geomagnetic storm, solar wind, forecasting, blackouts, solar-terrestrial couplings
Citation: Khabarova O and Price C (2024) Importance and challenges of geomagnetic storm forecasting. Front. Astron. Space Sci. 11:1493917. doi: 10.3389/fspas.2024.1493917
Received: 10 September 2024; Accepted: 10 October 2024;
Published: 24 October 2024.
Edited by:
Joseph E. Borovsky, Space Science Institute (SSI), United StatesReviewed by:
Subhamoy Chatterjee, Southwest Research Institute Boulder, United StatesCopyright © 2024 Khabarova and Price. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Olga Khabarova, b2xnYWtoYWJhckB0YXVleC50YXUuYWMuaWw=
 Olga Khabarova
Olga Khabarova Colin Price
Colin Price