Non-Maxwellian ion distribution in the equatorial and auroral electrojets

Strong electric fields in the auroral and equatorial electrojets can distort the background ion distribution function away from the Maxwellian. We developed a collisional plasma kinetic model using the Boltzmann equation and a simple BGK collision operator to predict a relatively simple relationship between the intensity of the background electric field and the resulting ion distribution function. To test the model, we perform 3-D plasma particle-in-cell simulations and compared the results to the model. Both the simulation and the analytical model assume a constant ion-neutral collision rate. The simulations show less ion heating in the Pedersen direction than in the analytical model but nearly identical overall heating. The model overestimates heating in the Pedersen direction because the simple BGK operator models collisions as a kinetic friction only in the Pedersen direction. On the other hand, the fully kinetic particle-in-cell code captures the physics of ion scattering in 3-D and therefore heats ions more isotropically. Although the simple BGK analytical theory does not precisely model the non-Maxwellian ion distribution function, it does capture the overall momentum and energy flows and therefore can provide the basis of further kinetic analysis of E-region wave evolution during strongly driven conditions.

1 Introduction

Strong DC electric fields in the auroral and equatorial electrojets drive plasma instabilities in the E-region ionosphere. When perpendicular to the global magnetic field, these electric fields generate strong cross-field plasma instabilities, such as the Farley–Buneman instability (Farley, 1963; Buneman, 1963), gradient drift instability (Hoh, 1963; Maeda et al., 1963; Simon, 1963), electron thermal instability (Dimant and Sudan, 1995; 1997; Robinson, 1998; St. -Maurice and Kissack, 2000), and ion thermal instability (Kagan and Kelley, 2000; Dimant and Oppenheim, 2004). These plasma instabilities serve to explain the plasma density irregularities that for many years have been observed in the E-region ionosphere by radar and sounding rockets.

Analytical kinetic models of plasma instabilities can accurately describe plasma wave growth and decay, but this often requires numerous approximations, such as eliminating nonlinear terms and simplifying collisional components. Such approximations can limit their applicability. Kinetic simulations of plasma using particle-in-cell (PIC) codes can also solve for wave evolution but can consume a lot of computer power and apply to only a limited range of parameters. For example, Oppenheim et al. (2008) expended 4 years of CPU time to simulate a 2-D patch of plasma for a quarter of a second, although the simulation required less than 24 h of wall clock time using a supercomputer (see also Oppenheim and Dimant, 2004, Oppenheim and Dimant, 2013, and Oppenheim et al., 2020)]. It is therefore practical to develop a fluid analytical kinetic model which is more computationally efficient than the PIC model while, at the same time, is able to capture the development of kinetic plasma instabilities.

Such a model will need to assume a 0^th-order ion distribution function which is not Maxwellian due to the Pedersen drift and collisions with the neutrals. To develop an accurate analytical kinetic model of plasma instabilities in the E-region ionosphere, we need to understand how the electric fields in the electrojets affect the background ion distribution function.

In the ionosphere, strong DC electric fields develop in two places: in high magnetic latitudes and within a few degrees of the magnetic equator. The electric fields in the auroral electrojet come from the current mapping between the magnetosphere and the ionosphere near the poles, while the electric fields in the equatorial electrojet come from the E-region dynamo effect driven by the zonal wind (Kelley, 2009). In the latter case, the zonal wind velocity $\vec{U}$ and the geomagnetic field $\vec{B}$ must satisfy the condition $\nabla \times \left(\vec{U}\times \vec{B}\right)\ne 0$ in order to generate an electrojet and its associated electric fields (Dimant et al., 2016).

The E-region ionosphere is weakly ionized, with neutrals outnumbering ions by more than $10^6$ to 1 (Schunk and Nagy, 2009). In the lower E-region, the ions do not gyrate around the geomagnetic field because frequent collisions with neutrals effectively cause them to become unmagnetized (Kelley, 2009). These collisions also prevent ions from accelerating ad infinitum along the electric field. As a result, the bulk of the ions in steady state drifts on average with the Pedersen velocity, which is proportional to the electric field divided by the ion-neutral collision rate. On the other hand, the electrons are highly magnetized and mostly drift with the Hall velocity perpendicular to the ions. The relative drift between the ions and electrons causes plasma instabilities such as the Farley–Bunemann instability.

If the external DC electric field in the electrojet is strong enough, it can leads to a large anisotropy in the ion distribution function with clear distortions from the Maxwellian. St-Maurice and Schunk (1979) developed the theory and showed observational evidence for non-Maxwellian ion distribution functions in the high-latitude E- and F-regions. The DC electric field can be especially strong at high latitudes during geomagnetic storms. Compared to the high-latitude E- and F-regions, the equatorial E-region has less intense electric fields, so we expect the typical distortion in the ion distribution to be smaller. Still, even there, extreme geomagnetic storms can intensify the electric fields enough to deviate the ion distribution function significantly from the Maxwellian.

Our study develops a collisional plasma kinetic model which relates the intensity of the external electric field to the ion velocity distribution function. We restrict our treatment to a spatially uniform and quasi-steady ionosphere which represents the background for developing instabilities. To describe the ion-neutral collisions, our kinetic model uses the BGK collision operator (Bhatnagar et al., 1954), which is a mathematically simple way of describing plasma collisions (Nicholson, 1983). Despite its inaccuracy, this simplified operator conserves the particle number and the average momentum and energy of the colliding particles. A hybrid simulation by Kovalev et al. (2008), based on the BGK collision term for ions, gave results comparable to the more accurate hybrid and full PIC simulations (Janhunen, 1995; Oppenheim et al., 1995; Oppenheim et al., 1996; Oppenheim et al., 2008; Oppenheim and Dimant, 2004; Young et al., 2020). Else et al. (2009) found that the constant collision rate BGK model agrees with a more realistic constant mean free path model in regimes where the Pedersen velocity is less than or comparable to the neutral thermal velocity. In this study, we quantify the accuracy of a BGK plasma kinetic model by comparing the analytical results to results from a more accurate fully kinetic PIC simulation.

The paper is organized as follows. Section 2 describes the simulation methods. Section 3 presents the analytical model and compares it to the simulation results. Section 4 discusses the discrepancies between the analytical results and the simulation. Section 5 summarizes our major results and forecasts future research.

2 Simulation methods

We used an EPPIC—electrostatic parallel plasma-in-cell simulator—to simulate the E-region background ions. EPPIC, like other particle-in-cell (PIC) codes, simulates plasma as individual particles. This enables PIC simulations to reproduce the kinetic behaviors of plasma. We are interested in the kinetic behavior of plasma—that is, the distortion of the ion distribution function. For more information about PIC codes, see Birdsall and Langdon (1991). For detailed explanations of EPPIC, see Oppenheim and Dimant (2004), Oppenheim et al. (2008), and Oppenheim and Dimant (2013).

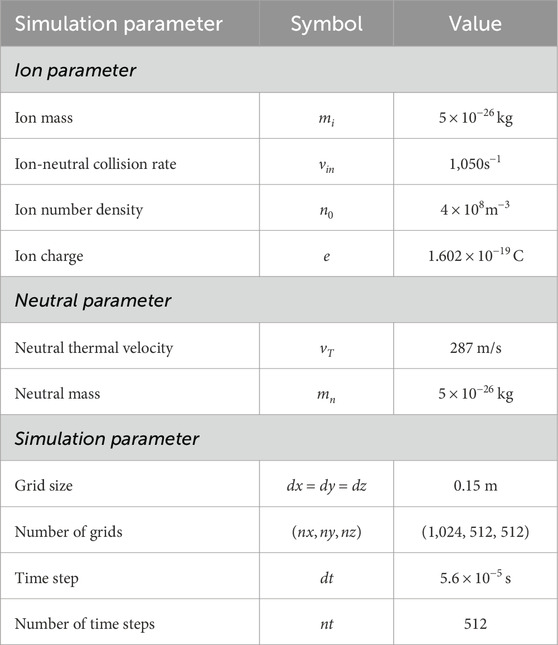
We set the magnetic field to zero in our simulation because the E-region background ions are unmagnetized. We also excluded electrons from our simulation, using instead a uniform background electron plasma that does not respond to any fields. We did this to avoid cross-drift between highly magnetized electrons and highly collisional background ions which would have led to internally generated electric fields and the Farley–Buneman instability (Farley, 1963; Buneman, 1963). This paper only explores the physics of the ion distribution function independent of the electron generated fields. EPPIC simulates background ions as PIC particles and neutrals as a uniform, constant background. Our simulation is in three dimensions (3-D), even though a two-dimensional (2-D) simulation would have sufficed for the behavior we were interested in. Table 1 gives the simulation parameters.

Table 1

Table 1. Simulation parameters.

The E-region background ions are highly collisional with the neutrals. In our simulation, we used a constant ion-neutral collision rate which does not depend on the particle’s velocity. This is analogous to the Maxwell molecule collision model in Schunk and Nagy (2009) which results in a velocity-independent collision rate. EPPIC employs a statistical method of applying collisional effects to ions. At each time step, it designates a number of ions for collision in accordance with the ion-neutral collision rate specified in the input deck; it then chooses that number of PIC particles at random, independent of ion location and velocity. For each collision, the code creates a neutral molecule assuming a random thermal distribution with the specified neutral temperature and velocity. The algorithm then collides the PIC ion and the neutral, assuming conservation of energy and momentum, changing the ion’s momentum. The algorithm then tabulates the neutral momentum and energy change and discards detailed information about the neutral particle. In the E-region, neutrals are many orders of magnitude more numerous than ions [$n_n/n_i>10^6$—Schunk and Nagy (2009)]. Therefore, neutrals that collide with ions constitute a very small part of the neutrals and do not affect their overall momentum and temperature.

Section 3.2 details the specific simulation setup as well as the analysis methods used for the simulation results.

3 Results

3.1 Analytical model of the background ion distribution function

3.1.1 Derivation of the distorted ion distribution function

The simplest kinetic equation for the ion distribution function (IDF) with the Bhatnagar–Gross–Krook (BGK) collision term (Bhatnagar et al., 1954) is given by

$\frac{\partial f}{\partial t}+\frac{e}{m_i}\vec{E}\cdot \frac{\partial f}{\partial \vec{V}}+\vec{v}\cdot \frac{\partial f}{\partial \vec{r}}=-{\nu }_{in}\left(f-\frac{n_i\left(\vec{r},t\right)}{n_0}{f}_0^{\text{Coll}}\right),(1)$

where $v=|\vec{v}|$ is the ion speed, ${\nu }_{in}$ is the ion-neutral collision frequency, $T_n$ is the neutral temperature (in energy units), $m_i$ is the ion mass (equal to the neutral mass), $\vec{E}$ is the external electric field, and

$f_0^{\text{Coll}}\left(v\right)\equiv n_0{\left(\frac{m_i}{2\pi T_n}\right)}^{3/2}\exp \left(-\frac{m_i{v}^2}{2T_n}\right).$

The function $f_0^{\text{Coll}}\left(v\right)$ is the spatially uniform and stationary ion Maxwellian distribution function, normalized to the mean ion density $n_0$ with no external electric field. The BGK collision term on the RHS of Equation 1 assumes Maxwell collisions (Schunk and Nagy, 2009) with the given constant a constant ion-neutral collision rate ${\nu }_{in}$ which accurately models Maxwell molecule collisions (Schunk and Nagy, 2009).

Below, we only consider the background conditions with the externally imposed electric field before developing any instabilities, $\vec{E}={\vec{E}}_0$. For the corresponding spatially uniform and stationary background ion distribution function $f_0(\vec{v})$, Equation 1 reduces to

${\vec{a}}_0\cdot \frac{\partial f_0}{\partial \vec{V}}=-{\nu }_{in}\left(f_0-f_0^{\text{Coll}}\right),(2)$

where ${\vec{a}}_0\equiv e{\vec{E}}_0/m_i$ is the free-ion acceleration. By introducing a Cartesian coordinate system with the axis $y$ directed along ${\vec{a}}_0$ and integrating Equation 2 over the perpendicular velocity components $v_y$ $v_x$ and $v_z$, we obtain

$a_0\frac{\partial F_0}{\partial V_y}=-{\nu }_{in}\left(F_0-F_0^{\text{Coll}}\right).(3)$

Here,

$F_0\left(v_y\right)\equiv \underset{-\infty }{\overset{+\infty }{\iint }}{f}_{0}d{v}_{x}d{v}_z(4)$

and

$F_0^{\text{Coll}}\left(v_y\right)\equiv \frac{n_0}{\sqrt{2\pi }{v}_{Ti}}\exp \left(-\frac{v_y^2}{2v_{Ti}^2}\right),(5)$

where $v_{Ti}\equiv \sqrt{T_n/m_i}$ is the thermal velocity of the neutral particles $(m_i=m_n)$. In the BGK approximation, the ion velocity distribution in the two perpendicular directions remains undisturbed by the field ${\vec{E}}_0$, so that the full 3-D IDF becomes

$f_0\left(v_x,v_y,v_z\right)=\frac{F_0\left(v_y\right)}{2\pi v_{Ti}^2}\exp \left(-\frac{v_x^2+v_z^2}{2v_{Ti}^2}\right).(6)$

Plugging Equation 5 into Equation 3 and solving the latter yields

$F_0\left(v_y\right)=\frac{n_0{\nu }_{in}}{2a_0}\exp \left[-\frac{{\nu }_{in}{v}_y}{a_0}+\frac{1}{2}{\left(\frac{{\nu }_{in}{v}_{Ti}}{a_0}\right)}^2\right]\left[1+erf\left(\frac{v_y-{\nu }_{in}{v}_T^2/a_0}{\sqrt{2}{v}_{Ti}}\right)\right],(7)$

where $erf(y)=(2/\sqrt{\pi }){\int }_0^y{e}^{-t^2}dt$ is the error function. Introducing the dimensionless ion velocity $u\equiv {\nu }_{in}{v}_y/a_0$ and the dimensionless neutral thermal velocity $u_T\equiv {\nu }_{in}{v}_{Ti}/a_0$, we can recast Equation 7 as

$\begin{array}{ll}\hfill G_0\left(u\right)& =\frac{1}{2}\exp \left(-u+\frac{u_T^2}{2}\right)\left[1+\text{erf}\left(\frac{u-u_T^2}{\sqrt{2}{u}_T}\right)\right]\hfill \\ \hfill & =\frac{1}{2}\exp \left(-\frac{u^2}{2u_T^2}\right)w\left(-i\frac{u-u_T^2}{\sqrt{2}{u}_T}\right),\hfill \end{array}(8)$

where $G_0(u)=[a_0/(n_0{\nu }_{in})]F_0(v_y)$ and $w(\zeta )=e^{-{\zeta }^2}\left[1+erf(i\zeta )\right]$. The function $w(\zeta )$ can be written in terms of the standard plasma dispersion function, $Z(\zeta )$, as $w(\zeta )=-(i/\sqrt{\pi })Z(\zeta )$.

The solution in the form of Equation 8 automatically conserves the number of particles and provides the correct expressions for the Pedersen velocity and effective temperature (see below), as can be deduced from the following integral relationships:

$\begin{array}{ll}\hfill {\int }_{-\infty }^{+\infty }{G}_0\left(u\right)du& =1,{\int }_{-\infty }^{+\infty }u{G}_0\left(u\right)du=1,\hfill \\ \hfill & {\int }_{-\infty }^{+\infty }{u}^2{G}_0\left(u\right)du=u_T^2+2.\hfill \end{array}(9)$

Figure 1 shows the normalized ion distribution function in Equation 8 for four values of $u_T$. Note that $u_T\propto E_0^{-1}$, so the four values of $u_T$ in Figure 1 correspond to four values of $E_0$. The ion distribution functions with large values of $u_T$ assume Maxwellian shapes, while the ion distribution functions with small values of $u_T$ appear right-skewed when compared to the Maxwellian. The distortion is such that their peaks lie to the left of their bulk velocity, which is equal to one according to Equation 9. Section 3.1.2 explains why the ion distribution function retains the Maxwellian shape at lower higher values of $u_T$ but is distorted at higher lower values of $u_T$.

Figure 1

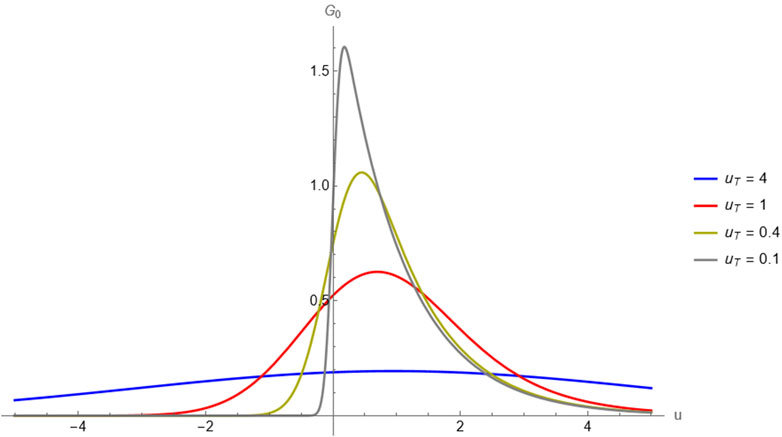
Figure 1. Normalized ion distribution function (IDF) for four values of $u_T\equiv v_T/v_{\mathrm{P}\mathrm{e}\mathrm{d}}$, where $v_{\mathrm{P}\mathrm{e}\mathrm{d}}=a_0/{\nu }_{in}$ is the ion Pedersen velocity proportional to $E_0$. The vertical axis is the function $G_0(u)$, as seen in Equation 8. The horizontal axis is the normalized ion velocity $u\equiv v_y/v_{\mathrm{P}\mathrm{e}\mathrm{d}}$. Since $u$ is normalized to $a_0^{-1}$, the IDF is compressed in the horizontal axis by a factor $\propto E_0$; therefore, effective heating does not relate to the full width at half maximum (FWHM) in the usual way. In this plot, curves with smaller FWHM are more strongly heated.

3.1.2 Distortion of the ion distribution function in the low and high $E_0$ limits

The antisymmetrical error function, $erf\left(\xi \right)$, at large $|\xi |$ can be approximated as

$\text{erf}\left(\xi \right)\approx \left\{\begin{array}{cc}1-\frac{\exp \left(-{\xi }^2\right)}{\xi \sqrt{\pi }}\hfill & \text{if}\xi >0\text{\hspace{0.17em}\hspace{0.17em}and\hspace{0.17em}\hspace{0.17em}}\xi \gg 1\hfill \\ -1+\frac{\exp \left(-{\xi }^2\right)}{\left(-\xi \right)\sqrt{\pi }}\hfill & \text{if\hspace{0.17em}\hspace{0.17em}}\xi <0\text{\hspace{0.17em}\hspace{0.17em}and\hspace{0.17em}\hspace{0.17em}}\left(-\xi \right)\gg 1\hfill \end{array}\right..(10)$

Using the bottom approximation from Equation 10, we can show that in the limit where $a_0\to 0$,

$G_0\left(u\right)\to \frac{1}{\sqrt{2\pi }{u}_T}\exp \left(-\frac{u^2}{2u_T^2}\right).(11)$

This corresponds to $f_0\to f_0^{\text{Coll}}$—the background ion distribution tends toward Maxwellian in the low $E_0$ limit. Equation 11 does not hold for all values of $u$. As seen from Equations 8, 11 does not hold if $u\gg u_T^2$. This means that the positive tail of the ion distribution function may deviate significantly from the Maxwellian.

The low $E_0$ limit can be expressed in terms of the ion Pedersen velocity, $v_{\mathrm{P}\mathrm{e}\mathrm{d}}=⟨v_y⟩=a_0/{\nu }_{in}=e{E}_0/(m_i{\nu }_{in})$, and the neutral thermal velocity $v_T$. If $v_{\mathrm{P}\mathrm{e}\mathrm{d}}\ll v_T$, then the distortion to the ion distribution function is weak, since the ion distribution function tends toward the Maxwellian. The effective temperature,

$T_{\text{eff}}=T_n+\frac{m{v}_{\mathrm{P}\mathrm{e}\mathrm{d}}^2}{2},(12)$

is only slightly higher than $T_n$, since $m{v}_{\mathrm{P}\mathrm{e}\mathrm{d}}^2\ll T_n$ in this limit.

In the high $E_0$ limit where $v_{\mathrm{P}\mathrm{e}\mathrm{d}}\gg v_T$, Equation 8 does not tend toward the Maxwellian, so the ion distribution function will be distorted along the ${\vec{E}}_0$ direction. The corresponding heating will be very considerable as well, since $m{v}_{\mathrm{P}\mathrm{e}\mathrm{d}}^2\gg T_n$ in Equation 12. Note that the effective thermal velocity, $\sqrt{T_{\text{eff}}/m_i}$, is of the order of the Pedersen velocity: $\sqrt{T_{\text{eff}}/m_i}\approx v_{\mathrm{P}\mathrm{e}\mathrm{d}}/\sqrt{2}$.

3.2 Background ion distribution functions from the PIC simulation

3.2.1 Kinetic simulation of highly collisional, unmagnetized, $\overrightarrow{E_0}$-driven background ions

Our model from Section 3.1 predicts that the background ion distribution function (IDF) will distort away from Maxwellian when $E_0$ is high enough. Equation 7 gives the one-dimensional IDF we expect to see in the $\overrightarrow{E_0}$ direction. To test the validity of our model, we ran four simulation cases using EPPIC. The values of $E_0$ used in the simulation cases are:

1. $E_0=0\text{m}\text{V}/\text{m}$, which corresponds to $u_T\to \infty$.

2. $E_0=24\text{m}\text{V}/\text{m}$, which corresponds to $u_T=4$.

3. $E_0=94\text{m}\text{V}/\text{m}$, which corresponds to $u_T=1$.

4. $E_0=235\text{m}\text{V}/\text{m}$, which corresponds to $u_T=0.4$.

As before, $u_T\equiv v_T/v_{\mathrm{P}\mathrm{e}\mathrm{d}}$ is the normalized neutral thermal velocity, $v_T=\sqrt{T_n/m_i}$ is the neutral thermal velocity, and $v_{\mathrm{P}\mathrm{e}\mathrm{d}}=e{E}_0/m_i{\nu }_{in}$ is the ion Pedersen velocity.

Our simulation includes one ion species, one neutral species, and no electrons. The imposed electric field $\overrightarrow{E_0}$ points in the y-direction, and there is no imposed magnetic field. As discussed in Section 2, the setup is representative of the plasma condition in the E-region ionosphere where ions are unmagnetized and highly collisional with the neutrals.

Table 1 gives the parameters used across all simulation cases.

3.2.2 Normalization of the discrete ion velocity distribution from the simulation

The simulation outputs a $(v_x\times v_y\times v_z)=(512\times 512\times 512)$ array of ion velocity distribution over a 3-D velocity domain. Each dimension of the array covers a 1-D velocity domain of [−20 km/s, 20 km/s]. The grid size is $\mathrm{\Delta }v=[20km/s-(-20km/s)]/512=78.125m/s$ in each dimension. We reduce the three-dimensional velocity distribution array $f(v_x,v_y,v_z)$ into three one-dimensional velocity distribution arrays—$F_x(v_x)$, $F_y(v_y)$, and $F_z(v_z)$—by summing over two other dimensions. This gives us

$F_x\left(v_x\right)={\displaystyle \sum _{v_y}}{\displaystyle \sum _{v_z}}f\left(v_x,v_y,v_z\right)$

and similarly for $F_y(v_y)$ and $F_z(v_z)$.

To facilitate the comparison with the theory, we normalize $F_x(v_x)$, $F_y(v_y)$, and $F_z(v_z)$ such that the sum of each distribution is equal to ${\left(\mathrm{\Delta }v\right)}^{-1}$. This process is analogous to letting the 0^th velocity moment of a continuous distribution function equal 1. This in effect normalizes the ion number density to 1. The normalized arrays are given by

$F_k^{\prime }\left(v_k\right)=\frac{F_k\left(v_k\right)}{{\sum }_{v_k}{F}_k\left(v_k\right)\mathrm{\Delta }v},(13)$

where $k$ is either $x$, $y$, or $z$. The normalization makes it so that ${\sum }_{v_k}{F}_x^{\prime }(v_x)={\left(\mathrm{\Delta }v\right)}^{-1}$ for all $k$.

3.2.3 Normalization of the continuous ion velocity distribution from the theory

The continuous one-dimensional ion distribution function in the direction parallel to ${\vec{E}}_0$ direction is given by the theory as $F_0(v_y)$ in Equation 7. For clarity, we reiterate Equation 7 as

$F^{{\mathrm{T}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r}\mathrm{y}}_y}\left(v_y\right)=\left\{\begin{array}{c}\frac{n_0{\nu }_{in}}{2a_0}\exp \left[-\frac{{\nu }_{in}{v}_y}{a_0}+\frac{1}{2}{\left(\frac{{\nu }_{in}{v}_T}{a_0}\right)}^2\right]\hfill \\ \left[1+erf\left(\frac{v_y-\frac{v_T^2{\nu }_{in}}{a_0}}{\sqrt{2}{v}_T}\right)\right],& \text{if\hspace{0.17em}}{a}_0\ne 0\hfill \\ \frac{n_0}{\sqrt{2\pi }{v}_T}\exp \left(-\frac{v_y^2}{2v_T^2}\right),\hfill & \text{if\hspace{0.17em}}{a}_0=0\hfill \end{array}\right.,$

where we incorporate the result in the low $E_0$ limit from Section 3.1.2.

For the directions perpendicular to $\overrightarrow{E_0}$, the theory assumes an undisturbed Maxwellian given by

$F_j^{\mathrm{T}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r}\mathrm{y}}\left(v_j\right)=\frac{n_0}{\sqrt{2\pi }{v}_T}\exp \left(-\frac{v_j^2}{2v_T^2}\right),$

where $j$ is either $x$ or $z$.

To facilitate the comparison with the simulation results, we normalize $F_x^{\mathrm{T}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r}\mathrm{y}}(v_x)$, $F^{{\mathrm{T}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r}\mathrm{y}}_y(v_y)}$, and $F^{{\mathrm{T}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r}\mathrm{y}}_z}(v_z)$ such that the area under the curve of each distribution is equal to one. This sets the 0^th velocity moment of the distribution to 1 and normalizes the ion number density to 1. The normalized distribution functions are given by

$F_k^{\prime \mathrm{T}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r}\mathrm{y}}\left(v_k\right)=\frac{F_k^{\mathrm{T}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r}\mathrm{y}}\left(v_k\right)}{{\int }_{-\infty }^{\infty }{F}_k^{\mathrm{T}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r}\mathrm{y}}\left(v\right)dv}=\frac{F_k^{\mathrm{T}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r}\mathrm{y}}\left(v_k\right)}{n_0},(14)$

where $k$ is either $x$, $y$, or $z$. The normalization makes it so that ${\int }_{-\infty }^{\infty }{F}_k^{\prime \mathrm{T}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r}\mathrm{y}}(v_k)d{v}_k=1$ for all $k$.

3.2.4 Choice of ${\nu }_{in}$ in the theoretical results

Although EPPIC used the ion-neutral collision rate ${\nu }_{in}=1050s^{-1}$ as its input, the outputted $F_y^{\prime }(v_y)$ instead exhibits ${\nu }_{in}=1082s^{-1}$ at an effective collision rate of $1082s^{-1}$. The simulation gives the ion bulk velocity $⟨v_y⟩$, and the relation $⟨v_y⟩=e{E}_0/(m_i{\nu }_{in})$ defines the effective ${\nu }_{in}$. To ensure compatibility between the simulation results and the theory, we chose the effective ${\nu }_{in}$ in $F_y^{\prime \mathrm{T}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r}\mathrm{y}}(v_y)$ such that

${\int }_{-\infty }^{\infty }{v}_y{F}_y^{\prime \mathrm{T}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r}\mathrm{y}}\left(v_y\right)d{v}_y={\displaystyle \sum _{v_y}}{v}_y{F}_y^{\prime }\left(v_y\right)\mathrm{\Delta }v.(15)$

The expression on the left-hand side of Equation 15 is the first velocity moment of $F_y^{\prime \mathrm{T}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r}\mathrm{y}}$, which gives the theoretical bulk velocity of the ions. The expression on the right-hand side of Equation 15 gives the bulk velocity of the simulated ions. By matching these two quantities, we ensure that the theoretical ion distribution function is representative of the condition in the simulated background ions to first order.

We numerically calculated both sides of Equation 15 for $E_0=24\text{m}\text{V}/\text{m}$, $E_0=94\text{m}\text{V}/\text{m}$, and $E_0=235\text{m}\text{V}/\text{m}$. For all of these cases, the effective ${\nu }_{in}=1082s^{-1}$ satisfies Equation 15 to within $\pm 2\text{m}/\text{s}$. On the other hand, the PIC ${\nu }_{in}=1050s^{-1}$ satisfies Equation 15 only to within $\pm 22m/s$. Therefore, the simulated background ions exhibit an effective ion-neutral collision rate of $1082s^{-1}$ and not $1050s^{-1}$.

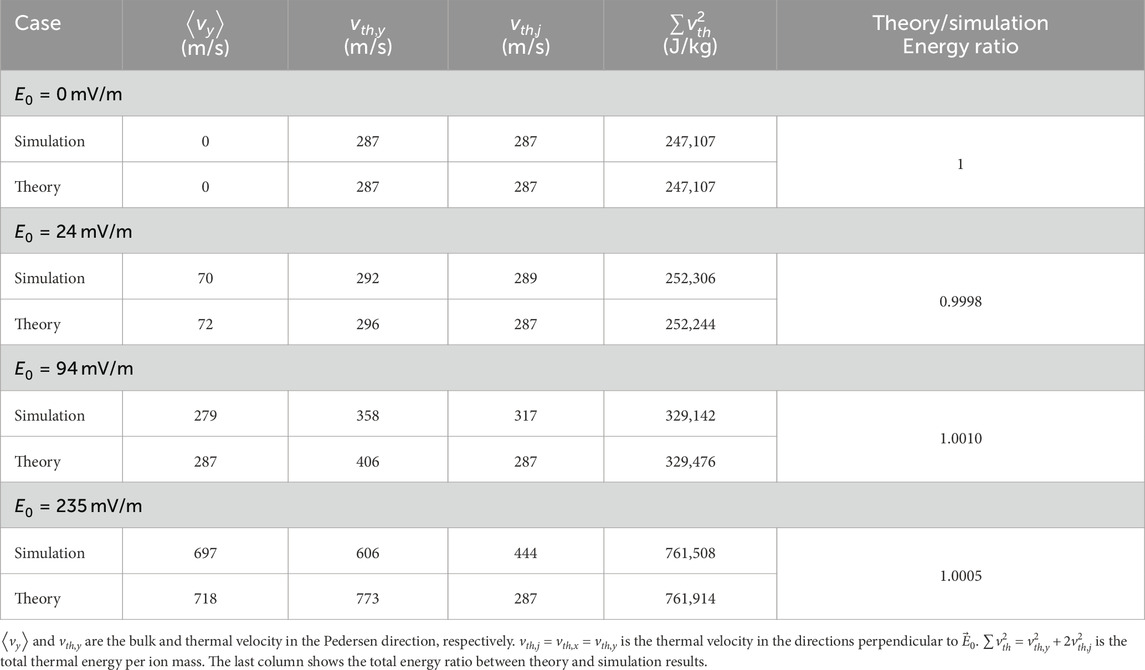
Table 2 shows the matching bulk velocities for the effective ${\nu }_{in}=1082s^{-1}$, while Table 3 shows the bulk velocity mismatch for the PIC ${\nu }_{in}=1050s^{-1}$. The choice of ${\nu }_{in}$ is irrelevant for $E_0=0\text{m}\text{V}/\text{m}$, since the theoretical ion distribution function is an undisturbed Maxwellian.

Table 2

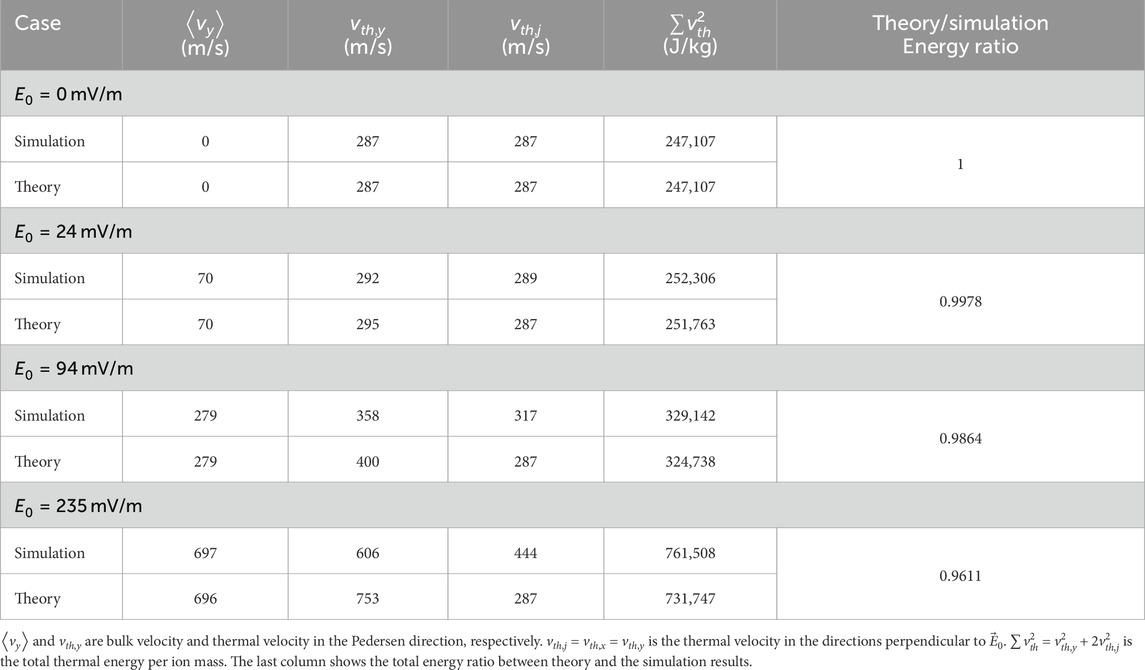
Table 2. Bulk velocities, directional thermal velocities, and total thermal energies for the effective ${\nu }_{in}=1082s^{-1}$.

Table 3

Table 3. Bulk velocities, directional thermal velocities, and total thermal energies for the PIC ${\nu }_{in}=1050s^{-1}$.

3.3 Comparison of the theoretical and simulated ion distribution functions

Figure 2A compares the theoretical and simulated ion distribution functions in the Pedersen direction—that is, the direction parallel to $\overrightarrow{E_0}$. Equation 14 gives the theoretical ion distribution functions in the Pedersen direction. Equation 13 gives the normalized ion distribution functions for the simulation results. Figure 2A also includes the Maxwellian distribution functions which have the same bulk velocities as the simulation results but assume a neutral thermal velocity of 287 m/s.

Figure 2

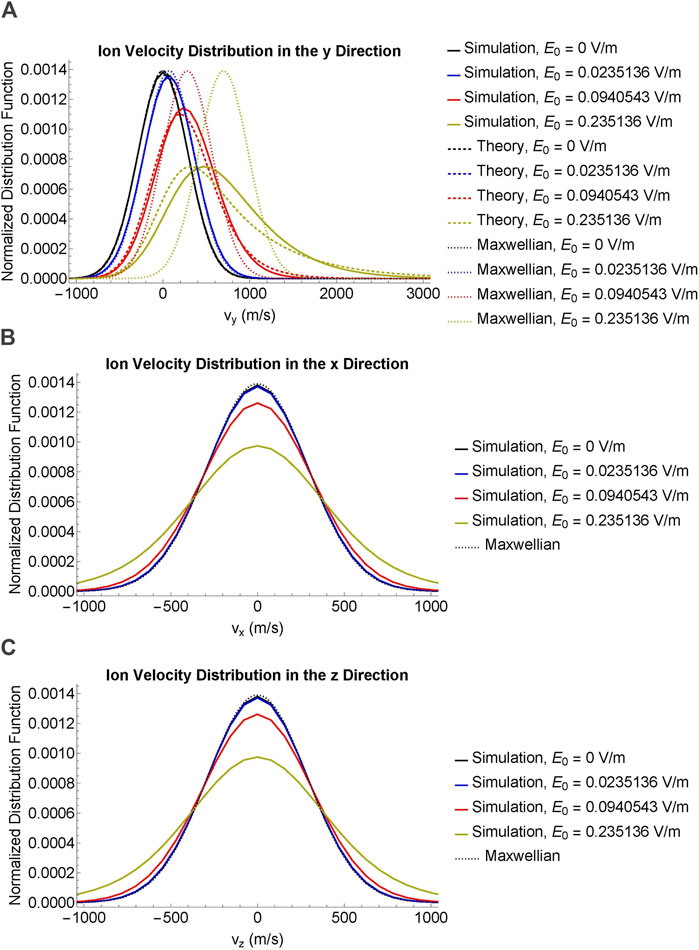
Figure 2. Comparison of simulated (solid) and theoretical (dashed) ion velocity distribution functions. Maxwellian functions (dotted) are included for comparison. The imposed electric field strengths are $E_0=0mV/m$ (black), $E_0=24mV/m$ (blue), $E_0=94mV/m$ (red), and $E_0=235mV/m$ (yellow). (A) Comparison of ion velocity functions in the Pedersen direction. (B, C) Comparison of ion velocity functions in directions perpendicular to $\overrightarrow{E_0}$. The theory assumes an undisturbed Maxwellian in (B, C). Due to symmetry, (B, C) are largely identical.

In the Pedersen direction, both the theory and the simulation results show ion heating beyond the Maxwellian, although the exact shapes of the distribution differ between the theory and the simulation results. The theoretical ion distribution functions are further right-skewed compared to the simulation, although both are right-skewed compared to the Maxwellian.

Figures 2B, C show the simulated ion distribution functions in directions perpendicular to $\overrightarrow{E_0}$. For comparison, the figure includes the undisturbed Maxwellian function which assumes the neutral temperature as the ion temperature. As mentioned in Section 3.1, the theory assumes this undisturbed Maxwellian distribution in the perpendicular directions. The simulation results show ion heating beyond the neutral temperature, especially when $E_0$ is high. Figures 2B, C are largely identical due to symmetry.

Table 2 reports the bulk and thermal velocities from the theory and simulation. Section 4 discusses the results in more detail.

4 Discussion

In this section, we mostly discuss discrepancies between the analytical results of Section 3.1 and the PIC simulations. On the one hand, the analytical model (hereinafter referred to as “theory”) is not perfectly accurate because it is based on the oversimplified BGK collision model. As a result, the theoretical 3-D shape of the ion distribution function turns out to be less accurate than the PIC-derived equivalent (over-distorted in the electric field direction and undisturbed Maxwellian in the two perpendicular directions). On the other hand, the integrated fluid characteristics, such as the ion bulk velocity and the total ion temperature, elevated due to frictional heating by the external electric field, should be accurately represented by this theory, even in the cases of very strong electric fields that result in efficient distortions of the ion distribution function. If there still remain small discrepancies, they may be attributed to imperfectly matching collision rates and to the velocity integration of the PIC determined ion distribution function being performed within an artificially restricted velocity domain. This is especially relevant to the strongly distorted ion distribution function when its high-energy tail can include a noticeable fraction of particles.

4.1 Thermal velocity mismatch between theory and simulation results

The simulated ion distribution functions show different thermal profiles from those predicted by the theory.

4.1.1 Definition of thermal velocity

For the theory, the thermal velocity in the Pedersen direction is defined in terms of the second velocity moment of the ion distribution function:

$v_{th,y}^{\text{Theory}}=\sqrt{{\int }_{-\infty }^{\infty }{\left(v_y-⟨v_y⟩\right)}^2{F}_y^{\prime \mathrm{T}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r}\mathrm{y}}\left(v_y\right)d{v}_y},$

where $F_y^{\prime \mathrm{T}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r}\mathrm{y}}$ is the normalized ion distribution function from Equation 14, and $⟨v_y⟩$ is the ion bulk velocity in the Pedersen direction as given in Table 2. In directions perpendicular to $\overrightarrow{E_0}$, the thermal velocity is equal to the neutral thermal velocity $v_T$, since the theory does not account for heating in these directions and assumes an undisturbed Maxwellian.

For the simulation results, the thermal velocity in direction $i$ is given by

$v_{th,i}=\sqrt{{\displaystyle \sum _{v_i}}{\left(v_i-⟨v_i⟩\right)}^2{F}_i^{\prime }\left(v_i\right)d{v}_i},$

where $i$ is either $x$, $y$, or $z$, $F_i^{\prime }$ is the normalized ion distribution function from Equation 13, and $⟨v_i⟩$ is the ion bulk velocity in direction $i$ as given in Table 2.

Table 2 shows the mismatch in directional heating between the theory and the simulation results. Section 4.1.2 discusses ion heating in directions perpendicular to ${\vec{E}}_0$, while Section 4.1.3 discusses ion heating in the Pedersen direction.

4.1.2 Underestimation of the thermal velocity in the directions $\perp {\vec{E}}_0$

The theory underestimates the ion heating in the directions perpendicular to ${\vec{E}}_0$. In the $x$ and $z$ directions, the theory predicts an ion thermal velocity of 287 m/s which is equal to the neutral thermal velocity $v_T$.

For larger values of $E_0$, the simulation shows an increase in the ion thermal velocity, whereas the theoretical thermal velocity remains at 287 m/s. The theory assumes an undisturbed Maxwellian in the directions perpendicular to ${\vec{E}}_0$, so it does not account for ion heating in these directions. The simulation shows that ion heating is more intense for larger values of $E_0$. In the most intense $E_0=235mV/m$, the simulated thermal velocity reaches as much as 444 m/s or about 1.5 times the undisturbed value. The increase in temperature is caused by ion frictional heating (Saint-Maurice and Hanson, 1982) which has been observed in the E-region ionosphere (e.g., Watanabe et al., 1991; Fujii et al., 2002; Zhang and Varney, 2024).

4.1.3 Overestimation of thermal velocity in the direction $\Vert {\vec{E}}_0$

The theory overestimates the heating in the Pedersen direction. In the $y$ direction, the theory predicts higher ion thermal velocities for higher values of $E_0$. Table 2 shows the theoretical predictions of the thermal velocities as well as the simulation results.

For larger values of $E_0$, both the theory and the simulation show increased ion thermal velocities beyond the neutral thermal velocity, as expected from ion frictional heating. However, the theory and the simulation results disagree on the exact amount of the heating. The simulation shows that ion heating is less intense in the Pedersen direction than the theory suggests. The discrepancy is larger for larger values of $E_0$. In the most intense case of $E_0=235mV/m$, the simulated thermal velocity only reaches 606 m/s or just 80% of the theoretical value of 753 m/s.

4.1.4 Angular scattering of ions due to elastic collisions with the neutrals

The major difference between the theory and the simulation is the angular scattering of ions in 3-D. The theory models ion heating only in the Pedersen direction; it does not account for ions scattering into directions perpendicular to ${\vec{E}}_0$. On the other hand, the PIC code is able to capture the physics of ion scattering in 3-D. Angular scattering causes ion heating to be more isotropic in the simulation. The theory underestimates the heating in the directions it does not account for, while at the same time overestimating in the direction it does account for.

We expect the total ion thermal energy to be the same between the theory and the simulation. Section 4.2 compares the total energy between the theory and the simulation.

4.2 Discrepancy in total energy between the theory and the simulation results

The total ion thermal energy differs between the theory and the simulation results. Table 2 gives the total thermal energy per ion mass as well as the total thermal energy ratio between the theory and the simulation results. Although the ratios are close to 1, the total thermal energy from the theory is consistently lower than the total thermal energy from the simulation. Larger values of $E_0$ exhibit larger energy discrepancies than smaller values of $E_0$. In the most intense case $E_0=235mV/m$, the theory captures 96.11% of the total simulated energy, while in the less intense case $E_0=24mV/m$, the theory captures as much as 98.85% of the total simulated energy.

A possible explanation for the discrepancy in total energy is our choice of ${\nu }_{in}$ as described in Section 3.2.4. The theoretical IDF depends on ${\nu }_{in}$ in the Pedersen direction. We chose ${\nu }_{in}$ retroactively such that the theory matches the simulation results to first order. Table 3 shows a hypothetical situation in which the theory uses the PIC ${\nu }_{in}=1050s^{-1}$ as its ion-neutral collision rate instead of the analytical effective value of $1082s^{-1}$. As seen by the mismatch in the bulk velocity, the PIC ${\nu }_{in}=1050s^{-1}$ does not satisfy Equation 15. However, the PIC ${\nu }_{in}=1050s^{-1}$ shows greater agreement with the simulation results in terms of the total thermal energy.

Comparing Tables 2, 3 shows how sensitive the theoretical IDF is to the value of ${\nu }_{in}$. We expect the theory to preserve the total thermal energy of the background ions while also giving the correct ion bulk velocity. The theory is able to do both within a margin of error.

4.3 Distortion of the ion distribution function in the equatorial E-region

A typical DC electric field strength in the equatorial E-region is $E_0=24\text{m}\text{V}/\text{m}$. Figure 2 shows only a small distortion in the ion distribution function for $E_0=24\text{m}\text{V}/\text{m}$. Table 2 gives the bulk and thermal velocities for $E_0=24\text{m}\text{V}/\text{m}$.

In the Pedersen direction, the theory predicts a thermal velocity of 295 m/s, while the simulation shows a thermal velocity of 294 m/s. In the directions perpendicular to the Pedersen direction, the simulation shows a thermal velocity of 291 m/s. These numbers are not so different from the Maxwellian thermal velocity of 287 m/s.

The background ion distribution in the equatorial E-region is not likely to distort much from the Maxwellian because the electric field is not strong enough. Both the theory and the simulation show that the distortion is stronger when $E_0$ is higher. In the Earth’s ionosphere, the distortion will be stronger in the auroral E-region where the DC electric field is more intense than the equatorial E-region, especially during periods of geomagnetic storms.

5 Conclusion

We developed a collisional plasma kinetic model for E-region background ions using the simple BGK collision operator (Section 3.1). This simplified analytical model results in the ion distribution function (IDF) distorted in the direction of the external DC electric field ${\vec{E}}_0$ (the Pedersen direction), while in the two perpendicular directions the velocity distribution remains the undisturbed Maxwellian (Equations 4–7). The reason for this extreme anisotropy lies in the fact that the BGK collisional operator does not include any ion angular scattering in the velocity space. At the same time, even this simplified model provides accurate values for the total Pedersen drift velocity and, given equal masses of the colliding ions and neutrals, for the total effective ion temperature elevated by the frictional heating. Under a sufficiently intense external electric field, the IDF is skewed in the direction of ${\vec{E}}_0$, so that a strong tail of superthermal-energy ions forms.

We compared this simplified model to the PIC simulation (Section 3.2). The simulation shows less ion heating in the Pedersen direction and more ion heating in the perpendicular directions than the analytical model. The difference in the thermal distribution is due to the ion angular scattering which, unlike the model, is present in the PIC code. There is also a small difference in the total thermal energy between the model and the simulation (Table 2). We have shown that the BGK model is sensitive to the choice of the ion-neutral collision rate, as shown by the alternate results in Table 3 which curiously give a total thermal energy that matches exactly with the simulation despite being unable to reproduce the ion bulk velocity. Still, the difference in Table 2 is not big enough to be consequential. The BGK model shows an overall similar total thermal energy to the PIC simulation.

The shapes of the ion distribution functions differ between the BGK model and the PIC simulation. The more accurate IDF determined by the PIC simulation is somewhere between the analytically determined IDF and the Pedersen-shifted Maxwellian distribution whose temperature equals the total elevated ion temperature. The latter, however, does not show any IDF skewness which is present in both analytical model and PIC simulations.

For the typical electric field strength of the equatorial E-region, the background ion distribution function is well-represented by the shifted and heated Maxwellian function. The situation may be very different at high latitudes where a strong external field may be present during periods of geomagnetic storms. Both the model and the PIC simulation show that, in these cases, the background ion velocity distribution can distort significantly from any Maxwellian. Any accurate model of plasma instabilities in a strongly driven E-region ionosphere must account for the potential non-Maxwellian distribution of the background ions. This modified distribution function can serve as the starting point when evaluating plasma wave growth characteristics using linear kinetic theory.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

RK: investigation, writing–original draft, and writing–review and editing. YD: conceptualization, methodology, writing–original draft, and writing–review and editing. MO: supervision, writing–review and editing, and software.

Funding

The authors declare that financial support was received for the research, authorship, and/or publication of this article. This work was funded by NASA Grants 80NSSC21K1322 and 80NSSC19K0080.

Acknowledgments

Computational resources were provided by the Anvil supercomputer through the NSF/ACCESS program.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor JC declared a past co-authorship with the author MO.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bhatnagar, P. L., Gross, E. P., and Krook, M. (1954). A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 94, 511–525. doi:10.1103/PhysRev.94.511

CrossRef Full Text | Google Scholar

Birdsall, C. K., and Langdon, A. B. (1991). Plasma physics via computer simulation.

Google Scholar

Buneman, O. (1963). Excitation of field aligned sound waves by electron streams. Phys. Rev. Lett. 10, 285–287. doi:10.1103/PhysRevLett.10.285

CrossRef Full Text | Google Scholar

Chen, F. F. (2016). Introduction to plasma physics and controlled fusion. doi:10.1007/978-3-319-22309-4

CrossRef Full Text | Google Scholar

Dimant, Y. S., and Oppenheim, M. M. (2004). Ion thermal effects on E-region instabilities: linear theory. J. Atmos. Solar-Terrestrial Phys. 66, 1639–1654. doi:10.1016/j.jastp.2004.07.006

CrossRef Full Text | Google Scholar

Dimant, Y. S., Oppenheim, M. M., and Fletcher, A. C. (2016). Generation of electric fields and currents by neutral flows in weakly ionized plasmas through collisional dynamos. Phys. Plasmas 23, 084503. doi:10.1063/1.4961085

CrossRef Full Text | Google Scholar

Dimant, Y. S., and Sudan, R. N. (1995). Kinetic theory of low-frequency cross-field instability in a weakly ionized plasma. II. Phys. Plasmas 2, 1169–1181. doi:10.1063/1.871395

CrossRef Full Text | Google Scholar

Dimant, Y. S., and Sudan, R. N. (1997). Physical nature of a new cross-field current-driven instability in the lower ionosphere. J. Geophys. Res. 102, 2551–2564. doi:10.1029/96JA03274

CrossRef Full Text | Google Scholar

Else, D., Kompaneets, R., and Vladimirov, S. V. (2009). On the reliability of the Bhatnagar-Gross-Krook collision model in weakly ionized plasmas. Phys. Plasmas 16, 062106. doi:10.1063/1.3152329

CrossRef Full Text | Google Scholar

Farley, J. D. T. (1963). A plasma instability resulting in field-aligned irregularities in the ionosphere. J. Geophys. Res. 68, 6083–6097. doi:10.1029/JZ068i022p06083

CrossRef Full Text | Google Scholar

Fujii, R., Oyama, S., Buchert, S. C., Nozawa, S., and Matuura, N. (2002). Field-aligned ion motions in the E and F regions. J. Geophys. Res. Space Phys. 107, 1049. doi:10.1029/2001JA900148

CrossRef Full Text | Google Scholar

Hoh, F. C. (1963). Instability of penning-type discharges. Phys. Fluids 6, 1184–1191. doi:10.1063/1.1706878

CrossRef Full Text | Google Scholar

Janhunen, P. (1995). On recent developments in E-region irregularity simulations and a summary of related theory. Ann. Geophys. 13, 791–806. doi:10.1007/s00585-995-0791-7

CrossRef Full Text | Google Scholar

Kagan, L. M., and Kelley, M. C. (2000). A thermal mechanism for generation of small-scale irregularities in the ionospheric E region. J. Geophys. Res. 105, 5291–5303. doi:10.1029/1999JA900415

CrossRef Full Text | Google Scholar

Kelley, M. C. (2009). The Earth’s ionosphere: plasma physics and electrodynamics. Academic Press.

Google Scholar

Kovalev, D. V., Smirnov, A. P., and Dimant, Y. S. (2008). Modeling of the Farley-Buneman instability in the E-region ionosphere: a new hybrid approach. Ann. Geophys. 26, 2853–2870. doi:10.5194/angeo-26-2853-2008

CrossRef Full Text | Google Scholar

Maeda, K., Tsuda, T., and Maeda, H. (1963). Theoretical interpretation of the equatorial sporadic E layers. Phys. Rev. Lett. 11, 406–407. doi:10.1103/PhysRevLett.11.406

CrossRef Full Text | Google Scholar

Nicholson, D. R. (1983). Introduction to plasma theory, 1. New York: Wiley.

Google Scholar

Oppenheim, M., Dimant, Y., Longley, W., and Fletcher, A. C. (2020). Newly discovered source of turbulence and heating in the solar chromosphere. Astrophysical J. 891, L9. doi:10.3847/2041-8213/ab75bc

CrossRef Full Text | Google Scholar

Oppenheim, M., Otani, N., and Ronchi, C. (1995). Hybrid simulations of the saturated Farley-Buneman instability in the ionosphere. Geophys. Res. Lett. 22, 353–356. doi:10.1029/94GL03277

CrossRef Full Text | Google Scholar

Oppenheim, M., Otani, N., and Ronchi, C. (1996). Saturation of the Farley-Buneman instability via nonlinear electron E×B drifts. J. Geophys. Res. 101, 17273–17286. doi:10.1029/96JA01403

CrossRef Full Text | Google Scholar

Oppenheim, M. M., Dimant, Y., and Dyrud, L. P. (2008). Large-scale simulations of 2-D fully kinetic Farley-Buneman turbulence. Ann. Geophys. 26, 543–553. doi:10.5194/angeo-26-543-2008

CrossRef Full Text | Google Scholar

Oppenheim, M. M., and Dimant, Y. S. (2004). Ion thermal effects on E-region instabilities: 2D kinetic simulations. J. Atmos. Solar-Terrestrial Phys. 66, 1655–1668. doi:10.1016/j.jastp.2004.07.007

CrossRef Full Text | Google Scholar

Oppenheim, M. M., and Dimant, Y. S. (2013). Kinetic simulations of 3-D Farley-Buneman turbulence and anomalous electron heating. J. Geophys. Res. Space Phys. 118, 1306–1318. doi:10.1002/jgra.50196

CrossRef Full Text | Google Scholar

Robinson, T. R. (1998). The effects of small scale field aligned irregularities on E-region conductivities: implications for electron thermal processes. Adv. Space Res. 22, 1357–1360. doi:10.1016/S0273-1177(98)80034-3

CrossRef Full Text | Google Scholar

Saint-Maurice, J. P., and Hanson, W. B. (1982). Ion frictional heating at high latitudes and its possible use for an in situ determination of neutral thermospheric winds and temperatures. J. Geophys. Res. 87, 7580–7602. doi:10.1029/JA087iA09p07580

CrossRef Full Text | Google Scholar

Schunk, R., and Nagy, A. (2009). Ionospheres: physics, plasma physics, and chemistry. Cambridge atmospheric and space science series (Cambridge University Press), 2.

Google Scholar

Simon, A. (1963). Instability of a partially ionized plasma in crossed electric and magnetic fields. Phys. Fluids 6, 382–388. doi:10.1063/1.1706743

CrossRef Full Text | Google Scholar

St. -Maurice, J. P., and Kissack, R. S. (2000). The role played by thermal feedback in heated Farley-Buneman waves at high latitudes. Ann. Geophys. 18, 532–546. doi:10.1007/s00585-000-0532-x

CrossRef Full Text | Google Scholar

St-Maurice, J. P., and Schunk, R. W. (1979). Ion velocity distributions in the high-latitude ionosphere. Rev. Geophys. Space Phys. 17, 99–134. doi:10.1029/RG017i001p00099

CrossRef Full Text | Google Scholar

Watanabe, S., Whalen, B. A., Wallis, D. D., and Pfaff, R. F. (1991). Observations of ion-neutral collisional effects in the auroral E region. J. Geophys. Res. 96, 9761–9771. doi:10.1029/91JA00561

CrossRef Full Text | Google Scholar

Young, M. A., Oppenheim, M. M., and Dimant, Y. S. (2020). The farley-buneman spectrum in 2-D and 3-D particle-in-cell simulations. J. Geophys. Res. Space Phys. 125, e27326. doi:10.1029/2019JA027326

CrossRef Full Text | Google Scholar

Zhang, Y., and Varney, R. H. (2024). A statistical survey of E-region anomalous electron heating using poker flat incoherent scatter radar observations. J. Geophys. Res. Space Phys. 129, e2023JA032360. doi:10.1029/2023JA032360

CrossRef Full Text | Google Scholar