Impact of meridional winds on the development of equatorial plasma bubbles: a review

The impact of meridional winds on the onset and evolution of equatorial plasma bubbles (EPBs) is reviewed. The conventional wisdom had been that transequatorial meridional winds have a stabilizing effect on the development of EPBs during equatorial spread F (ESF). However, this result is based on a uniform transequatorial meridional wind. Subsequently, it was demonstrated that a non-uniform meridional wind could have a stabilizing or destabilizing effect on EPB formation depending on the direction of wind gradient. The destabilization of EPBs associated with equatorward flowing meridional winds has recently been investigated during a midnight temperature maximum event and a geomagnetic storm. Although the neutral wind is a direct destabilizing influence in these cases, the large decrease in the Pedersen conductance caused by meridional equatorward winds is the primary reason for the large increase in the growth rate of the generalized Rayleigh-Taylor instability. We review the theoretical and modeling studies of this topic as well as observational studies that have been made to assess the relationship between meridional winds and ESF.

1 Introduction

The subject of the impact of meridional winds on the development of equatorial plasma bubbles (EPBs) has received considerable attention over the last 35 years (Huba and Krall, 2013; Huba et al., 2023; Huba and Lu, 2024). The generalized Rayleigh-Taylor instability (GRTI) (Sultan, 1996; Huba, 2022) is believed responsible for the generation of EPBs (Booker and Wells, 1938; Haerendel, 1974; Hysell, 2000) and a number of theoretical studies have focused on the impact of meridional winds on the GRTI to assess their role in EPB development.

The first study was performed by Maruyama (1988). He demonstrated that a uniform transequatorial meridional wind enhances the field-line integrated Pedersen conductivity and that this can reduce the growth rate of the generalized Rayleigh-Taylor instability. Zalesak and Huba (1991) extended the analysis of Maruyama (1988) to consider the direct effect of the wind on the development of the instability. They found that, in fact, the instability can be completely stabilized for a sufficiently strong meridional wind. These results were borne out in a 3D simulation study by Krall et al. (2009).

The work of Maruyama (1988) spurred interest in observational studies to assess the relationship between meridional winds and equatorial spread $F$ (ESF). The study by Mendillo et al. (1992) was limited to only two nights but the observations suggested the meridional wind suppressed (ESF) on one of the nights. A subsequent study (Mendillo et al., 2001) did not find convincing evidence for the “wind suppression” mechanism for ESF. In contrast, the observational study by Abdu et al. (2006) concluded that magnetic meridional winds negatively influence ESF development by reducing the pre-reversal enhancement electric field and direct suppression of the instability. Yet in other studies, Devasia et al. (2002) and Jyoti et al. (2004) found that under certain circumstances equatorward neutral winds appeared to be needed for ESF to develop. Thus, the observational studies of the impact of meridional winds on EPB development is mixed: in some cases the wind appears to suppress ESF, and in other cases the wind appears necessary to generate ESF.

A possible resolution to these “conflicting” observations was suggested by Huba and Krall (2013). They revisited this problem and demonstrated that a non-uniform meridional wind could have a stabilizing or destabilizing effect on EPB formation depending on the direction of wind gradient. Thus, the exact nature of the meridional wind is a key factor in how it affects the development of EPBs.

Recently, Huba et al. (2023) and Huba and Lu (2024) focused on equatorward flowing neutral winds and showed that they can be very destabilizing and generate EPBs. The primary reason for the large increase in the growth rate of the GRTI is a large decrease in the Pedersen conductivity. This is in contrast to the work of Maruyama (1988) who found that a uniform transequatorial meridional wind increased the Pedersen conductivity which led to a decrease in the growth rate of the GRTI.

We review the aforementioned theoretical and modeling studies, as well as the observational studies relating measurements of the meridional wind to the onset and evolution of ESF.

2 Theory

The theory of the stabilizing effects of meridional winds on the Rayleigh-Taylor instability was first developed by Maruyama (1988) and expanded upon by Zalesak and Huba (1991). Krall et al. (2009) elaborated on the theory and confirmed the stabilizing influence of meridional winds on the GRTI through numerical simulation studies using SAMI3/ESF (Huba et al., 2008). Recently, a more thorough analysis of the GRTI was presented by Huba (2022).

$\gamma ={\gamma }_g+{\gamma }_{wc},(1)$

where

${\gamma }_g=-\frac{\int {\sigma }_{Hc}\left(g_p/L_n\right)ds}{\int {\sigma }_{P}ds}(2)$

and

${\gamma }_{wc}=-\frac{\int {\sigma }_P\left(V_{wc}/L_n\right)ds}{\int {\sigma }_{P}ds},(3)$

with $L_n^{-1}=\partial \ln n_0/\partial p$ and

${\sigma }_P\simeq {\displaystyle \sum _i}\frac{nec}{B}\frac{{\nu }_{in}}{{\mathrm{\Omega }}_i}{\sigma }_{Hc}\simeq {\displaystyle \sum _i}\frac{nec}{B}\frac{1}{{\mathrm{\Omega }}_i}.$

Gravity being directed downwards, $g_p<0$ and ${\gamma }_g$ is always positive (destabilizing) in the bottomside $F$-layer. $V_{wc}=V_{mp}-V_p$ provides both positive and negative contributions depending on the sign of ${\mathbf{V}}_{wc}\cdot \nabla n$; here, $V_{mp}$ is the meridional wind and $V_p$ is the E $\times$ B drift in the meridional plane.

In Figure 1 we show a schematic indicating the important factors that affect the growth rate of the Rayleigh-Taylor instability associated with a meridional wind. In this figure we show a meridional wind (dark blue vector) in the northward direction and an upward density gradient (dark green vector) in the bottomside $F$ layer. The components of the meridional wind relative to the geomagnetic field are also shown: $V_{ms}$ is the component along the geomagnetic field and $V_{mp}$ is the component transverse to the geomagnetic field.

Figure 1

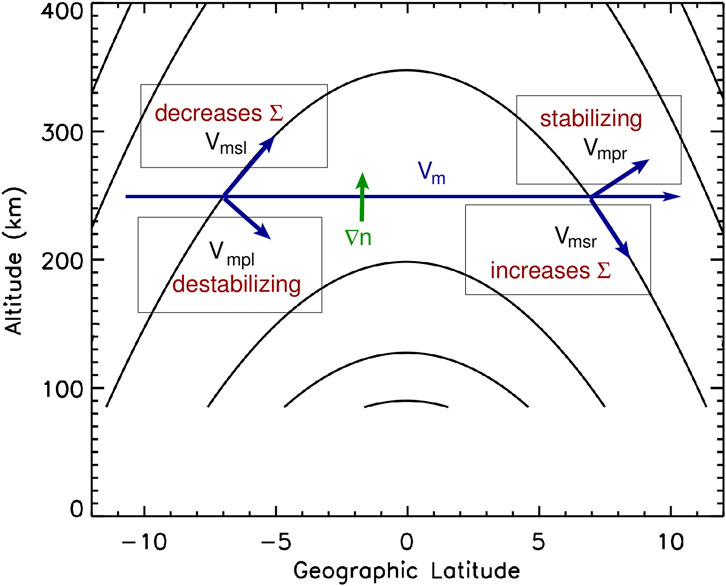
Figure 1. Schematic of the impact of meridional wind components on the growth rate and conductivity.

First, the component of the neutral wind along the geomagnetic field $(V_{ms})$ alters the local conductivity because of collisional drag on the ions. When the wind moves the plasma to higher altitudes $(V_{\mathit{msl}})$ the conductivity is decreased and when the wind moves the plasma to lower altitudes $(V_{\mathit{msr}})$ is increased. For a uniform meridional wind this leads to an increase in the field-line integrated Pedersen conductivity (for the ionosphere-thermosphere models used in Maruyama (1988); Krall et al. (2009)). This reduces the growth rate of the instability because $\int {\sigma }_{P}ds$ is in the denominator in Equation 1 and is the stabilizing effect first recognized by Maruyama (1988). However, if the meridional wind has a gradient such the $V_{\mathit{msl}}\gg V_{\mathit{msr}}$ this stabilizing effect is mitigated or possibly reversed. Alternatively, if $V_{\mathit{msl}}\ll V_{\mathit{msr}}$ then the stabilizing effect is amplified (Huba and Krall, 2013).

Second, the component of the neutral wind transverse to the geomagnetic field $(V_{mp})$ is a stabilizing influence when ${\mathbf{V}}_{mp}\cdot \nabla n>0$ which is the case for $V_{\mathit{mpr}}$; it is a destabilizing influence when ${\mathbf{V}}_{mp}\cdot \nabla n<0$ which is the case for $V_{\mathit{mpl}}$. The affect on the growth rate is complicated because it involves the field-line integration of neutral wind weighted by the Pedersen conductivity as shown in Equation 3. For the case of a uniform neutral wind, the stabilizing influence dominates and can completely stabilize the instability for a sufficiently strong meridional wind. This is the stabilizing effect described by Zalesak and Huba (1991). However, non-uniform meridional winds can have a destabilizing affect on the instability when $\partial V_m/\partial \theta <0$, i.e., $V_{\mathit{msl}}>V_{\mathit{msr}}$ in Figure 1. This effect is especially pronounced for the case of equatorward winds when the meridional wind both reduces the field-line integrated conductivity and is directed opposite to the density gradient (Huba and Krall, 2013).

3 Modeling

Krall et al. (2009) performed an extensive simulation study of the impact of the meridional wind on the development of equatorial plasma bubbles (EPBs). They used a constant transhemispheric meridional wind and their results confirmed the results of Maruyama (1988) and Zalesak and Huba (1991). As an example we show Figure 2 which plots the maximum vertical E $\times$ B velocity (${\mathrm{u}}_{p,max}$) as a function of time for different values of the meridional wind. The slope of each curve is a proxy for the growth rate. As the meridional neutral wind speed increases the slope of each curve up to 50 m/s decreases indicating a stabilizing effect. For the case where the wind speed is 60 m/s the slope is negative indicating the instability is completely suppressed as suggested by Zalesak and Huba (1991).

Figure 2

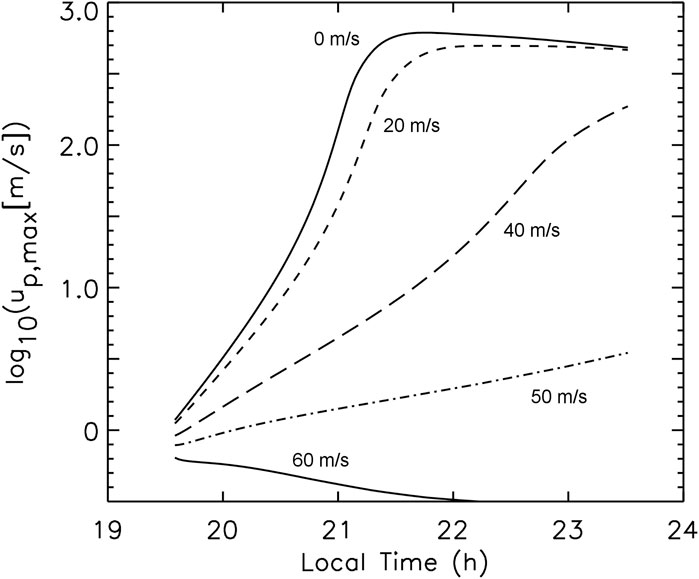
Figure 2. Line plots showing ${\mathrm{l}\mathrm{o}\mathrm{g}}_{10}(u_{p,max})$ versus local time for no wind (solid), 20 m/s (dashes), 40 m/s (long dashes), and 50 m/s (dash-dot), and 60 m/s (lower solid line). [from Krall et al. (2008)].

Huba and Krall (2013) expanded the previous work of Krall et al. (2009) to include an inhomogeneous meridional wind; they demonstrated that, depending on the direction of the latitudinal gradient of the wind, the meridional wind could be stabilizing or destabilizing. Specifically, a wind profile with a positive gradient as a function of latitude $(\partial V_m/\partial \theta \ge 0)$ is a stabilizing influence on the generalized Rayleigh-Taylor instability; however, a wind profile with a negative gradient $(\partial V_m/\partial \theta <0)$ can have a destabilizing influence. Here, $V_m$ is the meridional wind and $\theta$ is the geographic latitude and is positive towards the north pole.

As “extreme” cases, they considered equatorward flowing winds $(\partial V_m/\partial \theta <0)$ and poleward flowing winds $(\partial V_m/\partial \theta >0)$. The wind profile used was

$V_m=\pm V_{m0}\tanh \left(\theta /\mathrm{\Delta }\theta \right)(4)$

where $V_{m0}=$ 40 m/s and $\mathrm{\Delta }\theta =5°$.

The results are shown in Figure 3 where the labels $eq$ and $po$ refer to equatorward winds and poleward winds, respectively. Figure 3A shows the meridional wind profiles as a function of latitude based on Equation 4. Figure 3B shows the maximum upward $E\times B$ drift as a function of time for the equatorward case and poleward case meridional wind profiles. The case for no meridional wind is labeled “0” (dashed curve). The growth times of the instability in each case is as follows: 80eq (13 min), 0 (22 min), and 80po (41 min). Thus, the equatorward meridional wind profile is destabilizing while the poleward meridional wind profile is stabilizing relative to the case of no meridional wind.

Figure 3

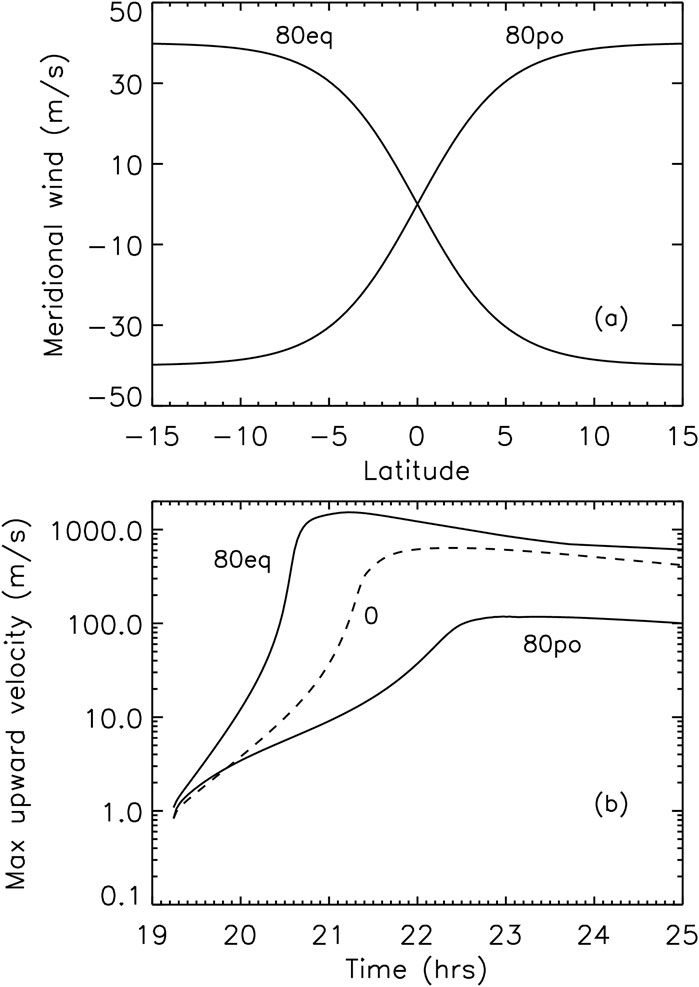
Figure 3. Plots of (A) the meridional neutral wind profiles as a function of latitude for $V_{m0}=\pm 40$ m/s, and (B) maximum upward $E\times B$ drift velocity as a function of time. [from Huba and Krall (2013)].

The contrast in the development of the generalized Rayleigh-Taylor instability for the equatorward and poleward meridional wind cases is exemplified in Figure 4. Electron density contours are shown at time $t=$ 20:44 LT as a function of longitude and altitude for cases 80eq (top) and 80po (bottom). The equatorward flow case has a well-developed plasma bubble that extends to almost 800 km while the poleward flow case has only developed a minor density undulation on the bottomside $F$ layer.

Figure 4

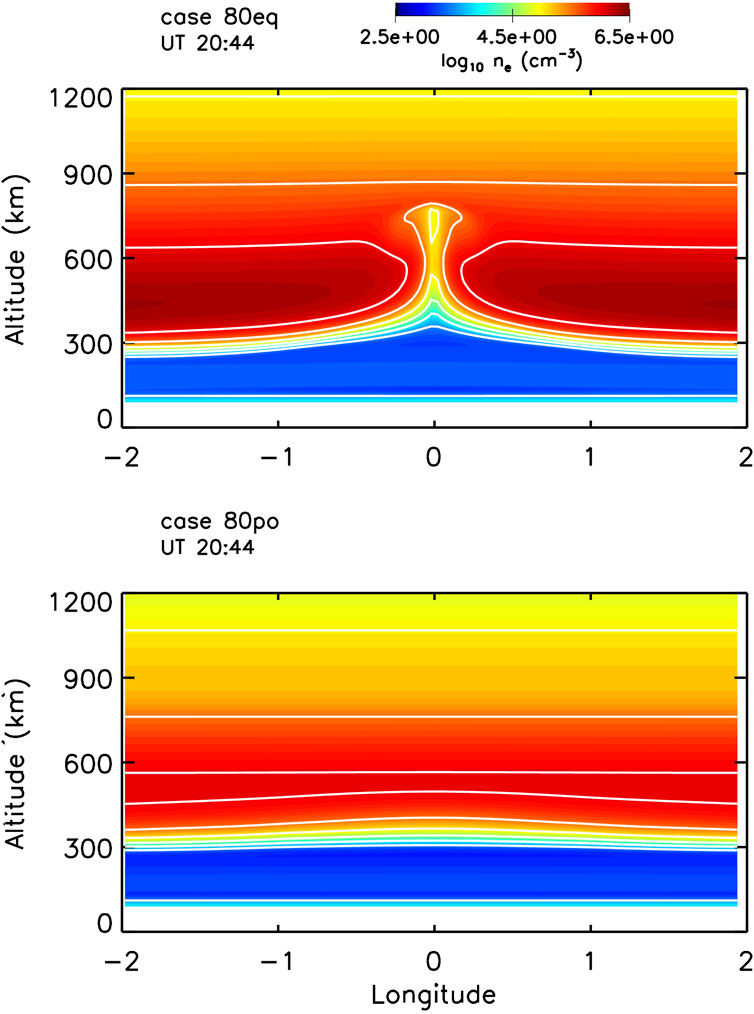
Figure 4. Contour plots of the electron density at time $t=$ 20:44 LT for the cases 80eq (top) and 80po (bottom). [from Huba and Krall (2013)].

The modeling results described above were based on the SAMI3/ESF code (Huba et al., 2008) which models a narrow range of longitude at night; nominally about $4°$ in longitude as shown in Figure 4. Recently, progress has been made in modeling the development of EPBs on a global scale (Huba and Liu, 2020) using the coupled SAMI3/WACCM-X code. Specifically the SAMI3 model (Huba and Joyce, 2010) has been one-way coupled to the global whole earth model WACCM-X (Liu et al., 2018). Here, the thermospheric variables (i.e., neutral densities, temperature, and winds) calculated by WACCM-X are used as inputs to SAMI3. There is no feedback from SAMI3 to WACCM-X though. The global models are run at high resolution in both latitude and longitude ($\sim$ $0.5°$–$0.625°$) which corresponds to grid scales $\sim$ 50–70 km.

Huba et al. (2023) investigated the development of an EPB during a period of low geomagnetic activity at solar minimum near the summer solstice using the coupled SAMI3/WACCM-X code. The parameters used were for August 22 with F10.7 = 71.6, F10.7A = 72.4, Ap = 6 and Kp = 1. The role of the meridional wind on the EPB growth is highlighted in Figure 5 which shows contour plots of the electron density (a, b), E × B velocity (c, d), zonal neutral wind (e, f), meridional neutral wind (g, i), latitude derivative of the meridional neutral wind (h, j), and neutral temperature (k, l) at times 11:59 UT (left panels) and 12:29 UT (right panels) as a function of latitude and altitude at longitude $168°$. As stated in Huba et al. (2023) we note the following. The early uplift of the EPB is apparent in Figure 5A at latitude $\theta \sim 6°$ with the development of ionization crests at $\theta \sim -5°\mathrm{a}\mathrm{n}\mathrm{d}15°$ as well as the enhanced E $\times$ B drift in the flux tubes with apex heights $\sim$ 400–500 km. At this time, there is also a reduction in both the zonal neutral wind (Figure 5E) and meridional neutral wind (Figure 5G). The meridional neutral wind is “equatorward” at latitude $\theta \sim$ $6°$, i.e., it is directed northward for $\theta <6°$ and is directed southward $\theta >6°$. This leads to a strong (negative) meridional gradient as well as an increase in the neutral temperature (Figure 5K) (i.e., midnight temperature maximum). Thirty minutes later, at 12:29 UT, the EPB has now fully developed and risen to $\sim$ 600 km (Figure 5B). The E $\times$ B drift inside the EPB has increased substantially to $\gtrsim$ 180 m/s (Figure 5D). The zonal neutral wind remains relatively weak (few 10 s m/s) at $168°$ (Figure 5F) but the meridional neutral wind is northward with a velocity $\sim$ 200 m/s (Figure 5H) at $\theta \sim 6°$. The derivative of the meridional neutral wind has significantly decreased (Figure 5I) at this latitude and the peak has shifted northward. Lastly, there is a relatively broad midnight temperature maximum in latitude (Figure 5L) (Herrero et al., 1993). Additionally, Meriwether et al. (2008) show both positive and negative gradients in the wind at ∼ 19:30 LT over Arequipa, Peru. They found converging (i.e., equatorward) neutral wind flows 1–2 hrs prior to the MTM. We note that there were several other bottom side irregularities in longitude away from $168°$ that did not develop EPBs. The important difference is that there were strong “equatorward” flows at $168°$ and not at the other longitudes with irregularities.

Figure 5

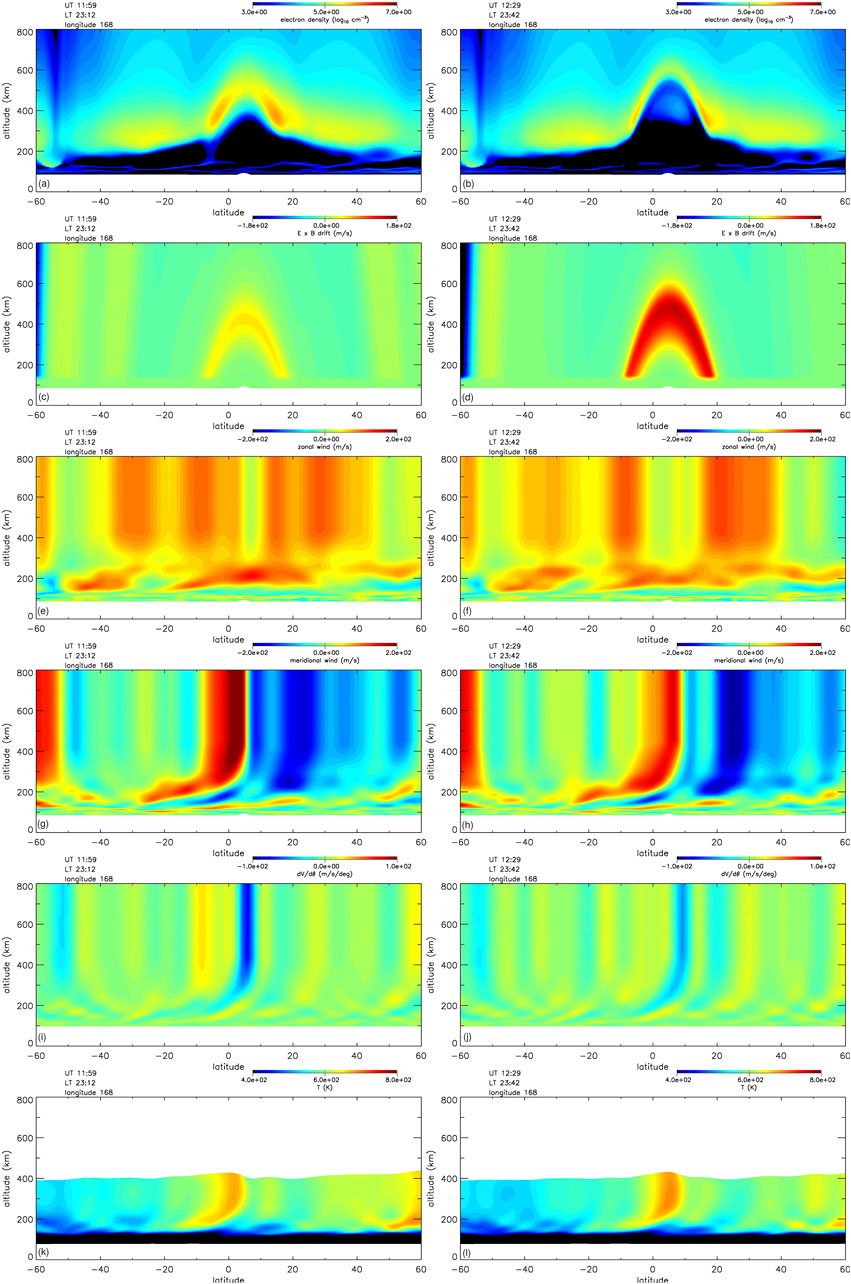
Figure 5. Contour plots of the electron density (A, B), E $\times$ B velocity (C, D), zonal neutral wind (E, F), meridional neutral wind (G, I), latitude derivative of the meridional neutral wind (H, J), and neutral temperature (K, L) at times 11:59 UT (A, C, E, G, I) and 12:29 UT (B, D, F, H, K) as a function of latitude and altitude at longitude $168°$.

The reason for the development of the EPB in Figure 5 is described in Figure 6 from Huba et al. (2023). This figure shows line plots of the (a) electron density $(n_e)$, E $\times$ B velocity $(V_{E\times B})$, derivative of the meridional neutral wind $(dV/d\theta )$, and (b) the Pedersen conductance as a function of time at longitude $168°$ and altitude 400 km, as well as (c) the maximum GRTI growth rates ($\gamma ,{\gamma }_g,\mathrm{a}\mathrm{n}\mathrm{d}{\gamma }_{wc}$) in the altitude range 250–800 km and the Pedersen conductance. In Figure 6A the electron density reaches a minimum of $\sim$ 2 $\times 10^3$ ${\mathrm{c}\mathrm{m}}^{-3}$ at 12:15 UT and the E $\times$ B velocity reaches a maximum of 120 m/s at 12:30 UT. Significantly, the derivative of the meridional neutral wind reaches a minimum of $\sim$ −70 m/s/deg at 12:00 UT. In Figure 6B we see a large increase in the GRTI growth rate $\gamma$ starting at $\sim$ 11:45 UT and peaking at $\sim$ 12:15 UT. During this period there is over an order-of-magnitude decrease in the Pedersen conductance ${\mathrm{\Sigma }}_P$. Decomposing the growth rate into the gravitational $({\gamma }_g)$ and wind/drift $({\gamma }_{wc})$ components we find that the dominant driving term is gravity; the wind/drift term leads to a positive growth rate but is much smaller than that associated with gravity. The reason for this is the large decrease in the Pedersen conductance that affects ${\gamma }_g$ much more than ${\gamma }_{wc}$ as evident in Equations 2, 3.

Figure 6

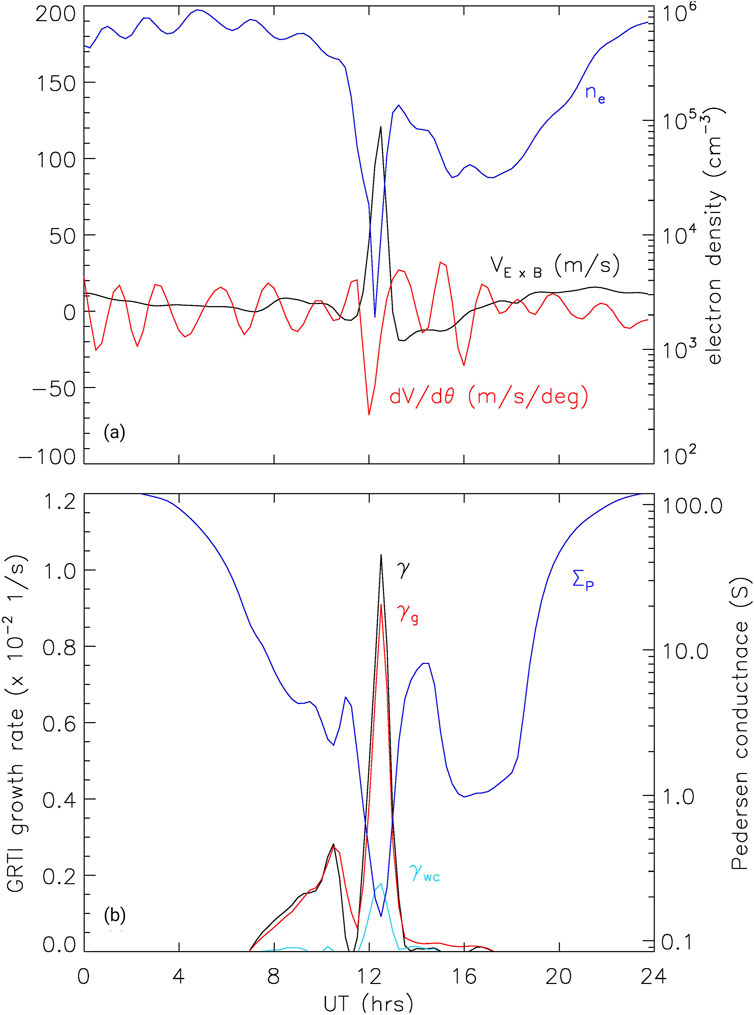
Figure 6. Line plots of (A) the electron density $(n_e)$, E × B velocity $(V_{E\times B})$, derivative of the meridional wind $(dV/d\theta )$, (B) the maximum GRTI growth rates ($\gamma ,{\gamma }_g,\mathrm{a}\mathrm{n}\mathrm{d}{\gamma }_{wc}$) in the altitude range 250–800 km. Here, local midnight is at 11:12 UT and the midnight temperature maximum (labeled MTM) occurs at $\sim$ 01:18 LT.

The aforementioned simulation study was for quiet geomagnetic conditions and generated a single EPB that rose to $\sim$ 600 km. However, a recent simulation study of the September 2018 (Huba and Lu, 2024) found that a series of large-scale EPBs formed in the western Pacific sector during the recovery phase of the storm on 8 September 2017. They attributed this behavior to large, equatorward flowing neutral winds caused by high latitude heating of the thermosphere during the storm.

The simulation used the coupled SAMI3/WACCM-X code to model the days 6–8 September 2017. The geophysical parameters considered are F10.7 = 134.9, 130.4, 118.5, F10.7A = 84.3, 84.3, 84.3, and Ap = 8, 36, 106 for each day, respectively. In Figure 7 contour plots of the electron density (a, e), meridional wind (b, f), E $\times$ B drift (d, h) (all at 494 km), and the Pedersen conductance (c, g) on September 8 are shown. The left panels (a, b, c, d) are at 14:14 UT and the right panels (e, f, g, h) are at 15:29 UT. There are “weak” EPBs evident in the longitude range $180°$ W to $90°$ W evident in Figure 7A; these are fossil EPBs that had formed earlier at 13:59 UT Of note, there are strong equatorward flowing meridional winds in the northern hemisphere between $90°$ E and $90°$ W and in the southern hemisphere between $135°$ E and $135°$ W in Figure 7B. There is a decrease in the Pedersen conductance in both the low- and mid-latitude regions associated with the equatorward winds as indicated in Figure 7C. Lastly, there is an increase in the E $\times$ B drift perpendicular to the magnetic field in the meridional plane (i.e., at the magnetic equator the drift is vertical while at mid-latitudes it has vertical and latitudinal components) in Figure 7D.

Figure 7

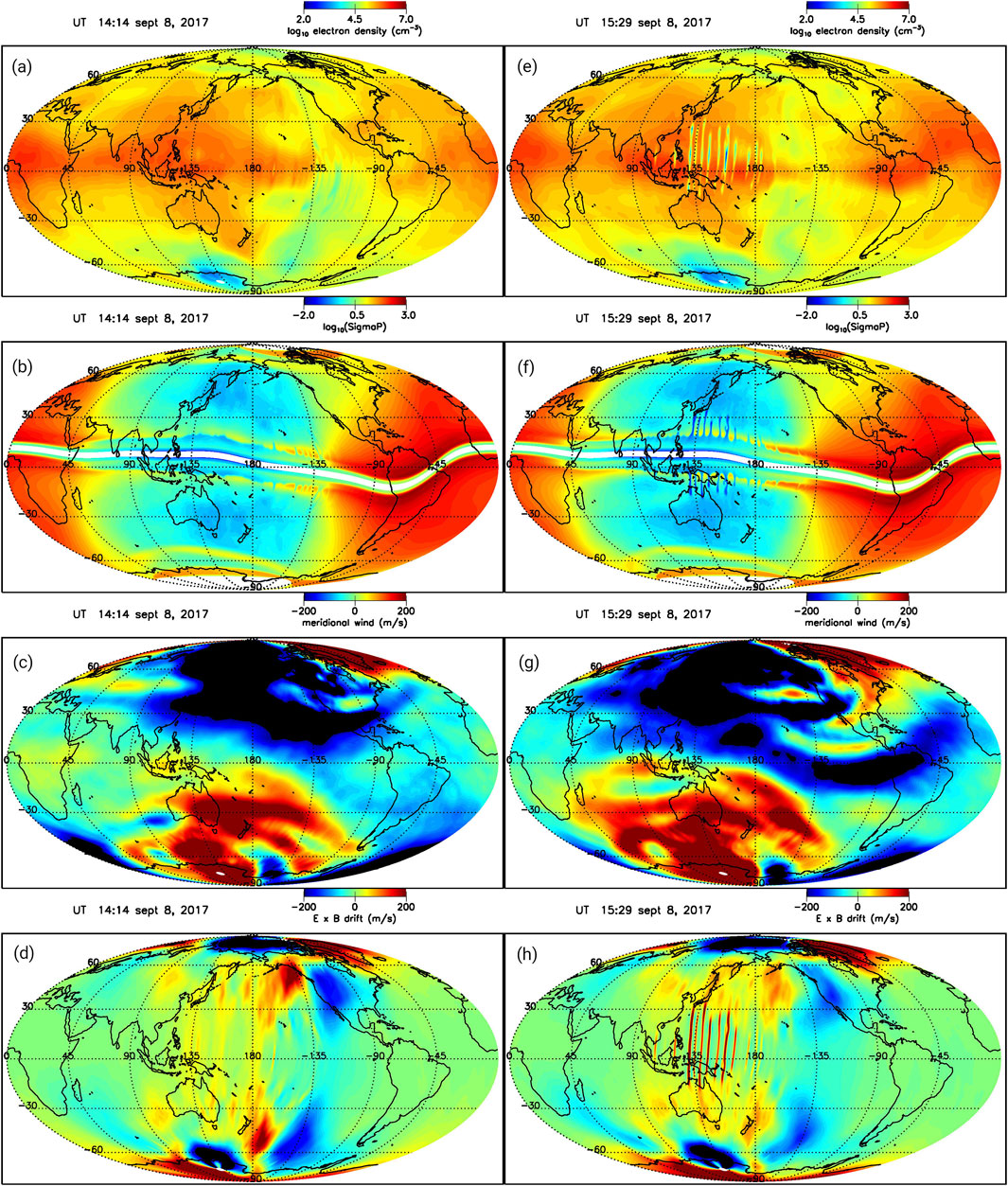
Figure 7. Contour plots of the electron density (A, E), meridional wind (B, F), E $\times$ B drift (D, H) (all at 394 km), and the Pedersen conductance (C, G). The left panels (A–D) are at 14:14 UT and the right panels (E–H) are at 15:29 UT.

Figures 7E–H correspond to Figures 7A–D but 75 min later at 15:29 UT. The equatorward meridional winds in Figure 7F have become more intense closer to the equator as well as a reduction in the Pedersen conductance at low- to mid-latitudes. However, the most striking features that have developed are shown in Figures 7E, H. In Figure 7E a span of EPBs developed in the longitude range $\sim$ $90°$ E to $180°$ E; several extend in latitude from $\sim$ −$15°$ to $30°$. Subsequently, several EPBs rise to over 2,000 km. Attendant with these EPBs are large E $\times$ B velocities that exceed 200 m/s as shown in Figure 7H.

4 Observations

The initial observational studies of the relationship between transhemispheric meridional winds and ESF focused on the suppression of ESF because of the work by Maruyama (1988). Mendillo et al. (1992) performed a two-day case study using the ALTAIR radar and optical imaging data. They found that ESF was suppressed on the first night (14 August 1988) but not the next night (15 August 1988). They attribute the suppression of ESF on the first night to a north-to-south meridional wind based on a reduction of the northern meridional gradient in 6,300 Å airglow. A subsequent study by Mendillo et al. (2001) during the Multi-Instrumented Studies of Equatorial Thermospheric Aeronomy (MISETA) campaign found “no convincing evidence for the wind suppression mechanism.”

Thampi et al. (2006) developed a prediction parameter $C$ based on observations that combined electrodynamic processes and meridional winds. The former is related to the E $\times$ B uplift of the ionosphere due to the pre-reversal enhancement of the eastward electric field and the latter to the asymmetry in the equatorial ionization crests (EIA) caused by the transhemispheric wind. They reported that an “EIA asymmetry alone does not suffice to make a deterministic forecast for the generation of ESF on a given day” because ESF was not observed on some days with a strong EIA asymmetry while observed on other days with a strong EIA asymmetry. This supports the suggestion that the actual behavior of the meridional wind can enhance or suppress ESF.

Maruyama et al. (2007) developed an ionosonde network in the Southeast Asian sector consisting of a meridional chain and a pair near the equator designed to estimate the meridional wind based on nighttime ionospheric height variations. Maruyama et al. (2009) used this network to infer the meridional winds for the spring and fall equinoxes in 2004 and 2005, and correlated the results with the occurrence of equatorial irregularities. They found that the transequatorial meridional winds were larger in September than March, and suggested that this was why equatorial irregularities occurred less frequently in September than in March. Numerical simulations were performed using the SAMI3/ESF model to support this contention. A Brazilian study during 1999 and 2001 by Abdu et al. (2006) also concluded that magnetic meridional winds negatively influence ESF development by reducing the pre-reversal enhancement electric field and direct suppression of the instability.

On the other hand, Devasia et al. (2002) and Jyoti et al. (2004) found that under certain circumstances equatorward neutral winds appeared to be needed for ESF to develop. Specifically, Devasia et al. (2002) argued that when the h’F base height of the $F$-layer is below 300 km, equatorward winds appear necessary to trigger ESF. However, they suggest that under these conditions there is a downward neutral wind that amplifies the instability; they did not consider changes in the conductance that could impact the instability. Jyoti et al. (2004) found a similar result and suggested that the effect of an equatorward neutral wind impacted the equatorial ionization anomaly (EIA), the equatorial temperature and wind anomaly (ETWA), and neutral dynamics to effectively enable instability at lower h’F heights (<300 km) via a downward wind (Sekar and Raghavarao, 1987).

Sreekumar and Sripathi (2016), Sreekumar and Sripathi (2017) studied nighttime thermospheric meridional winds in the Indian sector during the period March–December 2013. They derived the wind structure based on the h’F and hpF2 methods using ionosonde data. Comparing the results of the two methods to the HWM07 empirical wind model, it was found that the h’F was in better agreement. They related their h’F wind measurements to GPS scintillation data (i.e., an indicator of equatorial spread $F$) and found that longer duration scintillation events were associated with equatorward winds while non-scintillation days the winds were poleward.

Gao et al. (2023) studied the relationship between geomagnetic substorms and the occurrence of equatorial spread $F$. They used Jicamarca incoherent and coherent (JULIA) radar measurements to identify periods of equatorial spread $F$, and an AL-based identification algorithm (Newell and Gjerloev, 2011) to identify substorm activity. They find a distinct correlation between ESF and substorms. Specifically, in the post-sunset sector (1,800–2,400 LT) the ESF occurrence rate was a maximum $\sim$ 0.5 h after sunset, while in the post-midnight sector (0000–0006 LT) it was $\sim$ 3.0–3.5 h after midnight. They attributed the former to a prompt penetration field enhancing the pre-reversal upward E $\times$ B drift, and the latter to the disturbance dynamo electric field generating an upward E $\times$ B drift. This last result is consistent with the stormtime simulation study by Huba and Lu (2024). In particular, an upward E $\times$ B drift developed prior to the development of post-midnight EPBs on the storm day (shown in their Figure 5C). On the previous (non-storm) day the post-midnight drift was negative.

Zhan and Rodrigues (2018) investigated the dynamics of equatorial spread $F$ in the American sector during the June solstice. Using incoherent scatter radar measurements and the ionosphere model SAMI2 (Huba et al., 2000) in conjunction with GRTI theory they also found that equatorward meridional winds are destabilizing. However, in their analysis they found that the equatorward winds increased the conductance and that the increase in the GRTI growth rate was attributed to a modification of the electron density profile.

5 Discussion

Although not surprising, the results of this paper highlight the potential importance of meridional neutral winds in the development of EPBs during equatorial spread $F$. Nominally, EPBs form in the post-sunset sector and are usually associated with enhanced upward E $\times$ B drifts (e.g., $>$ 30 m/s) driven by the pre-reversal eastward electric field (e.g., Hysell et al., 2015). For this situation it is not clear meridional winds play a significant role in the development of ESF. However, during periods of low solar activity (e.g., F10.7 $\lesssim$ 80) the post-sunset E $\times$ B is typically small (Scherliess and Fejer, 1999) and ESF is unlikely to occur. On the other hand, for example, there are observations of ESF occurring in the post-midnight sector during solar minimum conditions (during the June solstice) in the absence of post-sunset EPBs (Heelis et al., 2010; Li et al., 2011; Zhan et al., 2018). During these periods it appears that the meridional wind can play a pivotal role in the generation of EPBs at the onset of ESF (Huba et al., 2023).

It also appears meridional winds can play a dramatic role in the development of large-scale EPBs during magnetic storms (Gao et al., 2023; Huba and Lu, 2024). During geomagnetic storms, heating of the thermosphere at high-latitude generates strong modifications to both the zonal and meridional winds that propagates equatorward over a period of several hours. This can lead to an upward E $\times$ B drift in the midnight sector because of modification of the zonal wind, and to an enhancement in the growth rate of the GRTI associated with the reduction in conductance caused by equatorward neutral winds.

The dominant theme of this review is that meridional winds can affect the onset and evolution of EPBs during ESF, primarily by modification of the conductance which directly impacts the growth rate of the GRTI. This doesn’t necessarily obviate the possibility of other factors playing a roll such as seeding mechanisms (e.g., gravity waves), modification of the lower $F$ layer gradient, or downward vertical winds. Moreover, the state of the ionosphere-thermosphere system is also a factor. For the theoretical and modeling studies described in this review, equatorward winds decrease the conductance while poleward winds increase the conductance as shown in Figure 1. It is possible that this is not always the case (e.g., Zhan and Rodrigues, 2018) and the blanket statement that “equatorward winds promote the development of ESF and poleward winds suppress the development of ESF” may not be universally true.

We also note that Kherani et al. (2005) presented a theoretical and modeling study of the collisional interchange instability. In this work a linear, local analysis was performed that considered a 3D potential equation (in contrast to the current analysis which assumes equipotential field lines). They found that a meridional wind can generate a density gradient along the magnetic field line that has a stabilizing influence on the instability when considering parallel oscillations (e.g., $k_{\Vert }$).

In conclusion, additional measurements of the neutral wind, in conjunction with observations of EPBs and ESF, are needed to provide a clearer understanding of ESF onset and evolution, and in particular the day-to-day variability of ESF. To this end the Ionospheric Connections Explorer (ICON) satellite mission data provides an invaluable resource for neutral wind and plasma data to address this problem (Immel et al., 2018).

Author contributions

JH: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was supported by NASA grants 80NSSC21K1305, ICON Explorers Program through contracts NNG12FA45C and NNG12FA42I, and DRIVE Science Center for Geospace Storms (CGS) under award (80NSSC22M0163), and AFOSR (FA9550-22-C-0001).

Conflict of interest

Author JH is employed by Syntek Technologies.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdu, M. A., Iyer, K. N., de Medeiros, R. T., Batista, I. S., and Sobral, J. H. A. (2006). Thermospheric meridional wind control of equatorial spread F and evening prereversal electric field. Geophys. Res. Lett. 33, L07106. doi:10.1029/2005GL024835

CrossRef Full Text | Google Scholar

Booker, H. G., and Wells, H. G. (1938). Scattering of radio waves by the F-region of the ionosphere. Terr. Mag. Atmos. Elec. 43, 249–256. doi:10.1029/te043i003p00249

CrossRef Full Text | Google Scholar

Devasia, C. V., Jyoti, N., Viswanathan, K. S., Tiwari, D., and Sridharan, R. (2002). On the plausible linkage of thermospheric meridional winds with equatorial spread F. J. Atmos. Sol. Terr. Phys. 64 (1), 1–12. doi:10.1016/s1364-6826(01)00089-x

CrossRef Full Text | Google Scholar

Gao, S., Cail, H., Zhan, W., Wan, X., Xiong, C., Zhang, H., et al. (2023). Characterization of local time dependence of equatorial spread F responses to substorms in the American sector. J. Space Weather Space Clim. 13 (2), 2. doi:10.1051/swsc/2022039

CrossRef Full Text | Google Scholar

Haerendel, G. (1974). Theory of equatorial spread F, Munich, Germany: Max Planck Institute for Extraterrestrial Physics.

Google Scholar

Heelis, R. A., Stoneback, R., Earle, G. D., Haaser, R. A., and Abdu, M. A. (2010). Medium-scale equatorial plasma irregularities observed by coupled ion-neutral dynamics investigation sensors aboard the communication navigation outage forecast system in a prolonged solar minimum. Ionosphere and Upper Atmosphere 115, A10321. doi:10.1029/2010JA015596

CrossRef Full Text | Google Scholar

Herrero, F. A., Spencer, N. W., and Mayr, H. G. (1993). Thermosphere and F-region plasma dynamics in the equatorial region. Adv. Space Res. 13, 201–220. doi:10.1016/0273-1177(93)90019-8

CrossRef Full Text | Google Scholar

Huba, J. D., Joyce, G., and Fedder, J. A. (2000). SAMI2 (Sami2 is another model of the Ionosphere): a new low-latitude Ionosphere model. J. Geophys. Res. 105, 23035

CrossRef Full Text | Google Scholar

Huba, J. D., Joyce, G., and Krall, J. (2008). Three-dimensional equatorial spread F modeling. Geophys. Res. Lett. 35, L10102. doi:10.1029/2008GL033509

CrossRef Full Text | Google Scholar

Huba, J. D., and Joyce, G. (2010). Global modeling of equatorial plasma bubbles. Geophys. Res. Lett. 37, L17104. doi:10.1029/2010GL044281

CrossRef Full Text | Google Scholar

Huba, J. D., and Krall, J. (2013). Impact of meridional winds on equatorial spread F: revisited. Geophys. Res. Lett. 40, 1268–1272. doi:10.1002/grl.50292

CrossRef Full Text | Google Scholar

Huba, J. D., and Liu, H.-L. (2020). Global modeling of equatorial spread F with SAMI3/WACCM-X. Geoophy. Res. Lett. 47, e2020GL088258. doi:10.1029/2020GL088258

CrossRef Full Text | Google Scholar

Huba, J. D. (2022). Generalized Rayleigh-Taylor instability: ion inertia, acceleration forces, and E region drivers. J. Geophys. Res. Space Phys. 127, e2022JA030474. doi:10.1029/2022JA030474

CrossRef Full Text | Google Scholar

Huba, J. D., Liu, H.-L., and McInerney, J. (2023). Modeling the development of an equatorial plasma bubble during a midnight temperature maximum with SAMI3/WACCM-X. Geoophy. Res. Lett. 50, e2023GL104388. doi:10.1029/2023GL104388

CrossRef Full Text | Google Scholar

Huba, J. D., and Lu, G. (2024). Modeling equatorial plasma bubbles with Sami3/WACCM-X september 2017 storm. Geophys. Res. Lett. 5, e2024GL109071. doi:10.1029/2024GL109071

CrossRef Full Text | Google Scholar

Hysell, D. L. (2000). An overview and synthesis of plasma irregularities in equatorial spread F. J. Atmos. Sol. Terr. Phys. 62, 1037–1056. doi:10.1016/s1364-6826(00)00095-x

CrossRef Full Text | Google Scholar

Hysell, D. L., Milla, M. A., Condori, L., and Vierinen, J. (2015). Data-driven numerical simulations of equatorial spread F in the Peruvian sector 3: solstice. J. Geophys. Res. Space Phys. 120 (10)–809. doi:10.1002/2015JA021877

CrossRef Full Text | Google Scholar

Immel, T. J., England, S. L., Mende, S. B., Heelis, R. A., Englert, C. R., Edelstein, J., et al. (2018). The ionospheric connection explorer mission: mission goals and design. Space Sci. Rev. 214, 13. doi:10.1007/s11214-017-0449-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Jyoti, N., Devasia, C. V., Sridharan, R., and Tiwari, D. (2004). Threshold height (h’F)c for the meridional wind to play a deterministic role in the bottom side equatorial spread F and its dependence on solar activity. Geophys. Res. Lett. 31, L12809. doi:10.1029/2004GL019455

CrossRef Full Text | Google Scholar

Kherani, A. E., Mascarenhas, M., de Paula, E. R., Sobral, J. H. A., and Bertoni, F. (2005). A three-dimensional simulation of collisional-interchange-instability in the equatorial-low-latitude ionosphere. Space Sci. Rev. 121, 253–269. doi:10.1007/s11214-006-6158-x

CrossRef Full Text | Google Scholar

Krall, J., Huba, J. D., Joyce, G., and Zalesak, S. T. (2009). Three-dimensional simulation of equatorial spread F with meridional wind effects. Ann. Geophys. 27, 1821–1830. doi:10.5194/angeo-27-1821-2009

CrossRef Full Text | Google Scholar

Li, G., Ning, B., Abdu, M. A., Yue, X., Liu, L., Wan, W., et al. (2011). On the occurrence of postmidnight equatorial F region irregularities during the June solstice. J. Geophys. Res. 116, A04318. doi:10.1029/2010JA016056

CrossRef Full Text | Google Scholar

Liu, H. L., Bardeen, C. G., Foster, B. T., Lauritzen, P., Liu, J., and Lu, G. (2018). Development and validation of the whole atmosphere community climate model with thermosphere and ionosphere extension (WACCM-X 2.0). J. Adv. Model. Earth Sys. 10, 381. doi:10.1002/2017MS001233

CrossRef Full Text | Google Scholar

Maruyama, T. (1988). A diagnostic model for equatorial spread F, 1, Model description and application to electric field and neutral wind effects. J. Geophys. Res. 93 (14), 14611–14622. doi:10.1029/ja093ia12p14611

CrossRef Full Text | Google Scholar

Maruyama, T., Kawamura, M., Saito, S., Nozaki, K., Kato, H., Hemmakorn, N., et al. (2007). Low latitude ionosphere-thermosphere dynamics studies with inosonde chain in Southeast Asia. Ann. Geophys. 25, 1569–1577. doi:10.5194/angeo-25-1569-2007

CrossRef Full Text | Google Scholar

Maruyama, T., Saito, S., Kawamura, M., Nozaki, K., Krall, J., and Huba, J. D. (2009). Equinoctial asymmetry of a low-latitude ionosphere-thermosphere system and equatorial irregularities: evidence for meridional wind control. Ann. Geophys. 27, 2027–2034. doi:10.5194/angeo-27-2027-2009

CrossRef Full Text | Google Scholar

Mendillo, M., Baumgardner, J., Pi, X., Sultan, P., and Tsunoda, R. (1992). Onset conditions for equatorial spread F. J. Geophys. Res. 97 (13), 13865–13876. doi:10.1029/92ja00647

CrossRef Full Text | Google Scholar

Mendillo, M., Meriwether, J., and Biondi, M. (2001). Testing the thermospheric neutral wind suppression mechanism for day-to-day variability of equatorial spread F. J. Geophys. Res. 106, 3655–3663. doi:10.1029/2000ja000148

CrossRef Full Text | Google Scholar

Meriwether, J., Faivre, M., Fesen, C., Sherwood, P., and Veliz, O. (2008). New results on equatorial thermospheric winds and the midnight temperature maximum. Ann. Geophys. 26, 447–466. doi:10.5194/angeo-26-447-2008

CrossRef Full Text | Google Scholar

Newell, P. T., and Gjerloev, J. W. (2011). Evaluation of SuperMAG auroral electrojet indices as indicators of substorms and auroral power. J. Geophys Res. Space Phys. 116. doi:10.1029/2011JA016779

CrossRef Full Text | Google Scholar

Scherliess, L., and Fejer, B. (1999). Radar and satellite global equatorial F region vertical drift model. J. Geophys. Res. 104, 6829–6842. doi:10.1029/1999ja900025

CrossRef Full Text | Google Scholar

Sekar, R., and Raghavarao, R. (1987). Role of vertical winds on the Rayleigh-Taylor mode instabilities of the night-time equatorial ionosphere. J. Atmos. Terr. Phys. 49, 981–985. doi:10.1016/0021-9169(87)90104-8

CrossRef Full Text | Google Scholar

Sreekumar, S., and Sripathi, S. (2016). Nighttime thermospheric meridional winds as inferred from ionosonde parameters over Indian region and their plausible effects on plasma irregularities. Adv. Space Res. 58 (92), 92–107. doi:10.1016/j.asr.2016.04.009

CrossRef Full Text | Google Scholar

Sreekumar, S., and Sripathi, S. (2017). A seasonal study on the role of h’F/meridional winds in influencing the development of ESF irregularities over Indian sector. Adv. Space Res. 60, 652–666. doi:10.1016/j.asr.2017.04.009

CrossRef Full Text | Google Scholar

Sultan, P. J. (1996). Linear theory and modeling of the Rayleigh-Taylor instability leading to the occurrence of equatorial spread F. J. Geophys. Res. 101 (26), 26875–26891. doi:10.1029/96ja00682

CrossRef Full Text | Google Scholar

Thampi, S. V., Ravindran, S., Pant, T. K., Devasia, C. V., Sreelatha, P., and Sridharan, R. (2006). Deterministic prediction of post-sunset ESF based on the strength and asymmetry of EIA from ground based TEC measurements: preliminary results. Geophys. Res. Lett. 33, L13103. doi:10.1029/2006GL026376

CrossRef Full Text | Google Scholar

Zalesak, S. T., and Huba, J. D. (1991). Effect of meridional winds on the development of equatorial spread F. Eos Trans. AGU 72, Spring Meet. Suppl. 211.

Google Scholar

Zhan, W., Rodrigues, F., and Milla, M. (2018). On the genesis of postmidnight equatorial spread F: results for the American/Peruvian sector. Geophys. Res. Lett. 45, 7354–7361. doi:10.1029/2018GL078822

CrossRef Full Text | Google Scholar

Zhan, W., and Rodrigues, F. S. (2018). June solstice equatorial spread F in the American sector: a numerical assessment of linear stability aided by incoherent scatter radar mearsurements. J. Geophys. Res. Space Phys. 123, 755. doi:10.1002/2017JA024969

CrossRef Full Text | Google Scholar