Estimating quasi-linear diffusion coefficients for varying values of density ratio

This paper considers a method for estimating bounce-averaged quasi-linear diffusion coefficients due to whistler-mode waves for a specified ratio of plasma frequency to gyrofrequency, ${\omega }_p/{\mathrm{\Omega }}_e$, using values precomputed for a different value of that ratio. This approach was recently introduced to facilitate calculations associated with the “POES technique,” generalized to infer both wave intensity and cold plasma density from measurements of particle fluxes near the loss cone. The original derivation was justified on the basis of parallel-propagating waves but applied to calculations with much more general models of the waves. Here, we justify the estimates, which are based on equating resonant frequencies for differing values of ${\omega }_p/{\mathrm{\Omega }}_e$ and energy, for wide ranges of wave normal angle, resonance number, energy, and equatorial pitch angle. Refinements of the original estimates are obtained and tested numerically against full calculations of the diffusion coefficients for representative wave models. The estimated diffusion coefficients can be calculated rapidly and generally give useful estimates for energies in the 30-keV–300-keV range, especially when both relevant values of the ratio ${\omega }_p/{\mathrm{\Omega }}_e$ are large.

1 Introduction

Cyclotron-resonant wave–particle interactions are a crucial aspect in magnetospheric dynamics, especially in radiation belts, and there is a vast tradition of simulating the process as quasi-linear diffusion of phase space density by a broad-band spectrum of small, incoherent waves, following the pioneering work of Kennel and Engelmann (1966) and Lerche (1968), with further development by Lyons et al. (1971) and Lyons (1974a). Modern formulations were given by Horne et al. (2005), Glauert and Horne (2005), and Albert (2005).

Known wave parameters can be used to calculate quasi-linear diffusion coefficients, which help determine decay lifetimes and levels of trapped and precipitating particle fluxes. Conversely, measurements of particle flux can be used to estimate the wave intensity, using a process often referred to as the “POES technique” (Li et al., 2013; Ni et al., 2014), which exploits the ability of low-altitude POES satellites to resolve the loss cone. Essentially, diffusion coefficients are calculated and used to estimate the ratio of trapped to precipitating flux, using assumed values for parameters including the wave amplitude, wave frequency, wave normal angle distributions, and cold plasma density; this is repeated for different wave amplitudes until an agreement with measurements is obtained. The wave amplitude is a specifically convenient, as well as important, parameter to vary because the diffusion coefficients simply scale with $B_{\text{wave}}^2$.

Longley et al. (2022) recently generalized this procedure to treat cold plasma density as an additional free parameter, using the additional constraint that the wave amplitude calculated from two POES energy channels remains the same. In principle, this requires extensive, time-consuming recalculations of diffusion coefficients for different values of the ratio of electron plasma frequency to gyrofrequency, $\mathcal{R}={\omega }_p/{\mathrm{\Omega }}_e$, referred to here as the density ratio. Repeated, rapid evaluation or approximation of diffusion coefficients is also required in many other settings, such as diffusion simulations using event-specific wave parameters (Watt et al., 2021; Yu et al., 2022) or when used to modify test particle trajectories to account for subscale wave–particle interactions in the evolving conditions of global MHD simulations (Chan et al., 2023; Michael et al., 2024).

One expedient for rapidly estimating diffusion coefficients is the “mean value approximation,” which replaces integration over the wave normal angle with evaluations at a few carefully chosen values (Albert, 2007b; 2008). Another approach, introduced by Longley et al. (2022), estimates diffusion coefficients for particle energy $E$ and pitch angle $\alpha$ and a chosen value of $\mathcal{R}$ from a table of values at a reference density value ${\mathcal{R}}_0$, for which the calculations are already done. This was done by finding adjusted values $\tilde{E}$ and $\tilde{\alpha }$ that equate an approximate expression for the resonant frequency for the two sets of parameters, so that

${\omega }_{\mathit{res}}\left(E,\alpha ,\mathcal{R}\right)\approx {\omega }_{\mathit{res}}\left(\tilde{E},\tilde{\alpha },{\mathcal{R}}_0\right).(1)$

In Section 2, we consider the approximations underlying Equation 1. Longley et al. (2022) only considered parallel-propagating waves (for which only the primary resonance contributes to diffusion) and characterized the validity of Equation 1 in terms of particle energy. In this study, constraints are developed in terms of wave frequency, justifying its use for a wide range of wave normal angle, particle energy, and resonant harmonic number. In Section 3, Equation 1 is used to estimate the diffusion coefficients, e.g.,

$D\left(E,\alpha ,\mathcal{R}\right)\approx D\left(\tilde{E},\tilde{\alpha },{\mathcal{R}}_0\right),(2)$

obtaining differing relativistic modifications for $D_{\alpha \alpha }$, $D_{\alpha p}$, and $D_{pp}$ and depending on whether $n\ne 0$ or $n=0$. Finally, in Section 4, we numerically compare calculated and estimated diffusion coefficients, using two very simple chorus wave models, for several representative combinations of $\mathcal{R}$ and ${\mathcal{R}}_0$.

2 Resonant frequencies

The condition for resonance between a gyrating charged particle and a plane wave is

$\omega -k_{\Vert }{v}_{\Vert }={\mathrm{\Omega }}_n,{\mathrm{\Omega }}_n\equiv sn{\mathrm{\Omega }}_c/\gamma ,(3)$

where the particle has parallel velocity $v_{\Vert }$, relativistic factor $\gamma$, and gyrofrequency $s{\mathrm{\Omega }}_c/\gamma$ (here, $s=\pm 1$ is the sign of the particle charge, with all frequencies unsigned), and the wave has a frequency $\omega$ and parallel wave number $k_{\Vert }$. The “harmonic number” $n$ can be any integer; $n=0$ indicates Landau resonance. After squaring, Equation 3 becomes

$\frac{{\omega }^2}{k^2{c}^2}=\frac{v^2}{c^2}\frac{{\omega }^2}{{\left(\omega -{\mathrm{\Omega }}_n\right)}^2}{\cos }^2\alpha {\cos }^2\theta .(4)$

The left-hand side is the inverse-squared index of refraction of the wave, and the particle pitch angle $\alpha$ and wave normal angle $\theta$ are given by $\cos \alpha =v_{\Vert }/v$ and $\cos \theta =k_{\Vert }/k$, respectively. Albert (1999, 2004, 2005, 2007a) noted the usefulness of this form for both analysis and approximation.

2.1 Full cold plasma refractive index

For completeness, we formulate the full cold plasma refractive index for R-mode (whistler) waves as

$\frac{{\omega }^2}{k^2{c}^2}=\left[\left(RL-PS\right){\sin }^2\theta +2PS-{\sigma }_{PD}\sqrt{{\left(RL-PS\right)}^2{\sin }^4\theta +4P^2{D}^2{\cos }^2\theta }\right]/2PRL,(5)$

where ${\sigma }_{PD}$ is the sign of $PD$ (typically negative), and the standard plasma quantities $R$, $L$, and $P$ for a single-component plasma (Stix, 1992) can be written as

$\begin{array}{cc}\hfill \left\{\genfrac{}{}{0pt}{}{R}{L}\right\}& =1\pm \frac{{\omega }_p^2\left(1+M\right)}{{\mathrm{\Omega }}_e^2}\frac{{\mathrm{\Omega }}_e/\omega }{1-M\mp \left(\omega /{\mathrm{\Omega }}_e-M{\mathrm{\Omega }}_e/\omega \right)},\hfill \\ \hfill P& =1-\frac{{\omega }_p^2\left(1+M\right)}{{\mathrm{\Omega }}_e^2}\frac{{\mathrm{\Omega }}_e^2}{{\omega }^2},S=\frac{R+L}{2},D=\frac{R-L}{2}.\hfill \end{array}(6)$

Here, ${\omega }_p$ is the electron plasma frequency ${(4\pi n{e}^2/m_e)}^{1/2}$, and the mass ratio $M$ is $m_e/m_p\approx 1/1836$.

To determine the resonant frequency $\omega$ as a function of $\theta$, Horne et al. (2005) and Glauert and Horne (2005) expanded these expressions into a ${10}^{th}$ order polynomial in $\omega$ (or $3^{rd}$ order in ${\omega }^2$ if $n=0$) and retained only the valid real roots. Ions heavier than ${\mathrm{H}}^{+}$ are ignored here, although treated by Albert (2003) for electromagnetic ion cyclotron (EMIC) waves. Albert (2005) and references therein developed criteria to isolate the roots of Equation 4 within restricted intervals of $\omega$, allowing the efficient use of real-valued, one-dimensional root finding and frequently reducing or even eliminating the consideration of irrelevant ranges of $\theta$ and $n$. Figure 1 shows the quantities on both sides of Equation 4 as functions of $\omega$ at fixed $\theta$, as well as various approximations of each, as discussed below.

Figure 1

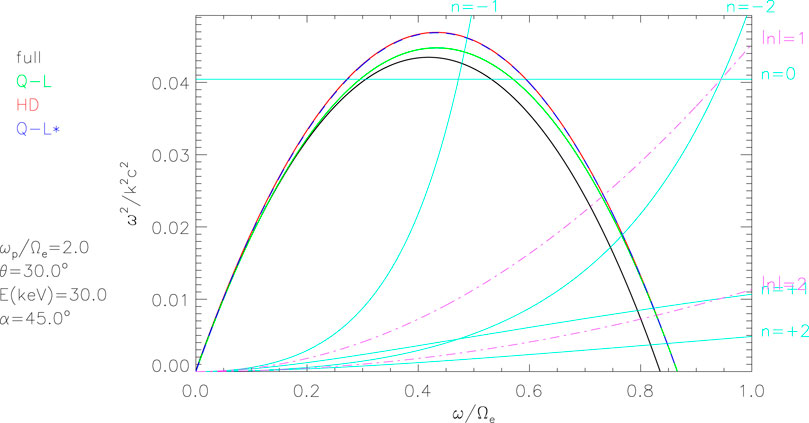
Figure 1. Versions of expressions constituting the resonance condition, for the parameter values shown in the plot. The inverted-U-shaped curves are the inverse-squared refractive index, given by Equation 5 (black), 7 (green), 11 (red), or 12 (blue). The upward-sloping (or horizontal) cyan curves show the corresponding term of the resonance condition (right-hand side of Equation 4) for several values of the harmonic number $n$. The upward-sloping magenta curves approximate the cyan curves according to Equation 14.

2.2 Quasi-longitudinal approximation

From Equation 5, the quasi-longitudinal approximation neglects the terms proportional to $M$ and ${\sin }^2\theta$, and further considers ${\omega }_p\gg \omega$ and ${\omega }_p^2({\mathrm{\Omega }}_e\cos \theta -\omega )\gg \omega ({\mathrm{\Omega }}_e^2-{\omega }^2)$. The well-known result is

$\frac{k^2{c}^2}{{\omega }^2}\approx \frac{RL}{S-D\cos \theta }\approx 1+\frac{{\omega }_p^2}{\omega \left({\mathrm{\Omega }}_e\cos \theta -\omega \right)},(7)$

which is illustrated in Figure 1. With $\theta =0$, Equation 7 is the same as Equation A13 of Longley et al. (2022). Using this in the resonance condition, Equation 4, gives a cubic equation in $\omega$, namely,

$c_3{\left(\omega /{\mathrm{\Omega }}_e\right)}^3-c_2{\left(\omega /{\mathrm{\Omega }}_e\right)}^2+c_1\left(\omega /{\mathrm{\Omega }}_e\right)-c_0=0,(8)$

with

$\begin{array}{cc}\hfill c_3& =\left({\gamma }^2-1\right)\left(1-{\cos }^2\alpha {\cos }^2\theta \right)+1,\hfill \\ \hfill c_2& =[\left({\gamma }^2-1\right)\left(1-{\cos }^2\alpha {\cos }^2\theta \right)+1]\cos \theta -2n\gamma ,\hfill \\ \hfill c_1& =\left({\omega }_p^2/{\mathrm{\Omega }}_e^2\right)\left({\gamma }^2-1\right){\cos }^2\alpha {\cos }^2\theta -2n\gamma \cos \theta +n^2,\hfill \\ \hfill c_0& =n^2\cos \theta .\hfill \end{array}(9)$

With $\theta =0$ (for which only $n=-1$ contributes to diffusion), these coefficients reduce to Equation 17 of Longley et al. (2022), who noted that ${\omega }_p/{\mathrm{\Omega }}_e$ entered only in the expression for $c_1$, which would be left unchanged by compensating changes in ${\gamma }^2-1$. Indeed, changing $\gamma$ also affects $c_2$ and $c_3$, but this effect was declared minor in the “weakly relativistic limit” such that $2n\gamma$ is approximately unchanged. By implication, ${\gamma }^2-1$ is also approximately unchanged, and further justification is provided by small values of $\alpha$. To this extent, the resonant value of $\omega$ depends on ${\omega }_p$ mainly through the combination $({\omega }_p^2/{\mathrm{\Omega }}_e^2)({\gamma }^2-1){\cos }^2\alpha$, or the square of $(p_{\Vert }/mc)\mathcal{R}$, where $\mathcal{R}={\omega }_p/{\mathrm{\Omega }}_e$.

With $n=0$, Equations 8, 9 reduce to the quadratic equation

$\frac{{\omega }^2}{{\mathrm{\Omega }}_e^2}-\frac{\omega }{{\mathrm{\Omega }}_e}\cos \theta +\frac{{\omega }_p^2}{{\mathrm{\Omega }}_e^2}\left[\frac{\left(v^2/c^2\right){\cos }^2\alpha {\cos }^2\theta }{1-\left(v^2/c^2\right){\cos }^2\alpha {\cos }^2\theta }\right]=0.(10)$

If $\cos \alpha \cos \theta \approx 1$, the bracketed expression in Equation 10 is $B\approx {(p/mc)}^2{\cos }^2\alpha {\cos }^2\theta$, regardless of energy, which suggests holding $(p_{\Vert }/mc)\mathcal{R}$ constant, as in the case $n\ne 0$. Alternatively, the approximation $B\approx {(v/c)}^2{\cos }^2\alpha {\cos }^2\theta$ applies if either $\cos \alpha \cos \theta$ is small or $v/c$ is small (of course neither can exceed 1), which motivates considering $(v_{\Vert }/c)\mathcal{R}$ constant. The two prescriptions coincide if both $\cos \alpha \cos \theta \approx 1$ and $v/c$ are small (since then $p_{\Vert }/mc$ and $v_{\Vert }/c$ are approximately equal). Thus, holding $(p_{\Vert }/mc)R$ constant rather than $(v_{\Vert }/c)R$ constant is favored only if both $\cos \alpha \cos \theta \approx 1$ and $v/c\sim 1$. Since the resonance condition for $n=0$ is $\cos \alpha \cos \theta =1/[(kc/\omega )(v/c)]$, this case implies $kc/\omega \approx 1$, which is an atypically low value, as illustrated in Figure 1.

2.3 High-density approximation

Lyons (1974b) and Albert (1999) used “high-density approximation,” which amounts to neglecting the leading term 1 relative to the terms proportional to ${\omega }_p^2/{\mathrm{\Omega }}_e^2$ in the definitions of $R$, $L$, and $P$. Then, Equation 5 reduces to

$\frac{{\omega }^2}{k^2{c}^2}=\frac{{\mathrm{\Omega }}_e^2}{{\omega }_p^2}\frac{1}{1+M}\left[M\left(1-\frac{{\sin }^2\theta }{2}\right)-\frac{{\omega }^2}{{\mathrm{\Omega }}_e^2}+\sqrt{\frac{M^2{\sin }^4\theta }{4}+\frac{{\omega }^2}{{\mathrm{\Omega }}_e^2}{\left(1-M\right)}^2{\cos }^2\theta }\right],(11)$

which is illustrated in Figure 1. A similar form applies to L-mode EMIC waves. Equation 11 should be accurate for a wider range of $\omega$ and $\theta$ than Equation 7, although for a narrower range of ${\omega }_p/{\mathrm{\Omega }}_e$. Indeed, it was introduced by Lyons and Thorne (1970) to study the magnetospheric reflection of whistler waves, which involves $\theta$ passing through $90°$. The full, quasi-longitudinal (QL), and high-density (HD) versions of the refractive index $\mu$ were compared for several combinations of ${\omega }_p/{\mathrm{\Omega }}_e$ and $\theta$ in Figure 4 of Albert (2005), where it was also shown analytically (in Appendix A) that ${\mu }_{\text{HD}}^2<{\mu }_{\text{full}}^2<{\mu }_{\text{QL}}^2$. Combining ${\mu }_{\text{HD}}^2$ with the resonance condition gives a $6^{th}$ order polynomial in $\omega$, but Albert (1999) showed that it yields at most three roots in the whistler range.

Setting $M=0$ in Equation 11 (which requires $\omega$ to be large compared to the lower hybrid frequency, ${\omega }_{LH}\approx \sqrt{M}{\mathrm{\Omega }}_e$) yields

$\frac{k^2{c}^2}{{\omega }^2}=\frac{{\omega }_p^2}{\omega \left({\mathrm{\Omega }}_e\cos \theta -\omega \right)},(12)$

which was used by Albert (2017) in a treatment of highly oblique whistler waves. It can also be regarded as a simplified version of quasi-longitudinal approximation. Combining it with the resonance condition yields a cubic equation of the form of Equation 8 with

$\begin{array}{cc}\hfill c_3& ={\gamma }^2,\hfill \\ \hfill c_2& ={\gamma }^2\cos \theta -2n\gamma ,\hfill \\ \hfill c_1& =\left({\omega }_p^2/{\mathrm{\Omega }}_e^2\right)\left({\gamma }^2-1\right){\cos }^2\alpha {\cos }^2\theta -2n\gamma \cos \theta +n^2,\hfill \\ \hfill c_0& =n^2\cos \theta .\hfill \end{array}(13)$

This set of coefficients agrees exactly with Equation 9 for $c_0$ and $c_1$, and approximately for $c_2$ and $c_3$ if $\cos \alpha \cos \theta \ll 1$. Changing ${\omega }_p/{\mathrm{\Omega }}_e$ and adjusting $\gamma$ to maintain the value of $c_1$ again modifies $c_2$ and $c_3$.

2.4 Approximate resonance condition

Lyons et al. (1972) and Albert (1994) considered $\omega \ll |{\mathrm{\Omega }}_n|$ in the resonance condition (Equation 4) for $n\ne 0$ to obtain

$\frac{{\omega }^2}{k^2{c}^2}=\frac{v^2{\gamma }^2}{c^2}\frac{{\omega }^2}{n^2{\mathrm{\Omega }}_e^2}{\cos }^2\alpha {\cos }^2\theta (14)$

and further approximated the refractive index (Equation 12) as

$\frac{k^2{c}^2}{{\omega }^2}=\frac{{\omega }_p^2}{\omega {\mathrm{\Omega }}_e\cos \theta }.(15)$

Both of these approximations are illustrated in Figure 1. At the risk of discarding two potential “anomalous” resonances with $\omega >|n|{\mathrm{\Omega }}_e/\gamma$ (Albert, 2005), they lead to the explicit expressions

$\frac{\omega }{{\mathrm{\Omega }}_e}=\left\{\begin{array}{cc}\left({\mathrm{\Omega }}_e^2/{\omega }_p^2\right){\left(mc/p_{\Vert }\right)}^2{n}^2\sec \theta ,\hfill & n\ne 0,\hfill \\ \left({\omega }_p^2/{\mathrm{\Omega }}_e^2\right)\left(v_{\Vert }^2/c^2\right)\cos \theta ,\hfill & n=0.\hfill \end{array}\right.(16)$

However, combining Equation 14 with Equation 11, instead of the cruder approximation Equation 15, replaces Equation 16 with a quadratic equation for ${\omega }^2$ (for $n\ne 0$), whose coefficients still depend on $\mathcal{R}={\omega }_p/{\mathrm{\Omega }}_e$ only through the combination $(p_{\Vert }/mc)\mathcal{R}$. For $n=0$, Equation 11 combined with the full resonance condition (Equation 4) gives a quadratic equation for ${\omega }^2$ whose coefficients depend on $\mathcal{R}$ only through the combination $\mathcal{R}(v_{\Vert }/c)$.

2.5 Compensating changes in R and energy

The various expressions in the preceding sections all suggest that the resonant frequency $\omega (E,\alpha ,\mathcal{R})$ can be approximated as $\omega (\tilde{E},\tilde{\alpha },{\mathcal{R}}_0)$, without restrictions on $(E,\alpha ,n)$, if $\tilde{E}$ and $\tilde{\alpha }$ are chosen such that

$\begin{array}{cc}\hfill {\tilde{p}}_{\Vert }& =\left(\mathcal{R}/{\mathcal{R}}_0\right)p_{\Vert },n\ne 0,\hfill \\ \hfill {\tilde{v}}_{\Vert }& =\left(\mathcal{R}/{\mathcal{R}}_0\right)v_{\Vert },n=0.\hfill \end{array}(17)$

The scaling for $n\ne 0$ is consistent with Equations 23, 25 (although not the reversed notation in Equations 24, 26) of Longley et al. (2022).

Equation 17 might further suggest that both the local pitch angle $\tilde{\alpha }$ and $\tilde{p}$ (or $\tilde{v}$) be considered free variables that are chosen to satisfy Equation 1. However, this would introduce undesirable dependence on latitude $\lambda$ in the relationship between the corresponding values of the equatorial pitch angle, ${\alpha }_{eq}$. For example, the choice $\tilde{p}=p$ in Equation 17 gives $\cos \tilde{\alpha }=(\mathcal{R}/{\mathcal{R}}_0)\cos \alpha$ or, converting from the local pitch angle $\alpha$ to the equatorial pitch angle ${\alpha }_{eq}$,

${\sin }^2{\tilde{\alpha }}_{eq}=\frac{{\mathcal{R}}^2}{{\mathcal{R}}_0^2}{\sin }^2{\alpha }_{eq}+\frac{1-{\mathcal{R}}^2/{\mathcal{R}}_0^2}{B\left(\lambda \right)/B_{eq}}.(18)$

The dependence on $\lambda$ in Equation 18 is not compatible with the use of a table of bounce-averaged diffusion coefficients evaluated on a grid of $(E,{\alpha }_{eq})$ values, as intended by Longley et al. (2022). Similarly, the approach hinges on being able to choose $\tilde{p}$ or $\tilde{v}$ in a manner independent of $\theta$ and $n$, which are also integrated or summed over in the calculation of diffusion coefficients.

Thus, with $\tilde{\alpha }=\alpha$ and using the relations $\gamma =1/\sqrt{1-v^2/c^2}=\sqrt{1+{(p/mc)}^2}=1+E/E_r$, where $E_r$ is the rest energy $m{c}^2$, Equation 17 yields

$\tilde{E}=\left\{\begin{array}{cc}\sqrt{E_r^2+E\left(E+2E_r\right)\left({\mathcal{R}}^2/{\mathcal{R}}_0^2\right)}-E_r,\hfill & n\ne 0,\hfill \\ E_r/\sqrt{1-\frac{E\left(E+2E_r\right)}{{\left(E+E_r\right)}^2}\left({\mathcal{R}}^2/{\mathcal{R}}_0^2\right)}-E_r,\hfill & n=0.\hfill \end{array}\right.(19)$

Longley et al. (2022) used this expression with $n=-1$ to estimate

$\frac{D_{\alpha \alpha }}{p^2}\left(E,\alpha ,\mathcal{R}\right)\approx \frac{D_{\alpha \alpha }}{{\tilde{p}}^2}\left(\tilde{E},\alpha ,{\mathcal{R}}_0\right).(20)$

For $n=0$, the implicit restriction in Equation 19 that $\mathcal{R}/{\mathcal{R}}_0$ cannot be too large for a given value of $E$ just reflects the requirement in Equation 17 that $\tilde{v}<c$. Figure 2 shows $\tilde{E}$ as a function of $E$ for two different choices of $\mathcal{R}$ and ${\mathcal{R}}_0$. It is evident that with $\mathcal{R}<{\mathcal{R}}_0$, the value $\tilde{E}$ is less than $E$ and may require the table based on ${\mathcal{R}}_0$ to extend to lower energy than the actual range of interest. Similarly, if $\mathcal{R}>{\mathcal{R}}_0$, the table may be required to extend to quite high energy, and, for $n=0$, Equation 19 for $\tilde{E}$ may become singular.

Figure 2

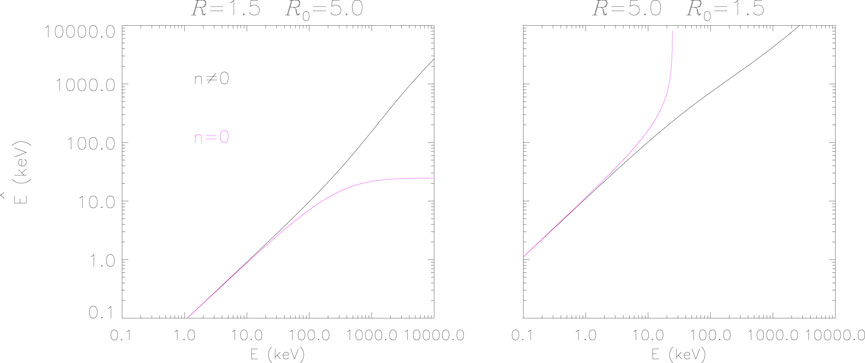
Figure 2. Values of $\tilde{E}$, according to Equation 19, used to estimate diffusion coefficients for $E$and $\mathcal{R}$ from values calculated for ${\mathcal{R}}_0$. Values for $n\ne 0$ are shown in black, and values for $n=0$ are shown in magenta, for two different choices of $\mathcal{R}$ and ${\mathcal{R}}_0$.

3 Diffusion coefficients

Even when $E$ can be adjusted to yield the same resonant frequency for two different values of $\mathcal{R}={\omega }_p/{\mathrm{\Omega }}_e$, it does not follow that the quasi-linear coefficients are the same since they are not functions of $\omega$ alone. However, approximate values of the corresponding values of $D$ can be related simply, as explained herein.

Using the expressions and notation of Albert (2005) and Albert (2007b) (which are exactly equivalent to those in Glauert and Horne (2005)), the local pitch angle diffusion coefficient is

$\frac{D_{\alpha \alpha }}{p^2}=\frac{{\mathrm{\Omega }}_c}{{\gamma }^2}\frac{B_{\text{wave}}^2}{B_o^2}{\displaystyle \sum _{n=-\infty }^{\infty }}{\displaystyle \sum _{{\omega }_n}}{\int }_{{\theta }_{\min }}^{{\theta }_{\max }}\sin \theta d\theta {\mathrm{\Delta }}_n{G}_1{G}_2,(21)$

where $D_{\alpha \alpha }/p^2$ has dimensions of $1/t$, and

$\begin{array}{cc}\hfill {\mathrm{\Delta }}_n& =\frac{\pi }{2}\frac{\sec \theta }{|v_{\Vert }/c{|}^3}{\mathrm{\Phi }}_n^2\frac{{\left(-{\sin }^2\alpha +{\mathrm{\Omega }}_n/\omega \right)}^2}{|1-{\left(\partial \omega /\partial k_{\Vert }\right)}_{\theta }/v_{\Vert }|},\hfill \\ \hfill G_1\left(\omega \right)& =\frac{{\mathrm{\Omega }}_c{B}^2\left(\omega \right)}{{\int }_{{\omega }_{LC}}^{{\omega }_{UC}}{B}^2\left({\omega }^{\prime }\right)d{\omega }^{\prime }},G_2\left(\omega ,\theta \right)=\frac{g_{\omega }\left(\theta \right)}{N\left(\omega \right)},\hfill \\ \hfill N\left(\omega \right)& ={\int }_{{\theta }_{\min }}^{{\theta }_{\max }}d{\theta }^{\prime }\sin {\theta }^{\prime }\mathrm{\Gamma }{g}_{\omega }\left({\theta }^{\prime }\right),\mathrm{\Gamma }={\mu }^2\left|\mu +\omega \frac{\partial \mu }{\partial \omega }\right|,\mu =\frac{kc}{\omega }.\hfill \end{array}(22)$

Furthermore, from Lyons (1974a),

$\frac{D_{\alpha p}}{D_{\alpha \alpha }}=\frac{\sin \alpha \cos \alpha }{-{\sin }^2\alpha +{\mathrm{\Omega }}_n/\omega },\frac{D_{pp}}{D_{\alpha \alpha }}={\left(\frac{D_{\alpha p}}{D_{\alpha \alpha }}\right)}^2.(23)$

Note that $G_1$ in Equation 22 does not depend on $\mathcal{R}$, $E$, or $\alpha$, but $G_2$ depends on $\mathcal{R}$ through $\mathrm{\Gamma }$. Using Equation 12 gives $\mathrm{\Gamma }=(\omega {\mathrm{\Omega }}_e\cos \theta /2{\omega }_p^2){\mu }^5$ (Albert, 2017), so $G_2\sim 1/\mathrm{\Gamma }\sim {\mathcal{R}}^2/{\mu }^5\sim 1/{\mathcal{R}}^3$ in this approximation.

To characterize ${\mathrm{\Delta }}_n$, substituting Equation 12 in Equation 6 of Albert (2005) yields

$\frac{1}{v_{\Vert }}{\left(\frac{\partial \omega }{\partial k_{\Vert }}\right)}_{\theta }=\frac{2\omega }{\omega -{\mathrm{\Omega }}_n}\frac{{\mathrm{\Omega }}_e\cos \theta -\omega }{{\mathrm{\Omega }}_e\cos \theta }\approx \left\{\begin{array}{cc}-2\omega /{\mathrm{\Omega }}_n,\hfill & n\ne 0,\hfill \\ 2,\hfill & n=0,\hfill \end{array}\right.(24)$

so the factor of ${\mathrm{\Delta }}_n$ involving ${(\partial \omega /\partial k_{\Vert })}_{\theta }$ is typically $\approx 1$. Similarly,

$-{\sin }^2\alpha +\frac{{\mathrm{\Omega }}_n}{\omega }\approx \left\{\begin{array}{cc}{\mathrm{\Omega }}_n/\omega \sim 1/\gamma ,\hfill & n\ne 0,\hfill \\ -{\sin }^2\alpha ,\hfill & n=0.\hfill \end{array}\right.(25)$

The factor ${\mathrm{\Phi }}_n^2$ is given in Equation 9 of Lyons (1974b). Using Equation 12, the only dependence on ${\omega }_p$ is through the argument of the Bessel functions, expressed by Albert (1999) as $\tan \alpha \tan \theta (s\omega \gamma /{\mathrm{\Omega }}_e-n)$. This is zero for parallel-propagating waves, and the dependence on $\gamma$ is otherwise neglected for both $n\ne 0$ and $n=0$. Thus, ${\mathrm{\Delta }}_n\sim 1/({\gamma }^2{v}_{\Vert }^3)\sim \gamma /p_{\Vert }^3$ for $n\ne 0$, and ${\mathrm{\Delta }}_n\sim {\sin }^4\alpha /v_{\Vert }^3$ for $n=0$.

The overall scaling of Equation 21 is therefore,

$\frac{D_{\alpha \alpha }}{p^2}\sim \left\{\begin{array}{cc}1/{\left(\mathcal{R}{p}_{\Vert }\right)}^3\gamma ,\hfill & n\ne 0,\hfill \\ {\sin }^4\alpha /{\left(\mathcal{R}{v}_{\Vert }\right)}^3{\gamma }^2,\hfill & n=0.\hfill \end{array}\right.(26)$

Thus, if $\tilde{E}$ and $\tilde{\alpha }$ are chosen in accordance with Equation 17, the corresponding values of $D_{\alpha \alpha }$ will be approximately related by

$\frac{D_{\alpha \alpha }}{p^2}\left(E,\alpha ,\mathcal{R}\right)\approx \frac{D_{\alpha \alpha }}{{\tilde{p}}^2}\left(\tilde{E},\tilde{\alpha },{\mathcal{R}}_0\right)\times \left\{\begin{array}{cc}\tilde{\gamma }/\gamma ,\hfill & n\ne 0,\hfill \\ {\left(\tilde{\gamma }/\gamma \right)}^2{\left(\sin \alpha /\sin \tilde{\alpha }\right)}^4,\hfill & n=0,\hfill \end{array}\right.(27)$

which refines Equation 20. Similarly, using Equations 23, 25, taking $\tilde{\alpha }=\alpha$, converting from local pitch angle $\alpha$ to equatorial pitch angle ${\alpha }_0$, and bounce averaging (which does not change any of the scaling) extend Equation 27 to

$\begin{array}{cc}\hfill \frac{D_{{\alpha }_0{\alpha }_0}}{p^2}\left(E,\mathcal{R}\right)& \approx \frac{D_{{\alpha }_0{\alpha }_0}}{{\tilde{p}}^2}\left(\tilde{E},{\mathcal{R}}_0\right)\times \left\{\begin{array}{cc}\tilde{\gamma }/\gamma ,\hfill & n\ne 0,\hfill \\ {\left(\tilde{\gamma }/\gamma \right)}^2,\hfill & n=0,\hfill \end{array}\right.\hfill \\ \hfill \frac{D_{{\alpha }_{0}p}}{p^2}\left(E,\mathcal{R}\right)& \approx \frac{D_{{\alpha }_{0}p}}{{\tilde{p}}^2}\left(\tilde{E},{\mathcal{R}}_0\right)\times \left\{\begin{array}{cc}1,\hfill & n\ne 0,\hfill \\ {\left(\tilde{\gamma }/\gamma \right)}^2,\hfill & n=0,\hfill \end{array}\right.\hfill \\ \hfill \frac{D_{pp}}{p^2}\left(E,\mathcal{R}\right)& \approx \frac{D_{pp}}{{\tilde{p}}^2}\left(\tilde{E},{\mathcal{R}}_0\right)\times \left\{\begin{array}{cc}\gamma /\tilde{\gamma },\hfill & n\ne 0,\hfill \\ {\left(\tilde{\gamma }/\gamma \right)}^2,\hfill & n=0.\hfill \end{array}\right.\hfill \end{array}(28)$

Mourenas and Ripoll (2012) and Artemyev et al. (2013), relying on the refractive index of Equation 15 and approximations of ${\mathrm{\Phi }}_n^2$, also obtained detailed analytical estimates for the total bounce-averaged pitch angle diffusion coefficient. With $\tilde{E}$ determined by Equation 19 and with $\omega \ll {\mathrm{\Omega }}_e/\gamma$, the scalings are consistent with those obtained here.

4 Numerical tests

Bounce-averaged quasi-linear diffusion coefficients were calculated using the simple chorus wave models of Glauert and Horne (2005) and Horne et al. (2005), namely,

$\begin{array}{cc}\hfill B^2\left(\omega \right)& =\exp [-{\left(\omega -{\omega }_m\right)}^2/\delta {\omega }^2],{\omega }_{LC}\le \omega \le {\omega }_{UC},\hfill \\ \hfill g_{\omega }\left(\theta \right)& =\exp [-{\left(\tan \theta -\tan {\theta }_m\right)}^2/{\tan }^2{\theta }_w],{\theta }_{\min }\le \theta \le {\theta }_{\max }.\hfill \end{array}(29)$

The parameter values used in Equation 29 are $\{{\omega }_m,\delta \omega ,{\omega }_{LC},{\omega }_{UC}\}$ $=\{0.35,0.15,0.125,0.575\}\times {\mathrm{\Omega }}_{eq}$ and $\{{\theta }_m,{\theta }_w,{\theta }_{\min },{\theta }_{\max }\}$ = $\{\mathrm{0,30}°,\mathrm{0,45}°\}$ at $L=5.25$. The “equatorial” model restricts the latitude to $0\le \lambda \le 15°$, while the “mid-latitude” model differs only in taking $15°\le \lambda \le 30°$. Cold plasma density was taken as a constant along dipole magnetic field lines, with chosen representative values of $\mathcal{R}={\omega }_p/{\mathrm{\Omega }}_{eq}$. For these comparisons, only the range $n=-5$ to 5 was included and, for concreteness, the wave amplitude was set to $B_{\text{wave}}=100$ pT. For each wave model and $\mathcal{R}$ value, diffusion coefficients were calculated for 80 (logarithmically spaced) values of $E$ between 100 eV and 10 MeV and 89 values of ${\alpha }_0$ between $1°$ and $89°$.

The top panel of Figure 3 shows values of $D_{\alpha 0\alpha 0}$ vs. energy, at a fixed equatorial pitch angle ${\alpha }_0=5°$, for the equatorial model. Values calculated for ${\mathcal{R}}_0=5.0$ are shown by dashed curves, values calculated for $\mathcal{R}=1.5$ are shown by solid curves, and symbols show values for $\mathcal{R}$ estimated using the values calculated for ${\mathcal{R}}_0$. Results for $n\ne 0$ and $n=0$ are shown separately, in black and magenta, respectively. Estimates based on Equation 20, denoted $D_{\ast }(\mathcal{R};{\mathcal{R}}_0)$, are indicated by asterisks, while estimates based on Equation 28, denoted $D(\mathcal{R};{\mathcal{R}}_0)$, are marked by diamonds. It is seen that the estimates are qualitatively close to the calculated values for much of the energy range, although less so for $n=0$ than for $n\ne 0$, and that the factors of $\tilde{\gamma }/\gamma$ in Equation 28 noticeably improve the agreement above a few hundred keV. Note that, from Figure 2 (left), $E$ below 1 keV would require $\tilde{E}$ below 100 eV, outside the range of the calculated table (100 eV–10 MeV).

Figure 3

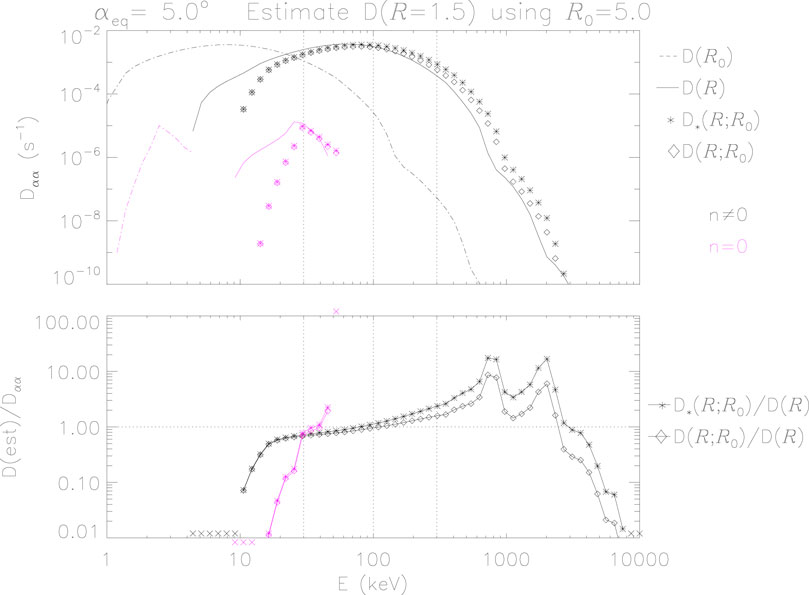
Figure 3. Calculated and estimated values of $D_{\alpha 0\alpha 0}$ vs. energy, at a fixed equatorial pitch angle, for a simple model of near-equatorial chorus waves. Black represents $n\ne 0$, and magenta represents $n=0$. Top: calculated values for ${\mathcal{R}}_0=5.0$ and $\mathcal{R}=1.5$ are shown by dashed and solid curves, respectively, and estimated values for $\mathcal{R}$ using ${\mathcal{R}}_0$ are shown by symbols. Factors of $\tilde{\gamma }/\gamma$ are included for $D(\mathcal{R};{\mathcal{R}}_0)$ but omitted for $D_{\ast }(\mathcal{R};{\mathcal{R}}_0)$. Bottom: ratio of the estimated and calculated values. The crosses at the bottom (top) of the plot indicate that the estimated value is zero, but the calculated value is nonzero (or the reverse).

The comparison is made clearer in the bottom panel of Figure 3, which shows the ratios of estimated to calculated values. For $n\ne 0$, especially with the factors of $\gamma$ included, the agreement is quite good between 30 keV and 300 keV, which is the range covered by the POES satellite and considered by Longley et al. (2022). However, the estimates are much less reliable for energy outside that range, giving underestimates at low and very high energy and overestimates in a broad range at approximately 1 MeV. Cases for which estimated values are zero (due to lack of resonances) but calculated values are nonzero are shown by crosses at the bottom of the panel, and crosses at the top of the panel indicate nonzero estimates where calculations result in zero.

The results of conversely using values calculated for ${\mathcal{R}}_0=1.5$ to estimate values for $\mathcal{R}=5.0$ are shown in Figure 4. For this combination of $\mathcal{R}$ and ${\mathcal{R}}_0$, the estimated values of $D$ are within a factor of approximately 10 for energy below approximately 2 MeV, with underestimates below 1 MeV and overestimates above 1 MeV. From Figure 2 (right), values of $\tilde{E}$ are outside the range of the calculated table for approximately $E>2.7$ MeV for $n\ne 0$ and $E>24$ keV for $n=0$.

Figure 4

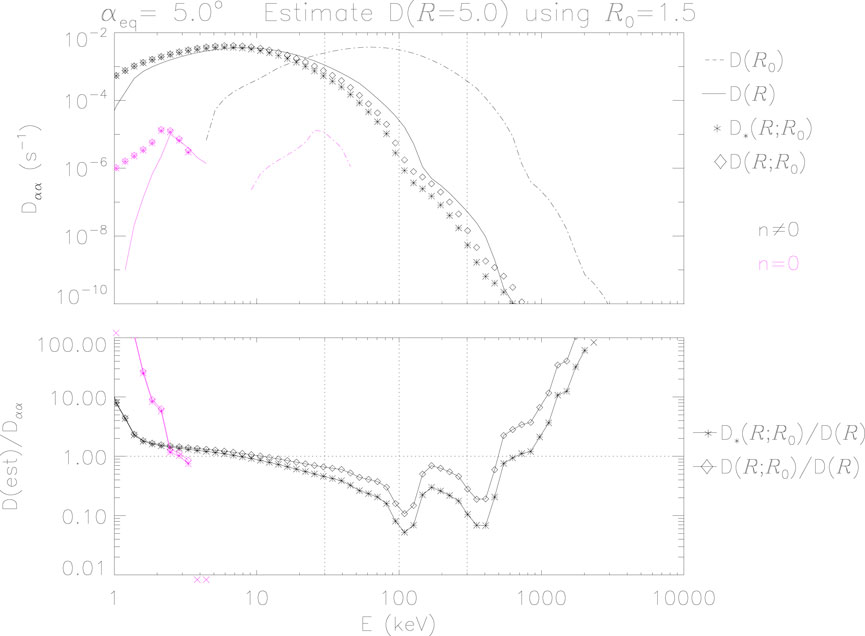
Figure 4. Calculated and estimated values of $D_{\alpha 0\alpha 0}$ vs. energy for a simple model of near-equatorial chorus waves, in the same format as Figure 3, showing values for $\mathcal{R}=5.0$ calculated and estimated from values for ${\mathcal{R}}_0=1.5$.

Figures 5, 6 repeat Figures 3, 4 using the mid-latitude chorus model. With $\mathcal{R}=1.5$ and ${\mathcal{R}}_0=5$, the estimates for $n\ne 0$ are within a factor of 10 in the range 100 keV to 2 MeV (if the relativistic factors are included), but they are lower at lower energy and higher at higher energy. For $n=0$, the estimates are with a factor of 10 between 20 keV and roughly 150 keV but predict nonzero values up to approximately 600 keV, while the full calculations indicate they should be zero. With $\mathcal{R}=5$ and ${\mathcal{R}}_0=1.5$, the estimates for $n\ne 0$ are fairly reliable between 10 keV and 2 MeV but fail above 2 MeV because (as shown in Figure 2) they require values beyond the computed table. For $n=0$, the estimates are fairly good between 2 keV and 10 keV but fail above 10 keV because, again, Equation 19 requires values of $\tilde{E}$ beyond the calculated table.

Figure 5

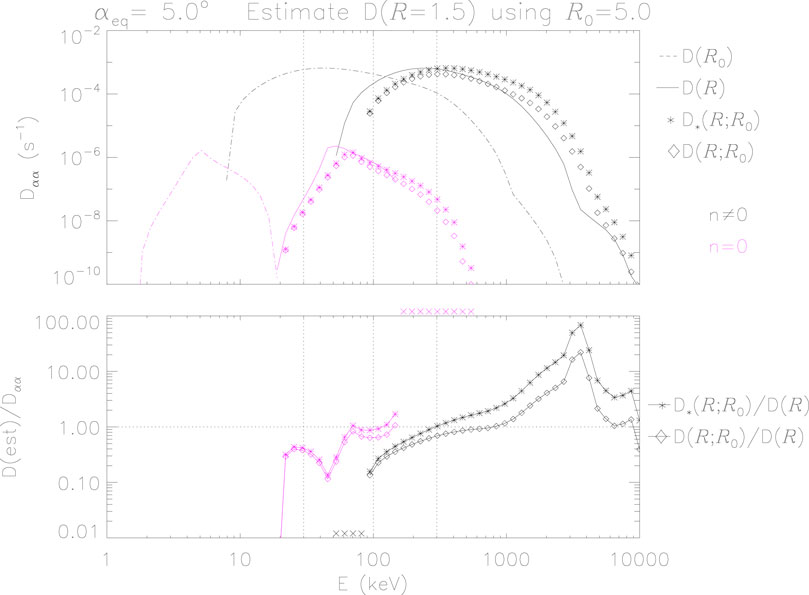
Figure 5. Calculated and estimated values of $D_{\alpha 0\alpha 0}$ vs. energy for a simple model of mid-latitude chorus waves, in the same format as Figure 3, showing values for $\mathcal{R}=1.5$ calculated and estimated from values for ${\mathcal{R}}_0=5.0$.

Figure 6

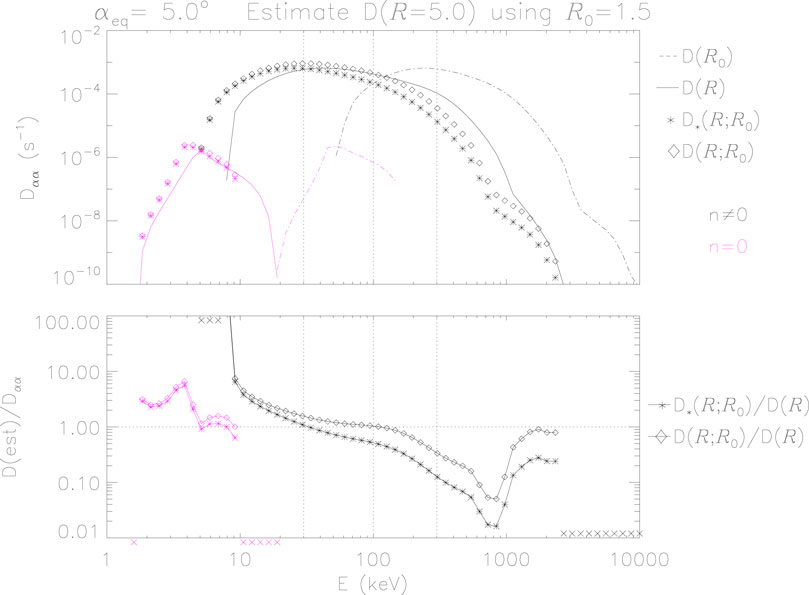
Figure 6. Calculated and estimated values of $D_{\alpha 0\alpha 0}$ vs. energy for a simple model of mid-latitude chorus waves, in the same format as Figure 3, showing values for $\mathcal{R}=5.0$ calculated and estimated from values for ${\mathcal{R}}_0=1.5$.

Figure 7 shows equatorial pitch angle diffusion coefficients for the equatorial chorus model as a function of both energy and pitch angle. Calculated values of $D(\mathcal{R})$, for $\mathcal{R}=\{1.2,1.5,2.5,5.0,7.5\}$, as shown in the plots along the main diagonal of the figure, while the ratios of estimated-to-calculated values, $D(\mathcal{R};{\mathcal{R}}_0)/D(\mathcal{R})$, are shown otherwise. For the values of $\mathcal{R}$ and ${\mathcal{R}}_0$ used, it can be seen that the ratios often fall between 0.10 and 10 but frequently exceed that range. Naturally, $D(\mathcal{R};{\mathcal{R}}_0)$ and $D({\mathcal{R}}_0)$ are closest when $\mathcal{R}$ and ${\mathcal{R}}_0$ are closest. The estimates are closer when $\mathcal{R}$ and ${\mathcal{R}}_0$ are both larger than when they are both small. Generally, $D(\mathcal{R};{\mathcal{R}}_0)$ is more likely to be an underestimate of $D(\mathcal{R})$ (blue regions) when $\mathcal{R}>{\mathcal{R}}_0$ and an overestimate (red regions) when $\mathcal{R}<{\mathcal{R}}_0$. The best agreement occurs roughly at approximately 100 keV at a low pitch angle and a few hundred keV for a larger pitch angle, with deteriorating agreement for energy above or below those values. Finally, similar trends are seen in Figure 8 for the mid-latitude chorus model.

Figure 7

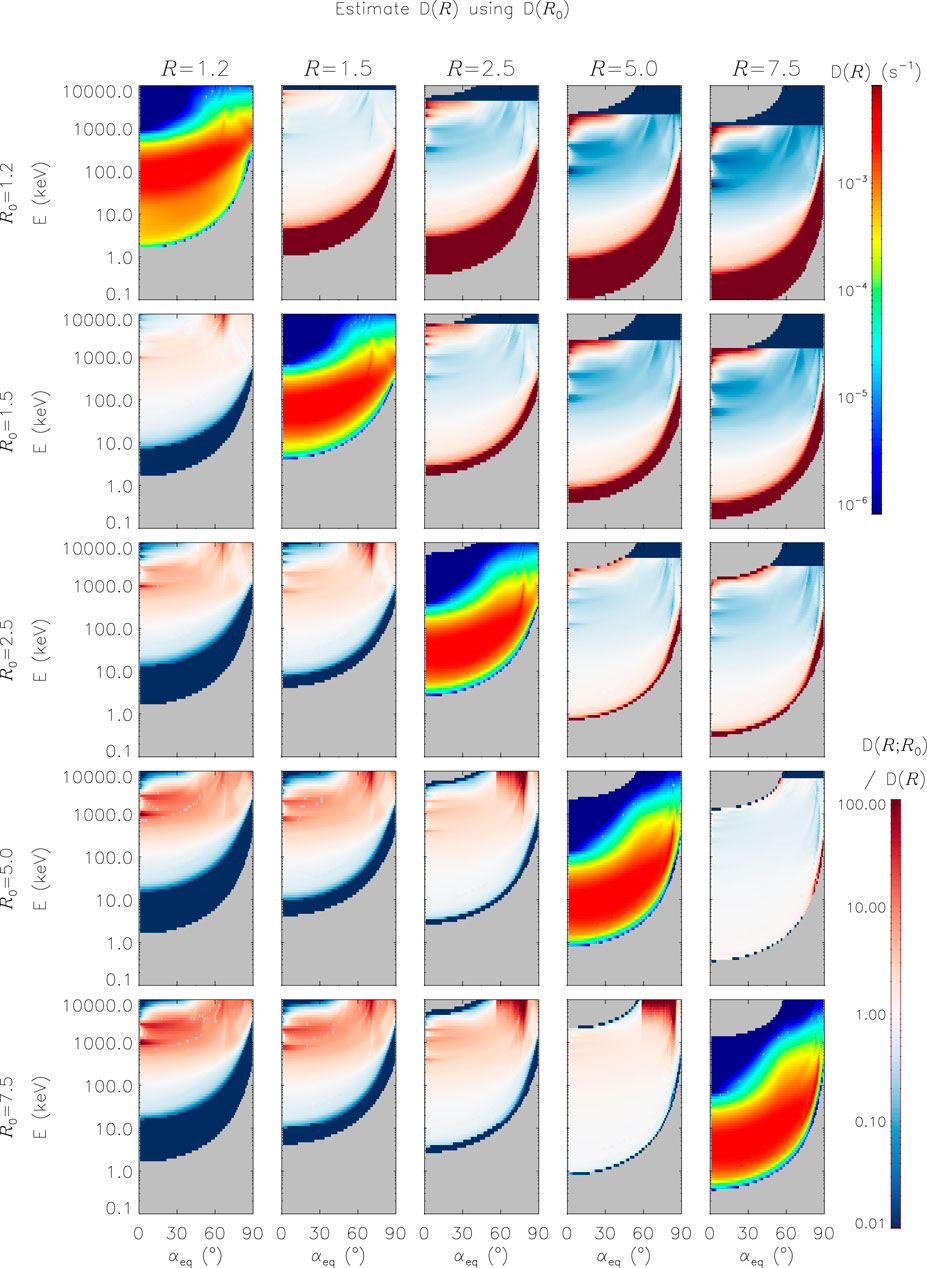
Figure 7. Calculated and estimated values of $D_{\alpha 0\alpha 0}$ vs. energy and equatorial pitch angle, for a simple model of near-equatorial chorus waves. The plots on the main diagonal (top left to bottom right) show calculated values of $D(\mathcal{R})$. The remaining plots show the ratio of $D(\mathcal{R})$ estimated using ${\mathcal{R}}_0$ to calculated values of $D(\mathcal{R})$. Fully saturated blue indicates values at or below the given limit of the appropriate color bar, while fully saturated red indicates values at or above the given limit; for the ratio plots, this includes a zero denominator but a nonzero numerator. Gray is used where $D=0$ for both calculated and estimated values.

Figure 8

Figure 8. Same as Figure 7 but for mid-latitude chorus waves.

5 Summary

This paper explored a method for quickly and easily estimating bounce-averaged quasi-linear diffusion coefficients for one value of “density ratio” $\mathcal{R}={\omega }_p/{\mathrm{\Omega }}_e$ using an existing set of values computed for a different value of $\mathcal{R}$. It was introduced by Longley et al. (2022) for the specific application of generalizing the “POES technique” to infer both wave intensity and cold plasma density from measurements of particle flux near the loss cone. In principle, that the procedure could be done without such approximations, although it would require repeated, time-consuming calculation of diffusion coefficients.

Although the original derivation was justified on the basis of parallel-propagating waves (wave normal angle $\theta =0$), for which only resonances with $n=-1$ contribute, the results were applied to diffusion coefficient calculations with much more general models of the waves. Here, we have justified the estimate of $D(E,\mathcal{R})$ by $D(E,{\mathcal{R}}_0)$, (Equation 2), based on equating the resonant frequency $\omega$ (Equation 1), for wide ranges of $\theta ,n$, $E$, and the equatorial pitch angle ${\alpha }_{eq}$, drawing on both the quasi-longitudinal and high-density approximations of the whistler-mode refractive index. Modifications accounting for dependence of $D$ on energy beyond that captured by the dependence on $\omega$ were obtained (Equation 28) and found to improve the agreement of the estimates with full calculations using two simple, idealized wave models.

The resulting agreement is far from perfect, however, especially when $\mathcal{R}$ and ${\mathcal{R}}_0$ differ greatly. For the tests done, the estimates were typically within a factor of 10 for energy between 10s of keV and 1 MeV for resonances with $n\ne 0$ but frequently worse for greater energy. For diffusion driven by Landau resonance, $n=0$, the estimates for ${\alpha }_0=5°$ were reliable only over limited ranges of energy below 100 keV. These results depend on the wave models: Landau resonance typically occurs near the particle mirror point, so it might be expected that values for the “equatorial” wave model, restricted to below $15°$ latitude, are difficult to estimate.

We note that all parameters specifying the wave frequency and wave normal angle distributions have been held fixed throughout. Sensitivity to these parameters was considered by Albert (2012). Furthermore, the quasi-linear diffusion paradigm itself has well-known caveats and limitations, e.g., Allanson et al. (2024). For use with the POES technique, which has additional sources of inaccuracy and uncertainty, the estimates here are probably acceptable. If nothing else, the wave amplitude and density values obtained can be used in more refined calculations. More generally, the tradeoff of accuracy for computational convenience should be carefully assessed for each intended application. One possible avenue toward improvement is to precompute several tables of diffusion coefficients, with different values of $\mathcal{R}$, and use the approach described here to scale from the nearest match to required $\mathcal{R}$ values. This is identical to the interpolation in $\mathcal{R}$ but in a manner that respects the (approximate) analytical form of the underlying expressions.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

JA: conceptualization, formal analysis, methodology, software, and writing–original draft. WL: conceptualization, formal analysis, and writing–review and editing. AC: conceptualization and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. JA was supported by the AFOSR grant 2021RVCOR002 and the Space Vehicles Directorate of the Air Force Research Laboratory. WL and AC acknowledge the NASA grant 80NSSC21K1323.

Acknowledgments

The views expressed are those of the author and do not necessarily reflect the official policy or position of the Air Force, the Department of Defense, or the U. S. Government. The appearance of external hyperlinks does not constitute endorsement by the United States Department of Defense (DoD) of the linked websites, or the information, products, or services contained therein. The DoD does not exercise any editorial, security, or other control over the information one may find at these locations.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Albert, J. M. (1994). Quasi-linear pitch angle diffusion coefficients: retaining high harmonics. J. Geophys. Res. 99 (23), 23741–23745. doi:10.1029/94JA02345

CrossRef Full Text | Google Scholar

Albert, J. M. (1999). Analysis of quasi-linear diffusion coefficients. J. Geophys. Res. 104, 2429–2441. doi:10.102910.1029/1998ja9001131998JA900113

CrossRef Full Text | Google Scholar

Albert, J. M. (2003). Evaluation of quasilinear diffusion coefficients for emic waves in a multi-species plasma. J. Geophys. Res. 108, 1249. doi:10.1029/2002JA009792

CrossRef Full Text | Google Scholar

Albert, J. M. (2004). Analytical bounds on the whistler mode refractive index. Phys. Plasmas 11, 4875–4877. doi:10.1063/.1.1792634

CrossRef Full Text | Google Scholar

Albert, J. M. (2005). Evaluation of quasi-linear diffusion coefficients for whistler mode waves in a plasma with arbitrary density ratio. J. Geophys. Res. 110, A03218. doi:10.1029/2004JA010844

CrossRef Full Text | Google Scholar

Albert, J. M. (2007a). Refractive index and wavenumber properties for cyclotron resonant quasilinear diffusion by cold plasma waves. Phys. Plasmas 14, 072901–1. doi:10.1063/1.2744363

CrossRef Full Text | Google Scholar

Albert, J. M. (2007b). Simple approximations of quasilinear diffusion coefficients. J. Geophys. Res. 112, A12202. doi:10.1029/2007JA012551

CrossRef Full Text | Google Scholar

Albert, J. M. (2008). Efficient approximations of quasilinear diffusion coefficients in the radiation belts. J. Geophys. Res. 113, A06208. doi:10.1029/2007JA012936

CrossRef Full Text | Google Scholar

Albert, J. M. (2012). Dependence of quasilinear diffusion coefficients on wave parameters. J. Geophys. Res. Space Phys. 113, A09224. doi:10.1029/2012JA017718

CrossRef Full Text | Google Scholar

Albert, J. M. (2017). Quasi-linear diffusion coefficients for highly oblique whistler mode waves. J. Geophys. Res. Space Phys. 122, 5339–5354. doi:10.1002/2017JA024124

CrossRef Full Text | Google Scholar

Allanson, O., Ma, D., Osmane, A., Albert, J. M., Bortnik, J., Watt, C. E. J., et al. (2024). The challenge to understand the zoo of particle transport regimes during resonant wave-particle interactions for given survey-mode wave spectra. Front. Astron. Space Sci. 11, 1332931. doi:10.3389/.fspas/2024.1332931

CrossRef Full Text | Google Scholar

Artemyev, A. V., Mourenas, D., Agapitov, O. V., and Krasnoselskikh, V. V. (2013). Parametric validations of analytical lifetime estimates for radiation belt electron diffusion by whistler waves. Ann. Geophys. 31, 599–624. doi:10.5194/angeo-31-599-2013

CrossRef Full Text | Google Scholar

Chan, A. A., Elkington, S. R., Longley, W. J., Aldhurais, S. A., Alam, S. S., Albert, J. M., et al. (2023). Simulation of radiation belt wave-particle interactions in an MHD-particle framework. Front. Astron. Space Sci. 10, 1239160. doi:10.3389/fspas.2023.1239160

CrossRef Full Text | Google Scholar

Glauert, S. A., and Horne, R. B. (2005). Calculation of pitch angle and energy diffusion coefficients with the PADIE code. J. Geophys. Res. 110, A04206. doi:10.1029/2004JA010851

CrossRef Full Text | Google Scholar

Horne, R. B., Thorne, R. M., Glauert, S. A., Albert, J. M., Meredith, N. P., and Anderson, R. R. (2005). Timescale for radiation belt electron acceleration by whistler mode chorus waves. J. Geophys. Res. 110, A03225. doi:10.1029/.2004JA010811

CrossRef Full Text | Google Scholar

Kennel, C. F., and Engelmann, F. (1966). Velocity space diffusion from weak plasma turbulence in a magnetic field. Phys. Fluids 9, 2377–2388. doi:10.1063/1.1761629

CrossRef Full Text | Google Scholar

Lerche, I. (1968). Quasilinear theory of resonant diffusion in a magneto-active, relativistic plasma. Phys. Fluids 11, 1720–1727. doi:10.1063/1.1692186

CrossRef Full Text | Google Scholar

Li, W., Ni, B., Thorne, R. M., Bortnik, J., Green, J. C., Kletzing, C. A., et al. (2013). Constructing the global distribution of chorus wave intensity using measurements of electrons by the POES satellites and waves by the Van Allen Probes. Geophys. Res. Lett. 40, 4526–4532. doi:10.1002/grl.50920

CrossRef Full Text | Google Scholar

Longley, W. J., Chan, A. A., Jaynes, A. N., Elkington, S. R., Pettit, J. M., Ross, J. P., et al. (2022). Using MEPED observations to infer plasma density and chorus intensity in the radiation belts. Front. Astron. Space Sci. 9, 1063329. doi:10.3389/fspas.2022.1063329

CrossRef Full Text | Google Scholar

Lyons, L. R. (1974a). General relations for resonant particle diffusion in pitch angle and energy. J. Plasma Phys. 12, 45–49. doi:10.1017/S0022377800024910

CrossRef Full Text | Google Scholar

Lyons, L. R. (1974b). Pitch angle and energy diffusion coefficients from resonant interactions with ion-cyclotron and whistler waves. J. Plasma Phys. 12, 417–432. doi:10.1017/.S002237780002537X

CrossRef Full Text | Google Scholar

Lyons, L. R., and Thorne, R. M. (1970). The magnetospheric reflection of whistlers. Planet. Space Sci. 18, 1753–1767. doi:10.1016/0032-0633(70)90009-7

CrossRef Full Text | Google Scholar

Lyons, L. R., Thorne, R. M., and Kennel, C. F. (1971). Electron pitch angle diffusion driven by oblique whistler-mode turbulence. J. Plasma Phys. 6, 589–606. doi:10.1017/S0022377800006310

CrossRef Full Text | Google Scholar

Lyons, L. R., Thorne, R. M., and Kennel, C. F. (1972). Pitch angle diffusion of radiation belt electrons within the plasmasphere. J. Geophys. Res. 77, 3455–3474. doi:10.1029/.JA077i019p03455

CrossRef Full Text | Google Scholar

Michael, A. T., Sorathia, K. A., Ukhorskiy, A. Y., Albert, J., Shen, X., Li, W., et al. (2024). Cross-scale modeling of storm-time radiation belt variability. J. Geophys. Res. Space Phys. 129, e2023JA032175. doi:10.1029/2023JA032175

CrossRef Full Text | Google Scholar

Mourenas, D., and Ripoll, J.-F. (2012). Analytical estimates of quasi-linear diffusion coefficients and electron lifetimes in the inner radiation belt. J. Geophys. Res. 117, A01204. doi:10.1029/2011JA016985

CrossRef Full Text | Google Scholar

Ni, B., Li, W., Thorne, R. M., Bortnik, J., Green, J. C., Kletzing, C. A., et al. (2014). A novel technique to construct the global distribution of whistler mode chorus wave intensity using low-altitude POES electron data. J. Geophys. Res. Space Phys. 119, 5685–5699. doi:10.1002/2014JA019935

CrossRef Full Text | Google Scholar

Stix, T. H. (1992). Waves in plasmas. American Institute of Physics.

Google Scholar

Watt, C. E. J., Allison, H. J., Thompson, R. L., Bentley, S. N., Meredith, N. P., Glauert, S. A., et al. (2021). The implications of temporal variability in wave-particle interactions in earth’s radiation belts. Geophys. Res. Lett. 48, e2020GL089962. doi:10.1029/2020GL089962

CrossRef Full Text | Google Scholar

Yu, Y., Hosokawa, K., Ni, B., Jordanova, V. K., Miyoshi, Y., Cao, J., et al. (2022). On the importance of using event-specific wave diffusion rates in modeling diffuse electron precipitation. J. Geophys. Res. Space Phys. 127, e2021JA029918. doi:10.1029/2021JA029918

CrossRef Full Text | Google Scholar