Magnetosonic wave instability by proton ring and shell distributions

Both proton ring and shell distributions, providing a positive gradient along the perpendicular direction, can trigger ion Bernstein instabilities and excite magnetosonic (MS) waves in the Earth’s inner magnetosphere. A thorough comparison of the ion Bernstein instability due to the proton ring and shell distributions has not been performed. In this study, we perform and compare the MS wave instabilities under different wave normal angles and parameters of ring and shell distributions. We find that (1) compared to shell-driven MS waves, ring-driven MS waves have narrower frequency and wavenumber ranges. (2) The peak growth rates of shell-driven MS waves are always near the first peaks of the square of first-kind Bessel function $J_n^2$. While, The peak growth rates of ring-driven MS waves are near the first peaks of $J_n^2$, and shift to the cold plasma dispersion relation as ring velocity or wave normal angle increases. (3) MS wave growth rates increase as first peaks of $J_n^2$ approach the cold plasma dispersion in frequency-wavenumber domain. This result can be used to explain dependences on ring (shell) velocity and wave normal angle. (4) The MS wave frequency range and growth rates decrease with increasing ring or shell temperature.

Highlights

• Compared to shell-driven MS waves, ring-driven MS waves have narrower frequency and wavenumber ranges.

• The peak growth rates of shell-driven MS waves are always near the first peaks of the square of the Bessel function $J_n^2$.

• The peak growth rates of ring-driven MS waves are near the first peak of $J_n^2$, and shift to the cold plasma dispersion relation as ring velocity or wave normal angle increases.

1 Introduction

Magnetosonic (MS) waves, also known as the ion Bernstein mode (IBM) or equatorial noise, are electromagnetic emissions with frequencies between the proton gyrofrequency and the lower hybrid resonant frequency (Laakso et al., 1990; Perraut et al., 1982; Santolík et al., 2004; Liu et al., 2018). The wave magnetic field is nearly linearly polarized, while the wave electric field is nearly circularly polarized. MS waves propagate quasi-perpendicularly to the ambient magnetic field and are thus confined near the geomagnetic equator (Russell et al., 1970; Santolík et al., 2002; Němec et al., 2005; Min et al., 2020). They occur both inside and outside the plasmasphere (Chen and Thorne, 2012; Xiao et al., 2012; Hrbáčková et al., 2015) with typical statistical amplitudes of $\sim 50pT$ (Ma et al., 2013) and peak amplitudes up to $\sim 1nT$ (Maldonado et al., 2016; Tsurutani et al., 2014).

MS waves have been investigated more in recent years due to their potential roles in accelerating and scattering energetic and relativistic electrons in the magnetosphere. Using quasi-linear theory and test particle simulations, it has been demonstrated that MS waves can scatter radiation belt MeV electrons through Landau resonance (Horne et al., 2007; Li et al., 2014), kick equatorially mirroring electrons out of the equatorial plane through bounce resonance (Chen, 2015; Li et al., 2015), and scatter electrons over the finite latitudinal extend near the magnetic equator through transit time scattering (Bortnik and Thorne, 2010).

MS waves can be excited near the perpendicular direction by the ion Bernstein instability, which is associated with a proton ring (Boardsen et al., 1992; Balikhin et al., 2015; Chen et al., 2010a; Gary et al., 2010) or shell distribution (Ashour-Abdalla et al., 2006; Liu et al., 2011; Min and Liu, 2015; Gao et al., 2017), providing a positive gradient in the proton velocity space distribution function (Chen et al., 2010a; Curtis and Wu, 1979; Gary et al., 2010; Liu et al., 2011). This physical mechanism has been confirmed by the consistent results of observations (e.g., Boardsen et al., 1992; Ashour-Abdalla et al., 2006; Balikhin et al., 2015), kinetic linear dispersion theory (Ashour-Abdalla et al., 2006; Gary et al., 2010; Min and Liu, 2015; Min and Liu, 2016a; Min et al., 2018), and numerical simulations (e.g., Chen, et al., 2010b; Liu et al., 2011; Chen et al., 2018; Min et al., 2020). Min and Liu (2016b) addressed differences of the MS wave linear growth rate patterns driven by the ring and shell velocity distributions. They used the cold plasma dispersion relation to approximate the MS wave frequencies and wavenumbers, and linear growth rates were determined only by the ring (shell) populations. They find that the growth rates of the ring-driven MS waves peak at the discrete harmonics of the proton gyrofrequency in quasi-perpendicular direction. Once wave normal angle decreases, those unstable modes broaden in frequency and eventually evolve to a continuum in the wave spectrum. Conversely, unstable modes driven by the proton shell are confined to a relatively small parallel wavenumber $k_{\Vert }$ and split into two local peaks on both sides of the harmonics of the proton gyrofrequency. The waves grow and damp alternatively in frequency-wavenumber domain due to the curved geometry of the shell distribution in velocity space. Min and Liu (2016b) uses an approximated wave dispersion solver that requires the trivial ring (shell) populations and limits wave dispersion relations to follow a cold dispersion relation instead of a realistic IBM dispersion relation. Moreover, to our knowledge, there has not been a thorough investigation of MS instability on the ring (shell) parameters.

Thus, in this study, we will perform a parametric comparison study of MS wave instability by proton ring and shell distributions by using a full wave dispersion relation solver. In Section 2, methodologies for instability analysis and shell distribution configuration are introduced. We provide a comparison of ring-driven and shell-driven MS waves in Section 3 and then present parametric dependences of ring/shell velocity, temperature and wave normal angles on the MS wave instability in Section 4, followed by the conclusion and discussion in Section 5.

2 Methodology

To perform instability analyses, we use a numerical electromagnetic linear wave dispersion relation and instability solver for Maxwellian ring-beam distributions (Umeda et al., 2012). The Maxwellian ring-beam distribution $f_{rb}$ can be written as (Min and Liu, 2015; Liu et al., 2022):

$\begin{array}{c}{f}_{rb}\left(v_d,v_r,a_{\Vert },a_{\perp };v_{\Vert },v_{\perp }\right)=\frac{1}{{\pi }^{1.5}{a}_{\Vert }{a}_{\perp }^2{C}_r}exp\left(-\frac{{\left(v_{\Vert }-v_d\right)}^2}{a_{\Vert }^2}\right)exp\left(-\frac{{\left(v_{\perp }-v_r\right)}^2}{a_{\perp }^2}\right),\hfill \\ C_r\left(v_r,a_{\perp }\right)=exp\left(-\frac{v_r^2}{a_{\perp }^2}\right)+\sqrt{\pi }\frac{v_r}{a_{\perp }}erfc\left(-\frac{v_r}{a_{\perp }}\right),\hfill \end{array}(1)$

where $v_d$, $a_{\Vert }$, $v_{\Vert }$, $v_r$, $a_{\perp }$, and $v_{\perp }$ are the beam velocity, beam thermal velocity, parallel velocity, ring velocity, ring thermal velocity and perpendicular velocity, respectively; $erfc$ is the complementary error function; and $C_r$ is a normalization constant and ensures that the density of the Maxwellian ring-beam distribution is 1. This ring-beam distribution can be reduced to a ring distribution once the beam velocity vanishes.

The isotropic shell distribution can be written as (Min and Liu, 2015):

$\begin{array}{c}\hfill f_s\left(v_s,a_s;v\right)=\frac{1}{C_s}exp\left(-\frac{{\left(v-v_s\right)}^2}{a_s^2}\right),\\ C_s\left(v_s,a_s\right)=\pi a_s^3\left[2exp\left(-\frac{v_s^2}{a_s^2}\right)\frac{v_s}{a_s}+\sqrt{\pi }\left(2\frac{v_s^2}{a_s^2}+1\right)\left(1+erf\left(\frac{v_s}{a_s}\right)\right)\right],\hfill \end{array}(2)$

where $v_s$, $a_s$, and $v$ are the shell velocity, shell thermal velocity and velocity, respectively; erf is the error function; and $C_s$ is a normalization constant and ensures that the density of the shell distribution is 1. As mentioned above, the linear wave solver used in this work is based on Maxwellian ring-beam distributions (Umeda et al., 2012). Thus, following Equations 3–8 of Min and Liu (2015), this shell distribution (Equation 2) is approximated by a summation of multiple isotropic ring-beam distributions (Equation 1), which are evenly distributed, which are evenly distributed along the pitch angle at the shell energy (i.e., $v_s^2=v_r^2+v_b^2$). The temperature of each ring-beam distribution equals that of the configured shell distribution (i.e., $a_{\Vert }=a_{\perp }=a_s$). The density of each ring-beam distribution can be determined by solving a linear equation with $M$ unknowns at the center of each ring-beam distribution, where $M$ is the number of ring-beam distributions.

Figures 1A, C show examples of isotropic ring and configured isotropic shell distributions with same density and temperature, respectively. The shell distribution is configured by 28 ring-beam distributions. According to Chen (2015), MS wave instability is dominated by resonant instability caused by the resonant protons near the $90°$ pitch angle with a finite $k_{\Vert }$ if $|\mathrm{\Gamma }|=|{\omega }_i/k_{\Vert }{a}_{\Vert }|\ll 1$, where $k_{\Vert }$ denotes parallel wavenumbers and ${\omega }_i$ denotes wave linear growth rates. However, when $|\mathrm{\Gamma }|>1$, for example, due to an increase of growth rates associated with relatively tenuous hot proton populations or a decrease in $k_{\Vert }$ by increasing wave normal angles, non-resonant instability driven by all hot protons will occur. Then, the growth rates ${\omega }_i$ are proportional to ${\int }_0^{+\infty }W(v_{\perp },{\omega }_r)d{\tilde{F}}_{\perp }/d{v}_{\perp }{J}_n^2(\frac{k_{\perp }{v}_{\perp }}{{\mathrm{\Omega }}_p})d{v}_{\perp }$ (Chen, 2015). Here, ${\tilde{F}}_{\perp }={\int }_{-\infty }^{+\infty }{f}_{hp}d{v}_{\Vert }$ and $f_{hp}$ are hot proton distributions. $d{\tilde{F}}_{\perp }/d{v}_{\perp }$ determines the wave growth or damping and ${\tilde{F}}_{\perp }$ is shown in Figures 1B, D for ring and shell distributions, respectively. The ring distribution can provide a sharp positive gradient in a narrow velocity range near the ring velocity (Figure 1B). In contrast, the shell distribution provides a smaller gradient, but over a wider velocity range (e.g., from 0 to shell velocity) (Figure 1D). $W(v_{\perp },{\omega }_r)$ and $J_n^2(\frac{k_{\perp }{v}_{\perp }}{{\mathrm{\Omega }}_p})$ are weighting functions for the phase space density gradient. Here ${\omega }_r$ denotes the wave frequency, $J_n$ is the first kind of Bessel function, $k_{\perp }$ denotes perpendicular wavenumbers, and ${\mathrm{\Omega }}_p$ denotes the proton gyrofrequency. A large growth rate may require a large value of $d{\tilde{F}}_{\perp }/d{v}_{\perp }$ near the maximum of $J_n^2(\frac{k_{\perp }{v}_{\perp }}{{\mathrm{\Omega }}_p})$ (i.e., near the first peak of $J_n^2$).

Figure 1

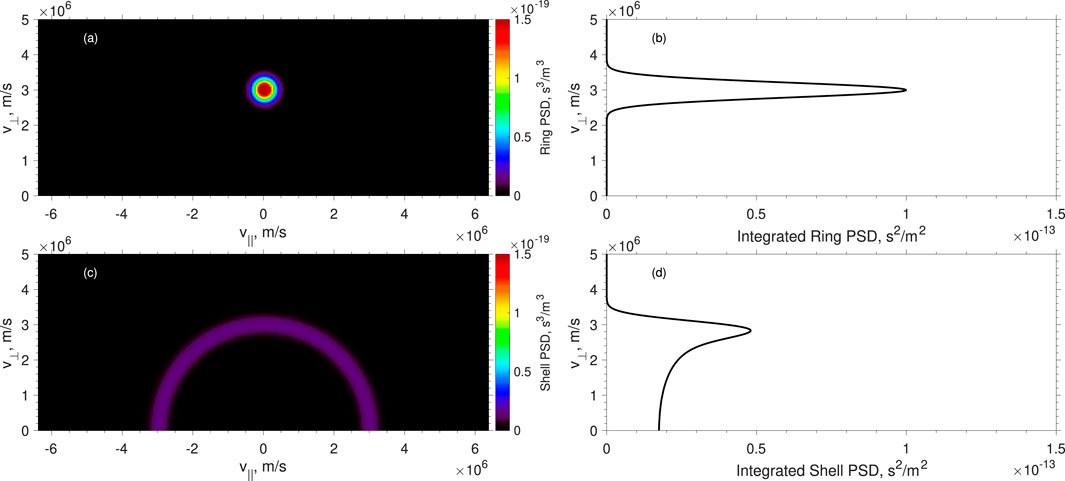
Figure 1. An example of proton ring and shell distributions. (A) Ring distribution ($v_r$ = $V_A$ and thermal velocity $a_r$ = $0.1V_A$) and (B) its integration along the parallel velocity. (C) Shell distribution ($v_s$ = $V_A$ and thermal velocity $a_s$ = $0.1V_A$) and (D) its integration along the parallel velocity. $V_A$ is the Alfven speed.

3 MS waves excited by ring and shell distributions

To investigate MS wave instability dependence, we use the numerical electromagnetic linear wave dispersion relation and instability solver. Such solver is extended to Maxwellian ring-beam distributions and tested by the particle-in-cell (PIC) simulation (Liu et al., 2022). Figure 2 shows a comparison of dispersion relations and growth rates of the ring-driven (left column) and shell-driven (right column) MS waves. Two black lines denote the cold dispersion relations. The large solid circles denote the growing modes, and the color denotes the growth rate values. The black squares denotes the first peaks of $J_n^2(\frac{k_{\perp }{v}_r}{{\mathrm{\Omega }}_p})$ for ring-driven MS waves and $J_n^2(\frac{k_{\perp }{v}_s}{{\mathrm{\Omega }}_p})$ for shell-driven MS waves, respectively. The black rectangle shows the zoomed-in parts. The parameters are set as follows. The ambient magnetic field $B_0$ is $143.5nT$ ($L=6$ in the dipole magnetic field model), and the electron density $n_e=1.1c{m}^{-3}$. The plasma consists of cold electrons, cold protons, and hot protons. The cold electrons and cold protons follow Maxwellian distributions with same temperatures $2eV$. The hot protons follow a ring or shell distribution with the ring/shell velocity equal to $1.3V_A$ and thermal velocity equal to $0.03V_A$. Here $V_A$ is the Alfven speed. The hot proton concentration is set to 0.08. The wave normal angle (WNA) is set as $85°$. The space and time are normalized by the proton inertial length ${\lambda }_p=V_A/{\mathrm{\Omega }}_p=1/k_0$ and ${\mathrm{\Omega }}_p^{-1}$, respectively.

Figure 2

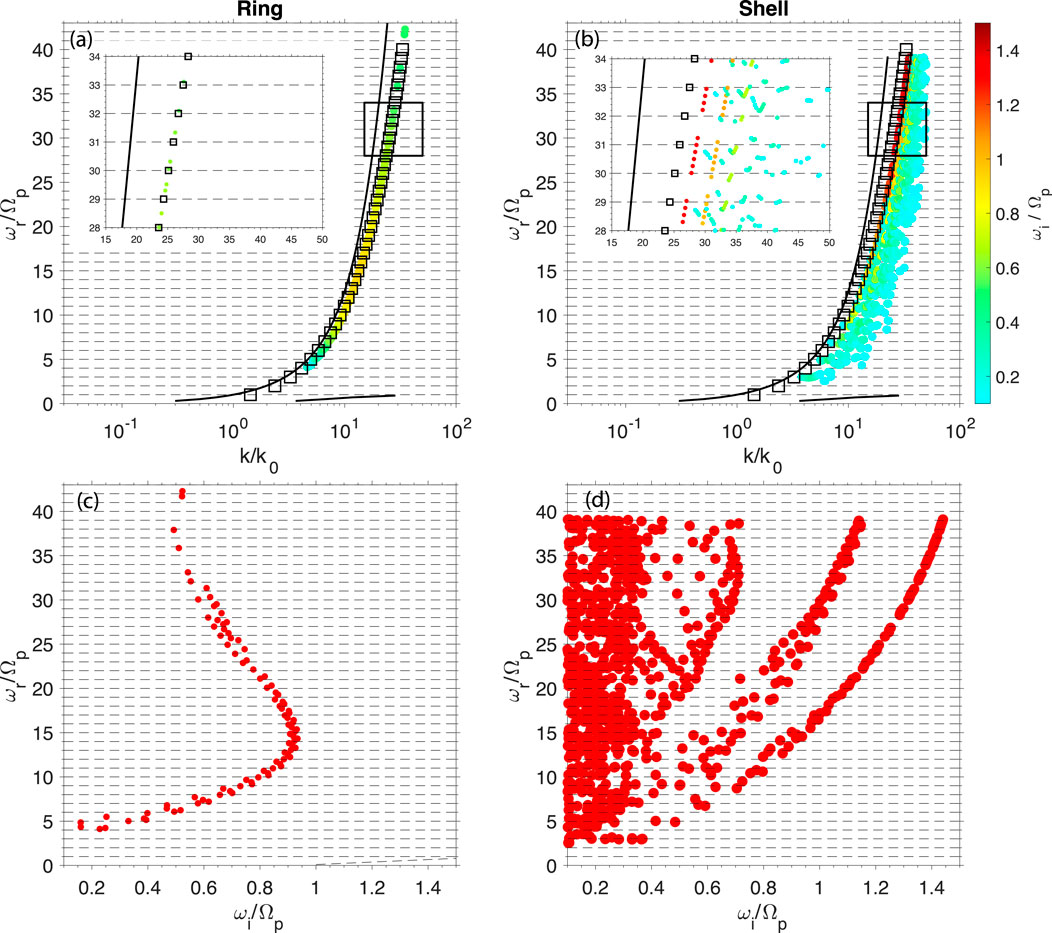
Figure 2. Comparison of the (A, C) ring-driven and (B, D) shell-driven MS waves using the full wave dispersion relation solver. (A, B) Full wave dispersion relations of ring-driven and shell-driven MS waves, respectively. Two black curves denote the cold plasma dispersion relations. The colored solid circles denote the growing modes. The black squares denote the first peak of the square of the Bessel function $J_n^2(\frac{k_{\perp }{v}_r}{{\mathrm{\Omega }}_p})$ or $J_n^2(\frac{k_{\perp }{v}_s}{{\mathrm{\Omega }}_p})$, where $k_{\perp }$ is the perpendicular wavenumber and $v_r$ $(v_s)$ is the ring (shell) velocity. ${\mathrm{\Omega }}_p$ is the proton gyrofrequency. (C, D) Relation between the wave growth rate and wave frequency for ring-driven and shell-driven MS waves, respectively. The two black rectangles in (A, B) indicate the zoomed-in region on the left upper part of each panel.

Both ring and shell distributions can excite MS waves near the wavenumber corresponding to the first peak of $J_n^2(\frac{k_{\perp }{v}_r}{{\mathrm{\Omega }}_p})$ (Figure 2A) and $J_n^2(\frac{k_{\perp }{v}_s}{{\mathrm{\Omega }}_p})$ (Figure 2B), respectively. However, there are several differences between ring- and shell-driven MS waves. (1) The large growth rates of ring-driven MS waves are almost following the first peak of $J_n^2(\frac{k_{\perp }{v}_r}{{\mathrm{\Omega }}_p})$ (zoomed-in region in Figure 2A). While, large growth rates of shell-driven MS waves (Figure 2B) is deviated from the first peak of $J_n^2(\frac{k_{\perp }{v}_s}{{\mathrm{\Omega }}_p})$, extend to much wider wavenumber range, and can have a second peak along the k direction for a harmonic band (consistent with Figure 1C in (Min and Liu, 2016b)). (2) The frequency range of ring-driven MS waves is narrower. The frequencies of ring-driven MS waves roughly range from $7{\mathrm{\Omega }}_p$ to $30{\mathrm{\Omega }}_p$ (${\omega }_i/{\mathrm{\Omega }}_p>0.6$, Figure 2C), while the frequencies of shell-driven MS waves can extend from $7{\mathrm{\Omega }}_p$ to $40{\mathrm{\Omega }}_p$ (Figure 2D). (3) The growth rates of ring-driven MS waves are not always larger than those of shell-driven MS waves even though ring distributions can provide larger gradient near the ring velocity. As mentioned in the introduction, once $|\mathrm{\Gamma }|>1$, non-resonant instability will occur and wave growth rates ${\omega }_i$ are proportional to ${\int }_0^{+\infty }W(v_{\perp },{\omega }_r)d{\tilde{F}}_{\perp }/d{v}_{\perp }{J}_n^2(\frac{k_{\perp }{v}_{\perp }}{{\mathrm{\Omega }}_p})d{v}_{\perp }$. In this case, $|\mathrm{\Gamma }|>10$. Thus, the differences between ring-driven and shell-driven MS waves can be explained by the differences in ${\tilde{F}}_{\perp }$ of ring and shell distributions, as shown in Figures 1B, D, respectively.

To achieve a large growth rate, $J_n^2(\frac{k_{\perp }{v}_{\perp }}{{\mathrm{\Omega }}_p})$ should be close to the maximum value (the first peak) in the $v_{\perp }$ range with a positive $d{\tilde{F}}_{\perp }/d{v}_{\perp }$. As a result, a small velocity range with positive $d{\tilde{F}}_{\perp }/d{v}_{\perp }$ in the ring distribution leads to a narrow $k_{\perp }$ range and a narrow $n$ range. Thus, the peak growth rates appear almost at the first peak of $J_n^2$ and exhibit a peak near $15{\mathrm{\Omega }}_p$. On the contrary, the shell distribution has a much wider velocity range with positive $d{\tilde{F}}_{\perp }/d{v}_{\perp }$, even though the largest value of such gradient is less than the one in the case of the ring distribution. Thus, such wider velocity range leads to a much wider $k_{\perp }$ and $n$ range. As the result, the peak growth rates of the shell-driven MS wave can appear over the $k_{\perp }$ range deviated from the first peak of $J_n^2$.

4 MS wave dependences on proton ring and shell distributions

In this section, we investigate the dependencies of MS wave instability on the velocity and temperature of proton ring and shell distributions and wave normal angles. We vary one of the three parameters and fix the other two at a time. The typical plasma parameters are shown in Section 2. To maintain the shell distribution, we change the numbers of ring-beam distributions used for the shell distribution configuration when the shell velocity or thermal velocity changes. For the sake of visualization, we only show the wave frequencies and growth rates for the peak growth rate in each harmonic band instead of showing all growing and damped modes.

4.1 Ring and shell velocity

Figure 3 shows the MS wave frequency and growth rate dependences on the velocity of proton ring (Figures 3A–H) and shell (Figures 3I–P) distributions for $V_r=V_s=0.6V_A$ (first column), $1.3V_A$ (second column), $1.5V_A$ (thrid column), and $3V_A$ (last column). With a small ring velocity (Figures 3A,B), no strong MS wave can be excited. The cold species with Maxwellian distributions contribute to damping of the MS waves. This damping effect is weak near the cold dispersion relation but becomes strong away from the cold dispersion relation. With the small ring velocity, the first peaks of $J_n^2$ are far from the cold dispersion relation. Damping from the cold species dominates over growth from the proton ring near the first peaks of $J_n^2$. However, the proton shell distribution (Figures 3I, J) can support MS waves in low harmonic bands and in a wider k range, where the damping from the cold species becomes weaker, even though the growth rates are weak. As the ring velocity increases (Figures 3C, D), the first peaks of $J_n^2$ become closer to the cold dispersion relation (because the argument $\frac{k_{\perp }{v}_r}{{\mathrm{\Omega }}_p}$ of $J_n^2$ is a constant), and the growth effect takes the domination role. Thus, ring-driven MS waves can be excited with a center frequency $\sim 14{\mathrm{\Omega }}_p$. For the same reason, the growth rates and wave frequency range of shell-driven MS waves increase as shell velocity increases (Figures 3K, L). As the ring (Figures 3E, F) and shell (Figures 3M, N) velocities increase further, the first peaks of $J_n^2$ and the cold dispersion relation become closer. The growth rates and frequency range of both ring-driven and shell-driven MS waves become larger.

Figure 3

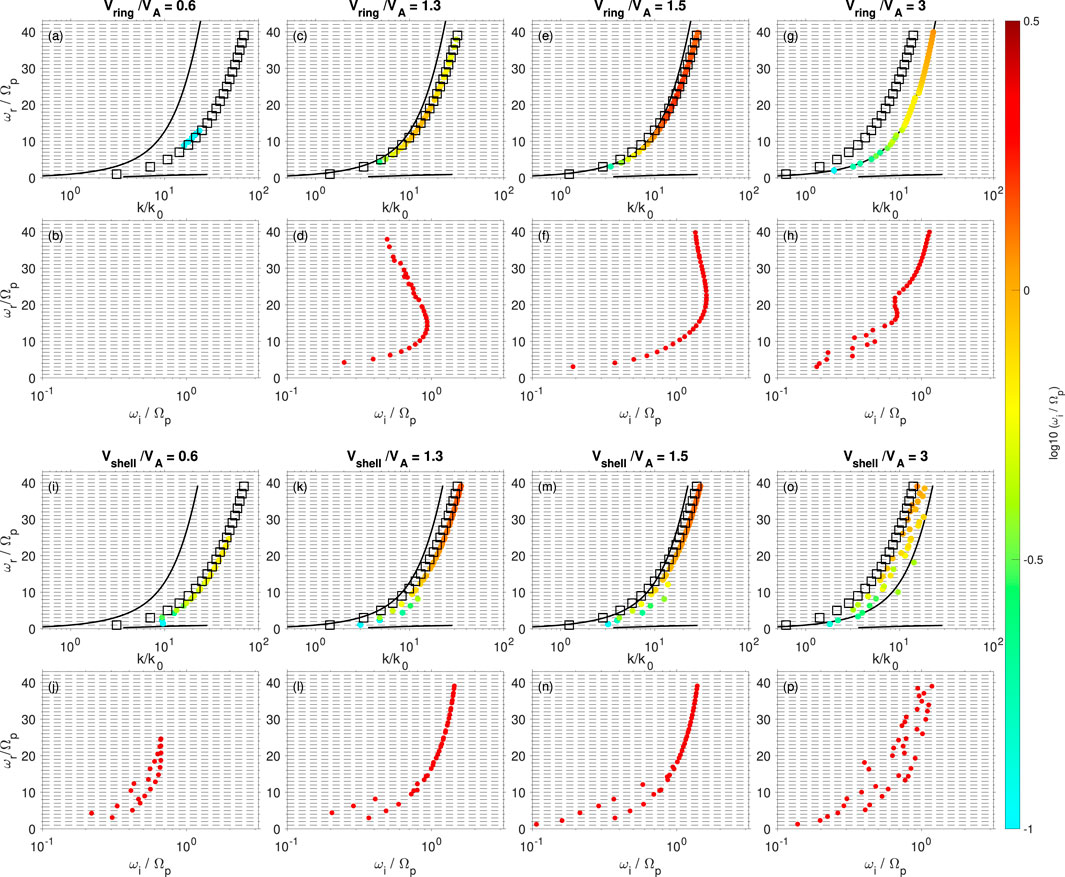
Figure 3. MS wave dependence on the velocity of the (A–H) ring and (I–P) shell distributions. $v_r/V_A$ = (A, B) 0.6, (C, D) 1.3, (E, F) 1.5, and (G, H) 3. $v_s/V_A$ = (I, J) 0.6, (K, L) 1.3, (M, N) 1.5, and (O, P) 3. The figure format is the same as Figure 2.

Once $k$ of the first peak of $J_n^2$ is smaller than that of the cold dispersion relation with larger ring (Figures 3G, H) and shell (Figures 3O, P) velocities, the ring-driven and shell-driven MS waves behave differently. The peak growth rates of ring-driven MS waves follow the cold dispersion relation instead of the first peak of $J_n^2$ (Figure 3G). The damping from the cold species becomes larger once $k$ is away from the cold plasma dispersion relation. Even though smaller, the values at the other $J_n^2$ peaks with larger $k$ are comparable to that at the first $J_n^2$ peak. This is particularly true for large $n$ (at which the first peak value of $J_n^2$ is small). As a result, the peak growth rates of ring-driven MS waves decrease (Figure 3H). These results are consistent with the ring-driven oxygen ion Bernstein mode (Liu et al., 2022). Unlike ring-driven MS waves, the peak growth rates of shell-driven MS waves always occur near the first peaks of $J_n^2$ (Figure 3O). A possible reason is that unlike the ring-driven MS waves, which are always confined near the harmonics of the proton gyrofrequency with a narrower k range, shell-driven MS waves occur between the harmonics of the proton gyrofrequency with a much wider k range, and thus, a set of wave frequency and wavenumber where the damping is weak is readily available.

4.2 Ring and shell temperature

Figure 4 shows the MS wave frequency and growth rate dependences on the thermal velocity (temperature) of the proton ring (Figures 4A–F) and shell (Figures 4G–L) distributions for $a_r=a_s=0.03V_A$ (left column), $0.1V_A$ (middle column), and $0.3V_A$ (right column). The temperature dependence is straightforward and same for ring-driven and shell-driven MS waves: as the ring (shell) temperature increases, the frequency range and growth rate of each harmonic band decrease. The peak growth rate of each harmonic band still occurs near the first peaks of $J_n^2$. As the temperature increases, the ring (shell) becomes smoother, and thus, $d{\tilde{F}}_{\perp }/d{v}_{\perp }$ decreases. As a result, the growth rates of all harmonic bands decrease. Once the growth from the proton ring (shell) becomes smaller than damping from the cold species (e.g., near high harmonic bands), the waves are damped, and the wave frequency range decreases.

Figure 4

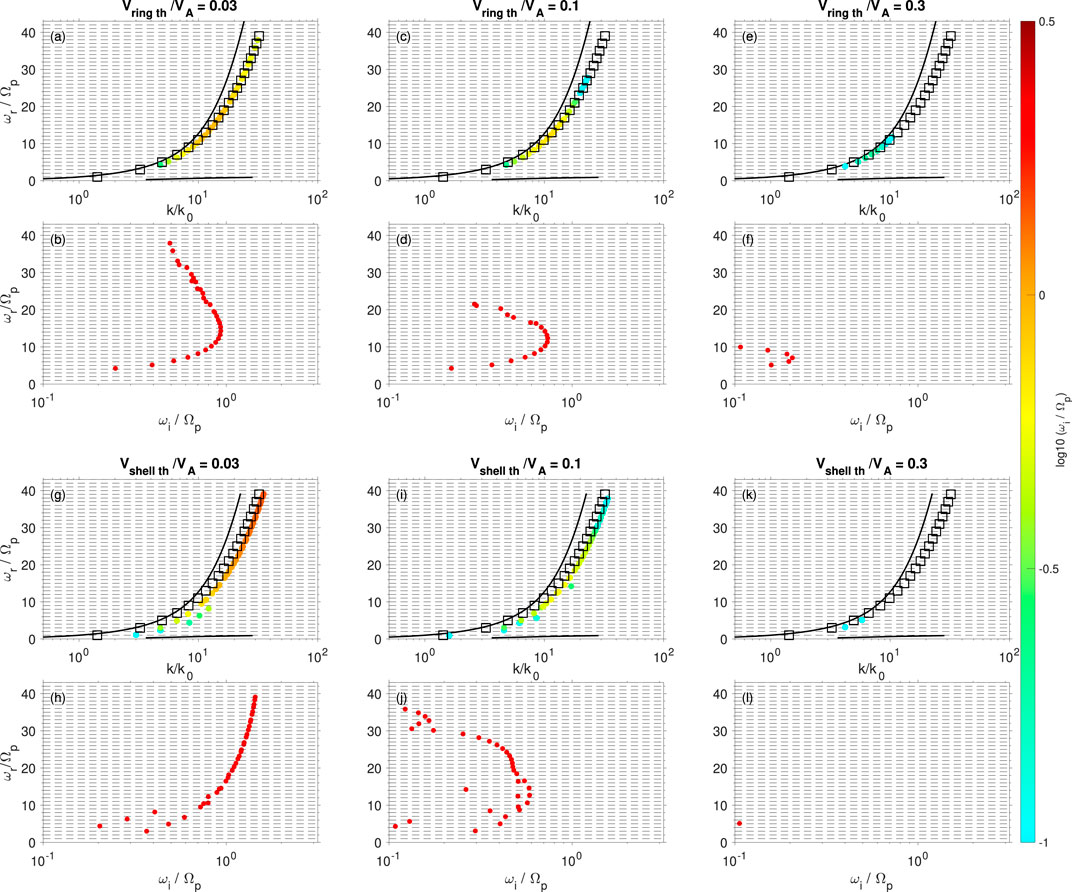
Figure 4. MS wave dependence on the thermal velocity (temperature) of the (A–F) ring and (G–L) shell distributions. $v_{r,th}/V_A$ = (A, B) 0.03, (c–d) 0.1, and (e–f) 0.3. $v_{s,th}/V_A$ = (G–H) 0.03, (I, J) 0.1, and (K, L) 0.3. The figure format is same as Figure 2.

4.3 Wave normal angle

Figure 5 shows the wave frequency and growth rate dependences on the wave normal angle for ring-driven (Figures 5A–F) and shell-driven (Figures 5G–L) MS waves with $WNA=81°$ (left column), $85°$ (middle column), and $89°$ (right column). As the WNA increases, the cold dispersion relation moves closer to the first peaks of $J_n^2$. Thus, the growth rate and wave frequency range increase with the WNA. For the ring-driven MS waves, once $k$ of the cold dispersion relation surpasses the first peaks of $J_n^2$, the peak growth rates follow the cold dispersion relation (Figure 5E), but for the shell-driven MS waves, they still follow the first peaks of $J_n^2$, similar to the ring (shell) velocity dependences.

Figure 5

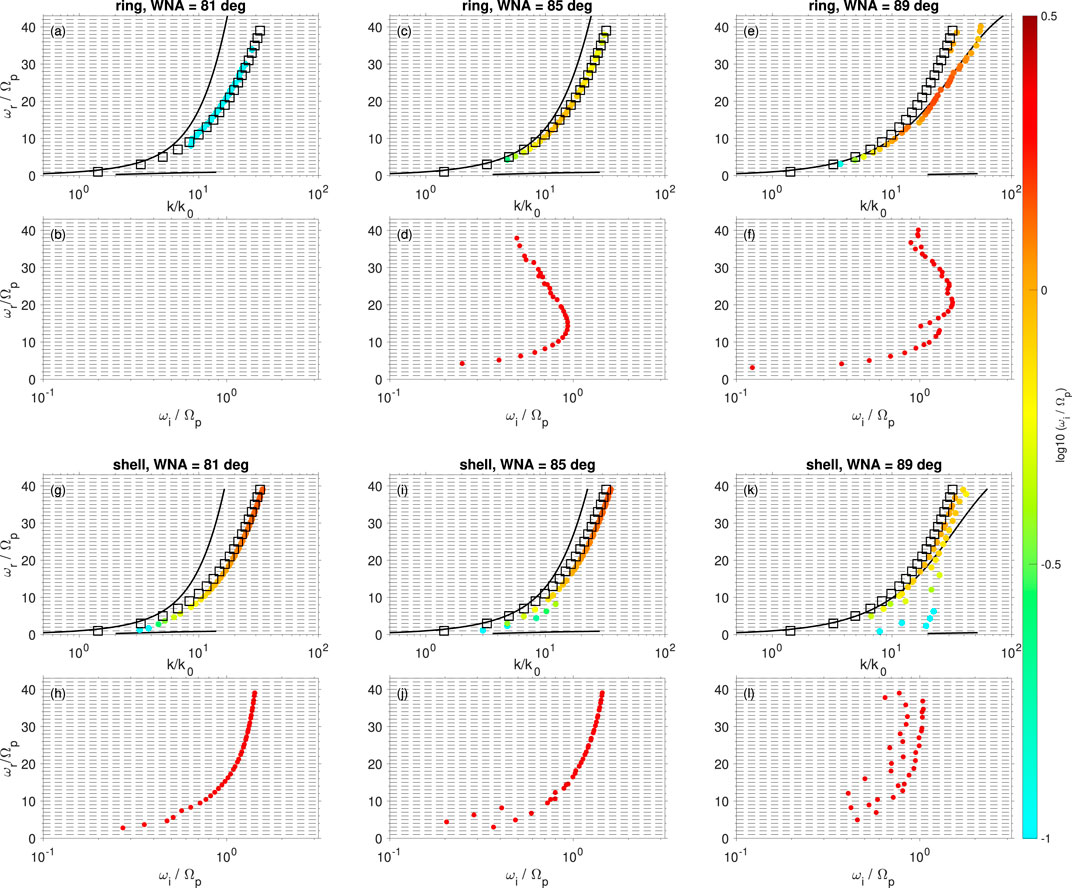
Figure 5. MS wave dependence on wave normal angles (WNAs) for (A–F) ring-driven and (G–L) shell-driven MS waves. $WNA$ = (A, B), (G, H) $81°$, (C, D), (I, J) $85°$, and (E, F), (K, L) $89°$. The figure format is the same as Figure 2.

The ring (shell) velocity and WNA dependences can be summarized by the relations between $k_{J_{n,1p}^2}$ and $k_{\mathit{cdr}}$, where $k_{J_{n,1p}^2}$ and $k_{\mathit{cdr}}$ are the wavenumbers corresponding to the first peak of $J_n^2$ for the ring (shell) velocity and cold plasma dispersion relation, respectively. The increase in the ring (shell) velocity leads to the decrease of $k_{J_{n,1p}^2}$ and the increase in the WNA leads to the increase of $k_{\mathit{cdr}}$. MS wave growth rates increase as $k_{J_{n,1p}^2}$ and $k_{\mathit{cdr}}$ become closer. For shell-driven MS waves, peak growth rates occur near the first peaks of $J_n^2$. While, for ring-driven MS waves, peak growth rates are near the first peaks of $J_n^2$ when $k_{J_{n,1p}^2}>k_{\mathit{cdr}}$ and follow the cold plasma dispersion relation when when $k_{J_{n,1p}^2}<k_{\mathit{cdr}}$.

5 Conclusion and discussion

In this study, we perform a parametric analysis of ring-driven and shell-driven MS waves by investigating their dependencies on the velocities and temperatures of the proton ring and shell distributions and wave normal angles using a full wave dispersion relation solver. The principal conclusions of this study are as follows.

1. Compared to shell-driven MS waves, ring-driven MS waves have narrower wavenumber ranges and narrower frequency ranges. This result occurs primarily because the ring distribution can provide a positive phase space density gradient along $v_{\perp }$ in a narrow velocity range, while the shell distribution can provide a gradient in a wide velocity range.

2. The MS wave growth rates increase as the ratio of $k_{J_{n,1p}^2}/k_{\mathit{cdr}}\sim 1$. When $k_{J_{n,1p}^2}>k_{\mathit{cdr}}$, the peak growth rate of each harmonic band is near the first peak of $J_n^2$. When $k_{J_{n,1p}^2}<k_{\mathit{cdr}}$, the peak growth rates of ring-driven MS waves are near the cold plasma dispersion relation, while the peak growth rates of shell-driven MS waves are still near the first peak of $J_n^2$. This result can be used to explain dependences on ring (shell) velocity and wave normal angle. The increase in the ring (shell) velocity will decrease $k_{J_{n,1p}^2}$ (due to constant arguments for the first peaks of $J_n^2$) and the increase in the wave normal angle will increase $k_{\mathit{cdr}}$.

3. The MS wave growth rates and frequency range decrease with increasing temperature of the ring (shell) distribution due to the smoothed phase space density by increasing the temperature.

In Figure 3, the MS wave frequency always extends from the low harmonic bands to high harmonic bands as the ring (shell) velocity increases. This phenomenon is different from a previous study, in which a proton ring with a small velocity excites high harmonic bands and a proton ring with a large velocity excites low harmonic bands (Chen et al., 2010b). This discrepancy is caused by the fact that the MS waves were studied under cold plasma conditions in Chen et al., 2010a, and the wave normal angle was quite large $(89.5°)$. However, in this study, a full wave dispersion relation solver is used, and thus, the wave dispersion relation follows the IBM and deviates from the cold plasma dispersion relation. By setting the temperatures of the cold species used in this study to 0 and decreasing the proton ring concentration to 0.02, we reproduce the relations between the wave frequency and ring velocity in Chen et al., 2010b (not shown).

The ring (shell)-driven MS waves (Figures 2A,B) show continuous growth rates across the proton harmonics. They correspond to continuous frequency spectra of MS waves (Gurnett, 1976; Tsurutani et al., 2014). The typical discrete MS waves can transit to continuous spectra once the growth rate satisfies ${\omega }_i>0.5{\mathrm{\Omega }}_p$ (Chen et al., 2016; Sun et al., 2016), which is consistent with this study of continuous growth rates $>0.6{\mathrm{\Omega }}_p$. A possible reason for the continuous growth rates is that the growth rate pattern of the MS waves will evolve from a discrete pattern to a continuous pattern as $k_{\Vert }$ increases (Min and Liu, 2016b). The minimum $k_{\Vert }$ for this pattern evolution decreases as $a_{\Vert }$ increases. In this study, $a_{\Vert }$ $(\ge 0.03V_A)$ is quite large so that the continuous growth rate pattern easily occurs.

Recently, a partial shell distribution was found in observations (Boardsen et al., 2018; Min et al., 2018; Ouyang et al., 2020) and simulations (Chen, Thorne, Jordanova, Wang, et al., 2010). This distribution acts as a shell distribution but is limited in a finite pitch angle range centered along the perpendicular direction so that it can be treated as a transition distribution between the two extreme cases, ring and shell distributions. Thus, the properties of the partial shell-driven MS waves should be in between the properties of the ring-driven and shell-driven MS waves and thus follow similar parametric dependences. Investigating this topic will be left for future research.

In this work, we use typical background parameters in the inner magnetosphere (such as background magnetic field and cold plasma density and temperature) and a realistic proton-electron-mass ratio. The dispersion relation and peak growth rates are highly dependent on the relation between the cold plasma wave mode and the first peak of $J_n^2$ related to the ring/shell distributions. Thus, a larger $V_r/V_A$ (or $V_s/V_A$) is corresponding to a smaller wave normal angle. A statistical observation of the Van Allen Probes shows that the wave normal angles inside the plasmapause are smaller than those outside the plasmapause (Figure 4 in Zou et al. (2019)). This result is consistent with our results that the denser plasma in the plasmasphere leads to a smaller Alfven speed, and thus, a larger $V_r/V_A$ (or $V_s/V_A$) and a smaller wave normal angle. Such the result is also tested by a 2-D PIC simulation (Sun et al., 2020). The thermal velocity is also a critical parameter. It can determine a threshold for the wave excitation.

In the Earth’s inner magnetosphere, ring and shell distributions can be formed at the dayside due to the energy-dependent proton drift paths. These ring or shell distributions will drive MS waves, and then, be relaxed after the wave excitation. Thus, how these distribution relaxations influence the proton drift and distribution is a significant topic in the wave-particle interaction, which we will address in the future.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://doi.org/10.5281/zenodo.11521879.

Author contributions

XL: Data curation, Formal Analysis, Investigation, Methodology, Software, Writing–original draft, Writing–review and editing. LC: Conceptualization, Funding acquisition, Supervision, Writing–review and editing. XW: Resources, Validation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The authors acknowledge NASA fundings NNX17AI52G, 80NSSC19K0283, 80NSSC20K0689, 80NSSC21K1679, and 80NSSC22K1637.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer IS declared a past co-authorship with the author LC to the handling editor.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ashour-Abdalla, M., Leboeuf, J. N., Schriver, D., Bosqued, J.-M., Cornilleau-Wehrlin, N., Sotnikov, V., et al. (2006). Instabilities driven by ion shell distributions observed by cluster in the midaltitude plasma sheet boundary layer. J. Geophys. Res. Space Phys. 111 (A10). doi:10.1029/2005JA011490

CrossRef Full Text | Google Scholar

Balikhin, M. A., Shprits, Y. Y., Walker, S. N., Chen, L., Cornilleau-Wehrlin, N., Dandouras, I., et al. (2015). Observations of discrete harmonics emerging from equatorial noise. Nat. Commun. 6 (1), 7703. doi:10.1038/ncomms8703

PubMed Abstract | CrossRef Full Text | Google Scholar

Boardsen, S. A., Gallagher, D. L., Gurnett, D. A., Peterson, W. K., and Green, J. L. (1992). Funnel-shaped, low-frequency equatorial waves. J. Geophys. Res. Space Phys. 97 (A10), 14967–14976. doi:10.1029/92JA00827

CrossRef Full Text | Google Scholar

Boardsen, S. A., Hospodarsky, G. B., Min, K., Averkamp, T. F., Bounds, S. R., Kletzing, C. A., et al. (2018). Determining the wave vector direction of equatorial fast magnetosonic waves. Geophys. Res. Lett. 45 (16), 7951–7959. doi:10.1029/2018GL078695

CrossRef Full Text | Google Scholar

Bortnik, J., and Thorne, R. M. (2010). Transit time scattering of energetic electrons due to equatorially confined magnetosonic waves. J. Geophys. Res. 115, 7213. doi:10.1029/2010JA015283

CrossRef Full Text | Google Scholar

Chen, L. (2015). Wave normal angle and frequency characteristics of magnetosonic wave linear instability. Geophys. Res. Lett. 42 (12), 4709–4715. doi:10.1002/2015GL064237

CrossRef Full Text | Google Scholar

Chen, L., Sun, J., Lu, Q., Gao, X., Xia, Z., and Zhima, Z. (2016). Generation of magnetosonic waves over a continuous spectrum. J. Geophys. Res. Space Phys. 121 (2), 1137–1147. doi:10.1002/2015JA022089

CrossRef Full Text | Google Scholar

Chen, L., Sun, J., Lu, Q., Wang, X., Gao, X., Wang, D., et al. (2018). Two-dimensional particle-in-cell simulation of magnetosonic wave excitation in a dipole magnetic field. Geophys. Res. Lett. 45 (17), 8712–8720. doi:10.1029/2018GL079067

CrossRef Full Text | Google Scholar

Chen, L., and Thorne, R. M. (2012). Perpendicular propagation of magnetosonic waves. Geophys. Res. Lett. 39 (14). doi:10.1029/2012GL052485

CrossRef Full Text | Google Scholar

Chen, L., Thorne, R. M., Jordanova, V. K., and Horne, R. B. (2010a). Global simulation of magnetosonic wave instability in the storm time magnetosphere. J. Geophys. Res. 115. doi:10.1029/2010JA015707

CrossRef Full Text | Google Scholar

Chen, L., Thorne, R. M., Jordanova, V. K., Wang, C., Gkioulidou, M., Lyons, L., et al. (2010b). Global simulation of EMIC wave excitation during the 21 April 2001 storm from coupled RCM-RAM-HOTRAY modeling. J. Geophys. Res. 115, 7209. doi:10.1029/2009JA015075

CrossRef Full Text | Google Scholar

Curtis, S. A., and Wu, C. S. (1979). Gyroharmonic emissions induced by energetic ions in the equatorial plasmasphere. J. Geophys. Res. 84, 2597–2607. doi:10.1029/JA084iA06p02597

CrossRef Full Text | Google Scholar

Gao, X., Liu, K., Wang, X., Min, K., Lin, Y., and Wang, X. (2017). Gyrokinetic electron and fully kinetic ion simulations of fast magnetosonic waves in the magnetosphere. Phys. Plasmas 24 (6), 062901. doi:10.1063/1.4985303

CrossRef Full Text | Google Scholar

Gary, S. P., Liu, K., Winske, D., and Denton, R. E. (2010). Ion Bernstein instability in the terrestrial magnetosphere: linear dispersion theory. J. Geophys. Res. Space Phys. 115, A12209. doi:10.1029/2010JA015965

CrossRef Full Text | Google Scholar

Gurnett, D. A. (1976). Plasma wave interactions with energetic ions near the magnetic equator. J. Geophys. Res. 81, 2765–2770. doi:10.1029/JA081i016p02765

CrossRef Full Text | Google Scholar

Horne, R. B., Thorne, R. M., Glauert, S. A., Meredith, N. P., Pokhotelov, D., and Santolík, O. (2007). Electron acceleration in the Van Allen radiation belts by fast magnetosonic waves. Geophys. Res. Lett. 34, L17107. doi:10.1029/2007GL030267

CrossRef Full Text | Google Scholar

Hrbáčková, Z., Santolík, O., Němec, F., Macúšová, E., and Cornilleau-Wehrlin, N. (2015). Systematic analysis of occurrence of equatorial noise emissions using 10 years of data from the cluster mission. J. Geophys. Res. Space Phys. 120 (2), 1007–1021. doi:10.1002/2014JA020268

CrossRef Full Text | Google Scholar

Laakso, H., Junginger, H., Schmidt, R., Roux, A., and de Villedary, C. (1990). Magnetosonic waves above c (H⁺) at geostationary orbit: GEOS 2 results. J. Geophys. Res. 95, 10609–10621. doi:10.1029/JA095iA07p10609

CrossRef Full Text | Google Scholar

Li, J., Ni, B., Xie, L., Pu, Z., Bortnik, J., Thorne, R. M., et al. (2014). Interactions between magnetosonic waves and radiation belt electrons: comparisons of quasi-linear calculations with test particle simulations. Geophys. Res. Lett. 41 (14), 4828–4834. doi:10.1002/2014GL060461

CrossRef Full Text | Google Scholar

Li, X., Tao, X., Lu, Q., and Dai, L. (2015). Bounce resonance diffusion coefficients for spatially confined waves. Geophys. Res. Lett. 42 (22), 9591–9599. doi:10.1002/2015GL066324

CrossRef Full Text | Google Scholar

Liu, K., Gary, S. P., and Winske, D. (2011). Excitation of magnetosonic waves in the terrestrial magnetosphere: particle-in-cell simulations. J. Geophys. Res. 116, A07212. doi:10.1029/2010JA016372

CrossRef Full Text | Google Scholar

Liu, X., Chen, L., Sun, J., Wang, X., and Usanova, M. E. (2022). A parametric study of oxygen ion cyclotron harmonic wave excitation and polarization by an oxygen ring distribution. J. Geophys. Res. Space Phys. 127 (11), e2022JA030828. doi:10.1029/2022JA030828

CrossRef Full Text | Google Scholar

Liu, X., Chen, L., Yang, L., Xia, Z., and Malaspina, D. M. (2018). One-dimensional full wave simulation of equatorial magnetosonic wave propagation in an inhomogeneous magnetosphere. J. Geophys. Res. Space Phys. 123 (1), 587–599. doi:10.1002/2017JA024336

CrossRef Full Text | Google Scholar

Ma, Q., Li, W., Thorne, R. M., and Angelopoulos, V. (2013). Global distribution of equatorial magnetosonic waves observed by themis. Geophys. Res. Lett. 40 (10), 1895–1901. doi:10.1002/grl.50434

CrossRef Full Text | Google Scholar

Maldonado, A. A., Chen, L., Claudepierre, S. G., Bortnik, J., Thorne, R. M., and Spence, H. (2016). Electron butterfly distribution modulation by magnetosonic waves. Geophys. Res. Lett. 43 (7), 3051–3059. doi:10.1002/2016GL068161

CrossRef Full Text | Google Scholar

Min, K., and Liu, K. (2015). Fast magnetosonic waves driven by shell velocity distributions. J. Geophys. Res. Space Phys. 120 (4), 2739–2753. doi:10.1002/2015JA021041

CrossRef Full Text | Google Scholar

Min, K., and Liu, K. (2016a). Proton velocity ring-driven instabilities in the inner magnetosphere: linear theory and particle-in-cell simulations. J. Geophys. Res. Space Phys. 121 (1), 475–491. doi:10.1002/2015JA022042

CrossRef Full Text | Google Scholar

Min, K., and Liu, K. (2016b). Understanding the growth rate patterns of ion bernstein instabilities driven by ring-like proton velocity distributions. J. Geophys. Res. Space Phys. 121 (4), 3036–3049. doi:10.1002/2016JA022524

CrossRef Full Text | Google Scholar

Min, K., Liu, K., Denton, R. E., Němec, F., Boardsen, S. A., and Miyoshi, Y. (2020). Two-dimensional hybrid particle-in-cell simulations of magnetosonic waves in the dipole magnetic field: on a constant l-shell. J. Geophys. Res. Space Phys. 125 (10), e2020JA028414. doi:10.1029/2020JA028414

CrossRef Full Text | Google Scholar

Min, K., Liu, K., Wang, X., Chen, L., and Denton, R. E. (2018). Fast magnetosonic waves observed by van allen probes: testing local wave excitation mechanism. J. Geophys. Res. Space Phys. 123 (1), 497–512. doi:10.1002/2017JA024867

CrossRef Full Text | Google Scholar

Němec, F., Santolík, O., Gereová, K., Macúšová, E., de Conchy, Y., and Cornilleau-Wehrlin, N. (2005). Initial results of a survey of equatorial noise emissions observed by the Cluster spacecraft. Planet. Space Sci. 53, 291–298. doi:10.1016/j.pss.2004.09.055

CrossRef Full Text | Google Scholar

Ouyang, Z., Yuan, Z., Yu, X., and Yao, F. (2020). Narrowband magnetosonic waves near the lower hybrid resonance frequency in the inner magnetosphere: wave properties and excitation conditions. J. Geophys. Res. Space Phys. 126, 2020JA028158. doi:10.1029/2020JA028158

CrossRef Full Text | Google Scholar

Perraut, S., Roux, A., Robert, P., Gendrin, R., Sauvaud, J., Bosqued, J., et al. (1982). A systematic study of ULF Waves above H+ from GEOS 1 and 2 Measurements and Their Relationships with proton ring distributions. J. Geophys. Res. 87, 6219–6236. doi:10.1029/JA087iA08p06219

CrossRef Full Text | Google Scholar

Russell, C. T., Holzer, R. E., and Smith, E. J. (1970). OGO 3 observations of ELF noise in the magnetosphere. 2. The nature of the equatorial noise. J. Geophys. Res. 75, 755–768. doi:10.1029/JA075i004p00755

CrossRef Full Text | Google Scholar

Santolík, O., Nemec, F., Gereová, K., Macúšová, E., Conchy, Y., and Cornilleau-Wehrlin, N. (2004). Systematic analysis of equatorial noise below the lower hybrid frequency. Ann. Geophys. 22, 2587–2595. doi:10.5194/angeo-22-2587-2004

CrossRef Full Text | Google Scholar

Santolík, O., Pickett, J. S., Gurnett, D. A., Maksimovic, M., and Cornilleau-Wehrlin, N. (2002). Spatiotemporal variability and propagation of equatorial noise observed by Cluster. J. Geophys. Res. 107, 1495. doi:10.1029/2001JA009159

CrossRef Full Text | Google Scholar

Sun, J., Chen, L., and Wang, X. (2020). Wave normal angle distribution of magnetosonic waves in the earth’s magnetosphere: 2-d pic simulation. J. Geophys. Res. Space Phys. 125 (5), e2020JA028012. doi:10.1029/2020JA028012

CrossRef Full Text | Google Scholar

Sun, J., Gao, X., Lu, Q., Chen, L., Tao, X., and Wang, S. (2016). A parametric study for the generation of ion bernstein modes from a discrete spectrum to a continuous one in the inner magnetosphere. ii. particle-in-cell simulations. Phys. Plasmas 23 (2), 022902. doi:10.1063/1.4941284

CrossRef Full Text | Google Scholar

Tsurutani, B. T., Falkowski, B. J., Pickett, J. S., Verkhoglyadova, O. P., Santolik, O., and Lakhina, G. S. (2014). Extremely intense elf magnetosonic waves: a survey of polar observations. J. Geophys. Res. Space Phys. 119 (2), 964–977. doi:10.1002/2013JA019284

CrossRef Full Text | Google Scholar

Umeda, T., Matsukiyo, S., Amano, T., and Miyoshi, Y. (2012). A numerical electromagnetic linear dispersion relation for maxwellian ring-beam velocity distributions. Phys. Plasmas 19 (7), 072107. doi:10.1063/1.4736848

CrossRef Full Text | Google Scholar

Xiao, F., Zhou, Q., He, Z., and Tang, L. (2012). Three-dimensional ray tracing of fast magnetosonic waves. J. Geophys. Res. Space Phys. 117 (A6). doi:10.1029/2012JA017589

CrossRef Full Text | Google Scholar

Zou, Z., Zuo, P., Ni, B., Wei, F., Zhao, Z., Cao, X., et al. (2019). Wave normal angle distribution of fast magnetosonic waves: a survey of van allen probes emfisis observations. J. Geophys. Res. Space Phys. 124 (7), 5663–5674. doi:10.1029/2019JA026556

CrossRef Full Text | Google Scholar