Solution of the dark matter riddle within standard model physics: from black holes, galaxies and clusters to cosmology

It is postulated that the energy density of the (quantum) vacuum acts firstly as dark energy and secondly as a part of dark matter. Assisted by electric fields arising from a small charge mismatch in the cosmic plasma, it can condense on mass concentrations. No longer participating in the cosmic expansion, this constitutes “electro-aether-energy” (EAE), “electro-zero-point-energy” or “electro-vacuum-energy”, which solves the dark matter riddle without new physics. A radial electric field of 1 kV/m is predicted in the Galaxy. For proper electric fields, EAE can cover the results deduced with MOND. An instability allows a speedy filling of dark matter cores. Hydrostatic equilibrium in galaxy clusters is obeyed. Flowing in aether energy of explains why black holes become supermassive, do not have mass gaps and overcome the final parsec problem. Rupture of charged clouds reduces, e.g., the primordial baryon cloud to the cosmic web. The large coherence scale of the electric field acts as a scaffold for gentle galaxy formation and their vast polar structures. In galaxy merging and bars, there occurs no dynamical friction. At cosmological scales, EAE acts as pressureless dark matter. Its amount increases in time, which likely solves the Hubble tension by its late time physics. A big crunch can occur. Of the large cosmological constant injected at the Big Bang, a small part kept that form, without fine-tuning.

1 Introduction

1.1 Short history of dark matter

The matter in the world and skies we experience is called “normal matter” by specialists. It consists of protons and neutrons, that are bound by the strong force in atomic nuclei, and electrons that encircle the nucleus due to the Coulomb attraction between the positive protons and the negative electrons.

Nowadays it is understood, however, that normal matter makes up only some 5% of the total mass budget in the Universe. In fact, the stars that we observe in the night sky make up only a modest four ‰of the total (Rich, 2009); most of the 5% lies in hydrogen clouds and hydrogen bridges between galaxies, which can be observed in the 21 cm radio line due to spin flipping in the hydrogen nucleus, as was discovered by Hendrik van de Hulst (Cook, 2001).

The remaining 95% of the total is matter that we do not perceive directly, even though its existence has been established rather firmly. After long suspicion of dark stars and the suggestion of dark matter based on stellar velocities by Jacobus Kapteyn in 1922 (Kapteyn, 2013), the existence of dark matter was established by Fritz Zwicky in 1933 (Zwicky, 1933) and much support for it has emerged. An account of the history of dark matter is given in (De Swart et al., 2017). Actually, this matter is not dark but transparent. Its French name “matière obscure” translates as “obscure matter”, hidden or unexplained matter, which does more justice to its nature.

Observations by Vera Rubin and Kent Ford in the seventies demonstrated that in the outer part of galaxies, circular orbits have nearly the same rotation speed (Rubin and Ford, 1970), constituting “flat rotation curves”. This has led to general acceptance of dark matter’s existence.

In 1998, it was established that there also exists dark energy (Riess et al., 1998; Perlmutter et al., 1999), which constitutes some 70% of the mass budget in the Universe, while dark matter makes up some 25%. Of all the matter/energy in the Universe, 95% is unexplained so far; it will be the focus of this work.

1.2 Present status

Dark matter must be cold, that is: slowly moving, in order to account for the creation of galaxies. Many searches have been carried out. The historical candidate, MACHOs, massive astrophysical compact halo objects such as dark stars or planets, has been ruled out as the main contributor (Alcock et al., 2000; Tisserand et al., 2007). The next candidate is the WIMP (weakly interacting massive particle) proposed by Jim Peebles and followers (Blumenthal et al., 1982; 1984; Bond et al., 1982; Peebles, 1982). Being massive and moving slowly, it is termed “cold” and leads to the present paradigm of Lambda cold dark matter (ΛCDM). Intensive searching for possible candidates has not yielded a discovery (Arcadi et al., 2018), and its 10 years window since 2010, during which various new searches should find it if it exists, has all but closed (Bertone, 2010). Nowadays, the focus is shifting to axions and axion-like-particles (Weinberg, 1978; Wilczek, 1978; Sikivie, 1983), to warm DM (Boyarsky et al., 2014), and to dark photons, see, e.g., (Pignol et al., 2015).

Of the many other approaches we mention theories without a new particle, like Modified Newtonian Dynamics (MOND) (Milgrom, 1983) and entropic (Verlinde, 2011) and emergent gravity (Verlinde, 2017), which leads to related predictions (Brouwer et al., 2017; Nieuwenhuizen, 2017). Here the Newton law is modified for weak acceleration. A definite test of general relativity versus extended theories of gravity has been worked out for gravitational wave observation (Corda, 2009).

The present paradigm, ΛCDM, is quite successful, among others for its widely employed Navarro-Frenk-White (NFW) profile (Navarro et al., 1997). Numerical codes for it are well developed, e.g., (Vogelsberger et al., 2014). Workers in the field have time and again achieved to model apparent “non-ΛCDM” aspects within the theory. However, ΛCDM remains loaded with issues; for reviews of challenges, see, e.g., (Kroupa, 2012; Bull et al., 2016; Bullock and Boylan-Kolchin, 2017; Perivolaropoulos and Skara, 2022).

The dark matter (DM) problem is still an outstanding riddle, but various aspects challenge ΛCDM: absence of dynamical friction in galaxy merging (Kroupa, 2015; Oehm and Kroupa, 2024) and in galactic bars (Roshan et al., 2021); as per MOND, structures in the baryons correspond to structures in the rotation velocity. The Hubble tension expresses the difference between the Hubble constant H₀ ≈ 68 km/s Gpc from the cosmic microwave radiation (Aghanim et al., 2020) versus the 73 km/s Gpc from supernovae in the nearby Universe (Brout et al., 2022). This is not solvable (within ΛCDM) with new physics at low redshift (Keeley and Shafieloo, 2023). Likewise, the Lithium-7 problem expressing a factor $\sim 3$ larger nucleosynthesis prediction than its observed Spite plateau (Spite and Spite, 1982; Coc and Vangioni, 2005; Pitrou et al., 2018), has remained open.

Observation by the James Webb telescope poses further challenges for ΛCDM. Black holes became supermassive early on. The black hole ULAS J1342 + 0928 has a mass of 8 10⁸M_⊙ at redshift z = 7.54 (Bañados et al., 2018). The one of GN-z11, an exceptionally luminous galaxy at z = 10.6, weighs several million solar masses and has accreted at about 5 times the Eddington rate (Maiolino et al., 2024). Early galaxies do not look chaotic but are more mature and heavier than predicted. A set of 12 of quiescent galaxies at redshifts 3 − 4 has masses in the 10¹¹M_⊙ range, comparable to massive galaxies in the local Universe, and are quenched for more than a billion years (Nanayakkara et al., 2024). For redshifts z = 0.5–8, many dwarf galaxies are prolate (van der Wel et al., 2014; Zhang et al., 2019), now termed “bananas” (Pandya et al., 2024). The current record holder is JADES-GS-z13-0, a galaxy with spectroscopically confirmed redshift of 13.2, which we observe as it existed 350 million years after the Big Bang (Curtis-Lake et al., 2023). As to clusters, an overdensity related to a galaxy protocluster is observed already at redshift z = 7.88 (Hashimoto et al., 2023).

These challenges put forward to abandon ΛCDM and start anew.

1.3 A new approach to the problem of dark matter

We propose an approach¹ towards many such riddles without new physics; it will suffice to take a new look at the vacuum of the quantum field theory for the Standard Model of particle physics. Let us consider an analogy with the atmosphere. A “particle” in the atmosphere can be identified with a tornado. Without “particles”, the atmosphere is in its “vacuum” state. But this is not a trivial state: the weather can be gentle or involve winds, rains, storms, …We shall take this notion over to the (quantum) vacuum, a state without matter, but not without energy. Because of Einstein’s relation E = mc², vacuum energy condensed on galaxies has similar (but not identical) gravitational effects as the purported particle dark matter.

Rather than invoking a new particle, we postulate that the zero point energy density of the quantum aether has specific properties: next to being uniform and acting as dark energy, it can be inhomogeneous and flow; it can condense on mass concentrations when assisted by electric fields; locally, it can be positive or negative.

Alternatively, we may view this vacuum as a classical aether (though not the historic fixed aether) with the said properties of its energy. Either way, the cosmological “constant” can slowly vary in space, and in time, while its local value can have either sign. The gradient of the related negative or positive pressure acts as a genuine force density that can counteract, e.g., the electrostatic force density. In this picture, dark energy partly acts, in combination with electrostatics, as the dark matter.

1.4 Nomenclature for the proposed form of dark matter

For our theory of dark matter as a combination of electrostatic energy and zero-point or aether energy, (or “ether of space”, an old term from Sir Oliver Lodge), we have initially employed the term “electro-zero-point energy” (EZPE) (Nieuwenhuizen, 2023b). The drawback is that this refers to a quantum concept, while such a connection is, for now, merely an assumption. A more neutral term is “electro-vacuum energy” (EVE) or “electro-aether energy” EAE. Another one is (the energy density related to) a local cosmological constant (LCC), a term we employed in our earlier work on black holes with a smooth (singularity-free) interior (Nieuwenhuizen, 2023a).

We are thus hampered by traditions for the use the term “vacuum” as energetically either empty or non-empty. Wishing to distinguish the standard vacuum of quantum field theory, we propose to call that “the vacuum”, and use “aether” for the (substance that sustains a) nontrivial vacuum, one with nonzero energy density and/or flow. Henceforward, we will use the acronym EAE.

1.5 Setup

The setup of this paper is as follows. Aspects of zero point energy are discussed in Section 2. The theoretical framework is presented in Section 3. The sizes of various effects are estimated in Section 4. Applications to black holes are discussed in Section 5. The working in galaxies and comparison with MOND is treated in Section 6. Section 7 analyses the application to galaxy clusters. An implementation for cosmology in various epochs is worked out in Section 8. The work closes with a conclusion, a summary and an outlook in Sections 9, 10, 11.

2 The standard model and its zero point energy

The standard model of particle physics (SMPP) is a quantum field theory for the U(1) × SU(2)× SU(3) gauge group with three families of quarks and leptons. Since its conception in the 1960s and 1970s, all its particles have been established, the latest ones being the top quark in 1995 and the Higgs boson in 2012. Like in the decades before, SMPP has been capable to explain all experiments so far, the latest success being to rule out the breaking of lepton universality which was suggested in earlier experiments (Collaboration et al., 2022).

In quantum mechanics there is the notion of zero point energy (ZPE). A harmonic oscillator has a ZPE of $\frac{1}{2}\hslash \omega$, where its oscillation frequency reads $\omega =\sqrt{k/m}$ with k the spring constant and m the mass. With n quanta, it has energy levels $(n+\frac{1}{2})\hslash \omega$. While the energy differences between the levels have clear experimental meaning, the meaning of ZPE is less obvious. Adiabatically changing either k or m, changes the ZPE; the difference has a physical meaning.

A quantum field decomposes in a large set of harmonic oscillators. Their total ZPE is formally a sum of $\pm \frac{1}{2}\hslash {\omega }_{\mathbf{k}}$ (+ for bosons, − for fermions) over the 3d momenta k, a quartically divergent expression. If the momenta are cut off at the Planck scale, there remains a result which is about 123 orders of magnitude² larger than the dark energy density in the present Universe. This enormous mismatch is a ground for unease to connection with ZPE.

The question we put forward is however: Is not there a more prominent role for the ZPE? Have not we, by focussing on the particles and taking the ZPE for granted, been picking out the raisins while overlooking the pudding? Is there room within the standard model to address its deficiencies like the description of the baryon asymmetry, dark matter and the dark energy related to the Universe’s accelerated expansion?

2.1 The essence: the Casimir effect

In 1948 Hendrik Casimir discovered that two parallel conducting plates of area A at distance d have an energy −π²ℏcA/720d³ (Casimir, 1948; Milton, 2003; Balian and Duplantier, 2004). It is generally understood that this energy is gained from the quantum aether when bringing the plates from infinity to distance d. Interpretations of the effect differ, however, since energy can not be localized in electrodynamics and neither in gravitation.

Upon adiabatically moving the plates to a distance d′ < d (or d′ > d), the aether energy changes, so one can say that more aether energy flows out (in). When taking them back to infinity, this energy has to be resupplied as work to readjust the boundary conditions at the surface of the plates: the Casimir effect works as an ideal battery (Nieuwenhuizen, 2023a).

While the Casimir energy for parallel conducting plates is negative, it is positive for a conducting spherical shell, which has a tendency to expand for small and large radii (Boyer, 1968). While the Casimir energy is always positive, a bump in the energy as function of the radius exposes an intermediate regime with tendency to contract (Cetto and De La Peña, 1993).

2.2 Zero point/aether energy in the black hole interior

The assumption that aether energy can behave as a fluid is the corner stone for the present work. It arose recently as sine qua non element in our singularity-free solution for the black hole interior (Nieuwenhuizen, 2021; 2023a). We propose that there is an extended core with a net (positive) charge. In the formation process, binding energy released by dissolving the protons and neutrons into free quarks is partly employed for electrostatic energy. Another part of the binding energy is proposed to be inserted in the quantum aether (without creating particles), which acts as a local cosmological constant (LCC).

The Einstein equations impose that the LCC and the electric field coexist. A change in the charge distribution changes the electric field and imposes a change in the LCC.

2.3 Zero point energy as a physical entity

In the black hole problem, the zero point energy was treated as physical. Let us motivate this. As said, the naive (bare) expression for the energy density of the quantum vacuum is divergent. That a constant can be subtracted from the bare value is compatible with the Callan-Symanzik equation, the renormalization equation in quantum field theory (Peskin and Schroeder, 2018). This allows to define the renormalized aether energy density as the physical energy density. It can be positive, negative or zero.

As for the single harmonic oscillator mentioned above, the aether modes can be deformed which relates to a finite aether energy density, positive or negative. For cosmological applications, no boundaries like Casimir plates or shells are present, but an electric field due to a mismatch of + and − charges may take their role.

In the application to the Casimir effect, to BHs and to the cosmos in the present work, the physical zero point energy does not vanish. In each of these cases, this is due to a physical effect. For the cosmos, we shall assume that ZPE was injected in the aether during the Big Bang, to turn, in the course of time, partly into particles, fields and dark matter.

2.4 Zero point energy as the dark energy

As a first step to give zero point energy a more prominent role, we identify the ZPE density of the quantum fields with the sought cosmic dark energy. In doing so, we follow our teacher Tini Veltman (Veltman, 1975) at the University of Utrecht, who cites Andrei Linde (Linde, 1974) and Joseph Dreitlein (Dreitlein, 1974), and our colleague Sander Bais with coauthor Robert Russell (Bais and Russell, 1975). The idea itself goes back to Yakov Zeldovich (Zel’dovich, 1967; Zel’dovich, 1968). The ZPE density is non-zero, having the “renormalized” (physical) value of 70% of the critical cosmic mass density ρ_c ≃ 9 10⁻³⁰gr/cm³, not the “bare” (unphysical) one which is 123 orders of magnitude too large–but see Section 8.8 for a fresh view.

In making this step, we explain–by default–the dark energy. Its merit is that the case is based on known physics and that we can postulate that the sought dark matter originates as a specific part of the very same ZPE. In Section 8.8 we argue that the present small value of the cosmological constant is a dynamical effect, not due to fine-tuning.

2.5 Electric field as partner in zero point energy condensation

In the plasma of galaxies and clusters, the first actors are the free charges. The electrons, protons and ions occur at high density $\sim 0.01/{\text{cm}}^3$, and in principle compensate each other. Small local mismatches produce an electric field with its negative longitudinal pressure, which has to be compensated by the ZPE in the way prescribed by the Einstein equations. Hereto, we view the ZPE as a dynamical quantity: energy stored in the aether can flow and partly condense on mass concentrations such as black holes, galaxies and clusters. The free charges are not an accidental property; they provide a skeleton to which the ZPE is attached.

Together, the ZPE and the electric field form a scaffold, a large correlated structure, for normal matter. It constitutes our proposal for the dark matter, which gets supported by various arguments.

3 Theoretical framework

3.1 Full Einstein equations

We start in general relativity and express the invariant line element ds² = g_μνdr^μdr^ν in spherical spatial coordinates, r^μ = (t, r, θ, ϕ) with μ = 0, 1, 2, 3, as³ (Nieuwenhuizen, 2021)

$\text{d}{s}^2=-N^2\bar{S}\text{d}{t}^2+\frac{1}{\bar{S}}\text{d}{r}^2-r^2\left(\text{d}{\theta }^2+{\sin }^2\theta \text{d}{\varphi }^2\right),\bar{S}=S-1,(3.1)$

with functions N(r) and S(r) to be specified later. As generalization of the Schwarzschild metric, it is the most general spherically symmetric one, see e.g., Weinberg’s book (Weinberg, 1972). It leads to a diagonal Einstein tensor $G_{\nu }^{\mu }$ with elements

$\begin{array}{l}{G}_0^0=\frac{S+r{S}^{\prime }}{r^2},G_1^1=\frac{S+r{S}^{\prime }}{r^2}+2\frac{N^{\prime }}{N}\frac{S-1}{r},\hfill \\ G_2^2=G_3^3=\frac{2S^{\prime }+r{S}^{″}}{2r}+\frac{N^{\prime }}{N}\frac{2S-2+3r{S}^{\prime }}{2r}+\frac{N^{″}}{N}\left(S-1\right),\hfill \end{array}(3.2)$

where $G_2^2=G_3^3$ due to the spherical symmetry. We express the stress energy tensor $T_{\nu }^{\mu }$ in parameters ρ_λ and ρ_E to be specified later, and parameters ρ_m, $p_r^{\text{m}}$ and $p_{\theta }^{\text{m}}=p_{\varphi }^{\text{m}}=p_{\perp }^{\text{m}}$ connected to normal matter (m), possibly thermal, with, in principle, an anisotropic material pressure,

$\begin{array}{ll}\hfill T_{\nu }^{\mu }& ={\rho }_{\lambda }{\delta }_{\nu }^{\mu }+{\rho }_E{C}_{\nu }^{\mu }+T_{\text{m}\nu }^{\mu },C_{\nu }^{\mu }=\text{diag}\left(\mathrm{1,1},-1,-1\right),\hfill \\ \hfill & T_{\text{m}\nu }^{\mu }=\text{diag}\left({\rho }_{\text{m}},-p_r^{\text{m}},-p_{\perp }^{\text{m}},-p_{\perp }^{\text{m}}\right),\hfill \end{array}(3.3)$

with all coefficients functions of r. They are fixed by the Einstein equations $G_{\nu }^{\mu }=8\pi G{T}_{\nu }^{\mu }$ and may be presented in a mixed way as.

${\bar{\rho }}_{\lambda }=\frac{2S+4r{S}^{\prime }+r^2{S}^{″}}{32\pi G{r}^2}+\frac{3N^{\prime }}{N}\frac{2\bar{S}+r{S}^{\prime }}{32\pi Gr}+\frac{N^{″}}{N}\frac{\bar{S}}{16\pi G},(3.4)$

${\bar{\rho }}_E=\frac{2S-r^2{S}^{″}}{32\pi G{r}^2}+\frac{N^{\prime }}{N}\frac{2\bar{S}-3r{S}^{\prime }}{32\pi Gr}-\frac{N^{″}}{N}\frac{\bar{S}}{16\pi G},(3.5)$

${\bar{\rho }}_{\text{m}}=-\frac{N^{\prime }\bar{S}}{4\pi GrN},(3.6)$

where

${\bar{\rho }}_{\lambda }\equiv {\rho }_{\lambda }-\frac{p_r^{\text{m}}+p_{\perp }^{\text{m}}}{2},{\bar{\rho }}_E\equiv {\rho }_E-\frac{p_r^{\text{m}}-p_{\perp }^{\text{m}}}{2},{\bar{\rho }}_{\text{m}}\equiv {\rho }_{\text{m}}+p_r^{\text{m}}.(3.7)$

In case the matter has an isotropic pressure, these reduce to

${\bar{\rho }}_{\lambda }\equiv {\rho }_{\lambda }-p_{\text{m}},{\bar{\rho }}_E\equiv {\rho }_E,{\bar{\rho }}_{\text{m}}\equiv {\rho }_{\text{m}}+p_{\text{m}}.(3.8)$

When material energy and pressure can be neglected, one simply has ${\bar{\rho }}_{\lambda }={\rho }_{\lambda }$, ${\bar{\rho }}_E={\rho }_E$ and ${\bar{\rho }}_{\text{m}}=0$. It implies that N(r) = 1, which simplifies the analysis.

Combining the above expressions, or by considering the $T_0^0$ component, Eq. 3.4 can be replaced by

${\rho }_{\mathrm{t}\mathrm{o}\mathrm{t}}\equiv {\rho }_{\lambda }+{\rho }_E+{\rho }_{\text{m}}=\frac{S+r{S}^{\prime }}{8\pi G{r}^2}.(3.9)$

This can be integrated to solve S(r) with vanishing value of S(0) as

$S\left(r\right)=\frac{2G{M}_{\mathrm{t}\mathrm{o}\mathrm{t}}\left(r\right)}{r},M_{\mathrm{t}\mathrm{o}\mathrm{t}}\left(r\right)=4\pi {\int }_0^r\text{d}u{u}^2{\rho }_{\mathrm{t}\mathrm{o}\mathrm{t}}\left(u\right).(3.10)$

(The singular behavior ρ_tot(r) ∼ 1/r² for r → 0 leads to a finite S (0) and a still regular metric.) Using (3.6), the function N can be eliminated from (3.5), to yield an equation for S alone,

${\rho }_E=\frac{2S-r^2{S}^{″}}{32\pi G{r}^2}+\frac{r{\bar{\rho }}_{\text{m}}^{\prime }}{4}+\frac{p_r^{\text{m}}-p_{\perp }^{\text{m}}}{2}+\frac{r{\bar{\rho }}_{\text{m}}{S}^{\prime }}{8\bar{S}}-\frac{\pi G{r}^2{\bar{\rho }}_{\text{m}}^2}{\bar{S}}.(3.11)$

The strategy to solve these equations is as follows. The energy densities and pressures of matter and electrostatics are assumed to be known, so that S can be solved from (3.11). It will determine M_tot and ρ_tot via (3.10), next ρ_λ via (3.9); lastly, N can be solved from (3.6). After these steps, ${\bar{\rho }}_{\lambda }$ can just be read off from (3.4); being determined by the electric charge density and normal matter, it is “enslaved”.

From (3.10) we can consider the rotation speed for circular orbits,

$v_{\mathrm{r}\mathrm{o}\mathrm{t}}^2\left(r\right)\equiv \frac{G{M}_{\mathrm{t}\mathrm{o}\mathrm{t}}\left(r\right)}{r}=\frac{1}{2}S\left(r\right),(3.12)$

hence any result for S can be expressed in terms of v_rot or M_tot.

The task simplifies when the energy and pressure (but not the charges) of normal matter can be neglected, so that N(r) = 1. For the application to singularity-free, cored black holes, this yields a class of exact solutions (Nieuwenhuizen, 2021).

3.2 Coulomb electrostatics in electrogravity

We consider a static potential $A_{\mu }={\delta }_{\mu }^0{A}_0(r)$ and define the radial electric field as $E(r)=-A_0^{\prime }(r)/N(r)$. It equals

$E\left(r\right)=\frac{Q\left(r\right)}{r^2},Q\left(r\right)=4\pi {\int }_0^r\text{d}u{u}^2{\rho }_q\left(u\right).(3.13)$

Here Q(r) is the total charge enclosed within radius r, given the charge density ρ_q. Since the metric (3.1) is diagonal, the stress energy tensor keeps its special relativistic form,

$\begin{array}{ll}\hfill & T_{E\nu }^{\mu }={\rho }_E{C}_{\nu }^{\mu },{\rho }_E\left(r\right)=\frac{E^2\left(r\right)}{2{\mu }_0}=\frac{E^2\left(r\right)}{8\pi },\hfill \\ \hfill & C_{\nu }^{\mu }=\text{diag}\left(\mathrm{1,1},-1,-1\right),\hfill \end{array}(3.14)$

as employed in (3.3). T_E is traceless, and involves a positive energy density and transversal pressures, but a negative longitudinal presssure; all equal in magnitude.

3.3 Linearized Einstein equations

For application to galaxies and clusters we can linearize around the vacuum N = 1 and S = 0. Indeed, the observed rotation speeds v_rot are much smaller than the speed of light c = 1, so that $S(r)=2v_{\text{rot}}^2(r)\ll 1$. Eq 3.6 yields

$N\left(r\right)=1-4\pi G{\int }_r^{\infty }\text{d}uu\left[{\rho }_{\text{m}}\left(u\right)+p_{\text{m}}\left(u\right)\right].(3.15)$

In linearized form, Eq. 3.11 reads

$\frac{2S-r^2{S}^{″}}{32\pi G{r}^2}={\rho }_E-\frac{r\left({\rho }_{\text{m}}^{\prime }+p_{\text{m}}^{\prime }\right)}{4}.(3.16)$

The homogenous solutions are S = r² and 1/r. The proper inhomogeneous solution,

$\begin{array}{ll}\hfill M_{\mathrm{t}\mathrm{o}\mathrm{t}}\left(r\right)& =\frac{rS\left(r\right)}{2G}=M_{\mathrm{\Lambda }}+M_{\text{m}}^{\rho }+M_{\text{m}}^p+\frac{4}{3}{M}_E+\frac{4\pi }{3}{r}^3{\rho }_E^{>},\hfill \\ \hfill & {\rho }_E^{>}\left(r\right)\equiv 4{\int }_r^{\infty }\text{d}u\frac{{\rho }_E\left(u\right)}{u},\hfill \end{array}(3.17)$

obeys M_tot (0) = 0 and S(r) ∼ r² at small r. The involved functions are

$\left(M_E,M_{\text{m}}^{\rho },M_{\text{m}}^p\right)=4\pi {\int }_0^r\text{d}u{u}^2\left({\rho }_E,{\rho }_{\text{m}},p_{\text{m}}\right),M_{\mathrm{\Lambda }}=\frac{4\pi }{3}{\rho }_{\mathrm{\Lambda }}{r}^3=\frac{\mathrm{\Lambda }{r}^3}{6G}.(3.18)$

where Λ, the standard cosmological constant, enters as an integration constant. Surprisingly, the last term in (3.17) involves the outer region u ≥ r. (This would be avoided by subtracting its integral from 0 to ∞, which connects to a homogenous solution S ∼ r², but, acting at large r as a huge negative cosmological constant, that is not acceptable.)

Equating (3.17) to the integral of ρ_tot in (3.9), viz. $M_{\mathrm{t}\mathrm{o}\mathrm{t}}=M_{\lambda }+M_E+M_{\text{m}}^{\rho }$, we can identify the LCC component,

$M_{\lambda }\left(r\right)=M_{\mathrm{\Lambda }}\left(r\right)+M_{\text{m}}^p\left(r\right)+\frac{1}{3}{M}_E\left(r\right)+\frac{4\pi }{3}{r}^3{\rho }_E^{>}\left(r\right).(3.19)$

The total excess ZPE $(M_{\lambda }-M_{\mathrm{\Lambda }}){|}_{r\to \infty }=\frac{1}{3}{M}_E(\infty )+M_{\text{m}}^p(\infty )$ is assumed to have flown in from infinity in the dynamics towards this phase. Notice that even without electric field, the aether already supplies the pressure term $M_{\text{m}}^p$, often called a “relativistic correction” to the matter term $M_{\text{m}}^{\rho }$.

The derivatives M_tot and M_λ yield

${\rho }_{\mathrm{t}\mathrm{o}\mathrm{t}}={\rho }_{\mathrm{\Lambda }}+{\rho }_E^{>}+{\rho }_{\text{m}}+p_{\text{m}},{\rho }_{\lambda }={\rho }_{\mathrm{\Lambda }}+{\rho }_E^{>}-{\rho }_E+p_{\text{m}}.(3.20)$

Setting $T_{\nu }^{\mu }=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}({\rho }_{\mathrm{t}\mathrm{o}\mathrm{t}},-p_{\mathrm{t}\mathrm{o}\mathrm{t}}^r,-p_{\mathrm{t}\mathrm{o}\mathrm{t}}^{\theta },-p_{\mathrm{t}\mathrm{o}\mathrm{t}}^{\varphi })$, this collects

$\begin{array}{l}{\rho }_{\mathrm{t}\mathrm{o}\mathrm{t}}={\rho }_{\lambda }+{\rho }_E+{\rho }_{\text{m}},\hfill \\ p_{\mathrm{t}\mathrm{o}\mathrm{t}}^r=-{\rho }_{\lambda }-{\rho }_E+p_{\text{m}},p_{\mathrm{t}\mathrm{o}\mathrm{t}}^{\theta }=p_{\mathrm{t}\mathrm{o}\mathrm{t}}^{\varphi }=p_{\mathrm{t}\mathrm{o}\mathrm{t}}^{\perp }=-{\rho }_{\lambda }+{\rho }_E+p_{\text{m}}.\hfill \end{array}(3.21)$

The total pressure is always anisotropic. After eliminating ρ_λ, the pressures (3.21) read

$p_{\mathrm{t}\mathrm{o}\mathrm{t}}^r=-{\rho }_{\mathrm{\Lambda }}-{\rho }_E^{>},p_{\mathrm{t}\mathrm{o}\mathrm{t}}^{\perp }=-{\rho }_{\mathrm{\Lambda }}-{\rho }_E^{>}+2{\rho }_E.(3.22)$

The cosmological constant ρ_Λ has been included for completeness; for applications to galaxies and clusters it is negligible. Outside a region with matter and a net charge Q, ${\rho }_E={\rho }_E^{>}=Q^2/8\pi r^4$ leads to ρ_λ = ρ_Λ + p_m. For galaxies and clusters, the net included charge will vanish at some radius, which can be identified with their outer border.

3.4 Electro-zero-point energy (electro-aether energy) as the dark matter

We have now arrived at the point to introduce EAE as the combination of the electric field energy and the ZPE in the LCC. In this paradigm we can identify the DM parts as

${\rho }_{\text{dm}}={\rho }_{\lambda }+{\rho }_E-p_{\text{m}}={\rho }_E^{>},M_{\text{dm}}=\frac{4}{3}{M}_E+\frac{4\pi }{3}{r}^3{\rho }_{\text{dm}},(3.23)$

$\begin{array}{ccc}\hfill & \hfill & p_{\text{dm}}^r=-{\rho }_E^{>},p_{\text{dm}}^{\perp }=2{\rho }_E-{\rho }_E^{>},{\rho }_E^{>}=4{\int }_r^{\infty }\text{d}u\frac{{\rho }_E\left(u\right)}{u},\hfill \\ \hfill & \hfill & {\rho }_E=\frac{E^2}{8\pi }.\hfill \end{array}(3.24)$

For small r, the expression for ρ_dm typically leads to a constant value, that is to say, EAE naturally involves constant-density dark matter cores. For empirical support of this, see Section 6.4. Nevertheless, powerlaw behavior S ∼ r²ⁿ at small r with n ≥ 0 is possible, with ρ_λ ∼ ρ_E ∼ r²⁽ⁿ⁻¹⁾ and E ∼ rⁿ⁻¹, ρ_q ∼ rⁿ⁻². The extreme case is n = 0, where S (0) is a constant between 0 and 1.

The build up of a net positive charge inside a central region of a galaxy or galaxy cluster, implies that some electrons must move outwards. Let us introduce a crossover radius by R_co; beyond it, the expelled electrons make up a net negative charge density. The included net charge Q(r) grows up to R_co but decays beyond it, making ρ_E = Q²/8πr⁴ decay quicker than 1/r⁴ at moderately large r. The radial size of the galaxy (cluster) R_g can be defined as the radius where Q(r) → 0; due to the large strength of electrostatics, this is a sharp boundary.

Approximating v²(r) here by GM_dm(r)/r (dark matter only) and denoting v²(r) = v₂(t) and Q²(r) = r²q₂(t)/4G with $t=\log \left(r/\right.$kpc), it follows that

$2q_2+{\dot{q}}_2=4v_2+4{\dot{v}}_2-{\ddot{v}}_2-{\stackrel{⃛}{v}}_2.(3.25)$

The crossover radius where Q′(R_co) = 0, now set by the condition $2q_2+{\dot{q}}_2=0$, is related to the rotation curve. In integral form Eq. 3.25 reads

$q_2=2v_2+{\dot{v}}_2-{\ddot{v}}_2.(3.26)$

These relations, extended to include normal matter, offer a test between the electric charge (and field) profile and the rotation curve.

3.5 A toy galaxy

Let us consider a toy galaxy, upon neglecting ρ_Λ, ρ_m and p_m. It has normalized radius R_g = 1 and normalized net charge density,

${\rho }_q\left(r\right)=\left(1-r\right)\left(3-5r\right),\left(0<r<1\right);{\rho }_q=0,\left(r>1\right),(3.27)$

which is positive for $0<r<R_{\mathrm{c}\mathrm{o}}=\frac{3}{5}$ and negative up to R_g. The included electric charge and energy density are

$Q\left(r\right)=4\pi r^3{\left(1-r\right)}^2,{\rho }_E=2\pi r^2{\left(1-r\right)}^4,(3.28)$

with Q (R_co) = 432π/3125 = 0.4343. The total charge vanishes, Q (1) = 0. Eq. 3.23 yields

$\begin{array}{ll}\hfill {\rho }_{\lambda }& =\frac{2\pi }{15}{\left(1-r\right)}^4\left(2+8r-25r^2\right),{\rho }_{\text{dm}}=\frac{4\pi }{15}{\left(1-r\right)}^5\left(1+5r\right),\hfill \\ \hfill & p_{\text{dm}}^r=-\frac{4\pi }{15}{\left(1-r\right)}^5\left(1+5r\right),p_{\text{dm}}^{\perp }=-\frac{4\pi }{15}{\left(1-r\right)}^4\left(1+4r-20r^2\right).\hfill \end{array}(3.29)$

While ρ_dm is strictly positive and $p_{\text{dm}}^r$ strictly negative, ρ_λ is positive up to r₀ = 0.4849 and then negative beyond. Notice that r₀ < R_co = 0.6. Conversely, $p_{\text{dm}}^{\perp }$ is negative up to r = 0.3449 and positive beyond. The profiles (3.29) vanish at R_g = 1. They are plotted in Figure 1. That ρ_λ has generally a negative tail follows from Eq. 3.20 near R_g, where ρ_E vanishes.

Figure 1

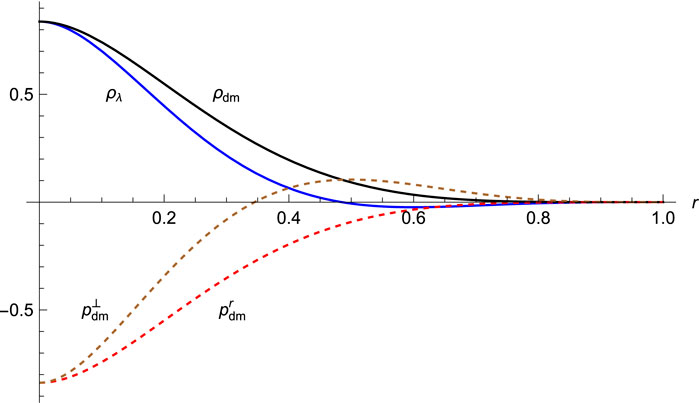
Figure 1. The local cosmological constant ρ_λ starts with positive value but has a negative tail, as shown here for a toy galaxy with charge distribution (3.27). While ρ_dm is strictly positive and $p_{\text{dm}}^r$ strictly negative, $p_{\text{dm}}^{\perp }$ starts out negatively and has a positive tail.

The accumulated zero point energy,

$M_{\lambda }\left(r\right)=\frac{8{\pi }^2}{15}\left(\frac{2r^3}{3}-9r^5+\frac{70r^6}{3}-\frac{180r^7}{7}+\frac{27r^8}{2}-\frac{25r^9}{9}\right),(3.30)$

has total M_λ ≡ M_λ(1) = 4π²/945 = 0.04177. Its positive density part between 0 and r₀ contains M_λ(r₀) = 1.652M_λ, while the tail between r₀ and 1 has value −0.652M_λ. With respect to M_λ, the ZPE imported from remote surroundings, this exhibits an additional 65.2% taken out of the vacuum in the outer region r₀ < r < 1, and transferred to the inner region r < r₀. With vanishing net total charge, Q(r) = 0 for r ≥ R_g, the total electrostatic energy $M_E=4\pi {\int }_0^1\text{d}r{r}^2{\rho }_E(r)$ equals 3M_λ.

These properties reflect our main assumption: zero point (vacuum) energy can be taken out or put into the (quantum) aether, at amounts governed by the Einstein equations.

3.6 The matter components

In a galaxy there is normal matter such as stars, planets, free floating planets, hydrogen gas clouds, and a plasma of protons, ions and electrons.

In a galaxy cluster, of all the galaxies, only the brightest cluster galaxy (bcg), located in the center and often the brightest X-ray source in the cluster, brings a relevant contribution to the enclosed mass M_tot(r); it can be described by its mass density ρ_bcg(r). This galaxy will also contain dark matter, which is a part of ρ_dm. Our fit profile ρ_bcg in Section 7.1 combines normal and dark matter; as of now, there are no data for the separate parts. For simplicity of notation, we shall nevertheless write

${\rho }_{\text{m}}={\rho }_{\mathrm{b}\mathrm{c}\mathrm{g}}+{\rho }_g,p_{\text{m}}=p_g,(3.31)$

where ρ_g and p_g describe the X-ray gas, see Eq. 3.32 below.

3.7 The X-ray gas

Free electrons, accompanied by protons and ions, occur in galaxies and clusters. The mass density ${\rho }_g=n_e{\bar{m}}_N$ involves the local free electron density n_e and the average molecular weight ${\bar{m}}_N\approx (7/6)m_N$ with m_N the nuclear weight (Morandi et al., 2010). The pressure is p_g = n_eT, where the typical scale of T(r) is several keV. So the X-ray gas involves

${\rho }_g\left(r\right)=n_e\left(r\right){\bar{m}}_N,p_g\left(r\right)=n_e\left(r\right)T\left(r\right).(3.32)$

With T in the keV regime, the gas is hot but the protons and nuclei are nonrelativistic, with p_g/ρ_g ∼ T/m_N ≲ 0.01.

In the EAE approach the X-ray plasma is indispensable, since by setting up a small charge mismatch (estimated in sec. 4.1), it creates the electric field that combines with ZPE as “dark matter”. Turned around, in this paradigm the presence of DM requires the presence of a net charge density and hence a (partial or full) plasma.

3.8 Hydrostatic equilibrium

For a fluid element in equilibrium, the balance of forces is expressed by hydrostatic equilibrium. Expressed by the energy conservation $T_{\nu ;\mu }^{\mu }=0$, this is automatically satisfied for a bona fide solution of the Einstein equations, since $G_{\nu ;\mu }^{\mu }=0$ by construction. For the stress energy tensor (3.3) in the metric (3.1) this leads to the exact force balance

$p_{\text{m}}^{\prime }+p_{\lambda }^{\prime }={\mathcal{F}}_E+{\mathcal{F}}_G\text{or}{\mathcal{F}}_{\text{m}}+{\mathcal{F}}_{\lambda }+{\mathcal{F}}_E+{\mathcal{F}}_G=0,(3.33)$

where we employed the cosmological pressure p_λ = −ρ_λ. In exact form, the respective force densities read, using ρ_E = E²/8π, E = Q(r)/r² and Q′ = 4πr²ρ_q(r),

$\begin{array}{ll}\hfill {\mathcal{F}}_{\text{m}}& =-p_{\text{m}}^{\prime },{\mathcal{F}}_{\lambda }=-p_{\lambda }^{\prime }={\rho }_{\lambda }^{\prime },{\mathcal{F}}_E={\rho }_E^{\prime }+4\frac{{\rho }_E}{r}=\frac{Q^{\prime }Q}{4\pi r^4}={\rho }_q\left(r\right)E\left(r\right),\hfill \\ \hfill & {\mathcal{F}}_G=-{\bar{\rho }}_{\mathrm{m}}\left(\frac{S^{\prime }}{2\bar{S}}+\frac{N^{\prime }}{N}\right)=-\frac{G}{r^2}\left({\rho }_{\mathrm{m}}+p_{\mathrm{m}}\right)\frac{M_{\mathrm{t}\mathrm{o}\mathrm{t}}-4\pi r^3\left({\rho }_{\lambda }+{\rho }_E-p_{\text{m}}\right)}{1-2G{M}_{\mathrm{t}\mathrm{o}\mathrm{t}}/r}.\hfill \end{array}(3.34)$

Here ${\mathcal{F}}_E={\rho }_{q}E$ is the Coulomb force on a unit volume with charge density ρ_q in an electric field E. Eq. 3.20 allows to replace the combination ρ_λ + ρ_E − p_m in ${\mathcal{F}}_G$ by ${\rho }_{\mathrm{\Lambda }}+{\rho }_E^{>}$.

In EAE, the leading terms are ${\mathcal{F}}_{\lambda }$ and ${\mathcal{F}}_E$; neglecting ${\mathcal{F}}_G$, one recognizes the derivative of ρ_λ in Eq. 3.20 as the solution for hydrostatic equilibrium. The exact approach adds the nonlinear, Newtonian ${\mathcal{F}}_G$ term, which is small, see Section. 4.4. Integrating (3.33) from r to ∞ yields the full nonlinear correction to ρ_λ; it becomes a self-consistent relation, since ρ_λ enters ρ_tot through Eq. 3.20, and hence through M_tot.

The fact that ${\mathcal{F}}_G$ contributes to ${\rho }_{\lambda }^{\prime }$, exhibits the malleability (enslavement) of the ZPE/AE, doing just the right thing in the situation at hand.

4 Physical estimates

4.1 Charge mismatch in the plasma

For the rotation speed v² = GM/r, Eq. 3.17 estimates the electric field as E ∼ v/cℓ_Pr. In the galaxy clusters A1689 and A1835, the free electron density in the center is of order n_e (0) = 0.05 − 0.09/cm³ (Nieuwenhuizen et al., 2021). The density n_p of plus charges (protons, ions) is very close to this. Equating E to e (n_p − n_e)r yields the relative mismatch δ_q ≡ (n_p − n_e)/(n_p + n_e) ∼ v/cen_eℓ_Pr² ∼ 6 10⁻¹⁵ for v = 1000 km/s and typical scale r = 100 kpc.

In our Galaxy near the Sun n_e ∼ 0.02/cm³ leads for r = 10 kpc and v = 200 km/s to δ_q ∼ 10^–13. In 2013, the Voyager-1 spacecraft observed electron plasma oscillations corresponding to an electron density n_e = 0.08/cm³, very close to the value expected in the interstellar medium and confirming the order of magnitude (Gurnett et al., 2013). The measured electric field of about 1 μV/m at kHz frequencies does not refer to a static field.

These tiny mismatches express that the plasma is not completely neutral, but slightly charged. The electric field is an average of spatially and temporally fluctuating E fields with their related B fields caused by the relatively high density of moving protons, ions and electrons. Since they are so light, it is easier to push out electrons than protons and ions; hence we assume that the inner galaxy is positively charged, and the outskirts negatively, separated by a crossover radius R_co. Due to the strength of the Coulomb force, a galaxy has a sharp boundary R_b, where the included charges cancel each other.

In reverse, the locally available amount of ZPE sets the size of the static E field. Such a correlation can be searched for via the determination of the dark matter, also in the intragalactic medium.

4.2 Galactic electric field

The possibility of a galactic electric field has been considered in the literature. Ref. (Reucroft, 2014) estimates from rotation curves a field of 1 V/m at the solar location. To keep most electrons in the stellar interior, ref. (Chakraborty et al., 2014) estimates a center-to-surface potential difference of 1000 V; giant galaxies to have a similar potential difference, and rich clusters ∼10 kV.

In our approach, the electric field joins the ZPE to make up the EAE. The DM density in the solar neighborhood is ${\rho }_{\text{dm}}^{\odot }=0.35_{-0.07}^{+0.08}$ GeV/${\mathrm{c}\mathrm{m}}^3=6.2_{-1.2}^{+1.4}10^{-25}\mathrm{g}\mathrm{r}/{\text{cm}}^3$ (Kafle et al., 2014). A recent, sharper estimate is ${\rho }_{\text{dm}}^{\odot }=0.447_{-0.004}^{+0.004}$ GeV/${\mathrm{c}\mathrm{m}}^3=7.96_{-0.07}^{+0.07}10^{-25}\mathrm{g}\mathrm{r}/{\text{cm}}^3$ (Ou et al., 2024). The total mass density (0.097 ± 0.013)M_⊙/pc³ = (6.6 ± 0.9)10⁻²⁴gr/cm³ is about 8 times larger. From Eq 3.23 we estimate that maximally

${\rho }_{\text{dm}}^{\odot }=4{\int }_r^{\infty }\text{d}u\frac{{\rho }_E\left(u\right)}{u}\approx 4{\rho }_E^{\odot }\log \frac{R_c}{r}\approx 10{\rho }_E^{\odot },(4.1)$

for R_c = 100 kpc and r = 8.1 kpc. Thus taking 10% of the DM density as electrostatic energy E²/8π leads to a local field E_⊙ = 0.042 statV/cm = 1.3 kV/m. It is likely shielded by the ionosphere. Notice that the Earth electric field is about 0.1 kV/m under fair weather conditions (Rycroft et al., 2000).

In Section 7.2.2; Figure 5 we predict similar electric fields of $\sim 1.5$ kV/m and 0.5 kV/m in the central $\sim 500$ kpc of the galaxy clusters A1689 and A1835, respectively.

4.3 Seeding of galactic magnetic fields

Large scale, quasi static magnetic fields abound in the cosmos and play an important role in the evolution of galaxies, but their origin is still debated (Beck et al., 2013). In EAE theory, the formation of a dark matter core is a dynamical effect with a slowly varying electric field, which, according to Maxwell law ${\epsilon }_0\dot{\mathbf{E}}=\nabla \times \mathbf{H}$, generates cosmic magnetic fields. In the local Galaxy and in the fat clusters A1689 and A1835 we predict electric fields in the 1 kV/m range, which corresponds in strength to a magnetic field of 0.029979 G, while observed magnetic fields lie typically in the 1-10 μG regime.

As to orders of magnitude, Maxwell’s law yields the estimate B ∼ LE/ct. For the Galaxy, E ∼ 1 kV/m, L ∼ 100 kpc and t ∼ 10 Gyr imply B ∼ 1 μG, and for clusters with L ∼ 1 Mpc it yields B ∼ 10 μG. As these rough estimates produce the right order of magnitude, this connection deserves a detailed analysis.

4.4 Implementation of hydrostatic stability

The net-charge ratio δ_q ∼ 10^–13 − 10^–14 needed in the EAE approach is actually relatively large and unexpected. A standard argument is to consider a sphere with mass M = Nm_N and charge Q = δ_qNe. In principle, the ratio of Coulomb and Newton forces at the surface, $Q^2/G{M}^2={(Q{m}_P/M)}^2$, can not exceed unity, which occurs for δ_q = m_N/2em_P = 0.5 10⁻¹⁸, quite smaller than the above estimates. Including dark matter by setting M ≈ 2Nm_N only alleviates this to 10^–18. While a huge charged cosmic object seems unrealistic, in the standard Einstein-Maxwell theory there cannot be a stable shell with negative charge density around a positively charged core, as it would add to rather than compensate the Newton attraction. Nevertheless, the typical value of only δ_q ∼ 10^–18 looks problematic for EAE theory, so let us analyze the situation.

In the EAE setting, the galaxy or cluster has a large core with net positive charge density, surrounded by a halo of negative net charge density. As a whole, it is not charged. One may define the boundary of a galaxy or cluster R_b as the radius where Q (R_b) = 0.

In the interior r < R_b, our starting point is Eq. 3.33, the hydrostatic equilibrium condition for the balance of forces acting on a fluid element. In terms of the local cosmological pressure p_λ = −ρ_λ, this takes to leading order the form

$\begin{array}{ll}\hfill & p_{\mathrm{m}}^{\prime }+p_{\lambda }^{\prime }={\mathcal{F}}_E+{\mathcal{F}}_G,{\mathcal{F}}_E={\rho }_E^{\prime }+4\frac{{\rho }_E}{r}=E{\rho }_q,\hfill \\ \hfill & {\mathcal{F}}_G\approx -G\left({\rho }_{\mathrm{m}}+p_{\mathrm{m}}\right)\frac{M_{\mathrm{t}\mathrm{o}\mathrm{t}}}{r^2}.\hfill \end{array}(4.2)$

In absence of ρ_E and $p_{\lambda }^{\prime }$ as in ΛCDM, the pressure must decay in such a way that ${\mathcal{F}}_G$, the Newton attraction per unit volume, is balanced. But notice that, according to (3.31), ρ_m = ρ_bcg + ρ_g includes both the gas and the normal matter mass densities. As we discuss in Section 7.2, this approach does not work out properly in clusters.

In EAE, the finite ${\mathcal{F}}_E=E{\rho }_q$ is the local Coulomb force density, involving a positive E = Q(r)/r² and a ρ_q that is positive for r < R_co and negative for r > R_co.

We can estimate ${\mathcal{F}}_G/{\mathcal{F}}_E$ as (ρ_m/ρ_E) (GM_tot/r) ≲ (GM_tot/r) ∼ 10^–7 for a galaxy with M_tot = 10¹¹M_⊙ and r = 100 kpc, and $\sim 510^{-5}$ for a fat cluster with M_tot = 10¹⁵M_⊙ and r = 1 Mpc. These values play the role of the above factor ${(m_N/{\delta }_{q}e{m}_P)}^2$, showing that δ_q is relatively large, and ${\mathcal{F}}_G$ relatively small, in the presence of EAE. Clearly, in Eq. 4.2 the combination $p_{\mathrm{m}}^{\prime }+p_{\lambda }^{\prime }$ should be balanced, not $p_{\text{m}}^{\prime }$ alone. Because $p_{\text{m}}^{\prime }\sim {\mathcal{F}}_G$ can even be neglected, the balance is in essence $p_{\lambda }^{\prime }={\mathcal{F}}_E$, obeyed grace to Eq. 3.20.

In conclusion, the above Newtonian argument fails, since it overlooks the stress (pressure) related to a positive (negative) aether energy density. On a fluid element of EAE, the strong Coulomb force (repulsive for r < R_co and attractive for r > R_co) is balanced by an equally strong (inward c. q. outward) force from the zero-point/aether pressure gradient. As a result, galaxies and clusters with charge ratios δ_q well exceeding 10^–18 are allowed in EAE.

4.5 Metastability vs. instability

Hydrostatic equilibrium for patches of matter describes stability at the macroscopic scale, but it does not automatically imply equilibrium at the microscopic scale. Indeed, an individual ion is affected by the strong outward Coulomb force but not know to involve a restoring force from the cosmological pressure, and neither an effect of the outer shell of negative charges. Likewise, an electron is strongly attracted inwards, the ones moving from r > R_co to r < R_co will lessen the charge mismatch. While for a reshuffling of the charge distribution, an accompanying reshuffling of the ZPE is required, an inherently unstable situation may remain.

This observation suggests that EAE cores are unstable, which in principle demonstrates the failure of the theory. But the involved timescales need not coincide, and may be cosmological, so that metastable cores on Gyr timescales are compatible with EAE.

We estimate the effects by connecting to observations. While galaxies and clusters clearly exist with dark matter supposedly arising from EAE theory, there are also indications for their subsequent dissolution. For galaxies these are discussed in Section 6.5.

5 Electro-aether-energy in black holes

5.1 Black hole metrics with a macroscopic core

The present work was inspired by our solutions for black holes (BHs) with a smooth core enclosed by the inner horizon and an empty mantle up to the event horizon. Assuming that in the stellar collapse a bit more electrons than protons were ejected, the core-collapsed BH will be positively charged. The protons may dissolve into up and down quarks, thereby releasing their binding energy, 98% of their mass. Upon neglecting the quark and electron masses, analytical solutions were presented based on what we now call EAE theory. The stress energy tensor takes the form

$T_{\nu }^{\mu }\left(r\right)={\rho }_{\lambda }\left(r\right){\delta }_{\nu }^{\mu }+{\rho }_E\left(r\right)C_{\nu }^{\mu }.(5.1)$

Given the charge distribution and hence ρ_E, a class of exact solutions of the Einstein Eq 3.5, viz. 2S − r²S^″ = 32πGr²ρ_E, was presented, after which the LCC (ZPE density) ρ_λ follows from (3.4), ρ_λ = (2S + 4rS′ + r²S^″)/32πGr², under the condition that it matches the trivial aether ρ_λ = 0 at the inner horizon. Special cases were worked out, and it was found that always $M_{\lambda }=\frac{1}{4}M$, $M_E=3M_{\lambda }=\frac{3}{4}M$. Next, accounting for quark and electron masses was carried out in a numerical analysis. It was also found that the fluctuation spectrum has oscillating modes, but no growing (unstable) ones.

Notice that with ${\rho }_{\mathrm{t}\mathrm{o}\mathrm{t}}=-p_{\mathrm{t}\mathrm{o}\mathrm{t}}^r={\rho }_{\lambda }+{\rho }_E$ the first law of thermodynamics is locally satisfied in the form $\text{d}U(r)\equiv {\rho }_{\mathrm{t}\mathrm{o}\mathrm{t}}(r)\text{d}V=-p_{\mathrm{t}\mathrm{o}\mathrm{t}}^r(r)\text{d}V$ with dV = 4πr²dr, confirming that neither a temperature nor a chemical potential is connected to EAE.

5.2 Super-Eddington accretion by aether energy inflow

Black holes grow by mass accretion. It falls firstly on the accretion disk, and from there into the back hole or get spit out in the jets. Elsewhere, we show that black holes can also become more massive by inflow of aether energy. Here neither an accretion disk nor angular momentum plays a role. But there is a caveat. In the limit where the energy density (but not the charge density) of the normal matter can be neglected, we have presented a class of exact solutions. They involve a charge distribution with a net charge with charge-to-mass ratio $Q/M\sqrt{G}\ge \frac{1}{2}\sqrt{3}$. When aether energy is absorbed, without additional charges, this limit will be reached. Further mass increase needs charge increase, which can come from the surroundings. This hints at a common growth of the supermassive black hole and the galaxy. Such has been detected. It is known as the M-σ relation.

The largest known black hole mass, 66 10⁹M_⊙ for Ton 618, is likely determined by super-Eddington accretion assisted by or even dominated by EAE absorption.

Recent observations support BH growth related to ZPE/AE. Ref. (Farrah et al., 2023b) reports statistics on hundreds of elliptical galaxies in three redshift bins in the domain 0 < z ≲ 2.5, showing that the supermassive BHs in massive, red-sequence elliptical galaxies must have grown in mass by a factor of seven from z ∼ 1 to z = 0, and a factor of 20 from z ∼ 2 to z = 0.

GN-z11 is an exceptionally luminous galaxy at redshift z = 10.6. Its spectral features indicate that GN-z11 hosts an accreting black hole. The assumption of local virial relations leads to a black hole mass of log₁₀ (M_BH/M_⊙) = 6.2 ± 0.3, which amounts to accretion at about 5 times the Eddington rate (Maiolino et al., 2024).

Both the existence of early black holes, even primordial ones (see later sections), with their super-Eddington accretion, is a central tenet of EAE theory.

5.3 The final parsec problem under EAE accretion

For two widely separated black holes to become bound and finally merge, potential energy must be lost. This can occur by dynamical friction, whereby kinetic energy is transferred to nearby matter. For example, a bypassing star can get a slingshot in which it gains kinetic energy and the BH pair becomes more bound. When the pair has a separation of a few parsecs, there is not enough matter to effectively continue this process, while gravitational radiation becomes relevant only at distances of 0.001–0.01 pc. This is called the final parsec problem (Milosavljević and Merritt, 2003). Various ways out have been proposed, including merging with help of further stars or a third BH. Also disk accretion during the merger of supermassive black hole binaries in galactic nuclei works for them (Armitage and Natarajan, 2002).

In the EAE paradigm, merging happens in a galaxy with a dark-matter core, which gets continuously filled up while being depleted by the BHs. For a BH pair this feeding increases both masses and also diminishes their distance, as we now discuss by a standard analysis.

For a two body problem, like a BH pair, the kinetic and potential energies are

$K=\frac{1}{2}{m}_1{\dot{\mathbf{r}}}_1^2+\frac{1}{2}{m}_2{\dot{\mathbf{r}}}_2^2,V=-G\frac{m_1{m}_2}{r}.(5.2)$

When m_1,2 depend on time, this reads in terms of the mutual position r = r₁ − r₂ and the barycentre R = (m₁r₁ + m₂r₂)/(m₁ + m₂) as

$K=\frac{1}{2}M{\left(\dot{\mathbf{R}}-\frac{{\dot{m}}_1{m}_2-m_1{\dot{m}}_2}{{\left(m_1+m_2\right)}^2}\mathbf{r}\right)}^2+\frac{1}{2}\mu {\dot{\mathbf{r}}}^2,(5.3)$

with, as usual, the total and reduced masses

$M=m_1+m_2,\mu =\frac{m_1{m}_2}{m_1+m_2}.(5.4)$

The center of mass motion involves the conserved momentum

$\mathbf{P}\left(t\right)\equiv M\left(\dot{\mathbf{R}}-\frac{m_2{\dot{m}}_1-m_1{\dot{m}}_2}{{\left(m_1+m_2\right)}^2}\mathbf{r}\right)={\mathbf{P}}_i,(5.5)$

so that the centre-of-mass energy ${\mathbf{P}}_i^2/2M$ decreases on mass inccrease. In the frame where P_i = 0, the energy reads as for constant masses,

$E=K+V=\frac{1}{2}\mu {\dot{\mathbf{r}}}^2-G\frac{m_1{m}_2}{r}=\frac{1}{2\mu }{\mathbf{p}}^2-G\frac{\mu M}{r},\mathbf{p}=\mu \dot{\mathbf{r}},(5.6)$

which leads to a $\dot{\mu }$ term in the equation of motion

$\frac{\text{d}}{\text{d}t}\mathbf{p}=\mu \ddot{\mathbf{r}}+\dot{\mu }\dot{\mathbf{r}}=-G\frac{\mu M}{r^3}\mathbf{r},(5.7)$

For the time-dependent masses, it results in the rate of change of energy

$\dot{E}=-\frac{\dot{\mu }}{\mu }K+\left(\frac{\dot{\mu }}{\mu }+\frac{\dot{M}}{M}\right)V,(5.8)$

with a minus sign in the kinetic term. As expected, only derivatives of the masses, not of the orbit, occur. The angular momentum in the rest frame

$\mathbf{L}\left(t\right)=\mathbf{r}\times \mathbf{p}=\mu \mathbf{r}\times \dot{\mathbf{r}}={\mathbf{L}}_i,(5.9)$

is conserved due to (5.7).

If m_1,2 change negligibly during one period, circular orbits involve K = −E, V = 2E, leading to $\dot{E}/E=3\dot{\mu }/\mu +2\dot{M}/M$. Integration from t_i to t_f and E = −GμM/2r yields

$\frac{E_f}{E_i}=\frac{{\mu }_f^3{M}_f^2}{{\mu }_i^2{M}_i^2}=\frac{{\mu }_f{m}_{1f}^2{m}_{2f}^2}{{\mu }_i{m}_{1i}^2{m}_{2i}^2},r_f=\frac{{\mu }_i{m}_{1i}{m}_{2i}}{{\mu }_f{m}_{1f}{m}_{2f}}{r}_i,(5.10)$

with i denoting initial and f final values, showing tighter binding upon mass accretion, $r_f\sim 1/m_f^3$. For Kepler orbits, the relations for E_f/E_i holds due to the virial theorem ⟨K⟩ = −E, ⟨V⟩ = 2E. Since the ellipticity parameter $\epsilon ={(1+2E{L}^2/G^2{\mu }^3{M}^2)}^{1/2}$ is nearly conserved, the relation between r_f and r_i still holds for the epicentre and the apocentre.

For m₁ = m₂ = m one has μ = m/2. Merging can be estimated to happen at the Schwartzschild value r_f = 2Gm_f. This leads to a final mass $m_f=m_i{(r_i/2G{m}_i)}^{1/4}$. In terms of $m_i={\bar{m}}_i{M}_{\odot }$ and $r_i={\bar{r}}_i$ kpc, this reads $m_f=10^4{({\bar{m}}_i^3{\bar{r}}_i)}^{1/4}{M}_{\odot }$, an appreciable mass gain from the aether. Relativistic corrections and gravitational radiation may bring corrections of order unity.

6 Electro-aether-energy in galaxies

6.1 Relation to MOND

Observations by Vera Rubin and Kent Ford in the seventies demonstrated that in the outer part of galaxies, circular orbits have nearly the same rotation speed (Rubin and Ford, 1970), constituting “flat rotation curves”. To explain this, Modified Newtonian Dynamics (MOND) was introduced by Milgrom in 1983 (Milgrom, 1983). It assumes that the Newton force decays as 1/r at large r, which can be expressed as an effective enclosed mass behaving as M(r) ∼ r. For recent reviews, see (Lelli et al., 2017; Banik and Zhao, 2022).

For a proper amount of EAE, our approach can explain the MOND results. Let the ρ_E profile take the form of an isothermal sphere, E²(r) = v²/Gr². This leads to ρ_λ ≈ ρ_E and GM/r ≈ v², so that v(r) = v exhibits the flat rotation curve. The acceleration g consists of the Newton term g_N = GM_b(r)/r² of the baryons (stars and hydrogen clouds) enclosed within r, and the DM term; they combine essentially as (Banik and Zhao, 2022)

$g=\mathrm{m}\mathrm{a}\mathrm{x}\left(g_N,\sqrt{g_N{a}_0}\right),a_0=\frac{v^4}{G{M}_b}.(6.1)$

(The true MOND relation g = g_N f (g_N/a₀), with $f(x)=\sqrt{x}$ at small x and f = 1 at large x, employed in applications is more rich than this form (Milgrom, 1983; Lelli et al., 2017; Banik and Zhao, 2022).) It was supposed that a₀ ∼ 1.2 10⁻¹⁰ m/s² is universal; empirical values fluctuate around this (Rodrigues et al., 2018), but confirm the baryonic Tully-Fisher relation M_b ∼ v⁴.

In our EAE approach, the amount of DM in a galaxy depends on its history, and there is no universal a₀. The next subsection discusses that constant-density cores are favored in EAE, and next we discuss various empirical evidence for that.

Renzo’s rule states that “for any feature in the luminosity profile” (due to stars, X ray gas or hydrogen clouds) “there is a corresponding feature” (a bump, a dip) “in the rotation curve and vice versa” (Sancisi, 2004). The EAE approach offers a mechanism for this: extra structures in the electric field of extra mass structures. However, data for the electric field is needed to give EAE predictive power. Presently, this is not available.

While MOND suffers from its conflict with wide binaries (Banik et al., 2024), EAE is just Einsteinian/Newtonian in this regime.

6.2 Stability analysis

The stability of the theory needs to be considered. Following ref. (Nieuwenhuizen, 2023a), we consider a perturbation of the electrostatic potential and of the accumulated charge,

$\begin{array}{ll}\hfill & \delta A_0\left(r,t\right)=\epsilon a_0\left(r\right)e^{-i\omega t},a_0^{\prime }\left(r\right)=-j\left(r\right)E\left(r\right),\hfill \\ \hfill & \delta Q\left(r,t\right)=\epsilon j\left(r\right)Q\left(r\right)e^{-i\omega t},\hfill \end{array}(6.2)$

with 0 < ɛ ≪ 1 and yet unspecified profiles j(r), while we again neglect the matter density, but not the charge density, keeping N(r) = 1. This induces radial fluctuations of the metric, δg_μμ(t, r) = 2ɛg_μμ(r)h_μ(r)e^−iωt with h₃ = h₂ for spherical symmetry. The Coulomb energy density picks up metric fluctuations,

$\delta {\rho }_E\left(r,t\right)=\epsilon {\rho }_E^{(1)}\left(r\right)e^{-i\omega t},{{\rho }_E}^{(1)}=2\frac{j\left(r\right)-h_0\left(r\right)-h_1\left(r\right)}{N^2\left(r\right)}{\rho }_E\left(r\right)(6.3)$

The remaining Einstein equations correspond to perturbations in the coefficients of (3.3),

$\begin{array}{ll}\hfill & T_{\nu }^{\mu }=\left({\bar{\rho }}_{\lambda }+\delta {\bar{\rho }}_{\lambda }\right){\delta }_{\nu }^{\mu }+\left({\rho }_E+\delta {\rho }_E\right)C_{\nu }^{\mu }+\left({\sigma }_{\text{m}}+\delta {\sigma }_{\text{m}}\right)U^{\mu }{U}_{\nu },\hfill \\ \hfill & \delta {\bar{\rho }}_{\lambda }=\epsilon {\rho }_{\lambda }^{(1)}\left(r\right)e^{-i\omega t},\hfill \end{array}(6.4)$

where $U^{\mu }={\delta }_0^{\mu }/\sqrt{g_{00}}$ with $U_{\nu }=g_{0\nu }/\sqrt{g_{00}}$ is the time-like unit vector. A first effect is the appearance of elements $G_1^0\sim G_0^1\sim \omega$, which must vanish since there is no energy current. (While the radial electric field is enhanced by a radial charge current, viz. $\dot{\mathbf{E}}=-{\mathbf{J}}_q$, this does not generate a magnetic field.) This imposes

$h_1=r{h}_2^{\prime }+h_2-h_2\frac{r{S}^{\prime }}{2\bar{S}},\left(\omega \ne 0\right),(6.5)$

a relation best employed only near the end of the analysis. The remaining Einstein equations correspond to the first order perturbations in the coefficients of (3.3),

$\delta {\rho }_{\lambda }=\epsilon {\rho }_{\lambda }^{(1)}\left(r\right)e^{-i\omega t},\delta {\rho }_E=\epsilon {{\rho }_E}^{(1)}\left(r\right)e^{-i\omega t}.(6.6)$

Since the baryons make up a minor part of the energy, we first omit their mass and pressure, neglecting σ_m and δσ_m, but keeping their net charge distribution. This sets N(r) = 1. One can eliminate h₀(r) in favor of a nucleus h(r),

$h=h_0+h_1-h_2-r{h}_2^{\prime },(6.7)$

after which the h_i functions follow as

$h_0=h-\frac{\bar{S}{S}^{\prime }}{2{\omega }^2}{h}^{\prime },h_1=-\frac{3\bar{S}{S}^{\prime }}{2{\omega }^2}{h}^{\prime }-\frac{{\bar{S}}^2}{{\omega }^2}{h}^{″},h_2=-\frac{{\bar{S}}^2}{{\omega }^{2}r}{h}^{\prime }.(6.8)$

This finally leads to an equation for h sourced by j,

${\bar{S}}^2{h}^{″}+2\bar{S}{S}^{\prime }{h}^{\prime }+\frac{E^{\prime }}{E}{\bar{S}}^2{h}^{\prime }-{\omega }^2\left(h-j\right)=0.(6.9)$

The E′ term enters through $S^{\prime \prime \prime }$ from $G_{\nu }^{\mu }$, while the other ones come from $T_{\nu }^{\mu }$.

In our nonrelativistic application we have S, S′ ≈ 0, $\bar{S}\approx -1$, so the leading terms are

$h_0=h+\frac{S^{\prime }{h}^{\prime }}{2{\omega }^2},h_1=-\frac{h^{″}}{{\omega }^2}+\frac{3S^{\prime }{h}^{\prime }+4S{h}^{″}}{2{\omega }^2},h_2=-\frac{h^{\prime }}{{\omega }^{2}r}+\frac{2S{h}^{\prime }}{{\omega }^{2}r}.(6.10)$

and

$h^{″}+\frac{E^{\prime }}{E}{h}^{\prime }-{\omega }^2\left(h-j\right)=0.(6.11)$

Eq 6.11 has a well behaved inhomogeneous solution, related to charge relocation coded by δQ ∼ j(r)Q(r) from Eq. 6.2. h behaves at large r as $h(r)=j(r)[1+\mathcal{O}(1/{\omega }^2{r}^2)]$. To determine it in general, let us denote the two real valued homogeneous solutions of (6.11) as J_E(r) and Y_E(r). Their Wronskian reads

$W_E\left(r\right)\equiv J_E\left(r\right)Y_E^{\prime }\left(r\right)-J_E^{\prime }\left(r\right)Y_E\left(r\right)=\frac{E_{*}}{E\left(r\right)},(6.12)$

where E_* > 0 follows by fixing the amplitudes and signs of J_E and Y_E. There is an inhomogenous solution of (6.11) that is well behaved at large r, reading

$h_{\text{i}}\left(r\right)=-{\omega }^2{\int }_r^{\infty }\text{d}u\frac{J_E\left(r\right)Y_E\left(u\right)-Y_E\left(r\right)J_E\left(u\right)}{W_E\left(u\right)}j\left(u\right).(6.13)$

6.3 An instability leading to explosive core growth

In our picture, dark matter stems from ZPE that flows in from infinity, and thereby creating a small mismatch between the charged particles so as to set up an E field. Does the inflowing DE fill up profiles ρ_E ∼ 1/r² and hence M_tot ∼ r and S(r) ∼ r⁰ at large r, and if so, how does this happen?

To investigate this, we assume $S(r)=2v_n^2{r}^{2n}$ for small and moderate r, for which the rotation speed equals v(r) = v_nrⁿ. While ${\rho }_{\lambda }=(1+n)(2n+1)v_n^2{r}^{2n-2}/8\pi G$, the related ${\rho }_E=(1-n)(2n+1)v_n^2{r}^{2n-2}/8\pi G$ must be non-negative, allowing $-\frac{1}{2}\le n\le 1$, with ρ_E → 0 for n → 1. For small r, our interest is 0 ≤ n < 1 where S ≪ 1 vanishes for r → 0 (it remains bounded for n = 0). For relatively large r, the regime of interest is $-\frac{1}{2}<n\le 0$. On this background, we consider an electric field perturbation δE (r, t) = ɛj(r)E(r)e^−iωt with ɛ ≪ 1 and some profile j(r). With the connection ρ_E = E²/8π = Q²(r)/8πr⁴ this is a special case of the treatment in subsection 6.2, with E ∼ rⁿ⁻¹. Equation 6.11 now reads

$h^{″}+\frac{1+2\nu }{r}{h}^{\prime }+{\omega }^{2}j={\omega }^{2}h,\nu =\frac{n}{2}-1,-\frac{5}{4}\le \nu \le -\frac{1}{2}.(6.14)$

For real ω, this has modes oscillating in time, involving modified Bessel functions I_ν(ωr) and K_ν(ωr). More interesting are the unstable (growing) modes j(r)e^ϖt, h(r)e^ϖt with ϖ > 0 and ω = iϖ, where Eq. 6.2 involves δQ (r, t) = ɛj(r)Q(r)e^ϖt. The case j(r) > 0 connects to increase of positive charge in the region r < R_co, making the region r > R_co more negatively charged; the case j(r) < 0 describes the reverse. Eq 6.13 reduces to

$\begin{array}{ll}\hfill h_{\text{i}}\left(r\right)& =\frac{\pi }{2}{\varpi }^2{r}^{-\nu }{\int }_r^{\infty }\text{d}u\left[J_{\nu }\left(\varpi r\right)Y_{\nu }\left(\varpi u\right)-Y_{\nu }\left(\varpi r\right)J_{\nu }\left(\varpi u\right)\right]u^{\nu +1}j\left(u\right),\hfill \end{array}(6.15)$

which involves the ordinary Bessel functions J_ν and Y_ν. Compared to Eqs 6.11, 6.12, it holds that J_E(r) = r^−νJ_ν(ϖr) and Y_E(r) = r^−νY_ν(ϖr), while W_E(u) = 2/πu^1+2ν. The homogeneous solutions J_E and Y_E behave as r^(1−n)/2 cos (ϖr − ϕ) at large r and have to be omitted. Conversely, h_i is well behaved and does not oscillate. With δρ_λ/ρ_λ = δρ_E/ρ_E, it follows that the increase of energy is exponential in time,

$\begin{array}{ll}\hfill \delta {\rho }_E+\delta {\rho }_{\lambda }& =\epsilon \left({\rho }_E+{\rho }_{\lambda }\right)G\left(r\right)e^{\varpi t},\hfill \\ \hfill G\left(r\right)& =\frac{2E^{\prime }{h}_{\text{i}}^{\prime }\left(r\right)}{{\varpi }^{2}E}=\frac{2\left(n-1\right)h_{\text{i}}^{\prime }\left(r\right)}{{\varpi }^{2}r}.\hfill \end{array}(6.16)$

With n ≤ 1 and, if j(r) > 0, $h_{\text{i}}^{\prime }<0$, it is seen that G(r) > 0 describes mass accretion triggered by the increasing enclosed charge. The profile G(r) is plotted in Figure 2 for the case $j(r)=1/\sqrt{r^2+1}$ and n = 0, so that ρ_q = cst/r². It shows that the “explosive” filling of the DM profile is most effective in the center.

Figure 2

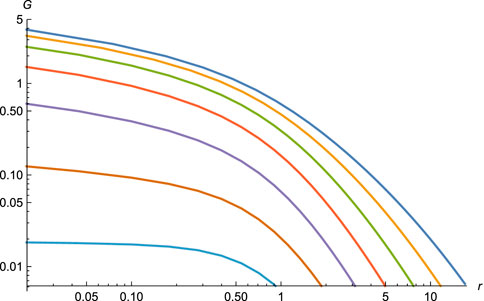
Figure 2. The growth factor G(r) of the mass density in Eq. 6.16 for a toy galaxy with only ν =−1 (n = 0, ρ_q = cst/r²) dark matter and enclosed-charge growth function $j(r)=1/\sqrt{r^2+1}$. The temporal growth rates are ϖ = 2^k with k from −3 (top) to 3 (bottom).

It came as a surprise to us that MOND, corresponding to n = 0 at large r, is not a limiting case, the allowed interval being $-\frac{1}{2}\le n\le 1$. Actually, the n = 0 case at small r, corresponding to a cusp ρ_q ∼ 1/r², E(r) ∼ 1/r, ρ_E ∼ ρ_λ ∼ 1/r², is an extremal case (Nieuwenhuizen, 2024).

There is evidence for the n = 1, constant-density case, see next section.

When j(r) < 0 in the galaxy or cluster center, the above argument exhibits a case of EAE flowing out of the core. This may be connected with expanding and diluting cores of galaxies, see Section. 6.5, and the cooling of cluster cores.

6.4 Evidence for constant-density, non-cusped cores

The NFW profile for ΛCDM (Navarro et al., 1997) has an 1/r singularity at the origin, expressing the mutual gravitational attraction of the CDM particles, playing out at their low (“cold”) speeds. Whether the CDM consists of axions, WIMPs or MACHOs is not relevant on the scale of galactic cores. The 1/r divergence is called a cusp. However, dark matter cores are often observed to be flat, and the issue is called the “cusp-core problem”; for recent reviews, see (Boldrini, 2021; Del Popolo and Le Delliou, 2021). Dark matter halos seem to have stopped growing: those of nearby quasars are not heavies than those at z ∼ 6 (Arita et al., 2023).

For EAE, Eq. 3.23 typically involves a constant-density DM core.

In galaxies, the nearly flat rotation curves occur since normal matter (stars, gas clouds) at small r adds to the DM which dominates at large r. In NGC 3626 the rotation curve keeps growing beyond eight kpc, for data up to 18 kpc. After accounting for stars and clouds, ref. (Shelest and Lelli, 2020) adds a DM component with v_dm ∼ rⁿ for n ≈ 1 or n = 1 in three galactic models. The same is done for NGC 2824 and NGC 6176, which do show flattening. The DM with index close to or equal to our limit n_max = 1 supports the above analysis.

In the Triangulum galaxy (M33, Cartwheel galaxy) the rotation speed increases as constant + linear beyond three kpc up to 15 kpc. It was modelled by determining the contribution from stars and gas, while DM was modeled by an NFW profile (López Fune et al., 2017). As in previous cases, modelling by an n = 1 (constant density) EAE profile may work.

A variety of observations are at odds with the presence of a cusp (Palunas and Williams, 2000; Salucci and Burkert, 2000; De Blok et al., 2001; Karukes and Salucci, 2017; Di Paolo et al., 2019); they favor a constant-density core of a few kpc in size. Ref. (Di Paolo et al., 2019) mentions a mysterious entanglement between the properties of the luminous and the dark matter, which has similarity to Renzo’s rule of Section 6.1. In EAE theory this occurs, since its ZPE dark matter is regulated by an electric field, due to a net charge distribution that has to adjust itself.

Our EAE explanation for the DM in the Galactic center is an indirect support for the binary milisecond pulsar interpretation of the 511 keV Fermi-LAT line (Bartels et al., 2018).

6.5 Dissolution of galactic cores

Another piece of evidence is the observational evidence of evolving constant-density dark matter profiles (Sharma et al., 2022). By subtracting the contributions from normal matter, these authors study the dark matter halos of a set of 256 star-forming disk-like galaxies at redshift z ∼ 1. They find constant-density DM cores, as expressed by Eq. 3.23 and corresponding to our above case n = 1. But, statistically, the DM cores at z ∼ 1 are denser by 1.5 dex than current ones and smaller by a factor of 0.3 dex compared to present.

Within EAE theory, this can be explained by a diminishing of the net charge ratio, related to the instability of cores mentioned in Section 4.5. It leads to ZPE moving outwards after having moved inwards; the same effect may also have caused the adiabatic expansion of the cluster gas in cool cores in clusters. In principle, this outflow can be described by an approach like the one in Section 6.3, with negative source function j(r), underlining once more the ZPE’s fluid character.

6.6 The electric field scaffold and the vast polar structure

It has been established that the Milky Way galaxy is surrounded by a vast polar structure of subsystems: satellite galaxies, globular clusters and streams of stars and gas, spreading from Galactocentric distances as small as 10 kpc out to 250 kpc (Metz and Kroupa, 2007; Pawlowski et al., 2012; 2014). A similar structure occurs in Andromeda (Kroupa, 2014). While an explanation was given as tidal tails of material expelled from interacting galaxies, the predicted EAE scaffold offers a fresh viewpoint. It presents a rather strong structure with which the matter inside it correlates in a smooth manner. This picture offers an alternative for the fortunate temporal alignment put forward recently for Gaia data interpreted within ΛCDM (Sawala et al., 2023).

7 Electro-aether-energy in clusters

7.1 Modified isothermal sphere as a fit for lensing

To apply the idea of isothermal spheres to the galaxy clusters, we consider the clusters A1689 and A1835. In ref. (Nieuwenhuizen et al., 2021), precise strong lensing and gas data and fits to them were presented. Here we consider a different modelling for the DM. A regularization of an isothermal sphere is

${\rho }_E=\frac{E^2\left(r\right)}{8\pi }=\frac{v^2}{8\pi G}\frac{r^2}{r^2+r_0^2}\frac{1}{r^2+r_1^2}\frac{r_2^{2n_{\mathrm{c}\mathrm{o}}}}{{\left(r^2+r_2^2\right)}^{n_{\mathrm{c}\mathrm{o}}}},(7.1)$

with r₀ ≪ r₁ ≪ r₂. At small r it yields E(r) ∼ r and a finite central charge density ρ_q (0). In the middle region, r₀ ≪ r ≪ r₂, it acts as a truncated isothermal sphere. At large r ≫ r₂, it exhibits incomplete build up (underfill) with index n_co.

The data for the cylindrical mass M_2d(r) are expressed in the cylindrical mass density $\bar{\mathrm{\Sigma }}(r)=M_{2d}(r)/\pi r^2$, which derives from the 3d mass density as

$\bar{\mathrm{\Sigma }}\left(r\right)=\frac{4}{r^2}{\int }_0^r\text{d}s{s}^2{\rho }_{\mathrm{t}\mathrm{o}\mathrm{t}}\left(s\right)+{\int }_r^{\infty }\text{d}s\frac{4s{\rho }_{\mathrm{t}\mathrm{o}\mathrm{t}}\left(s\right)}{s+\sqrt{s^2-r^2}}.(7.2)$

We consider the profile (7.1); the case n_co = 2 works well; an analytic expression for its contribution to $\bar{\mathrm{\Sigma }}$ can be derived. For the brightest cluster galaxy (bcg) with mass M_bcg, we add a stretched exponential (se) profile ${\rho }_{\text{bcg}}=[M_{\text{bcg}}/4\pi \mathrm{\Gamma }(3n_{\mathrm{s}\mathrm{e}})n_{\mathrm{s}\mathrm{e}}{R}_{\mathrm{s}\mathrm{e}}^3]\times \exp [-{(r/R_{\mathrm{s}\mathrm{e}})}^{1/n_{\mathrm{s}\mathrm{e}}}]$, while the X-ray gas has also been modelled in (Nieuwenhuizen et al., 2021). In Figure 3 we present the data for $\bar{\mathrm{\Sigma }}(r)$ and fit this to ${\bar{\mathrm{\Sigma }}}_{\mathrm{b}\mathrm{c}\mathrm{g}}+{\bar{\mathrm{\Sigma }}}_{\text{dm}}+{\bar{\mathrm{\Sigma }}}_{\text{gas}}$ with r₀ → 0. The further parameters are for A1689:

$\begin{array}{ll}\hfill & M_{\mathrm{b}\mathrm{c}\mathrm{g}}=110^{12}{M}_{\odot },R_{\mathrm{s}\mathrm{e}}=3\mathrm{k}\mathrm{p}\mathrm{c},n_{\mathrm{s}\mathrm{e}}=1,v=3480\frac{\text{km}}{\mathrm{s}},\hfill \\ \hfill & r_1=50\mathrm{k}\mathrm{p}\mathrm{c},r_2=1.5\mathrm{M}\mathrm{p}\mathrm{c},\hfill \end{array}(7.3)$

and for A1835:

$\begin{array}{ll}\hfill & M_{\mathrm{b}\mathrm{c}\mathrm{g}}=910^{12}{M}_{\odot },R_{\mathrm{s}\mathrm{e}}=6\mathrm{k}\mathrm{p}\mathrm{c},n_{\mathrm{s}\mathrm{e}}=1.25,v=3350\frac{\text{km}}{\mathrm{s}},\hfill \\ \hfill & r_1=100\mathrm{k}\mathrm{p}\mathrm{c},r_2=2.1\mathrm{M}\mathrm{p}\mathrm{c}.\hfill \end{array}(7.4)$

These values work well, but are not optimized; the error bars will be comparable to the ones in related fits (Nieuwenhuizen et al., 2021). Since the bcg is poorly constrained, other shapes may function as well. The “underfill” for r ≳ r₂ expresses that the surplus electrons pushed outwards are dominant there and diminish the net enclosed charge Q(r) and hence ρ_E.

Figure 3

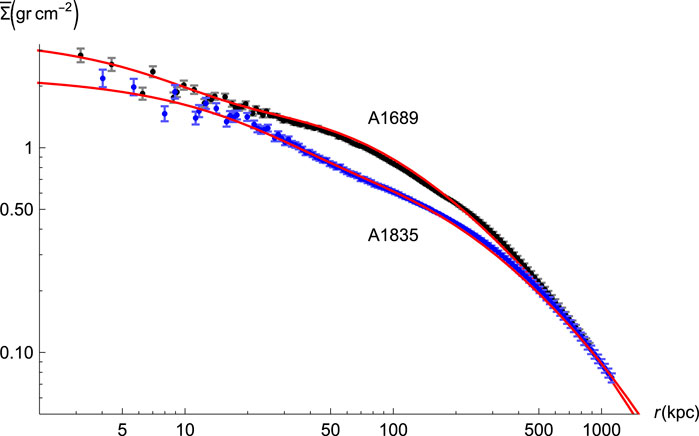
Figure 3. Cylindrical mass density as function of r in the galaxy clusters A1689 (upper) and A1835 (lower) with their fits to the truncated isothermal profile of Eq. 7.1 with index n_co= 2.

According to (3.20), the LCC ρ_λ(r) equals ${\rho }_E^{>}(r)-{\rho }_E(r)$. For ρ_E in Eq. 7.1 with n_co = 2, the ${\rho }_E^{>}$ term can be solved analytically,

$\begin{array}{ll}\hfill {\rho }_E^{>}\left(r\right)& =4{\int }_r^{\infty }\text{d}u\frac{{\rho }_E\left(u\right)}{u}=\frac{r_2^4{v}^2}{4\pi G}\left(\frac{1}{r_{20}^2{r}_{21}^2\left(r^2+r_2^2\right)}-\frac{L_0}{r_{10}^2{r}_{20}^4}\right.\hfill \\ \hfill & \left.+\frac{L_1}{r_{10}^2{r}_{21}^4}-\frac{r_{20}^2+r_{21}^2}{r_{20}^4{r}_{21}^4}{L}_2\right),\hfill \end{array}(7.5)$

with $r_{10}^2=r_1^2-r_0^2$, $r_{20}^2=r_2^2-r_0^2$, $r_{21}^2=r_2^2-r_1^2$ and $L_i=\log (r^2+r_i^2)$. As in the toy galaxy of sec. 3.5, ρ_λ is positive for small and moderate r, while it has a negative tail $-r_2^4{v}^2/24\pi G{r}^6$. Its zero crossing lies at 1.2 Mpc for A1689 and at 1.7 Mpc for A1835.

The crossover radius which separates the inner region with positive net charge density ρ_q from the outer region with a negative one, occurs for d (r⁴ρ_E)/dr = 0, implying R_co ≈ r₂ for n_co = 2, so that R_co = 1.5 and 2.1 Mpc for A1689 and A1835, respectively.

7.2 The hydrostatic equilibrium puzzle in clusters

In the Earth’s atmosphere, hydrostatic equilibrium is broken by lightning, after which its restoration leads to thunder. In studies of clusters, hydrostatic equilibrium of the X-ray gas is investigated, but found to be dissatisfied (Morandi et al., 2010; Lemze et al., 2011; Morandi et al., 2012); it leads to a $\sim 40\%$ “nonthermal pressure” component in the center of A1689 (Molnar et al., 2010), supposedly due to turbulence, spurious gas dynamics or the dynamical build up of the cluster. Figure 4 of our ref. (Nieuwenhuizen and Morandi, 2013). shows that for hydrostatic equilibrium the gas temperature (and with it, the pressure) should be larger than observed by a factor $\sim 1.5$.

Figure 4

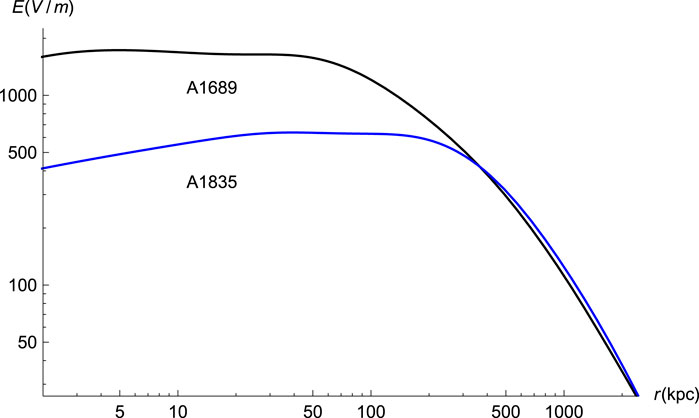
Figure 4. Fits to the TT, EE and TE spectra of the cosmic microwave background observed by the Planck satellite for l up to 2000. The large value of the Hubble constant of 73 km/s Mpc is compatible with the data due to the dynamical nature of electro-zero-point energy.

This riddle can be solved in EAE theory. The condition for hydrostatic equilibrium, Eq. 3.33, reads $p_{\text{m}}^{\prime }+p_{\lambda }^{\prime }={\mathcal{F}}_E+{\mathcal{F}}_G$, with

${\mathcal{F}}_E={\rho }_E^{\prime }+4\frac{{\rho }_E}{r},{\mathcal{F}}_G\approx -G\left({\rho }_{\mathrm{m}}+p_{\mathrm{m}}\right)\frac{M_{\mathrm{t}\mathrm{o}\mathrm{t}}+4\pi r^3\left(p_{\text{m}}-{\rho }_{\lambda }-{\rho }_E\right)}{r^2}.(7.6)$

7.2.1 Hydrostatic equilibrium in ΛCDM

In ΛCDM one has ρ_E = 0 and p_λ(r) = −Λ/8πG, a constant; employing ρ_m = ρ_bcg + ρ_g and p_m = p_g from (3.31), Eq. 7.6 results in

$p_g^{\prime }\approx -G\left({\rho }_{\mathrm{b}\mathrm{c}\mathrm{g}}+{\rho }_g\right)\frac{M_{\mathrm{t}\mathrm{o}\mathrm{t}}}{r^2},\left(\mathrm{\Lambda }\text{CDM}\right).(7.7)$

This exhibits the ΛCDM hydrodynamic equilibrium condition for the gas pressure, but notice that ρ_m = ρ_bcg + ρ_g also involves the bcg, a point generally overlooked.

A consistent approach in ΛCDM simulations should satisfy (7.7), but observed clusters need not, and, as mentioned above, the analyzed ones do not satisfy it. Away from the bcg, where ρ_bcg → 0, the relation remains violated.

7.2.2 Hydrostatic equilibrium in EAE

In the EAE approach, the ρ_E and p_λ terms are present with |p_λ|∼ ρ_E, and they are by far the dominant terms, making (7.6) a relation between them with the matter terms as spectators. As we realized in our fitting of the lensing profiles of the clusters A1689 and A1835 (Nieuwenhuizen and Morandi, 2013; Nieuwenhuizen, 2017; 2020; Nieuwenhuizen et al., 2021), the gas is just a spectator, with right nor need for “its own” hydrostatic equilibrium.

In the description of section 3.3 the nonlinear ${\mathcal{F}}_G$ terms were left out, which led to the ρ_λ in Eq. 3.20 as solution for hydrostatic equilibrium. ${\mathcal{F}}_G$ indeed acts as a small correction; compared to ${\mathcal{F}}_E$, it is of relative size 10^–6 − 10^–5. Integrating it from r to ∞ yields a correction to ρ_λ, which exhibits the malleability of the ZPE, doing just the right thing in the situation at hand.

The respect for hydrostatic equilibrium in EAE implies that no big effects of turbulence or other (gas) dynamics are to be sought for. Rather, it underlines that its violation in ΛCDM is a real deficit.

While ρ_λ + ρ_E − p_m can be identified with the empirical ρ_dm profile, data for ρ_E are needed to test the hydrostatic equilibrium condition. Unlike the ZPE density, that can only be inferred gravitationally, the electric field acts on charges, and can in principle be determined. Eq 3.20 yields the prediction $E(r)={[-r{\rho }_{\mathrm{t}\mathrm{o}\mathrm{t}}^{\prime }(r)/2{\epsilon }_0]}^{1/2}$; it is plotted in Figure 5 for A1689 and A1835. The central regions involve electric fields of $\sim 1.5$ and $\sim 0.5$ kV/m, respectively.

Figure 5

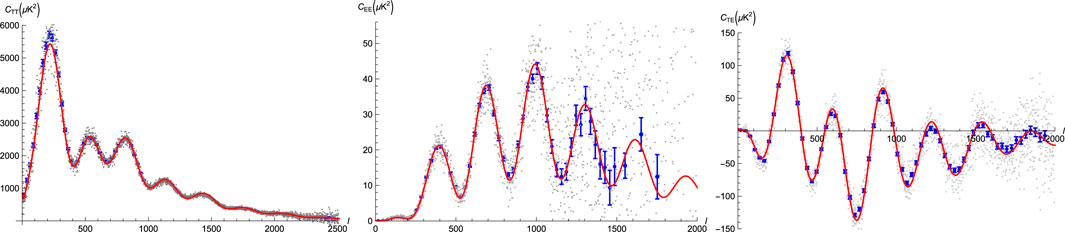
Figure 5. Prediction for the static electric field (in V/m) as function of the radius in the galaxy clusters A1689 (upper, black) and A1835 (lower, blue).

8 Electro-aether-energy in cosmology

8.1 Zero pressure EAE equation of state

On cosmological scales, one considers the spatial average of the mass density and pressure over a large cosmological volume V with many galaxies.

For a given galaxy (cluster), the electrons compensate the positively charged interior of the galaxy (cluster) beyond the crossover length R_co, making ρ_E decay faster than 1/r⁴. The integral in Eq. 3.17 vanishes in the limit r → ∞, so as to keep the limits

$M_{\lambda }+M_E+M_{\text{m}}^{\rho }=\frac{4}{3}{M}_E+M_{\text{m}}^p.(8.1)$

Likewise, consider the energy stored in the pressures,

$P_{\mathrm{t}\mathrm{o}\mathrm{t}}^i=4\pi {\int }_0^{\infty }\text{d}u{u}^2{p}_{\mathrm{t}\mathrm{o}\mathrm{t}}^i\left(u\right),i=r,\theta ,\varphi .(8.2)$

Eq 3.22 yields the values

$P_{\mathrm{t}\mathrm{o}\mathrm{t}}^r=-\frac{4}{3}{M}_E,P_{\mathrm{t}\mathrm{o}\mathrm{t}}^{\theta }=P_{\mathrm{t}\mathrm{o}\mathrm{t}}^{\varphi }=P_{\mathrm{t}\mathrm{o}\mathrm{t}}^{\perp }=\frac{2}{3}{M}_E.(8.3)$

A large cosmological volume V with many galaxies at random positions has a mass density and an isotropic pressure. The mass density can be obtained by smearing out the mass of each galaxy over V and summing. The 3 × 3 pressure matrix is, on the average, diagonal and isotropic. For each galaxy, the contribution to the pressure is obtained as 1/3V times the trace of the pressure matrix integrated over space. Eq 8.3 implies that this trace vanishes for each galaxy and hence for their combination. This leads to the equation of state for the EAE

$p_e=0,w_e\equiv \frac{p_e}{{\rho }_e}=0,(8.4)$

which coincides with the standard p_dm = 0 for particle cold dark matter like ΛCDM.

In an alternative approach, we only use that the trace of the EM stress energy tensor vanishes. Averaging over a large volume V with many galaxies yields an isotropic pressure $p_E=\frac{1}{3}{\rho }_E$. With p_λ = −ρ_λ and ${\rho }_{\lambda }=\frac{1}{3}{\rho }_E$⁴, Eq. 8.4 follows again from p_e = p_λ + p_E.

8.2 The Hubble tension and the increasing amount of dark matter

The so-called Hubble tension is the fact that local measurements of the Hubble constant via supernovas yield H₀ ≈ 73 km/s Mpc (Brout et al., 2022), while the cosmic microwave background fixes it at $\approx 68$ km/s Mpc (Aghanim et al., 2020), with smaller and smaller error bars bringing it to a $\sim 5\sigma$ discrepancy. It is often argued that late time physics cannot solve the Hubble tension, see, e.g., the “most general” scenario (Keeley and Shafieloo, 2023). The reason for this is simple, at the present low temperature of the cosmos, no new dark matter particles can be created, so there cannot be an increase of cold dark matter. But it is also early-time new physics alone cannot solve the Hubble tension (Vagnozzi, 2023). Apparently, the situation is presently in a limbo.

While the EAE acts as a pressureless type of cold dark matter, its mass density can grow in time, since more and more ZPE/AE can be condense locally on BHs, galaxies, clusters, filaments, etc. This will lead to a growth equation for the cosmic dark matter fraction Ω_dm; a modelling is given in Eq. 8.11 below. It fixes the “enslaved” global dark energy density Ω_λ by energy conservation, see Eq. 8.15 below.

8.3 Friedmannology for aether energy condensation

The Friedman equations for the cosmic scale factor a(t) with a (now) = 1, are

$H^2=\frac{{\dot{a}}^2}{a^2}=\frac{8\pi G}{3}\rho ,\frac{\ddot{a}}{a}=-\frac{4\pi G}{3}\left(\rho +3p\right),\text{d}\left(\rho a^3\right)=-p\text{d}{a}^3.(8.5)$

Two of these three equations are independent; the last one expresses energy conservation. It is customary to divide out the critical density ${\rho }_c=3H_0^2/8\pi G$, where the Hubble constant H₀ is the present value of H, and to split up in various components Ω_i = ρ_i/ρ_c,

$\frac{H^2}{H_0^2}=E\left(a\right),E\left(a\right)={\displaystyle \sum _i}{\mathrm{\Omega }}_i\left(a\right).(8.6)$

We will consider radiation (r), baryons (b), dark matter (dm), and aether energy (λ).

$\begin{array}{ll}\hfill E\left(a\right)& =E_r\left(a\right)+E_b\left(a\right)+E_{\text{dm}}\left(a\right)+E_{\lambda }\left(a\right)\hfill \\ \hfill & \equiv \frac{{\mathrm{\Omega }}_r\left(a\right)}{a^4}+\frac{{\mathrm{\Omega }}_b\left(a\right)}{a^3}+\frac{{\mathrm{\Omega }}_{\text{dm}}\left(a\right)}{a^3}+{\mathrm{\Omega }}_{\lambda }\left(a\right).\hfill \end{array}(8.7)$

With w_dm ≡ w_e = 0, see Eq. 8.4, the respective equation of state parameters are

$w_r=\frac{1}{3},w_b=w_{\text{dm}}=w_e=0,w_{\lambda }=-1.(8.8)$

Energy conservation gets expressed as

${\mathrm{\Omega }}_{\lambda }^{\prime }=-{\displaystyle \sum _{i\ne \lambda }}\left[E_i^{\prime }\left(a\right)+3\left(1+w_i\right)\frac{E_i\left(a\right)}{a}\right]=-\frac{{\mathrm{\Omega }}_r^{\prime }}{a^4}-\frac{{\mathrm{\Omega }}_b^{\prime }}{a^3}-\frac{{\mathrm{\Omega }}_{\text{dm}}^{\prime }}{a^3},(8.9)$

with the solution

$\begin{array}{ll}\hfill {\mathrm{\Omega }}_{\lambda }\left(a\right)& ={\mathrm{\Omega }}_{\mathrm{\Lambda }}+{\int }_a^1\text{d}b\left[\frac{{\mathrm{\Omega }}_r^{\prime }\left(b\right)}{b^4}+\frac{{\mathrm{\Omega }}_m^{\prime }\left(b\right)}{b^3}+\frac{{\mathrm{\Omega }}_{\text{dm}}^{\prime }\left(b\right)}{b^3}\right],\hfill \\ \hfill & E\left(a\right)=1+{\int }_a^1\frac{\text{d}b}{b}\left[4\frac{{\mathrm{\Omega }}_r\left(b\right)}{b^4}+3\frac{{\mathrm{\Omega }}_b\left(b\right)}{b^3}+3\frac{{\mathrm{\Omega }}_{\text{dm}}\left(b\right)}{b^3}\right],\hfill \\ \hfill & {\mathrm{\Omega }}_{\mathrm{\Lambda }}+{\mathrm{\Omega }}_r\left(1\right)+{\mathrm{\Omega }}_b\left(1\right)+{\mathrm{\Omega }}_{\text{dm}}\left(1\right)=1.\hfill \end{array}(8.10)$

In the present epoch, Ω_r(a) = Ω_r and Ω_b(a) = Ω_b are constants, but they change when neutrinos become nonrelativistic due to their small, finite masses; in the past such changes happened during the freeze out of the various species, accompanied by a change in Ω_λ.

Deviating from the standard assumption that also Ω_dm and Ω_λ are constants, we will consider an increasing Ω_dm(a) with an appropriate, non-constant Ω_λ(a).

The prediction of a growing Ω_dm is supported by observational values for the cosmic matter fraction Ω_m = Ω_dm + Ω_b. The early time value 0.315 ± 0.007 from the cosmic microwave background (CMB) observed by the Planck satellite (Aghanim et al., 2020), is smaller than the late time (“now”) value 0.334 ± 0.018 deduced from supernovae in the nearby cosmos (Brout et al., 2022).

To deal properly with the problem, a unified approach covering these epochs is needed. Here we connect to ref. (Dainotti et al., 2021). By parting the Pantheon supernova data in redshift bins, a weak time-dependence of Hubble constant H₀ is found and fit to the form $H_0(z)=H_0^{\mathrm{n}\mathrm{o}\mathrm{w}}{(1+z)}^{-\alpha }$ with α ≈ 0.01. Inspired by this, we consider the DM growth function

${\mathrm{\Omega }}_{\text{dm}}\left(a\right)={\mathrm{\Omega }}_e{a}^{{\delta }_e},(8.11)$

where δ_e ∼ 0.02, deviating from δ_e = 0 in ΛCDM. (For simplicity, we neglect a possible a-dependence of δ_e). This small value is compatible with the non-growth of dark matter halos of quasars since z ∼ 6 (Arita et al., 2023).

So, next to radiation (r), baryons (b), we consider EAE (e) dark matter, and a time dependent dark energy (λ). Since Ω_b and Ω_e thus have negligible pressure, the total pressure reads

$\frac{p}{{\rho }_c}=\frac{{\mathrm{\Omega }}_r}{3a^4}-{\mathrm{\Omega }}_{\lambda }\left(a\right).(8.13)$

The total energy content is now

$E\left(a\right)=\frac{{\mathrm{\Omega }}_r}{a^4}+\frac{{\mathrm{\Omega }}_b}{a^3}+\frac{{\mathrm{\Omega }}_{\text{dm}}\left(a\right)}{a^3}+{\mathrm{\Omega }}_{\lambda }\left(a\right)=\frac{{\mathrm{\Omega }}_r}{a^4}+\frac{{\mathrm{\Omega }}_b}{a^3}+\frac{{\mathrm{\Omega }}_e{a}_e^{\delta }}{a^3}+{\mathrm{\Omega }}_{\lambda }\left(a\right).(8.14)$

Like in other applications, the aether, here expressed in the component Ω_λ, is enslaved. Eq. 8.9, expressing energy conservation, fixes it as

${\mathrm{\Omega }}_{\lambda }\left(a\right)={\mathrm{\Omega }}_{\mathrm{\Lambda }}+\frac{{\delta }_e}{3-{\delta }_e}{\mathrm{\Omega }}_e\left(a^{{\delta }_e-3}-1\right),(8.15)$

with Ω_Λ the present cosmological constant. The a-depencence exhibits that Ω_λ(a) was much larger in the past than now, and will be smaller in the future: Throughout the history of the Universe, aether energy is turned into other forms of energy. In this setup, the smallness of Ω_λ(1) = Ω_Λ is not a result of fine-tuning, but of dynamics, set by the integration constant Ω_Λ.

Equations 8.14 and 8.15 lead to

$E\left(a\right)=\frac{{\mathrm{\Omega }}_r}{a^4}+\frac{{\mathrm{\Omega }}_b}{a^3}+\frac{3a^{{\delta }_e-3}-{\delta }_e}{3-{\delta }_e}{\mathrm{\Omega }}_e+{\mathrm{\Omega }}_{\mathrm{\Lambda }},(8.16)$

which can be written in the effective form

$\begin{array}{ll}\hfill E\left(a\right)& =\frac{{\mathrm{\Omega }}_r}{a^4}+\frac{{\mathrm{\Omega }}_b}{a^3}+\frac{{\bar{\mathrm{\Omega }}}_e}{a^{3-{\delta }_e}}+{\bar{\mathrm{\Omega }}}_{\mathrm{\Lambda }}=\frac{{\mathrm{\Omega }}_r}{a^4}+\frac{{\mathrm{\Omega }}_b}{a^3}+\frac{{\bar{\mathrm{\Omega }}}_{\text{dm}}\left(a\right)}{a^3}+{\bar{\mathrm{\Omega }}}_{\mathrm{\Lambda }},\hfill \\ \hfill & {\bar{\mathrm{\Omega }}}_{\text{dm}}\left(a\right)={\bar{\mathrm{\Omega }}}_e{a}^{{\delta }_e},{\bar{\mathrm{\Omega }}}_e=\frac{3{\mathrm{\Omega }}_e}{3-{\delta }_e},{\bar{\mathrm{\Omega }}}_{\mathrm{\Lambda }}={\mathrm{\Omega }}_{\mathrm{\Lambda }}-\frac{{\delta }_e{\mathrm{\Omega }}_e}{3-{\delta }_e},\hfill \end{array}(8.17)$

with, as usual, the present-time sum rule

$E\left(1\right)={\mathrm{\Omega }}_r+{\mathrm{\Omega }}_b+{\mathrm{\Omega }}_e+{\mathrm{\Omega }}_{\mathrm{\Lambda }}={\mathrm{\Omega }}_r+{\mathrm{\Omega }}_b+{\bar{\mathrm{\Omega }}}_e+{\bar{\mathrm{\Omega }}}_{\mathrm{\Lambda }}=1.(8.18)$

Eq. 8.17 has the familiar form, only modified by an increasing dark matter component. Unlike other rather ad hoc approaches, our ongoing EAE condensation Ansatz (8.11) fits in a bigger picture, the one where EAE also acts as the dark matter in galaxies and clusters, as ingredient of singularity-free black holes, and more.

8.4 A fit to CMB data

Identifying $H_0^{\text{cm}b}\equiv z_{\text{cm}b}^{-3/2}{[H(z_{\text{cm}b})]}^{1/2}$ leads to

$H_0^{\text{cm}b}\approx H_0^{\mathrm{n}\mathrm{o}\mathrm{w}}{\left(\frac{{\mathrm{\Omega }}_b+{\mathrm{\Omega }}_{\text{dm}}{z}_{\text{cm}b}^{-{\delta }_e}}{{\mathrm{\Omega }}_b+{\mathrm{\Omega }}_{\text{dm}}}\right)}^{1/2},(8.19)$

with z_cmb ≈ 1080. The value δ_e = 0.025 maps $H_0^{\mathrm{n}\mathrm{o}\mathrm{w}}=73$ km/s Mpc to $H_0^{\text{cm}b}\approx 68$ km/s Mpc, apparently solving the Hubble tension with late-time physics, an option unjustly ruled out by restricting in ref. (Keeley and Shafieloo, 2023) to the “most general” scenario.

Of course, a more fundamental analysis is warranted. Employing the CLASS code (Blas et al., 2011; Di Dio et al., 2013), it is possible to find reasonable parameter fits to the Planck CMB TT, EE and TE spectra (Aghanim et al., 2020) up to angular index l = 2000. A specific case⁵ is depicted in Figure 5. While encouraging by its good fit, this is only indicative. In a proper approach one has to derive the theoretical CMB spectra for the EAE situation of (8.11), considering effects of the electric fields, and fit those predictions to the various data sets, such as CMB, baryon acoustic oscillations and supernovae. At the next level of description, one determines a practical shape for Ω_dm(z) from Monte Carlo simulation or otherwise. These steps are beyond the aim of the present paper; we restrict ourselves to stating that the Hubble tension is eased and likely solvable in EAE.

8.5 The large hubble constant and the age of the universe

Though too seldomly stressed, a large Hubble constant leads to a small age of the Universe, bringing it close to physical lower bounds. The value H₀ = 73 km/s Mpc leads to

$\text{Age\hspace{0.17em}of\hspace{0.17em}Universe}\approx 12.8\text{\hspace{0.17em}Gyr},(8.20)$

rather than the 13.8 Gyr in ΛCDM. This is slightly older than the age of the oldest cluster M4 based on main sequence stars 12.6 ± 1.1 Gyr, or based on the oldest white dwarfs 12.7 ± 0.7 Gyr (Rich, 2009). But it is younger than the estimated age 13.7 ± 0.7 Gyr for the Methusalah star HD 140283 (Creevey et al., 2015), and the accurate 13.535 ± 0.002 Gyr of the ultra-metal poor 2MASS J18082002–5104,378 B (Schlaufman et al., 2018).

These and related estimates are based on fitting to simulations of ΛCDM, not to EAE theory. Its predicted early structure formation is suited for early objects. Anyhow, in no consistent theory an age larger than its age of the Universe should appear.

8.6 The lopsidedness of the cosmos and the axis of evil

Another challenge to the standard cosmological model concerns the cosmological principle: the expansion of the Universe is homogeneous and isotropic. The largest effect in the cosmic microwave background fluctuations is the so-called the dipole asymmetry. Is it simply due to the motion of the Galaxy through the cosmos, or is it due to a genuine asymmetry in the distribution of matter? Analysis of X ray galaxy clusters (Migkas et al., 2020) and radio galaxies and quasars (Secrest et al., 2022) suggests that the universe is lopsided in our frame. This correlates with the mysterious “Axis of evil” (Land and Magueijo, 2005), the fact that the plane of the Galaxy correlates with the alignment of the low-l (l = 2, 3, 4, 5) multipoles of the CMB: the “top half” of the cosmos is sllghtly cooler than the “bottom half”, and the axes of the quadrupole and octopole correlate with it.

It is natural to imagine that the cosmic expansion occurred in an anisotropic way, and, consequently, that the cosmological constant was anisotropic. EAE theory can accommodate that, since it connects the cosmological constant (as vacuum energy) to matter, via the necessary electric fields carried by charge mismatches.

8.7 Beyond present

Except for special periods in the early Universe, ${\mathrm{\Omega }}_r^{\prime }$ and ${\mathrm{\Omega }}_b^{\prime }$ are zero, so that Ω_r,b(a) = Ω_r,b keep their present values in the future. (For simplicity, we neglect the fact that neutrinos have a small mass and that BHs radiate). If Ω_e(a) were also constant, we would have the ΛCDM connection Ω_λ(a) = Ω_Λ. Since Ω_e(a) = a³E_dm(a) is the cosmic EAE fraction in a comoving volume, it can continue to increase by further condensation as DM.

Let us consider the far future where expansion leads to a scale factor a > 1 or even ≫ 1 and the integral in the expression for E(a) in (8.10) is negative. The EAE condensation will likely go on until the dissolution of EAE in galaxies and clusters possibly takes the overhand, which could be modeled by a parameter δ_e < 0. Finally this leads to a “true” cosmological constant,

${\mathrm{\Omega }}_{\mathrm{\Lambda }}^e\equiv {\mathrm{\Omega }}_{\lambda }\left(a_{\text{max}}\right)={\mathrm{\Omega }}_{\mathrm{\Lambda }}-{\int }_1^{a_{\text{max}}}\text{d}b\frac{{{\mathrm{\Omega }}_e}^{\prime }\left(b\right)}{b^3}.(8.21)$

with finite or infinite a_max. In the latter case, it results in

${\mathrm{\Omega }}_{\lambda }\left(a\right)={\mathrm{\Omega }}_{\mathrm{\Lambda }}^e+{\int }_a^{\infty }\text{d}b\frac{{{\mathrm{\Omega }}_e}^{\prime }\left(b\right)}{b^3},E\left(a\right)={\mathrm{\Omega }}_{\mathrm{\Lambda }}^e+\frac{{\mathrm{\Omega }}_r}{a^4}+\frac{{\mathrm{\Omega }}_b}{a^3}+3{\int }_a^{\infty }\frac{\text{d}b}{b}\frac{{\mathrm{\Omega }}_e\left(b\right)}{b^3}.(8.22)$

The proposed shape ${\mathrm{\Omega }}_e(a)={\mathrm{\Omega }}_e{a}^{{\delta }_e}$ leads for δ_e < 3 to

${\mathrm{\Omega }}_{\lambda }\left(a\right)={\mathrm{\Omega }}_{\mathrm{\Lambda }}^e+\frac{{\delta }_e{\mathrm{\Omega }}_e}{3-{\delta }_e}\frac{a^{{\delta }_e}}{a^3},E\left(a\right)=\frac{{\mathrm{\Omega }}_r}{a^4}+\frac{{\mathrm{\Omega }}_b}{a^3}+\frac{3{\mathrm{\Omega }}_e}{3-{\delta }_e}\frac{a^{{\delta }_e}}{a^3}+{\mathrm{\Omega }}_{\mathrm{\Lambda }}^e.(8.23)$

The case δ_e = 1 connects to Ω_e(a)/a³ = Ω_e (1)/a² which is commonly connected to curvature of space; here it is a special–and relatively large–parameter δ_e.

The deceleration parameter defined as

$q=-\frac{a\ddot{a}}{{\dot{a}}^2}=-1-\frac{a{E}^{\prime }\left(a\right)}{2E\left(a\right)}.(8.24)$

The present value,

$q_0=-1+2{\mathrm{\Omega }}_r+\frac{3}{2}{\mathrm{\Omega }}_b+\frac{3}{2}{\mathrm{\Omega }}_e\approx -0.55,(8.25)$

exhibits acceleration (q₀ < 0). It coincides with the Planck value (Aghanim et al., 2020). Analysis of the Pantheon supernovae sample (Camarena and Marra, 2020a; b) leads, however, to q₀ = −1.1 ± 0.3, disagreeing at 2σ. The Dark Energy Survey finds $q_0=-0.530_{-0.017}^{+0.018}$ (Abbott et al., 2024), at 1.5σ from (8.25).

8.7.1 Black holes and the big crunch

Ref. (Farrah et al., 2023a). considers that supermassive BHs in the redshift interval 0.7 < z < 2.5 have a mass $M=M_i{(a/a_i)}^k$ growing with the scale factor as a^k since time t_i where a (t_i) = a_i, where a = 1/(1 + z), and construct a histogram of the distribution p(k), normalized as ∫dk p(k) = 1. Being centred around k = 3, it appears to have weight between k_min = 0 and k_max ≈ 6. These authors put forward that black holes are the source of dark energy, whereas we assume that dark energy can condense on galaxies and end up in black holes.

When supermassive black holes are relevant for the mass budget, there will be an extra term in (8.14). Assuming for simplicity that p(k) does not depend on a and holds also for a > 1, it takes the form

$E_{\text{bh}}\left(a\right)={\mathrm{\Omega }}_{\text{bh}}\int \text{d}kp\left(k\right)a^{k-3},(8.26)$

Black holes do not create pressure (Hawking radiation is negligible), so for w_bh = 0 the energy conservation (8.9) yields an extra term to (8.10),

${\mathrm{\Omega }}_{\lambda }^{\text{bh}}\left(a\right)=-{\mathrm{\Omega }}_{\text{bh}}\int \text{d}kp\left(k\right)k\frac{a^{k-3}-1}{k-3},(8.27)$

vanishing at a = 1, in accord with the definition Ω_Λ = Ω_λ(1). Equation 8.16 now reads

$E\left(a\right)=\frac{{\mathrm{\Omega }}_r}{a^4}+\frac{{\mathrm{\Omega }}_b}{a^3}+\frac{3a^{{\delta }_e-3}-{\delta }_e}{3-{\delta }_e}{\mathrm{\Omega }}_e+{\mathrm{\Omega }}_{\mathrm{\Lambda }}+{\mathrm{\Omega }}_{\text{bh}}\int \text{d}kp\left(k\right)\frac{k-3a^{k-3}}{k-3},(8.28)$

with the closure Ω_r + Ω_b + Ω_e + Ω_Λ + Ω_bh = 1. For large a the integral behaves as $\sim -a^{k_{\text{max}}-3}\ll -1$, demonstrating that more energy is extracted from the aether than transferred to the black holes, due to the work cost to get it there.

Apparently, black holes have a tendency to make E negative, but since $E=H^2/H_0^2$, this is physically impossible. If E reaches zero at some a_max, this implies $\dot{a}=0$. Since values $\ddot{a}<0$ must then hold already, it describes a Big Crunch with $\dot{a}<0$ from thereon.

8.8 Times near the big bang

Let us return to Eq. 8.9 and add a term Ω_ϕ(a) from an unspecified degree of freedom ϕ,

$E\left(a\right)=\frac{{\mathrm{\Omega }}_r\left(a\right)}{a^4}+\frac{{\mathrm{\Omega }}_b\left(a\right)}{a^3}+\frac{{\mathrm{\Omega }}_e\left(a\right)}{a^3}+{\mathrm{\Omega }}_{\lambda }\left(a\right)+{\mathrm{\Omega }}_{\varphi }\left(a\right),(8.29)$

Assuming that Ω_r(a), Ω_b(a), Ω_e(a) and Ω_ϕ(a) (but not Ω_λ) all start at zero at a = 0, and grow slowly enough, the quantity Ω_dS, where dS stands for de Sitter, takes a finite value,

${\mathrm{\Omega }}_{\text{dS}}={\mathrm{\Omega }}_{\mathrm{\Lambda }}+{\int }_0^1\text{d}b\left[\frac{{\mathrm{\Omega }}_r^{\prime }\left(b\right)}{b^4}+\frac{{\mathrm{\Omega }}_b^{\prime }\left(b\right)}{b^3}+\frac{{{\mathrm{\Omega }}_e}^{\prime }\left(b\right)}{b^3}+3\frac{{\mathrm{\Omega }}_{\varphi }\left(b\right)}{b}\right]+{\mathrm{\Omega }}_{\varphi }\left(1\right),(8.30)$

Energy conservation (8.9) allows to express Ω_λ with Ω_λ(1) = Ω_Λ as

$\begin{array}{ll}\hfill {\mathrm{\Omega }}_{\lambda }\left(a\right)& ={\mathrm{\Omega }}_{\text{dS}}-{\int }_0^a\text{d}b\left[\frac{{\mathrm{\Omega }}_r^{\prime }\left(b\right)}{b^4}+\frac{{\mathrm{\Omega }}_b^{\prime }\left(b\right)}{b^3}+\frac{{{\mathrm{\Omega }}_e}^{\prime }\left(b\right)}{b^3}\right.\hfill \\ \hfill & \left.+3\left(1+w_{\varphi }\right)\frac{{\mathrm{\Omega }}_{\varphi }\left(b\right)}{b}\right]-{\mathrm{\Omega }}_{\varphi }\left(a\right).\hfill \end{array}(8.31)$

After partial integration, Eq. 8.29 reads

$\begin{array}{ll}\hfill E\left(a\right)& ={\mathrm{\Omega }}_{\text{dS}}-{\int }_0^a\frac{\text{d}b}{b}\left[4\frac{{\mathrm{\Omega }}_r\left(b\right)}{b^4}+3\frac{{\mathrm{\Omega }}_b\left(b\right)}{b^3}\right.\hfill \\ \hfill & \left.+3\frac{{\mathrm{\Omega }}_e\left(b\right)}{b^3}+3\left(1+w_{\varphi }\right){\mathrm{\Omega }}_{\varphi }\left(b\right)\right].\hfill \end{array}(8.32)$

The decay of E(a) is expressed here by the growth of the integral.

8.8.1 High zero-point energy initial state: Automatic inflation

The product ρ_cΩ_dS is the aether energy density at the big bang (a ≈ 0). It may have the Planck value $\sim m_P^4$, so that Ω_dS ∼ 10¹²³, which is commonly seen as a catastrophic mismatch between theory and observation. But, as mentioned in Section 2.3, that refers to the bare ZPE, which is unphysical; here it refers to the physical energy content at the Big Bang.

Rather than doing away with the large ZPE, we make it a cornerstone. We now assume that ${\rho }_c{\mathrm{\Omega }}_{\text{dS}}={\rho }_P\sim m_P^4$ is the physical zero point energy density injected in the quantum aether during the Big Bang, where Ω_dS ∼ 10¹²³. This ZPE gets subsequently diluted by the expansion, by creating gravitational waves, by turning it into particles and electrostatic energy, and by participating in the dark matter.

The initial phase of the Universe is a de Sitter universe, with cosmological constant H_dS The Friedman equation ${\dot{a}}^2/a^2=H_0^{2}E(a)$ leads at early times, when only E ≈ Ω_dS ≫ 1 matters, to exponential expansion, a(t) ≈ a_P exp H_dSt with $H_{\text{dS}}=\sqrt{{\mathrm{\Omega }}_{\text{dS}}}{H}_0$, the inverse of the de Sitter time ${\tau }_{\text{dS}}=1/\sqrt{{\mathrm{\Omega }}_{\text{dS}}}{H}_0\approx 25t_P$ for Ω_P = 10¹²³ and 100t_P for Ω_P = 10¹²⁰ with $t_P=\sqrt{\hslash G/c^5}=5.3910^{-44}$ s the Planck time. This behavior is called “inflation”; in EAE theory, it happens automatically; an inflaton field ϕ seems needed to end the inflation. In this classical approach, the initial time where a = 0 appears to be t_i = −∞.

In the course of time, the subtraction terms in (8.31) and 8.32 grow in size and diminish E(a). We assume that, after a certain period, these integrals creep towards Ω_dS, leaving a relatively small E(a), and essentially make an end to the period of inflation. Such an end is generally expected to be smooth and called “graceful exit” (gx).

A candidate for enforcing the gx may be primordial black holes. It happens around a = a_gx where

${\mathrm{\Omega }}_{\text{dS}}-3{\int }_0^{a_{\text{gx}}}\frac{\text{d}b}{b}{\mathrm{\Omega }}_{\varphi }\left(b\right)\ll {\mathrm{\Omega }}_{\text{dS}}.(8.33)$

From then on, the two terms in (8.32) nearly cancel, and the expansion is more effectively expressed by the familiar form (8.14) with Ω_ϕ(a) added, and with Ω_λ from (8.31) and 8.30 expressed in only moderately large terms,

$\begin{array}{ll}\hfill {\mathrm{\Omega }}_{\lambda }& ={\mathrm{\Omega }}_{\mathrm{\Lambda }}+{\int }_a^1\text{d}b\left[\frac{{\mathrm{\Omega }}_r^{\prime }\left(b\right)}{b^4}+\frac{{\mathrm{\Omega }}_b^{\prime }\left(b\right)}{b^3}+\frac{{{\mathrm{\Omega }}_e}^{\prime }\left(b\right)}{b^3}+3\frac{{\mathrm{\Omega }}_{\varphi }\left(b\right)}{b}\right]\hfill \\ \hfill & +{\mathrm{\Omega }}_{\varphi }\left(1\right)-{\mathrm{\Omega }}_{\varphi }\left(a\right),\hfill \end{array}(8.34)$

In order not to “overshoot”, i.e., not to make E negative, Ω_ϕ(a) must have become relatively small near a_gx. For black holes, this may occur by Hawking evaporation, which leads to particle creation and thus increase of their temperature, the so-called reheating.

8.8.2 Low entropy initial state

Roger Penrose has estimated the final entropy of the Universe by considering it as a huge black hole and applying the Bekenstein-Hawking formula. The result S ∼ 10¹²³ (Penrose, 1989) coincides with the above ${\mathrm{\Omega }}_{\text{dS}}\approx m_P^4/{\rho }_c$. This is much larger than the entropy $\sim 10^{88}$ in the CMB radiation. Due to the second law, the entropy kept on increasing in the past, so it must even have been much smaller during the Big Bang. The volume of phase space is V = exp S ∼ exp (10¹²³), hence the question arises how the Creator could select our low entropy Universe out of this enormous number of candidates (Penrose, 1989).

In the above EAE initial state, only EZP/VE is present but no particles, neither photons nor gluons nor black holes, so that all field modes lie in their quantum ground state. Though general quantum systems are described by a mixed state, this case can be described by a pure quantum state, roughly as a product of individual ground states, like the Hartle-Hawking state (Hartle and Hawking, 1983), but with modified individual zero point energies to code the ZPE injection. The fine grained entropy, in this situation the von Neumann entropy, vanishes in a pure state. Being conserved under quantum dynamics, it vanishes at all times. This puts many constraints on the ensuing dynamics, some of which are coded in known conservation laws.

Neglecting these correlations leads to a coarse grained entropy, that increases in time. Starting from zero, this solves Penrose’s conundrum: in EAE theory a zero–or at least, a low–entropy initial state is a consistency property, for which neither fine-tuning nor selection out of a vast set of candidate universes is involved.

9 Conclusion

At the time of writing, there are two standard models. The first is the standard model of particle physics, formulated as a quantum field theory which is shown to be renormalizable by our teachers Gerard ’t Hooft and Tiny Veltman. The second is ΛCDM, the standard model of cosmology, based on the assumptions of a cosmological constant and cold dark matter. Next to the no-show in multiple CDM searches, this approach suffers from the Hubble tension.

Here we put forward that such a new type of matter is neither wanted nor needed, and that standard models of cosmology and particle physics are actually one and the same. No dark matter particle, which would require an extension of the standard model, is involved; a new view on the zero point energy of the vacuum suffices to explain the main constituents of the Universe, the 95% fraction of dark matter and dark energy. Given that the Casimir effect for moving parallel conducting plates involves an inflow or outflow of zero point energy (ZPE), we consider the ZPE as a fluid that can partly act as dark matter. Interpretation of our analytical results leads to consider the energy of the vacuum itself as zero, or unmeasurable in any way, while energy added to it, or taken out from it, acts as “aether” energy (though not the historic aether ruled out by the Michelson-Morley experiment), a physical component, subject to the Einstein equations.

In this interpretation, we are led by the principle that one should first solve the mathematics and then provide a physical interpretation of the results, as applied to our approach to dynamics of quantum measurement and the ensuing statistical interpretation of quantum mechanics (Allahverdyan et al., 2013; 2017; 2024).

The Einstein equations require that ZPE is assisted by an electric field, which can arise from a tiny mismatch between plus and minus charges in cosmic plasmas. The combination is termed electro-zero-point energy (EZPE) or electro-aether-energy (EAE), which aims to replace the popular cold dark matter. In fact, the connection to an electric field seems natural but is not compulsary; its role may be taken by any vector field producing the structure ${\rho }_E{C}_{\nu }^{\mu }$ in Eq. 3.3.

Rather than invoking new physics, EAE theory takes a new view on the capacities of the zero point energy of the (quantum) vacuum or just the energy of the classical vacuum. We are led to view it not as a static, uniform entity but as a type of fluid, that can condense on mass concentrations. This application of the standard model appoints an indispensable, and even leading role for the aether, to function as the main actor in cosmic structures by providing, presently, 70% of the total mass/energy as dark energy and 6% involved as the ZPE part of the dark matter, combined with 19% electrostatic energy in the dark matter. Particles, in the form of normal matter, only play a secondary role, coming into existence later in the early Universe and forming presently some 5% of the total mass.

EAE theory predicts that the dark matter present during the emission of cosmic background radiation arose from ZPE/AE condensation; this leads naturally to the assumption of primordial black holes. They may have grown by EAE condensation and merging. Black holes from stellar collapse can likewise grow by gentle inflow of EAE, filling “mass gaps” and triggering the growth of supermassive BHs not dominated by merging. Massive BHs may “steal” the EAE from small surrounding ones, the tidal field effect.

Next, the BHs organize the galaxy around them, by an interdependent propensity for the available zero point energy, that partly streams in from infinity and is partly taken out of the vacuum in the outskirts. To achieve this, the charge mismatch has to be optimal according to the Einstein-Coulomb equations. In a galaxy and in a cluster there is a dynamical connection with the baryons: in order to host more ZPE coming in from infinity, an adjustment of the local net charge mismatch has to take place. Flow of aether energy into black holes requires inflow of charges, assuring a dynamical connection between the central BH and the whole galaxy.

A dynamical instability is identified, which assists in a speedy buildup of galactic and cluster cores with constant DM density, supporting EAE theory and observations on the cusp-core problem. The reverse mechanism can explain the expansion and possible dissolution of galactic and cluster cores.

Hydrostatic equilibrium in galaxy clusters satisfied in EAE.

On cosmological scales the EAE acts as a pressureless type of cold dark matter. EAE theory goes even one step further: the “cosmological constant” measured from supernovae is merely the present value of the dynamical zero point energy, that may have started out at the Big Bang with the field theoretic value larger by some 123 orders of magnitude. In EAE theory there is no fine-tuning, the “cosmological constant” is small, since it is the present value of a decaying function.

Despite Einstein’s most famous equation E = mc², EAE theory involves a discrepancy between mass and energy. Mass and matter are related to particles, including photons, while energy relates to a modified aether without further particles. The kinetic energy of particles remains included in the “mass”.

The analysis of the present section shows that the final parsec problem is solved by mass accretion as it happens for EAE. Two supermassive BHs at parsec distance will finally merge by absorbing aether energy, which enhances the probability for observing gravitational waves from merging events by the future LISA system.

10 Summary

Electro aether energy (EAE, or, equivalently, electro-vacuum energy EVE, or electro-zero-point energy EZPE) relies on electric fields and the zero point energy of the quantum fields of the standard model of particle physics. Alternatively, it is just a property of the “classical” vacuum. The energy, often equated to a cosmological constant, actually gets depleted in its condensation as part of dark matter. These insights explain a cornucopia of phenomena.

After considering various aspects of ZPE in Section 2, the EAE framework is laid out in Section 3. For spherically symmetric setups, it is shown how a non-uniform ZPE, combined with an electric field, is compatible with the Einstein Eq. ZPE is absorbed from the environment, while subject to a reshuffling inside the galaxy or cluster; its density is positive inside a core region and negative in the halo region. There results a core with a net plus charge, surrounded by a halo with net minus charge; the total charge is zero.

A stability analysis is carried out. An inhomogeneous solution is connected to the formation of dark matter cores made up of EAE, and their later dissolution.

Estimates for various quantities are discussed in Section 4. Particular attention is paid to the net charge fraction in the plasma. While standard estimates allow maximally a fraction of 10^–18, EAE involves a fraction that can perhaps be 10⁵ times larger. Analysis of the hydrostatic equilibrium shows that the strong Coulomb repulsion and attraction is counteracted by the negative casu quo positive gradient of the ZPE pressure.

Section 5 deals with black holes. They can grow by EAE accretion, which rules out the “mass gaps” from standard arguments, and is supported by some gravitational wave events. It is shown that the final parsec problem for black hole merging is overcome by ongoing mass accretion within EAE theory.

Section 6 considered the application to galaxies. It is postulated that results from Modified Newtonian Dynamics (MOND) can be modeled by EAE theory, and that the involved electric field and underlying charge density regulates a connection between the dark matter structure, the shape of the rotation curve and the central supermassive black hole. It is pointed out that constant-density dark matter cores, more than cusped ones, should be expected, and support for this is reviewed.

In the application to galaxy clusters of Section 7, first an isothermal sphere-type of fit is worked out for strong lensing data of two fat clusters and the relation to the charge distributions and ZPE profiles is worked out. Special attention is payed to their hydrodynamic equilibrium puzzle, solved in EAE theory.

For the application to cosmology, Section 8 first shows that at cosmological scales, the pressure connected to EAE dark matter vanishes, as desired. It is pointed out that ongoing ZPE condensation leads to a late-time increasing amount of dark matter. A fit of the ΛCDM theory for the Planck data for the cosmic microwave background already softens the Hubble tension between its value H₀ = 68 km/s Mpc and the late-time value H₀ = 73 km/s Mpc from supernovae. To investigate a full resolution of the problem, the CMB theory within EAE theory needs to be worked out and fitted. Next, the cosmologically-near and far future is considered. A big crunch scenario is worked out involving a dominant role of black holes. Finally, attention is paid to the Big Bang period, where it is assumed that a large cosmological “constant” is inserted, leading to an initial state with large aether energy and zero entropy. Inflation occurs automatically.

Various further dark matter aspects in galaxies, clusters and cosmology seem to fall into place like pieces of a jigsaw puzzle, see Section 9 of ref. (Nieuwenhuizen, 2023b).

11 Outlook

In EAE cosmology, there is no dark matter particle, as supported by the no-show in dark matter searches, but the EAE theory gets ruled out when such a detection is made.

Simulations for the EAE paradigm are desired to test it on various observations, replacing the current ΛCDM simulations. Given the great expertise in the latter, the situation seems hopeful. Irrespective of our proposal, the recent James Webb Space Telescope observation of very early onset of massive galaxy formation (Labbé et al., 2022) already seems to demand a new understanding of structure formation.

With the arrival of a new standard model, many issues in cosmology may hope for explanation. We have mentioned the Hubble tension, softened already, the Lithium-7 problem and hinted at black holes for a big crunch and, perhaps, a gentle exit of inflation.

The predicted smaller age of the Universe of some 12.8 Gyr poses questions regarding the earliest stars and structures; these are not new, however, since they follow mainly from adopting the large value of the present Hubble constant. In this regard, early black hole growth by EAE accretion and early galaxy formation due to rupture of hydrogen clouds may emerge as a consistent picture, allowing vast polar structures of matter around them due to the EAE scaffold. Being charged locally, the expanding primordial hydrogen cloud will be subject to lightnings, after which the thunders may provide the onset of prolate and/or barred structure formation.

The question “why is the cosmological constant so small” gets the EAE answer: the cosmological “constant” depends on space and time; there is no fine-tuning, during the Big Bang a large zero point energy was inserted, which decreased. It was a cold Big Bang, that quickly became hot. The possibility for a recollapsing Universe may relate to a cyclic repetition of expansions and collapses.

In all these processes, aether energy (vacuum energy) is the ideal servant, an obedient, malleable agency, doing just the right thing at the right time. One may wonder whether it plays a similar role in standard, terrestrial electrostatic and perhaps magnetostatic problems. Progress in this direction will be reported elsewhere (Nieuwenhuizen, 2024). Lastly, one may wonder whether, as in black holes, also in cosmology, the rotation of structures can carry some of the burden of the net charges.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

TN: Investigation, Methodology, Writing–original draft, Writing–review and editing, Conceptualization.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

It is a pleasure to thank Rudolf Sprik, Ben van Linden van den Heuvell, Ralph Wijers, Indranil Banik, Piet Mulders, Peter Keefe, Rudy Schild and Jasper van Wezel for discussion.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹This manuscript is an update of arXiv:2303.04637, submitted to the arXiv on 23 February 2023.

²Other sources report 120 orders of magnitude; both are estimates. The factor 10123 is sometimes called the Penrose number, named after the Nobel laureate Roger Penrose.

³Unless indicated otherwise, we employ units ℏ = c = 1, ɛ₀ = 1/4π, μ₀ = 4π.

⁴A factor 3 between electric and zero point contributions was first encountered in integral form in the exact solutions for black holes with a regular interior (Nieuwenhuizen, 2023a), and also occurred in the present work at the end of sec. 3.5.

⁵H₀ = 74, δ_e = 0.015, τ = 0.1225, ω_b = 0.0231, ω_c = 0.128, ln 1010A_s = 3.162, n_s = 1.029, Y_He = 0.2398, N_ur = 3.719, Ω_k = 0.00466, χ2/ν = 1.177.

References

Abbott, T., Acevedo, M., Aguena, M., Alarcon, A., Allam, S., Alves, O., et al. (2024) The Dark Energy Survey: cosmology results with ∼1500 new high-redshift type ia supernovae using the full 5-year dataset. arXiv preprint arXiv:2401.02929.

Google Scholar

Aghanim, N., Akrami, Y., Ashdown, M., Aumont, J., Baccigalupi, C., Ballardini, M., et al. (2020). Planck 2018 results-vi. cosmological parameters. Astronomy Astrophysics 641, A6.

Google Scholar

Alcock, C., Allsman, R., Alves, D. R., Axelrod, T., Becker, A. C., Bennett, D., et al. (2000). The macho project: microlensing results from 5.7 years of Large Magellanic Cloud observations. Astrophysical J. 542, 281–307. doi:10.1086/309512

CrossRef Full Text | Google Scholar

Allahverdyan, A. E., Balian, R., and Nieuwenhuizen, T. M. (2013). Understanding quantum measurement from the solution of dynamical models. Phys. Rep. 525, 1–166. doi:10.1016/j.physrep.2012.11.001

CrossRef Full Text | Google Scholar

Allahverdyan, A. E., Balian, R., and Nieuwenhuizen, T. M. (2017). A sub-ensemble theory of ideal quantum measurement processes. Ann. Phys. 376, 324–352. doi:10.1016/j.aop.2016.11.001

CrossRef Full Text | Google Scholar

Allahverdyan, A. E., Balian, R., and Nieuwenhuizen, T. M. (2024). Teaching ideal quantum measurement, from dynamics to interpretation. Comptes Rendus Phys.

CrossRef Full Text | Google Scholar

Arcadi, G., Dutra, M., Ghosh, P., Lindner, M., Mambrini, Y., Pierre, M., et al. (2018). The waning of the WIMP? a Review of models, searches, and constraints. Eur. Phys. J. C 78, 203–257. doi:10.1140/epjc/s10052-018-5662-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Arita, J., Kashikawa, N., Matsuoka, Y., He, W., Ito, K., Liang, Y., et al. (2023). Subaru high-z exploration of low-luminosity quasars (SHELLQs). XVIII. The dark matter halo mass of quasars at z ∼ 6. Astrophysical J. 954, 210. doi:10.3847/1538-4357/ace43a

CrossRef Full Text | Google Scholar

Armitage, P. J., and Natarajan, P. (2002). Accretion during the merger of supermassive black holes. Astrophysical J. 567, L9–L12. doi:10.1086/339770

CrossRef Full Text | Google Scholar

Bais, F., and Russell, R. (1975). Magnetic-monopole solution of non-Abelian gauge theory in curved spacetime. Phys. Rev. D. 11, 2692–2695. doi:10.1103/physrevd.11.2692

CrossRef Full Text | Google Scholar

Balian, R., and Duplantier, B. (2004) Geometry of the Casimir effect. arXiv preprint quant-ph/0408124.

Google Scholar

Bañados, E., Venemans, B. P., Mazzucchelli, C., Farina, E. P., Walter, F., Wang, F., et al. (2018). An 800-million-solar-mass black hole in a significantly neutral Universe at a redshift of 7.5. Nature 553, 473–476. doi:10.1038/nature25180

PubMed Abstract | CrossRef Full Text | Google Scholar

Banik, I., Pittordis, C., Sutherland, W., Famaey, B., Ibata, R., Mieske, S., et al. (2024). Strong constraints on the gravitational law from Gaia DR3 wide binaries. Mon. Notices R. Astronomical Soc. 527, 4573–4615. doi:10.1093/mnras/stad3393

CrossRef Full Text | Google Scholar

Banik, I., and Zhao, H. (2022). From galactic bars to the Hubble tension: weighing up the astrophysical evidence for Milgromian gravity. Symmetry 14, 1331. doi:10.3390/sym14071331

CrossRef Full Text | Google Scholar

Bartels, R., Calore, F., Storm, E., and Weniger, C. (2018). Galactic binaries can explain the Fermi Galactic centre excess and 511 keV emission. Mon. Notices R. Astronomical Soc. 480, 3826–3841. doi:10.1093/mnras/sty2135

CrossRef Full Text | Google Scholar

Beck, R., Balogh, A., Bykov, A., Treumann, R. A., and Widrow, L. M. (2013) Large-scale magnetic fields in the universe. Springer.

Google Scholar

Bertone, G. (2010) Particle dark matter: observations, models and searches. Cambridge University Press.

Google Scholar

Blas, D., Lesgourgues, J., and Tram, T. (2011). The cosmic linear anisotropy solving system (class). Part II: approximation schemes. J. Cosmol. Astropart. Phys. 2011, 034. doi:10.1088/1475-7516/2011/07/034

CrossRef Full Text | Google Scholar

Blumenthal, G. R., Faber, S., Primack, J. R., and Rees, M. J. (1984). Formation of galaxies and large-scale structure with cold dark matter. Nature 311, 517–525. doi:10.1038/311517a0

CrossRef Full Text | Google Scholar

Blumenthal, G. R., Pagels, H., and Primack, J. R. (1982). Galaxy formation by dissipationless particles heavier than neutrinos. Nature 299, 37–38. doi:10.1038/299037a0

CrossRef Full Text | Google Scholar

Boldrini, P. (2021). The cusp–core problem in gas-poor dwarf spheroidal galaxies. Galaxies 10 (5), 5. doi:10.3390/galaxies10010005

CrossRef Full Text | Google Scholar

Bond, J. R., Szalay, A. S., and Turner, M. S. (1982). Formation of galaxies in a gravitino-dominated Universe. Phys. Rev. Lett. 48, 1636–1639. doi:10.1103/physrevlett.48.1636

CrossRef Full Text | Google Scholar

Boyarsky, A., Ruchayskiy, O., Iakubovskyi, D., and Franse, J. (2014). Unidentified line in X-ray spectra of the Andromeda galaxy and Perseus galaxy cluster. Phys. Rev. Lett. 113, 251301. doi:10.1103/physrevlett.113.251301

PubMed Abstract | CrossRef Full Text | Google Scholar

Boyer, T. H. (1968). Quantum electromagnetic zero-point energy of a conducting spherical shell and the Casimir model for a charged particle. Phys. Rev. 174, 1764–1776. doi:10.1103/physrev.174.1764

CrossRef Full Text | Google Scholar

Brout, D., Scolnic, D., Popovic, B., Riess, A. G., Carr, A., Zuntz, J., et al. (2022). The Pantheon+ analysis: cosmological constraints. Astrophysical J. 938, 110. doi:10.3847/1538-4357/ac8e04

CrossRef Full Text | Google Scholar

Brouwer, M. M., Visser, M. R., Dvornik, A., Hoekstra, H., Kuijken, K., Valentijn, E. A., et al. (2017). First test of Verlinde’s theory of emergent gravity using weak Gravitational lensing measurements. Mon. Notices R. Astronomical Soc. 466, 2547–2559. doi:10.1093/mnras/stw3192

CrossRef Full Text | Google Scholar

Bull, P., Akrami, Y., Adamek, J., Baker, T., Bellini, E., Jiménez, J. B., et al. (2016). Beyond λCDM: problems, solutions, and the road ahead. Phys. Dark Universe 12, 56–99. doi:10.1016/j.dark.2016.02.001

CrossRef Full Text | Google Scholar

Bullock, J. S., and Boylan-Kolchin, M. (2017). Small-scale challenges to the λCDM paradigm. Annu. Rev. Astron. Astrophys. 55, 343–387. doi:10.1146/annurev-astro-091916-055313

CrossRef Full Text | Google Scholar

Camarena, D., and Marra, V. (2020a). Local determination of the Hubble constant and the deceleration parameter. Phys. Rev. Res. 2, 013028. doi:10.1103/physrevresearch.2.013028

CrossRef Full Text | Google Scholar

Camarena, D., and Marra, V. (2020b). A new method to build the (inverse) distance ladder. Mon. Notices R. Astronomical Soc. 495, 2630–2644. doi:10.1093/mnras/staa770

CrossRef Full Text | Google Scholar

Casimir, H. B. (1948). On the attraction between two perfectly conducting plates. Proc. Kon. Ned. Akad. Wet. 51, 793.

Google Scholar

Cetto, A., and De La Peña, L. (1993). Casimir effect for bodies of arbitrary size. Il Nuovo Cimento B 108, 447–458. doi:10.1007/bf02828725

CrossRef Full Text | Google Scholar

Chakraborty, K., Rahaman, F., Ray, S., Nandi, A., and Islam, N. (2014). Possible features of galactic halo with electric field and observational constraints. General Relativ. Gravit. 46, 1807–1824. doi:10.1007/s10714-014-1807-y

CrossRef Full Text | Google Scholar

Coc, A., and Vangioni, E. (2005). Lithium and big-bang nucleosynthesis. Proc. Int. Astronomical Union 1, 13–22. doi:10.1017/s1743921305005156

CrossRef Full Text | Google Scholar

Collaboration, L., et al. (2022) Measurement of lepton universality parameters in B⁺↦K⁺ℓ⁺ℓ⁻ and B⁰↦K*⁰ℓ⁺ℓ⁻ decays. arXiv preprint arXiv:2212.09153.

Google Scholar

Cook, A. (2001). Hendrik Christoffel van de Hulst Ridder in de Orde van Nederlandse Leeuw. 19 November 1918-31 July 2000. Biogr. Memoirs Fellows R. Soc. 47, 465–479. doi:10.1098/rsbm.2001.0028

CrossRef Full Text | Google Scholar

Corda, C. (2009). Interferometric detection of gravitational waves: the definitive test for general relativity. Int. J. Mod. Phys. D 18, 2275–2282. doi:10.1142/s0218271809015904

CrossRef Full Text | Google Scholar

Creevey, O., Thévenin, F., Berio, P., Heiter, U., Von Braun, K., Mourard, D., et al. (2015). Benchmark stars for Gaia Fundamental properties of the Population ii star HD 140283 from interferometric, spectroscopic, and photometric data. Astronomy Astrophysics 575, A26. doi:10.1051/0004-6361/201424310

CrossRef Full Text | Google Scholar

Curtis-Lake, E., Carniani, S., Cameron, A., Charlot, S., Jakobsen, P., Maiolino, R., et al. (2023). Spectroscopic confirmation of four metal-poor galaxies at z = 10.3–13.2. Nat. Astron. 7, 622–632. doi:10.1038/s41550-023-01918-w

CrossRef Full Text | Google Scholar

Dainotti, M. G., De Simone, B., Schiavone, T., Montani, G., Rinaldi, E., and Lambiase, G. (2021). On the Hubble constant tension in the SNe ia Pantheon sample. Astrophysical J. 912, 150. doi:10.3847/1538-4357/abeb73

CrossRef Full Text | Google Scholar

De Blok, W., McGaugh, S. S., Bosma, A., and Rubin, V. C. (2001). Mass density profiles of low surface brightness galaxies. Astrophysical J. 552, L23–L26. doi:10.1086/320262

CrossRef Full Text | Google Scholar

Del Popolo, A., and Le Delliou, M. (2021). Review of solutions to the cusp-core problem of the λCDM model. Galaxies 9, 123. doi:10.3390/galaxies9040123

CrossRef Full Text | Google Scholar

De Swart, J., Bertone, G., and van Dongen, J. (2017). How dark matter came to matter. Nat. Astron. 1, 0059–9. doi:10.1038/s41550-017-0059

CrossRef Full Text | Google Scholar

Di Dio, E., Montanari, F., Lesgourgues, J., and Durrer, R. (2013). The CLASSgal code for relativistic cosmological large scale structure. J. Cosmol. Astropart. Phys. 2013, 044. doi:10.1088/1475-7516/2013/11/044

CrossRef Full Text | Google Scholar

Di Paolo, C., Salucci, P., and Erkurt, A. (2019). The universal rotation curve of low surface brightness galaxies–IV. The interrelation between dark and luminous matter. Mon. Notices R. Astronomical Soc. 490, 5451–5477. doi:10.1093/mnras/stz2700

CrossRef Full Text | Google Scholar

Dreitlein, J. (1974). Broken symmetry and the cosmological constant. Phys. Rev. Lett. 33, 1243–1244. doi:10.1103/physrevlett.33.1243

CrossRef Full Text | Google Scholar

Farrah, D., Croker, K. S., Zevin, M., Tarlé, G., Faraoni, V., Petty, S., et al. (2023a). Observational evidence for cosmological coupling of black holes and its implications for an astrophysical source of dark energy. Astrophysical J. Lett. 944, L31. doi:10.3847/2041-8213/acb704

CrossRef Full Text | Google Scholar

Farrah, D., Petty, S., Croker, K. S., Tarlé, G., Zevin, M., Hatziminaoglou, E., et al. (2023b). A preferential growth channel for supermassive black holes in elliptical galaxies at z ≤ 2. Astrophysical J. 943, 133. doi:10.3847/1538-4357/acac2e

CrossRef Full Text | Google Scholar

Gurnett, D., Kurth, W., Burlaga, L., and Ness, N. (2013). In situ observations of interstellar plasma with Voyager 1. Science 341, 1489–1492. doi:10.1126/science.1241681

PubMed Abstract | CrossRef Full Text | Google Scholar

Hartle, J. B., and Hawking, S. W. (1983). Wave function of the universe. Phys. Rev. D. 28, 2960–2975. doi:10.1103/physrevd.28.2960

CrossRef Full Text | Google Scholar

Hashimoto, T., Álvarez-Márquez, J., Fudamoto, Y., Colina, L., Inoue, A., Nakazato, Y., et al. (2023). Reionization and the ISM/stellar origins with JWST and ALMA (RIOJA): the core of the highest-redshift galaxy overdensity at z = 7.88 confirmed by NIRSpec/JWST. Astrophysical J. Lett. 955, L2. doi:10.3847/2041-8213/acf57c

CrossRef Full Text | Google Scholar

Kafle, P. R., Sharma, S., Lewis, G. F., and Bland-Hawthorn, J. (2014). On the shoulders of giants: properties of the stellar halo and the Milky Way mass distribution. Astrophysical J. 794, 59. doi:10.1088/0004-637x/794/1/59

CrossRef Full Text | Google Scholar

Kapteyn, J. C. (2013). “First attempt at a theory of the arrangement and motion of the sidereal system,” in A source book in Astronomy and astrophysics (Harvard University Press), 542–549.

Google Scholar

Karukes, E. V., and Salucci, P. (2017). The universal rotation curve of dwarf disc galaxies. Mon. Notices R. Astronomical Soc. 465, 4703–4722. doi:10.1093/mnras/stw3055

CrossRef Full Text | Google Scholar

Keeley, R. E., and Shafieloo, A. (2023). Ruling out new physics at low redshift as a solution to the h₀ tension. Phys. Rev. Lett. 131, 111002. doi:10.1103/physrevlett.131.111002

PubMed Abstract | CrossRef Full Text | Google Scholar

Kroupa, P. (2012). The dark matter crisis: falsification of the current standard model of cosmology. Publ. Astronomical Soc. Aust. 29, 395–433. doi:10.1071/as12005

CrossRef Full Text | Google Scholar

Kroupa, P. (2014). “The planar satellite distributions around Andromeda, the Milky Way and other galaxies, and their implications for fundamental physics,” in Multi-Spin Galaxies, ASP Conference Series 486, 183. Available at: https://ui.adsabs.harvard.edu/abs/2014ASPC.486.183K/abstract

Google Scholar

Kroupa, P. (2015). Galaxies as simple dynamical systems: observational data disfavor dark matter and stochastic star formation. Can. J. Phys. 93, 169–202. doi:10.1139/cjp-2014-0179

CrossRef Full Text | Google Scholar

Labbé, I., van Dokkum, P., Nelson, E., Bezanson, R., Suess, K., Leja, J., et al. (2022) A very early onset of massive galaxy formation. arXiv preprint arXiv:2207.12446.

Google Scholar

Land, K., and Magueijo, J. (2005). Examination of evidence for a preferred axis in the cosmic radiation anisotropy. Phys. Rev. Lett. 95, 071301. doi:10.1103/physrevlett.95.071301

PubMed Abstract | CrossRef Full Text | Google Scholar

Lelli, F., McGaugh, S. S., Schombert, J. M., and Pawlowski, M. S. (2017). One law to rule them all: the radial acceleration relation of galaxies. Astrophysical J. 836, 152. doi:10.3847/1538-4357/836/2/152

CrossRef Full Text | Google Scholar

Lemze, D., Rephaeli, Y., Barkana, R., Broadhurst, T., Wagner, R., and Norman, M. L. (2011). Quantifying the collisionless nature of dark matter and galaxies in A1689. Astrophysical J. 728, 40. doi:10.1088/0004-637x/728/1/40

CrossRef Full Text | Google Scholar

Linde, A. D. (1974). Is the Lee constant a cosmological constant. JETP Lett. 19, 183.

Google Scholar

López Fune, E., Salucci, P., and Corbelli, E. (2017). Radial dependence of the dark matter distribution in M33. Mon. Notices R. Astronomical Soc. 468, 147–153. doi:10.1093/mnras/stx429

CrossRef Full Text | Google Scholar

Maiolino, R., Scholtz, J., Witstok, J., Carniani, S., D’Eugenio, F., de Graaff, A., et al. (2024). A small and vigorous black hole in the early Universe. Nature 627, 59–63. doi:10.1038/s41586-024-07052-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Metz, M., and Kroupa, P. (2007). Dwarf spheroidal satellites: are they of tidal origin? Mon. Notices R. Astronomical Soc. 376, 387–392. doi:10.1111/j.1365-2966.2007.11438.x

CrossRef Full Text | Google Scholar

Migkas, K., Schellenberger, G., Reiprich, T., Pacaud, F., Ramos-Ceja, M., and Lovisari, L. (2020). Probing cosmic isotropy with a new x-ray galaxy cluster sample through the lx–t scaling relation. Astronomy Astrophysics 636, A15. doi:10.1051/0004-6361/201936602

CrossRef Full Text | Google Scholar

Milgrom, M. (1983). A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophysical J. 270, 365–370. doi:10.1086/161130

CrossRef Full Text | Google Scholar

Milosavljević, M., and Merritt, D. (2003). “The final parsec problem,” in AIP conference proceedings (American Institute of Physics), 686, 201–210. doi:10.1063/1.1629432

CrossRef Full Text | Google Scholar

Milton, K. A. (2003) The Casimir effect: physical manifestations of zero-point energy. American Association of Physics Teachers.

Google Scholar

Molnar, S., Chiu, I.-N., Umetsu, K., Chen, P., Hearn, N., Broadhurst, T., et al. (2010). Testing strict hydrostatic equilibrium in simulated clusters of galaxies: implications for A1689. Astrophysical J. Lett. 724, L1–L4. doi:10.1088/2041-8205/724/1/l1

CrossRef Full Text | Google Scholar

Morandi, A., Limousin, M., Sayers, J., Golwala, S. R., Czakon, N. G., Pierpaoli, E., et al. (2012). X-ray, lensing and Sunyaev-Zel’dovich triaxial analysis of Abell 1835 out to R 200. Mon. Notices R. Astronomical Soc. 425, 2069–2082. doi:10.1111/j.1365-2966.2012.21196.x

CrossRef Full Text | Google Scholar

Morandi, A., Pedersen, K., and Limousin, M. (2010). Unveiling the three-dimensional structure of galaxy clusters: resolving the discrepancy between X-ray and lensing masses. Astrophysical J. 713, 491–502. doi:10.1088/0004-637x/713/1/491

CrossRef Full Text | Google Scholar

Nanayakkara, T., Glazebrook, K., Jacobs, C., Kawinwanichakij, L., Schreiber, C., Brammer, G., et al. (2024). A population of faint, old, and massive quiescent galaxies at 3 < z < 4 revealed by JWST NIRSpec spectroscopy. Sci. Rep. 14, 3724. doi:10.1038/s41598-024-52585-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Navarro, J. F., Frenk, C. S., and White, S. D. (1997). A universal density profile from hierarchical clustering. Astrophysical J. 490, 493–508. doi:10.1086/304888

CrossRef Full Text | Google Scholar

Nieuwenhuizen, T. M. (2017). How Zwicky already ruled out modified gravity theories without dark matter. Fortschritte Phys. 65, 1600050. doi:10.1002/prop.201600050

CrossRef Full Text | Google Scholar

Nieuwenhuizen, T. M. (2020). Subjecting dark matter candidates to the cluster test. Fluctuation Noise Lett. 19, 2050016. doi:10.1142/s0219477520500169

CrossRef Full Text | Google Scholar

Nieuwenhuizen, T. M. (2021) The interior of hairy black holes in standard model physics. arXiv preprint arXiv:2108.01422.

Google Scholar

Nieuwenhuizen, T. M. (2023a) Exact solutions for black holes with a smooth quantum core. arXiv preprint arXiv:2302.14653.

Google Scholar

Nieuwenhuizen, T. M. (2023b) Solution of the dark matter riddle within standard model physics: from galaxies and clusters to cosmology. arXiv preprint arXiv:2303.04637v1.

Google Scholar

Nieuwenhuizen, T. M. (2024) How the aether rescues the Lorentz electron and imprints its Newtonian and geodesic motion, and the equivalence principle. submitted.

Google Scholar

Nieuwenhuizen, T. M., Limousin, M., and Morandi, A. (2021). Accurate modeling of the strong and weak lensing profiles for the galaxy clusters Abell 1689 and 1835. Eur. Phys. J. Special Top. 230, 1137–1148. doi:10.1140/epjs/s11734-021-00101-4

CrossRef Full Text | Google Scholar

Nieuwenhuizen, T. M., and Morandi, A. (2013). Are observations of the galaxy cluster A1689 consistent with a neutrino dark matter scenario? Mon. Notices R. Astronomical Soc. 434, 2679–2683. doi:10.1093/mnras/stt1216

CrossRef Full Text | Google Scholar

Oehm, W., and Kroupa, P. (2024). The relevance of dynamical friction for the MW/LMC/SMC triple system. Universe 10, 143. doi:10.3390/universe10030143

CrossRef Full Text | Google Scholar

Ou, X., Eilers, A.-C., Necib, L., and Frebel, A. (2024). The dark matter profile of the Milky Way inferred from its circular velocity curve. Mon. Notices R. Astronomical Soc. 528, 693–710. stae034. doi:10.1093/mnras/stae034

CrossRef Full Text | Google Scholar

Palunas, P., and Williams, T. (2000). Maximum disk mass models for spiral galaxies. Astronomical J. 120, 2884–2903. doi:10.1086/316878

CrossRef Full Text | Google Scholar

Pandya, V., Zhang, H., Iyer, K. G., McGrath, E., Barro, G., Finkelstein, S. L., et al. (2024). Galaxies going bananas: inferring the 3d geometry of high-redshift galaxies with JWST-CEERS. Astrophysical J. 963, 54. doi:10.3847/1538-4357/ad1a13

CrossRef Full Text | Google Scholar

Pawlowski, M., Pflamm-Altenburg, J., and Kroupa, P. (2012). The VPOS: a vast polar structure of satellite galaxies, globular clusters and streams around the Milky Way. Mon. Notices R. Astronomical Soc. 423, 1109–1126. doi:10.1111/j.1365-2966.2012.20937.x

CrossRef Full Text | Google Scholar

Pawlowski, M. S., Famaey, B., Jerjen, H., Merritt, D., Kroupa, P., Dabringhausen, J., et al. (2014). Co-orbiting satellite galaxy structures are still in conflict with the distribution of primordial dwarf galaxies. Mon. Notices R. Astronomical Soc. 442, 2362–2380. doi:10.1093/mnras/stu1005

CrossRef Full Text | Google Scholar

Peebles, P. (1982). Large scale background temperature and mass fluctuations due to scale invariant primeval perturbations. Astrophys. J. 263, L1. doi:10.1086/183911

CrossRef Full Text | Google Scholar

Penrose, R. (1989) The emperor’s new mind: concerning computers, minds, and the laws of physics. Oxford University Press.

Google Scholar

Perivolaropoulos, L., and Skara, F. (2022). Challenges for λcdm: an update. New Astron. Rev. 95, 101659. doi:10.1016/j.newar.2022.101659

CrossRef Full Text | Google Scholar

Perlmutter, S., Aldering, G., Goldhaber, G., Knop, R., Nugent, P., Castro, P. G., et al. (1999). Measurements of ω and λ from 42 high-redshift supernovae. Astrophysical J. 517, 565–586. doi:10.1086/307221

CrossRef Full Text | Google Scholar

Peskin, M. E., and Schroeder, D. V. (2018) An introduction to quantum field theory. Cambridge, MA: CRC Press.

Google Scholar

Pignol, G., Clement, B., Guigue, M., Rebreyend, D., and Voirin, B. (2015) Constraints on dark photon dark matter using Voyager magnetometric survey. arXiv preprint arXiv:1507.06875.

Google Scholar

Pitrou, C., Coc, A., Uzan, J.-P., and Vangioni, E. (2018). Precision Big Bang nucleosynthesis with improved helium-4 predictions. Phys. Rep. 754, 1–66. doi:10.1016/j.physrep.2018.04.005

CrossRef Full Text | Google Scholar

Reucroft, S. (2014) Galactic charge. arXiv preprint arXiv:1409.3096.

Google Scholar

Rich, J. (2009) Fundamentals of cosmology. Springer Science and Business Media.

Google Scholar

Riess, A. G., Filippenko, A. V., Challis, P., Clocchiatti, A., Diercks, A., Garnavich, P. M., et al. (1998). Observational evidence from supernovae for an accelerating Universe and a cosmological constant. Astronomical J. 116, 1009–1038. doi:10.1086/300499

CrossRef Full Text | Google Scholar

Rodrigues, D. C., Marra, V., del Popolo, A., and Davari, Z. (2018). Absence of a fundamental acceleration scale in galaxies. Nat. Astron. 2, 668–672. doi:10.1038/s41550-018-0498-9

CrossRef Full Text | Google Scholar

Roshan, M., Ghafourian, N., Kashfi, T., Banik, I., Haslbauer, M., Cuomo, V., et al. (2021). Fast galaxy bars continue to challenge standard cosmology. Mon. Notices R. Astronomical Soc. 508, 926–939. doi:10.1093/mnras/stab2553

CrossRef Full Text | Google Scholar

Rubin, V. C., and Ford, W. K. (1970). Rotation of the Andromeda nebula from a spectroscopic survey of emission regions. Astrophysical J. 159, 379. doi:10.1086/150317

CrossRef Full Text | Google Scholar

Rycroft, M., Israelsson, S., and Price, C. (2000). The global atmospheric electric circuit, solar activity and climate change. J. Atmos. Solar-Terrestrial Phys. 62, 1563–1576. doi:10.1016/s1364-6826(00)00112-7

CrossRef Full Text | Google Scholar

Salucci, P., and Burkert, A. (2000). Dark matter scaling relations. Astrophysical J. 537, L9–L12. doi:10.1086/312747

CrossRef Full Text | Google Scholar

Sancisi, R. (2004). “The visible matter-dark matter coupling,” in Symposium international astronomical union (Cambridge University Press), 220, 233–240.

CrossRef Full Text | Google Scholar

Sawala, T., Cautun, M., Frenk, C., Helly, J., Jasche, J., Jenkins, A., et al. (2023). The Milky Way’s plane of satellites is consistent with ΛCDM. Nat. Astron. 7, 481–491. doi:10.1038/s41550-022-01856-z

CrossRef Full Text | Google Scholar

Schlaufman, K. C., Thompson, I. B., and Casey, A. R. (2018). An ultra metal-poor star near the hydrogen-burning limit. Astrophysical J. 867, 98. doi:10.3847/1538-4357/aadd97

CrossRef Full Text | Google Scholar

Secrest, N. J., von Hausegger, S., Rameez, M., Mohayaee, R., and Sarkar, S. (2022). A challenge to the standard cosmological model. Astrophysical J. Lett. 937, L31. doi:10.3847/2041-8213/ac88c0

CrossRef Full Text | Google Scholar

Sharma, G., Salucci, P., and van de Ven, G. (2022). Observational evidence of evolving dark matter profiles at z ≤ 1. Astronomy Astrophysics 659, A40. doi:10.1051/0004-6361/202141822

CrossRef Full Text | Google Scholar

Shelest, A., and Lelli, F. (2020). From spirals to lenticulars: evidence from the rotation curves and mass models of three early-type galaxies. Astronomy Astrophysics 641, A31. doi:10.1051/0004-6361/202038184

CrossRef Full Text | Google Scholar

Sikivie, P. (1983). Experimental tests of the “invisible” axion. Phys. Rev. Lett. 51, 1415–1417. doi:10.1103/physrevlett.51.1415

CrossRef Full Text | Google Scholar

Spite, F., and Spite, M. (1982). Abundance of lithium in unevolved halo stars and old disk stars-interpretation and consequences. Astronomy Astrophysics 115, 357–366.

Google Scholar

Tisserand, P., Le Guillou, L., Afonso, C., Albert, J., Andersen, J., Ansari, R., et al. (2007). Limits on the Macho content of the galactic halo from the EROS-2 Survey of the Magellanic clouds. Astronomy Astrophysics 469, 387–404. doi:10.1051/0004-6361:20066017

CrossRef Full Text | Google Scholar

Vagnozzi, S. (2023). Seven hints that early-time new physics alone is not sufficient to solve the hubble tension. Universe 9, 393. doi:10.3390/universe9090393

CrossRef Full Text | Google Scholar

van der Wel, A., Chang, Y.-Y., Bell, E., Holden, B., Ferguson, H., Giavalisco, M., et al. (2014). Geometry of star-forming galaxies from sdss, 3d-hst, and candels. Astrophysical J. Lett. 792, L6. doi:10.1088/2041-8205/792/1/l6

CrossRef Full Text | Google Scholar

Veltman, M. (1975). Cosmology and the Higgs mass. Phys. Rev. Lett. 34, 777. doi:10.1103/physrevlett.34.777

CrossRef Full Text | Google Scholar

Verlinde, E. (2011). On the origin of gravity and the laws of Newton. J. High Energy Phys. 2011, 29–27. doi:10.1007/jhep04(2011)029

CrossRef Full Text | Google Scholar

Verlinde, E. (2017). Emergent gravity and the dark Universe. SciPost Phys. 2, 016. doi:10.21468/scipostphys.2.3.016

CrossRef Full Text | Google Scholar

Vogelsberger, M., Genel, S., Springel, V., Torrey, P., Sijacki, D., Xu, D., et al. (2014). Introducing the Illustris Project: simulating the coevolution of dark and visible matter in the Universe. Mon. Notices R. Astronomical Soc. 444, 1518–1547. doi:10.1093/mnras/stu1536

CrossRef Full Text | Google Scholar

Weinberg, S. (1972) Gravitation and cosmology: principles and applications of the general theory of relativity. John Wiley and Sons.

Google Scholar

Weinberg, S. (1978). A new light boson? Phys. Rev. Lett. 40, 223–226. doi:10.1103/physrevlett.40.223

CrossRef Full Text | Google Scholar

Wilczek, F. (1978). Problem of strong P and T invariance in the presence of instantons. Phys. Rev. Lett. 40, 279–282. doi:10.1103/physrevlett.40.279

CrossRef Full Text | Google Scholar

Zel’dovich, Y. B. (1967). Cosmological constant and elementary particles. ZhETF Pisma Redaktsiiu 6, 883.

Google Scholar

Zel’dovich, Y. B. (1968). The cosmological constant and the theory of elementary particles. Sov. Phys. Uspekhi 11, 381–393. doi:10.1070/pu1968v011n03abeh003927

CrossRef Full Text | Google Scholar

Zhang, H., Primack, J. R., Faber, S., Koo, D. C., Dekel, A., Chen, Z., et al. (2019). The evolution of galaxy shapes in candels: from prolate to discy. Mon. Notices R. Astronomical Soc. 484, 5170–5191. doi:10.1093/mnras/stz339

CrossRef Full Text | Google Scholar

Zwicky, F. (1933). Die Rotverschiebung von extragalaktischen Nebeln. Helvetica Phys. Acta 6, 110–127.

Google Scholar