Cosmic rays escape from their sources

Cosmic rays (CRs) are accelerated in diverse astrophysical objects like supernova remnants, massive star clusters, or pulsars. Fermi acceleration mechanisms built a power-law distribution controlled by the ratio of the acceleration to escape timescales in the acceleration site. Hence, escape is an essential mechanism to establish the particle distribution at cosmic-ray sources and to control the flux of cosmic rays injected into the galaxy. Different models have tried to account for the escape process. However, all show some limitations due to the complexity of the particle release mechanism, usually involving 3D geometry, with specific magnetic turbulence properties linked to the process itself. The escape process is also time dependent and results from the interplay of particle acceleration and injection efficiency in the astrophysical source. Once injected into the interstellar medium, freshly released particles are channelled by the ambient magnetic field, which is itself turbulent. In a simplified view, we mainly focus on the propagation of CRs along 1D magnetic flux tubes before turbulent motions start to mix them over a turbulent coherence length, and then we further question this assumption. Close to their sources, one can also expect cosmic rays to harbour higher pressure with respect to their mean value in the interstellar medium. This intermittency in the CR distribution is prone to trigger several types of kinetic and macro instabilities, among which the resonant streaming instability has been the most investigated. In this article, we review recent observational and theoretical studies treating cosmic-ray escape and propagation in the vicinity of their source. We will consider three main astrophysical contexts: association with massive star clusters, gamma-ray halos around pulsars, and, more specifically, supernova remnants. In particular, we discuss in some detail the cosmic-ray cloud (CRC) model, which has been widely used to investigate CR propagation in the environment of supernova remnants. The review also discusses recent studies on CR-induced feedback over the interstellar medium surrounding the sources associated with the release process, as well as alternative types of driven instabilities.

1 Scientific context

The origin of the cosmic ray (hereafter CR) phenomenon is still a widely open issue in modern astrophysics. CRs are mostly composed of protons and helium nuclei, plus some traces of heavier elements. The CR spectrum also has a leptonic component dominated by electrons. Several sources likely contribute to the CR spectrum observed on Earth: citing a few of the most-invoked ones, supernova remnants (SNRs), massive star clusters (MSCs), and pulsars and their nebula, see Gabici et al. (2019) and references therein. There is clear observational evidence from radio to X- and gamma-ray wavebands that these sources accelerate non-thermal particles; the highest energies reach several tens to hundreds of TeV (Vink and Bamba, 2022; Tibaldo et al., 2021; Bykov et al., 2020; Funk, 2015). The CR energy spectrum at sources is harder, $N(E)\propto E^{-2.2/-2.3}$, than the one in the local interstellar medium (ISM) that is within a few hundred parsecs around the solar system, which follows a power law in energy scaling as $E^{-2.7}$ up to a few PeV. This is a consequence of the highest energies escaping the galaxy diffusively with a mean free path increasing with energy. This effect is probed by the measurement of the ratio of the product of spallation reaction to their primary component (see Génolini et al. (2019) and references therein), hereafter denominated secondary to primary ratio. Although phenomenological models can now reproduce the mean CR transport in our Milky Way, the physics that describes the transition from in-source to galactic CR spectrum is still not fully understood. It, in effect, relies on specific MHD turbulence models (Beresnyak and Lazarian, 2019), sometimes triggered by CRs themselves. It then comprises complex non-linear plasma physics, which requires multi-dimensional kinetic simulations that are still out of reach for modern supercomputers.

In addition to understanding the link between CRs in sources and in the local ISM, it is also important to realise that CRs can have much dynamical feedback over ISM dynamics. First, CRs can have a dynamic role because of their pressure and the gradient of their pressure (Ruszkowski and Pfrommer, 2023; Zweibel, 2013). In the local ISM, this role is devoted to particles with kinetic energies close to 1 GeV due to the softness of the above-mentioned spectrum. The local ISM CR pressure $P_{CR,\odot }\sim 1\mathrm{e}\mathrm{V}/\mathrm{c}{\mathrm{m}}^{\mathrm{3}}$ is in a close balance with thermal gas and magnetic pressures. However, on their road to Earth, while being freshly injected from their sources, CRs still carry a pressure in far excess of $P_{\mathrm{C}\mathrm{R},\odot }$. Then, it seems reasonable to consider specific dynamical effects in the ISM closely surrounding CR sources. Theoretical models then aim to evaluate the time and spatial scales where this source effect is substantial. Second, CRs with energies below GeV, even if they do not carry strong pressure, can be an important source of ionisation (Padovani et al., 2020; Grenier et al., 2015). Because of CR overabundance, it also seems reasonable to expect enhanced ionisation rates close to CR sources. Hence, it appears to be important to have a better assessment of the propagation of CRs in the environment close to their sources. This is the main subject of this short review.

CR-modified propagation around their sources has been discussed in several astrophysical contexts: around SNRs, around MSCs, at the galactic centre, and to explain the gamma-ray halo phenomenon around evolved pulsars. The evidence for such modification (which must be understood with respect to the diffusive regime derived from secondary to primary, or S/P, ratio studies) starts to have a better observational basis, itself completed by a diversity of models from purely phenomenological to models involving plasma microphysics. Gamma-ray data can be used to support the CR-modified propagation in the environment of sources (Mitchell et al., 2021). Reduced diffusion coefficients are derived from the radial fit of the gamma-ray profile applied around a given source. In most of the cases, the fit assumes a constant but reduced diffusion coefficient (one-zone model), a continuous particle injection from a point source and no advective transport [see, e.g., the cases of Cygnus cocoon and Westerlund 1 MSCs in Aharonian et al. (2019)]. The solution of the transport CR equation in spherical geometry gives a particle profile $N_{CR}\propto Q(E)/r{\kappa }_s(E)$, see, for example, Celli et al. (2019) for a detailed derivation. The injection spectrum at source is $Q(E)$. The particle profile is modulated by a function dependent on the diffusive radius $r_{\text{diff}}=\sqrt{2{\kappa }_{s}t}$, where ${\kappa }_s$ is the local diffusion coefficient inferred from gamma-ray profile fits. By applying this method, diffusion coefficient reduction factors $\chi ={\kappa }_s/{\kappa }_0$ can inferred for different classes of objects. Here, ${\kappa }_0$ is the diffusion coefficient at the same energy inferred from phenomenological propagation S/P models. Usually, ${\kappa }_s$ is allowed to vary with the CR energy E as a power law, namely, ${\kappa }_s\propto E^{\delta }$. One advantage of reducing the value of the diffusion coefficient for a given gamma-ray emission flux is to reduce the amount of energy imparted into CRs with respect to the case of standard diffusion. Below, we briefly review recent observations that have interpreted gamma-ray profiles in the framework of reduced CR diffusivity for three categories of objects: SNRs, MSCs, and pulsar gamma-ray halos. It is important to keep in mind that the below-mentioned analysis is restricted to this framework and that other interpretations of the gamma-ray profile are valuable, as, for instance, modified local turbulence properties in the case of pulsar gamma-ray halos (López-Coto and Giacinti, 2018).

Before discussing specific observations, let us specify some technical aspects of the models used in these analyses. First, there are two ways CRs can be injected in a halo, either continuously with time or at a given time, in a burst-like way. Most of the below-analysis adopt a burst-like injection, which means that a particle with a given energy is injected at a given time t, as has been modelled in Ohira et al. (2011) and more accurately described in Section 2. Second, the CR transport equation is usually treated in spherical geometry, as again done by Ohira et al. (2011). But some approaches use a Cartesian geometry and allow for anisotropic particle diffusion along two directions: a parallel diffusion described by a specific diffusion coefficient ${\kappa }_{s,\Vert }$ along the background (mean) magnetic field direction and a perpendicular diffusion described by another specific diffusion coefficient ${\kappa }_{s,\perp }$, see Nava and Gabici (2013) for further details. It should be noted that all models discussed below are restricted to 1D, 2D, or 3D but with some axisymmetry. No 3D models (analytical/numerical) have been yet developed due to the complexity and requested resources for solving kinetic and/or magnetohydrodynamic equations. We hereafter specify the transport geometry and injection method for each observational work.

1.1 Supernova remnants

Uchiyama et al. (2012) investigate the GeV gamma-ray emission detected by the Fermi-LAT from molecular clouds in the vicinity of the SNR W44. The CR model is adapted from Ohira et al. (2011). CRs are injected in a burst-like manner. Reduced diffusion solutions are possible with $\chi$ taking values down to 0.1 (notice that in this study $\delta$ was kept fixed to 0.6). Peron et al. (2020) propose an updated analysis of W44 and its surroundings using 9.7 years of Fermi data. Interestingly, their analysis shows that two clouds lying along the galactic plane have enhanced gamma-ray emission that is incompatible with a contribution of the local CR background. These observations likely necessitate anisotropic CR diffusion from W44. Complementary observations are needed in order to infer constraints on the values of the diffusion coefficients ${\kappa }_{s,\Vert }$ and ${\kappa }_{s,\perp }$.

Using both GeV and TeV data and an isotropic spherical diffusion model with burst-like injection, Hanabata et al. (2014) propose $\chi$ to be in the range 1/20–1/2 to explain the gamma-ray profiles around W28, while ${\kappa }_s$ is found to have a mild dependence with the CR energy $E^{0.1-0.3}$.

These two first studies triggered several others with diverse conclusions: The MAGIC collaboration (MAGIC Collaboration et al., 2023) fits extended emission around the $\gamma$Cygni SNR and finds (spherical model, burst-like injection) $\chi$ in the range 0.03–0.1; Li et al. (2023) using Fermi data find (spherical model, burst-like injection at an energy-independent time) solutions with $\chi <1$ and $\delta$ in the range of 0.5–1 around G15.4 + 0.1 SNR; using a similar model, Xin and Guo (2023) using Fermi data find results consistent with $\chi \sim 1$ around DA 530 SNR; Oka and Ishizaki (2022) arrive (spherical model, burst-like injection) to similar conclusions in the case of HB 89 SNR. Finally, Katagiri et al. (2016) used Fermi data to find (spherical model, continuous injection) an enhanced CR energy density by a factor of approximately 10 with respect to local values in the environment of the HB3 SNR, in particular in the W3 source associated with an HII complex in interaction with the SNR.

1.2 Massive star clusters

Aharonian et al. (2019) use Fermi, HESS, and ARGO data to investigate the extended emission around the Westerlund 1 massive star cluster, around the Arches, Quintuplet clusters in the central molecular zone, as well as the Cygnus cocoon. In each case, the radial profile of the gamma-ray emission shows a 1/r decline within 50 pc around the central source. The objects also show an energy spectrum scaling as $E^{-2.2}$ without any noticeable cut-off above 10 TeV. Fixing a maximum value of the overall wind mechanical power $W_{\text{max}}$ and a maximum acceleration efficiency for protons above 10 TeV to not exceed 0.01, it is possible to derive an upper limit of the diffusion, still above 10 TeV, not exceeding $10^{28}\mathrm{c}{\mathrm{m}}^{\mathrm{2}}/\mathrm{s}$, giving $\chi \le 0.01$.Recent investigations propose some re-analysis of some of these clusters and obtain more mitigated results. Aharonian et al. (2022), using HESS observations of Westerlund 1, do not show strong evidence of CRs leaking out of the cluster region. Adopting a distance of 3.9 kpc to fix the CO map around the object, they still obtain a density radial profile compatible with the results by Aharonian et al. (2019). Abeysekara et al. (2021) propose a deep analysis of the Cygnus cocoon combining Fermi and HAWC data. If a GeV gamma-ray profile reproduces a 1/r profile well, a TeV gamma-ray profile may be well explained by a constant CR density produced by a bursting event. Constraints on the diffusion coefficient still conclude a suppression of CR diffusivity with $0.002\le \chi$ but still $\ll 1$.

1.3 Gamma-ray halos around pulsars

Gamma-ray halos around evolved pulsars are a new phenomenon detected in the GeV and multi-TeV bands. This shows extended diffuse structures of several pc scales; hence, they are much extended compared to the pulsar wind nebula. López-Coto et al. (2022) propose a review of the gamma-ray halo phenomenon based on the discovery of Geminga and Monogem pulsar halos. Fang (2022) proposes a complement to this list, including two more objects, namely, LHAASO J0621 + 3,755 [see also Liu (2022)] and HESSJ 1831-098. For each of these objects, the gamma-ray profile centred on the pulsar and its nebula (whose extension is small with respect to the halo), a spherical gamma-ray profile either in the GeV or multi-TeV range fits a $1/r$ law well. The particle injection is time dependent with an amplitude scaling with the pulsar spin-down power evolution. Typical reduced particle diffusivity can be deduced for this list of objects in the range $510^{-3}$ (for LHAASO J0621 + 3,755) to 0.03 (for Monogem); see Fang (2022) and the references therein.

In this short review, we first detail in Section 2 the kinetic models describing cosmic-ray escape from their sources and then present the cosmic-ray cloud (CRC) model. We consider three types of sources: supernova remnants, massive star clusters, and pulsars through their gamma-ray halos. Then, Section 3 describes the potential dynamical effects associated with CR pressure and current effects. The effects due to ionisation are also invoked in this section. Section 4 concludes and proposes some perspectives.

2 Cosmic-ray halos: theoretical aspects

2.1 Acceleration and escape models

Modified CR propagation is usually invoked in the framework of CR self-generated turbulence; that is, CRs can produce the turbulence that they scatter off. However, specific local properties of a background (or extrinsic) turbulence can also explain, to some extent, the gamma-ray and CR halo phenomena. We now examine these two possibilities in more detail.

The first step for the production of a CR halo comprises the escape of these particles from the accelerator. One could define a CR halo as a cloud of energetic particles confined in the close spatial and temporal environment of a source (the spatial and temporal extension of the cloud need to be properly estimated) but disconnected from the acceleration process [see Malkov et al. (2013) for more discussion]. Let us illustrate the properties of a halo in the case of SNRs. The above definition is, in fact, a bit arbitrary. Indeed, in the diffusive shock acceleration process, likely at the heart of the acceleration of CRs, a more correct approach would be to consider that the most energetic particles have a 3D random walk and a probability to return to the shock, which is dropping to 0, as discussed by Drury (2011). This description, however, requires a minimum level of extrinsic turbulence to allow particles close to the maximum energy to not freely escape; otherwise, the escape process is controlled by the energy flux carried by the highest CR to bootstrap the acceleration process (Bell et al., 2013); (Blandford et al., 2023). However, 3D modelling of the escape process is out of reach of current computational resources. The authors are reduced to adopting a 1D spatial description in which the escape process is controlled by a physical boundary (named the far escape boundary) or even simply setting a maximum energy; see the discussion in Reville et al. (2009). Physically, this boundary may mark the transition between a zone where the presence of CRs triggers a magnetic dynamo and the interstellar medium (Xu and Lazarian, 2022b). Notice that CRs can also escape from downstream if, for instance, the turbulence level drops (Ptuskin and Zirakashvili, 2005.

Several models have attempted to describe the escape process and the transition from the in-source to around-source CR distribution. These models focus on SNRs. In these approaches, the maximum CR energy $E_{\text{max}}$ or momentum $p_{\text{max}}$ is either fixed or parameterised as a function of time and in some cases, derived from source modelling. We describe some of them below. The main assumptions are resumed in Table 1 for conciseness.

Table 1

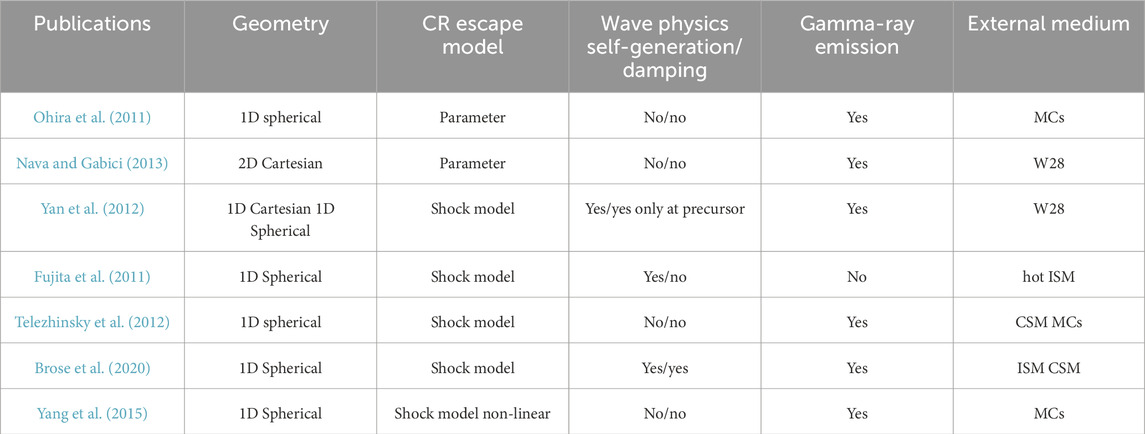
Table 1. Main physical assumptions and background medium properties of several CR escape models from SNRs in order of appearance in the text. MCs: molecular clouds, ISM: interstellar medium, and CSM: circumstellar medium.

Ohira et al. (2011) consider the case of SNRs close or in interaction with molecular clouds (MCs). They use a 1D spherical model and introduce a parameterised form for $p_{\text{max}}=p_0{(t/t_{\text{Sed}})}^{-\alpha }$, where $p_0=1$ PeV/c, and $t_{\text{Sed}}$ is the Sedov timescale and $\alpha =6.5$. However, this value can be modulated in the case that the SNR interacts with an MC directly because particles can escape due to the damping of magnetic perturbations by ion-neutral collisions. The authors apply their model to four specific SNRs: W51C, W44, W28, and IC443. They derive the effective CR spectrum, which is marked by a succession of energy spectral breaks quoting the population of CRs reaching the inner and outer bound of the MCs. In order to fit the gamma-ray data, a reduced diffusion coefficient is necessary in all cases. Makino et al. (2019) continue with similar modelling but also derive the contribution of MeV protons to the iron 6.4 keV fluorescence line if the SNRs interact with a molecular cloud.

Nava and Gabici (2013) propose a similar model using 2D cylindrical geometry. In this model, the maximum CR energy is also parameterised as by Ohira et al. (2011) but with $p_0=5$ PeV/c. Particles are injected in a magnetic flux tube in the (x, y) plane at z = 0 within a circular region given the SNR radius corresponding to the escape time of particles at a given energy E. The model is 2D because it includes the effect of magnetic field random walk due to magnetic, turbulent, chaotic motions. The diffusion coefficient is parameterised with the two above-defined parameters, $\chi$ and $\delta$ (fixed to be 0.5). The authors show that because anisotropic diffusion concentrates the CR flux in flux tubes, it can alleviate low $\chi$ values (the authors use normal values with $\chi =1$) when it matters to reproduce the gamma-ray signal from MCs surrounding the W28 SNR.

Yan et al. (2012) propose a 1D Cartesian model for the CR precursor ahead, the SNR shock. They accurately derive a value for $p_{\text{max}}$ based on a physical model accounting for magnetic amplification by the CRs themselves. They treat CR propagation around the SNR using a 1D spherical approach where the diffusion coefficient is scaled down by a factor $\chi$ with respect to its ISM values. The CR distribution is obtained using the solution of a stationary 1D diffusion. Wave growth and damping are only derived in the CR precursor region. The $\chi$ factor is constrained by comparing the model with gamma-ray data from W28, leading to a reduced diffusivity with $\chi \simeq 0.05$.

Fujita et al. (2011) adopt a 1D spherical two-zone model: a shock zone corresponding to a CR precursor and an escape zone where particles at high energy move diffusively with a diffusion coefficient derived from quasi-linear theory (or QLT, see next). The coefficient includes the amplitude of the self-generated waves. In each zone, an equation for the self-generated waves is solved using a quasi-linear expression for the growth rate. The authors consider three types of models: A, B, and C. Model A corresponds to the general case where the amplitude of the waves is derived in parallel to the evolution of the CR distribution; models B and C are used as tests. In model B (C), the diffusion coefficient is fixed to its Bohm value (the amplitude of the wave is fixed). In all cases, there is no explicit calculation for $p_{\text{max}}$, which is likely fixed. The authors find that wave self-generation can strongly limit CR expansion in a zone around 2$R_s$, where $R_s$ is the SNR radius. The extension of the CR distribution in model A lies between the two other models.

Telezhinsky et al. (2012) include a treatment of particle acceleration at the SNR shock in 1D spherical geometry, including hydrodynamics of fluid evolution. The model can hence derive a physically based expression for $p_{\text{max}}$. For this, the authors define different diffusion regions (their D2 model): one region around the shock with radii between 0 and $R_{sh}(1+\ell )$ with $\ell =0.05$ where Bohm diffusion $\kappa ={\kappa }_B=\frac{E}{qB}$ (B is the total magnetic field accounting for magnetic field amplification) is adopted, a transition region where $\kappa =\chi {\kappa }_0$, and then an outer region beyond $2R_{sh}$ where $\kappa ={\kappa }_0$. Hence, $p_{\text{max}}$ is fixed by comparing the spectra of escaped CRs and diffusion models. The authors consider two scenarios for the interacting material producing gamma rays: either a molecular cloud in the case of a type Ia SNR or a dense wind-blown shell in the case of a core-collapse SNR. In a recent work, Brose et al. (2020) further elaborate on Telezhinsky et al. (2012) calculations, including 1D hydrodynamic solutions for the thermal gas. The calculation is performed in the test-particle limit and so does not account for CR pressure effects. The large-scale magnetic field is fixed up- and downstream of the SNR shock. The CR injection and transport are extended to include the SNR radiative phase. The authors also include an explicit treatment of the wave amplitude, including self-generation and damping, following Brose et al. (2016). They also include an explicit calculation of the CR electron spectrum. Finally, the authors allow for a time-dependent injection of CRs at the SNR forward shock; it scales as a power-law function over time. Figure 1 illustrates the propagation modes of CRs near their sources, which is interesting in terms of the purpose of this review. Figure 1up shows the CR solutions over the whole volume of integration: around the shock and upstream, as defined in Telezhinsky et al. (2012). It illustrates the impact of the CR transport over the maximum energy reachable by the particles. Bohm diffusion maximises particle confinement and leads to higher energies than in the case of self-generated wave solutions. The latter model also produces an energy break around 10 GeV at late evolution timescales where the energy CR spectrum passes from a power law with an index of 2–2.4, consistent with the required injection spectrum for galactic propagation models. Figure 1(down) shows the spectra of escaped CRs at distances of 7.5 pc from the SNR shock in a 2-pc-thick layer at a time of 37 kyr. Four models are displayed: Bohm and self-generated transport with or without the inclusion of a background CR population (not shown in Figure 1). The main impact of background CRs is to compensate for the CR normalisation decrease at low energy because of reacceleration. The self-generated solutions lead to less CR pressure but a wider distribution than the Bohm case, where the escaped particles are more peaked and populate higher energies. This difference in shapes is explained by the fact that the maximum particle energy evolves more rapidly with time in the case of the self-generated wave model.

Figure 1

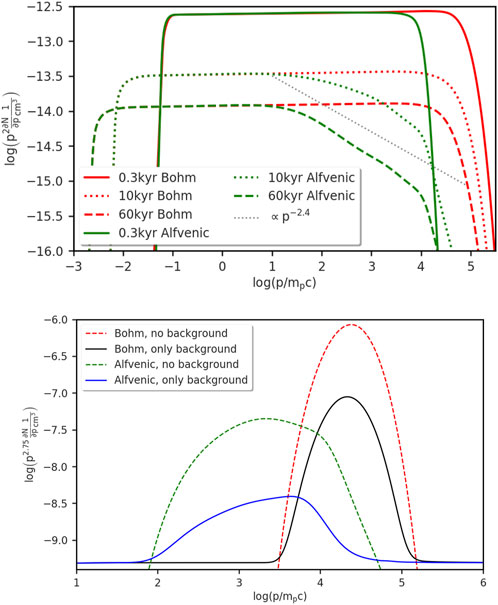
Figure 1. CR distribution over the whole volume of integration (up) and a particular distance of 7.5 pc from the SNR (down) for different models (see text for details). From Brose et al. (2020).

Yang et al. (2015) also elaborate on Telezhinsky et al. (2012) but go beyond the test-particle limit by including non-linear effects over magnetohydrodynamics of shock solutions following the numerical recipes by Zirakashvili and Ptuskin (2012). The authors propose a calculation of the CR distribution outside the acceleration zone by modulating the escaped CR distribution (so a distribution based on a non-linear acceleration model) by the kernel obtained from the 1D spherical solution of the diffusion equation. This is their model B. Their model A is similar to the approach adopted by Telezhinsky et al. The main trend of the results, regardless of age and distance (up to 100 pc ahead of the SNR), is that model A leads to a moderately enhanced CR component with respect to model B, which includes non-linear effects in the source. The difference is, at most, one order of magnitude in the energy flux.

A recent analysis considered the escape of CRs from SNRs propagating in the Parker spiral produced by a massive progenitor star (Kamijima and Ohira, 2022). Test-particle solutions show that the energy of escaping particle $E_{\text{max}}$ is partly controlled by the electrostatic potential difference between the pole and the equator $\mathrm{\Delta }\varphi$, with $E_{\max }\ge e\mathrm{\Delta }\varphi$. Red supergiant stars can contribute to producing CRs above 10 TeV if Gauss-level magnetic fields can be maintained in the wind. Fast-rotating Wolf–Rayet stars can contribute to producing CRs above 1 PeV. The same study in an ISM magnetic field, when adapted to type Ia SNRs, gives maximum energies of several tens of TeV (Kamijima and Ohira, 2021).

At this stage, an alternative approach combines acceleration, escape, and transport in the ISM. In this model, Petrosian and Chen (2014), instead of adjusting data with model parameters, revert the analysis by using CR data from sources and direct measurements to infer the CR momentum diffusion coefficient and angular scattering frequency. The authors concentrate their analysis on electron spectra (for instance, from SNR RXJ1713.7–3946 or SN 1993J). They conclude that it is likely that complex relationships beyond a simple random walk should link escape and scattering times, possibly invoking the presence of stochastic interaction with compression perturbations, as discussed in Section 2.3.8.

Summarising briefly, the aforementioned models all tend to show that an SNR can inject a CR distribution harder than the background ISM population over relatively long timescales of a few tens of kyr. When self-generated waves are included, the confinement of particles is reduced with respect to the case of prescribed transport [see, e.g., Brose et al. (2020)], that is, by fixing a reduced factor $\chi$. In all cases, MCs can track CRs and are good test targets to probe the escaping CR distribution.

We now turn to the cosmic-ray cloud (CRC) model, which is a different class of model. These are 1D Cartesian. They calculate the propagated CR spectrum along a magnetic flux tube surrounding the mother source and provide a parallel solution of the self-generated wave spectra. In some senses, CRC models are less accurate about the escaping process from the accelerator but propose a more accurate treatment of the propagated particles once these are disconnected from the acceleration process. Notice that assuming a population of particles can be completely disconnected from acceleration processes occurring at the SNR is the main assumption of the CRC model. The assumption somehow hides the physics of escape and, hence, the transition from in-source to near-source propagation. This subject is still open, and the above-described models only treat this aspect in a phenomenological way. In reality, this issue requires a refined modelling of the microphysical processes responsible for this transition [see discussions in Malkov et al. (2013) and Bykov et al. (2017)].

2.2 The cosmic-ray cloud model

The cosmic-ray cloud model has been developed by Ptuskin et al. (2008) and Malkov et al. (2013). In this model, CR acceleration and escape phases are decoupled, and acceleration is not explicitly treated separately in the construction of the CR injection term $Q_{CR}$.

2.2.1 Model equations

The complete set of the CR-wave diffusion-convection equations is given by Schwartz and Skilling (1978) and Dewar (1970). We consider only waves propagating along the background magnetic field (slab waves); hence:

$\begin{array}{ll}\hfill {\partial }_t{P}_{CR}\left(E\right)+{\vec{V}}_{st}.\vec{\nabla }{P}_{CR}\left(E\right)& =\vec{\nabla }.\overline{\stackrel{̄}{\kappa }}.\vec{\nabla }{P}_{CR}\left(E\right)+\frac{E}{3}\left\{{\vec{V}}_{st},P_{CR}\right\}\hfill \\ \hfill & -\frac{4}{3}\vec{\nabla }.{\vec{V}}_{st}{P}_{CR}+Q_{CR}\left(E,t\right).\hfill \end{array}(1)$

$\begin{array}{ll}\hfill {\partial }_{t}W\left(k_{\Vert }\right)& +{\vec{V}}_{st}.\vec{\nabla }W\left(k_{\Vert }\right)=-W\left(k_{\Vert }\right)\vec{\nabla }.{\vec{V}}_{st}+\vec{b}.\vec{\nabla }\left(\vec{b}.{\vec{V}}_{st}\right)\hfill \\ \hfill & \left(W\left(k_{\Vert }\right)-k_{\Vert }{\partial }_{k_{\Vert }}W\left(k_{\Vert }\right)\right)+Q\left(W\right).\hfill \end{array}(2)$

$Q\left(W\right)={\mathrm{\Gamma }}_g\left(k_{\Vert }\right)W\left(k_{\Vert }\right)-{\mathrm{\Gamma }}_d\left(k_{\Vert }\right)\left(W\left(k_{\Vert }\right)-W_0\left(k_{\Vert }\right)\right).$

$P_{CR}(E)$ and $W(k_{\Vert })$ are CR pressure and wave pressure in modes parallel to the background magnetic field ${\vec{B}}_0$, respectively. We have $\vec{b}={\vec{B}}_0/B_0$ and $W_0=B_0^2/4\pi$, which stems from the amplitude of the background turbulence (the one that is not CR self-generated). $\overline{\stackrel{̄}{\kappa }}$ is the spatial diffusion coefficient tensor. ${\mathrm{\Gamma }}_g$ and ${\mathrm{\Gamma }}_d$ are the growing and damping rates of CR-generated perturbations. ${\vec{V}}_{st}$ is the CR streaming speed, which may be space-dependent as the ISM changes or because it adapts to the level of scattering waves. The CR streaming speed may also be energy or wavenumber dependent if the scattering waves are dispersive.

If we restrict ourselves to a 1D description with a spatial variable along z, then ${\vec{B}}_0=B_0\vec{z}$. We only consider slab-type waves; hence $\vec{k}=k\vec{z}$. We have ${\left\{{\vec{V}}_{st},P_{CR}\right\}}_{\Vert }={\partial }_z{V}_{st}{\partial }_E{P}_{CR}-{\partial }_E{V}_{st}{\partial }_z{P}_{CR}$. The previous relation also assumes that a direct relationship between k and E exists because the scattering waves are in resonance with CRs. We also consider Alfvén-type waves, and $W(k)=\delta B^2(k)/4\pi$, where $\delta B(k)$ is the amplitude of magnetic perturbations at a wavenumber k. The quasi-linear theory limit gives simple expressions for ${\mathrm{\Gamma }}_g$ and ${\mathrm{\Gamma }}_d$ and ${\kappa }_{\Vert }$. To be valid, this limit requires a low level of turbulent fluctuations at the scale of the particle gyroradius and the turbulence to be fully developed in order for the particle scattering time to be larger than the correlation time of fluctuating forces acting on the particle motion. See Casse et al. (2001) for further details. We have

${\kappa }_{\Vert }=\frac{2{\kappa }_B{W}_0}{W\left(k\right)}.(3)$

At this stage, it should be clear that CR resonant scattering in the quasi-linear regime is a rather restricted way of describing the propagation of CRs in magnetic turbulence. We also neglect CR perpendicular transport completely at this point [see, e.g., Zhang and Xu (2023) and Xu (2021) for recent investigations]. For the wave growth rate, we restrict ourselves for now to the case of the resonant streaming instability, although many other instabilities are possible (see Section 3). In the quasi-linear limit, the wave growth rate is proportional to the CR pressure gradient along the background magnetic field (Skilling, 1975; Marcowith et al., 2021).

${\mathrm{\Gamma }}_g=\frac{1}{2W\left(\vec{k}\right)}{\vec{V}}_{st}.\vec{\nabla }{P}_{CR}{|}_{\Vert }=\frac{1}{2W\left(k\right)}{V}_{st}{\partial }_z{P}_{CR},(4)$

where ${\kappa }_B=\frac{4}{3\pi }Ec/q{B}_0$ is the Bohm diffusion coefficient. Hereafter, we use normalised pressure quantities, namely, $W(k)\equiv W(k)/W_0(k)$ and $P_{CR}\equiv P_{CR}/W_0$.

The damping rate depends on the ISM environment. In ionised phases, wave damping can be due to linear damping (LD), non-linear Landau damping (NLLD), or turbulent damping (TD). The latter is due to the non-linear interaction of self-generated waves with background perturbations part of large-scale-injected turbulence. In partially ionised phases, rapid ion-neutral collisions (IND) take over the other processes (see the next sections for further discussion on these damping processes).

An important quantity in the CRC model is the adimensional variable $\mathrm{\Pi }$, defined as (Malkov et al. (2013):

$\mathrm{\Pi }\left(E\right)=\frac{V_{st}}{{\kappa }_B}{\mathrm{\Phi }}_{\text{CR}}\left(E\right);{\mathrm{\Phi }}_{CR}\left(E\right)={\int }_0^{\infty }dz{P}_{\text{CR}}\left(E,z,t=0\right).(5)$

This quantity is conserved along the magnetic flux tube in which CRs propagate. CR and wave pressure equations can be solved simultaneously either using semi-analytical calculations (Malkov et al.. 2013 or numerically (Nava et al., 2016; Brahimi et al. 2020).

2.2.2 Model physics

The model requires some assumptions about the injection spectrum $Q_{CR}$ in the CRC. Usually, a fraction ${\xi }_{CR}$ of the SNR total mechanical energy is assumed to be imparted into CRs in most related work—see Nava et al. (2016), which used ${\xi }_{CR}=0.1$. The injection spectrum also has some specified energy dependence, such as a power law with an index $-{\alpha }_{CR}$. Particles are injected time dependently over a face of the magnetic flux tube with a surface scaling as $a{(t)}^2$ (in practice, $a(t)$ is proportional to the SNR shock radius $R_{sh}(t)$; see the sketch of the model in Figure 2). Hence, in Equation 5, ${\mathrm{\Phi }}_{CR}(E)=a(t)P_{CR}(E,t=0)$.

Figure 2

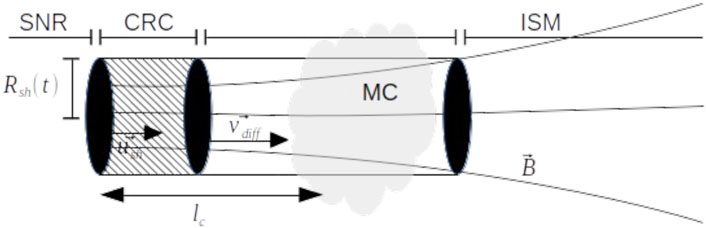
Figure 2. Sketch of the CRC model: at a time t, CRs are injected on the left side of the magnetic flux tube. The SNR expands at a speed $u_{sh}(t)$ towards the right and transversely. CRs propagate in the cloud at speed $v_{\text{diff}}$ fixed by the diffusion coefficient given by Equation 3 where a CR gradient applies. The background magnetic field has a typical coherence length ${\ell }_c$ before the 3D field line’s wandering due to background turbulence starts to induce a 3D transport of the particles. A molecular cloud (MC) can eventually lie in the flux tube.

Another important quantity is the half-life of the CRC, $t_{1/2}$: the time after which half of the primarily injected CR pressure has escaped diffusively. This quantity is related to SNR physics. At a given energy E, a series of $t_{1/2}$ are calculated for different values of $a(t)$ and then compared to solutions of the SNR shock expansion radius with time. The latter comprises the adiabatic and radiative phases (see Figure 3 for details). The shapes of $t_{1/2}$ curves can be understood by the form of $\mathrm{\Pi }$ as a function of the main model parameters. From Nava et al. (2016), we have

$\mathrm{\Pi }\left(E\right)\simeq 3\times 10^4\left(\frac{E_{CR}}{10^{50}\mathrm{e}\mathrm{r}\mathrm{g}}\right)R_1^{-2}{E}_1^{-{\alpha }_{CR}+1}{n}_{i,-1}^{-1/2},$

Figure 3

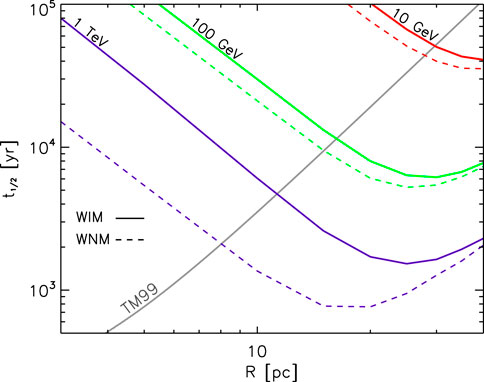
Figure 3. Solutions for the CRC half-life $t_{1/2}$. A series of solutions are derived from the non-linear evolution of the CRC for different values of $a(t)$ and compared with SNR expansion solutions, here labelled by TM99 for Truelove and McKee (1999). Three different energies are shown: red denotes 10 GeV CRs, green denotes 100 GeV CRs, and purple denotes 1 TeV CRs. Solutions for the warm ionised phase (WIM) are on the solid line, while solutions for the warm neutral phase (WNM) are on the dashed line. The intersection of the two sets of solutions gives the injection radius $a(t)=2/3R_{sh}(t)$. Notice that a and R are interchangeable. From Nava et al. (2016).

where $R_{sh}=10\mathrm{p}\mathrm{c}{R}_1$, $E_1=10\mathrm{G}\mathrm{e}\mathrm{V}{E}_1$, $n_i=0.1\mathrm{c}{\mathrm{m}}^{-\mathrm{3}}{n}_{i,-1}$ is the ambient ion density, and $E_{CR}$ is the total energy injected into CRs. As long as $\mathrm{\Pi }(E)\gg 1$, non-linear effects (the effect due to self-generated waves) are strong enough for CR diffusion to be substantially reduced with respect to mean ISM values. Hence, Figure 3 $t_{1/2}$ shows two different trends. First, at small values of a (or R in the figure), the CR pressure gradient in the CRC is strong enough to drive Alfvénic perturbations. As the cloud radius increases, the CR gradient decreases, and fewer waves are produced. Consequently, $t_{1/2}$ drops with the cloud radius. Then, at even higher R, we come to a point such that both $\mathrm{\Pi }$ and the CR pressure gradient drop, and the background turbulence takes over for the control of CR transport and $t_{1/2}\simeq {(R/{\kappa }_0)}^{1/2}$, where ${\kappa }_0$ is the parallel diffusion coefficient fixed by the background turbulence.

The next section discusses applying the CRC model to different ISM phases.

2.3 Astrophysical models for SNR halos

2.3.1 Interstellar medium phases

In Table 2, we briefly summarise the physical properties of the ISM phases, namely, different regions of the ISM characterised by specific thermodynamical quantities like density, temperature, or ionisation fraction (McKee and Ostriker, 1977; Cox, 2005). These quantities will be helpful in estimating the different damping rates.

Table 2

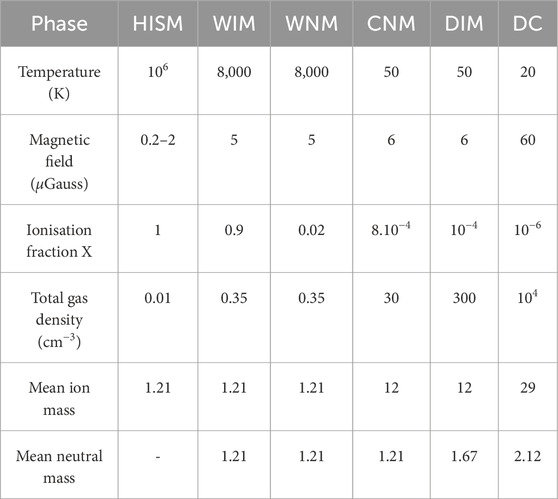
Table 2. Mean thermodynamical properties of the different ISM phases. HISM: hot ISM, WIM: warm ionised medium, WNM: warm neutral medium, CNM: cold neutral medium, DIM: diffuse molecular, and DC: dark clouds. Notice that the molecular phase is decomposed into DIM and DC. The different values are extracted from Jean et al. (2009), Snow and McCall (2006), and Neufeld et al. (2005). The total gas density is the sum of ion density $n_i$ and neutral density $n_n$. The ionisation fraction $X=n_i/(n_n+n_i)$. The mean ion (neutral) mass is the mass of the dominant ion (neutral) species reported to be the hydrogen mass. In all cases, a fraction of 0.1 of abundance in helium nuclei is assumed. The different dominant ion species are hydrogen in hot and warm phases, $C^{+}$ in CNM and DIM, and $HC{O}^{+}$ in DC. The dominant neutral species in warm and atomic phases is hydrogen. It is the $H_2$ molecule in DC and an equal mixture of $H$ and $H_2$ in DIM.

2.3.2 Damping processes

Ion-neutral damping does not operate in ionised phases. The main mechanisms responsible for CR-driven wave damping are linear and non-linear Landau damping and turbulent damping. Linear Landau damping (LD) involves the damping of collective plasma motion by the resonant interaction with thermal background plasma (thermal ions). This damping does not affect the Alfvén slab modes considered here but does affect magnetosonic waves [see Yan and Lazarian (2004)].

Non-linear landau damping (NLLD) is a process that can be viewed as the non-linear interaction of two (here Alfvén) waves with a thermal particle (Hasegawa, 1975). Calculations of the NLLD rate can be found in Lee and Völk (1973) and Hollweg (1971). We use the expression from Wiener et al. (2013),

${\mathrm{\Gamma }}_{\text{NLLD}}=\frac{1}{2}\sqrt{\frac{\pi }{2}}k{v}_i{\left(\frac{\delta B\left(k\right)}{B_0}\right)}^2,$

where $v_i$ is the ion sound speed and $\delta B(k)/B_0$ is the amplitude of the perturbed magnetic field reported to the background one $B_0$.

As previously stated, turbulent damping occurs because of the interaction of CR-driven waves with background turbulence injected at large-scale L of the ISM (Farmer and Goldreich, 2004; Lazarian, 2016; Xu and Lazarian, 2022a; Cerri, 2024). A general expression is

${\mathrm{\Gamma }}_{\text{turb}}=\frac{k^{1/2}{V}_a}{L^{1/2}}.$

Viscous (collisional) damping effects do not affect slab Alfvén wave cascades (Jean et al., 2009).

As stated above, because we are dealing with resonant wave-particle interaction, for slab-type Alfvén waves, we will hereafter apply a direct relation between the wave number and the particle Larmor radius (taken in the background magnetic field $B_0$), namely, $k{R}_L\sim 1$.

Ion-neutral collisions can affect CR-driven Alfvén waves in a partially ionised phase (in fact, ion-neutral damping is already relevant in the warm ionised medium (WIM) phase). The damping rate is fixed by the ordering of the phase frequency $\omega$ with respect to neutral-ion ${\nu }_{ni}$ and ion-neutral ${\nu }_{in}={\nu }_{ni}{\rho }_n/{\rho }_i$ collision frequencies (where ${\rho }_i=n_i{m}_i$ and $\rho =n_n{m}_n$ are the mass density in ions and neutrals). In atomic phases, ${\nu }_{in}$ depends on the temperature [see Jean et al. (2009) and references therein; Xu et al. (2015)]

${\nu }_{in}\simeq n_n\times 1.710^{-8}{\left(\frac{T}{10^4\mathrm{K}}\right)}^{0.4}{\mathrm{s}}^{-\mathrm{1}}.$

T is the gas temperature. In molecular phases, it is

${\nu }_{in}\simeq n_n\times 2.110^{-9}{\mathrm{s}}^{-\mathrm{1}}.$

More accurate estimations that include the contribution of helium can be found in Recchia et al. (2022). Ion-neutral collisions most efficiently damp high-frequency waves with $\omega \gg {\nu }_{in}>{\nu }_{ni}$ because, in that case, ion and neutral motions cannot adjust each other. In that decoupled regime, Kulsrud and Pearce (1969) find

${\mathrm{\Gamma }}_{in}=\frac{{\nu }_{in}}{2}.(6)$

The Alfvén wave is ported by the ions and is expressed as $V_{a,\mathrm{t}\mathrm{o}\mathrm{t}}=B/\sqrt{4\pi {\rho }_i}$. Alternatively, for low-frequency waves with ${\nu }_{in}>{\nu }_{ni}\gg \omega$, the momentum transfer between the two species allows adjusting their relative motion and the damping rate drops as $k^2$. This is the coupled regime and

${\mathrm{\Gamma }}_{in}=\frac{V_{A,\mathrm{t}\mathrm{o}\mathrm{t}}^2{k}^2}{2{\nu }_{in}}.(7)$

Because ions and neutrals move in phase in this regime, the Alfvén speed includes the contribution of neutrals, $V_{a,\mathrm{t}\mathrm{o}\mathrm{t}}=B/\sqrt{4\pi ({\rho }_i+{\rho }_n)}$. In the intermediate regime, that is, for ${\nu }_{in}>\omega >{\nu }_{ni}$, neutral-ion collisions are efficient to damp magnetic perturbations but not efficient enough to transfer momentum to neutrals before magnetic fluctuations are fully damped. In this domain, the real part of $\omega$ vanishes, and Alfvén waves become evanescent (Kulsrud and Pearce, 1969). A recent re-analysis of this problem by Reville et al. (2021), however, concludes that CR-triggered waves can still propagate in this regime provided the waves are strongly driven (in a regime where the CR drift speed is in far excess of the Alfvén speed). This conjecture still needs to be fully verified.

2.3.3 Results in the fully ionised phase

CR clouds propagating in fully ionised phases have been treated by Nava et al. (2019). In the HISM phase, the adiabatic phases of the SNR expansion last over much longer timescales than in other media. It may even happen that the SNR merges with the ISM before reaching any radiative phases, as the upstream sound speed is much higher there, namely, $c_s\sim 100$ km/s. As a consequence, low-energy particles may even stay in the SNR before the merging phase occurs. Figure 4 illustrates this issue. In effect, no solution shows an intersection between the shock solution from Truelove and McKee (1999) and the different half-life solutions obtained for different values of the cloud R for CRs at 10 GeV. Figure 4 also illustrates the dominant role of the NLLD process in controlling the growth of CR-driven turbulence. In effect, two types of solutions are depicted: dotted lines only include turbulent damping, while solid lines combine both NLLD and turbulent damping. NLLD clearly contributes to reducing the CRC half-life in the non-linear phase (on the right part of the curves before $t_{1/2}$ increases as $R^{1/2}$). The amplitude of self-generated waves is high enough to sustain the NLLD effect. NLLD drops at larger radii. The main CRC half-lives at 1 TeV and 100 GeV are approximately 15 kyr and 50 kyr, respectively, corresponding to large escape radii between 40 pc and 80 pc.

Figure 4

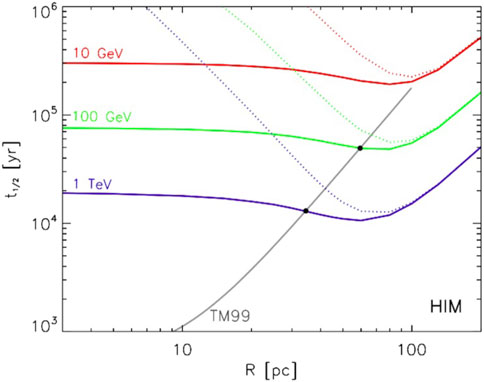
Figure 4. CRC half-life in the HISM phase. Red, green, and purple curves refer to CR energies at 10 GeV, 100 GeV, and 1 TeV, respectively. Dotted lines are the solutions if only the turbulent damping is included, whereas the solid lines combine the contribution of both turbulent and non-linear Landau damping processes. The grey curve depicts the SNR shock dynamical solution obtained in Truelove and McKee (1999). From Nava et al. (2019).

Figure 5 displays the time evolution of the CR spectrum (upper figures) and the spatial parallel diffusion coefficient (lower figures, reported as the diffusion coefficient deduced from direct CR measurements) as a function of CR energy. From this figure, one can clearly see the time sequence of CR escape, with the highest energies escaping first. The diffusion coefficient can be non-linearly reduced over a broad range of CR energies up to one order of magnitude, especially closer to the cloud centre (left figures). At larger distances, the final CR spectrum is softer than the injected one ($E^{-2.4}$ instead of $E^{-2.2}$) because of the larger diffusivity of high-energy particles. At this distance, the CR diffusion can be reconstructed over a larger energy dynamical range. Reduced diffusivity (by a factor of 2) is obtained even at late times of about 150 kyr.

Figure 5

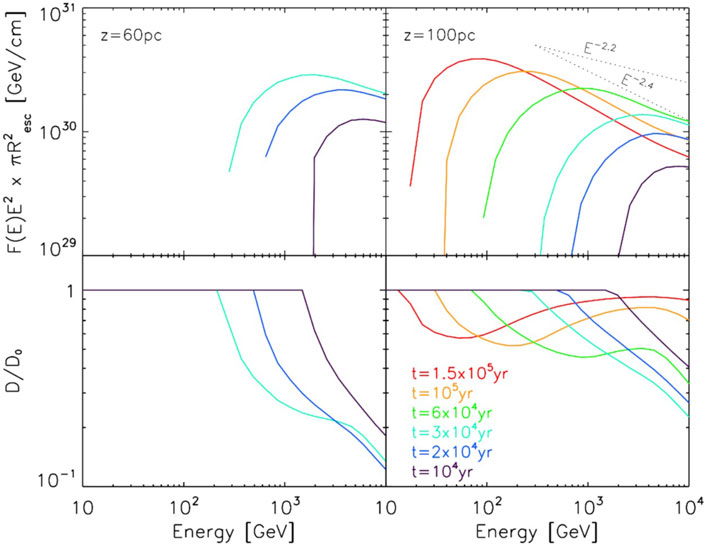
Figure 5. Upper figures: Time-dependent CR spectrum at two distances from the cloud centre: 60 pc (left) and 100 pc (right). Lower figure: Time-dependent evolution of the self-controlled parallel spatial diffusion coefficient as a function of the CR energy. The coefficient is normalised to the background diffusion $D_0$ (noted as ${\kappa }_0$ in the text). From Nava et al. (2019).

2.3.4 Results in partially ionised phases

As stated above, the wave growth in partially ionised phases is mainly controlled by ion-neutral collisions. Ion-neutral damping depends on the perturbation frequency. At high frequencies, Equation 6 applies, whereas Equation 7 applies at low frequencies. As we are dealing with resonant wave-particle interaction, for slab-type Alfvén waves, we have $\omega =k{V}_a$ and still $k{R}_L\sim 1$; hence, $\omega =V_a/R_L$. The Alfvén speed must be interpreted either as the ionic one at high frequencies or as the total one at low frequencies. Another important effect in partially ionised phases is the scale extension of the evanescent propagation zone. It can be the case in some phases that this zone covers almost one order of magnitude in scale (or energy, as in our case). For instance, in the DIM phase, waves in resonance with particles in the band 10 GeV–100 GeV are evanescent (Brahimi et al., 2020). Finally, ion-neutral damping modifies the cut-off scale of the background turbulence and the amplitude of the turbulent damping (Lazarian, 2016). Typical half-life timescales in WIM, warm neutral medium (WNM), and cold neutral medium (CNM) phases are between one kyr to tens of kyr for CR energies between 1 TeV and 10 GeV, respectively (Nava et al., 2016; Brahimi et al., 2020). Denser phases imply a supplementary difficulty. As the ISM is denser, the SNR evolution is slowed. Particles are released while the SNR is smaller and may eventually be released when the SNR reaches the radiative snowplough phase. In that case, it is not clear how particles are released. They can be released at once when the radiative phase is reached or stay confined longer if the ionisation level at the shock precursor is high enough (see the discussion in Brahimi et al. (2020). The escape process has some impact on the final result because if CRs are released earlier, the SNR radius is smaller, and hence, the CR density is higher (see the discussion in Section 2.3.8).

Globally, partially ionised phases lead to less confinement, especially at low energies (10–100 GeV), because the damping rate is maximal. Figure 6 presents the space dependence of the CR pressure, the CR pressure gradient, and the wave spectrum amplitude and diffusion coefficient values in the CNM phase (Brahimi et al., 2020). The zone over which modified propagation extends is typically up to a few tens of pc, while the diffusion coefficient is reduced by factors up to 100 but for a limited time. The larger extension of the modified propagation zone at TeV can be explained because of the high CR gradient associated with a small CR cloud radius and because resonant waves are in the coupled regime in this energy regime; hence, the ion-neutral damping rate is reduced and scales as $E^{-2}$ (see Equation 7).

Figure 6

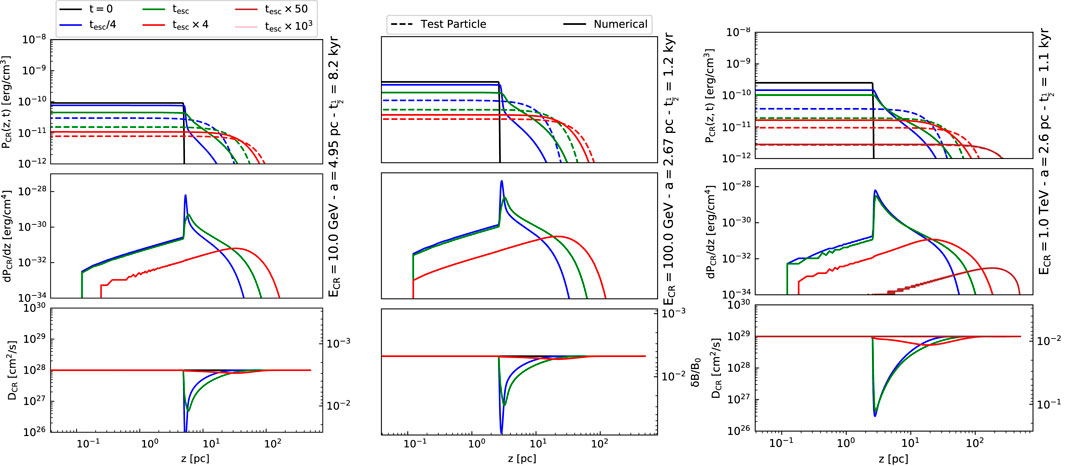
Figure 6. CR pressure (upper row), pressure gradient (middle row), relative diffusion coefficient, and wave amplitude (lower row) at three different CR energies (left: 10 GeV, middle: 100 GeV, and right: 1 TeV) if the SNRs propagate in the CNM. The cloud half-lives are 8.2 kyr, 1.2 kyr, and 1.1 kyr at 10 GeV, 100 GeV, and 1 TeV, respectively. In each case, the escape radius $a$ does not exceed a few pc. Solid lines show the non-linear solutions, and the dashed lines show the linear solutions. The colour codes show the solutions at different times: black t = 0, blue $t_{1/2}/4$, green $t_{1/2}$, red $t_{1/2}\times 4$ and, at 1 TeV, brown $t_{1/2}\times 50$. From Brahimi et al. (2020).

2.3.5 Grammage around CR sources

As CRs harbour a reduced diffusivity around SNRs, a substantial fraction of their grammage (the amount of matter intercepted during their journey to the Earth) could be due to these peculiar regions of the ISM (D’Angelo et al., 2016). This aspect could potentially affect the interpretation of secondary to primary ratio in direct measurements. Using a CRC model, D’Angelo et al. (2016) infer such a vicinity source grammage as a function of the fraction of neutrals from a completely ionised medium to a medium composed of approximately 10% of neutrals. The model considers a CR population released with an energy spectrum of $E^{-2}$ contributing to 20% of the SNR released energy (taken to be $10^{51}$ erg). The particles are released from an SNR of 20 pc radius. Figure 7 presents the main results for different ISM models (see the figure caption for details). It appears that neutrals considerably reduce the near-source grammage as they damp the self-generated waves. It requires a rather high density of ions to allow reaching a vicinity source grammage on the order of 10%–20% of the total grammage, depending on the grammage model.

Figure 7

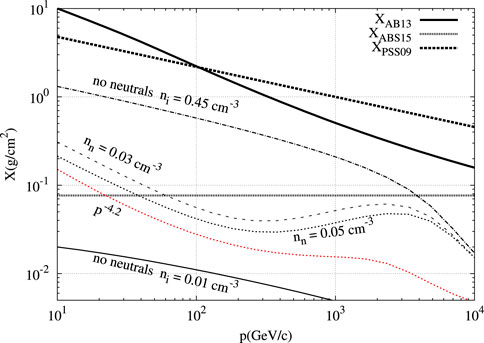
Figure 7. Near-source grammage as a result of the triggering of the resonant streaming instability. The solid thick line is the grammage inferred in Aloisio and Blasi (2013), the dotted line is from Ptuskin et al. (2009), and the light dotted line is from Aloisio et al. (2015). The different ISM models are: (1) thin solid line: no neutrals and ion density $n_i=0.01\mathrm{c}{\mathrm{m}}^{-\mathrm{3}}$, (2) short dashed line: neutral density $n_n=0.055\mathrm{c}{\mathrm{m}}^{-\mathrm{3}}$ and ion density $n_i=0.45\mathrm{c}{\mathrm{m}}^{-\mathrm{3}}$ (dashed red line correspond to a softer CR injection spectrum), (3) long dashed line: neutral density $n_n=0.035\mathrm{c}{\mathrm{m}}^{-\mathrm{3}}$ and ion density $n_i=0.45\mathrm{c}{\mathrm{m}}^{-\mathrm{3}}$, (4) long-short dashed line: no neutrals and ion density $n_i=0.01\mathrm{c}{\mathrm{m}}^{-\mathrm{3}}$. From D’Angelo et al. (2016).

Nava et al. (2019) similarly find that the nearby-source grammage does not contribute more than $10^{-2}\mathrm{g}/\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$ at 10 GeV in HISM [corresponding to model 4 in D’Angelo et al. (2016)] because the CR cloud radius at the release time is large and because the external medium has only a low density. In the HISM, the grammage is inherently reduced because the diffusion coefficient is high. Diffusion due to CR scattering dominates the effect of a larger streaming speed due to enhanced Alfvén speed in HISM. This can be easily checked by defining a diffusion coefficient from the streaming of CRs proportional to $L_{CR}{v}_a$ (Dubois et al., 2019) where $L_{CR}$ is the CR gradient along the background magnetic field. The latter is two orders of magnitude lower than the non-linear diffusion coefficient resulting from CR scattering off Alfvén waves. Recchia et al. (2022) reexamine this question by considering a detailed ion-neutral model that includes both charge exchange and momentum transfer with neutral helium. The latter process was not considered in D’Angelo et al. (2016). In this model, the authors also evaluate the CR cloud model following a procedure described previously in Section 2. As a consequence, the CR cloud at the release of 10 GeV CRs is larger than 20 pc. The fraction of SNR energy imparted into CRs is also twice as small as in D’Angelo et al. (2016). All these effects likely explain why Recchia et al. (2022) find near-source grammage one order of magnitude smaller and, hence, negligible in the WNM and WIM phases.

2.3.6 Cases of inhomogeneous interstellar medium

The discussion in the previous sections was restricted to a homogeneous ISM. In reality, the ISM is all but homogeneous, especially in the galactic disc, close to star formation sites. The inhomogeneous character of the ISM can modify the CRC model in several ways. First, depending on the position in the disc, the coherence scale of the large-scale-injected turbulence can vary from a few parsecs in spiral arms to typically 100 parsecs in inter-arm regions [see, e.g., Haverkorn et al. (2008)]. Then, if immersed in different phases, the ionisation fraction can substantially vary along the magnetic flux tube. In addition, a variation of the magnetic field strength and gas density induces a variation of the local Alfvén speed and hence inflicts supplementary adiabatic losses to CRs while they propagate (see the second term in the RHS of Equation 1).

We provide here an example of a simulation combining different ISM phases (see Brahimi et al. (2020), see also¹). In Figure 8, we present a test comprising several ISM phases along the magnetic flux tube, namely, WNM, CNM, and diffuse molecular (DIM) phases. CNM and DIM phases cover 80 pc and 20 pc, respectively, while the WMN phase in which the SNR is embedded covers 100 pc. Of course, it is quite debatable to assume a flux to be conserved over such large distances [i.e., more than 200 pc; see discussions in Chandran (2000)], but this set-up must be rather seen as a test bed case. What can be noticed from this figure is first that the presence of the DIM phase is almost imperceptible. Then, it can be noted that adiabatic losses can have an effect on the CR distribution. At low energies, the term ${\partial }_z{V}_A{\partial }_E{P}_{\text{CR}}$ is important to account for at the WNM/CNM interface where the CR pressure suffers from an advection towards the low energies. This effect is also amplified by the term ${\partial }_z{V}_A{P}_{\text{CR}}$. At high energy, in the coupled regime ion-neutrals collisions drop as $E^{-2}$, and the term $-{\partial }_E{V}_{\text{A,tot}}\partial P_{\text{CR}}$ becomes important and compensates the two terms, including the gradient of the Alfvén speed. The effects of adiabatic losses are hence less pronounced in that domain of CR energy.

Figure 8

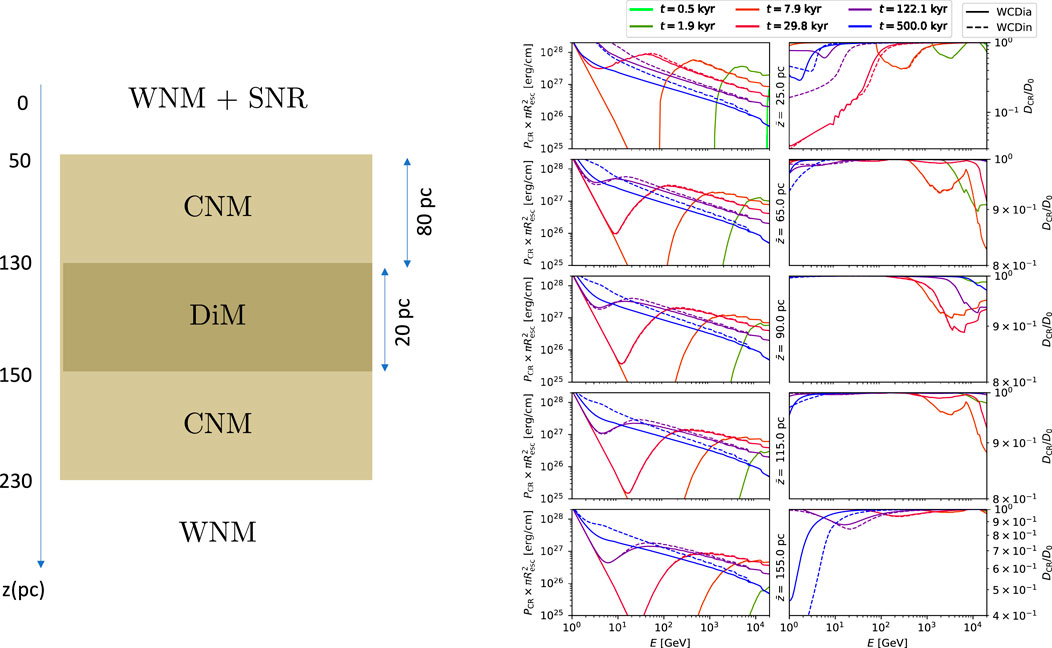
Figure 8. CR escape in an inhomogeneous ISM setup. Left panel: Inhomogeneous ISM sketch: the SNR is placed in a WNM phase, while the magnetic flux tube along which propagated CRs pass by a succession of CNM-DIM-CNM sequences. Right panel: CR pressure and diffusion coefficients as a function of the CR energy at six different times and five different distances from the SNR corresponding to the WNM, CNM, DIM, CNM, and WNM phases, respectively. The CR pressure is multiplied by the surface of the flux tube at the escape time. The CR diffusion coefficient is normalised to the background diffusion coefficient. Two setups are displayed: WCDia and WCDin. WCD designs the phase sequence WNM-CNM-DIM; (i) means that the background CR diffusion is independent of the ISM phase, (a) means that all terms in Equation 1 are retained, and (n) means that the energy terms are skipped. From L. Brahimi’s PhD Thesis.

2.3.7 The release of low-energy cosmic rays

In the previous sections, we have limited our analysis to CR energies larger than 10 GeV. However, the release of less energetic particles in the ISM must also be properly addressed. In effect, protons with MeV kinetic energies or electrons with sub-keV kinetic energies are the main drivers of ISM non-thermal ionisation (Padovani et al., 2009). In addition to ionisation, GeV protons are involved in MeV gamma-ray line production, whereas keV electrons are involved in iron line fluorescence emission (Tatischeff, 2003).

The release of low-energy CRs in the CRC model framework has been considered by Jacobs et al. (2022). In this model, ionisation/Coulomb losses are taken into account for low-energy particles and pp interaction for high-energy particles. The wave equation (Equation 2) also accounts for the damping due to self-interaction between waves involved in a self-generated turbulent cascade. Ion-neutral and turbulent damping terms are also included in the wave equation. CRs are released before, or at most at the start of, the radiative evolution phase of the SNR and carry 10% of the ejecta kinetic energy. We describe the main results below.

Figure 9 presents the CR distribution and diffusion coefficients in the case of an SNR propagating in two different phases, namely, the WIM and WNM phases. It appears that the timescales over which the CR diffusion coefficient is modified due to non-linear effects induced by self-generated turbulence are longer than for higher energetic particles (see Nava et al. (2016) for a comparison): the diffusion coefficient can be reduced by approximately one order of magnitude over several hundred kyr after the release over distances of several tens of parsecs. This has some important consequences for the uniformity of low-energy CRs in our galaxy. Contrary to multi-GeV and TeV CRs, multi-MeV particles do have a much more intermittent distribution. This means that the fit of Voyager data must be interpreted in a statistical sense (Phan et al., 2023), but solutions exist which fit these data. The grammage at energies below 1 GeV is found to be enhanced, in particular in the WIM phase, where it reaches approximately 0.8 $\mathrm{g}/\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$ at 200 MeV before dropping at lower energies because of ionisation/Coulomb losses.

Figure 9

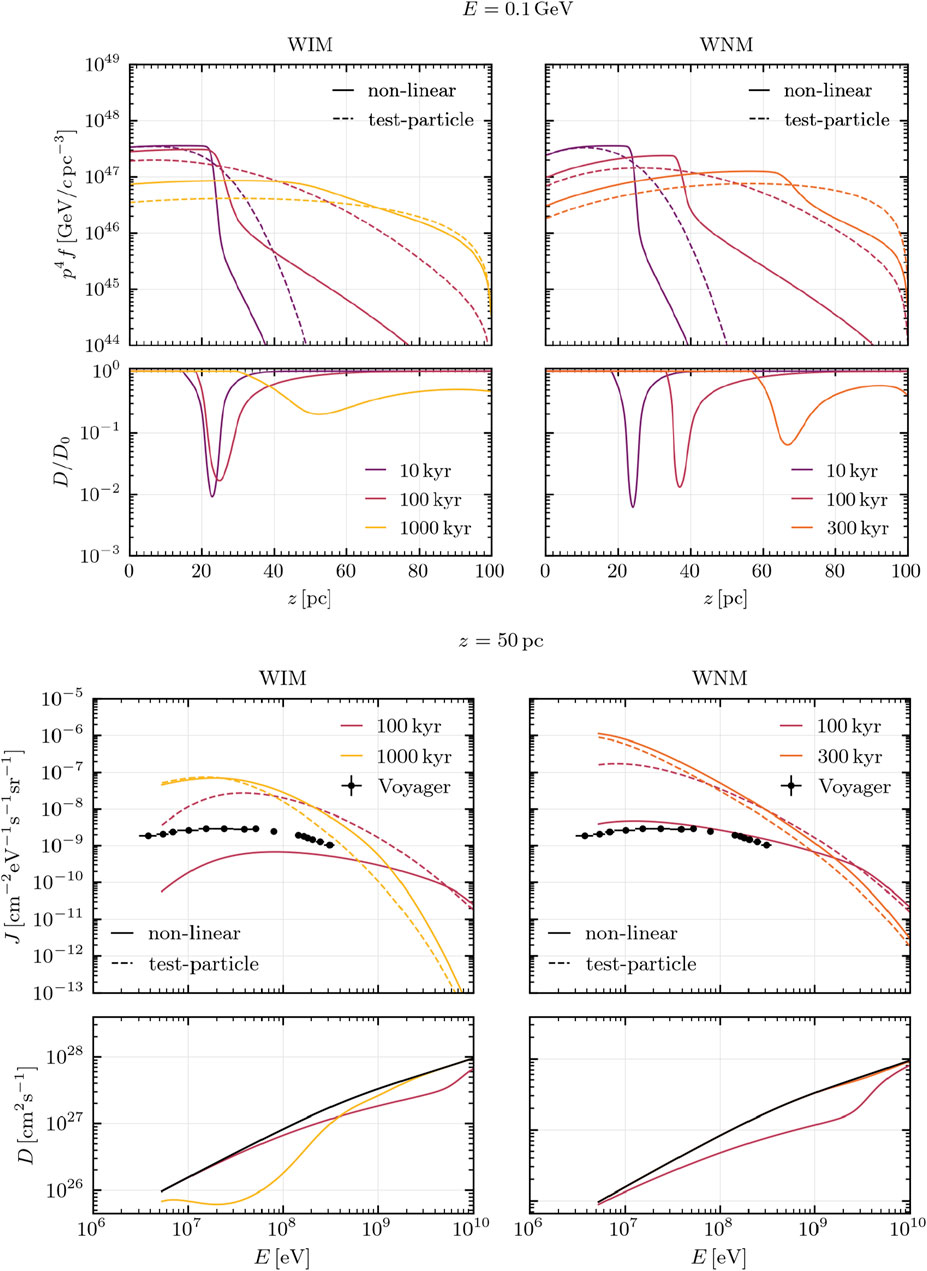
Figure 9. CR distribution (upper row) and normalised diffusion coefficients (lower row) for 100 MeV CRs at three different times in the WIM (left) and WNM (right) phases, respectively. CR distribution (upper row) and normalised diffusion coefficients (lower row) are plotted as a function of CR energy at a distance of 50 pc from the SNR in the WIM (left) and WNM (right) phases. Voyager data are superimposed. The solid black line for the diffusion coefficient is the one extrapolated from background S/P measurements. From Jacobs et al. (2022).

Notice that apart from the above-mentioned sources (SNRs, pulsars, and massive star clusters), low-energy CRs can be injected by different types of sources like the galactic centre, HII regions, and young stellar jets. See Padovani et al. (2020) for a review.

2.3.8 Escape from SNRs: conclusions from the CRC model and alternative approaches

The CRC model is an interesting tool for investigating the development of self-generated CR turbulence once these particles propagate along a magnetic flux tube surrounding an SNR in expansion. The model hence considers that such a flux tube can be maintained over a timescale larger than the particle propagation time (typically at most a few tens of 10 kyr for supra-GeV particles and 1 Myr for MeV particles). The main conclusions we can extract from this model are the following. First, the propagation process is sensitive to the physical properties of the SNR environment, that is, to ISM phases. In ionised phases, particles adopt non-linearly modified propagation over longer timescales and larger distances because turbulence-damping processes have large enough characteristic times. Typical values of the $\chi$ parameter on the order of 0.1 at TeV energies for a few tens of kyr can be obtained, but the parameter is larger for GeV particles. In partially ionised phases, ion-neutral collisions induce strong damping of resonant Alfvén-type waves, especially in the GeV domain. It reduces the residence time of the particles in the halo to a few kyr. The $\chi$ parameter can adopt values down to 0.01 in these timescales. The diffusion is suppressed only in the rather close region around the SNR, although not much in excess of a few tens of pc. The grammage accumulated by CRs around their sources has been shown to be not in excess of 10% of the total grammage in WNM and WIM phases deduced from direct measurements. It is even smaller in HISM phases.

Although interesting and predictive, the CRC model has several limitations. It disconnects acceleration and escapes from the source. There are large uncertainties in the way CRs are released once the SNR enters the radiative phase. The model only considers resonant slab-type Alfvén waves as a source of CR scattering. It is 1D and assumes that a magnetic flux tube can be maintained around an SNR over large dynamical times. The model assumes that QLT applies to both CR scattering regimes and wave growth rates. As QLT is applied, the model neglects perpendicular CR superdiffusion. The dynamical feedback of CRs and their self-generated turbulence is not retained, and the ambient ISM is assumed to be homogeneous and characterised by a specific phase.

We discuss below other physical processes that could address the above limitations.

$•$ Acceleration and escape connection. In Section 2.1, we discussed different models that attempt to account for both sequences; see, for example, Telezhinsky et al. (2012). These models are 1D and rely on some prescribed assumptions about particle transport diffusion coefficients. It could be interesting to redo the analysis performed by Petrosian and Chen (2014) for protons using gamma-ray data. It should also be of great interest to investigate particle acceleration and escape using multi-dimensional simulations or to design a relevant set-up to be tested in laboratory experiments (Reville et al., 2013; Marcowith et al., 2020).

$•$ CR acceleration and escape in radiative SNR evolving phases. The question of whether radiative shocks are good particle accelerators has scarcely been investigated. A recent analysis based on a multi-zone model tends to show that most particles around a radiative SNR shock are accelerated during the adiabatic phase. The injection efficiency decreases rapidly with the age of the shock as its Mach number drops (Diesing et al., 2024).

$•$ Slab-type Alfvén waves. If slab turbulence is the main driver for CR scattering, then as CRs drift out of the source, it is likely, at least in a zone close to the source, that the self-generated turbulence can harbour some cross-helicity or imbalance (a differential number of forward and backward propagating waves) (Weidl et al., 2015). This aspect must still be properly accounted for in CR propagation. It is then a strong restriction to assume a pure Alfvénic slab-type turbulence. Consider, for instance, the influence of magnetosonic waves: the latter can modify parallel CR transport. They can support some gyroresonance if they are not absorbed above the CR Larmor radius scale (Yan and Lazarian, 2004), and they can support large-scale non-resonant magnetic compressions. The latter can induce parallel diffusion due to the perpendicular superdiffusion of CRs (Lazarian and Xu, 2021; Zhang and Xu, 2023) and provide a solution to the ${90}^o$ scattering problem of the QLT that predicts a vanishing pitch-angle cosine diffusion coefficient as $\mu =\widehat{k}.\widehat{B}\to 0$.² This effect can suppress CR propagation near the source. Xu (2021) finds a typical value for the parallel diffusion coefficient at 10 GeV of about $10^{24}\mathrm{c}{\mathrm{m}}^{\mathrm{2}}/\mathrm{s}$. The parallel diffusion coefficient, however, increases with energy rapidly as $E^{0.91}$. Finally, let us mention that the turbulence phenomenon is far more complex than is being described in terms of waves (Beresnyak and Lazarian, 2019). It is well-known to include some structures that lead to intermittency that likely impact CR propagation (Shukurov et al., 2017; Kempski et al., 2023; Lemoine, 2023).

$•$ QLT for CR transport and wave growth. It appears that the QLT conditions in the CRC model are sometimes marginally satisfied. In particular, this is the case if the ambient gas is in the atomic or molecular phases. In that case, Brahimi et al. (2020) find that because the SNR size is reduced in comparison to warm or hot phases, the normalisation of the CR pressure spectrum is larger even if $10^{50}$ erg are injected into CRs. Even if the CR gradient scale is similar, the total CR gradient is larger in that case, leading to larger growth rates. In these regimes, the amplitude of the self-generated waves is larger, and $\delta B(k)/B_0\lesssim 1$ especially for TeV CRs, questioning the applicability of the QLT (Brahimi et al., 2020). This regime may necessitate more refined transport models like the second-order quasi-linear theory (Shalchi, 2005). In addition, the use of the QL growth rate over the whole sequence to fix the turbulence level is also an approximation. This aspect can be tested using numerical simulations with a set-up that includes several CR components to investigate the multi-scale generation of magnetic perturbations.

$•$ Perpendicular superdiffusion. While engaged in stochastic diffusion in a magnetic mirror, CRs cannot completely retrace the magnetic field line back because, at scales smaller than the coherence length, the shearing motion produced by Alfvénic perturbations leads to a superdiffusion of the field lines. This is the Richardson diffusion regime (Eyink et al., 2011; Lazarian and Yan, 2014; Lazarian and Xu, 2021; Hu et al., 2022a). This effect can be accentuated in case of imbalanced turbulence (Beresnyak, 2013). This effect induces a transversal dispersal of the CR content released by the source, which remains to be properly evaluated but may impact any gamma-ray signature of a molecular cloud in the environment (Nava and Gabici, 2013) and the dynamical feedback of the particles (see Section 3).

$•$ Magnetic flux tube coherence. CRs can affect the main properties of the turbulence near sources if the level of magnetic fluctuations is not small in comparison with the background magnetic field amplitude, such as by modifying the coherence length and, hence, the background magnetic flux tube properties. However, testing this potential effect would require fully accounting for the CR feedback. This could only be done numerically and is largely unexplored. It would also necessitate accounting for several CR energy components in order to address the expected final turbulence spectrum. As particles start to diffuse in the flux tube, the highest energy components start to produce long-wavelength perturbations that may dampen after these particles escape into the ISM. Hence, one may expect this coherence length to be time-dependently connected to the main component of particles diffusing at a given time.

$•$ CR feedback. This effect is connected with the previous item questioning magnetic flux tube stability. This aspect is further discussed in Section 3.

2.4 Gamma-ray halos around pulsars

The gamma-ray halo phenomenon briefly described in Section 1 has also been interpreted in the framework of CR self-confinement. In that case, self-generated waves are produced by electron–positron pairs injected from the pulsar termination shock and the pulsar wind nebula, although other interpretations are possible [see (Giacinti et al., 2020)]. Evoli et al. (2018) derive the theory of resonant streaming instability in the context of gamma-ray halos. In this model, electron–positron pairs trigger magnetic fluctuations following $k{r}_L\sim 1$. Pairs are injected with a power-law distribution $f(p)\propto p^{-a}$. The growth rate of the resonant modes can be derived using an alternative form to the one proposed in Equation 4, which implicitly assumes particles are diffusing. The growth rate can be expressed in terms of the drift speed of the pair beam $V_d$:

${\mathrm{\Gamma }}_g\simeq \frac{\pi }{2}\frac{a-3}{a-2}\frac{V_d}{V_a}\frac{n_{ee}}{n_g}{\mathrm{\Omega }}_{cp}{\left(k{r}_{l,0}\right)}^{a-4},$

where $r_{l,0}$ is the Larmor radius of the particles with the minimum momentum in the distribution. The solution is obtained by solving a similar system to Equations 1, 2. The nonlinear Landau damping process (see Equation 1) is the damping process retained in this work. The electron–positron diffusion coefficient is obtained by solving Equation 3. Mukhopadhyay and Linden (2022) use a similar approach but include supplementary damping processes in the wave equation, namely, ion-neutral damping and turbulent damping. The authors added two more ingredients to the model: a 3D description of the propagation that is still in spherical geometry and the presence of an SNR, which contributes by injecting cosmic rays (electrons and protons) as supplementary sources of self-generated waves. The authors consider two models for their 3D runs. Both have a pulsar injection efficiency of 100% into pairs (or $\alpha =1$). The “tuned” model has a harder injection distribution with $a=3$ instead of $a=3.5$ in the fiducial case. This model also has a smaller spin-down time and a smaller background magnetic field strength. Figure 10 presents the solutions of the electron-positron diffusion coefficients as a function of time at 10 TeV (at energies corresponding to the gamma rays probed by HAWC). The solutions clearly show that reducing the diffusion coefficient by several orders of magnitude is challenging in this framework. The maximum reduction occurs close to the pulsar, at 5 pc. The addition of the turbulence generated by the particles injected at the SNR can help in reducing the coefficient further but requires the transfer of much of the SNR mechanical energy into protons, about 40%. Mukhopadhyay and Linden (2022) also propose a 1D model where a diffusion coefficient reduction by more than two orders of magnitude is recovered, although this model predicts diffusion suppression over scales larger than 100 pc. The latter effect partly motivated the above-mentioned 3D developments. From this analysis, it seems difficult to fully account for the gamma-ray halo phenomenon in the framework of self-generated waves or, at least, it requires other sources of turbulence, such as the one generated by the SNR. However, self-generated wave models can be invoked if the electron–positron beam is injected after the pulsar birth if 1D propagation can be sustained, which requires specific properties of the background turbulence (Malik et al., 2023). As stated in Section 2.3.8, another possible explanation for pulsar halos is to have multiple processes contributing: self-generated waves close to the pulsar wind nebula, other sources of turbulence farther away, and specific magnetic geometries. Time-dependent effects should also be important in shaping the halo.

Figure 10

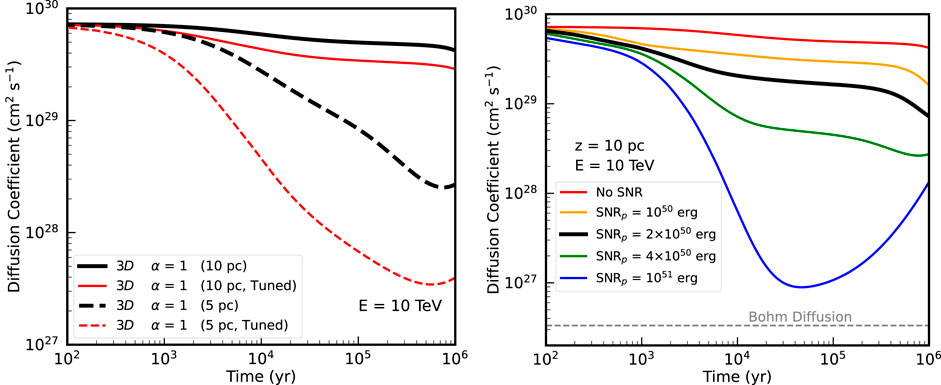
Figure 10. Electron–positron diffusion coefficients at 10 TeV from a 3D model of gamma-ray pulsar halo as a function of time (in yr). Left panel: Solutions at two distances: 10 pc (in black) and 5 pc (in red) for two different models (fiducial and tuned; see the text for details). Right panel: Solution at 10 pc, including the contribution of the SNR, for different total energy imparted into the proton component. From Mukhopadhyay and Linden (2022).

3 Dynamical effects associated with cosmic-ray release

As they carry momentum and pressure, CRs can provide some feedback over the ISM gas coupled to magnetic fields. These effects are expected to be even stronger, close to CR sources. In some sense, the previous section already treats the feedback effect through CR-driven instability. Here, we would like to focus more on recent numerical simulations addressing this effect in the context of multi-scale ISM dynamics.

3.1 Feedback from the CR-resonant streaming instability

This instability has been considered the main instability driving magnetic field turbulence in the ISM (Morlino, 2018; Blasi, 2019; Marcowith et al., 2021). Through this instability, CRs transfer their momenta into the background gas via the production of Alfvén waves and ultimately participate in heating the ISM (Wiener et al., 2013). Once they can trigger resonant magnetic fluctuations, CRs are rapidly locked to the gas (Skilling, 1971). Their bulk speed is the ambient Alfvén speed, or $f{V}_a$, with $f>1$ being a boost factor fixed by the main wave damping process (Ruszkowski et al., 2017).

The main application of this theory concerns the CR feedback in star formation through the sustaining of galactic winds. In effect, while driving the background gas in motion, CRs extract some gas from the galactic disk, lowering the star formation rate [see the review by Ruszkowski and Pfrommer (2023) and references therein]. This review is, however, restricted to smaller-than-kpc-scale ISM. The interested reader is referred to the above-mentioned review for details about CR-driven physics at larger galactic scales.

Around sources, the pressure gradient set by the onset of the CR streaming instability can have dynamical effects over the ambient gas because $\vec{\nabla }{P}_{\text{CR}}$ is a force term in the gas momentum equation. Commerçon et al. (2019) have used CR-magnetohydrodynamic simulations to investigate the necessary condition under which CRs can become trapped with gas at meso-galactic scales, close to their sources, in practice around SNRs. In the ISM, turbulence imposes some scaling relations, known as the empirical Larson laws (Larson, 1979; Larson, 1981), linking the turbulent velocity $\sigma$ and the size of the probed turbulent region. Namely, we have

$\sigma =\sigma \left(\mathrm{1}\mathrm{p}\mathrm{c}\right)L^q,$

where $q=1/3$ corresponds to a Kolmogorov turbulence, and $\sigma (\mathrm{1}\mathrm{p}\mathrm{c})$ is the turbulent rms speed at 1 pc. In ionised gas, a recent investigation using the WHAM survey dataset improves the estimated density fluctuations at large scales (Chepurnov and Lazarian, 2010). Improving the lever arm of the data permits a better fit with a Kolmogorov spectrum, with $q=1/3$. Lines broadening studies in the partially ionised atomic gas allow, for instance, deriving $q\simeq 0.35$ and $\sigma (\mathrm{1}\mathrm{p}\mathrm{c})\simeq 1-1.5$ km/s (Roy et al., 2008). In molecular gas, we have $q\simeq 0.5$ and $\sigma (\mathrm{1}\mathrm{p}\mathrm{c})\simeq 1$ km/s (Hennebelle and Falgarone, 2012). If CRs scatter some magnetic fluctuations leading to a typical diffusion coefficient $\kappa$ along the mean magnetic field lines, then, for a region of size L, CRs can be trapped in the gas if $t_{\text{diff}}=L^2/\kappa >t_{\text{turb}}=L/\sigma (L)$. Hence, the diffusion coefficient must be limited to

$\kappa \le \sigma \left(L\right)L.(8)$

In that situation, the CR gradient along the magnetic field lines is high enough to produce some feedback effects. This condition is true regardless of the ISM phase. If $\kappa$ fulfils the condition in Equation 8, then the gas is entrained by the streaming CR motion, and the local sound speed is also modified as the effective pressure now combines the gas and the CR pressure. All macro instabilities that are important for ISM dynamics (Parker–Jeans, Rayleigh–Taylor, Kelvin–Helmoltz, and magneto-rotational) have a modified growth rate partly controlled by $\kappa$ [see Marcowith (2023)]. In particular, close to SNRs, Commerçon et al. (2019) estimate that the CR gradient sustained by the presence of an SNR must exceed a typical ISM value of $P_{CR,\mathrm{r}\mathrm{e}\mathrm{f}}^{\prime }\simeq 5\times 10^{-33}\mathrm{d}\mathrm{y}\mathrm{n}\mathrm{e}\mathrm{s}/\mathrm{c}{\mathrm{m}}^{\mathrm{2}}\frac{P_{\text{CR}}}{1\mathrm{e}\mathrm{V}/\mathrm{c}{\mathrm{m}}^{\mathrm{3}}}{\left(\frac{L_{CR}}{100\mathrm{p}\mathrm{c}}\right)}^{-1}$, where the prime denotes the gradient taken along the mean magnetic field direction, and $L_{\text{CR}}$ is the CR gradient length, here set with respect to the galactic disc height. The triggering of the resonant modes is, in principle, an efficient way to reduce $\kappa$ and to increase $P_{\text{CR}}^{\prime }$ above $P_{CR,\mathrm{r}\mathrm{e}\mathrm{f}}^{\prime }$. A rough calculation balances the resonant streaming growth rate with the dominant damping rate and fixes the expected level of turbulence. It is found that for an SNR propagating in the atomic phase of the ISM (WNM, CNM), the ratio $P_{\text{CR}}^{\prime }/P_{CR,\mathrm{r}\mathrm{e}\mathrm{f}}^{\prime }\ge 100$ for GeV CRs. Hence, one should expect CRs recently released in such an ISM phase to possibly have substantial feedback because of pressure gradient effects. This simple estimate, however, requires that dedicated numerical simulations be confirmed or invalidated.

3.2 CR current-driven feedback

Schroer et al. (2022) and Schroer et al. (2021) have considered a different scenario than the ones invoked in the framework of the CRC model. In their setup, CRs escaping the SNR can carry a current $J_{\text{CR}}$ strong enough to trigger the non-resonant branch of the steaming instability (Bell, 2004). In that case, magnetic perturbations grow due to the return shielding current ported by thermal background electrons. The non-resonant streaming instability grows faster than the resonant one, but non-resonant modes only grow from wavenumbers $k>r_l^{-1}$ to $k_{\text{max}}=\frac{B_0{J}_{\text{CR}}}{2\rho V_a^2}$, with a maximum growth rate ${\mathrm{\Gamma }}_{\text{max}}=k_{\text{max}}{V}_a$ reached at $k_{\text{max}}/2$ [hence the non-resonant character of the instability; see Amato and Blasi (2009)]. Here, $B_0$ and $\rho$ are the background magnetic field amplitude and gas density, respectively. In this model, CRs are released in a single burst from the SNR. CR distribution follows a power-law distribution with $f(p)\propto p^{-4}$. The condition for triggering the non-resonant branch of the instability is (Zweibel and Everett, 2010; Bell, 2004)

$\frac{U_{\text{CR}}}{U_{B_0}}>\frac{c}{V_D},(9)$

which translates into $k_{\text{max}}{r}_L>1$. This is the necessary condition for this instability to become destabilised. However, even if the non-resonant modes are strongly driven, the instability growth time must be short enough with respect to the residence timescale of the CRs $t_{\text{res}}$, either upstream of a shock front in an SNR or in a flux tube. In the former case, this timescale is set by the CR shock precursor size, ${\ell }_{\text{prec}}\simeq \kappa /u_{\text{sh}}$, where $u_{\text{sh}}$ is the shock speed, and $\kappa$ the diffusion coefficient of the most energetic CRs. Hence, we have $t_{\text{res}}={\ell }_{\text{res}}/u_{\text{sh}}$. In the latter case, the residence time is $t_{\text{res}}\simeq {\ell }_c/V_D$, and the ratio of the flux tube coherence length to the CR drift speed. Hence, the condition is ${\mathrm{\Gamma }}_{\text{max}}{t}_{\text{res}}>1$.

In Schroer et al. (2022) and Schroer et al. (2021), 2D and then 3D hybrid simulations are conducted where CRs are injected on a subpart of the left boundary to mimic the injection by an SNR into the magnetic flux tube. Figure 11 shows the evolution of the 3D morphology of the flux tube using the hybrid approach. The simulation setup respects the condition in Equation 9, even if the CR density is upscaled with respect to a realistic object. A clear inflation due to the lateral CR pressure effect can be noticed. The diffusion coefficient along the flux tube direction converges to a value a few times its Bohm limit. This work shows that while being injected around the SNR, CRs may modify the surrounding ISM gas and magnetic distribution. This effect should be accounted for while dealing with any gamma-ray halo morphology. However, the effective expansion of the flux tube in realistic situations is not clear at this stage. In effect, if only 10% of the mechanical energy is imparted into CRs at the position of the SNR, 90% is still available to inflate the magnetic flux tube. The inflation information propagates at a speed corresponding to the maximum between the local sound and the Alfvén speed. While moving ballistically, the CRs will reach regions of the flux tube far ahead, but as they start to trigger magnetic fluctuations, their mean speed slows to $V_a$ or a few times $V_a$, depending the main damping mechanism. Hence, the total effect due to CRs should not exceed the effect produced by the SNR expansion. Still, if CRs can be more efficiently scattered by adding the contribution of the magnetic fluctuations issued from the generation of the non-resonant instability, then one may expect an enhancement of the CR grammage around a source.

Figure 11

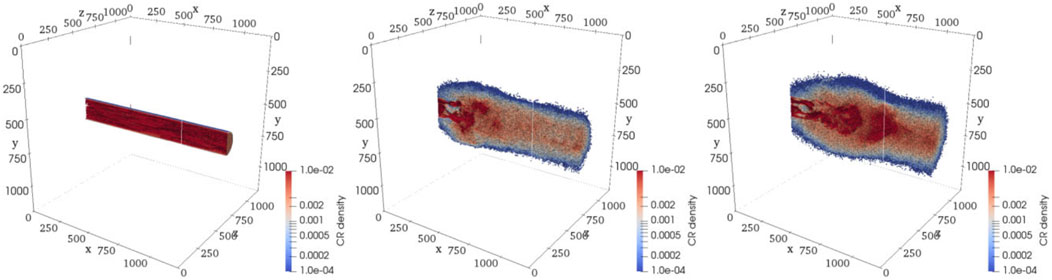
Figure 11. 3D contour plots of CR density as a function of time (here in units of ${\mathrm{\Omega }}_{\text{cp}}^{-1}$, the inverse of the proton cyclotron frequency. From Schroer et al. (2022).

Blasi and Amato (2019) propose a similar approach for the case of CRs escaping the galactic disc. CRs escape diffusively the galactic disc with a flux ${\varphi }_{\text{CR}}$. The flux escaping from the disc is proportional to the disc CR luminosity $L_{\text{CR}}\sim 10^{41}$ erg/s dispersed over a surface proportional to $R_d^2$, $R_d$ being the disc radius. The flux thus obtained is found to be high enough to sustain the onset of the non-resonant streaming instability based on Equation 9 and a background magnetic field not in excess of approximately $210^{-2}\mu$ G. Once the instability grows, magnetic perturbations also grow, and CRs start to propagate diffusively. This induces a CR gradient, which drives the background gas into motion to a speed close to the Alfvén speed. The non-resonant instability can be a source of magnetic field injection into the galactic halo. Finally, CRs can produce diffuse gamma-ray and high-energy neutrino emissions while interacting with circum-galactic gas.

3.3 CR pressure-driven feedback

By CR pressure-driven feedback, we mean the induced effects associated with second-order anisotropy in the CR distribution function (Bykov et al., 2014; Zweibel, 2020). Zweibel (2020) proposes an ensatz for the particle distribution function given by

$F\left(p\right)=F_0\left(p\right)+\zeta p{\partial }_p{F}_0\left(p\right)P_2\left(\mu \right),(10)$

where $F_0(p)$ is the isotropic part of the CR distribution and $P_2(\mu )$ is the Legendre second-order function as a function of the CR velocity pitch-angle cosine $\mu$. The controlling anisotropy parameter is $\zeta =\frac{5}{12}\frac{\mathrm{\Delta }{P}_{\text{CR}}}{P_{CR}}$, where $P_{\text{CR}}=(2P_{CR,\perp }+P_{CR,\Vert })$ and $P_{CR,\perp },P_{CR,\Vert }$ are the perpendicular and parallel CR pressures with respect to the mean magnetic field direction, respectively. The pressure excess is derived from the second term in the RHS of Equation 10. For $F_0(p)\propto p^{-a}$, we directly reproduce the pressure-anisotropy-driven instability growth rate [see also Lazarian and Beresnyak (2006)]

${\mathrm{\Gamma }}_{CR,A}\left(k\right)\simeq \frac{\pi }{8}\frac{a-2}{a-3}\times {\mathrm{\Omega }}_{cp}\times \frac{n_{CR}\left(p>p_1\right)}{n_g}\left(\frac{3a\left(a-2\right)}{a^2-1}\frac{c}{V_a}\zeta -1\right),$

where $p_1=m_p{\mathrm{\Omega }}_{cp}/k_{\Vert }$. The CR scattering frequency in the pressure-driven turbulence can be fixed by balancing the above growth rate with the appropriate damping rate. Zweibel (2020) showed that the CR pressure-driven usually leads to a less efficient ISM heating and CR scattering frequency than the resonant streaming instability by a typical factor of $V_a/c$. This is explained by the fact that magnetic field expansion, which occurs at a typical speed of $V_a$, is balanced CR scattering, whereas, in the case of streaming instability, CRs tend to move along the magnetic field at the speed of light. However, this instability is interesting, as it is a source of CR work in the transversal direction of the magnetic flux tube. This instability can also be relevant close to CR sources where stronger anisotropy should be expected, such as those induced by the CR escape process (Bykov et al., 2017) (In this study, other types of CR pressure instabilities may be triggered, namely, the non-resonant firehose/mirror modes that control the CR anisotropy). Again, as for the streaming instability, it seems important to develop new numerical tools and set-ups capable of integrating different degrees of CR anisotropy to address the effect of triggering both pressure-driven and streaming instabilities (Reville et al., 2021).

4 Conclusion and perspectives

The advent of GeV and TeV gamma-ray detectors starts to shed light on the complex structure of our galaxy. It appears that the high-angular resolution capacity of Cherenkov imagers allows us to derive a gamma-ray profile around different classes of sources like supernova remnants, massive star clusters, and pulsar gamma-ray halos. In several cases, the radial profile is consistent with a 1/r scaling, which can be associated with a diffusive particle dilution. The profile width allows for constraining the amplitude of the diffusion coefficients, which is found to be reduced with respect to the values expected from diffusion laws reconstructed from secondary to primary CR ratios in direct measurements. One can then invoke some specific processes reducing the particle diffusivity around CR sources. However, the process of CR escape and propagation in the interstellar medium is still not a formally settled issue in modern astrophysics. This is largely due to a combination of complex effects that are difficult to handle with even the most powerful supercomputers. Escape traces the transition between in-source turbulence, which is often self-generated by the cosmic rays themselves, like in supernova remnants, to the propagation in the large-injected turbulence in the interstellar medium. One may then expect particles to first propagate along magnetic flux tubes over distances comparable to the background turbulence coherence length. In this framework, the CRC model describes the injection of a component of cosmic rays disconnected from their acceleration process. The particles, because they carry a pressure dominating the background gas and magnetic pressures, can trigger their own turbulence through various instabilities, among which the resonant streaming instability has been the most frequently investigated. The amplitude of the self-generated turbulence is controlled by different damping processes. The dominant damping mechanism depends on the phase of the interstellar medium surrounding the source. Globally, the cloud model predicts a reduction of cosmic-ray diffusivity by 1–2 orders of magnitude depending on the particle energy. Higher (TeV) CR energies are confined over shorter timescales than GeV particles. Below GeV, the self-generated waves may confine cosmic rays efficiently enough to impose a strong intermittency distribution.In addition to this progress, several aspects of the escape-close source propagation problem must be improved. On the observational side, it seems important to have a better assessment of CR content around sources, whatever its type. This probably requires a careful analysis of the surrounding emissions from molecular clouds or any dense material target (e.g., shells or HII regions). On the theoretical side, several aspects are worth considering. First, the factors that affect the interconnection between acceleration and escape must be understood to have a better description of the time evolution of the maximum particle energies and how they are connected to the injection. This aspect has not been effectively investigated because of the scale separation between the two processes. It appears that high-energy CRs, while accelerated, produce copious magnetic perturbations that participate in a strong corrugation of the shock front (van Marle et al., 2019). The corrugation modifies the local magnetic field orientation—or obliquity—with respect to the shock front, which itself impacts the injection efficiency of the whole shock acceleration process (Caprioli and Spitkovsky, 2014; van Marle et al., 2022). Now, this aspect has only been investigated over rather short timescales and usually in 2D because of high computational costs. It deserves an accurate description in 3D and over longer timescales to catch a possible self-similar particle injection-acceleration behaviour (Simon et al., 2024). Another aspect often overlooked in shock theory is that the ISM medium is all but homogeneous. Upstream density and magnetic fluctuations can impact the acceleration process itself (Xu and Lazarian, 2022b; Hu et al., 2022b). Second, once released, CRs can be subject to or be submitted to many effects, as discussed in this review. In reality, the physics is quite complex. The ISM is turbulent, and what we call phases is only an idealised view. For instance, as an SNR reaches scales like 1–10 pc in the galactic plane, the ambient medium can be diverse, and the view of a straight magnetic flux tube over 100 pc is certainly an oversimplification. Simulations combining phases or accounting for the magnetic flux tube distortion (Chandran, 2000) seem to be timely now. Another aspect is that until now, the CRC model investigated the non-linear modification of the particle transport only considering the perturbations produced by one CR component in energy: one can anticipate rather that the self-generated turbulence triggered by high-energy particles would interfere with the propagation of less-energetic particles released later. Finally, as invoked by Schroer et al. (2021), the dynamics of magnetic flux tubes can be strongly modified by the presence of CRs in overpressure with respect to the background magnetic plasma. All these aspects should be investigated to make substantial progress in that particular important field of cosmic-ray research.

Author contributions

AM: writing–original draft and writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The author would like to thank S. Manconi, S. Recchia, and S. Xu for a careful reading of the manuscript and very valuable comments. The author thanks S. Gabici for enlightening discussions, particularly on the aspect of the development of the non-resonant streaming instability around SNRs. The author thanks ANR for support to the GAMALO project under reference ANR-19-CE31-0014. The author thanks IN2P3 for the support of the INTERCOS project.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹https://www.theses.fr/2020MONTS048

²$\widehat{k}=\vec{k}/k$ and $\widehat{B}=\vec{B}/B$

References

Abeysekara, A. U., Albert, A., Alfaro, R., Alvarez, C., Camacho, J. R. A., Arteaga-Velázquez, J. C., et al. (2021). HAWC observations of the acceleration of very-high-energy cosmic rays in the Cygnus Cocoon. Nat. Astron. 5, 465–471. doi:10.1038/s41550-021-01318-y

CrossRef Full Text | Google Scholar

Aharonian, F., Ashkar, H., Backes, M., Barbosa Martins, V., Becherini, Y., Berge, D., et al. (2022). A deep spectromorphological study of the γ-ray emission surrounding the young massive stellar cluster Westerlund 1. A& 666, A124. doi:10.1051/0004-6361/202244323

CrossRef Full Text | Google Scholar

Aharonian, F., Yang, R., and de Oña Wilhelmi, E. (2019). Massive stars as major factories of Galactic cosmic rays. Nat. Astron. 3, 561–567. doi:10.1038/s41550-019-0724-0

CrossRef Full Text | Google Scholar

Aloisio, R., and Blasi, P. (2013). Propagation of galactic cosmic rays in the presence of self-generated turbulence. JCAP 2013, 001. doi:10.1088/1475-7516/2013/07/001

CrossRef Full Text | Google Scholar

Aloisio, R., Blasi, P., and Serpico, P. D. (2015). Nonlinear cosmic ray Galactic transport in the light of AMS-02 and Voyager data. A& 583, A95. doi:10.1051/0004-6361/201526877

CrossRef Full Text | Google Scholar

Amato, E., and Blasi, P. (2009). A kinetic approach to cosmic-ray-induced streaming instability at supernova shocks. MNRAS 392, 1591–1600. doi:10.1111/j.1365-2966.2008.14200.x

CrossRef Full Text | Google Scholar

Bell, A. R. (2004). Turbulent amplification of magnetic field and diffusive shock acceleration of cosmic rays. MNRAS 353, 550–558. doi:10.1111/j.1365-2966.2004.08097.x

CrossRef Full Text | Google Scholar

Bell, A. R., Schure, K. M., Reville, B., and Giacinti, G. (2013). Cosmic-ray acceleration and escape from supernova remnants. MNRAS 431, 415–429. doi:10.1093/mnras/stt179

CrossRef Full Text | Google Scholar

Beresnyak, A. (2013). Asymmetric diffusion of magnetic field lines. ApJl 767, L39. doi:10.1088/2041-8205/767/2/L39

CrossRef Full Text | Google Scholar

Beresnyak, A., and Lazarian, A. (2019). Turbulence in magnetohydrodynamics.

Google Scholar

Blandford, R., Simeon, P., Globus, N., Mukhopadhyay, P., Peretti, E., and Barrow, K. S. S. (2023). “A hierarchical framework for explaining the cosmic ray spectrum using diffusive shock acceleration,” in 38th ICRC conference, Nagoya, Japan. arXiv:2309.09116doi. doi:10.48550/arXiv.2309.09116

CrossRef Full Text | Google Scholar

Blasi, P. (2019). The self-control of cosmic rays. Galaxies 7, 64. doi:10.3390/galaxies7020064

CrossRef Full Text | Google Scholar

Blasi, P., and Amato, E. (2019). Escape of cosmic rays from the galaxy and effects on the circumgalactic medium. PRL 122, 051101. doi:10.1103/PhysRevLett.122.051101

PubMed Abstract | CrossRef Full Text | Google Scholar

Brahimi, L., Marcowith, A., and Ptuskin, V. S. (2020). Nonlinear diffusion of cosmic rays escaping from supernova remnants: Cold partially neutral atomic and molecular phases. A& 633, A72. doi:10.1051/0004-6361/201936166

CrossRef Full Text | Google Scholar

Brose, R., Pohl, M., Sushch, I., Petruk, O., and Kuzyo, T. (2020). Cosmic-ray acceleration and escape from post-adiabatic supernova remnants. A& 634, A59. doi:10.1051/0004-6361/201936567

CrossRef Full Text | Google Scholar

Brose, R., Telezhinsky, I., and Pohl, M. (2016). Transport of magnetic turbulence in supernova remnants. A& 593, A20. doi:10.1051/0004-6361/201527345

CrossRef Full Text | Google Scholar

Bykov, A. M., Brandenburg, A., Malkov, M. A., and Osipov, S. M. (2014). “Microphysics of cosmic ray driven plasma instabilities,”. Microphysics of cosmic plasmas. Editors A. Balogh, A. Bykov, P. Cargill, R. Dendy, T. Dudok de Wit, and J. Raymond, 125, 125–156. doi:10.1007/978-1-4899-7413-6_6

CrossRef Full Text | Google Scholar

Bykov, A. M., Ellison, D. C., and Osipov, S. M. (2017). Nonlinear Monte Carlo model of superdiffusive shock acceleration with magnetic field amplification. PRE 95, 033207. doi:10.1103/PhysRevE.95.033207

PubMed Abstract | CrossRef Full Text | Google Scholar

Bykov, A. M., Marcowith, A., Amato, E., Kalyashova, M. E., Kruijssen, J. M. D., and Waxman, E. (2020). High-energy particles and radiation in star-forming regions. Space Sci. Rev. 216, 42. doi:10.1007/s11214-020-00663-0

CrossRef Full Text | Google Scholar

Caprioli, D., and Spitkovsky, A. (2014). Simulations of ion acceleration at non-relativistic shocks. I. Acceleration efficiency. ApJ 783, 91. doi:10.1088/0004-637X/783/2/91

CrossRef Full Text | Google Scholar

Casse, F., Lemoine, M., and Pelletier, G. (2001). Transport of cosmic rays in chaotic magnetic fields. PRD 65, 023002. doi:10.1103/PhysRevD.65.023002

CrossRef Full Text | Google Scholar

Celli, S., Morlino, G., Gabici, S., and Aharonian, F. A. (2019). Exploring particle escape in supernova remnants through gamma rays. MNRAS 490, 4317–4333. doi:10.1093/mnras/stz2897

CrossRef Full Text | Google Scholar

Cerri, S. S. (2024). Revisiting the role of cosmic-ray driven Alfvén waves in pre-existing magnetohydrodynamic turbulence. I. Turbulent damping rates and feedback on background fluctuations. arXiv e-prints, arXiv:2402, 02901doi. doi:10.48550/arXiv.2402.02901

CrossRef Full Text | Google Scholar

Chandran, B. D. G. (2000). Confinement and isotropization of galactic cosmic rays by molecular-cloud magnetic mirrors when turbulent scattering is weak. ApJ 529, 513–535. doi:10.1086/308232

CrossRef Full Text | Google Scholar

Chepurnov, A., and Lazarian, A. (2010). Extending the big power law in the sky with turbulence spectra from Wisconsin hα mapper data. ApJ 710, 853–858. doi:10.1088/0004-637X/710/1/853

CrossRef Full Text | Google Scholar

Commerçon, B., Marcowith, A., and Dubois, Y. (2019). Cosmic-ray propagation in the bi-stable interstellar medium. I. Conditions for cosmic-ray trapping. A& 622, A143. doi:10.1051/0004-6361/201833809

CrossRef Full Text | Google Scholar

Cox, D. P. (2005). The three-phase interstellar medium revisited. Annu. Rev. A& 43, 337–385. doi:10.1146/annurev.astro.43.072103.150615

CrossRef Full Text | Google Scholar

D’Angelo, M., Blasi, P., and Amato, E. (2016). Grammage of cosmic rays around Galactic supernova remnants. PRD 94, 083003. doi:10.1103/PhysRevD.94.083003

CrossRef Full Text | Google Scholar

Dewar, R. L. (1970). Interaction between hydromagnetic waves and a time-dependent, inhomogeneous medium. Phys. Fluids 13, 2710–2720. doi:10.1063/1.1692854

CrossRef Full Text | Google Scholar

Diesing, R., Guo, M., Kim, C.-G., Stone, J., and Caprioli, D. (2024). Nonthermal signatures of radiative supernova remnants. arXiv e-prints , arXiv:2404.15396 974, 201. doi:10.3847/1538-4357/ad74f0

CrossRef Full Text | Google Scholar

Drury, L. O. (2011). Escaping the accelerator: how, when and in what numbers do cosmic rays get out of supernova remnants? MNRAS 415, 1807–1814. doi:10.1111/j.1365-2966.2011.18824.x

CrossRef Full Text | Google Scholar

Dubois, Y., Commerçon, B., Marcowith, A., and Brahimi, L. (2019). Shock-accelerated cosmic rays and streaming instability in the adaptive mesh refinement code Ramses. 631, A121. doi:10.1051/0004-6361/201936275

CrossRef Full Text | Google Scholar

Evoli, C., Linden, T., and Morlino, G. (2018). Self-generated cosmic-ray confinement in TeV halos: implications for TeV γ-ray emission and the positron excess. PRD 98, 063017. doi:10.1103/PhysRevD.98.063017

CrossRef Full Text | Google Scholar

Eyink, G. L., Lazarian, A., and Vishniac, E. T. (2011). Fast magnetic reconnection and spontaneous stochasticity. ApJ 743, 51. doi:10.1088/0004-637X/743/1/51

CrossRef Full Text | Google Scholar

Fang, K. (2022). Gamma-ray pulsar halos in the Galaxy. Front. Astronomy Space Sci. 9, 1022100. doi:10.3389/fspas.2022.1022100

CrossRef Full Text | Google Scholar

Farmer, A. J., and Goldreich, P. (2004). Wave damping by magnetohydrodynamic turbulence and its effect on cosmic-ray propagation in the interstellar medium. ApJ 604, 671–674. doi:10.1086/382040

CrossRef Full Text | Google Scholar

Fujita, Y., Takahara, F., Ohira, Y., and Iwasaki, K. (2011). Alfvén wave amplification and self-containment of cosmic rays escaping from a supernova remnant. MNRAS 415, 3434–3438. doi:10.1111/j.1365-2966.2011.18980.x

CrossRef Full Text | Google Scholar

Funk, S. (2015). Ground- and space-based gamma-ray astronomy. Annu. Rev. Nucl. Part. Sci. 65, 245–277. doi:10.1146/annurev-nucl-102014-022036

CrossRef Full Text | Google Scholar

Gabici, S., Evoli, C., Gaggero, D., Lipari, P., Mertsch, P., Orlando, E., et al. (2019). The origin of Galactic cosmic rays: challenges to the standard paradigm. Int. J. Mod. Phys. D 28, 1930022–1930339. doi:10.1142/S0218271819300222

CrossRef Full Text | Google Scholar

Génolini, Y., Boudaud, M., Batista, P. I., Caroff, S., Derome, L., Lavalle, J., et al. (2019). Cosmic-ray transport from AMS-02 boron to carbon ratio data: benchmark models and interpretation. PRD 99, 123028. doi:10.1103/PhysRevD.99.123028

CrossRef Full Text | Google Scholar

Giacinti, G., Mitchell, A. M. W., López-Coto, R., Joshi, V., Parsons, R. D., and Hinton, J. A. (2020). Halo fraction in TeV-bright pulsar wind nebulae. A& 636, A113. doi:10.1051/0004-6361/201936505

CrossRef Full Text | Google Scholar

Grenier, I. A., Black, J. H., and Strong, A. W. (2015). The nine lives of cosmic rays in galaxies. Annu. Rev. A& 53, 199–246. doi:10.1146/annurev-astro-082214-122457

CrossRef Full Text | Google Scholar

Hanabata, Y., Katagiri, H., Hewitt, J. W., Ballet, J., Fukazawa, Y., Fukui, Y., et al. (2014). Detailed investigation of the gamma-ray emission in the vicinity of SNR W28 with FERMI-LAT. ApJ 786, 145. doi:10.1088/0004-637X/786/2/145

CrossRef Full Text | Google Scholar

Hasegawa, A. (1975). Plasma instabilities and nonlinear effects, 8. Springer Verlag Springer Series on Physics Chemistry Space.

Google Scholar

Haverkorn, M., Brown, J. C., Gaensler, B. M., and McClure-Griffiths, N. M. (2008). The outer scale of turbulence in the magnetoionized galactic interstellar medium. ApJ 680, 362–370. doi:10.1086/587165

CrossRef Full Text | Google Scholar

Hennebelle, P., and Falgarone, E. (2012). Turbulent molecular clouds. A&Rev 20, 55. doi:10.1007/s00159-012-0055-y

CrossRef Full Text | Google Scholar

Hollweg, J. V. (1971). Nonlinear Landau damping of Alfvén waves. PRL 27, 1349–1352. doi:10.1103/PhysRevLett.27.1349

CrossRef Full Text | Google Scholar

Hu, Y., Lazarian, A., and Xu, S. (2022a). Superdiffusion of cosmic rays in compressible magnetized turbulence. MNRAS 512, 2111–2124. doi:10.1093/mnras/stac319

CrossRef Full Text | Google Scholar

Hu, Y., Xu, S., Stone, J. M., and Lazarian, A. (2022b). Turbulent magnetic field amplification by the interaction of a shock wave and inhomogeneous medium. ApJ 941, 133. doi:10.3847/1538-4357/ac9ebc

CrossRef Full Text | Google Scholar

Jacobs, H., Mertsch, P., and Phan, V. H. M. (2022). Self-confinement of low-energy cosmic rays around supernova remnants. JCAP 2022, 024. doi:10.1088/1475-7516/2022/05/024

CrossRef Full Text | Google Scholar

Jean, P., Gillard, W., Marcowith, A., and Ferrière, K. (2009). Positron transport in the interstellar medium. A& 508, 1099–1116. doi:10.1051/0004-6361/200809830

CrossRef Full Text | Google Scholar

Kamijima, S. F., and Ohira, Y. (2021). Escape of cosmic rays from perpendicular shocks in the interstellar magnetic field. PRD 104, 083028. doi:10.1103/PhysRevD.104.083028

CrossRef Full Text | Google Scholar

Kamijima, S. F., and Ohira, Y. (2022). Escape of cosmic rays from perpendicular shocks in the circumstellar magnetic field. PRD 106, 123025. doi:10.1103/PhysRevD.106.123025

CrossRef Full Text | Google Scholar

Katagiri, H., Yoshida, K., Ballet, J., Grondin, M. H., Hanabata, Y., Hewitt, J. W., et al. (2016). Fermi LAT discovery of extended gamma-ray emissions in the vicinity of the HB 3 supernova remnant. ApJ 818, 114. doi:10.3847/0004-637X/818/2/114

CrossRef Full Text | Google Scholar

Kempski, P., Fielding, D. B., Quataert, E., Galishnikova, A. K., Kunz, M. W., Philippov, A. A., et al. (2023). Cosmic ray transport in large-amplitude turbulence with small-scale field reversals. MNRAS 525, 4985–4998. doi:10.1093/mnras/stad2609

CrossRef Full Text | Google Scholar

Kulsrud, R., and Pearce, W. P. (1969). The effect of wave-particle interactions on the propagation of cosmic rays. ApJ 156, 445. doi:10.1086/149981

CrossRef Full Text | Google Scholar

Larson, R. B. (1979). Stellar kinematics and interstellar turbulence. MNRAS 186, 479–490. doi:10.1093/mnras/186.3.479

CrossRef Full Text | Google Scholar

Larson, R. B. (1981). Turbulence and star formation in molecular clouds. MNRAS 194, 809–826. doi:10.1093/mnras/194.4.809

CrossRef Full Text | Google Scholar

Lazarian, A. (2016). Damping of Alfvén waves by turbulence and its consequences: from cosmic-ray streaming to launching winds. ApJ 833, 131. doi:10.3847/1538-4357/833/2/131

CrossRef Full Text | Google Scholar

Lazarian, A., and Beresnyak, A. (2006). Cosmic ray scattering in compressible turbulence. MNRAS 373, 1195–1202. doi:10.1111/j.1365-2966.2006.11093.x

CrossRef Full Text | Google Scholar

Lazarian, A., and Xu, S. (2021). Diffusion of cosmic rays in MHD turbulence with magnetic mirrors. ApJ 923, 53. doi:10.3847/1538-4357/ac2de9

CrossRef Full Text | Google Scholar

Lazarian, A., and Yan, H. (2014). Superdiffusion of cosmic rays: implications for cosmic ray acceleration. ApJ 784, 38. doi:10.1088/0004-637X/784/1/38

CrossRef Full Text | Google Scholar

Lee, M. A., and Völk, H. J. (1973). Damping and non-linear wave-particle interactions of alfvén-waves in the solar wind. Astr. Sp.Sc 24, 31–49. doi:10.1007/BF00648673

CrossRef Full Text | Google Scholar

Lemoine, M. (2023). Particle transport through localized interactions with sharp magnetic field bends in MHD turbulence. J. Plasma Phys. 89, 175890501. doi:10.1017/S0022377823000946

CrossRef Full Text | Google Scholar

Li, Y., Xin, Y., Liu, S., and He, Y. (2023). Advanced γ-ray emission studies of G15.4+0.1 with fermi-LAT: evidence of escaping cosmic rays interacting with surrounding molecular clouds. ApJ 945, 21. doi:10.3847/1538-4357/acb81d

CrossRef Full Text | Google Scholar

Liu, R.-Y. (2022). The physics of pulsar halos: research progress and prospect. Int. J. Mod. Phys. A 37, 2230011. doi:10.1142/S0217751X22300113

CrossRef Full Text | Google Scholar

López-Coto, R., de Oña Wilhelmi, E., Aharonian, F., Amato, E., and Hinton, J. (2022). Gamma-ray haloes around pulsars as the key to understanding cosmic-ray transport in the Galaxy. Nat. Astron. 6, 199–206. doi:10.1038/s41550-021-01580-0

CrossRef Full Text | Google Scholar

López-Coto, R., and Giacinti, G. (2018). Constraining the properties of the magnetic turbulence in the Geminga region using HAWC γ-ray data. MNRAS 479, 4526–4534. doi:10.1093/mnras/sty1821

CrossRef Full Text | Google Scholar

MAGIC Collaboration Acciari, V. A., Ansoldi, S., Antonelli, L. A., Artero, M., Asano, K., et al. (2023). Study of the GeV to TeV morphology of the γ Cygni SNR (G 78.2+2.1) with MAGIC and Fermi-LAT. Evidence for cosmic ray escape. A& 670, A8. doi:10.1051/0004-6361/202038748

CrossRef Full Text | Google Scholar

Makino, K., Fujita, Y., Nobukawa, K. K., Matsumoto, H., and Ohira, Y. (2019). Interaction between molecular clouds and MeV-TeV cosmic-ray protons escaped from supernova remnants. PASJ 71, 78. doi:10.1093/pasj/psz058

CrossRef Full Text | Google Scholar

Malik, S., Yuen, K. H., and Yan, H. (2023). Diagnosis of 3D magnetic field and mode composition in MHD turbulence with Y-parameter. MNRAS 524, 6102–6113. doi:10.1093/mnras/stad2225

CrossRef Full Text | Google Scholar

Malkov, M. A., Diamond, P. H., Sagdeev, R. Z., Aharonian, F. A., and Moskalenko, I. V. (2013). Analytic solution for self-regulated collective escape of cosmic rays from their acceleration sites. ApJ 768, 73. doi:10.1088/0004-637X/768/1/73

PubMed Abstract | CrossRef Full Text | Google Scholar

Marcowith, A. (2023). Cosmic-Ray-modified and driven instabilities. arXiv e-prints. arXiv:2312.17134doi. doi:10.48550/arXiv.2312.17134

CrossRef Full Text | Google Scholar

Marcowith, A., Ferrand, G., Grech, M., Meliani, Z., Plotnikov, I., and Walder, R. (2020). Multi-scale simulations of particle acceleration in astrophysical systems. Living Rev. Comput. Astrophysics 6, 1. doi:10.1007/s41115-020-0007-6

CrossRef Full Text | Google Scholar

Marcowith, A., van Marle, A. J., and Plotnikov, I. (2021). The cosmic ray-driven streaming instability in astrophysical and space plasmas. Phys. Plasmas 28, 080601. doi:10.1063/5.0013662

CrossRef Full Text | Google Scholar

McKee, C. F., and Ostriker, J. P. (1977). A theory of the interstellar medium: three components regulated by supernova explosions in an inhomogeneous substrate. ApJ 218, 148–169. doi:10.1086/155667

CrossRef Full Text | Google Scholar

Mitchell, A. M. W., Rowell, G. P., Celli, S., and Einecke, S. (2021). Using interstellar clouds to search for Galactic PeVatrons: gamma-ray signatures from supernova remnants. MNRAS 503, 3522–3539. doi:10.1093/mnras/stab667

CrossRef Full Text | Google Scholar

Morlino, G. (2018). Effects of self-generated turbulence on Galactic Cosmic Ray propagation and associated diffuse γ-ray emission. Nucl. Part. Phys. Proc. 297-299, 39–48. doi:10.1016/j.nuclphysbps.2018.07.006

CrossRef Full Text | Google Scholar

Mukhopadhyay, P., and Linden, T. (2022). Self-generated cosmic-ray turbulence can explain the morphology of TeV halos. PRD 105, 123008. doi:10.1103/PhysRevD.105.123008

CrossRef Full Text | Google Scholar

Nava, L., and Gabici, S. (2013). Anisotropic cosmic ray diffusion and gamma-ray production close to supernova remnants, with an application to W28. MNRAS 429, 1643–1651. doi:10.1093/mnras/sts450

CrossRef Full Text | Google Scholar

Nava, L., Gabici, S., Marcowith, A., Morlino, G., and Ptuskin, V. S. (2016). Non-linear diffusion of cosmic rays escaping from supernova remnants - I. The effect of neutrals. MNRAS 461, 3552–3562. doi:10.1093/mnras/stw1592

CrossRef Full Text | Google Scholar

Nava, L., Recchia, S., Gabici, S., Marcowith, A., Brahimi, L., and Ptuskin, V. (2019). Non-linear diffusion of cosmic rays escaping from supernova remnants - II. Hot ionized media. MNRAS 484, 2684–2691. doi:10.1093/mnras/stz137

CrossRef Full Text | Google Scholar

Neufeld, D. A., Wolfire, M. G., and Schilke, P. (2005). The chemistry of fluorine-bearing molecules in diffuse and dense interstellar gas clouds. ApJ 628, 260–274. doi:10.1086/430663

CrossRef Full Text | Google Scholar

Ohira, Y., Murase, K., and Yamazaki, R. (2011). Gamma-rays from molecular clouds illuminated by cosmic rays escaping from interacting supernova remnants. MNRAS 410, 1577–1582. doi:10.1111/j.1365-2966.2010.17539.x

CrossRef Full Text | Google Scholar

Oka, T., and Ishizaki, W. (2022). Detection of gamma-rays around SNR HB9 and its implications for the diffusive shock-acceleration history. PASJ 74, 625–638. doi:10.1093/pasj/psac024

CrossRef Full Text | Google Scholar

Padovani, M., Galli, D., and Glassgold, A. E. (2009). Cosmic-ray ionization of molecular clouds. A& 501, 619–631. doi:10.1051/0004-6361/200911794

CrossRef Full Text | Google Scholar

Padovani, M., Ivlev, A. V., Galli, D., Offner, S. S. R., Indriolo, N., Rodgers-Lee, D., et al. (2020). Impact of low-energy cosmic rays on star formation. Space Sci. Rev. 216, 29. doi:10.1007/s11214-020-00654-1

CrossRef Full Text | Google Scholar

Peron, G., Aharonian, F., Casanova, S., Zanin, R., and Romoli, C. (2020). On the gamma-ray emission of W44 and its surroundings. ApJL 896, L23. doi:10.3847/2041-8213/ab93d1

CrossRef Full Text | Google Scholar

Petrosian, V., and Chen, Q. (2014). Determination of acceleration mechanism characteristics directly and nonparametrically from observations: application to supernova remnants. PRD 89, 103007. doi:10.1103/PhysRevD.89.103007

CrossRef Full Text | Google Scholar

Phan, V. H. M., Recchia, S., Mertsch, P., and Gabici, S. (2023). Stochasticity of cosmic rays from supernova remnants and the ionization rates in molecular clouds. PRD 107, 123006. doi:10.1103/PhysRevD.107.123006

CrossRef Full Text | Google Scholar

Ptuskin, V. S., Strelnikova, O. N., and Sveshnikova, L. G. (2009). On leaky-box approximation to GALPROP. Astropart. Phys. 31, 284–289. doi:10.1016/j.astropartphys.2009.02.004

CrossRef Full Text | Google Scholar

Ptuskin, V. S., and Zirakashvili, V. N. (2005). On the spectrum of high-energy cosmic rays produced by supernova remnants in the presence of strong cosmic-ray streaming instability and wave dissipation. A& 429, 755–765. doi:10.1051/0004-6361:20041517

CrossRef Full Text | Google Scholar

Ptuskin, V. S., Zirakashvili, V. N., and Plesser, A. A. (2008). Non-linear diffusion of cosmic rays. Adv. Space Res. 42, 486–490. doi:10.1016/j.asr.2007.12.007

CrossRef Full Text | Google Scholar

Recchia, S., Galli, D., Nava, L., Padovani, M., Gabici, S., Marcowith, A., et al. (2022). Grammage of cosmic rays in the proximity of supernova remnants embedded in a partially ionized medium. A& 660, A57. doi:10.1051/0004-6361/202142558

CrossRef Full Text | Google Scholar

Reville, B., Bell, A. R., and Gregori, G. (2013). Diffusive shock acceleration at laser-driven shocks: studying cosmic-ray accelerators in the laboratory. New J. Phys. 15, 015015. doi:10.1088/1367-2630/15/1/015015

CrossRef Full Text | Google Scholar

Reville, B., Giacinti, G., and Scott, R. (2021). Cosmic-ray current-driven instabilities - revisiting environmental conditions. MNRAS 502, 4137–4153. doi:10.1093/mnras/stab296

CrossRef Full Text | Google Scholar

Reville, B., Kirk, J. G., and Duffy, P. (2009). Steady-state solutions in nonlinear diffusive shock acceleration. ApJ 694, 951–958. doi:10.1088/0004-637X/694/2/951

CrossRef Full Text | Google Scholar

Roy, N., Peedikakkandy, L., and Chengalur, J. N. (2008). Turbulence measurements from HI absorption spectra. MNRAS 387, L18–L22. doi:10.1111/j.1745-3933.2008.00473.x

CrossRef Full Text | Google Scholar

Ruszkowski, M., and Pfrommer, C. (2023). Cosmic ray feedback in galaxies and galaxy clusters. A&Rev 31, 4. doi:10.1007/s00159-023-00149-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Ruszkowski, M., Yang, H. Y. K., and Reynolds, C. S. (2017). Cosmic-ray feedback heating of the intracluster medium. ApJ 844, 13. doi:10.3847/1538-4357/aa79f8

CrossRef Full Text | Google Scholar

Schroer, B., Pezzi, O., Caprioli, D., Haggerty, C., and Blasi, P. (2021). Dynamical effects of cosmic rays on the medium surrounding their sources. ApJL 914, L13. doi:10.3847/2041-8213/ac02cd

CrossRef Full Text | Google Scholar

Schroer, B., Pezzi, O., Caprioli, D., Haggerty, C. C., and Blasi, P. (2022). Cosmic-ray generated bubbles around their sources. MNRAS 512, 233–244. doi:10.1093/mnras/stac466

CrossRef Full Text | Google Scholar

Schwartz, S. J., and Skilling, J. (1978). The escape of cosmic rays from supernova remnants. A&A 70, 607.

Google Scholar

Shalchi, A. (2005). Second-order quasilinear theory of cosmic ray transport. Phys. Plasmas 12, 052905. doi:10.1063/1.1895805

CrossRef Full Text | Google Scholar

Shukurov, A., Snodin, A. P., Seta, A., Bushby, P. J., and Wood, T. S. (2017). Cosmic rays in intermittent magnetic fields. ApJl 839, L16. doi:10.3847/2041-8213/aa6aa6

CrossRef Full Text | Google Scholar

Simon, E., Caprioli, D., Haggerty, C., and Reville, B. (2024). Maximum energy achievable in supernova remnants: self-consistent simulations. arXiv e-prints, arXiv:2402, 01048doi. doi:10.48550/arXiv.2402.01048

CrossRef Full Text | Google Scholar

Skilling, J. (1971). Cosmic rays in the galaxy: convection or diffusion? ApJ 170, 265. doi:10.1086/151210

CrossRef Full Text | Google Scholar

Skilling, J. (1975). Cosmic ray streaming - II. Effect of particles on Alfvén waves. MNRAS 173, 245–254. doi:10.1093/mnras/173.2.245

CrossRef Full Text | Google Scholar

Snow, T. P., and McCall, B. J. (2006). Diffuse atomic and molecular clouds. Annu. Rev. A& 44, 367–414. doi:10.1146/annurev.astro.43.072103.150624

CrossRef Full Text | Google Scholar

Tatischeff, V. (2003). “X- and gamma-ray line emission processes,”. EAS publications series. Editors C. Motch, and J.-M. Hameury (Aussois, France: 7 of EAS Publications Series), 79, 79. doi:10.1051/eas:2003038

CrossRef Full Text | Google Scholar

Telezhinsky, I., Dwarkadas, V. V., and Pohl, M. (2012). Time-dependent escape of cosmic rays from supernova remnants, and their interaction with dense media. A& 541, A153. doi:10.1051/0004-6361/201118639

CrossRef Full Text | Google Scholar

Tibaldo, L., Gaggero, D., and Martin, P. (2021). Gamma rays as probes of cosmic-ray propagation and interactions in galaxies. Universe 7, 141. doi:10.3390/universe7050141

CrossRef Full Text | Google Scholar

Truelove, J. K., and McKee, C. F. (1999). Evolution of nonradiative supernova remnants. ApJs 120, 299–326. doi:10.1086/313176

CrossRef Full Text | Google Scholar

Uchiyama, Y., Funk, S., Katagiri, H., Katsuta, J., Lemoine-Goumard, M., Tajima, H., et al. (2012). Fermi large area telescope discovery of GeV gamma-ray emission from the vicinity of SNR W44. ApJL 749, L35. doi:10.1088/2041-8205/749/2/L35

CrossRef Full Text | Google Scholar

van Marle, A. J., Bohdan, A., Morris, P. J., Pohl, M., and Marcowith, A. (2022). Diffusive shock acceleration at oblique high Mach number shocks. ApJ 929, 7. doi:10.3847/1538-4357/ac5962

CrossRef Full Text | Google Scholar

van Marle, A. J., Casse, F., and Marcowith, A. (2019). Three-dimensional simulations of non-resonant streaming instability and particle acceleration near non-relativistic astrophysical shocks. MNRAS 490, 1156–1165. doi:10.1093/mnras/stz2624

CrossRef Full Text | Google Scholar

Vink, J., and Bamba, A. (2022). “Nonthermal processes and particle acceleration in supernova remnants,” in Handbook of X-ray and gamma-ray Astrophysics (Springer), 52. doi:10.1007/978-981-16-4544-0_90-1

CrossRef Full Text | Google Scholar

Weidl, M. S., Jenko, F., Teaca, B., and Schlickeiser, R. (2015). Cosmic-ray pitch-angle scattering in imbalanced MHD turbulence simulations. ApJ 811, 8. doi:10.1088/0004-637X/811/1/8

CrossRef Full Text | Google Scholar

Wiener, J., Zweibel, E. G., and Oh, S. P. (2013). Cosmic ray heating of the warm ionized medium. ApJ 767, 87. doi:10.1088/0004-637X/767/1/87

CrossRef Full Text | Google Scholar

Xin, Y., and Guo, X. (2023). Detection of the extended γ-ray emission around supernova remnant DA 530 with fermi-LAT. ApJ 955, 84. doi:10.3847/1538-4357/acf455

CrossRef Full Text | Google Scholar

Xu, S. (2021). Mirror diffusion of cosmic rays in highly compressible turbulence near supernova remnants. ApJ 922, 264. doi:10.3847/1538-4357/ac2d8f

CrossRef Full Text | Google Scholar

Xu, S., and Lazarian, A. (2022a). Cosmic ray streaming in the turbulent interstellar medium. ApJ 927, 94. doi:10.3847/1538-4357/ac4dfd

CrossRef Full Text | Google Scholar

Xu, S., and Lazarian, A. (2022b). Shock acceleration with oblique and turbulent magnetic fields. ApJ 925, 48. doi:10.3847/1538-4357/ac3824

CrossRef Full Text | Google Scholar

Xu, S., Lazarian, A., and Yan, H. (2015). The line width difference of neutrals and ions induced by MHD turbulence. ApJ 810, 44. doi:10.1088/0004-637X/810/1/44

CrossRef Full Text | Google Scholar

Yan, H., and Lazarian, A. (2004). Cosmic-ray scattering and streaming in compressible magnetohydrodynamic turbulence. ApJ 614, 757–769. doi:10.1086/423733

CrossRef Full Text | Google Scholar

Yan, H., Lazarian, A., and Schlickeiser, R. (2012). Cosmic-ray streaming from supernova remnants and gamma-ray emission from nearby molecular clouds. ApJ 745, 140. doi:10.1088/0004-637X/745/2/140

CrossRef Full Text | Google Scholar

Yang, C., Zhang, L., and Wang, J. (2015). On the escape and propagation of high-energy protons near young supernova remnants. MNRAS 448, 3423–3428. doi:10.1093/mnras/stv255

CrossRef Full Text | Google Scholar

Zhang, C., and Xu, S. (2023). Numerical testing of mirror diffusion of cosmic rays. ApJL 959, L8. doi:10.3847/2041-8213/ad0fe5

CrossRef Full Text | Google Scholar

Zirakashvili, V. N., and Ptuskin, V. S. (2012). Numerical simulations of diffusive shock acceleration in SNRs. Astropart. Phys. 39, 12–21. doi:10.1016/j.astropartphys.2011.09.003

CrossRef Full Text | Google Scholar

Zweibel, E. G. (2013). The microphysics and macrophysics of cosmic rays. Phys. Plasmas 20, 055501. doi:10.1063/1.4807033

CrossRef Full Text | Google Scholar

Zweibel, E. G. (2020). The role of pressure anisotropy in cosmic-ray hydrodynamics. ApJ 890, 67. doi:10.3847/1538-4357/ab67bf

CrossRef Full Text | Google Scholar

Zweibel, E. G., and Everett, J. E. (2010). Environments for magnetic field amplification by cosmic rays. ApJ 709, 1412–1419. doi:10.1088/0004-637X/709/2/1412

CrossRef Full Text | Google Scholar