Comparison of terrestrial exospheric hydrogen 3D distributions at solar minimum and maximum using TWINS Lyman-α observations

Remote sensing observations of far-ultraviolet (FUV) emissions have been used to estimate 3D neutral hydrogen (H) density models of the terrestrial exosphere under solar minimum (2008) and solar maximum (2013 and 2015) conditions. Specifically, we used Lyman-alpha (Lyman-$\alpha$, FUV at 121.6 nm) radiance data acquired by the Lyman-alpha detectors (LADs) onboard NASA’s TWINS satellites, collected over several days for each of the 3 years to provide sufficient coverage of the exospheric region. The datasets included Lyman-$\alpha$ measurements taken only above Earth radii (R_e) of 3.75, assumed to be the optically thin region of the exosphere, where the measured Lyman-$\alpha$ intensity along a line of sight (LOS) is linearly proportional to the atomic hydrogen column density. Based on the calibration using multiple UV-bright stars, a significant decrease in TWINS1 LAD1/2 sensitivities was found for 2013 (LAD2 ∼1/2, LAD ∼1/3) and 2015 (LAD2 ∼1/3, LAD ∼1/7) compared to 2008. The calibration uncertainty was derived to be, on average, 5%. We estimated the 3D global hydrogen density distributions from these radiance data using two different tomographic inversion methods: first, a parametric fitting method based on a spherical harmonic function of order 3 and second, a high degree-of-freedom retrieval approach to validate our retrievals of H density. Both inversion methods consistently incorporate the effects of Lyman-$\alpha$ absorption within the exosphere and Lyman-$\alpha$ re-emission from Earth’s albedo. Our results reveal that H densities during solar maximum conditions are, on average, 30%–40% higher than those during solar minimum. All models showed a high concentration of atomic H on the dayside and nightside near the Sun–Earth line, which determines a nose/geotail structure consistent with theoretical effects from the solar radiation pressure. Furthermore, we identified that H-density enhancements during solar maximum with respect to solar minimum conditions occur at mid-to-high latitudes, particularly on the dusk side, while no significant enhancement seems to occur near the dayside nose.

1 Introduction

The exosphere is the uppermost layer of the terrestrial atmosphere that extends from ∼500 km (its inner boundary, known as the exobase) up to Earth radii of ∼60 (R_e; 1 R_e = 6,371 km) (Baliukin et al., 2019). This region is mainly populated with atomic neutral hydrogen (H), which resonantly scatters solar Lyman-alpha (Lyman-$\alpha$) photons at 121.6 nm, producing the global glow phenomenon called the geocorona. Above 3 R_e, the exosphere is in an optically thin regime such that a measurement of a column-integrated Lyman-$\alpha$ emission exhibits a linear relationship with the local exospheric column density. This property has been used by several scientists to derive exospheric H-density models from Lyman-$\alpha$ data using a variety of inversion techniques. Knowledge about H-density distributions at this altitude range is crucial to understanding the drivers responsible for the permanent escape of H to space and investigating the role of atomic H in several ion-neutral processes within the inner magnetospheric region, such as plasmaspheric refilling and ring current recovery, especially during geomagnetic storms (Krall et al., 2018). Exospheric H-density reactions to geomagnetic storms have been analyzed by Kuwabara et al. (2017); Zoennchen et al. (2017); and Cucho-Padin and Waldrop (2019). Other possible contributions of non-thermal hydrogen to the exosphere are discussed [see Qin and Waldrop (2016); Fahr et al. (2018)].

Several efforts to estimate H density from far-ultraviolet (FUV) observations have been thoroughly conducted in the last four decades. For example, Rairden et al. (1986) generated an H-density profile utilizing Lyman-$\alpha$ measurements from the ultraviolet photometer of the University of Iowa Spin-scan Auroral Imaging instrumentation on board the Dynamics Explorer 1 satellite. Specifically, the radiance data were fitted to an isothermal Chamberlain model (Brandt and Chamberlain, 1959) that produces radial H-density profiles ranging from the exobase up to 12 R_e. The data were acquired during 1981–1985 under both solar maximum and minimum conditions. Østgaard et al. (2003) used optically thin, nightside Lyman-$\alpha$ observations of the exosphere acquired by the Geocoronal Imager (GEO) instrument on board NASA’s Imager for Magnetopause-to-Aurora Global Exploration (IMAGE) to derive a set of H-density profiles ranging from 90 to 180° solar zenith angles (SZAs). These radiance data were fitted to a double-exponential function featuring high data/model agreement, which indicates the presence of two-temperature populations of H in the terrestrial exosphere. Furthermore, data used for this analysis were acquired during the 2000–2001 period under solar maximum conditions.

Since June 2008, NASA’s Two Wide-angle Imaging Neutral-atom Spectrometers (TWINS) mission, which includes two satellites TWINS1 and TWINS2, has been acquiring routine measurements of geocoronal H Lyman-$\alpha$ from the two Lyman-Alpha Detectors (LAD1 and LAD2) on each spacecraft. The satellites are placed in elliptical Molniya orbits having 63.4° inclination, apogees in the Northern Hemisphere at ∼7.2 R_e, and sufficient longitudinal inter-satellite separation appropriate for stereoscopic sensing of the magnetospheric and exospheric regions. The LADs have a 4-degree field of view (FOV) with a 100-Å filter bandwidth and are placed on a rotating platform whose axis is nadir pointing, and the detectors are 40 degrees off, such that line-of-sight (LOS) measurements cover altitudes beyond ∼1,000 km [instrumental details are given in the study by McComas et al. (2009)]. Since the LAD sensitivity has decreased over the years, the correct inflight calibration (including uncertainty) is a very important issue when comparing Lyman-α observations from different years.

TWINS/LAD radiance data have been used to estimate 3D H-density models using more sophisticated inversion methods. Zoennchen et al. (2015) used a parametric fitting approach to a spherical harmonics function of order 2 to estimate a set of exospheric density models. Data acquired in June 2008 and June 2010 during quiet geomagnetic conditions were used to generate a solar minimum model. Similarly, data acquired from October to December 2012 were used to generate a model for solar maximum conditions. This study reported, for the first time, the response of the exospheric density and structure to the solar cycle. More recently, Cucho-Padin and Waldrop (2018) implemented a high degree-of-freedom (DOF) tomography approach, which allows the estimation of density distributions without the dependence on ad hoc functions, allowing the identification of intricate spatial structures. Data for a single day in 2008 (solar minimum) were used to demonstrate the feasibility of this technique. Radial H-density profiles of the outer exosphere, in particular close to the subsolar point (SSP) derived from Lyman-α observations, are discussed by Cucho-Padin et al. (2022) and Zoennchen et al. (2022). Furthermore, H-density values at 10 R_e near the subsolar point derived from different observations from Lyman-α are also discussed [i.e., with XMM-Newton X-ray by Connor and Carter (2019) or with IBEX-ENA/MMS by Fuselier et al. (2020)].

In this article, we implement three models of the H exosphere using TWINS LAD data acquired during solar minimum (2008) and solar maximum conditions (2013 and 2015) to investigate the response of the density distributions to a solar cycle. Each dataset is formed using several days of data to provide an appropriate coverage of the exospheric region. We process data from each year independently and introduce a self-consistent handling of two different Lyman-$\alpha$ absorption processes within the exosphere. Furthermore, we expand the spherical harmonic representation (SHR) model from order 2 to order 3 to allow complex spatial structures of the H density. To validate our results, we also implement a high-DOF tomography approach to reconstruct the 3D exospheric density using the same Lyman-$\alpha$ datasets. In order to examine the models under different solar conditions, we quantify the number of H atoms within the 3.75–6-R_e region, where the uncertainty of the reconstruction is low. Finally, we provide a set of SHR model parameters for each model to allow the scientific community to reproduce these H densities.

2 Materials and methods

2.1 Approach and LOS corrections

Under the assumption of single scattering in the optically thin regime, the local exospheric density $n\left(S\right)$ [atoms/cm³] and the exospheric backscattered Lyman-α column brightness $B$ in Rayleighs (1 [R] = 10⁶ photons [$4\pi ·{cm}^2·s·sr$]⁻¹, see Østgaard et al. (2003) along a line-of-sight $S$ are related to each other:

$B=4\pi I=\frac{g^{*}}{{10}^6}{\int }_0^{S_{\mathit{max}}}n\left(S\right)\epsilon \left(S\right)\gamma \left(S\right)\mathit{\Psi }\left(\alpha \left(S\right)\right)dS,(1)$

with $\epsilon \left(S\right)$ being the (dimensionless) local Earth albedo correction term, γ(S) being the (dimensionless) local loss term of photons on their way back to the detector, and Ψ(α(S)) being the (dimensionless) local intensity correction due to the dependence of the scattering efficiency on the angle α between the line-of-sight S and the incident solar photon (Brandt and Chamberlain, 1959). The scattering rate g* [photons/atom/s] is the product of the scattering cross section σ [cm²] and the effective solar Lyman-α flux at line center F_eff [photons/cm²/s] (* at g indicates its adjustment from 1 AU to the actual Earth–Sun distance). The values for σ and F_eff, shown in Equations 2–4, were obtained from the studies by Østgaard et al. (2003) and Bishop (1999):

$\sigma =5.9·{10}^{-12}·{\left(1050\left[K\right]\right)}^{-\frac{1}{2}},(2)$

$F_{eff}=\pi f·∆{\gamma }_D\sqrt{\pi }\text{\hspace{1em}with\hspace{0.17em}}{f}_{line-center}=\pi f,(3)$

$\text{Doppler\hspace{1em}line\hspace{1em}width}∆{\gamma }_D=5.21·{10}^{-4}·\sqrt{1050\left[K\right]},(4)$

where 1,050 K is an exospheric reference temperature derived by Rairden et al. (1986).

The solar Lyman-α line-center flux can be calculated from the total solar Lyman-α flux (which is provided by SEE/TIMED) using the relation given by Emerich et al. (2005).

In addition to the exospheric contribution, every measurement contains a background from the Lyman-α glow of the interplanetary H atoms (IPH background), which needs to be subtracted. Here, we used a hot model of the interplanetary H-density distribution (Fahr, 1971; Thomas, 1978). Based on that model, we calculated daily all-sky maps of the Lyman-α flux from the IPH background. The model parameters and assumptions used are widely described by Zoennchen et al. (2015).

The Earth albedo correction term $\epsilon \left(S\right)$ consists of two additive components.

First is the backscattered Lyman-α re-emission from lower (optically thick) exospheric shells with high H densities at the dayside (acts as a secondary source of Lyman-α). This secondary dayside Lyman-α radiation was modeled using a Monte Carlo (MC) model based on the solar minimum 3D H-density distribution proposed by Zoennchen et al. (2015). The largest enhancement of the local g-factor due to this effect is located at the dayside (near the subsolar point) at low distances. At our lower model boundary at 3.75 R_e, the local g-factor is enhanced by ∼15%. The dayside enhancement decreases rapidly with increasing radial distance. The influence of H-density variations during the solar cycle on the local g-factor enhancement is expected to be very small. One reason is the expected low variance of the H-density level with the solar cycle at low distances near the exobase (Chamberlain, 1963), where most of Earth’s albedo Lyman-α emissions originate from. Therefore, in this work, we used the same modeled local g-factor enhancement due to albedo emission for all inversions.

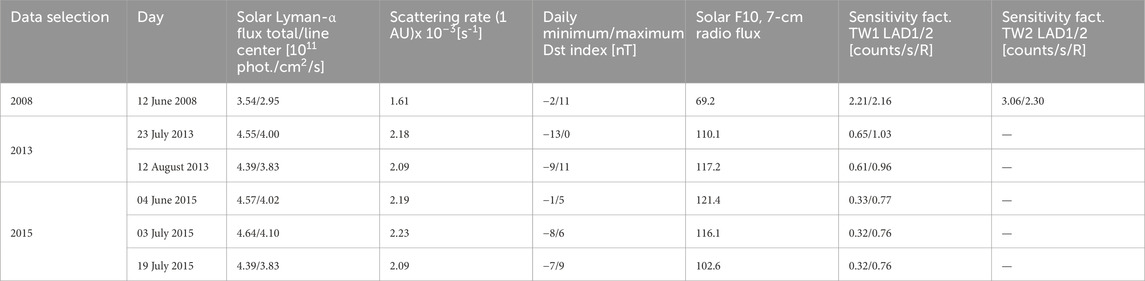
Second is the self-absorption term of the solar Lyman-α flux when it enters the exosphere at the dayside (i.e., at 10 R_e) and transits toward the nightside (see blue arrow in Figure 1). This correction term was implemented self-consistently in the model fitting process by considering the optical depth ${\tau }_1=\int \sigma ·n_{H}d{S}_1$ (with local H density $n_H$ and cross section $\sigma$) along the exospheric penetration path of the solar light to an LOS position at $S_{Scattering}$. The solar Lyman-α flux at this position is reduced by exp ($-{\tau }_1$). The combined effect of these two correction terms on the local g-factor is shown within the ecliptic plane in Figure 2 (as an example of the solar minimum H-density distribution). With the exceptions of the inner exospheric dayside region (enhanced g-factor) and the nightside penumbra region (reduced g-factor), the combined correction factor is elsewhere close to 1, signifying small deviations from the purely single-scattering case.

Figure 1

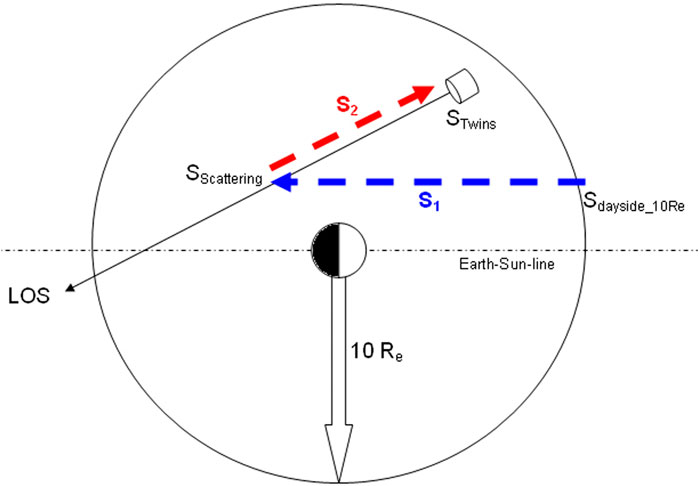
Figure 1. Two corrections (blue and red arrows) for geocoronal Lyman-α absorption at an integration LOS-position S_Scattering: (1) blue arrow: absorption due to the optical depth between S_Scattering and S_{dayside_10Re} (dimming of solar Lyman-α flux penetrating the exosphere); (2) red arrow: loss of scattered exospheric Lyman-α photons to the detector due to the optical depth between S_Scattering and S_Twins.

Figure 2

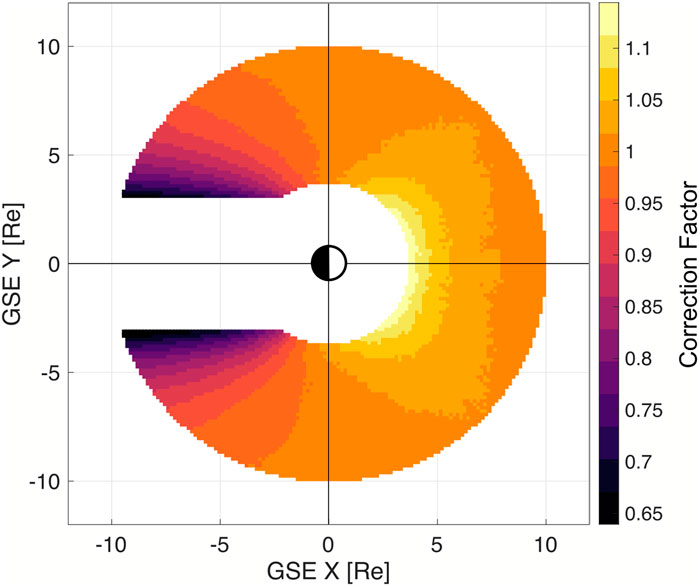
Figure 2. Ecliptic map (in GSE coordinates) of the combined effect of secondary Lyman-α from Earth re-emission (mostly at the Earth dayside) and exospheric self-absorption of solar Lyman-α radiation (mostly on the Earth nightside). This map is based on the H-density distribution from the solar minimum SHR model inversion (2008).

Additionally, our emission model includes a third correction term, $\gamma \left(S\right)$, that accounts for a loss of scattered photons on their way from the position of origin at $S_{Scattering}$ to the detector at $S_{Twins}$ (along the inverse LOS direction $S_2$; see red arrow in Figure 1). This term acts as a first-order correction of the optically thin assumption and was also implemented self-consistently into the model by considering the optical depth ${\tau }_2=\int \sigma ·n_{H}d{S}_2$ (and the scattered flux reduction $\gamma \left(S\right)=$ exp ($-{\tau }_2$)) along the path $S_2$).

The local cross section σ needed for the calculation of optical depths τ₁ and τ₂ is a function of the local exospheric temperature T_exo (see Equation 2). As an approximation of the local T_exo, we used a relation from COSPAR. Working Group IV (1965), where it is a function of the solar activity level (solar F_{10.7 cm} radio flux) and the Geocentric Solar Ecliptic (GSE) longitude. Note that there is a relation between solar F_{10.7 cm} radio flux and total solar Lyman-α flux (Vidal-Madjar, 1975). Figure 3 shows the GSE-longitudinal T_exo values used in this work for our data selections of solar minimum and maximum to calculate the local cross section σ.

Figure 3

Figure 3. Longitudinal variation in the exospheric temperature [K] for the total solar Lyman-α fluxes 3.5 (black—solar minimum) and 4.5 (red—solar maximum) based on temperature profiles from COSPAR. Working Group IV (1965).

2.2 Reconstruction of the exospheric 3D H-density distribution

For the reconstruction of the exospheric 3D H-density distribution, we applied two independent tomographic inversion methods as described in the following subsections. The expression “tomographic inversion” refers to a method that retrieves a local 3D distribution from a sample of (intersecting) multipositional and multidirectional line-of-sight integrated observations.

2.2.1 Method A: 3D inversion based on an SHR model

SHRs are widely used as a functional base to reconstruct the exospheric H-density distribution [(Hodges, 1994) with a polynomial number L = 3 (Nass et al., 2006; Zoennchen et al., 2015; Bailey and Gruntman, 2011) and L = 2].

To calculate the modeled LOS column brightness, we used the exospheric H-density model proposed by Zoennchen et al. (2015) with improvements in two aspects.

First, the radial power law function was enhanced by an additional term since it better fits the radial behavior of the column brightness data compared to a pure power law. Second, the polynomial number of the SHR was increased from L = 2 to 3 in order to capture spatial variations having higher angular frequencies.

$n_H\left(r,\vartheta ,\varphi \right)=c·r^{-k}·d^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$r$}\right.}·SHR\left(r,\vartheta ,\varphi \right),(5)$

$\begin{array}{ll}\hfill \text{with\hspace{1em}}SHR\left(r,\vartheta ,\varphi \right)& =\sqrt{4\pi }·{\displaystyle \sum _{l=0}^3}{\displaystyle \sum _{m=0}^l}\left[A_{lm}\left(r\right)·\cos \left(m\varphi \right)+B_{lm}\left(r\right)·\sin \left(m\varphi \right)\right]\hfill \\ \hfill & ·Y_{lm}\left(\vartheta \right),\hfill \end{array}(6)$

$\text{where\hspace{0.17em}}{A}_{lm}\left(r\right)=a_{lm}+b_{lm}·\ln \left(r\right);B_{lm}\left(r\right)=p_{lm}+q_{lm}·\ln \left(r\right).(7)$

Here, $Y_{lm}\left(\vartheta \right)$, used in Equation 6, represents the spherical harmonic Legendre polynomials [for reference, see “Appendix” in the study by Hodges (1994)] and $\vartheta$ is the co-latitude measured from the GSE north pole.

To take into account that the maximal impact distance (at the Earth tangent point) of the available LOSs is approximately 6 R_e, we limited the radial variation of $A_{lm}\left(r\right)$ and $B_{lm}\left(r\right)$ up to that distance. This assumption implies that the angular shape of our model at r > 6 R_e is fixed to its shape at 6 R_e, with the total H density decaying with further increases in radial distance according to Equation 5.

With a least squares fit procedure, the difference between observed and modeled LOS column brightness can be minimized:

$\mathit{min}\left({\left(I_{observed}-I_{model}\right)}^2\right).(8)$

Since the observational global coverage of the exosphere by TWINS LAD is incomplete, this fit function is expanded by a regularization term c, described below, to enforce a solution with optimal angular smoothness:

$\mathit{min}\left({\left(I_{observed}-I_{model}\right)}^2+c\right).(9)$

An inversion of TWINS Lyman-α data with the additional use of 3D regularization was first introduced by Cucho-Padin and Waldrop (2018). Since our inversion is based on a parametric density model with an r-dependence constraint in terms of an approximate power law, we only need to regularize the two angular dimensions (2D). The regularization term $c$, shown in Equation 10, in our work expresses the longitudinal and latitudinal gradient of the angular H-density variation onto a shell at the distance of the LOS Earth impact. The shell was split into 10° × 10° angular segments. Then, the squared modeled H-density gradients between neighbored segments at this shell were summed (longitudinal and latitudinal separately). It can be written as

$c=\lambda \left(\sum {\left(\frac{{\left({N_i-N}_{\left(i-1\right)}\right)}_{longitudinal}}{10°}\right)}^2+\sum {\left(\frac{{\left({N_j-N}_{\left(j-1\right)}\right)}_{latitudinal}}{10°}\right)}^2\right).(10)$

Factor λ scales the strength of the angular smoothness against the ${\left(I_{observed}-I_{model}\right)}^2$ term within the least squares fit. To evaluate the value of λ, we used the method of “K-fold” cross-validation, which can be used to optimize the predictability of our fitted model. The LAD data were separated into “training” and “testing” subsets. The fitted model reached its highest predictability if the fit based on “training” data (with a pre-defined λ) can best predict the observations of the “testing” data.

For the “training” subset, we used TWINS1 LAD1 and TWINS2 LAD2 data of 12 June 2008. The “testing” subset contained TWINS1 LAD2 and TWINS2 LAD1 data of the same day. Using these subsets, we found the optimal model predictability with λ = 2.01. This value for λ was also used for the density inversion from the data of 2013 and 2015 (for the description of the LAD data selections, see Section 2.3).

2.2.2 Method B: 3D inversion based on the “high-DOF” method

In order to validate the parametric estimations of 3D H-density distributions, we also utilized a parametric-free approach to reconstruct exospheric density from TWINS radiance data. In contrast to parametric estimation, this possesses a high DOF to reproduce intricate spatial structures in the H density. This method is thoroughly described by Cucho-Padin et al. (2022) and is briefly summarized here. First, we adopted a spherical solution domain that includes only the optically thin region (valid zone for Equation 1). This sphere has an inner and outer radius equal to 3 and 25 R_e, respectively. Second, we discretized the solution domain into uniform spherical voxels with dimensions ∆r = 0.25 R_e and ∆ϕ = ∆θ = ${12}^{\circ }$, which provide sufficient resolution to capture spatial gradients of the exospheric density distributions. We selected a spherical grid instead of a Cartesian grid for two reasons: (a) to reduce the computational load of the reconstruction problem since the number of spherical voxels required to cover the desired region of interest is around ∼10³ times less than the number of cubic voxels with similar resolution (∆r = 0.25 R_e) and (b) since the H density decreases with radial distance, spatial variability beyond ∼12 Re also decreases, and a low-resolution grid (spherical voxels) is sufficient to capture the 3D structural shape of the high-altitude exosphere. Thus, our selection of voxel sizes yields a total number of voxels of $N=39600$. Third, the forward emission model presented in Equation 1 is also discretized, resulting in the compact algebraic system $\mathit{y}=L\mathit{x}$. Here, $\mathit{y}$ is an $\left[M\times 1\right]$ vector of background-free measurements of LOS-integrated brightness B in units of Rayleigh, i.e., the $m^{th}$ measurement $y_m=I-I_{bkg}$. The term $\mathit{x}$ is the $\left[N\times 1\right]$ vector of H-density distributions corresponding to all voxels in the solution domain and arranged into a column vector. We assume that $n_H$ in a given voxel is constant within the voxel volume. The term $\mathit{L}$ is the $\left[M\times N\right]$ observation matrix that is generated by intersecting each LOS measurement with the solution domain. To clarify, the length of the line sector within a given voxel is used to populate matrix $\mathit{L}$. Additionally, each row of $\mathit{L}$ incorporates the corresponding factor $g^{*}\cdot \mathrm{\Psi }\left(\alpha \left(S\right)\right)/{10}^6$. Note that LOSs that are parallel to a given voxel’s edges have intersection length values that cannot be calculated; these are discarded as data constraints. The percentage of LOSs discarded from each Lyman-α dataset due to this geometry constraint is ∼2%.

In this study, we generated $\mathit{y}$ using TWINS observations, and each row of $\mathit{L}$ can be calculated with the corresponding direction of a measurement’s LOS, the TWINS’s spatial location, and the voxel sizes. Thus, the vector of densities $\mathit{x}$ is the only unknown in the system of equations. To solve this inverse problem, we used the statistical approach known as maximum a posteriori (MAP) estimation, which is formulated as follows (Norberg et al., 2023; 2018):

${\widehat{\mathit{x}}}_{MAP}={\left({\mathit{L}}^T{\mathit{R}}^{-1}\mathit{L}+{\mathit{Q}}^{-1}\right)}^{-1}\left({\mathit{L}}^T{\mathit{R}}^{-1}\mathit{y}+{\mathit{Q}}^{-1}{\mathit{x}}_{ref}\right),(11)$

where $\mathit{R}$ is the $\left[M\times M\right]$ covariance matrix of measurements, $\mathit{Q}$ is an approximation to the $\left[N\times N\right]$ covariance matrix of states (in this case, H density in the voxels), and ${\mathit{x}}_{ref}$ represents a physical model of the exosphere that supports the estimation process when data do not provide enough coverage of the solution domain.

To generate the covariance matrix of measurements, $\mathit{R}$, we consider that the Lyman-$\alpha$ brightness observations, $\mathit{y}$, are subject to primarily Poisson-distributed shot noise, i.e., $\mathit{y}$ $\sim$ Poiss ($\lambda$), where $\lambda$ is the mean and variance of the probability distribution. Since MAP establishes that all random vectors involved in the inverse problem should follow a Gaussian probability distribution, we use the approximation Poiss ($\lambda$) $\approx \mathcal{N}\left(\lambda ,\lambda \right)$ for each measurement [see Feller (1968); Hajek (2015); Cucho-Padin et al. (2024); Butala et al. (2010) for further details]. Additionally, we consider that each measurement is independent of the others such that their covariance is zero, and the value of $\lambda$ is the actual $\mathit{y}$ measurement as it is the high-probability realization of Poiss ($\lambda$). As a result, $\mathit{R}$ is defined as a diagonal matrix whose variance elements are the values of $\mathit{y}$, i.e., $\mathit{R}$ = diag($\left.\mathit{y}\right)$.

To generate the “precision matrix” ${\mathit{Q}}^{-1}$, we closely follow the implementation provided in Equations 7–9 by Cucho-Padin et al. (2022). This formulation requires (i) 3D correlation lengths and (ii) a standard deviation function $\mathit{\sigma }$ in the form of an $\left[N\times 1\right]$ vector. A correlation length ($l$) is a positive factor needed in the formulation of the precision matrix that, in simple words, establishes an interconnection among adjacent spherical voxels such that a variation in the density of a single voxel is propagated to its neighbors, ultimately imposing a level of smoothness in the 3D reconstruction, which is proportional to $l$. We selected correlation lengths that have been previously tested and used by Cucho-Padin et al. (2022) with values $l_r=l_{\varphi }$ = $l_{\theta }$ = 4 [R_e]. The vector $\mathit{\sigma }$ is formulated as $\eta \cdot {\mathit{x}}_{ref}$, where ${\mathit{x}}_{ref}$ is a vector of densities estimated using a spherically symmetric Chamberlain profile (Chamberlain, 1963) with temperature and density at the exobase equal to ${n_H}_{exo}$ = 2.3 $\times {10}^5$ and $T_{exo}$ = 850 K for the 2008 dataset, ${n_H}_{exo}$ = 8.4 $\times {10}^4$ and $T_{exo}$ = 1,060 K for the 2013 dataset, and ${n_H}_{exo}$ = 1.2 $\times {10}^5$ and $T$ = 1,000 K for the 2015 dataset. These exobase parameters were extracted from the NRLMSIS 2.0 model (Emmert et al., 2021). The scalar value of $\eta$ is fixed at 0.5 and represents the degree of confidence in this physics-based model used in the reconstruction. That is, the estimated density in a given voxel n, $x_{MAP}^n$, has a high probability of being in the range [$x_{ref}^n\cdot$ 0.5, $x_{ref}^n\cdot$ 1.5]. Furthermore, the formulation of ${\mathit{Q}}^{-1}$ includes penalization to the first and second derivatives, which enforces smoothness in the solution.

In this methodology, we also included the correction for geocoronal Lyman-α absorption, as well as the correction for Earth’s albedo. To do so, we first estimated the H-density distributions with no corrections and used the new ${\mathit{n}}_{\mathit{H}}$ profile to calculate the optical depth values, as explained in Section 2.1. Then, a correction factor for each voxel and measurement is estimated and included in the observation matrix $\mathit{L}.$ The inversion process (Equation 11) is performed iteratively until the variation between the previous and current H-density numbers is smaller than 5%. Our experiments showed that this threshold is met after four iterations.

2.3 Selections of TWINS LAD data

As a representation of the solar minimum near the summer solstice, our first selection contains LAD observations of TWINS1 and 2 from 12 June 2008. This day corresponds to quiet solar conditions, 3 days before a geomagnetic storm onset. On this day, the apogees of TWINS1 and 2 are situated longitudinally (GSE) on the dawn and dusk side at an angle of ∼20° from the noon–midnight meridian. This viewing geometry enables stereoscopic coverage of the dayside H-geocorona. For the solar maximum dataset, we used near-summer solstice TWINS1 LAD observations from 2013 to 2015. We created two separate selections with quiet-time data (with Dst-indexes near 0) from 2013 (23 July and 12 August) and 2015 (04 June, 03 July, and 19 July). These selections involve LAD data from multiple days in order to obtain a stereoscopic view, which is comparable to the viewing geometry in the 2008 data selection described above. As a result, the solar minimum and maximum data selections are very comparable in terms of angular viewing geometry, season, and geomagnetic activity.

We restricted the data to LOSs having geocentric impact distances ≥3.75 R_e. Beyond this distance, the relevant scattering processes correspond to an optically thin regime. All observations with LOS-Sun angles ≤90° are omitted from the data because they are contaminated by scattered sunlight. LOSs with tangent point radial distances ≤3 R_e are also excluded from the negative GSE x-axis (nightside) to avoid LOSs that cross regions near the shadow of Earth’s penumbra. Lastly, all LOSs crossing the 8° angular region around one of the tracked UV-bright stars [list of stars taken from the study by Snow et al. (2013)] are removed.

2.4 Solar and geomagnetic conditions

The data selection of 12 June 2008 represents the H-geocorona on a quiet day near the summer solstice in solar minimum. The solar total Lyman-α flux is very low at 3.54 [$\left.·{10}^{11}\right[$photons/cm²/s], and the Dst index (daily averaged) is stable near 0 [nT].

The other two data selections used here, from mid-2013 and mid-2015, represent the H-geocorona in the same season but during solar maximum conditions. The selected days can also be considered geomagnetic quiet with daily averaged Dst indexes near 0 [nT], which rules out the direct onset of a geomagnetic storm. Nevertheless, the total solar Lyman-α flux is significantly higher, with averaged values of 4.47 (2013) and 4.53 (2015) [$·{10}^{11}$ photons/cm²/s], compared to the 2008 data selection. A higher total solar Lyman-α flux is associated with a higher line center flux, which is relevant for geocoronal scattering (Emerich et al., 2005). The solar and geomagnetic conditions for all days used in this work are listed in Table 1.

Table 1

Table 1. Data selections of TWINS Lyman-α data with calibration factors and solar conditions.

2.5 LAD sensitivity calibration

The TWINS LAD detectors observed exospheric Lyman-α column brightness (in [counts/s]) along LOSs with a field of view of approximately 4°. The observed count rates were converted into the physical unit Rayleigh [R]. This was done using the LAD sensitivity factors $f_{cal}$ (in [counts/s/R]), which vary with time independently for each detector. In general, semiconductor detectors exhibit decreasing $f_{cal}$ values over their lifetime due to a loss of sensitivity by aging and exhaustion.

The calibration procedure presented here is customized for this study. To the best of our knowledge, no citable standard TWINS LAD calibration and no high data levels are available at this time. Nevertheless, the stellar peak levels, together with the related LAD sensitivity factors found in this work, might be useful for the community as standards of the analyzed periods.

The LAD sensitivity values from the data selections for 2013 and 2015 deviate significantly from their initial values in 2008, which motivates the recalibration conducted for this study. The TWINS LAD sensitivity $f_{cal}\left(t\right)$ at a given time $t$ can be calculated based on Equation 12 from the ratio of the Lyman-α peak fluxes of a UV-bright star at this time relative to an initial time $t_{init}$ (where the initial sensitivity $f_{cal,init}$ is known from a ground-based calibration [see also Zoennchen et al. (2015)]):

$f_{cal}\left(t\right)=f_{cal,init}·\frac{{Ly}_{\alpha }fluxstellarpeak\left(t\right)}{{Ly}_{\alpha }fluxstellarpeak\left(t_{init}\right)}(12)$

For the TWINS1 LAD2 data from 2015, we used the initial Lyman-α peak flux of June 2008 of the star Spica and compared it directly to the peak value measured from observations in mid-2015 (see Figure 4, upper row). A depletion in the TWINS1 LAD2 sensitivity by a factor of about 0.35 was derived. Regarding the TWINS1 LAD2 data from 2013, an additional cross-calibration step of Spica with the second star β Cen (galactic long/lat: 311.7°/1.25°) in mid-2010 was necessary since Spica was not observed by LAD2 on the days of our 2013 selection (see Figure 4, lower row). For validation, the stars α Cru and λ Sco were also used.

Figure 4

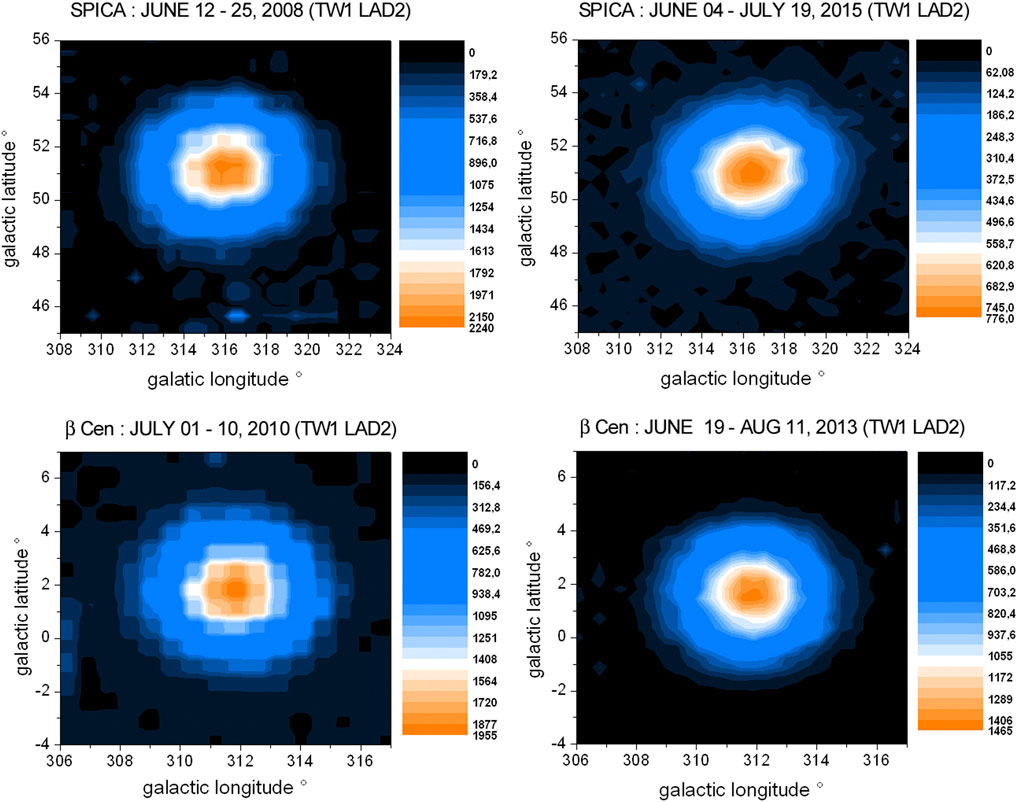
Figure 4. Cross-calibration of TWINS1 LAD2 for mid-2015 and 2013 (upper row: June 2008 versus June–July 2015 using observations of star Spica; lower row: July 2010 versus June–August 2013 using observations from star β Cen).

Furthermore, the sensitivities of both LADs of TWINS2 (as used in the 2008 data selection) are recalibrated against the LADs of TWINS1 (see Figure 5) using the stars σ Sgr and α Cru. All sensitivity factors used in this work are listed in Table 1.

Figure 5

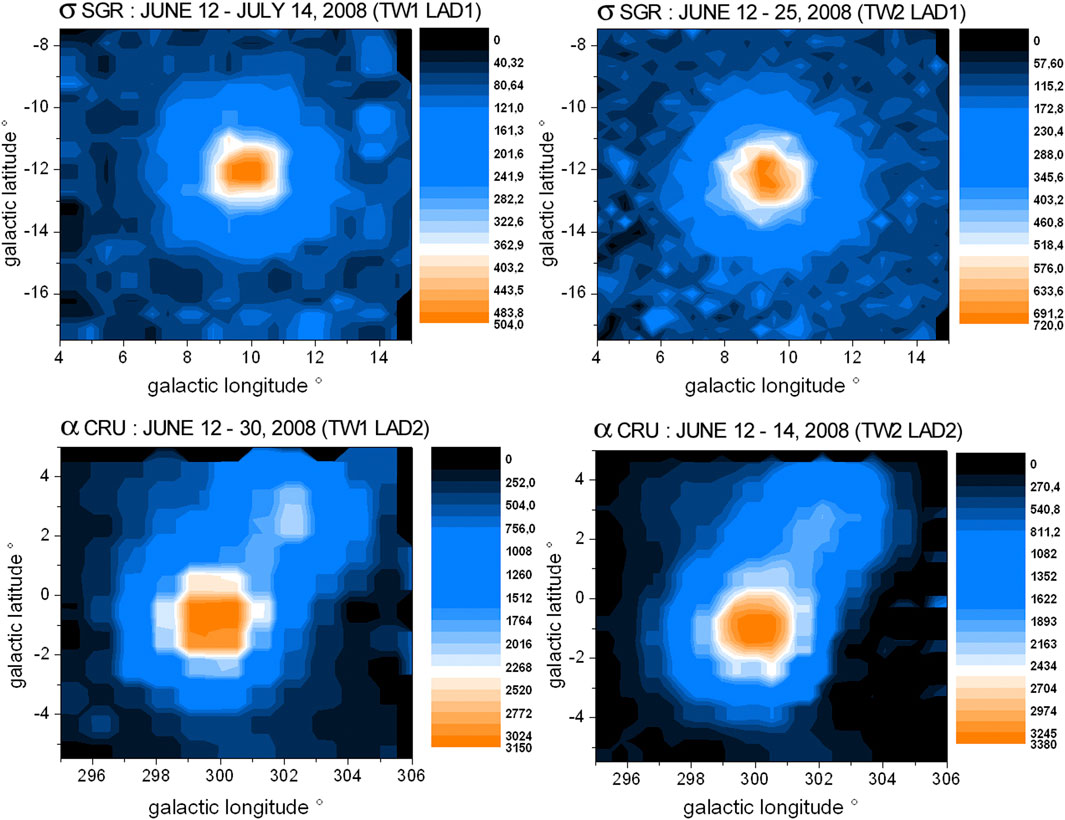
Figure 5. Lyman-α detector cross-calibration of TWINS2 against TWINS1 in 2008 (upper row: TWINS1 LAD1 versus TWINS2 LAD1 using LAD observations of star σ Sgr in June/July 2008; lower row: TWINS1 LAD2 versus TWINS2 LAD2 using LAD observations of star α Cru in June 2008).

An estimate of the calibration uncertainty is needed to evaluate the H-density variation between solar minimum (2008) and maximum (2013, 2015) found in this work. As shown in Table 1, for TWINS1 in 2015, the sensitivities of both LADs experienced a heavy decrease (LAD1 to ∼1/7 and LAD2 to ∼1/3) with respect to their initial values. In 2013, the decrease was not that strong but was also significant (LAD1 to ∼1/3 and LAD2 to ∼1/2). Besides the noise-to-peak ratio of the reconstructed stellar images, there is uncertainty due to the intrinsic stellar UV-flux variation over the considered time period. Both effects can be quantified (in sum) by analyzing the standard deviation of the individual peak-level decreases of multiple stars. As shown in Table 2, the values for the relative peak-level decrease derived from different stars for the same period/same LAD are quantitatively very close together. This speaks for a good noise-to-peak ratio in the images and for stable stellar UV-fluxes of the used stars. For TWINS1, it was found that the LAD2 calibration based on α Cru and λ Sco has 4.6% (2013) and 4.2% (2015) uncertainty with respect to the Spica-based value, respectively. The LAD1 calibration uncertainties are 3.2% (2013) and 6.2% (2015). From these values, we assume an averaged calibration uncertainty of ∼5% for both LADs and both solar max years.

Table 2

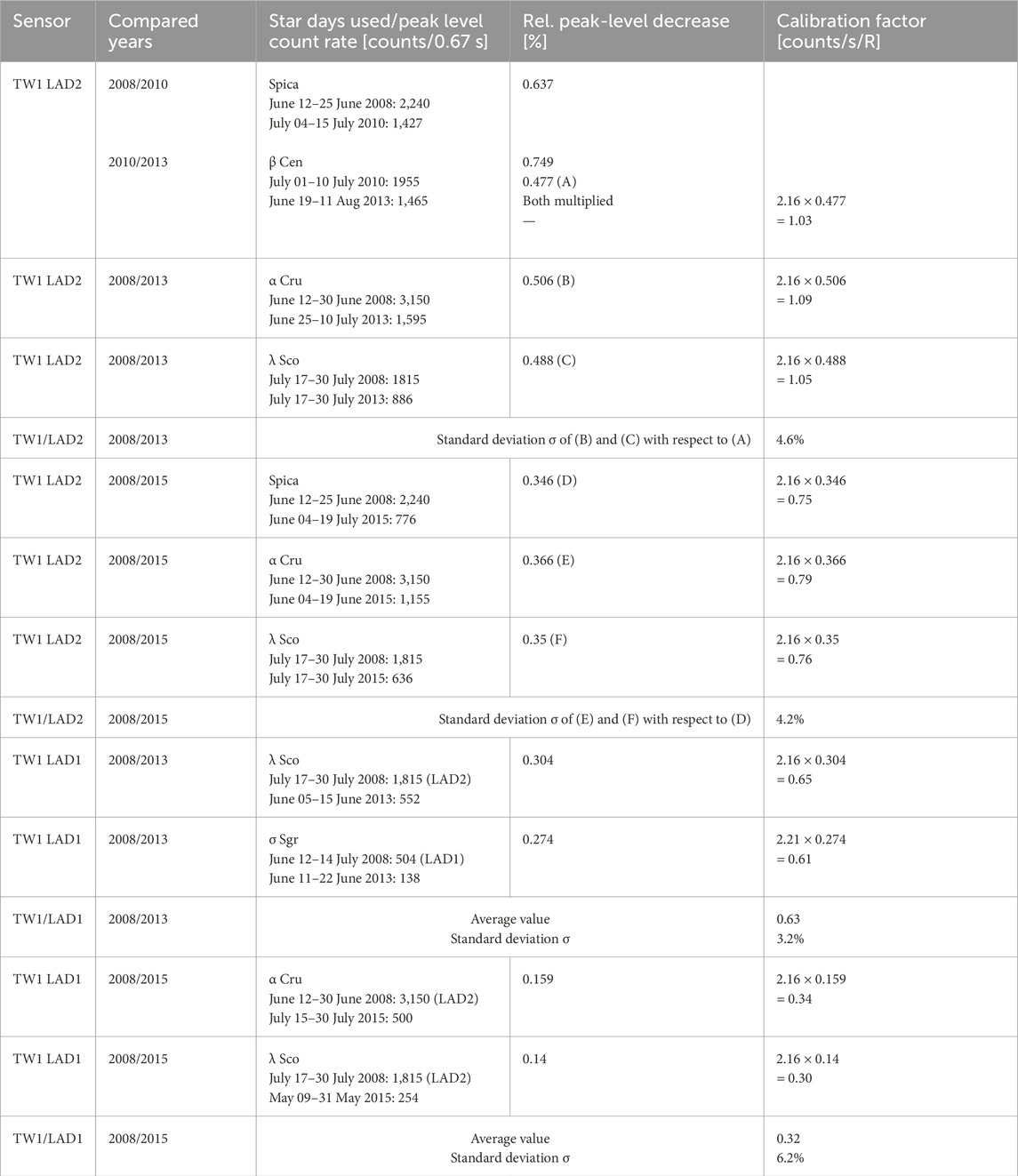
Table 2. Lyman-α peak-level count rates of different UV-bright stars measured with the two LADs of TWINS1 near summer 2008, 2013, and 2015. The reduction in the LAD-sensitivity between 2 years is equivalent to the reduction in the peak-level count rates of a given star during the same time. By comparing the peak-level reductions of multiple stars over a period (observed by the same LAD), the uncertainty of this calibration method was found to be 3%–6% (on average, ∼5%).

3 Results

3.1 Normalized radial Lyman-α profiles at solar minimum and maximum

Figure 6 shows the normalized radial profiles of the measured exospheric Lyman-α column brightness between 3.75 and 6.0 R_e (LOS impact distance) for solar minimum and maximum (IPH background and the effect of the scattering phase function are removed). Here, normalized means that the effect of a brighter solar Lyman-α illumination at solar maximum than at solar minimum is removed by normalizing the solar maximum profiles to the lower scattering rate of the total solar Lyman-α flux at solar minimum. As shown in Figure 6, the solar maximum profiles (2013 and 2015) both show significantly higher Lyman-α column brightness values than the solar minimum profile. Since the effect of a brighter solar illumination is removed, the remaining higher values at solar maximum reflect larger hydrogen column densities than those at solar minimum. This result is evident directly from the column brightness profiles shown in Figure 6.

Figure 6

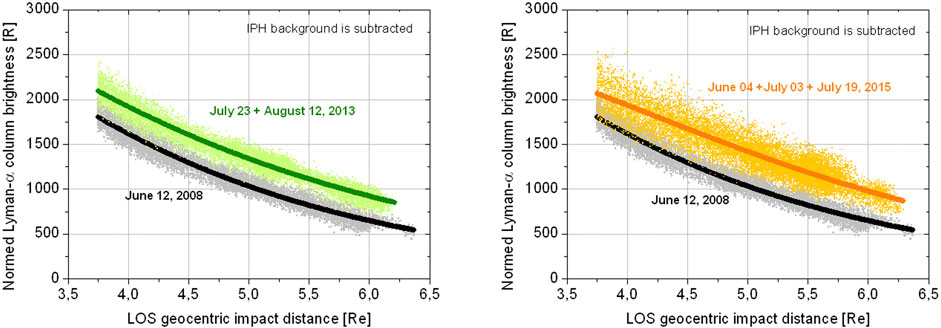
Figure 6. TWINS LAD Lyman-α column brightness profiles observed at spacecraft distances ≥6.5 R_e (LOSs impacting the bright dayside nose within an angular distance <75° from the subsolar point are excluded from these plots).

A correct calibration of the LAD sensitivity between the years of solar minimum (2008) and maximum (2013 and 2015) is essential when comparing exospheric H-density levels. The relative uncertainty of the calibration method used in this work, which, based on the peak values of multiple UV-bright stars, was found to be, on average, ∼5%. This is significantly smaller than the enhancement of the Lyman-α column brightness profile at solar maximum compared to minimum (as shown in Figure 6).

3.2 Comparison of the 3D H-density distributions

Figure 7 shows the 3D H-density distributions for solar minimum (2008) and maximum (2013 and 2015) derived from the two independent 3D inversion techniques described in Section 2.2.1 (with the SHR formulation) and Section 2.2.2 (“high degree-of-freedom” method). The results from both inversion techniques are very similar in terms of angular distribution and total exospheric H density at the lower and upper boundary of 3.75 and 6.0 R_e, respectively. Since the angular resolution of the SHR method is limited by its polynomial order (=3), the H-density distributions from the HDOF method show slightly more structures than the SHR results. The numerical values for the SHR model coefficients are listed in Table 3.

Figure 7

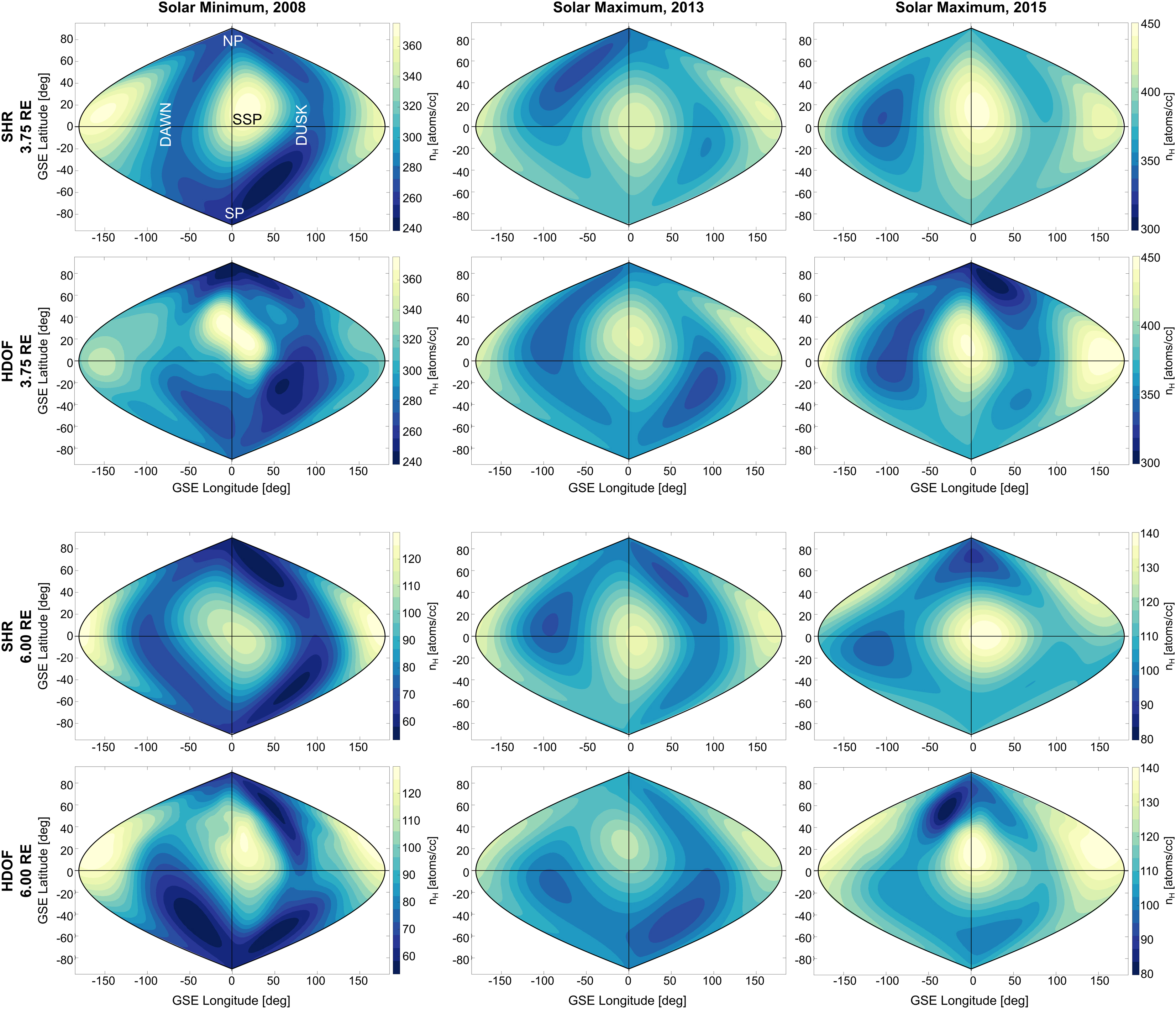
Figure 7. H-density distributions estimated from both inversion methods: SHR model (see section 2.2.1) and HDOF technique (see section 2.2.2). The first and second rows show estimated H-density distributions at a geocentric distance of 3.75 R_e using the SHR model and HDOF technique, respectively. Tomographic estimations used data on near summer solstice for 2008 (left column), 2013 (middle column), and 2015 (right column). The third and fourth rows show H densities at 6.00 R_e using the SHR model and HDOF technique, respectively. Most significant regions of enhanced H density are at the dayside (“nose”) near the subsolar point at GSE longitude/latitude ∼15°/10° and at the nightside (“tail”) near midnight. Density enhancements near the nose and tail are visible in the inversions for both solar minimum and maximum. Both the absolute H density and its angular distribution (nose and tail features) are very similar to the results found with the SHR model inversion. NP, North ecliptic pole; SP, South ecliptic pole.

Table 3

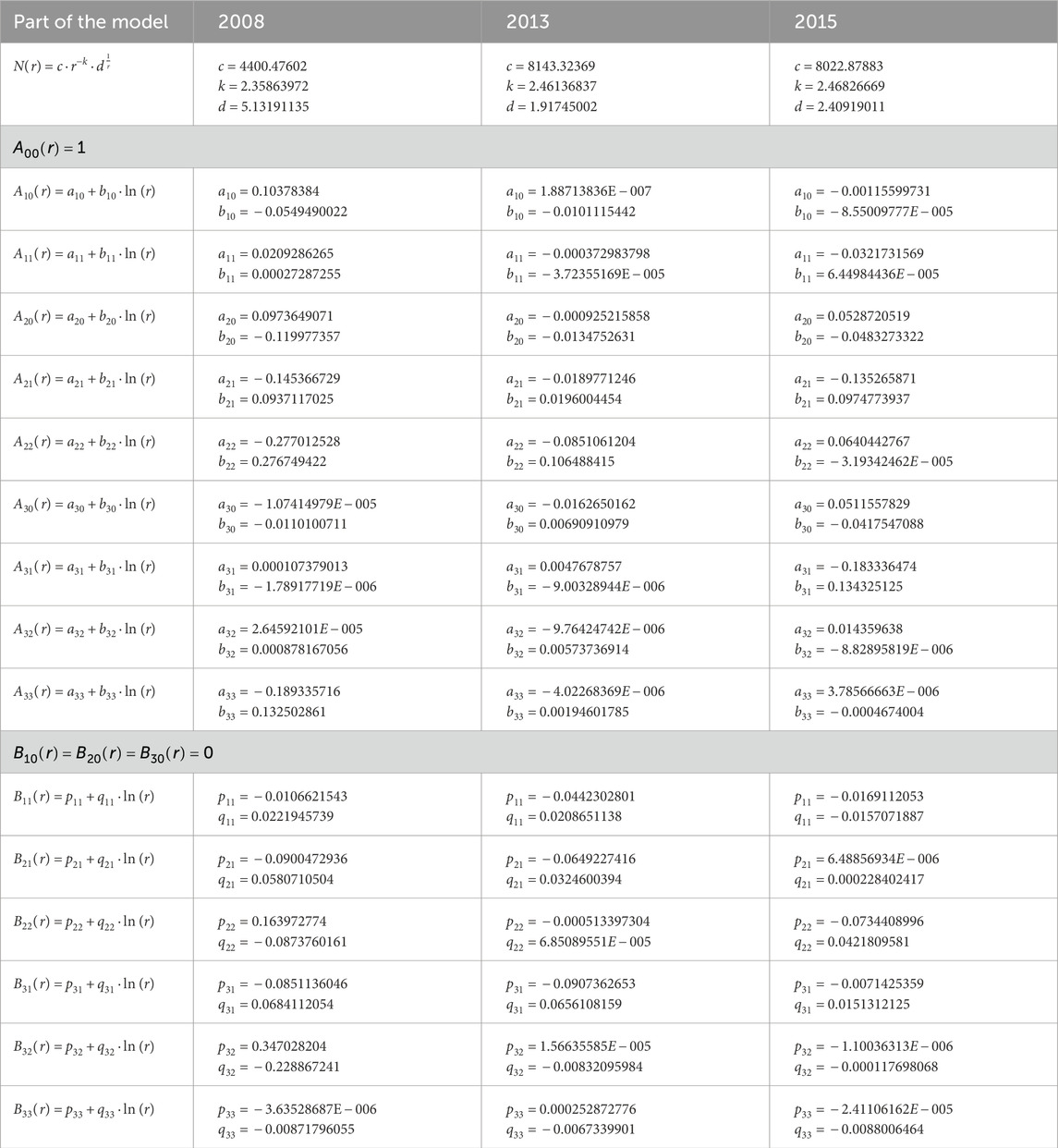
Table 3. Model fit coefficients for the spherical harmonic models of the 3D hydrogen density distribution at solar minimum (2008) and solar maximum (2013 and 2015).

The exosphere over this distance range clearly deviates from a radial symmetric distribution. Most significant is a strongly enhanced region on the dayside near the SSP. This dayside “nose” is visible in all inversions and provides an H-density peak value that is 20%–50% larger than the H densities of the surrounding “off-nose” angular regions on the same radial shell. A second region of enhanced H densities is present on the nightside near midnight. This “tail” structure also appears in all inversions with a varying level of significance.

The integrated (over 1° × 1° angular segments) number of H-atoms within 3.75–6.0 R_e is shown in Figure 8 separately for both inversion methods. The described “nose” and “tail” regions of enhanced H densities appear in these images with their highest significance and contrast. To identify angular regions with the largest solar cycle-dependent H-density enhancement, the ratio of solar maximum to minimum of the integrated H-atom number density at every angular segment was calculated. The result is plotted for both inversion techniques in Figure 9 (left image: SHR model; right image: “high degree-of-freedom” method). The most significant relative H-density enhancements are at the dayside (mostly at mid-to-high latitudes), with a preference for the dusk side. It is noteworthy that the enhancement close to the dayside nose (near the SSP) appears to be relatively low.

Figure 8

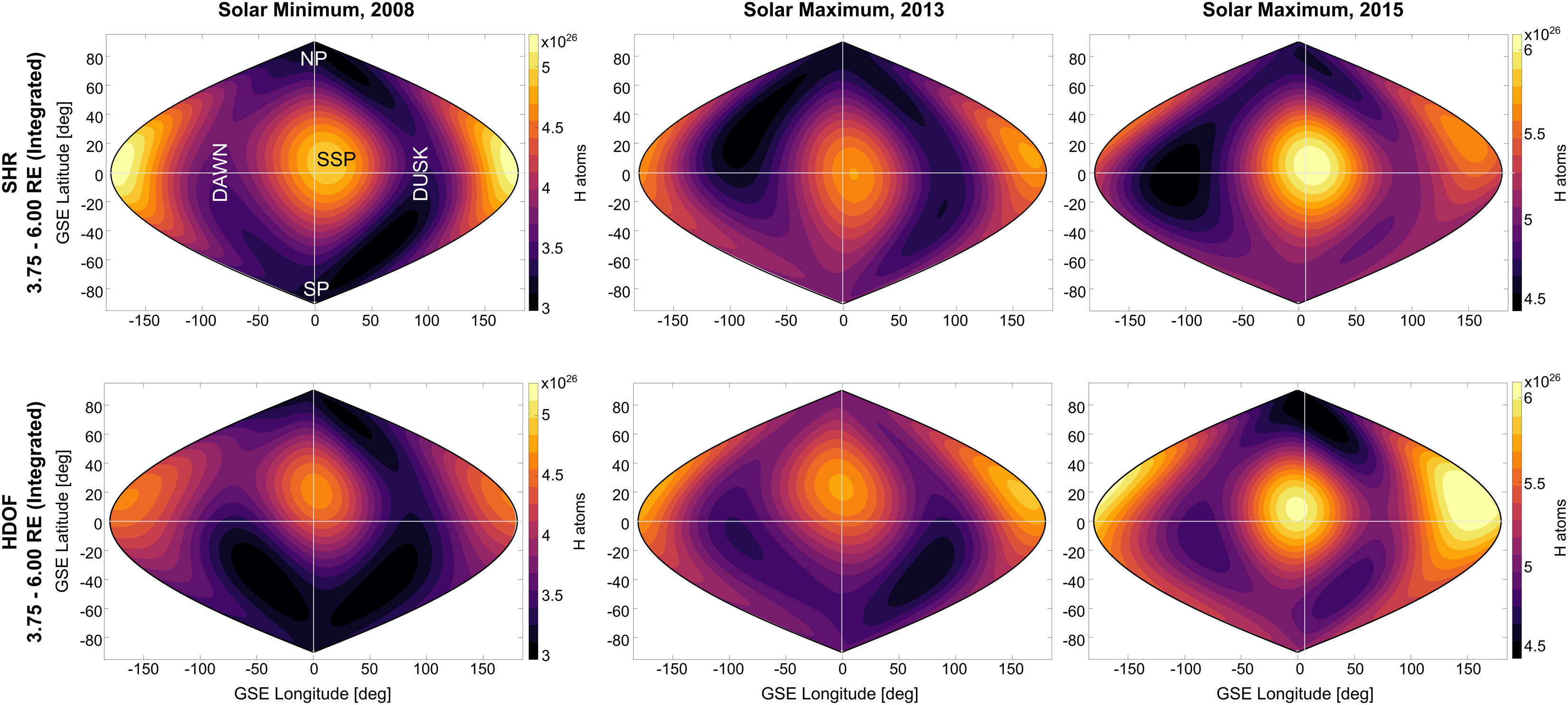
Figure 8. Total number of neutral exospheric H-atoms between 3.75 and 6.00 R_e near the summer solstice for 2008 (left), 2013 (middle), and 2015 (right). The first row shows the total H content in the 3.75–6.00 Re region derived from the tomographic estimations using the SHR model. Similarly, the second row shows results using the HDOF technique. Dayside nose and nightside tail structures are present in all reconstructions during solar minimum and solar maximum conditions.

Figure 9

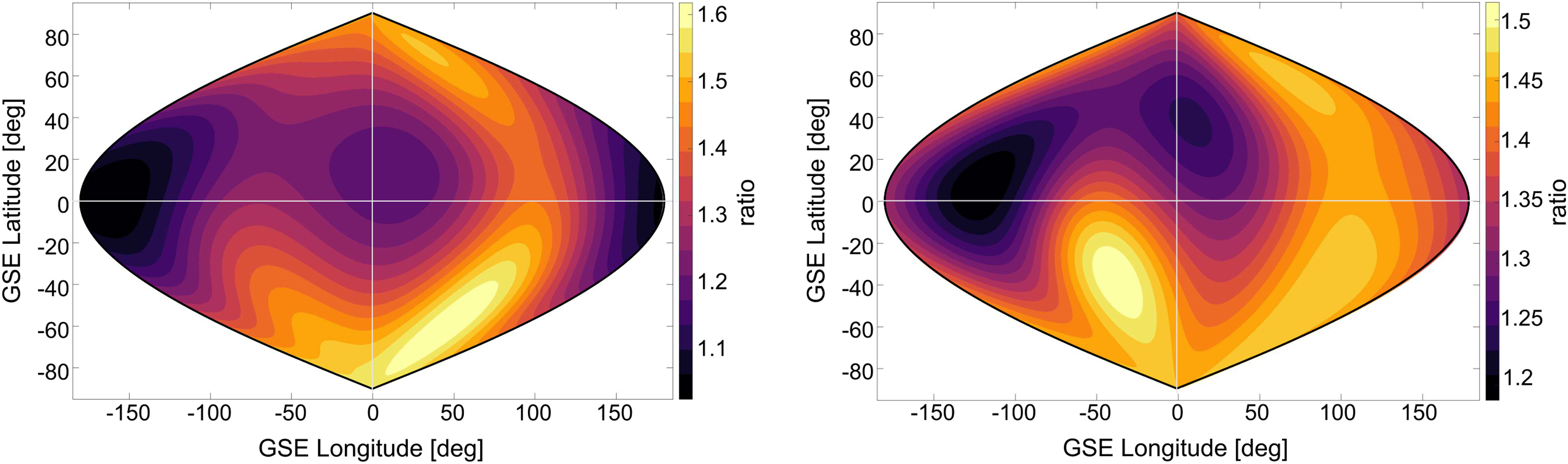
Figure 9. Angular view of the relative solar cycle enhancement of H density integrated between 3.75 and 6 R_e (left: based on the SHR model; right: based on the “high degree-of-freedom” method). Plotted is the ratio of the H-atom number density (integrated from 3.75 to 6.0 R_e near the summer solstice) at solar maximum (2013 and 2015 averaged) relative to solar minimum (2008). The most significant relative H-density enhancements are visible at mid-to-high latitudes with a preference for the dusk side. Surprisingly, the enhancement close around the dayside nose (near the SSP) appears to be relatively low.

The total number of H-atoms within 3.75–6.0 R_e, calculated as the sum of H-atoms within all 1° × 1° angular segments, is approximately 35% larger at solar maximum than at solar minimum [based on the SHR model: 33% (2013) and 36% (2015); based on the “high degree-of-freedom” method: 35% (2013) and 37% (2015)].

A major result of this work is that within 3.75–6.0 R_e, the solar maximum H density is larger than that of solar minimum at the same geocentric distance r₀ and angular position. This finding can be interpreted as a more expanded exosphere during solar maximum. To quantify the amount of radial expansion, we calculated the geocentric distance, r_exp, where the H density at solar maximum equals the solar minimum H density at r₀. The amount of radial expansion can then be defined as $a=r_{\mathit{exp}}-r_0$. The exospheric expansion at solar maximum compared to a minimum was found to be ∼2,500 km at the lower boundary r₀ = 3.75 R_e and ∼5,000 km at the upper boundary r₀ = 6.0 R_e (based on the SHR model results). The amount of exospheric expansion at solar maximum seems to increase with geocentric distance. This finding suggests that the expansion (or equivalently H-density enhancement) at solar maximum decreases with decreasing radial distance and may vanish (or even turn into a thinner exosphere than that at solar minimum) at some lower radial distance <<3.75 R_e [see also Joshi et al. (2019); Waldrop and Paxton (2013); Chamberlain (1963)]. This idea is mostly speculative and might be tested by analyzing exospheric Lyman-α observations from below 3 R_e.

Furthermore, to analyze quantitatively the difference in exospheric H content between solar maximum and minimum conditions, we implemented histograms of integrated H-atoms from radial shells at 3.75–6 R_e for both inversion techniques, which are shown in Figure 10 (note that the data have been taken from Figure 8). For solar minimum conditions, integrated H-atoms range from 3 to 5 × 10²⁶, while during solar maximum conditions, they range from 4 to 6 × 10²⁶. Both techniques display a similar trend for these results and clearly show the solar seasonal dependence of the H content. The peaks of each histogram are particularly defined by H-atoms located in both nose and tail regions, while the dispersion (or width of the histogram) can be interpreted as a qualitative measurement of the spherical symmetry of the exosphere. In this context, the solar maximum exosphere of 2013, with the smallest dispersion, exhibits higher spherical symmetry than the other two cases. Although the scope of this paper is mainly to report our data-based models, quantify global H densities, and specify particular features that depend on the solar cycle, the use of physics-based models is crucial to understanding the role of thermalization processes below the exobase and/or charge exchange with magnetospheric plasma in forming the 3D structure of the exosphere. The observational results suggest that future physics-based models need to consider radiation pressure (i.e., to be in accordance with the nose and tail features) and should include (new) physical processes, which account for the higher H densities at solar maximum in the analyzed distance range.

Figure 10

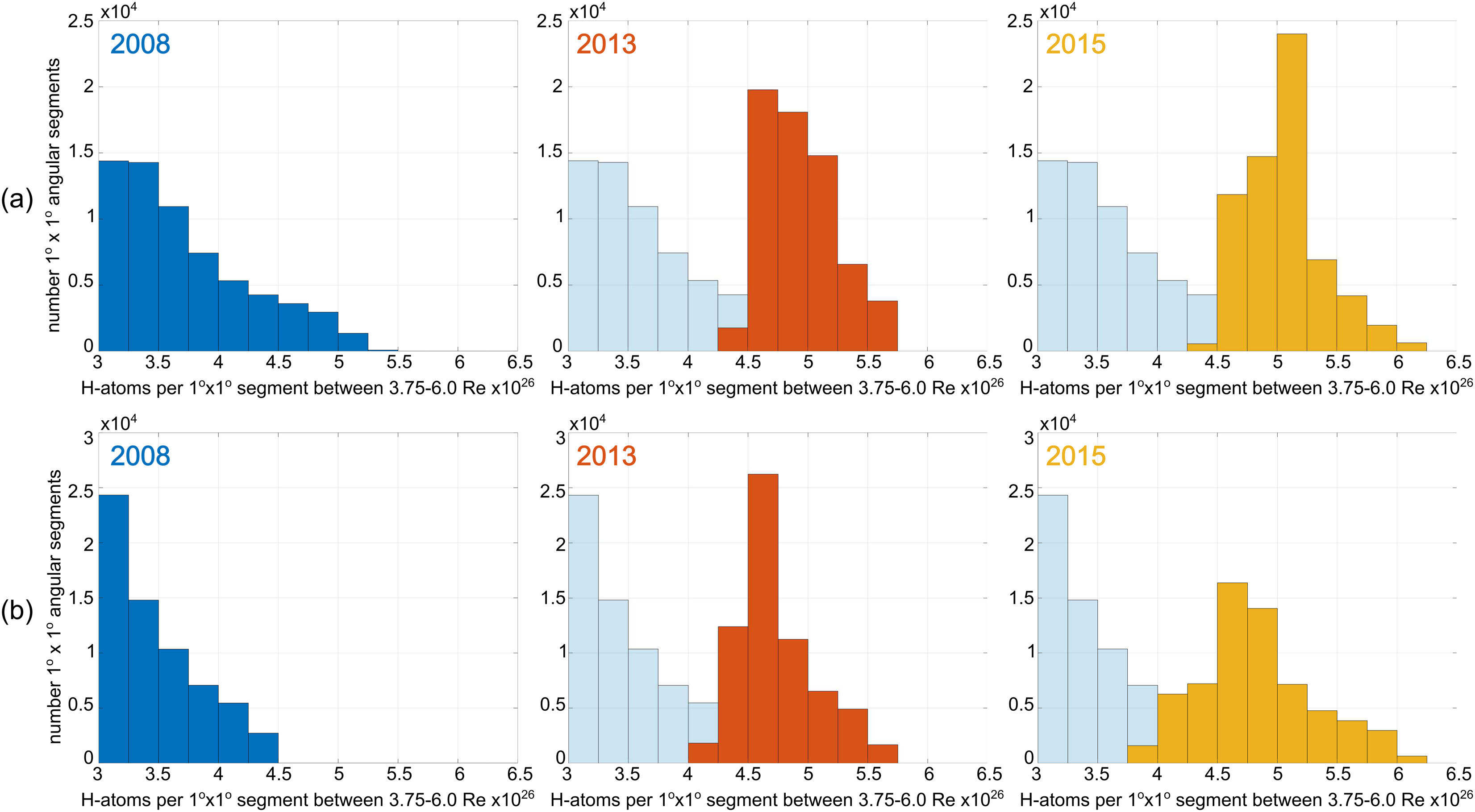
Figure 10. Histograms of the number of H-atoms (in 1 ° × 1 ° angular segments) between 3.75 and 6 R_e for the inversions at solar minimum (2008) and maximum (2013 and 2015)—top row (A): based on the SHR model; bottom row (B): based on the “high degree-of-freedom” method.

In order to quantify the estimation error from both techniques (parametric fitting and “high degree-of-freedom” reconstruction), we calculate the relative inversion error or ratio of the observed to modeled LOS column brightness. Figure 11 shows histograms and the derived relative inversion errors (as the width of a Gauss fit) for each of the three datasets used in this study. A larger relative error in the 2015 dataset than that from the 2008 dataset is mainly due to the significant enhancement of instrumental noise as a result of the LAD sensitivity depletion. Since the count rates decrease similar to the decrease in sensitivity (in 2015 LAD1 by a factor of ∼7 and LAD2 by a factor of ∼3), the statistical error of the measurements increases accordingly. A second reason for the enhanced error in 2015 might be the large time span of the 2015 data selection, which covers 45 days (2008 = 1 day and 2013 = 20 days). Within these 45 days, the LADs can observe minor seasonal variations in the exosphere or variations due to the 27-day solar rotation cycle, which also increases the inversion error.

Figure 11

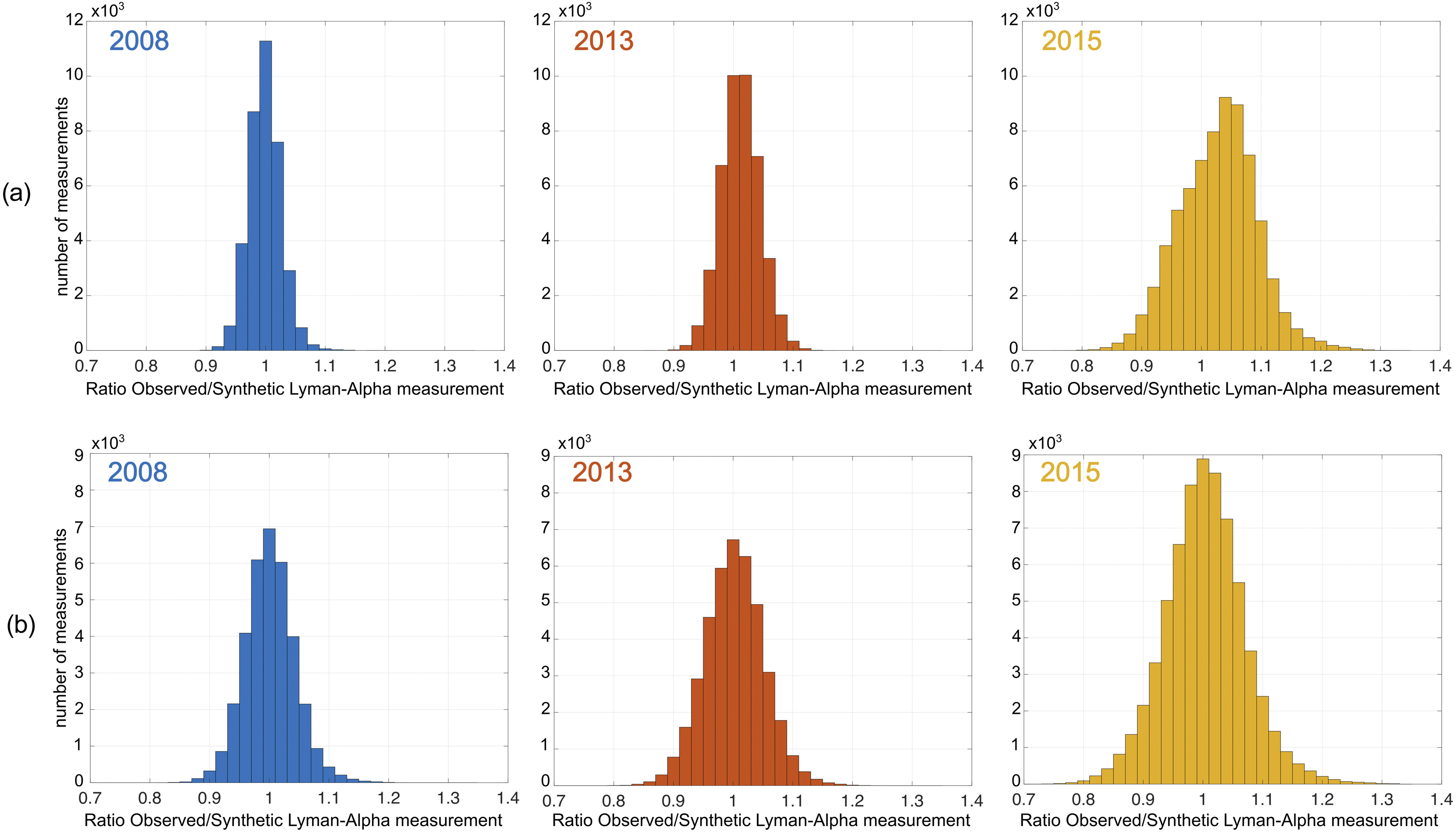
Figure 11. Histograms of the relative inversion error (ratio of the observed and modeled LOS column brightness) for the 3 years used—top row (A): based on the SHR model; bottom row (B): based on the “high degree-of-freedom” method. The relative errors are derived from Gauss curve fits of these histograms (top row: (A) 2008: 2.56%; 2013: 3.2%; and 2015: 6.4%; bottom row (B): 2008: 3.9%; 2013: 4.8%; and 2015: 6.0%). Larger relative errors in 2015 than in 2008 are mainly caused by the significant decrease in LAD sensitivity, which causes a higher statistical error in the observations due to accordingly reduced count rates. Furthermore, minor seasonal or solar rotation cycle-based exospheric H-density variations might contribute to the enhanced error in 2015, which has, with 45 days, the largest time span of all selections used (2008: 1 day; 2013: 20 days).

The uncertainty in the relative H-density enhancement at solar maximum (2013 or 2015) compared to solar minimum (2008) is calculated based on the following equation:

${\delta }_{2013/2015}=\sqrt{{\left({\delta }_{inv,2008}\right)}^2+{\left({\delta }_{inv,2013/2015}\right)}^2+{\left({\delta }_{calib}\right)}^2}(13)$

with the relative inversion errors of 2008 ${\delta }_{inv,2008}$ and the solar maximum year ${\delta }_{inv,2013/2015}$ (δ values for 2013 and 2015 are given in Figure 11) and the averaged relative calibration uncertainty (assumed for both LADs and years ${\delta }_{calib}$ = 0.05; see Section 2.5).

For the two inversion methods, the uncertainties in the H-density enhancements based on Equation 13 were found to be SHR 6.5% (2013) and 8.5% (2015) and HDOF 7.9% (2013) and 8.7% (2015). The average uncertainty for both methods and both solar max years is approximately 8%.

The SHR results for 12 June 2008 (solar minimum) can be compared to SHR results of the same day from an earlier analysis by Zoennchen et al. (2015), which was done with a lower angular resolution (L-order = 2) and a simple radial power law function. The solar minimum H-density distribution from this earlier work already shows both features, “nose” and “tail.” Nevertheless, the new results with the higher angular resolution, the better radial adaptation, and finally, the newly introduced regularization show deviations from the earlier results. The most obvious are a stronger “nose” feature and a significantly weaker “tail” in the presented results than those obtained by Zoennchen et al. (2015). Furthermore, the variation in the angular H density around the average value on a radial shell is generally lower in the new results.

The solar maximum results obtained by Zoennchen et al. (2015) are only partially comparable to those presented in this work. First, they are based on data from October to December 2012, meaning that they are from a different season and year (shortly before the solar maximum). Second, the data selection was not restricted to days with quiet geomagnetic conditions. However, the H-density enhancement of approximately +20% in 2012 found by Zoennchen et al. (2015) confirms the trend of higher H densities near the solar maximum.

4 Conclusion

The study of three independent datasets for solar minimum and maximum conditions enabled us to identify clear differences in the H density as a response to solar cycle 24. We summarize our scientific and technical findings as follows:

1. H-density distributions are, on average, ∼35 (±8)% higher during solar maximum than those under solar minimum conditions.

2. The presence of a nose/tail structure in all reconstructed models (see Figures 7, 8) is in good agreement with the radiation pressure theory, which establishes how the continuous scattering of Lyman-$\alpha$ photons by exospheric H-atoms exerts anti-sunward pressure over this neutral population, resulting in an enhancement of H densities at the dayside region near the subsolar point and the formation of a “geotail” in the nightside (Beth et al., 2016; Bishop and Chamberlain, 1989).

3. Comparison between integrated H-atoms between solar minimum and solar maximum reconstructions reveals that the enhancement of the H population occurs from mid-to-high latitudes, with a preference for the dusk side (see Figure 9). Furthermore, only a ∼20% increase is seen near the SSP region, which has the highest H density and integrated H-atoms.

4. Analysis of the histograms of integrated H-atoms (see Figure 10) shows that the exosphere during solar maximum 2013 is more spherically symmetric than other reconstructions.

5. The use of two different and independent tomographic reconstruction techniques provides a high degree of confidence in the estimated H-density values.

6. Estimated errors in the tomographic reconstruction based on the comparison of observed and modeled column-integrated Lyman-alpha emission are ∼3–6% (see Figure 11). The average uncertainty in the LAD sensitivity decrease between 2008 and the solar maximum years 2013 and 2015 was found to be ∼5%

Our study provides important insights into the 3D structure of the exosphere. In this work, we included more sophisticated optical calibration and correction processes than in our previous studies (Zoennchen et al., 2015; Cucho-Padin and Waldrop, 2018). Furthermore, we compared two independent approaches for 3D reconstructions, and the results demonstrate excellent agreement, thereby providing confidence in the reported density values.

Structural differences between SHR and HDOF—caused by the different modeling techniques—can be summarized with a brighter nose and tail (particularly at the lower border) from the SHR inversion compared to the HDOF. However, regarding the principal validity of the main statements of this work (higher solar maximum H densities and similar angular features like nose, tail, or polar depletion), they are of minor significance. The continuously ongoing process of improving the model techniques will help minimize those structural differences.

Our results of higher H density during solar maximum than during solar minimum conditions contradict the findings from the physics-based model of the exosphere developed by Hodges (1994). Using an MC approach, this model includes an extensive number of reactions and interactions (e.g., between atomic H and several molecules and ions within the thermospheric and inner magnetospheric regions). Although the MC model exhibits spatial structures similar to our results, it has an evident opposite solar cycle dependence of the neutral H density at high altitudes (>2 R_e) under similar solar conditions used in our study. On the other hand, the trend displayed by the density derived from the spherically symmetric Chamberlain model (Chamberlain, 1963) for both solar minimum and maximum is in better agreement with our results. Specifically, this model shows that at distances near the exobase (∼500 km), the H density is higher for solar minimum conditions than for solar maximum; however, this trend is reversed beyond ∼1.1 R_e owing solely to the scale height effect for atomic H.

Nevertheless, we acknowledge that for a better interpretation of estimated H densities, data analysis may be assisted by physics-based modeling. Three drivers are crucial to define the exosphere structure: (a) the temperature and hydrogen density at the exobase region, which depend on the atmospheric (molecular and atomic) composition, winds in the thermosphere/mesosphere regions, and the solar radiation (Chamberlain, 1963); (b) the charge-exchange interaction with dense plasma regions such as the plasmasphere and magnetosheath (Kuwabara et al., 2017; Qin and Waldrop, 2016); and (c) solar radiation pressure, especially at high altitudes (Beth et al., 2016). A model that can account for these three mechanisms could be used to quantitatively identify the role of each of them in the exosphere formation. Furthermore, the identification of the energy partition of exospheric H-atoms is of great importance. Driver (a) defines the thermal population of atomic H that usually follows a Maxwellian distribution of 3D velocities with an average energy of ∼0.01 eV, while driver (b) produces the non-thermal H atoms with energies greater than 1 eV as plasma is usually hotter than neutrals. Investigation of the energization process will improve our understanding of the permanent upper-atmospheric escape to space.

Finally, this research work is timely and directly supports the upcoming NASA mission Carruthers Geocorona Observatory to be launched in 2025. This mission will image the terrestrial exosphere in Lyman-α with a wide field-of-view imager from the Sun–Earth L1 Lagrangian point (∼250 R_e from Earth) and will be used to estimate the 3D global distributions of H densities, especially during solar maximum conditions. The description of our techniques in this paper may serve as guidance for software development, and the estimated H densities can be used as a first approximation ground-truth model to validate the estimation process.

Data availability statement

Publicly available datasets were analyzed in this study. These data can be found at: https://cdaweb.gsfc.nasa.gov/, https://lasp.colorado.edu/lisird/data/composite_lyman_alpha, http://omniweb.sci.gsfc.nasa.gov

Author contributions

JZ: Conceptualization, writing–original draft and writing–review and editing. GC-P: Conceptualization, writing–original draft and writing–review and editing. LW: writing–review and editing. HF: writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was supported by the Deutsche Forschungsgemeinschaft (grant no. 469043535) and the NASA Goddard Space Flight Center through Cooperative Agreement 80NSSC21M0180 to Catholic University, Partnership for Heliophysics and Space Environment Research (PHaSER).

Acknowledgments

The authors thank the TWINS team (PI Dave McComas) for making this work possible. Jochen Zoennchen acknowledges the funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation, grant no. 469043535) and the support of the Argelander Institut für Astronomie at the University of Bonn. Gonzalo Cucho-Padin thanks Drs. Dolon Bhattacharyya and John Clarke for important discussions on radiative transfer theory. The authors also acknowledge the International Space Science Institute on the ISSI team titled “The Earth’s Exosphere and its Response to Space Weather.” The authors thank the topical editor and the referees for the discussions for their extensive help in improving the paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The Editor DB is currently organizing a Research Topic with the author GC-P.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bailey, J., and Gruntman, M. (2011). Experimental study of exospheric hydrogen atom distributions by Lyman-alpha detectors on the TWINS mission. J. Geophys. Res. Space Phys. 116 (19), 1–9. doi:10.1029/2011JA016531

CrossRef Full Text | Google Scholar

Baliukin, I., Bertaux, J.-L., Quemerais, E., Izmodenov, V., and Schmidt, W. (2019). SWAN/SOHO Lyman-α mapping: the hydrogen geocorona extends well beyond the Moon. J. Geophys. Res.-Space 124, 861–885. doi:10.1029/2018JA026136

CrossRef Full Text | Google Scholar

Beth, A., Garnier, P., Toublanc, D., Dandouras, I., and Mazelle, C. (2016). Theory for planetary exospheres: I. Radiation pressure effect on dynamical trajectories. Icarus 266, 410–422. doi:10.1016/j.icarus.2015.10.018

CrossRef Full Text | Google Scholar

Bishop, J. (1999). Transport of resonant atomic hydrogen emissions in the thermosphere and geocorona: model description and applications. J. Quantitative Spectrosc. Radiat. Transf. 61, 473–491. doi:10.1016/S0022-4073(98)00031-4

CrossRef Full Text | Google Scholar

Bishop, J., and Chamberlain, J. W. (1989). Radiation pressure dynamics in planetary exospheres: a “natural” framework. Icarus 81, 145–163. doi:10.1016/0019-1035(89)90131-0

CrossRef Full Text | Google Scholar

Brandt, J. C., and Chamberlain, J. W. (1959). Interplanetary gas. I. Hydrogen radiation in the night sky. Astrophysical J. 130, 670–682. doi:10.1086/146756

CrossRef Full Text | Google Scholar

Butala, M. D., Hewett, R. J., Frazin, R. A., and Kamalabadi, F. (2010). Dynamic three-dimensional tomography of the solar corona. Sol. Phys. 262, 495–509. doi:10.1007/s11207-010-9536-1

CrossRef Full Text | Google Scholar

Chamberlain, J. W. (1963). Planetary coronae and atmospheric evaporation. Planet. Space Sci. 11, 901–960. doi:10.1016/0032-0633(63)90122-3

CrossRef Full Text | Google Scholar

Connor, H. K., and Carter, J. A. (2019). Exospheric neutral hydrogen density at the nominal 10 R_E subsolar point deduced from xmm-Newton X-ray observations. J. Geophys. Res.-Space 124, 1612–1624. doi:10.1029/2018JA026187

CrossRef Full Text | Google Scholar

COSPAR. Working Group IV (1965). Cira 1965: COSPAR international reference atmosphere 1965, COSPAR series. North-Holland Publishing Company. doi:10.1038/2101305a0

CrossRef Full Text | Google Scholar

Cucho-Padin, G., Connor, H., Jung, J., Walsh, B., and Sibeck, D. G. (2024). Finding the magnetopause location using soft x-ray observations and a statistical inverse method. Earth Planet. Phys. 8, 184–203. doi:10.26464/epp2023070

CrossRef Full Text | Google Scholar

Cucho-Padin, G., Kameda, S., and Sibeck, D. G. (2022). The earth’s outer exospheric density distributions derived from procyon/laica uv observations. J. Geophys. Res. Space Phys. 127, e2021JA030211. doi:10.1029/2021JA030211

CrossRef Full Text | Google Scholar

Cucho-Padin, G., and Waldrop, L. (2018). Tomographic estimation of exospheric hydrogen density distributions. J. Geophys. Res. Space Phys. 123 (Issue 6), 5119–5139. doi:10.1029/2018ja025323

CrossRef Full Text | Google Scholar

Cucho-Padin, G., and Waldrop, L. (2019). Time-dependent response of the terrestrial exosphere to a geomagnetic storm. Geophys. Res. Lett. 46, 11661–11670. doi:10.1029/2019GL084327

CrossRef Full Text | Google Scholar

Emerich, C., Lemaire, P., Vial, J.-C., Curdt, W., Schühle, U., and Wilhelm, K. (2005). A new relation between the central spectral solar HI Lyman-α irradiance and the line irradiance measured by SUMER/SOHO during the cycle 23. Icarus 178, 429–433. doi:10.1016/j.icarus.2005.05.002

CrossRef Full Text | Google Scholar

Emmert, J. T., Drob, D. P., Picone, J. M., Siskind, D. E., Jones, M., Mlynczak, M. G., et al. (2021). NRLMSIS 2.0: a whole-atmosphere empirical model of temperature and neutral species densities. Earth Space Sci. 8, e2020EA001321. doi:10.1029/2020EA001321

CrossRef Full Text | Google Scholar

Fahr, H. J. (1971). The interplanetary hydrogen cone and its solar cycle variations. Astron. Astrophys. 14, 263–274.

Google Scholar

Fahr, H. J., Nass, U., Dutta-Roy, R., and Zoennchen, J. H. (2018). Neutralized solar wind ahead of the Earth’s magnetopause as contribution to non-thermal exospheric hydrogen. Ann. Geophys. 36, 445–457. doi:10.5194/angeo-36-445-2018

CrossRef Full Text | Google Scholar

Feller, W. (1968). An introduction to probability theory and its applications. New York, USA: Wiley.

Google Scholar

Fuselier, S. A., Dayeh, M. A., Galli, A., Funsten, H. O., Schwadron, N. A., Petrinec, S. M., et al. (2020). Neutral atom imaging of the solar wind-magnetosphere-exosphere interaction near the subsolar magnetopause. Geophys. Res. Lett. 47, e2020GL089362. doi:10.1029/2020GL089362

PubMed Abstract | CrossRef Full Text | Google Scholar

Hajek, B. (2015). Random processes for engineers. Cambridge: Cambridge University Press.

Google Scholar

Hodges, R. R. (1994). Monte Carlo simulation of the terrestrial hydrogen exosphere. J. Geophys. Res. Space Phys. 99, 23229–23247. doi:10.1029/94JA02183

CrossRef Full Text | Google Scholar

Joshi, P. P., Phal, Y. D., and Waldrop, L. S. (2019). Quantification of the vertical transport and escape of atomic hydrogen in the terrestrial upper atmosphere. J. Geophys. Res. Space Phys. 124, 10468–10481. doi:10.1029/2019JA027057

CrossRef Full Text | Google Scholar

Krall, J., Glocer, A., Fok, M. C., Nossal, S. M., and Huba, J. D. (2018). The unknown hydrogen exosphere: Space weather implications. Space Weather. 16, 205–215. doi:10.1002/2017SW001780

CrossRef Full Text | Google Scholar

Kuwabara, M., Yoshioka, K., Murakami, G., Tsuchiya, F., Kimura, T., Yamazaki, A., et al. (2017). The geocoronal responses to the geomagnetic disturbances. J. Geophys. Res. Space Phys. 122, 1269–1276. doi:10.1002/2016JA023247

CrossRef Full Text | Google Scholar

McComas, D. J., Allegrini, F., Baldonado, J., Blake, B., Brandt, P. C., Burch, J., et al. (2009). The two wide-angle imaging neutral-atom Spectrometers (TWINS) NASA mission-of-opportunity. Space Sci. Rev. 142 (1–4), 157–231. doi:10.1007/s11214-008-9467-4

CrossRef Full Text | Google Scholar

Nass, H. U., Zoennchen, J. H., Lay, G., and Fahr, H. J. (2006). The TWINS-LAD mission: observations of terrestrial Lyman-α fluxes. ASTRA Astrophysics Space Sci. Trans. 2, 27–31. doi:10.5194/astra-2-27-2006

CrossRef Full Text | Google Scholar

Norberg, J., Käki, S., Roininen, L., Mielich, J., and Virtanen, I. I. (2023). Model-free approach for regional ionospheric multi-instrument imaging. J. Geophys. Res. Space Phys. 128, e2022JA030794. doi:10.1029/2022JA030794

CrossRef Full Text | Google Scholar

Norberg, J., Vierinen, J., Roininen, L., Orispää, M., Kauristie, K., Rideout, W. C., et al. (2018). Gaussian markov random field priors in ionospheric 3-d multi-instrument tomography. IEEE Trans. Geoscience Remote Sens. 56, 7009–7021. doi:10.1109/tgrs.2018.2847026

CrossRef Full Text | Google Scholar

Østgaard, N., Mende, S. B., Frey, H. U., Gladstone, G. R., and Lauche, H. (2003). Neutral hydrogen density profiles derived from geocoronal imaging. J. Geophys. Res. Space Phys. 108 (A7), 1–12. SMP 18. doi:10.1029/2002JA009749

CrossRef Full Text | Google Scholar

Qin, J., and Waldrop, L. (2016). Non-thermal hydrogen atoms in the terrestrial upper thermosphere. Nat. Commun. 7, 13655. doi:10.1038/ncomms13655

PubMed Abstract | CrossRef Full Text | Google Scholar

Rairden, R. L., Frank, L. A., and Craven, J. D. (1986). Geocoronal imaging with dynamics explorer. J. Geophys. Res. Space Phys. 91, 13613–13630. doi:10.1029/ja091ia12p13613

CrossRef Full Text | Google Scholar

Snow, M., Reberac, A., Quémerais, E., Clarke, J., McClintock, W. E., and Woods, T. N. (2013). A new catalog of ultraviolet stellar spectra for calibration. ISSI Sci. Rep. Ser. 13, 191–226. doi:10.1007/978-1-4614-6384-9_7

CrossRef Full Text | Google Scholar

Thomas, G. E. (1978). The interstellar wind and its influence on the interplanetary environment. Annu. Rev. earth Planet. Sci. 6, 173–204. doi:10.1146/annurev.ea.06.050178.001133

CrossRef Full Text | Google Scholar

Vidal-Madjar, A. (1975). Evolution of the solar Lyman alpha flux during four consecutive years. Sol. Phys. 40, 69–86. doi:10.1007/BF00183153

CrossRef Full Text | Google Scholar

Waldrop, L., and Paxton, L. J. (2013). Lyman-α airglow emission: implications for atomic hydrogen geocorona variability with solar cycle. J. Geophys. Res. Space Phys. 118, 5874–5890. doi:10.1002/jgra.50496

CrossRef Full Text | Google Scholar

Zoennchen, J. H., Connor, H. K., Jaewoong, J., Nass, U., and Fahr, H. J. (2022). Terrestrial exospheric dayside H-density profile at 3–15 R_e from UVIS/HDAC and TWINS Lyman-α data combined. Ann. Geophys. 40, 271–279. doi:10.5194/angeo-40-271-2022

CrossRef Full Text | Google Scholar

Zoennchen, J. H., Nass, U., and Fahr, H. J. (2015). Terrestrial exospheric hydrogen density distributions under solar minimum and solar maximum conditions observed by the TWINS stereo mission. Ann. Geophys. 33, 413–426. doi:10.5194/angeo-33-413-2015

CrossRef Full Text | Google Scholar

Zoennchen, J. H., Nass, U., Fahr, H. J., and Goldstein, J. (2017). The response of the H geocorona between 3 and 8 R_e to geomagnetic disturbances studied using TWINS stereo Lyman-α data. Ann. Geophys. 35 (1), 171–179. doi:10.5194/angeo-35-171-2017

CrossRef Full Text | Google Scholar