Magnetopause MHD surface wave theory: progress & challenges

Sharp boundaries are a key feature of space plasma environments universally, with their wave-like motion (driven by pressure variations or flow shears) playing a key role in mass, momentum, and energy transfer. This review summarises magnetohydrodynamic surface wave theory with particular reference to Earth’s magnetopause, due to its mediation of the solar-terrestrial interaction. Basic analytic theory of propagating and standing surface waves within simple models are presented, highlighting many of the typically-used assumptions. We raise several conceptual challenges to understanding the nature of surface waves within a complex environment such as a magnetosphere, including the effects of magnetic topology and curvilinear geometry, plasma inhomogeneity, finite boundary width, the presence of multiple boundaries, turbulent driving, and wave nonlinearity. Approaches to gain physical insight into these challenges are suggested. We also discuss how global simulations have proven a fruitful tool in studying surface waves in more representative environments than analytic theory allows. Finally, we highlight strong interdisciplinary links with solar physics which might help the magnetospheric community. Ultimately several upcoming missions provide motivation for advancing magnetopause surface wave theory towards understanding their global role in filtering, accumulating, and guiding turbulent solar wind driving.

1 Introduction

The plasma Universe hosts a wide variety of different environments. Since over large scales plasmas from different sources cannot mix, these systems tend to be bounded by sharp discontinuities—typically large-scale sheets of electrical currents. Figure 1A illustrates several of these environments and discontinuities across the heliosphere. Akin to waves on water or the membrane of a drum, space plasma boundaries are observed to be in almost continual wave-like motion, including (but not limited to): coronal loops (Nakariakov et al., 2016; Wang, 2016); coronal mass ejections (Nykyri and Foullon, 2013); the heliospheric current sheet (Smith, 2001); termination shock/heliopause (Zirnstein et al., 2022); and the planetary magnetospheres of Earth (Plaschke et al., 2009a; Plaschke et al., 2009b; He et al., 2020), Mercury (Boardsen et al., 2010; Sundberg et al., 2012), Mars (Wang et al., 2023), Saturn (Masters et al., 2009; Ma et al., 2015), and Jupiter (Volwerk et al., 2013; Montgomery et al., 2023). These surface waves, driven by pressure variations and/or velocity shears, play a key role in mass, momentum, and energy transfer across boundaries (Kivelson and Chen, 1995), meaning they have a major impact on their environment’s energy budget.

Figure 1

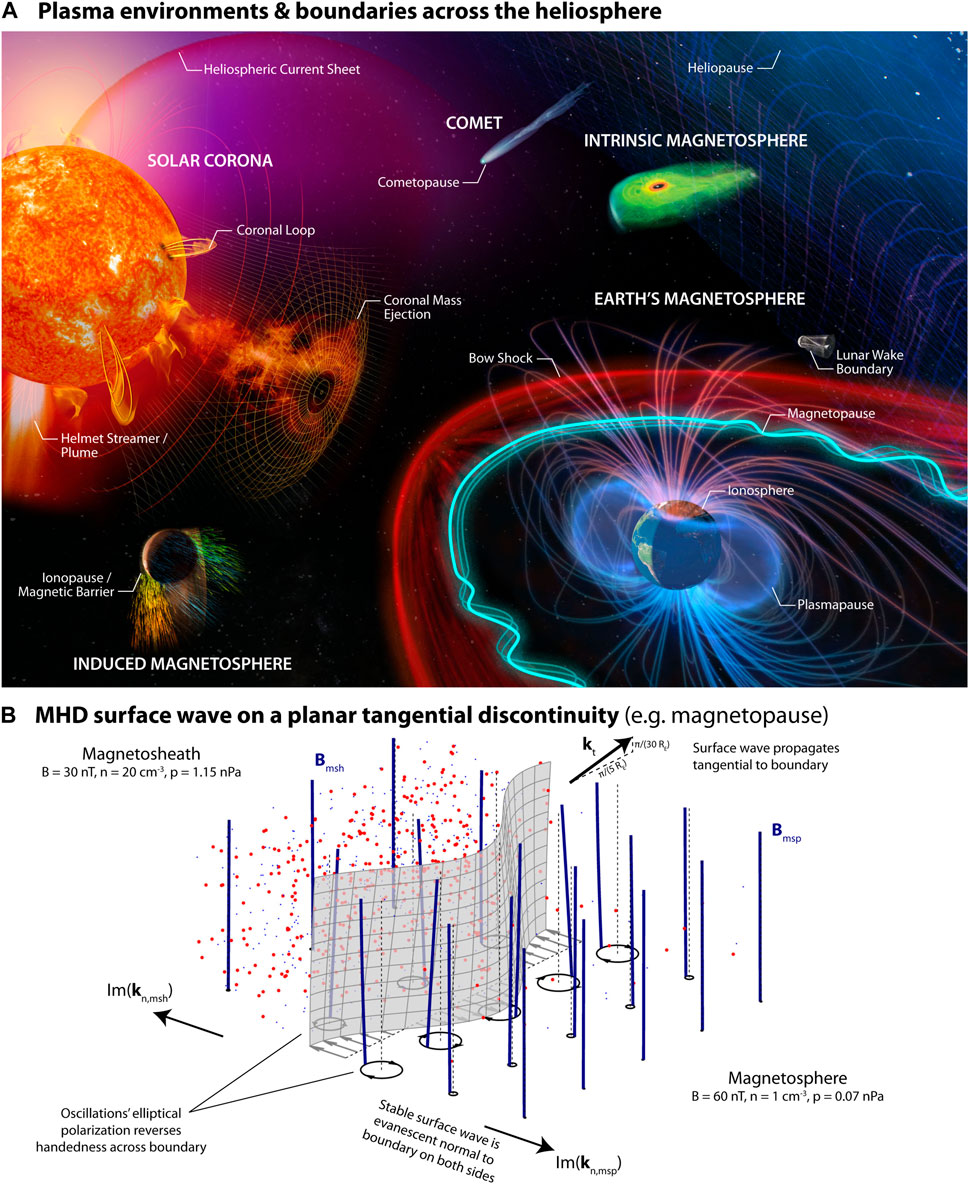
Figure 1. (A) Illustration across the heliosphere of different plasma environments and their boundaries which support surface waves (adapted from images by NASA and Emmanuel Masongsong). (B) Diagram of a surface wave on a tangential discontinuity, such as the magnetopause. Displayed are the discontinuity (grey), magnetic field lines (navy), and relative numbers of ions (red) and electrons (blue). An animated version can be found in the Supplementary Material.

A prime example is Earth’s magnetopause, the interface of the solar-terrestrial interaction that leads to space weather’s impacts on vital infrastructure. Magnetopause dynamics have wide-ranging consequences throughout geospace—both directly and through the magnetospheric ultra-low frequency (ULF) waves they generate—affecting radiation belts, magnetotail plasmasheet, auroral oval, mid-latitude ionosphere, and geomagnetic/geoelectric fields (e.g., Elkington, 2006; Summers et al., 2013; Hwang and Sibeck, 2016). These impacts make magnetopause dynamics a cornerstone of solar-terrestrial physics research.

This review concerns magnetohydrodynamic (MHD) surface wave theory through the lens of Earth’s magnetopause. Basic theory is briefly discussed (see Plaschke, 2016, for more and relation to observations) though we focus on current challenges, posing suggestions of how to advance progress.

2 MHD theory

2.1 Surface waves

Like body MHD waves able to propagate through the bulk plasma, surface waves at the interface of two media can be derived from wave solutions in displacement

$\mathit{\xi }\left(\mathbf{r},t\right)=\mathit{\xi }\left(\mathbf{k},\omega \right)e^{i\left(\mathbf{k}\cdot \mathbf{r}-\omega t\right)}$

about equilibrium (subscript 0’s) in the linearised Ideal MHD equation

$\begin{array}{ll}\hfill {\rho }_0\frac{{\partial }^2\mathit{\xi }}{\partial t^2}& =\nabla \left(\mathit{\xi }\cdot \nabla p_0+\gamma p_0\nabla \cdot \mathit{\xi }\right)+\frac{1}{{\mu }_0}\left(\nabla \times {\mathbf{B}}_0\right)\times \left[\nabla \times \left(\mathit{\xi }\times {\mathbf{B}}_0\right)\right]\hfill \\ \hfill & +\frac{1}{{\mu }_0}\left[\nabla \times \nabla \times \left(\mathit{\xi }\times {\mathbf{B}}_0\right)\right]\times {\mathbf{B}}_0,\hfill \end{array}$

which has corresponding density ρ, pressure p, and magnetic field B perturbations

$\delta \rho =-{\rho }_0\nabla \cdot \mathit{\xi }-\mathit{\xi }\cdot \nabla {\rho }_0$

$\delta p=-\gamma p_0\nabla \cdot \mathit{\xi }-\mathit{\xi }\cdot \nabla p_0$

$\delta \mathbf{B}=\nabla \times \left(\mathit{\xi }\times {\mathbf{B}}_0\right),$

with γ being the adiabatic index.

Often surface waves are considered at discontinuities with the most studied being unbounded tangential discontinuities (TDs; Kruskal and Schwartzschild, 1954; Sen, 1963; Southwood, 1968; Goedbloed, 1971; Walker, 1981; Pu and Kivelson, 1983a; Pu and Kivelson, 1983b), pressure balanced surfaces with no threaded mass/magnetic flux—a reasonable approximation to the magnetopause in the absence of reconnection. Surface waves are, however, also supported by the other MHD discontinuities and shocks (Lubchich and Pudovkin, 1999; Lubchich and Despirak, 2005; Ruderman et al., 2018), as well as transition layers (Chen and Hasegawa, 1974; Lee and Roberts, 1986; Uberoi, 1989; De Keyser et al., 1999).

Figure 1B demonstrates the key features of a surface wave on a planar TD with uniform half-spaces. They are collective modes of vortical plasma motions, mathematically constructed from magnetosonic waves on each side independently obeying dispersion relation

$k_{n,a}^2=-k_t^2+\frac{{\omega }_a^4}{v_{\text{A},a}^2{\omega }_a^2+c_{\text{S},a}^2\left[{\omega }_a^2-{\left({\mathbf{k}}_t\cdot {\mathbf{v}}_{\text{A},a}\right)}^2\right]},(1)$

where a represents one half-space (magnetosphere/magnetosheath), n and t denote normal and tangential directions, v_A and c_S are the Alfvén and sound speeds, and ω_a is the rest frame angular frequency. If the plasma has velocity u_0,a in the local frame, the Doppler shift gives ω = ω_a + k_t ⋅u_0,a.

Surface waves are necessarily localised to their discontinuity, hence exhibit evanescence normal to the boundary, i.e., $\mathrm{R}\mathrm{e}(k_{n,a}^2)<0$. Fluctuations’ decay scale depends on plasma conditions, thus can be different on either side. Amplitudes peak at the discontinuity, necessitating a reversal of polarisation across the boundary (Southwood, 1974).

The two wave solutions are tied together through boundary conditions: the tangential wave vector k_t and wave frequency ω are the same on both sides, and the normal displacement ξ_n (or equivalently velocity) and total pressure perturbation δp_tot = δp + B₀ ⋅ δB/μ₀ are continuous. This leads to general surface wave dispersion relation applied to the magnetopause.

$\frac{k_{n,\mathrm{m}\mathrm{s}\mathrm{h}}}{{\rho }_{0,\mathrm{m}\mathrm{s}\mathrm{h}}\left[{\omega }_{\text{msh}}^2-{\left({\mathbf{k}}_t\cdot {\mathbf{v}}_{\text{A},\mathrm{m}\mathrm{s}\mathrm{h}}\right)}^2\right]}=\frac{k_{n,\mathrm{m}\mathrm{s}\mathrm{p}}}{{\rho }_{0,\mathrm{m}\mathrm{s}\mathrm{p}}\left[{\omega }_{\text{msp}}^2-{\left({\mathbf{k}}_t\cdot {\mathbf{v}}_{\text{A},\mathrm{m}\mathrm{s}\mathrm{p}}\right)}^2\right]},(2)$

where subscripts msh and msp represent the magnetosheath and magnetosphere sides, respectively. Eq. 2 must be solved numerically and yields quasi-fast and quasi-slow modes (Pu and Kivelson, 1983a). It can be simplified assuming incompressibility (c_S → ∞), where $k_n^2=-k_t^2$ on both sides and Eq. 2 becomes.

$\begin{array}{ll}\hfill \omega & =\frac{{\mathbf{k}}_t\cdot \left({\rho }_{0,\mathrm{m}\mathrm{s}\mathrm{h}}{\mathbf{u}}_{0,\mathrm{m}\mathrm{s}\mathrm{h}}+{\rho }_{0,\mathrm{m}\mathrm{s}\mathrm{p}}{\mathbf{u}}_{0,\mathrm{m}\mathrm{s}\mathrm{p}}\right)}{{\rho }_{0,\mathrm{m}\mathrm{s}\mathrm{h}}+{\rho }_{0,\mathrm{m}\mathrm{s}\mathrm{p}}}\hfill \\ \hfill & \pm \sqrt{\frac{{\rho }_{0,\mathrm{m}\mathrm{s}\mathrm{h}}{\left({\mathbf{k}}_t\cdot {\mathbf{v}}_{\text{A},\mathrm{m}\mathrm{s}\mathrm{h}}\right)}^2+{\rho }_{0,\mathrm{m}\mathrm{s}\mathrm{p}}{\left({\mathbf{k}}_t\cdot {\mathbf{v}}_{\text{A},\mathrm{m}\mathrm{s}\mathrm{p}}\right)}^2}{{\rho }_{0,\mathrm{m}\mathrm{s}\mathrm{h}}+{\rho }_{0,\mathrm{m}\mathrm{s}\mathrm{p}}}-\frac{{\rho }_{0,\mathrm{m}\mathrm{s}\mathrm{h}}{\rho }_{0,\mathrm{m}\mathrm{s}\mathrm{p}}}{{\left({\rho }_{0,\mathrm{m}\mathrm{s}\mathrm{h}}+{\rho }_{0,\mathrm{m}\mathrm{s}\mathrm{p}}\right)}^2}{\left[{\mathbf{k}}_t\cdot \left({\mathbf{u}}_{0,\mathrm{m}\mathrm{s}\mathrm{h}}-{\mathbf{u}}_{0,\mathrm{m}\mathrm{s}\mathrm{p}}\right)\right]}^2}.\hfill \end{array}$

This has forward and backward propagating solutions with respect to k_t, though as the flow shear increases one is reversed becoming a “negative energy” wave (e.g., Mann et al., 1999). Increasing the shear further results in exponential growth in time, corresponding to the classical criterion for the Kelvin-Helmholtz Instability (KHI, Chandrasekhar, 1961). While intimately related to surface waves, we shall not discuss KHI further here (see instead review Masson and Nykyri, 2018). At the magnetopause typically u_0,msh ≫ u_0,msp, ρ_0,msh ≫ ρ_0,msp and B_0,msh ≪ B_0,msp, hence the approximate relation

$\omega \approx {\mathbf{k}}_t\cdot {\mathbf{u}}_{0,\mathrm{m}\mathrm{s}\mathrm{h}}\pm {\omega }_0$

${\omega }_0=\sqrt{\frac{{\left({\mathbf{k}}_t\cdot {\mathbf{B}}_{0,\mathrm{m}\mathrm{s}\mathrm{p}}\right)}^2+{\left({\mathbf{k}}_t\cdot {\mathbf{B}}_{0,\mathrm{m}\mathrm{s}\mathrm{h}}\right)}^2}{{\mu }_0\left({\rho }_{0,\mathrm{m}\mathrm{s}\mathrm{p}}+{\rho }_{0,\mathrm{m}\mathrm{s}\mathrm{h}}\right)}}\approx \frac{{\mathbf{k}}_t\cdot {\mathbf{B}}_{0,\mathrm{m}\mathrm{s}\mathrm{p}}}{\sqrt{{\mu }_0{\rho }_{0,\mathrm{m}\mathrm{s}\mathrm{h}}}}(3)$

holds for ${\left({\mathbf{k}}_t\cdot {\mathbf{u}}_{0,\mathrm{m}\mathrm{s}\mathrm{h}}\right)}^2{\rho }_{0,\mathrm{m}\mathrm{s}\mathrm{p}}/{\rho }_{0,\mathrm{m}\mathrm{s}\mathrm{h}}\ll {\omega }_0^2$, consisting of a natural frequency ω₀ for no flow shear (Chen and Hasegawa, 1974; Plaschke and Glassmeier, 2011) along with an advective Doppler shift.

In reality the magnetopause has finite thickness $\sim 100\text{–}2500\mathrm{k}\mathrm{m}$ (Berchem and Russell, 1982; Paschmann et al., 2005), whereas the above theory treated it as infinitesimally thin. While this limit is valid for wavelengths much larger than the thickness, a finite-width boundary has been considered through either a continuously-varying transition (Chen and Hasegawa, 1974; De Keyser et al., 1999) or uniform layer bounded by two discontinuities (Lee et al., 1981). Finite thickness introduces inner and outer surface modes, and can allow waves to propagate inside the layer due to the presence of turning points. Surface waves may resonantly convert to Alfvén or slow magnetosonic waves if their resonance conditions, ${\omega }^2={\left({\mathbf{k}}_t\cdot {\mathbf{v}}_A\right)}^2$ or ${\omega }^2={\left({\mathbf{k}}_t\cdot {\mathbf{v}}_A\right)}^2{c}_S^2/\left(v_A^2+c_S^2\right)$, become locally fulfilled within the transition. This irreversible mode conversion leads to damping of the surface mode, even in the absence of any dissipation in the system (Chen and Hasegawa, 1974; Lee and Roberts, 1986; Uberoi, 1989). Damping (or conversely growth) of surface waves results, through Eq. 1, in the evanescent magnetosonic waves exhibiting phase motion along the normal direction (Pu and Kivelson, 1983a; Archer et al., 2021).

2.2 Surface eigenmodes

The theory presented in Section 2.1 holds for unbounded TDs, whereas magnetospheric field lines are necessarily terminated at their intersection with the ionosphere, as displayed in Figures 2A, B for simple box and cylindrical magnetospheric models (e.g., Southwood, 1974; Kivelson et al., 1984). The ionospheric boundary conditions are highly reflecting for magnetosonic modes, even more than for Alfvén waves (Kivelson and Southwood, 1988), meaning standing surface waves might form between conjugate ionospheres, known as surface eigenmodes (Chen and Hasegawa, 1974; Plaschke and Glassmeier, 2011). These modes have been considered on either the magnetopause or plasmapause, with quantization condition

$\frac{{\mathbf{k}}_t\cdot {\mathbf{B}}_{0,\mathrm{m}\mathrm{s}\mathrm{p}}}{B_{0,\mathrm{m}\mathrm{s}\mathrm{p}}}=\pm \frac{j\pi }{S},(4)$

where $j\in \mathbb{N}$ and S is the field line length. Surface eigenmodes have conceptual similarities to field line resonances, Alfvén waves locally standing on field lines due to ionospheric reflection (e.g., Southwood, 1974). They are, however, rather different from cavity (for a closed magnetosphere with quantized azimuthal wavenumbers; Kivelson et al., 1984; Kivelson and Southwood, 1985) and waveguide (for an open-ended magnetotail with a spectrum of azimuthal wavenumbers; Samson et al., 1992; Wright, 1994) modes. These eigenmodes instead consist of propagating, rather than evanescent, magnetosonic waves that form approximately radially standing structure from reflection by boundaries or turning points. See Archer et al. (2022) for further comparison.

Figure 2

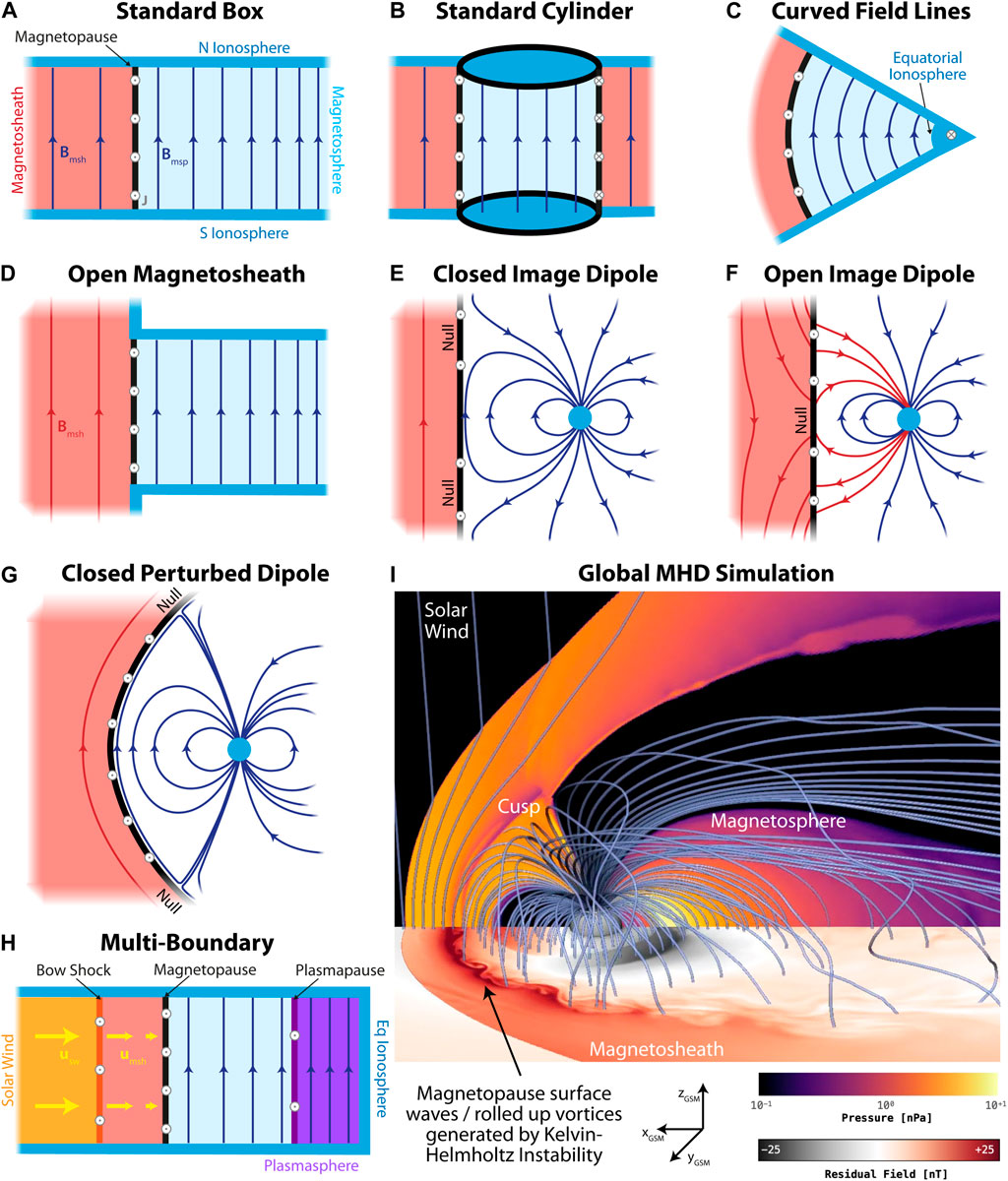
Figure 2. Diagrams of analytic MHD magnetosphere models that have been applied to magnetopause surface wave theory (A, B), and model setups which could advance current challenges to this theory (C–H). These may be complemented by global MHD simulations of the magnetosphere (I), such as GAMERA (Zhang et al., 2019). Depicted is a northward IMF run exhibiting KHI waves/vortices at the magnetopause, with equatorial plane showing residual magnetic field from a dipole, and meridional plane showing thermal pressure.

Magnetopause surface eigenmodes (MSEs) are typically considered around the subsolar meridian, where flow shears are low. Its eigenfrequency in an incompressible box model is thus given by Eq. 3, making it the lowest frequency magnetospheric normal mode and highly penetrating into the magnetosphere due to expected low azimuthal wavenumbers (Plaschke et al., 2009b; Plaschke and Glassmeier, 2011; Archer and Plaschke, 2015). The frequency has an approximately linear dependence on solar wind speed—via balance of magnetospheric magnetic and solar wind dynamic pressures, proportionality of magnetosheath and solar wind densities, and “stiffness” of the magnetosphere (Chen and Hasegawa, 1974; Archer et al., 2013a; Archer and Plaschke, 2015; Nenovski, 2021). Compressibility should modify this only slightly (Pu and Kivelson, 1983a).

It had been suggested fast solar wind might inhibit MSE, as meridional magnetosheath flow could reverse one of the counter-propagating surface waves (Plaschke and Glassmeier, 2011). Later this was considered important only for large dipole tilts, based on time-of-flight calculations within empirical models (Archer and Plaschke, 2015). Away from the subsolar meridian it was thought MSE would be advected tailward by the magnetosheath. However, it was shown theoretically (as well as in observations and simulations) that MSE can stand stationary against the flow across a wide local time range on the dayside, trapping wave energy locally (Archer et al., 2021).

In box models MSE currents flow only within the magnetopause, forming field-aligned currents at low altitudes which close via ionospheric Pedersen currents (Plaschke and Glassmeier, 2011). Whether surface modes directly have significant effects on the ionosphere or ground, and where these might map to, has been debated (Kivelson and Southwood, 1988; Southwood and Kivelson, 1990; Southwood and Kivelson, 1991; Kozyreva et al., 2019; Archer et al., 2023a).

2.3 Theoretical challenges

Numerous fundamental conceptual challenges concerning magnetopause surface waves remain, even in the linear theory. These are due to standard box/cylindrical models (Figures 2A, B) being oversimplifications of the magnetospheric environment, neglecting aspects of the full physics.

Standard models feature straight equilibrium field lines, however, field line curvature significantly affects MHD waves. To account for this one requires a magnetic (field-aligned) coordinate system with corresponding metric tensor (Stern, 1970; Stern, 1976; D’haeseleer et al., 1991). Note an orthogonal system may not exist, e.g., in the case of background field-aligned currents (Salat and Tataronis, 2000; Rankin et al., 2006). Such methods applied to the magnetospheric Alfvén continuum have shown eigenfrequencies differ from time-of-flight estimates typically by $\sim 20\text{–}75\%$ and vary with polarisation (Singer et al., 1981; Rankin et al., 2006; Elsden and Wright, 2020). The problem is more complex for surface waves, since solutions in each half-space, with likely different magnetic coordinate systems, must be tied together. Nonetheless, a simple model to determine surface waves’ sensitivity to field line curvature is the hydromagnetic wedge (Radoski, 1970) depicted in Figure 2C. Here cylindrical coordinates describe axial field lines, each with a constant radius of curvature (their radial coordinate), confined between two angles of azimuth corresponding to ionospheric boundaries.

Field lines are terminated in the ionosphere on both sides of the discontinuity in standard models. While this is valid for the plasmapause, at the magnetopause field lines in the magnetosheath should be open (Kozyreva et al., 2019). A modified box model with open magnetosheath flux is illustrated in Figure 2D. While the quantization condition on closed magnetospheric field lines (Eq. 4) should be unaffected, continuity of normal displacement across the boundary (Walker, 1981; Plaschke and Glassmeier, 2011) requires zero perturbation above/below the intersection of the magnetopause with the ionosphere, i.e., ${\xi }_x\left(x=0,y,z,t\right)=\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}\left(\pi z/S\right)\cos \left(k_{z}z\right)\exp \left(i\left[k_{y}y-\omega t\right]\right)$. The Fourier decomposition of this boundary condition introduces additional magnetosheath wavenumbers. These must also follow the magnetosonic dispersion relation (Eq. 1), hence may consist of propagating components in addition to evanescent waves. The overall effect would be a form of diffraction into the magnetosheath.

The magnetic field models presented have still been highly simplified. Close to Earth the field is reasonably approximated by a dipole, but differs substantially from this in the outer magnetosphere. Dipole equilibrium magnetic field models have been used to explore surface modes due to velocity shears (Leonovich and Kozlov, 2019), though by definition these models cannot include background currents or thermal pressure gradients. Placing an image dipole in the solar wind gives an analytic closed magnetosphere with planar infinitely conducting magnetopause and two magnetic null points at the cusps, as shown in Figure 2E (Chapman and Bartels, 1940). More representative closed magnetosphere models, like in Figure 2G, can be constructed by perturbing a dipole. Introducing (just two) spherical harmonic corrections to dipole Euler potentials produces a reasonable magnetosphere (Stern, 1967), though how to describe magnetosheath field lines in this framework is unclear. Alternatively, expressing the field as a scalar potential in parabolic harmonics with contributions from the dipole and magnetopause currents allows one to confine the geomagnetic field within a paraboloidal magnetopause (Stern, 1985), though magnetic coordinates must be determined numerically (Degeling et al., 2010).

In closed magnetosphere models the magnetopause is a TD. While it is often stated the magnetopause may be treated as a rotational discontinuity for an open magnetosphere (e.g., Sonnerup and Ledley, 1974), this neglects any density/pressure gradients present between the two media. Therefore, for an open magnetosphere the magnetopause must consist of both compressional and rotational boundaries (Dorville et al., 2014). The image dipole model (Figure 2E) can be simply extended to represent an open magnetosphere, as shown in Figure 2F (Kan and Akasofu, 1974). Constructing a realistic open magnetosphere model analytically remains an outstanding challenge (Zaharia and Birn, 2005).

These more representative models (Figures 2E–G) may help understanding effects of the polar cusps. Alfvén wave propagation is significantly affected by local variations in magnetic field strength and/or curvature when wavelengths are comparable to inhomogeneity scales (Pilipenko et al., 1999; Pilipenko et al., 2005), leading to reflection up to $\sim 80\text{–}90\%$. If similar holds for surface waves, surface eigenmodes might stand between reflection points in conjugate cusps rather than ionospheres. Another benefit to these models would be in probing non-resonant wave coupling. While Alfvén and magnetosonic modes are independent in uniform media, when inhomogeneities are introduced waves necessarily have mixed properties (Radoski, 1971; Goossens et al., 2019). Understanding the partial, irreversible conversion of surface waves’ compressional energy into Alfvén waves could help determine potential impacts of surface waves on the system and any filtering/processing the magnetosphere imposes upon them (cf. Pilipenko et al., 1999).

Thus far surface waves on a single boundary have been considered. However, it is clear from Figure 1A numerous boundaries exist within the magnetosphere. Given the large-scale nature of surface eigenmodes across the magnetic field, they cannot exist in isolation. This motivates a multi-boundary approach, such as in Figure 2H. Some progress towards this has considered eigenmodes of the outer magnetosphere, modeled as a slab or annular cylinder bounded by magnetopause and plasmapause (Nenovski et al., 2007; Nenovski, 2021). How the surface eigenmodes of individual boundaries are modified by, and couple to, the existence of another boundary has yet to be explored. Furthermore, introduction of the bow shock and equatorial ionospheric boundaries is required for a more complete description.

Resonant absorption for a finite-width boundary has been poorly explored outside of standard models. Where (either inside or outside) the transition layer mode conversion occurs and how this varies with surface mode harmonics is not well understood in more realistic setups. Since mode conversion provides a means for field-aligned current generation from a purely compressional wave (Southwood and Kivelson, 1990; Itonaga et al., 2000; Plaschke and Glassmeier, 2011) it is an important topic relevant to the ionospheric and ground-based impacts of surface modes (Kivelson and Southwood, 1988; Archer et al., 2023a).

Linear surface wave theory typically solves either initial value (where the boundary is perturbed and allowed to evolve) or eigenvalue problems (where normal modes are sought). Under these approaches it is not possible to self consistently consider variable solar wind forcing. However, solar wind and magnetosheath plasmas are highly turbulent, modifying conditions present adjacent to the magnetopause over timescales comparable to (or shorter than) surface wave periodicities. It has been suggested, by analogy with a driven harmonic oscillator with stochastically varying eigenfrequency, magnetosheath turbulence might suppress the surface mode (Pilipenko et al., 2017). The potential damping factor in such a toy model using representative turbulent amplitudes/spectra have not yet been estimated. Expanding this approach to self-consistently treat turbulent driving in addition to its effect on the eigenfrequency is required to more realistically formulate this problem.

It is finally worth noting only linear wave theory has been discussed. Nonlinear effects have been investigated analytically on planar TDs (cf. Figure 1B) for incompressible plasmas (Hollweg, 1987; Alì and Hunter, 2003). While this is of greatest relevance to a KH-unstable boundary, even in the marginally stable and weakly nonlinear regimes surface waves undergo wave steepening, crest/trough sharpening, and non-local self-interactions, leading to their breakdown in finite time. There is certainly more scope to explore this topic.

Many of these current challenges simply cannot be realistically treated by analytic theory. Nonetheless, modifications to simple models will likely provide insight into the physics. However, to more representatively model them in a complex environment like the magnetosphere necessitates numerical simulations.

3 Global simulations

Global simulations (mostly MHD, as shown in Figure 2I) have become a valuable tool in studying geospace, though correctly interpreting their results requires understanding the underlying physics and numerics (Raeder, 2003; Zhang et al., 2019; Raeder et al., 2021). The choice of grid, resolution, algorithms, and solver order have implications on whether boundary layers are resolved/smeared, in turn affecting surface wave growth/damping rates and wavelengths (Hartinger et al., 2015; Sorathia et al., 2017; Michael et al., 2021).

Magnetopause dynamics driven by upstream pressure changes (e.g., Børve et al., 2011; Desai et al., 2021; Horaites et al., 2023) and KHI (e.g., Slinker et al., 2003; Collado-Vega et al., 2007; Fairfield et al., 2007) have been explored in global simulations. These have included reproducing impulsively-excited MSE, showing this eigenmode can be sustained in a realistic magnetosphere (Hartinger et al., 2015; Archer et al., 2021).

Distinct inner and outer surface modes for continuous transition layers have been demonstrated. Results vary on whether their local frequencies are the same (Claudepierre et al., 2008; Archer et al., 2022; Archer et al., 2023a) or slightly different (Li et al., 2012), but agree these modes have different local wavelengths. Similarly, even just for intrinsic KHI-generated waves, differences are reported on whether surface wave frequencies are global (Claudepierre et al., 2008; Guo et al., 2010) or locally varying (Merkin et al., 2013; Archer et al., 2021), though their wavelengths clearly vary with local time from noon (Guo et al., 2010; Li et al., 2012; Merkin et al., 2013; Archer et al., 2021). Surface wave frequencies appear correlated with solar wind speed (Claudepierre et al., 2008; Li et al., 2012). Dayside MSE have been demonstrated seeding tailward-travelling surface waves that subsequently amplify via KHI despite not being at the instability’s intrinsic frequency (Hartinger et al., 2015; Archer et al., 2021), highlighting different driving mechanisms can be coupled thus may not always be as simple as often assumed.

The mixed properties of MHD waves from non-resonant wave coupling of the surface mode in a realistic plasma environment have been reported. These lead to field-aligned current generation throughout the magnetosphere, peaking at the inner edge of the boundary layer rather than the Open-Closed Boundary (Archer et al., 2023a). They also affect velocity polarisations, exhibiting axes aligned to the local (highly distorted) geomagnetic field (Li et al., 2013) and orientations perpendicular to amplitude gradients (Archer et al., 2023a), more akin to Alfvénic modes (Southwood and Kivelson, 1984). Resonant coupling of surface waves to Alfvén and cavity/waveguide body eigenmodes has been demonstrated in regions where frequencies match (Merkin et al., 2013; Archer et al., 2021; Archer et al., 2022).

Simulation results suggest the cusps do not reflect surface modes, but do introduce additional magnetic field nodes/antinodes and polarisation reversals compared to the velocity (Archer et al., 2022). They have also demonstrated standing structure and plasma inhomogeneities can alter the standard magnetosonic plasma–magnetic field correlation (Archer et al., 2023b). Finally, simulations have provided insight into potential impacts of surface waves on energetic particles (Claudepierre et al., 2008; Sorathia et al., 2017) and the ionosphere/ground (Archer et al., 2023a).

Global simulations have, therefore, provided valuable insight to some of the theoretical challenges raised in section 2.3, though further work in resolving inconclusive results and addressing outstanding questions remains.

4 Discussion

Boundary processes are key to the global dynamics and energetics of space plasma systems. Indeed it has been appreciated that the magnetopause may act as a (slow roll-off) low-pass filter (Smit, 1968; Freeman et al., 1995; Børve et al., 2011; Archer et al., 2013b; Desai et al., 2021), with surface waves contributing by processing, accumulating, and guiding upstream disturbances. Given magnetopause surface waves have natural frequencies (dependent on plasma conditions, Chen and Hasegawa, 1974; Miura and Pritchett, 1982; Archer and Plaschke, 2015), they may act as a magnetospheric resonator providing an efficient mechanism for frequency-dependent absorption of turbulent driving. Further theoretical/modelling work addressing the challenges raised in this review are required to assess this prospect. We have only considered MHD theory; extensions include kinetic surface wave theory (Lee, 2019) and/or coupling to Kinetic Alfvén Waves within the magnetopause (Hasegawa, 1976; Lee et al., 1994).

The connection between magnetospheric and solar waves has long been recognized (Nakariakov et al., 2016). For example, the best observed solar collective motions—transverse fundamental kink modes of coronal loops (Nakariakov et al., 2021)—can be strikingly well understood in terms of surface waves supported by interfaces of vanishing (Goossens et al., 2009) or finite widths (Hollweg and Yang, 1988) in models similar to Figure 2B. Though historically classified as “body modes” (Edwin and Roberts, 1983), in the long-wavelength linear limit kink modes are relatively insensitive to the details of the MHD environment (Goossens et al., 2009) and their dispersion relation reduces to exactly that of the surface eigenmode (Eq. 3). While theoretical understanding of their resonant interplay with the Alfvén continuum benefitted considerably from magnetospheric studies (Pascoe et al., 2011), their remotely-sensed nature have enabled effects like field line curvature (Van Doorsselaere et al., 2004; van Doorsselaere et al., 2009) and the localization of wave exciters (Nakariakov et al., 2004) to be addressed. Concepts such as wave packets have been elucidated by the stationary phase method (Guo et al., 2022; Li et al., 2023), addressing effects of waveguide dispersion (Kolotkov et al., 2021). These advancements from the solar environment could aid current challenges in the magnetospheric context.

Overall, advancing magnetopause surface wave theory will provide vital underpinning in interpreting data from upcoming missions. These include SMILE, which aims to uncover the fundamental modes of the dayside solar wind–magnetosphere interaction through soft X-ray imaging (Wang and Branduardi-Raymont, 2022), and HelioSwarm, which among its objectives is to assess the impact of solar wind turbulence on the magnetosphere (Klein et al., 2023).

Author contributions

MA: Funding acquisition, Project administration, Visualization, Writing–original draft. VP: Conceptualization, Writing–review and editing. BL: Writing–review and editing. KS: Visualization, Writing–review and editing. VN: Writing–review and editing. TE: Writing–review and editing. KN: Funding acquisition, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This review was supported by the International Space Science Institute (ISSI) in Bern, through ISSI International Team project #546 “Magnetohydrodynamic Surface Waves at Earth’s Magnetosphere (and Beyond)”. MOA was supported by UKRI (STFC/EPSRC) Stephen Hawking Fellowship EP/T01735X/1 and UKRI Future Leaders Fellowship MR/X034704/1.

Acknowledgments

We thank Ferdinand Plaschke, Anatoly Leonovich, and Harley M. Kelly for helpful discussions. For the purpose of open access, the author(s) has applied a Creative Commons attribution (CC BY) licence to any Author Accepted Manuscript version arising.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2024.1407172/full#supplementary-material

References

Alì, G., and Hunter, J. K. (2003). Nonlinear surface waves on a tangential discontinuity in magnetohydrodynamics. Q. Appl. Math. 61, 451–474. doi:10.1090/qam/1999831

CrossRef Full Text | Google Scholar

Archer, M. O., Hartinger, M. D., and Horbury, T. S. (2013a). Magnetospheric “magic” frequencies as magnetopause surface eigenmodes. Geophys. Res. Lett. 40, 5003–5008. doi:10.1002/grl.50979

CrossRef Full Text | Google Scholar

Archer, M. O., Hartinger, M. D., Plaschke, F., Southwood, D. J., and Rastaetter, L. (2021). Magnetopause ripples going against the flow form azimuthally stationary surface waves. Nat. Commun. 12, 5697. doi:10.1038/s41467-021-25923-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Archer, M. O., Hartinger, M. D., Rastaetter, L., Southwood, D. J., Heyns, M., Eggington, J. W. B., et al. (2023a). Auroral, ionospheric and ground magnetic signatures of magnetopause surface modes. J. Geophys. Res. Space Phys. 128, e2022JA031081. doi:10.1029/2022JA031081

CrossRef Full Text | Google Scholar

Archer, M. O., Horbury, T. S., Eastwood, J. P., Weygand, J. M., and Yeoman, T. K. (2013b). Magnetospheric response to magnetosheath pressure pulses: a low pass filter effect. J. Geophys. Res. Space Phys. 118, 5454–5466. doi:10.1002/jgra.50519

CrossRef Full Text | Google Scholar

Archer, M. O., and Plaschke, F. (2015). What frequencies of standing surface waves can the subsolar magnetopause support? J. Geophys Res. Space Phys. 120, 3632–3646. doi:10.1002/2014JA020545

CrossRef Full Text | Google Scholar

Archer, M. O., Southwood, D. J., Hartinger, M. D., Rastaetter, L., and Wright, A. N. (2022). How a realistic magnetosphere alters the polarizations of surface, fast magnetosonic, and alfvén waves. J. Geophys. Res. Space Phys. 127, e2021JA030032. doi:10.1029/2021JA030032

PubMed Abstract | CrossRef Full Text | Google Scholar

Archer, M. O., Southwood, D. J., Rastaetter, L., and Nykyri, K. (2023b). Magnetosonic ULF waves with anomalous plasma–magnetic field correlations: standing waves and inhomogeneous plasmas. Geophys. Res. Lett. 50, e2023GL104762. doi:10.1029/2023GL104762

CrossRef Full Text | Google Scholar

Berchem, J., and Russell, C. T. (1982). The thickness of the magnetopause current layer: ISEE 1 and 2 observations. J. Geophys. Res. 87, 2108–2114. doi:10.1029/JA087iA04p02108

CrossRef Full Text | Google Scholar

Boardsen, S. A., Sundberg, T., Slavin, J. A., Anderson, B. J., orth, H., Solomon, S. C., et al. (2010). Observations of Kelvin-Helmholtz waves along the dusk-side boundary of Mercury’s magnetosphere during MESSENGER’s third flyby. Gephys. Res. Lett. 37, L12101. doi:10.1029/2010GL043606

CrossRef Full Text | Google Scholar

Børve, S., Sato, H., Pécseli, H. L., and Trulsen, J. K. (2011). Minute-scale period oscillations of the magnetosphere. Ann. Geophys. 29, 663–671. doi:10.5194/angeo-29-663-2011

CrossRef Full Text | Google Scholar

Chandrasekhar, S. (1961) Hydrodynamic and hydromagnetic stability. Oxford, UK: Oxford University Press.

Google Scholar

Chapman, S., and Bartels, J. (1940) Geomagnetism. Oxford, UK: Oxford University Press.

Google Scholar

Chen, L., and Hasegawa, A. (1974). A theory of long-period magnetic pulsations: 2. impulse excitation of surface eigenmode. J. Geophys. Res. 79, 1033–1037. doi:10.1029/JA079i007p01033

CrossRef Full Text | Google Scholar

Claudepierre, S. G., Elkington, S. R., and Wiltberger, M. (2008). Solar wind driving of magnetospheric ULF waves: pulsations driven by velocity shear at the magnetopause. J. Geophys. Res. Space Phys. 113, A05218. doi:10.1029/2007JA012890

CrossRef Full Text | Google Scholar

Collado-Vega, Y. M., Kessel, R. L., Shao, X., and Boller, R. A. (2007). MHD flow visualization of magnetopause boundary region vortices observed during high-speed streams. J. Geophys. Res. Space Phys. 112, A06213. doi:10.1029/2006JA012104

CrossRef Full Text | Google Scholar

Degeling, A. W., Rankin, R., Kabin, K., Rae, I. J., and Fenrich, F. R. (2010). Modeling ULF waves in a compressed dipole magnetic field. J. Geophys. Res. 115, A10212. doi:10.1029/2010JA015410

CrossRef Full Text | Google Scholar

De Keyser, J., Roth, M., Reberac, F., Rezeau, L., and Belmont, G. (1999). Resonant amplification of MHD waves in realistic subsolar magnetopause configurations. J. Geophys. Res. Space Phys. 104, 2399–2409. doi:10.1029/1998JA900060

CrossRef Full Text | Google Scholar

Desai, R. T., Freeman, M. P., Eastwood, J. P., Eggington, J. W. B., Archer, M. O., Shprits, Y. Y., et al. (2021). Interplanetary shock-induced magnetopause motion: comparison between theory and global magnetohydrodynamic simulations. Geophys. Res. Lett. 48, e2021GL092554. doi:10.1029/2021GL092554

CrossRef Full Text | Google Scholar

D’haeseleer, W. D., Hitchon, W. N. G., Callen, J. D., and Shohet, J. L. (1991) Flux coordinates and magnetic field structure: a guide to a fundamental tool of plasma theory. Berlin, Germany: Springer. doi:10.1007/978-3-642-75595-8

CrossRef Full Text | Google Scholar

Dorville, N., Belmont, G., Rezeau, L., Grappin, R., and Retinó’, A. (2014). Rotational/compressional nature of the magnetopause: application of the bv technique on a magnetopause case study. J. Geophys. Res. Space Phys. 119, 1898–1908. doi:10.1002/2013JA018927

CrossRef Full Text | Google Scholar

Edwin, P. M., and Roberts, B. (1983). Wave propagation in a magnetic cylinder. Sol. Phys. 88, 179–191. doi:10.1007/BF00196186

CrossRef Full Text | Google Scholar

Elkington, S. R. (2006). “A review of ULF interactions with radiation belt electrons,” in Magnetospheric ULF waves: synthesis and new directions. Editors K. Takahashi, P. J. Chi, R. E. Denton, and R. L. Lysak (United States: John Wiley and Sons). 169 of Geophysical Monograph Series. doi:10.1029/169GM06

CrossRef Full Text | Google Scholar

Elsden, T., and Wright, A. (2020). Evolution of high-m poloidal alfvén waves in a dipole magnetic field. J. Geophys. Res. Space Phys. 125, e2020JA028187. doi:10.1029/2020JA028187

CrossRef Full Text | Google Scholar

Fairfield, D. H., Kuznetsova, M. M., Mukai, T., Nagai, T., Gombosi, T. I., and Ridley, A. J. (2007). Waves on the dusk flank boundary layer during very northward interplanetary magnetic field conditions: observations and simulation. J. Geophys. Res. Space Phys. 112, A08206. doi:10.1029/2006JA012052

CrossRef Full Text | Google Scholar

Freeman, M. P., Freeman, N. C., and Farrugia, C. J. (1995). A linear perturbation analysis of magnetopause motion in the Newton-Busemann limit. Ann. Geophys. 13, 907–918. doi:10.1007/s00585-995-0907-0

CrossRef Full Text | Google Scholar

Goedbloed, J. P. (1971). Stabilization of magnetohydrodynamic instabilities by force-free magnetic fields: I. plane plasma layer. Physica 53, 412–444. doi:10.1016/0031-8914(71)90127-3

CrossRef Full Text | Google Scholar

Goossens, M., Terradas, J., Andries, J., Arregui, I., and Ballester, J. L. (2009). On the nature of kink MHD waves in magnetic flux tubes. A&A 503, 213–223. doi:10.1051/0004-6361/200912399

CrossRef Full Text | Google Scholar

Goossens, M. L., Arregui, I., and Van Doorsselaere, T. (2019). Mixed properties of MHD waves in non-uniform plasmas. Front. Astron. Space Sci. 6, 20. doi:10.3389/fspas.2019.00020

CrossRef Full Text | Google Scholar

Guo, M., Li, B., Van Doorsselaere, T., and Shi, M. (2022). Impulsively generated kink wave trains in solar coronal slabs. MNRAS 515, 4055–4064. doi:10.1093/mnras/stac2006

CrossRef Full Text | Google Scholar

Guo, X. C., Wang, C., and Hu, Y. Q. (2010). Global MHD simulation of the Kelvin-Helmholtz instability at the magnetopause for northward interplanetary magnetic field. J. Geophys. Res. Space Phys. 115, A10218. doi:10.1029/2009JA015193

CrossRef Full Text | Google Scholar

Hartinger, M. D., Plaschke, F., Archer, M. O., Welling, D. T., Moldwin, M. B., and Ridley, A. (2015). The global structure and time evolution of dayside magnetopause surface eigenmodes. Geophys. Res. Lett. 42, 2594–2602. doi:10.1002/2015GL063623

CrossRef Full Text | Google Scholar

Hasegawa, A. (1976). Particle acceleration by MHD surface wave and formation of aurora. J. Geophys. Res. 81, 5083–5090. doi:10.1029/JA081i028p05083

CrossRef Full Text | Google Scholar

He, F., Guo, R.-L., Dunn, W. R., Yao, Z.-H., Zhang, H.-S., Hao, Y.-X., et al. (2020). Plasmapause surface wave oscillates the magnetosphere and diffuse aurora. Nat. Commun. 11, 1668. doi:10.1038/s41467-020-15506-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Hollweg, J. V. (1987). Incompressible magnetohydrodynamic surface waves: nonlinear aspects. ApJ 317, 918–925. doi:10.1086/165341

CrossRef Full Text | Google Scholar

Hollweg, J. V., and Yang, G. (1988). Resonance absorption of compressible magnetohydrodynamic waves at thin “surfaces”. J. Geophys. Res. Space Phys. 93, 5423–5436. doi:10.1029/JA093iA06p05423

CrossRef Full Text | Google Scholar

Horaites, K., Rintamäki, E., Zaitsev, I., Turc, L., Grandin, M., Cozzani, G., et al. (2023). Magnetospheric response to a pressure pulse in a three-dimensional hybrid-vlasov simulation. J. Geophys. Res. Space Phys. 128, e2023JA031374. doi:10.1029/2023JA031374

CrossRef Full Text | Google Scholar

Hwang, K.-J., and Sibeck, D. G. (2016) Low-frequency waves in space plasmas. Washington DC, USA: American Geophysical Union, 213–239. doi:10.1002/9781119055006.ch13

CrossRef Full Text | Google Scholar

Itonaga, M., Yoshikawa, A., and Fujita, S. (2000). A wave equation describing the generation of field-aligned current in the magnetosphere. Earth Planet Sp. 52, 503–507. doi:10.1186/BF03351654

CrossRef Full Text | Google Scholar

Kan, J. R., and Akasofu, S.-I. (1974). A model of the open magnetosphere. J. Geophys. Res. 79, 1379–1384. doi:10.1029/JA079i010p01379

CrossRef Full Text | Google Scholar

Kivelson, M. G., and Chen, S.-H. (1995). The magnetopause: surface waves and instabilities and their possible dynamical consequences. Geophys. Monogr. Ser., 257–268. doi:10.1029/GM090p0257

CrossRef Full Text | Google Scholar

Kivelson, M. G., Etcheto, J., and Trotignon, J. G. (1984). Global compressional oscillations of the terrestrial magnetosphere: the evidence and a model. J. Geophys Res. 89, 9851–9856. doi:10.1029/JA089iA11p09851

CrossRef Full Text | Google Scholar

Kivelson, M. G., and Southwood, D. J. (1985). Resonant ULF waves: a new interpretation. Geophys. Res. Lett. 12, 49–52. doi:10.1029/GL012i001p00049

CrossRef Full Text | Google Scholar

Kivelson, M. G., and Southwood, D. J. (1988). Hydromagnetic waves and the ionosphere. Geophys. Res. Lett. 15, 1271–1274. doi:10.1029/GL015i011p01271

CrossRef Full Text | Google Scholar

Klein, K. G., Spence, H., Alexandrova, O., Argall, M., Arzamasskiy, L., Bookbinder, J., et al. (2023). Helioswarm: a multipoint, multiscale mission to characterize turbulence. Space Sci. Rev. 219, 74. doi:10.1007/s11214-023-01019-0

CrossRef Full Text | Google Scholar

Kolotkov, D. Y., Nakariakov, V. M., Moss, G., and Shellard, P. (2021). Fast magnetoacoustic wave trains: from tadpoles to boomerangs. MNRAS 505, 3505–3513. doi:10.1093/mnras/stab1587

CrossRef Full Text | Google Scholar

Kozyreva, O., Pilipenko, V., Lorentzen, D., Baddeley, L., and Hartinger, M. (2019). Transient oscillations near the dayside open-closed boundary: evidence of magnetopause surface mode? J. Geophys. Res. Space Phys. 124, 9058–9074. doi:10.1029/2018JA025684

CrossRef Full Text | Google Scholar

Kruskal, M., and Schwartzschild, M. (1954). Some instabilities of a completely ionized plasma. Proc. R. Soc. Lond. Ser. A 223, 348–360. doi:10.1098/rspa.1954.0120

CrossRef Full Text | Google Scholar

Lee, H. J. (2019) Fundamentals of theoretical plasma physics: mathematical description of plasma waves. Singapore: World Scientific Publishing. doi:10.1142/11168

CrossRef Full Text | Google Scholar

Lee, L. C., Albano, R. K., and Kan, J. R. (1981). Kelvin-Helmholtz Instability in the magnetopause-boundary layer region. J. Geophys. Res. Space Phys. 86, 54–58. doi:10.1029/JA086iA01p00054

CrossRef Full Text | Google Scholar

Lee, L. C., Johnson, J. R., and Ma, Z. W. (1994). Kinetic alfvén waves as a source of plasma transport at the dayside magnetopause. J. Geophys. Res. Space Phyiscs 99, 17405–17411. doi:10.1029/94JA01095

CrossRef Full Text | Google Scholar

Lee, M. A., and Roberts, B. (1986). On the behavior of hydromagnetic surface waves. Astrophysical J. 30, 430–439. doi:10.1086/163911

CrossRef Full Text | Google Scholar

Leonovich, A., and Kozlov, D. A. (2019). Kelvin-helmholtz instability in a dipole magnetosphere: the magnetopause as a tangential discontinuity. J. Geophys. Res. Space Phys. 124, 7936–7953. doi:10.1029/2019JA026842

CrossRef Full Text | Google Scholar

Li, B., Guo, M., Yu, H., Chen, S.-X., and Shi, M. (2023). Three-dimensional propagation of kink wave trains in solar coronal slabs. MNRAS 518, L57–L62. doi:10.1093/mnrasl/slac139

CrossRef Full Text | Google Scholar

Li, W., Wang, C., Tang, B., Guo, X., and Lin, D. (2013). Global features of Kelvin-Helmholtz waves at the magnetopause for northward interplanetary magnetic field. J. Geophys. Res. Space Phys. 118, 5118–5126. doi:10.1002/jgra.50498

CrossRef Full Text | Google Scholar

Li, W. Y., Guo, X. C., and Wang, C. (2012). Spatial distribution of Kelvin-Helmholtz instability at low-latitude boundary layer under different solar wind speed conditions. J. Geophys. Res. Space Phys. 117, A08230. doi:10.1029/2012JA017780

CrossRef Full Text | Google Scholar

Lubchich, A. A., and Despirak, I. V. (2005). Magnetohydrodynamic waves within the medium separated by the plane shock wave or rotational discontinuity. Ann. Geophys. 23, 1889–1908. doi:10.5194/angeo-23-1889-2005

CrossRef Full Text | Google Scholar

Lubchich, A. A., and Pudovkin, M. I. (1999). “Transmission of fast magnetosonic wave through rotational discontinuity,” in Conference: XXII Annual seminar Physics of Auroral Phenomena, March 14 to March 18, 2022.

Google Scholar

Ma, X., Stauffer, B., Delamere, P. A., and Otto, A. (2015). Asymmetric Kelvin-Helmholtz propagation at Saturn’s dayside magnetopause. J. Geophys. Res. Space Phys. 120, 1867–1875. doi:10.1002/2014JA020746

CrossRef Full Text | Google Scholar

Mann, I. R., Wright, A. N., Mills, K. J., and Nakariakov, V. M. (1999). Excitation of magnetospheric waveguide modes by magnetosheath flows. J. Geophys Res. Space Phys. 104, 333–353. doi:10.1029/1998JA900026

CrossRef Full Text | Google Scholar

Masson, A., and Nykyri, K. (2018). Kelvin-Helmholtz instability: lessons learned and ways forward. Space Sci. Rev. 214, 71. doi:10.1007/s11214-018-0505-6

CrossRef Full Text | Google Scholar

Masters, A., Achilleos, N., Bertucci, C., Dougherty, M. K., Kanani, S. J., Arridge, C. S., et al. (2009). Surface waves on Saturn’s dawn flank magnetopause driven by the Kelvin–Helmholtz instability. Planet. Space Sci. 57, 1769–1778. doi:10.1016/j.pss.2009.02.010

CrossRef Full Text | Google Scholar

Merkin, V. G., Lyon, J. G., and Clausepierre, S. G. (2013). Kelvin-Helmholtz instability of the magnetospheric boundary in a three-dimensional global MHD simulation during northward IMF conditions. J. Geophys. Res. Space Phys. 118, 5478–5496. doi:10.1002/jgra.50520

CrossRef Full Text | Google Scholar

Michael, A. T., Sorathia, K. A., Merkin, V. G., Nykyri, K., Burkholder, B., Ma, X., et al. (2021). Modeling Kelvin-Helmholtz instability at the high-latitude boundary layer in a global magnetosphere simulation. Geophys. Res. Lett. 48, e2021GL094002. doi:10.1029/2021GL094002

PubMed Abstract | CrossRef Full Text | Google Scholar

Miura, A., and Pritchett, P. L. (1982). Nonlocal stability analysis of the MHD Kelvin-Helmholtz instability in a compressible plasma. J. Geophys. Res. Space Phys. 87, 7431–7444. doi:10.1029/JA087iA09p07431

CrossRef Full Text | Google Scholar

Montgomery, J., Ebert, R. W., Allegrini, F., Bagenal, F., Bolton, S. J., DiBraccio, G. A., et al. (2023). Investigating the occurrence of Kelvin-Helmholtz instabilities at Jupiter’s dawn magnetopause. Geophys. Res. Lett. 50, e2023GL102921. doi:10.1029/2023GL102921

CrossRef Full Text | Google Scholar

Nakariakov, V. M., Anfinogentov, S. A., Antolin, P., Jain, R., Kolotkov, D. Y., Kupriyanova, E. G., et al. (2021). Kink oscillations of coronal loops. Space Sci. Rev. 217, 73. doi:10.1007/s11214-021-00847-2

CrossRef Full Text | Google Scholar

Nakariakov, V. M., Arber, T. D., Ault, C. E., Katsiyannis, A. C., Williams, D. R., and Keenan, F. P. (2004). Time signatures of impulsively generated coronal fast wave trains. MNRAS 349, 705–709. doi:10.1111/j.1365-2966.2004.07537.x

CrossRef Full Text | Google Scholar

Nakariakov, V. M., Pilipenko, V., Heilig, B., Jelínek, P., Karlický, M., Klimushkin, D. Y., et al. (2016). Magnetohydrodynamic oscillations in the solar corona and Earth’s magnetosphere: towards consolidated understanding. Space Sci. Rev. 200, 75–203. doi:10.1007/s11214-015-0233-0

CrossRef Full Text | Google Scholar

Nenovski, P. (2021). MHD surface waves - a source of global magnetospheric modes (resonances)? Adv. Space Res. 67, 731–738. doi:10.1016/j.asr.2020.09.039

CrossRef Full Text | Google Scholar

Nenovski, P., Villante, U., Francia, P., Vellante, M., and Bochev, A. (2007). Do we need a surface wave approach to the magnetospheric resonances? Planet. Space Sci. 55, 680–693. doi:10.1016/j.pss.2006.04.038

CrossRef Full Text | Google Scholar

Nykyri, K., and Foullon, C. (2013). First magnetic seismology of the CME reconnection outflow layer in the low corona with 2.5-D MHD simulations of the Kelvin-Helmholtz instability. Geophys. Res. Lett. 40, 4154–4159. doi:10.1002/grl.50807

CrossRef Full Text | Google Scholar

Paschmann, G., Haaland, S., Sonnerup, B. U. O., Hasegawa, H., Georgescu, E., Klecker, B., et al. (2005). Characteristics of the near-tail dawn magnetopause and boundary layer. Ann. Geophys. 23, 1481–1497. doi:10.5194/angeo-23-1481-2005

CrossRef Full Text | Google Scholar

Pascoe, D. J., Wright, A. N., and De Moortel, I. (2011). Propagating coupled alfvén and kink oscillations in an arbitrary inhomogeneous corona. ApJ 731, 73. doi:10.1088/0004-637X/731/1/73

CrossRef Full Text | Google Scholar

Pilipenko, V., Federov, E., Mazur, N. G., Engebretson, M. J., and Hughes, W. J. (1999). Magnetohydrodynamic waveguide/resonator for pc3 ULF pulsations at cusp latitudes. Earth Planets Space 51, 441–448. doi:10.1186/BF03352248

CrossRef Full Text | Google Scholar

Pilipenko, V. A., Kozyreva, O., Baddeley, L., Lorentzen, D. A., and Belakhovsky, V. B. (2017). Suppression of the dayside magnetopause surface modes. Sol.-Terr. Phys. 3, 17–25. doi:10.12737/stp-34201702

CrossRef Full Text | Google Scholar

Pilipenko, V. A., Mazur, N. G., Federov, E. N., Engebretson, M. J., and Murr, D. L. (2005). Alfvén wave reflection in a curvilinear magnetic field and formation of alfvénic resonators on open field lines. J. Geophys. Res. Space Phys. 110, A10S05. doi:10.1029/2004JA010755

CrossRef Full Text | Google Scholar

Plaschke, F. (2016) Low-frequency waves in space plasmas. Washington DC, USA: AGU, 193–212. doi:10.1002/9781119055006.ch12

CrossRef Full Text | Google Scholar

Plaschke, F., and Glassmeier, K. H. (2011). Properties of standing Kruskal-Schwarzschild-modes at the magnetopause. Ann. Geophys. 29, 1793–1807. doi:10.5194/angeo-29-1793-2011

CrossRef Full Text | Google Scholar

Plaschke, F., Glassmeier, K.-H., Auster, H. U., Angelopoulos, V., Constantinescu, O. D., Fornaçon, K.-H., et al. (2009a). Statistical study of the magnetopause motion: first results from THEMIS. J. Geophys. Res. Space Phys. 114, A00C10. doi:10.1029/2008JA013423

CrossRef Full Text | Google Scholar

Plaschke, F., Glassmeier, K.-H., Auster, H. U., Constantinescu, O. D., Magnes, W., Angelopoulos, V., et al. (2009b). Standing Alfvén waves at the magnetopause. Geophys. Res. Lett. 36, L02104. doi:10.1029/2008GL036411

CrossRef Full Text | Google Scholar

Pu, Z.-Y., and Kivelson, M. G. (1983a). Kelvin-Helmholtz Instability at the magnetopause: solution for compressible plasmas. J. Geophys. Res. Space Phys. 88, 841–852. doi:10.1029/JA088iA02p00841

CrossRef Full Text | Google Scholar

Pu, Z.-Y., and Kivelson, M. G. (1983b). Kelvin-Helmholtz Instability at the magnetopause: energy flux into the magnetosphere. J. Geophys. Res. Space Phys. 88, 853–861. doi:10.1029/JA088iA02p00853

CrossRef Full Text | Google Scholar

Radoski, H. R. (1970). The resonance barrier theory of hydromagnetic waves. J. Geomag. Geoelec. 22, 361–379. doi:10.5636/jgg.22.361

CrossRef Full Text | Google Scholar

Radoski, H. R. (1971). A note on the problem of hydromagnetic resonances in the magnetosphere. Planet. Space Sci. 19, 1012–1013. doi:10.1016/0032-0633(71)90152-8

CrossRef Full Text | Google Scholar

Raeder, J. (2003) Space plasma simulation. Berlin, Heidelberg, Germany: Springer.

Google Scholar

Raeder, J., Germaschewski, K., Cramer, W. D., and Lyon, J. (2021). Magnetospheres in the Solar System (Washington DC, USA: AGU), chap. Global simulations. Geophys. Monogr. Ser., 595–606. doi:10.1002/9781119815624.ch37

CrossRef Full Text | Google Scholar

Rankin, R., Kabin, K., and Marchand, R. (2006). Alfvénic field line resonances in arbitrary magnetic field topology. Adv. Space Res. 38, 1720–1729. doi:10.1016/j.asr.2005.09.034

CrossRef Full Text | Google Scholar

Ruderman, M. S., Vickers, E., Ballai, I., and Erdelyi, R. (2018). Propagation of leaky surface waves on contact magnetohydrodynamic discontinuities in incompressible plasmas. Phys. Plasmas 25, 122107. doi:10.1063/1.5050591

CrossRef Full Text | Google Scholar

Salat, A., and Tataronis, J. A. (2000). Conditions for existence of orthogonal coordinate systems oriented by magnetic field lines. J. Geophys. Res. 105, 13055–13062. doi:10.1029/1999JA000221

CrossRef Full Text | Google Scholar

Samson, J. C., Harrold, B. G., Ruohoniemi, J. M., Greenwald, R. A., and Walker, A. D. M. (1992). Field line resonances associated with MHD waveguides in the magnetosphere. Geophys. Res. Lett. 19, 441–444. doi:10.1029/92GL00116

CrossRef Full Text | Google Scholar

Sen, A. K. (1963). Stability of hydromagnetic kelvin-helmholtz discontinuity. Phys. Fluids 6, 1154–1163. doi:10.1063/1.1706875

CrossRef Full Text | Google Scholar

Singer, H. J., Southwood, D. J., Walker, R. J., and Kivelson, M. G. (1981). Alfvén wave resonances in a realistic magnetospheric magnetic field geometry. J. Geophys. Res. 86, 4589–4596. doi:10.1029/JA086iA06p04589

CrossRef Full Text | Google Scholar

Slinker, S. P., Fedder, J. A., Sibeck, D. G., Lyon, J. G., Frank, L. A., and Mukai, T. (2003). Simulation of magnetopause oscillations observed january 9, 1996. Geophys. Res. Lett. 30, 1569. doi:10.1029/2003GL017063

CrossRef Full Text | Google Scholar

Smit, G. R. (1968). Oscillatory motion of the nose region of the magnetopause. J. Geophys. Res. 73, 4990–4993. doi:10.1029/JA073i015p04990

CrossRef Full Text | Google Scholar

Smith, E. J. (2001). The heliospheric current sheet. J. Geophys. Res. Space Phys. 106, 15819–15831. doi:10.1029/2000JA000120

CrossRef Full Text | Google Scholar

Sonnerup, B. U. O., and Ledley, B. G. (1974). Magnetopause rotational forms. J. Geophys. Res. 79, 4309–4314. doi:10.1029/JA079i028p04309

CrossRef Full Text | Google Scholar

Sorathia, K. A., Merkin, V. G., Ukhorskiy, A. Y., Mauk, B. H., and Sibeck, D. G. (2017). Energetic particle loss through the magnetopause: a combined global mhd and test-particle study. J. Geophys. Res. Space Phys. 122, 9329–9343. doi:10.1002/2017JA024268

CrossRef Full Text | Google Scholar

Southwood, D. J. (1968). The hydromagnetic stability of the magnetospheric boundary. Planet. Space Sci. 16, 587–605. doi:10.1016/0032-0633(68)90100-1

CrossRef Full Text | Google Scholar

Southwood, D. J. (1974). Some features of field line resonances in the magnetosphere. Planet. Space Sci. 22, 483–491. doi:10.1016/0032-0633(74)90078-6

CrossRef Full Text | Google Scholar

Southwood, D. J., and Kivelson, M. G. (1984). Relations between polarization and the structure of ULF waves in the magnetosphere. J. Geophys. Res. 89, 5523–5529. doi:10.1029/JA089iA07p05523

CrossRef Full Text | Google Scholar

Southwood, D. J., and Kivelson, M. G. (1990). The magnetohydrodynamic response of the magnetospheric cavity to changes in solar wind pressure. J. Geophys. Res. Space Phys. 95, 2301–2309. doi:10.1029/JA095iA03p02301

CrossRef Full Text | Google Scholar

Southwood, D. J., and Kivelson, M. G. (1991). An approximate description of field-aligned currents in a planetary magnetic field. J. Geophys. Res. Space Phys. 96, 67–75. doi:10.1029/90JA01806

CrossRef Full Text | Google Scholar

Stern, D. (1967). Geomagnetic euler potentials. J. Geophys. Res. 72, 3995–4005. doi:10.1029/JZ072i015p03995

CrossRef Full Text | Google Scholar

Stern, D. P. (1970). Euler potentials. Am. J. Phys. 35, 494–501. doi:10.1119/1.1976373

CrossRef Full Text | Google Scholar

Stern, D. P. (1976). Representation of magnetic fields in space. Rev. Geophys. 14, 199–214. doi:10.1029/RG014i002p00199

CrossRef Full Text | Google Scholar

Stern, D. P. (1985). Parabolic harmonics in magnetospheric modeling: the main dipole and the ring current. J. Geophys. Res. Space Phys. 90, 10851–10863. doi:10.1029/JA090iA11p10851

CrossRef Full Text | Google Scholar

D. Summers, I. R. Mann, D. N. Baker, and M. Schulz (2013). Dynamics of the Earth’s radiation belts and inner magnetosphere (Washington, D.C., United States: American Geophysical Union). doi:10.1029/GM199

CrossRef Full Text | Google Scholar

Sundberg, T., Boardsen, S. A., Slavin, J. A., Anderson, B. J., amd, T. H., Zurbuchen, H. K., et al. (2012). MESSENGER orbital observations of large-amplitude Kelvin-Helmholtz waves at Mercury’s magnetopause. J. Geophys. Res. Space Phys. 117, A04216. doi:10.1029/2011JA017268

CrossRef Full Text | Google Scholar

Uberoi, C. (1989). Resonant absorption of Alfvén compressional surface waves. J. Geophys. Res. 94, 6941–6944. doi:10.1029/JA094iA06p06941

CrossRef Full Text | Google Scholar

Van Doorsselaere, T., Debosscher, A., Andries, J., and Poedts, S. (2004). The effect of curvature on quasi-modes in coronal loops. A&A 424, 1065–1074. doi:10.1051/0004-6361:20041239

CrossRef Full Text | Google Scholar

van Doorsselaere, T., Verwichte, E., and Terradas, J. (2009). The effect of loop curvature on coronal loop kink oscillations. Space Sci. Rev. 149, 299–324. doi:10.1007/s11214-009-9530-9

CrossRef Full Text | Google Scholar

Volwerk, M., Jia, X., Paranicas, C., Kurth, W. S., Kivelson, M. G., and Khurana, K. K. (2013). Ulf waves in Ganymede’s upstream magnetosphere. Ann. Geophys. 31, 45–59. doi:10.5194/angeo-31-45-2013

CrossRef Full Text | Google Scholar

Walker, A. D. M. (1981). The Kelvin-Helmholtz instability in the low-latitude boundary layer. Planet. Space Sci. 29, 1119–1133. doi:10.1016/0032-0633(81)90011-8

CrossRef Full Text | Google Scholar

Wang, C., and Branduardi-Raymont, G. (2022). Progress of solar wind magnetosphere ionosphere link explorer (SMILE) mission. Chin. J. Space Sci. 38, 657–661. doi:10.11728/cjss2018.05.657

CrossRef Full Text | Google Scholar

Wang, L., Huang, C., Du, A., Ge, Y., Chen, G., Yang, Z., et al. (2023). Kelvin–Helmholtz instability at mars: in situ observations and kinetic simulations. ApJ 947, 51. doi:10.3847/1538-4357/acc655

CrossRef Full Text | Google Scholar

Wang, T. J. (2016). “Low-frequency Waves in space plasmas (Washington DC, USA: AGU), chap. Waves,” in Solar coronal loops, 395–418. doi:10.1002/9781119055006.ch23

CrossRef Full Text | Google Scholar

Wright, A. N. (1994). Dispersion and wave coupling in inhomogeneous MHD waveguides. J. Geophys. Res. Space Phys. 99, 159–167. doi:10.1029/93JA02206

CrossRef Full Text | Google Scholar

Zaharia, S., Birn, J., and Cheng, C. Z. (2005). Toward a global magnetospheric equilibrium model. J. Geophys. Res. Space Phys. 110, A09228. doi:10.1029/2005JA011101

CrossRef Full Text | Google Scholar

Zhang, B., Sorathia, K. A., Lyon, J. G., Merkin, V. G., Garretson, J. S., and Wiltberger, M. (2019). GAMERA: a three-dimensional finite-volume MHD solver for non-orthogonal curvilinear geometries. ApJ 244, 20. doi:10.3847/1538-4365/ab3a4c

CrossRef Full Text | Google Scholar

Zirnstein, E. J., Shrestha, B. L., McComas, D. J., Dayeh, M. A., Heerikhuisen, J., Reisenfeld, D. B., et al. (2022). Oblique and rippled heliosphere structures from the interstellar boundary explorer. Nat. Astron. 6, 1398–1413. doi:10.1038/s41550-022-01798-6

PubMed Abstract | CrossRef Full Text | Google Scholar