Infrared-radio-follow-up observations for detection of the magnetic radio emission of extra solar planets: a new window to detect exoplanets

There are several methods for indirectly detecting exoplanets, such as transit, radial velocity, astrometry, and the conventional gravitational microlensing approach. These methods rely on observing the effects of exoplanets on the emission or motion of observed stars. All these techniques have focused on the optical or infrared domains. However, an alternative method for exoplanet detection via microlensing events involves planets orbiting the source star, creating a binary source system. In this study, we explore a novel approach to detecting and studying exoplanets exclusively through their radio emissions resulting from magnetospheric processes. We propose utilizing the Roman telescope as a survey observer to detect microlensing events. Subsequently, we investigate the potential for detecting planetary radio signals through follow-up observations of these microlensing events in the radio band using the SKA telescope. This method is viable due to the comparable radio emission levels of exoplanets and their parent stars, unlike optical and infrared emissions. We conduct a Monte Carlo simulation to replicate the observations by the Nancy Roman Telescope, followed by a follow-up observation in radio frequencies using the SKA telescope. We determine that approximately 1,317 exoplanets exhibit detectable signals by the SKA telescope during the 7-season observations by the Nancy Roman Telescope. This result indicates that such a method cannot only facilitate the direct detection of exoplanets but also enable the measurement of their magnetic field strength through analysis of their radio emissions.

1 Introduction

A planetary magnetic field is one of the few observable quantities that contain information about the properties of the planetary interior since the internal dynamo produces it. Further, the extent to which exoplanets retain their atmospheres over geological time scales depends on whether they are exposed directly to stellar winds. Also, planetary magnetic fields could potentially serve as indicators of plate tectonics. Therefore, information about the magnetic fields of extrasolar planets is essential to assess their habitability. So far, our knowledge of planetary magnetic fields is limited to our Solar System’s planets, which are not representative of the vast array of possible planets, such as hot Jupiters (Lammer et al., 2009; Cockell et al., 2016; Kane, 2021; Lingam and Loeb, 2021).

But how can we observe and measure the magnetic field of exoplanets? The magnetospheres of Earth, Jupiter, Saturn, Uranus, and Neptune all show evidence of nonthermal continuum radiation emission resulting from the solar wind’s interaction with the planet’s magnetic field (Zarka, 1998). The electron cyclotron maser instability (ECMI) is a phenomenon that occurs in plasmas where electrons emit coherent electromagnetic radiation due to confinement by magnetic field lines along which they travel, gyrate, and accelerate (Melrose and Dulk, 1982; Dulk, 1985). The ECMI is the most efficient radio emission mechanism, dominating all other emissions (beam-plasma instabilities and others). Based on our knowledge of the Solar System planets, the average ECMI is related to the total solar wind power and the magnetic field of the planet by using the Radiometric Bode’s Law (RBL) model (Zarka et al., 2001; Zarka, 2004; 2007). Therefore, observations of this emission type can indirectly measure and classify the planetary magnetic field. This quantification of the magnetic field gives us constraints on internal structure models and planetary rotation, informing us about the evolutionary history of the planet and host system (Hess et al., 2011). Furthermore, the exoplanets’ radio emission may reveal the presence of exomoons around them. For example, it has been shown that part of the Jovian decameter radio emission is “controlled” by the satellite Io (Bigg, 1964). Noyola et al. (2014) argues that the Io-Jupiter interaction could also be found in exoplanet-moon pairs, and the exoplanets’ radio emissions could be used to detect such systems directly.

A multitude of exoplanet detection techniques rely on indirect optical/infrared wavelength observations (Mandel and Agol, 2002; Seager and Hui, 2002; Guyon et al., 2005; Traub and Oppenheimer, 2010; Gaudi, 2012; Wright et al., 2012; Knutson et al., 2014; Bagheri et al., 2019). However, measurements of the planetary magnetic fields require direct observations at the low-frequency radio wavelengths. Despite efforts to detect exoplanets in the radio band via ground-based radio telescopes, no promising detection of planetary radio emissions has been successful (Murphy et al., 2015; Lazio et al., 2018; Turner et al., 2021), primarily due to the low sensitivity of ground-based radio telescopes. Consequently, direct confirmation of the existence of exomoons has so far remained impossible.

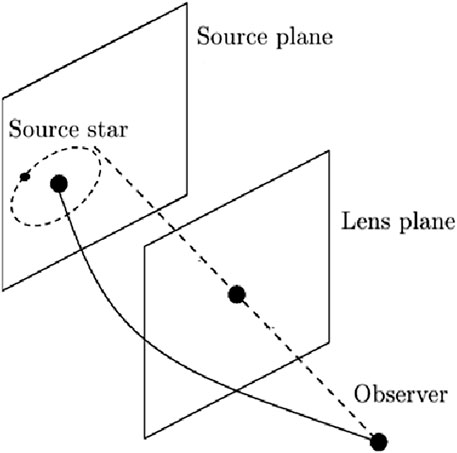
In this work, we combine two different exoplanet detection methods to make the radio emission of exoplanets detectable. The novel idea behind this study is that during a microlensing event, light intensity will be magnified at all frequencies. Therefore, a microlensing event can serve as a natural light magnifier. The idea is to use an optical/infrared telescope to detect a microlensing event that would trigger follow-up observations by radio telescopes upon detection. If the source star has at least one exoplanet in microlensing events, we can directly measure the light emitted from the exoplanet (Figure 1). The magnified light of the exoplanet could be observable in the infrared wavelength as we have shown in (Bagheri et al., 2019). However, the radio band is the most desirable wavelength window to detect exoplanets (Foster et al., 2020; Vedantham et al., 2020; Viswanath et al., 2020) since the planetary radio emission, which includes the effects of exomoons, may dominate the signal from the parent star (Zarka, 2004; Cauley et al., 2019). This method will enable us to measure the magnetic fields of exoplanets and provide us with information about the existence of exomoons. To show this, we simulate the Nancy Grace Roman Space Telescope (previously named Wide Filed Infrared Space Telescope, WFIRST) as an infrared survey telescope to alert the Square Kilometre Array (SKA) radio telescope to the occurrence of microlensing events for follow-up observations.

Figure 1

Figure 1. A schematic view of a binary-source microlensing event.

2 Methodology

2.1 Microlensing events

Microlensing, a powerful tool in the study of astrophysics, involves the gravitational bending of light by massive objects, typically stars, within the lensing galaxy. This phenomenon, predicted by Einstein’s theory of general relativity, manifests as a temporary increase in the brightness of a background source, such as a distant star, as the foreground lensing object passes in front of it. The gravitational field of the foreground object acts as a lens, magnifying and distorting the light from the background source. In lensing, the magnification, denoted by A, represents the factor by which the flux of the source is amplified during the microlensing event. Therefore it is given by the ratio of the image size to the source size:

$A=\frac{\text{Image} \text{size}}{\text{Source} \text{size}}.(1)$

For point source magnification in microlensing, where the source size is negligible compared to the Einstein radius (R_E), the magnification can be simplified as:

$A=\frac{u^2+2}{u\sqrt{u^2+4}}(2)$

where u is the impact parameter, defined as the closest approach of the source to the lens normalized by the Einstein radius (Gaudi, 2012). The lensing system may comprise either a single object (single-lens) or two objects (binary-lens), with the possibility of additional components (Daněk and Heyrovskỳ, 2019). The presence of two lenses introduces additional complexity to the gravitational lensing phenomenon, leading to more intricate and often asymmetric light curves. Source systems can also consist of one or more objects. The conventional technique utilized in gravitational microlensing for exoplanet detection relies on the premise that the lens star hosts an exoplanet, constituting a binary lens system. Alternatively, another microlensing approach involves a scenario where the planet orbits the source star, resulting in a binary source configuration (Bagheri et al., 2019) as illustrated in Figure 1. In this study we simulate binary-source microlensing events by assuming both single-lens and binary-lens configurations. We consider the finite source effect for the source star while neglecting limb darkening.

2.2 Source and Lens stars parameters

To characterize the star mass density within the Milky Way galaxy, we rely on the Bésançon model, extensively discussed in previous works (Robin et al., 2003; Gardner et al., 2014; Spergel et al., 2015). This model presents the distribution of matter in our galaxy as a superposition of eight thin disk structures with varying ages, a thick disk component, and a central (old) bar structure consisting of two components. Our choice is the updated model proposed by (Gardner et al., 2014). We select the model parameters fitted to a two ellipsoid bar. This refined model, utilizing star distribution data from the Hipparcos catalog, has proven effective in interpreting microlensing data from the EROS collaboration in the direction of the spiral arms (Moniez et al., 2017). When generating binary lenses, the mass ratio between the two lenses is determined from the distribution function proposed by (Duquennoy and Mayor, 1991). We choose the semi-major axis s of the binary orbit of microlenses from the Öpik’s law where the distribution function for the primary-secondary distance is proportional to ρ(s) = dN/dss⁻¹ in the range of [0.6, 30] au.

2.3 Exoplanet parameters and their occurrence

In our simulations, we categorize the characteristic parameters of exoplanets into two primary groups: rocky planets and Jovian planets. According to the conventional planet formation theory, rocky planets are situated within the snow line of their parent star (Kennedy et al., 2006; Kennedy and Kenyon, 2008). The snowline of a star, also known as the frost line or ice line, refers to the distance from the star where volatile compounds, such as water, can condense into solid form due to the decrease in temperature. Beyond the snowline, the temperature drops low enough for these volatile compounds to freeze, forming icy grains or particles (Kennedy and Kenyon, 2008). This snowline can be expressed with the snowline of the Sun as

$R_{\text{SL},\star }=R_{{\text{SL}}_{\odot }}\times \frac{M_{\star }}{M_{\odot }},(3)$

where M_⋆ is the mass of the parent star (Gould et al., 2010). For Jovian planets, as they can migrate towards their parent star from distant orbits (as discussed by (Murray et al., 1998; Papaloizou and Terquem, 2005), we set the maximum distance from the parent star at 10 au. This range is consistent with observations from MOA microlensing studies, indicating at least one bound planet per star within this range, represented as a = 0.01–10 au (Sumi et al., 2011). We assume that the distribution of exoplanet semi-major axes follows the Öpik’s.

The planetary mass range in our simulation is 0.002–10M_J (Schlaufman, 2018). For planets with masses $>100M_{\oplus }$ orbiting host stars with masses greater than 0.6 solar masses, we utilized the correlation between giant planet occurrence and host star mass and metallicity as outlined by (Johnson et al., 2010; Fulton et al., 2021). Following the occurrence dependencies discussed in (Santerne et al., 2016; Wittenmyer et al., 2020; Fulton et al., 2021; Winn and Petigura, 2024), we adopted their result of planet occurrence. We summarized the frequencies of various exoplanet types from our simulation in Table 1.

Table 1

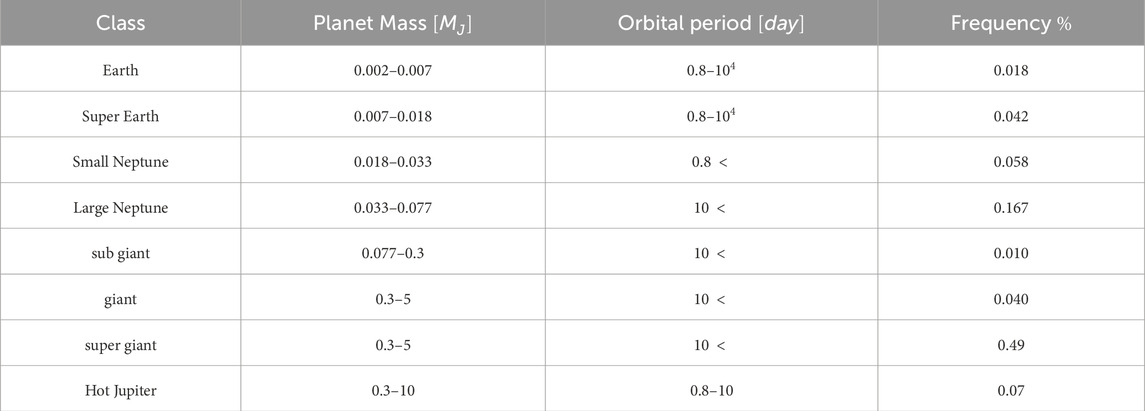
Table 1. Summary of the planet occurrence frequencies in our simulation, as a function of planet mass and period.

Generally, exoplanets exhibit a wide range of mass-radius relationships, reflecting their diverse compositions and evolutionary histories. However, a commonly used empirical relationship for estimating the radius of exoplanets based on their mass and incident flux is the following power-law scaling relation

$\frac{R_p}{R_{\oplus }}=1.78{\left(\frac{M_p}{M_{\oplus }}\right)}^{0.53}{\left(\frac{F}{erg{s}^{1}c{m}^2}\right)}^{0.03}\text{for}{M}_p<150M_{\oplus }$

$\frac{R_p}{R_{\oplus }}=2.45{\left(\frac{M_p}{M_{\oplus }}\right)}^{-0.039}{\left(\frac{F}{erg{s}^{1}c{m}^2}\right)}^{0.094}\text{for}{M}_p>150M_{\oplus }(4)$

where F is the bolometric incident flux from the parent star and can be calculated by

$F=\sigma T_{\text{eff}}^4\frac{R_{\star }^2}{a^2}\sqrt{\frac{1}{1-e^2}},(5)$

where R_⋆ is the stellar radius, T_eff is the effective stellar temperature, a is the semi-major axis, and e is the orbital eccentricity (Weiss et al., 2013).

2.4 Estimation of exoplanets radio emission

To simulate the detection process involving the Roman telescope for surveying microlensing events and subsequent follow-up observations with the SKA telescope, a model is necessary to estimate the emission of exoplanets based on their characteristics and the attributes of their parent stars. In general, the flux received from a planet contains thermal radiation due to its intrinsic temperature, as well as the reflection radiation from the parent star and radio emission if it has a magnetic field due to the electron cyclotron maser instability (ECMI) (Melrose and Dulk, 1982; Dulk, 1985). The thermal and reflection radiation can be readily computed from the planet’s characteristics and its parent star (Bagheri et al., 2019). The ECMI radiation is characterized by strong circular polarization and high anisotropy. ECMI stands out as the most efficient mechanism for radio emission, superseding other mechanisms like beam-plasma instabilities. Consequently, it plays a dominant role in the generation of radio emissions. This dominance is exemplified in the brightness of auroral radio emissions from planets in the Solar System, particularly Jupiter, which rival the intensity of solar radio bursts.

Based on observations of the magnetized Solar system planets, we know that all auroral radio emissions power is related to incident energy flux of the stellar wind (Zarka et al., 2001; Zarka, 2004; Zarka, 2007; Zarka et al., 2018). In all cases in our Solar System, about 2 × 10⁻³ of the electrons’ energy goes into radio waves (Zarka et al., 2018). Therefore, the average ECMI radiation can be linked to both the total power of the solar wind and the magnetic field strength of the planet, utilizing the RBL model (Zarka et al., 2001; Zarka, 2004; Zarka, 2007). The gyrofrequency can be expressed mathematically as:

$\nu =\frac{eB}{2\pi m}(6)$

where ν is the emitted pick frequency, e is the charge of the emitting particles (in this case, electrons), B is the magnetic field strength, and m is the mass of the emitting particles (electron mass in this case). This equation shows that the emitted frequency is directly proportional to the magnetic field strength of the planet. Therefore, observations of this emission type can provide an indirect means of measuring and classifying the planetary magnetic field. This quantification of the magnetic field gives us constraints on internal structure models and planetary rotation, informing us about the evolutionary history of the planet and host system (Hess et al., 2011).

The RBL model is frequently used to estimate the radio emission of extrasolar planets (Farrell et al., 1999; Zarka et al., 2001; Joseph et al., 2004; Zarka, 2007; Christensen, 2010). The simplicity of this model has some advantages, but it does not provide a complete picture of all processes involved, in particular for close-in exoplanets as discussed in (Bagheri et al., 2024b) (for Examples of studies that extend beyond the RBL model for calculating radio emission (Vidotto, 2017; Vidotto and Donati, 2017; Dong et al., 2018; Li et al., 2023)). However, the RBL model facilitates comparative analyses between the radio emissions of exoplanets and those observed within the Solar System, thereby enhancing our contextual understanding of planetary magnetospheric dynamics. This capacity for comparative analysis underscores the utility of the RBL model in advancing our comprehension of exoplanetary environments and their potential habitability while also serving as a foundation for future investigations into the broader astrophysical implications of planetary radio emissions. Thus, in this paper, we follow the approach outlined by (Joseph et al., 2004) to estimate the radio flux density of exoplanets. As described by (Farrell et al., 1999), the radio power from an exoplanet is related to the incident power of the stellar winds. Following (Farrell et al., 1999), the Jovian decametric component is considered at least partly related to the solar wind kinetic energy input and is used as the base power level to give

$\begin{array}{ll}\hfill P_{\mathit{rad}}& =4\times 10^{18}erg{s}^{-1}{\left(\frac{{\dot{M}}_{\mathit{ion}}}{10^{-14}{M}_{\odot }y{r}^{-1}}\right)}^{0.8}{\left(\frac{v_{\infty }}{400km{s}^{-1}}\right)}^2\hfill \\ \hfill & {\left(\frac{a}{5au}\right)}^{-1.6}{\left(\frac{\omega }{{\omega }_J}\right)}^{0.8}{\left(\frac{M_p}{M_J}\right)}^{1.33},\hfill \end{array}(7)$

where a is the semi-major axis of the planet’s orbit in au, $\dot{M}$ ion is the stellar ionized mass-loss rate, v_∞ is the terminal velocity of the stellar wind, and ω is the corotation speed. For the terminal velocity of stellar wind, we use

$v_{\infty }=0.75\times 617.5\times \sqrt{R_{\star }/M_{\star }},(8)$

where R_⋆ and M_⋆ are the host star radius and mass in solar radius and mass units (O’Gorman et al., 2018). Eq. 8 serves as a mere approximation for low-mass stars, however, recent study (Mesquita and Vidotto, 2020) indicates that the terminal velocity of M dwarf stellar winds either aligns well with predictions from Parker wind models, in which stellar winds are driven by radiation pressure mechanism, or exceed these model estimates. As a result, employing this equation may yield conservative estimations of stellar winds terminal velocity and the overall count of planets with detectable signals. Then, the radio flux density (S_ν) emitted by an exoplanet can be estimated using the following equation

$S_{\nu }=\frac{P_{\mathit{rad}}}{\mathrm{\Delta }\nu \mathrm{\Omega }{d}^2},(9)$

where P_rad is the total radio emission power of the exoplanet (7), d is the distance between the exoplanet and the observer, and ν is the frequency of the radio emission,

${\nu }_c=23.5\mathbf{MHz}\left(\frac{\omega }{{\omega }_J}\right){\left(\frac{M_p}{M_J}\right)}^{5/3}{\left(\frac{R_p}{R_J}\right)}^3,(10)$

where R_p is the planetary radius. Substituting (9) into (7) gives.

$\begin{array}{lll}{S}_{\nu }\hfill & =\hfill & 7.6\text{mJy}{\left(\frac{\omega }{{\omega }_J}\right)}^{-0.2}{\left(\frac{M_p}{M_J}\right)}^{-0.33}{\left(\frac{R_p}{R_J}\right)}^{-3}\hfill \\ \hfill & \hfill & {\left(\frac{\mathrm{\Omega }}{1.6sr}\right)}^{-1}{\left(\frac{d}{10pc}\right)}^{-2}\times {\left(\frac{a}{1au}\right)}^{-1.6}\hfill \end{array}(11)$

${\left(\frac{{\dot{M}}_{\mathit{ion}}}{10^{-11}{M}_{\odot }y{r}^{-1}}\right)}^{0.8}{\left(\frac{v_{\infty }}{100km{s}^{-1}}\right)}^2,(12)$

where ω_J, M_J, and R_J, are Jupiter’s corotation speed, mass, and radius and Ω is the beaming solid angle of the emission. In deriving this expression, we have followed (Farrell et al., 1999) and assumed that the planet will emit ECMI emission between the frequencies 0.3ν_c and ν_c, where ν_c is the maximum radiation frequency.

The planetary corotational speed (ω) is a crucial parameter in estimating radio flux from exoplanets. Exoplanets orbiting closely around their host stars experience significant tidal dissipation, resulting in considerably slowed corotation or complete tidal locking. This phenomenon has a profound impact on the production of auroral radiation due to the permanent orientation of one side of the planet towards the star, causing asymmetrical ionospheric conductance (Zarka et al., 2001; Seager and Hui, 2002). To consider the effect of tidal locking, we assume all the exoplanets with orbits $<0.1$ au are tidally locked, so the orbital period is equal to their corotation period. For all other exoplanets, we use the Darwin-Radau relation to relate corotation and oblateness (Murray and Dermott, 2000)

$\omega =\sqrt{\frac{fG{M}_p}{R_{eq}^2}\left[\frac{5}{2}{\left(1-1.5C\right)}^2+\frac{2}{5}\right]}(13)$

where C is 0.4 for rocky planets and for gas giant planets C = 0.25 (Hubbard, 1984). In this equation, f is the planet’s oblateness; the oblateness of planets refers to the degree to which a planet deviates from a perfect sphere, taking on a slightly flattened shape due to the centrifugal force generated by its corotation. This deviation from sphericity is more pronounced for rapidly rotating planets. The oblateness of a planet is quantified by

$f=\frac{R_{eq}-R_{\mathit{pole}}}{R_{eq}}(14)$

where R_eq and R_pole are the equatorial and polar radii of the planet. In our simulation, for the Jovian planet with orbital distance a > 0.1 au, we use the oblateness of Jupiter (f = 0.064), and for rocky planets, we use the Earth’s value which is f = 0.00335 (Barnes and Fortney, 2003). In Our simulation we also assume no planets rotate faster than Jupiter.

In this paper, the arrangement considered for the lens, source star, and planet entails that the observed light curve of microlensing events results from a combination of two distinct light curves: one originating from the source star and the other from the planet. Consequently, the final light curve results from merging these two light curves. To calculate host stars’ radio flux at the desired frequency, we use the relationship between the luminosity of the host star in the X band and the radio band. Stars emit X-rays primarily through high-energy processes such as magnetic reconnection events, coronal heating, and interactions between fast-moving charged particles and the stellar atmosphere. The X-ray luminosity of a star is thus influenced by its magnetic activity level, mass, age, and evolutionary stage. On the other hand, radio emission from stars is more associated with non-thermal processes, such as ECMI. The strength of radio emission depends on factors including the density and strength of the stellar magnetic field, the presence of energetic particles, and the efficiency of acceleration mechanisms. While there is no universal scaling relationship between X-ray and radio luminosity for all types of stars, correlations have been observed within specific stellar populations, such as active stars with strong magnetic fields or those undergoing rapid evolution. One can use empirical relationships based on observations for the radio luminosity of main sequence stars. One such relationship is the Gudel-Benz relation, which relates the X-ray and radio luminosities:

$L_X=L_R\times 10^{15\pm 1}(15)$

where L_X is the X-ray luminosity and L_R is the radio luminosity (Guedel and Benz, 1993). Notably, ECMI radiation exhibits strong circular polarization, whereas solar or stellar plasma radiation lacks polarization and occurs sporadically. Additionally, ECMI radiation is beamed anisotropically, resulting in significant modulation by the planetary rotation (Zarka et al., 2014). Therefore, polarization and temporal variations should enable the differentiation between stellar and exoplanetary radio emissions, as gravitational lensing does not change the polarization of the light rays.

2.4.1 Induced radio emission by exomoons

There are more than 200 moons in our Solar System, many of which orbit gas giants like Jupiter and Saturn. Despite significant efforts, the successful detection of exomoons remains elusive (Narang et al., 2023). If an exomoon resides within the magnetosphere of its host planet, it can influence the planet’s radio emissions by injecting plasma that accelerates electrons within the magnetosphere. A notable example is Io, a moon characterized by intense volcanic activity within Jupiter’s magnetosphere. This activity generates a tenuous atmosphere around Io (Lopes et al., 2007), contributing ions to Jupiter’s magnetosphere and generating a plasma (Reich et al., 2009). These ions in motion accelerate electrons, ultimately leading to the formation of an ECMI along the field lines, resulting in radio emissions known as Io-DAM (Cecconi, 2014; Crary, 1997; Mauk et al., 2001). Similar effects are observed with other Galilean moons and moons orbiting Saturn, such as Titan and Enceladus. Consequently, it is reasonable to anticipate moon-planet interactions in other stellar systems (Green et al., 2021). ECMI radio emissions from exomoon magnetosphere have not had a confirmed detection, but there are three candidate systems under study (Turner et al., 2021).

To simulate the induced radio emission by exomoons, one should know the probability of having a moon such as Io. The results of N-body simulations in (Sasaki et al., 2010; Heller et al., 2014) show that 80% of Jovian planets have moons with masses M_m/M_p ≈ 10^–5. However, stellar tidal forces serve to slow down a planet’s rotation and in conjunction with tidal migration, contribute to removing moons; At short a, migration of moons is significant and occurs quickly, which can lead to orbital instabilities (Sucerquia et al., 2020). This process limits the lifetimes of larger moons in extrasolar planetary systems (Barnes and O’brien, 2002). Therefore, in our simulation, we assume 80% of Jovian planets with masses M_p ≥ 0.1 M_J with a ≥ 0.1 au have one moon. So exoplanet with the semi-major axis less than 0.1 au do not have any moons, which in consistent with assuming they are tidally-locked.

Noyola et al. (2014) proposed that interactions akin to those between Io and Jupiter’s magnetosphere could also occur in exoplanet-moon pairs. The frequency of the moon-induced radio emission is slightly different,

${\nu }_{ci}={\nu }_c\times \sqrt{4-3\frac{R_p}{a_m}},(16)$

where ν_ci is the frequency of radio emission induced by a moon, such as Io, a_m is the same-major axis of the moon’s orbit, and ν_c can be obtained by (10). Eq. 16 is asymptotic, approaching a maximum value of ν_c as a_m becomes very large (Noyola et al., 2016). Assuming the plasma density of the exomoon is equal to the Io’s plasma density, the optimal distance for the exomoon to have the maximum of the induced radio emission can be obtained by (Noyola et al., 2014)

$a_{m_{\mathit{optimal}}}=5.4\times M_p^{0.3}.(17)$

Therefore, the total radio flux induced by a moon is

$S_{{\nu }_i}=\frac{2\pi \beta R_m^2{B}_m^2{V}_0}{{\mu }_0{\nu }_{ci}\mathrm{\Omega }{d}^2}\sqrt{\frac{{\rho }_m}{{\rho }_m+{\rho }_c}},(18)$

where d is the distance of star-planet-moon system to Earth, ρ_m is the moon’s plasma density, R_m is the moon’s radius, and β is the efficiency coefficient of converting Joule dissipation to radio waves (we assume β ≈ 1% as is in the Jupiter–Io system (Zarka et al., 2001)). B_m is the magnetic field affecting the exomoon, and so $B_m=B_p\times {(R_p/a_m)}^3$, where B_p is the magnetic field of the exoplanet at its poles. The plasma speed, V₀, is computed assuming it corotates with the planet’s magnetic field. Therefore, $V_0={\omega }_p\times a_m-\sqrt{G{M}_p/a_m}$, where G is the gravitational constant, M_pis the planet’s mass, and ω_p is the planet’s corotation speed. Finally, ρ_c is the critical density which is defined as ${\rho }_c={\mu }_0^{-1}{(B_m/V_0)}^2$ (Noyola et al., 2014). In our simulation, we assume IO’s plasma density and IO’s radius for ρ_m and R_m. We also assume Ω = 0.2 (Noyola et al., 2014). In our simulation, the induced radio emission by an Io-like moon accounts for a maximum of 0.2% of the total radiation emitted by the exoplanets.

2.5 Observation strategy

The NASA Roman Space Telescope is a next-generation space observatory designed to investigate various astrophysical phenomena using infrared observations. Named in honor of the astronomer Nancy Grace Roman, often regarded as the “Mother of Hubble” for her pivotal role in the development of the Hubble Space Telescope (Roman, 2019), this advanced instrument is slated to launch in the mid-2020s. With its wide field of view, the telescope is designed to conduct large-scale surveys to explore dark energy, dark matter, and the formation and evolution of galaxies with unprecedented detail (Rose et al., 2021). The Roman Space Telescope will also be crucial in advancing our knowledge of exoplanets using microlensing events. Roman W 149 filter (0.9–2 μm) will have a significantly low detection threshold, with a zero-point magnitude of 27.61. The microlensing survey of Roman will monitor 1.97deg² of the Galactic bulge (in the direction of b = −1.5 and l = 0.5 in the Galactic coordinate) with 15-min cadence, over six 72-day per season (Spiegel et al., 2005), potentially detecting thousands of exoplanets via the perturbations that they produce on the microlensing light curves (Bagheri et al., 2019). Since microlensing events usually have a duration of a few days up to a few weeks, we propose to use the Roman telescope as a survey observer to detect a microlensing event and then alert that event to a ground-based radio telescope for a follow-up observation of that microlensing event in the radio band. The most suitable ground-based telescope to detect planetary radio emission is the Square Kilometre Array (SKA) telescope. As the world’s largest radio telescope, the SKA comprises two arrays: SKA1-Low, optimized for low-frequency observations between 50 MHz and 350 MHz, and SKA1-Mid, designed for mid-frequency observations between 350 MHz and 14 GHz. The vast collecting area of the SKA, totaling one square kilometer when fully operational, enables it to detect faint radio signals from cosmic phenomena spanning a wide range of scales, from nearby planets to distant galaxies and beyond. Furthermore, the SKA’s innovative design incorporates advanced signal processing techniques and data analysis algorithms, maximizing its scientific output while minimizing data volumes and processing requirements.

2.6 Detectablity of the planetary radio signal

The detectablity of the radio signal of exoplanets depends on, first, the detection of the microlensing event by the Roman telescope, and, second, the frequency and the intensity of the radio emission of the star-planet system. To address the first condition, we calculate the host star and planet magnitude in Roman’s W149 filter. For the flux received from the host stars, we consider both the distance-dependent effects of the source stars and the reddening of their apparent magnitudes due to interstellar dust. Using the host stars’ position and stellar type, we estimate the extinction caused by interstellar dust along the line of sight, using the comprehensive 3D extinction map provided by (Marshall et al., 2006). We use the relationships outlined in (Nishiyama et al., 2008; Nishiyama et al., 2009) to convert the extinction values from V bands to the band of W149 filter (Bagheri et al., 2019; Penny et al., 2019). The flux received from a planet comprises both thermal radiation originating from the planet’s intrinsic temperature and reflected radiation from its parent star. The planet’s temperature can be calculated by assuming that the planet’s thermal emission adheres to blackbody radiation principles (López-Morales and Seager, 2007). This calculation incorporates the absorption of radiation from the parent star by the planet, which is then re-emitted following Boltzmann’s law,

$T_p=T_{\mathit{eff}}\sqrt{\frac{R_{\star }}{a}}{\left[f\times \left(1-A_B\right)\right]}^{1/4}(19)$

where T_p indicates the temperature of the planet, A_B denotes the albedo (0.15 and 0.52 for rocky and Jovian planets), while f characterizes the proportion of re-radiated energy absorbed by the planet (Harrington et al., 2006; Knutson et al., 2007). Since hot Jupiters are the most frequently detected, we adopt a value of 2/3 for f across all planets. Assuming blackbody radiation, the thermal flux (F_th) at the specified frequency ν can be expressed using Planck’s law as follows:

$I\left(\nu ,T_p\right)=\frac{2h{\nu }^3}{c^2}\frac{1}{\exp \left(h\nu /k{T}_p\right)-1}(20)$

where, I(ν, T_p) denotes the emitted power per unit area of the emitting surface, per unit solid angle, and unit frequency. Integrating it across the energy range of the W149 filter and over a hemisphere yields the thermal flux of the planet as observed by Roman. The flux of the planet resulting from the reflection (F_ref) of the parent star’s light is determined by

$F_{\mathit{ref}}=A_{g}g\left(\mathrm{\Phi }\right)F_{\star }\left(\frac{R_p}{a}\right)(21)$

where g(Φ) denotes the fraction of the illuminated portion of the planet visible to the observer, A_g represents the geometric albedo. We utilize a geometric albedo formula: A_g = 2/3 A_B (Bagheri et al., 2019). While this relationship may not hold true for all phase angles, its alteration does not significantly impact results. This is because the thermal radiation emitted by planets is much weaker than the flux of host stars in the Roman W149 filter. Thus, any changes in this relationship would only affect the total flux received by the Roman telescope at the order of 10^–4 at most. Consequently, the overall flux received from the planet (F_p) can be calculated as the combined sum of the thermal flux and the reflection flux. At the final stage we add realistic noise. The total noise consists of the intrinsic Poisson fluctuation in the flux received from the microlensing event in a single exposure, the intrinsic Poisson fluctuation within the point spread function (PSF) representing the background sky flux in a single exposure, the read-out and dark noise (Bagheri et al., 2019). Finally, we determine the range within which the noisy signal exhibits magnitudes below the zero-point magnitude of Roman and above the saturation magnitude of 14.8 (Penny et al., 2019).

For the follow-up observation by the SKA, we consider the SKA1-low and SKA1-mid frequency ranges up to 890 MHz. The image noise is given by,

$\sigma =S_D\frac{SEFD}{{\eta }_S\sqrt{{\eta }_{\mathit{pol}}\nu \mathrm{\Delta }\tau }},(22)$

where S_D = 2.5 is a degradation factor relative to the natural array sensitivity for the specific target Gaussian FWHM resolution of the image, η_S = 0.9 is a system efficiency that takes account of the finite correlator efficiency, and η_pol = 2 is the number of contributing polarizations and for SKA1 with orthogonal linear polarizations (Braun et al., 2019). The imaging sensitivity for SKA1-Low and SKA1-mid up to 890 MHz is listed in Table 2 by assuming a continuum observation with fractional bandwidth of Δν/ν_c ≈ 0.3, together with an integration time Δτ = 1 h.

Table 2

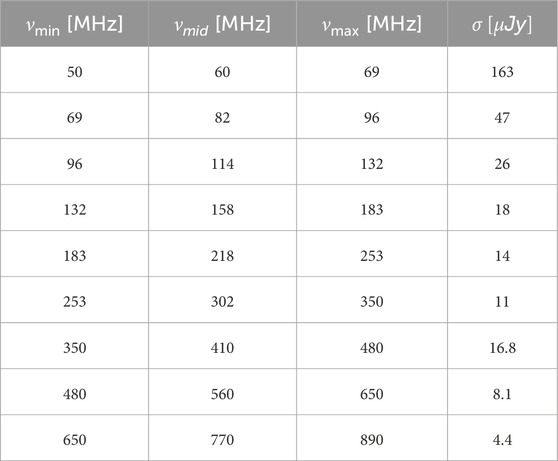
Table 2. Image sensitivity of SKA1-Low and SKA1-mid within the indicated frequency bands for continuum observations (Braun et al., 2019).

We use the SKA image sensitivity for different ranges of frequencies as summarized in Table 2. Therefore, any event with flux density greater than the SKA sensitivity for at least 4 h of imaging is considered a detected event.

3 Results

We simulate 150,000 single-lens and binary-lens microlensing events. Our Monte Carlo simulations indicate the likelihood of detecting radio emission of rocky planets using either single-lens or binary-lens configurations is exceedingly low with the SKA telescope. Consequently, Jovian planets exhibit the highest detection probabilities in both scenarios. This outcome primarily stems from their stronger magnetic field and higher frequency of radio emission relative to rocky planets, resulting in a substantial portion of their radiation falling within the SKA sensitivity. Simulations of Roman-SKA data predict, under the assumption of single-lens configuration, that the number of detecting a Jovian planet with orbital periods of 2 days–10 years is about 3.54%. For the binary-lens simulation, this number increases to 8.25% due to the high magnification of caustic crossings.

Figure 2 shows our simulation’s distributions of planetary parameters. Exoplanets with detected radio fluxes are in orange. As depicted in Figures 2A, it is notable that the majority of exoplanets exhibiting detectable signals are situated at orbital distances lower than two au. However, for planets with higher masses, the orbital distance can extend up to eight au. The planetary radio flux in terms of magnification of the microlensing events is shown in Figures 2B. Exoplanets within the shaded region exhibit emission frequencies below 50 MHz, rendering their signals undetectable despite their radio emissions being of high intensity and possessing a significant magnification factor during microlensing events. Figures 2D,E represent the distance of the star-planet system relative to the exoplanet mass and the magnification of the microlensing events. Notably, the range extends up to 10 kpc for exoplanets with detectable signals, underscoring the importance of this observation method. These exoplanets are beyond the reach of current technologies for detection in any other wavelength bands using conventional methods. Identifying such star-planet systems can enhance our understanding of planet formation rates within the galactic bulge and facilitate the detection of extragalactic exoplanets.

Figure 2

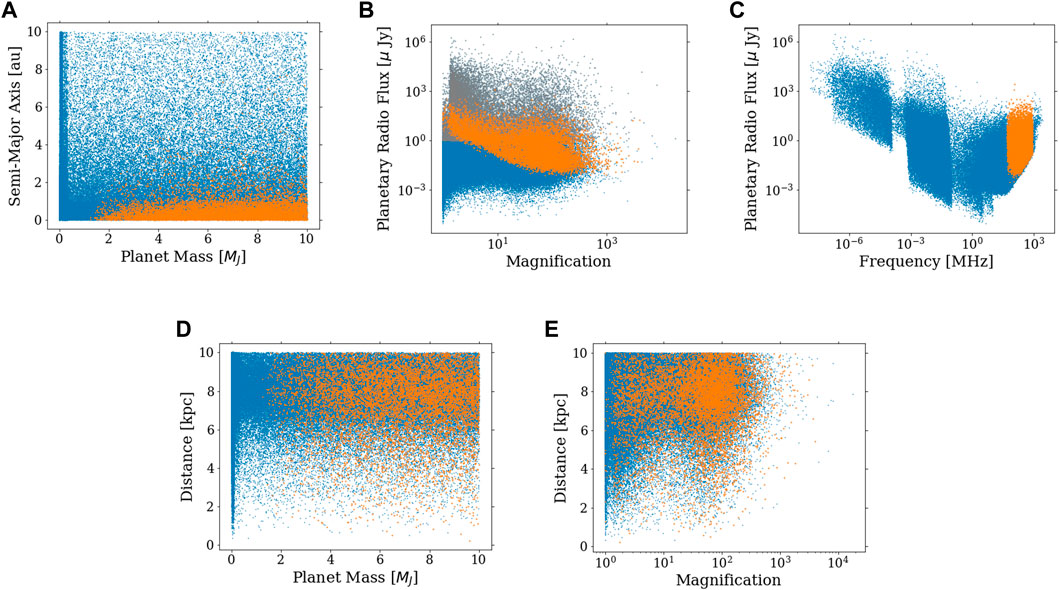
Figure 2. Characteristics of the exoplanets within the simulated event. Exoplanets exhibiting detectable radio signals are highlighted in orange; (A) distribution of semi-major axis as a function of planetary mass, (B) planetary radio flux vs. magnification of the microlensing events, (C) planetary radio flux as a function of the frequency of the planetary radio emissions, (D) distance of the star-planet system vs. planetary mass, and (E) distance of the star-planet system vs. magnification of the microlensing events.

The detection efficiency in terms of mass and semi-major axis of the exoplanets is illustrated in Figure 3. Detected planets exhibit masses ranging from M_p = 1–10M_J and semi-major axes spanning from a = 0.01 to 10 au.

Figure 3

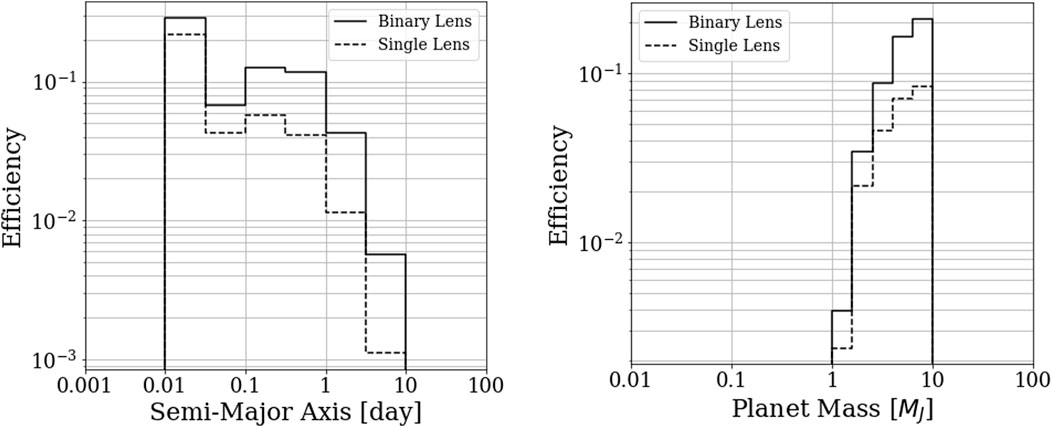
Figure 3. The detection efficiency of the planetary radio emission in terms of the mass and semi-major axis of the exoplanet in our Monte Carlo simulation.

We conducted simulations targeting coordinates l = 0.5° and b = −1.5°. In this direction, as reported by (Penny et al., 2019), the estimated number of source stars detectable by the Roman telescope with magnitudes below 25 is 240 × 10⁶. Hence, the number of microlensing events that could be deteted via Roman observation can be given by:

$N=\frac{2}{\pi }{T}_{\mathit{obs}}\times N_{\star }\times <ϵ\left(t_E\right)>\tau (23)$

where T_obs is the observational time, N_⋆ is the number of background stars detectable by Roman, ϵ(t_E) is the Roman efficiency for detecting microlensing events with the duration of t_E, and τ is the optical depth (Bagheri et al., 2019). The optical depth, averaged over the distances of the source stars, is τ = 2.4 × 10⁻⁶ (Mróz et al., 2019), and our simulation yields an average value of $<ϵ/t_E>=0.035$. Therefore, around 27,000 microlensing events can be detected by Roman observation (Penny et al., 2019). Consequently, approximately 1,317 exoplanets could be detected with Roman-SKA observations toward the Galactic bulge. However, it may not be feasible to follow up on all Roman’s detected microlensing events; nonetheless, a 10%–20% follow-up of these events could significantly impact exoplanet sciences and the measurement of exoplanetary magnetic fields. These findings are summarized in Table 3.

Table 3

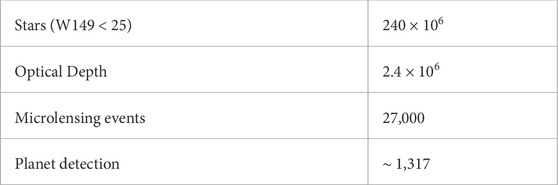
Table 3. Estimated number of detectable planetary radio emissions in the Roman-SKA follow-up observation.

4 Discussion

Our comprehension of planetary magnetic fields remains largely confined to the Solar System. Expanding our knowledge and observation of exoplanetary magnetic fields could provide valuable insights into their internal compositions and dynamics, which are otherwise challenging to ascertain. The detection of radio emissions from confirmed exoplanets has been investigated in multiple studies (e.g., Li et al., 2023; Bagheri et al., 2024a). In this study, we investigate an alternative approach to detecting exoplanets through their radio emissions magnified by microlensing events. Our findings reveal that the planetary radio emissions of approximately 5% of microlensing events could be detected through follow-up observations with Roman-SKA (equivalent to $\sim 8\%$ for binary-lens and $\sim 3.5\%$ for single-lens events). This finding gains significance when considering that, to date, only 210 exoplanets have been detected via microlensing events¹. These detections primarily occurred due to caustic crossings in binary-lens events, making follow-up observations of these planets nearly impracticable. In contrast, we consider exoplanets as companions within the source system of microlensing events, enabling us to conduct follow-up observations on the star-planet system.

Our results underscore the potential of infrared-radio follow-up observations to enhance the rates of direct exoplanet detections while yielding valuable insights into the magnetic fields and internal structure of exoplanets. The observation strategy outlined in this study demonstrates heightened sensitivity to detecting the radio emissions of giant and close-in exoplanets. Observing the radio emissions of close-in exoplanets broadens our comprehension of planetary responses to their space environment and evolutionary trajectories. Hot Jupiters’ magnetospheres serve as compelling subjects for study, highlighting the intricate complex interplay between magnetic fields, stellar wind, and atmospheric escape processes. Observing radio emissions of close-in exoplanets and further investigations into these magnetospheric properties will deepen our understanding of exoplanetary systems and their diverse environments. Such insights will significantly contribute to our comprehension of planet formation, migration, and the potential habitability of exoplanets.

The outcomes of this project are important for the prospects of Exoplanet radio emission detection by the contemporary and planned surveys as well as the next-generation of Radio telescopes. In a wider view, the results of this work pave the way toward actual infrared-radio follow-up observations of exoplanets/exomoons using the method introduced in this study. The knowledge of the magnetic field and the magnetospheric emissions of exoplanets are considered a science frontier for the next decade, as highlighted in the Origins, Worlds, and Life Planetary Science & Astrobiology Decadal Survey report. Two Priority Science Question Topics identified in this survey report incorporate aspects of planetary magnetic fields and their interplay with the solar wind. These are identified as Q6: “Solid body atmospheres, exospheres, magnetospheres, and climate evolution” and Q12.7: “Exoplanets, Giant planet structure and evolution.”(National Academies of Sciences Engineering Medicine, 2022).

We acknowledge the use of the Cheyenne supercomputer at the National Center for Atmospheric Research (NCAR) (Computational and Information System Laboratory, 2017) and Texas Advanced Computing Center (TACC) supercomputing resources. We acknowledge the support of the US National Science Foundation (NSF) under Grant No. 2138122.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

FB: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. RL: Supervision, Writing–review and editing. AS: Methodology, Writing–review and editing, Formal Analysis.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. We acknowledge the support of the US National Science Foundation (NSF) under Grant No. 2138122.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹NASA Exoplanet Archive.

References

Bagheri, F., Garga, A., and Lopez, R. E. (2024a). Exploring radio emissions from confirmed exoplanets using SKA. arXiv e-prints, arXiv:2404.14468. doi:10.48550/arXiv.2404.14468

CrossRef Full Text | Google Scholar

Bagheri, F., Lopez, R. E., and Pham, K. (2024b). A fresh look into the interaction of exoplanets magnetosphere with stellar winds using MHD simulations. arXiv e-prints, arXiv:2404.14377. doi:10.48550/arXiv.2404.14377

CrossRef Full Text | Google Scholar

Bagheri, F., Sajadian, S., and Rahvar, S. (2019). Detection of exoplanet as a binary source of microlensing events in wfirst survey. Mon. Notices R. Astronomical Soc. 490, 1581–1587. doi:10.1093/mnras/stz2682

CrossRef Full Text | Google Scholar

Barnes, J. W., and Fortney, J. J. (2003). Measuring the oblateness and rotation of transiting extrasolar giant planets. Astrophysical J. 588, 545–556. doi:10.1086/373893

CrossRef Full Text | Google Scholar

Barnes, J. W., and O’brien, D. (2002). Stability of satellites around close-in extrasolar giant planets. Astrophysical J. 575, 1087–1093. doi:10.1086/341477

CrossRef Full Text | Google Scholar

Bigg, E. (1964). Influence of the satellite i o on jupiter’s decametric emission. Nature 203, 1008–1010. doi:10.1038/2031008a0

CrossRef Full Text | Google Scholar

Braun, R., Bonaldi, A., Bourke, T., Keane, E., and Wagg, J. (2019). Anticipated performance of the square kilometre array–phase 1 (ska1). arXiv preprint arXiv:1912.12699.

Google Scholar

Cauley, P. W., Shkolnik, E. L., Llama, J., and Lanza, A. F. (2019). Magnetic field strengths of hot jupiters from signals of star–planet interactions. Nat. Astron. 3, 1128–1134. doi:10.1038/s41550-019-0840-x

CrossRef Full Text | Google Scholar

Cecconi, B. (2014). Goniopolarimetry: space-borne radio astronomy with imaging capabilities. Comptes Rendus Phys. 15, 441–447. doi:10.1016/j.crhy.2014.02.005

CrossRef Full Text | Google Scholar

Christensen, U. R. (2010). Dynamo scaling laws and applications to the planets. Space Sci. Rev. 152, 565–590. doi:10.1007/978-1-4419-5901-0_17

CrossRef Full Text | Google Scholar

Cockell, C. S., Bush, T., Bryce, C., Direito, S., Fox-Powell, M., Harrison, J. P., et al. (2016). Habitability: a review. Astrobiology 16, 89–117. doi:10.1089/ast.2015.1295

PubMed Abstract | CrossRef Full Text | Google Scholar

Computational and Information System Laboratory (2017). Cheyenne: hpe/sgi ice xa system (climate simulation laboratory).

Google Scholar

Crary, F. (1997). On the generation of an electron beam by io. J. Geophys. Res. Space Phys. 102, 37–49. doi:10.1029/96ja02409

CrossRef Full Text | Google Scholar

Daněk, K., and Heyrovskỳ, D. (2019). Triple-lens gravitational microlensing: critical curves for arbitrary spatial configuration. Astrophysical J. 880, 72. doi:10.3847/1538-4357/ab2982

CrossRef Full Text | Google Scholar

Dong, C., Jin, M., Lingam, M., Airapetian, V. S., Ma, Y., and van der Holst, B. (2018). Atmospheric escape from the trappist-1 planets and implications for habitability. Proc. Natl. Acad. Sci. 115, 260–265. doi:10.1073/pnas.1708010115

PubMed Abstract | CrossRef Full Text | Google Scholar

Dulk, G. A. (1985). Radio emission from the sun and stars. Annu. Rev. astronomy astrophysics 23, 169–224. doi:10.1146/annurev.astro.23.1.169

CrossRef Full Text | Google Scholar

Duquennoy, A., and Mayor, M. (1991). Multiplicity among solar-type stars in the solar neighbourhood. ii-distribution of the orbital elements in an unbiased sample. Astronomy Astrophysics 248, 485–524.

Google Scholar

Farrell, W., Desch, M., and Zarka, P. (1999). On the possibility of coherent cyclotron emission from extrasolar planets. J. Geophys. Res. Planets 104, 14025–14032. doi:10.1029/1998je900050

CrossRef Full Text | Google Scholar

Foster, G., Poppenhaeger, K., Alvarado-Gómez, J., and Schmitt, J. (2020). The corona of gj 1151 in the context of star–planet interaction. Mon. Notices R. Astronomical Soc. 497, 1015–1019. doi:10.1093/mnras/staa1982

CrossRef Full Text | Google Scholar

Fulton, B. J., Rosenthal, L. J., Hirsch, L. A., Isaacson, H., Howard, A. W., Dedrick, C. M., et al. (2021). California legacy survey. ii. occurrence of giant planets beyond the ice line. Astrophysical J. Suppl. Ser. 255, 14. doi:10.3847/1538-4365/abfcc1

CrossRef Full Text | Google Scholar

Gardner, E., Debattista, V. P., Robin, A. C., Vásquez, S., and Zoccali, M. (2014). N-body simulation insights into the x-shaped bulge of the milky way: kinematics and distance to the galactic centre. Mon. Notices R. Astronomical Soc. 438, 3275–3290. doi:10.1093/mnras/stt2430

CrossRef Full Text | Google Scholar

Gaudi, B. S. (2012). Microlensing surveys for exoplanets. Annu. Rev. Astronomy Astrophysics 50, 411–453. doi:10.1146/annurev-astro-081811-125518

CrossRef Full Text | Google Scholar

Gould, A., Dong, S., Gaudi, B., Udalski, A., Bond, I., Greenhill, J., et al. (2010). Frequency of solar-like systems and of ice and gas giants beyond the snow line from high-magnification microlensing events in 2005–2008. Astrophysical J. 720, 1073–1089. doi:10.1088/0004-637x/720/2/1073

CrossRef Full Text | Google Scholar

Green, J., Boardsen, S., and Dong, C. (2021). Magnetospheres of terrestrial exoplanets and exomoons: implications for habitability and detection. Astrophysical J. Lett. 907, L45. doi:10.3847/2041-8213/abd93a

CrossRef Full Text | Google Scholar

Guedel, M., and Benz, A. O. (1993). X-ray/microwave relation of different types of active stars. Astrophysical J. 405, L63–L66. doi:10.1086/186766

CrossRef Full Text | Google Scholar

Guyon, O., Pluzhnik, E. A., Galicher, R., Martinache, F., Ridgway, S. T., and Woodruff, R. A. (2005). Exoplanet imaging with a phase-induced amplitude apodization coronagraph. i. principle. Astrophysical J. 622, 744–758. doi:10.1086/427771

CrossRef Full Text | Google Scholar

Harrington, J., Hansen, B. M., Luszcz, S. H., Seager, S., Deming, D., Menou, K., et al. (2006). The phase-dependent infrared brightness of the extrasolar planet ʊ andromedae b. Science 314, 623–626. doi:10.1126/science.1133904

PubMed Abstract | CrossRef Full Text | Google Scholar

Heller, R., Williams, D., Kipping, D., Limbach, M. A., Turner, E., Greenberg, R., et al. (2014). Formation, habitability, and detection of extrasolar moons. Astrobiology 14, 798–835. doi:10.1089/ast.2014.1147

PubMed Abstract | CrossRef Full Text | Google Scholar

Hess, S. L., Bonfond, B., Zarka, P., and Grodent, D. (2011). Model of the jovian magnetic field topology constrained by the io auroral emissions. J. Geophys. Res. Space Phys. 116. doi:10.1029/2010ja016262

CrossRef Full Text | Google Scholar

Hubbard, W. B. (1984). Planetary interiors. New York: Van Nostrand Reinhold.

Google Scholar

Johnson, J. A., Aller, K. M., Howard, A. W., and Crepp, J. R. (2010). Giant planet occurrence in the stellar mass-metallicity plane. Publ. Astronomical Soc. Pac. 122, 905–915. doi:10.1086/655775

CrossRef Full Text | Google Scholar

Joseph, T., Lazio, W., Farrell, W., Dietrick, J., Greenlees, E., Hogan, E., et al. (2004). The radiometric bode’s law and extrasolar planets. Astrophysical J. 612, 511–518. doi:10.1086/422449

CrossRef Full Text | Google Scholar

Kane, S. R. (2021). Planetary habitability. United Kingdom: IOP Publishing.

Google Scholar

Kennedy, G. M., and Kenyon, S. J. (2008). Planet formation around stars of various masses: hot super-earths. Astrophysical J. 682, 1264–1276. doi:10.1086/589436

CrossRef Full Text | Google Scholar

Kennedy, G. M., Kenyon, S. J., and Bromley, B. C. (2006). Planet formation around low-mass stars: the moving snow line and super-earths. Astrophysical J. 650, L139–L142. doi:10.1086/508882

CrossRef Full Text | Google Scholar

Knutson, H. A., Charbonneau, D., Allen, L. E., Fortney, J. J., Agol, E., Cowan, N. B., et al. (2007). A map of the day–night contrast of the extrasolar planet hd 189733b. Nature 447, 183–186. doi:10.1038/nature05782

PubMed Abstract | CrossRef Full Text | Google Scholar

Knutson, H. A., Fulton, B. J., Montet, B. T., Kao, M., Ngo, H., Howard, A. W., et al. (2014). Friends of hot jupiters. i. a radial velocity search for massive, long-period companions to close-in gas giant planets. Astrophysical J. 785, 126. doi:10.1088/0004-637x/785/2/126

CrossRef Full Text | Google Scholar

Lammer, H., Bredehöft, J., Coustenis, A., Khodachenko, M., Kaltenegger, L., Grasset, O., et al. (2009). What makes a planet habitable? Astronomy astrophysics Rev. 17, 181–249. doi:10.1007/s00159-009-0019-z

CrossRef Full Text | Google Scholar

Lazio, J., Hallinan, G., Airapetian, V., Brain, D., Dong, C., Driscoll, P., et al. (2018). Magnetic fields of extrasolar planets: planetary interiors and habitability. arXiv preprint arXiv:1803.06487.

Google Scholar

Li, B., Zhang, L., Su, T., Han, X. L., Misra, P., and Long, L. (2023). Statistical and radio analysis of exoplanets and their host stars. Universe 9, 475. doi:10.3390/universe9110475

CrossRef Full Text | Google Scholar

Lingam, M., and Loeb, A. (2021). Life in the cosmos: from biosignatures to technosignatures. United States: Harvard University Press.

Google Scholar

Lopes, R. M., Spencer, J. R., Perry, J., Lopes, R. M., Spencer, J. R., and Alexander, C. (2007). “A summary of the galileo mission and its observations of io,” in Io after galileo: a new view of Jupiter’s volcanic moon (Springer), 35–59.

Google Scholar

López-Morales, M., and Seager, S. (2007). Thermal emission from transiting very hot jupiters: prospects for ground-based detection at optical wavelengths. Astrophysical J. 667, L191–L194. doi:10.1086/522118

CrossRef Full Text | Google Scholar

Mandel, K., and Agol, E. (2002). Analytic light curves for planetary transit searches. Astrophysical J. 580, L171–L175. doi:10.1086/345520

CrossRef Full Text | Google Scholar

Marshall, D. J., Robin, A., Reylé, C., Schultheis, M., and Picaud, S. (2006). Modelling the galactic interstellar extinction distribution in three dimensions. Astronomy Astrophysics 453, 635–651. doi:10.1051/0004-6361:20053842

CrossRef Full Text | Google Scholar

Mauk, B., Williams, D., and Eviatar, A. (2001). Understanding io’s space environment interaction: recent energetic electron measurements from galileo. J. Geophys. Res. Space Phys. 106, 26195–26208. doi:10.1029/2000ja002508

CrossRef Full Text | Google Scholar

Melrose, D., and Dulk, G. A. (1982). Electron-cyclotron masers as the source of certain solar and stellar radio bursts. Astrophysical J. 259, 844–858. doi:10.1086/160219

CrossRef Full Text | Google Scholar

Mesquita, A. L., and Vidotto, A. A. (2020). Global trends in winds of m dwarf stars. Mon. Notices R. Astronomical Soc. 494, 1297–1307. doi:10.1093/mnras/staa798

CrossRef Full Text | Google Scholar

Moniez, M., Sajadian, S., Karami, M., Rahvar, S., and Ansari, R. (2017). Understanding eros2 observations toward the spiral arms within a classical galactic model framework. Astronomy Astrophysics 604, A124. doi:10.1051/0004-6361/201730488

CrossRef Full Text | Google Scholar

Mróz, P., Udalski, A., Skowron, J., Szymański, M. K., Soszyński, I., Wyrzykowski, Ł., et al. (2019). Microlensing optical depth and event rate toward the galactic bulge from 8 yr of ogle-iv observations. Astrophysical J. Suppl. Ser. 244, 29. doi:10.3847/1538-4365/ab426b

CrossRef Full Text | Google Scholar

Murphy, T., Bell, M. E., Kaplan, D. L., Gaensler, B., Offringa, A. R., Lenc, E., et al. (2015). Limits on low-frequency radio emission from southern exoplanets with the murchison widefield array. Mon. Notices R. Astronomical Soc. 446, 2560–2565. doi:10.1093/mnras/stu2253

CrossRef Full Text | Google Scholar

Murray, C. D., and Dermott, S. F. (2000). Solar system dynamics. Cambridge, England: Cambridge University Press.

Google Scholar

Murray, N., Hansen, B., Holman, M., and Tremaine, S. (1998). Migrating planets. Science 279, 69–72. doi:10.1126/science.279.5347.69

PubMed Abstract | CrossRef Full Text | Google Scholar

Narang, M., Oza, A. V., Hakim, K., Manoj, P., Tyagi, H., Banerjee, B., et al. (2023). Ugmrt observations of the hot-saturn wasp-69b: radio-loud exoplanet–exomoon survey ii (rlees ii). Mon. Notices R. Astronomical Soc. 522, 1662–1668. doi:10.1093/mnras/stad1027

CrossRef Full Text | Google Scholar

National Academies of Sciences Engineering Medicine (2022). Origins, worlds, and life: a decadal strategy for planetary science and astrobiology 2023-2032.

Google Scholar

Nishiyama, S., Nagata, T., Tamura, M., Kandori, R., Hatano, H., Sato, S., et al. (2008). The interstellar extinction law toward the galactic center. II.V,J,H, andK_<i>s</i>Bands. Astrophysical J. 680, 1174–1179. doi:10.1086/587791

CrossRef Full Text | Google Scholar

Nishiyama, S., Tamura, M., Hatano, H., Kato, D., Tanabé, T., Sugitani, K., et al. (2009). Interstellar extinction law toward the galactic center iii: J, h, ks bands in the 2mass and the mko systems, and 3.6, 4.5, 5.8, 8.0 μm in the spitzer/irac system. Astrophysical J. 696, 1407–1417. doi:10.1088/0004-637x/696/2/1407

CrossRef Full Text | Google Scholar

Noyola, J., Satyal, S., and Musielak, Z. (2016). On the radio detection of multiple-exomoon systems due to plasma torus sharing. Astrophysical J. 821, 97. doi:10.3847/0004-637x/821/2/97

CrossRef Full Text | Google Scholar

Noyola, J. P., Satyal, S., and Musielak, Z. E. (2014). Detection of exomoons through observation of radio emissions. Astrophysical J. 791, 25. doi:10.1088/0004-637x/791/1/25

CrossRef Full Text | Google Scholar

O’Gorman, E., Coughlan, C. P., Vlemmings, W., Varenius, E., Sirothia, S., Ray, T. P., et al. (2018). A search for radio emission from exoplanets around evolved stars. Astronomy Astrophysics 612, A52. doi:10.1051/0004-6361/201731965

CrossRef Full Text | Google Scholar

Papaloizou, J. C., and Terquem, C. (2005). Planet formation and migration. Rep. Prog. Phys. 69, 119–180. doi:10.1088/0034-4885/69/1/r03

CrossRef Full Text | Google Scholar

Penny, M. T., Gaudi, B. S., Kerins, E., Rattenbury, N. J., Mao, S., Robin, A. C., et al. (2019). Predictions of the wfirst microlensing survey. i. bound planet detection rates. Astrophysical J. Suppl. Ser. 241 (3), 3. doi:10.3847/1538-4365/aafb69

CrossRef Full Text | Google Scholar

Reich, W., Reich, P., Strassmeier, K., Kosovichev, A., and Beckman, J. (2009). Cosmic magnetic fields: from planets, to stars and galaxies. IAU Symp. 259, 603.

Google Scholar

Robin, A. C., Reylé, C., Derrière, S., and Picaud, S. (2003). A synthetic view on structure and evolution of the milky way. Astronomy Astrophysics 409, 523–540. doi:10.1051/0004-6361:20031117

CrossRef Full Text | Google Scholar

Roman, N. G. (2019). Nancy grace roman and the dawn of space astronomy. Annu. Rev. Astronomy Astrophysics 57, 1–34. doi:10.1146/annurev-astro-091918-104446

CrossRef Full Text | Google Scholar

Rose, B., Baltay, C., Hounsell, R., Macias, P., Rubin, D., Scolnic, D., et al. (2021). A reference survey for supernova cosmology with the nancy grace roman space telescope. arXiv preprint arXiv:2111.03081.

Google Scholar

Santerne, A., Moutou, C., Tsantaki, M., Bouchy, F., Hébrard, G., Adibekyan, V., et al. (2016). SOPHIE velocimetry ofKeplertransit candidates: XVII. The physical properties of giant exoplanets within 400 days of period⋆⋆⋆. Astronomy Astrophysics 587, A64. doi:10.1051/0004-6361/201527329

CrossRef Full Text | Google Scholar

Sasaki, T., Stewart, G. R., and Ida, S. (2010). Origin of the different architectures of the jovian and saturnian satellite systems. Astrophysical J. 714, 1052–1064. doi:10.1088/0004-637x/714/2/1052

CrossRef Full Text | Google Scholar

Schlaufman, K. C. (2018). Evidence of an upper bound on the masses of planets and its implications for giant planet formation. Astrophysical J. 853, 37. doi:10.3847/1538-4357/aa961c

CrossRef Full Text | Google Scholar

Seager, S., and Hui, L. (2002). Constraining the rotation rate of transiting extrasolar planets by oblateness measurements. Astrophysical J. 574, 1004–1010. doi:10.1086/340994

CrossRef Full Text | Google Scholar

Spergel, D., Gehrels, N., Baltay, C., Bennett, D., Breckinridge, J., Donahue, M., et al. (2015). Wide-field infrarred survey telescope-astrophysics focused telescope assets wfirst-afta 2015 report. arXiv preprint arXiv:1503.03757.

Google Scholar

Spiegel, D. S., Zamojski, M., Gersch, A., Donovan, J., and Haiman, Z. (2005). Can we probe the atmospheric composition of an extrasolar planet from its reflection spectrum in a high-magnification microlensing event? Astrophysical J. 628, 478–486. doi:10.1086/430696

CrossRef Full Text | Google Scholar

Sucerquia, M., Ramírez, V., Alvarado-Montes, J. A., and Zuluaga, J. I. (2020). Can close-in giant exoplanets preserve detectable moons? Mon. Notices R. Astronomical Soc. 492, 3499–3508. doi:10.1093/mnras/stz3548

CrossRef Full Text | Google Scholar

Sumi, T., Kamiya, K., Bennett, D. P., Bond, I. A., Abe, F., Botzler, C. S., et al. (2011). Unbound or distant planetary mass population detected by gravitational microlensing. Nature 473, 349–352. doi:10.1038/nature10092

PubMed Abstract | CrossRef Full Text | Google Scholar

Traub, W. A., and Oppenheimer, B. R. (2010). Direct imaging of exoplanets. Tucson: University of Arizona Press.

Google Scholar

Turner, J. D., Zarka, P., Grießmeier, J.-M., Lazio, J., Cecconi, B., Enriquez, J. E., et al. (2021). The search for radio emission from the exoplanetary systems 55 cancri, υ andromedae, and τ boötis using lofar beam-formed observations. Astronomy Astrophysics 645, A59. doi:10.1051/0004-6361/201937201

CrossRef Full Text | Google Scholar

Vedantham, H., Callingham, J., Shimwell, T., Tasse, C., Pope, B., Bedell, M., et al. (2020). Coherent radio emission from a quiescent red dwarf indicative of star–planet interaction. Nat. Astron. 4, 577–583. doi:10.1038/s41550-020-1011-9

CrossRef Full Text | Google Scholar

Vidotto, A., and Donati, J.-F. (2017). Predicting radio emission from the newborn hot jupiter v830 tauri b and its host star. Astronomy Astrophysics 602, A39. doi:10.1051/0004-6361/201629700

CrossRef Full Text | Google Scholar

Vidotto, A. A. (2017). Stellar coronal and wind models: impact on exoplanets. arXiv preprint arXiv:1709.07800.

Google Scholar

Viswanath, G., Narang, M., Manoj, P., Mathew, B., and Kartha, S. S. (2020). A statistical search for star–planet interaction in the ultraviolet using galex. Astronomical J. 159, 194. doi:10.3847/1538-3881/ab7d3b

CrossRef Full Text | Google Scholar

Weiss, L. M., Marcy, G. W., Rowe, J. F., Howard, A. W., Isaacson, H., Fortney, J. J., et al. (2013). The mass of koi-94d and a relation for planet radius, mass, and incident flux. Astrophysical J. 768, 14. doi:10.1088/0004-637x/768/1/14

CrossRef Full Text | Google Scholar

Winn, J. N., and Petigura, E. (2024). Planet occurrence from Doppler and transit surveys. arXiv preprint arXiv:2401.16451.

Google Scholar

Wittenmyer, R. A., Wang, S., Horner, J., Butler, R., Tinney, C., Carter, B., et al. (2020). Cool jupiters greatly outnumber their toasty siblings: occurrence rates from the anglo-australian planet search. Mon. Notices R. Astronomical Soc. 492, 377–383. doi:10.1093/mnras/stz3436

CrossRef Full Text | Google Scholar

Wright, J., Marcy, G., Howard, A., Johnson, J. A., Morton, T., and Fischer, D. (2012). The frequency of hot jupiters orbiting nearby solar-type stars. Astrophysical J. 753, 160. doi:10.1088/0004-637x/753/2/160

CrossRef Full Text | Google Scholar

Zarka, P. (1998). Auroral radio emissions at the outer planets: observations and theories. J. Geophys. Res. Planets 103, 20159–20194. doi:10.1029/98je01323

CrossRef Full Text | Google Scholar

Zarka, P. (2004). Fast radio imaging of jupiter’s magnetosphere at low-frequencies with lofar. Planet. Space Sci. 52, 1455–1467. doi:10.1016/j.pss.2004.09.017

CrossRef Full Text | Google Scholar

Zarka, P. (2007). Plasma interactions of exoplanets with their parent star and associated radio emissions. Planet. Space Sci. 55, 598–617. doi:10.1016/j.pss.2006.05.045

CrossRef Full Text | Google Scholar

Zarka, P., Lazio, T. J. W., and Hallinan, G. (2014). Magnetospheric radio emissions from exoplanets with the ska. in Proceedings of Advancing Astrophysics with the Square Kilometre Array (AASKA14). Giardini Naxos, Italy, 9 -13 June, 2014.

Google Scholar

Zarka, P., Marques, M., Louis, C., Ryabov, V., Lamy, L., Echer, E., et al. (2018). Jupiter radio emission induced by ganymede and consequences for the radio detection of exoplanets. Astronomy Astrophysics 618, A84. doi:10.1051/0004-6361/201833586

CrossRef Full Text | Google Scholar

Zarka, P., Treumann, R. A., Ryabov, B. P., and Ryabov, V. B. (2001). “Magnetically-driven planetary radio emissions and application to extrasolar planets,” in Physics of space: growth points and problems (Springer), 293–300.

CrossRef Full Text | Google Scholar