- 1NASA Goddard Space Flight Center, Greenbelt, MD, United States
- 2Physics Department, University of Texas at Arlington, Arlington, TX, United States
- 3High Altitude Observatory (HAO), Boulder, CO, United States
Numerous numerical studies have been carried out in recent years that simulate different aspects of exoplanets’ magnetosphere and stellar winds. These studies have focused primarily on hot Jupiters with sun-like stars. This study addresses the challenges inherent in utilizing existing MHD codes to model hot Jupiter-star systems. Due to the scaling of the system and the assumption of a uniformly flowing stellar wind at the outer boundary of the simulation, MHD codes necessitate a minimum distance of greater than 0.4 au for a Jupiter-like planet orbiting a sun-like star to avoid substantial violations of the code’s assumptions. Additionally, employing the GAMERA (Grid Agnostic MHD for Extended Research Applications) MHD code, we simulate star-planet interactions considering various stellar types (Sun-like and M Dwarf stars) with both Jupiter-like and rocky planets positioned at varying orbital distances. Furthermore, we explore the impact of tidal locking on the total power within the magnetosphere-ionosphere systems.
1 Introduction
The study of exoplanets has emerged as a captivating frontier in astrophysics, providing unprecedented insights into the diversity and potential habitability of distant worlds. The discovery of the first exoplanets (Mayor and Queloz, 1995) has revolutionized our understanding of planetary systems and expanded the scope of the search for extraterrestrial life. Advancements in the exoplanet detection techniques, such as the transit method, radial velocity measurements, microlensing, and direct imaging have led to the discovery of thousands of exoplanets and characterized their properties with increasing precision (Wright et al., 2012; Knutson et al., 2014; Mandel and Agol, 2002; Seager and Mallen-Ornelas, 2003; Gaudi, 2012; Bagheri et al., 2019; 2024b; a; Traub and Oppenheimer, 2010; Guyon et al., 2005). So far, more than 5,000 exoplanets have been detected, presenting a rich tapestry of planetary populations that help find habitable planets. Habitability, defined as the conditions suitable for life as we know it on Earth, encompasses a complex interplay of factors ranging from a planet’s size, composition, and atmosphere to its orbital characteristics and the nature of its host star. While Earth remains the sole known haven for life in the cosmos, the prospect of discovering habitable environments beyond our solar system has been an ongoing research topic.
In the quest to unravel the mysteries of exoplanetary habitability, one fundamental and often overlooked factor emerges as a critical player: the magnetic field. On Earth, the geomagnetic field acts as a protective shield, deflecting charged particles from the solar wind and cosmic rays that could otherwise strip away our atmosphere and erode the conditions conducive to life (Griessmeier et al., 2005). Although it was previously believed that Magnetic fields shield against stellar winds and influence atmospheric gas escape rates, recent studies show that a magnetosphere clearly impacts ionospheric outflow. An intrinsic magnetic field is not necessarily needed to prevent atmospheric erosion (Gronoff et al., 2020; Ramstad and Barabash, 2021). Rather, it is a combination of the planet’s magnetic field and stellar wind, as well as the characteristic of the planetary atmosphere, that represents a delicate equilibrium that governs habitability. Magnetic fields not only shield against stellar winds but also influence the escape rates of atmospheric gases. It can regulate the long-term stability of a planet’s atmosphere if field strength is strong enough relative to the upstream stellar wind and EUV flux from the host star and the gravity of the planet (Lundin et al., 2007; Ramstad and Barabash, 2021). This, in turn, influences surface temperatures and the potential for liquid water to exist, shaping the very foundation of habitability. Another significant yet less explored factor in determining the habitability of exoplanets involves the magnetic characteristics of associated exomoons. Recent studies (Green et al., 2021; 2023), reveals that the combined magnetospheres of terrestrial exoplanets and their exomoons collaborate to shield their early atmospheres. When exomoon magnetospheres intersect with the exoplanet’s magnetospheric cavity, the exomoon’s magnetic field forms an additional protective layer, akin to a magnetic bubble, which helps counteract stellar winds when the exomoon is on the dayside. This arrangement also facilitates plasma exchange between the exoplanet and its moon, potentially preserving a historical record of volatile evolution. Conversely, if the exomoon’s magnetosphere extends beyond the exoplanet’s magnetosphere, it serves as the primary defense against strong stellar winds, thereby reducing atmospheric loss.
One possible way to study exoplanets’ magnetic fields is by observing their radio emission. Within our solar system, Jupiter stands out as a prominent radio emitter, producing powerful bursts of radiation originating from its intense magnetic field. However, all magnetized planets in our solar system, even seemingly less dynamic planets, such as Earth and Saturn, contribute their own distinct radio signatures, each revealing the unique intricacies of their magnetospheric environments. Like Earth, Jupiter and Saturn have auroras, which are bright and dynamic displays of light near the polar regions caused by the interaction of charged particles with the planet’s atmosphere. Within the auroral zones, the magnetic fields trap energetic electrons. Some of these electrons can undergo a process called the Electron Cyclotron Maser Instability (ECMI). This process amplifies electromagnetic waves in the kilometric range. The amplified waves manifest as radio emission known as Auroral Kilometric Radiation (AKR). The emitted radio waves are detected at kilometric wavelengths, typically ranging from a few hundred kilohertz to a few megahertz. The exploration of AKR presents a promising avenue for directly detecting exoplanets, offering an independent means of inquiry distinct from their influence on host stars. The extension of AKR detection methods holds the potential for direct exoplanet detection and offers a unique opportunity to unravel the origins of exoplanetary magnetic fields.
Ground-based observatories and spaceborne instruments, such as the Voyager and Cassini spacecraft, have provided crucial data, enabling scientists to probe the radio signals emanating from the gas giants and icy moons of our solar system (Asmar et al., 2021). Beyond these familiar realms, detecting radio emissions from exoplanets promises to unveil new dimensions of planetary diversity and magnetospheric complexity. In recent decades, advances in radio telescopes, such as the Square Kilometre Array (SKA) telescope, have extended our capacity to explore and even detect planetary radio emissions beyond our immediate neighborhood. Understanding the average AKR emission of an exoplanet involves grappling with significant fluctuations caused by the stellar cycle. When EUV radiation increases, it boosts ionospheric densities, thereby diminishing the overall intensity and frequency of AKR by reducing the depth of the auroral density cavity (Green et al., 2004). In addition, atmospheric transmission acts as a barrier to radio signals, making it impossible to detect emissions below roughly 10 MHz due to the opacity of much of the radio spectrum within our atmosphere. Consequently, ground-based radio telescopes encounter challenges in observing the AKR emission of certain exoplanets, akin to the difficulty in detecting emissions from gas giant planets in our solar system, except Jupiter.
Two Priority Science Question Topics in the Origins, Worlds, and Life Planetary Science & Astrobiology Decadal Survey report have elements involving the existence of planetary magnetic fields and their interactions with the solar wind, Q6: “Solid body atmospheres, exospheres, magnetospheres, and climate evolution” and Q12.7: “Exoplanets, Giant planet structure and evolution” (National Academies of Sciences, 2022). To answer these questions, in this paper, we study the interaction of the exoplanets’ magnetosphere and stellar winds using Magneto-Hydro-Dynamic (MHD) simulations. Field-aligned currents (FACs) are identified as the primary and most effective sources of planetary ECMI emission (Treumann, 2006). Therefore, this paper aims to estimate FACs and the total power within the magnetosphere of two types of exoplanets under different conditions. We use a variant of MHD numerical simulations known as GAMERA (Zhang et al., 2019). We determine the overall power within the planetary magnetosphere by accounting for various stellar types, the influence of tidal locking and exoplanet rotation, and different orbital distances. Our approach involves conducting GAMERA simulations to explore different scenarios of the star-planet interaction, including a Sun-like star with both a rocky and a Jovian planet and an M Dwarf star with similar planetary configurations. The GAMERA simulation outputs ionospheric power data for each scenario based on stellar wind parameters, orbital distance, and conductance within the exoplanet’s ionosphere. The paper’s structure is outlined as follows: Section 2 details the methodology for the MHD simulations, while Section 3 summarizes the results. Section 4 discusses the implications of these findings and presents the conclusion.
2 Magneto-hydro-dynamic simulations and their limitations in exoplanet sciences
Based on our knowledge of the solar system planets, the average ECMI is related to the total solar wind power and the magnetic field of the planet by using the RBL model (Zarka et al., 2001; Zarka, 2004; 2007). However, the auroral radio emission strongly correlates with solar wind fluctuations (density, velocity, and/or ram pressure) (Gallagher and D’angelo, 1981; Desch, 1982; Genova et al., 1989; Bagheri and Lopez, 2022). Regardless of its origins, the existence of this correlation indicates that different types of stellar winds can significantly change the power of the auroral radio emission (Grießmeier et al., 2007a). For example, planets around young stars may be more luminous in radio emission than the solar system planets (Wood et al., 2005). More realistic estimates of the planetary radio emission are possible via MHD simulations of the interactions between the stellar wind and the planetary magnetic field. Global MHD simulations have been extensively used to study magnetospheric dynamics and ionosphere phenomena for the Earth and other solar system planets since the late 70s and early 80s. In recent years, a few studies have used MHD simulations to study the magnetosphere of exoplanets, especially giant close-in exoplanets. Close-in planets (semimajor axis
The magnetosphere structure of giant close-in exoplanets can also be different. All magnetized planets in our solar system have a magnetosphere with a structure similar to Earth’s magnetosphere. They are characterized by the following main elements: a bow shock, transition region, magnetopause, radiation belts, and a magnetospheric tail. The similarity of the magnetosphere in all magnetized planets in our solar system is because they all are located in the super-Alfvénic region of the solar wind since the Alfvén radius in the solar wind is
For giant close-in exoplanets, the tidal force, and XUV-driven heating are strong contributors to drive the expansion of the planetary atmosphere beyond the Roche lobe so that there is a gaseous open envelope around the planet, formed in the presence of outflows from the nearest Lagrange points. Therefore, hot Jupiters can experience significant hydrodynamic escapes (Johnstone et al., 2018; 2019; Shaikhislamov et al., 2020). Hydrodynamic escape has been observed for exoplanets close to their host star, including the hot Jupiters HD 209458b. Results in (Weber et al., 2017) show that high ionospheric plasma densities in hydrodynamically expanded upper atmospheres of close-in extrasolar giant planets prevent the radio emission from escaping the source region or render the generation of radio waves via the ECMI mechanism impossible.
Despite efforts to use MHD codes for simulating the magnetospheres of giant exoplanets orbiting close to their host stars [e.g., Turnpenney et al. (2020)], MHD codes frequently encounter inherent gaps and limitations, often compensated for through empirical fitting or simplifying assumptions. These empirical constraints and other assumptions derived from the properties of Earth or planets within the solar system may not be universally applicable to other planetary systems. As a result, modeling the plasma environments of exoplanets poses notable challenges to conventional MHD models. A crucial feature in any MHD simulation is how boundary conditions are treated. In MHD codes, the outer boundaries include the upstream, side, and downstream. The upstream boundary where the solar wind enters the simulation is placed upstream from the planet (in the case of Earth at 1 au, about 30 Earth radii
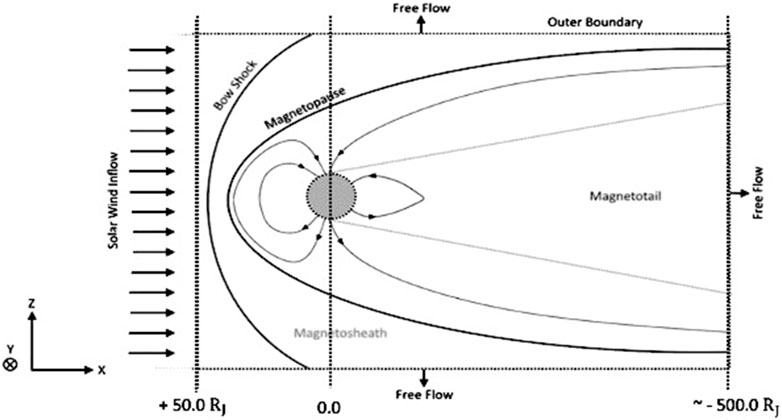
Figure 1. A Schematic view of the boundaries in the MHD codes for a Jupiter-like planet with the same size and magnetic field strength as Jupiter.
The downstream boundary is sufficiently far so that plasma flow velocity has become super-Alfvénic at the back of the box to avoid reflections off the back boundary. The side boundary conditions are just the solar wind variables propagated to the corresponding star-ward direction by the solar wind velocity. These conditions are usually in the form of Neumann boundary conditions, i.e.,
Beyond the Alfvén surface, where the stellar flow is super Alfvénic, MHD waves generated at the planet cannot flow upstream. Instead, the solar wind generates a bow shock when encountering planetary obstacles. This bow shock decelerates and redirects the solar wind, influencing its interaction with the magnetosphere-ionosphere system of the planet (Garcia-Sage et al., 2023). On the other hand, within the Alfvén surface, the transfer of energy can occur in both directions, towards and away from the star, enabling direct interaction between the planet and its host star [e.g., Cohen et al. (2014); Saur et al. (2013)]. Therefore, including the stellar wind magnetic field formally leads to a change in the regime for the wind flowing around the hot Jupiter from supersonic to subsonic (Zhilkin and Bisikalo, 2019). As a result, no bow shock should form in front of the atmosphere in the subsonic regime (Ip et al., 2004); i.e., the wind flowing around the planet should have a shockless character (for example, TRAPPIST-1e (Harbach et al., 2021) or AU Mic b (Cohen et al., 2022)). Analyses show that many typical hot Jupiters should have shockless-induced magnetospheres (Zhilkin and Bisikalo, 2019) [e.g., the magnetosphere of Ganymede (Jia and Kivelson, 2021)]. However, for close-in planets that possess high Keplerian velocities and are frequently located at regions where the host star’s wind is still accelerating, a shock may develop in the direction of the planet’s orbital motion (for example, WASP-12b (Vidotto et al., 2011)).
Cohen et al. (2011) use an MHD stellar corona model to predict the ambient coronal radio emission and its modulations induced by a close planet on its host star. This work focuses on studying the effect of a close-in planet on the corona. Basically, the exoplanet in this simulation is considered as an additional boundary condition in the corona model (Cohen et al., 2014; 2018). Therefore, the number of grids corresponding to the planet’s size in this model needs to be increased to capture all the magnetospheric/ionospheric features of the planet. Hence it cannot be used to calculate the auroral radio emission from the planet.
Our discussion pertains exclusively to giant close-in exoplanets like hot Jupiters. Studies involving MHD simulations of Super-Earths or sub-Neptune-sized exoplanets with short orbital periods (such as (Cohen et al., 2022; Garraffo et al., 2022)) are not applicable to this argument due to their small size, although, they may encounter challenges due to variations in stellar wind parameters between the upstream and downstream boundaries, which can reduce the reliability of their results.
3 An exoplanet with a sun-like star
The closest feasible orbital distance for a gas giant planet to adhere to the assumptions within MHD codes is approximately at the orbit of Mercury (about 0.4 au). The key alteration involves the side boundary conditions occurring over a range of
For 0.4 au, we use solar wind values based on actual measurements of the solar wind at the location of Mercury (Diego et al., 2020). The typical values for solar wind parameters are, IMF
Throughout all simulations presented in this study, we maintain a constant ionospheric Pedersen conductance. To determine the Pedersen conductance at varying orbital distances, we employ
where
Figure 2 illustrates the simulation outcomes depicting FACs, Joule heating, energy distribution, and Pedersen Conductance for both a rocky planet and a Jovian Planet. The right panel of Figure 2 showcases the northern hemisphere’s FACs, energy flux, and Joule heating distribution. In this simulation, the Pedersen conductance, calculated using Equation 1, was
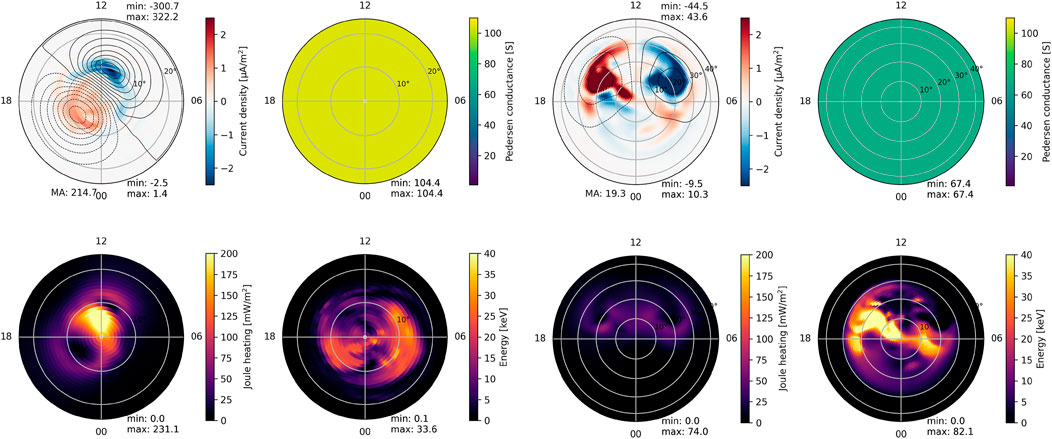
Figure 2. The simulations output for current density, Joule heating, and energy, the northern hemisphere of left-a Jovian and right-a rocky planet, both at 0.4 au with the IMF = −32 nT.
4 Tidally locked exoplanets
A crucial factor in estimating the radio flux of exoplanets is the planetary magnetic moment, a quantity assumed in MHD simulations. Two theoretical approaches underlie its calculation (Farrell et al., 1999; Weber et al., 2017). The first relies on scaling laws, linking the planetary magnetic dipole moment to its rotational speed (Grießmeier et al., 2004), indicating a direct influence of planetary rotations on the magnetic field. Conversely, the second hypothesis attributes the planetary magnetic moment primarily to energy flux from the planetary core (Reiners and Christensen, 2010), largely unaffected by tidal locking. Tidal locking, a consequence of strong tidal dissipation in exoplanets orbiting at smaller distances, significantly impacts the generation of auroral radiation due to asymmetrical conductance in the ionosphere (Zarka et al., 2001; Seager and Hui, 2002). Consequently, to model exoplanetary radio emissions accurately, MHD simulations must consider the effects of tidal locking and exoplanet rotation, critical factors that have yet been unexplored in previous studies. Notably, a planet at 0.4 au would become tidally locked much sooner than one at 1 au or beyond. A slower rotation rate may weaken the dynamo effect, resulting in weaker magnetic fields and smaller magnetospheres. However, recent studies (Zuluaga et al., 2013) show a non-trivial relationship between rotation period and magnetic properties, suggesting that tidally locked planets could still exhibit intense magnetic fields and extended magnetospheres with larger polar cap areas.
In this section, we aim to explore the influence of tidal locking on magnetospheric dynamics and its interaction with stellar winds. Specifically, we seek to elucidate the impact of rotation speed on magnetospheric energy flow, comparing two scenarios: one featuring a rapidly rotating planet akin to Jupiter and the other exhibiting synchronous rotation matching its orbital angular velocity. To address this inquiry, we conduct simulations mirroring the preceding section, focusing on a Jovian planet positioned at 0.4 au but assuming a rotational period equivalent to its orbital period. Changing the rotation period means changing the corotation potential in the magnetosphere-ionosphere system. Basically, corotation potential denotes the electrostatic potential arising from the dynamic interplay between a planet’s magnetosphere and the surrounding plasma environment. This phenomenon manifests prominently in regions where the planet’s rotational velocity synchronizes with the flow of the surrounding plasma, particularly in the outer reaches of the magnetosphere. In such zones of corotation, the plasma particles co-rotate with the planet’s magnetic field lines, resulting in a characteristic distribution of electrostatic potential. This potential can be driven by
where
The simulation outcomes, detailing the characteristics of magnetospheric magnetic and electric fields, are illustrated in Figure 3. The right panel of Figure 3 illustrates current density, Joule heating, energy distribution, and Pedersen conductance within the ionosphere-magnetosphere system of a tidally-locked Jovian planet at 0.4 au. A comparison between Figures 2, 3 reveals that in the tidally-locked scenario, FACs exhibit a symmetric pattern and higher magnitude attributable to reduced heating dissipation.
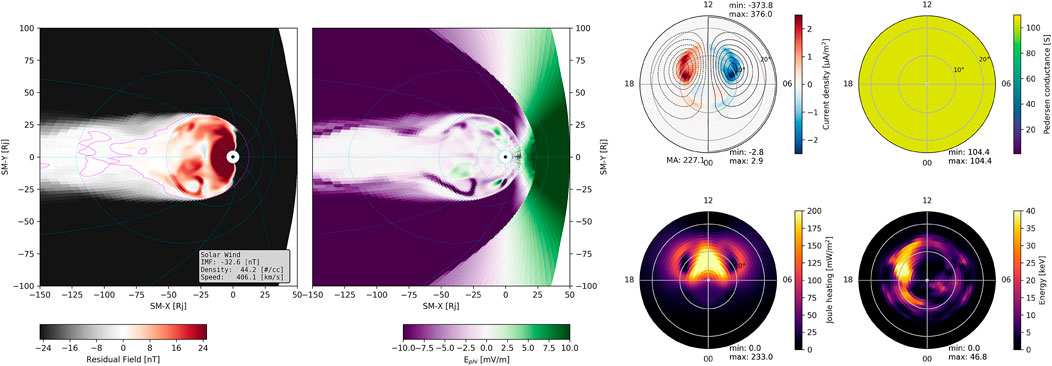
Figure 3. Left- Azimuthal component of electric field and Residual Field for a tidally-locked Jupiter-like planet at 0.4 au with the IMF = −32 nT. Right- The simulations output for current density, Joule heating, and energy in the northern hemisphere, a tidally-locked Jupiter-like planet at 0.4 au.
One of the principal distinctions observed in the context of tidal locking pertains to the evolution of the Cross-Polar Cap Potential (CPCP) throughout the simulation. Illustrated in the left panel of Figure 4, the CPCP for a rapidly rotating planet reaches its zenith approximately 5 hours into the simulation period. Conversely, in the scenario featuring a tidally locked planet (right panel), the CPCP exhibits continual escalation, ultimately peaking at approximately twice that of the CPCP observed in the fast-rotating planet configuration with an equivalent magnetic field. This trend can be understood by considering that tidally locked planets possess an expanded polar cap region, which in turn contributes to higher CPCP (Zuluaga et al., 2013).
We also explore the influence of corotation on the magnetospheric dynamics of a rocky planet possessing a rocky magnetic field. Figure 5 depicts CPCP, FACs, and Hemispheric Power (HP) of the northern (left) and southern hemispheres (right), considering various corotation periods. Although there are some differences, the overall pattern remains similar for all rotation speeds, unlike what we see with Jovian planets. A comprehensive analysis is needed to explain the observed elevation in CPCP in simulations of tidally-locked Jovian planets. However, this falls beyond the scope of the present study and is undergoing comprehensive investigation in a subsequent paper.
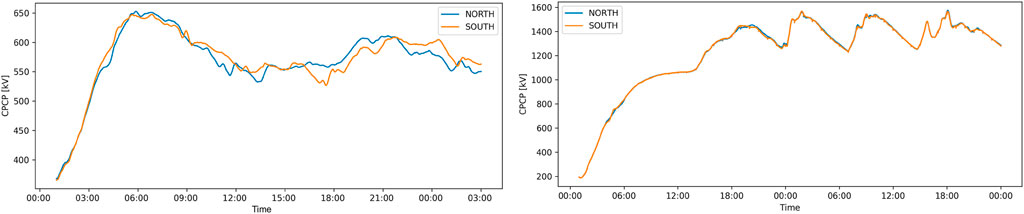
Figure 4. Cross Polar Cap Potential in the northern and southern hemispheres for left-a fast rotating planet (10 h rotation period), and right-a tidally locked planet.
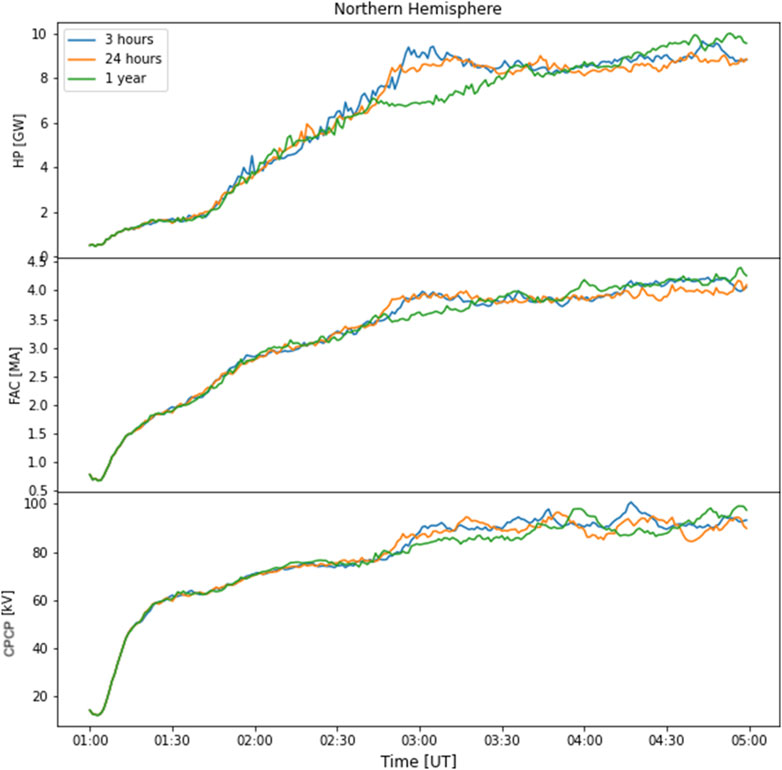
Figure 5. HP, FACs, and Cross potential polar cap with different corotation periods in left- northern and right-southern hemisphere.
5 Orbital distance effects
To investigate the influence of orbital distance on the magnetosphere of planets, we replicate the experimental setup with planets positioned at 1 au. Considering a Sun-like star, the stellar wind parameters at this distance are typical values observed near Earth. These include an incident plasma velocity of 400
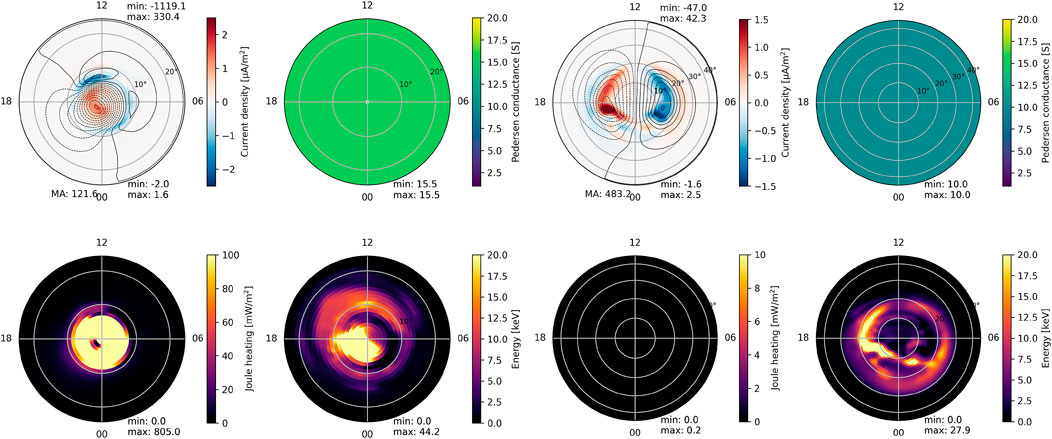
Figure 6. The simulations output for current density, Joule heating, and energy, the northern hemisphere of left-a Jovian and right-a rocky planet at 1 au with a Sun-like star.
6 An exoplanet with an M dwarf star
To contrast the preceding outcomes with the planetary interaction under the influence of a cooler stellar body, we conduct a simulation using standard values for M dwarf stellar wind parameters. In the scenario involving an M dwarf star, we use the data of GJ 436 as a representative sample (Vidotto and Bourrier, 2017). The stellar wind parameters at 1 au encompass an incident plasma velocity of 370
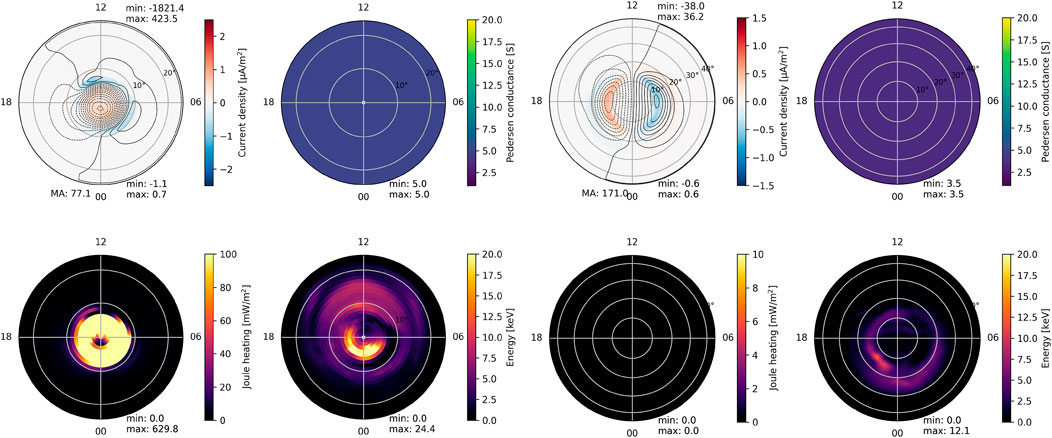
Figure 7. The simulations output for current density, Joule heating, and energy, the northern hemisphere of left-a Jovian and right-a rocky planet at 1 au with an M Dwarf star.
7 Conclusion
As previously mentioned, current 3D MHD simulations like GAMERA/LFM or SWMF are constrained by assumptions based on the solar system and Earth, rendering them inadequate for modeling systems with giant close-in exoplanets. Consequently, we cannot position a planet with a Jupiter-sized (or larger) magnetic field closer than 0.4 au to its host star. The magnetospheric structure of giant close-in exoplanets markedly differs from that of solar system planets. Close-in exoplanets tend to possess shock-less magnetospheres and are typically situated within the sub-Alfvénic zone of their host stars. Their proximity to host stars and relatively large sizes often fill their Roche lobes, leading to outflows from Lagrange points L1 and L2. The close proximity of these exoplanets to their host stars causes intense heating, ionization, and chemical alteration of their upper atmospheres due to stellar X-ray/EUV radiation, prompting hydrodynamic expansion of ionized atmospheric material. Consequently, modeling the magnetosphere-ionosphere interactions of exoplanets necessitates substantial modifications to established MHD models.
This study, we focused on “warm Jupiter” systems instead of hot Jupiters due to the limitations we discussed regarding MHD codes. We placed our Jupiter-sized planet at 0.4 au, which corresponds to an orbital period of approximately 90 days, to ensure a reasonably realistic simulation scenario. This configuration is supported by confirmed exoplanets such as TIC 260130483 b or TOI-1859 b (Montalto et al., 2020; Dong et al., 2021). We explored the impact of tidal locking on the system dynamics. The observed rise in CPCP in simulations of tidally-locked planets warrants further examination, which we plan to address in a subsequent manuscript. It is essential to acknowledge that conductance is variable in actual conditions, particularly for tidally locked planets. These findings represent an initial step toward understanding such star-planet systems.
Furthermore, we change the orbital distance from 0.4 to 1 au. When considering a Sun-like star, the conductance of a planet positioned at an orbital distance of 0.4 au surpasses that at 1 au by approximately an order of magnitude. This differential conductance results in diminished CPCP (Lopez et al., 2010), elevated total power, and heightened FACs for the planet located at 0.4 au relative to 1 au.
Moreover, the host stars of exoplanets may exhibit a range of spectral types, extending from F to M. Hence, we consider two scenarios, one with a sun-like star and another with an M dwarf stellar wind, to contrast simulation outcomes. Notably, the total power within the planet’s ionosphere-magnetosphere system is amplified when under the influence of a sun-like star.
This amplification stems from the planet’s conductance being approximately threefold greater than the M dwarf scenario. Consequently, the CPCP is correspondingly lower in the case of the sun-like star.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
FB: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. RL: Supervision, Validation, Writing–review and editing. KP: Resources, Software, Visualization, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research is supported by NSF grant number 2138122.
Acknowledgments
We acknowledge the use of the Cheyenne supercomputer at the National Center for Atmospheric Research (NCAR) (Computational and Laboratory, 2017).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Asmar, S., Preston, R., Vergados, P., Atkinson, D., Andert, T., Ando, H., et al. (2021). Solar system interiors, atmospheres, and surfaces investigations via radio links: goals for the next decade. Bull. AAS 53. doi:10.3847/25c2cfeb.9d29ef85
Bagheri, F., Garga, A., and Lopez, R. E. (2024a). Exploring radio emissions from confirmed exoplanets using ska. arXiv Prepr. arXiv:2404, 14468. doi:10.48550/arXiv.2404.14468
Bagheri, F., Lopez, R., and Shahmoradi, A. (2024b). Infrared-radio-follow-up observations for detection of the magnetic radio emission of extra solar planets: a new window to detect exoplanets. Front. Astronomy Space Sci. 11. doi:10.3389/fspas.2024.1400032
Bagheri, F., and Lopez, R. E. (2022). Solar wind magnetosonic mach number as a control variable for energy dissipation during magnetic storms. Front. Astronomy Space Sci. 9, 960535. doi:10.3389/fspas.2022.960535
Bagheri, F., Sajadian, S., and Rahvar, S. (2019). Detection of exoplanet as a binary source of microlensing events in wfirst survey. Mon. Notices R. Astronomical Soc. 490, 1581–1587. doi:10.1093/mnras/stz2682
Cauley, P. W., Shkolnik, E. L., Llama, J., and Lanza, A. F. (2019). Magnetic field strengths of hot jupiter from signals of star–planet interactions. Nat. Astron. 3, 1128–1134. doi:10.1038/s41550-019-0840-x
Cohen, O., Alvarado-Gómez, J. D., Drake, J. J., Harbach, L. M., Garraffo, C., and Fraschetti, F. (2022). Space-weather-driven variations in lyα absorption signatures of exoplanet atmospheric escape: MHD simulations and the case of AU mic b. Astrophysical J. 934, 189. doi:10.3847/1538-4357/ac78e4
Cohen, O., Drake, J., Glocer, A., Garraffo, C., Poppenhaeger, K., Bell, J., et al. (2014). Magnetospheric structure and atmospheric joule heating of habitable planets orbiting m-dwarf stars. Astrophysical J. 790, 57. doi:10.1088/0004-637x/790/1/57
Cohen, O., Kashyap, V., Drake, J., Sokolov, I., Garraffo, C., and Gombosi, T. (2011). The dynamics of stellar coronae harboring hot jupiter. i. a time-dependent magnetohydrodynamic simulation of the interplanetary environment in the hd 189733 planetary system. Astrophysical J. 733, 67. doi:10.1088/0004-637x/733/1/67
Cohen, O., Moschou, S.-P., Glocer, A., Sokolov, I. V., Mazeh, T., Drake, J. J., et al. (2018). Exoplanet modulation of stellar coronal radio emission. Astronomical J. 156, 202. doi:10.3847/1538-3881/aae1f2
Computational and Laboratory (2017). Cheyenne: hpe/sgi ice xa system (climate simulation laboratory)
Desch, M. D. (1982). Evidence for solar wind control of saturn radio emission. J. Geophys. Res. Space Phys. 87, 4549–4554. doi:10.1029/ja087ia06p04549
Diego, P., Piersanti, M., Laurenza, M., and Villante, U. (2020). Properties of solar wind structures at mercury’s orbit. J. Geophys. Res. Space Phys. 125, e2020JA028281. doi:10.1029/2020ja028281
Dong, J., Huang, C. X., Dawson, R. I., Foreman-Mackey, D., Collins, K. A., Quinn, S. N., et al. (2021). Warm jupiter in tess full-frame images: a catalog and observed eccentricity distribution for year 1. Astrophysical J. Suppl. Ser. 255 (6), 6. doi:10.3847/1538-4365/abf73c
Farrell, W., Desch, M., and Zarka, P. (1999). On the possibility of coherent cyclotron emission from extrasolar planets. J. Geophys. Res. Planets 104, 14025–14032. doi:10.1029/1998je900050
Fleming, D. P., Barnes, R., Luger, R., and VanderPlas, J. T. (2020). On the xuv luminosity evolution of trappist-1. Astrophysical J. 891, 155. doi:10.3847/1538-4357/ab77ad
Freeman, J. W., and Lopez, R. E. (1985). The cold solar wind. J. Geophys. Res. Space Phys. 90, 9885–9887. doi:10.1029/ja090ia10p09885
Gallagher, D. L., and D’angelo, N. (1981). Correlations between solar wind parameters and auroral kilometric radiation intensity. Geophys. Res. Lett. 8, 1087–1089. doi:10.1029/gl008i010p01087
Garcia-Sage, K., Farrish, A., Airapetian, V., Alexander, D., Cohen, O., Domagal-Goldman, S., et al. (2023). Star-exoplanet interactions: a growing interdisciplinary field in heliophysics. Front. Astron. Space Sci. 10. doi:10.3389/fspas.2023.1064076
Garraffo, C., Alvarado-Gómez, J. D., Cohen, O., and Drake, J. J. (2022). Revisiting the space weather environment of proxima centauri b. Astrophysical J. Lett. 941, L8. doi:10.3847/2041-8213/aca487
Gaudi, B. S. (2012). Microlensing surveys for exoplanets. Annu. Rev. Astronomy Astrophysics 50, 411–453. doi:10.1146/annurev-astro-081811-125518
Genova, F., Zarka, P., and Lecacheux, A. (1989). In Time-variable Phenomena in the Jovian System: Proceedings of the Workshop on Time-variable Phenomena in the Jovian System, Lowell Observatory, Flagstaff, Arizona. NASA Special Publication, 25–27.
Green, J., Boardsen, S., and Dong, C. (2021). Magnetospheres of terrestrial exoplanets and exomoons: implications for habitability and detection. Astrophysical J. Lett. 907, L45. doi:10.3847/2041-8213/abd93a
Green, J., Boardsen, S., and Dong, C. (2023). Effects of the evolving early moon and earth magnetospheres. Front. Astronomy Space Sci. 10, 1112233. doi:10.3389/fspas.2023.1112233
Green, J. L., Boardsen, S., Garcia, L., Fung, S. F., and Reinisch, B. (2004). Seasonal and solar cycle dynamics of the auroral kilometric radiation source region. J. Geophys. Res. Space Phys. 109. doi:10.1029/2003ja010311
Griessmeier, J.-M., Stadelmann, A., Motschmann, U., Belisheva, N., Lammer, H., and Biernat, H. (2005). Cosmic ray impact on extrasolar earth-like planets in close-in habitable zones. Astrobiology 5, 587–603. doi:10.1089/ast.2005.5.587
Grießmeier, J.-M., Preusse, S., Khodachenko, M., Motschmann, U., Mann, G., and Rucker, H. (2007a). Exoplanetary radio emission under different stellar wind conditions. Planet. Space Sci. 55, 618–630. doi:10.1016/j.pss.2006.01.008
Grießmeier, J.-M., Stadelmann, A., Penz, T., Lammer, H., Selsis, F., Ribas, I., et al. (2004). The effect of tidal locking on the magnetospheric and atmospheric evolution of “hot jupiters”. Astronomy and Astrophysics 425, 753–762. doi:10.1051/0004-6361:20035684
Grießmeier, J.-M., Zarka, P., and Spreeuw, H. (2007b). Predicting low-frequency radio fluxes of known extrasolar planets. Astronomy and Astrophysics 475, 359–368. doi:10.1051/0004-6361:20077397
Gronoff, G., Arras, P., Baraka, S., Bell, J. M., Cessateur, G., Cohen, O., et al. (2020). Atmospheric escape processes and planetary atmospheric evolution. J. Geophys. Res. Space Phys. 125, e2019JA027639. doi:10.1029/2019ja027639
Guyon, O., Pluzhnik, E. A., Galicher, R., Martinache, F., Ridgway, S. T., and Woodruff, R. A. (2005). Exoplanet imaging with a phase-induced amplitude apodization coronagraph. i. principle. Astrophysical J. 622, 744–758. doi:10.1086/427771
Harbach, L. M., Moschou, S. P., Garraffo, C., Drake, J. J., Alvarado-Gómez, J. D., Cohen, O., et al. (2021). Stellar winds drive strong variations in exoplanet evaporative outflow patterns and transit absorption signatures. Astrophysical J. 913, 130. doi:10.3847/1538-4357/abf63a
Ip, W.-H., Kopp, A., and Hu, J.-H. (2004). On the star-magnetosphere interaction of close-in exoplanets. Astrophysical J. 602, L53–L56. doi:10.1086/382274
Jackson, B., Greenberg, R., and Barnes, R. (2008). Tidal evolution of close-in extrasolar planets. Astrophysical J. 678, 1396–1406. doi:10.1086/529187
Jia, X., and Kivelson, M. G. (2021). The magnetosphere of ganymede. Magnetos. Sol. Syst., 557–573. doi:10.1002/9781119815624.ch35
Johnstone, C., Khodachenko, M., Lüftinger, T., Kislyakova, K., Lammer, H., and Güdel, M. (2019). Extreme hydrodynamic losses of earth-like atmospheres in the habitable zones of very active stars. Astronomy and Astrophysics 624, L10. doi:10.1051/0004-6361/201935279
Johnstone, C. P., Güdel, M., Lammer, H., and Kislyakova, K. G. (2018). Upper atmospheres of terrestrial planets: carbon dioxide cooling and the earth’s thermospheric evolution. Astronomy and Astrophysics 617, A107. doi:10.1051/0004-6361/201832776
Knutson, H. A., Benneke, B., Deming, D., and Homeier, D. (2014). A featureless transmission spectrum for the neptune-mass exoplanet gj 436b. Nature 505, 66–68. doi:10.1038/nature12887
Koskinen, T., Harris, M., Yelle, R., and Lavvas, P. (2013). The escape of heavy atoms from the ionosphere of hd209458b. i. a photochemical–dynamical model of the thermosphere. Icarus 226, 1678–1694. doi:10.1016/j.icarus.2012.09.027
Lopez, R., Bruntz, R., Mitchell, E., Wiltberger, M., Lyon, J., and Merkin, V. (2010). Role of magnetosheath force balance in regulating the dayside reconnection potential. J. Geophys. Res. Space Phys. 115. doi:10.1029/2009ja014597
Lopez, R. E. (2016). The integrated dayside merging rate is controlled primarily by the solar wind. J. Geophys. Res. Space Phys. 121, 4435–4445. doi:10.1002/2016ja022556
Lundin, R., Lammer, H., and Ribas, I. (2007). Planetary magnetic fields and solar forcing: implications for atmospheric evolution. Space Sci. Rev. 129, 245–278. doi:10.1007/978-0-387-74288-5_9
Mandel, K., and Agol, E. (2002). Analytic light curves for planetary transit searches. Astrophysical J. 580, L171–L175. doi:10.1086/345520
Mayor, M., and Queloz, D. (1995). A jupiter-mass companion to a solar-type star. nature 378, 355–359. doi:10.1038/378355a0
Montalto, M., Borsato, L., Granata, V., Lacedelli, G., Malavolta, L., Manthopoulou, E., et al. (2020). A search for transiting planets around fgkm dwarfs and subgiants in the tess full frame images of the southern ecliptic hemisphere. Mon. Notices R. Astronomical Soc. 498, 1726–1749. doi:10.1093/mnras/staa2438
National Academies of Sciences, E., Medicineet al. (2022). Origins, worlds, and life: a decadal strategy for planetary science and astrobiology 2023-2032.
Nichols, J., and Milan, S. (2016). Stellar wind–magnetosphere interaction at exoplanets: computations of auroral radio powers. Mon. Notices R. Astronomical Soc. 461, 2353–2366. doi:10.1093/mnras/stw1430
Ramstad, R., and Barabash, S. (2021). Do intrinsic magnetic fields protect planetary atmospheres from stellar winds? lessons from ion measurements at mars, venus, and earth. Space Sci. Rev. 217, 36–39. doi:10.1007/s11214-021-00791-1
Reiners, A., and Christensen, U. R. (2010). A magnetic field evolution scenario for brown dwarfs and giant planets. Astronomy and Astrophysics 522, A13. doi:10.1051/0004-6361/201014251
Saur, J., Grambusch, T., Duling, S., Neubauer, F., and Simon, S. (2013). Magnetic energy fluxes in sub-alfvénic planet star and moon planet interactions. Astronomy and Astrophysics 552, A119. doi:10.1051/0004-6361/201118179
Seager, S., and Hui, L. (2002). Constraining the rotation rate of transiting extrasolar planets by oblateness measurements. Astrophysical J. 574, 1004–1010. doi:10.1086/340994
Seager, S., and Mallen-Ornelas, G. (2003). A unique solution of planet and star parameters from an extrasolar planet transit light curve. Astrophysical J. 585, 1038–1055. doi:10.1086/346105
Shaikhislamov, I., Khodachenko, M., Lammer, H., Berezutsky, A., Miroshnichenko, I., and Rumenskikh, M. (2020). Three-dimensional modelling of absorption by various species for hot jupiter hd 209458b. Mon. Notices R. Astronomical Soc. 491, 3435–3447. doi:10.1093/mnras/stz3211
Tasker, E. J., Unterborn, C., Laneuville, M., Fujii, Y., Desch, S. J., and Hartnett, H. E. (2020). Planetary Diversity: Rocky planet processes and their observational signatures. IOP Publishing.
Traub, W. A., and Oppenheimer, B. R. (2010). Direct imaging of exoplanets. Tucson: University of Arizona Press.
Treumann, R. A. (2006). The electron–cyclotron maser for astrophysical application. Astronomy Astrophysics Rev. 13, 229–315. doi:10.1007/s00159-006-0001-y
Turnpenney, S., Nichols, J. D., Wynn, G. A., and Jia, X. (2020). Magnetohydrodynamic modelling of star–planet interaction and associated auroral radio emission. Mon. Notices R. Astronomical Soc. 494, 5044–5055. doi:10.1093/mnras/staa824
Vidotto, A., and Bourrier, V. (2017). Exoplanets as probes of the winds of host stars: the case of the m dwarf gj 436. Mon. Notices R. Astronomical Soc. 470, 4026–4033. doi:10.1093/mnras/stx1543
Vidotto, A., Llama, J., Jardine, M., Helling, C., and Wood, K. (2011). Shock formation around planets orbiting m-dwarf stars. Astron. Nachrichten 332, 1055–1061. doi:10.1002/asna.201111622
Weber, C., Lammer, H., Shaikhislamov, I. F., Chadney, J., Khodachenko, M., Grießmeier, J.-M., et al. (2017). How expanded ionospheres of hot jupiters can prevent escape of radio emission generated by the cyclotron maser instability. Mon. Notices R. Astronomical Soc. 469, 3505–3517. doi:10.1093/mnras/stx1099
Wood, B. E., Müller, H.-R., Zank, G. P., Linsky, J. L., and Redfield, S. (2005). New mass-loss measurements from astrospheric lyα absorption. Astrophysical J. 628, L143–L146. doi:10.1086/432716
Wright, J., Marcy, G., Howard, A., Johnson, J. A., Morton, T., and Fischer, D. (2012). The frequency of hot jupiters orbiting nearby solar-type stars. Astrophysical J. 753, 160. doi:10.1088/0004-637x/753/2/160
Xi, S., Lotko, W., Zhang, B., Brambles, O., Lyon, J., Merkin, V., et al. (2015). Poynting flux-conserving low-altitude boundary conditions for global magnetospheric models. J. Geophys. Res. Space Phys. 120, 384–400. doi:10.1002/2014ja020470
Zarka, P. (2004). Fast radio imaging of jupiter’s magnetosphere at low-frequencies with lofar. Planet. Space Sci. 52, 1455–1467. doi:10.1016/j.pss.2004.09.017
Zarka, P. (2007). Plasma interactions of exoplanets with their parent star and associated radio emissions. Planet. Space Sci. 55, 598–617. doi:10.1016/j.pss.2006.05.045
Zarka, P., Marques, M., Louis, C., Ryabov, V., Lamy, L., Echer, E., et al. (2018). Jupiter radio emission induced by ganymede and consequences for the radio detection of exoplanets. Astronomy and Astrophysics 618, A84. doi:10.1051/0004-6361/201833586
Zarka, P., Treumann, R. A., Ryabov, B. P., and Ryabov, V. B. (2001). “Magnetically-driven planetary radio emissions and application to extrasolar planets,” in Physics of space: growth points and problems (Springer), 293–300.
Zhang, B., Sorathia, K. A., Lyon, J. G., Merkin, V. G., Garretson, J. S., and Wiltberger, M. (2019). Gamera: a three-dimensional finite-volume mhd solver for non-orthogonal curvilinear geometries. Astrophysical J. Suppl. Ser. 244, 20. doi:10.3847/1538-4365/ab3a4c
Zhilkin, A., and Bisikalo, D. (2019). On possible types of magnetospheres of hot jupiters. Astron. Rep. 63, 550–564. doi:10.1134/s1063772919070096
Keywords: exoplanet, MHD simulations, AKR emission, planetary magnetic field, close-in exoplanet
Citation: Bagheri F, Lopez R and Pham K (2024) A fresh look into the interaction of exoplanets magnetosphere with stellar winds using MHD simulations. Front. Astron. Space Sci. 11:1398379. doi: 10.3389/fspas.2024.1398379
Received: 09 March 2024; Accepted: 08 August 2024;
Published: 21 August 2024.
Edited by:
Joseph E. Borovsky, Space Science Institute (SSI), United StatesReviewed by:
Vladimir Airapetian, National Aeronautics and Space Administration, United StatesJames L. Green, Independent Researcher, Silver Spring, Maryland, United States
Copyright © 2024 Bagheri, Lopez and Pham. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fatemeh Bagheri, ZmF0ZW1laC5iYWdoZXJpQG5hc2EuZ292
 Fatemeh Bagheri
Fatemeh Bagheri Ramon Lopez
Ramon Lopez Kevin Pham3
Kevin Pham3