
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
BRIEF RESEARCH REPORT article
Front. Astron. Space Sci. , 31 May 2024
Sec. Space Physics
Volume 11 - 2024 | https://doi.org/10.3389/fspas.2024.1394817
This article is part of the Research Topic Energy Transfer And Exchange With Low-Energy Plasma Via Cross-Energy And Cross-Scale Interactions Throughout The Magnetosphere View all articles
 K. Seki1*
K. Seki1* Y. Matsumoto2
Y. Matsumoto2 N. Terada3
N. Terada3 T. Hara4
T. Hara4 D. A. Brain5
D. A. Brain5 H. Nakagawa3
H. Nakagawa3 J. P. McFadden4
J. P. McFadden4 J. S. Halekas6
J. S. Halekas6 S. Ruhunusiri5
S. Ruhunusiri5 D. L. Mitchell4
D. L. Mitchell4 L. Andersson5
L. Andersson5 J. R. Espley7
J. R. Espley7 D. N. Baker5
D. N. Baker5 J. G. Luhmann4
J. G. Luhmann4 B. M. Jakosky5
B. M. Jakosky5Boundaries between space plasmas occur in numerous contexts and scales, from astrophysical jets to planetary magnetospheres. Mass and momentum transport across boundaries poses a fundamental problem in magnetospheric physics. Kelvin–Helmholtz instability (KHI) is a promising mechanism to facilitate transport. Although previous studies have suggested KHI occurrence in various space plasmas, theory predicts that compressibility prevents KHI excitation at boundaries with large density gradients because of previously considered boundary structures where density varies with velocity. Based on the observations of a large density gradient boundary by MAVEN at Mars, where we can observe an extreme case, in this study, we show that it is the entropy, instead of the previously considered density, that varies with the velocity in the real velocity-sheared boundary. The entropy-based boundary structure places the velocity shear in a lower-density region than the traditional density-based structure and weakens the compressibility effect. This new boundary structure thus enables KHI excitation even at large density gradient boundaries, such as at the ionopause of unmagnetized planets and the plasmapause of magnetized planets. The result suggests the ubiquitous occurrence of KHI in the plasma universe and emphasizes its important role in planetary cold plasma escape from unmagnetized planets.
Momentum and mass transport mechanisms at a velocity-sheared boundary in the space plasma are important processes that affect the supply of magnetospheric plasma at various planets. In various space plasmas, collisions are often negligible (Matthaeus et al., 2003), and thus, momentum and mass transport primarily occurs through couplings between constituent charged particles and the electric/magnetic fields (Seki et al., 2003). When two different plasma regimes come into contact, instabilities facilitate mass and momentum transport across the ambient magnetic field. Such boundaries occur in numerous contexts and scales from astrophysical plasmas such as at neutron star mergers (Price and Rosswog, 2006), star-forming molecular clouds (Berne et al., 2010), nova explosions (Casanova et al., 2011), and solar corona (Hillier and Arregui, 2019), in addition to various planetary magnetospheres (Hasegawa et al., 2004; Slavin et al., 2008; Delamere et al., 2013). The Kelvin–Helmholtz instability (KHI) (Fujimoto and Terasawa, 1994) is considered a promising candidate to facilitate momentum and mass transfers across boundaries.
One of the important parameters for assessment of the occurrence of KHI is compressibility. The stability analysis of compressional plasma predicts that KHI excitation is suppressed when the density ratio across the boundary (
In Earth, which has a strong intrinsic magnetic field, KHI has been identified by in situ satellite observations at the boundary between the shocked solar wind and terrestrial magnetosphere (Hasegawa et al., 2004), where the density gradient is usually small (with the density ratio between the two sides of the boundary being
In the case of unmagnetized planets such as Mars and Venus, that do not have a global intrinsic magnetic field, the velocity-sheared boundary appears between the shocked solar wind and the ionized upper atmosphere (ionosphere), i.e., around the ionopause. The magnetic field geometry effects are also important at Venus and Mars, and KHI is mainly excited in the perpendicular plane to the IMF (Dang et al., 2022). Due to the large density in the ionosphere, the compressibility effects are expected to be important and can suppress the occurrence of KHI. Despite this expectation from theory, KHI vortex-like signatures (boundary waves) have been observed on Mars (Ruhunusiri et al., 2016; Poh et al., 2021; Wang et al., 2022) and Venus (Chong et al., 2018), where
Particularly on Mars,
Using a comprehensive in situ plasma observation at Mars by MAVEN and MHD simulations of KHI, in this study, we investigate the characteristics of plasma boundaries with large density gradients and their effects on Kelvin–Helmholtz instability. Following the description of the instrumentation and model in Section 2, the results of the comparison between the observations and simulations are shown in Section 3. Based on observations, we propose a new realistic boundary structure for the velocity-sheared layer with a large density gradient based on entropy and conduct MHD simulations of KHI. In Section 4 and Section 5, discussions and conclusion are provided, respectively.
A comprehensive in situ observation of plasma at Mars by MAVEN (Andersson et al., 2015; Connerney et al., 2015; Halekas et al., 2015; McFadden et al., 2015) provides an ideal opportunity to investigate the fundamental question described in Section 1. We used the data obtained in the MAVEN orbit #118 on 20 October 2014 from the MAG instrument (Connerney et al., 2015) for the vector magnetic fields, STATIC (McFadden et al., 2015)/SWIA (Halekas et al., 2015) for ion moments with/without mass discrimination, and LPW (Andersson et al., 2015) for electron density in the ionosphere. We used SWIA density and velocity data only for the time period when the SupraThermal and Thermal Ion Composition (STATIC) energy coverage was limited due to its observation mode, as described in Section 3.1.
A high-resolution, numerically robust magnetohydrodynamic (MHD) simulation code CANS+ (Matsumoto et al., 2019) is used to simulate KHI in velocity-sheared boundary layers with large density gradients. The nonlinear evolution of the physical quantities—plasma number density, pressure, velocity, and magnetic field B—is followed on the basis of MHD equations. We numerically solve the equations by using the fifth-order MP5 scheme (Suresh and Huynh, 1997) and the approximate Rieman solver of the HLLD scheme (Miyoshi and Kusano, 2005). In order to compare traditional density-based and new entropy-based initial structures of the velocity-sheared boundary, we conducted two sets of two-dimensional MHD simulations. Two models of the boundary structure will be described in detail, together with observations, in Section 3.1. Based on the observations, the number density, velocity, temperature, and magnetic field strength in the shocked solar wind (ionosphere) side are set to 2 (104) cm−3, 177 (0) km/s, 275 (0.055) eV, and 8 (8) nT, respectively. It corresponds to
Since Mars does not possess a global magnetic field, the solar wind directly interacts with the ionosphere. As it approaches Mars, the supersonic solar wind forms a bow shock in front of the planet (Figure 1), and the decelerated, shocked solar wind interacts with the dense ionosphere. At the boundary between the shocked solar wind and the ionosphere, the density gradient is large, with a typical density ratio of
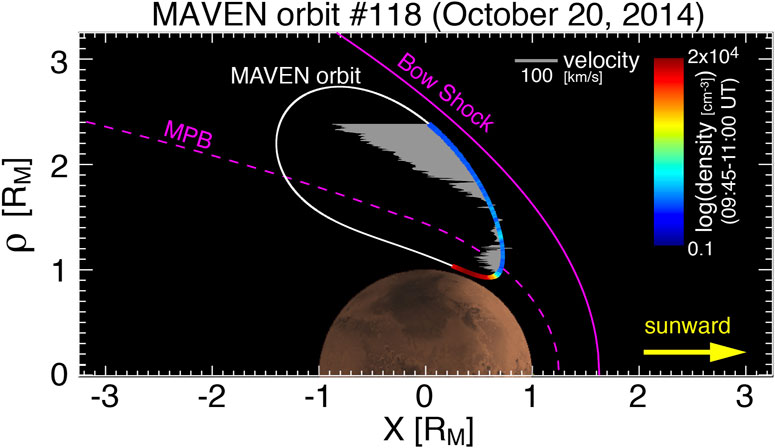
Figure 1. Orbital configuration of the MAVEN spacecraft around Mars during 07:30–12:07 UT on 20 October 2014 (orbit #118). The x-axis points sunward from the center of Mars, and
MAVEN observed an example of a velocity-sheared boundary with a large density gradient of
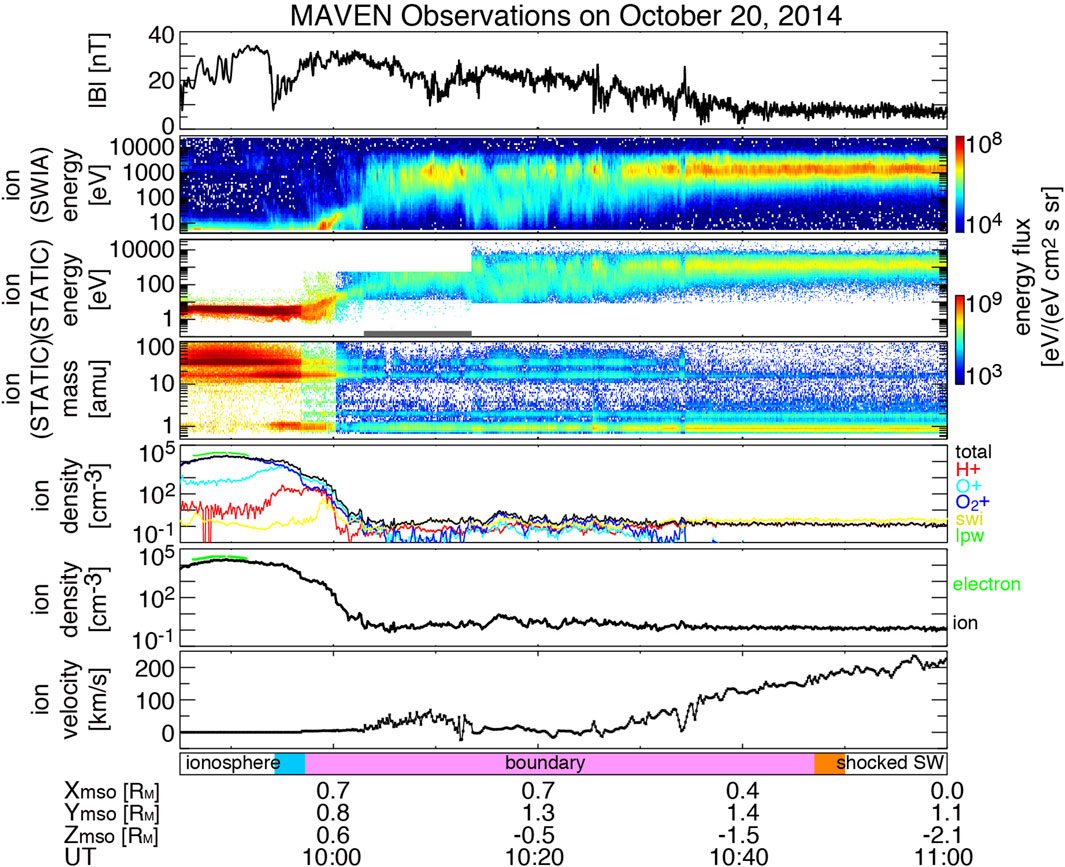
Figure 2. Summary of MAVEN observations in a large density gradient boundary between the shocked solar wind and the ionosphere. From the top of the figure, each panel shows magnetic field strength from the MAG instrument (Connerney et al., 2015), the ion energy–time, mass–time spectrograms, density of each species, combined electron/ion density, velocity, and region identification bar, respectively. The black line in the sixth panel of the ion density shows the total ion density obtained both from STATIC (McFadden et al., 2015) and SWIA (Halekas et al., 2015) in addition to electron density from LPW (Andersson et al., 2015) in the ionosphere (green) to confirm the accuracy of the density observation. The ion velocity panel displays the bulk velocity component in the direction of the shocked solar wind flow averaged over the orange bar time interval at the bottom. Note that we used SWIA density and velocity data for the time period shown in the gray bar at the bottom of the third panel due to the limited energy coverage of STATIC. The bottom color bar indicates time intervals used in the data analysis. Light blue (orange) corresponds to the interval used to calculate ionospheric (shocked solar wind) parameters, while pink indicates the boundary region in which the velocity shear and density gradient are observed.
In order to investigate the location of the velocity shear relative to the density gradient, the observed relation between the density and velocity is determined and plotted in Figure 3A. In theoretical considerations (Miura and Pritchett, 1982; Amerstorfer et al., 2010; Matsumoto and Seki, 2010), the velocity shear, taking the X-axis in the original shocked solar wind direction and Y across the shear, is often expressed with the hyperbolic tangent as
in the rest frame of the ionosphere, where
where
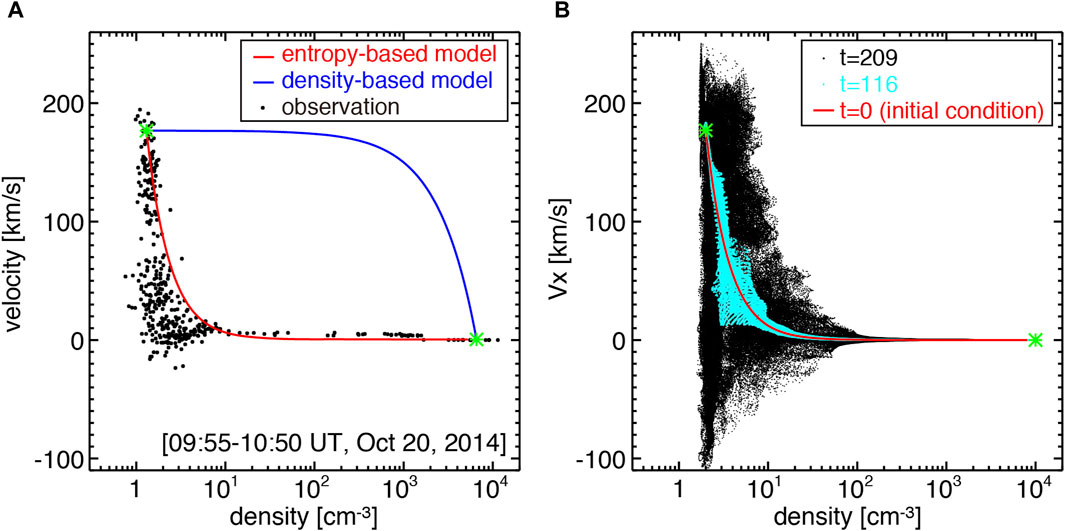
Figure 3. Relations between ion density and velocity (A) observed in the large-density gradient boundary by MAVEN and (B) obtained in the MHD simulation with the entropy-based model as the initial condition. In panel (A), black dots show the ion density and velocity in the boundary interval observed by MAVEN (the same data shown in Figure 2 for the time interval indicated by the pink bar at the bottom of Figure 2), while red and blue lines display the newly proposed entropy-based model and classical density-based model, respectively, calculated based on parameters (green symbols) derived from observations in both ends of the boundary, i.e., the shocked solar wind (high speed and low density) and the ionosphere (low speed and high density). In panel (B), light blue and black dots indicate different time evolution stages, i.e.,
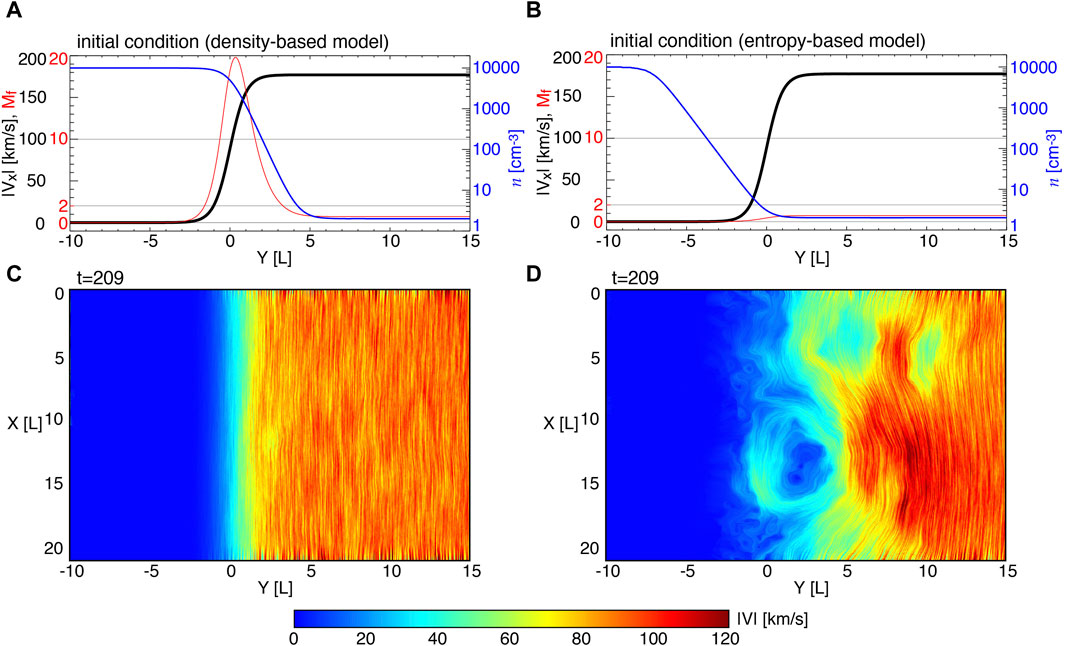
Figure 4. Comparison between MHD simulations with two different boundary structures (red and blue lines in Figure 3A) as initial conditions. Panels (A) and (C) and (B) and (D) correspond to the density-based model and entropy-based model cases, respectively. Top panels show initial profiles of velocity (black line), density (blue), and the magnetosonic Mach number
In order to describe the observed boundary structure, we here introduce the entropy per unit mass,
where
We here conducted two-dimensional MHD simulations of KHI with a transverse magnetic field for the two initial conditions, i.e., the density-based model (Figure 4A) and entropy-based model (Figure 4B). The density, velocity, temperature, and magnetic field strength in the shocked solar wind (ionosphere) side are set to 2 (104) cm−3, 177 (0) km/s, 275 (0.055) eV, and 8 (8) nT based on observations shown in Section 3.1, respectively. These parameters correspond to
The center upper part of Figure 4D shows a well-developed vortex with its center at approximately
The real boundary structure with velocity shear and density gradient in space plasma reported here requires alteration of the initial boundary structure in theoretical studies of KHI to estimate mass and momentum transport across the boundary. In collisionless space plasmas, plasma mixing across the magnetic field lines occurs at small-scale structures, caused by secondary instabilities excited in the rolled-up vortex of KHI, i.e., at a well-developed KHI. To understand the momentum and mass transport mechanisms across the velocity-sheared boundary, high-resolution kinetic simulations of KHI have been conducted (Matsumoto and Seki, 2010; Dargent et al., 2019). Some of the previous studies have identified the importance of including electron inertial effects when assessing mass transport mechanisms across the boundaries. The observed entropy-based boundary structure presented here has a fundamental difference from the traditional initial conditions of the various simulation studies of KHI (density-based model) (Suresh and Huynh, 1997; Casanova et al., 2011; Andersson et al., 2015; Matsumoto et al., 2019; Hwang et al., 2023). The change in the initial condition largely alters the time evolution of KHI, even in the small and moderate density gradient cases. For example, the usage of the proposed entropy-based model based on the observations will be important for understanding the interplay between KHI and the lower-hybrid drift instability in plasma mixing (Dargent et al., 2019).
Although kinetic particle-in-cell (PIC) simulations are important to investigate plasma mixing processes, MHD (Michael et al., 2021; Dang et al., 2022) or hybrid (Wang et al., 2023) simulations have the advantage of conducting three-dimensional global simulations of the interaction between the solar wind and planetary magnetosphere/ionosphere. The comparison between MHD and PIC simulations indicates that the MHD approximation can capture important features of the plasma mixing layer in certain conditions when the grid resolution and numerical dissipation are small enough (Matsumoto and Seki, 2010). Thus, this study encourages investigations of dayside velocity-sheared boundary structures in the global simulation, which determine the initial condition for KHI growth, to compare them with the entropy-based boundary structure obtained from observations in this study.
The specific entropy
The entropy-based model obtained in this study has no artificial peak in the magnetosonic Mach number
Based on comprehensive plasma observations by MAVEN at Mars, we investigated the real structure of velocity-sheared boundaries with a large density gradient (density ratio of 5000), and the two cases of MHD simulations of KHI with two different initial boundary structure models are compared. The results are as follows:
• The observations show that the boundary structure has a fundamental difference from the traditional density-based model used in previous simulation studies. Based on the observations, a new entropy-based boundary model is proposed.
• In the proposed entropy-based model, the relative location of the velocity shear to the density gradient changed so that the velocity shear is located in the lower-density region than in the density-based model.
• The comparison between simulations with two boundary models shows that KHI cannot develop in the density-based boundary model, while it can be excited in the entropy-based model due to the difference in compressibility effects at the velocity shear layer.
These results suggest that the suppression of KHI can be weakened in the realistic velocity-sheared boundary structure even when the density gradient across the boundary is large, and it can facilitate the ubiquitous occurrence of Kelvin–Helmholtz instability in various planetary magnetospheres and astrophysical plasmas. It will be useful to use the entropy-based boundary model for future simulation studies of velocity-sheared boundaries with a density gradient.
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below. The Mars Atmosphere and Volatile EvolutioN (MAVEN) data are available from the NASA Planetary Data System (https://pds.nasa.gov) and the MAVEN Science Data Center (https://lasp.colorado.edu/maven/sdc/public/). The simulation data used in this study are available from the UTokyo Repository (https://repository.dl.itc.u-tokyo.ac.jp/).
KS: conceptualization, formal analysis, funding acquisition, investigation, methodology, project administration, visualization, writing–original draft, and writing–review and editing. YM: investigation, methodology, validation, visualization, writing–review and editing, writing–original draft, and software. NT: conceptualization, validation, and writing–review and editing. TH: formal analysis, validation, writing–review and editing, and software. DB: validation, writing–review and editing, and investigation. HN: funding acquisition, writing–review and editing, and validation. JM: data curation, software, supervision, validation, and writing–review and editing. JH: data curation, validation, and writing–review and editing. SR: investigation and writing–review and editing. DM: data curation and writing–review and editing. LA: data curation, validation, writing–review and editing, and investigation. JE: data curation, validation, and writing–review and editing. DB: supervision and writing–review and editing. JL: supervision, writing–review and editing, and investigation. BJ: funding acquisition, resources, supervision, writing–review and editing, and project administration.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is conducted under NASA’s MAVEN Participating Scientist Program (Proposal #12-MAVENPS12-0017, PI: KS). This work was supported by a Grant-in-Aid for Scientific Research (A) #20H00192 and #22H00164 and Fostering Joint International Research (B) 18KK0093 by the Japan Society for the Promotion of Science.
The authors thank M. Fujimoto for useful discussion and J. E. P. Connerney for his contribution to MAG data.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Amerstorfer, U. V., Erkaev, N. V., Taubenschuss, U., and Biernat, H. K. (2010). Influence of a density increase on the evolution of the Kelvin–Helmholtz instability and vortices. Phys. Plasmas 17, 072901. doi:10.1063/1.3453705
Andersson, L., Ergun, R. E., Delory, G. T., Eriksson, A., Westfall, J., Reed, H., et al. (2015). The Langmuir probe and waves (LPW) instrument for MAVEN. Space Sci. Rev. 195, 173–198. doi:10.1007/s11214-015-0194-3
Barabash, S., Fedorov, A., Lundin, R., and Sauvaud, J. A. (2007). Martian atmospheric erosion rates. Science 315, 501–503. doi:10.1126/science.1134358
Berne, O., Marcelino, N., and Cernicharo, J. (2010). Waves on the surface of the Orion molecular cloud. Nature 466, 947–949. doi:10.1038/nature09289
Borovsky, J. E., and Cayton, T. E. (2011). Entropy mapping of the outer electron radiation belt between the magnetotail and geosynchronous orbit. J. Geophys. Res. 116, A06216. doi:10.1029/2011JA016470
Cabral, B., and Leedom, L. C. (1993). “Imaging vector fields using line integral convolution,” in Proceedings of the 20th annual conference on Computer graphics and interactive techniques (SIGGRAPH 93), 263–270.
Casanova, J., José, J., García-Berro, E., Shore, S. N., and Calder, A. C. (2011). Kelvin–Helmholtz instabilities as the source of inhomogeneous mixing in nova explosions. Nature 478, 490–492. doi:10.1038/nature10520
Chaston, C. C. (2022). Flow channels and the generation of Alfvenic turbulence along storm-time inner magnetospheric field-lines. Geophys. Res. Lett. 49, e2022GL101321. doi:10.1029/2022GL101321
Chong, G. S., Pope, S., Walker, S. N., Frahm, R. A., Zhang, T. L., and Futaana, Y. (2018). A statistical study of ionospheric boundary wave formation at Venus. J. Geophys. Res. 123, 7668–7685. doi:10.1029/2018JA025644
Connerney, J. E. P., Espley, J., Lawton, P., Murphy, S., Odom, J., Oliversen, R., et al. (2015). The MAVEN magnetic field investigation. Space Sci. Rev. 195, 257–291. doi:10.1007/s11214-015-0169-4
Dang, T., Lei, J., Zhang, B., Zhang, T., Yao, Z., Lyon, J., et al. (2022). Oxygen ion escape at Venus associated with three-dimensional Kelvin-Helmholtz instability, Geophys. Res. Lett. 49, e2021GL096961. doi:10.1029/2021GL096961
Dargent, J., Lavorenti, F., Califano, F., Henri, P., Pucci, F., and Cerri, S. S. (2019). Interplay between Kelvin Helmholtz and lower-hybrid drift instabilities. J. Plasma Phys. 85, 805850601. doi:10.1017/S0022377819000758
Delamere, P. A., Wilson, R. J., Eriksson, S., and Bagenal, F. (2013). Magnetic signatures of Kelvin-Helmholtz vortices on Saturn's magnetopause: global survey. J. Geophys. Res. 118, 393–404. doi:10.1029/2012JA018197
Fujimoto, M., and Terasawa, T. (1994). Anomalous ion mixing within an MHD scale Kelvin-Helmholtz vortex. J. Geophys. Res. 99, 8601–8613. doi:10.1029/93ja02722
Halekas, J. S., Taylor, E. R., Dalton, G., Johnson, G., Curtis, D. W., McFadden, J. P., et al. (2015). The solar wind ion analyzer for MAVEN. Space Sci. Rev. 195, 125–151. doi:10.1007/s11214-013-0029-z
Hasegawa, H., Fujimoto, M., Phan, T. D., Rème, H., Balogh, A., Dunlop, M. W., et al. (2004). Transport of solar wind into Earth’s magnetosphere through rolled-up Kelvin–Helmholtz vortices. Nature 430, 755–758. doi:10.1038/nature02799
Hillier, A., and Arregui, I. (2019). Coronal cooling as a result of mixing by the nonlinear kelvin–helmholtz instability. ApJ 885, 101. doi:10.3847/1538-4357/ab4795
Hwang, K.-J., Wang, C.-P., Nykyri, K., Hasegawa, H., Tapley, M. B., Burch, J. L., et al. (2023). Kelvin-Helmholtz instability-driven magnetopause dynamics as turbulent pathway for the solar wind-magnetosphere coupling and the flank-central plasma sheet communication. Front. Astron. Space Sci. 10, 1151869. doi:10.3389/fspas.2023.1151869
Inui, S., Seki, K., Sakai, S., Brain, D. A., Hara, T., McFadden, J. P., et al. (2019). Statistical study of heavy ion outflows from Mars observed in the Martian-induced magnetotail by MAVEN. J. Geophys. Res. 124, 5482–5497. doi:10.1029/2018JA026452
Jakosky, B. M., Brain, D., Chaffin, M., Curry, S., Deighan, J., Grebowsky, J., et al. (2018). Loss of the Martian atmosphere to space: present-day loss rates determined from MAVEN observations and integrated loss through time. Icarus 315, 146–157. doi:10.1016/j.icarus.2018.05.030
Kavosi, S., Raeder, J., Johnson, J. R., Nykyri, K., and Farrugia, C. J. (2023). Seasonal and diurnal variations of Kelvin-Helmholtz Instability at terrestrial magnetopause. Nat. Comm. 14, 2513. doi:10.1038/s41467-023-37485-x
Matsumoto, Y., Asahina, Y., Kudoh, Y., Kawashima, T., Matsumoto, J., Takahashi, H. R., et al. (2019). Magnetohydrodynamic simulation code CANS+: assessments and applications. Publ. Astron. Soc. Jpn. 71. doi:10.1093/pasj/psz064
Matsumoto, Y., and Seki, K. (2010). Formation of a broad plasma turbulent layer by forward and inverse energy cascades of the Kelvin-Helmholtz instability. J. Geophys. Res. 115, A10231. doi:10.1029/2009JA014637
Matthaeus, W. H., Qin, G., Bieber, J. W., and Zank, G. P. (2003). Nonlinear collisionless perpendicular diffusion of charged particles. Astrophys. J. 590, L53–L56. doi:10.1086/376613
McFadden, J. P., Kortmann, O., Curtis, D., Dalton, G., Johnson, G., Abiad, R., et al. (2015). MAVEN SupraThermal and thermal ion compostion (STATIC) instrument. Space Sci. Rev. 195, 199–256. doi:10.1007/s11214-015-0175-6
Michael, A. T., Sorathia, K. A., Merkin, V. G., Nykyri, K., Burkholder, B., Ma, X., et al. (2021). Modeling Kelvin-Helmholtz instability at the high latitude boundary layer in a global magnetosphere simulation. Geophys. Res. Lett. 48, e2021GL094002. doi:10.1029/2021GL094002
Miura, A., and Pritchett, P. L. (1982). Nonlocal stability analysis of the MHD Kelvin-Helmholtz instability in a compressible plasma. J. Geophys. Res. 87, 7431–7444. doi:10.1029/ja087ia09p07431
Miyoshi, T., and Kusano, K. (2005). A multi-state HLL approximate Riemann solver for ideal magnetohydrodynamics. J. Comput. Phys. 208, 315–344. doi:10.1016/j.jcp.2005.02.017
Poh, G., Espley, J. R., Nykyri, K., Fowler, C. M., Ma, X., Xu, S., et al. (2021). On the growth and development of nonlinear Kelvin–Helmholtz instability at Mars: MAVEN observations. J. Geophys. Res. 126, e2021JA029224. doi:10.1029/2021JA029224
Price, D. J., and Rosswog, S. (2006). Producing ultrastrong magnetic fields in neutron star mergers. Science 312, 719–722. doi:10.1126/science.1125201
Ruhunusiri, S., Halekas, J. S., McFadden, J. P., Connerney, J. E. P., Espley, J. R., Harada, Y., et al. (2016). MAVEN observations of partially developed Kelvin-Helmholtz vortices at Mars. Geophys. Res. Lett. 43, 4763–4773. doi:10.1002/2016gl068926
Seki, K., Hirahara, M., Hoshino, M., Terasawa, T., Elphic, R. C., Saito, Y., et al. (2003). Cold ions in the hot plasma sheet of Earth’s magnetotail. Nature 422, 589–592. doi:10.1038/nature01502
Slavin, J. A., Acuna, M. H., Anderson, B. J., Baker, D. N., Benna, M., Gloeckler, G., et al. (2008). Mercury's magnetosphere after MESSENGER's first flyby. Science 321, 85–89. doi:10.1126/science.1159040
Suresh, A., and Huynh, H. T. (1997). Accurate monotonicity-preserving schemes with Runge–Kutta time stepping. J. Comput. Phys. 136, 83–99. doi:10.1006/jcph.1997.5745
Trotignon, J. G., Mazelle, C., Bertucci, C., and Acuña, M. (2006). Martian shock and magnetic pile-up boundary positions and shapes determined from the Phobos 2 and Mars Global Surveyor data sets. Planet. spa. Sci. 52, 357–369. doi:10.1016/j.pss.2006.01.003
Wan, W. C., Malamud, G., Shimony, A., Di Stefano, C., Trantham, M., Klein, S., et al. (2015). Observation of single-mode, kelvin-helmholtz instability in a supersonic flow. Phys. Rev. Lett. 115, 145001. doi:10.1103/PhysRevLett.115.145001
Wang, L., Huang, C., Du, A., Ge, Y., Chen, G., Yang, Z., et al. (2023). Kelvin–helmholtz instability at Mars: in situ observations and kinetic simulations. Astrophys. J. 947, 51. doi:10.3847/1538-4357/acc655
Keywords: Kelvin–Helmholtz instability, Mars, density gradient, compressibility, cold plasma, MAVEN
Citation: Seki K, Matsumoto Y, Terada N, Hara T, Brain DA, Nakagawa H, McFadden JP, Halekas JS, Ruhunusiri S, Mitchell DL, Andersson L, Espley JR, Baker DN, Luhmann JG and Jakosky BM (2024) Characteristics of plasma boundaries with large density gradients and their effects on Kelvin–Helmholtz instability. Front. Astron. Space Sci. 11:1394817. doi: 10.3389/fspas.2024.1394817
Received: 02 March 2024; Accepted: 29 April 2024;
Published: 31 May 2024.
Edited by:
Gian Luca Delzanno, Los Alamos National Laboratory (DOE), United StatesReviewed by:
Kareem Sorathia, Johns Hopkins University, United StatesCopyright © 2024 Seki, Matsumoto, Terada, Hara, Brain, Nakagawa, McFadden, Halekas, Ruhunusiri, Mitchell, Andersson, Espley, Baker, Luhmann and Jakosky. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: K. Seki, ay5zZWtpQGVwcy5zLnUtdG9reW8uYWMuanA=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.