Numerical model of the QiTai radio Telescope PAF receiver signal and simulation of interference mitigation

Xinjiang Qitai is constructing a 110-m fully steerable radio telescope (QiTai radio Telescope [QTT]) equipped with a phased array feeds (PAF) receiver, which will install the focal plane operating from 0.7 to 1.8 GHz. In this article, we introduce a PAF receiver model for beamforming, and the numerical model of the internal and external noise for this PAF receiver is provided using electromagnetic field simulation software. The linear constraint minimum variance (LCMV) algorithm is used to simulate the interference mitigation. The interference mitigation rate is from 0.581 to 0.921, and the signal restoration rate is from 0.998 to 1.512 within the error range of an interference arrival angle of 10°. This conclusion can be used in the signal correction of the PAF receiver for interference mitigation.

1 Introduction

The phased array feeds (PAF) receiver has been extensively studied worldwide as it is considered the next-generation receiver for telescopes. Compared to the horn receiver, which has a single-point receiving system, the PAF receiver is a multi-point (19–200) receiving system placed on the focal plane of telescopes (Warnick et al., 2016). The benefits of PAF receivers include a continuous field of view, flexible beam control, and active interference mitigation.

The search for faint astronomical signals is often limited by relatively large noise and interference in radio telescopes. The utilization of a PAF receiver in a telescope can result in increased system fluctuations, thereby leading to an increase in noise variance. This effect cannot be eliminated by integration (Jeffs et al., 2008). For single-dish radio telescopes, these noise sources include, but are not limited to, spillover noise observed by the PAF receiver from beyond the reflector edge; sky noise collected by the main and side beams of the telescope pattern, as shown in Figure 1; cross-coupling between the closely packed elements of the array (Warnick et al., 2009b); and additional noise due to resistance losses in the connector between the antenna, cable, and low-noise amplifier (LNA), as shown in Figure 2.

The QiTai radio Telescope (QTT), the largest fully steerable single-dish radio telescope currently under construction, has been selected by $Nature$ as the most noteworthy science project in 2023¹. The QTT will install a 192-element $(96\times 2)$ array dual-polarized PAF (QTT-PAF) receiver operating from 0.7 to 1.8 GHz (Wang, 2014; Ma et al., 2019). A parabolic antenna of 110 m and a single-polarized PAF composed of 25 Vivaldi antennas have been established and simulated, with a 2D model of a Vivaldi antenna being presented. Based on this model, the detailed noise environment of this telescope model is established, followed by the application of the linear constraint minimum variance (LCMV) algorithm for beamforming. The operational performance of the telescope is affected by errors arising from telescope pointing, receiver–telescope matching, and system phase shift, resulting in deviations in estimating the arrival angle of interference. Within the error range of 10° interference arrival angle, we calculate the interference mitigation rate and the signal restoration rate, which are valuable in the correction of cosmic signal power estimation.

Figure 1

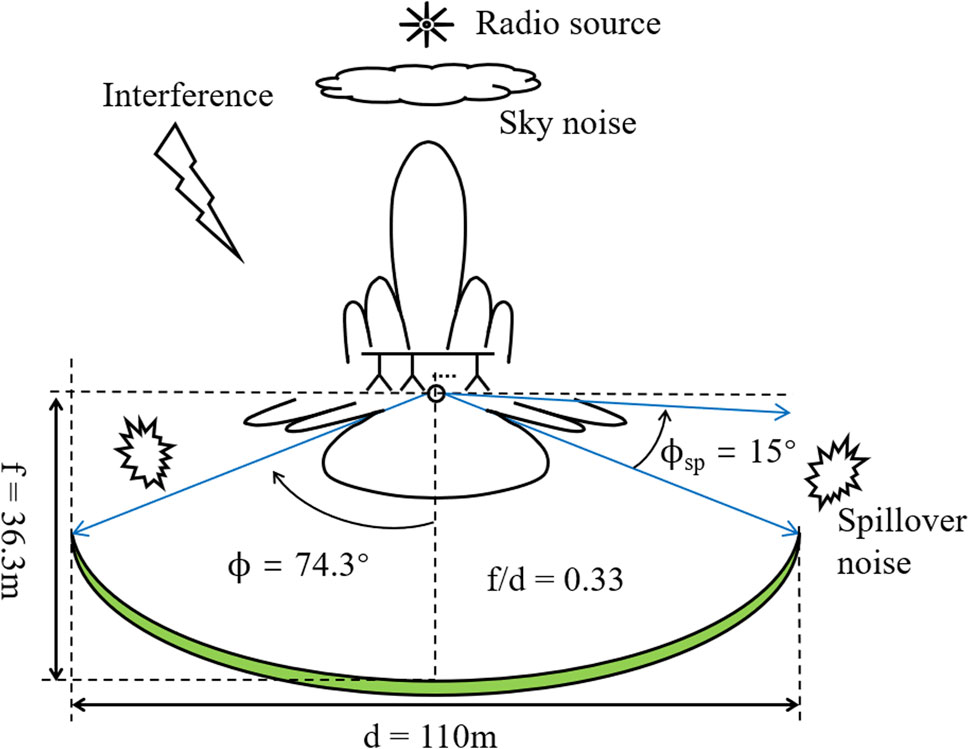
Figure 1. Sky noise and spillover noise diagram of the QTT-PAF receiver, when the telescope is pointed at the zenith.

Figure 2

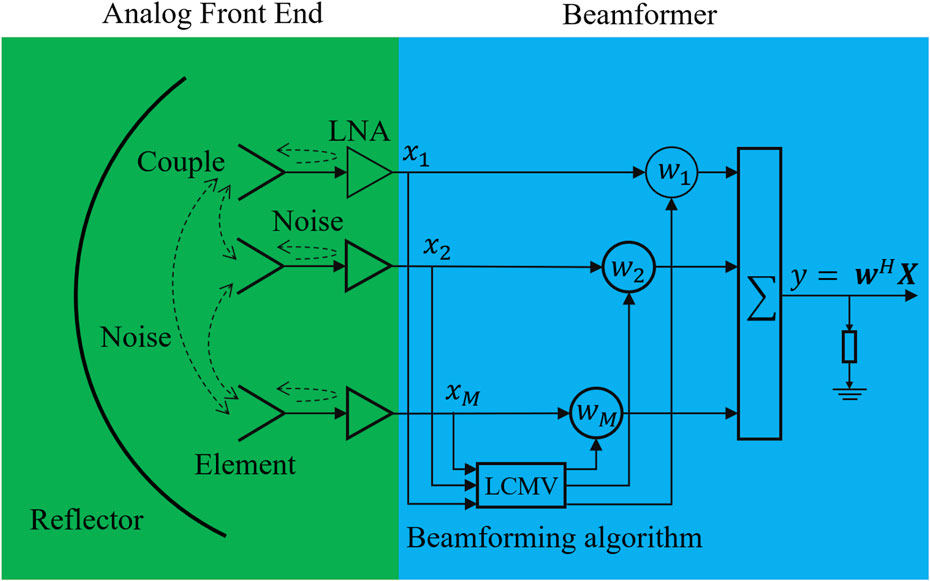
Figure 2. Beamforming schematic diagram of the PAF receiver. Here, the dashed line represents the noise caused by the coupling, connector, and LNA.

This paper aims to investigate and establish the noise environment of the QTT-PAF receiver and to offer a numerical model for noise and interference mitigation in the design of the array and beamforming algorithm of the QTT-PAF receiver. At the same time, it is also important to obtain the relation between the interference arrival angle error, interference mitigation, and signal restoration, which is helpful in the correction of system errors and the estimation of cosmic signal power. Furthermore, this research can also provide theoretical validation and an experimental foundation for the pre-project research and development.

2 The mathematical principles of the PAF beamformer

2.1 Signal stream of the PAF receiver

Figure 2 shows a PAF receiving system with $M$ elements. This system is divided into two parts: 1) analog front end, which consists of a reflector, PAF, and LNA, and 2) beamformer, which consists of a beamforming algorithm and power adder with complex weight. Here, $\mathit{X}={[x_1,\dots ,x_M]}^T$ represents the input of the beamformer (the output of the LNA), ${[\cdot ]}^T$ for transpose. In addition, ${\mathit{w}}^H=[w_1^{*},\dots ,w_M^{*}]$ is the complex weight of the power adder (the LCMV algorithm output), and ${[\cdot ]}^{*}$ and ${[\cdot ]}^H$ represent the conjugate and conjugate transpose, respectively. It is obtained by using a beamforming algorithm to calculate sampling data in a short-time integration (STI) window. Therefore, the accuracy of the interference arrival angle is negatively correlated with the size of the STI window. At this point, the output of the beamformer is displayed as $y={\mathit{w}}^H\mathit{X}$.

2.2 Signal analysis

The sensitivity metric $A_{\mathit{eff}}/T_{\mathit{sys}}$, which is the effective area of the antenna system divided by the system equivalent noise temperature, can be expressed in terms of the signal-to-noise ratio (SNR) and the normalized flux density $F_{\mathit{source}}$ of the radio source (in jansky, $1[Jy]=10^{-26}[W{m}^{-2}H{z}^{-1}]$) as (Warnick and Jeffs, 2008)

$\frac{A_{\mathit{eff}}}{T_{\mathit{sys}}}=\frac{2k_B}{F_{\mathit{source}}}\text{SNR},\text{SNR}=\frac{\mathit{w}{\mathit{R}}_X\mathit{w}}{\mathit{w}{\mathit{R}}_{n+I}\mathit{w}},(1)$

where $k_B$ is Boltzmann’s constant, ${\mathit{R}}_X$ is the signal-of-interest (SOI) covariance matrix, and ${\mathit{R}}_{n+I}$ is the sum of covariance matrix interference ${\mathit{R}}_I$ and noise ${\mathit{R}}_n$. Improving the SNR by matching $\mathit{w}$ in Eq. 1 is the main method to improve the sensitivity. Eliminating ${\mathit{R}}_I$ is the main work when interference is present. ${\mathit{R}}_n$ is reduced as much as possible when there is no interference. At the same time, due to the pursuit of extreme sensitivity in radio astronomy, ${\mathit{R}}_n$ cannot be described by a simple covariance matrix of white noise. It needs to reflect the contribution of the internal and external noise of a telescope, described as ${\mathit{R}}_n={\mathit{R}}_{sp}+{\mathit{R}}_{\mathit{sky}}+{\mathit{R}}_{\mathit{ant}}+{\mathit{R}}_{\mathit{LNA}}$. ${\mathit{R}}_{sp}$ is a spillover noise matrix with non-white noise characteristics as the pattern of the PAF beamforming extends beyond the edge of the reflector surface, collecting unwanted signals from the spillover area within a limited range of angles. The main component of ${\mathit{R}}_{\mathit{ant}}$ is LNA noise, which is due to the use of the high-gain LNA at the beginning of the receiver chain. The off-diagonal terms in ${\mathit{R}}_{\mathit{ant}}$ are non-zero due to the LNA noise coupling back through array elements to neighboring closely packed antennas. As a result, the receiver noise temperature is increased by a mutual coupling noise penalty. ${\mathit{R}}_{\mathit{sky}}$ is sky background noise, including atmospheric, constant cosmic microwave background (CMB), and galactic background (GB) noise. It enters mainly from the main and side beams of a telescope, and the non-diagonal parts of ${\mathit{R}}_{\mathit{sky}}$ are also non-zero. ${\mathit{R}}_{\mathit{LNA}}$ represents the noise power of a high-gain LNA at the beginning of the receiver chain. As the thermal motion power of the electron is independent of frequency, the covariance matrix exhibits non-zero values only on the diagonal (James, 2012).

2.3 Beamforming algorithm

At present, the main algorithms used in the beamformer are based on the maximum signal-to-noise ratio (MaxSNR), minimum variance distortionless response (MVDR), subspace projection (SP), and LCMV (Jeffs et al., 2008; Warnick et al., 2009a; Ivashina et al., 2011; Young et al., 2013). The LCMV algorithm can achieve interference mitigation without affecting the main beam response. When there is no interference, it is the MVDR algorithm. Suppressing the power of interference is equivalent to controlling the PAF pattern on interference orientation in a telescope. At the same time, because of the good control of the beam, it is also applied to the multi-beam joint optimization problem of PAF. Mathematically, the weight vector ${\mathit{w}}_{\mathit{LCMV}}$ of the LCMV beamformer can be set by solving the following optimization problems:

$\begin{array}{cc}\hfill {\mathit{w}}_{\mathit{LCMV}}=& \underset{\mathit{w}}{\min }{\mathit{w}}^{H}R\mathit{w}\hfill \\ \hfill s.t.B\left({\theta }_0,{\varphi }_0,\mathit{w}\right)=& 1\hfill \\ \hfill & B\left({\theta }_k,{\varphi }_k,\mathit{w}\right)=0,k=\mathrm{1,2},\dots ,M-2,\hfill \end{array}(2)$

where ${\theta }_0$ (azimuth) and ${\varphi }_0$ (elevation) are the solid angles of the SOI for the PAF receiver. ${\theta }_k$ and ${\varphi }_k$ are $k$ interference spherical angles. Since $M$ arrays can provide $M-1$ constraints, the number of disturbances that need to be constrained should not exceed $M-2$ for a given astronomical information response constraint. Since all constraints are linear in the complex field, the solution can be obtained using the Lagrange multiplier method.

3 Simulation

This section presents the simulated signals used for beamforming and the hardware model to generate these signals. Antenna simulation software and the PAF signal generator mentioned by Wu et al. (2024) are mainly used in the experiment. Finally, the relationship between the interference arrival angle and interference mitigation and signal restoration in the LCMV beamfromer of Eq. 2 is calculated.

3.1 Model of the 110-m reflector and 25 Vivaldi PAF antennas

The QTT-PAF receiver is designed to operate at a center frequency of 1.25 GHz, with the array element being a Vivaldi antenna, and the operating temperature is 20 k in a cryogenic environment. The design of the QTT-PAF receiver has not yet been completed. The antenna model used for generating the simulation signal consists of 25 Vivaldi antennas arranged in a quadrilateral pattern on the focal plane of a 110-m parabolic reflector, as depicted in Figure 3. This section introduces a 2D Vivaldi antenna model, which does not compromise the principle of beamforming. Figure 4 illustrates the Vivaldi antenna model and the parameters of its quadrilateral arrangement. Due to computer memory constraints, the antenna model is divided into 192,680 grids. The pattern of all array elements under uniform excitation is shown in Figure 5.

Figure 3

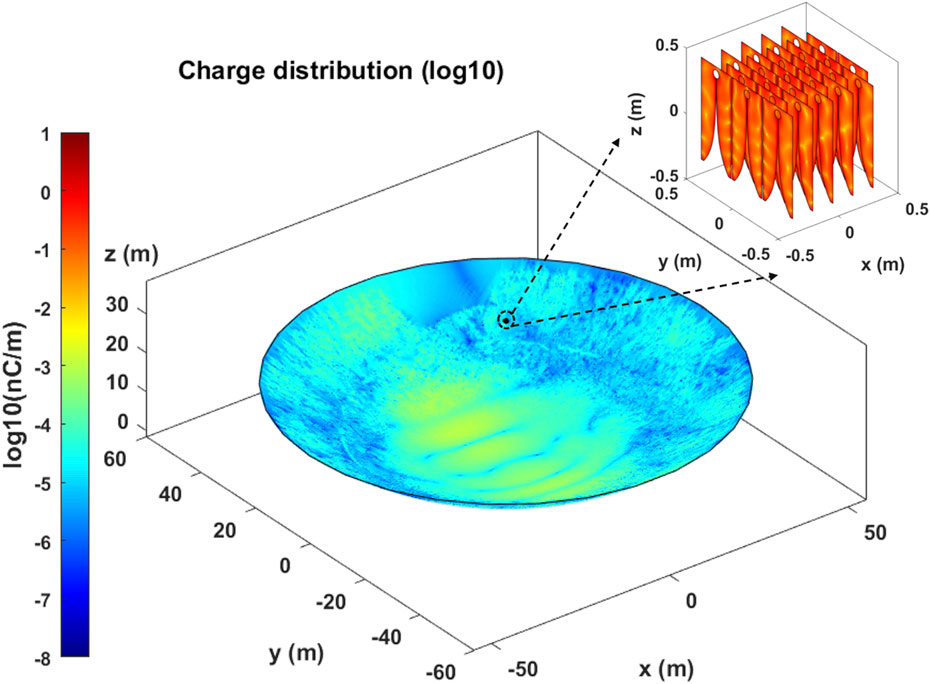
Figure 3. Charge distribution of a 110-m parabola antenna in the illumination of a PAF receiver consisting of 25 Vivaldi antennas. All Vivaldi antennas are unit-excited and operate at 1.25 GHz.

Figure 4

Figure 4. Planar diagram of the array and charge diagram of the 2D Vivaldi model (unit excitation).

Figure 5

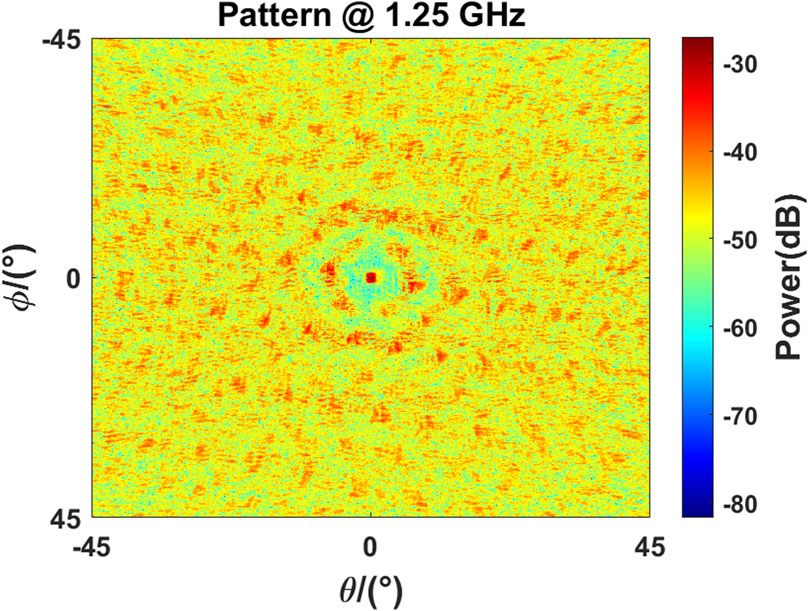
Figure 5. 2D beam image in the model in Figure 3; the display range is 90 square degrees, and the operating frequency is 1.15 GHz.

3.2 The numerical model of noise

In radio astronomy, electric power is equated to temperature. The relationship between the average electrical power $P$ per unit bandwidth and the temperature $T$ is $P=k_{B}T$, when the impedance is matched. The numerical model of PAF system noise can be established by using antenna analysis technology and electromagnetic field simulation software. According to the principle of electromagnetic reciprocity, the signal response of the array in the $(\theta ,\varphi )$ orientation can be obtained from the pattern $P(\theta ,\varphi )$, which is the pattern of the array under unit excitation. Then, the array response in an orientation can also be obtained from $P(\theta ,\varphi )$. The correlation matrix of the signal response (Jeffs et al., 2008) of the non-point source is described as

$R=16k_{B}TB\mathfrak{C}{A}_{\mathrm{\Omega }}{\mathfrak{C}}^H,(3)$

where $B$ is the bandwidth, $A_{\mathrm{\Omega }}$ is the integral matrix of the non-point source pattern, and $A_{\mathrm{\Omega }}={\iint }_{\mathrm{\Omega }}p(\theta ,\varphi )p^{*}(\theta ,\varphi )d\theta d\varphi$, where $\mathrm{\Omega }$ is the solid angle of the noise reception. $\mathfrak{C}$ is the impedance coefficient vector calculated using electromagnetic field simulation software. Figure 6 shows a correlation matrix of impedance coefficients of 25 elements, i.e., $\mathfrak{C}{\mathfrak{C}}^H$. For ${\mathit{R}}_{sp}$, the focal ratio of the 110-m parabolic antenna is 0.33, and the spillover angle of the PAF receiver ranges from 0° to −15.7°. To facilitate the calculation and avoid considering noise from long distances near the horizon, the spillover angle selected for the simulation ranges from −1° to −15°, as depicted in Figure 1. The angle interval used is 0.1°, consistent throughout the experiment. The spillover pattern of the 25 Vivaldi antennas under uniform excitation is shown in Figure 7. Assuming that the temperature of the warm ground is 298.5 K, the resulting ${\mathit{R}}_{sp}$ is shown in Figure 8. For ${\mathit{R}}_{\mathit{sky}}$, we consider noise entering the elevation range from 35° to 90°, which predominantly includes the main beam and several side beams. The pattern, shown in Figure 9, is obtained through the joint simulation of all array elements and the parabolic antenna under uniform excitation. Assuming that the atmospheric noise is 15 K and the cosmic microwave background (CMB) is 3 K, the resulting ${\mathit{R}}_{\mathit{sky}}$ is depicted in Figure 10. For ${\mathit{R}}_{\mathit{LNA}}$, the LNA of the QTT-PAF receiver has a design index of 6 k under cryogenic conditions, which cannot be represented by white noise only due to the mutual coupling, as shown in Figure 11. Due to the scope simulation, the loss of the antenna is not included. Finally, for the overall receiver operating temperature of 20 k, the remaining 14 k noise contribution is replaced by white noise.

Figure 6

Figure 6. Correlation matrix of impedance coefficients of 25 elements.

Figure 7

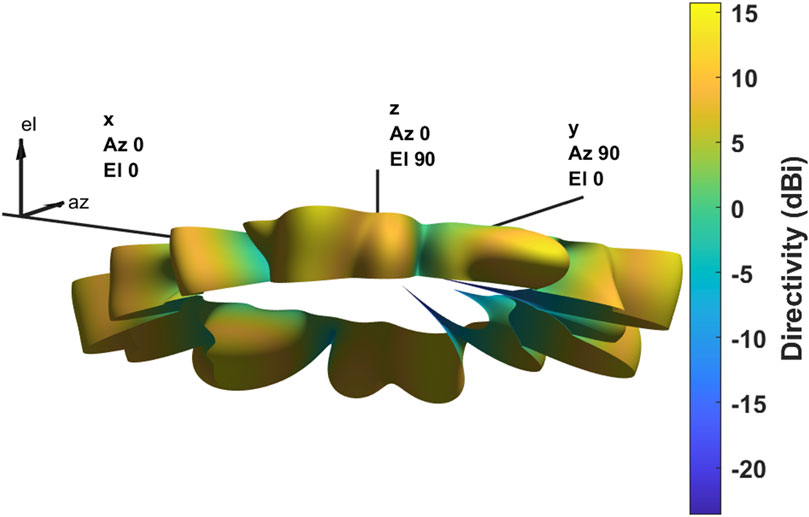
Figure 7. Pattern of PAF spillover noise, i.e., the pattern of ${\varphi }_{sp}$ in Figure 1.

Figure 8

Figure 8. Covariance matrix of spillover noise in the telescope.

Figure 9

Figure 9. Pattern of the telescope-collected noise from the sky.

Figure 10

Figure 10. Covariance matrix of sky noise in the telescope.

Figure 11

Figure 11. Covariance matrix of LNA noise in the PAF receiver.

3.3 Beamforming and interference mitigation

The minimum signal power that a radio telescope can detect is limited by the variance of the noise. Usually, the SOI enters along the main beam of a telescope, and the interference enters through the side beam, and these and the noise are uncorrelated to each other. The covariance matrix of the output signal of the PAF receiver can be described as ${\mathit{R}}_x={\mathit{R}}_{\mathit{SOI}}+{\mathit{R}}_I+{\mathit{R}}_{\mathit{noise}}$, where ${\mathit{R}}_{\mathit{SOI}}$ and ${\mathit{R}}_I$ are the covariance matrix of the SOI and interference, respectively. The models for these two contributions are also described by Eq. 3, except that these are both considered point sources. The power of the SOI is limited to −20 dB below noise power and 30 dB above noise power for interference. At the same time, the STI window size is set to 1,024. In this window, interference that occurs is 40% of the size, the SOI appears 20% of the size, and they are simultaneous in time. The output of the LCMV beamformer (assuming that the arrival angle of interference is unambiguous) is shown in Figure 12. We define the interference mitigation rate as $1-\frac{P_I^{\mathit{LCMV}}}{P_I}$, where $P_I^{\mathit{LCMV}}$ is the average output power of the LCMV beamformer over the interference period and $P_I$ is the average power of the input interference. The SOI restoration rate is defined as $\frac{P_{\mathit{SOI}}^{\mathit{LCMV}}}{P_{\mathit{SOI}}}$, where $P_{\mathit{SOI}}^{\mathit{LCMV}}$ is the average output power of the LCMV beamformer during the time of SOI occurrence and $P_{\mathit{SOI}}$ is the set average power of the SOI. Finally, we present the graphical depiction of the interference mitigation rate and SOI restoration rate when the error of the spherical angle of interference remains below 10°, as shown in Figures 13, 14. Here, the beamforming weight vector ${\mathit{w}}_{\mathit{LCMV}}(\theta ,\varphi )$ for the telescope at the orientation $(\theta ,\varphi )$ during one STI is obtained by the Hadamard product of the steering vector $\mathit{w}(\theta ,\varphi )$ with the LCMV weight vector ${\mathit{w}}_{\mathit{LCMV}}$. Mathematically, this can be expressed as $\mathit{w}(\theta ,\varphi )\ast {\mathit{w}}_{\mathit{LCMV}}={\mathit{w}}_{\mathit{LCMV}}(\theta ,\varphi )$, where $\ast$ is the Hadamard product operation.

Figure 12

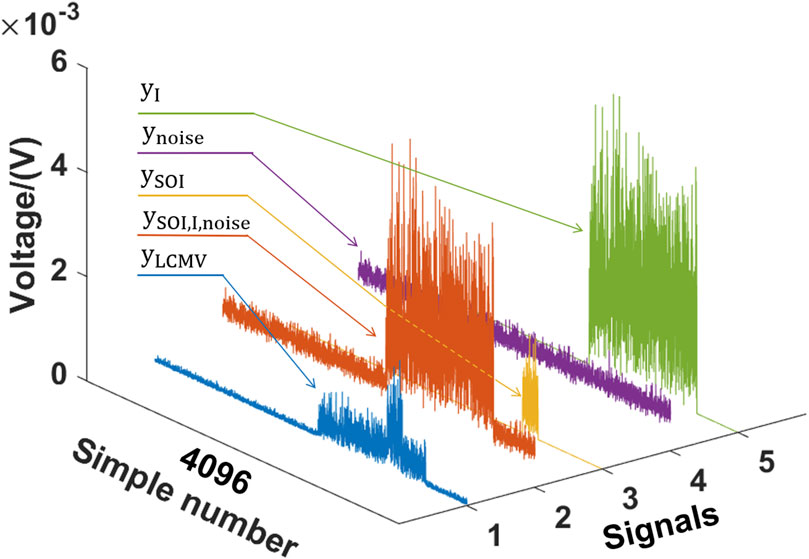
Figure 12. Voltage images of each signal over time, which are the average result of 10 STI windows. ${\mathrm{y}}_{\mathrm{I}}$, ${\mathrm{y}}_{\mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}}$, and ${\mathrm{y}}_{\mathrm{S}\mathrm{O}\mathrm{I}}$ are the given interference, noise, and SOI, respectively. ${\mathrm{y}}_{\mathrm{S}\mathrm{O}\mathrm{I},\mathrm{I},\mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}}$ is the average output of the 25 ports of LNAs. ${\mathrm{y}}_{\mathrm{l}\mathrm{c}\mathrm{m}\mathrm{v}}$ is the output of the LCMV beamformer.

Figure 13

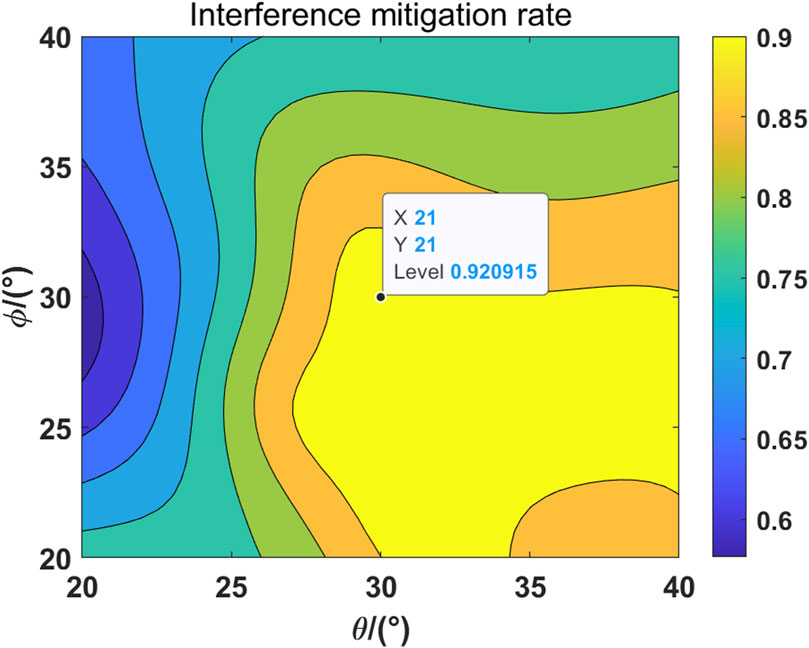
Figure 13. The relationship between the estimation of the interference arrival angle and the interference mitigation rate is plotted.

Figure 14

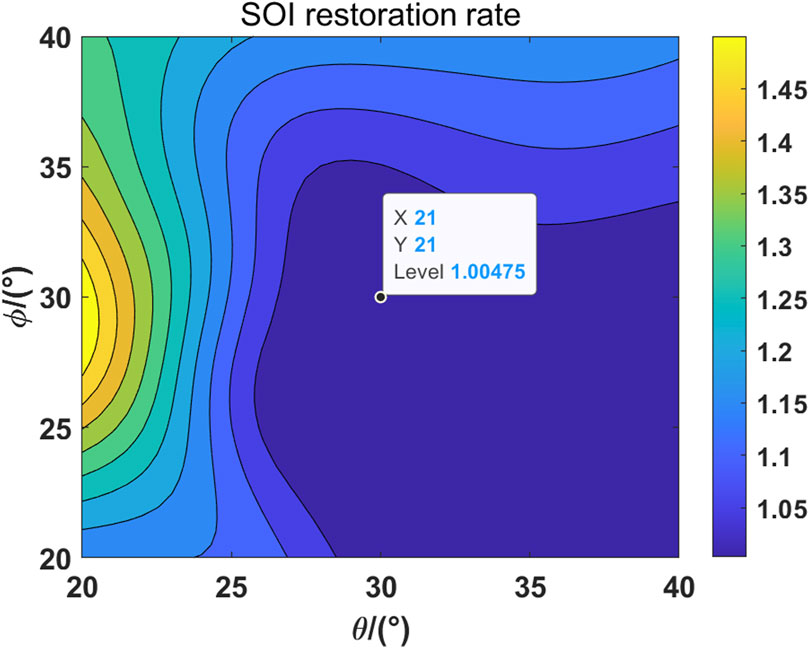
Figure 14. The relationship between the estimation of the interference arrival angle and the SOI restoration rate is plotted.

By examining Figures 12–14, it becomes evident that when there is a clear interference orientation, the LCMV algorithm demonstrates significant interference reduction. The interference mitigation rate is 0.921, and the SOI restoration rate is 1.005. It should be noted that the ratio is greater than 1 due to interference. The interference orientation vector and the SOI orientation vector are not orthogonal. With the change in the spherical angle of interference, the interference mitigation rate and the SOI restoration rate show similar patterns. We believe that the primary factors are the pattern and single polarization of the telescope. Regarding the pattern, the telescope exhibits an approximately 10 dB variation in gain on the interference within the estimated range of interference orientations. Given that the telescope’s overall dynamic range exceeds 50 dB, this change is not substantial. Furthermore, the PAF model considers only single polarization. Consequently, when the interference shifts in an orientation not aligned with the polarization, the telescope does not respond sensitively to these changes.

4 Conclusion

In this paper, the signal numerical model and interference mitigation verification under the QTT-PAF model are implemented. The PAF receiver and parabolic antenna composed of 25 array elements are co-simulated under the Vivaldi antenna model, and the internal and external noise of the system is given from the perspective of covariance. Finally, the noise is mixed into the SOI and interference, and the interference is mitigated by the LCMV algorithm. The mitigation results show that the LCMV algorithm has a good mitigation ability for interference under this model and has a small impact on the SOI, but the premise is that the interference orientation is accurately estimated.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

PW: writing–original draft and writing–review and editing. JL: funding acquisition and writing–review and editing. M-ZC: funding acquisition, project administration, supervision, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was funded by the National Key R&D Program of China under Grant No. 2022YFC2205300, the National Natural Science Foundation of China (12073067), and the Chinese Academy of Sciences (CAS) “Light of West China” Program under Grant No. 2022-XBQNXZ-012.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹https://www.nature.com/articles/d41586-022-04444-3

References

Ivashina, M. V., Iupikov, O., Maaskant, R., van Cappellen, W. A., and Oosterloo, T. (2011). An optimal beamforming strategy for wide-field surveys with phased-array-fed reflector antennas. IEEE Trans. Antennas Propag. 59, 1864–1875. doi:10.1109/TAP.2011.2123865

CrossRef Full Text | Google Scholar

James, E. M. (2012) Improved methods for phased array feed beamforming in single dish radio astronomy. Provo, UT, United States; Brigham Young University. Ph.D. thesis.

Google Scholar

Jeffs, B. D., Warnick, K. F., Landon, J., Waldron, J., Jones, D., Fisher, J. R., et al. (2008). Signal processing for phased array feeds in radio astronomical telescopes. IEEE J. Sel. Top. Signal Process. 2, 635–646. doi:10.1109/JSTSP.2008.2005023

CrossRef Full Text | Google Scholar

Ma, J., Pei, X., Wang, N., Li, J., Wang, K., and Liu, Y. (2019). Ultra wideband and multi-beam signal receiving and processing system of qtt. Sci. Sinica Phys. Mech. Astronomica 49, 99502, 1–13. doi:10.1360/SSPMA-2019-0014

CrossRef Full Text | Google Scholar

Wang, N. (2014). Xinjiang Qitai 110 m radio telescope. Sci. Sinica Phys. Mech. Astronomica 44, 783–794. doi:10.1360/SSPMA2014-00039

CrossRef Full Text | Google Scholar

Warnick, K. F., and Jeffs, B. D. (2008). Efficiencies and system temperature for a beamforming array. IEEE Antennas Wirel. Propag. Lett. 7, 565–568. doi:10.1109/LAWP.2008.2001752

CrossRef Full Text | Google Scholar

Warnick, K. F., Jeffs, B. D., Landon, J., Waldron, J., Jones, D., Richard Fisher, J., et al. (2009a). “Beamforming and imaging with the byu/nrao l-band 19-element phased array feed,” in 2009 13th International Symposium on Antenna Technology and Applied Electromagnetics and the Canadian Radio Science Meeting, Banff, AB, February 15–18, 2009 (IEEE) 1–4. doi:10.1109/ANTEMURSI.2009.4805125

CrossRef Full Text | Google Scholar

Warnick, K. F., Maaskant, R., Ivashina, M. V., Davidson, D. B., and Jeffs, B. D. (2016). High-sensitivity phased array receivers for radio astronomy, Proc. IEEE 104 (3), 607–622. doi:10.1109/JPROC.2015.2491886

CrossRef Full Text | Google Scholar

Warnick, K. F., Woestenburg, B., Belostotski, L., and Russer, P. (2009b). Minimizing the noise penalty due to mutual coupling for a receiving array. IEEE Trans. Antennas Propag. 57, 1634–1644. doi:10.1109/TAP.2009.2019898

CrossRef Full Text | Google Scholar

Wu, P., Li, J., and Chen, M.-Z. (2024). Simulation of rfi cancellation using subspace projection algorithm for paf receiver. Res. Astron. Astrophys. 24, 015019. doi:10.1088/1674-4527/ad0b84

CrossRef Full Text | Google Scholar

Young, A., Ivashina, M. V., Maaskant, R., Iupikov, O. A., and Davidson, D. B. (2013). Improving the calibration efficiency of an array fed reflector antenna through constrained beamforming. IEEE Trans. Antennas Propag. 61, 3538–3545. doi:10.1109/TAP.2013.2255577

CrossRef Full Text | Google Scholar