First direct observations of interplanetary shock impact angle effects on actual geomagnetically induced currents: The case of the Finnish natural gas pipeline system

Oliveira, Denny M.; Zesta, Eftyhia; Vidal-Luengo, Sergio

doi:10.3389/fspas.2024.1392697

ORIGINAL RESEARCH article

Front. Astron. Space Sci., 10 July 2024

Sec. Space Physics

Volume 11 - 2024 | https://doi.org/10.3389/fspas.2024.1392697

This article is part of the Research Topic Space weather: Magnetosphere Ionosphere Thermosphere (M-I-T) Coupling View all 6 articles

First direct observations of interplanetary shock impact angle effects on actual geomagnetically induced currents: The case of the Finnish natural gas pipeline system

Denny M. Oliveira^1,2*

Eftyhia Zesta²

Sergio Vidal-Luengo³

¹Goddard Planetary Heliophysics Institute, University of Maryland, Baltimore, MD, United States
²Geospace Physics Laboratory, NASA Goddard Space Flight Center, Greenbelt, MD, United States
³Laboratory for Atmospheric and Space Physics, University of Colorado, Boulder, CO, United States

The impact of interplanetary (IP) shocks on the Earth’s magnetosphere can greatly disturb the geomagnetic field and electric currents in the magnetosphere-ionosphere system. At high latitudes, the current systems most affected by the shocks are the auroral electrojet currents. These currents then generate ground geomagnetically induced currents that couple with and are highly detrimental to ground artificial conductors including power transmission lines, oil/gas pipelines, railways, and submarine cables. Recent research has shown that the shock impact angle, the angle the shock normal vector performs with the Sun-Earth line, plays a major role in controlling the subsequent geomagnetic activity. More specifically, due to more symmetric magnetospheric compressions, nearly frontal shocks are usually more geoeffective than highly inclined shocks. In this study, we utilize a subset (332 events) of a shock list with more than 600 events to investigate, for the first time, shock impact angle effects on the subsequent GICs right after shock impact (compression effects) and several minutes after shock impact (substorm-like effects). We use GIC recordings from the Finnish natural gas pipeline performed near the Mäntsälä compression station in southern Finland. We find that GIC peaks ( $>$ 5 A) occurring after shock impacts are mostly caused by nearly frontal shocks and occur in the post-noon/dusk magnetic local time sector. These GIC peaks are presumably triggered by partial ring current intensifications in the dusk sector. On the other hand, more intense GIC peaks ( $>$ 20 A) generally occur several minutes after shock impacts and are located around the magnetic midnight terminator. These GIC peaks are most likely caused by intense energetic particle injections from the magnetotail which frequently occur during substorms. The results of this work are relevant to studies aiming at predicting GICs following solar wind driving under different levels of asymmetric solar wind forcing.

1 Introduction

Interplanetary (IP) shocks correspond to a kind of perturbation frequently observed in the solar wind at many locations in the heliosphere (Smith et al., 1985; Szabo et al., 2001; Aryan et al., 2014; Echer, 2019; Pérez-Alanis et al., 2023). IP shocks are formed when the relative speed between the Rankine-Hugoniot-determined shock velocity and the upstream solar wind velocity is greater than the environment magnetosonic speed (Priest, 1981; Kennel et al., 1985; Parks, 2004; Piel, 2010). This results from sharp enhancements of solar wind plasma properties (velocity, number density, temperature) and interplanetary magnetic field, known as IMF, characterizing the formation of fast forward shocks (Tsurutani et al., 2011; Oliveira, 2017). IP shocks are expected to occur during all phases of the solar cycle, but they are much more common during solar maxima (Kilpua et al., 2015; Oliveira and Raeder, 2015; Rudd et al., 2019). Strengths of IP shocks are usually represented by magnetosonic Mach numbers, the ratio between the shock/solar wind relative speed and the local magnetosonic speed (Tsurutani and Lin, 1985; Lugaz et al., 2016; Oliveira, 2017). IP shocks are usually driven by coronal mass ejections (CMEs, Tsurutani et al., 1988; Veenadhari et al., 2012) and corotating interaction regions (CIRs, Smith and Wolfe, 1976; Fisk and Lee, 1980).

The impact of IP shocks on the magnetosphere often causes geomagnetic disturbances observed in the geospace, ionosphere, and on the ground. Such responses are characterized by magnetic field disturbances at geosynchronous orbit (Kokubun, 1983; Nagano and Araki, 1984; Wing and Sibeck, 1997), field-aligned currents in the magnetosphere-ionosphere system (Moretto et al., 2000; Araki et al., 2009; Belakhovsky et al., 2017; Liu et al., 2023), sudden impulses observed in ground magnetometer data (Echer et al., 2005; Shinbori et al., 2009; Wang et al., 2010), and magnetospheric substorms triggered by explosive energy release by the Earth’s magnetotail (Kokubun et al., 1977; Zhou and Tsurutani, 2001; Milan et al., 2017). More important for this work, IP shocks trigger ground dB/dt variations that can be observed at high latitudes (Pulkkinen et al., 2017; Ngwira et al., 2018), mid latitudes (Marshall et al., 2011; Fiori et al., 2014), low/equatorial latitudes (Carter et al., 2015; Nilam et al., 2023), and everywhere (Tsurutani and Lakhina, 2014). Such field variations connect to ground conductors through geoelectric fields according to Faraday’s law $(\vec{\nabla} \times \vec{E} = - \partial \vec{B} / \partial t)$ which in turn generate geomagnetically induced currents (GICs) (Boteler et al., 1998; Viljanen, 1998; Tsurutani and Lakhina, 2014). Therefore, ground dB/dt variations and auroral electroject variations (in the east-west and other directions) are recognized as the space weather drivers of GICs (Dimmock et al., 2019; Tsurutani and Hajra, 2023; ?). However, a model of the Earth’s conductivity must be used in order to characterize GICs triggered by enhanced geoelectric fields (Viljanen et al., 2006; Pulkkinen et al., 2007; Bedrosian and Love, 2015). GIC effects can be detrimental to artificial conductors found in ground power transmission lines (Erinmez et al., 2002; Trivedi et al., 2007; Pulkkinen et al., 2017; Piccinelli and Krausmann, 2018), old telegraph wires (Barlow, 1849, Arcimis, 1903; Hayakawa et al., 2020b), oil and gas pipelines (Campbell, 1980; Martin, 1993; Gummow and Eng, 2002), railways (Kasinskii et al., 2007; Love et al., 2019; Patterson et al., 2023), and submarine cables (Chakraborty et al., 2022; Boteler et al., 2024).

Geomagnetic activity triggered by IP shocks is significantly controlled by shock impact angles, which correspond to the angle the normal vector performs with the Sun-Earth line. More specifically, the more frontal the shock impact, the higher the subsequent geomagnetic activity. In general, for Earth-bound shocks observed at L1 CME-driven shocks have their shock normals aligned with the Sun-Earth line due to radial CME propagation (Klein and Burlaga, 1982; Gulisano et al., 2010; Salman et al., 2020), whereas CIR-driven shocks are more inclined due to the twisted nature of the Parker spiral (Pizzo, 1991; Jian et al., 2006; Rout et al., 2017). Thus, possible shock normal deviations caused by interplanetary medium variations, such as magnetic field and plasma density (Temmer et al., 2023), are neglegible. Many numerical and experimental studies have shown that shocks with small inclinations tend to trigger more intense field-aligned currents (Guo et al., 2005; Selvakumaran et al., 2017; Shi et al., 2019); cause sudden impulse events with shorter rise times (Takeuchi et al., 2002; Wang et al., 2006; Rudd et al., 2019), and can determine whether substorms are triggered or not (Oliveira and Raeder, 2014; 2015; Oliveira et al., 2021). In addition, Oliveira et al. (2018) showed that nearly frontal and high-speed shocks drive more intense ground dB/dt variations at all latitudes right after shock impacts. Oliveira et al. (2021) showed in a comparative study that a nearly frontal shock triggered a substorm much more intense than a substorm triggered by a highly inclined shock, even though both shocks had similar strengths. They attributed these observations to the fact that the magnetosphere was more rapidly and symmetrically compressed in the nearly frontal shock case, while the compression was slower and asymmetric in the highly inclined case. As a result, ground dB/dt variations were more intense, occurred earlier, and covered larger geographic areas in North America and Greenland as indicated by a large array of ground magnetometers. These results were confirmed by the superposed epoch analysis study reported by Oliveira et al. (2024) with similar data. In general, most works agree that more frontal shocks, in comparison to inclined shocks, tend to compress the magnetosphere more symetrically enhancing current systems in the magnetosphere and ionosphere more effectively, which in turn leads to higher geomagnetic activity, as reviewed by Oliveira and Samsonov (2018) and more recently by Oliveira (2023a).

Viljanen et al. (2010) reported on a statistical study of GICs in southern Finland covering approximately one solar cycle. The authors catalogued the highest GIC amplitudes in the period of 1999–2010. Viljanen et al. (2010) concluded that the GIC peaks occurred mostly during intense magnetic storms near solar maximum. Tsurutani and Hajra (2021) used the same GIC data set to investigate the solar wind and magnetospheric conditions associated with GIC peaks larger than 30 A in a more extensive period (1999–2019). In that work, it was concluded that such extremely high GIC peaks mostly occurred during magnetospheric super substorms, which take place when ground magnetometers show intense activity of the westward auroral electrojet with lower envelope indices $< -$ 2,500 nT (Tsurutani et al., 2015; Hajra and Tsurutani, 2018; Zong et al., 2021). Although these works advanced our understanding of GIC enhancements at high latitudes during magnetic storm times, they did not provide a link between magnetospheric compressions caused and substorms triggered by IP shocks with different inclinations. As we will show in this paper, shock-induced GICs can also pose serious threats to artificial conductors in long-, mid-, and short-term regimes. The results presented in this work also have important implications to GIC forecasting, since IP shock impact angles can be forecasted in a time window of up to 2 h before shock impacts on the Earth’s magnetosphere (Paulson et al., 2012; Oliveira et al., 2018; Smith et al., 2020).

Although some works have shown that shock impact angles significantly affect ground dB/dt variations, direct shock impact angle effects on actual GICs flowing in ground conductors have not been shown yet. The main goal of this work is to show, for the first time, with GIC data collected at a natural gas pipeline in southern Finland, how shock impact angles, combined with the pipeline’s local time, affect the subsequent GIC enhancements. The remainder of the paper is organized as follows. Section 2 presents the data. Section 3 presents the results. The main results are discussed in section 4. Finally, Section 5 summarizes and concludes the article.

2 Data

2.1 Solar wind plasma and IMF data

In this work, we use the IP shock list provided by Oliveira (2023b). The list currently contains 603 events from January 1995 to May 2023. However, due to GIC data availability (see below), only 332 events from the list can be used in this study. The available events occurred from January 1999 to May 2023. Wind and ACE (Advanced Composition Explorer) solar wind plasma (particle number density, velocity, and temperature), and IMF data are used for shock detection and property computations. Solar wind data is explained by Ogilvie et al. (1995) for Wind, and by McComas et al. (1998) for ACE, whereas IMF data is detailed in Lepping et al. (1995) for Wind, and in Smith et al. (1998) for ACE. Before the computation of shock properties, the data was processed and interpolated as described in detail by Oliveira (2023b).

2.2 Computation of shock impact angles and speeds

Shock properties including shock impact angles $(θ_{x_{n}})$ and shock speeds are computed with the Rankine-Hugoniot (RH) conditions. These conditions assume that energy and momentum across the shock front, normal magnetic field component, and tangential electric field component are conserved (Priest, 1981; Parks, 2004; Piel, 2010). Such effects are computed with RH equations using solar wind velocity data, magnetic field data, and equations that combine both data sets. For example, a shock normal vector can be calculated with the equation (Oliveira, 2017; 2023b):

\vec{n} = \pm \frac{{\vec{B}}_{u} \times ({\vec{V}}_{d} - {\vec{V}}_{u}) \times ({\vec{B}}_{d} - {\vec{B}}_{u})}{| {\vec{B}}_{u} \times ({\vec{V}}_{d} - {\vec{V}}_{u}) \times ({\vec{B}}_{d} - {\vec{B}}_{u}) |} . (1)

In Equation 1, $\vec{B}$ is the magnetic field vector, and $\vec{V}$ is the solar wind velocity vector. The indices u and d indicate observations in the upstream (non-shocked) and downstream (shocked) environments, respectively. Then, from a three-dimensional shock vector calculated with Equation 1 and given by $\vec{n} = (n_{x}, n_{y}, n_{z})$ , $θ_{x_{n}}$ can be computed as

θ_{x_{n}} = \cos^{- 1} (n_{x}) . (2)

We choose the (−) sign of $\vec{n}$ for $θ_{x_{n}}$ defined in Geocentric Solar Ecliptic (GSE) coordinates because shock normals point toward the Earth in this case (Schwartz, 1998). Since the shocks are defined in GSE coordinates, a shock with $θ_{x_{n}}$ = 180° indicates a purely frontal shock, whereas a shock with 90 $° < θ_{x_{n}}$ $<$ 180° indicates an inclined shock, with the shock being more inclined as $θ_{x_{n}}$ decreases. Figure 1 of Oliveira (2023a) shows pictorial representations of a purely frontal shock and a highly inclined shock. Additionally, animations showing simulations of two shocks with different inclinations using real data can be found here: https://dennyoliveira.weebly.com/phd.html.

Figure 1

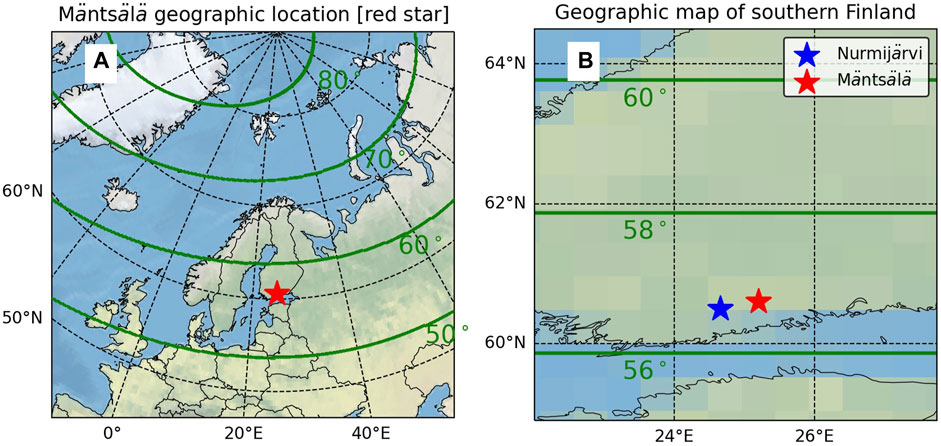
Figure 1. Panel (A) Geographic position of the Mäntsälä compression station in southern Finland (red star). The thick green lines are the magnetic latitudes from 50° in increments of 10° poleward. Panel (B) snapshot of a southern Finland map showing the Nurmijärvi station (blue star), and the Mäntsälä compression station (red star).

According to the RH conditions, shock speeds of shocks with different inclinations can be calculated according to the expression (Oliveira, 2017; 2023b):

v_{s} = \frac{(N_{d} {\vec{V}}_{d} - N_{u} {\vec{V}}_{u}) \cdot \vec{n}}{N_{d} - N_{u}}, (3)

where N is the solar wind particle number density. As a result, the magnetosonic Mach number M_s is computed as M_s = $u_{r} / v_{m s}^{f}$ , where $u_{r} = v_{s} - | {\vec{V}}_{u} |$ , and $v_{m s}^{f}$ is the fast magnetosonic speed. A solar wind structure is classified as a true IP shock if M_s > 1. See section 2.3 of Oliveira (2023b) for more details.

2.3 Ground magnetometer data

Geomagnetic activity is represented by SuperMAG ground geomagnetic indices. SuperMAG data comprises of an array with hundreds of stations located worldwide for the computation of several geomagnetic indices to capture effects of magnetospheric and ionospheric currents at different latitudes (Gjerloev, 2009). Ring current effects are accounted for by the SuperMAG ring current SMR index (Newell and Gjerloev, 2012), whereas auroral electrojet effects are represented by the SuperMAG total and regional SMU (upper envelope) and SML (lower envelope) indices (Newell and Gjerloev, 2012). As detailed by Newell and Gjerloev (2012), the SMR index is similar to the SYM-H index (Iyemori, 1990), but more low- and mid-latitude stations are used to compute the SMR index. Similar explanations are provided by Newell and Gjerloev (2011), who detail how the SMU and SML indices are calculated with more high-latitude stations in comparison to the traditional AU and AL indices (Davis and Sugiura, 1966). All SuperMAG data used in this study are 1-min resolution data.

Local ground-based magnetic field response is represented by IMAGE (International Monitor for Auroral Geomagnetic Effects) data (Viljanen and Häkkinen, 1997). IMAGE provides high-resolution data in northern Europe and eastern Greenland for studies of large-scale field-aligned current structures and dynamics of the high-latitude auroral electrojets (Tanskanen, 2009). IMAGE data resolutions are usually 10 s. In this study, we use data recorded at a single station, namely, the Nurmijärvi (NUR) station, located in southern Finland at geographic coordinates 60.50° latitude and 24.65° longitude. The magnetic field components of the NUR data are represented in the north-ward direction (x component), eastward direction (y component), and downward direction (z component).

2.4 GIC data from the Finnish natural gas pipeline

GIC data recordings come from locations near the Mäntsälä pipeline compression station in southern Finland (latitude 25.20°, longitude 60.60°) maintained by the Finnish Meteorological Institute and the European Community’s Seventh Framework Programme. The Mäntsälä GIC data is obtained by two magnetometers, one located at Mäntsälä, and the other at NUR (Pulkkinen et al., 2001b; Viljanen et al., 2010). The ground dB/dt variations at and auroral dynamics above NUR account for natural variations of the geomagnetic field. The NUR field values are then subtracted from the Mäntsälä field values, and the difference is interpreted as field variations due to GIC effects (Pulkkinen et al., 2001b; Viljanen et al., 2010). Finally, by knowing the electromagnetic and geometric properties of the pipeline, along with the geoelectric field modeled by a framework shown in Pulkkinen et al. (2001a), the actual measurements of GICs are determined. GICs measured at Mäntsälä have an error of up to 1 A, which are smaller than the GIC peaks we intend to investigate in this work (GIC $>$ 5 A). Such GIC levels can cause overtime damage (Béland and Small, 2005; Gaunt and Coetzee, 2007; Rodger et al., 2017) and power disruptions in electric power transmission systems (Allen et al., 1989; Bolduc, 2002; Oliveira and Ngwira, 2017). The Mäntsälä GIC data and the NUR geomagnetic field data have both resolutions of 10 s. As recommended by Viljanen et al. (2010), daily GIC average values were substrcted from the GIC data shown in this paper, even though these average values are very close to zero.

3 Results

3.1 Localizing geomagnetic field and GIC data in space and time

Panel A of Figure 1 shows the approximate location near the Mäntsälä compression station in southern Finland. The thick green lines represent magnetic latitudes computed with the Altitude-Adjusted Corrected GeoMagnetic (AACGM) model (Baker and Wing, 1989; Shepherd, 2014) for the year 2015. This figure shows that Mäntsälä can certainly be underneath the auroral oval during intense geomagnetic storms and substorms, where it can reach magnetic latitudes as low as 50° (e.g., Boteler, 2019; Hayakawa et al., 2020a). Panel B in the same figure shows a snapshot of southern Finland with the geographic locations of Mäntsälä (red star) and NUR (blue star). NUR is located approximately 40 km southwest of Mäntsälä, which is way within the separation of 600 km between ground stations for adequate GIC modeling (Ngwira et al., 2008). The time evolution of Mäntsälä’s magnetic latitude in the time span of this study (1999–2023) is shown in Figure 2. The variation of the magnetic latitudes was near 0.5° in the period, which is neglegible for this study. Therefore, effects caused by different MLATs at Mäntsälä can safely be ignored in this study.

Figure 2

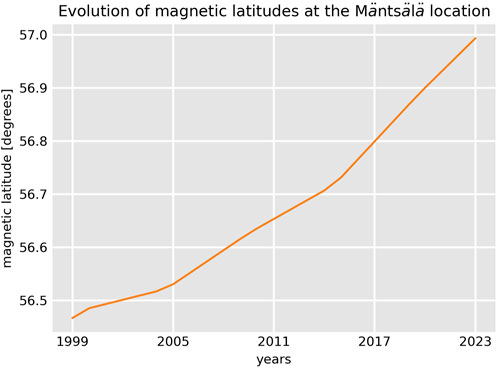
Figure 2. Time evolution of magnetic latitudes at Mäntsälä’s geographic location from 1999 to 2023. This time span covers the full Mäntsälä GIC pipeline system data set. The magnetic coordinates were calculated with the AACGM model.

Figure 3 shows a comparison between the two main data sets used in this study, namely, the shock and GIC data sets. Panel A shows annual number distributions of IP shocks in the Oliveira (2023b) data base (salmon bars), and Carrington-averaged ( $\sim 27$ days) sunspot numbers from January 1995 to May 2023 (solid black line) (Clette et al., 2015). As discussed by Oliveira (2023b), both numbers of shocks and sunspots correlate quite well, meaning that shocks are more likely to occur during solar maxima (Oh et al., 2002; Kilpua et al., 2015; Oliveira and Raeder, 2015). Panel B of Figure 3 shows observation numbers of GIC observations plotted and color coded in 1 year × 1-h MLT (AACGM magnetic local time) bins. The plot shows that there are no GIC measurements recorded at the Mäntsälä pipeline before 1999. On the other hand, the number of observations in all MLT bins for a particular year are nearly the same, which indicates that eventual lack of observations may cover a few days. In addition, most years provide on average 8–10× 10⁴ data points (1 data point ≡ 10 s). Although there are good coverages for the maximum and declining phases of solar cycle 23 (SC23), there is good coverage for the ascending phase of SC24, but lower coverages during maximum and initial declining phases of SC24 (years 2015 and 2016). Finally, GIC data has good coverage in the ascending phase of the current SC25. Therefore, for this study, there’s coverage of approximately two entire solar cycles with shocks and GIC concomitant data.

Figure 3

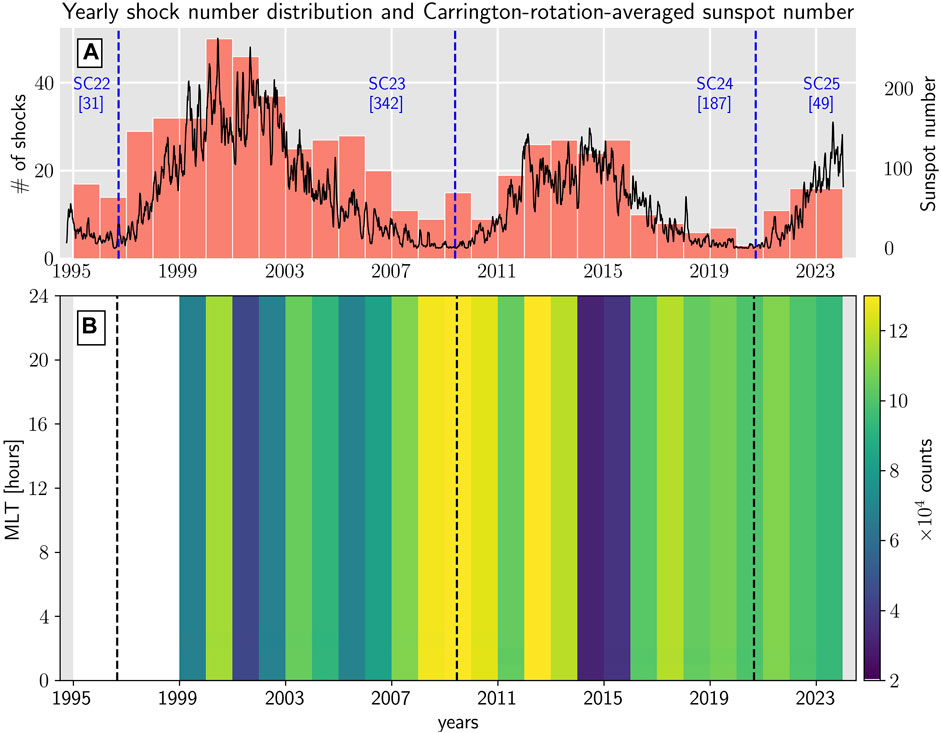
Figure 3. Panel (A) Shock number distribution (salmon bars) and Carrington-rotation-averaged sunspot numbers (solid black line) from January 1995 to May 2023. This time span corresponds to the shock data base provided by Oliveira (2023b). Panel (B) Number of GIC observations (counts) plotted as a function of year and magnetic local time (AACGM) at the Mäntsälä natural gas pipeline system in the time span of the GIC data set (January 1999 to May 2023).

3.2 Effects of $θ_{x_{n}}$ on GICs: shock compression effects

In this subsection, we compare GIC effects caused by the impacts of two shocks with different inclinations, but with similar strengths as represented by magnetosonic Mach numbers. We choose a nearly frontal shock, hereafter NFS1, with $θ_{x_{n}}$ = 161.77° and M_s = 2.3, that struck the magnetosphere at 1400 UT on 18 April 2023. We also select a highly inclined shock, hereafter HFS1, with $θ_{x_{n}}$ = 128.92° and M_s = 2.6, that hit the magnetosphere at 1708 UT on 11 November 2004. This approach has been shown to be very effective for comparisons of geomagnetic activity triggered by shocks with different inclinations (Wang et al., 2006; Selvakumaran et al., 2017; Oliveira et al., 2018; Shi et al., 2019; Xu et al., 2020). As will become clearer later, these shocks were also chosen because their impacts on the magnetosphere occurred when Mäntsälä was around dusk (MLT ∼16 h and MLT $\sim 19$ hr, respectively). In both plots, the black dashed vertical lines indicate the corresponding UT of shock impact of the magnetosphere. NFS1 was observed by Wind, whereas HIS1 was observed by ACE. Table 1 summarizes some general properties of the shocks used for comparisons of compression effects.

Table 1

Table 1. Comparison of parameters for a nearly frontal shock and a highly inclined shock. The focus is on shock compression effects.

Figure 4 and Figure 5 show time series for solar wind, IMF, geomagnetic index, ground magnetic field, and GIC data for the NFS1 and HFS1, respectively. Both figures show the three components of the IMF (panels A), IMF magnitude (panel B), three components of the solar wind velocity (x, panel C; y and z, panel D), plasma number density (panel E), dynamic pressure m_pNV², where m_p is the proton mass (panel F), temperature (panel G), SMR (panel H), SMU (panel I), regional SMU plotted as a function of time and MLT (panel J), ground dB/dt at NUR (panel K); and GIC at Mäntsälä (panel L). In order to compare geomagnetic effects caused by IP shock compression, we plot data ±1 h around shock impact time (dashed black vertical line) and focus on the following 20 min. This time has been shown to be adequate to focus only on shock compression effects (Selvakumaran et al., 2017; Oliveira et al., 2018; Rudd et al., 2019).

Figure 4

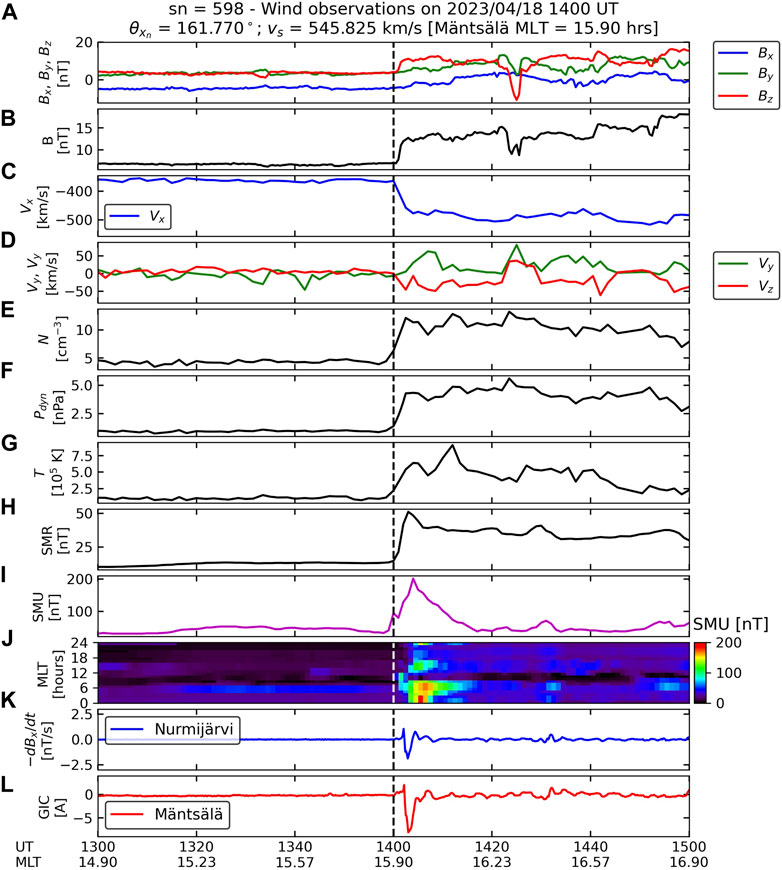
Figure 4. Solar wind and IMF, geomagnetic index, ground magnetometer, and Mäntsälä GIC data for the shock event of 18 April 2023. Solar wind and IMF data were recorded by Eind in this case. (A): three components of the IMF; (B), IMF magnitude; (C), x component of the solar wind velocity; (D), y and z components of the solar wind velocity; (E), solar wind number density; (F), solar wind ram pressure; (G), solar wind temperature; (H), SuperMAG SMR index; (I), SuperMAG SMU index; (J), regional SuperMAG SMU index; (K), −dBx/dt recorded at Nurmijärvi; and (L), GIC measurements at Mäntsälä. Note that NUR ground magnetic field variations are plotted as–dB/dt to follow GIC trends at Mäntsälä.

Figure 5

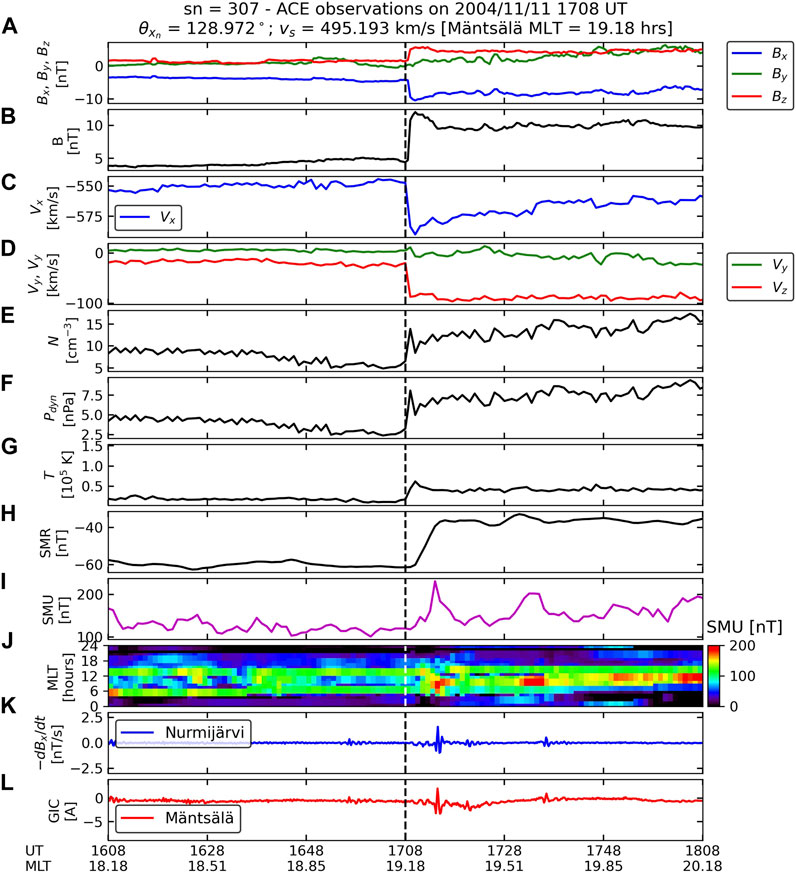
Figure 5. Solar wind and IMF, geomagnetic index, ground magnetometer, and Mäntsälä GIC data for the shock event of 11 November 2004. Solar wind and IMF data were recorded by ACE in this case. The figure is organized in the same way as Figure 4.

Both figures show that IMF conditions are very similar before shock impacts (B_x slightly negative, with B_y and B_z near zero values). After shock impacts, the IMF magnitudes increase from values near 5 nT to values around 13 nT. In both time series, V_x shows a sharper decrease, with V_z showing a much more intense variation in the HIS1 case with respect to the NFS1 case. Although the shock compression rates (downstream to upstream plasma number density ratio) are similar (2.6 and 2.2, respectively), the dynamic pressure compression ratio is higher in the case of the NFS1 (see Table 1). These observations indicate that the HIS1 is indeed more inclined and stronger than NFS1. As theoretically demonstrated by Samsonov (2011), nearly frontal shocks compress the magnetosphere mostly in the x direction, whereas highly inclined shocks compress the magnetosphere more significantly in the y and z directions in comparison to y and z directions in nearly frontal shocks. As demonstrated by many works (see, e.g., Oliveira, 2023a), these asymmetric compression effects caused by highly inclined shocks usually lead to very different geomagnetic activity in terms of asymmetries and intensities in comparison to nearly frontal shocks.

The shock impact angle effects caused by the two shocks can be clearly seen in the remaining panels of Figure 4 and Figure 5. Panels H and I show that SMR and SMU are more intense and develop faster in the NFS1 case in comparison to the HIS1 case. These effects have been shown in many works, including simulations and observations (Takeuchi et al., 2002; Guo et al., 2005; Wang et al., 2006; Rudd et al., 2019; Shi et al., 2019; Oliveira et al., 2021). The regional SMU index shows strong enhancements around MLT = 6 h, but a relative SMU change is higher in the NFS1 case. Ground–dB/dt variations at NUR are more intense (magnitude near 2.5 nT/s) and peak earlier in the first case in comparison to the second case. These effects have already been reported to be observed in ground magnetometer data in geospace (Oliveira et al., 2020) and on the ground (Takeuchi et al., 2002; Oliveira et al., 2020; 2021). As expected, similar trends are observed in the GIC observations shown by the red lines in both plots, which are supported by the papers mentioned above and many others (Oliveira and Samsonov, 2018; Oliveira, 2023a). Finally, our NUR–dB/dt and Mäntsälä GIC observations agree with a trend reported by Viljanen et al. (2010), who pointed out that GIC measurements almost always follow–dB/dt measurements (which are plotted in the figures) in the x direction because the Mäntsälä pipeline is positive-oriented in the eastward direction from Mäntsälä.

3.3 Effects of $θ_{x_{n}}$ on GICs: substorm effects

Now we focus on GIC enhancements caused by substorm effects triggered by shocks. We select two shocks, a nearly frontal shock (NFS2), with $θ_{x_{n}}$ = 162.62° and M_s = 2.4, and a highly inclined shock (HFS2), with $θ_{x_{n}}$ = 130.78° and M_s = 2.4. The impact of the NFS2 on the magnetosphere occurred at 2300 UT of 07 September 2017, whereas the impact of the HFS2 took place at 1833 UT of 15 February 2010. Table 2 summarizes the main properties of NFS2 and HIS2. These shocks were selected because their impacts occurred at MLT = 0.9 h and MLT = 20.6 h at Mäntsälä for NFS2 and HIS2, which allows for the observation of magnetotail effects on GICs around the magnetic midnight terminator (MLT = 00 h). Solar wind, IMF, geomagnetic index, ground magnetic field, and GIC data are plotted for the NFS2 and HFS2 in Figure 6 and Figure 7. These figures are similar to Figure 4 and Figure 5, except for two differences: first, the SMU index time series and regional SMU index are replaced by SML, and data is plotted 1 and 2 h around the shock impact onset. The time span after the shock impacts are adequate to account for substorm activity triggered by solar wind driving including shocks (Bargatze et al., 1985; Freeman and Morley, 2004; Oliveira and Raeder, 2014; Oliveira et al., 2024).

Table 2

Table 2. Comparison of parameters for a nearly frontal shock and a highly inclined shock. The focus is on effects caused by shock-triggered substorms.

Figure 6

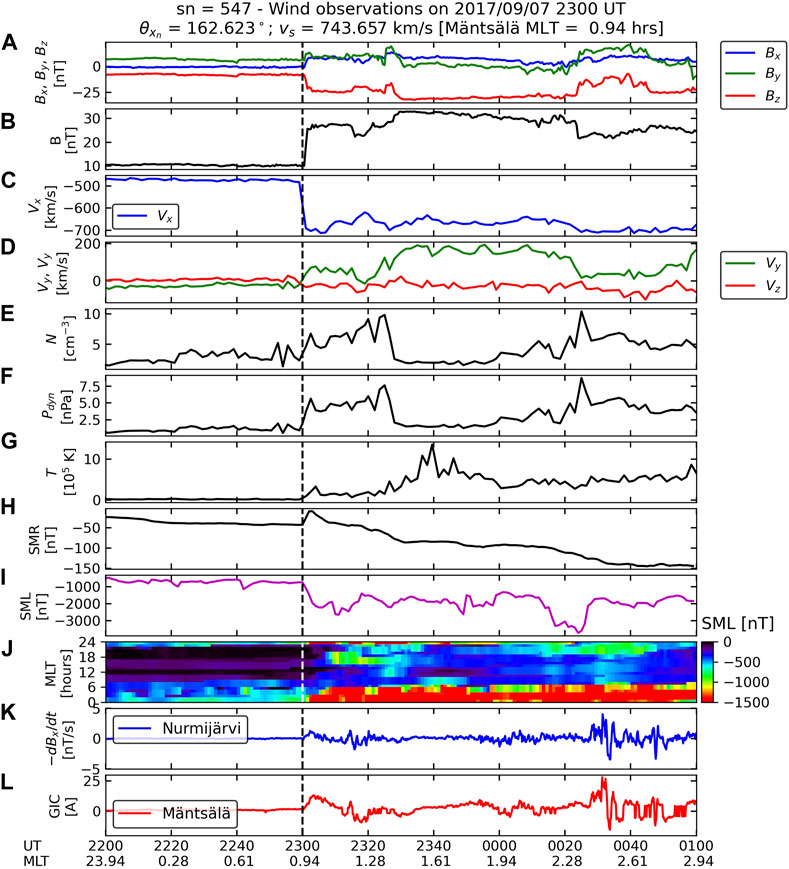
Figure 6. Solar wind and IMF, geomagnetic index, ground magnetometer, and Mäntsälä GIC data for the shock event of 7 September 2017. Solar wind and IMF data were recorded by Wind in this case. The figure is organized in the same way as Figure 4, with two differences: the total and regional SuperMAG SMU indices are replaced by the total and regional SuperMAG SML index, and 2) data is plotted 1 and 2 h around shock onset.

Figure 7

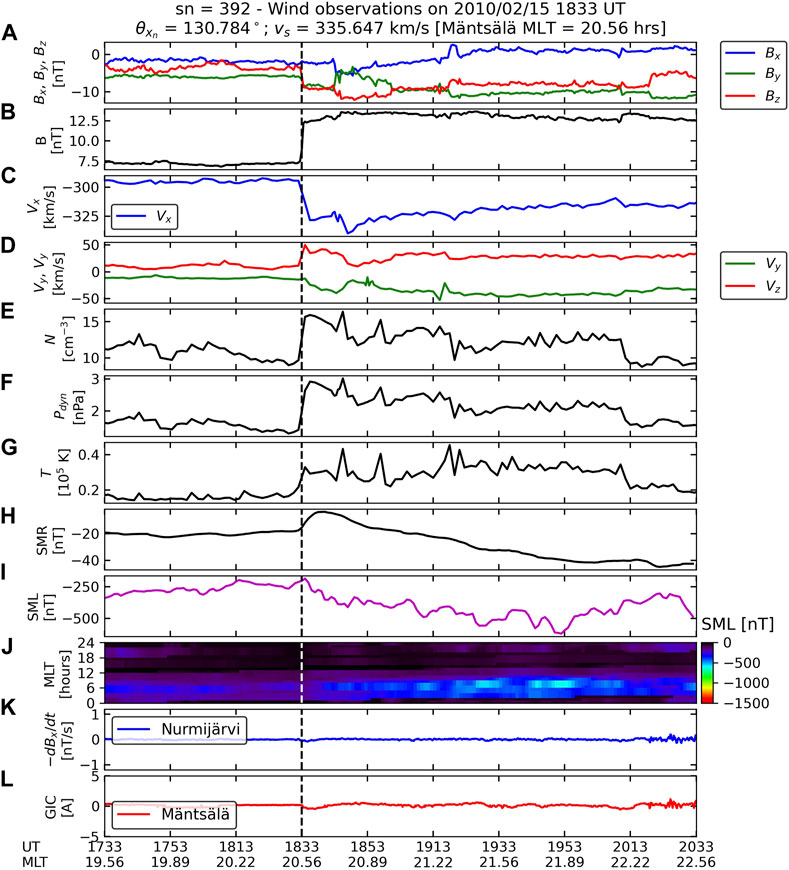
Figure 7. Solar wind and IMF, geomagnetic index, ground magnetometer, and Mäntsälä GIC data for the shock event of 15 February 2010. Solar wind and IMF data were recorded by Wind in this case. The figure is organized in the same way as Figure 4, with two differences: the total and regional SuperMAG SMU indices are replaced by the total and regional SuperMAG SML index, and 2) data is plotted 1 and 2 h around shock onset.

In both shock cases, IMF B_z values in the upstream region were close to −5 nT. Preconditioning effects are very important conditions for substorm triggering (Zhou and Tsurutani, 2001; Yue et al., 2010), and they determine whether a substorm is triggered or not. On the other hand, it is very clear that IMF B_z is much more depleted in the NSF2 case in comparison to the HFS2 case because the nearly head-on impact amplifies the southward condition of IMF B_z in comparison to the other case. These different magnetospheric compression conditions were shown with simulation by Oliveira and Raeder (2014) to be very effective in determining the intensity of substorm triggering, being much more intense in the frontal case in comparison to the inclined case. This is clearly seen in Table 2, with the downstream to upstream ram pressure ratio being higher in the NFS2 case in comparison to the HIS2 case. SMR amplitudes are more intense and occur earlier in the nearly frontal case in comparison to the highly inclined case (Guo et al., 2005; Selvakumaran et al., 2017; Rudd et al., 2019). Time series for the SML index (magenta lines) indicate much more intense magnetotail activity in the first case (SML $<$ −3,000 nT) in comparison to the second case (SML around −600 nT). Similar effects were shown with SuperMAG data by Oliveira and Raeder (2015). The regional SuperMAG index data show very intense SML activity (SML $<$ −1,500 nT) around the magnetic midnight for the NFS2, whereas mild SML activity (SML ∼ −500 nT) is seen near dawn for the HIS2. These results agree with the simulations conducted by Oliveira and Raeder (2014) for shocks with different orientations.

As depicted in Figure 6 and Figure 7, after shock impacts, some NUR–dB/dt variations and Mäntsälä GIC variations are observed at their respective locations in the NFS2 case, but close to none observations are seen after shock impact in the HIS2 case (note that panels K and L in the figures are not to scale). Later, intense ground–dB/dt and GIC variations are seen around 90 min after shock impacts in the NFS2 case, whereas no noticeable observations are recorded at NUR and Mäntsälä. These observations strongly agree with the results shown by Oliveira et al. (2021): ground–dB/dt variations are more intense during substorms triggered by nearly head-on shock impacts on the magnetosphere. These results are also supported by the statistical and superposed epoch analysis study reported by Oliveira et al. (2024).

3.4 Statistical results

A superposed epoch analysis of GIC peaks for all shocks is shown in Figure 8. The top panels show counts or number of data points or observations (1 data point ≡ 10 s) of GIC peaks caused by shock compressions (panel A) and substorm effects (panel B). The lower panels show the GIC peaks associated with shock compression effects (panel C) and substorm effects (panel D). In all panels, data are plotted as a function of MLT and $θ_{x_{n}}$ , with the color codes representing number of observations (panels A and B) and GIC peaks (panels C and D).

Figure 8

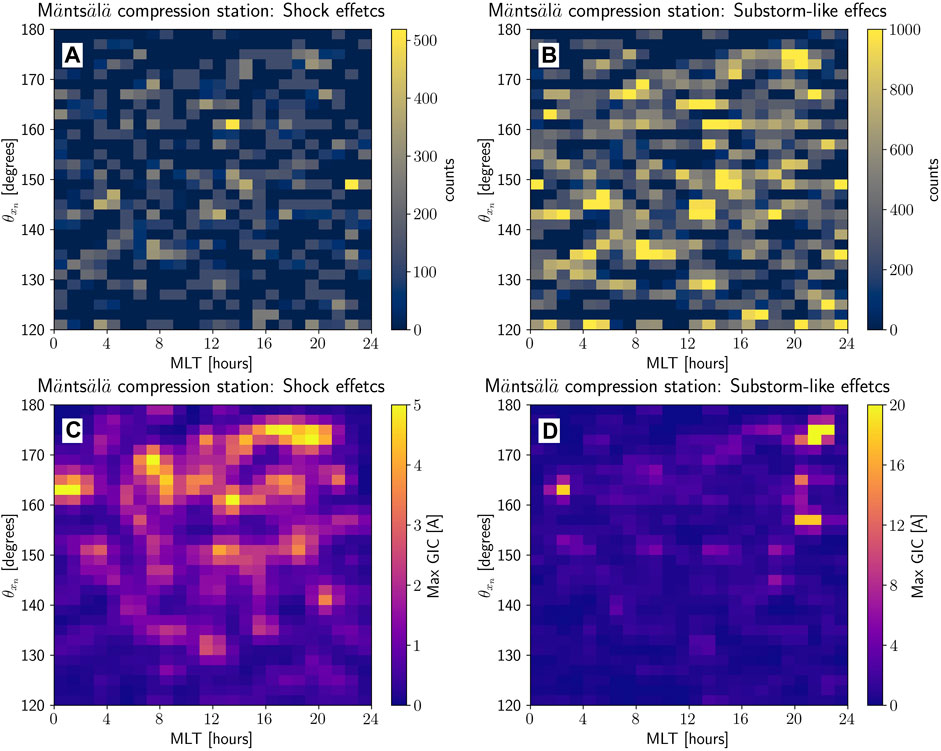
Figure 8. Superposed epoch analysis of GIC response recorded at the Mäntsälä compression station during shock compression effects (first 20 min after shock impat, first column) and during substorm-like effects (within 20 and 120 min after shock impact, second column). Color-codes represent observation counts (panels (A, B)), and GIC peaks (panels (C, D)). All data are plotted in MLT $\times θ_{x_{n}}$ bins.

In order to explore shock impact angle effects on the subsequent GIC peak response, we classify events as highly inclined shocks (HIS, with $θ_{x_{n}}$ $<$ 140°); moderately inclined shocks (MIS, 140 $° \leq θ_{x_{n}} <$ 160°); and nearly frontal shocks (NFS, $θ_{x_{n}} \geq$ 160°). Such shock impact angle classifications have been shown to be very effective in capturing impact angle effects on the following geomagnetic activity caused by shocks (e.g., Wang et al., 2006; Oliveira and Raeder, 2015; Selvakumaran et al., 2017; Oliveira et al., 2018; Rudd et al., 2019; Shi et al., 2019; Xu et al., 2020; Oliveira et al., 2024).

In the shock compression case, panels show that observation counts indicate that most bins show observation numbers less than 200, but a few bins show observation numbers greater than 300. In the other case, most bins indicate observation numbers greater than 600, and fewer bins indicate observation numbers greater than 800. Therefore, although the numbers of observations are spread out in the bins, there are no particular biases introduced by either MLT or $θ_{x_{n}}$ in the observations. The overall number of observations is higher in the substorm effects case in comparison to the shock compression case due to the time span of observations around shock onset (within 20 min and within 20 and 120 min for both cases, respectively).

GIC peaks ( $>$ 5 A) in the shock compression case (Figure 8C) occur more often for NFSs. There are very few peaks (1–2 A) for the HIS case, but they are apparently more concentrated around MLT = 12 h. MISs show peak intensities in between the HIS and NFS categories, with MLT coverage in between. Although these observations agree with previous works (Oliveira et al., 2018; Xu et al., 2020), our results are novel in two ways: first, this is the first time IP shock impact angle effects are observed on actual GICs, and, second, there is broader and more intense GIC peak response around the dusk sector (MLT ∼ 18 h), which is much more evident for NFSs.

In Figure 8D, GIC peaks are shown in the same way as in panel C, but for the case accounting for substorm effects. However, since GIC peaks in this case are more intense, the panel highlights GIC peaks greater than 10 A. Most of these peaks occur around MLT = 00 h for NFSs, but a few peaks occur for MISs with 20 h $<$ MLT $<$ 22 h. These results agree withVsubstorm effects triggered by nearly head-on shock impacts on the subsequent ground dB/dt variations in the case study reported by Oliveira et al. (2021), and the statistical study provided by Oliveira et al. (2024).

Figure 9 shows the same data represented in panels C and D of Figure 8, but organized in pie diagrams with the relative occurrence number of events with GIC peaks greater than 5 A (panels A and B), and GIC peaks greater than 10 A (panel C) and greater than 20 A (panel D). Shock inclination categories are represented in blue, NFS; magenta, MIS; and green, HIS. The first column is for events caused by magnetospheric compression by the shocks (within 20 min after shock onset), whereas the second column is for magnetotail or substorm effects (between 20 min and 120 min after shock onset).

Figure 9

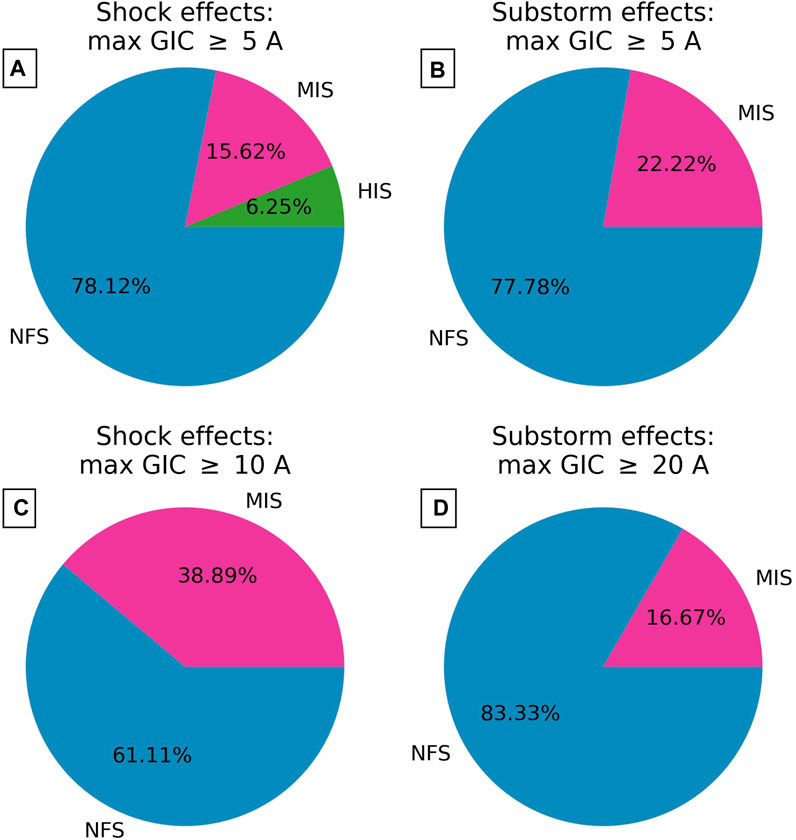
Figure 9. Pie diagrams documenting relative GIC peak response ≥5 A for shock effects (A), and substorm effects (B). GIC peaks ≥10 A are shown in panel (C) (shock effects), whereas GIC peaks (≥20 (A) resulting from magnetotail activity are shown in panel (D). Blue colors indicate NFS; magenta colors, MIS; and green colors, HIS.

Results show that NFSs dominate GIC peaks for both GIC thresholds and space weather drivers (magnetospheric compression and substorm effects). For GIC peaks ≥5 A, compression effects, NFSs account for more than three-quarters of the events, with ∼16% of events classified as MISs, and ∼6% classified as HISs. As shown in Table 3, there is only one event classified as HIS. Still for compression effects, nearly three-quarters of the events are NFS, whereas nearly one-quarter of the events are MIS. There are no HIS events. Therefore, these results clearly show that shock impact angles significantly control the subsequent GIC peaks at Mäntsälä, particularly for GIC peaks greater than 20 A occurring during substorm events (panel D). Tables 3 (shock compression effects) and 4 (substorm effects) summarize the shock properties, geomagnetic index, and GIC peak responses to all events investigated in this study with GIC peaks grater than 5 A.

4 Discussion

In this investigation, we used the shock data base provided by Oliveira (2023b) and GIC data measurements from the Finnish natural gas pipeline system to study shock impact angle effects on the subsequent GICs. Our observations are based on previous studies of shock impact angle effects on ground dB/dt variations, which are the space weather drivers of GICs. For example, Oliveira et al. (2018) showed that nearly frontal shocks trigger more intense ground dB/dt variations following the shock impact in comparison to highly inclined shocks at all latitudes. In another work, Oliveira et al. (2021) demonstrated with a case study that a nearly frontal shock triggered a super substorm (SML $<$ −2,500 nT), and a highly inclined shock triggered an intense substorm (−2,500 nT $<$ SML ≤ −2,000 nT), even though both shocks had similar strengths. As a result, ground dB/dt variations were more intense, occurred earlier, and covered larger geographic areas in North America and western Greenland in the first case in comparison to the second case. All these results suggest that nearly frontal shocks compress the magnetosphere more symmetrically in comparison to highly inclined shocks, with the former enhancing more effectively the most important current systems in the magnetosphere-ionosphere system leading to higher geomagnetic activity (Takeuchi et al., 2002; Guo et al., 2005; Wang et al., 2006; Oliveira and Raeder, 2014; 2015; Samsonov et al., 2015; Selvakumaran et al., 2017; Oliveira and Samsonov, 2018; Shi et al., 2019; Xu et al., 2020; Oliveira, 2023a).

The statistical study of Oliveira et al. (2024) confirmed the case study of Oliveira et al. (2021) by showing that ground dB/dt variations induced by nearly frontal shocks i) are more intense, ii) cover larger geographic areas including iii) more equator-ward regions in comparison to highly inclined shocks. However, as outlined in the introductory section, though ground dB/dt variations are considered the space weather drivers of GICs, actual GIC effects can only be adequately quantified with the use of ground conductivity models (Beggan, 2015; Espinosa et al., 2019; Wang et al., 2021). This is a difficult task because GICs present a spectral dependence on ground dB/dt variations due to their interaction with the non-uniform Earth’s conductivity structures in many layers whose modeling is quite complex (Gannon et al., 2017; Juusola et al., 2020; Kelbert and Lucas, 2020). In addition, the geometry of the conductors of interest must be known for accurate computation of GICs. However, since this has been accomplished with the Mäntsälä GIC data set, we were able to investigate shock impact angle effects on actual GIC measurements for the first time. Although GICs were tackled on in very similar magnetic latitudes, we can clearly conclude from our results that the more frontal the shock, the more intense the GIC amplitudes during compressions after the shocks (GIC $>$ 5 A), and during magnetotail energy inputs due to energetic particle injections during substorm times (GIC $>$ 20). These results build upon the work of Tsurutani and Hajra (2021) who observed very intense storm-time GIC peaks ( $>$ 30 A), but our contribution indicates that intense GICs ( $>$ 5 A and $>$ 20 A) can follow shock impacts, which can pose serious risks to ground artificial conductors in short-, mid-, and long-term regimes (Allen et al., 1989; Béland and Small, 2005; Gaunt and Coetzee, 2007; Oliveira et al., 2018). Therefore, our results are consistent with previous reports showing nearly symmetric compressions generally cause more intense ground dB/dt variations associated with GICs (Oliveira et al., 2018; Xu et al., 2020; Oliveira et al., 2021; 2024).

Our results clearly show that GICs are enhanced promptly in the following 20 min after shock impacts, particularly resulting from nearly frontal shock impacts. This is consistent with the works of Oliveira et al. (2018) and Xu et al. (2020), but for ground dB/dt variations. We then show for the first time that most intense GIC peaks ( $>$ 5 A) occurred in the noon/dusk region (Figure 8) mostly due to nearly frontal shocks, with a very few being caused by highly inclined shocks. This noon/dusk preference is consistent with Madelaire et al. (2022b), who showed that ground magnetic field responses to solar wind dynamic pressure enhancements usually occur in the dusk sector $\sim 30$ minutes after the pressure pulse onset. The authors attributed this effect to partial ring current (Fukushima and Kamide, 1973) enhancements at high latitudes including Mäntsälä’s latitudes. In another work, Madelaire et al. (2022a) used ground magnetometer data and a model to derive equivalent ionospheric currents in response to solar wind dynamic pressure enhancements. The authors showed that a current vortex was mostly localized on the high-latitude duskside whereas a current vortex on high-latitude dawnside travelled with a significant velocity westward. These results also agree with the localized GIC peaks located on the duskside resulting from shock compression effects, being amplified by nearly frontal shock impacts, as shown by our case comparisons (Figure 4; Figure 5) and statistical results (Figure 8). This is also shown in higher intensifications of the SuperMAG regional SMU index in the same region (MLT ∼ 18 h) in response to impact of all shocks regardless of inclinations, but the SMR response becomes more enhanced as the shock becomes more frontal. These results will be reported in a forthcoming work.

Ngwira et al. (2018) and Oliveira et al. (2021) showed that very intense ground dB/dt variations are highly correlated and coincident in time with energetic particle injections originated in the magnetotail. The authors used spacecraft observations (Time History of Events and Macroscale Interactions during Substorms and Los Alamos National laboratory) located on the nightside tail around local magnetic midnight which were magnetically conjugated with ground magnetometers in North America. All stations and satellites were located a few hours around MLT = 00 h. Ngwira et al. (2018) and Oliveira et al. (2021) observed intense dB/dt variations occurring a few seconds after sharp and intense energetic particle injections observed by the spacecraft. The authors also noted intense aurora brightening associated with substorm occurrence and its subsequent poleward expansion of the auroral oval. These works associated these energetic particle injections to the tailward stretching of the local geomagnetic field at the magnetic midnight, usually caused by substorm-time flux growth phase dropouts (Sauvaud et al., 1996; Reeves and Henderson, 2001). Additionally, Oliveira et al. (2021) showed that the effects described above were more intense and occurred earlier in the case of a NFS in comparison to a HIS. These works support our findings concerning GIC peaks during substorm times occurring near the local magnetic midnight associated with substorm effects. This is clearly shown in our case examples (Figure 6; Figure 7) and superposed epoch analysis (Figure 8D; Figure 9D).

As kindly suggested by a reviewer, we looked at time intervals between shock onsets and GIC peaks for all events (ΔMLT = MLT2—MLT1 in Table 3; Table 4 for shock and substorm effects) as a function of $θ_{x_{n}}$ . As shown in the L panels of Figure 4 and Figure 5, there is a time delay of ∼3 min and ∼7.5 min in MLT between shock onsets and GIC peaks for the NFS1 and HIS1, respectively. This is supported by a comparative study (Oliveira et al., 2021) and statistical analyses (Oliveira et al., 2024) showing that dB/dt variations are more intense and occur earlier as a result of nearly head-on shock impacts in comparison to highly inclined shock impacts. However, a clear correlations between ΔMLT and $θ_{x_{n}}$ were not found in our study. As mentioned before in this article, many works focusing on observations and simulations found a significant correlation between sudden impulse rise times and shock impact angles, with the shorter the rise time, the more frontal the shock impact (Takeuchi et al., 2002; Guo et al., 2005; Wang et al., 2006; Selvakumaran et al., 2017; Rudd et al., 2019). Therefore, those works report on magnetopause current effects recorded by ground magnetometer located at low- and mid-latitude regions. However, the GIC effects reported in this work were most likely caused by auroral electrojet dynamics above the Mäntsälä compression station location (Wawrzaszek et al., 2023). Thus, the current data set we have in hands does not show strong correlations between GIC peak time delays and shock impact angles preasumably due to two reasons: 1) data collected at only one location is not enough to successfully address such correlation effetcs; and 2) such strong correlations do not occur at all. Therefore, more GIC measurements recorded at mid and low latitudes (e.g., New Zealand, Brazil, United States, Europe) are needed to address such possible correlation effects.

Table 3

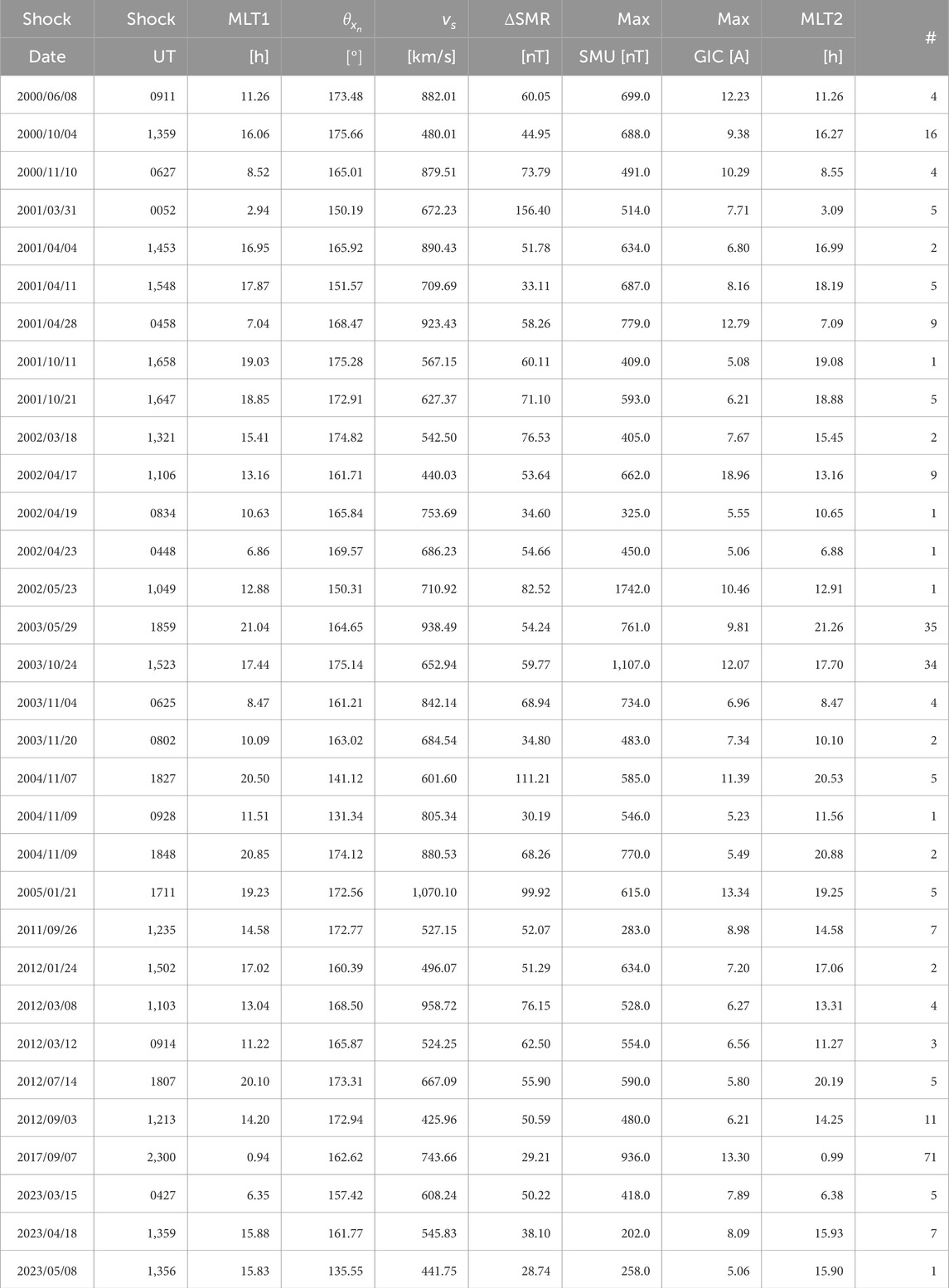
Table 3. Table for shock properties and the subsequent geomagnetic index/GIC peak responses. In the table, MLT1 indicates Mäntsälä MLT at shock impact; v_s, shock speed; ΔSMR, SMR index variation (SMR peak after shock compression minus background); MLT2, Mäntsälä MLT at GIC peak occurrence; and the rightmost column indicates the number of GIC peaks greater than 5 A within 20 min of shock impact for each event.

Table 4

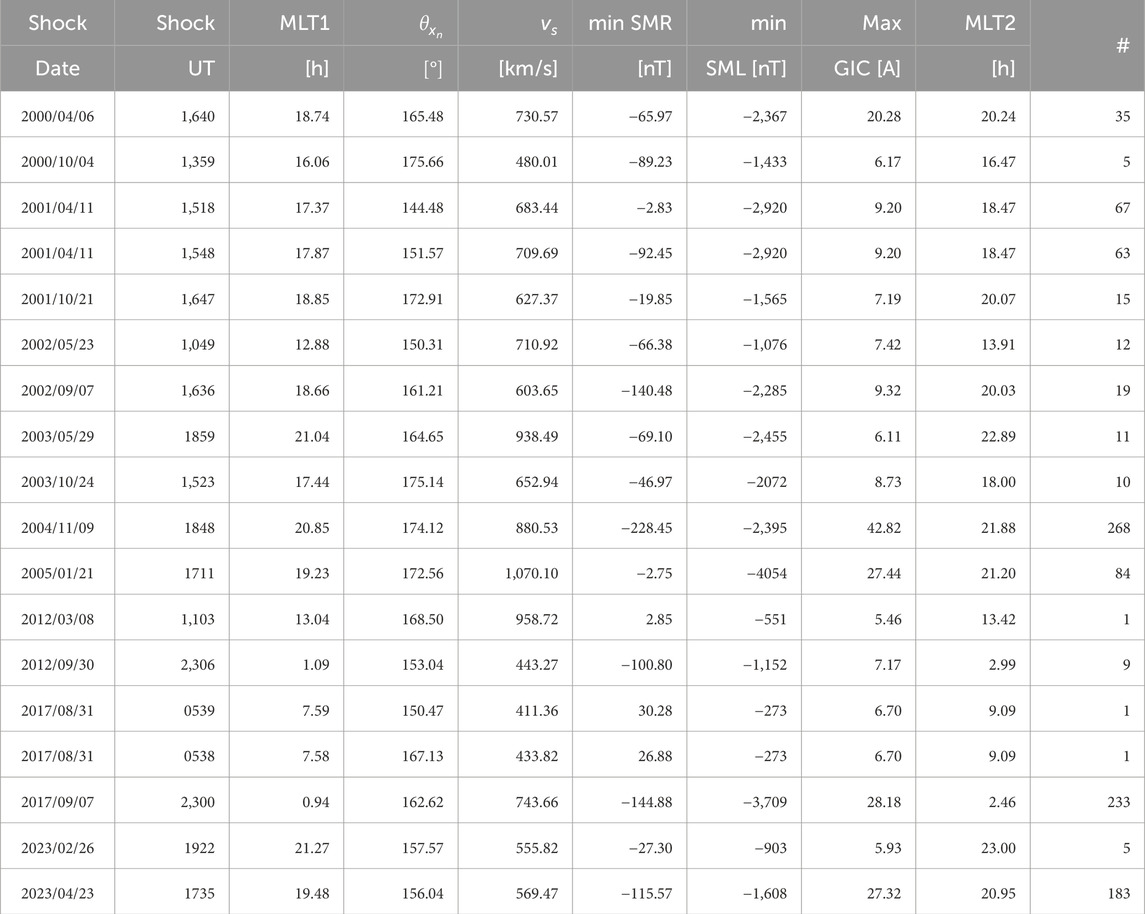
Table 4. Table for substorm effects and the subsequent geomagnetic index/GIC peak responses. This table is similar to Table 3, but with two modification: ΔSMR and maximum SMU are now replaced by minimum SMR and minimum SML values, respectively. The time of interest is in between 20 min and 120 min after shock impacts.

Furthermore, we strongly recommend modelers to simulate the impact of IP shocks with different inclinations on the Earth’s magnetosphere in GIC-related investigations. For example, Welling et al. (2021) simulated the impact of the “perfect” coronal mass ejection on the Earth’s magnetosphere suggested by Tsurutani and Lakhina (2014) to investigate the subsequent ground dB/dt response. The authors noted that the dB/dt response was amplified by the purely head-on nature of the CME impact, which is a very particular case. However, for more realistic results, we encourage modelers to undertake simulations of IP shocks impacts with different orientations on the magnetosphere. Therefore, the combination of asymmetric ground dB/dt variations (Oliveira et al., 2018; 2021; 2024) and varying ground conductivity (Viljanen and Pirjola, 2017; Liu et al., 2019; Wang et al., 2021) will most likely produced more realistic results, since most shocks detected in the solar wind at 1 AU have moderate inclinations of nearly $\sim 130 °$ -140° with respect tot he Sun-Earth line (Oliveira, 2023b; Oliveira et al., 2024).

5 Summary and conclusion

In this work, we used a subset with 332 events of a larger data set (603 events) of IP shocks from January 1999 to May 2023. We looked at IP shock impact angle effects on GICs recorded at the Mäntsälä natural gas pipeline in southern Finland during two distinct moments: up to 20 min after shock impacts, due to shock compressions, and between 20 and 120 min after shock impacts, due to magnetotail activity. We summarize our findings as follows.

1. IP shock impact angles control GIC response at Mäntsälä: nearly frontal shocks tend to trigger more intense GIC peaks. This is supported by previous observations of ground dB/dt response to shocks with different orientations (Oliveira et al., 2018; Xu et al., 2020; Oliveira et al., 2021; 2024).

2. GIC peaks greater than 5 A tend to occur more after shock impacts. These peaks occur more around dusk as a response to nearly frontal shock impacts. These effects are explained by the enhancement of the partial ring current at Mäntsälä latitudes in the dusk sector (Madelaire et al., 2022b) associated with localized current vortices located around the dusk sector (Madelaire et al., 2022a).

3. Very intense GIC peaks ( $>$ 20 A) occur during substorm times around the magnetic midnight terminator. This occurs due to geomagnetic field line stretching around MLT = 00 h in geospace caused by flux growth phase dropouts (Sauvaud et al., 1996; Reeves and Henderson, 2001). Such flux dropouts generate intense energetic particle injections which in turn cause intense auroral brightening and intense ground dB/dt variations nearly simultaneously (Ngwira et al., 2018; Oliveira et al., 2021). Our GIC peak observations are also supported by intense dB/dt variations caused by nearly frontal shocks around the magnetic midnight (Oliveira et al., 2021; 2024).

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

DO: Conceptualization, Formal Analysis, Funding acquisition, Investigation, Writing–original draft, Writing–review and editing. EZ: Conceptualization, Investigation, Writing–review and editing. SV-L: Conceptualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. DMO and EZ thank the financial support provided by the NASA HGIO program through grant 80NSSC22K0756. DMO and SVL acknowledge the financial support provided by NASA LWS program through grant NNH22ZDA001N-LWS.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Allen, J., Sauer, H., Frank, L., and Reiff, P. (1989). Effects of the March 1989 solar activity. Eos Trans. AGU 70, 1479–1488. doi:10.1029/89EO00409

ORIGINAL RESEARCH article

First direct observations of interplanetary shock impact angle effects on actual geomagnetically induced currents: The case of the Finnish natural gas pipeline system

1 Introduction

2 Data

2.1 Solar wind plasma and IMF data

2.2 Computation of shock impact angles and speeds

2.3 Ground magnetometer data

2.4 GIC data from the Finnish natural gas pipeline

3 Results

3.1 Localizing geomagnetic field and GIC data in space and time

3.2 Effects of θxn on GICs: shock compression effects

3.3 Effects of θxn on GICs: substorm effects

3.4 Statistical results

4 Discussion

5 Summary and conclusion

Data availability statement

Author contributions

Funding

Conflict of interest

Publisher’s note

References

3.2 Effects of $θ_{x_{n}}$ on GICs: shock compression effects

3.3 Effects of $θ_{x_{n}}$ on GICs: substorm effects