
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Astron. Space Sci. , 24 June 2024
Sec. Space Physics
Volume 11 - 2024 | https://doi.org/10.3389/fspas.2024.1385472
Impulsive radial transport events occurring in the radiation belts leave lasting marks in the form of drift echoes, that is, energy-dependent drift phase structures in the radiation belts that evolve at the drift frequency. Drift echoes are known to be transient structures that dissipate due to phase mixing. The objective of this paper is to discuss how much time it takes for drift echoes to dissipate, and what drives this phase-mixing process. While any uncertainty or perturbation in the variables controlling trapped particles’ drift frequency contributes to phase mixing, we highlight two main drivers: the observational uncertainty associated with the finite size of the instrument energy channels, and the natural field fluctuations driving perturbations in trapped particles’ drift frequency. It is the combination of both instrumental and natural sources of phase mixing that determines the observed dissipation and lifetime of drift echoes. This means that the observed magnitude and lifetime of a drift echo are always underestimations of the natural magnitude and lifetime of the structure. This calls into question the applicability of the standard, drift-averaged formulation of radial diffusion. The three key points of the study are the following: First, the time it takes for particles initially localized in local time to phase-mix is measured in hours in the Earth’s radiation belts. Second, phase mixing at the drift scale is primarily due to uncertainties in measured kinetic energy and field perturbations. Third, our analysis can be utilized to set an energy resolution requirement for future particle instruments.
Observations of drift phase structures in the radiation belts have multiplied over the last decade, facilitated by the use of instruments with high energy resolution channels (Krimigis et al., 2004; Sauvaud et al., 2006; 2013; Mitchell et al., 2013; Ukhorskiy et al., 2014; Hartinger et al., 2018). They have been the object of statistical analyses in the Earth’s inner belt (e.g., Lejosne and Mozer, 2020), in the outer belt (e.g., Zhao et al., 2022), and even at Saturn (e.g., Sun et al., 2021). Drift phase structures in radiation belt measurements are indicative of a transient magnetic local time (MLT) dependence in phase space density (PSD). As such, they are a direct challenge to the purely diffusive framework commonly utilized in radiation belt modeling and data analysis.
Indeed, the current picture for radiation belt acceleration (e.g., Jaynes et al., 2015) relies on the assumption that the effect of radial transport on radiation belt intensity is well captured by a diffusive equation (e.g., Lejosne et al., 2022a). That said, the validity of the radial diffusion equation relies on the assumption that radiation belts are fully phase mixed at all scales, including at the drift scale (e.g., Lejosne and Albert, 2023). As such, it excludes the possibility of any MLT dependence along a drift shell. One could expect any MLT-dependent PSD fluctuation to dissipate rapidly thanks to some efficient phase-mixing process (e.g., Schulz and Lanzerotti, 1974). Yet, ubiquitous observations of drift phase structures in the radiation belts suggest that: a) processes generating significant MLT-dependent structures in radiation belt fluxes (i.e., non-diffusive radial transport events) occur frequently and/or that b) the characteristic time for phase-mixing at the drift scale can be significant. Quantifying the latter is the object of this paper. Determining the amount of time it takes for a drift phase structure to dissipate and fully phase mix at the drift scale is important, because it provides information on the amount of time during which the radial diffusion equation cannot fully represent the effect of radial transport on radiation belt intensity once a MLT-dependent perturbation has occurred.
In this paper, we propose a thorough analysis of the characteristic time for drift phase mixing in the Earth’s radiation belts. While drift phase mixing is usually viewed as an effect related to the finite energy resolution of particle detectors at the drift scale (e.g., Schulz and Lanzerotti, 1974), we show that field perturbations also lead to natural phase mixing. The results of this analysis have theoretical and practical implications. From the theoretical standpoint, they contribute to clarifying the limits of the radial diffusion framework. From the practical standpoint, they provide analytical grounds to improve the analysis of measured drift phase structures and to specify resolution requirements for future particle detectors designed for radiation belt measurements.
Drift phase mixing at the drift scale corresponds to a process by which trapped particles with similar characteristics (adiabatic invariants, charge) initially located in a limited MLT sector along a drift shell end up covering all MLT sectors uniformly. We are interested in determining how long it takes for this phase homogenization process to occur. This defines the characteristic time for drift phase mixing, and the calculation of this time is the focus of this work. Within this section, we describe the framework by which fluctuations or uncertainties within the system drive phase mixing and the procedure by which the resulting phase mixing time can be extracted.
Drift frequency perturbations are required for a population with similar initial characteristics (adiabatic invariants, charge, MLT) to start covering different MLT locations. Because drift frequency varies with energy, pitch angle, radial location, and field magnitude, any fluctuation in any of these quantities has the potential to drive phase mixing. Specifically, the drift frequency of energetic particles trapped in the Earth’s magnetic dipole field,
In this formula,
In the following, we will divide the sources of variations in drift frequency in two categories: 1. Variations associated with observational uncertainties due to the finite resolution of the instrument, and 2. Variations associated with natural field fluctuations present in the space environment. The elements of each category will be discussed individually (Section 3; Section 4) before being combined (Section 5) to determine a realistic time for phase mixing. The mathematical derivations of the formulas provided in Sections 2–4 will be provided in Sections 7–10 for the interested reader. In the remainder, we will consider that the Earth’s magnetic field is well represented by a dipole to determine analytical expressions for drift phase mixing.
To quantify the characteristic time for phase-mixing, we need to set a criterion that determines whether a particle distribution along a drift shell is homogeneous, i.e., phase-mixed. To quantify the spread in MLT of the population, we propose to consider the variance of the drift phase locations. The greater the variance, the more the population is phase-mixed. If we assume that a) the distribution of the drift phase locations along a drift shell is random, and that b) the random distribution is well described by a wrapped normal distribution, then it is possible to show that a phase-mixed state is reached when the variance of the distribution is greater than
Since the variance of the drift phase locations of the trapped particles is expected to (strictly) increase with time,
An efficient phase mixing process will reach a phase mixed state after a relatively short time,
While the choice of a Gaussian distribution to model the distribution of drift phase locations may appear somewhat artificial, in particular when it comes to characterizing instrumental drift phase mixing (Section 3), it is consistent with the characteristics of the field fluctuations assumed to characterize natural drift phase mixing (Section 4). Since natural drift phase mixing is the process of interest for theoretical analysis of radiation belt dynamics, we opt for a Gaussian distribution as a first approximation. Other assumptions would result in different analytical formulas, but we expect the order of magnitude to be similar.
In radiation belt textbooks (e.g., Schulz and Lanzerotti, 1974), phase mixing at the drift scale is usually attributed to the instrument finite energy resolution: energy channels are sensitive to a given energy range,
We consider particles of the same charge starting from a single location and with a Gaussian energy distribution. Specifically, the variations in kinetic energy are randomly distributed around
where
Combining Eqs 3–5, the characteristic time for phase mixing associated with the instrument finite energy resolution,
where
To reformulate the standard deviation in energy,
The characteristic time for phase mixing,
Let us mention that the characteristic time for phase mixing associated with the finite energy resolution of the instrument is usually defined as
With a theoretical estimate in hand, we now turn to a numerical investigation of the problem from a particle-based description. Figure 1A shows the dissipation of a drift echo, measured from L = 3, MLT = 00±0.5 h, associated with equatorial electrons of energies distributed normally around 250 keV, with
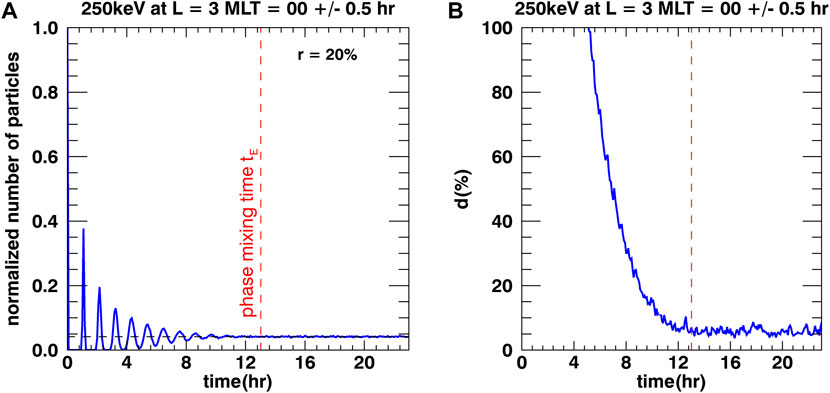
Figure 1. (A) Time evolution of the normalized number of particles situated at L = 3 and MLT = 00±0.5 h. We launch 30,000 equatorial electrons with average energy 250 keV and a standard deviation in energy of
Figure 2 presents a quantification of the characteristic time for phase mixing,
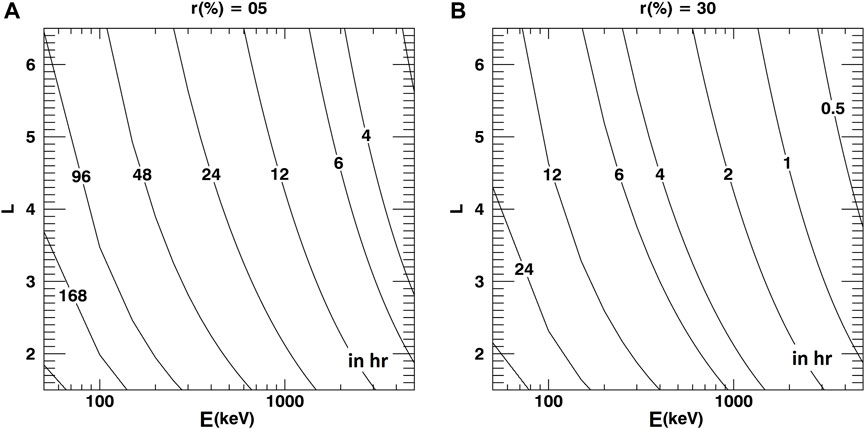
Figure 2. Characteristic time for phase mixing, in hours, due to the finite resolution in particles’ measured kinetic energy. The information is provided as a function of kinetic energy,
Because particles with different pitch angles have slightly different drift frequencies (Eq. 1), the finite pitch angle resolution of an instrument can also play a role in phase mixing. Since the dependence of the drift frequency on pitch angle,
Let us now consider a cluster of particles with normally distributed equatorial pitch angles, with a mean sine equal to
As a result, combining Eqs 3, 4, 8, the characteristic time for phase mixing associated with the instrument finite pitch angle resolution,
This expression is again directly proportional to the drift period, as was the case for the energy resolution mixing time (Equation 7). Its dependence on
The expression 9) permits us to explore the impact of an instrument’s pitch angle resolution on the phase mixing process. To best do so, let us first consider a particularly coarse resolution where the pitch angles are normally distributed around
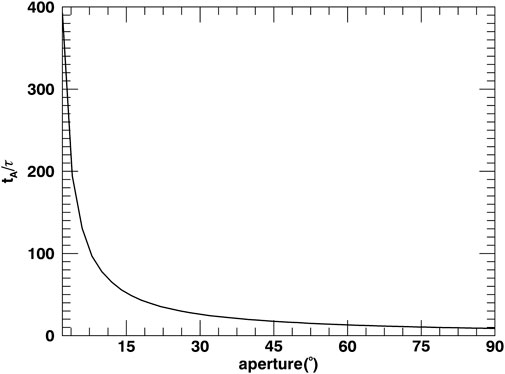
Figure 3. Ratio between the characteristic time for phase mixing associated with the finite pitch angle resolution of the instrument,
Figure 3 suggests that phase mixing due to the finite pitch angle resolution of the instrument is not a significant process to account for when dealing with unidirectional measurements (with an aperture of <
That said, in practice, the distribution of the drift phase locations along a drift shell may not always be very well described by a wrapped normal distribution when dealing with a population with a variety of pitch angles. Assuming a pitch angle distribution peaked around
In the theoretical case of a perfectly resolved instrument (measuring one exact set of kinetic energy and pitch angle values), the characteristic times for phase mixing computed in Section 3,
The omnipresence of small, slow, electric and magnetic field fluctuations means that the radial location of radiation belt particles is constantly disturbed. We show in Section 9 that the variance of the phase locations along a given drift shell is, as a first approximation for equatorial particles:
where
Thus, the characteristic time for phase mixing,
Wave-particle interactions driving diffusion in energy and/or pitch angle, can also contribute to natural drift phase mixing. That said, because the dependence of the drift frequency in pitch angle is relatively weak (see also Section 3.2), we expect the effect of pitch angle diffusion on phase mixing time to be a secondary process. Regarding energy diffusion, we show in Section 10 that the variance of the phase locations when considering a constant energy value is, as a first approximation for equatorial particles:
And the characteristic time for phase mixing associated with energy diffusion,
Comparing the effects of energy diffusion (Eqs 12, 13) and radial diffusion (Eqs 10, 11) on phase mixing, we see that they are of similar magnitude when
Particle injections have been observed even at very low L values (e.g., Turner et al., 2015), down to the inner belt and below (e.g., Selesnick et al., 2019). In our numerical experiment, we launched 30,000 equatorially mirroring electrons with 250 keV in the inner belt, from L = 3, MLT = 00. The particles are trapped in a magnetic dipole field and their drift motion is perturbed by a special case of random electric potential fluctuations, identical to the one described in the article by Lejosne et al. (2023). Specifically, we model the total electric potential,
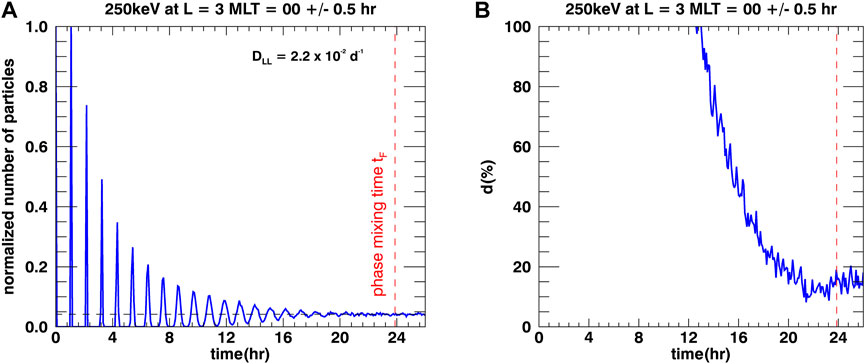
Figure 4. (A) Time evolution of the normalized number of particles situated at L = 3 and MLT = 00±0.5 h. We launch 30,000 equatorial electrons with kinetic energy 250 keV from L = 3, MLT = 00 at t = 0 and we assume a radial diffusion coefficient
To provide a first quantification of the characteristic time for phase mixing associated with fluctuations in trapped particles’ radial location,
In order to get information on the range of values for the characteristic time for phase mixing associated with field fluctuations,
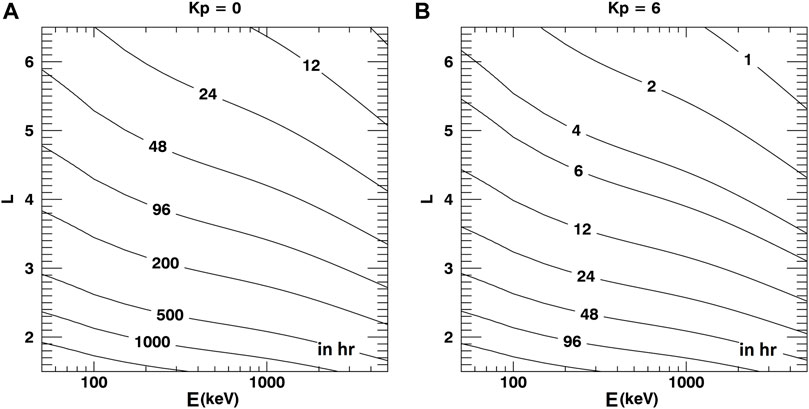
Figure 5. Characteristic time for phase mixing due to radial diffusion,
Although we have explored and characterized each mixing process individually, it is clear that in practice none of them operate in isolation. The “true” mixing time, therefore, is the cumulative effect of all operating in tandem. The focus of this section will be to use the analytic expressions for each individual process to construct an overall mixing time for the particles in MLT.
When all processes discussed in Sections 3, 4 coexist, we expect the resulting characteristic time for phase mixing,
Because the sources of perturbations are independent from each other, we can consider that the variance of the drift phase locations resulting from the combination of all instrumental and natural processes is the sum of the variances associated with each process:
where the indices
By definition, the characteristic time for phase mixing associated with each process,
Assuming that every variance
Thus, the characteristic time for phase-mixing due to the co-existence of all processes,
Let us first focus on determining the total, natural time for phase mixing in the outer belt in presence of both radial diffusion and energy diffusion,
Assuming
Let us now consider equatorial particles, with a total phase mixing time,
We solve numerically Eq. 20, to provide a quantification of the total characteristic time for phase mixing, leveraging the model for electromagnetic radial diffusion proposed by Brautigam and Albert (2000) to quantify
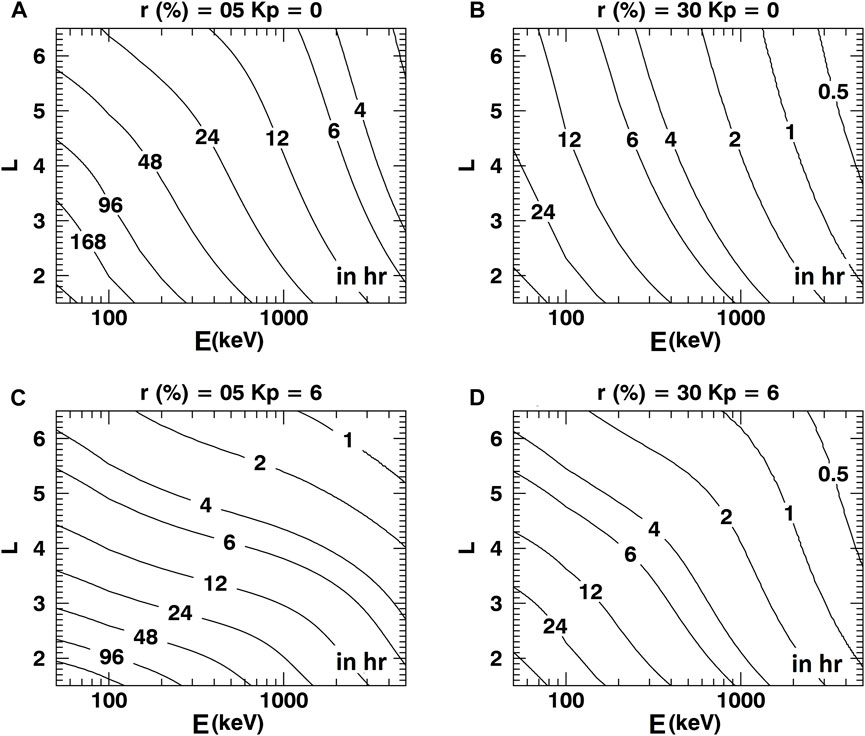
Figure 6. Characteristic time for phase mixing due to the combined effects of radial diffusion and the finite resolution in particles’ measured kinetic energy,
Figure 7 compares and contrasts the time evolution of the same drift echo, dissipating under the effect of slow field fluctuations (radial diffusion), a) in the theoretical case of an instrument that is perfectly resolved in energy (r = 0%), as was presented in Section 4.3.1, and b) as observed by an instrument with a finite energy resolution (r = 20%). Figure 7 contributes to explaining why observations of drift phase structures have multiplied with the use of instruments with higher energy resolution (e.g., Hartinger et al., 2018). It suggests that the measured amplitude and lifetime of a drift echo are always an underestimation of the real (
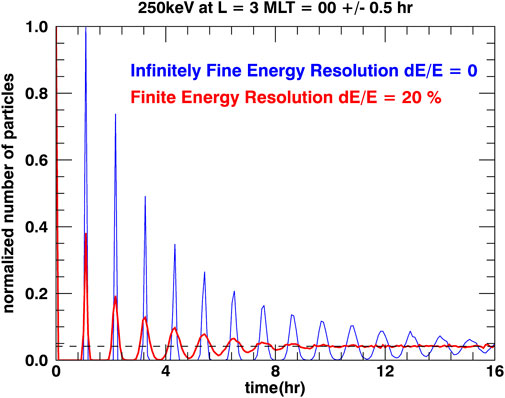
Figure 7. (In blue) Time evolution of the natural dissipation of a drift echo under radial diffusion (similar to Figure 4A)), and (in red) as viewed by an instrument with finite energy resolution (
It is interesting to compare the results of this numerical experiment in presence of both radial diffusion and finite energy resolution (
In this section, we propose a way to determine the energy resolution requirements needed to guarantee that the observed dissipation of the drift echo is dominated by natural processes, rather than observational artifacts. This is of interest since the natural dissipation of drift echoes provides information on the field perturbations sampled by the particles (See Section 4.1).
In the case discussed in Section 5.1.2.2, in which total phase mixing results from the combination of radial diffusion and the finite energy resolution of the instrument, the resolution,
Which occurs when
Combining Eqs 7, 11, 22, this means that:
This threshold resolution,
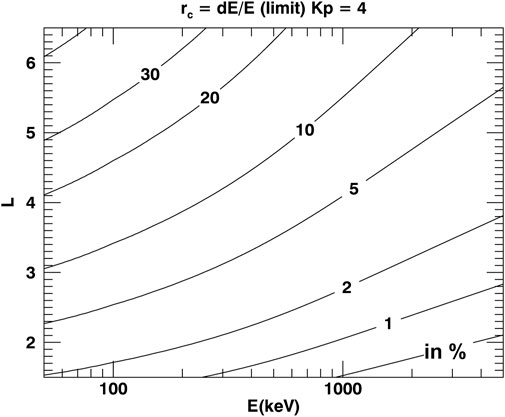
Figure 8. Minimum energy resolution required,
Therefore, this kind of analysis could be utilized to obtain the energy resolution requirements of future particle instruments. Reciprocally, when working with a known instrument resolution, the same kind of analysis can be utilized to determine the minimum magnitude of radial and/or energy diffusion needed to guarantee that the observed dissipation of drift echoes is dominated by natural phase mixing, rather than observational artifacts.
In practice, the initial injection may not be strictly localized in MLT. In that case, the variance at the onset time,
which can also be written as:
In the presence of a rather localized injection, such that
In all cases, the estimates for the characteristic times for phase mixing at the drift scale presented in this paper can be interpreted as estimates for drift echoes’ lifetime. The presence of drift phase structures with significantly longer lifetimes could be indicative of the presence of a process maintaining phase coherence, such as drift resonance.
Physics-based radiation belt models usually consist of solving a three-dimensional Fokker-Planck equation reduced to a three-dimensional fully diffusive equation (e.g., Beutier and Boscher, 1995; Subbotin and Shprits, 2009; Su et al., 2010; Tu et al., 2013; Glauert et al., 2014).
While first implemented in the case of the Earth’s radiation belts, this theoretical framework has also been applied to the radiation belts of Jupiter and Saturn (e.g., Woodfield et al., 2014; 2018; Nénon et al., 2017). All these models rely on the assumption that radiation belts are fully phase mixed at all scales, including at the drift scale.
When the theoretical framework underlying these models was first put forward (e.g., Schulz and Lanzerotti, 1974), drift echoes had already been measured by the ATS-1 satellite at the geostationary orbit (e.g., Brown, 1968; Lanzerotti et al., 1971). Yet, it was assumed that rendering MLT-dependences in radiation belts could be omitted to first order. The radial diffusion framework was indeed designed to render radiation belt dynamics on long timescales (longer than the drift period). A new generation of particle instruments, equipped with very high-energy resolution channels, highlighted the omnipresence of drift phase structures in the radiation belts. This further challenged the validity of the radial diffusion approximation to model the effect of radial transport on radiation belt dynamics, a long-standing issue in radiation belt science which is currently the object of renewed scientific interest (e.g., Riley and Wolf, 1992; Ukhorskiy et al., 2006; Ukhorskiy and Sitnov, 2008; Degeling et al., 2008; Obrien et al., 2022; Osmane et al., 2023).
The objective of this work was to quantify the time it takes for a MLT-dependent structure to phase-mix at the drift scale, that is, the time during which the (purely diffusive) radial diffusion equation does not provide an accurate description of the effect of radial transport on radiation belt intensity once a MLT-dependent perturbation has occurred. Using relatively simple first assumptions to describe instrumental response and field perturbations, we found that the time it takes for particles initially localized in local time to phase-mix is measured in hours in the Earth’s radiation belts, determining timescales during which drift remains an important driver of the dynamics. Future studies could consist of describing the effects of radial transport on radiation belt intensity using a drift-diffusion model, following an approach similar to the one presented by Lejosne et al. (2023) for instance, to determine the role played by PSD’s radial gradients (e.g., Hartinger et al., 2020) in drift echoes’ lifetimes. Several analyses of electrostatic drift echoes present in the Earth’s inner radiation belt (also known as “zebra stripes”) showed that these structures can be observed up to 14 h after generation (e.g., Lejosne and Roederer, 2016; Liu et al., 2016; Lejosne and Mozer, 2020) by the Radiation Belt Storm Probes Ion Composition Experiment (RBSPICE) instruments (Gkioulidou et al., 2023) onboard the Van Allen Probes (
Regarding theoretical studies, the parameter of interest should be independent of the instrument. Thus, it is the characteristic time for natural phase mixing associated with radial diffusion and energy diffusion,
The validity of the radial diffusion equation relies on the assumption that radiation belts are fully phase mixed at all scales, including at the drift scale, even though in reality, this is not necessarily the case. A more realistic implementation of the effects of radial transport on radiation belt intensity using a drift-diffusion model (e.g., Birmingham et al. (1967); Shprits et al., 2015; Lejosne and Albert, 2023) will contribute to determining how different from the radial diffusion paradigm the picture for large-scale radiation belt dynamics is when non-diffusive radial transport events are accounted for.
We assume that the drift phase locations of the trapped particles along the drift shell are distributed randomly, and described by a normal (Gaussian) distribution,
For illustrative purposes, we set
In terms of error function, with:
The distribution,
Introducing the notations:
yields
When the standard deviation,
The contribution of the
For a phase-mixed distribution, we expect the resulting distribution,
Figure 9A represents the normalized number of particles per MLT bin (with a size of one hour MLT), for three different values of the variance,
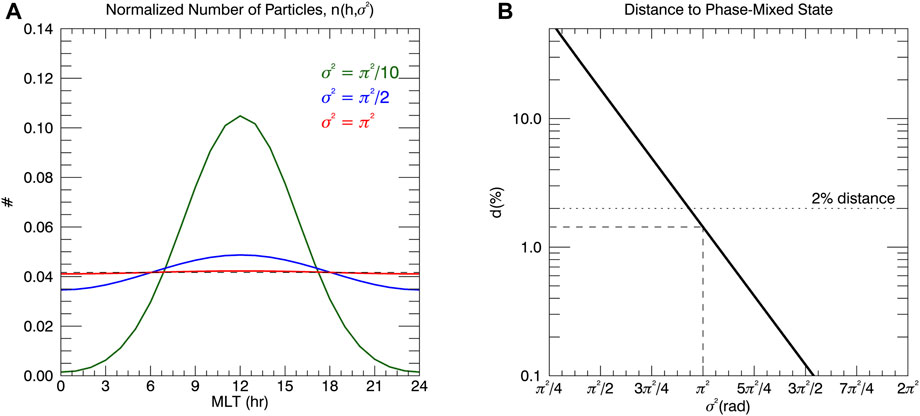
Figure 9. (A) Normalized number of particles per hour MLT, for three different values of the variance,
In this section, we consider a population with kinetic energies randomly distributed around
The average phase location of the population at time, t,
where the integral over
A first order Taylor expansion of
and Eq. 34 can be reformulated as:
Because the integral in Eq. 36 is 0, the square of the average phase location is:
To compute the average of the square of the phase locations, we follow a similar approach. Given that:
and
The result Eq. 33 is obtained by subtracting Eq. 37 from Eq. 40.
In this section, we show that the variance of the drift phase locations associated with radial diffusion, is, to first order:
for equatorial particles. For the sake of simplicity, let us first consider particles at high enough energy that
where
The variation in phase,
Given Eq. 44, this is also:
In a first approximation,
The statistical properties of random walks (e.g., Brockwell and Davis, 2002, p.14) are such that the autocovariance of
where
Thus:
Because
At this point in the derivation, it is important to realize that the population of particles for which we are quantifying the variance of the drift phase locations is scattering in radial distance as it is scattering in azimuthal location. To compute the characteristic time for phase mixing, it is preferable to stay on the same drift shell instead, meaning, it is preferable to focus on
Leveraging Eqs 46, 48, the covariance between
Given that the variance in radial location,
the correlation coefficient,
And the variance of the drift phase locations at
This relationship can be obtained by considering the joint probability density function of a bivariate normal distribution (in
Small perturbations of the fields of electrostatic origin do not yield first-order perturbations in
Finally, let us mention that this derivation relies on the standard assumption that the variance in radial location grows linearly in time (e.g., eq. (C-12)). While this is a typical assumption in radial diffusion research (e.g., Ukhorskiy et al., 2005, their Figure 5; Lejosne and Kollmann, 2020, their equation (5.19)), super-diffusive and/or sub-diffusive regimes could also exist (e.g., Desai et al., 2021; Osmane and Lejosne, 2021). Assuming different statistical models for radial transport would of course lead to different results in this analysis.
In this section, we show that the variance of the drift phase locations associated with energy diffusion, is, to first order:
for equatorial particles. Any perturbation in energy,
The variation in phase,
In a first approximation,
By definition of energy diffusion and the random walk, the autocovariance of
At this point in the derivation, it is important to realize that the population of particles for which we are quantifying the variance of the drift phase locations is scattering in energy as it is scattering in azimuthal location. To compute the characteristic time for phase mixing, it is preferable to focus on a given energy, meaning, it is preferable to focus
Leveraging Eqs 56, 57, the covariance between
Given that the variance in energy,
The correlation coefficient,
And the variance of the drift phase locations at
The combination of Eqs 59, 63 yields Eq. 55.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
SL: Conceptualization, Visualization, Writing–original draft, Writing–review and editing. JA: Conceptualization, Writing–review and editing. DR: Conceptualization, Writing–review and editing.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. SL work was performed under NASA Grant Award 80NSSC23K0518. JA was supported by NASA grant 80NSSC20K1270, AFOSR grant 22RVCOR002, and the Space Vehicles Directorate of the Air Force Research Laboratory.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The views expressed are those of the authors and do not reflect the official guidance or position of the United States Government, the Department of Defense or of the United States Air Force. The appearance of external hyperlinks does not constitute endorsement by the United States Department of Defense (DoD) of the linked websites, or the information, products, or services contained therein. The DoD does not exercise any editorial, security, or other control over the information you may find at these locations.
Beutier, T., and Boscher, D. (1995). A three-dimensional analysis of the electron radiation belt by the Salammbô code. J. Geophys. Res. 100 (8), 14853–14861. doi:10.1029/94JA03066
Brand, A., Allen, L., Altman, M., Hlava, M., and Scott, J. (2015). Beyond authorship: attribution, contribution, collaboration, and credit. Learn. Pub. 28, 151–155. doi:10.1087/20150211
Brautigam, D. H., and Albert, J. M. (2000). Radial diffusion analysis of outer radiation belt electrons during the October 9, 1990, magnetic storm. J. Geophys. Res. 105 (A1), 291–309. doi:10.1029/1999JA900344
Birmingham, T. J., Northrop, T. G., and Fälthammar, C. G. (1967). Charged particle diffusion by violation of the third adiabatic invariant. Phys. Fluids 10 (11), 2389. doi:10.1063/1.1762048
P. J. Brockwell, and R. A. Davis (2002). Introduction to time series and forecasting (New York, NY: Springer New York).
Brown, W. L. (1968). “Energetic outer-belt electrons at synchronous altitude,” in Earth's particles and fields. Editor B. M. McCormac (New York: Reinhold), 33.
Degeling, A. W., Ozeke, L. G., Rankin, R., Mann, I. R., and Kabin, K. (2008). Drift resonant generation of peaked relativistic electron distributions by pc 5 ULF waves. J. Geophys. Res. 113, a–n. doi:10.1029/2007JA012411
Desai, R. T., Eastwood, J. P., Horne, R. B., Allison, H. J., Allanson, O., Watt, C. E. J., et al. (2021). Drift orbit bifurcations and cross-field transport in the outer radiation belt: global MHD and integrated test-particle simulations. J. Geophys. Res. Space Phys. 126, e2021JA029802. doi:10.1029/2021JA029802
Gkioulidou, M., Mitchell, D. G., Manweiler, J. W., Lanzerotti, L. J., Gerrard, A. J., Ukhorskiy, A. Y., et al. (2023). Radiation belt storm probes ion composition experiment (RBSPICE) revisited: in-flight calibrations, lessons learned and scientific advances. Space Sci. Rev. 219, 80. doi:10.1007/s11214-023-00991-x
Glauert, S. A., Horne, R. B., and Meredith, N. P. (2014). Three-dimensional electron radiation belt simulations using the BAS Radiation Belt Model with new diffusion models for chorus, plasmaspheric hiss, and lightning-generated whistlers. J. Geophys. Res. Space Phys. 119, 268–289. doi:10.1002/2013JA019281
Hartinger, M. D., Claudepierre, S. G., Turner, D. L., Reeves, G. D., Breneman, A., Mann, I. R., et al. (2018). Diagnosis of ULF wave-particle interactions with megaelectron volt electrons: the importance of ultrahigh-resolution energy channels. Geophys. Res. Lett. 45 (11), 883–892. doi:10.1029/2018GL080291
Hartinger, M. D., Reeves, G. D., Boyd, A., Henderson, M. G., Turner, D. L., Komar, C. M., et al. (2020). Why are there so few reports of high-energy electron drift resonances? Role of radial phase space density gradients. J. Geophys. Res. Space Phys. 125, e2020JA027924. doi:10.1029/2020JA027924
Hogg, R. V., and Craig, A. T. (1970). Introduction to mathematical statistics. 3rd Edition. New York: Macmillan Publishing Company.
Jaynes, A. N., Baker, D. N., Singer, H. J., Rodriguez, J. V., Loto'aniu, T. M., Ali, A. F., et al. (2015). Source and seed populations for relativistic electrons: Their roles in radiation belt changes. J. Geophys. Res. Space Physics 120, 7240–7254. doi:10.1002/2015JA021234
Krimigis, S. M., Mitchell, D. G., Hamilton, D. C., Livi, S., Dandouras, J., Jaskulek, S., et al. (2004). Magnetosphere imaging instrument (MIMI) on the cassini mission to saturn/titan. Space Sci. Rev. 114, 233–329. doi:10.1007/s11214-004-1410-8
Lanzerotti, L. J., Maclennan, C. G., and Robbins, M. F. (1971). Proton drift echoes in the magnetosphere. J. Geophys. Res. 76, 259. doi:10.1029/JA076i001p00259
Lejosne, S., and Albert, J. M. (2023). Drift phase resolved diffusive radiation belt model: 1. Theoretical framework. Front. Astron. Space Sci. 10, 1200485. doi:10.3389/fspas.2023.1200485
Lejosne, S., Albert, J. M., and Walton, S. D. (2023). Drift phase resolved diffusive radiation belt model: 2. Implementation in a case of random electric potential fluctuations. Front. Astron. Space Sci. 10, 1232512. doi:10.3389/fspas.2023.1232512
Lejosne, S., Allison, H. J., Blum, L. W., Drozdov, A. Y., Hartinger, M. D., Hudson, M. K., et al. (2022a). Differentiating between the leading processes for electron radiation belt acceleration. Front. Astronomy Space Sci. 144. doi:10.3389/fspas.2022.896245
Lejosne, S., Fejer, B. G., Maruyama, N., and Scherliess, L. (2022b). Radial transport of energetic electrons as determined from the zebra stripes measured in the Earth's inner belt and slot region. Front. Astronomy Space Sci. 9, 823695. doi:10.3389/fspas.2022.823695
Lejosne, S., and Kollmann, P. (2020). Radiation belt radial diffusion at Earth and beyond. Space Sci. Rev. 216, 19. doi:10.1007/s11214-020-0642-6
Lejosne, S., and Mozer, F. S. (2020). Experimental determination of the conditions associated with “zebra stripe” pattern generation in the earth's inner radiation belt and slot region. J. Geophys. Res. Space Phys. 125, e2020JA027889. doi:10.1029/2020JA027889
Lejosne, S., and Roederer, J. G. (2016). The “zebra stripes”: an effect of F region zonal plasma drifts on the longitudinal distribution of radiation belt particles. J. Geophys. Res. Space Phys. 121, 507–518. doi:10.1002/2015JA021925
Liu, Y., Zong, Q.-G., Zhou, X.-Z., Foster, J. C., and Rankin, R. (2016). Structure and evolution of electron “zebra stripes” in the inner radiation belt. J. Geophys. Res. Space Phys. 121, 4145–4157. doi:10.1002/2015JA022077
Mitchell, D., Lanzerotti, L. J., Kim, C. K., Stokes, M., Ho, G., and Cooper, S. (2013). Radiation belt storm probes ion composition experiment (RBSPICE). Space Sci. Rev. 179, 263–308. doi:10.1007/s11214-013-9965-x
Nénon, Q., Sicard, A., and Bourdarie, S. (2017). A new physical model of the electron radiation belts of Jupiter inside Europa's orbit. J. Geophys. Res. Space Phys. 122, 5148–5167. doi:10.1002/2017JA023893
O'Brien, T. P., Claudepierre, S. G., Guild, T. B., Fennell, J. F., Turner, D. L., Blake, J. B., et al. (2016). Inner zone and slot electron radial diffusion revisited. Geophys. Res. Lett. 43, 7301–7310. doi:10.1002/2016GL069749
O'Brien, T. P., Green, J. C., Halford, A. J., Kwan, B. P., Claudepierre, S. G., and Ozeke, L. G. (2022). Drift phase structure implications for radiation belt transport. J. Geophys. Res. Space Phys. 127, e2022JA030331. doi:10.1029/2022JA030331
Osmane, A., Kilpua, E., George, H., Allanson, O., and Kalliokoski, M. (2023). Radial transport in the earth's radiation belts: linear, quasi-linear, and higher-order processes. ApJS 269, 44. doi:10.3847/1538-4365/acff6a
Osmane, A., and Lejosne, S. (2021). Radial diffusion of planetary radiation belts’ particles by fluctuations with finite correlation time. Astrophys. J. 912, 142. doi:10.3847/1538-4357/abf04b
Riley, P., and Wolf, R. A. (1992). Comparison of diffusion and particle drift descriptions of radial transport in the earth's inner magnetosphere. J. Geophys. Res. 97 (A11), 16865–16876. doi:10.1029/92JA01538
Sauvaud, J. A., Moreau, T., Maggiolo, R., Treilhou, J.-P., Jacquey, C., Cros, A., et al. (2006). High-energy electron detection onboard DEMETER: the IDP spectrometer, description and first results on the inner belt. Planet. Space. Sci. 54, 502–511. doi:10.1016/j.pss.2005.10.019
Sauvaud, J.-A., Walt, M., Delcourt, D., Benoist, C., Penou, E., Chen, Y., et al. (2013). Inner radiation belt particle acceleration and energy structuring by drift resonance with ULF waves during geomagnetic storms. J. Geophys. Res. Space Phys. 118, 1723–1736. doi:10.1002/jgra.50125
Schulz, M. (1991). “The magnetosphere,” in Geomagnetism. Editor J. A. Jacobs (London, UK: Academic Press), 4, 87–293. cli. 2.
Schulz, M., and Lanzerotti, L. J. (1974). Particle diffusion in the radiation belts. Berlin: Springer. doi:10.1007/978-3-642-65675-0
Selesnick, R. S. (2012). Atmospheric scattering and decay of inner radiation belt electrons. J. Geophys. Res. 117, A08218. doi:10.1029/2012JA017793
Selesnick, R. S., Su, Y.-J., and Sauvaud, J.-A. (2019). Energetic electrons below the inner radiation belt. J. Geophys. Res. Space Phys. 124, 5421–5440. doi:10.1029/2019JA026718
Shprits, Y. Y., Kellerman, A. C., Drozdov, A. Y., Spence, H. E., Reeves, G. D., and Baker, D. N. (2015). Combined convective and diffusive simulations: VERB-4D comparison with 17 March 2013 Van Allen Probes observations. Geophys. Res. Lett. 42, 9600–9608. doi:10.1002/2015GL065230
Su, Z., Xiao, F., Zheng, H., and Wang, S. (2010). Steerb: a three-dimensional code for storm-time evolution of electron radiation belt. J. Geophys. Res. 115, A09208. doi:10.1029/2009JA015210
Subbotin, D. A., and Shprits, Y. Y. (2009). Three-dimensional modeling of the radiation belts using the Versatile Electron Radiation Belt (VERB) code. Space weather. 7, S10001. doi:10.1029/2008SW000452
Sun, Y., Roussos, E., and Hao, Y. (2021). Saturn’s inner magnetospheric convection in the view of zebra stripe patterns in energetic electron spectra. J. Geophys. Res. Space Phys. 125 (5), e2019JA027621. doi:10.1029/2021ja029600
Tu, W., Cunningham, G. S., Chen, Y., Henderson, M. G., Camporeale, E., and Reeves, G. D. (2013). Modeling radiation belt electron dynamics during GEM challenge intervals with the DREAM3D diffusion model. J. Geophys. Res. Space Phys. 118, 6197–6211. doi:10.1002/jgra.50560
Turner, D. L., Claudepierre, S. G., Fennell, J. F., O'Brien, T. P., Blake, J. B., Lemon, C., et al. (2015). Energetic electron injections deep into the inner magnetosphere associated with substorm activity. Geophys. Res. Lett. 42, 2079–2087. doi:10.1002/2015GL063225
Ukhorskiy, A., Sitnov, M., Mitchell, D., Takahashi, K., Lanzerotti, L. J., and Mauk, B. H. (2014). Rotationally driven ‘zebra stripes’ in Earth’s inner radiation belt. Nature 507, 338–340. doi:10.1038/nature13046
Ukhorskiy, A. Y., Anderson, B. J., Brandt, P. C., and Tsyganenko, N. A. (2006). Storm time evolution of the outer radiation belt: transport and losses. J. Geophys. Res. 111, A11S03. doi:10.1029/2006JA011690
Ukhorskiy, A. Y., and Sitnov, M. I. (2008). Radial transport in the outer radiation belt due to global magnetospheric compressions. J. Atmos. Sol.-Terr. Phys. 70, 1714. doi:10.1016/j.jastp.2008.07.018
Wong, J.-M., Meredith, N. P., Horne, R. B., Glauert, S. A., and Ross, J. P. J. (2024). New chorus diffusion coefficients for radiation belt modeling. J. Geophys. Res. Space Phys. 129, e2023JA031607. doi:10.1029/2023JA031607
Woodfield, E. E., Horne, R. B., Glauert, S. A., Menietti, J. D., and Shprits, Y. Y. (2014). The origin of Jupiter's outer radiation belt. J. Geophys. Res. Space Phys. 119, 3490–3502. doi:10.1002/2014JA019891
Woodfield, E. E., Horne, R. B., Glauert, S. A., Menietti, J. D., Shprits, Y. Y., and Kurth, W. S. (2018). Formation of electron radiation belts at Saturn by Z-mode wave acceleration. Nat. Commun. 9, 5062. doi:10.1038/s41467-018-07549-4
Zhao, H., Sarris, T. E., Li, X., Huckabee, I. G., Baker, D. N., Jaynes, A. J., et al. (2022). Statistics of multi-MeV electron drift-periodic flux oscillations using Van Allen Probes observations. Geophys. Res. Lett. 49, e2022GL097995. doi:10.1029/2022GL097995
Keywords: radiation belt, drift, phase-mixing, radial diffusion, energy diffusion, instrument resolution
Citation: Lejosne S, Albert JM and Ratliff D (2024) Characteristic times for radiation belt drift phase mixing. Front. Astron. Space Sci. 11:1385472. doi: 10.3389/fspas.2024.1385472
Received: 12 February 2024; Accepted: 17 April 2024;
Published: 24 June 2024.
Edited by:
Georgios Balasis, National Observatory of Athens, GreeceReviewed by:
Stavros Dimitrakoudis, National and Kapodistrian University of Athens, GreeceCopyright © 2024 Lejosne, Albert and Ratliff. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Solène Lejosne, c29sZW5lQGJlcmtlbGV5LmVkdQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.