
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
MINI REVIEW article
Front. Astron. Space Sci. , 04 March 2024
Sec. Cosmology
Volume 11 - 2024 | https://doi.org/10.3389/fspas.2024.1346820
This article is part of the Research Topic Scalar Fields and the Dark Universe View all 6 articles
 Brandon Bautista
Brandon Bautista Juan Carlos Degollado*
Juan Carlos Degollado*We consider static solutions to the spherically symmetric Einstein-scalar field systems with an axion potential known as axion stars, originally described by Guerra et al., JCAP (2019, 09 (09)). We construct numerically families of axion stars in the ground state, for different values of the decay constant fa. It is shown that the existence diagram becomes richer than the mini-boson star case, and several regions of stability appear as the value of fa decreases, yielding to more massive configurations with larger compactness. Some intrinsic properties, such as isotropy and compactness of such stars, are also discussed. Finally, we describe the motion of test particles around these objects.
Bosonic stars are formed when the density of bosons in a region of space becomes high enough to allow them to gravitationally attract each other and form a self-gravitating configuration overcoming their quantum-mechanical repulsion (Kaup, 1968; Ruffini and Bonazzola, 1969; Mielke and Scherzer, 1981; Colpi et al., 1986; Seidel and Suen, 1990; Mielke and Schunck, 2000; Steven, 2012). Several types of bosonic stars have been proposed, depending on the type of boson involved. These include vector bosonic fields known as Proca stars (Brito et al., 2016; Herdeiro et al., 2019), oscillations (Seidel and Suen, 1991; Alcubierre et al., 2003) or Q-balls (Alexander and Shaposhnikov, 1998; Enqvist and McDonald, 1998). One the simplest configurations are boson stars with a complex scalar field (Jetzer, 1992). Interest in these self-gravitating objects has recently increased due to developments in particle physics and cosmology, suggesting that in the early stages of the universe, bosonic stars may have formed out of fundamental scalar fields and could play a role in understanding the origin of dark matter (Matos and Arturo Urena-Lopez, 2000; Matos et al., 2000; Matos and Arturo Urena-Lopez, 2001; Matos and Arturo Urena-Lopez, 2002; Marsh and Ferreira, 2010; Marsh and Pop, 2015; Marsh, 2016). Among the myriad of candidates proposed to explain this cosmic enigma, axions have emerged as one of the leading candidates to explain the nature of dark matter in the universe (Peccei and Quinn, 1977; Matos and Arturo Urena-Lopez, 2007; Matos et al., 2008; Arvanitaki et al., 2010; Arvanitaki and Dubovsky, 2011; Marsh and Silk, 2014; Porayko and Postnov, 2014; Schive et al., 2014; Sikivie, 2014; Marsh and Pop, 2015; Marsh, 2016). Axion particles were originally proposed in the 1970s as a possible solution to the strong CP problem in particle physics and are the best motivated candidates because of naturally suppressed CP violation in the strong nuclear force. The fundamental theory for the axion field is a renormalizable extension of the standard model in which the Peccei–Quinn symmetry is broken spontaneously by the ground state of a scalar field.
After the original proposal, axion can refer to any low-mass spin-zero particle characterized by a periodic self-interaction potential (Graham et al., 2015; Caso et al., 2018). String theory, for instance, provides grounds for considering the existence of numerous axions with masses spanning several orders of magnitude, and such possibility has been referred as the Axiverse (Arvanitaki et al., 2010; Di Luzio et al., 2020), and the observational consequences of these axions on astrophysical black holes through the Penrose super-radiance process have been explored (Arvanitaki and Dubovsky, 2011; Brito et al., 2015). Additionally, extremely light bosonic particles, with masses of the order of 10–22 eV, as a candidate for dark matter, have been discussed (Arturo Ureña-López and Matos, 2000; Matos et al., 2000; Matos and Arturo Urena-Lopez, 2007; Lam et al., 2017). Astrophysical constraints coming from the mechanism of cooling of stars due to the emission of axions provide a lower bound on the axion decay constant of the order of fa ≥ 3 × 109 GeV. On the other hand, the cosmological constraint in the early universe provides a bound of the order of fa ≤ 1012 GeV (Marsh, 2016).
Due to the bosonic nature, axions can form a Bose–Einstein condensate (BEC), whose collective behavior can be slightly different compared to an ideal gas of bosons. In this work, we focus on the case of static axion stars, which are spherically symmetric self-gravitating solutions for a scalar field with a periodic potential. Axion boson stars were first studied by Guerra et al. (2019) and later generalized to include rotation by Delgado et al. (2020) and Zeng et al. (2023). More recently, the fermion–axion system has also been studied by Zeng et al. (2021) and Di Giovanni et al. (2022).
We begin by describing the set up to construct self-gravitating axion stars in Einstein theory and provide some basic definitions. We focus on isolated axion stars and summarize some basic features of the equations. Then, we construct families of spherically symmetric solutions with different values of the decay constant fa and describe some of their properties. Finally, we discuss the motion of test particles, both null and massive, moving in the vicinity of the central object.
We consider a complex scalar field minimally coupled to gravity with an action given by
where R represents the Ricci scalar, g = det (gμν), κ = 16π, Φ represents the scalar field, and the star stands for the complex conjugate. V represents the self-interacting potential. The variation of the action 2.1 with respect to the metric tensor gμν leads to Einstein’s equations.
where the stress–energy tensor is given by
The conservation of energy applied to the stress–energy tensor (2.3) reduces to the equation
and its complex conjugate, where □Φ = gμν∇μ∇νΦ.
We are interested in static spherically symmetric spacetimes, so we assume the metric can be written as
where dΩ2 = dθ2 + sin2θdφ2 is the metric defined on the two-sphere. In order to construct stationary configurations, we assume a scalar field with a time harmonic dependence of the form
As described in the work of Guerra et al. (2019), axion stars are constructed with the potential
where B = 0.22 is a numerical factor that depends on the mass of the up and down quarks and μ is identified as the mass of the particles. In the limit fa ≫ ϕ, the leading term in the power series of the potential leads to a potential with a quartic self-interaction of the form
From 2.8 we thus expect, the major contributions of the periodic potential appear in the limit of small fa. With the ansatz for metric 2.5 and form 2.6 of the field, the Einstein-scalar field system 2.2, 2.4, 2.7 in spherical symmetry becomes
To solve systems 2.9–2.11, one must choose appropriate boundary conditions, which are as follows. In order to guarantee that the spacetime is locally flat at the origin, the condition a (0) = 1 is required. Furthermore, we ask for
After substituting this scaling 2.12 in systems 2.9–2.11, the rescaled system is left in units of the mass parameter μ, which fixes the scale. Given a value of the field at the origin ϕc as a free parameter, we choose a trial value of the lapse and integrate the system outward from the origin using a fourth-order Runge–Kutta scheme with an adaptive step size. This adaptive scheme allowed us to reach smaller values of fa. Then, we use a shooting algorithm to find the value of the lapse that corresponds to asymptotically flat solutions. We construct families of axion boson stars for different values of the parameter fa and different values of the central scalar field. We also focus on solutions with no nodes in the scalar field corresponding to the ground state.
As demonstrated by Guerra et al. (2019), in the limit of large fa, mini-boson stars are recovered, and this happens for values
The energy density ρ, radial pressure pr, and tangential pressure pt are defined in terms of the stress–energy tensor 2.3 as
The total mass of the object M is given by the limit r → ∞ of the function
In our numerical calculations, we approach M as the value of this function evaluated at the outer point of the numerical grid. Alternatively, one can also find the total mass of the system by assuming that far away, the metric reduces to the Schwarzschild metric (Misner et al., 1973) so that
This expression converges very rapidly as r grows due to the exponential decay of the scalar field, and nonetheless, we checked that the results obtained with both expressions 2.16, 2.17 agree in the limit of large r.
The periodic potential for the axion as given in Equation 2.7 is shown in Figure 1 for some representative values of fa. Close to the minimum around ϕ ≈ 0, as the value of fa increases, the quadratic behavior of the field dominates the potential and the solutions resemble the mini-boson stars. We show some results for the families of solutions corresponding to different values of fa in the following.
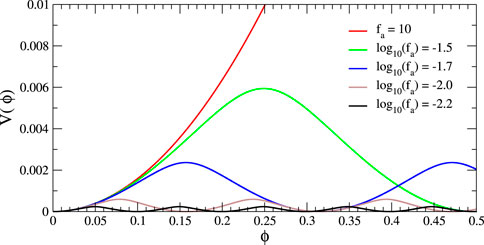
FIGURE 1. Periodic scalar field potential, as given in (2.7), for some values of the decaying constant fa. For larger values of fa ∼ 10, the potential tends to a quadratic behavior. We consider μ = 1; however, the potential can be rescaled with μ2.
It is known since the pioneer works of Kaup (1968) and Ruffini and Bonazzola (1969) that the mass of mini-boson stars has a maximum value
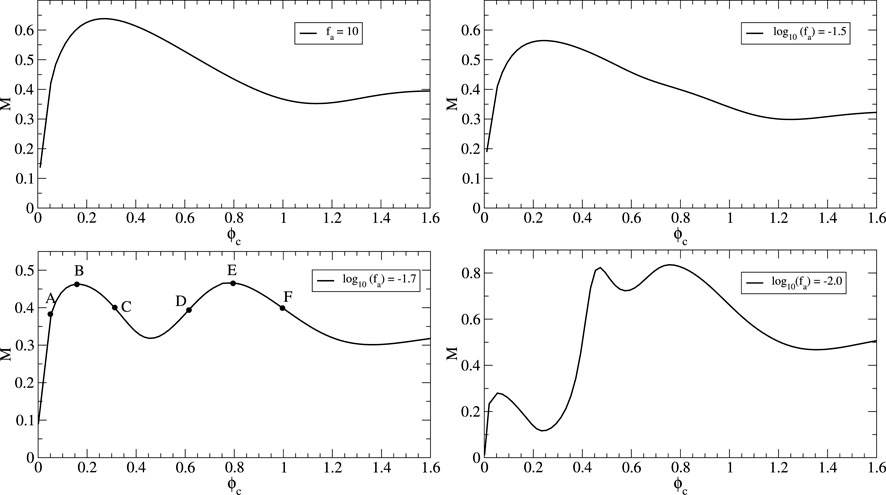
FIGURE 2. Existence plots. Each point on these curves corresponds to a solution of the Einstein-scalar field system. The local maxima separate the stable and unstable regions. The solutions with fa = 10 are consistent with the mini-boson stars described by Kaup (1968). For smaller values of the decay constant fa, a richer structure appears with more than one maximum and more than one minimum. The value of the maximum mass configurations increases as the value of fa decreases.
For larger fa, the solutions reduce to the standard mini-boson stars, but in the limit fa → 0, solutions with the appropriate boundary conditions, representing localized objects, are more difficult to find.
We now move to the description of the stars for a fixed value of fa. For the sake of simplicity, we show the results for log10 (fa) = −1.7. Figure 4 shows the parametric plots of radial and tangential pressures [pr(r), pt(r)] as given by (2.14 and 2.15. In the figure, the dashed line corresponds to the identity pr = pt. Larger deviations from this line, thus, correspond to larger anisotropy. The plots correspond to configurations marked with dots in Figure 2 and labeled with letters from A–F. Configuration A, with smaller values of ϕc, display only a small deviation from isotropy; however, as the value of ϕc increases, the stars become more anisotropic. For configuration E, the change of sign in the tangential pressure becomes more evident. However, the anisotropy is not as large as the one presented in other boson stars (Steven, 2012; Alcubierre et al., 2018; Alcubierre et al., 2019). The values of the radius, mass, and compactness for configurations A–F are listed in Table 1. As one moves to the right in the existence plot, with larger values of ϕc, axion stars become more compact. In the last column of Table 1, the numerical values of compactness are listed. As one moves to higher values of ϕc, the compactness increases. This trend is also present for the smaller values of fa used in this work. Nonetheless, it seems that the compactness does not reach the maximum compactness limit (Buchdahl, 1966). Figure 5 displays the profiles of radial and tangential pressure as well as the density given in 2.13 of the configuration with the local maximum mass labeled as B and E in Figure 2. For configuration B, the difference in terms of absolute values between pr and pt is quite small. For configuration E, the same trend holds, but the tangential pressure becomes negative in the more exterior parts of the star. In both models, the maximum density is attained in the origin as in the usual mini-boson stars. Figure 5 shows the radial profiles of the metric coefficients α and a. In both models, the relation a/α → 1 holds at infinity, which is consistent with a Schwarzschild asymptotic behavior. In the more compact model E, a lower value of the lapse is attained at the origin, which is related with the fact that this configuration is more compact.
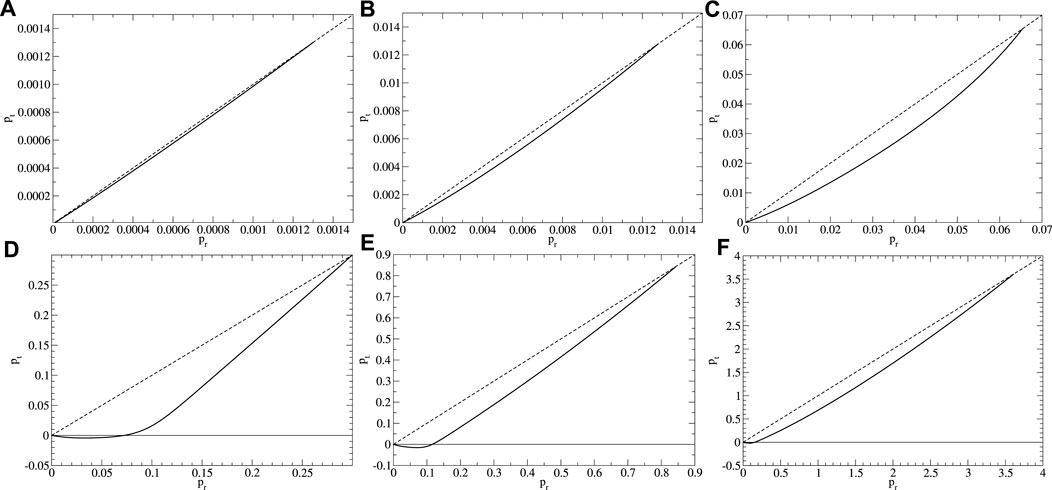
FIGURE 4. The measure of the anisotropy of axion stars is given by the difference between radial and tangential pressure. The dashed line represents the identity pt = pr. The configurations displayed correspond to the ones in the bottom panel of Figure 2 labeled from (A–F).
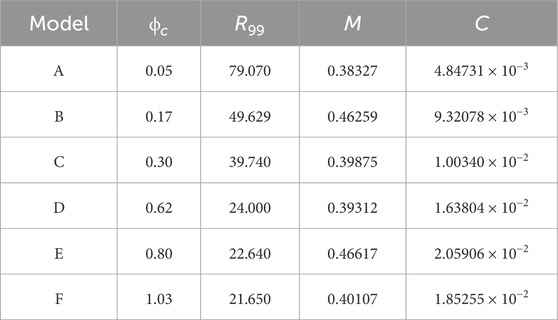
TABLE 1. Parameters of the configurations shown in Figure 2 with log10 (fa) = −1.7: the value of the field at the origin, ϕc, the effective size as determined by the R99 radius, the total mass M, and the compactness.
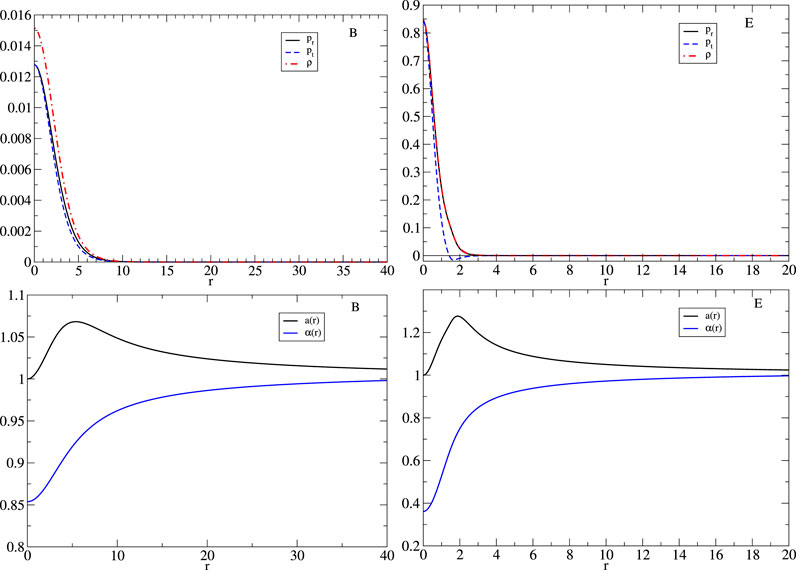
FIGURE 5. Top panels: energy density and radial and tangential pressure profiles for configurations B and E in Figure 2. These configurations correspond to local maximum masses. Bottom panels display the corresponding metric coefficient a and the lapse function α.
In general relativity, the maximum compactness of a self-gravitating, isotropic and spherically symmetric object made of a perfect fluid is M/R = 4/9, where M represents the mass of the object and R represents its radius. However, the above number, known as Buchdahl’s bound, relies strongly on the hypothesis of isotropy (Buchdahl, 1966). Considerable effort has been dedicated to model the properties of anisotropic matter, with the hope of finding physically viable models of compact stars. While anisotropies are generally negligible as compared to the pressure, it has been shown that even small anisotropies in fluid stars may induce significant changes on the mass and compactness of the star (Raposo et al., 2019). To determine the structure of a compact star, a widely followed path is to specify an equation of state and then solve the field equations. Customarily, this is carried out considering hydrodynamical equilibrium; however, in this work, we found that moderate anisotropic configurations exist for the potential (2.7), yielding to highly compact objects. Nonetheless, our results indicate that for the axion periodic potential, it is not possible to surpass Buchdahl’s bound.
It will also be helpful in identifying some general properties of the motion of test particles propagating in the spacetime associated with the previously found stars and, in particular, in determining whether the solutions admit stable circular orbits or light rings. The interest of studying light rings in compact objects has been renewed because of the correspondence between the quasi-normal modes of black holes and light ring oscillations to describe the initial part of the ringdown gravitational-wave signal of black holes (Cardoso et al., 2009; Cardoso and Pani, 2017; Khanna and Price, 2017).
In order to describe the motion of test particles in the spacetime (2.5), let us consider the Lagrangian equation as follows:
where “dot” denotes the derivative with respect to the affine parameter τ. It is possible to consider
Since the spacetime is spherically symmetric, we focus on particles in the plane θ = π/2 in 3.1. Associated to the time and angular symmetry, there are two conserved quantities during the motion of the particles, namely, the energy at infinity E and the angular momentum ℓ given by
Normalization of the four velocities uμuμ = −k can be written in terms of the conserved quantities 3.2 yielding the equation
Equation 3.3 can be written as
Defining a new variable z, through
where the effective potential in 3.5 is defined as
Circular motion of particles is possible when the conditions
where the prime denotes the derivative with respect to r. For null geodesics, the existence of circular orbits is given by the condition h(r) = α − rα′ = 0 for which expressions (3.7) are undetermined. Moreover, it has been proven that regular configurations can have two light rings, of which one is stable (Pedro et al., 2017). However, not all configurations considered here admit light rings, and their appearance will depend on the compactness of the star. On the other hand, regarding massive particles, there always exist stable circular orbits. Figure 6 shows the potential (3.6) for null geodesics (with k = 0) for configurations A to F in Figure 2 with log10 (fa) = −1.7. For this value of fa, configurations are not compact enough to have light rings. Since the potential for these configurations is very alike, the motion of null particles around them is quite similar. In the right panel of Figure 6, the function h(r) is displayed, and the change of behavior close the origin for configurations D–F is observed, and there is a slight decay on the value of h(r). It can be seen in the figure that as the configurations become more compact, h decreases in such a way that it will cross the origin twice, giving rise to the existence of a pair of light rings. For configurations with lower values of log10 (fa) ≈ − 2.3, this is actually the case, and a pair of light rings appear. Figure 7 displays the effective potential for massive particles (k = 1) with ℓ = 1 for configurations A–F. In all cases, the potential is minimum, indicating the existence of circular orbits.
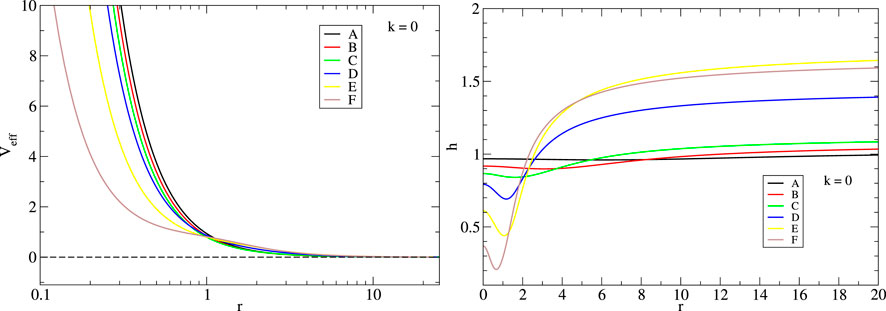
FIGURE 6. Left: effective potential (3.6) for null geodesics. Right: function h(r) = α − rα′. The zeroes of h determine the existence of light rings. For configurations A–F in Figure 2, there are no light rings.
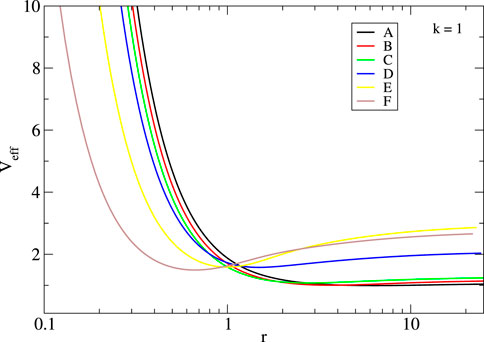
FIGURE 7. Effective potential for massive particles for the configurations A–F shown in Figure 2 with ℓ = 1. The location of the minimum indicates the position of the circular orbit.
In this work, we considered solutions to the spherically symmetric stationary Einstein-axion field system known as axion stars, which have been previously studied by Guerra et al. (2019). This system is characterized because the scalar field potential is periodic on the field. We presented solutions with no nodes on the scalar field (also known as ground state solutions) varying the value of the axion decay constant fa. Axion stars with fa ≫ ϕ have similar properties as mini-boson stars in the sense that they have a local maximum of the total mass M for a finite value of the central value of the field ϕc. As the value of the constant fa decreases, more local maxima appear, and it is possible to find solutions with larger values of mass with larger values of ϕc. However, as a consequence, local minima also appear, leading to a different region of stability. For smaller values of fa, it becomes extremely difficult to find solutions since the system is quite sensible to the values of ϕc. Configurations with larger values of ϕc present larger anisotropies in the sense that the ratio between the tangential and radial pressures pt/pr differs slightly from unity. Furthermore, for values of ϕc beyond the first maximum in the mass, solutions with negative tangential pressure are found. Finally, regarding the motion of test particles, stars with small values of fa may have high compactness that allow the existence of light rings, while for time-like particles, the existence of circular orbits is possible. This characteristic may be used to explore the astrophysical features of axion stars.
BB: writing–original draft and writing–review and editing. JD: writing–original draft and writing–review and editing.
The authors declare that financial support was received for the research, authorship, and/or publication of this article. This work was partially supported by DGAPA-UNAM through grant IN110523, by the CONACyT Network Project No. 376127 “Sombras, lentes y ondas gravitatorias generadas por objetos compactos astrofisicos,” and No. 304001 “Estudio de campos escalares con aplicaciones en cosmología y astrofísica,” and by the European Union’s Horizon 2020 research and innovation (RISE) program H2020-MSCARISE- 2017, Grant No. FunFiCO-777740, and the European Horizon Europe staff exchange (SE) program HORIZONMSCA- 2021-SE-01, Grant No. NewFunFiCO-101086251.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Alcubierre, M., Barranco, J., Bernal, A., Degollado, J. C., Diez-Tejedor, A., Megevand, M., et al. (2018). Cl. Quant. Grav. 35 (19), 19LT01. doi:10.1088/1361-6382/aadcb6
Alcubierre, M., Barranco, J., Bernal, A., Degollado, J. C., Diez-Tejedor, A., Megevand, M., et al. (2019). Dynamical evolutions of ℓ-boson stars in spherical symmetry. Cl. Quant. Grav. 36 (21), 215013. doi:10.1088/1361-6382/ab4726
Alcubierre, M., Becerril, R., Guzman, S. F., Matos, T., Nunez, D., and Arturo Urena-Lopez, L. (2003). Numerical studies of Phi**2 oscillatons. Cl. Quant. Grav. 20, 2883–2904. doi:10.1088/0264-9381/20/13/332
Alexander, K., and Shaposhnikov, M. E. (1998). Supersymmetric Q balls as dark matter. Phys. Lett. B 418, 46–54. doi:10.1016/s0370-2693(97)01375-0
Arturo Ureña-López, L., and Matos, T. (2000). New cosmological tracker solution for quintessence. Phys. Rev. D62, 081302. doi:10.1103/PhysRevD.62.081302
Arvanitaki, A., Dimopoulos, S., Dubovsky, S., Kaloper, N., and March-Russell, J. (2010). String Axiverse. Phys. Rev. D81, 123530. doi:10.1103/physrevd.81.123530
Arvanitaki, A., and Dubovsky, S. (2011). Exploring the string Axiverse with precision black hole physics. Phys. Rev. D83, 044026. doi:10.1103/physrevd.83.044026
Brito, R., Cardoso, V., CarlosHerdeiro, A. R., and Radu., E. (2016). Proca stars: gravitating Bose–Einstein condensates of massive spin 1 particles. Phys. Lett. B 752, 291–295. doi:10.1016/j.physletb.2015.11.051
Brito, R., Cardoso, V., and Pani, P. (2015). Superradiance: new Frontiers in black hole physics. Lect. Notes Phys. 906, 1–237. doi:10.1007/978-3-030-46622-0
Buchdahl, H. A. (1966). General relativistic fluid spheres. II. General inequalities for regular spheres. Astrophys. J. 146, 275. doi:10.1086/148875
Cardoso, V., Miranda, A. S., Berti, E., Witek, H., and Vilson, T. Z. (2009). Geodesic stability, Lyapunov exponents and quasinormal modes. Phys. Rev. D. 79 (6), 064016. doi:10.1103/physrevd.79.064016
Cardoso, V., and Pani, P. (2017). Tests for the existence of black holes through gravitational wave echoes. Nat. Astron 1 (9), 586–591. doi:10.1038/s41550-017-0225-y
Caso, C., Conforto, , Gurtu, A., Aguilar-Benitez, M., Amsler, C., Barnett, R. M., et al. (2018). Review of particle physics. Phys. Rev. D. 98 (3), 030001–030783. doi:10.1007/s10052-998-0104-x
Colpi, M., Shapiro, S. L., and Wasserman, I. (1986). Boson stars: gravitational equilibria of self-interacting scalar fields. Phys. Rev. Lett. 57, 2485–2488. doi:10.1103/physrevlett.57.2485
Delgado, J. F. M., Herdeiro, C. A. R., and Radu., E. (2020). Rotating axion boson stars. JCAP 06. 037. doi:10.1088/1475-7516/2020/06/037
Di Giovanni, F., Guerra, D., Albanesi, S., Miravet-Tenés, M., and Tseneklidou, D. (2022). Fermion-axion stars: static solutions and dynamical stability. Phys. Rev. D. 106 (8), 084013. doi:10.1103/physrevd.106.084013
Di Luzio, L., Giannotti, M., Nardi, E., and Visinelli, L. (2020). The landscape of QCD axion models. Phys. Rept. 870, 1–117. doi:10.1016/j.physrep.2020.06.002
Enqvist, K., and McDonald, J. (1998). Q balls and baryogenesis in the MSSM. Phys. Lett. B 425, 309–321. doi:10.1016/s0370-2693(98)00271-8
Graham, P. W., Irastorza, I. G., Lamoreaux, S. K., Lindner, A., and van Bibber, K. A. (2015). Experimental searches for the axion and axion-like particles. Ann. Rev. Nucl. Part. Sci. 65, 485–514. doi:10.1146/annurev-nucl-102014-022120
Guerra, D., CaioMacedo, F. B., and Pani, P. (2019). Axion boson stars. JCAP 09 (09), 061. [Erratum: JCAP 06, E01 (2020)]. doi:10.1088/1475-7516/2019/09/061
Herdeiro, C., Perapechka, I., Radu, E., and Shnir, Ya. (2019). Asymptotically flat spinning scalar, Dirac and Proca stars. Phys. Lett. B 797, 134845. doi:10.1016/j.physletb.2019.134845
Khanna, G., and Price, R. H. (2017). Black hole ringing, quasinormal modes, and light rings. Phys. Rev. D. 95 (8), 081501. doi:10.1103/physrevd.95.081501
Lam, H., Ostriker, J. P., Scott, T., and Witten, E. (2017). Ultralight scalars as cosmological dark matter. Phys. Rev. D95 (4), 043541. doi:10.1103/PhysRevD.95.043541
Marsh, D. J. E., and Ferreira, P. G. (2010). Ultra-light scalar fields and the growth of structure in the universe. Phys. Rev. D82, 103528. doi:10.1103/physrevd.82.103528
Marsh, D. J. E., and Pop, A.-R. (2015). Axion dark matter, solitons and the cusp?core problem. Mon. Not. Roy. Astron. Soc. 451 (3), 2479–2492. doi:10.1093/mnras/stv1050
Marsh, D. J. E., and Silk, J. (2014). A model for halo formation with axion mixed dark matter. Mon. Not. Roy. Astron. Soc. 437 (3), 2652–2663. doi:10.1093/mnras/stt2079
Matos, T., and Arturo Urena-Lopez, L. (2000). Quintessence and scalar dark matter in the universe. Cl. Quantum Grav. 17, L75–L81. doi:10.1088/0264-9381/17/13/101
Matos, T., and Arturo Urena-Lopez, L. (2001). A further analysis of a cosmological model of quintessence and scalar dark matter. Phys. Rev. D63, 063506. doi:10.1103/PhysRevD.63.063506
Matos, T., and Arturo Urena-Lopez, L. (2002). Scalar field dark matter, cross section and Planck-scale physics. Phys. Lett. B538, 246–250. doi:10.1016/s0370-2693(02)02002-6
Matos, T., and Arturo Urena-Lopez, L. (2007). Flat rotation curves in scalar field galaxy halos. Gen. Rel. Grav. 39, 1279–1286. doi:10.1007/s10714-007-0470-y
Matos, T., Bernal, A., and Núñez, D. (2008). Flat central density profiles from scalar field dark matter halo. Rev. Mex. A. A 44, 149.
Matos, T., Guzman, F. S., and Arturo Urena-Lopez, L. (2000). Scalar field as dark matter in the universe. Cl. Quantum Grav. 17, 1707–1712. doi:10.1088/0264-9381/17/7/309
Mielke, E. W., and Scherzer, R. (1981). Mielke and reinhard scherzer. Geon-Type solutions of the nonlinear heinsenberg-klein-gordon equation. Phys. Rev. D24, 2111–2126. doi:10.1103/PhysRevD.24.2111
Mielke, E. W., and Schunck, F. E. (2000). Boson stars: alternatives to primordial black holes? Nucl. Phys. B564, 185–203. doi:10.1016/s0550-3213(99)00492-7
Misner, C. W., Thorne, K. S., and Wheeler, J. A. (1973). Gravitation. San Francisco: Academic Press.
Peccei, R. D., and Quinn, H. R. (1977). Cp conservation in the presence of pseudoparticles. Phys. Rev. Lett. 38, 1440–1443. doi:10.1103/physrevlett.38.1440
Pedro, V. P. C., Emanuele, B., and Herdeiro, C. A. R. (2017). Light-ring stability for ultracompact objects. Phys. Rev. Lett. 119 (25), 251102. doi:10.1103/physrevlett.119.251102
Porayko, N. K., and Postnov, K. A. (2014). Constraints on ultralight scalar dark matter from pulsar timing. Phys. Rev. D. 90 (6), 062008. doi:10.1103/physrevd.90.062008
Raposo, G., Pani, P., Bezares, M., Palenzuela, C., and Cardoso, V. (2019). Anisotropic stars as ultracompact objects in General Relativity. Phys. Rev. D. 99 (10), 104072. doi:10.1103/physrevd.99.104072
Ruffini, R., and Bonazzola, S. (1969). Systems of self-gravitating particles in general relativity and the concept of an equation of state. Phys. Rev. 187, 1767–1783. doi:10.1103/physrev.187.1767
Schive, H.-Yu, Chiueh, T., and Broadhurst, T. (2014). Cosmic structure as the quantum interference of a coherent dark wave. Nat. Phys. 10, 496–499. doi:10.1038/nphys2996
Seidel, E., and Suen, W.-Mo (1990). Dynamical evolution of boson stars: perturbing the ground state. Phys. Rev. D. 42, 384–403. doi:10.1103/physrevd.42.384
Seidel, E., and Suen, W. M. (1991). Oscillating soliton stars. Phys. Rev. Lett. 66, 1659–1662. doi:10.1103/physrevlett.66.1659
Sikivie, P. (2014). Axion dark matter detection using atomic transitions. Phys. Rev. Lett. 113 (20), 201301. [Erratum: Phys.Rev.Lett. 125, 029901 (2020)]. doi:10.1103/physrevlett.113.201301
Steven, L. (2012). Liebling and carlos palenzuela. Dynamical boson stars. Living Rev. Rel. 15 (6). doi:10.1007/s41114-017-0007-y
Zeng, Y.-Bo, Li, H.-Bo, Sun, S.-X., Cui, S.-Y., and Wang, Y.-Q. (2021). Rotating hybrid axion-miniboson stars. 3 Available at: https://arxiv.org/abs/2103.10717.
Zeng, Y.-Bo, Sun, S.-X., Cui, S.-Y., Zhang, Y.-P., and Wang, Y.-Q. (2023). Rotating multistate axion boson stars. 9 Available at: https://arxiv.org/abs/2309.05743.
Keywords: boson stars, compact object, black holes, general relativity, scalar fields
Citation: Bautista B and Degollado JC (2024) Static axion stars revisited. Front. Astron. Space Sci. 11:1346820. doi: 10.3389/fspas.2024.1346820
Received: 30 November 2023; Accepted: 31 January 2024;
Published: 04 March 2024.
Edited by:
Luis Arturo Urena-Lopez, University of Guanajuato, MexicoReviewed by:
Ricardo Becerril, Michoacana University of San Nicolás de Hidalgo, MexicoCopyright © 2024 Bautista and Degollado. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Juan Carlos Degollado, amNkZWdvbGxhZG9AY2llbmNpYXMudW5hbS5teA==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.