- Astronomical Institute of the Czech Academy of Sciences, Prague, Czechia
Radiation transport plays a crucial role in star formation models, as certain questions within this field cannot be accurately addressed without taking it into account. Given the high complexity of the interstellar medium from which stars form, numerical simulations are frequently employed to model the star formation process. This study reviews recent methods for incorporating radiation transport into star formation simulations, discussing them in terms of the used algorithms, treatment of radiation frequency dependence, the interaction of radiation with the gas, and the parallelization of methods for deployment on supercomputers. Broadly, the algorithms fall into two categories: i) moment-based methods, encompassing the flux-limited diffusion approximation, M1 closure, and variable Eddington tensor methods, and ii) methods directly solving the radiation transport equation, including forward and reverse ray tracing, characteristics-based methods, and Monte Carlo techniques. Beyond discussing advantages and disadvantages of these methods, the review also lists recent radiation hydrodynamic codes implemented the described methods.
1 Introduction
Electromagnetic radiation plays a fundamental role in the process of star formation as it regulates the dynamics, thermodynamics, and chemistry of star-forming regions. The interstellar radiation field (ISFR) heats the interstellar dust, dissociates molecules and affects the ionization balance, which is critical for the chemistry of the interstellar medium and the formation of molecular clouds. During the collapse of molecular cores, the dust absorbs the cooling radiation and once the medium becomes optically thick, the first proto-stellar core is formed. When the first stars are formed, their radiation exerts a profound influence on the surrounding gas and dust shaping the morphology of molecular clouds. This set of processes is called the radiative feedback as it regulates the rate and efficiency of star formation. Extreme ultraviolet photons from young, massive stars can ionize the surrounding gas, creating HII regions. The ionizing radiation also influences the chemistry of the gas, affecting the abundance of molecules necessary for the cooling and fragmentation of the cloud. Furthermore, radiation pressure from newly formed stars can counteract gravitational collapse, slow down the gas inflow and drive the winds and outflows.
The inclusion of radiation transport in star formation simulations is therefore desirable. However, it is also very hard due to both the high computational costs and the complexity of the processes that have to be taken into account. The radiation transport equation (RTE) in its general form reads
where the radiation field is represented by the specific intensity Iν. It is defined through the element of the radiation energy dEν flowing across an area element da located at position x in time dt in the solid angle dΩ about the direction n in the frequency interval ν + dν as
where θ is the angle that n makes with a normal to the area element da. The first term on the r.h.s of Eq. 1 represents the radiation losses due to absorption (described by the absorption opacity κν,a) and scattering (described by the scattering opacity κν); ρ is the mass density of the medium through which the radiation propagates. The second term on the r.h.s of Eq. 1 represents the emission of radiation describe by the emission coefficient jν, the last r.h.s term represents contribution of the radiation scattered from other directions. Note that in the above equations, the specific intensity is expressed in the frame of coordinate system, however, emission coefficient and opacities are defined in the comoving frame.
The structure of Eqs 1, 2 reveals that the computational costs associated with solving them directly in their complete generality are exceedingly high. Specifically, in the case of three-dimensional problems, Iν becomes a function of three components of x, two components of n, time t, and the frequency of the radiation ν (written as a subscript, as it is often grouped into several ranges known as wavebands)—amounting to seven independent variables. This issue becomes particularly pronounced when implementing the radiation transport algorithm within a star formation simulation that demands high resolution and, consequently, a substantial number of computational points along the aforementioned variables. To address this, various computational techniques have been developed that solve only a portion of Eq. 1 (e.g., incorporating only a subset of the processes it describes) or utilize diverse approximations, including those transforming it into a different (albeit related) equation that can be solved more computationally efficiently.
This paper reviews the most common techniques to solve the radiation transport equation within (magneto-)hydrodynamic simulations of star formation. The focus of this work is primarily on continuum radiation transport, rather than line transport (atomic or molecular). There is an extensive amount of work on solving radiation transport on static grids or as tools for synthetic observations, however, covering it is beyond the scope of this work. Additional information can be found, e.g., in classical works on radiation hydrodynamics Mihalas and Mihalas (1984); Castor (2004), in a review of dust radiative transfer by Steinacker et al. (2013) and in a review of numerical methods in simulations of star formation by Teyssier and Commerçon (2019). The paper is organised as follows. Section §2 describes different way how radiation transport codes can be classified. Section §3 reviews the most common radiation transport algorithms used in star formation, consisting of §3.1 discussing the moment-based methods and §3.2 describing the methods solving Eq. 1 directly. Finally, Section §4 summarizes this review.
2 Classifications of the radiation transport treatments
There are several criteria based on which radiation transport codes can be classified.
Firstly, the method can either explicitly include the first term of Eq. 1 (partial time derivative) or assume the infinite speed of light and solve the RTE equation implicitly. The former approach, also known as the evolutionary method, is typically employed by moment-based methods. In some cases, the speed of light is artificially reduced to avoid excessively small time steps mandated by the stability conditions of an explicit solver—a technique demonstrated to be useful in other fields as well (e.g., Cohen et al., 1999). The implicit approach, alternatively termed the instantaneous method, is often utilized by codes based on the method of characteristics, ray tracing, and Monte Carlo methods.
Secondly and related to the above, the method can either directly solve Eq. 1 (albeit with some approximations) or transform it into another type of equation. The former approach includes ray tracing, long and short characteristic methods, and Monte Carlo methods. While ray tracing and long characteristic methods are among the most accurate, they are also computationally expensive. The computational cost of ray tracing typically scales with the number of discrete radiation sources, making it particularly expensive for simulations with a high number of sources. In the latter approach, Eq. 1 is commonly transformed into a hyperbolic system (M1 closure methods) or a parabolic system (flux-limited diffusion method).
Thirdly, various methods concentrate on distinct wavelengths of radiation, incorporating different physical processes related to the interaction between radiation and matter. In the simplest approach, termed monochromatic, all photons are assumed to possess a single (representative) frequency. A slightly more complex method is the grey approximation, where a specific constant spectrum—often the black body spectrum—is assumed for all radiation. In certain scenarios, it becomes necessary to categorize radiation based on its frequency into multiple groups that exhibit qualitative differences (e.g., where only some frequencies ionize a specific species). This approach is referred to as multi-group frequency treatment. Lastly, certain codes have the capability to encompass full frequency dependence by sampling the frequency with a designated number of bins.
An essential consideration in implicit radiation transport methods is whether the opacity at a specific location is depends on the radiation intensity at that point. A notable instance of this behavior is the treatment of ionizing (EUV) radiation using the on-the-spot approximation. In this approach, ionizing photons are effectively destroyed by case B recombinations, as they do not result in the replication of ionizing photons. The number of case B recombinations occurring in a given gas parcel needs to be distributed among all the rays passing through it, particularly when using ray tracing or the long characteristic method. Consequently, such methods necessitate iteration, leading to an increase in computational cost.
Finally, different methods pose varying challenges in terms of parallelization, with particular emphasis on the parallelization using domain decomposition suitable for distributed memory machines. Many hydrodynamic codes opt for this type of parallelization, as distributed memory machines offer extensive memory and processor core capabilities. Unfortunately, this parallelization scheme is also the most complex from a coding perspective. Radiation transport, being primarily a long-distance interaction problem, presents significant difficulties in parallelization. This is especially true for ray tracing, the long characteristics method, and Monte Carlo, where numerous calculations over considerable distances must be executed within a limited timeframe.
3 Radiation transport algorithms
3.1 Moment-based methods
Instead of the specific intensity Iν, the radiation field can be described by its moments obtained by integrating Iν over all directions. The first three moments are defined as (see, e.g., Shu, 1991):
where n is a unit vector. The mean radiation energy density Eν, the radiation flux Fν, and the radiation pressure tensor
Moments of Eq. 1 can be obtained by multiplying it with a certain power of n and integrating it over all directions. The scattering is assumed to be isotropic. Then, the first two moment equations are
and
In the above equations, the opacity and the emission coefficient are expressed in the frame of reference co-moving with the fluid (where they are typically isotropic), however, Eν, Fν and
and
where u is the velocity of the gas. For details on the mixed frame formulation see e.g., Mihalas and Klein (1982). The advantage of the mixed frame approach is that the radiation transfer equations are significantly simpler and that it conserves the total energy, however, it is not suitable for computing for instance line opacities in the supersonic flow due to their rapid changes (Moens et al., 2022).
3.1.1 Flux limited diffusion (FLD)
The simplest moment-based method was derived as an extension of the radiation transport in a diffusion limit (Minerbo, 1978; Levermore and Pomraning, 1981). If the photon free mean path is small and the optical depth is high, the radiation is isotropic and the Eddington tensor has form
and the radiation transport problem reduces to the Fick’s diffusion law.
Relation 8 is not valid if the optical depth is low, because Fν can exceed the physical limit Fmax = cEν there. Therefore, the FLD method introduces the so called flux limiter λ and modifies Eq. 8 in the following way
The flux limiter λ(R) is defined as a function of the normalized radiation energy density gradient
in such a way that it ensures Eq. 9 reduces to the Fick’s law in the optically thick regime (i.e., λ = 1/3) and to the maximum allowed flux, Fmax, in the optically thin regime (i.e., λ = 1/R). Various flux limiters fulfilling the above requirements have been suggested in the literature (see, e.g., Minerbo, 1978; Levermore and Pomraning, 1981; Levermore, 1984; Turner and Stone, 2001). As an example we give the flux limiter of Levermore and Pomraning (1981) in the form
and the corresponding approximate Eddington tensor
The FLD method then solves only the 0-th moment equation in the form
which is, from a mathematical point of view, a parabolic equation, and hence the standard parabolic solvers can be used.
The above equations are monochromatic, i.e., they are written for a single wavelength of the radiation. However, it is often practical to use the FLD method (and other methods as well) for radiation with a certain range of wavelengths. Then we speak about the grey radiation transport if there is a single range covering the broad wavelength range important for a given problem, or about the multi-group/multi-band radiation transport if there are several wavelength ranges. Additionally, the grey methods often use the Planck black body law, Bν(T), as the source function, and then the 0-th moment equation has form
where Er ≡∫Eνdν is the bolometric radiation energy density, T is the gas/dust temperature, ar = 4σB/c is the radiation constant, σB is the Stefan-Boltzmann constant, and κP and κR are Planck and Rosseland mean opacities defined as
and
RHD codes using the FLD method are discussed below and summarized in Table 1 giving a reference to the code paper, code name, whether it uses co-moving or mixed frame of reference, whether it is parallel with the domain decomposition and some additional information. The first usage of the FLD method is probably by Alme and Wilson (1973) for the problem of the X-ray emission resulting from the accretion of material onto a neutron star. In the field related to star formation, the grey FLD method was used by Kley (1989); Bodenheimer et al. (1990); Klahr et al. (1999); Boss (2001) for simulations of accretion discs around young low mass stars. It yielded reasonably correct temperatures in the optically thick and optically thing regions, however, it showed deviations from the correct solution in the transition regions (Boley et al., 2007). The treatment of radiation in such models has been significantly improved by Kuiper et al. (2010) who developed a hybrid scheme combining the grey FLD method with the frequency dependent ray tracing, and implemented it to the MHD code PLUTO. They at first calculate the stellar radiation up to the first absorption by a simple ray tracing algorithm and subsequently, they use FLD to calculate the radiation re-emitted by the dust. This approach turned out to be very successful and many other authors implemented this or similar schemes into their codes. Bitsch et al. (2013) used it with the NIRVANA code to study the influence of opacity and stellar irradiation on the disc structure and on the migration of planets. Flock et al. (2013) and Kolb et al. (2013) created two independent implementations of this hybrid method for the PLUTO code. Klassen et al. (2014) generalized this method for multiple sources and arbitrary geometry wrote it as a module for the MHD code FLASH. Similarly, Ramsey and Dullemond (2015) implemented a generalized version of this method for the AZEUS code—a ZEUS family AMR code with a fully staggered mesh.
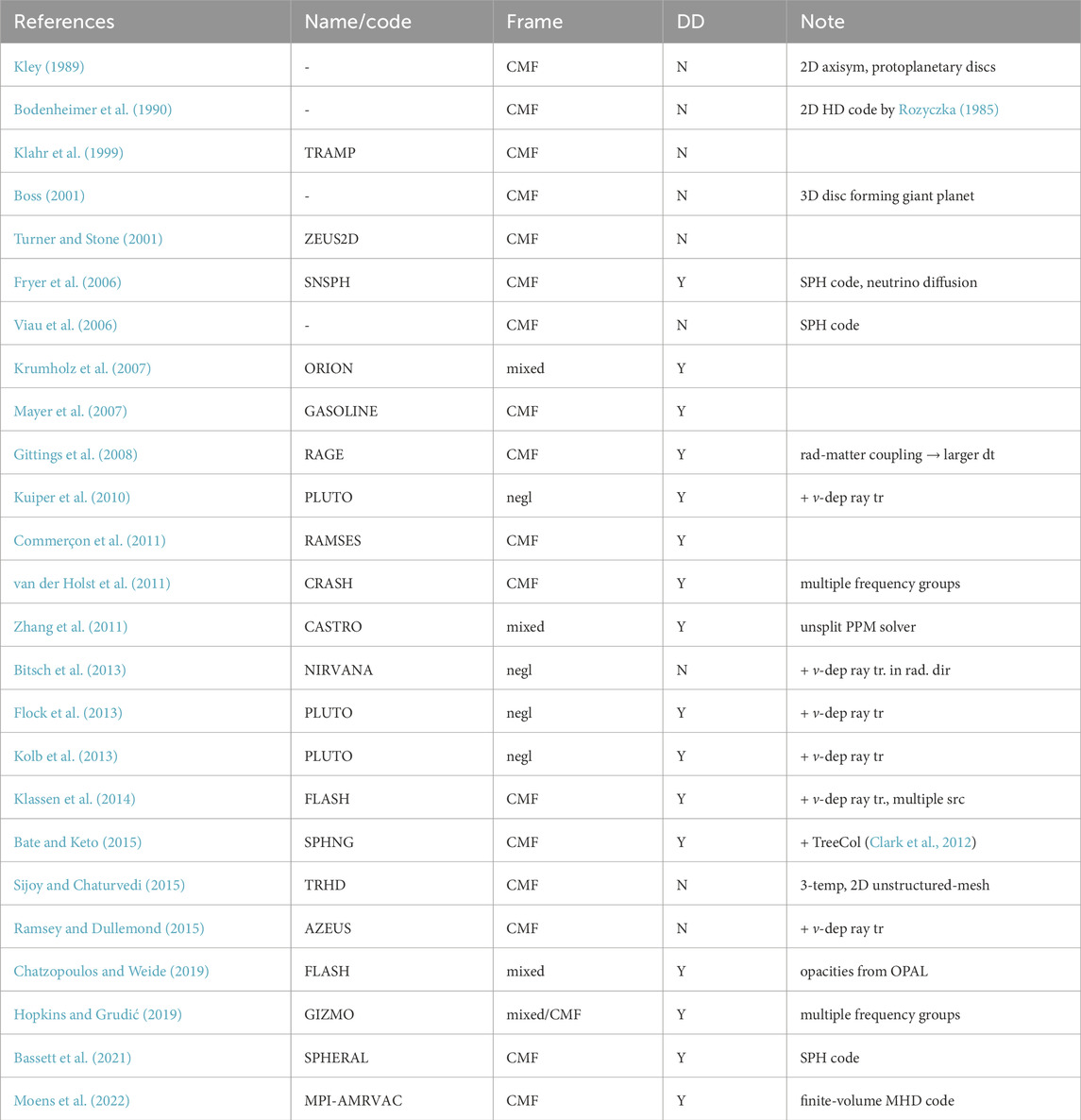
TABLE 1. Radiation transport codes using the flux limited diffusion (FLD) approximation. The first column gives the reference to the work describing the code or algorithm; the second column give the name of the radiation transport code or RHD code (if they exist); the third column specifies the frame of reference in which the radiation energy equation is formulated (mixed, co-moving–CMF, or radiation energy advection terms are neglected); the fourth column tells whether the code is parallel using the domain decomposition; and the last column gives eventually an additional information.
The simplicity of the FLD method allowed it to be implemented into many general purpose (magneto-) hydrodynamic codes used in astrophysics. The widely used ZEUS2D code was originally released with the radiation module based on the tensor variable Eddington factor, however, the FLD method was written for it by Turner and Stone (2001). The ORION code used for many simulations of star formation, including the feedback from massive stars, was developed with FLD method being part of it (Krumholz et al., 2007). Gittings et al. (2008) developed the AMR code RAGE including the grey FLD, for which they introduce a new technique of solving the diffusion and material energy equations, allowing larger time steps and more robust behavior. Commerçon et al. (2011) implemented FLD into the AMR code RAMSES, and Commerçon et al. (2014) added adaptive time stepping and the implicit time integration. The block AMR code CRASH (van der Holst et al., 2011) was developed with grey FLD where electrons and ions are allowed to have different temperatures. The grey FLD method in its mixed-frame formulation is also part of the AMR code CASTRO (Zhang et al., 2011), one of the first 3D RHD codes using the unsplit PPM solver. TRHD (Sijoy and Chaturvedi, 2015) is two-dimensional unstructured mesh Lagrangian code using the grey FLD with three temperature approach (ions, electrons and radiation are allowed to have different temperatures). The FLASH code (Fryxell et al., 2000), a computational framework consisting of modules implementing various physical processes including hydrodynamics and radiation transport, was provided by the FLD module implemented by Chatzopoulos and Weide (2019) and tested on 1D simulations of supernova Ia explosions. The general fluid dynamics code GIZMO (Hopkins and Grudić, 2019) includes several radiation transport solvers including the one based on FLD. Recently, the grey FLD method was implemented into the finite-volume MHD code MPI-AMRVAC (Moens et al., 2022).
The FLD method was implemented also into the Smoothed Particle Hydrodynamics (SPH) codes. Basic methods for calculating radiative heat diffusion were described in seminal works on SPH by Lucy (1977) and Brookshaw (1985). The full grey FLD method was implemented into the SPH by Whitehouse and Bate (2004) and Whitehouse et al. (2005). Later, this code originating from code SPHNG (Benz, 1990) was used by Price and Bate (2009); Bate and Keto (2015); Bate (2019) and many other works for simulating star forming clouds, where the FLD method can be efficiently used to follow collapsing pre-stellar cores with high optical depths. Mayer et al. (2007) used implemented FLD into SPH code GASOLINE and used it to study the gravitational instability in protoplanetary discs. Fryer et al. (2006) developed code SNSPH including the FLD radiation transport and used it for simulating supernova explosions, where FLD can also be used efficiently due to high optical depths. Another implementations of FLD into SPH codes are by Viau et al. (2006) and recently by Bassett et al. (2021) (code SPHERAL).
3.1.2 M1 closure
A more complex and accurate two-moments method is the M1 closure (Dubroca and Feugeas, 1999). It assumes that the Eddington tensor is axially symmetric around the flux vector and hence can be expressed as
where χ is a scalar function called the Eddington factor. The M1 closure method uses one of its simplest forms discussed in Levermore (1984), corresponding to the Lorentz boosted isotropic distribution of the radiation,
where f = |Fν|/cEν is the reduced flux. Then, the method solves Eqs 6, 7 or their equivalent in the mixed frame approach.
The advantage of the M1 closure is that it captures correctly the two extremes of the radiation field: i) the free streaming (or optically thin) limit with |f| = 1 and χ = 1, and ii) the diffusion (or optically thick) limit with |f| = 0 and χ = 1/3. The ability to maintain the original direction of the free streaming radiation is a pronounced improvement in comparison to the FLD method leading to the artificial diffusion of the free streaming radiation. On the other hand, the assumed simple form of the radiation pressure tensor cannot correctly describe more complex radiation fields as for instance the radiation from multiple sources in which case the nonphysical interaction would occur.
A specific feature of the M1 closure making is suitable for the implementation into (magneto-) hydrodynamic codes is that the system of Eqs 6, 7 is hyperbolic and hence it can be solved with the same algorithms as the equations of the fluid dynamics. Table 2 gives a list of star formation and related fields codes implementing the M1 closure method. The first such code was HERACLES (González et al., 2007) designed to study radiative shocks (and compare the results with laboratory experiments), jets of young stars, formation of pre-stellar cores and protoplanetary disks. This method was implemented into the cosmic reionisation code ATON (Aubert and Teyssier, 2008), and later ported to the general RHD code RAMSES (Rosdahl et al., 2013; Rosdahl and Teyssier, 2015). Sądowski et al. (2013) included the M1 closure method into the general relativistic code KORAL formulating the RHD equations in the covariant form. Skinner and Ostriker (2013) describe the M1 closure module for the ATHENA code, in which they use the reduced speed of light approximation to improve the performance. The general fluid dynamics code GIZMO includes the M1 closure as one of its radiation transport solvers. Kannan et al. (2019) describe the radiation transport module for the unstructured moving mesh code AREPO, based on a new higher order implementation of the M1 closure method. This method is also included into code FORNAX (Skinner et al., 2019) primarily intended for core collapse supernova simulations, general fuild dynamics code PLUTO (Melon Fuksman and Mignone, 2019), and hybrid OpenMP/MPI/GPU parallel code ARK-RT (Bloch et al., 2021). Chan et al. (2021) present module SPH-M1RT for task-based parallel SPH code SWIFT.
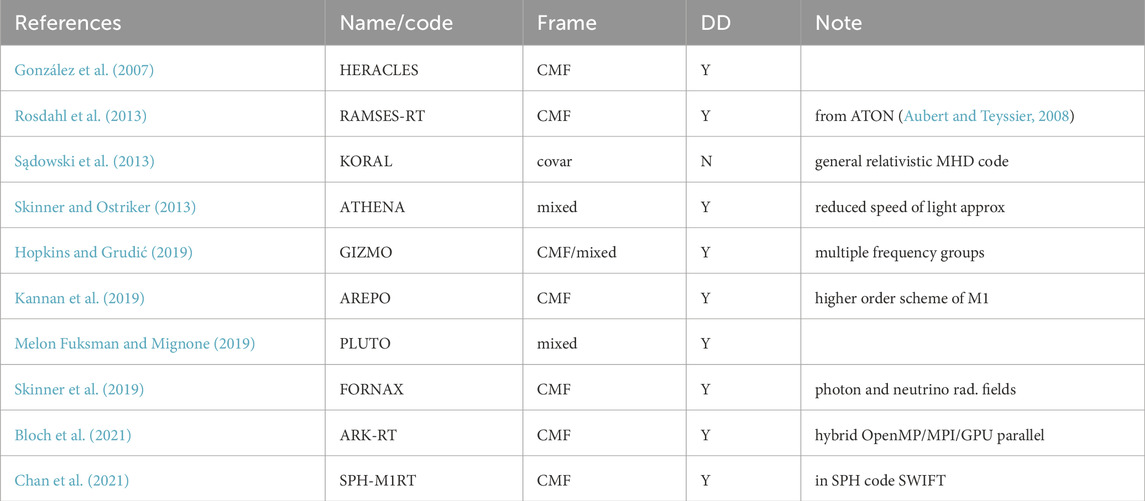
TABLE 2. Radiation transport codes using the M1 closure method. The meaning of columns is the same as in Table 1.
3.1.3 Variable Eddington Tensor methods
Another approach to solve moment Eqs 4, 5, as opposed to the closure assuming an approximate form of the Eddington tensor, is to calculate the Eddington tensor self consistently by directly solving the radiation transport Eq. 1. Methods using it (Table 3) are referred to as Variable Eddington Tensor (VET) methods, and the Eddington tensor,
The VET method was developed for 1D calculations of plane-parallel stellar atmospheres by Auer and Mihalas (1970), however, the idea of iterating the ratio of second and zeroth radiation moments dates back to Eddington (1926). The first multi-dimensional astrophysical code using this method was ZEUS2D (Stone et al., 1992), where
3.2 Methods solving RTE directly
Table 4 lists codes that employ the direct solution of the RTE: forward and reverse ray tracing, methods of characteristics, and Monte Carlo methods.
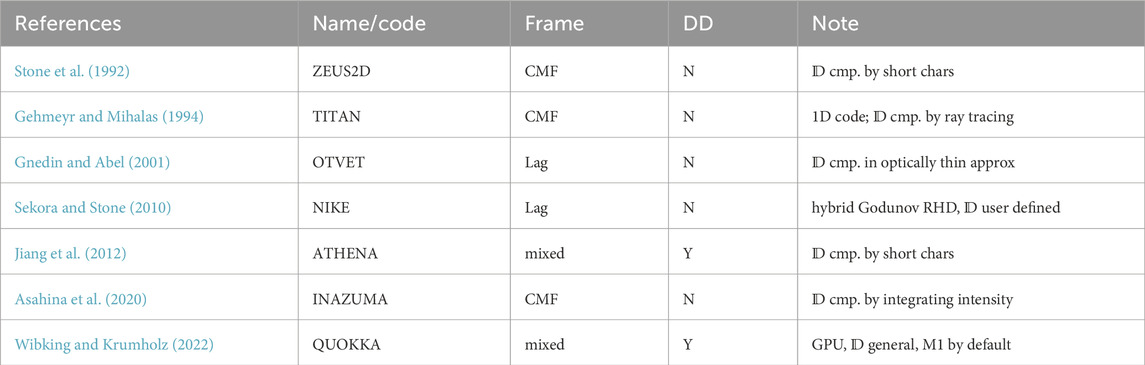
TABLE 3. Radiation transport codes using the Variable Eddington Tensor (VET) approach. The meaning of columns is the same as in Table 1.
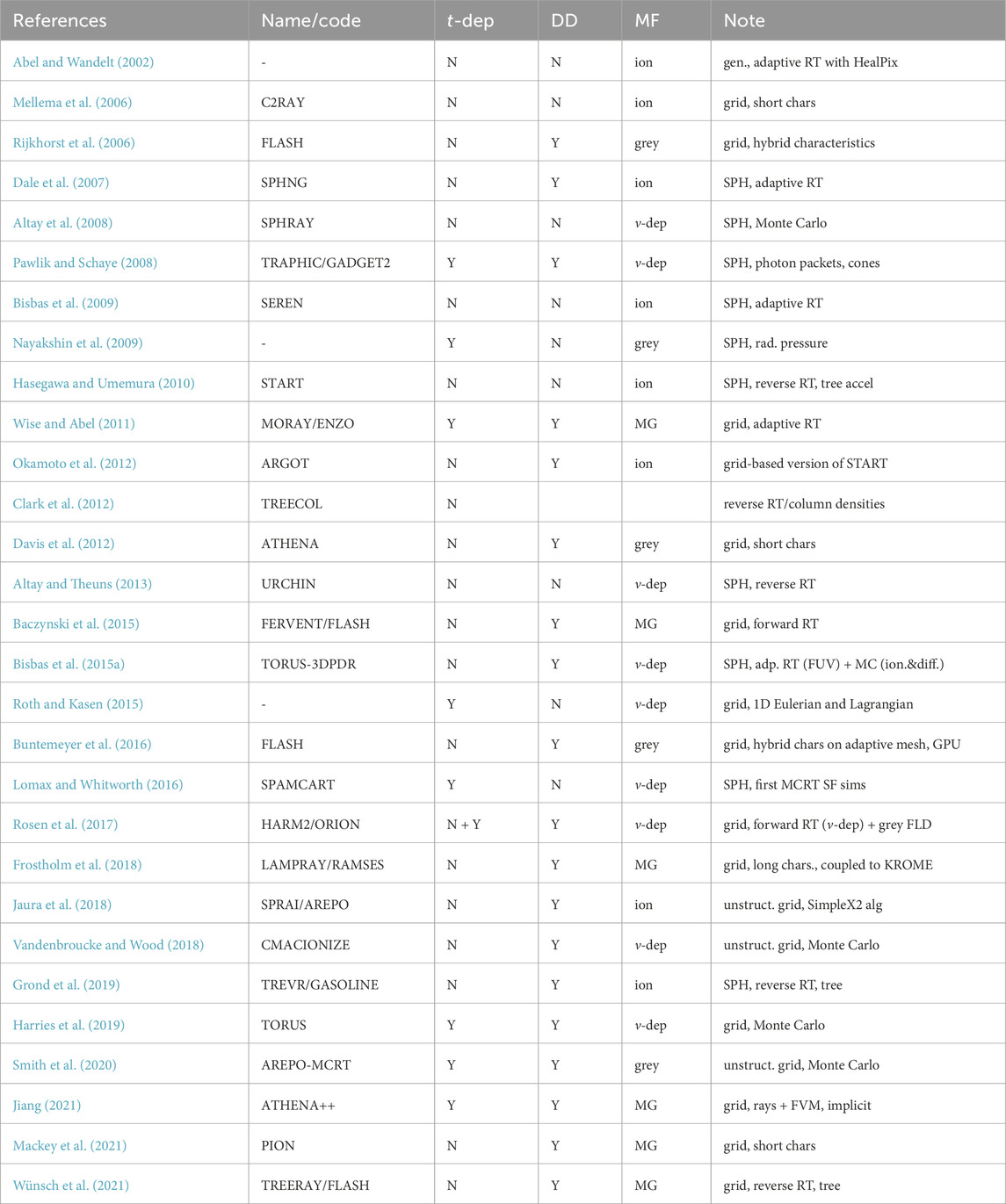
TABLE 4. Radiation transport codes using ray tracing and methods of characteristics. The first column gives the reference to the work describing the code or algorithm; the second column give the name of the radiation transport code or RHD code (if they exist); the third column whether the code solves time-dependent RTE; the fourth column tells whether the code is parallel using the domain decomposition; the fifth column gives how the code deals with the frequency dependence (grey, ion. - a single band of ionising photons, MG - multi-group approach, ν-dep - full frequency dependence); and the last column gives eventually an additional information.
3.2.1 Ray tracing
The most straightforward method to solve the radiation transport Eq. 1 is to follow the radiation from its sources along the lines of its propagation, a technique called ray tracing. It is widely used in many other fields, in particular in the computer image generation. The original idea of ray tracing dates back to 16th century to Albrecht Dürer who described multiple techniques for projecting 3D scenes onto an image plane (Hofmann, 1990).
As previously mentioned, the primary challenge in directly solving Eq. 1 is its high dimensionality, resulting in high computational costs. Therefore, a key characteristic of a ray tracing algorithm is a set of approximations designed to reduce the complexity of problem. A crucial aspect is the method by which the radiation field is discretized in both space and its propagation directions. The simplest approach, employed by many early and recent codes, involves calculating the radiation on the same grid as the gas dynamics. This confines the direction of radiation propagation to the coordinate axes. Examples of this approach include Wolfire and Cassinelli (1986) in a 1D spherical grid, Murray et al. (1994); Garcia-Segura and Franco (1996) in a 2D spherical grid, and numerous other works, the review of which exceeds the scope of this study. This method is particularly well-suited for treating radiation emanating from a single source (e.g., a central star) located at the center of the coordinate system. It can be effectively combined with other methods that describe the diffuse radiation component (e.g., FLD, as mentioned in Section 3.1.1; Table 1).
In many cases, confining the radiation propagation solely along the hydrocode grid axes is overly restrictive. Therefore, general radiation transport codes typically employ an independent method to define rays, making ray tracing algorithms particularly suitable for implementation into unstructured grid or smooth particle hydrodynamic codes. One approach is to cast rays from a source in spherical coordinates, associating each ray with a spherical segment of the same size (Abel et al., 1999; Razoumov and Scott, 1999). This method was later refined in the HEAlPix library (Górski et al., 2005), which has become a de facto standard. HEALPix facilitates the tessellation of the sphere surface into equal area regions in a hierarchical manner, a feature utilized by adaptive ray tracing algorithms that split rays in regions requiring finer angular resolution (Abel and Wandelt, 2002). This approach has proven highly successful and has been employed by various authors, including Pawlik and Schaye (2008) (TRAPHIC code linked to SPH code GADGET2), Bisbas et al. (2009) (SPH code SEREN), Wise and Abel (2011) (MORAY code linked to AMR code ENZO), Baczynski et al. (2015) (FERVENT code within the AMR code FLASH), and others.
Depending on the number of cast rays, ray tracing algorithms can achieve high accuracy, although with correspondingly higher computational costs that typically scale with the number of radiation sources. As a result, they are occasionally employed in conjunction with other methods where ray tracing specifically handles radiation from a relatively low number of discrete sources, such as massive stars. An example is the HARM2 code (Rosen et al., 2017), which calculates ionizing stellar radiation using adaptive ray tracing and the diffuse component using the FLD method in the ORION code. Similarly, the TORUS-3DPDR code (Bisbas et al., 2015a) utilizes adaptive ray tracing for FUV radiation and the Monte Carlo method for the ionizing and diffuse components.
A slightly different approach to spatially adaptive ray tracing was used by Dale et al. (2007) who integrated the RTE on the line-of-sight between the source and the target particle using evaluation points defined by SPH particles close to the line-of-sight selected using method by Kessel-Deynet and Burkert (2000).
Ritzerveld and Icke (2006) developed algorithm SimpleX to solve Eq. 1 on an unstructured grid calculated from the properties of the medium in which the radiation propagates, using the Delaunay triangulation (Delaunay, 1934). The computational costs of this method do not depend on the number of sources, similarly to moment-based methods or some reverse ray tracing schemes. It is typically less diffusive that moment based methods and it is more suitable for parallelisation with domain decomposition than most of the ray tracing methods. It is particularly suitable for being used with SPH or unstructured grid codes, Clementel et al. (2014) implemented it into an SPH code. The SimpleX algorithm was improved and parallelized by Paardekooper et al. (2010) and implemented as code SPRAI integrated into code AREPO by Jaura et al. (2018).
3.2.2 Characteristics-based methods
A specific way of ray tracing are methods of characteristics, which solve the RTE along predefined rays (characteristics) covering the entire computational domain rather than casting rays from discrete sources. In this manner, characteristics-based methods can describe the diffuse radiation component. They can be categorized into long, short and hybrid characteristics based on the end points of the rays. Long characteristics extend across the entire computational domain, with their separation comparable to the size of the computational elements and defined in specific directions. While long characteristics are among the most accurate methods, they are also the most expensive, depending on the number of rays. Another disadvantage, applicable to some extent to all ray tracing methods, is that they are difficult to get parallelized within codes that use domain decomposition on distributed memory machines. This challenge arises because rays crossing multiple domains typically represent a substantial amount of information that needs to be communicated over the (relatively) slow network. An example of a code utilizing long characteristics is LAMPRAY (Frostholm et al., 2018), implemented into the RAMSES code. LAMPRAY calculates both diffuse and discrete sources radiation on an adaptive oct-tree mesh, allowing the definition of several frequency bins for both ionizing and non-ionizing radiation. It is coupled with the non-equilibrium chemistry code KROME (Grassi et al., 2014), providing the chemical networks to evolve species abundances.
The short characteristics methods create rays only among the neighbour cells (or generally computational elements) and interpolate the radiation intensity at the cell borders. This makes this class of methods more diffusive, but also computationally cheaper and much easier to parallelize with domain decomposition codes. Short characteristics are used, e.g., by code C2RAY (Mellema et al., 2006), code ATHENA (Davis et al., 2012), or code PION (Mackey et al., 2021). They have been also used together with the moment-based VET method to calculate the local radiation pressure tensor
Rijkhorst et al. (2006) developed the hybrid characteristics method, combining the advantages of both long and short characteristics, particularly in reducing the necessary parallel communication. This method is implemented within the block-based daptive AMR code FLASH. It divides the radiation field into two components: i) the local component within the blocks, calculated using the long characteristics method, and ii) the global component, transporting radiation among blocks (and parallel sub-domains) using interpolation similar to the short characteristics method. This algorithm was further enhanced by Peters et al. (2010) and later re-implemented by Buntemeyer et al. (2016) to also handle diffuse radiation and operate on GPU-accelerated architectures.
Jiang (2021) developed an implicit radiation transport algorithm for MHD code ATHENA++. It represents the radiation by its specific intensities along discrete rays, and evolves them using a conservative finite volume method. It avoids using a closure as in moment-based methods and the related artificial diffusion. On the other hand, it solves time-dependent radiation transport equation, contrary to majority of ray or characteristics based methods. The original implementation was grey, however, Jiang (2022) extended it to include the frequency dependence using the multi-group approach.
3.2.3 Reverse ray tracing
An alternative approach is the so-called reverse ray tracing. In contrast to the “standard” forward ray tracing, which casts rays from the source outward, reverse ray tracing schemes cast rays from the target point where the radiation interacts with the gas (e.g., grid cell or SPH particle) and transport the radiation inward to the target point. This approach offers several advantages, including the highest density of rays (i.e., the highest spatial resolution) near the location where radiation interacts with the gas. Another advantage is its suitability for handling external diffuse radiation. Hasegawa and Umemura (2010) implemented this algorithm into the SPH code START, incorporating tree-based acceleration to group distant sources into oct-tree nodes. A grid-based version of this algorithm was developed by Okamoto et al. (2012) for the code ARGOT. Altay and Theuns (2013) created the reverse ray tracing code URCHIN and integrated it into an SPH code focused on cosmological simulations. Another implementation of this approach is TREVR for the SPH code GASOLINE by Grond et al. (2019), who introduced adaptive refinement along rays and directionally dependent absorption coefficients for tree nodes. Wünsch et al. (2021) developed the code TREERAY, implementing tree-accelerated reverse ray tracing for the Adaptive Mesh Refinement (AMR) code FLASH. It utilizes a fast parallel tree solver described in Wünsch et al. (2018) and is coupled with the chemical network developed by Glover and Mac Low (2007). Later, it was extended by Klepitko et al. (2023), who added diffuse grey infrared radiation and related radiation pressure, and by Gaches et al. (2023), who added frequency-dependent X-ray radiation. TREERAY has been used in the SILCC project (Walch et al., 2015, and follow-up papers) using RMHD simulations to model the full cycle of molecular clouds in a part of a galactic disc.
3.2.4 Monte Carlo methods
Monte Carlo Radiation Transport (MCRT) algorithms belong to a broad category of statistical sampling methods that share this name. They simulate the movement of individual photons through a medium by stochastically sampling random events, including interactions with matter. Given that tracking individual photons is prohibitively expensive, MCRT algorithms introduce “photon packets” that carry information about the position, direction, frequency distribution, etc., of the group of photons they represent. This approach closely mirrors the reality of propagating radiation, making it highly versatile, and facilitating the inclusion of various complex processes such as scattering.
However, the statistical nature of this method introduces Poisson noise, and maintaining it below a required level often necessitates a very large number of photon packets. Consequently, MCRT codes have historically mostly been used for static problems (e.g., the code MOCASSIN by Ercolano et al., 2003, the code HYPERION by Robitaille, 2011, or the code RADMC3D by Dullemond et al., 2012). Due to the potential long distances photon packets can travel, Monte Carlo methods are relatively challenging to parallelize using domain decomposition. On the other hand, thread-based parallelization on shared memory architectures is typically straightforward.
As this method does not rely on any grid, it is natural to use it with SPH or unstructured grid codes. An algorithm to incorporate MCRT into SPH codes was proposed by Lucy (1999). A Monte Carlo-based ray-tracing algorithm was developed by Altay et al. (2008) and implemented into the publicly available code SPHRAY, primarily focused on cosmological simulations. Another implementation of MCRT into an SPH code was done by Nayakshin et al. (2009), who used it to calculate the radiation pressure force. Roth and Kasen (2015) developed a 1D MCRT code and coupled it with both Eulerian and Lagrangian hydrodynamic codes. The first star formation simulations with MCRT were performed by Lomax and Whitworth (2016), who developed the code SPAMCART coupled with SPH hydrodynamics. They used it to calculate synthetic intensity maps and spectra of an embedded protostellar multiple system. Vandenbroucke and Wood (2018) developed the radiation hydrodynamic code CMACIONIZE, which works on an unstructured moving grid and is based on the Monte Carlo method calculating ν-dependent transport of ionizing photons. The code is parallelized using a task-based scheme and has an option to work in a distributed memory configuration. Code TORUS, developed by Harries et al. (2019), is an MCRT that includes native AMR grid-based hydrodynamics and can also be coupled with the SPH code SPHNG. It implements numerous microphysics modules, including atomic and molecular line transport in moving media, dust radiative equilibrium, photoionization equilibrium, and time-dependent radiative transfer, and has been used, e.g., for modelling massive stars feedback in turbulent clouds (Ali et al., 2018). It is also designed for postprocessing the output of several other (magneto-)hydrodynamic codes. Recently, MCRT has also been implemented into the unstructured moving mesh code AREPO by Smith et al. (2020).
3.3 Other approximations
Many studies conducting hydrodynamic simulations of star formation further simplify the radiation transport problem. For example, Vázquez-Semadeni et al. (2017) include stellar ionizing radiation feedback by calculating the Strömgren sphere radius from the EUV photon production rate of a star and the characteristic density obtained as the geometric mean of the density at the star and at the target cell. Subsequently, they set the gas temperature within the sphere to 104 K.
A specific case involves non-ionizing diffuse ambient interstellar radiation fields, crucial for the physics of molecular clouds as they provide heating and affect molecular gas chemistry. In molecular clouds, this radiation intensity strongly depends on shielding, i.e., the optical depth between a given location and the edge of the cloud. This consideration led Clark et al. (2012) to develop the TREECOL algorithm, implemented into the code GADGET2. It efficiently calculates optical depths in all directions (discretized by HealPix) for each SPH particle using a tree, enabling the determination of heating and dissociation rates. This algorithm was later implemented by Valdivia and Hennebelle (2014) into RAMSES and by Wünsch et al. (2018) into FLASH.
A different approach to solving a very similar problem was suggested by Stamatellos et al. (2007), who estimate the mean optical depth from local density, temperature, and gravitational potential using a set of precalculated models of collapsing clouds. This method provides reasonably good results for almost zero computational costs.
The simplest treatment of radiation is to modify the gas equation of state to calculate the equilibrium gas temperature from local gas density, thus accounting for the most probable result of the heating-cooling balance. A popular choice is the barotropic equation of state (e.g., Bonnell, 1994; Whitworth et al., 1995; Bate, 1998), a simple analytical formula designed to mimic the thermodynamics of spherically symmetric collapse of a single, isolated protostar.
4 Summary
This work reviews methods to solve radiation transport equation (RTE) in simulations of star formation and related fields. According to the algorithm, they can be roughly divided into two groups: moment-based methods and methods solving the RTE directly.
Moment-based methods approximate the radiation specific intensity by integrating it over all directions and expressing it in terms of several moments. The order of the moments in the sequence closure determines the level of approximation, leading to artificial diffusion of the radiation, unphysical self-interaction, and other artificial effects. These methods typically include the time-dependent term of the RTE and sometimes artificially decrease the speed of light to reduce computational costs. Their computational expenses are independent of the number of sources, making them well-suited for calculating diffuse radiation. Frequency-wise, moment-based methods often use the grey approximation or, occasionally, the multi-group frequency approach. They are sometimes combined with ray tracing, which calculates radiation from one or several discrete sources, while the moment-based method addresses the diffuse radiation component. The most commonly used methods of this type include flux-limited diffusion, the M1 closure, and the variable Eddington tensor method.
Methods that directly solve the RTE integrate it along specific lines, commonly referred to as rays. These methods include forward and reverse ray tracing, long, hybrid, and short characteristics, as well as Monte Carlo methods. Ray tracing and characteristics-based methods typically do not include the time-dependent RTE term, utilizing the infinite speed of light approximation; however, there are exceptions. Monte Carlo methods are usually time-dependent. Depending on angular discretization, ray tracing and long/hybrid characteristics can achieve high accuracy but at the expense of high computational costs. Short characteristics methods tend to be more diffusive. While Monte Carlo methods can be highly accurate, achieving this requires a substantial number of photon packets, leading to increased computational costs. Monte Carlo methods are also versatile, suitable, e.g., for treating radiation scattering. Computational costs for most of these methods scale with the number of sources, with exceptions like reverse ray tracing methods that group distant sources and methods combining ray tracing with advection schemes. Various treatments of radiation frequency dependence are employed; generally, methods designed for a small number of sources can incorporate detailed frequency dependence. Forward ray tracing and long characteristics methods are typically challenging to parallelize using domain decomposition, whereas short characteristics are relatively straightforward. Hybrid characteristics, reverse ray tracing, and Monte Carlo methods fall in the middle ground regarding parallelization difficulty.
Radiation transport has become a well-established component of star formation simulations, with many methods and codes available, continuously advancing in both maturity and complexity. Consequently, it becomes imperative to not only validate these codes against standard tests but also to benchmark them against each other and, ideally, against realistic problems inherent in the realm of star formation. In this regard, initiatives such as the code comparison projects, such as those conducted by Iliev et al. (2006), Iliev et al. (2009) for cosmological radiation transport codes and the STARBENCH project led by Bisbas et al. (2015b) that compares radiation transport codes for star formation, prove to be very valuable. Moreover, there is a growing need for more comparison projects to enhance our understanding and confidence in the capabilities of these codes.
Author contributions
RW: Writing–original draft, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study has been supported by the institutional project RVO:67985815.
Acknowledgments
I thank the referees for their constructive comments that have helped to improve this work.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abel, T., Norman, M. L., and Madau, P. (1999). Photon-conserving radiative transfer around point sources in multidimensional numerical cosmology. ApJ 523, 66–71. doi:10.1086/307739
Abel, T., and Wandelt, B. D. (2002). Adaptive ray tracing for radiative transfer around point sources. MNRAS 330, L53–L56. doi:10.1046/j.1365-8711.2002.05206.x
Ali, A., Harries, T. J., and Douglas, T. A. (2018). Modelling massive star feedback with Monte Carlo radiation hydrodynamics: photoionization and radiation pressure in a turbulent cloud. MNRAS 477, 5422–5436. doi:10.1093/mnras/sty1001
Alme, M. L., and Wilson, J. R. (1973). X-ray emission from a neutron star accreting material. ApJ 186, 1015–1026. doi:10.1086/152566
Altay, G., Croft, R. A. C., and Pelupessy, I. (2008). SPHRAY: a smoothed particle hydrodynamics ray tracer for radiative transfer. MNRAS 386, 1931–1946. doi:10.1111/j.1365-2966.2008.13212.x
Altay, G., and Theuns, T. (2013). URCHIN: a reverse ray tracer for astrophysical applications. MNRAS 434, 748–764. doi:10.1093/mnras/stt1067
Asahina, Y., Takahashi, H. R., and Ohsuga, K. (2020). A numerical scheme for general relativistic radiation magnetohydrodynamics based on solving a grid-based Boltzmann equation. ApJ 901, 96. doi:10.3847/1538-4357/abaf51
Aubert, D., and Teyssier, R. (2008). A radiative transfer scheme for cosmological reionization based on a local Eddington tensor. MNRAS 387, 295–307. doi:10.1111/j.1365-2966.2008.13223.x
Auer, L. H., and Mihalas, D. (1970). On the use of variable Eddington factors in non-LTE stellar atmospheres computations. MNRAS 149, 65–74. doi:10.1093/mnras/149.1.65
Baczynski, C., Glover, S. C. O., and Klessen, R. S. (2015). Fervent: chemistry-coupled, ionizing and non-ionizing radiative feedback in hydrodynamical simulations. MNRAS 454, 380–411. doi:10.1093/mnras/stv1906
Bassett, B. R., Owen, J. M., and Brunner, T. A. (2021). Efficient smoothed particle radiation hydrodynamics I: thermal radiative transfer. J. Comput. Phys. 429, 109996. doi:10.1016/j.jcp.2020.109996
Bate, M. R. (1998). Collapse of a molecular cloud core to stellar densities: the first three-dimensional calculations. ApJ Let. 508, L95–L98. doi:10.1086/311719
Bate, M. R. (2019). The statistical properties of stars and their dependence on metallicity. MNRAS 484, 2341–2361. doi:10.1093/mnras/stz103
Bate, M. R., and Keto, E. R. (2015). Combining radiative transfer and diffuse interstellar medium physics to model star formation. MNRAS 449, 2643–2667. doi:10.1093/mnras/stv451
Benz, W. (1990). “Smooth particle hydrodynamics - a review,” in Numerical modelling of nonlinear stellar pulsations problems and prospects. Editor J. R. Buchler (Netherlands: Springer), 269.
Bisbas, T. G., Haworth, T. J., Barlow, M. J., Viti, S., Harries, T. J., Bell, T., et al. (2015a). TORUS-3DPDR: a self-consistent code treating three-dimensional photoionization and photodissociation regions. MNRAS 454, 2828–2843. doi:10.1093/mnras/stv2156
Bisbas, T. G., Haworth, T. J., Williams, R. J. R., Mackey, J., Tremblin, P., Raga, A. C., et al. (2015b). STARBENCH: the D-type expansion of an H II region. MNRAS 453, 1324–1343. doi:10.1093/mnras/stv1659
Bisbas, T. G., Wünsch, R., Whitworth, A. P., and Hubber, D. A. (2009). Smoothed particle hydrodynamics simulations of expanding H II regions. I. Numerical method and applications. A&A 497, 649–659. doi:10.1051/0004-6361/200811522
Bitsch, B., Crida, A., Morbidelli, A., Kley, W., and Dobbs-Dixon, I. (2013). Stellar irradiated discs and implications on migration of embedded planets. I. Equilibrium discs. A&A 549, A124. doi:10.1051/0004-6361/201220159
Bloch, H., Tremblin, P., González, M., Padioleau, T., and Audit, E. (2021). A high-performance and portable asymptotic preserving radiation hydrodynamics code with the M1 model. A&A 646, A123. doi:10.1051/0004-6361/202038579
Bodenheimer, P., Yorke, H. W., Rozyczka, M., and Tohline, J. E. (1990). The Formation phase of the solar nebula. ApJ 355, 651. doi:10.1086/168798
Boley, A. C., Durisen, R. H., Nordlund, Å., and Lord, J. (2007). Three-dimensional radiative hydrodynamics for disk stability simulations: a proposed testing standard and new results. ApJ 665, 1254–1267. doi:10.1086/519767
Bonnell, I. A. (1994). A new binary formation mechanism. MNRAS 269, 837–848. doi:10.1093/mnras/269.3.837
Boss, A. P. (2001). Gas giant protoplanet formation: disk instability models with thermodynamics and radiative transfer. ApJ 563, 367–373. doi:10.1086/323694
Brookshaw, L. (1985). A method of calculating radiative heat diffusion in particle simulations. PASA 6, 207–210. doi:10.1017/S1323358000018117
Buntemeyer, L., Banerjee, R., Peters, T., Klassen, M., and Pudritz, R. E. (2016). Radiation hydrodynamics using characteristics on adaptive decomposed domains for massively parallel star formation simulations. New Astron. 43, 49–69. doi:10.1016/j.newast.2015.07.002
Chan, T. K., Theuns, T., Bower, R., and Frenk, C. (2021). Smoothed particle radiation hydrodynamics: two-moment method with local Eddington tensor closure. MNRAS 505, 5784–5814. doi:10.1093/mnras/stab1686
Chatzopoulos, E., and Weide, K. (2019). Gray radiation hydrodynamics with the FLASH code for astrophysical applications. ApJ 876, 148. doi:10.3847/1538-4357/ab18f9
Clark, P. C., Glover, S. C. O., and Klessen, R. S. (2012). TreeCol: a novel approach to estimating column densities in astrophysical simulations. MNRAS 420, 745–756. doi:10.1111/j.1365-2966.2011.20087.x
Clementel, N., Madura, T. I., Kruip, C. J. H., Icke, V., and Gull, T. R. (2014). 3D radiative transfer in η Carinae: application of the SIMPLEX algorithm to 3D SPH simulations of binary colliding winds. MNRAS 443, 2475–2491. doi:10.1093/mnras/stu1287
Commerçon, B., Debout, V., and Teyssier, R. (2014). A fast, robust, and simple implicit method for adaptive time-stepping on adaptive mesh-refinement grids. A&A 563, A11. doi:10.1051/0004-6361/201322858
Commerçon, B., Teyssier, R., Audit, E., Hennebelle, P., and Chabrier, G. (2011). Radiation hydrodynamics with adaptive mesh refinement and application to prestellar core collapse. I. Methods. A&A 529, A35. doi:10.1051/0004-6361/201015880
Dale, J. E., Ercolano, B., and Clarke, C. J. (2007). A new algorithm for modelling photoionizing radiation in smoothed particle hydrodynamics. MNRAS 382, 1759–1767. doi:10.1111/j.1365-2966.2007.12486.x
Davis, S. W., Stone, J. M., and Jiang, Y.-F. (2012). A radiation transfer solver for athena using short characteristics. ApJS 199, 9. doi:10.1088/0067-0049/199/1/9
Delaunay, B. (1934). Sur la sphère vide. A la mémoire de Georges Voronoï. Bull. de l’Académie des Sci. de l’URSS. Cl. des Sci. mathématiques naturelles 6, 793–800.
Dubroca, B., and Feugeas, J. (1999). Etude théorique et numérique d’une hiérarchie de modèles aux moments pour le transfert radiatif. Acad. Des. Sci. Paris Comptes Rendus Ser. Sci. Math. 329, 915–920. doi:10.1016/S0764-4442(00)87499-6
Dullemond, C. P., Juhasz, A., Pohl, A., Sereshti, F., Shetty, R., Peters, T., et al. (2012). RADMC-3D: a multi-purpose radiative transfer tool. N/A ascl (Astrophysics Source Code Library). record ascl:1202.015.
Ercolano, B., Barlow, M. J., Storey, P. J., and Liu, X. W. (2003). MOCASSIN: a fully three-dimensional Monte Carlo photoionization code. MNRAS 340, 1136–1152. doi:10.1046/j.1365-8711.2003.06371.x
Flock, M., Fromang, S., González, M., and Commerçon, B. (2013). Radiation magnetohydrodynamics in global simulations of protoplanetary discs. A&A 560, A43. doi:10.1051/0004-6361/201322451
Frostholm, T., Haugbølle, T., and Grassi, T. (2018). Lampray: multi-group long characteristics ray tracing for adaptive mesh radiation hydrodynamics. arXiv e-prints , arXiv:1809.05541. doi:10.48550/arXiv.1809.05541
Fryer, C. L., Rockefeller, G., and Warren, M. S. (2006). SNSPH: a parallel three-dimensional smoothed particle radiation hydrodynamics code. ApJ 643, 292–305. doi:10.1086/501493
Fryxell, B., Olson, K., Ricker, P., Timmes, F. X., Zingale, M., Lamb, D. Q., et al. (2000). FLASH: an adaptive mesh hydrodynamics code for modeling astrophysical thermonuclear flashes. ApJS 131, 273–334. doi:10.1086/317361
Gaches, B. A. L., Walch, S., Wünsch, R., and Mackey, J. (2023). Tree-based solvers for adaptive mesh refinement code FLASH - IV. An X-ray radiation scheme to couple discrete and diffuse X-ray emission sources to the thermochemistry of the interstellar medium. MNRAS 522, 4674–4690. doi:10.1093/mnras/stad1206
Garcia-Segura, G., and Franco, J. (1996). From ultracompact to extended H II regions. ApJ 469, 171. doi:10.1086/177769
Gehmeyr, M., and Mihalas, D. (1994). Adaptive grid radiation hydrodynamics with TITAN. Phys. D. Nonlinear Phenom. 77, 320–341. doi:10.1016/0167-2789(94)90143-0
Gittings, M., Weaver, R., Clover, M., Betlach, T., Byrne, N., Coker, R., et al. (2008). The RAGE radiation-hydrodynamic code. Comput. Sci. Discov. 1, 015005. doi:10.1088/1749-4699/1/1/015005
Glover, S. C. O., and Mac Low, M.-M. (2007). Simulating the formation of molecular clouds. I. Slow formation by gravitational collapse from static initial conditions. ApJS 169, 239–268. doi:10.1086/512238
Gnedin, N. Y., and Abel, T. (2001). Multi-dimensional cosmological radiative transfer with a Variable Eddington Tensor formalism. New Astron. 6, 437–455. doi:10.1016/S1384-1076(01)00068-9
González, M., Audit, E., and Huynh, P. (2007). HERACLES: a three-dimensional radiation hydrodynamics code. A&A 464, 429–435. doi:10.1051/0004-6361:20065486
Górski, K. M., Hivon, E., Banday, A. J., Wandelt, B. D., Hansen, F. K., Reinecke, M., et al. (2005). HEALPix: a framework for high-resolution discretization and fast analysis of data distributed on the sphere. ApJ 622, 759–771. doi:10.1086/427976
Grassi, T., Bovino, S., Schleicher, D. R. G., Prieto, J., Seifried, D., Simoncini, E., et al. (2014). KROME - a package to embed chemistry in astrophysical simulations. MNRAS 439, 2386–2419. doi:10.1093/mnras/stu114
Grond, J. J., Woods, R. M., Wadsley, J. W., and Couchman, H. M. P. (2019). TREVR: A general N log2N radiative transfer algorithm. MNRAS 485, 3681–3695. doi:10.1093/mnras/stz525
Harries, T. J., Haworth, T. J., Acreman, D., Ali, A., and Douglas, T. (2019). The TORUS radiation transfer code. Astronomy Comput. 27, 63–95. doi:10.1016/j.ascom.2019.03.002
Hasegawa, K., and Umemura, M. (2010). START: smoothed particle hydrodynamics with tree-based accelerated radiative transfer. MNRAS 407, 2632–2644. doi:10.1111/j.1365-2966.2010.17100.x
Hayes, J. C., and Norman, M. L. (2003). Beyond flux-limited diffusion: parallel algorithms for multidimensional radiation hydrodynamics. ApJS 147, 197–220. doi:10.1086/374658
Hopkins, P. F., and Grudić, M. Y. (2019). Numerical problems in coupling photon momentum (radiation pressure) to gas. MNRAS 483, 4187–4196. doi:10.1093/mnras/sty3089
Iliev, I. T., Ciardi, B., Alvarez, M. A., Maselli, A., Ferrara, A., Gnedin, N. Y., et al. (2006). Cosmological radiative transfer codes comparison project - I. The static density field tests. MNRAS 371, 1057–1086. doi:10.1111/j.1365-2966.2006.10775.x
Iliev, I. T., Whalen, D., Mellema, G., Ahn, K., Baek, S., Gnedin, N. Y., et al. (2009). Cosmological radiative transfer comparison project - II. The radiation-hydrodynamic tests. MNRAS 400, 1283–1316. doi:10.1111/j.1365-2966.2009.15558.x
Jaura, O., Glover, S. C. O., Klessen, R. S., and Paardekooper, J. P. (2018). SPRAI: coupling of radiative feedback and primordial chemistry in moving mesh hydrodynamics. MNRAS 475, 2822–2834. doi:10.1093/mnras/stx3356
Jiang, Y.-F. (2021). An implicit finite volume scheme to solve the time-dependent radiation transport equation based on discrete ordinates. ApJS 253, 49. doi:10.3847/1538-4365/abe303
Jiang, Y.-F. (2022). Multigroup radiation magnetohydrodynamics based on discrete ordinates including compton scattering. ApJS 263, 4. doi:10.3847/1538-4365/ac9231
Jiang, Y.-F., Stone, J. M., and Davis, S. W. (2012). A Godunov method for multidimensional radiation magnetohydrodynamics based on a variable Eddington tensor. ApJS 199, 14. doi:10.1088/0067-0049/199/1/14
Kannan, R., Vogelsberger, M., Marinacci, F., McKinnon, R., Pakmor, R., and Springel, V. (2019). AREPO-RT: radiation hydrodynamics on a moving mesh. MNRAS 485, 117–149. doi:10.1093/mnras/stz287
Kessel-Deynet, O., and Burkert, A. (2000). Ionizing radiation in smoothed particle hydrodynamics. MNRAS 315, 713–721. doi:10.1046/j.1365-8711.2000.03451.x
Klahr, H. H., Henning, T., and Kley, W. (1999). On the azimuthal structure of thermal convection in circumstellar disks. ApJ 514, 325–343. doi:10.1086/306926
Klassen, M., Kuiper, R., Pudritz, R. E., Peters, T., Banerjee, R., and Buntemeyer, L. (2014). A general hybrid radiation transport scheme for star formation simulations on an adaptive grid. ApJ 797, 4. doi:10.1088/0004-637X/797/1/4
Klepitko, A., Walch, S., Wünsch, R., Seifried, D., Dinnbier, F., and Haid, S. (2023). Tree-based solvers for adaptive mesh refinement code FLASH - III: a novel scheme for radiation pressure on dust and gas and radiative transfer from diffuse sources. MNRAS 521, 160–184. doi:10.1093/mnras/stad385
Kley, W. (1989). Radiation hydrodynamics of the boundary layer in accretion disks. I - numerical methods. A&A 208, 98–110.
Kolb, S. M., Stute, M., Kley, W., and Mignone, A. (2013). Radiation hydrodynamics integrated in the PLUTO code. A&A 559, A80. doi:10.1051/0004-6361/201321499
Krumholz, M. R., Klein, R. I., McKee, C. F., and Bolstad, J. (2007). Equations and algorithms for mixed-frame flux-limited diffusion radiation hydrodynamics. ApJ 667, 626–643. doi:10.1086/520791
Kuiper, R., Klahr, H., Dullemond, C., Kley, W., and Henning, T. (2010). Fast and accurate frequency-dependent radiation transport for hydrodynamics simulations in massive star formation. A&A 511, A81. doi:10.1051/0004-6361/200912355
Levermore, C. D. (1984). Relating Eddington factors to flux limiters. J. Quant. Spec. Radiat. Transf. 31, 149–160. doi:10.1016/0022-4073(84)90112-2
Levermore, C. D., and Pomraning, G. C. (1981). A flux-limited diffusion theory. ApJ 248, 321–334. doi:10.1086/159157
Lomax, O., and Whitworth, A. P. (2016). SPAMCART: a code for smoothed particle Monte Carlo radiative transfer. MNRAS 461, 3542–3551. doi:10.1093/mnras/stw1568
Lucy, L. B. (1977). A numerical approach to the testing of the fission hypothesis. AJ 82, 1013–1024. doi:10.1086/112164
Mackey, J., Green, S., Moutzouri, M., Haworth, T. J., Kavanagh, R. D., Zargaryan, D., et al. (2021). PION: simulating bow shocks and circumstellar nebulae. MNRAS 504, 983–1008. doi:10.1093/mnras/stab781
Mayer, L., Lufkin, G., Quinn, T., and Wadsley, J. (2007). Fragmentation of gravitationally unstable gaseous protoplanetary disks with radiative transfer. ApJ Let. 661, L77–L80. doi:10.1086/518433
Mellema, G., Iliev, I. T., Alvarez, M. A., and Shapiro, P. R. (2006). C 2-ray: a new method for photon-conserving transport of ionizing radiation. New Astron. 11, 374–395. doi:10.1016/j.newast.2005.09.004
Melon Fuksman, J. D., and Mignone, A. (2019). A radiative transfer module for relativistic magnetohydrodynamics in the PLUTO code. ApJS 242, 20. doi:10.3847/1538-4365/ab18ff
Mihalas, D., and Klein, R. I. (1982). On the solution of the time-dependent inertial-frame equation of radiative transfer in moving media to. J. Comput. Phys. 46, 97–137. doi:10.1016/0021-9991(82)90007-9
Mihalas, D., and Mihalas, B. W. (1984). Foundations of radiation hydrodynamics. Mineola, New York: Courier Corporation.
Minerbo, G. N. (1978). Maximum entropy Eddington factors. J. Quant. Spec. Radiat. Transf. 20, 541–545. doi:10.1016/0022-4073(78)90024-9
Moens, N., Sundqvist, J. O., El Mellah, I., Poniatowski, L., Teunissen, J., and Keppens, R. (2022). Radiation-hydrodynamics with MPI-AMRVAC. Flux-limited diffusion. A&A 657, A81. doi:10.1051/0004-6361/202141023
Murray, S. D., Castor, J. I., Klein, R. I., and McKee, C. F. (1994). Accretion disk coronae in high-luminosity systems. ApJ 435, 631. doi:10.1086/174842
Nayakshin, S., Cha, S.-H., and Hobbs, A. (2009). Dynamic Monte Carlo radiation transfer in SPH: radiation pressure force implementation. MNRAS 397, 1314–1325. doi:10.1111/j.1365-2966.2009.15091.x
Okamoto, T., Yoshikawa, K., and Umemura, M. (2012). ARGOT: accelerated radiative transfer on grids using oct-tree. MNRAS 419, 2855–2866. doi:10.1111/j.1365-2966.2011.19927.x
Paardekooper, J. P., Kruip, C. J. H., and Icke, V. (2010). SimpleX2: radiative transfer on an unstructured, dynamic grid. A&A 515, A79. doi:10.1051/0004-6361/200913821
Pawlik, A. H., and Schaye, J. (2008). TRAPHIC - radiative transfer for smoothed particle hydrodynamics simulations. MNRAS 389, 651–677. doi:10.1111/j.1365-2966.2008.13601.x
Peters, T., Banerjee, R., Klessen, R. S., Mac Low, M.-M., Galván-Madrid, R., and Keto, E. R. (2010). H II regions: witnesses to massive star formation. ApJ 711, 1017–1028. doi:10.1088/0004-637X/711/2/1017
Petkova, M., and Springel, V. (2009). An implementation of radiative transfer in the cosmological simulation code GADGET. MNRAS 396, 1383–1403. doi:10.1111/j.1365-2966.2009.14843.x
Price, D. J., and Bate, M. R. (2009). Inefficient star formation: the combined effects of magnetic fields and radiative feedback. MNRAS 398, 33–46. doi:10.1111/j.1365-2966.2009.14969.x
Ramsey, J. P., and Dullemond, C. P. (2015). Radiation hydrodynamics including irradiation and adaptive mesh refinement with AZEuS. I. Methods. A&A 574, A81. doi:10.1051/0004-6361/201424954
Razoumov, A. O., and Scott, D. (1999). Three-dimensional numerical cosmological radiative transfer in an inhomogeneous medium. MNRAS 309, 287–298. doi:10.1046/j.1365-8711.1999.02775.x
Rijkhorst, E. J., Plewa, T., Dubey, A., and Mellema, G. (2006). Hybrid characteristics: 3D radiative transfer for parallel adaptive mesh refinement hydrodynamics. A&A 452, 907–920. doi:10.1051/0004-6361:20053401
Ritzerveld, J., and Icke, V. (2006). Transport on adaptive random lattices. Phys. Rev. E 74, 026704. doi:10.1103/PhysRevE.74.026704
Robitaille, T. P. (2011). HYPERION: an open-source parallelized three-dimensional dust continuum radiative transfer code. A&A 536, A79. doi:10.1051/0004-6361/201117150
Rosdahl, J., Blaizot, J., Aubert, D., Stranex, T., and Teyssier, R. (2013). RAMSES-RT: radiation hydrodynamics in the cosmological context. MNRAS 436, 2188–2231. doi:10.1093/mnras/stt1722
Rosdahl, J., and Teyssier, R. (2015). A scheme for radiation pressure and photon diffusion with the M1 closure in RAMSES-RT. MNRAS 449, 4380–4403. doi:10.1093/mnras/stv567
Rosen, A. L., Krumholz, M. R., Oishi, J. S., Lee, A. T., and Klein, R. I. (2017). Hybrid Adaptive Ray-Moment Method (HARM2): a highly parallel method for radiation hydrodynamics on adaptive grids. J. Comput. Phys. 330, 924–942. doi:10.1016/j.jcp.2016.10.048
Roth, N., and Kasen, D. (2015). Monte Carlo radiation-hydrodynamics with implicit methods. ApJS 217, 9. doi:10.1088/0067-0049/217/1/9
Rozyczka, M. (1985). Two-dimensional models of stellar wind bubbles. I - numerical methods and their application to the investigation of outer shell instabilities. A&A 143, 59–71.
Sądowski, A., Narayan, R., Tchekhovskoy, A., and Zhu, Y. (2013). Semi-implicit scheme for treating radiation under M1 closure in general relativistic conservative fluid dynamics codes. MNRAS 429, 3533–3550. doi:10.1093/mnras/sts632
Sekora, M. D., and Stone, J. M. (2010). A hybrid Godunov method for radiation hydrodynamics. J. Comput. Phys. 229, 6819–6852. doi:10.1016/j.jcp.2010.05.024
Shu, F. H. (1991). The physics of astrophysics. Volume 1: radiation. Mill Valley, CA: University Science Books.
Sijoy, C. D., and Chaturvedi, S. (2015). TRHD: three-temperature radiation-hydrodynamics code with an implicit non-equilibrium radiation transport using a cell-centered monotonic finite volume scheme on unstructured-grids. Comput. Phys. Commun. 190, 98–119. doi:10.1016/j.cpc.2015.01.019
Skinner, M. A., Dolence, J. C., Burrows, A., Radice, D., and Vartanyan, D. (2019). FORNAX: a flexible code for multiphysics astrophysical simulations. ApJS 241, 7. doi:10.3847/1538-4365/ab007f
Skinner, M. A., and Ostriker, E. C. (2013). A two-moment radiation hydrodynamics module in athena using a time-explicit Godunov method. ApJS 206, 21. doi:10.1088/0067-0049/206/2/21
Smith, A., Kannan, R., Tsang, B. T. H., Vogelsberger, M., and Pakmor, R. (2020). AREPO-MCRT: Monte Carlo radiation hydrodynamics on a moving mesh. ApJ 905, 27. doi:10.3847/1538-4357/abc47e
Stamatellos, D., Whitworth, A. P., Bisbas, T., and Goodwin, S. (2007). Radiative transfer and the energy equation in SPH simulations of star formation. A&A 475, 37–49. doi:10.1051/0004-6361:20077373
Steinacker, J., Baes, M., and Gordon, K. D. (2013). Three-dimensional dust radiative transfer. Annu. Rev. Astronomy Astrophysics 51, 63–104. doi:10.1146/annurev-astro-082812-141042
Stone, J. M., Mihalas, D., and Norman, M. L. (1992). ZEUS-2D: a radiation magnetohydrodynamics code for astrophysical flows in two space dimensions. III. The radiation hydrodynamic algorithms and tests. ApJS 80, 819. doi:10.1086/191682
Teyssier, R., and Commerçon, B. (2019). Numerical methods for simulating star formation. Front. Astronomy Space Sci. 6, 51. doi:10.3389/fspas.2019.00051
Turner, N. J., and Stone, J. M. (2001). A module for radiation hydrodynamic calculations with ZEUS-2D using flux-limited diffusion. ApJS 135, 95–107. doi:10.1086/321779
Valdivia, V., and Hennebelle, P. (2014). A fast tree-based method for estimating column densities in adaptive mesh refinement codes. Influence of UV radiation field on the structure of molecular clouds. A&A 571, A46. doi:10.1051/0004-6361/201423720
Vandenbroucke, B., and Wood, K. (2018). The Monte Carlo photoionization and moving-mesh radiation hydrodynamics code CMACIONIZE. Astronomy Comput. 23, 40–59. doi:10.1016/j.ascom.2018.02.005
van der Holst, B., Tóth, G., Sokolov, I. V., Powell, K. G., Holloway, J. P., Myra, E. S., et al. (2011). CRASH: a block-adaptive-mesh code for radiative shock hydrodynamics—implementation and verification. ApJS 194, 23. doi:10.1088/0067-0049/194/2/23
Vázquez-Semadeni, E., González-Samaniego, A., and Colín, P. (2017). Hierarchical star cluster assembly in globally collapsing molecular clouds. MNRAS 467, stw3229–1328. doi:10.1093/mnras/stw3229
Viau, S., Bastien, P., and Cha, S.-H. (2006). An implicit method for radiative transfer with the diffusion approximation in smooth particle hydrodynamics. ApJ 639, 559–570. doi:10.1086/499328
Walch, S., Girichidis, P., Naab, T., Gatto, A., Glover, S. C. O., Wünsch, R., et al. (2015). The SILCC (SImulating the LifeCycle of molecular Clouds) project - I. Chemical evolution of the supernova-driven ISM. MNRAS 454, 246–276. doi:10.1093/mnras/stv1975
Whitehouse, S. C., and Bate, M. R. (2004). Smoothed particle hydrodynamics with radiative transfer in the flux-limited diffusion approximation. MNRAS 353, 1078–1094. doi:10.1111/j.1365-2966.2004.08131.x
Whitehouse, S. C., Bate, M. R., and Monaghan, J. J. (2005). A faster algorithm for smoothed particle hydrodynamics with radiative transfer in the flux-limited diffusion approximation. MNRAS 364, 1367–1377. doi:10.1111/j.1365-2966.2005.09683.x
Whitworth, A. P., Chapman, S. J., Bhattal, A. S., Disney, M. J., Pongracic, H., and Turner, J. A. (1995). Binary star formation: accretion-induced rotational fragmentation. MNRAS 277, 727–746. doi:10.1093/mnras/277.2.727
Wibking, B. D., and Krumholz, M. R. (2022). QUOKKA: a code for two-moment AMR radiation hydrodynamics on GPUs. MNRAS 512, 1430–1449. doi:10.1093/mnras/stac439
Wise, J. H., and Abel, T. (2011). ENZO+MORAY: radiation hydrodynamics adaptive mesh refinement simulations with adaptive ray tracing. MNRAS 414, 3458–3491. doi:10.1111/j.1365-2966.2011.18646.x
Wolfire, M. G., and Cassinelli, J. P. (1986). The temperature structure in accretion flows onto massive protostars. ApJ 310, 207. doi:10.1086/164676
Wünsch, R., Walch, S., Dinnbier, F., Seifried, D., Haid, S., Klepitko, A., et al. (2021). Tree-based solvers for adaptive mesh refinement code FLASH - II: radiation transport module TreeRay. MNRAS 505, 3730–3754. doi:10.1093/mnras/stab1482
Wünsch, R., Walch, S., Dinnbier, F., and Whitworth, A. (2018). Tree-based solvers for adaptive mesh refinement code FLASH - I: gravity and optical depths. MNRAS 475, 3393–3418. doi:10.1093/mnras/sty015
Keywords: star formation, interstellar medium, numerical techniques, radiation transport, astrophysical fluid dynamics
Citation: Wünsch R (2024) Radiation transport methods in star formation simulations. Front. Astron. Space Sci. 11:1346812. doi: 10.3389/fspas.2024.1346812
Received: 30 November 2023; Accepted: 13 February 2024;
Published: 01 March 2024.
Edited by:
James Wurster, University of St Andrews, United KingdomReviewed by:
Thomas Haworth, Queen Mary University of London, United KingdomTim Harries, University of Exeter, United Kingdom
Copyright © 2024 Wünsch. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Richard Wünsch, cmljaGFyZC53dW5zY2hAYXN1LmNhcy5jeg==
 Richard Wünsch
Richard Wünsch