Large-scale magnetic field oscillations and their effects on modulating energetic electron precipitation

In this study, we present simultaneous multi-point observations of magnetospheric oscillations on a time scale of tens of minutes (forced-breathing mode) and modulated whistler-mode chorus waves, associated with concurrent energetic electron precipitation observed through enhanced BARREL X-rays. Similar fluctuations are observed in X-ray signatures and the compressional component of magnetic oscillations, spanning from ∼9 to 12 h in MLT and 5 to 11 in L shell. Such magnetospheric oscillations covering an extensive region in the pre-noon sector have been suggested to play a potential role in precipitating energetic electrons by either wave scattering or loss cone modulation, showing a high correlation with the enhancement in X-rays. In this event, the correlation coefficients between chorus waves (smoothed over 8 min), ambient magnetic field oscillations and X-rays are high. We perform an in-depth quasi-linear modeling analysis to evaluate the role of magnetic field oscillations in modulating energetic electron precipitation in the Earth’s magnetosphere through modulating whistler-mode chorus wave amplitude, resonance condition between chorus waves and electrons, as well as loss cone size. Model results further show that the modulation of chorus wave amplitude plays a dominant role in modulating the electron precipitation. However, the effect of the modulation in the resonant energy between chorus waves and energetic electrons due to the background magnetic field oscillations cannot be neglected. The bounce loss cone modulation, affected by the magnetic oscillations, has little influence on the electron precipitation modulation. Our results show that the low frequency magnetospheric oscillations could play a significant role in modulating the electron precipitation through modulating chorus wave intensity and the resonant energy between chorus waves and electron.

1 Introduction

Pitch angle diffusion of energetic electrons into the atmospheric bounce loss cone has been considered to be an important loss mechanism of radiation belt electrons. In this process, energetic electrons are precipitated into the atmosphere through resonant interactions with various plasma waves (e.g., Millan and Thorne., 2007), such as electromagnetic ion cyclotron (EMIC) waves (Summers and Thorne, 2003; Clilverd et al., 2015; Hendry et al., 2017; Qin et al., 2018; Qin et al., 2019; Qin et al., 2020; Capannolo et al., 2019a; Capannolo et al., 2019b; Zhang et al., 2021), whistler-mode chorus waves (e.g., Nishimura et al., 2010; Thorne, 2010; Ma et al., 2020) and hiss waves in the plasmasphere and plumes (Summers et al., 2008; Li et al., 2019; Ma et al., 2021).

Fluctuations with frequencies below tens of millihertz (mHz) have been extensively observed in the signatures of energetic electron precipitation from riometer pulsations (Heacock and Hunsucker, 1977; Spanswick et al., 2005), radars (Buchert et al., 1999), optical auroral emissions (Rae et al., 2007; Jaynes et al., 2015) and balloon X-ray spectra (Brito et al., 2012; Motoba et al., 2013; Breneman et al., 2015; Halford et al., 2015; Rae et al., 2018; Breneman et al., 2020; Qin et al., 2021). These fluctuations have been shown to be usually associated with ultra-low frequency (ULF) waves or quasi-static breathing mode of the magnetosphere with similar periodicities. Pc 3–5 ULF waves (1.7–100 mHz, Jacobs et al., 1964) can be driven by upstream solar wind dynamic pressure impulses (e.g., Claudepierre et al., 2009; Claudepierre et al., 2010; Shen et al., 2015; Shen et al., 2017), solar wind speed changes (Mathie and Mann, 2000), as well as internal sources like substorms (e.g., Olson, 1999; Hsu and McPherron, 2007). The magnetosphere also responds to external solar wind conditions via a quasi-static forced breathing mode, with periods longer than the Alfven wave travel time in the dayside magnetosphere (∼4 min, 4 mHz) (Kepko et al., 2002; Kepko and Spence, 2003; Kepko and Viall, 2019). Because the period of these ambient magnetic field oscillations is much longer than the gyroperiod and the bounce period of energetic electrons, they are only supposed to be in drift resonance with electrons (Elkington et al., 2003), rather than directly scatter the electrons into loss cone through cyclotron-resonance interaction.

Many mechanisms have been employed to explain the commonly observed energetic electron precipitation modulated by ULF wave or forced-breathing mode oscillations. Theoretically, ULF waves or forced-breathing mode magnetic field fluctuations can modulate electron precipitation mainly in three ways. 1) ULF waves/breathing mode oscillations can modulate the EMIC wave and whistler-mode wave growth rate. Breneman et al. (2015) showed that 1–10 min ULF modulations of X-rays generated by electron precipitation on a Balloon Array for Radiation-belt Relativistic Electron Losses (BARREL) balloon (Millan et al., 2013; Woodger et al., 2015) were nearly identical to modulations in whistler-mode hiss amplitude observed by the Van Allen Probes (RBSP, Mauk et al., 2013) during a close magnetic conjunction. Breneman et al. (2020) reported large-scale electron precipitation observed as X-rays on BARREL. Their analysis suggested that hiss waves modulated by forced-breathing mode magnetic field fluctuations are directly responsible for the observed loss. 2) ULF waves/breathing mode oscillations could modulate the resonance condition and thus cause an increase/decrease of the resonant energy with electrons by modulating the ambient magnetic field or total electron density. Zhang et al. (2019) investigated the mechanism of electron precipitation through quasi-linear pitch angle scattering by EMIC waves when simultaneous ULF waves exist. It was shown that the ULF wave fluctuations could lead to a significant decrease in the minimum resonant energy when the magnetic field diminishes. 3) ULF waves can cause electron precipitation by modulating the size of the bounce loss cone (BLC) (Rae et al., 2018) and electron pitch angles (Brito et al., 2012; Brito et al., 2015; Yin et al., 2023). Brito et al. (2012); Brito et al. (2015) used MHD simulations to show that when electrons encounter compressional magnetic field oscillations, their trajectories move closer to the Earth into a stronger magnetic field with shorter field lines where the loss cone is larger, leading to enhanced precipitation. However, due to a lack of equatorial wave observations and direct comparison between observed and simulated electron precipitation features, it remains unclear whether ULF waves were fully responsible for the electron precipitation or act as a minor role in modulating electron precipitation. ULF waves/breathing mode oscillations could also modulate the BLC by modulating the ambient magnetic field (Rae et al., 2018). Although the direct modulation of the BLC by ULF waves/quasi-static breathing mode only influences electrons near the loss cone, it could potentially enhance the modulation of precipitation during the presence of EMIC/whistler-mode waves due to pitch angle scattering. However, in Rae et al. (2018), there are no means to test other precipitation sources, such as pitch angle scattering by whistler-mode waves, due to the lack of conjugated high frequency wave measurement near the equatorial plane.

In this paper, we primarily use observations from BARREL-1H (Millan et al., 2013) and THEMIS-E (Angelopoulos, 2008), which were in close conjunction, to separately evaluate the effect of whistler-mode chorus wave amplitude, loss cone size and the resonant energy (between plasma waves and electrons) in modulating energetic electron precipitation in the Earth’s magnetosphere. We also augment our observations with other equatorial satellite magnetometer data from THEMIS-D, RBSP-A, B and GOES-13, 15 (Singer et al., 1996), as well as the observations of X-rays generated by electron precipitation from other BARREL payloads (BARREL 1A, 1I, 1Q, 1T and 1U). The BARREL payloads drift slowly in space, enabling the investigation of temporal evolution features of electron precipitation. The THEMIS spacecraft were operating in near-equatorial orbits to measure waves and plasma parameters.

The content of the paper is outlined as follows. In Section 2, an overview of the event and detailed correlation between the measured chorus emissions, BARREL X-rays and quasi-static breathing mode fluctuations are presented. In Section 3, through a physics-based technique based on the quasi-linear theory, we quantify the role of background magnetic field in modulating the chorus-driven electron precipitation by turning on and off the background quasi-static magnetic field fluctuations respectively and compare the time evolution of the modeled electron precipitation with the observed modulated X-rays. In Section 4, we discuss the potential roles of loss cone change and the shift of resonant energy in modulating the energetic electron precipitation. The conclusions are summarized in Section 5.

2 Observation

2.1 Event overview

Figure 1A shows the trajectories of the available equatorial satellites (THEMIS-D, E; RBSP-B and GOES-13, 15) and BARREL payloads (BARREL 1A, 1H, 1I, 1Q, 1T and 1U) in the L-MLT map (determined using the IGRF magnetic field model) over 18:30 UT—20:30 UT on 28 January 2013. Figures 1B–D show solar wind and geomagnetic conditions, indicating little change in the interplanetary magnetic field and the solar wind dynamic pressure, as well as a modest substorm activity at around 18:30 UT. Figures 1F, G show the fluxgate magnetometer data from GOES and THEMIS. During this event, GOES-15 and GOES-13 were located in the pre-noon and post-noon sectors respectively (Figure 1A), providing observations of magnetic field at geosynchronous orbit with 0.512 s time resolution. THEMIS-D and THEMIS-E were located in the pre-noon sector outside the geosynchronous orbit. Following the substorm onset (18:30 UT), similar magnetic field modulations (correlation coefficient >0.5) on a timescale of ∼10 s of minutes (forced-breathing mode) were observed by GOES-15, THEMIS-D, and THEMIS-E. Such low frequency magnetospheric oscillations are often related to solar wind pressure variations (Kepko et al., 2002; Kepko and Spence, 2003). In this event, frequency analysis (not shown) suggests that source of the forced-breathing mode magnetic oscillations lies in the solar wind speed (OMNI database, propagated from measurements at the Lagrange-1 point by either ACE or Wind satellite to the Earth’s bow shock nose). GOES-13, which was located near post-noon, however, shows a different modulation in the background magnetic field (Figure 1F).

FIGURE 1

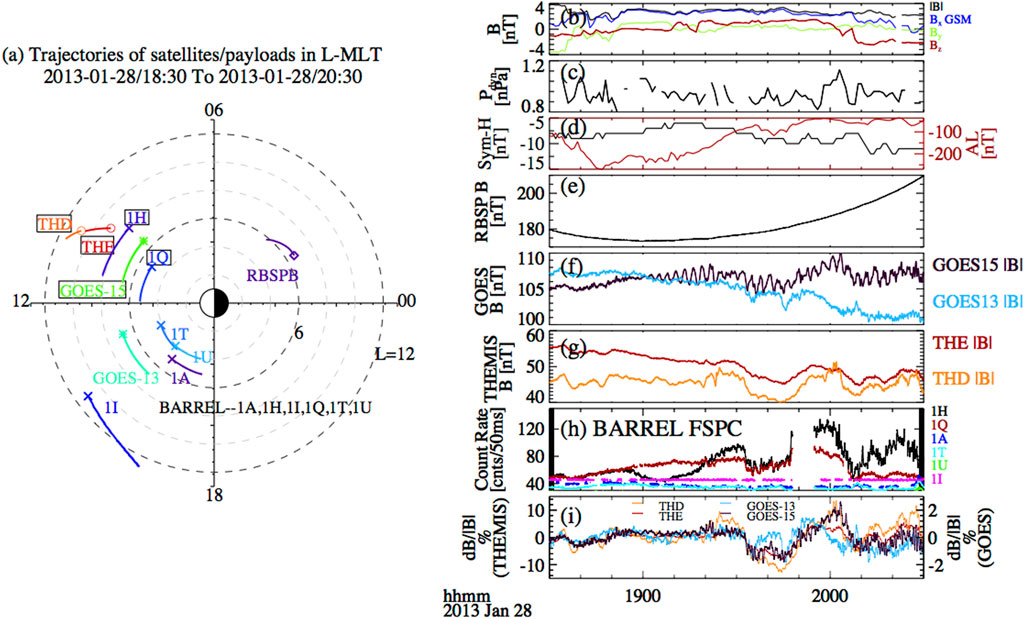
FIGURE 1. (A) Trajectories of BARREL payloads, RBSP, THEMIS and GOES satellites in the L-MLT map (IGRF model) during 18:30–20:30 UT. The circle, cross, asterisk, and diamond symbols indicate the start point of THEMIS, BARREL, RBSP and GOES. Satellites and payloads that observed the similar features of fluctuation are highlighted in the black box. The observations from the solar wind, magnetospheric spacecraft and BARREL payloads are shown in Panels (B–G). (B) Total magnetic field (black), Bx (blue), By (green), and Bz component (red) of the interplanetary magnetic field in GSM coordinates and (C) solar wind dynamic pressure obtained from OMNI database (a compilation of records made on ACE, WIND, and IMP-8 spacecraft that were time-shifted to the Earth’s bow shock subsolar point); (D) Sym-H (black) and AL indices (red) showing a substorm onset at ∼18:30 UT; (E) Total magnetic field measured by RBSP-B; (F) Total magnetic field strength measured by GOES-13 (cyan) and 15 (black); (G) Total magnetic field measured by THEMIS D (orange) and E (red); (H) 25–180 keV X-ray count rate (smoothed over 0.5 s) measured by BARREL 1A (blue), 1H (black), 1I (magenta), 1Q (red), 1T (cyan) and 1U (green); (I) Percent variation (over 60 min smoothed background) of the magnetic field observed by THEMIS-D (orange), THEMIS-E (red), GOES-13 (cyan) and GOES-15 (black) relative to their 60 min smoothed data.

Observations from the full BARREL array are shown in the 25–180 keV X-ray fast spectrum smoothed over 0.5 s (Millan et al., 2013; Woodger et al., 2015) in Figure 1H. Similar modulations were observed on BARREL 1H and 1Q, which were located in the prenoon sector. The count rate level of X-rays was higher for BARREL 1H (L ∼ 8) than 1Q (L ∼ 5), which might be either caused by the different trapped flux levels at different L shells or the location of the plasmapause. Enhancements were not observed on BARREL-1A, 1I, 1T and 1U, which were located in the afternoon sector. Those satellites and payloads with similar fluctuations (correlation coefficient >0.5) are highlighted in the black boxes in Figure 1A. The spatial scale with the similar modulation timescale is large, with MLT spanning from ∼9 to 12 and L shell from 5 to 11. It was also shown that moderate changes in the ambient magnetic field can cause a significant change in the BLC (Rae et al., 2018), the plasma wave growth rate and the resonance condition between waves and energetic electrons (Zhang et al., 2019). In this case, the relative change (relative to the 60 min smoothed data) of the magnetic field on THEMIS-D and E reached up to around 10% (Figure 1I). Our results indicate a potential link between the low frequency magnetic field fluctuations and the electron precipitation observed through BARREL X-rays.

To explore the large-scale background magnetic field fluctuations in modulating the electron precipitation, we analyze the observations from BARREL-1H and THEMIS-E which were in closer conjunction (Figure 2). Figure 2A shows three components of the magnetic field in the field-aligned coordinates observed by THEMIS-E fluxgate magnetometers (FGM) (Auster et al., 2008), which were detrended over 60 min to show the ULF/quasi-static forced breathing mode variations. It is shown that the compressional component (red line) has a similar fluctuation to the BARREL X-rays shown in Figure 2E. Figure 2B shows the magnetic spectral density observed by the Search Coil Magnetometer (SCM) (Roux et al., 2008), which detects low-frequency magnetic field fluctuations and waves in three directions over a frequency bandwidth up to ∼8 kHz. The superimposed magenta line represents total electron density inferred from the spacecraft potential (Pedersen et al., 2008) measured by the Electric Field Instrument (EFI) (Bonnell et al., 2008). The lower-band chorus wave was also observed by THEMIS-E and the wave intensity was positively correlated with the total electron density, with the lower cutoff frequency of waves extending down to a lower value with a higher density. The density modulation can lead to modulation of chorus wave growth through modulating the fraction of resonant electrons (Li et al., 2011a) or through wave trapping by density crests or troughs (Chen et al., 2012; Liu et al., 2021). Figure 2C shows the magnetic spectral density calculated from the low frequency fluctuations (up to 64 Hz) of the background magnetic field measured by the FGM instrument, using fast Fourier transform method with a window size of 256 s and a shifted time window by 32 s. EMIC waves were also detected during this event. However, the enhancement in X-rays were only observed in the lowest energy channel (25–180 keV). EMIC waves, which are known to interact with high-energy electrons (>∼ a few hundred keV; Capannolo et al., 2019a; Capannolo et al., 2019b; Grach et al., 2022) and would lead to enhanced X-ray count rates in higher energy channels (Li et al., 2014), are unlikely to play a major role during this precipitation event. Figure 2D shows the Morlet mother wavelet analysis of the FGM measurement. The horizontal lines in panel (d) indicate frequencies of 4 and 30 mHz. ULF waves between 4 mHz and 30 mHz were relatively weak, while the quasi-static forced breathing mode, with wave frequency lower than 4 mHz, was stronger. The forced breathing mode of the magnetosphere was associated with the enhancement of the 25–180 keV BARREL X-rays with a similar fluctuation, as shown in Figure 2E.

FIGURE 2

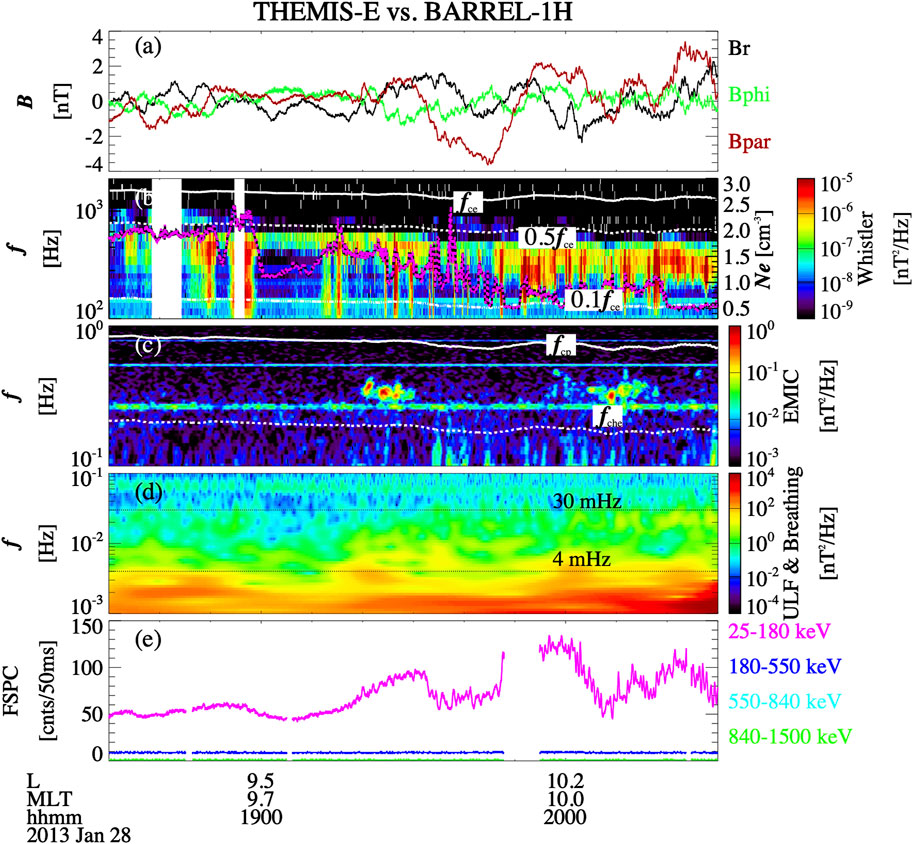
FIGURE 2. (A) Three components of the magnetic field in field-aligned coordinates (black: radial component, green: azimuthal component, red: compressional component) detrended over 60 min. (B) Magnetic spectral density observed by the Search Coil Magnetometer (SCM) onboard THEMIS-E. The white lines in panel (B) represent the electron cyclotron frequency (f_ce), 0.5 f_ce and 0.1 f_ce from top to bottom. The superimposed magenta line is the total electron density obtained from the spacecraft potential. (C) Magnetic spectral density calculated from the fluxgate magnetometer (FGM) onboard THEMIS-E. The white lines in panel (C) indicate proton, helium, and oxygen cyclotron frequencies. (D) Wavelet analysis of the magnetometer measurements, where the 4 and 30 mHz frequencies are shown as the two black dotted lines. (E) BARREL 1H fast spectrum X-rays at energies of 25–180 (pink), 180–550 (blue), 550–840 (cyan), and 840–1,500 keV (green).

2.2 Modulation of waves and electron precipitation

In order to examine the correlation between the observed electron precipitation and the chorus waves or ambient magnetic field oscillations, we show the correlation coefficients (C. C.) between them in Figure 3. During this period, chorus waves were observed outside the plasmasphere, as shown in Figure 2B. The blue line in Figure 3A shows chorus wave amplitude (8-s time resolution, blue line) observed by THEMIS-E, which was calculated by integrating the wave intensity over the frequency range from 100 to 1,000 Hz. The black line in Figure 3A shows the total electron density inferred from the spacecraft potential. It shows that the chorus wave intensity has similar fluctuations with the local electron density on a timescale of approximately 1 minute. However, when considering a longer time scale (10 s of minutes), the fluctuations of chorus waves and electron density are quite different. This is evident in the correlation coefficient over the entire time window (19:10–20:30), which is close to 0 (Figure 3A). To analyze the correlation on a shorter timescale, Figure 3F presents the calculation of the correlation coefficient within a 4-min box with a time-shifted window of 2 min. Figure 3F shows that the chorus wave intensity is highly correlated (>0.5 at most times) with the local electron density, further supporting that the chorus waves are modulated by local density. Figure 3B shows the amplitudes of chorus waves (blue line) and the compressional component of the ambient magnetic field oscillations (0.5–30 mHz, 4-s time resolution, black line), with a low correlation coefficient only about 0.17. Figure 3C shows the X-ray count rate (black line) and the chorus wave amplitude (blue line), also with a low correlation of about 0.20. Similarly, we calculate the short-time scale correlation, which is shown in Figure 3E and further demonstrates the overall low correlation (C. C. < 0.5 at most times). Figure 3D shows the compressional component of the ambient magnetic field oscillations (black line) and the X-ray count rate (magenta line), with a correlation coefficient ∼0.57, much higher than that between X-ray count rate and chorus wave amplitude. This indicates that the breathing mode fluctuations observed by THEMIS-E is highly correlated with the enhancement in X-rays. Combining with the fact that a similar modulation (C. C. > 0.5) was also observed by BARREL-1Q and GOES-15 (Figure 1A), we conclude that the quasi-static breathing mode may have played a significant role in modulating the electron precipitation. Previous studies show high correlation between chorus waves and ASI auroral intensity when the electron precipitation is driven by chorus waves (Nishimura et al., 2011; Hosokawa et al., 2020). In those work, the observations were specifically chosen at latitudes with the highest correlation (corresponding to highest correlation L shell), within a narrow window of a few minutes. In this case, however, the correlation is calculated on a point-to-point basis, rather than the point-to-plane comparison (Nishimura et al., 2011; Hosokawa et al., 2020). The low correlation between chorus wave amplitude and X-ray count rate (Figure 3E) might be due to the spatial difference of THEMIS-E and BARREL-1H, which were at rough conjugate locations with a separation in L shell of ∼1.5–2.5. This is much larger than the coherent scale size of the chorus elements, which is about hundreds to thousands of kilometers (Agapitov et al., 2017; Shen et al., 2019), thus the electron precipitation is not expected to have one-to-one correspondence with the chorus wave elements.

FIGURE 3

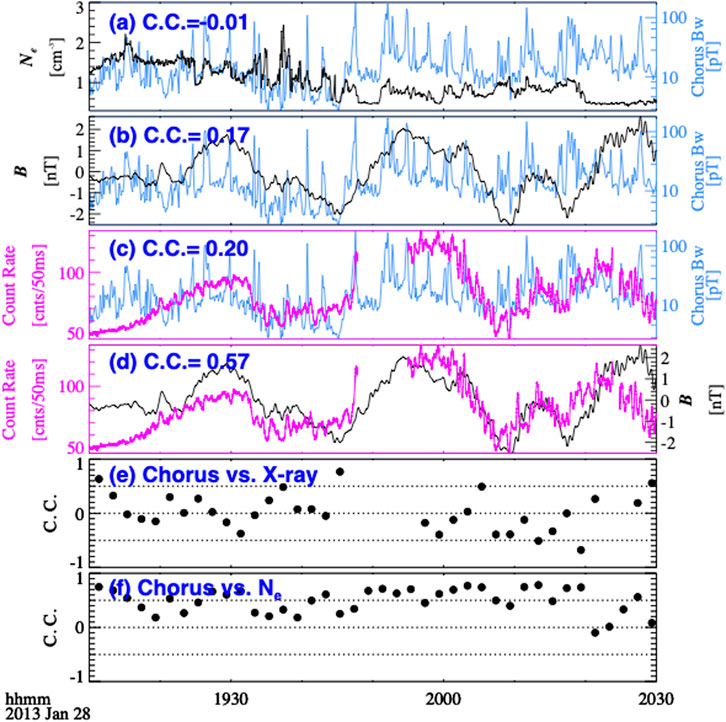
FIGURE 3. (A) Total electron density (black) obtained from spacecraft potential and chorus wave amplitude (blue) observed by THEMIS-E. (B) Ambient magnetic field fluctuations (0.5–30 mHz, black) and chorus wave amplitude (blue) observed by THEMIS-E with the time resolution of 4 s and 8 s, respectively. (C) Fast spectrum X-ray count rate (25–180 keV) from BARREL smoothed over 0.5 s (magenta) and chorus wave amplitude (blue). (D) Fast spectrum X-ray count rate (25–180 keV) from BARREL smoothed over 0.5 s (magenta) and ambient magnetic field fluctuations (0.5–30 mHz, black). Correlation coefficient between (E) chorus wave amplitude and X-ray count rate and (F) chorus wave amplitude and electron density. Correlation coefficients in panels (A–D) are calculated over the entire time window (19:10–20:30), while in panels (E–F), the correlation coefficients are calculated within a 4-min box with a time-shifted window of 2 min.

The chorus wave intensity is not only shown to be correlated (at times) with the local electron density (Figure 3F), but also tends to increase (decrease) when the ambient background magnetic field increases (decreases). The ambient magnetic field oscillations can modulate the whistler mode growth rate by modulating the magnetic field inhomogeneity (Zhou et al., 2015) and the radial transport of resonant electron populations (Brenaman et al., 2020). To smooth out the modulation in association with local plasma density, whistler-mode chorus wave amplitude is smoothed over 8 min to evaluate the temporal modulation on forced-breathing time scale. The results are shown in Figure 4, which is similar to Figure 3 except that chorus wave amplitude is smoothed over 8 min. The analysis reveals that there is a notable increase in the correlation coefficient between chorus wave intensity (smoothed over 8-min) and the amplitude of the ambient magnetic field fluctuations (Figure 4A), reaching 0.39. This value is higher when compared to the correlation coefficient of 0.17 for unsmoothed chorus wave amplitude in Figure 3B. Additionally, the correlation coefficient between the smoothed chorus wave amplitude and X-ray count rate (Figure 4B) increased to 0.61. This value is much higher compared to the unsmoothed case in Figure 3C (C. C. ∼ 0.2) and comparable to the correlation coefficient between the ambient magnetic field fluctuations and X-ray count rate (Figure 4C). These findings suggest that the overall temporal evolution of chorus wave amplitude is also modulated by quasi-static breathing mode oscillations of the ambient magnetic field, which can further modulate the X-ray count rate generated by electron precipitation. Since the magnetic field oscillations can also modulate electron precipitation through modulating resonance condition and the loss cone size, the correlation analysis itself cannot determine the main driver of the electron precipitation modulation. To further examine the role of each mechanism, a further physics-based modeling is performed in Section 3 and Section 4.

FIGURE 4

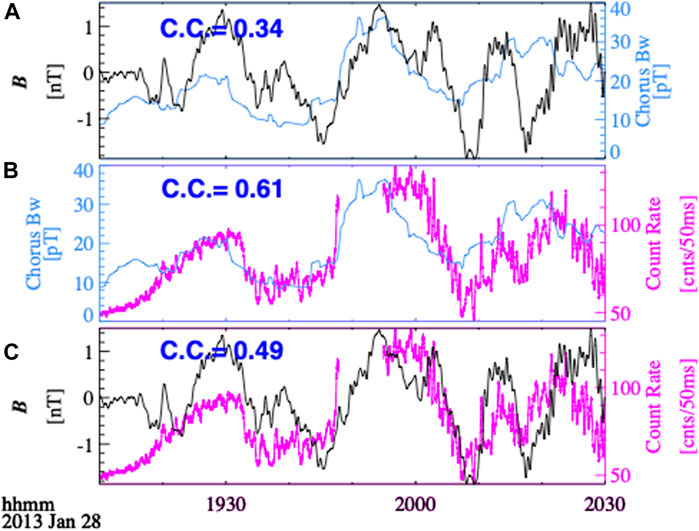
FIGURE 4. (A) Ambient magnetic field fluctuations (0.5–30 mHz, black) and chorus wave amplitude smoothed over 8 min (blue) observed by THEMIS-E with the time resolution of 4 s and 8 s, respectively. (B) Fast spectrum X-ray count rate (25–180 keV) from BARREL smoothed over 0.5 s (magenta) and chorus wave amplitude smoothed over 8 min (blue). (C) Fast spectrum X-ray count rate (25–180 keV) from BARREL smoothed over 0.5 s (magenta) and ambient magnetic field fluctuations (0.5–30 mHz, black).

3 Comparison between observations and simulations

Figure 5A shows the modulation in equatorial bounce loss cone (blue) due to large amplitude magnetic field oscillations (black). The equatorial bounce loss cone ${\alpha }_{LC}$ is defined as the maximum pitch angle of particles at the equatorial plane that have a mirror point below 100 km altitude in the atmosphere (${\mathit{sin}}^2{\alpha }_{LC}$ = $B_0/B_m$, where $B_0$ is the equatorial magnetic field and $B_m$ is the magnetic field at 100 km altitude). Since the variation in $B_m$ is only a small fraction of $B_m$ as compared to $B_0$, we assume that the variation in ${\alpha }_{LC}$ is mainly caused by modulation in $B_0$ with very little loss in accuracy (Rae et al., 2018). Magnetic field strength of $B_m$ was calculated by mapping the THEMIS-E position to the foot point at 100 km using the IGRF magnetic field model. The ratio of the corresponding background magnetic field and loss cone size under the two circumstances are shown in Figure 5G, where the black line represents magnetic field and the blue line is for the equatorial loss cone size. When $B_0$ increases, the equatorial loss cone size also increases, which allows more particles to be precipitated. It is shown that there is an up to 8% variation in loss cone size caused by ambient magnetic field fluctuations.

FIGURE 5

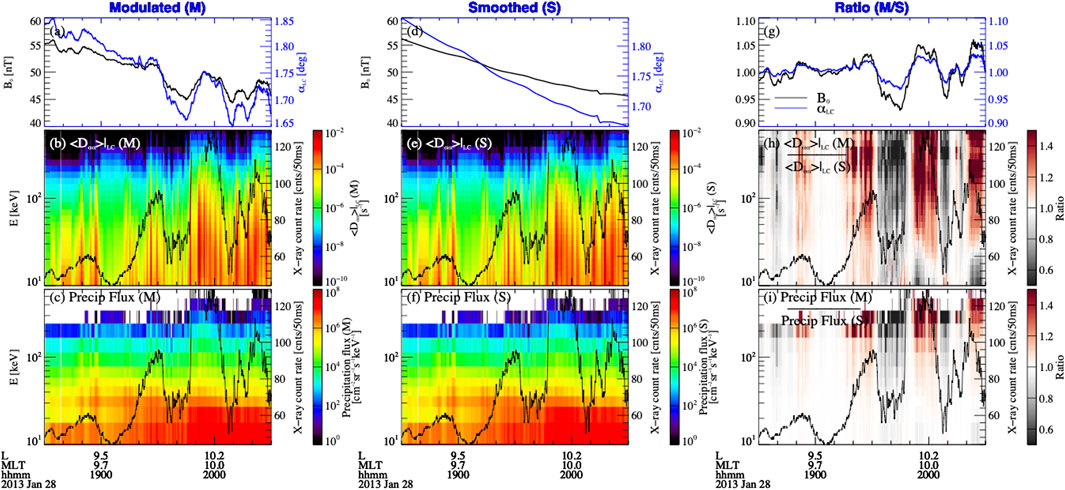
FIGURE 5. Analysis of electron precipitation due to chorus waves when the quasi-static breathing mode magnetic field modulation is considered (A–C) and excluded (D–F). (A) Measured ambient magnetic field strength and the corresponding bounce loss cone size calculated from the IGRF model; (B) Bounce-averaged pitch angle diffusion coefficients at the loss cone as a function of time and electron energy; (C) Model calculated electron precipitation at the equilibrium state from the quasi-linear theory as a function of time and electron energy. (D, E) Same format as panels (A–C) but with the quasi-static breathing mode turned off (Smoothed). Right panels (G–I) show the ratio between the left panels and the middle panels. The superimposed black lines in the bottom two rows represent fast spectrum X-ray count rate (25–180 keV) observed by BARREL.

The pitch angle scattering rates driven by chorus waves are quantified using a physics-based approach with the Full Diffusion Code to calculate the quasi-linear diffusion coefficients (Ni et al., 2008). Landau resonance and multiple cyclotron harmonic resonances (−10 to 10) are considered. It is assumed that chorus wave normal angles are quasi-parallel to the magnetic field line near the equatorial plane and increase as magnetic latitudes increase (Ni et al., 2013). Total electron density is derived from the spacecraft potential measured by THEMIS-E and assumed to be constant along the field lines. With the diffusion coefficient < D_αα>_LC and the electron flux near the equatorial loss cone ${\alpha }_{LC}$, we then determine the equatorial pitch angle distribution of electrons inside the loss cone using the solution for the Fokker-Planck equation under the quasi-equilibrium state (Kennel and Petschek, 1966; Li et al., 2011b; Ma et al., 2020; Ma et al., 2021), which can be estimated as:

$J_{in}\left({\alpha }_{eq,in},E\right)=\frac{S\left(E\right)}{D^{*}}\left\{\frac{I_0\left(\frac{{\alpha }_{eq,in}}{{\alpha }_{LC}}{z}_0\right)}{z_0{I}_1\left(z_0\right)}\right\}(1)$

where $I_{0}and{I}_1$ are the modified Bessel functions; $S\left(E\right)$ is the rate that the particles enter the loss cone, which is calculated based on the electron flux measured by solid state telescope (SST) onboard THEMIS-E at the lowest pitch angle bin (11.25°); $D^{*}\approx {<D_{aa}>}_{LC}\times cos\left({\alpha }_{LC}\right)$ and $z_0=\frac{{\alpha }_{LC}}{\sqrt{D^{*}\tau }}$ , where $\tau$ is a quarter of the electron bounce period. The integral electron flux inside the loss cone is further calculated as:

$J_{integral}\left(E\right)={\displaystyle {\int }_0^{{\alpha }_{LC}}}{J}_{in}\left({\alpha }_{eq,in},E\right)\bullet \mathit{sin}\alpha \bullet d\alpha (2)$

In order to evaluate the effects of ambient magnetic field oscillations in electron precipitation through modulating the resonance condition and loss cone size, we perform simulations by turning on (“modulated”) and turning off (“smoothed”) the background ambient magnetic field fluctuations in the Full Diffusion Code and in calculating the resultant integral electron precipitation inside the loss cone using Eqs 1, 2. In the “modulated” case, the modulation of chorus wave amplitude and modulation of the resonant energy are included to calculate the diffusion coefficients with the Full Diffusion Code (Figure 5B) and the modulation of the loss cone size is further included to calculate the resultant electron precipitation using Eqs 1, 2 (Figure 5C). In the “smoothed” case, only the modulation of the chorus wave amplitude is included to calculate the diffusion coefficients (Figure 5E) and the electron precipitation (Figure 5F). The ratios of them are shown in the right panels (g-i).

The diffusion coefficients at the loss cone < D_αα>_LC corresponding to these two circumstances are shown in Figure 5B (Modulated) and 5e (Smoothed). The superimposed black lines are BARREL X-ray counts at 25–180 keV. Figure 5H is the ratio between them. When background magnetic field increases, chorus waves tend to interact with higher energy electrons more efficiently, leading to a higher ratio in <D_αα>_LC (modulated/smoothed) at higher energies and a lower ratio at lower energies. Above 30 keV, breathing mode can decrease the diffusion coefficient to half at minimum $B_0$ and increase the diffusion coefficient by 50% at maximum $B_0$. The modulations of <D_αα>_LC caused by chorus wave amplitude variations are more noticeable than the difference of <D_αα>_LC caused by the modulation of resonant condition (mainly due to the modulation of background magnetic field), as shown in Figures 5B, E. This indicates that the temporal modulation of the chorus wave amplitude dominates the fluctuations in electron precipitation.

Figures 5C, F show the integral precipitating flux under the two circumstances and Figure 5I is the ratio between them. It was shown that the integral precipitating flux is similar for the two circumstances when the background magnetic field fluctuation is turned on (Figure 5C) and turned off (Figure 5F). The ratio in Figure 5I further shows that the precipitating fluxes at higher energy (>∼100 keV) are significantly modulated. The modeled precipitation can increase by 1.5–3 times as magnetic field varies from the minimum to maximum value when we turn on the breathing mode fluctuation. This result indicates that although the temporal modulation of the chorus wave amplitude dominates the fluctuations in electron precipitation, the effects of the modulation of resonance condition through modulating the background magnetic field cannot be neglected.

4 Discussion

In this work, we evaluate the role of large-scale forced-breathing mode magnetic field oscillations in modulating the electron precipitation. Although the ambient magnetic field oscillations alone only affect the small electron population near the loss cone, they can play an important role in modulating the electron precipitation ratio with the presence of chorus waves, through modulating the chorus wave amplitude, the resonance condition and the loss cone size.

ULF waves/forced-breathing mode magnetic field fluctuations can modulate the electron precipitation through modulating chorus wave growth rate (e.g., Li et al., 2011a; Breneman et al., 2015; Jaynes et al., 2015; Xia et al., 2016; Qin et al., 2021). In our study, the whistler-mode chorus wave amplitude is modulated by both magnetic field fluctuations (Figure 4A) and local electron density (Figure 3F). The correlation coefficient between chorus wave amplitude (8 s time resolution without smoothing) and the electron precipitation is low (0.22). This is because the separation in L shell between chorus wave and electron precipitation is ∼1.5–2.5, much larger than the coherent scale size of the chorus elements, which is about hundreds to thousands of kilometers (Agapitov et al., 2017; Shen et al., 2019). Therefore, the electron precipitation is not expected to have one-to-one correspondence with the chorus wave elements. The smoothed chorus wave amplitude, which shows the averaged properties of a group of chorus wave elements, however, exhibits a higher correlation (0.62) with X-ray count rate (Figure 4B). This suggests that the magnetic field oscillations could modulate the electron precipitation through modulating the whistler-mode chorus wave amplitude. The maximum value of the smoothed chorus wave amplitude is about 4 times larger than the minimum value, which can lead to a significant modulation (16 times) in the electron precipitation. Unfortunately, chorus wave intensity measured at the exactly same location as BARREL was not available, and thus the accurate role of the modulation of chorus wave intensity in modulating the energetic electron precipitation is difficult to quantify.

ULF waves/forced-breathing mode magnetic field fluctuations can also modulate the electron precipitation through modulating the resonance condition and the loss cone size. On one hand, the minimum energy of electrons to interact with chorus waves depends on the background magnetic field strength (Li et al., 2011a). It was shown that the minimum resonant energy increases when the magnetic field increases. On the other hand, chorus waves can move electrons toward pitch angles near the loss cone through cyclotron resonance. The quasi-static breathing mode magnetic field oscillations can then take over and enhance (reduce) the precipitation by increasing (decreasing) the loss cone size, as suggested by Rae et al. (2018). In our case, we show that magnetic field fluctuations could affect the resonant energy and the pitch angle diffusion rate (Figure 5). When the magnetic field increases (decreases), the minimum energy for electrons to be in resonance with chorus waves increases (decreases, approximately ∼10%). For electrons above 30 keV, the diffusion coefficients at the loss cone increase by up to ∼1.5 times when the magnetic field increases by 5%. Correspondingly, the diffusion coefficients for electrons with energy below 30 keV show an anti-correlation with the magnetic field oscillations. Since BARREL X-rays are only sensitive to electrons with energy approximately above 30 keV, the X-ray count rate is expected to increase when the background magnetic field increases.

In order to separate the effect of bounce loss cone size modulation and the effect of diffusion coefficient modulation on the precipitating flux, we further compare the simulation results corresponding to three cases: 1) in the “smoothed” case, only the modulation of the chorus wave amplitude is included to calculate the diffusion coefficient and electron precipitation; 2) in the case of “modulated loss cone,” the modulation of the chorus wave amplitude is included to calculate the diffusion coefficient and the modulation of loss cone is further included to calculate the electron precipitation (the modulation of resonant energy is not included to calculate the diffusion coefficient and the resultant integral electron precipitation inside the loss cone); 3) in the case of “modulated diffusion coefficient”, both modulation of the chorus wave amplitude and modulation of the resonant energy are included to calculate the diffusion coefficient. Variation of loss cone size is not included when calculating the resultant electron precipitation using Eqs 1, 2. We calculate the ratio of the modeled precipitating flux with modulation of the equatorial loss cone size (“Modulated ${\alpha }_{LC}$”) to the precipitating flux without ambient magnetic field modulation (“Smoothed”) (Figure 6A), as well as the ratio of the precipitating flux with modulated < D_αα>_LC to the precipitating flux without modulation in <D_αα>_LC (“Smoothed”) (Figure 6B). Rae et al. (2018) showed that the percent change in precipitating flux driven by the change in the equatorial loss cone depends significantly on electron pitch angle distribution close to the loss cone. In our case, it is shown that when there is only bounce loss cone modulation (Figure 6A), the precipitating flux increases (decreases) about 10% when magnetic field increases (decreases) by 10% for electrons with a broad range of energy (10–300 keV). However, for higher energy electrons, the precipitating flux shows an opposite trend, i.e., increases when ${\alpha }_{LC}$ decreases. This is caused by the competing effects of the loss cone size and averaged flux inside the loss cone. When loss cone size increases, it is harder for these higher energy electrons to form a filled loss cone under the equilibrium between pitch angle scattering and precipitation into the atmosphere, and the averaged flux inside the loss cone is smaller, leading to a lower value of total integrated precipitation. When there is only modulation in <D_αα>_LC (Figure 6B), the change in electron precipitation ratio also depends on their energies, increasing (decreasing) by up to about 20% for electrons with energy at 30 keV and about 50% for ∼100 keV electrons when $B_0$ increases (decreases). We conclude that the magnetic field oscillation-driven modulation in <D_αα>_LC, i.e., the resonance condition in precipitating rates, are larger than the effects of modulation in loss cone size by the ambient magnetic field oscillations.

FIGURE 6

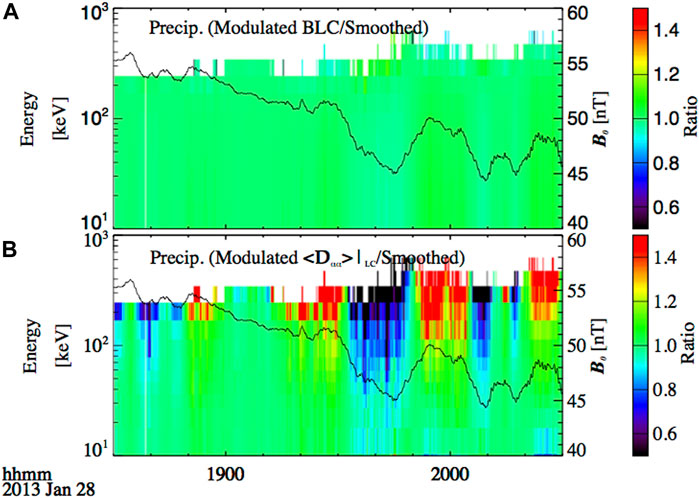
FIGURE 6. (A) Ratio of the calculated precipitating electron flux inside the loss cone with quasi-static breathing mode modulation of the equatorial loss cone size (Modulated BLC) to the precipitating flux without quasi-static breathing mode modulation (Smoothed). (B) Ratio of the calculated precipitating electron flux inside the loss cone with quasi-static breathing mode modulation of <D_αα>_LC to the precipitating flux without quasi-static breathing mode modulation (Smoothed). The superimposed black lines represent the background magnetic field strength observed by THEMIS-E.

5 Summary

We present simultaneous multi-point observations of whistler-mode chorus waves and magnetospheric oscillations on a time scale of ∼10 s min, associated with concurrent energetic electron precipitation observed through enhanced BARREL X-rays. Similar fluctuations on a time scale of ∼10 s min are observed in X-ray signatures and the compressional component of magnetic field oscillations. The spatial scale of oscillations spans from ∼9 to 12 h in MLT and from 5 to 11 in L shell. Such large-scale magnetic field oscillations, which have been suggested to play a potential role in precipitating energetic electrons by either wave amplitude, resonance energy or loss cone modulation, show high correlations with enhancement in X-rays.

We evaluate the relative role of breathing mode magnetic field oscillations in modulating the electron precipitation through modulating the minimum resonant energy, the loss cone size and the chorus wave amplitude. We show that the modulation in energetic electron precipitation is dominated by the modulation of chorus wave amplitude. However, the effects of modulation in the resonance condition due to breathing mode magnetic field oscillations cannot be neglected. The ambient magnetic field oscillation could significantly modulate the electron precipitation observed through BARREL X-ray (25–180 keV), increasing the precipitating flux by 50% when magnetic field increases by 5% by modulating the resonance condition. The modulation in the loss cone size has a much smaller effect on the electron precipitation modulation, increasing the precipitating flux by 10% when the ambient magnetic field increases by 5%.

The study examines the relative role of different mechanisms that could be responsible for the electron precipitation modulated on ULF timescales or a longer period, which is important for understanding the radiation belt electron loss. Nevertheless, multi-case or statistical studies are needed in the future to systematically evaluate the relative roles of various mechanisms in different events and regions.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

MQ: Writing–original draft. WL: Supervision, Writing–review and editing. Qianli Ma: Methodology, Writing–review and editing. X-CS: Writing–review and editing. LW: Data curation, Writing–review and editing. RM: Writing–review and editing. VA: Data curation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. NASA grants of 80NSSC20K0698, 80NSSC19K0845, 80NSSC20K0196, 80NSSC21K1312, and the NSF grant of AGS-1847818.

Acknowledgments

WL, QM, and X-CS would like to acknowledge NASA grants of 80NSSC20K0698, 80NSSC19K0845, 80NSSC20K0196, 80NSSC21K1312, and the NSF grant of AGS-1847818. We acknowledge the BARREL team developers of IDL BDAS program for use of BARREL data. We thank the NOAA National Geophysical Data Center for GOES data. We acknowledge VA for use of data from the THEMIS mission. We also acknowledge, specifically, C.W. Carlson and J. P. McFadden for use of ESA data; K.H. Glassmeier, U. Auster, and W. Baumjohann for the use of FGM data provided under the lead of the Technical University of Braunschweig. The content of this manuscript has been presented in part at EGU22, the 24th EGU General Assembly. Citation: MQ, WL, QM, X-CS: Global magnetic field oscillations on the breathing-mode timescale and their effects on energetic electron precipitation, EGU General Assembly 2022, Vienna, Austria, 23–27 May 2022, EGU22-4057, https://doi.org/10.5194/egusphere-egu22-4057, 2022.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Agapitov, O., Blum, L. W., Mozer, F. S., Bonnell, J. W., and Wygant, J. (2017). Chorus whistler wave source scales as determined from multipoint Van Allen Probe measurements. Geophys. Res. Lett. 44, 2634–2642. doi:10.1002/2017GL072701

CrossRef Full Text | Google Scholar

Angelopoulos, V. (2008). The THEMIS mission. Space Sci. Rev. 141, 5–34. doi:10.1007/s11214-008-9336-1

CrossRef Full Text | Google Scholar

Auster, H. U., Glassmeier, K. H., Magnes, W., Aydogar, O., Baumjohann, W., Constantinescu, D., et al. (2008). The THEMIS fluxgate magnetometer. Space Sci. Rev. 141, 235–264. doi:10.1007/s11214-008-9365-9

CrossRef Full Text | Google Scholar

Bonnell, J. W., Mozer, F. S., Delory, G. T., Hull, A. J., Ergun, R. E., Cully, C. M., et al. (2008). The electric field instrument (EFI) for THEMIS. Space Sci. Rev. 141, 303–341. doi:10.1007/s11214-008-9469-2

CrossRef Full Text | Google Scholar

Breneman, A. W., Halford, A., Millan, R., McCarthy, M., Fennell, J., Sample, J., et al. (2015). Global-scale coherence modulation of radiation-belt electron loss from plasmaspheric hiss. Nature 523 (7559), 193–195. doi:10.1038/nature14515

PubMed Abstract | CrossRef Full Text | Google Scholar

Breneman, A. W., Halford, A. J., Millan, R. M., Woodger, L. A., Zhang, X.-J., Sandhu, J. K., et al. (2020). Driving of outer belt electron loss by solar wind dynamic pressure structures: analysis of balloon and satellite data. J. Geophys. Res. Space Phys. 125 (12). doi:10.1029/2020ja028097

CrossRef Full Text | Google Scholar

Brito, T., Hudson, M., Kress, B., Paral, J., Halford, A., Millan, R., et al. (2015). Simulation of ULF wave-modulated radiation belt electron precipitation during the 17 March 2013 storm. J. Geophys. Res. Space Phys. 120 (5), 3444–3461. doi:10.1002/2014ja020838

CrossRef Full Text | Google Scholar

Brito, T., Woodger, L., Hudson, M., and Millan, R. (2012). Energetic radiation belt electron precipitation showing ULF modulation. Geophys. Res. Lett. 39 (22). doi:10.1029/2012gl053790

CrossRef Full Text | Google Scholar

Buchert, S. C., Fujii, R., and Glassmeier, K.-H. (1999). Ionospheric conductivity modulation in ULF pulsations. J. Geophys. Res. Space Phys. 104 (A5), 10119–10133. doi:10.1029/1998ja900180

CrossRef Full Text | Google Scholar

Capannolo, L., Li, W., Ma, Q., Chen, L., Shen, X.-C., Spence, H. E., et al. (2019a). Direct observation of subrelativistic electron precipitation potentially driven by EMIC waves. Geophys. Res. Lett. 46 (22), 12711–12721. doi:10.1029/2019gl084202

CrossRef Full Text | Google Scholar

Capannolo, L., Li, W., Ma, Q., Shen, X.-C., Zhang, X.-J., Redmon, R. J., et al. (2019b). Energetic electron precipitation: multievent analysis of its spatial extent during EMIC wave activity. J. Geophys. Res. Space Phys. 124 (4), 2466–2483. doi:10.1029/2018ja026291

CrossRef Full Text | Google Scholar

Chen, L., Thorne, R. M., Li, W., Bortnik, J., Turner, D., and Angelopoulos, V. (2012). Modulation of plasmaspheric hiss intensity by thermal plasma density structure. Geophys. Res. Lett. 39, L14103. doi:10.1029/2012GL052308

CrossRef Full Text | Google Scholar

Claudepierre, S., Hudson, M., Lotko, W., Lyon, J., and Denton, R. (2010). Solar wind driving of magnetospheric ULF waves: field line resonances driven by dynamic pressure fluctuations. J. Geophys. Res. 115, A11202. doi:10.1029/2010ja015399

CrossRef Full Text | Google Scholar

Claudepierre, S. G., Wiltberger, M., Elkington, S. R., Lotko, W., and Hudson, M. K. (2009). Magnetospheric cavity modes driven by solar wind dynamic pressure fluctuations. Geophys. Res. Lett. 36, L13101. doi:10.1029/2009gl039045

CrossRef Full Text | Google Scholar

Clilverd, M. A., Duthie, R., Hardman, R., Hendry, A. T., Rodger, C. J., Raita, T., et al. (2015). Electron precipitation from EMIC waves: a case study from 31 May 2013. J. Geophys. Res. Space Phys. 120 (5), 3618–3631. doi:10.1002/2015ja021090

CrossRef Full Text | Google Scholar

Elkington, S. R., Hudson, M. K., and Chan, A. A. (2003). Resonant acceleration and diffusion of outer zone electrons in an asymmetric geomagnetic field. J. Geophys. Res. 108, 1116. doi:10.1029/2001ja009202

CrossRef Full Text | Google Scholar

Grach, V. S., Artemyev, A. V., Demekhov, A. G., Zhang, X.-J., Bortnik, J., Angelopoulos, V., et al. (2022). Relativistic electron precipitation by EMIC waves: importance of nonlinear resonant effects. Geophys. Res. Lett. 49, e2022GL099994. doi:10.1029/2022GL099994

CrossRef Full Text | Google Scholar

Halford, A., McGregor, S., Murphy, K., Millan, R., Hudson, M., Woodger, L., et al. (2015). BARREL observations of an ICME-shock impact with the magnetosphere and the resultant radiation belt electron loss. J. Geophys. Res. Space Phys. 120 (4), 2557–2570. doi:10.1002/2014ja020873

CrossRef Full Text | Google Scholar

Heacock, R., and Hunsucker, R. (1977). A study of concurrent magnetic field and particle precipitation pulsations, 0.005 to 0.5 Hz, recorded near College, Alaska. J. Atmos. Terr. Phys. 39 (4), 487–501. doi:10.1016/0021-9169(77)90158-1

CrossRef Full Text | Google Scholar

Hendry, A. T., Rodger, C. J., and Clilverd, M. A. (2017). Evidence of sub-MeV EMIC-driven electron precipitation. Geophys. Res. Lett. 44 (3), 1210–1218. doi:10.1002/2016gl071807

CrossRef Full Text | Google Scholar

Hosokawa, K., Miyoshi, Y., Ozaki, M., Oyama, S. I., Ogawa, Y., Kurita, S., et al. (2020). Multiple time-scale beats in aurora: precise orchestration via magnetospheric chorus waves. Sci. Rep. 10, 3380. doi:10.1038/s41598-020-59642-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Hsu, T., and McPherron, R. L. (2007). A statistical study of the relation of Pi 2 and plasma flows in the tail. J. Geophys. Res. 112, A05209. doi:10.1029/2006ja011782

CrossRef Full Text | Google Scholar

Jacobs, J. A., Kato, Y., Matsushita, S., and Troitskaya, V. A. (1964). Classification of geomagnetic micropulsations. J. Geophys. Res. 69 (1), 180–181. doi:10.1029/JZ069i001p00180

CrossRef Full Text | Google Scholar

Jaynes, A., Lessard, M., Takahashi, K., Ali, A., Malaspina, D., Michell, R., et al. (2015). Correlated Pc4–5 ULF waves, whistler-mode chorus, and pulsating aurora observed by the Van Allen Probes and ground-based systems. J. Geophys. Res. Space Phys. 120 (10), 8749–8761. doi:10.1002/2015ja021380

CrossRef Full Text | Google Scholar

Kennel, C. F., and Petschek, H. E. (1966). Limit on stably trapped particle fluxes. J. Geophys. Res. 71 (1), 1–28. doi:10.1029/jz071i001p00001

CrossRef Full Text | Google Scholar

Kepko, L., and Spence, H. E. (2003). Observations of discrete, global magnetospheric oscillations directly driven by solar wind density variations. J. Geophys. Res. 108 (A6), 1257. doi:10.1029/2002JA009676

CrossRef Full Text | Google Scholar

Kepko, L., Spence, H. E., and Singer, H. J. (2002). ULF waves in the solar wind as direct drivers of magnetospheric pulsations. Geophys. Res. Lett. 29 (8). doi:10.1029/2001GL014405

CrossRef Full Text | Google Scholar

Kepko, L., and Viall, N. M. (2019). The source, significance, and magnetospheric impact of periodic density structures within stream interaction regions. J. Geophys. Res. Space Phys. 124, 7722–7743. doi:10.1029/2019JA026962

CrossRef Full Text | Google Scholar

Li, W., Bortnik, J., Thorne, R. M., Nishimura, Y., Angelopoulos, V., and Chen, L. (2011b). Modulation of whistler mode chorus waves: 2. Role of density variations. J. Geophys. Res. 116, A06206. doi:10.1029/2010ja016313

CrossRef Full Text | Google Scholar

Li, W., Shen, X.-C., Ma, Q., Capannolo, L., Shi, R., Redmon, R. J., et al. (2019). Quantification of energetic electron precipitation driven by plume whistler mode waves, plasmaspheric hiss, and exohiss. Geophys. Res. Lett. 46 (7), 3615–3624. doi:10.1029/2019gl082095

CrossRef Full Text | Google Scholar

Li, W., Thorne, R. M., Bortnik, J., Nishimura, Y., and Angelopoulos, V. (2011a). Modulation of whistler mode chorus waves: 1. Role of compressional Pc4–5 pulsations. J. Geophys. Res. 116, A06205. doi:10.1029/2010ja016312

CrossRef Full Text | Google Scholar

Li, Z., Millan, R. M., Hudson, M. K., Woodger, L. A., Smith, D. M., Chen, Y., et al. (2014). Investigation of EMIC wave scattering as the cause for the BARREL 17 January 2013 relativistic electron precipitation event: a quantitative comparison of simulation with observations. Geophys. Res. Lett. 41, 8722–8729. doi:10.1002/2014GL062273

CrossRef Full Text | Google Scholar

Liu, X., Gu, W., Xia, Z., Chen, L., and Horne, R. B. (2021). Frequency-dependent modulation of whistler-mode waves by density irregularities during the recovery phase of a geomagnetic storm. Geophys. Res. Lett. 48, e2021GL093095. doi:10.1029/2021GL093095

CrossRef Full Text | Google Scholar

Ma, Q., Connor, H. K., Zhang, X.-J., Li, W., Shen, X.-C., Gillespie, D., et al. (2020). Global survey of plasma sheet electron precipitation due to whistler mode chorus waves in Earth's magnetosphere. Geophys. Res. Lett. 47, e2020GL088798. doi:10.1029/2020GL088798

CrossRef Full Text | Google Scholar

Ma, Q., Li, W., Zhang, X.-J., Bortnik, J., Shen, X.-C., Connor, H. K., et al. (2021). Global survey of electron precipitation due to hiss waves in the Earth’s plasmasphere and plumes. J. Geophys. Res. Space Phys. 126, e2021JA029644. doi:10.1029/2021JA029644

CrossRef Full Text | Google Scholar

Mathie, R. A., and Mann, I. R. (2000). A correlation between extended intervals of ULF wave power and storm-time geosynchronous relativistic electron flux enhancements. Geophys. Res. Lett. 27 (20), 3261–3264. doi:10.1029/2000gl003822

CrossRef Full Text | Google Scholar

Millan, R. M., McCarthy, M. P., Sample, J. G., Smith, D. M., Thompson, L. D., McGaw, D. G., et al. (2013). The balloon array for RBSP relativistic electron losses (BARREL). Space Sci. Rev. 179 (1-4), 503–530. doi:10.1007/s11214-013-9971-z

CrossRef Full Text | Google Scholar

Millan, R. M., and Thorne, R. M. (2007). Review of radiation belt relativistic electron losses. J. Atmos. Sol. Terr. Phys. 69, 362–377. doi:10.1016/j.jastp.2006.06.019

CrossRef Full Text | Google Scholar

Motoba, T., Takahashi, K., Gjerloev, J., Ohtani, S., and Milling, D. (2013). The role of compressional Pc5 pulsations in modulating precipitation of energetic electrons. J. Geophys. Res. Space Phys. 118 (12), 7728–7739. doi:10.1002/2013ja018912

CrossRef Full Text | Google Scholar

Ni, B., Bortnik, J., Thorne, R. M., Ma, Q., and Chen, L. (2013). Resonant scattering and resultant pitch angle evolution of relativistic electrons by plasmaspheric hiss. J. Geophys. Res. Space Phys. 118, 7740–7751. doi:10.1002/2013JA019260

CrossRef Full Text | Google Scholar

Ni, B., Thorne, R. M., Shprits, Y. Y., and Bortnik, J. (2008). Resonant scattering of plasma sheet electrons by whistler-mode chorus: contribution to diffuse auroral precipitation. Geophys. Res. Lett. 35, L11106. doi:10.1029/2008GL034032

CrossRef Full Text | Google Scholar

Nishimura, Y., Bortnik, J., Li, W., Thorne, R. M., Chen, L., Lyons, L. R., et al. (2011). Multievent study of the correlation between pulsating aurora and whistler mode chorus emissions. J. Geophys. Res. 116, A11221. doi:10.1029/2011JA016876

CrossRef Full Text | Google Scholar

Nishimura, Y., Bortnik, J., Li, W., Thorne, R. M., Lyons, L. R., Angelopoulos, V., et al. (2010). Identifying the driver of pulsating aurora. Science 330, 81–84. doi:10.1126/science.1193186

PubMed Abstract | CrossRef Full Text | Google Scholar

Olson, J. V. (1999). Pi2 pulsations and substorm onsets: a review. J. Geophys. Res. 104 (17), 17499–17520. doi:10.1029/1999ja900086

CrossRef Full Text | Google Scholar

Pedersen, A., Lybekk, B., André, M., Eriksson, A., Masson, A., Mozer, F. S., et al. (2008). Electron density estimations derived from spacecraft potential measurements on Cluster in tenuous plasma regions. J. Geophys. Res. 113, A07S33. doi:10.1029/2007JA012636

CrossRef Full Text | Google Scholar

Qin, M., Hudson, M., Li, Z., Millan, R., Shen, X., Shprits, Y., et al. (2019). Investigating loss of relativistic electrons associated with EMIC waves at low L values on 22 june 2015. J. Geophys. Res. Space Phys. 124 (6), 4022–4036. doi:10.1029/2018ja025726

CrossRef Full Text | Google Scholar

Qin, M., Hudson, M., Millan, R., Woodger, L., and Shekhar, S. (2018). Statistical investigation of the efficiency of EMIC waves in precipitating relativistic electrons. J. Geophys. Res. Space Phys. 123 (8), 6223–6230. doi:10.1029/2018ja025419

CrossRef Full Text | Google Scholar

Qin, M., Hudson, M., Millan, R., Woodger, L., and Shen, X. (2020). Statistical dependence of EMIC wave scattering on wave and plasma parameters. J. Geophys. Res. Space Phys. 125 (4). doi:10.1029/2020ja027772

CrossRef Full Text | Google Scholar

Qin, M., Li, W., Ma, Q., Woodger, L., Millan, R., Shen, X.-C., et al. (2021). Multi-point observations of modulated whistler-mode waves and energetic electron precipitation. J. Geophys. Res. Space Phys. 126, e2021JA029505. doi:10.1029/2021ja029505

CrossRef Full Text | Google Scholar

Rae, I. J., Mann, I. R., Dent, Z. C., Milling, D. K., Donovan, E. F., and Spanswick, E. (2007). Multiple field line resonances: optical, magnetic and absorption signatures. Planet. Space Sci. 55 (6), 701–713. doi:10.1016/j.pss.2006.02.009

CrossRef Full Text | Google Scholar

Rae, J. I., Murphy, K. R., Watt, C. E., Halford, A. J., Mann, I. R., Ozeke, L. G., et al. (2018). The role of localized compressional ultra-low frequency waves in energetic electron precipitation. J. Geophys. Res. Space Phys. 123 (3), 1900–1914. doi:10.1002/2017ja024674

CrossRef Full Text | Google Scholar

Roux, A., Le Contel, O., Coillot, C., Bouabdellah, A., de la Porte, B., Alison, D., et al. (2008). The search coil magnetometer for THEMIS. Space Sci. Rev. 141, 265–275. doi:10.1007/s11214-008-9455-8

CrossRef Full Text | Google Scholar

Shen, X., Zong, Q.-G., Shi, Q., Tian, A., Sun, W., Wang, Y., et al. (2015). Magnetospheric ULF waves with increasing amplitude related to solar wind dynamic pressure changes: the time history of events and macroscale interactions during substorms (THEMIS) observations. J. Geophys. Res. Space Phys. 120, 7179–7190. doi:10.1002/2014ja020913

CrossRef Full Text | Google Scholar

Shen, X.-C., Li, W., Ma, Q., Agapitov, O., and Nishimura, Y. (2019). Statistical analysis of transverse size of lower band chorus waves using simultaneous multisatellite observations. Geophys. Res. Lett. 46, 5725–5734. doi:10.1029/2019GL083118

CrossRef Full Text | Google Scholar

Shen, X. C., Shi, Q. Q., Zong, Q., Tian, A. M., Nowada, M., Sun, W. J., et al. (2017). Dayside magnetospheric ULF wave frequency modulated by a solar wind dynamic pressure negative impulse. J. Geophys. Res. Space Phys. 122, 1658–1669. doi:10.1002/2016ja023351

CrossRef Full Text | Google Scholar

Singer, H., Matheson, L., Grubb, R., Newman, A., and Bouwer, D. (1996). “Monitoring space weather with the GOES magnetometers,” in GOES-8 and beyond (Bellingham, Washington: International Society for Optics and Photonics), 299–308. doi:10.1117/12.254077

CrossRef Full Text | Google Scholar

Spanswick, E., Donovan, E., and Baker, G. (2005). Pc5 modulation of high energy electron precipitation: particle interaction regions and scattering efficiency. Ann. Geophys. 23 (5), 1533–1542. doi:10.5194/angeo-23-1533-2005

CrossRef Full Text | Google Scholar

Summers, D., Ni, B., Meredith, N. P., Horne, R. B., Thorne, R. M., Moldwin, M. B., et al. (2008). Electron scattering by whistler-mode ELF hiss in plasmaspheric plumes. J. Geophys. Res. 113, A04219. doi:10.1029/2007ja012678

CrossRef Full Text | Google Scholar

Summers, D., and Thorne, R. M. (2003). Relativistic electron pitch-angle scattering by electromagnetic ion cyclotron waves during geomagnetic storms. J. Geophys. Res. 108 (A4), 1143. doi:10.1029/2002JA009489

CrossRef Full Text | Google Scholar

Thorne, R. M. (2010). Radiation belt dynamics: the importance of wave-particle interactions. Geophys. Res. Lett. 37, L22107. doi:10.1029/2010gl044990

CrossRef Full Text | Google Scholar

Woodger, L. A., Halford, A. J., Millan, R. M., McCarthy, M. P., Smith, D. M., Bowers, G. S., et al. (2015). A summary of the BARREL campaigns: technique for studying electron precipitation. J. Geophys. Res. Space Phys. 120, 4922–4935. doi:10.1002/2014JA020874

PubMed Abstract | CrossRef Full Text | Google Scholar

Xia, Z., Chen, L., Dai, L., Claudepierre, S. G., Chan, A. A., Soto-Chavez, A. R., et al. (2016). Modulation of chorus intensity by ULF waves deep in the inner magnetosphere. Geophys. Res. Lett. 43, 9444–9452. doi:10.1002/2016GL070280

CrossRef Full Text | Google Scholar

Yin, Z.-F., Zhou, X.-Z., Li, W., Shen, X.-C., Rankin, R., Liu, J., et al. (2023). Characteristics of electron precipitation directly driven by poloidal ULF waves. J. Geophys. Res. Space Phys. 128, e2022JA031163. doi:10.1029/2022JA031163

CrossRef Full Text | Google Scholar

Zhang, X.-J., Mourenas, D., Artemyev, A. V., Angelopoulos, V., and Sauvaud, J.-A. (2019). Precipitation of MeV and sub-MeV electrons due to combined effects of EMIC and ULF waves. J. Geophys. Res. Space Phys. 124, 7923–7935. doi:10.1029/2019ja026566

CrossRef Full Text | Google Scholar

Zhang, X.-J., Mourenas, D., Shen, X.-C., Qin, M., Artemyev, A. V., Ma, Q., et al. (2021). Dependence of relativistic electron precipitation in the ionosphere on EMIC wave minimum resonant energy at the conjugate equator. J. Geophys. Res. 126 (5), e2021JA029193. doi:10.1029/2021ja029193

CrossRef Full Text | Google Scholar

Zhou, C., Li, W., Thorne, R. M., Bortnik, J., Ma, Q., An, X., et al. (2015). Excitation of dayside chorus waves due to magnetic field line compression in response to interplanetary shocks. J. Geophys. Res. Space Phys. 120, 8327–8338. doi:10.1002/2015JA021530

CrossRef Full Text | Google Scholar