Ultra-low-mass and small-radius white dwarfs made of heavy elements

Seven possible ultra-low-mass and small-radius white dwarfs have been recently identified, with masses ranging from ∼0.02 M_⊙ to ∼0.08 M_⊙ and radii ranging from ∼ 4,270 km to 10670 km. The mass–radius measurements of these white dwarfs pose challenges to traditional white dwarf models, assuming they are mostly made of nuclei lighter than ⁵⁶Fe. In this work, we consider the possibility that those white dwarfs are made of heavier elements. Due to the small charge-to-mass ratios in heavy elements, the electron number density in white dwarf matter is effectively reduced, which reduces the pressure with additional contributions of lattice energy and electron polarization corrections. This consequently leads to white dwarfs with much smaller masses and radii, which coincide with the seven ultra-low-mass and small-radius white dwarfs. The mass of the most massive white dwarfs is effectively reduced and could possibly account for the sub-Chandrasekhar progenitors in underluminous Type Ia supernovae. The corresponding equation of state and matter contents of dense stellar matter with and without reaching the cold-catalyzed ground state are presented, which are obtained using the latest Atomic Mass Evaluation (AME 2020). Further observations are necessary to unveil the actual matter contents in those white dwarfs via, e.g., spectroscopy, asteroseismology, and the discoveries of other ultra-low-mass and small-radius white dwarfs.

1 Introduction

White dwarfs represent the final destiny of the vast majority of stars, which may reach a temperature of ∼100 eV and a density of $\sim 10^6$ g/cm³ in their centers (Saumon et al., 2022). The matter contents of typical white dwarfs are ¹²C and ¹⁶O, covered by a thin envelope of ⁴He (and ¹H, if not burned entirely). If the progenitor star approaches the 10M_⊙ limit, white dwarfs are thought to be made of ¹⁶O and ²⁰Ne (Siess, L., 2007); however, He white dwarfs are also possible if the progenitors are of very low mass and in a binary system (Iben and Livio, 1993; Marsh et al., 1995). As a white dwarf slowly cools down, a crystallized core will be formed, releasing latent heat that delays the cooling process (Tremblay et al., 2019). Most white dwarfs are expected to go through at least one pulsation phase during their evolution, displaying periodic variations in their brightness that arise from global oscillations (Fontaine and Brassard, 2008; Córsico et al., 2019). Additionally, various oscillation modes can be excited during the late inspiral or merger of white dwarf binaries, which may emit gravitational waves that are detectable for future space-borne gravitational wave detectors (Tang and Lin, 2023).

Combined with the measurements of the distance and surface temperature T_eff of a white dwarf (Blouin et al., 2019), its radius R can be inferred according to the observational flux. The surface gravity of a white dwarf can also be measured according to the gravitational redshift of the spectrum lines from the atmosphere (Fontaine et al., 2001; Gentile Fusillo et al., 2018; Chandra et al., 2020), which can be used to fix the mass with additional information on its radius. Throughout the available data on the masses and radii of white dwarfs in the Montreal White Dwarf Database (MWDD; Dufour et al., 2017), as indicated in Table 1, seven ultra-low-mass and small-radius white dwarfs have been identified with masses ranging from ∼0.02 M_⊙ to ∼0.08 M_⊙ and radii ranging from ∼ 4,270 km to 10,670 km (Kurban et al., 2022), which deviate from the M–R relation of typical white dwarfs. It should be noted that no spectral lines have been identified in those stars, and the surface gravity needs to be inferred theoretically (Blouin et al., 2019), which results in large uncertainties. Further confirmation of those white dwarfs may pose challenges to traditional white dwarf models, which are considered to be made of light elements such as ¹²C, ¹⁶O, ⁴He, and ²⁰Ne. Consequently, traditional white dwarf models predict much larger radii than those indicated in Table 1. In addition to these anomalous white dwarfs, there are underluminous Type Ia supernovae whose progenitor masses appear to be well below 1.4 M_⊙ (Blondin et al., 2017; Flörs et al., 2019), which again challenges the large Chandrasekhar mass limit (∼1.4 M_⊙) predicted by traditional white dwarf models.

TABLE 1

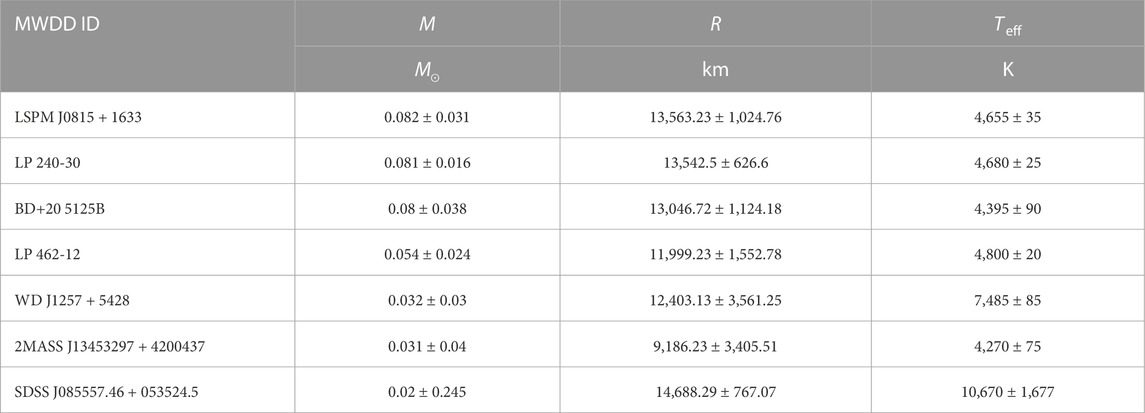
TABLE 1. Masses, radii, and surface temperatures of seven ultra-low-mass and small-radius white dwarfs (Rebassa-Mansergas et al., 2016; Blouin et al., 2019; Kurban et al., 2022).

To understand the physical origin of such low-mass and small-radius white dwarfs, possible candidates made of various exotic materials were considered. For example, Kurban et al. (2022) proposed that they are, in fact, strange dwarfs comprised of a strange quark matter (SQM) core and a thick normal matter crust (Glendenning et al., 1995). It was suggested that the intermittent fractional collapses of the crust induced by the refilling of materials accreted from its low-mass companion lead to repeating fast radio bursts (Geng et al., 2021). Additionally, there are possibilities that these white dwarfs may be strangelet dwarfs (Alford et al., 2012) or ud quark matter (udQM) dwarfs (Wang et al., 2021a; Xia et al., 2022) comprised of strangelets or udQM nuggets immersed in a sea of electrons.

In this work, we consider the possibility that those low-mass and small-radius white dwarfs are made of heavy elements such as ⁵⁶Fe, ⁶²Ni, ¹⁰⁸Pd, and ²⁰⁸Pb, which significantly reduces the mass and radius of a white dwarf in comparison with those made of light elements. In fact, there exist extensive observations of (DZ) white dwarfs contaminated by heavy elements, which were identified by the characteristic spectral lines (Farihi, 2016; Zuckerman and Young, 2018; Coutu et al., 2019). It is, thus, reasonable to consider the possibility that white dwarfs can also be made entirely of heavy elements, where the shell of light elements is either stripped by its companion object in a binary system or by a nuclear explosion, e.g., in a thermonuclear electron-capture supernova event (Tauris and Janka, 2019).

The remainder of this paper is organized as follows. Section 2 presents the theoretical framework for obtaining the properties of white dwarf matter under various constraints on the mass numbers of nuclei, including either light or heavy elements. The obtained equation of state (EOS) and matter contents that minimize the energy density of cold white dwarf matter are presented in Section 3, while the corresponding white dwarf structures are investigated and compared with the low-mass and small-radius white dwarfs. Section 4 presents our conclusion.

2 Theoretical framework

For cold white dwarf matter comprised of crystallized nuclei immersed in a sea of electrons, the energy density can be divided into three parts (Chamel, 2020), i.e.,

$E=\frac{M_N{n}_e}{Z}+\left(1+\frac{\alpha }{2\pi }\right)E_e+K_M\alpha {\left(\frac{4\pi n_e^4{Z}^2}{3}\right)}^{1/3}\sigma \left(Z\right),(1)$

where n_e is the average electron number density and α = 1/137.03599911 is the fine structure constant. The first term in Eq. 1 represents the energy density of nuclei, with M_N(Z, A) being the mass of a nucleus with Z protons and A nucleons, which is determined by

$M_N\left(Z,A\right)=M_A\left(Z,A\right)-Z{m}_e+B_e\left(Z\right),(2)$

where M_A(Z, A) is the measured atomic mass (AME 2020; Huang et al., 2021; Wang et al., 2021b), m_e = 510998.95 eV is the electron mass, and $B_e(Z)=\left(14.4381Z^{2.39}+1.55468\times 10^{-6}{Z}^{5.35}\right)$ eV is the electron binding energy (Lunney et al., 2003). The baryon number density is then given by n_b = n_e/f_Z with the charge-to-mass ratio f_Z = Z/A. The second term in Eq. 1 corresponds to the energy density of electrons, including exchange contributions. E_e is the energy density of free electron gas, which is given by

$E_e=\frac{{m_e}^4}{8{\pi }^2}\left[x_e\left(2x_e^2+1\right)\sqrt{x_e^2+1}-\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{s}\mathrm{h}\left(x_e\right)\right],(3)$

with $x_e\equiv {(3{\pi }^2{n}_e)}^{1/3}/m_e$. The third term in Eq. 1 represents the lattice energy density, including electron polarization corrections. For a body-centered cubic lattice, the Madelung constant is K_M = −0.895929255682 (Baiko et al., 2001), and the function σ(Z) (Potekhin and Chabrier, 2000; Chamel, 2020) is given by

$\sigma \left(Z\right)=1+\frac{12^{4/3}{Z}^{2/3}\alpha }{35{\pi }^{1/3}}\left(1-\frac{1.1866}{Z^{0.267}}+\frac{0.27}{Z}\right).(4)$

For nuclei to stably exist inside white dwarfs, they should be stable against electron capture and β-decay reactions, i.e.,

${}_Z{}^{A}X+e^{-}\to {}_{Z-1}{}^{A}X+{\nu }_e;(5)$

${}_Z{}^{A}X\to {}_{Z+1}{}^{A}X+e^{-}+{\bar{\nu }}_e.(6)$

This indicates the following stability condition, i.e.,

$E\left(Z\pm 1,A,n_{\text{b}}\right)-E\left(Z,A,n_{\text{b}}\right)>0,(7)$

with the energy density E fixed by Eq. 1. It should be noted that the electron number density changes to n_e(Z ± 1)/Z as we vary the charge number of a nucleus from Z to Z ± 1. A vast number of nuclei species fulfilling the stability condition (7) are obtained, which could all stably exist inside white dwarfs if there are no other decay channels. At a fixed baryon number density n_b, we search for the nucleus that minimizes the energy density of white dwarf matter under three different considerations, i.e.,

1. Massive white dwarfs comprised of light elements (A ≤ 16, 24, 28)

2. Catalyzed ones with all possible nuclear species

3. Ultra-low-mass and small-radius white dwarfs made of heavy elements (A ≥ 62, 108, 208)

Once the nucleus is fixed, the energy density can then be obtained using Eq. 1. A similar procedure is carried out in a vast density range with n_b ≈ 10^–13–10⁻⁴ fm⁻³. At larger densities, the nucleus becomes too neutron-rich, causing neutrons to start dripping out and forming a neutron gas, a phenomenon beyond the scope of the current study. According to basic thermodynamic relations, the pressure of white dwarf matter is then determined by

$P=\left(1+\frac{\alpha }{2\pi }\right)P_e+K_M\alpha {\left(\frac{4\pi n_e^4{Z}^2}{3^4}\right)}^{1/3}\sigma \left(Z\right),(8)$

with $P_e=m_e\sqrt{x_e^2+1}{n}_e-E_e$.

At smaller densities with pressure P ≲ 0.4P_e ≈ 10^–17 MeV/fm³, nuclei are not fully ionized as few electrons start to bind to them. In such cases, the EOS predicted by Eqs 1, 8 is no longer valid. We follow the treatment outlined by Baym et al. (1971) and employ the results obtained by Feynman et al. (1949), where the pressure of white dwarf matter now becomes

$P=\frac{3^{2/3}{\pi }^{4/3}}{5m_e}{\left[f\left(Z,n_e\right)n_e\right]}^{5/3}.(9)$

It should be noted that a dampening factor f(Z, n_e) is introduced, where Eq. 9 represents the pressure of non-interacting electrons in the non-relativistic limit when f = 1. The exact value of f(Z, n_e) is determined by interpolating the results presented in Figure 1 of the work of Feynman et al. (1949).

FIGURE 1

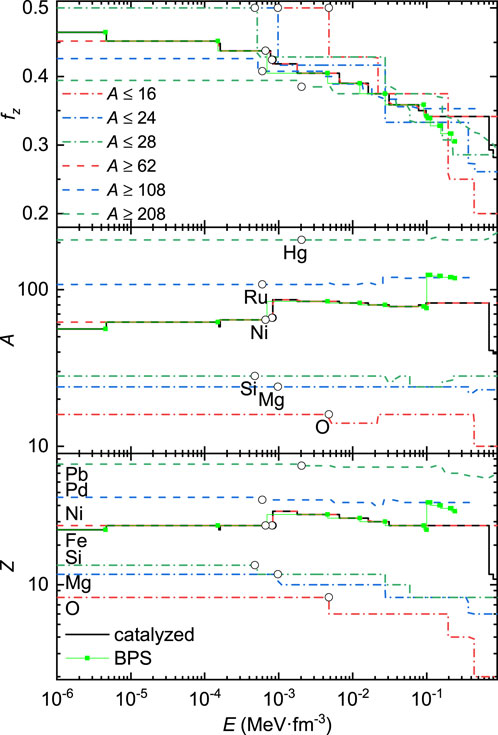
FIGURE 1. Proton number Z, mass number A, and charge-to-mass ratio f_Z = Z/A of nuclei in white dwarf matter under different considerations, using the latest Atomic Mass Evaluation (AME 2020; Huang et al., 2021; Wang et al., 2021b). For comparison, the nuclear species from the BPS EOS is presented (Baym et al., 1971). The open circles indicate the central densities of the most massive white dwarfs, corresponding to the values in the sixth column of Table 2.

3 Results and discussion

In Figure 1, we present the proton number Z, mass number A, and charge-to-mass ratio f_Z = Z/A of nuclei in white dwarf matter as functions of energy density, where various constraints on the mass numbers of nuclei are adopted with A ≤ 16, 24, 28 or A ≥ 62, 108, 208. Similar to the BPS model (Baym et al., 1971), the catalyzed one indicated by the black solid curve is obtained by searching for all possible nuclear species without any restriction on A, which generally agrees with the BPS EOS at E ≲ 0.1 MeV/fm³. The latest data from the Atomic Mass Evaluation (AME 2020) have been adopted in our calculations (Wang et al., 2021b; Huang et al., 2021). It is found that the nuclear species remains unchanged at E ≲ 3 × 10⁻⁴ MeV/fm³ except for the catalyzed one, which covers most of the density range in white dwarfs. As indicated by the symbols in the bottom panel of Figure 1 and in the second column of Table 2, at small densities, the nuclei ¹⁶O, ²⁴Mg, ²⁸Si, ⁵⁶Fe, ⁶²Ni, ¹⁰⁸Pd, and ²⁰⁸Pb minimize the energy density of white dwarf matter under various constraints on A. The corresponding charge-to-mass ratio f_Z starts to decrease with A at A ≥ 62, which reduces the electron number density with n_e = f_Zn_b. As will be shown later, this will consequently reduce the pressure and make white dwarfs more compact. At larger densities, the nuclear species starts to change, which typically takes place at the center of the most massive white dwarfs (indicated by the open circles in Figure 1), except for the catalyzed one. If we further increase the density, the nuclear species continues to change, which decreases the charge-to-mass ratio f_Z.

TABLE 2

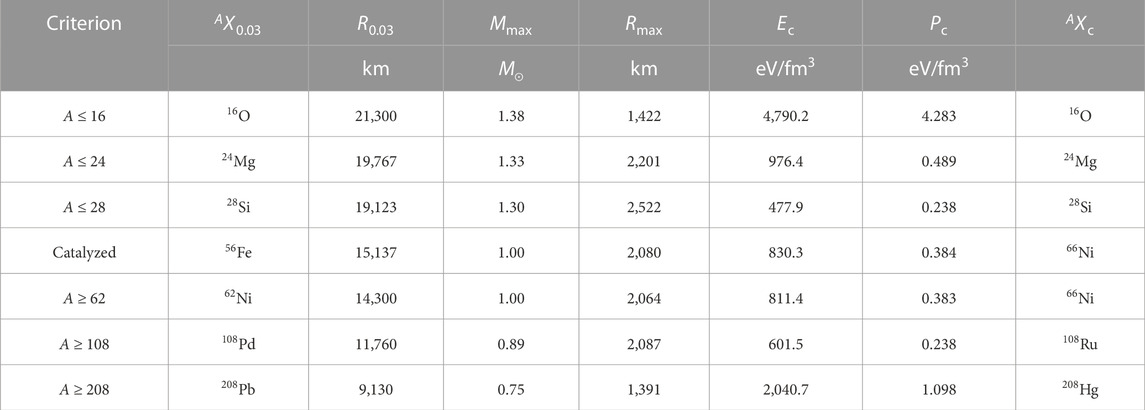
TABLE 2. Summary of white dwarf properties obtained under different constraints on nuclear mass numbers. The radii (R_0.03) of 0.03M_⊙ white dwarfs and their matter contents (^AX_0.03) are indicated in the third and second columns. The masses (M_max) and radii (R_max) of the most massive white dwarfs are presented, along with the energy density E_c, pressure P_c, and nuclei species (^AX_c) at the center of these white dwarfs.

Based on the nuclear species indicated in Figure 1, the pressure of white dwarf matter can then be fixed using Eqs 8, 9. The corresponding EOSs under various constraints are then presented in Figure 2. At E ≳ 10^–4 MeV/fm³, the EOSs of white dwarf matter generally coincide with each other, while there are slight variations due to the sudden changes in nuclear species causing mild first-order phase transitions. At E ≲ 10^–4 MeV/fm³, the effects of chemical composition become evident, and the pressure is effectively reduced if white dwarf matter is made of heavy elements. This is attributed to the reduction in the charge-to-mass ratio f_Z at A ≥ 62, which decreases the electron number density and, consequently, the pressure. The pressure reduction becomes more evident at smaller densities, where the variations in lattice energy density and electron polarization corrections become sizable even for cases with the same f_Z value.

FIGURE 2

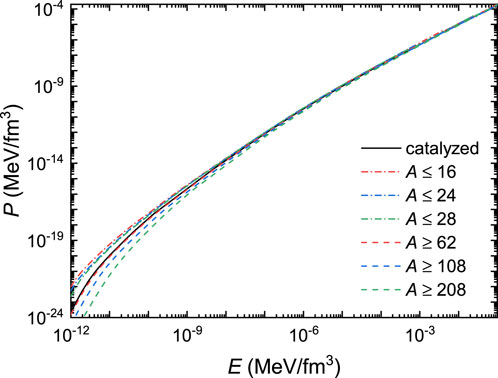
FIGURE 2. Pressure of white dwarf matter as a function of energy density, where the corresponding nuclear species is indicated in Fig. 1.

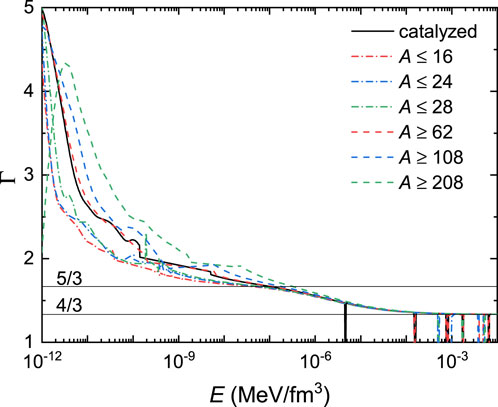
To better illustrate the effects of heavy elements on the EOSs of white dwarf matter, in Figure 3, we present the corresponding adiabatic index as a function of energy density, which is determined by

$\mathrm{\Gamma }=\frac{\text{d}\ln P}{\text{d}\ln n_{\text{b}}}.(10)$

FIGURE 3

FIGURE 3. Adiabatic index of white dwarf matter as a function of energy density.

For electron gas in the non-relativistic limit, one expects Γ = 5/3, which turns into 4/3 in the extreme relativistic limit with a softer EOS. This is indeed the case for white dwarf matter at E ≳ 10^–4 MeV/fm³, where the EOSs in Figure 2 generally coincide with each other with Γ = 4/3. Nevertheless, there are few exceptions during the first-order phase transitions with sudden changes in nuclear species, which reduces the adiabatic index to Γ = 0. At smaller densities, however, Γ easily exceeds the non-relativistic limit of 5/3. In particular, as density decreases, Γ quickly increases and becomes larger if white dwarf matter is made of heavy elements with a larger A. This can be attributed to the additional contributions of lattice energy and electron polarization corrections, which are sizable at small densities.

Based on the EOSs presented in Figure 2, the structures of white dwarfs are fixed by solving the TOV equation.

$\frac{\text{d}P}{\text{d}r}=-\frac{GmE}{r^2}\frac{\left(1+P/E\right)\left(1+4\pi r^{3}P/m\right)}{1-2Gm/r},(11)$

$\frac{\text{d}m}{\text{d}r}=4\pi E{r}^2,(12)$

where G = 6.707 × 10⁻⁴⁵ MeV⁻² is the gravitational constant. In Figure 4, we present the mass–radius relations of white dwarfs under various constraints on their matter contents. Typical white dwarfs with M > 0.5M_⊙ (Bond et al., 2017) and seven ultra-low-mass and small-radius white dwarfs are indicated by the dots with the corresponding error bars (Kurban et al., 2022). It is evident that the typical white dwarfs are made of light elements with A ≤ 28, where the mass and radius could become slightly larger if lighter elements (¹²C, ⁴He, and ¹H), magnetic field, and temperature effects are accounted for. However, compared with the seven ultra-low-mass and small-radius white dwarfs, the radii of these normal white dwarfs are too large. To resolve this, it was suggested that the low-mass and small-radius white dwarfs are made of exotic matter such as SQM or udQM. As illustrated by Kurban et al. (2022), a strange dwarf with a mass similar to that of a normal white dwarf could harbor an extremely dense SQM core, resulting in a smaller radius that coincides with that of the seven white dwarfs. For absolute stable SQM or udQM with sufficiently small surface tension, it was shown that strangelets or udQM nuggets of a certain size can be more stable than others (Heiselberg, 1993); consequently, the surface of a quark star fragments into a crystalline crust comprised of strangelets or udQM nuggets immersed in a sea of electrons (Jaikumar et al., 2006). Further investigations have revealed that the crustal material could also form strangelet (Alford et al., 2012) or udQM dwarfs (Wang et al., 2021a; Xia et al., 2022), where the radii are typically smaller than those of normal white dwarfs, and can, thus, accommodate the seven small-radius white dwarfs.

FIGURE 4

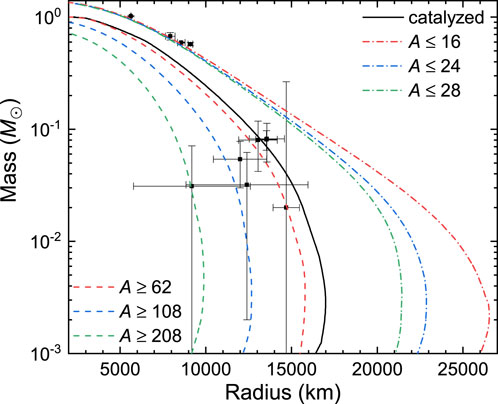
FIGURE 4. Mass–radius relations of white dwarfs obtained with the EOSs presented in Figure 2. The dots with M >0.5M_⊙ represent four typical white dwarfs, namely, Sirius B, Stein 2051 B, Procyon B, and 40 Eri B (Bond et al., 2017), while the seven dots below correspond to the ultra-low-mass and small-radius white dwarfs, namely, LSPM J0815 + 1633, LP 240-30, BD+20 5125B, LP 462-12, WD J1257 + 5428, 2MASS J13453297 + 4200437, and SDSS J085557.46 + 053524.5 (Kurban et al., 2022).

In this work, we resort to the more familiar explanation that the white dwarfs are made of heavier elements. As indicated in Figure 4, the masses and radii of white dwarfs decrease significantly if they are made of heavy elements, which coincide with the observed seven ultra-low-mass and small-radius white dwarfs (Kurban et al., 2022). In particular, to accommodate the extreme small radius of 2MASS J13453297 + 4200437, the white dwarf should be comprised of elements with mass numbers A ≥ 108. Similar cases are observed for other small-radius white dwarfs LSPM J0815 + 1633, LP 240-30, BD+20 5125B, LP 462-12, WD J1257 + 5428, and SDSS J085557.46 + 053524.5, whose radii are too small if they are made of light elements with A ≤ 28. This is attributed to the reduction in pressure at small densities if white dwarfs are made of heavy elements, causing them to become more compact than typical white dwarfs. The maximum mass of white dwarfs is also reduced, reaching 0.75 M_⊙ if they are made of heavy elements, which could be the progenitor for underluminous Type Ia supernovae.

To show this explicitly, in Figure 5, we present the internal energy density profiles of 0.03M_⊙ white dwarfs, where the horizontal axis corresponds to the total mass m(r) enclosed in a sphere of radius r in Eq. 12. The corresponding nuclear species that makes up the white dwarf and its radius are indicated in the second and third columns of Table 2. It is evident that the energy density of white dwarf matter increases with the nuclear mass number A, leading to more compact white dwarfs with smaller radii.

FIGURE 5

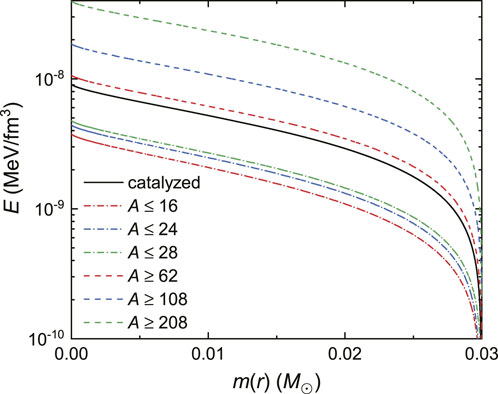
FIGURE 5. Energy density profiles of 0.03M_⊙ white dwarfs as a function of the total mass m(r) enclosed in a sphere of radius r in Eq. 12, where the corresponding nuclear species and radius are indicated in the second and third columns of Table 2.

Finally, it is worth mentioning that we considered only ideal scenarios in which white dwarfs are made entirely of elements with fixed upper or lower limits on the mass number A, while in reality, we expect they are comprised of elements with various mass numbers and fractions. In that case, the EOS can be obtained as a combination of the EOSs indicated in Figure 2, connected at certain critical pressures, where the corresponding mass–radius relation lies between those indicated in Figure 4. Meanwhile, the possible existence of a strong magnetic field could alter significantly the mass–radius relations of white dwarfs (Deb et al., 2022), while the temperature effects are expected to have a minor impact.

4 Conclusion

The recent observations of the seven possible ultra-low-mass and small-radius white dwarfs, namely, LSPM J0815 + 1633, LP 240-30, BD+20 5125B, LP 462-12, WD J1257 + 5428, 2MASS J13453297 + 4200437, and SDSS J085557.46 + 053524.5, have posed challenges to traditional white dwarf models assuming that they are mostly made of nuclei lighter than ⁵⁶Fe. To resolve this, previous investigations suggest that they may be made of exotic matter such as SQM or udQM (Alford et al., 2012; Wang et al., 2021a; Kurban et al., 2022; Xia et al., 2022). In this work, we consider the possibility that these white dwarfs are made of heavier elements, which effectively reduces the pressure and leads to white dwarfs with much smaller masses and radii. In such cases, we can accommodate the low-mass and small-radius white dwarfs without introducing any exotic matter. The maximum mass of white dwarfs is also reduced if they are made of heavier elements, which could possibly account for the sub-Chandrasekhar progenitors in underluminous Type Ia supernovae.

It should be noted that we assumed white dwarfs are made entirely of elements with fixed upper or lower limits on the mass numbers, where the predicted radii should be viewed as lower limits for white dwarfs containing lighter elements. Additional theoretical uncertainties are also expected under the influence of a strong magnetic field and high temperatures. These issues should be considered in our future study, where their impacts on various properties of white dwarfs aside from mass–radius relations need to be addressed. Meanwhile, the uncertainty in the mass and radius measurements of the seven anomalous white dwarfs is still large, which may originate from possible unresolved binary systems or extrapolation errors at small masses. Further observations are, thus, necessary to unveil the actual structures and matter contents in those white dwarfs via, e.g., their cooling processes (Tremblay et al., 2019), characteristic spectral lines emitted by the heavy elements (Farihi, 2016; Zuckerman and Young, 2018; Coutu et al., 2019), pulsation that arises from their global oscillations (Fontaine and Brassard, 2008; Córsico et al., 2019), gravitational waves excited during the late inspiral or merger of white dwarf binaries (Tang and Lin, 2023), and searching for other white dwarfs with similar low-mass and small-radius characteristics (Kurban et al., 2022).

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

C-JX: conceptualization, funding acquisition, investigation, and writing–original draft. Y-FH: conceptualization, funding acquisition, and writing–review and editing. H-BL: conceptualization, validation, and writing–review and editing. LS: funding acquisition, investigation, and writing–review and editing. R-XX: conceptualization, funding acquisition, and writing–review and editing.

Funding

The authors declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China (Grant Nos. 12275234, 12342027, 12233002, and 12041306), the National SKA Program of China (Grant Nos. 2020SKA0120300 and 2020SKA0120100), and the National Key R&D Program of China (Grant No. 2021YFA0718500).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alford, M. G., Han, S., and Reddy, S. (2012). Strangelet dwarfs. J. Phys. G. 39, 065201. doi:10.1088/0954-3899/39/6/065201

CrossRef Full Text | Google Scholar

Baiko, D. A., Potekhin, A. Y., and Yakovlev, D. G. (2001). Thermodynamic functions of harmonic coulomb crystals. Phys. Rev. E 64, 057402. doi:10.1103/PhysRevE.64.057402

PubMed Abstract | CrossRef Full Text | Google Scholar

Baym, G., Pethick, C., and Sutherland, P. (1971). The ground state of matter at high densities: equation of state and stellar models. Astrophys. J. 170, 299. doi:10.1086/151216

CrossRef Full Text | Google Scholar

Blondin, S., Dessart, L., and Hillier, D. J. (2017). The detonation of a sub-Chandrasekhar-mass white dwarf at the origin of the low-luminosity Type Ia supernova 1999by. Mon. Not. R. Astron. Soc. 474, 3931–3953. doi:10.1093/mnras/stx3058

CrossRef Full Text | Google Scholar

Blouin, S., Dufour, P., Thibeault, C., and Allard, N. F. (2019). A new generation of cool white dwarf atmosphere models. iv. revisiting the spectral evolution of cool white dwarfs. Astrophys. J. 878, 63. doi:10.3847/1538-4357/ab1f82

CrossRef Full Text | Google Scholar

Bond, H. E., Bergeron, P., and Bédard, A. (2017). Astrophysical implications of a new dynamical mass for the nearby white dwarf 40 eridani b. Astrophys. J. 848, 16. doi:10.3847/1538-4357/aa8a63

CrossRef Full Text | Google Scholar

Chamel, N. (2020). Analytical determination of the structure of the outer crust of a cold nonaccreted neutron star. Phys. Rev. C 101, 032801. doi:10.1103/PhysRevC.101.032801

CrossRef Full Text | Google Scholar

Chandra, V., Hwang, H.-C., Zakamska, N. L., and Cheng, S. (2020). A gravitational redshift measurement of the white dwarf mass-radius relation. Astrophys. J. 899, 146. doi:10.3847/1538-4357/aba8a2

CrossRef Full Text | Google Scholar

Córsico, A. H., Althaus, L. G., Miller Bertolami, M. M., and Kepler, S. O. (2019). Pulsating white dwarfs: new insights. Astron. Astrophys. Rev. 27, 7. doi:10.1007/s00159-019-0118-4

CrossRef Full Text | Google Scholar

Coutu, S., Dufour, P., Bergeron, P., Blouin, S., Loranger, E., Allard, N. F., et al. (2019). Analysis of helium-rich white dwarfs polluted by heavy elements in the gaia era. Astrophys. J. 885, 74. doi:10.3847/1538-4357/ab46b9

CrossRef Full Text | Google Scholar

Deb, D., Mukhopadhyay, B., and Weber, F. (2022). Anisotropic magnetized white dwarfs: unifying under- and overluminous peculiar and standard type ia supernovae. Astrophys. J. 926, 66. doi:10.3847/1538-4357/ac410b

CrossRef Full Text | Google Scholar

Dufour, P., Blouin, S., Coutu, S., Fortin-Archambault, M., Thibeault, C., Bergeron, P., et al. (2017). “The Montreal White dwarf Database: a tool for the community,” in 20th European white dwarf workshop of astronomical society of the pacific conference series. Editors P. E. Tremblay, B. Gaensicke, and T. Marsh, 509, 3. doi:10.48550/arXiv.1610.00986

CrossRef Full Text | Google Scholar

Farihi, J. (2016). Circumstellar debris and pollution at white dwarf stars. New Astron. Rev. 71, 9–34. doi:10.1016/j.newar.2016.03.001

CrossRef Full Text | Google Scholar

Feynman, R. P., Metropolis, N., and Teller, E. (1949). Equations of state of elements based on the generalized fermi-thomas theory. Phys. Rev. 75, 1561–1573. doi:10.1103/PhysRev.75.1561

CrossRef Full Text | Google Scholar

Flörs, A., Spyromilio, J., Taubenberger, S., Blondin, S., Cartier, R., Leibundgut, B., et al. (2019). Sub-Chandrasekhar progenitors favoured for Type Ia supernovae: evidence from late-time spectroscopy. Mon. Not. R. Astron. Soc. 491, 2902–2918. doi:10.1093/mnras/stz3013

CrossRef Full Text | Google Scholar

Fontaine, G., and Brassard, P. (2008). The pulsating white dwarf stars. Publ. Astron. Soc. Pac. 120, 1043–1096. doi:10.1086/592788

CrossRef Full Text | Google Scholar

Fontaine, G., Brassard, P., and Bergeron, P. (2001). The potential of white dwarf cosmochronology. Publ. Astron. Soc. Pac. 113, 409–435. doi:10.1086/319535

CrossRef Full Text | Google Scholar

Geng, J., Li, B., and Huang, Y. (2021). Repeating fast radio bursts from collapses of the crust of a strange star. Innovation 2, 100152. doi:10.1016/j.xinn.2021.100152

PubMed Abstract | CrossRef Full Text | Google Scholar

Gentile Fusillo, N. P., Tremblay, P.-E., Gänsicke, B. T., Manser, C. J., Cunningham, T., Cukanovaite, E., et al. (2018). A Gaia Data Release 2 catalogue of white dwarfs and a comparison with SDSS. Mon. Not. R. Astron. Soc. 482, 4570–4591. doi:10.1093/mnras/sty3016

CrossRef Full Text | Google Scholar

Glendenning, N. K., Kettner, C., and Weber, F. (1995). Possible new class of dense white dwarfs. Phys. Rev. Lett. 74, 3519–3522. doi:10.1103/PhysRevLett.74.3519

PubMed Abstract | CrossRef Full Text | Google Scholar

Heiselberg, H. (1993). Screening in quark droplets. Phys. Rev. D. 48, 1418–1423. doi:10.1103/PhysRevD.48.1418

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, W., Wang, M., Kondev, F., Audi, G., and Naimi, S. (2021). The ame 2020 atomic mass evaluation (i). evaluation of input data, and adjustment procedures. Chin. Phys. C 45, 030002. doi:10.1088/1674-1137/abddb0

CrossRef Full Text | Google Scholar

Iben, I., and Livio, M. (1993). Common envelopes in binary star evolution. Publ. Astron. Soc. Pac. 105, 1373. doi:10.1086/133321

CrossRef Full Text | Google Scholar

Jaikumar, P., Reddy, S., and Steiner, A. W. (2006). Strange star surface: a crust with nuggets. Phys. Rev. Lett. 96, 041101. doi:10.1103/PhysRevLett.96.041101

PubMed Abstract | CrossRef Full Text | Google Scholar

Kurban, A., Huang, Y.-F., Geng, J.-J., and Zong, H.-S. (2022). Searching for strange quark matter objects among white dwarfs. Phys. Lett. B 832, 137204. doi:10.1016/j.physletb.2022.137204

CrossRef Full Text | Google Scholar

Lunney, D., Pearson, J. M., and Thibault, C. (2003). Recent trends in the determination of nuclear masses. Rev. Mod. Phys. 75, 1021–1082. doi:10.1103/RevModPhys.75.1021

CrossRef Full Text | Google Scholar

Marsh, T. R., Dhillon, V. S., and Duck, S. R. (1995). Low-mass white dwarfs need friends: five new double-degenerate close binary stars. Mon. Not. R. Astron. Soc. 275, 828–840. doi:10.1093/mnras/275.3.828

CrossRef Full Text | Google Scholar

Potekhin, A. Y., and Chabrier, G. (2000). Equation of state of fully ionized electron-ion plasmas. ii. extension to relativistic densities and to the solid phase. Phys. Rev. E 62, 8554–8563. doi:10.1103/PhysRevE.62.8554

PubMed Abstract | CrossRef Full Text | Google Scholar

Rebassa-Mansergas, A., Ren, J. J., Parsons, S. G., Gänsicke, B. T., Schreiber, M. R., García-Berro, E., et al. (2016). The SDSS spectroscopic catalogue of white dwarf-main-sequence binaries: new identifications from DR 9-12. Mon. Not. R. Astron. Soc. 458, 3808–3819. doi:10.1093/mnras/stw554

CrossRef Full Text | Google Scholar

Saumon, D., Blouin, S., and Tremblay, P.-E. (2022). Current challenges in the physics of white dwarf stars. Phys. Rep. 988, 1–63. doi:10.1016/j.physrep.2022.09.001

CrossRef Full Text | Google Scholar

Siess, L. (2007). Evolution of massive AGB stars: II. model properties at non-solar metallicity and the fate of Super-AGB stars. Astron. Astrophys. 476, 893–909. doi:10.1051/0004-6361:20078132

CrossRef Full Text | Google Scholar

Tang, Y.-T., and Lin, L.-M. (2023). Oscillations and tidal deformations of crystallized white dwarfs. Mon. Not. R. Astron. Soc. 521, 926–936. doi:10.1093/mnras/stad634

CrossRef Full Text | Google Scholar

Tauris, T. M., and Janka, H.-T. (2019). J0453+1559: a neutron star-white dwarf binary from a thermonuclear electron-capture supernova? Astrophys. J. Lett. 886, L20. doi:10.3847/2041-8213/ab5642

CrossRef Full Text | Google Scholar

Tremblay, P.-E., Fontaine, G., Gentile Fusillo, N. P., Dunlap, B. H., Gänsicke, B. T., Hollands, M. A., et al. (2019). Core crystallization and pile-up in the cooling sequence of evolving white dwarfs. Nature 565, 202–205. doi:10.1038/s41586-018-0791-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, L., Hu, J., Xia, C.-J., Xu, J.-F., Peng, G.-X., and Xu, R.-X. (2021a). Stable up-down quark matter nuggets, quark star crusts, and a new family of white dwarfs. Galaxies 9, 70. doi:10.3390/galaxies9040070

CrossRef Full Text | Google Scholar

Wang, M., Huang, W., Kondev, F., Audi, G., and Naimi, S. (2021b). The ame 2020 atomic mass evaluation (ii). tables, graphs and references. Chin. Phys. C 45, 030003. doi:10.1088/1674-1137/abddaf

CrossRef Full Text | Google Scholar

Xia, C.-J., Xu, J.-F., Peng, G.-X., and Xu, R.-X. (2022). Interface effects of quark matter: light-quark nuggets and compact stars. Phys. Rev. D. 106, 034016. doi:10.1103/PhysRevD.106.034016

CrossRef Full Text | Google Scholar

Zuckerman, B., and Young, E. D. (2018). Characterizing the chemistry of planetary materials around white dwarf stars. Cham: Springer International Publishing, 1545–1566. doi:10.1007/978-3-319-55333-7_14

CrossRef Full Text | Google Scholar