Coherence of Elsässer Variables in the slow solar wind from 0.1 au to 0.3 au

The highly Alfvénic fluctuations (AF) and magnetic-velocity alignment structures (MVAS) are two distinguished components in the near-Sun slow solar wind observed by Parker Solar Probe. The amplitudes of the Els$\ddot{\mathrm{a}}$sser Variables z^± of AF and MVAS show distinct features. However, how these fluctuations contribute to the slow solar wind turbulence remains unknown. Here we investigate the coherence between z⁺ and z⁻ for the first time using the Parker Solar Probe measurements with a high resolution 0.8738 s in the slow solar wind from 0.1–0.3 au. We find that the coherence spectra of z⁺ and z⁻ in the perpendicular directions for MVAS are remarkable higher than that for AF, in particular at large scale. There exists a break around 10 d_i (d_i is the ion inertial length) where the coherence decreases to a lower level for MVAS. A bump around 10 d_i appears on the coherence spectra of all three components for AF. The coherence of z⁺ and z⁻ may relate to the possible nonlinear interactions reflected by the time series, the power spectra, and the self-correlation functions. These results help to understand the roles of AF and MVAS in the slow solar wind turbulence.

1 Introduction

The solar wind is a natural laboratory for the study of MHD turbulence (Tu and Marsch, 1995; Bruno and Carbone, 2013), which is often described theoretically by MHD equations in terms of Els$\ddot{\mathrm{a}}$sser Variables z^± (Elsasser, 1950). The nonlinear interactions between z⁺ and z⁻ lead to the energy cascade from large scales to small scales. MHD cascade models (Kraichnan, 1965; Goldreich and Sridhar, 1995; Boldyrev, 2006) often take z⁺ and z⁻ as counter-propagating Alfvén wave packets respectively. This picture is incorporated in several solar wind turbulence models (e.g., Marsch and Tu, 1989; Breech et al., 2008; Howes et al., 2008; Zank et al., 2012). Velli et al. (1989) proposed that the nonlinear interactions in the solar wind are mediated by the co-traveling z⁻ generated by the linear coupling of the dominant species to the large-scale gradients. Recently Yang et al. (2023) find that the energy transfer of imbalanced Alfvénic turbulence is completed by coherent interaction between Alfvén waves and co-propagating anomalous fluctuations that continuously generated through the nonlinearity. The interaction between z⁺ and z⁻ are of importance for the understanding of solar wind turbulence.

It is widely accepted that z⁺ represents the outward Alfvén fluctuations in the solar wind originating from the solar atmosphere. However, the origin and nature of z⁻ are controversial. Assumptions include the inward Alfvén waves produced by parametric instabilities (Marsch and Tu, 1993;Del Zanna, 2001; Malara et al., 2001; Shi et al., 2017), the reflection of the outward Alfvén waves (Velli et al., 1989; Chandran et al., 2009; Chandran and Perez, 2019), the velocity shear (Zank et al., 2012; Shi et al., 2020), the compressive fluctuations (Grappin et al., 1990); the convective structures originating from the solar atmosphere (Tu and Marsch, 1990; Tu and Marsch, 1993); and the pseudo structures in the highly Alfvénic solar winds (Wang et al., 2018). The determination of the nature of z⁻ is of importance for the understanding of solar wind turbulence. Whether z − is inward wave, co-propagating fluctuation, or structure directly influences the interaction between z + and z −.

The properties of the turbulent fluctuations reflect their nature. The typical slow solar wind has a lower degree of Alfvénicity than the fast solar wind, being more strongly intermixed with structures of non-Alfvénic nature (Tu and Marsch, 1995). The information in the σ_c − σ_r plane provides an important approach to investigate the properties of solar wind fluctuations, in which σ_c is the cross helocity and σ_r is the normalized residual energy. Bruno et al. (2007) studied the radial evolution of the distributions in the σ_c − σ_r plane and found that there exist advected magnetic structures in the solar wind. Alberti et al. (2022) and Sioulas et al. (2023) both presented the radial evolution of the distribution in the σ_c − σ_r plane and argued that more non-Alfvénic fluctuations occurs during the solar wind expansion, resulting in the transition of magnetic spectral index from −5/3 to −3/2 (Chen et al., 2020). The evolution of σ_c − σ_r plane reflects that the fluctuations are higher Alfvénic close to the Sun and less Alfvénic away from the Sun. The more Alfvénicity and −3/2 scaling are consistent with the IK phenomenology (Kraichnan, 1965) and the −5/3 scaling is consistent with the Kolmogorov phenomenology (Kolmogorov, 1941) and critical balance models (Goldreich and Sridhar, 1995; Boldyrev, 2006).

Wang et al. (2020) pointed out that σ_c and σ_r are dependent with each other and used $C_{\text{vb}}^{\prime }$ and σ_r instead to analyze the properties of the fluctuations, where $C_{\text{vb}}^{\prime }$ is the correlation coefficient between the magnetic and velocity fluctuations multiplied by the opposite sign of the radial component of the mean magnetic field. They studied the pixel averaged amplitude distributions of the fluctuations in the $C_{\text{vb}}^{\prime }-{\sigma }_{\text{r}}$ plane in the slow solar wind using WIND measurements at 1 au and found that the amplitude distributions of velocity and magnetic field present a vertical stripe in the region with $|C_{\text{vb}}^{\prime }|>0.85$ and σ_r ∈ (−0.9, −0.2). This region on the $C_{\text{vb}}^{\prime }-{\sigma }_{\text{r}}$ plane reflects the magnetic-dominated structures with high correlation between magnetic-field fluctuations and velocity fluctuations, which were defined as magnetic-velocity alignment structures (MVAS) by Wang et al. (2020). Wu et al. (2021) perform the analyses using the same method for the near-Sun solar wind. They find that there is a domain in the $C_{\text{vb}}^{\prime }-{\sigma }_{\text{r}}$ plane for Alfvénic fluctuations with $C_{\text{vb}}^{\prime }>0.95$ (AF) and σ_r ∼ 0 in the near-Sun region while this domain almost disappear at 1 au and MVAS already exists in the near-Sun region. They found that z⁺ is large but z⁻ is just above the observational uncertainty for AF and z⁺ and z⁻ are both large for MVAS. It is still unknown that what is the nature of z⁻ in AF and MVAS respectively and whether the MVAS takes part in the nonlinear interactions in the solar wind turbulence.

The correlation between magnetic and velocity fluctuations is an effective parameter to investigate the fluctuations. Coherence is the correlation as a function of frequency (or scale). Denskat and Neubauer (1983) analyzed the coherence between magnetic and velocity fluctuations in the fast solar wind observed by Helios and found that the coherence is low at low frequency below 2.4 × 10⁻⁵ Hz, and high at higher frequency. They concluded that at low frequency the fluctuations are generated by larger-scale dynamical process and at high frequency the fluctuations are Alfvénic turbulence. Since turbulence is an multi-scale phenomenon, the coherence provides more information about the fluctuations than the correlation. Here we investigate the coherence between z⁺ and z⁻ for both AF and MVAS. We utilize the PSP measurements inside 0.3 au in the slow solar wind and analyze the fluctuations of z⁺ and z⁻ in the $C_{\text{vb}}^{\prime }-{\sigma }_{\text{r}}$ plane. We present the coherence spectra of z⁺ and z⁻ for both AF and MVAS for the first time. We find that the coherence for MVAS is higher than that for AF at all scales. We analyze two intervals in the slow solar wind in detail in three aspects: the time series, the self-correlation function, and the power spectrum. We propose the possibility that there are two different interactions between z⁺ and z⁻ in the slow solar wind turbulence. This paper is organized as follows. In Section 2, we describe the data and method. In Section 3, we show coherence spectra of z⁺ and z⁻ for both AF and MVAS and the detailed analyses on two intervals. In Section 4, we discuss our results and draw our conclusions.

2 Data and methods

Here we use measurements from PSP from 2018 October 31 to 2023 April 30. The perihelion reached 0.09 au in the sixth orbit. The fluxgate magnetometer (MAG) in the FIELDS instrument suite (Bale et al., 2016) measures the magnetic field B and the Solar Probe Cup [SPC (Case et al., 2020)] in the Solar Wind Electrons, Protons, and Alphas [SWEAP (Kasper et al., 2016)] instrument suite measures the proton velocity distribution function (VDF), whose moments including proton density n_p, solar wind velocity V are used. We cut the near-Sun solar wind data from 0.1 au to 0.3 au into 1-h intervals with no overlapping and only reserve the high resolution data with good data coverage (time resolution of 0.8738 and a total data coverage of 95% or better) and obtain 1339 intervals. Most of them are slow solar wind with the average velocity V₀ < 450 km/s. We focus our analyses on the 1187 slow solar wind intervals. We fit plasma and magnetic field data to an uniform time grid with the resolution of Δ = 0.8738 s.

The magnetic and velocity are calculated as δv = V − V₀ and $\delta \mathbf{b}=(\mathbf{B}-{\mathbf{B}}_0)/\sqrt{4\pi n_{\text{p}}{m}_{\text{p}}}$, respectively. B₀ is the average magnetic field and m_p is the proton mass. B₀ and V₀ are the averaged value of each interval. Note that this is a zeroth order approximation since that the determination of B₀ and V₀ may be influenced by the one-sided fluctuations (Matteini et al., 2014). The normalized residual energy σ_r and the correlation coefficient C_vb between δb and δv are defined as

${\sigma }_{\text{r}}=\frac{<\delta {\mathbf{v}}^2>-<\delta {\mathbf{b}}^2>}{<\delta {\mathbf{v}}^2>+<\delta {\mathbf{b}}^2>},(1)$

$C_{\text{vb}}=\frac{<\delta \mathbf{v}\cdot \delta \mathbf{b}>}{\sqrt{<\delta {\mathbf{v}}^2><\delta {\mathbf{b}}^2>}},(2)$

where the angled-bracket $<>$ denotes an ensemble time average. These dimensionless parameters reflect the nature of solar wind fluctuations (Tu and Marsch, 1995; Wang et al., 2020). We calculate $C_{\text{vb}}^{\prime }=-C_{\text{vb}}\cdot B_R/|B_R|$, where B_R is the R component of B₀ in the RTN coordinates (R is the direction from the Sun to the spacecraft, T is cross product of the solar rotation axis and R, N completes the right-handed coordinates). In this way, the positive (negative) sign of $C_{\text{vb}}^{\prime }$ indicates the outward (inward) sense of the fluctuations.

The fluctuations of the Els$\ddot{\mathrm{a}}$sser Variable z^± are defined as

${\mathbf{z}}^{\pm }=\delta \mathbf{v}\pm \frac{C_{\text{vb}}}{|C_{\text{vb}}|}\cdot \delta \mathbf{b},(3)$

So that z⁺ always refers to the dominated fluctuations, whether the Els$\ddot{\mathrm{a}}$sser variable propagates parallel or anti-parallel to the background magnetic field line. The pixel average fluctuation amplitudes of z^± are calculated in the $C_{\text{vb}}^{\prime }-{\sigma }_{\text{r}}$ plane with 40 × 40 pixels. We require that each pixel has more than 4 intervals for statistical purpose. We further focus on the AF and the MVAS defined by Wu et al. (2021) for the near-Sun slow solar wind. There are 60 intervals in the AF region and 173 intervals in the MVAS region.

We calculate the coherence between z⁺ and z⁻. The coherence measures the correlation between z⁺ and z⁻ in the frequency domain. We construct the field-aligned coordinate system, in which ‖ refers to the direction of B₀, ⊥₁ refers to the direction perpendicular to both B₀ and V₀ and ⊥₂ completes this orthogonal coordinate system. The coherence spectra is the normalized cross-spectral density of two time signals z⁺ and z⁻:

${\mathrm{c}\mathrm{o}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}}_i=\frac{|PS{D}_i^{+-}{|}^2}{PS{D}_i^{++}\cdot PS{D}_i^{--}},(4)$

Where i denotes the ‖, ⊥₁, and ⊥₂ components, PSD⁺⁺, PSD⁻⁻ are the power spectra of z⁺ and z⁻, and PSD⁺⁻ is the cross spectral density of z⁺ and z⁻. The power spectral density (PSD) of a variable u can be computed by applying the fast Fourier transform (FFT) or wavelet method (Torrence and Compo, 1998) using Morlet wavelet. The coherence can also reflect the phase difference between the fluctuations of z⁺ and z⁻. The coherence equals to 1 when the phase difference is 0° or 180° and equals to 0 when the phase difference is 90° or 270°. We transfer the frequency f to the wavenumber kd_i in units of the ion inertial scale d_i using Tayler hypothesis (Taylor, 1938). The applicability of Taylor’s hypothesis in the analysis of PSP data requires to be investigated (Klein et al., 2014; Perez et al., 2021). Several modified Taylor’s hypothesis are proposed to validate the transform from frequency to wavenumber (Klein et al., 2015; Bourouaine and Perez, 2018; Perez et al., 2021; Zank et al., 2022). We apply the modified Taylor’s hypothesis as in Zank et al. (2022), the difference between the original and modified Taylor’s hypothesis is a $\sim 20\%$ shift of the wavenumber. Other main features remain. Since most of these modified Taylor’s hypothesis are related to the dispersion relation for the fluctuations and we are not sure for the nature of z⁻, we only show the results using the original Taylor’s hypothesis in this work. We obtain the averaged coherence spectra for both the AF and the MVAS in a smaller wavenumber domain, in which range every interval covers.

We present a typical case of MVAS with high coherence and another typical case of the AF with low coherence. We analyze their time series, power spectra and self-correlation function. The power spectral density (PSD) of a variable u are computed by applying the fast Fourier transform (FFT). The estimated spectral indices are given by the least-squares regressions to the corresponding spectra within 0.004–0.04kdi in the log-log space. The self-correlation function of u is calculated as CF(τ) =< δu(t) ⋅ δu (t + τ) > (Matthaeus and Goldstein, 1982), where $<>$ denotes an ensamble time average and τ = 0, Δ, 2Δ, … , 500Δ. We obtain the normalized self-correlation function NCF(τ) = CF(τ)/CF(0). The correlation length is given as the time scale where NCF(τ) = 1/e (Smith et al., 2001). The results are presented in Section 3.

3 Results

Figure 1 shows the number distribution in the $C_{\text{vb}}^{\prime }-{\sigma }_{\text{r}}$ plane for the 1-h intervals in the slow solar wind from 0.1 to 0.3 au. $C_{\text{vb}}^{\prime }>0.5$ for most intervals and σ_r spreads from −0.6 to 0.2. Most intervals locate at around $C_{\text{vb}}^{\prime }\sim 0.9$. We mark the AF with $C_{\text{vb}}^{\prime }>0.95$ and σ_r ∈ (−0.1, 0.1) in magenta rectangle and the MVAS with $C_{\text{vb}}^{\prime }>0.8$ and σ_r ∈ (−0.6, −0.3) in black rectangle. There are 60 AF intervals and 173 MVAS intervals respectively.

FIGURE 1

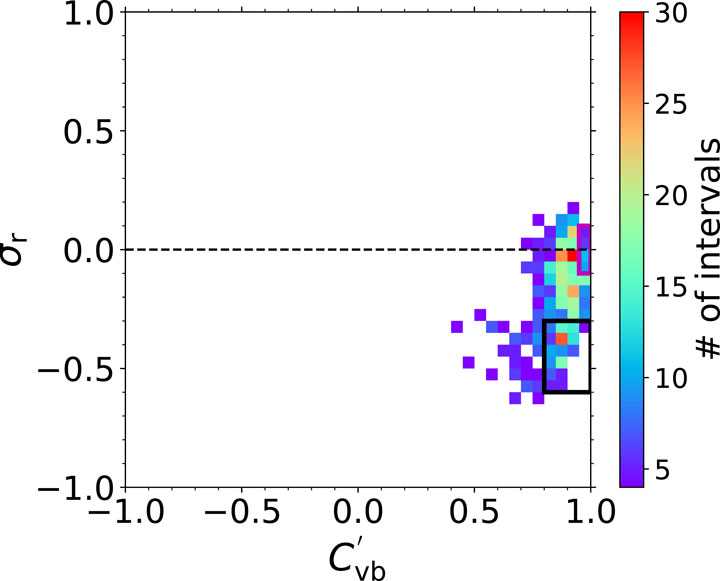
FIGURE 1. Number distribution in the $C_{\text{vb}}^{\prime }-{\sigma }_{\text{r}}$ plane observed in the slow solar wind. The magenta denotes the AF region and the black denotes the MVAS region.

Figure 2 presents the pixel average amplitudes (top) and the corresponding standard deviations (bottom) of z⁺ (left) and z⁻ (right) in the $C_{\text{vb}}^{\prime }-{\sigma }_{\text{r}}$ plane. The average amplitude of z⁺ is around 160 km/s in the AF and 100 km/s in the MVAS region. While the amplitudes of z⁻ is around 20 km/s in the AF and 35 km/s in the MVAS region. Their standard deviations are all much smaller than the average amplitudes. The properties of the AF and the MVAS for these 1-h intervals in the near-Sun slow solar wind are consistent with those 6-min intervals in the near-Sun slow solar wind (Wu et al., 2021).

FIGURE 2

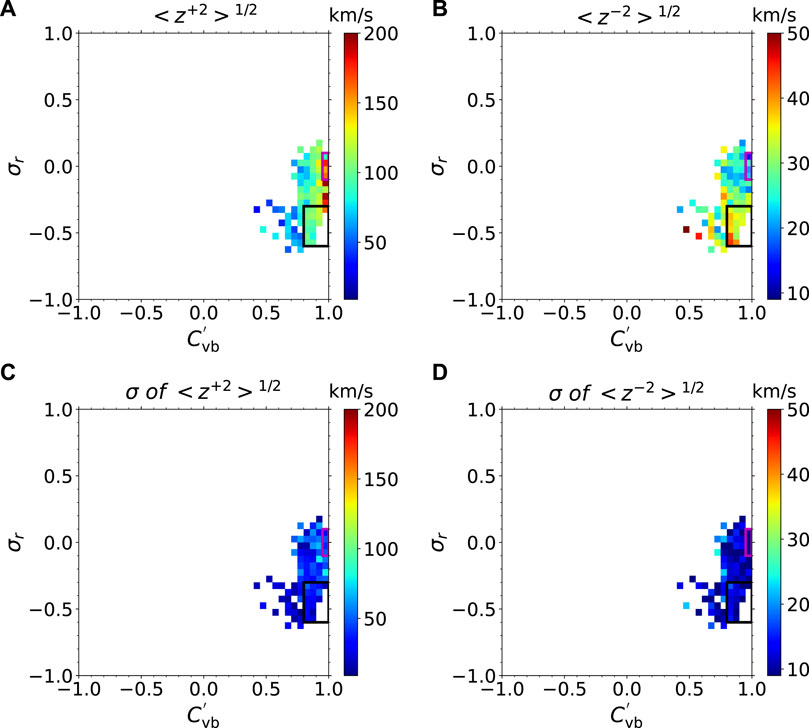
FIGURE 2. Top panels: pixel average amplitudes of z⁺ (A) and z⁻ (B) in the $C_{\text{vb}}^{\prime }-{\sigma }_{\text{r}}$ plane observed in the slow solar wind. The magenta denotes the AF region and the black denotes the MVAS region. Bottome panels: the standard deviations of z⁺ (C) and z⁻ (D) in the same format of top panels.

The average coherence spectra between three components of z⁺ and z⁻ are shown in Figure 3. The differences on the average coherence spectra are obvious for the AF and the MVAS. For the MVAS, the average coherence for the perpendicular components can reach 0.55 at large scale, gradually declines to 0.4 around 0.1kd_i and drop to 0.25 around 0.2kd_i. The parallel components has a lower coherence at all scales and a bump around 0.07kd_i. The bump indicates a slight higher coherence. The spectra illustrate an obvious 2D anisotropy that the coherence in the perpendicular direction is larger than that in the parallel direction, while it is almost isotropic in the plane perpendicular to the magnetic field. For those AF, the coherence spectra show little anisotropy. The values of the average coherence are lower than 0.3 at all scales with a nearly constant coherence at large scales. All three components have a bump around 0.07kd_i.

FIGURE 3

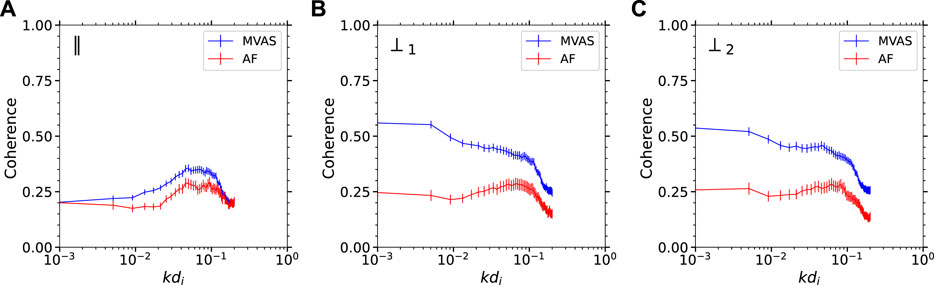
FIGURE 3. The averaged coherence spectra between z⁺ and z⁻in the three directions (‖ (A); ⊥₁ (B); ⊥₂ (C)) of the field-aligned coordinates as shown on the top left corner for the AF and the MVAS, respectively. The error bars represent the standard errors.

Figure 4 shows an interval on 2022 May 29 (interval A). Interval A is measured at 0.17 au and with correlation coefficient C_vb = −0.97 and Alfvén ratio σ_r = −0.44. Thus, it is a interval of MVAS. Figure 4A shows the magnetic field fluctuations δb and the velocity fluctuations δv in the ⊥₁ of the field-aligned coordinates. We can see that the correlation between δb and δv is high but δb is dominated over δv. Figure 4B presents z⁺ and z⁻ in unit of km/s. It is clear that z⁺ is much larger than z⁻. δz⁻, the root mean square of z⁻, is 38.5 km/s. Figure 4C displays the wavelet spectrum of coherence between z⁺ and z⁻ in the ⊥₁ direction. The red patch illustrates a high coherence at large scales and the green and blue patch indicates a lower coherence at small scales. Figure 4D presents the corresponding phase difference between z⁺ and z⁻. The yellow patch indicates phase difference being 180° at most scales and instants, demonstrating that the peaks of z⁺ are accompanied by the troughs of z⁻ and vice versa.

FIGURE 4

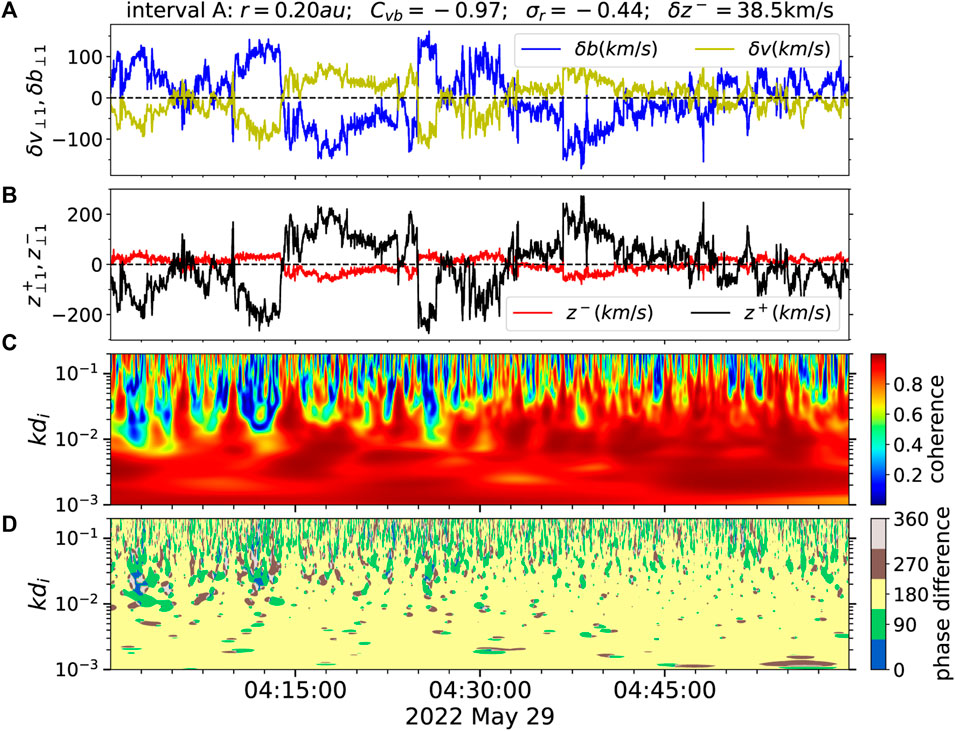
FIGURE 4. The C_vb, σ_r and z⁻ are given in the title for interval A measured on 2022 May 29 at 0.20 au. (A) The time variations of the components of magnetic field (blue) and velocity fluctuations (yellow) in the ⊥₁ direction of the field-aligned coordinates in unit of km/s. (B) The time series of z⁺ (black) and z⁻ (red) in unit of km/s. (C) The wavelet spectrum of coherence between z⁺ and z⁻. (D) The phase difference between z⁺ and z⁻.

Figure 5 shows an interval on 2022 December 8 (interval B). Interval B is measured at 0.16 au and with C_vb = 0.97 and Alfvén ratio σ_r = −0.01. This time interval is highly Alfvénic with δz⁻ = 18.8 km/s. It is obvious that z⁻ is much smaller than z⁺. The wavelet spectrum shows a large patch of low coherence in blue, corresponding to phase differences of 90° or 270°, implying that the peak values of z⁺ are accompanied by a zero value of z⁻ and vice versa.

FIGURE 5

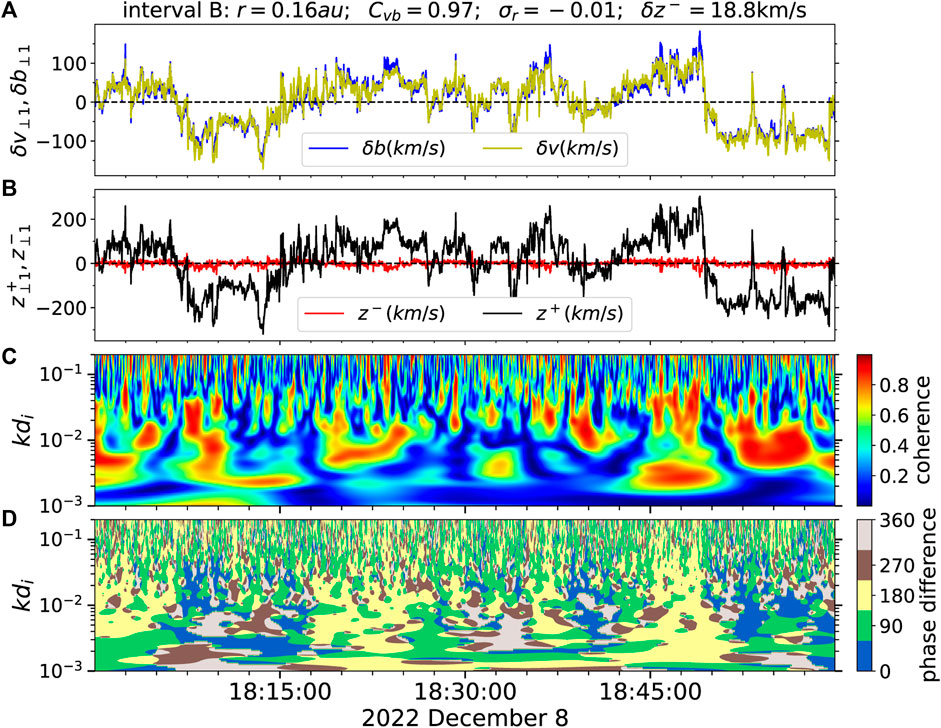
FIGURE 5. The interval B measured on 2022 December 8 at 0.16 au with same format as Figure 4 (A–D).

In the top panels of Figure 6, we show the coherence spectra between z⁺ and z⁻ in the three directions in the field-aligned coordinates. The differences between those two intervals are obvious. For interval A, the values of coherence between z⁺ and z⁻ of the ⊥₁ and ⊥₂ components reach 0.8 at the largest scale and decline to around 0.4 at small scale. The coherence of the ‖ component is around 0.3 at all scales. For interval B, the values of coherence between z⁺ and z⁻ of the three components are all lower than 0.2 at all scales. The coherence of the ⊥₂ component is close to 0.2 and the values of coherence of the ⊥₁ and ‖ components are close to 0.

FIGURE 6

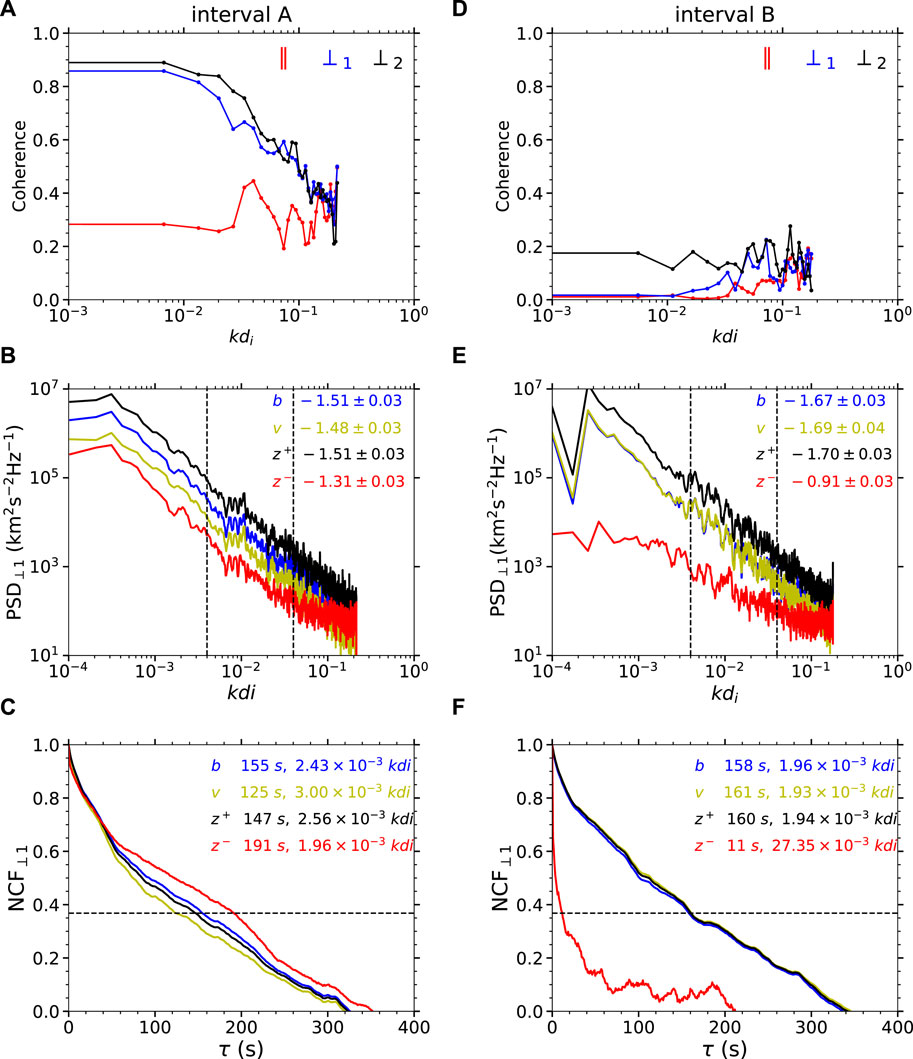
FIGURE 6. Left panels are for interval (A). (A) The coherence spectra between z⁺ and z⁻ in the three directions in the field-aligned coordinates (‖ in red; ⊥₁ in blue and ⊥₂ in black). (B) The power spectra of four variables (b in blue; v in yellow; z⁺ in black; z⁻ in red) in the ⊥₁ direction with the corresponding slopes and their standard deviations obtained from the linear fit in the log-log space shown at the right corner. The two black dashed lines mark the range for the least squares fit to the spectra on the log-log plot. (C) The normalized self-correlation functions (NCF) of four variables (b in blue; v in yellow; z⁺ in black; z⁻ in red) in the ⊥₁ direction with the corresponding correlation length (where NCF = 1/e) shown at the right corner. The black dashed line denotes 1 = e. Right panels (D–F) are for interval B with the same format as the left panels (A–C).

In the middle panels of Figure 6, we show the power spectra of δb, δv, z⁺, and z⁻ for the ⊥₁ component to be clear. We can see for both interval A in the left panel and interval B in the right panel, the power spectra of z⁻ are much lower than those of z⁺. The magnetic spectrum of interval A is dominated over the velocity spectra, while the magnetic spectrum and the velocity spectrum of interval B almost overlap. We perform the least squares fit to the spectra on the log-log plot from 0.004 to 0.04 kdi and obtained the estimated spectral indices. For interval A, the spectral indices of magnetic field, velocity and z⁺ are all close to −3/2 and the spectral index of z⁻ is −1.31. For interval B, the spectral indices of magnetic field, velocity and z⁺ are all close to −5/3 and the spectral index of z⁻ is −0.91.

In the bottom panels of Figure 6, we show the normalized self-correlation functions of the ⊥₁ components of δb, δv, z⁺, and z⁻. NCFs of δb, δv, z⁺ for both interval A and interval B decrease gradually as time lags τ increase. The correlation lengths are of the same order around 150 s. However, z⁻ is distinguished from the others: NCFs is similar with that of z⁺ for interval A but drops dramatically to 1/e at only 11 s for intervals B. This means that the relation of the value of z⁻ at a time instant with another instant for intervals B weakens quickly as the distance increases.

4 Conclusions and discussion

In this study, we use the PSP measurements in the slow solar wind from 0.1–0.3 au and calculate the coherence spectra between Els$\ddot{\mathrm{a}}$sser Variable z⁺ and z⁻ for 60 intervals of the AF and 173 intervals of the MVAS defined in the $C_{\text{vb}}^{\prime }-{\sigma }_{\text{r}}$ plane. The average coherence spectra of MVAS are higher than those of AF for all components at all scales in the field-aligned coordinate system, especially for the perpendicular components. The average coherence spectra of MVAS show a distinct 2D anisotropy while that of AF is nearly isotropic and low. Both MVAS and AF show a bump around 0.07kd_i on the average coherence spectra of parallel component. For the perpendicular components, the coherence decreases with the increasing kd_i for MVAS but presents a bump around 0.07kd_i for AF.

We analyze two intervals in detail. Interval A is a typical event of MVAS with high coherence and interval B is highly Alfvénic with low coherence. The wavelet spectra of coherence is shown together with the phase difference for the ⊥₁ component of z⁺ and z⁻. For interval A, the high coherence corresponds to a close to 180° phase difference. The coherence spectra present a clear 2D anisotropy with high (up to 0.85) coherence at large scale for the perpendicular components. The spectral indices of δb, δv, z⁺ are all around −3/2, while the spectra of z⁻ is flatter with the spectral indices −1.31. The correlation lengths of z⁺ and z⁻ are at the same order. These results support the scenario that the fluctuations of MVAS are involved in the nonlinear interactions of the solar wind turbulence as proposed in IK theory. The high coherence of z⁺ and z⁻ may indicate that z⁺ and z⁻ both originate from MVAS, which complete the nonlinear interactions in the MVAS and contribute to the slow solar wind turbulence.

For interval B, the low coherence corresponds to a close to 90° or 270° phase difference. The coherence spectra are nearly isotropically low with a slight higher (around 0.2) coherence for the ⊥₂ component. The spectral indices of δb, δv, z⁺ are all around −5/3, while the spectra of z⁻ is flatter with the spectral indices −0.91. The correlation lengths of z⁺ are at the same order with that of δb and δv. However, the normalized self-correlation function of z⁻ drops very quickly and comes to 1/e at only 11 s. The highly Alfvénic fluctuations, the close to −1 spectral index and the small correlation length of z⁻ all imply that z⁻ could not be the inward Alfvénic fluctuations as suggested by Wang et al. (2018). It may be the co-propagating anomalous fluctuations generated in the imbalanced Alfvénic turbulence (Yang et al., 2023). The different origin of z⁺ and z⁻ may indicate different nonlinear interactions in AF from that in MVAS.

Coherence is a useful window to unveil the nonlinear interactions. Our work suggests that there may exist two kinds of nonlinear interactions in the slow solar wind turbulence. One is in the MVAS, completed by the z⁺ and z⁻ generated by the MVAS. Another is in the AF between the outward Alfvénic fluctuations and the possible co-propagating anomalous fluctuations. The two kinds may have other different properties, for example, the spectral index of z⁺. However, due to the limitation of the data, we do not obtain two clearly different statistical distributions of the spectral index for both Alfvénic fluctuations and MVAS. The uncertainty of density measurements may be a major reason. Using the proton density estimated from QTN, we find that the number of MVAS greatly decreases. Thus part of the MVAS determined using SPC data could be pseudo structures and z⁺ and z⁻ both are influenced by the uncertainty, leading to a larger value of their coherence. The measurement effect should be investigated in the future. The differences between interval A and interval B could also reflect two stages of the evolution of the solar wind turbulence across scale or during the solar wind expansion.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: NASA’s Space Physics Data Facility (https://cdaweb.gsfc.nasa.gov/index.html/).

Author contributions

HW: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Visualization, Writing–original draft, Writing–review and editing. LY: Conceptualization, Data curation, Formal Analysis, Methodology, Writing–review and editing. SH: Data curation, Formal Analysis, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work is supported by the National Key R&D Program of China (Grant No. 2022YFF0503700), the National Natural Science Foundation of China under contract Nos. 42104152 and 41974198.

Acknowledgments

We acknowledge the NASA Parker Solar Probe mission team and the SWEAP team led by J.C. Kasper, and the FIELDS team led by S.D. Bale, for the use of PSP data.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alberti, T., Benella, S., Consolini, G., Stumpo, M., and Benzi, R. (2022). Reconciling parker solar probe observations and magnetohydrodynamic theory. Astrophysical J. Lett. 940, L13. doi:10.3847/2041-8213/aca075

CrossRef Full Text | Google Scholar

Bale, S. D., Goetz, K., Harvey, P. R., Turin, P., Bonnell, J. W., Dudok de Wit, T., et al. (2016). The FIELDS instrument suite for solar probe plus. Measuring the coronal plasma and magnetic field, plasma waves and turbulence, and radio signatures of solar transients. Space Sci. Rev. 204, 49–82. doi:10.1007/s11214-016-0244-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Boldyrev, S. (2006). Spectrum of magnetohydrodynamic turbulence. Phys. Rev. Lett. 96, 115002. doi:10.1103/PhysRevLett.96.115002

PubMed Abstract | CrossRef Full Text | Google Scholar

Bourouaine, S., and Perez, J. C. (2018). On the limitations of taylor’s hypothesis in parker solar probe’s measurements near the alfvén critical point. Astrophysical J. Lett. 858, L20. doi:10.3847/2041-8213/aabccf

CrossRef Full Text | Google Scholar

Breech, B., Matthaeus, W. H., Minnie, J., Bieber, J. W., Oughton, S., Smith, C. W., et al. (2008). Turbulence transport throughout the heliosphere. J. Geophys. Res. Space Phys. 113. doi:10.1029/2007JA012711

CrossRef Full Text | Google Scholar

Bruno, R., and Carbone, V. (2013). The solar wind as a turbulence laboratory. Living Rev. Sol. Phys. 10, 2. doi:10.12942/lrsp-2013-2

CrossRef Full Text | Google Scholar

Bruno, R., D’Amicis, R., Bavassano, B., Carbone, V., and Sorriso-Valvo, L. (2007). Magnetically dominated structures as an important component of the solar wind turbulence. Ann. Geophys. 25, 1913–1927. doi:10.5194/angeo-25-1913-2007

CrossRef Full Text | Google Scholar

Case, A. W., Kasper, J. C., Stevens, M. L., Korreck, K. E., Paulson, K., Daigneau, P., et al. (2020). The solar probe cup on the parker solar probe. Astrophysical J. Suppl. Ser. 246, 43. doi:10.3847/1538-4365/ab5a7b

CrossRef Full Text | Google Scholar

Chandran, B. D. G., Quataert, E., Howes, G. G., Xia, Q., and Pongkitiwanichakul, P. (2009). Constraining low-frequency alfvénic turbulence in the solar wind using density-fluctuation measurements. Astrophysical J. 707, 1668–1675. doi:10.1088/0004-637x/707/2/1668

CrossRef Full Text | Google Scholar

Chandran, B. D. G., and Perez, J. C. (2019). Reflection-driven magnetohydrodynamic turbulence in the solar atmosphere and solar wind. J. Plasma Phys. 85, 905850409. doi:10.1017/S0022377819000540

CrossRef Full Text | Google Scholar

Chen, C. H. K., Bale, S. D., Bonnell, J. W., Borovikov, D., Bowen, T. A., Burgess, D., et al. (2020). The evolution and role of solar wind turbulence in the inner heliosphere. Astrophysical J. Suppl. Ser. 246, 53. doi:10.3847/1538-4365/ab60a3

CrossRef Full Text | Google Scholar

Del Zanna, L. (2001). Parametric decay of oblique arc-polarized alfvén waves. Geophys. Res. Lett. 28, 2585–2588. doi:10.1029/2001GL012911

CrossRef Full Text | Google Scholar

Denskat, K. U., and Neubauer, F. M. (1983). Observations of hydromagnetic turbulence in the solar wind. Solar Wind Five, 81–92.

Google Scholar

Elsasser, W. M. (1950). The hydromagnetic equations. Phys. Rev. 79, 183. doi:10.1103/PhysRev.79.183

CrossRef Full Text | Google Scholar

Goldreich, P., and Sridhar, S. (1995). Toward a theory of interstellar turbulence. 2: strong alfvenic turbulence. Astrophys. J. 438, 763–775. doi:10.1086/175121

CrossRef Full Text | Google Scholar

Grappin, R., Mangeney, A., and Marsch, E. (1990). On the origin of solar wind MHD turbulence: Helios data revisited. J. Geophys. Res. 95, 8197–8209. doi:10.1029/JA095iA06p08197

CrossRef Full Text | Google Scholar

Howes, G. G., Cowley, S. C., Dorland, W., Hammett, G. W., Quataert, E., and Schekochihin, A. A. (2008). A model of turbulence in magnetized plasmas: implications for the dissipation range in the solar wind. J. Geophys. Res. Space Phys. 113. doi:10.1029/2007JA012665

CrossRef Full Text | Google Scholar

Kasper, J. C., Abiad, R., Austin, G., Balat-Pichelin, M., Bale, S. D., Belcher, J. W., et al. (2016). Solar wind Electrons Alphas and protons (SWEAP) investigation: design of the solar wind and coronal plasma instrument suite for solar probe plus. Space Sci. Rev. 204, 131–186. doi:10.1007/s11214-015-0206-3

CrossRef Full Text | Google Scholar

Klein, K. G., Howes, G. G., and TenBarge, J. M. (2014). The violation of the taylor hypothesis in measurements of solar wind turbulence. Astrophysical J. Lett. 790, L20. doi:10.1088/2041-8205/790/2/l20

CrossRef Full Text | Google Scholar

Klein, K. G., Perez, J. C., Verscharen, D., Mallet, A., and Chandran, B. D. G. (2015). A modified version of taylor’s hypothesis for solar probe plus observations. Astrophysical J. Lett. 801, L18. doi:10.1088/2041-8205/801/1/L18

CrossRef Full Text | Google Scholar

Kolmogorov, A. (1941). The local structure of turbulence in incompressible viscous fluid for very large Reynolds’ numbers. Akad. Nauk. SSSR Dokl. 30, 301–305.

Google Scholar

Kraichnan, R. H. (1965). Inertial-range spectrum of hydromagnetic turbulence. Phys. Fluids 8, 1385–1387. doi:10.1063/1.1761412

CrossRef Full Text | Google Scholar

Malara, F., Primavera, L., and Veltri, P. (2001). Nonlinear evolution of the parametric instability: numerical predictions versus observations in the heliosphere. Nonlinear Process. Geophys. 8, 159–166. doi:10.5194/npg-8-159-2001

CrossRef Full Text | Google Scholar

Marsch, E., and Tu, C. Y. (1989). Dynamics of correlation functions with Elsässer variables for inhomogeneous MHD turbulence. J. Plasma Phys. 41, 479–491. doi:10.1017/S0022377800014033

CrossRef Full Text | Google Scholar

Marsch, E., and Tu, C. Y. (1993). Modeling results on spatial transport and spectral transfer of solar wind Alfvénic turbulence. J. Geophys. Res. 98, 21045–21059. doi:10.1029/93JA02365

CrossRef Full Text | Google Scholar

Matteini, L., Horbury, T. S., Neugebauer, M., and Goldstein, B. E. (2014). Dependence of solar wind speed on the local magnetic field orientation: role of Alfvénic fluctuations. Geophys. Res. Lett. 41, 259–265. doi:10.1002/2013GL058482

CrossRef Full Text | Google Scholar

Matthaeus, W. H., and Goldstein, M. L. (1982). Measurement of the rugged invariants of magnetohydrodynamic turbulence in the solar wind. J. Geophys. Res. 87, 6011–6028. doi:10.1029/JA087iA08p06011

CrossRef Full Text | Google Scholar

Perez, J. C., Bourouaine, S., Chen, C. H. K., and Raouafi, N. E. (2021). Applicability of taylor’s hypothesis during parker solar probe perihelia. A&A 650, A22. doi:10.1051/0004-6361/202039879

CrossRef Full Text | Google Scholar

Shi, C., Velli, M., Tenerani, A., Rappazzo, F., and Réville, V. (2020). Propagation of alfvén waves in the expanding solar wind with the fast-slow stream interaction. Astrophysical J. 888, 68. doi:10.3847/1538-4357/ab5fce

CrossRef Full Text | Google Scholar

Shi, M., Li, H., Xiao, C., and Wang, X. (2017). The parametric decay instability of alfvén waves in turbulent plasmas and the applications in the solar wind. Astrophysical J. 842, 63. doi:10.3847/1538-4357/aa71b6

CrossRef Full Text | Google Scholar

Sioulas, N., Huang, Z., Shi, C., Velli, M., Tenerani, A., Bowen, T. A., et al. (2023). Magnetic field spectral evolution in the inner heliosphere. Astrophysical J. Lett. 943, L8. doi:10.3847/2041-8213/acaeff

CrossRef Full Text | Google Scholar

Smith, C. W., Matthaeus, W. H., Zank, G. P., Ness, N. F., Oughton, S., and Richardson, J. D. (2001). Heating of the low-latitude solar wind by dissipation of turbulent magnetic fluctuations. J. Geophys. Res. Space Phys. 106, 8253–8272. doi:10.1029/2000JA000366

CrossRef Full Text | Google Scholar

Taylor, G. I. (1938). The spectrum of turbulence. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 164, 476–490. doi:10.1098/rspa.1938.0032

CrossRef Full Text | Google Scholar

Torrence, C., and Compo, G. P. (1998). A practical guide to wavelet analysis. Bull. Am. Meteorological Soc. 79, 61–78. doi:10.1175/1520-0477(1998)079<0061:apgtwa>2.0.co;2

CrossRef Full Text | Google Scholar

Tu, C. Y., and Marsch, E. (1990). Evidence for a “background” spectrum of solar wind turbulence in the inner heliosphere. J. Geophys. Res. 95, 4337–4341. doi:10.1029/JA095iA04p04337

CrossRef Full Text | Google Scholar

Tu, C. Y., and Marsch, E. (1993). A model of solar wind fluctuations with two components: alfvén waves and convective structures. J. Geophys. Res. 98, 1257–1276. doi:10.1029/92JA01947

CrossRef Full Text | Google Scholar

Tu, C.-Y., and Marsch, E. (1995). MHD structures, waves and turbulence in the solar wind: observations and theories. Space Sci. Rev. 73, 1–210. doi:10.1007/BF00748891

CrossRef Full Text | Google Scholar

Velli, M., Grappin, R., and Mangeney, A. (1989). Turbulent cascade of incompressible unidirectional alfvén waves in the interplanetary medium. Phys. Rev. Lett. 63, 1807–1810. doi:10.1103/PhysRevLett.63.1807

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X., Tu, C., and He, J. (2020). Fluctuation amplitudes of magnetic-field directional turnings and magnetic-velocity alignment structures in the solar wind. Astrophysical J. 903, 72. doi:10.3847/1538-4357/abb883

CrossRef Full Text | Google Scholar

Wang, X., Tu, C. Y., He, J. S., Wang, L. H., Yao, S., and Zhang, L. (2018). Possible noise nature of elsässer variable z⁻ in highly alfvénic solar wind fluctuations. J. Geophys. Res. (Space Phys. 123, 57–67. doi:10.1002/2017JA024743

CrossRef Full Text | Google Scholar

Wu, H., Tu, C., Wang, X., and Yang, L. (2021). Magnetic and velocity fluctuations in the near-sun region from 0.1-0.3 au observed by parker solar probe. Astrophysical J. 922, 92. doi:10.3847/1538-4357/ac3331

CrossRef Full Text | Google Scholar

Yang, L., He, J., Verscharen, D., Li, H., Bowen, T., Bale, S., et al. (2023). Energy transfer of imbalanced Alfvénic turbulence in the heliosphere. Nat. Commun. 14, 7955. doi:10.1038/s41467-023-43273-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Zank, G. P., Dosch, A., Hunana, P., Florinski, V., Matthaeus, W. H., and Webb, G. M. (2012). The transport of low-frequency turbulence in astrophysical flows. I. Governing equations. Astrophysical J. 745, 35. doi:10.1088/0004-637X/745/1/35

PubMed Abstract | CrossRef Full Text | Google Scholar

Zank, G. P., Zhao, L.-L., Adhikari, L., Telloni, D., Kasper, J. C., Stevens, M., et al. (2022). Turbulence in the sub-alfvénic solar wind. Astrophysical J. Lett. 926, L16. doi:10.3847/2041-8213/ac51da

CrossRef Full Text | Google Scholar