Electron precipitation caused by intense whistler-mode waves: combined effects of anomalous scattering and phase bunching

Resonant interactions with whistler-mode waves are a crucial mechanism that drives the precipitation of energetic electrons. Using test particle simulations, we investigated the impact of nonlinear interactions of whistler-mode waves on electron precipitation across a broad energy range (10 keV- 1 MeV). Specifically, we focused on the combined effects of conventional phase bunching and anomalous scattering, which includes anomalous trapping and positive bunching. It is shown that anomalous scattering transports electrons away from the loss cone and the only process directly causing precipitation in the nonlinear regime is the phase bunching. We further show that their combined effects result in a precipitation-to-trapped flux ratio lower than the quasilinear expectations in a quasi-equilibrium state. Additionally, we calculated the diffusion and advection coefficients associated with the nonlinear trapping and bunching processes, which are vital for understanding the underlying mechanisms of the precipitation. Based on these coefficients, we characterized the phase bunching boundary, representing the innermost pitch angle boundary where phase bunching can occur. A further analysis revealed that electrons just outside this boundary, rather than near the loss cone, are directly precipitated, while electrons within the boundary are prevented from precipitation due to anomalous scattering. Moreover, we demonstrated that the regime of dominant nonlinear precipitation is determined by the combination of the phase bunching boundary and the inhomogeneity ratio. This comprehensive analysis provides insights into the nonlinear effects of whistler-mode waves on electron precipitation, which are essential for understanding physical processes related to precipitation, such as microbursts, characterized by intense and bursty electron precipitation.

1 Introduction

Electron precipitation into the Earth’s upper atmosphere is a crucial process for the loss of energetic electrons in the radiation belts. Resonant interactions with whistler-mode waves play a significant role in scattering electron pitch angles into the loss cone, resulting in efficient electron precipitation. For instance, the short and intense electron precipitation events, known as microbursts, are widely attributed to be driven by whistler-mode chorus waves (Breneman et al., 2017; Miyoshi et al., 2020; Chen et al., 2022). These waves contribute to the depletion of the outer radiation belt (e.g., Blake et al., 1996; O’Brien et al., 2004; Thorne et al., 2005). Specifically, ∼1 MeV (mega-electron-volt) electrons can be precipitated through interactions with ducted chorus waves at high magnetic latitudes (Chen et al., 2022), while sub-MeV electrons are subject to resonances with chorus waves at moderate magnetic latitudes (Douma et al., 2018; Shumko et al., 2018; Zhang et al., 2022a).

Quasilinear theory, which assumes diffusive resonant interactions between electrons and whistler-mode waves (Kennel and Engelmann, 1966; Lyons, 1974), is commonly employed in modeling interactions between electrons and whistler-mode waves. It has been successful in simulating long-term energetic electron dynamics associated with whistler-mode waves (e.g., Horne et al., 2005; Albert et al., 2009; Thorne et al., 2013; Li et al., 2014; Ma et al., 2018). However, recent observations have revealed that whistler-mode waves can often possess sufficient intensity to drive nonlinear interactions with energetic electrons (Zhang et al., 2018; Zhang et al., 2019). Comparisons between numerical and observational results have also shown that quasilinear theory (Kennel and Engelmann, 1966) alone is inadequate to explain the intense electron precipitation observed at both low Earth orbit (Mozer et al., 2018) and in the near-equatorial region (Shumko et al., 2018). Hence, it is believed that nonlinear interactions between electrons and whistler-mode waves play a significant role in these processes.

Nonlinear interactions between electrons and whistler-mode waves typically involve two main mechanisms: nonlinear phase trapping and phase bunching (Bortnik et al., 2008). In the case of phase trapping, electrons become trapped in resonance with whistler-mode waves and are rapidly accelerated to higher energies and larger pitch angles (Albert, 2000; Omura et al., 2007; Artemyev et al., 2014; Vainchtein et al., 2018). On the other hand, phase bunching scatters electrons to lower energies and smaller pitch angles (Albert, 1993; Artemyev et al., 2018), which is believed to drive the intense electron precipitation. Recent studies have also highlighted additional nonlinear effects, namely anomalous trapping (Kitahara and Katoh, 2019) and positive bunching (Gan et al., 2020).

Both anomalous trapping and positive bunching occur for electrons with small equatorial pitch angles. Anomalous trapping can efficiently accelerate electrons to higher energies and pitch angles, similar to standard phase trapping. However, electrons “anomalously” trapped at small pitch angles exhibit a much larger ratio of trapped electrons compared to the entire electron population, as compared to phase trapping. Positive bunching electrons, on the other hand, undergo the process similar to phase bunching but in the opposite direction. While phase bunching always decreases electron pitch angle and energy, positive bunching increases the pitch angles and energies of electrons with small pitch angles. The theoretical analysis of these two processes was conducted in earlier studies by Neishtadt (1975) and Henrard and Lemaitre (1983), as well as a more recent study by Bellan (2013), by utilizing the Hamiltonian approach. Building upon these previous studies, Albert et al. (2021) and Artemyev et al. (2021a) discussed the anomalous trapping process specifically in the context of interactions between electrons and whistler-mode waves, providing theoretical criteria for the occurrence of anomalous trapping. Later in this paper, these criteria are examined in detail and compared to numerical results.

Previously, it was believed that intense electron precipitation events were associated with nonlinear interactions. However, electrons near the loss cone experience anomalous trapping and positive bunching, collectively referred to as anomalous scattering (AS) from now on. Anomalous scattering always increases electron pitch angles, which reduces precipitation. Conversely, phase bunching can transport electrons non-locally into the loss cone in phase space, thereby increasing precipitation. The combined effects of anomalous scattering and phase bunching on electron precipitation represent a key question in understanding nonlinear electron precipitation caused by whistler-mode waves, which remains unanswered. Anomalous scattering can also occur when electrons interact with electromagnetic ion cyclotron (EMIC) waves. Grach and Demekhov. (2020) showed that nonlinear interactions with parallel and intense EMIC waves lead to a higher level of loss cone filling near the minimum resonance energy. Bortnik et al. (2022) specifically discussed the effects of anomalous scattering, referred to as force bunching, and concluded that force bunching could potentially block electron precipitation caused by EMIC waves. Subsequently, Grach et al. (2022) and Hanzelka et al. (2023) evaluated the effects of force bunching on the precipitation phase space density (PSD) and demonstrated that force bunching does not reduce the precipitation PSD. This is because the electrons scattered outward are balanced by the inward transport of electrons within the loss cone.

In this paper, we address the question of the combined effects of anomalous scattering and phase bunching by parallel whistler-mode waves. Such effects have been discussed for EMIC waves, as introduced above, but not for the case of whistler-mode waves. We use test particle simulations to numerically evaluate the nonlinear interactions. Quasilinear theory and nonlinear Hamiltonian approaches are also compared to numerical results. Section 2 describes the numerical methodology including test particle and quasilinear methods. Section 3 describes the main results of this paper. Section 4 discusses the implications of our results and summarizes the main conclusions.

2 Methodology

2.1 Test particle simulation

This paper uses the test particle simulations to model the interactions between electrons and whistler-mode waves, following the method of Gan et al. (2020). In this study, a 1-D dipole geometry is employed for the background magnetic field, with the equatorial field intensity equivalent to that at L = 6. The cold electron density follows an empirical density model, $n_e\left(\lambda \right)=n_e^{eq}{\cos }^{-4}\lambda$ (Denton et al., 2004), where $n_e^{eq}=5c{m}^{-3}$ is the equatorial electron density. The upper atmosphere boundary is set at an altitude of 100 km, where electrons are considered lost. All whistler-mode waves are released from the equator and propagate with wave normal angle of $0^{\circ }$ to both hemispheres up to magnetic latitude of ${30}^{\circ }$. The whistler-mode wave frequency is set to $0.3f_{ce}^{eq}$ for all simulations, where $f_{ce}^{eq}$ is the equatorial electron gyrofrequency. The latitudinal distribution of wave amplitude follows $B_w\left({\lambda }_{\mathit{deg}}\right)=B_w^0\tanh \left({\lambda }_{eq}\right)\tanh \left({{30}^{\circ }-\lambda }_{eq}\right)$. Here $B_w^0$ is the wave amplitude of choice for each simulation, which is assumed to be uniform versus time, and ${\lambda }_{\mathit{deg}}$ is the magnetic latitude measured in unit of degrees. Initial electron energy ranges from 10 keV to 1 MeV, with 20 energy bins uniformly distributed in logarithmic space.

Initial electron equatorial pitch angle ranges from $0^{\circ }$ to ${90}^{\circ }$, with 360 uniform bins. For simulations of electron PSD distribution, electrons are released with 90 uniform bins of gyro-phase from $0^{\circ }$ to $360^{\circ }$, and 30 uniform bins of magnetic latitudes between the two mirror points. Initial electron PSD distribution is:

$f\left({\alpha }_{eq},E\right)=\left\{\begin{array}{l}j\left(E\right)\sin {\alpha }_{eq}{\alpha }_{eq}>{\alpha }_{lc}\\ 0{\alpha }_{eq}\le {\alpha }_{lc}\end{array}\right.(1)$

$j\left(E\right)={10}^{11.45-3.11{\log }_{10}\left(E\right)}(2)$

Here, ${\alpha }_{eq}$ is the equatorial pitch angle, ${\alpha }_{lc}$ is the loss cone calculated at the equator, and $E$ is the electron energy in keV. This distribution is calculated based on the time averaged electron flux measured by Van Allen Probe A during the time interval of 19:40:00 to 20:10:00 UT on 20th January 2016, during a microburst conjunction event reported in Breneman et al. (2017). The full initial PSD distribution in pitch angle-energy space is shown in Figure 2A. The fitting of the Van Allen Probe measurements is shown in Supplementary Figure S1 in the Supplementary Material. For simulations calculating the electron diffusion and advection coefficients, 360 electrons are released from the equator with initial gyro-phase uniformly distributed between $0^{\circ }$ and ${360}^{\circ }$ within each pitch angle-energy bin. The calculation of diffusion and advection coefficients for different resonant interactions is discussed in more detail in Section 3.3.

2.2 Quasilinear theory and quasi-equilibrium state (QES) of electron precipitation

Test particle simulation results are quantitatively compared to quasilinear results. Quasilinear diffusion coefficients are calculated based on Ma et al. (2018), using the same background and wave parameters, as described in Section 2.1. Electron PSD distribution near the loss cone at the quasi-equilibrium state is calculated following Kennel and Petschek (1966):

$J_{in}\left({\alpha }_{eq,in},E\right)=\frac{S\left(E\right)}{D^{*}}\left\{\frac{I_0\left(\frac{{\alpha }_{eq,in}}{{\alpha }_{lc}}{z}_0\right)}{z_0{I}_1\left(z_0\right)}\right\}(3)$

$J_{out}\left({\alpha }_{eq,out},E\right)=\frac{S\left(E\right)}{D^{*}}\left\{\frac{I_0\left(z_0\right)}{z_0{I}_1\left(z_0\right)}+\ln \left(\frac{\mathit{sin}{\alpha }_{eq,out}}{\mathit{sin}{\alpha }_{lc}}\right)\right\}(4)$

Here $S\left(E\right)$ is the rate of electrons entering the loss cone, $z_0=\frac{{\alpha }_{lc}}{\sqrt{D^{*}\tau }}$, $D^{*}\approx D_{\alpha \alpha }{|}_{\alpha ={\alpha }_{lc}}\times \cos \left({\alpha }_{lc}\right)$, $D_{\alpha \alpha }{|}_{\alpha ={\alpha }_{lc}}$ is the pitch angle diffusion coefficient at the equatorial loss cone ${\alpha }_{lc}$, ${\alpha }_{eq,in}$ and ${\alpha }_{eq,out}$ are the equatorial pitch angles inside and outside the loss cone, respectively, $E$ is the electron energy, $\tau$ is a quarter of the electron bounce period, and $I_0$ and $I_1$ are the modified Bessel functions. Electron precipitation flux ratio, which is the ratio of precipitation to trapped flux, is calculated based on Eqs 3, 4.

$\chi \left(E\right)=\frac{\frac{1}{{\alpha }_{lc}}{\int }_0^{{\alpha }_{lc}}{J}_{in}\mathit{sin}\alpha d\alpha }{\frac{1}{{\alpha }_{sc}-{\alpha }_{lc}}{\int }_{{\alpha }_{lc}}^{{\alpha }_{sc}}{J}_{out}\mathit{sin}\alpha d\alpha }(5)$

Here, ${\alpha }_{sc}=\arcsin \left(\sqrt{\frac{B_{eq}}{B_{sc}}}\right)$, where $B_{eq}$ is the Earth’s equatorial dipole magnetic field intensity at L shell of 6, and $B_{sc}$ is the field intensity at magnetic latitude of ${64.72}^{\circ }$ at the same L shell, which corresponds to an altitude of 600 km. This is the altitude of the FIREBIRD (Focused Investigations of Relativistic Electron Burst Intensity, Range, and Dynamics) CubeSat as reported in Breneman et al. (2017). Equation 5 is set to mimic the flux ratio one would observe by a typical LEO CubeSat. The precipitation flux ratio from test particle simulations is also calculated using Eq. 5.

2.3 Identification of phase trapping electrons

To quantify the contribution of different nonlinear processes, we identify the electrons that are phase trapped or anomalously trapped during simulations of half bounce-period. The key characteristic of nonlinearly trapped electrons is that they stay in resonance with whistler-mode waves for an extensive amount of time. The resonance is identified by calculating the relative phase speed $\dot{\zeta }=d\zeta /dt$, where $\zeta$ is the phase angle between the electron perpendicular velocity and the wave magnetic field vector (for detailed definition of $\zeta$, see Tao and Bortnik (2010)). $\dot{\zeta }=0$ marks the moment when an electron is in resonance with whistler-mode waves. Electrons that cross the resonance line for more than n = 5 times are identified as the phase/anomalous trapping electrons. The criterion of 5 is arbitrarily selected to exclude any electrons that are detrapped quickly.

3 Results

3.1 Electron precipitation in nonlinear regime

Figure 1 illustrates the typical trajectories of electrons interacting with intense whistler-mode waves of 1 nT, which represents typical nonlinear interactions. In Figures 1A, B, 360 electrons initially with an energy of 50 keV and an equatorial pitch angle of 10° move from the mirror point to the equator. All of these electrons experience anomalous trapping, leading to a significant increase in their pitch angles and energies. In this particular case, none of the electrons are precipitated, but their pitch angles increase due to the nonlinear interactions. Electrons with the same energy, but smaller pitch angles also undergo anomalous trapping, preventing any electrons close to the loss cone from being precipitated in the typical nonlinear regime. For electrons with the same energy (50 keV) but slightly larger pitch angles (13.5°), the probability of anomalous trapping decreases, as shown in Figures 1C, D. The non-trapping electrons experience positive bunching (Gan et al., 2020), which also leads to an increase in their pitch angles. Consequently, all electrons in this scenario are further affected by the anomalous scattering, resulting in no precipitation. When the pitch angles are even higher (18°), electrons exhibit the typical nonlinear phase trapping and phase bunching features. Figures 1E, F demonstrate that phase trapping increases the electron pitch angle and energy, while phase bunching decreases them. In this case, phase bunching scatters electrons into the loss cone, driving precipitation. The typical nonlinear interactions depicted in Figure 1 indicate that electron precipitation in the nonlinear regime is primarily driven by phase bunching, which only occurs when the equatorial pitch angle is sufficiently large, surpassing the pitch angle range considered in the quasilinear theory.

FIGURE 1

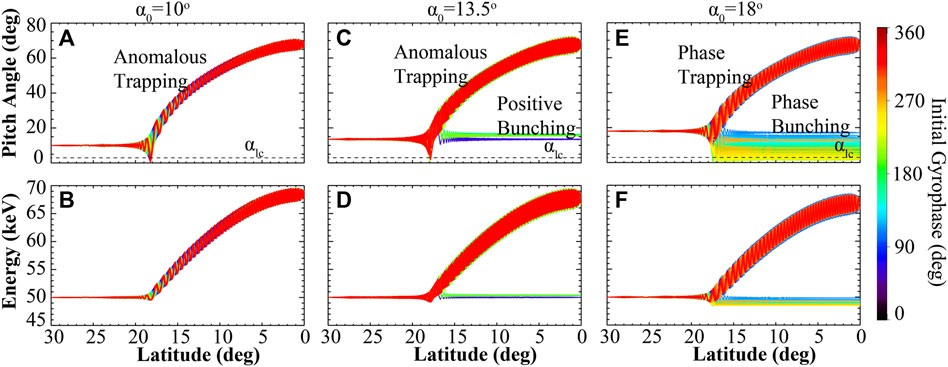
FIGURE 1. Typical interactions between electrons ($E_k=50keV$) and intense whistler-mode waves ($B_w=1nT$). (A) Pitch angle variation versus magnetic latitude of electrons with an initial equatorial pitch angle of ${10}^{\circ }$, undergoing anomalous trapping, color coded for different initial gyro-phases; (B) energy variation of the same electrons as those in (A); (C,D) same as (A,B) but for electrons with an initial equatorial pitch angle of ${13.5}^{\circ }$, undergoing anomalous trapping and positive bunching; (E,F) same as (A,B) but for electrons with an initial equatorial pitch angle of ${18}^{\circ }$, undergoing phase trapping and phase bunching. The horizontal black dashed lines mark the equatorial loss cone. Note that only interactions in Panels (E,F) lead to electron precipitation.

To assess the combined effects of various nonlinear processes on electron precipitation, we conducted three sets of test particle simulations lasting for 20 s each. These simulations employed three different wave amplitudes: 50 pT, 200 pT, and 1 nT. All models shared the same initial PSD distribution, described by Eqs 1 2 and displayed in Figure 2A. The PSD evolution of the precipitating electrons is illustrated in Figure 2B (Nunn and Omura, 2015), with colors representing different energies. Dashed, dotted, and solid lines correspond to wave amplitudes of 50 pT, 200 pT, and 1 nT, respectively. A common characteristic observed in all models and energy ranges is the significant variability of precipitating electron PSD during the initial few seconds of the simulations. However, it tends to stabilize within 20 s, indicating the quasi-equilibrium state. In this state, the overall shapes of the electron PSD distributions in pitch angle and energy change slowly and can be considered stable. This paper will primarily focus on discussing the QES derived from the test particle simulations and comparing it to the results obtained from the quasilinear approach. It is important to note that the precipitation PSD in the QES is lower than that observed within the first 1–2 s. Consequently, some of the conclusions drawn from the QES may not be applicable to events observed on timescales shorter than approximately 1 s, such as microbursts (Zhang et al., 2022b).

FIGURE 2

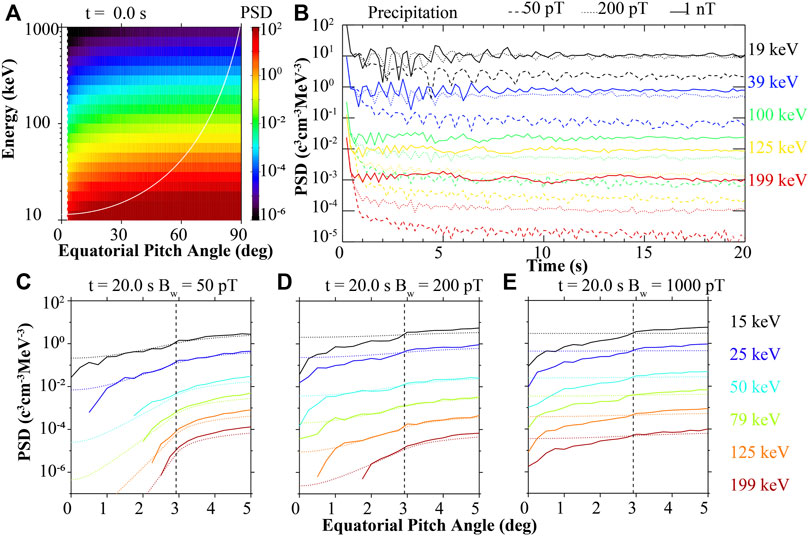
FIGURE 2. The PSD evolution of the precipitating electrons driven by whistler-mode waves with different wave amplitudes. (A) Initial PSD distribution in equatorial pitch angle-energy space. The vertical black dashed line marks the loss cone. The white solid line marks the minimum resonant energy. (B) Precipitation PSD variation versus time, color coded for different energies. Dashed, dotted, and solid lines represent the model results using whistler-mode amplitude of 50 pT, 200 pT, and 1 nT, respectively. (C–E) Pitch angle distribution of electron PSD near the loss cone after 20 s of simulations using wave amplitude of 50 pT, 200 pT, and 1 nT, respectively, color coded for different energies. The loss cone is marked by the vertical dashed lines. The dotted lines are the results calculated with quasilinear methods.

Based on the evolution of the precipitation PSD presented in Figure 2B, we extracted a snapshot of the electron PSD at a simulation time of 20 s and compared it to the expected QES based on the calculations from quasilinear theory (Eqs 3, 4). The results are displayed in Figures 2C, D, E for wave amplitudes of 50 pT, 200 pT, and 1 nT, respectively, with colors indicating different energy levels. The corresponding dotted lines represent the quasilinear results. As depicted in Figure 2C, for a wave amplitude of 50 pT, the test particle results align well with the quasilinear results, except for deep within the loss cone at low energies. The lack of electrons deep within the loss cone is attributed to the method used for setting the atmosphere boundary in test particle simulations, which does not include any backscattering processes. This demonstrates the applicability of quasilinear models when the wave amplitude is not sufficiently intense to induce nonlinear interactions. For an amplitude of 200 pT, the test particle results match the quasilinear predictions for energies above approximately 50 keV. However, at lower energies, the test particle PSD is lower than the quasilinear results within the loss cone. Additionally, the test particle results exhibit a similar shape in the PSD distribution within the loss cone. For a wave amplitude of 1 nT, similar PSD distributions are observed for all energy levels, and they are consistently smaller than the quasilinear expectations. The outcomes depicted in Figures 2D, E highlight that nonlinear interactions generate comparable PSD pitch angle distributions for different energy levels within the loss cone, all of which are lower than the quasilinear expectations. The specific nonlinear processes driving these observed features are analyzed in Section 3.2.

3.2 Nonlinear processes driving electron precipitation

To investigate the specific nonlinear processes driving electron precipitation, we tracked the electrons that were precipitated at time $t_1=20s$. Their PSD distributions in the equatorial pitch angle-energy space at different times $t_0$ are illustrated in Figure 3. Figures 3A, B display the tracing results for models using a wave amplitude of 200 pT at $t_0$ of 19.8 s and 19 s, respectively. The typical quarter-bounce period of electrons is about 0.3 s (energy of 100 keV and pitch angle of $5^{\circ }$). For a whistler-mode wave with a fixed single frequency, electrons can only resonate with the wave once during one quarter-bounce period. Thus, the two timesteps illustrated the precipitation effects of 1 ($t_0=19.8$ s) to about 3 cyclotron resonant interactions ($t_0=19.0s$) with whistler-mode waves. In both cases, sources located away from the loss cone contribute to the precipitation PSD for energies below 30 keV, where PSD distributions of nonlinear characteristics were observed in Figures 3C, D. These source electrons are transported into the loss cone by the nonlinear phase bunching processes since diffusive processes cannot transport electrons nonlocally in just 1-3 cyclotron resonances. A diffusive precipitation mechanism would also result in a continuous PSD distribution, while discrete distributions are shown in Figure 3. Specifically, for an amplitude of 1 nT, the contribution of phase bunching electrons and anomalous scattering is dominant over diffusive processes. For the case of 200 pT, both diffusive scattering and phase bunching contribute to precipitation, as denoted by the two initial PSD distributions separated by a gap (Figures 3A, B). The gaps of PSD distribution are exhibited for both cases of 200 pT and 1 nT. These gaps arise due to the presence of anomalous scattering, which transport electrons to sufficiently large pitch angles and prevent them from precipitation. This pattern, observed in Figures 3A, B, is more pronounced when the wave amplitude is 1 nT by crossing the entire resonant energy range, as shown in Figures 3C, D. In this scenario, anomalous scattering dominates a significant range of pitch angle and energy, resulting in the substantial gaps illustrated in Figures 3C, D. Moreover, the advection effects of nonlinear phase bunching are evident in Figure 3C, as they transport electrons into the loss cone from pitch angles as large as 30° within a time span of 0.2 s. The outer pitch angle boundary of the gaps, which corresponds to the inner boundary of the phase bunching source, converges to smaller pitch angles as the energy increases. This observation aligns with the theoretical predictions presented by Albert et al. (2021) and Artemyev et al. (2021b). The tracing results in Figure 3 demonstrate that anomalous scattering plays a prominent role at lower energies and larger wave amplitudes, effectively preventing a majority of electrons from undergoing precipitation, as indicated by the gap right outside of the loss cone in Figure 3. The pitch angle range of the gaps resulting from these two nonlinear processes can extend up to 20° (30°) for wave amplitudes of 200 pT (1 nT). The only mechanism directly driving precipitation in the nonlinear regime is phase bunching.

FIGURE 3

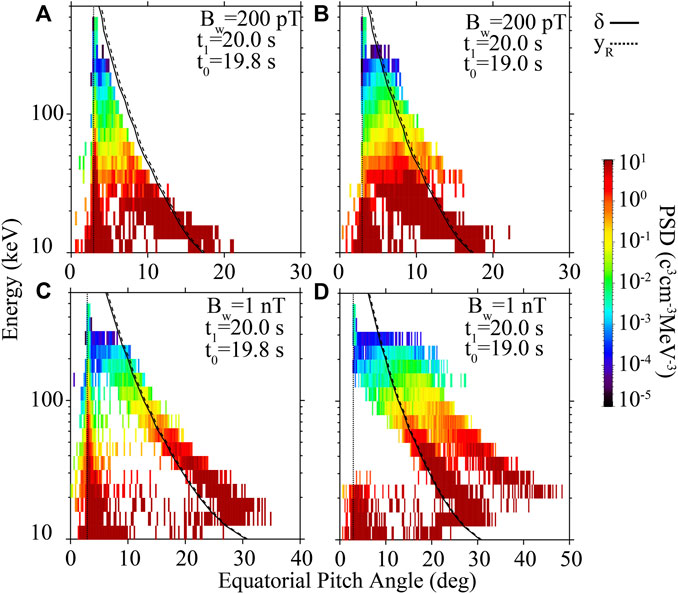
FIGURE 3. PSD distribution of precipitated electrons at time $t_0$, with $t_1$ being the time of precipitation. (A) PSD distribution at 19.8 s with an amplitude of 200 pT; (B) PSD distribution at 19 s with an amplitude of 200 pT; (C,D) same as (A,B) but with an amplitude of 1 nT. The solid and dashed black lines are contours of $\delta =0$ and $y_R=1$, respectively, depicting the theoretical boundary of anomalous trapping.

We further confirm this mechanism we propose, by comparing the tracing results with the theoretical analysis by Albert et al. (2021) and Artemyev et al. (2021a). For anomalous trapping to occur, Albert et al. (2021) provides the criterion $\delta <0$, where

$\delta =\frac{2}{3}\frac{{\eta }^2{\left(1-\frac{1}{{\eta }^2}\right)}^{\frac{2}{3}}}{{\left(\frac{B_w}{B_0}\right)}^{\frac{2}{3}}}\frac{\omega }{{\mathrm{\Omega }}_c}{I}_{res}-1.(6)$

Here, $\eta$ is the refractive index, $B_w$ is the wave amplitude, $B_0$ is the background magnetic field, $\omega$ is the wave frequency, ${\mathrm{\Omega }}_c$ is the electron gyrofrequency, and $I_{res}$ is the resonant value of action $I$ (for the full definition see Equation (5) in Albert et al. (2021)). Similarly, Artemyev et al. (2021b) provides the criterion for anomalous trapping as $y_R<1$, where

$y_R=\frac{2}{3}\frac{{\kappa }^{\frac{2}{3}}{k}^2{c}^2}{{\gamma }_0^{\frac{4}{3}}{\mathrm{\Omega }}_c^2}\frac{I_R{\mathrm{\Omega }}_c}{m_e{c}^2{\left(\frac{B_w}{B}\right)}^{\frac{2}{3}}}.(7)$

Here, $\kappa ={\gamma }_0^2-{\left(\frac{{\mathrm{\Omega }}_c}{kc}+\sqrt{{\gamma }_0^2-1}\right)}^2$, ${\gamma }_0$ is the Lorentz factor of electrons, $k$ is the wave vector, $c$ is the speed of light, and $I_R$ is the resonant value of action I (for full definition see Eq. 6 in Artemyev et al. (2021a)). $\delta$ and $y_R$ are equivalent parameters only in a slightly different format. For completeness, we show both parameters here. $\delta =0$ and $y_R=1$ are plotted in Figure 3 with solid and dashed lines, respectively. As is shown in Figure 3, the outer boundary of the gap qualitatively agrees with the theoretical boundaries. This confirms our proposed mechanism that the gap is due to nonlinear anomalous scattering. Note that the agreement between the test particle result and the theoretical boundaries is better for the amplitude of 1 nT than 200 pT. This is because the theoretical analysis is focused on the anomalous trapping while the positive bunching is not included, and the anomalous trapping probability is much larger for 1 nT. We will discuss the comparison with theoretical results in more detail in Section 3.3.

Based on the analysis presented above, we discuss the mechanisms governing electron precipitation in the presence of nonlinear interactions. Figure 4B provides an illustration of the pitch angle-energy space, where the phase bunching boundary is depicted. This boundary represents the inner limit within which phase bunching can occur, transporting electrons toward the vicinity of the loss cone. The advection and diffusion effects associated with the phase bunching process determine whether the electrons move into or out of the loss cone. For equatorial pitch angles smaller than the phase bunching boundary values, the dominant effect of anomalous scattering causes electrons to scatter into higher pitch angles. Consequently, electrons within the phase bunching boundary cannot undergo direct precipitation through nonlinear interactions with whistler-mode waves. However, once they are transported outside of this boundary, they undergo precipitation through the phase bunching process. Furthermore, the phase bunching boundary converges to smaller pitch angles as the energy increases, as indicated by the values $\delta =0$ and $y_R=1$ in Figure 3.

FIGURE 4

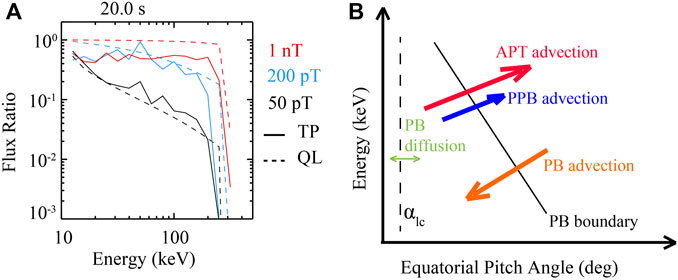
FIGURE 4. (A) Precipitation to trapped electron flux ratio versus energy, color coded for different wave amplitudes. The dashed lines mark the quasilinear results, and the solid lines represent the test particle results. (B) Illustration of electron precipitation mechanisms in the pitch angle and energy space in the nonlinear regime. Here, APT represents Anomalous Phase Trapping; PPB represents Positive Phase Bunching; PB represents Phase Bunching.

We further quantify the precipitation in the nonlinear regime by calculating the precipitation flux ratio and comparing it to the quasilinear QES expectations defined in Eq. 5. The comparison is presented in Figure 4A, where solid lines represent the test particle results and dashed lines represent the quasilinear results. Different colors correspond to different wave amplitudes. In the quasilinear regime, the test particle flux ratio aligns well with the quasilinear results, as demonstrated by the black lines representing an amplitude of 50 pT. For an amplitude of 1 nT, the quasilinear theory predicts a completely filled loss cone for all resonant energies. However, the test particle simulations, which are dominated by nonlinear processes across the entire energy range, yield a smaller flux ratio compared to the quasilinear theory. For an amplitude of 200 pT, nonlinear processes dominate the precipitation for energies below approximately 30 keV, as evidenced by the results in Figures 3A, B, which were discussed earlier. Consistently, Figure 4A illustrates that the test particle flux ratio is smaller than the quasilinear results below approximately 30 keV. However, for higher energies, the test particle results closely match the quasilinear ones, indicating that quasilinear processes are the main driving mechanism for electron precipitation in that energy range. Overall, the results suggest that nonlinear precipitation leads to a flux ratio smaller than that predicted by quasilinear expectations.

3.3 Nonlinear diffusion and advection

As is shown in Figure 4A, electron precipitation in the nonlinear regime is driven by the combination of various nonlinear processes. Thus, quantification of the nonlinear diffusion and advection is critical for the understanding of nonlinear precipitation processes. Figure 5 shows the diffusion coefficients based on quasilinear theory and test particle simulations for nonlinear waves (200 pT and 1 nT). The bounce-averaged quasilinear coefficients are calculated based on Ma et al. (2018), and are shown in Figures 5A, D for amplitudes of 200 pT and 1 nT, respectively. Quasilinear diffusion coefficients at the equatorial loss cone ($D_{\alpha \alpha }{|}_{\alpha ={\alpha }_{lc}}$) are used to calculate the flux ratio in Figure 4A following Eq. 5. As is shown in both panels, $D_{\alpha \alpha }{|}_{\alpha ={\alpha }_{lc}}$ decreases with increasing energy. $D_{\alpha \alpha }{|}_{\alpha ={\alpha }_{lc}}$ with the amplitude of 1 nT (Figure 5D) is also much larger than that with the amplitude of 200 pT (Figure 5A), since $D_{\alpha \alpha }\propto B_w^2$. Diffusion coefficients calculated using test particle simulations are shown in Figures 5B, E. The test particle diffusion coefficients $D_{\alpha \alpha }$ are:

$D_{\alpha \alpha }^{TP}=\frac{1}{2\tau }\overline{{\left({\alpha }_{eq}-\overline{{\alpha }_{eq}}\right)}^2}(8)$

FIGURE 5

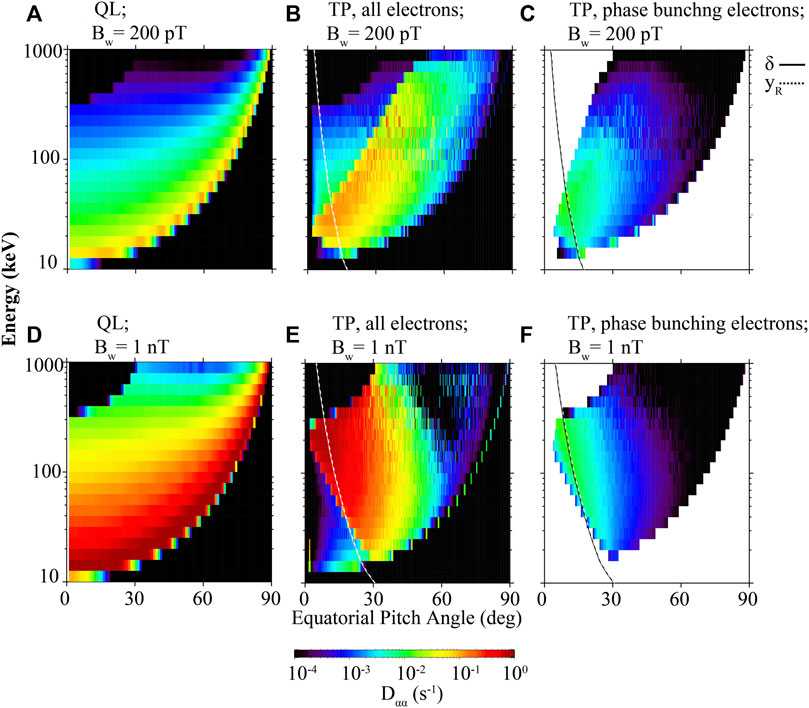
FIGURE 5. Diffusion coefficients of different electron populations and wave amplitudes, within the equatorial pitch angle-energy space. (A) Quasilinear diffusion coefficients; (B) diffusion coefficients of all electrons from test particle simulations; (C) diffusion coefficients of phase bunching electrons for the amplitude of 200 pT from test particle simulations. (D–F) Same as (A–C) but for the amplitude of 1 nT. The solid and dashed white lines are contours of $\delta =0$ and $y_R=1$, respectively.

Here, $\tau$ is a quarter of electron bounce period, ${\alpha }_{eq}$ is the electron equatorial pitch angle. For the amplitude of 200 pT, test particle diffusion coefficients show a similar range of values compared to the quasilinear results, but with a different distribution. The peak diffusion values are distributed in the middle of the resonant region (Figure 5B), instead of being near the minimum resonant energy (Figure 5A). Two sharp transition boundaries correspond to the maximum diffusion coefficients in Figure 5B. One is at the region of low energy and small pitch angle, extending from pitch angle near the loss cone and energy of ∼30 keV to pitch angle of ∼ ${15}^{\circ }$ and energy of ∼15 keV, which is at minimum resonant energy boundary. This boundary marks the phase bunching boundary defined in Figure 4B. The solid and dashed lines represent the theoretical boundaries from Albert et al. (2021) and Artemyev et al. (2021b), as is shown above in Figure 3. Similar to the conclusions in Section 3.2, the theoretical boundaries agree with numerical phase bunching boundary qualitatively but show a small offset in pitch angle. For regions to the left of the boundary, diffusion coefficients from test particle simulations are much smaller than quasilinear results. This is because anomalous trapping is dominant for this region, and trapping processes result in only advection without diffusion. The other sharp transition boundary extends from pitch angles near the loss cone and energy of ∼30 keV to pitch angle of ∼ ${45}^{\circ }$ and energy of 500 keV. This is the nonlinear boundary, i.e., the boundary between nonlinear and quasilinear regimes. Electrons to the left of this boundary interact with whistler-mode waves through quasilinear processes, which shows a similar diffusion coefficient distribution as the quasilinear results shown in Figure 5A. For the amplitude of 1 nT, only one of these two sharp boundaries exists, specifically the phase bunching boundary. This is because nonlinear interactions are dominant for the entire resonant region, and thus the nonlinear boundary disappeared. The theoretical bunching boundaries, also shown by solid and dashed lines, agree with the numerical boundary better compared to the case of 200 pT. The maximum diffusion coefficients shown in both Figures 5B, C are located at the upper nonlinear or resonant boundaries. Such distributions are due to the strong modulation of diffusion coefficients caused by the nonlinear phase trapping, which is most significant when the resonant latitude is largest (Gan et al., 2020). However, as is shown in Section 3.2, phase bunching is the only process that directly precipitates electrons into the nonlinear regime. Thus, we calculate the diffusion coefficients specifically for phase bunching electrons by excluding the modulation from phase trapping in the nonlinear regime. The phase bunching diffusion coefficients are calculated following the equation below:

$D_{\alpha \alpha }^{PB}=\frac{1}{2\tau }\overline{{\left({\alpha }_{eq}^{PB}-\overline{{\alpha }_{eq}^{PB}}\right)}^2}(9)$

The parameters are the same as those of Eq. 8 but for phase bunching electrons only. The phase bunching electrons are identified by excluding the phase trapping electrons. Identification of phase trapping is described in Section 2.3. $D_{\alpha \alpha }^{PB}$ for amplitudes of 200 pT and 1 nT are shown in Figures 5C, F, respectively. Phase bunching diffusion coefficients are much smaller than the diffusion coefficients calculated from quasilinear theory or from all electron populations in the test particle simulations. This simulation result confirms the previous theoretical analysis as shown in Figure 8 of Frantsuzov et al. (2023). For the amplitude of 200 pT (Figure 5C), phase bunching diffusion coefficients are only distributed in the region below the nonlinear boundary. This is because phase bunching only exists within this nonlinear regime. The maximum phase bunching diffusion coefficients are distributed close to the two boundaries defined above. For the amplitude of 1 nT, phase bunching diffusion coefficients are distributed to the right of the phase bunching boundary since anomalous trapping dominates the region to the right. The maximum diffusion coefficients for the amplitude of 1 nT is also located close to the phase bunching boundary.

Advection coefficients and the ratio of phase/anomalous trapping electrons are presented in Figure 6. Results for the amplitude of 200 pT and 1nT are shown in Figures 6A–C, and Figures 6D–F, respectively. As is shown in Figure 6A, phase trapping ratio, i.e., the ratio between the number of phase trapping electrons and the total population, is highest to the left of the phase bunching boundary, which reaches a value of 50%. Phase trapping advection is shown in Figure 6B, which is quantified by the average of equatorial pitch angle variation of the phase trapping electrons. Phase trapping advection is highest at the nonlinear boundary. Advection of the phase bunching is also denoted by the average of equatorial pitch angles for the phase bunching electrons. For small pitch angle region, phase bunching advection is positive due to dominant positive bunching processes, as shown in Figure 1B. The boundary of the positive advection agrees with the theoretical boundaries qualitatively well. Regarding the results for the amplitude of 1 nT (Figures 6D–F), anomalous trapping probability reaches 100% within the phase bunching boundary. Phase trapping advection shows a similar distribution to that of 200 pT, with the highest advection at the upper resonant energy boundary, which corresponds to the highest resonant latitude. For advection of bunching electrons, positive bunching only occurs for pitch angles close to the phase bunching boundary with high energy. It is worth noting that the bunching processes are not possible for most regions left of the phase bunching boundary, due to the 100% trapping ratio.

FIGURE 6

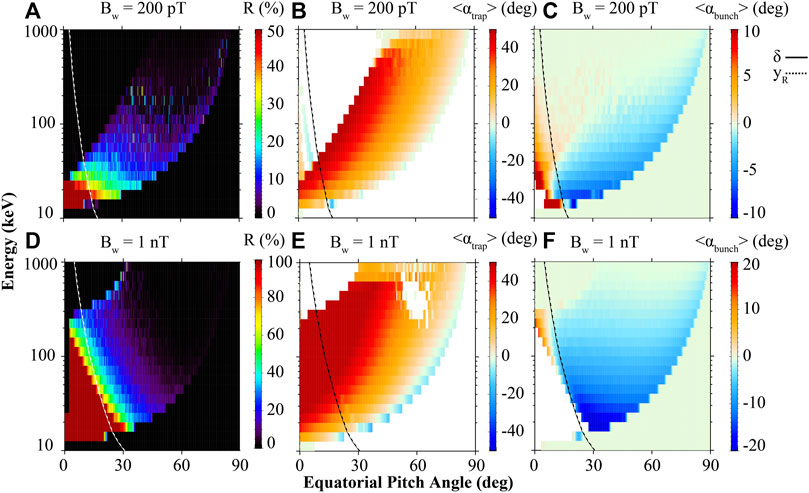
FIGURE 6. Phase trapping ratio and advection coefficients of both phase trapping and bunching distribution in equatorial pitch angle-energy space. (A) Phase trapping ratio; (B) advection coefficients of phase trapping electrons; (C) advection coefficients of phase bunching electrons for the amplitude of 200 pT. (D–F) Same as (A–C) but for the amplitude of 1 nT. Solid and dashed lines mark the theoretically calculated phase bunching boundary based on Albert et al. (2021) and Artemyev et al. (2021a), respectively.

In Figure 7, we show the diffusion coefficients and advection coefficients of nonlinear processes with color coded lines for different energies to present their characteristics more clearly. Diffusion coefficients of phase bunching electrons for the wave amplitude of 200 pT are shown in Figure 7A in solid lines. As is shown in Figure 5C, for the amplitude of 200 pT, wave-particle interactions transit to the quasilinear regime as the electron pitch angle decreases and energy increases. We also show quasilinear diffusion coefficients of this region with dotted lines in Figure 7A for completeness, as phase bunching is not possible within the quasilinear regime. Pitch angle diffusion coefficients, shown in logarithmic scale, mostly decrease linearly as pitch angle increases. For nonlinear energy range (<40 keV), diffusion coefficients have similar values for a specific pitch angle, with the nonlinear pitch angle range extending to smaller pitch angles for lower energies. For higher energies, the quasilinear process is dominant. Quasilinear diffusion coefficients increase with pitch angle and decrease with energy. Such reverse in energy dependence corresponds to the flux ratio distribution versus energy shown in Figure 4A. The flux ratio also increases with energy in the nonlinear regime and decreases in the quasilinear regime for amplitude of 200 pT. Advection coefficients of phase bunching electrons (200 pT) are shown in Figure 7B. For energies within the nonlinear regime, phase bunching shows positive advection for small pitch angles and negative advection for larger pitch angles. The absolute values of phase bunching advection coefficients decrease with increasing energy. For quasilinear energies (above 40 keV), close-to-zero advection is shown due to the dominant diffusion process. Advection coefficients of phase trapping electrons are presented in Figure 7C, and they increase with increasing energy, as discussed above. Results of the amplitude of 1 nT are shown in the same format in Figures 7D–F. In this case, all energies shown are in the nonlinear regime. Phase bunching diffusion coefficients of 1 nT for energies also follow the same trend, except for the pitch angle range close to the inner-most phase bunching boundary. Maximum diffusion coefficients also increase with increasing energy similar to what is shown in Figure 7A for the amplitude of 200 pT, but for all energies. Advection coefficients of phase bunching electrons decrease with increasing energy in the case of 1 nT. For lower energy electrons (<40 keV), only negative phase bunching advection is observed. For higher energies, advection is positive at small pitch angles, and negative at larger pitch angles. Advection coefficients of trapping electrons exhibit a similar pitch angle distribution and increase with increasing energy.

FIGURE 7

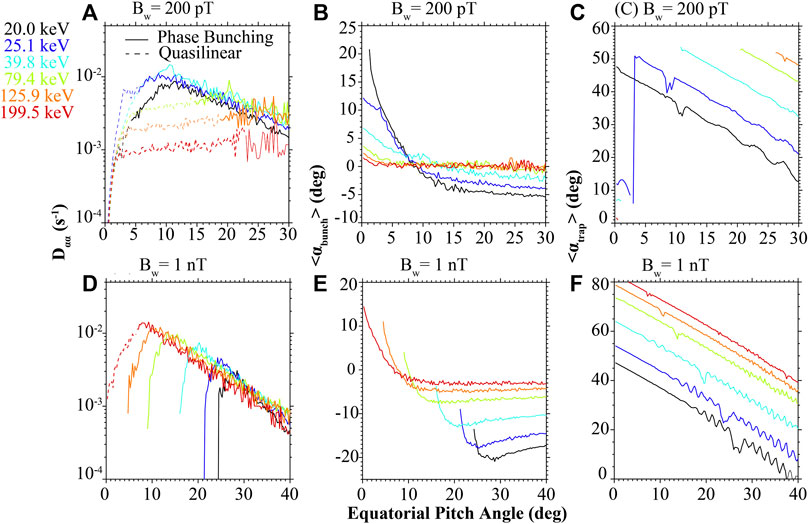
FIGURE 7. Diffusion coefficients and advection coefficients of phase bunching and trapping electrons. (A) Diffusion coefficients of phase bunching electrons interacting with the wave amplitude of 200 pT shown in solid lines, color coded for different energies. The dashed lines show the quasilinear diffusion coefficients in the quasilinear regime, where phase bunching is not possible. (B) Advection coefficients of phase bunching electrons; (C) advection coefficients of phase trapping electrons. (D–F) Same as (A–C) but for the amplitude of 1 nT.

4 Discussion

As discussed above, the precipitation flux ratio transits from nonlinear characteristics at low energies to quasilinear characteristics at high energies, when the wave amplitude is 200 pT. For the amplitude of 1 nT, however, nonlinear characteristics persist for all resonant energies. The distribution of such nonlinear characteristics can be quantitatively analyzed through the nonlinear inhomogeneity ratio. In Figures 8A, B, we show the distribution of inhomogeneity ratio S, which follows Omura et al. (2007):

$S=\frac{1}{2{\omega }_t^2{\delta }_{*}^2}\left\{\left[\left(2+{\delta }_{*}^2\frac{{\mathrm{\Omega }}_e-\gamma \omega }{{\mathrm{\Omega }}_e-\omega }\right)V_R-\frac{k\gamma v_{\perp }^2}{{\mathrm{\Omega }}_e}\right]\frac{\partial {\mathrm{\Omega }}_e}{\partial h}\right\}(10)$

FIGURE 8

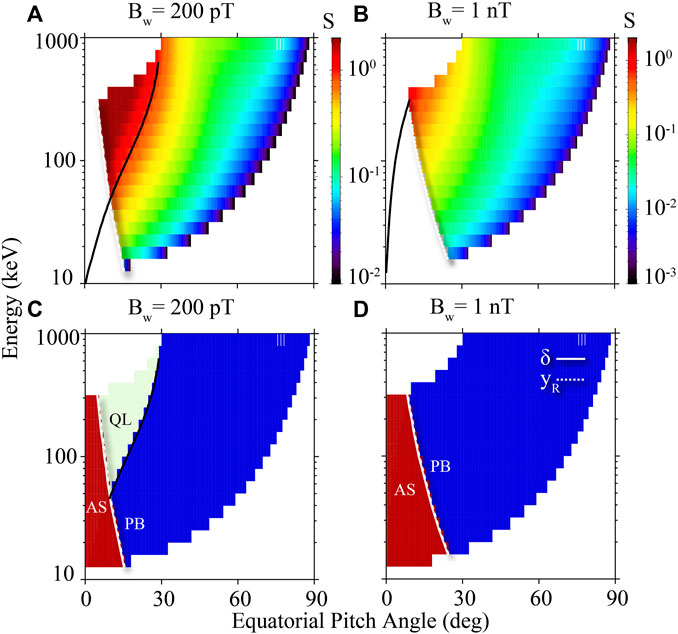
FIGURE 8. The distribution of inhomogeneity ratio and different regimes in electron equatorial pitch angle-energy space. (A) Inhomogeneity ratio (S) distribution for the amplitude of 200 pT. Black solid line marks the points where S = 1. The white solid and dashed lines mark the theoretically derived phase bunching boundary from Albert et al. (2021) and Artemyev et al. (2021b). (B) Inhomogeneity ratio S distribution for the amplitude of 1 nT. (C) Distribution of different regimes in pitch angle-energy space for the amplitude of 200 pT. Green region represents quasilinear regime, where electrons are diffused into the loss cone via quasilinear processes. Red region marks the region where electrons are anomalously trapped or positively bunched away from the loss cone. Blue region marks the region where electrons can be precipitated through phase bunching processes. (D) Same as (C) but for the amplitude of 1 nT.

Here, $\omega =0.3{\mathrm{\Omega }}_{e0}$, $v_{\perp }$ is the perpendicular electron velocity, and the definition of other parameters can be found in Eqs 1–11 in Omura et al. (2007). It is worth noting that ${\delta }_{*}$ is marked as $\delta$ in Omura et al. (2007). A different notation is applied here to avoid confusion with Eq. 6. The criterion of $\left|S\right|<1$ characterizes the nonlinear regime. The boundaries of nonlinear regimes defined by $\left|S\right|=1$ are marked with black solid lines in Figures 8A, B, corresponding to amplitudes of 200 pT and 1 nT. Within the nonlinear regime, $\delta =0$ and $y_R=1$ define the phase bunching boundary, which are represented by white solid and dashed lines in Figure 8. Nonlinear boundary and phase bunching boundary collectively define three regimes of different wave-particle interaction characteristics that are related to electron precipitation. The distributions of these three regimes are shown in Figures 8C, D for the amplitudes of 200 pT and 1 nT, respectively. Quasilinear regime, where only electrons very close to the loss cone are scattered into it and precipitated, is marked by green regions in Figure 8C. The red regions in these two panels mark the regime where electrons interact with whistler-mode waves through anomalous scattering. The blue regions mark the region where electrons undergo nonlinear phase trapping and phase bunching processes. As shown in Figure 8C, for the amplitude of 200 pT and energy below ∼40 keV, anomalous trapping and positive bunching transport electrons away from the loss cone and phase bunching dominates electron precipitation process. For energy above 40 keV, quasilinear diffusion drives the electron precipitation as the phase bunching boundary shifts closer to the loss cone. Such transition of driving mechanisms for precipitation at energy of 40 keV explains the flux ratio distribution shown in Figure 4A, which converges to quasilinear theory for energy above ∼40 keV. For the amplitude of 1 nT, anomalous trapping remains as the dominant wave-particle interaction for small pitch angles in the entire resonant energy range. Thus, phase bunching drives electron precipitation for all resonant energies. This corresponds to the nonlinear flux ratio for all energies, as shown in Figure 4A for the amplitude of 1 nT.

As shown in Figures 8A, B, the inhomogeneity ratio S is not calculated for small pitch angle regions, i.e., within the phase bunching boundary, which results in the gaps. This is because the inhomogeneity ratio S from Omura et al. (2007) is not suitable for analyzing electrons with very small equatorial pitch angles. The inhomogeneity ratio S is derived from Equation (5) of Omura et al. (2007): $\frac{d\zeta }{dt}=k\left(v_{\parallel }-V_R\right)$, where $\zeta$ is the relative phase between electron perpendicular velocity and wave magnetic field vector, $v_{\parallel }$ is the parallel velocity of electrons, and $V_R=\left(\omega -{\mathrm{\Omega }}_e/\gamma \right)/k$ is the resonance velocity. For small pitch angles, this simplified equation of phase variation is not accurate and a full version needs to be applied (Kitahara and Katoh, 2019):

$\frac{d\zeta }{dt}=k\left(v_{\parallel }-V_R\right)+\frac{e\left(E_w-v_{\parallel }{B}_W\right)}{m\gamma v_{\perp }}\mathit{cos}\zeta (11)$

Here, $e$ is the electron charge, $m$ is the electron mass, $E_w$ and $B_w$ are the wave electric and magnetic field respectively. The second term in Eq. 11 becomes comparable to or even much larger than the first term when electron pitch angle is small and thus cannot be dropped out of the equation. This complication at the small electron pitch angle requires the derivation of a new form of inhomogeneity for the electron precipitation scenario. Albert et al. (2021) presented parameters $R_0$, $R_2$, and $R_3$ which generalize the inhomogeneity parameter for small pitch angles regions. This is, however, not the focus of this paper and is left as future work. Although the current inhomogeneity is not applicable to the left of the phase bunching boundary (white lines), it is applicable to the right of it, when the second term in Eq. 11 becomes much smaller than the first term. Thus, the transition energy determined from intersection between the black and white lines is still qualitatively valid. In conclusion, by combining the current version of inhomogeneity ratio and bunching boundary, we can roughly estimate the energy at which precipitation transits from nonlinear to quasilinear characteristics, which increases with increasing wave amplitude. However, a more accurate expression for inhomogeneity ratio is still crucial for accurate quantification of the nonlinear precipitation regime.

The simulations in this paper assume a uniform wave amplitude, which may be approximated by a very long wave packet. As shown by Zhang et al. (2019), short and intense whistler-mode wave packets are also commonly observed in the Earth’s radiation belts. These short packets are able to resonate with electrons nonlinearly, but would significantly reduce the trapping effects, including the anomalous trapping (Mourenas et al., 2018; Gan et al., 2020; Artemyev et al., 2021a). This may lead to a more diffusive precipitation process, which was discussed in Mourenas et al. (2022). The effects of wave packet length, and the wave coherency (Zhang et al., 2020) need to be considered in the numerical simulations and are left as future extensions of this paper.

5 Conclusion

In this paper, we systematically estimate the combined effects of anomalous scattering and phase bunching caused by intense whistler-mode waves on electron precipitation. We proposed a new physical picture of energetic electron precipitation in the nonlinear regime. The transition of electron precipitation from quasilinear to nonlinear regimes is analyzed using current theories. Nonlinear diffusion and advection coefficients, which are crucial for the nonlinear precipitation processes, are also calculated using the test particle simulations. The key findings of this paper are summarized below:

1. Nonlinear electron precipitation is driven by phase bunching right outside the phase bunching boundary, instead of right outside of the loss cone.

2. Anomalous trapping and positive phase bunching prevent electrons within the phase bunching boundary from precipitation.

3. Nonlinear precipitation region is determined by both the phase bunching boundary and inhomogeneity ratio and is dominant at lower energies. The maximum energy for nonlinear precipitation increases with increasing wave amplitude.

4. Phase bunching driven precipitation leads to a smaller flux ratio compared to quasilinear expectations at the quasi-equilibrium state.

5. Maximum phase bunching diffusion coefficients are much smaller than those from quasilinear theory. Phase bunching diffusion coefficients near the phase bunching boundary increase with increasing energy.

The results from this study are based on purely parallel whistler-mode waves. Previous studies have also shown abundant large amplitude oblique whistler-mode waves with wave normal angles close to the resonance cone angle (e.g., Cattell et al., 2008; Li et al., 2016). The nonlinear effects for these quasi-electrostatic whistler-mode waves can be very different from parallel waves (Artemyev et al., 2013; Goyal et al., 2017; Goyal et al., 2018; Zhang et al., 2022a) and further investigation is needed to fully understand their roles in electron precipitation.

Determination of phase bunching boundary is crucial to understanding precipitation in the nonlinear regime. Previous theoretical analyses have provided rough estimates of this boundary. However, these theoretical analyses are focused on anomalous trapping and do not consider positive bunching process. Thus, the theoretical results do not agree with the numerical results well for the case of 200 pT where positive bunching also plays a significant role. Further numerical and theoretical studies that quantitatively determine the phase bunching are important and left as future work.

As shown in this paper, the pitch angle distribution of precipitation PSD is different from quasilinear expectations in the nonlinear regime, which leads to a smaller flux ratio. This could be due to the fact that phase bunching diffusion coefficients near the phase bunching boundary is much smaller than quasilinear diffusion coefficients near the loss cone. Theoretical expressions of the nonlinear precipitation PSD distribution using nonlinear diffusion and advection coefficients could serve as an interesting future study. Potential results from these future studies could also contribute to improving the method of calculating whistler-mode wave intensity based on the electron precipitation ratio proposed by Li et al. (2013), which relies on quasilinear theory (Kennel and Petschek, 1966). It is also important to evaluate the relative contributions of the advection and diffusion coefficients in driving the electron precipitation, as well as determine the precipitation to trapped flux ratio. For short timescales of several bounces, if the phase bunching advection coefficients are the dominant term, the precipitation ratio will be more sensitive to the electron pitch angle distribution and the large pitch angle gradient of the PSD near the phase bunching boundary could potentially lead to local peaks or an inverse PSD gradient within the loss cone. On the other hand, if phase bunching diffusion coefficients are dominant, the electron pitch angle distribution near the loss cone are not sensitive to the electron pitch angle distribution, similar to what was predicted by the quasilinear theory (e.g., Kennel and Petschek, 1966), although the distribution would be different from the quasilinear prediction due to the different diffusion coefficients from phase bunching, as discussed above. For longer timescales which is the focus of this study, the initial distribution should not have significant effects on electron precipitation with intense whistler-mode waves.

Inhomogeneity ratio has been commonly used to estimate the nonlinear effects of whistler-mode waves. However, as discussed in this paper, previous analytical expressions of the inhomogeneity ratio are not applicable concerning the precipitation problem, since the electron pitch angle is small and major assumptions of the derivation of these inhomogeneity ratios become invalid. Further studies on the correct form of inhomogeneity ratio at very small pitch angles are essential to our understanding of the role of nonlinear interactions in electron precipitation. This is beyond the scope of this paper and is left as a follow-up study.

Data availability statement

The original contributions presented in the study are publicly available. This data can be found here: https://doi.org/10.6084/m9.figshare.23282702.v1.

Author contributions

LG: Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. WL: Funding acquisition, Supervision, Writing–review and editing. MH: Writing–review and editing. QM: Writing–review and editing. JA: Writing–review and editing. AA: Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. At Boston University, this research is supported by NASA grants 80NSSC20K0698, 80NSSC19K0845, 80NSSC21K1312, and 80NSSC20K0196, NSF grants AGS-1847818, AGS-2019950, and AGS-2225445. LG gratefully acknowledges the NASA FINESST grant 80NSSC20K1506.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2023.1322934/full#supplementary-material

References

Albert, J. M. (1993). Cyclotron resonance in an inhomogeneous magnetic field. Phys. Fluids B Plasma Phys. 5 (8), 2744–2750. doi:10.1063/1.860715

CrossRef Full Text | Google Scholar

Albert, J. M., Meredith, N. P., and Horne, R. B. (2009). Three-dimensional diffusion simulation of outer radiation belt electrons during the 9 October 1990 magnetic storm. J. Geophys. Res. Space Phys. 114 (A9). doi:10.1029/2009JA014336

CrossRef Full Text | Google Scholar

Albert, J. M. (2000). Gyroresonant interactions of radiation belt particles with a monochromatic electromagnetic wave. J. Geophys. Res. Space Phys. 105 (A9), 21191–21209. doi:10.1029/2000JA000008

CrossRef Full Text | Google Scholar

Albert, J. M., Artemyev, A. V., Li, W., Gan, L., and Ma, Q. (2021). Models of resonant wave-particle interactions. J. Geophys. Res. Space Phys. 126 (6), e2021JA029216. doi:10.1029/2021JA029216

CrossRef Full Text | Google Scholar

Artemyev, A. V., Neishtadt, A. I., Albert, J. M., Gan, L., Li, W., and Ma, Q. (2021a). Theoretical model of the nonlinear resonant interaction of whistler-mode waves and field-aligned electrons. Phys. Plasmas 28 (5), 052902. doi:10.1063/5.0046635

CrossRef Full Text | Google Scholar

Artemyev, A. V., Neishtadt, A. I., Vainchtein, D. L., Vasiliev, A. A., Vasko, I. Y., and Zelenyi, L. M. (2018). Trapping (capture) into resonance and scattering on resonance: summary of results for space plasma systems. Commun. Nonlinear Sci. Numer. Simulations 65, 111–160. doi:10.1016/j.cnsns.2018.05.004

CrossRef Full Text | Google Scholar

Artemyev, A. V., Neishtadt, A. I., Vasiliev, A. A., and Mourenas, D. (2021b). Transitional regime of electron resonant interaction with whistler-mode waves in inhomogeneous space plasma. Phys. Rev. E 104 (5), 055203. doi:10.1103/PhysRevE.104.055203

PubMed Abstract | CrossRef Full Text | Google Scholar

Artemyev, A. V., Vasiliev, A. A., Mourenas, D., Agapitov, O. V., Krasnoselskikh, V., Boscher, D., et al. (2014). Fast transport of resonant electrons in phase space due to nonlinear trapping by whistler waves. Geophys. Res. Lett. 41 (16), 5727–5733. doi:10.1002/2014GL061380

CrossRef Full Text | Google Scholar

Artemyev, A. V., Vasiliev, A. A., Mourenas, D., Agapitov, O. V., and Krasnoselskikh, V. V. (2013). Nonlinear electron acceleration by oblique whistler waves: landau resonance vs. cyclotron resonance. Phys. Plasmas 20 (12), 122901. doi:10.1063/1.4836595

CrossRef Full Text | Google Scholar

Bellan, P. M. (2013). Pitch angle scattering of an energetic magnetized particle by a circularly polarized electromagnetic wave. Phys. Plasmas 20 (4), 042117. doi:10.1063/1.4801055

CrossRef Full Text | Google Scholar

Blake, J. B., Looper, M. D., Baker, D. N., Nakamura, R., Klecker, B., and Hovestadt, D. (1996). New high temporal and spatial resolution measurements by SAMPEX of the precipitation of relativistic electrons. Adv. Space Res. 18 (8), 171–186. doi:10.1016/0273-1177(95)00969-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Bortnik, J., Albert, J. M., Artemyev, A., Li, W., Jun, C.-W., Grach, V. S., et al. (2022). Amplitude dependence of nonlinear precipitation blocking of relativistic electrons by large amplitude EMIC waves. Geophys. Res. Lett. 49 (12), e2022GL098365. doi:10.1029/2022GL098365

PubMed Abstract | CrossRef Full Text | Google Scholar

Bortnik, J., Thorne, R. M., and Inan, U. S. (2008). Nonlinear interaction of energetic electrons with large amplitude chorus. Geophys. Res. Lett. 35 (21), 35500. doi:10.1029/2008GL035500

CrossRef Full Text | Google Scholar

Breneman, A. W., Crew, A., Sample, J., Klumpar, D., Johnson, A., Agapitov, O., et al. (2017). Observations directly linking relativistic electron microbursts to whistler mode chorus: van allen probes and FIREBIRD II. Geophys. Res. Lett. 44 (22), 265–272. doi:10.1002/2017GL075001

CrossRef Full Text | Google Scholar

Cattell, C., Wygant, J. R., Goetz, K., Kersten, K., Kellogg, P. J., Rosenvinge, T. V., et al. (2008). Discovery of very large amplitude whistler-mode waves in Earth’s radiation belts. Geophys. Res. Lett. 35 (1), 32009. doi:10.1029/2007GL032009

CrossRef Full Text | Google Scholar

Chen, L., Zhang, X.-J., Artemyev, A., Angelopoulos, V., Tsai, E., Wilkins, C., et al. (2022). Ducted chorus waves cause sub-relativistic and relativistic electron microbursts. Geophys. Res. Lett. 49 (5), e2021GL097559. doi:10.1029/2021GL097559

CrossRef Full Text | Google Scholar

Denton, R. E., Menietti, J. D., Goldstein, J., Young, S. L., and Anderson, R. R. (2004). Electron density in the magnetosphere. J. Geophys. Res. Space Phys. 109 (A9), 10245. doi:10.1029/2003JA010245

CrossRef Full Text | Google Scholar

Douma, E., Rodger, C. J., Clilverd, M. A., Hendry, A. T., Engebretson, M. J., and Lessard, M. R. (2018). Comparison of relativistic microburst activity seen by SAMPEX with ground-based wave measurements at Halley, Antarctica. J. Geophys. Res. Space Phys. 123 (2), 1279–1294. doi:10.1002/2017JA024754

CrossRef Full Text | Google Scholar

Frantsuzov, V. A., Artemyev, A. V., Zhang, X.-J., Allanson, O., Shustov, P. I., and Petrukovich, A. A. (2023). Diffusive scattering of energetic electrons by intense whistler-mode waves in an inhomogeneous plasma. J. Plasma Phys. 89 (1), 905890101. doi:10.1017/S0022377822001271

CrossRef Full Text | Google Scholar

Gan, L., Li, W., Ma, Q., Albert, J. M., Artemyev, A. V., and Bortnik, J. (2020). Nonlinear interactions between radiation belt electrons and chorus waves: dependence on wave amplitude modulation. Geophys. Res. Lett. 47 (4), e2019GL085987. doi:10.1029/2019GL085987

CrossRef Full Text | Google Scholar

Goyal, R., Sharma, R. P., and Gupta, D. N. (2018). Whistler mode localization and turbulence implicating particle acceleration in radiation belts. Phys. Plasmas 25 (12), 122903. doi:10.1063/1.5054635

CrossRef Full Text | Google Scholar

Goyal, R., Sharma, R. P., and Kumar, S. (2017). Nonlinear effects associated with quasi-electrostatic whistler waves relevant to that in radiation belts. J. Geophys. Res. Space Phys. 122 (1), 340–348. doi:10.1002/2016JA023274

CrossRef Full Text | Google Scholar

Grach, V. S., Artemyev, A. V., Demekhov, A. G., Zhang, X.-J., Bortnik, J., Angelopoulos, V., et al. (2022). Relativistic electron precipitation by EMIC waves: importance of nonlinear resonant effects. Geophys. Res. Lett. 49 (17), e2022GL099994. doi:10.1029/2022GL099994

CrossRef Full Text | Google Scholar

Grach, V. S., and Demekhov, A. G. (2020). Precipitation of relativistic electrons under resonant interaction with electromagnetic ion cyclotron wave packets. J. Geophys. Res. Space Phys. 125 (2), e2019JA027358. doi:10.1029/2019JA027358

CrossRef Full Text | Google Scholar

Hanzelka, M., Li, W., and Ma, Q. (2023). Parametric analysis of pitch angle scattering and losses of relativistic electrons by oblique EMIC waves. Front. Astronomy Space Sci. 10, 1163515. doi:10.3389/fspas.2023.1163515

CrossRef Full Text | Google Scholar

Henrard, J., and Lemaitre, A. (1983). A second fundamental model for resonance. Celest. Mech. 30 (2), 197–218. doi:10.1007/BF01234306

CrossRef Full Text | Google Scholar

Horne, R. B., Thorne, R. M., Glauert, S. A., Albert, J. M., Meredith, N. P., and Anderson, R. R. (2005). Timescale for radiation belt electron acceleration by whistler mode chorus waves. J. Geophys. Res. Space Phys. 110 (A3), 10811. doi:10.1029/2004JA010811

CrossRef Full Text | Google Scholar

Kennel, C. F., and Engelmann, F. (1966). Velocity space diffusion from weak plasma turbulence in a magnetic field. Phys. Fluids 9 (12), 2377–2388. doi:10.1063/1.1761629

CrossRef Full Text | Google Scholar

Kennel, C. F., and Petschek, H. E. (1966). Limit on stably trapped particle fluxes. J. Geophys. Res. 71 (1), 1–28. doi:10.1029/JZ071i001p00001

CrossRef Full Text | Google Scholar

Kitahara, M., and Katoh, Y. (2019). Anomalous trapping of low pitch angle electrons by coherent whistler mode waves. J. Geophys. Res. Space Phys. 124 (7), 5568–5583. doi:10.1029/2019JA026493

CrossRef Full Text | Google Scholar

Li, W., Ni, B., Thorne, R. M., Bortnik, J., Green, J. C., Kletzing, C. A., et al. (2013). Constructing the global distribution of chorus wave intensity using measurements of electrons by the POES satellites and waves by the Van Allen Probes. Geophys. Res. Lett. 40 (17), 4526–4532. doi:10.1002/grl.50920

CrossRef Full Text | Google Scholar

Li, W., Santolik, O., Bortnik, J., Thorne, R. M., Kletzing, C. A., Kurth, W. S., et al. (2016). New chorus wave properties near the equator from Van Allen Probes wave observations. Geophys. Res. Lett. 43 (10), 4725–4735. doi:10.1002/2016GL068780

CrossRef Full Text | Google Scholar

Li, W., Thorne, R. M., Ma, Q., Ni, B., Bortnik, J., Baker, D. N., et al. (2014). Radiation belt electron acceleration by chorus waves during the 17 March 2013 storm. J. Geophys. Res. Space Phys. 119 (6), 4681–4693. doi:10.1002/2014JA019945

CrossRef Full Text | Google Scholar

Lyons, L. R. (1974). Pitch angle and energy diffusion coefficients from resonant interactions with ion–cyclotron and whistler waves. J. Plasma Phys. 12 (3), 417–432. doi:10.1017/S002237780002537X

CrossRef Full Text | Google Scholar

Ma, Q., Li, W., Bortnik, J., Thorne, R. M., Chu, X., Ozeke, L. G., et al. (2018). Quantitative evaluation of radial diffusion and local acceleration processes during GEM challenge events. J. Geophys. Res. Space Phys. 123 (3), 1938–1952. doi:10.1002/2017JA025114

CrossRef Full Text | Google Scholar

Miyoshi, Y., Saito, S., Kurita, S., Asamura, K., Hosokawa, K., Sakanoi, T., et al. (2020). Relativistic electron microbursts as high-energy tail of pulsating aurora electrons. Geophys. Res. Lett. 47, e90360. doi:10.1029/2020GL090360

CrossRef Full Text | Google Scholar

Mourenas, D., Zhang, X.-J., Artemyev, A. V., Angelopoulos, V., Thorne, R. M., Bortnik, J., et al. (2018). Electron nonlinear resonant interaction with short and intense parallel chorus wave packets. J. Geophys. Res. Space Phys. 123 (6), 4979–4999. doi:10.1029/2018JA025417

CrossRef Full Text | Google Scholar

Mourenas, D., Zhang, X.-J., Nunn, D., Artemyev, A. V., Angelopoulos, V., Tsai, E., et al. (2022). Short chorus wave packets: generation within chorus elements, statistics, and consequences on energetic electron precipitation. J. Geophys. Res. Space Phys. 127 (5), e2022JA030310. doi:10.1029/2022JA030310

PubMed Abstract | CrossRef Full Text | Google Scholar

Mozer, F. S., Agapitov, O. V., Blake, J. B., and Vasko, I. Y. (2018). Simultaneous observations of lower band chorus emissions at the equator and microburst precipitating electrons in the ionosphere. Geophys. Res. Lett. 45 (2), 511–516. doi:10.1002/2017GL076120

CrossRef Full Text | Google Scholar

Neishtadt, A. I. (1975). Passage through a separatrix in a resonance problem with a slowly-varying parameter: PMM. J. Appl. Math. Mech. 39 (4), 594–605. doi:10.1016/0021-8928(75)90060-X

CrossRef Full Text | Google Scholar

Nunn, D., and Omura, Y. (2015). A computational and theoretical investigation of nonlinear wave-particle interactions in oblique whistlers. J. Geophys. Res. (Space Phys. 120 (4), 2890–2911. doi:10.1002/2014JA020898

CrossRef Full Text | Google Scholar

O’Brien, T. P., Looper, M. D., and Blake, J. B. (2004). Quantification of relativistic electron microburst losses during the GEM storms. Geophys. Res. Lett. 31 (4), 18621. doi:10.1029/2003GL018621

CrossRef Full Text | Google Scholar

Omura, Y., Furuya, N., and Summers, D. (2007). Relativistic turning acceleration of resonant electrons by coherent whistler mode waves in a dipole magnetic field. J. Geophys. Res. Space Phys. 112 (A6), 12243. doi:10.1029/2006JA012243

CrossRef Full Text | Google Scholar

Shumko, M., Turner, D. L., O’Brien, T. P., Claudepierre, S. G., Sample, J., Hartley, D. P., et al. (2018). Evidence of microbursts observed near the equatorial plane in the outer van allen radiation belt. Geophys. Res. Lett. 45 (16), 8044–8053. doi:10.1029/2018GL078451

CrossRef Full Text | Google Scholar

Tao, X., and Bortnik, J. (2010). Nonlinear interactions between relativistic radiation belt electrons and oblique whistler mode waves. Nonlinear Process. Geophys. 17 (5), 599–604. doi:10.5194/npg-17-599-2010

CrossRef Full Text | Google Scholar

Thorne, R. M., Li, W., Ni, B., Ma, Q., Bortnik, J., Chen, L., et al. (2013). Rapid local acceleration of relativistic radiation-belt electrons by magnetospheric chorus. Nature 504 (7480), 411–414. doi:10.1038/nature12889

PubMed Abstract | CrossRef Full Text | Google Scholar

Thorne, R. M., O’Brien, T. P., Shprits, Y. Y., Summers, D., and Horne, R. B. (2005). Timescale for MeV electron microburst loss during geomagnetic storms. J. Geophys. Res. Space Phys. 110 (A9). doi:10.1029/2004JA010882

CrossRef Full Text | Google Scholar

Vainchtein, D., Zhang, X.-J., Artemyev, A. V., Mourenas, D., Angelopoulos, V., and Thorne, R. M. (2018). Evolution of electron distribution driven by nonlinear resonances with intense field-aligned chorus waves. J. Geophys. Res. (Space Phys. 123 (10), 8149–8169. doi:10.1029/2018JA025654

CrossRef Full Text | Google Scholar

Zhang, X.-J., Agapitov, O., Artemyev, A. V., Mourenas, D., Angelopoulos, V., Kurth, W. S., et al. (2020). Phase decoherence within intense chorus wave packets constrains the efficiency of nonlinear resonant electron acceleration. Geophys. Res. Lett. 47 (20), e2020GL089807. doi:10.1029/2020GL089807

CrossRef Full Text | Google Scholar

Zhang, X. J., Angelopoulos, V., Mourenas, D., Artemyev, A., Tsai, E., and Wilkins, C. (2022a). Characteristics of electron microburst precipitation based on high-resolution ELFIN measurements. J. Geophys. Res. Space Phys. 127 (5), e2022JA030509. doi:10.1029/2022JA030509

CrossRef Full Text | Google Scholar

Zhang, X. J., Artemyev, A., Angelopoulos, V., Tsai, E., Wilkins, C., Kasahara, S., et al. (2022b). Superfast precipitation of energetic electrons in the radiation belts of the Earth. Nat. Commun. 13 (1), 1611. doi:10.1038/s41467-022-29291-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X.-J., Mourenas, D., Artemyev, A. V., Angelopoulos, V., Bortnik, J., Thorne, R. M., et al. (2019). Nonlinear electron interaction with intense chorus waves: statistics of occurrence rates. Geophys. Res. Lett. 46 (13), 7182–7190. doi:10.1029/2019GL083833

CrossRef Full Text | Google Scholar

Zhang, X.-J., Thorne, R., Artemyev, A., Mourenas, D., Angelopoulos, V., Bortnik, J., et al. (2018). Properties of intense field-aligned lower-band chorus waves: implications for nonlinear wave-particle interactions. J. Geophys. Res. (Space Phys. 123 (7), 5379–5393. doi:10.1029/2018JA025390

CrossRef Full Text | Google Scholar