Numerical simulation of the equatorial plasma bubble: the effect of seeding by the vertical winds and random background noise perturbations

A wide variety of small-amplitude waves widely exist in the ionosphere and have significant effects on the evolution of equatorial plasma bubbles. In this paper, we simulated equatorial plasma bubbles (EPB) seeded by vertical neutral wind perturbations with wavelengths of 125 km and 250 km, and compared the morphology characteristics of plasma bubble structures with those under random noise perturbations in the background density. The numerical results showed that both vertical winds and random background noise perturbations can contribute to the growth of plasma bubbles, and the perturbations under additional random background noise can promote the growth of the plasma bubble structures faster. Additionally, several processes of the nonlinear behavior of bifurcated EPB structures, including bifurcation, pinching, and small-scale turbulent structures, were successfully obtained. Our simulation captured supersonic flows within the low-density plasma structures characterized by vertical velocities of about 1.5 km/s, which is consistent with experimental studies found in the literature.

1 Introduction

The upwellings of the low-density ionospheric phenomenon caused by the plasma instabilities, which are termed equatorial spread F (ESF) or equatorial plasma bubble (EPB), are one of the most important scientific subjects in the equatorial F region. They commonly occur after sunset as a result of the prereversal enhancement in the upward plasma velocity that lifts the F layer (Eccles, 1998). The spatial scale of the fully developed EPB structures ranges from tens of km to tens of cm (Yokoyama, 2017; Huba, 2021). It is well known that the existence of the EPB structure can cause severe radio wave scintillation, and then degrade communication and navigation systems (Woodman, 2009).

Observations reveal that EPBs often undergo bifurcation, pinching, and small-scale turbulent structures at the topside F region (Hysell, 1999; Hysell et al., 2005; Makela et al., 2006; Tsunoda, 2007; Huba et al., 2015; Carrasco et al., 2020). Theoretically, the equatorial ionospheric low-density structure grows when the vertical plasma density gradient steepens at the bottomside F-region due to the generalized Rayleigh-Taylor instability, and then the EPB structures generate and penetrate through the topside of the F-region. Numerical simulation is widely used to reproduce the dynamic, nonlinear evolution of the well-developed plasma bubble structure on the magnetic equatorial plane. To date, the nonlinear development of the EPBs has been followed in a series of increasingly sophisticated models, including the simple two-dimensional equatorial plane models (Scannapieco and Ossakow, 1976; Zalesak and Ossakow, 1980; Zalesak et al., 1982; Sekar et al., 1994; Huang and Kelley, 1996; Alam Kherani et al., 2004; Huba and Joyce, 2007; Carrasco et al., 2020; Li et al., 2021; Gao et al., 2023) and fully three-dimensional high-resolution models (Huba et al., 2008; Retterer, 2010; Aveiro and Huba, 2013; Hysell et al., 2014; Yokoyama et al., 2014; Hysell et al., 2015; Yokoyama et al., 2015; Li et al., 2023). Although the dynamic evolution of EPBs has been successfully obtained, researchers are still confused by the complicated patterns of plasma density depletion structure, including the bifurcation, pinching, and small-scale turbulent structures.

Based on the three-layer numerical model, Zalesak et al. (1982) studied the simple bifurcation of EPB structures seeded by the eastward neutral wind. Huang and Kelley (1996) found that the generation of multiple plumes on the west wall of a plasma upwelling was well-correlated with the neutral wind perturbations. Aveiro and Hysell (2010) reported that the asymmetric bifurcation of EPBs could be captured by seeding with Gaussian white noise, electric field, and neutral wind. In fact, a wide variety of small-amplitude waves exist in the background ionosphere (Kirchengast, 1996), and their inhomogeneity reasonably has an important influence on the generation of EPB bifurcations. This has been confirmed by Huba et al. (2015), who found that the varied bubble structures are possibly linked to asymmetric initial perturbation. Based on the High-Resolution Bubble (HIRB) model, Yokoyama et al. (2015) proposed that the east-west asymmetry of EPB likely originates from a westward plasma shear flow initiated by two-wavelength perturbations. Recently, Huba et al. (2020) found that the appearance of bifurcated bubbles is strongly affected by the E-region metal ion layers with random noise perturbations in the background ionosphere. These results indicate that the nonlinear bifurcation and pinching processes of the EPBs are possibly related to the seed perturbations.

To further understand the mechanism of bifurcated plasma bubbles in the magnetic equatorial plane, we first give a brief description of the numerical model of EPB, which is available in the literature (e.g., Huba and Joyce, 2007; Zalesak et al., 1982). Then, we will present four case studies under different seed conditions combined with vertical winds and random noise perturbations in the background density. Finally, this paper closes with discussions and conclusions of the main results.

2 Model description

The two-dimensional electrostatic ESF model is used in the present study, and the basic equations of this model are written as:

$\frac{\partial N_i}{\partial t}+\nabla \cdot \left(N_i{\mathbf{V}}_i\right)=S_i(1)$

$q\left(\mathbf{E}+{\mathbf{V}}_i\times \mathbf{B}\right)-\frac{\nabla \left(N_i{k}_{B}T\right)}{N_i}+M_i\mathbf{g}+M_i{\nu }_{in}\left(\mathbf{U}-{\mathbf{V}}_i\right)=M_i\left(\frac{\partial }{\partial t}+{\mathbf{V}}_i\cdot \nabla \right){\mathbf{V}}_i(2)$

$-q\left(\mathbf{E}+{\mathbf{V}}_e\times \mathbf{B}\right)-\frac{\nabla \left(N_e{k}_{B}T\right)}{N_e}+M_e\mathbf{g}+M_e{\nu }_{en}\left(\mathbf{U}-{\mathbf{V}}_e\right)=M_e\left(\frac{\partial }{\partial t}+{\mathbf{V}}_e\cdot \nabla \right){\mathbf{V}}_e(3)$

$\nabla \cdot \mathbf{J}=\nabla \cdot \left[qN\left({\mathbf{V}}_i-{\mathbf{V}}_e\right)\right]=0(4)$

where the subscript i and e mean ions and electrons. $N_{i,e}$ is the ions/electrons density under quasi-neutrality condition ($N_i=N_e=N$). $S_i$ represents the chemical terms, $q$ is the electron charge, $\mathbf{E}=-\nabla \varphi$ is the electric field, $B$ is the geomagnetic field, ${\mathbf{V}}_{i,e}$ is the ion/electron velocity, $k_B$ is the Boltzmann constant, $T$ is the temperature, $M_{i,e}$ is the ion/electron mass, $\mathbf{g}$ is the gravitational acceleration, ${\nu }_{in,en}$ is the ion/electron collision frequency with neutrals, $\mathbf{U}$ is the neutral wind velocity, and $\mathbf{J}$ is the current density.

In this model, it has been assumed that the dominant ion in the ionospheric F region is the atomic oxygen ion ($O^{+}$). Similar to the work of Zalesak and Ossakow (1980) and Li et al. (2021), the inertial terms of Eqs 2, 3 are ignored when considering $\omega \ll {\mathrm{\Omega }}_i$, Where $\omega$ is the frequency of plasma perturbations and ${\mathrm{\Omega }}_i=eB/M_i$ is the ion gyrofrequency. Considering the finite temperature effects, we can obtain Eqs 5, 6 from Eqs 2, 3.

$q\left(\mathbf{E}+{\mathbf{V}}_i\times \mathbf{B}\right)+M_i\mathbf{g}+M_i{\nu }_{in}\left(\mathbf{U}-{\mathbf{V}}_i\right)=0(5)$

$-q\left(\mathbf{E}+{\mathbf{V}}_e\times \mathbf{B}\right)+M_e\mathbf{g}+M_e{\nu }_{en}\left(\mathbf{U}-{\mathbf{V}}_e\right)=0(6)$

Taking $M_e\ll M_i$ ${\nu }_{en}/{\mathrm{\Omega }}_e\approx 0$, ${\nu }_{in}/{\mathrm{\Omega }}_i\ll 1$, we can obtain the velocity of electron and ion.

${\mathbf{V}}_{e\perp }=\frac{-\nabla \varphi \times \mathbf{B}}{B^2}(7)$

${\mathbf{V}}_{i\perp }=\frac{-\nabla \varphi \times \mathbf{B}}{B^2}-\frac{M_i{\nu }_{in}}{q{B}^2}\nabla \varphi +\frac{M_i}{q{B}^2}\mathbf{g}\times \mathbf{B}+\frac{M_i{\nu }_{in}}{q{B}^2}\mathbf{U}\times \mathbf{B}+\frac{M_i^2{\nu }_{in}^2}{q^2{B}^2}\mathbf{U}(8)$

where ${\nabla }_{\perp }=\overrightarrow{x}\partial /\partial x+\overrightarrow{z}\partial /\partial z$, $\overrightarrow{x}$ represents the eastward direction, $\overrightarrow{z}$ represents the upward direction, and $\varphi$ represents the polarization electric potential. Substituting Eqs 7, 8 into Eq. 4, we can derive the Eq. 9.

${\nabla }^2\varphi +\frac{1}{N{\nu }_{in}}\nabla \left(N{\nu }_{in}\right)\cdot \nabla \varphi =\frac{gB}{N{\nu }_{in}}\frac{\partial N}{\partial x}+\frac{\nabla \cdot \left(N{\nu }_{in}\mathbf{U}\times \mathbf{B}\right)}{N{\nu }_{in}}+\frac{M_i}{q}\frac{\nabla \cdot \left(N{\nu }_{in}^2\mathbf{U}\right)}{N{\nu }_{in}}(9)$

The initial plasma density profile is a Chapman layer with (Huba and Joyce, 2007):

$N_0\left(z\right)=N_{peak}\exp \left[1-\xi -\exp \left(-\xi \right)\right](10)$

Here, we set $N_{peak}={10}^6$ cm^-3, $\xi =\left(z-z_0\right)/\Delta h$, $z_0=438$ km, and $\Delta h=80$ km. The ion-neutral collision frequency is given by ${\nu }_{in}={\nu }_0\exp \left(-z/L_z\right)$ where ${\nu }_0=26.7$ s^-1 and $L_z=81.4$ km, which is the same as the profile used in Huba and Joyce (2007). It should be noted that the density profile can also be initiated by some more realist models (e.g., IRI 2016), but this does not make against representing the process of seeding EPBs.

The main purpose of this study is to examine the effect of vertical winds and additional random background noise perturbation on the evolution of the EPB structures. The initial seeds of vertical wind perturbations along the west-east direction used in this simulation are shown in Figure 1. Perturbation 1 is a sine function with a wavelength of 125 km and an initial amplitude of 10 m/s. Perturbation 2 is similar to Perturbation 1 but with a wavelength of 250 km. Such amplitude of vertical winds is approximately consistent with the previous simulation and observation results near the equator (Raghavarao et al., 1999; Yokoyama et al., 2019). Appling this disturbance, we can more realistically simulate the evolution process of EPB. We assume that the amplitude of vertical wind decreases exponentially until it reaches 5 m/s at about t = 600 s in the simulation. The initial 5% amplitude random noise perturbation in the background density is used to compare the morphology characteristics of plasma bubbles structures. Different initial perturbation cases in the simulation are shown in Table 1.

FIGURE 1

FIGURE 1. Vertical wind used in the simulation.

TABLE 1

TABLE 1. Different initial perturbation cases in the simulation

The recombination loss term in Eq. 1 is ignored. Note that appropriately conserving mass must be applied to numerically solve the Eq. 1. Li et al. (2021) and Huba (2021) found that the evolution of the plasma bubble structures is highly correlated with numerical method. In general, oscillations and unphysical values such as negative densities occur easily without the total variation diminishing (TVD) constraint. Therefore, we adopted a second-order accurate TVD approach for the solution of two-dimensional generalized continuity equations (Trac and Pen, 2003). The algorithm of spatial discretization in this paper is implemented with finite-difference method, time integration is performed using a second-order Runge-Kutta scheme, and the Van Leer limiter is used to determine the appropriate second-order correction. Despite significant numerical diffusion, second-order accurate TVD algorithm has been proven effective in capturing small-scale EPB structures (Li et al., 2021). The potential Eq. 9 is solved using a successive over-relaxation (SOR) method in this study. Periodic boundary conditions are imposed on the horizontal direction for both the $N$ and the $\varphi$. In the vertical directions, the Neumann boundary conditions are used for the top and bottom boundary for the $N$ and the $\varphi$. The numerical simulation is performed on a two-dimension uniform Cartesian mesh with $200\times 250$ cells with a resolution of 1.25 km in the west-east direction and 1.6 km in the vertical direction.

3 Simulation results

Figure 2 presents the evolution of plasma density on the magnetic equatorial plane over six different times: 2,500 s, 3,000 s, 4,000 s, 4,500 s, 5,000 s, and 5,500 s (case 1). The seeding of EPBs produced by a vertical wind cosine perturbation with a wavelength of 125 km is applied, and the initial amplitude of the vertical wind is 10 m/s. As the lower-density plasma rises from the bottomside of the F region, both bubble structures begin to bifurcate around t = 4,000 s. Note that the first bifurcation of the lower-density plasma structure occurs below the F layer peak height. When the plasma bubbles reach the higher density F region, small structures emerge on the interior walls of the two main bifurcated density structures. At t = 5,500 s, the eastern channel of the plasma density depletion structure has merged into the middle one. Although the initial seeding with symmetric vertical wind is applied, it is found that the right side grows faster than the left side after about 4,500 s, but there is no significant difference before that point.

FIGURE 2

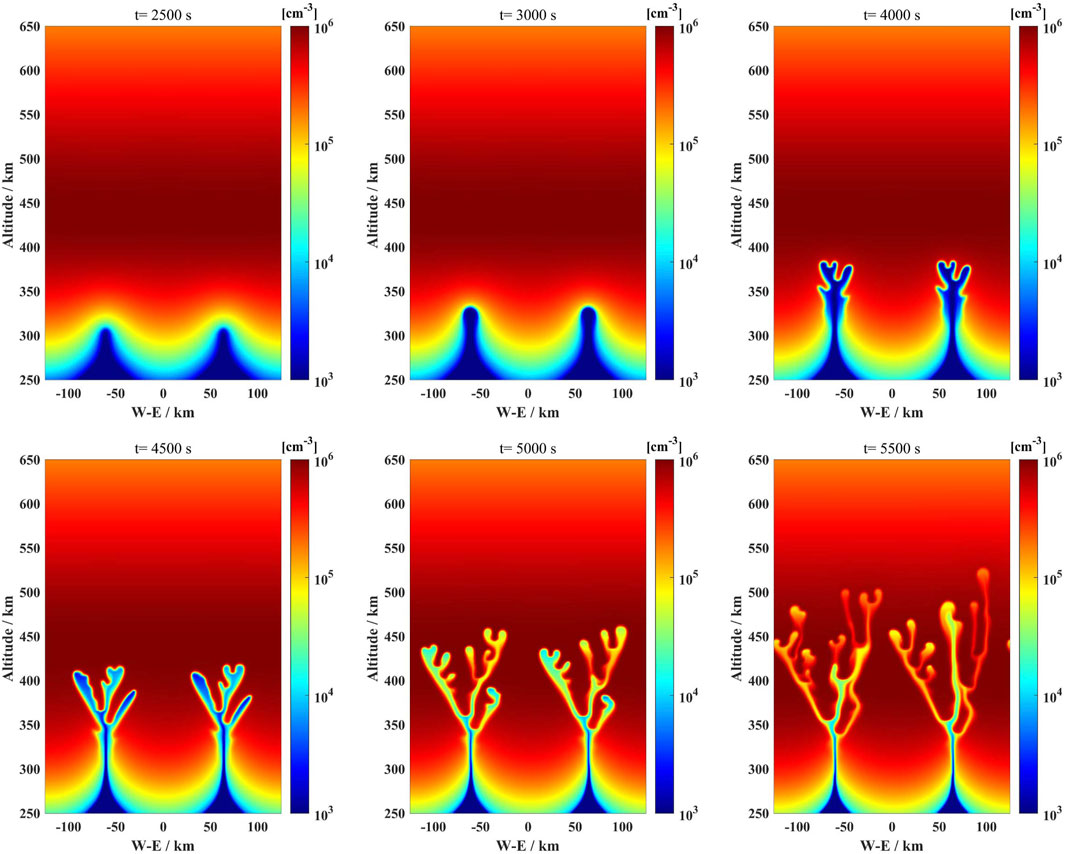
FIGURE 2. Plasma density distribution as a function of west-east coordinate and altitude on magnetic equatorial plane at the times 2,500 s, 3,000 s, 4,000 s, 4,500 s, 5,000 s, and 5,500 s, respectively.

Figure 3 presents the evolution of plasma density on the magnetic equatorial plane over six different times: 3,000 s, 4,000 s, 4,500 s, 5,000 s, 5,500 s, and 6,000 s (case 2). The seeding of EPBs produced by vertical wind cosine perturbation with a wavelength of 250 km is applied, and the initial amplitude of the vertical wind is 10 m/s. In this case, the initial bifurcated structures of the EPB occur at 4,500 s and the height of the secondary instability is significantly lower than case 1. After the first bifurcation of the EPB structure, both channels of the plasma density depletion structure are pinched off, and then secondary instability occurs only along the middle channel. Obviously, the evolution of the EPB structures seeding with vertical wind depends on the zonal wavelength, and the shorter wavelength perturbation works more effectively.

FIGURE 3

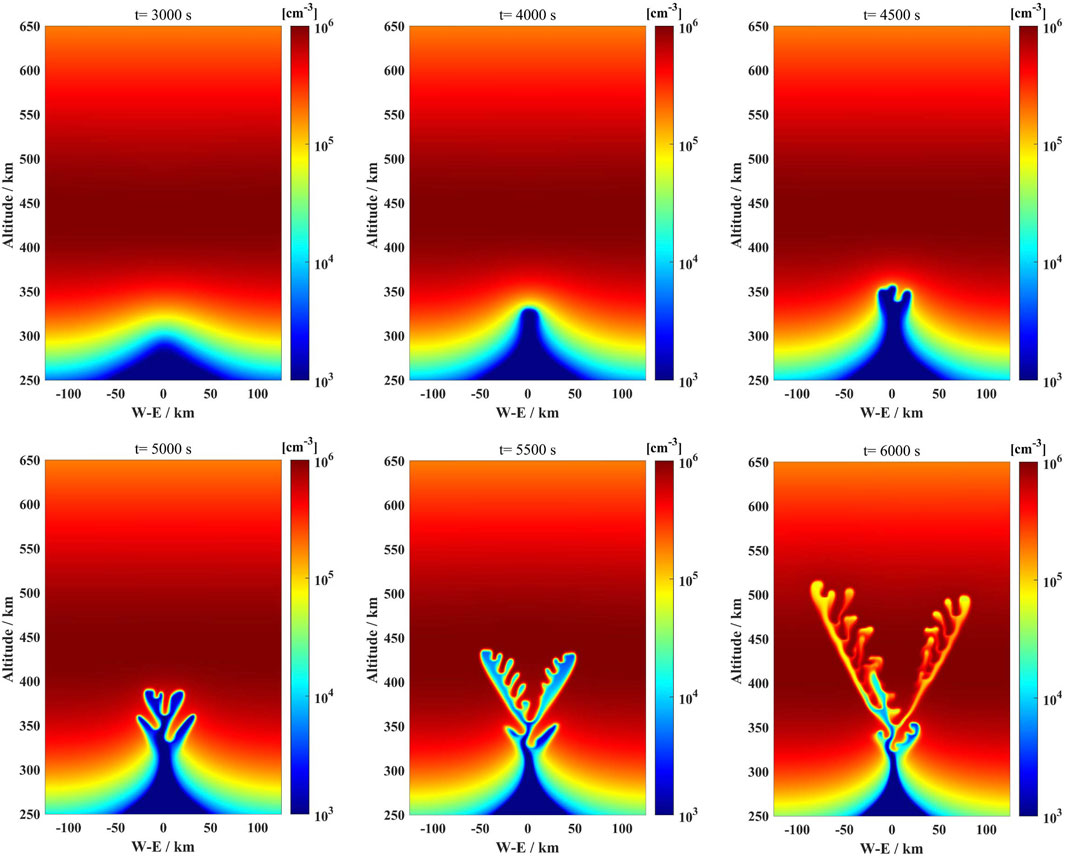
FIGURE 3. Plasma density distribution as a function of west-east coordinate and altitude on magnetic equatorial plane at the times 3,000 s, 4,000 s, 4,500 s, 5,000 s, 5,500 s, and 6,000 s, respectively.

Figure 4 presents the evolution of plasma density on the magnetic equatorial plane over six different times: 2,500 s, 3,500 s, 4,000 s, 4,500 s, 5,000 s, and 5,500 s, respectively (case 3). The amplitude of the random noise perturbation imposed in background density is 5%, and the initial amplitude imposed with the vertical wind at the wavelength of 125 km is 10 m/s. Different from cases 1 and 2, the low-density plasma structures more easily grow in the western channel in the early stage of the simulation. The initial bifurcated structures of the EPB occur below 300 km, and the small amplitude ripples are apparent below the peak height of the F layer. About t = 4,500 s, the plasma bubble with small-amplitude structures quickly rises to the peak height through the narrow channel. Soon later, small-amplitude EPB structures interact and merge when the plasma bubble rises to the topside F-region. Overall, the asymmetric bifurcated structures occur on both the two main plasma bubbles.

FIGURE 4

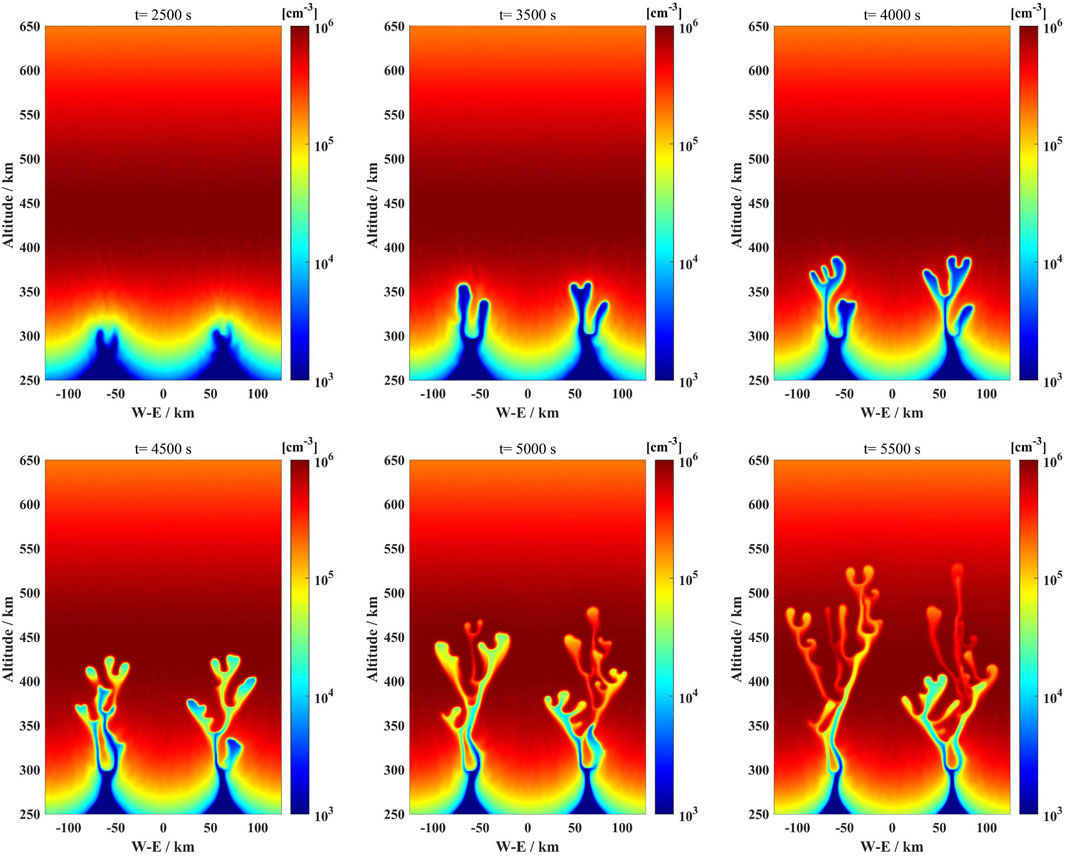
FIGURE 4. Plasma density distribution as a function of west-east coordinate and altitude on magnetic equatorial plane for at the times 2,500 s, 3,500 s, 4,000 s, 4,500 s, 5,000 s, and 5,500 s, respectively.

Figure 5 presents the evolution of plasma density on the magnetic equatorial plane over six different times: 3,000 s, 3,500 s, 4,000 s, 4,500 s, 5,000 s, and 5,500 s (case 4). In this case, both the random noise perturbation and the vertical wind are considered. The initial amplitude imposed by random noise perturbation in the background density is 5%, and the amplitude imposed with the vertical wind at the wavelength of 250 km is 10 m/s. When the low-density bubbles begin to rise, multiple small-amplitude structures within the plume form gradually. After that, three plasma bubble structures in the bottomside of the F layer are well developed. Compared to the above cases without random noise perturbation, the growth of plasma bubbles is faster in this case. At t = 5,500 s, the low-density plasma bubbles can rise to a height of more than 500 km. However, the east-west expansion scale of the low-density plasma bubble structure above the peak height of the F layer is less than 100 km.

FIGURE 5

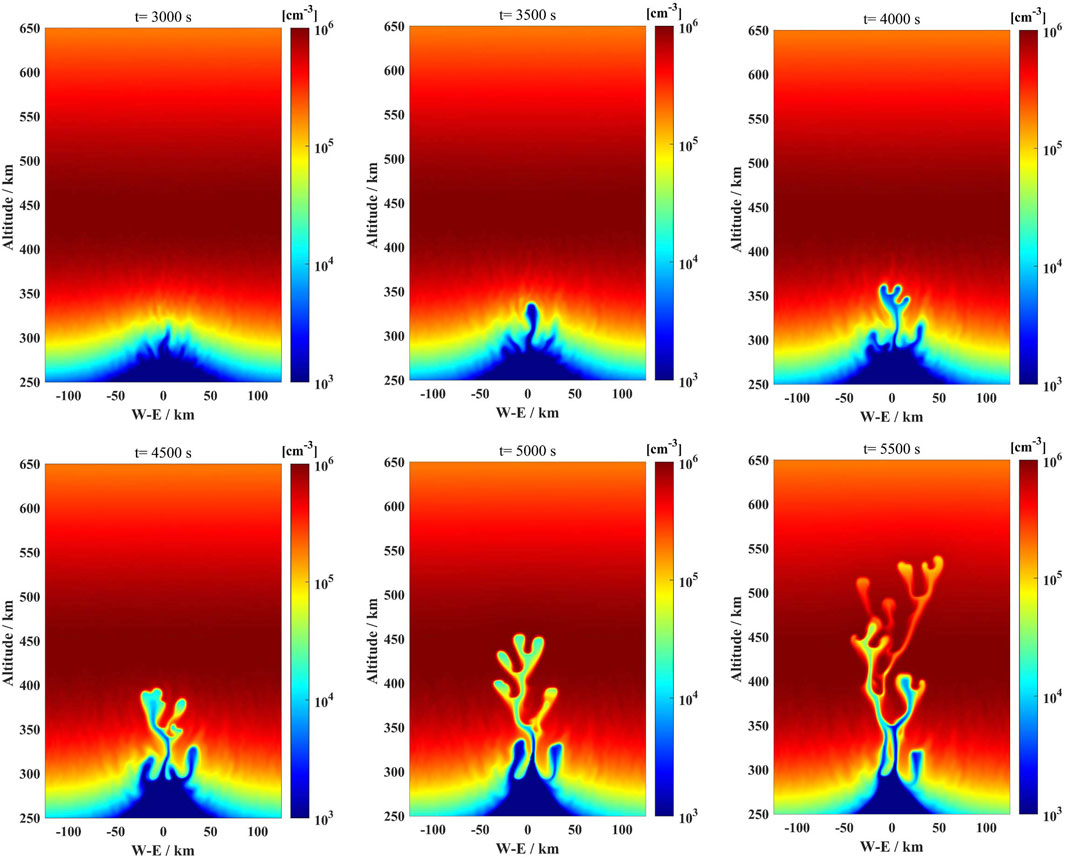
FIGURE 5. Plasma density distribution as a function of west-east coordinate and altitude on magnetic equatorial plane for at the times 3,000 s, 3,500 s, 4,000 s, 4,500 s, 5,000 s, and 5,500 s, respectively.

Figure 6 shows the variation of the maximum upward velocity and horizontal velocity. It can be seen from Figure 6 that the maximum upward velocity is higher for the cases with longer-wavelength vertical wind perturbations, reaching up to 1.5 km/s, while for shorter-wavelength perturbations, it is around 0.8 km/s. These results suggest that the flows within the low-density plasma structures are supersonic (Huba and Joyce, 2007). It is clear that in vertical directions, the peak velocity values of the plasma bubbles are higher for those with longer-wavelength vertical wind perturbations.

FIGURE 6

FIGURE 6. The variation of the maximum upward velocity.

Figure 7 shows plasma density variations at the height of 330 km and 442 km, respectively. Generally, the plasma density gradient at the bottomside of the F layer appears to be steepened and is not affected by the background seeding perturbations. In these four cases, the plasma density at the height of 330 km can even reduce by up to 2 orders of magnitude within the plasma flows. However, above the peak height of the F layer, it does not change dramatically, and the magnitude of the numerical density is ${10}^4\sim {10}^6$ cm^-3 at the altitude of 442 km. Additionally, we note that the wavelength scale of the vertical wind perturbation affects the depletion within the plasma flows, with longer wavelengths resulting in more severe depletion. This may be attributed to numerical artifacts due to limitations in the numerical method’s resolution and insufficient grid resolution.

FIGURE 7

FIGURE 7. Plasma density distribution at the height of 330 km (blue line) and 442 km (red line).

4 Discussion

In this paper, we performed the numerical simulation of the equatorial plasma bubble by seeding with vertical wind and additional random noise perturbations. The simulation results show that both the vertical wind and random noise perturbations in the background density contribute to the growth of the plasma bubbles. Although the generation mechanism of F region plasma depletion is generally attributed to the Rayleigh-Taylor instability, the relationship between the wave characteristics of fluctuations and the seeding mechanism on the background ionosphere is still not well understood.

Observational results demonstrate that the significant role of the vertical winds associated with gravity waves perturbations propagating from the lower atmosphere affects the growth of EPBs (Hysell et al., 1990; Raghavarao et al., 1999; Fritts et al., 2008; Shinagawa et al., 2018). Vertical winds associated with gravity waves are inferred from the layering of ESF structures measured by the Jicamarca radar (Hysell et al., 1990). Fritts et al. (2008) found that the vertical wind perturbations can potentially affect the plasma instability growth rates and plasma bubble seeding. Theoretical studies and simulations also reveal the association between the seeding mechanism of the EPBs and vertical wind perturbations. Krall et al. (2013) showed that the effect of the background vertical wind can suppress equatorial spread F, while Wu et al. (2015) reported that vertical wind perturbations are most effective in seeding ESF bubbles. Yokoyama et al. (2019) presented that shorter wavelength vertical wind perturbations can contribute to the growth of EPB structures. In their models, the amplitude of the vertical wind perturbations is generally at the range from 4 to 50 m/s. It has also been observed that the peak amplitude of the vertical wind component can reach about 20 m/s near the equator (Raghavarao et al., 1999). In this paper, the EPB structures seeded by vertical wind perturbations with the amplitude of 10 m/s are well-developed. The asymmetric bubbles arose on the case 2 may be caused by the numerical calculation, which has been observed by the previous works (Yokoyama et al., 2019).

The vertical wind seeding mechanism can generate the plasma bubble structures, while the small-scale amplitude fluctuations on the background density can also affect the evolution of the EPB patterns. Previous investigations demonstrate that a wide variety of small-amplitude waves exist in the background ionosphere play an important role in the evolution of EPB bifurcations (Aveiro and Hysell, 2010; Retterer, 2010). Based on the three-dimension numerical simulation, Aveiro and Hysell (2010) successfully reproduced the transient and asymptotic growth of collisional shear instability as well as generalized Rayleigh instability using the random white noise with a relative amplitude of 20% in the initial number density. Huba et al. (2020) found that the appearance of bifurcated bubbles is strongly affected by the E-region metal ion layers with the additional random noise perturbations in the background. In our work, as shown in Figure 3 and Figure 5, the initial random noise perturbation applied to the numerical model is additionally used, and the relative amplitude of the background density is 5%. This amplitude value is quietly moderate compared to previous numerical models (Sekar et al., 1994; Huang and Kelley, 1996). As a result, we found that the different evolution process occurred in the cases of seeding with vertical winds and additional random noise perturbations in the background density. Therefore, we conclude that the evolution process of the EPB structure seeded with additional random noise perturbations is different from that seeded only by vertical winds.

The formation of the EPB structures involves a series of processes, including bifurcation, pinching, and small-scale turbulent structures (Yokoyama et al., 2014). The simulated plasma bubble structures in this paper exhibit both similarities and differences compared to previous simulation results. Previous studies show that the first bifurcation of the low-density plasma structures usually occurs above the peak height of the F-region (Huang and Kelley, 1996; Retterer, 2010; Yokoyama et al., 2014; Carrasco et al., 2020). In our works, however, the first bifurcation occurred below the F peak heights, which is limited but some exist (Huba and Joyce, 2007; Huba, 2021). Yokoyama et al. (2014) attributed this phenomenon to the absence of background E-region conductivity. However, Carrasco et al. (2020) argued that the absence of E-region conductivity cannot explain the simulation results obtained by Huang and Kelley (1996). Carrasco et al. (2020) concluded that the bifurcation height of low-density plasma structures is determined by the polarization electric field inside the EPB structures. To consider the effect of polarization electric fields, the characteristics of $E_z^{\max }\approx E_x^{\min }$ ($E_z^{\max }$ and $E_x^{\min }$ represent the electric fields through the narrow channel in vertical and zonal direction, respectively) that determine the bifurcation height of the low-density depletion structures are examined. As shown in Figure 8, the value of the vertical electric field (red line) is approximately equal to the zonal electric field (blue line) in the narrow channel only when the bifurcation of the low-density plasma structures occurs. Before this, the vertical electric field is smaller than the zonal electric field. This indicates that the first bifurcation height of the plasma depletion in this study is possibly related to the transformation between vertical and zonal electric fields.

FIGURE 8

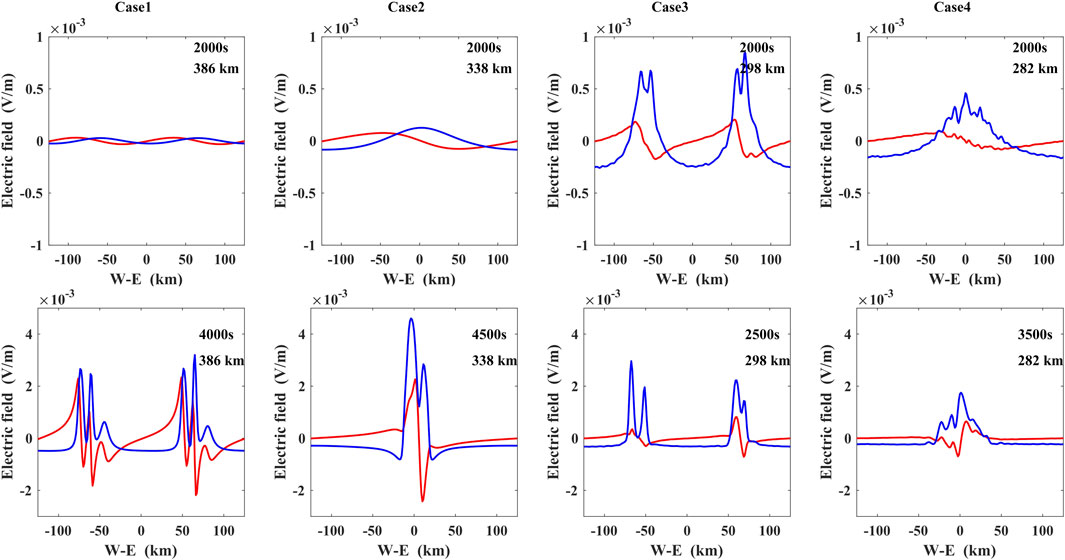
FIGURE 8. Plot of the zonal and vertical components electric field inside the bubble for case 1 to case 4, the red line represents the vertical electric field, and the blue line represents the zonal electric field.

Except for the bifurcation process mentioned above, the processes of pinching and small-scale turbulent structures simulated in this study also exhibit both similarities and differences compared to the previous reports. For example, the supersonic flows within the low-density plasma structures have also been reported in observation and simulation results (Aggson et al., 1992; Hysell et al., 1994; Huang et al., 2007; Huba and Joyce, 2007; Astafyeva and Zakharenkova, 2015; Huba et al., 2020). Based on the Naval Research Laboratory equatorial spread F (NRLESF2) model, Huba and Joyce (2007) demonstrated that the vertical velocity of the plasma flow is as high as about 2 km/s below the F peak height, while Retterer (2010) reported that the peak velocities within the plumes are generally in the range of 0.3–0.6 km/s. Based on the (Saim3 is Also a Model of the Ionosphere) SAMI3/ESF model, Huba, Joyce and Krall (2008) reported that the upward velocities of the EPB structures can reach approach 1.0 km/s. In this work, the peak vertical velocity, seeding only with the vertical winds, can reach about 1.5 km/s as shown in Figure 6. It is very evident that there is a distinct moment when the growth rate of the EPB undergoes a clear transition. The upward velocities increase as the plasma bubble structures grows and saturates, and then decrease slowly. Similar results have been reported by Li et al. (2023). Huba et al. (2020) thought that the variations of the background conductance may be responsible for this phenomenon on the basis of the SAMI3/ESF model. Since EPBs tend to nonlinearly form very narrow channel near the F peak height, the seeding perturbation with a shorter wavelength can generate polarization electric fields more effectively (Yokoyama et al., 2019). It has been found in Figure 8 that the maximum upward electric field (associated with maximum upward velocity) occurs in the narrow channel. Generally, there is a significant density gradient in narrow channels (Yokoyama et al., 2014; Huba et al., 2015). Thus, the velocity differences of the EPB structures between different wavelength perturbations may be related to the plasma density gradient generated in the narrow channel as shown in Figure 7. The issue of velocity differences of EPB structures associated with wavelength perturbation needs more investigation. In addition, the plasma bubble characterized by small structures arising on the interior walls can also grow through the narrow channel in response to the Rayleigh-Tylor instability, which has been previously reported by Huba and Joyce (2007), Yokoyama et al. (2019) and Li et al. (2021). However, a slight difference is that the EPB structures reproduced in the HIRB model can grow along both sides of the wall. Overall, serval processes associated with the nonlinear behavior of EPB structures have been captured in our simulation results.

Our purpose is to improve the understanding of the effects of the vertical wind and additional random noise perturbations on the plasma bubbles. However, it should be noted that the current numerical model is still unable to entirely simulate the sophisticated patterns of the EPB structures. Retterer (2010) mentioned that the major component leading to the variability of the EPB structures is that of the ambient background ionosphere. However, due to the lack of real-time background, we are still unable to obtain the specific patterns of the EPB structures. On the other hand, researchers are still confused by how the gravity wave interacts with the ionosphere, drives the density perturbations in the background, and generates the small-scale EPB structures with a meter magnitude. Particularly, the meridional flows of the neutral wind and the E-region drivers in controlling the EPB growth have also been simulated by the SAMI3/ESF and HIRB models (Huba et al., 2009; Yokoyama et al., 2019; Huba et al., 2020), which surely affects the development of the resulting plumes. This cannot be simulated from the two-dimension model in the paper. Due to the limitations of numerical algorithms, the scale size of the EPB structures captured in this paper is significantly inferior to the HIRB model on the fine details (Yokoyama et al., 2014). Therefore, further studies are required to improve the numerical model, including the development of the high-resolution three-dimension EPB model and the coupling with the lower ionosphere.

5 Conclusion

In this paper, we conducted the numerical simulation of the equatorial plasma bubble by seeding with vertical wind and additional random noise perturbations in the two-dimension magnetic equatorial plane. The important morphological characteristics of bifurcated plasma bubbles in the magnetic equatorial plane were discussed in this work. The main conclusions are summarized as follows:

1. The importance of a wide variety of small-amplitude waves in the background ionosphere on the evolution of the EPB is recognized. Simulation results show that the vertical wind seeding mechanism can generate the plasma bubble structures, while the role of random noise fluctuations in the background density will also affect the evolution process of the EPB patterns.

2. The characteristic of the bifurcation height of the low-density depletion structures is reexamined in this work. The first bifurcation height of the plasma depletion is possibly related to the transformation between vertical and zonal electric fields.

3. Supersonic flows within the low-density plasma structures were captured in our simulation, which is consistent with experimental studies found in previous investigations.

Data availability statement

The data used in this paper are available in the repository of ZENODO (https://doi.org/10.5281/zenodo.10149218).

Author contributions

YZ: Writing–original draft. QT: Writing–review and editing. TX: Writing–review and editing. YL: Writing–review and editing. CZ: Writing–review and editing. ZD: Writing–review and editing. YZ: Writing–review and editing. ZZ: Writing–review and editing. FW: Writing–review and editing. BX: Writing–review and editing. SS: Writing–review and editing.

Funding

This work was supported by the National Key Research and Development Program of China (grant No. 2022YFF0503904), National Natural Science Foundation of China (NSFC Grant Nos. 42204161, 42074187, 41574146, 41774162, 42004130, and 42104150), the fellowship of China Postdoctoral Science Foundation (2022M710941), the Foundation of National Key Laboratory of Electromagnetic Environment (Grant Nos. 6142403180204, 6142403200303, 20200101, and JCKY2021210C614240302), Chinese Academy of Sciences, Key Laboratory of Geospace Environment, University of Science and Technology of China (GE2020-01), and the Fundamental Research Funds for the Central Universities (2042021kf0020), and the Excellent Youth Foundation of Hubei Provincial Natural Science Foundation (Grant No. 2019CFA054).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aggson, T. L., Burke, W. J., Maynard, N. C., Hanson, W. B., Anderson, P. C., Slavin, J. A., et al. (1992). Equatorial bubbles updrafting at supersonic speeds. J. Geophys. Res. Space Phys. 97 (A6), 8581–8590. doi:10.1029/92JA00644

CrossRef Full Text | Google Scholar

Alam Kherani, E., De Paula, E. R., and Bertoni, F. C. (2004). Effects of the fringe field of Rayleigh-Taylor instability in the equatorial E and valley regions. J. Geophys. Res. Space Phys. 109 (A12). doi:10.1029/2003JA010364

CrossRef Full Text | Google Scholar

Astafyeva, E., and Zakharenkova, I. (2015). First detection of the supersonic upward plasma flow structures in the early morning sector. Geophys. Res. Lett. 42, 9642–9649. doi:10.1002/2015GL066369

CrossRef Full Text | Google Scholar

Aveiro, H., and Huba, J. (2013). Equatorial spread F studies using Sami3 with two-dimensional and three-dimensional electrostatics. Ann. Geophys. 31, 2157–2162. doi:10.5194/angeo-31-2157-2013

CrossRef Full Text | Google Scholar

Aveiro, H. C., and Hysell, D. L. (2010). Three-dimensional numerical simulation of equatorial F region plasma irregularities with bottomside shear flow. J. Geophys. Res. Space Phys. 115 (A11). doi:10.1029/2010JA015602

CrossRef Full Text | Google Scholar

Carrasco, A., Pimenta, A., Wrasse, C., Batista, I., and Takahashi, H. (2020). Why do equatorial plasma bubbles bifurcate? J. Geophys. Res. Space Phys. 125 (11), e2020JA028609. doi:10.1029/2020JA028609

CrossRef Full Text | Google Scholar

Eccles, J. V. (1998). Modeling investigation of the evening prereversal enhancement of the zonal electric field in the equatorial ionosphere. J. Geophys. Res. 103 (A11), 26709–26719. doi:10.1029/98JA02656

CrossRef Full Text | Google Scholar

Fritts, D., Vadas, S., Riggin, D., Abdu, M., Batista, I., Takahashi, H., et al. (2008). Gravity wave and tidal influences on equatorial spread F based on observations during the Spread F Experiment (SpreadFEx). Ann. Geophys. 26, 3235–3252. doi:10.5194/angeo-26-3235-2008

CrossRef Full Text | Google Scholar

Gao, J.-F., Xu, Z.-W., Guo, L.-X., Xue, K., and Zhao, H.-S. (2023). Controlling factors of artificial irregularities triggered by chemical release at low latitude ionosphere. Space weather. 21, e2022SW003229. doi:10.1029/2022SW003229

CrossRef Full Text | Google Scholar

Huang, C.-S., Foster, J. C., and Sahai, Y. (2007). Significant depletions of the ionospheric plasma density at middle latitudes: a possible signature of equatorial spread F bubbles near the plasmapause. J. Geophys. Res. 112, A05315. doi:10.1029/2007JA012307

CrossRef Full Text | Google Scholar

Huang, C.-S., and Kelley, M. C. (1996). Nonlinear evolution of equatorial spread F: 4. Gravity waves, velocity shear, and day-to-day variability. J. Geophys. Res. Space Phys. 101 (A11), 24521–24532. doi:10.1029/96JA02332

CrossRef Full Text | Google Scholar

Huba, J., Ossakow, S., Joyce, G., Krall, J., and England, S. (2009). Three-dimensional equatorial spread F modeling: zonal neutral wind effects. Geophys. Res. Lett. 36 (19). doi:10.1029/2009GL040284

CrossRef Full Text | Google Scholar

Huba, J. D. (2021). Theory and modeling of equatorial spread F. Ionos. Dyn. Appl., 185–200. doi:10.1002/9781119815617.ch10

CrossRef Full Text | Google Scholar

Huba, J. D., and Joyce, G. (2007). Equatorial spread F modeling: multiple bifurcated structures, secondary instabilities, large density ‘bite-outs,’ and supersonic flows. Geophys. Res. Lett. 34 (7). doi:10.1029/2006GL028519

CrossRef Full Text | Google Scholar

Huba, J. D., Joyce, G., and Krall, J. (2008). Three-dimensional equatorial spread F modeling. Geophys. Res. Lett. 35 (10). doi:10.1029/2008gl033509

CrossRef Full Text | Google Scholar

Huba, J. D., Krall, J., and Drob, D. (2020). Modeling the impact of metallic ion layers on equatorial spread with Sami3/ESF. Geophys. Res. Lett. 47 (5), e2020GL087224. doi:10.1029/2020GL087224

CrossRef Full Text | Google Scholar

Huba, J. D., Wu, T.-W., and Makela, J. J. (2015). Electrostatic reconnection in the ionosphere. Geophys. Res. Lett. 42 (6), 1626–1631. doi:10.1002/2015GL063187

CrossRef Full Text | Google Scholar

Hysell, D. (1999). Imaging coherent backscatter radar studies of equatorial spread F. J. Atmos. solar-terrestrial Phys. 61 (9), 701–716. doi:10.1016/S1364-6826(99)00020-6

CrossRef Full Text | Google Scholar

Hysell, D., Kelley, M., Swartz, W., and Farley, D. (1994). VHF radar and rocket observations of equatorial spread F on Kwajalein. J. Geophys. Res. Space Phys. 99 (A8), 15065–15085. doi:10.1029/94JA00476

CrossRef Full Text | Google Scholar

Hysell, D., Kelley, M., Swartz, W., and Woodman, R. (1990). Seeding and layering of equatorial spread F by gravity waves. J. Geophys. Res. Space Phys. 95 (A10), 17253–17260. doi:10.1029/JA095iA10p17253

CrossRef Full Text | Google Scholar

Hysell, D. L., Jafari, R., Fritts, D. C., and Laughman, B. (2014). Gravity wave effects on postsunset equatorial F region stability. J. Geophys. Res. Space Phys. 119 (7), 5847–5860. doi:10.1002/2014JA019990

CrossRef Full Text | Google Scholar

Hysell, D. L., Larsen, M. F., Swenson, C. M., Barjatya, A., Wheeler, T. F., Sarango, M. F., et al. (2005). Onset conditions for equatorial spread F determined during EQUIS II. Geophys. Res. Lett. 32 (24). doi:10.1029/2005GL024743

CrossRef Full Text | Google Scholar

Hysell, D. L., Milla, M. A., Condori, L., and Vierinen, J. (2015). Data-driven numerical simulations of equatorial spread F in the Peruvian sector 3: solstice. J. Geophys. Res. Space Phys. 120 (12), 809–810. doi:10.1002/2015JA021877

CrossRef Full Text | Google Scholar

Kirchengast, G. (1996). Elucidation of the physics of the gravity wave-TID relationship with the aid of theoretical simulations. J. Geophys. Res. Space Phys. 101 (A6), 13353–13368. doi:10.1029/96JA00750

CrossRef Full Text | Google Scholar

Krall, J., Huba, J., and Fritts, D. (2013). On the seeding of equatorial spread F by gravity waves. Geophys. Res. Lett. 40 (4), 661–664. doi:10.1002/grl.50144

CrossRef Full Text | Google Scholar

Li, Z., Lei, J., and Zhang, B. (2021). Numerical considerations in the simulation of equatorial spread F. J. Geophys. Res. Space Phys. 126 (10), e2021JA029622. doi:10.1029/2021JA029622

CrossRef Full Text | Google Scholar

Li, Z., Lei, J., and Zhang, B. (2023). Three-dimensional simulation of equatorial spread F: effects of field-aligned plasma flow and ionospheric conductivity. J. Geophys. Res. Space Phys. 128 (3), e2022JA031070. doi:10.1029/2022JA031070

CrossRef Full Text | Google Scholar

Makela, J. J., Kelley, M. C., and Nicolls, M. J. (2006). Optical observations of the development of secondary instabilities on the eastern wall of an equatorial plasma bubble. J. Geophys. Res. Space Phys. 111 (A9). doi:10.1029/2006JA011646

CrossRef Full Text | Google Scholar

Raghavarao, R., Suhasini, R., Mayr, H., Hoegy, W., and Wharton, L. (1999). Equatorial spread-F (ESF) and vertical winds. J. Atmos. solar-terrestrial Phys. 61 (8), 607–617. doi:10.1016/S1364-6826(99)00017-6

CrossRef Full Text | Google Scholar

Retterer, J. M. (2010). Forecasting low-latitude radio scintillation with 3-D ionospheric plume models: 1. Plume model. J. Geophys. Res. Space Phys. 115 (A3). doi:10.1029/2008JA013839

CrossRef Full Text | Google Scholar

Scannapieco, A. J., and Ossakow, S. L. (1976). Nonlinear equatorial spread F. Geophys. Res. Lett. 3 (8), 451–454. doi:10.1029/GL003i008p00451

CrossRef Full Text | Google Scholar

Sekar, R., Suhasini, R., and Raghavarao, R. (1994). Effects of vertical winds and electric fields in the nonlinear evolution of equatorial spread F. J. Geophys. Res. Space Phys. 99 (A2), 2205–2213. doi:10.1029/93JA01849

CrossRef Full Text | Google Scholar

Shinagawa, H., Jin, H., Miyoshi, Y., Fujiwara, H., Yokoyama, T., and Otsuka, Y. (2018). Daily and seasonal variations in the linear growth rate of the Rayleigh–Taylor instability in the ionosphere obtained with GAIA. Prog. Earth Planet. Sci. 5, 16. doi:10.1186/s40645-018-0175-8

CrossRef Full Text | Google Scholar

Trac, H., and Pen, U. L. (2003). A primer on eulerian computational fluid dynamics for astrophysics. Publ. Astronomical Soc. Pac. 115 (805), 303–321. doi:10.1086/367747

CrossRef Full Text | Google Scholar

Tsunoda, R. T. (2007). Seeding of equatorial plasma bubbles with electric fields from an Es-layer instability. J. Geophys. Res. Space Phys. 112 (A6). doi:10.1029/2006JA012103

CrossRef Full Text | Google Scholar

Woodman, R. (2009). Spread F–an old equatorial aeronomy problem finally resolved? Ann. Geophys. 27, 1915–1934. doi:10.5194/angeo-27-1915-2009

CrossRef Full Text | Google Scholar

Wu, T. W., Huba, J., Krall, J., Fritts, D., and Laughman, B. (2015). Seeding equatorial spread F with turbulent gravity waves: phasing effects. Geophys. Res. Lett. 42 (1), 15–21. doi:10.1002/2014GL062348

CrossRef Full Text | Google Scholar

Yokoyama, T. (2017). A review on the numerical simulation of equatorial plasma bubbles toward scintillation evaluation and forecasting. Prog. Earth Planet. Sci. 4, 37. doi:10.1186/s40645-017-0153-6

CrossRef Full Text | Google Scholar

Yokoyama, T., Jin, H., and Shinagawa, H. (2015). West wall structuring of equatorial plasma bubbles simulated by three-dimensional HIRB model. J. Geophys. Res. Space Phys. 120 (10), 8810–8816. doi:10.1002/2015JA021799

CrossRef Full Text | Google Scholar

Yokoyama, T., Jin, H., Shinagawa, H., and Liu, H. (2019). Seeding of equatorial plasma bubbles by vertical neutral wind. Geophys. Res. Lett. 46 (13), 7088–7095. doi:10.1029/2019GL083629

CrossRef Full Text | Google Scholar

Yokoyama, T., Shinagawa, H., and Jin, H. (2014). Nonlinear growth, bifurcation, and pinching of equatorial plasma bubble simulated by three-dimensional high-resolution bubble model. J. Geophys. Res. Space Phys. 119 (12), 474–482. doi:10.1002/2014JA020708

CrossRef Full Text | Google Scholar

Zalesak, S., and Ossakow, S. (1980). Nonlinear equatorial spread F: spatially large bubbles resulting from large horizontal scale initial perturbations. J. Geophys. Res. Space Phys. 85 (A5), 2131–2142. doi:10.1029/JA085iA05p02131

CrossRef Full Text | Google Scholar

Zalesak, S. T., Ossakow, S. L., and Chaturvedi, P. K. (1982). Nonlinear equatorial spread F: the effect of neutral winds and background Pedersen conductivity. J. Geophys. Res. Space Phys. 87 (A1), 151–166. doi:10.1029/JA087iA01p00151

CrossRef Full Text | Google Scholar