- 1Department of Mathematics, Division of Science and Technology, University of Education, Lahore, Pakistan
- 2Department of Mathematics, Government College Women University, Sialkot, Pakistan
- 3Department of Physics, Zhejiang Normal University, Jinhua, China
- 4Astrophysics Research Centre, School of Mathematics, Statistics and Computer Science, University of KwaZulu-Natal, Durban, South Africa
- 5Department of Physics, College of Sciences, University of Bisha, Bisha, Saudi Arabia
This paper develops the stellar interior geometry for charged anisotropic spherical matter distribution by developing an exact solution of the field equations of Rastall gravity using the notion of gravitational decoupling. The main purpose of this investigation is the extension of the well-known isotropic model within the context of charged isotropic Rastall gravity solutions. The second aim of this work is to apply gravitational decoupling via a minimal geometric deformation scheme in Rastall gravity. Finally, the third one is to derive an anisotropic version of the charged isotropic model previously obtained by applying gravitational decoupling technology. We construct the field equations which are divided into two sets by employing the geometric deformation in radial metric function. The first set corresponds to the seed (charged isotropic) source, while the other one relates the deformation function with an extra source. We choose a known isotropic solution for spherical matter configuration including electromagnetic effects and extend it to an anisotropic model by finding the solution of the field equations associated with a new source. We construct two anisotropic models by adopting some physical constraints on the additional source. To evaluate the unknown constants, we use the matching of interior and exterior spacetimes. We investigate the physical feasibility of the constructed charged anisotropic solutions by the graphical analysis of the metric functions, density, pressure, anisotropy parameter, energy conditions, stability criterion, mass function, compactness, and redshift parameters. For the considered choice of parameters, it is concluded that the developed solutions are physically acceptable as all the physical aspects are well-behaved.
1 Introduction
Gravity is believed to be a natural phenomenon in general relativity (GR), which has revolutionized cosmological and astronomical conceptions. One fundamental reality that presents several obstacles for modern science is the universe’s accelerating expansion. In order to collect data of an exotic source that is enigmatic and participating to the expansion of the universe, astronomers have used a variety of probes, including gamma-ray bursts, large-scale structure, cosmic microwave background radiation, the integrated Sachs–Wolfe effect, and type Ia supernovas (Riess et al., 1998; Perlmutter et al., 1999; Bennett et al., 2003; Boughn and Crittenden, 2004; Eisenstein et al., 2005; Kodama et al., 2008). The cosmic period before radiation and the current condition after the matter-dominated phase are suggested to represent two stages of rapid expansion by these data. In recent decades, a broad agreement has developed on the origin of this accelerated behavior: dark energy (DE), an extraordinary anti-gravitational force. In the early 1980s, physicists researching the creation of galaxies in space initially hypothesized the existence of DE (Hinshaw et al., 2009). Due to its unusual character, DE is not consistent with the strong energy condition (SEC), which results in a large amount of the cosmic contents unknown. In the literature, multiple efforts have been undertaken to comprehend the enigmatic nature of DE. Extensive techniques have been taken as a substitute for dark sources in the lack of strong evidence to support them. Two methods have been used to demonstrate the study of such exotic terms: one is the use of changed matter sources, and the other is the modification of gravity by adding additional degrees of freedom to the action.
Modifying the matter sector of the Einstein–Hilbert Lagrangian density is one approach of describing the universe’s dynamic behavior. This may be accomplished by the use of numerous ideas such as quintessence energy, phantom, tachyon field, k-essence, and generalized equations of state such as Chaplygin gas (Caldwell et al., 1998; Kamenshchik et al., 2001; Bento et al., 2002; Carroll et al., 2003; Chimento, 2004; Gorini et al., 2004). These theories perfectly represent the universe’s dynamic behavior and offer an intriguing avenue for further investigation. Another strategy is to improve the gravitational portion of general relativity by introducing a DE source while leaving the matter component unchanged. This can help us comprehend the expansion of the cosmos and the nature of DE. However, there are major ambiguities with this procedure, making it less promising than other methods. Another method that might be effective in cosmological applications is modified gravity frameworks. These frameworks change gravity rules to better describe the behavior of the cosmos and can be employed to assess different gravity theories. They provide a potential route for future study on the nature of DE and the expansion of the cosmos.
The function of a curvature invariant is substituted or introduced in the geometric part of the Einstein–Hilbert action to develop alternative gravity theories. The simplest extension of GR is
Several alternative gravity theories have been presented, and recently, Rastall theory (Rastall, 1972) has been considered one of the most prominent and attractive theories. Many researchers have explored various cosmological aspects in the context of Rastall gravity. Visser (Abbas and Shahzad, 2020) explored that Rastall gravity is equivalent to general relativity and found that Rastall’s stress–energy tensor corresponds to an artificially isolated portion of the physical conserved stress–energy. The study of compact stars has been conducted by Abbas and Shahzad (2018a), Abbas and Shahzad (2018b), Salako et al. (2018), Abbas and Shahzad (2019), Hansraj et al. (2019), Mota et al. (2019), Javed et al. (2022a), and Ashraf et al. (2023); black hole (BH) solutions by Heydarzade and Darabi (2017), Heydarzade et al. (2017), Ma and Zhao (2017), Kumar and Ghosh (2018), Xu et al. (2018), and Liu et al. (2023); thermodynamics of BHs by Bamba et al. (2018), Lobo et al. (2018), Soroushfar et al. (2019), Ditta et al. (2023), and Gulzoda et al. (2023); wormhole (WH) solutions by Moradpour et al. (2017a) and Halder et al. (2019); and cosmology by Batista et al. (2012) and Moradpour (2016). Moreover, some studies on the generalization of Rastall theory (Moradpour et al., 2017b; Lin and Qian, 2020) and a combination of this with other modified theories (Wolf, 1986; Carames et al., 2014) have also been performed. Recently, Javed et al. (2022b) developed a WH solution in the background of Rastall gravity. They also analyzed the stable configuration of a thin-shell around the constructed wormhole solution by using the speed of sound parameter.
Oliveira et al. (2015) used static spherically symmetric Rastall gravity solutions to represent neutron stars and realistic equations of state for these stars to establish a conservative constraint on Rastall theory’s non-general relativity behavior. Moradpour et al. (2019) determined the conformally flat and non-singular BH solutions in generalized Rastall theory and discussed the thermodynamics of obtained BHs. They concluded that the pressure components in the equations for the gravitational field are not always equivalent to the thermodynamic pressure. They also discussed the conformally flat BHs in the Rastall scenario. Övgün et al. (2020) studied the energy emission rate and shadow of spherical non-commutative BH in Rastall gravity. They found that the non-commutative parameter affects the visibility of shadow. In the framework of Rastall gravity, Lobo et al. (2020) created thin-shell WH solutions for static BHs supplied by an anisotropic fluid using the cut-and-paste method. They explored the energy bounds and traversability condition at the WH throat and identified the stability zones. In the Rastall framework, Abbas and Shahzad (2020) proposed a hybrid compact star model made up of regular baryonic matter distribution and strange quark matter. They deduced that the resulting model satisfies the criteria for a realistic model. The same authors solved the Rastall field equations for isotropic matter content with quintessence field by adopting Krori and Barua ansatz and investigated several physical characteristics for the obtained model (Shahzad and Abbas, 2020). In this theory, Zubair et al. (2020) used a linear equation of state to construct the dynamical equations for static spherical symmetry and solved them numerically by choosing a certain gravitational potential. They showed that the obtained solutions are both stable and physically acceptable.
Many astrophysical researchers are interested in studying exact isotropic and anisotropic solutions of static spherically symmetric celestial configurations. The non-linear nature of the Einstein field equations generates difficulties in the construction of the analytical solutions. A potential technique which is most convenient and efficient in determining the analytical and physically acceptable solutions of non-linear field equations is gravitational decoupling (Ovalle and Linares, 2013). The addition of a new source as dust or anisotropic fluid in the stress–energy tensor is a significant feature of this method. This approach assists in the conversion of known isotropic solutions to anisotropic solutions. Ovalle et al. (2018a) studied the implications of anisotropic spherically symmetric gravitational sources on isotropic interior solutions for static self-gravitating systems by considering the minimal geometric deformation (MGD) approach. Mustafa et al. (2020a), Mustafa et al. (2020b), Mustafa et al. (2020c), Mustafa et al. (2021a), Mustafa et al. (2021b), Mustafa et al. (2021c), and Mustafa et al. (2021d) explored the stellar structures for the spherically static symmetric space–time in the background of Rastall gravity and different modified gravities via the embedding approach. They also studied the modified field equations by plugging the different sources like quintessence field with an anisotropic source of fluid. Furthermore, by imposing the junction conditions, we calculate the values of involved parameters by considering observational data of 4U 1608-52, Cen X-3, and EXO 1785-240. They found that the physical parameters show the viability and stability of the stellar objects in Rastall gravity and modified theories of gravities.
The effect of charge in self-gravitating systems is of great importance. Using the gravitational decoupling technique, the charged anisotropic spherical solutions and anisotropic uncharged cylindrical solutions were investigated by Sharif and Sadiq (2018). Implementing the same approach, Gabbanelli et al. (2018) investigated the observable influence of surface redshift for general anisotropies. For a spherical symmetric fluid distribution, Ovalle et al. (2018b) used the same method to develop a modified Schwarzschild vacuum solution. Graterol (2018) considered the Buchdahl perfect fluid distribution in the stellar structure and found the components of the stress–energy tensor using Einstein’s field equations. He also deformed the Buchdahl solution to get the anisotropic solution with the help of matching conditions. The study of WH solutions and thin-shell around the calculated WHs is conducted in different theories as in teleparallel gravity (Javed et al., 2022c), f(R, T) gravity (Javed et al., 2022d), f(Q) gravity (Mustafa et al., 2022), and with consideration of quantum wave dark matter (Mustafa et al., 2023). Furthermore, the dynamical evolution of thin-shell composed of scalar field was explored in the framework of GR and metric affine gravity in the work of Javed (2023a) and Javed (2023b). Sharif and Ama-Tul-Mughani (2020) and Sharif and Ahmed (2021) formulated some gravitational decoupled solutions of axial string cosmology and non-static anisotropic spherical solutions. Making use of this technique, several anisotropic solutions have been obtained (Maurya, 2019; Singh et al., 2019; Maurya et al., 2020a; Maurya and Tello-Ortiz, 2020a; Maurya et al., 2020b; Tello-Ortiz, 2020; Maurya et al., 2021a; Maurya et al., 2021b; Maurya et al., 2021c; Maurya et al., 2021d; Maurya et al., 2022).
In the context of modified theories of gravity, the gravitational decoupling via the MGD approach has also gained much attention. Sharif and Waseem (2019), Maurya et al. (2020), Azmat and Zubair (2021), and Sharif and Aslam (2021) derived the charged and uncharged anisotropic spherical solutions by employing this technique in the frameworks of f(R) and f(R, T) theories. In Rastall gravity, Maurya and Tello-Ortiz (2020b) obtained the stellar interior solutions for anisotropic matter distribution via the gravitational decoupling approach. In order to examine the viability of their obtained anisotropic solutions, they adopted the Tolman IV solution.
Motivated by the abovenarrated works, in this paper, we derived the charged anisotropic spherical solutions through the gravitational decoupling approach in Rastall gravity by considering the well-known metric function. So, the paper is organized in the following pattern. The next section deals with the basics of Rastall theory and constructs its field equations corresponding to multiple factors. Section 3 discusses the gravitational decoupled solutions through the MGD technique. The mimic constraints and their physical implications are examined in Section 4. discusses the mass function. The last section provides the final outcomes of the problem examined in this paper.
2 Rastall gravity and the MGD approach
In a curved spacetime, the primary notion behind Rastall theory is to renounce the divergence-free stress–energy tensor, i.e.,
where
For χ → 0, the field equations of general relativity are recovered from the above equation. The above field equations can be rewritten as follows (Mustafa et al., 2021a; Mustafa et al., 2021c):
where
Here, ξ = χκ with κ = 1 denotes the Rastall gravitational constant. Moreover, the necessary condition is 4ξ − 1 ≠ 0 to avoid singularities. In the present study, we consider multiple sources to analyze the internal structure of stellar objects. In this case, the standard field equations become
where
The matter constitution is taken to be charged perfect as
The terms ρ, P and
where Jδ denotes the four-current. In comoving coordinates, we have the following equation:
where γ = γ(r) represents the charge density. For the considered geometry, the Maxwell field equations yield
where prime indicates the differentiation with respect to r. The integration of above equation yields
Here,
where
The conservation law
We observe that the system, consisting of non-linear differential Eqs 13–15, contains seven unknowns, i.e., thermodynamic factors (ρ(eff), P(eff)), metric potentials (η, ζ), and the factors of an additional term
It is clear that the presence of Θ leads to anisotropic behavior of the system when
where
where f and h are the deformations defined by the radial and temporal metric constituents, respectively. It should be noted that the mentioned deformations are entirely radial functions that assure the spherical symmetry of the solution. Here, we take h = 0, meaning that the temporal part stays unaltered, and the anisotropy is based on the radial part. The substitution of Eq. 20 in field Eqs 13–15 yields two groups of equations. The first group yields α = 0, i.e., charged isotropic configuration given as
representing the Einstein–Maxwell–Rastall system. From the above equations, the explicit expressions of ρ, P, and q in terms of metric functions are obtained as follows:
where
The other group leads to the source Θ given as follows:
The sets of Eqs 21–23 and Eqs 28–30 satisfy the following conservation equations:
whose linear combination by means of coupling parameter α corresponds the conservation equation for
The last term of the above equation indicates the Rastall contribution or the so-called Rastall force which can be attractive or repulsive depending on the sign of Rastall parameter χ. At this point, the components of the total energy–momentum tensor are defined as follows:
where ρ and P are expressed in Eqs 24 and 25, respectively, and contains the additional geometric factors given by the Rastall participation. In this manner, the Rastall factors occur in the decoupler function f(r) and further in the additional source Θ. The junction conditions are an important factor to study significant characteristics and the evolution of stellar configurations. They provide a linear matching between interior
Making use of Eq. 26, the mass function becomes
where
The proper mass may be greater or less than that of the general relativistic case as α does not need to be purely positive and binding energy changes accordingly.
The exterior manifold can include some factors arising from the source Θ meaning that the outer spacetime binding the stellar structure is no more a vacuum. The most general exterior geometry is considered as follows:
To match the interior geometry with the outer one, the famous Israel–Darmois junction conditions (Darmois, 1966) are employed. The first fundamental form of these conditions (continuity of metric functions about Σ) yields
where M = m(R) and Q = q(R) display the total gravitational mass and charge surrounded by the fluid distribution, respectively. The second fundamental form (continuity of the extrinsic curvature) gives
The above equation illustrates that the source Θ and the Rastall parameter contribute to the outer spacetime. So, while discussing the compact objects within the context of modified gravitational theories, the exterior region is not a vacuum due to the presence of modified terms. Such participation can provide some extensions on the standard matching constraints. Senovilla (2013) discussed such constraints in the context of f(R) theory by adopting isotropic and anisotropic distributions and concluded that these constraints are not fulfilled in this arena. If we talk about the factors arising from the Rastall theory, the external spacetime is no more vacuum as it is occupied by an effective cosmological constant illustrating the (anti) de Sitter spacetime (Heydarzade et al., 2017). Here, we drop out the Rastall contributions in the exterior region
So, the exterior geometry is considered deformed Reissner–Nordström spacetime, i.e.,
where g(r) manifests the geometric deformation corresponding to the external Reissner–Nordström spacetime connected with Θηζ. Using Eq. 29 in (41), we obtain the following equation:
If we take the geometric deformation function g(r) to be zero, then the original Reissner–Nordström exterior solution is recovered. Consequently, the above equation leads to the following condition:
In the next section, we find the anisotropic solution by solving the field equations for the source Θ.
3 Gravitational decoupled anisotropic solution
Here, to evaluate the deformation function f(r), we determine the solutions of Eqs 28–30 by implementing some feasible conditions on the factors of Θδς and then compute
where S and a are arbitrary constants that can be determined from matching conditions, B is the integration constant, and G ≥ 0 represents the measure of charge. This solution is singularity-free and satisfies the physical conditions inside the sphere and illustrated by the following thermodynamic factors
where
Now, in order to close the system, we consider the mimic constraint approach (Ovalle et al., 2018a).
3.1 Pressure constraint
After applying the decoupling mechanism, the mimic constraints are implemented on the components of sources. These impositions result in solutions that are well-behaved, i.e., without any unfavorable mathematical/physical conducts like increasing thermodynamic factors, singularities, and the contravention of the conservation law. Some other assumptions could include a direct and appropriate description of the geometric deformation function f(r) that satisfies the fundamental standards of physical and mathematical admissibility or connecting the parts of Θ via barotropic, polytropic, or linear equation of state. Here, we take the situation where the radial component
This choice indicates that for the seed solution, the stress–energy tensor coincides with the anisotropy in the radial direction. Using Eqs 47, 48, and 29 in the above equation, we use Mathematica to find the explicit expression of deformation parameter f(r) in terms of the metric functions (44) as
where Cχ is as expressed in Supplementary Appendix SA1. To describe the inner solution, the unknown constants a, B, and S can be computed from the matching conditions. The temporal metric function (ζ = ν) is given in Eq. 44, while the deformed radial metric function (η) can be obtained by substituting the value of μ in Eq. 20. Using these metric functions in Eq. 39, i.e., the continuity of metric functions, the following result is obtained:
yielding the value of S and B, which are not mentioned here due to lengthy expression. In this case, the expressions of the components of Θ (
where Dχ, Eχ, and Fχ are as presented in Supplementary Appendix SA1.
The graphical analysis of metric functions is shown in Figure 1, while the behavior of main matter variables that specifies the system such as density, radial and tangential pressures, and anisotropic factor is presented in Figure 2 for different values of G to inspect the effect of the charge parameter. In order to determine a physically viable stellar model, we consider the values of parameters which lead to the viable behavior of all physical parameters, energy conditions, and stability criterion. For this reason, we take the negative values of χ. Moreover, in the literature, the positive and negative values of the Rastall parameter have been used. So, there is no limitation on the Rastall parameter except that
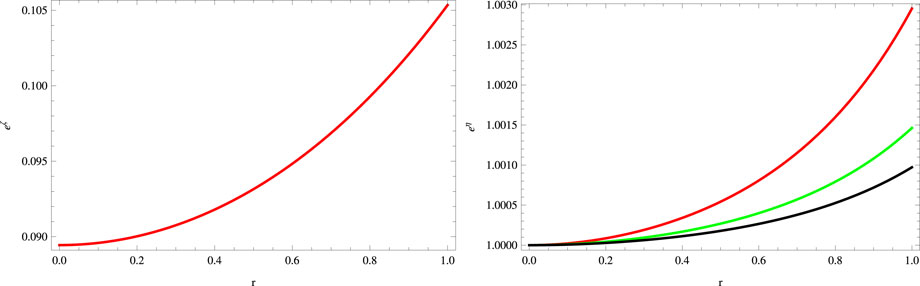
FIGURE 1. Plots of metric functions for a = 0.045, S = 1, B = −0.7, χ = −0.2, G = 0.05, α = 0.5 (red), α = 1 (green), and α = 1.5 (black).
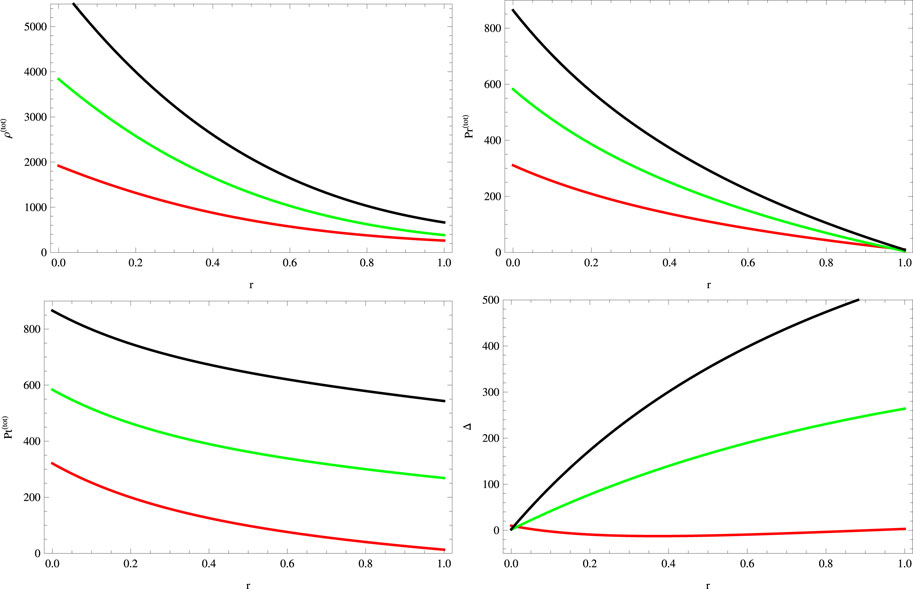
FIGURE 2. Plots of physical quantities for a = 0.045, S = 1, B = −0.7, χ = −2, G = 0.05, α = 0.5 (red), α = 1 (green), and α = 1.5 (black).
We show the energy constraints for the case under consideration in Figure 3, which shows that our charged anisotropic solution for the chosen parameters satisfies all the above inequalities. Using the sound speed criterion, we examine the stability of the system. The following formula is used to evaluate the radial
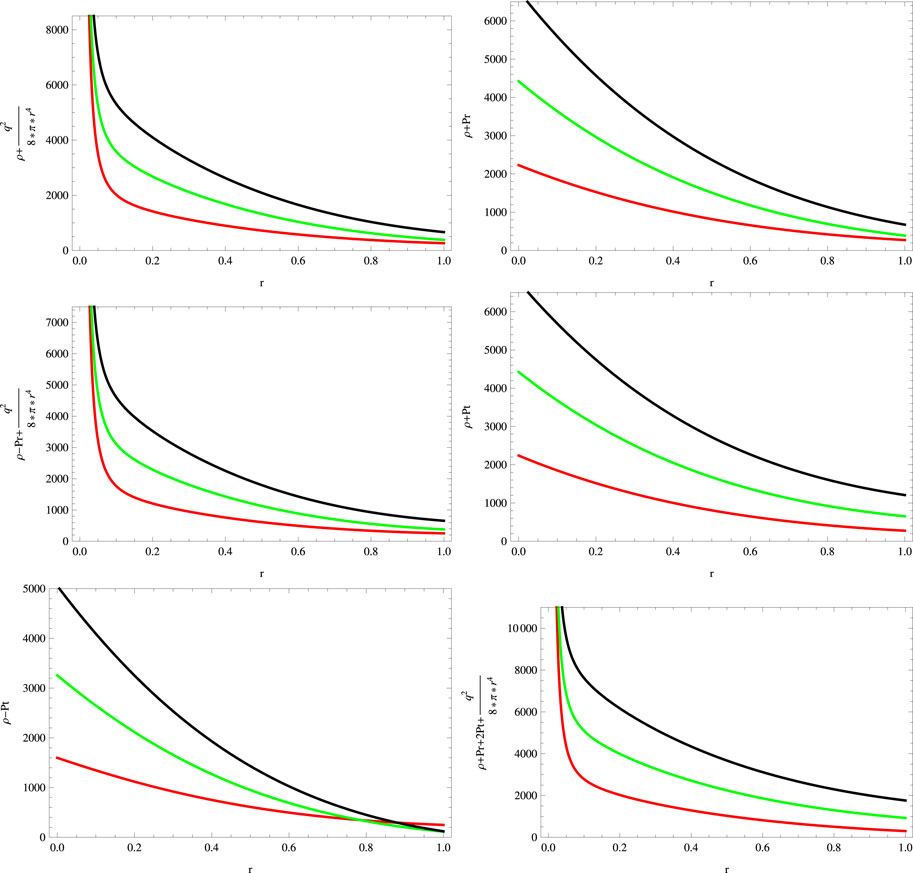
FIGURE 3. Plots of energy conditions for a = 0.045, S = 1, B = −0.7, χ = −2, G = 0.05, α = 0.5 (red), α = 1 (green), and α = 1.5 (black).
As shown by the causality condition, the sound speed ought to be smaller than the speed of light whenever it passes through the anisotropic fluid configuration in stellar objects. According to this condition,
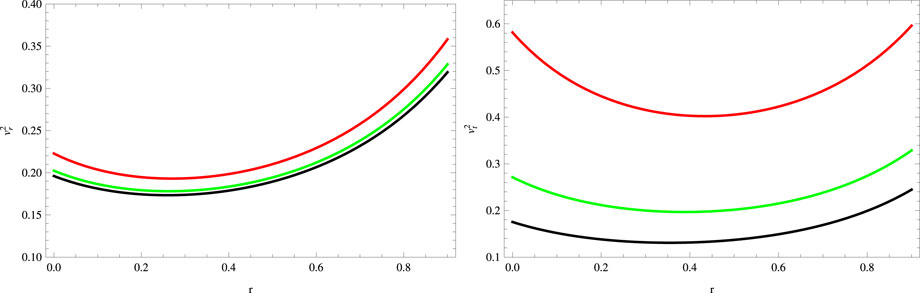
FIGURE 4. Plots of radial and tangential squared speed of sound for a = 0.045, S = 1, B = −0.7, χ = −2, G = 0.05, α = 0.5 (red), α = 1 (green), and α = 1.5 (black).
We plot the radial adiabatic index in Figure 5, showing that Γ > 4/3. Now, we examine the outcomes produced by the gravitational decoupling through minimal geometric deformation on the mass function and compactness parameter. The mass function for the considered system is found to be
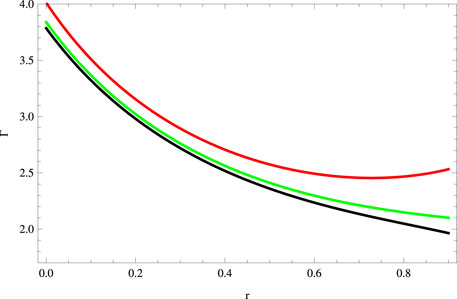
FIGURE 5. Plot of the adiabatic index for a = 0.045, S = 1, B = −0.7, χ = −2, G = 0.05, α = 0.5 (red), α = 1 (green), and α = 1.5 (black).
For the considered mimic constraint, the behavior of the gravitational decoupled mass function, compactness parameter, and redshift parameter is presented in Figure 6. All these factors vanish at the center of stellar structures and manifest the required viable physical behavior.
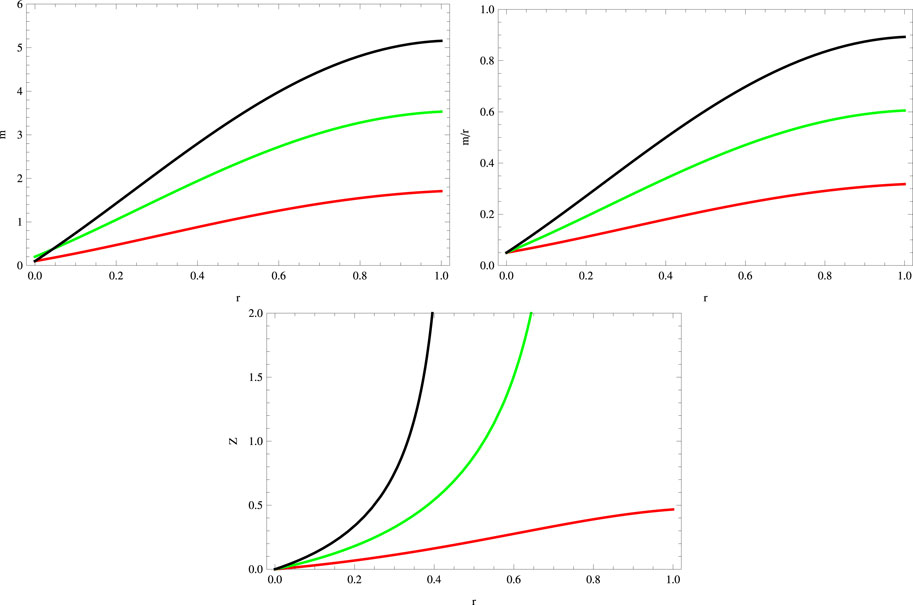
FIGURE 6. Plots of mass function, compactness, and redshift parameters for a = 0.045, S = 1, B = −0.7, χ = −2, G = 0.05, α = 0.5 (red), α = 1 (green), and α = 1.5 (black).
It is worth mentioning here that the obtained anisotropic solution is not unique because different choices and possibilities on the decoupler function f(r) and Θ constituents can be chosen. A different constraint is taken into account in the following section providing a distinct anisotropic solution.
3.2 Density constraint
Here, we consider a mimic constraint on density to close system (28)–(30) and determine an admissible solution, i.e.,
Equating Eqs 28 and 46, we get a general form of deformation factor f(r) presented as follows:
where Gχ is as displayed in Supplementary Appendix SA1, and the temporal and radial metric functions can be obtained from Eq. 20. The anisotropic solutions in this case become
Using the matching conditions (39), we find the expressions of constants which are not written here due to lengthy expressions. The graphical analysis in this case is displayed in Figures 7–12. The behavior of the metric function and matter variables is positive, regular, finite, and viable within the interior geometry of the stellar object (Figures 7, 8). The stellar model in this case exhibits the same radius as for the model obtained by pressure constraint. The energy conditions are also satisfied for this constraint (Figure 9). Our second solution also presents the stable structure of the stellar system (Figure 10). The graphical behavior of adiabatic index is shown in Figure 11. For density constraint, the graphical structure of the gravitational decoupled mass function, redshift, and compactness parameters is shown in Figure 12. These factors exhibit the same behavior as determined in case of pressure constraint, i.e., the physically acceptable behavior.
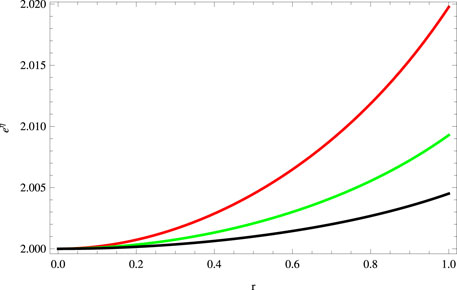
FIGURE 7. Plot of metric function eη for a = 0.045, S = 1, B = −0.7, χ = −2, G = 0.05, α = 0.5 (red), α = 1 (green), and α = 1.5 (black).
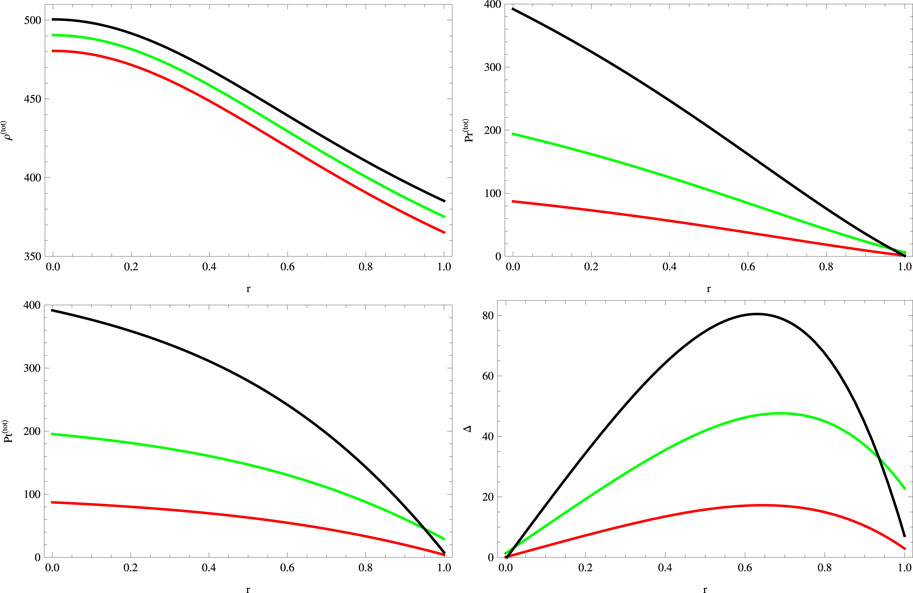
FIGURE 8. Plots of physical quantities for a = 0.045, S = 1, B = −0.7, χ = −2, G = 0.05, α = 0.5 (red), α = 1 (green), and α = 1.5 (black).
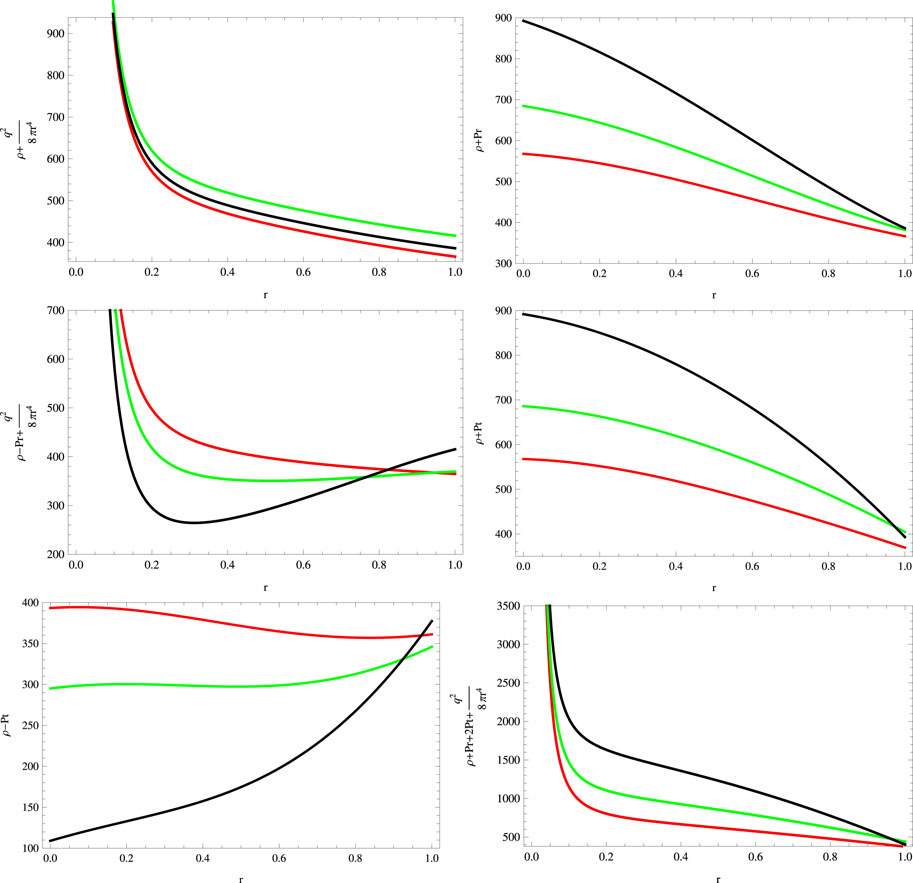
FIGURE 9. Energy conditions for a = 0.045, S = 1, B = −0.7, χ = −2, G = 0.05, α = 0.5 (red), α = 1 (green), and α = 1.5 (black).
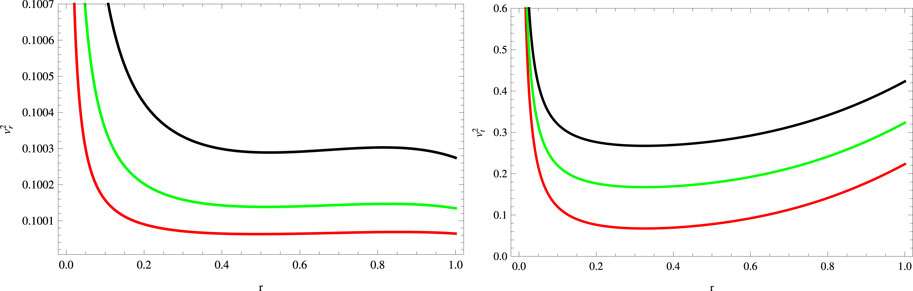
FIGURE 10. Plots of squared speed of sound for a = 0.045, S = 1, B = −0.7, χ = −2, G = 0.05, α = 0.5 (red), α = 1 (green), and α = 1.5 (black).
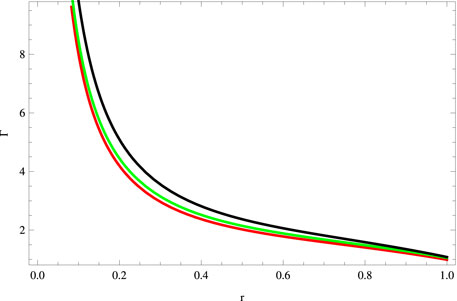
FIGURE 11. Plot of the adiabatic index for a = 0.045, S = 1, B = −0.7, χ = −2, G = 0.05, α = 0.5 (red), α = 1 (green), and α = 1.5 (black).
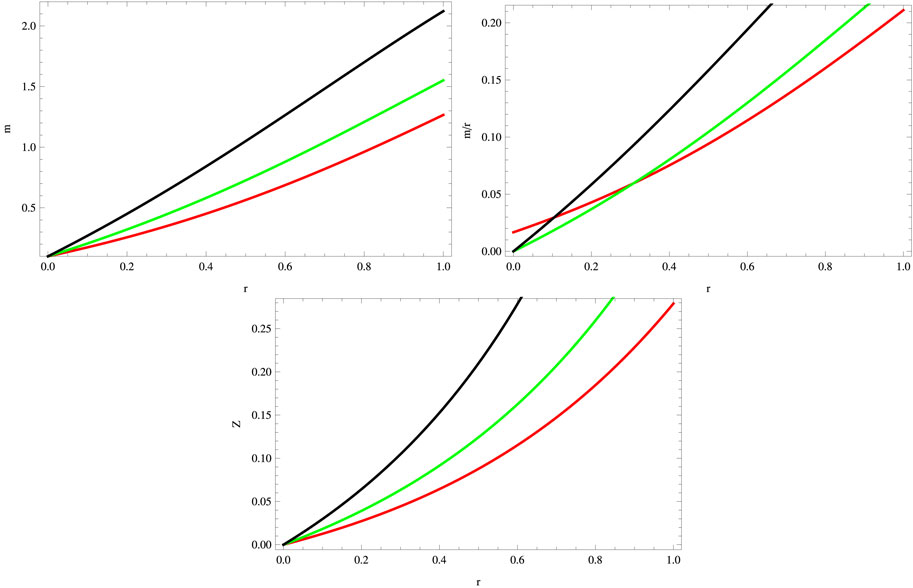
FIGURE 12. Plots of mass function, compactness, and redshift parameters for a = 0.045, S = 1, B = −0.7, χ = −2, G = 0.05, α = 0.5 (red), α = 1 (green), and α = 1.5 (black).
4 Final remarks
In order to analyze the structural features and stability criterion of the stellar models, the notion of gravitational decoupling by means of a minimal geometric deformation and the complete geometric deformation possesses great significance. This approach provides us a new window to obtain new anisotropic solutions to the Einstein field equations. Despite its simplicity, this powerful technique yields a better understanding about self-gravitating anisotropic configurations. One of the most important advantages of this approach lies in the fact that it splits a complicated system of equations into two simple separated sets of equations, one corresponds to the usual Einstein field equations associated with an isotropic matter distribution and the second one governed by an extra gravitational source which encodes the anisotropic sector (this system of equations is also known as quasi-Einstein equations). In the present study, we have employed this technique to formulate a new anisotropic stellar model with the inclusion of electromagnetic field by taking into account a known isotropic solution in the light of Rastall theory.
According to the MGD approach, an additional source is adjoined with the charged perfect fluid stress–energy tensor, which provides the effective field equations. Here, the first set corresponds to the field equations for perfect fluid along with the charge, whereas the second set is associated with the new source and the deformed metric function. We compared our interior spacetime with the deformed RN metric and evaluated the junction conditions. To solve the equations, we took the known charged perfect fluid model and then integrated the impact of the new source. As Rastall gravity includes an additional factor which displays the deviation from the behavior of general relativity, therefore, in this paper, we also observed the impact of that additional factor and the influence of electromagnetic field and the chances to attain the compact celestial configurations, which could lead to narrate quark or neutron stars.
In order to analyze the physical consistency of the obtained solutions, we examined the nature of some physical parameters, energy conditions, and stability criteria corresponding to the two mimic constraints for the particular choice of parametric values. It is found that the energy density and the radial/tangential pressures are well-behaved throughout the matter distribution. The radial/tangential pressures monotonically decrease and disappear at the surface of the stars. At the center of stellar structures, fluid distribution shows isotropic structure, whereas the increment in the anisotropic factor occurs as one travels toward the surface of a star. In addition, for the first constraint, the anisotropy parameter is negative just for smaller values of α, while for other cases, Δ > 0, intending the existence of the repulsive nature of gravitational force which may help in the development of more compact celestial objects. From the graphical description, it is observed that the proposed formalism (considered metric functions) exhibits suitable behavior in the presence of decoupling and Rastall parameters.
The graphical analysis of all energy conditions manifests that these are satisfied assuring the physical viability and acceptability of the obtained solutions. The stability criterion is inspected through the adiabatic index criterion and the cracking method. It is seen that these conditions are fulfilled, and henceforth, the developed solutions are stable corresponding to both mimic constraints. The mass function, compactness parameter, and redshift parameter also exhibit the required consistent behavior for both constraints. Finally, it is concluded that the adopted charged perfect fluid metric potentials (Estevez-Delgado et al., 2020) show viable and consistent configuration of stellar structures for the specific choices of decoupling and Rastall parameters.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
SS: writing–original draft. AW: writing–review and editing. FJ: writing–original draft. AE: writing–review and editing. AA-A: writing–review and editing.
Funding
The authors declare that financial support was received for the research, authorship, and/or publication of this article. The authors are thankful to the Deanship of Scientific Research at University of Bisha for supporting this work through the Fast-Track Research Support Program.
Acknowledgments
FJ acknowledges Grant No. YS304023917 to support his Postdoctoral Fellowship at Zhejiang Normal University, China. AE thanks the National Research Foundation (NRF) of South Africa for the award of a postdoctoral fellowship. The authors are thankful to the Deanship of Scientific Research at University of Bisha for supporting this work through the Fast-Track Research Support Program.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2023.1320081/full#supplementary-material
References
Abbas, G., and Shahzad, M. R. (2018a). A new model of quintessence compact stars in the Rastall theory of gravity. Eur. Phys. J. A 54, 211. doi:10.1140/epja/i2018-12642-y
Abbas, G., and Shahzad, M. R. (2018b). Isotropic compact stars model in Rastall theory admitting conformal motion. Astrophys. Space Sci. 363, 251. doi:10.1007/s10509-018-3472-1
Abbas, G., and Shahzad, M. R. (2019). Models of anisotropic compact stars in the Rastall theory of gravity. Astrophys. Space Sci. 364, 50. doi:10.1007/s10509-019-3537-9
Abbas, G., and Shahzad, M. R. (2020). Hybrid compact stars model in Rastall gravity: a comparative study. Astrophys. Space Sci. 365, 147. doi:10.1007/s10509-020-03861-y
Azmat, H., and Zubair, M. (2021). An anisotropic version of Tolman VII solution in f(R, T) gravity via gravitational decoupling MGD approach. Eur. Phys. J. Plus 136, 112. doi:10.1140/epjp/s13360-021-01081-z
Bamba, K., Jawad, A., Rafque, S., and Moradpour, H. (2018). Thermodynamics in Rastall gravity with entropy corrections. Eur. Phys. J. C 78, 986. doi:10.1140/epjc/s10052-018-6446-0
Batista, C. E., Daouda, M. H., Fabris, J. C., Piattella, O. F., and Rodrigues, D. C. (2012). Rastall cosmology and theΛCDMmodel. Phys. Rev. D. 85, 084008. doi:10.1103/physrevd.85.084008
Bento, M. C., Bertolami, O., and Sen, A. A. (2002). Generalized Chaplygin gas, accelerated expansion, and dark-energy-matter unification. Phys. Rev. D. 66, 043507. doi:10.1103/physrevd.66.043507
Boughn, S. P., and Crittenden, R. G. (2004). A correlation between the cosmic microwave background and large-scale structure in the Universe. Nature 427, 45–47. doi:10.1038/nature02139
Caldwell, R. R., Dave, R., and Steinhardt, P. J. (1998). Cosmological imprint of an energy component with general equation of state. Phys. Rev. Lett. 80, 1582–1585. doi:10.1103/physrevlett.80.1582
Carames, T. R., Daouda, M. H., Fabris, J. C., Oliveira, A. M., Piattella, O. F., and Strokov, V. (2014). The brans–dicke–rastall theory. Eur. Phys. J. C 74, 3145. doi:10.1140/epjc/s10052-014-3145-3
Darmois, G. (1966). M’emorial des Sciences Math’ematiques, Fascicule 25 (Gauthier-Villars, Paris, 1927); W. Israel, Singular hypersurfaces and thin shells in general relativity. Nuovo Cim. B 44S10, 1.
Ditta, A., Javed, F., Maurya, S., Mustafa, G., and Atamurotov, F. (2023). Thermal stability and effects of thermal fluctuations on the static and spherically symmetric hairy black hole by gravitational decoupling. Phys. Dark Universe 42, 101345. doi:10.1016/j.dark.2023.101345
Estevez-Delgado, J., Cabrera, J. V., Paulin-Fuentes, J. M., Rodriguez Ceballos, J. A., and Duran, M. P. (2020). A charged perfect fluid solution. Mod. Phys. Lett. A 35, 2050120. doi:10.1142/s0217732320501205
Gabbanelli, L., Rincon, A., and Rubio, C. (2018). Gravitational decoupled anisotropies in compact stars. Eur. Phys. J. C 78, 370. doi:10.1140/epjc/s10052-018-5865-2
Graterol, R. P. (2018). A new anisotropic solution by MGD gravitational decoupling. Eur. Phys. J. Plus 133, 244. doi:10.1140/epjp/i2018-12074-2
Gulzoda, R., Atamurotov, F., Javed, F., Abdujabbarov, A., and Mustafa, G. (2023). Thermodynamical analysis of charged rotating black hole surrounded by perfect fluid dark matter. Nucl. Phys. B 996, 116363. doi:10.1016/j.nuclphysb.2023.116363
Halder, S., Bhattacharya, S., and Chakraborty, S. (2019). Wormhole solutions in Rastall gravity theory. Mod. Phys. Lett. A 34, 1950095. doi:10.1142/s0217732319500950
Hansraj, S., Banerjee, A., and Channuie, P. (2019). Impact of the Rastall parameter on perfect fluid spheres. Ann. Phys. 400, 320–345. doi:10.1016/j.aop.2018.12.003
Harko, T., Lobo, F. S. N., Nojiri, S., and Odintsov, S. D. (2011). f(R,T)gravity. Phys. Rev. D. 84, 024020. doi:10.1103/physrevd.84.024020
Heydarzade, Y., Moradpour, H., and Darabi, F. (2017). Black hole solutions in Rastall theory. Can. J. Phys. 95, 1253–1256. doi:10.1139/cjp-2017-0254
Javed, F. (2023a). Stability and dynamics of scalar field thin-shell for renormalization group improved Schwarzschild black holes. Euro. Phys. J. C 83, 513. doi:10.1140/epjc/s10052-023-11686-6
Javed, F. (2023b). Computational analysis of thin-shell with scalar field for class of new black hole solutions in metric-affine gravity. Ann. Phys. 458, 169464. doi:10.1016/j.aop.2023.169464
Javed, F., Jan, M., Ditta, A., and Qaisar, S. (2022a). Anisotropic strange stars with off-diagonal tetrad in f(T,𝒯) gravity. Int. J.Geo. M. Mod. Phys. 19, 2250190. doi:10.1142/s0219887822501900
Javed, F., Mumtaz, S., Mustafa, G., Hussain, I., and Liu., W.-M. (2022c). New wormhole models with stability analysis via thin-shell in teleparallel gravity. Euro. Phys. J. C 82, 825. doi:10.1140/epjc/s10052-022-10780-5
Javed, F., Mustafa, G., Ovgun, A., and Shamir, M. F. (2022b). Epicyclic frequencies and stability of thin shell around the traversable phantom wormholes in Rastall gravity. Eur. Phys. J. Plus 137, 61. doi:10.1140/epjp/s13360-021-02291-1
Javed, F., Sadiq, S., Mustafa, G., and Hussain, I. (2022d). A comparative study of new generic wormhole models with stability analysis via thin-shell. Phys. Scr. 97, 125010. doi:10.1088/1402-4896/ac9ff6
Kamenshchik, A., Moschella, U., and Pasquier, V. (2001). An alternative to quintessence. Phys. Lett. B 511, 265–268. doi:10.1016/s0370-2693(01)00571-8
Kumar, R., and Ghosh, S. G. (2018). Rotating black hole in Rastall theory. Eur. Phys. J. C 78, 750. doi:10.1140/epjc/s10052-018-6206-1
Lin, K., and Qian, W. L. (2020). Cosmic evolution of dark energy in a generalized Rastall gravity. Available at: https://arxiv.org/abs/2006.03229.
Lobo, I. P., Moradpour, H., Morais Graca, J., and Salako, I. (2018). Thermodynamics of black holes in Rastall gravity. Int. J. Mod. Phys. D. 27, 1850069. doi:10.1142/s0218271818500694
Lobo, I. P., Richarte, M. G., Graça, J. M., and Moradpour, H. (2020). Thin-shell wormholes in Rastall gravity. Eur. Phys. J. Plus 135, 550. doi:10.1140/epjp/s13360-020-00553-y
Ma, M. S., and Zhao, R. (2017). Noncommutative geometry inspired black holes in Rastall gravity. Eur. Phys. J. C 77, 629. doi:10.1140/epjc/s10052-017-5217-7
Maurya, S. K., Errehymy, A., Singh, K. N., Tello-Ortiz, F., and Daoud, M. (2020b). Gravitational decoupling minimal geometric deformation model in modified f(R,T) gravity theory. Phys. Dark Univ. 30, 100640–100654. doi:10.1016/j.dark.2020.100640
Maurya, S. K., Pradhan, A., Tello-Ortiz, F., Banerjee, A., and Nag, R. (2021d). Minimally deformed anisotropic stars by gravitational decoupling in Einstein–Gauss–Bonnet gravity. Eur. Phys. J. C 81, 848–866. doi:10.1140/epjc/s10052-021-09628-1
Maurya, S. K., and Tello-Ortiz, F. (2020a). Decoupling gravitational sources by MGD approach in Rastall gravity. Phys. Dark Univ. 29, 100577–100595. doi:10.1016/j.dark.2020.100577
Maurya, S. K., and Tello-Ortiz, F. (2020b). Decoupling gravitational sources by MGD approach in Rastall gravity. Phys. Dark Uni. 29, 100577. doi:10.1016/j.dark.2020.100577
Maurya, S. K., Tello-Ortiz, F., and Govender, M. (2021a). Exploring physical properties of gravitationally decoupled anisotropic solution in 5D einstein-gauss-bonnet gravity. Fortschr. Phys. 69, 2100099–2100113. doi:10.1002/prop.202100099
Maurya, S. K., Tello-Ortiz, F., and Jasim, M. K. (2020a). An EGD model in the background of embedding class I space–time. Eur. Phys. J. C 80, 918–934. doi:10.1140/epjc/s10052-020-08491-w
Maurya, S. K., Tello-Ortiz, F., and Ray, S. (2021c). Decoupling gravitational sources in f(R,T) gravity under class I spacetime. Phys. Dark Univ. 31, 100753–100766. doi:10.1016/j.dark.2020.100753
Misner, C. W., and Sharp, D. H. (1964). Relativistic equations for adiabatic, spherically symmetric gravitational collapse. Phys. Rev. 136, B571–B576. doi:10.1103/physrev.136.b571
Moradpour, H., Heydarzade, Y., Corda, C., Ziaie, A. H., and Ghaffari, S. (2019). Black hole solutions and Euler equation in Rastall and generalized Rastall theories of gravity. Mod. Phys. Lett. A 34, 1950304. doi:10.1142/s0217732319503048
Moradpour, H., Heydarzade, Y., Darabi, F., and Salako, I. G. (2017b). A generalization to the Rastall theory and cosmic eras. Eur. Phys. J. C 77, 259. doi:10.1140/epjc/s10052-017-4811-z
Moradpour, H., Sadeghnezhad, N., and Hendi, S. (2017a). Traversable asymptotically flat wormholes in Rastall gravity. Can. J. Phys. 95, 1257–1266. doi:10.1139/cjp-2017-0040
Mota, C. E., Santos, L. C., da Silva, F. M., Flores, C. V., da Silva, T. J., and Menezes, D. P. (2019). Anisotropic compact stars in rastall-rainbow gravity. Available at: https://arxiv.org/abs/1911.03208.
Mustafa, G., Farasat Shamir, M., and Tie-Cheng, X. (2020a). Physically viable solutions of anisotropic spheres in f(R,G) gravity satisfying the Karmarkar condition. Phys. Rev. D. 101, 104013. doi:10.1103/physrevd.101.104013
Mustafa, G., Gao, X., and Javed, F. (2022). Twin peak quasi-periodic oscillations and stability via thin-shell formalism of traversable wormholes in symmetric teleparallel gravity. Fortschritte Phys. 70, 2200053. doi:10.1002/prop.202200053
Mustafa, G., Hussain, I., Farasat Shamir, M., and Tie-Cheng, X. (2021c). Realistic and dark stellar models via embedding approach in the Rastall gravity. Phys. Scr. 96, 045009. doi:10.1088/1402-4896/abe0f0
Mustafa, G., Tie-Cheng, X., Ahmad, M., and Farasat Shamir, M. (2021d). Anisotropic spheres via embedding approach in R+βR2 gravity with matter coupling. Phys. Dark Univ. 31, 100747. doi:10.1016/j.dark.2020.100747
Mustafa, G., Tie-Cheng, X., and Farasat Shamir, M. (2020b). Realistic solutions of fluid spheres in f(G,T) Gravity under Karmarkar condition. Ann. Phys. 413, 168059. doi:10.1016/j.aop.2019.168059
Mustafa, G., Tie-Cheng, X., and Farasat Shamir, M. (2021a). Self-consistent embedded anisotropic quintessence compact stars in Rastall gravity via linear equation of state. Phys. Scr. 96, 105008. doi:10.1088/1402-4896/ac0ee6
Oliveira, A. M., Velten, H. E. S., Fabris, C., and Casarini, L. (2015). Neutron stars in Rastall gravity. Phys. Rev. D. 92, 044020. doi:10.1103/physrevd.92.044020
Ovalle, J., Casadio, R., da Rocha, R., and Sotomayor, A. (2018a). Anisotropic solutions by gravitational decoupling. Eur. Phys. J. C 78, 122. doi:10.1140/epjc/s10052-018-5606-6
Ovalle, J., Casadio, R., da Rocha, R., Sotomayor, A., and Stuchlik, Z. (2018b). Black holes by gravitational decoupling. Eur. Phys. J. C 78, 960. doi:10.1140/epjc/s10052-018-6450-4
Ovalle, J., and Linares, F. (2013). Tolman IV solution in the Randall-Sundrum braneworld. Phys. Rev. D. 88, 104026. doi:10.1103/physrevd.88.104026
Övgün, A., Sakalli, I., Saavedra, J., and Leiva, C. (2020). Shadow cast of noncommutative black holes in Rastall gravity. Mod. Phys. Lett. A 35, 2050163. doi:10.1142/s0217732320501631
Rastall, P. (1972). Generalization of the Einstein theory. Phys. Rev. D. 6, 3357–3359. doi:10.1103/physrevd.6.3357
Salako, I. G., Jawad, A., and Moradpour, H. (2018). Anisotropic compact stars in non-conservative theory of gravity. Int. J. Geomet. Meth. Mod. Phys. 15, 1850093. doi:10.1142/s0219887818500937
Shahzad, M. R., and Abbas, G. (2020). Models of quintessence compact stars in Rastall gravity consistent with observational data. Eur. Phys. J. Plus 135, 502. doi:10.1140/epjp/s13360-020-00508-3
Sharif, M., and Ahmed, S. (2021). Gravitationally decoupled non-static anisotropic spherical solutions. Mod. Phys. Lett. A 36, 2150145. doi:10.1142/s0217732321501455
Sharif, M., and Ama-Tul-Mughani, Q. (2020). Gravitational decoupled solutions of axial string cosmology. Mod. Phys. Lett. A 35, 2050091–2050104. doi:10.1142/s0217732320500911
Sharif, M., and Aslam, M. (2021). Compact objects by gravitational decoupling in f(R) gravity. Eur. Phys. J. C 81, 641. doi:10.1140/epjc/s10052-021-09436-7
Sharif, M., and Sadiq, S. (2018). Gravitational decoupled anisotropic solutions for cylindrical geometry. Eur. Phys. J. Plus 133, 245. doi:10.1140/epjp/i2018-12075-1
Singh, K. N., Maurya, S. K., Jasim, M. K., and Rahaman, F. (2019). Minimally deformed anisotropic model of class one space-time by gravitational decoupling. Eur. Phys. J. C 79, 851–865. doi:10.1140/epjc/s10052-019-7377-0
Soroushfar, S., Saffari, R., and Upadhyay, S. (2019). Thermodynamic geometry of a black hole surrounded by perfect fluid in Rastall theory. Gen. Relativ. Grav. 51, 130. doi:10.1007/s10714-019-2614-2
Xu, Z., Hou, X., Gong, X., and Wang, J. (2018). Kerr–Newman-AdS black hole surrounded by perfect fluid matter in Rastall gravity. Eur. Phys. J. C 78, 513. doi:10.1140/epjc/s10052-018-5991-x
Keywords: electromagnetic field, gravitational decoupling, modified theory, anisotropy, PACS: 04.40.Nr, 97.10.Cv, stability analysis
Citation: Sadiq S, Waseem A, Javed F, Errehymy A and Abdel-Aty A-H (2024) Gravitationally decoupled charged anisotropic solutions in Rastall gravity. Front. Astron. Space Sci. 10:1320081. doi: 10.3389/fspas.2023.1320081
Received: 11 October 2023; Accepted: 05 December 2023;
Published: 18 January 2024.
Edited by:
Ghulam Abbas, Department of Mathematics, PakistanReviewed by:
Oktay Aydogdu, Mersin University, TürkiyeMehrab Momennia, Benemérita Universidad Autónoma de Puebla, Mexico
Copyright © 2024 Sadiq, Waseem, Javed, Errehymy and Abdel-Aty. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Faisal Javed, ZmFpc2FsamF2ZWQubWF0aEBnbWFpbC5jb20=
 Sobia Sadiq
Sobia Sadiq Arfa Waseem2
Arfa Waseem2 Faisal Javed
Faisal Javed Abdelghani Errehymy
Abdelghani Errehymy Abdel-Haleem Abdel-Aty
Abdel-Haleem Abdel-Aty