Statistical analysis of equatorial electrojet responses to the transient changes of solar wind conditions

Introduction: Prior case studies have indicated that changes in solar wind conditions have a significant impact on equatorial ionospheric electrodynamics. However, there have been limited statistical studies on this topic, impairing our understanding of the coupling between solar wind, magnetosphere, and equatorial ionosphere electrodynamics.

Methods: In this study, we conducted a superposed epoch analysis of long-term data from the South America equatorial electrojet (EEJ) spanning from 2001 to 2021 examining the responses of the equatorial ionospheric electric field to step-like changes in solar wind velocity, density, dynamic pressure, and interplanetary magnetic field (IMF) B_z.

Result: Our study shows that step-like changes in solar wind velocity, density, and dynamic pressure can trigger changes in EEJ within ∼20–40 min. EEJ exhibits the highest sensitivity to variations in solar wind velocity while being relatively less sensitive to changes in dynamic pressure. Furthermore, the response of EEJ shows greater responsiveness to northward IMF B_z compared to southward IMF B_z.

Discussion: Our work provides statistical evidence of how changes in solar wind can lead to changes in low-latitude ionospheric EEJ. We inferred that the changes in solar wind conditions cause magnetospheric deformation and changes in magnetic reconnection rates, leading to the fluctuations of the ionospheric electric field and the resultant EEJ variations.

1 Introduction

The ionospheric electric fields and currents can vary greatly due to the transient changes in solar wind conditions. When a substantial amount of solar wind energy and momentum is injected into the magnetosphere, it can result in large-scale magnetospheric convection through processes like magnetic reconnection and viscous interaction (Axford and Hines, 1961; Dungey, 1961; Bruntz et al., 2012). This, in turn, triggers the redistribution of polarization charges within the inner magnetosphere, leading to disturbances in the magnetospheric electric field, which propagate to the high-latitude ionosphere along magnetic field lines, giving rise to prompt penetration electric field (PPEF) to the low-latitude ionosphere (Sastri, 1988; Spiro et al., 1988; Abdu et al., 1995; 1997). The pioneering work of Nishida (1968) demonstrated that the geomagnetic field perturbations are correlatedwith the reorientations of the interplanetary magnetic field (IMF). Subsequently, the field of magnetosphere-ionosphere coupling has extensively studied the penetration electric field (e.g., Kikuchi et al., 2000; Bhaskar and Vichare, 2013; Ebihara et al., 2014; Xiong et al., 2016; Venkatesh et al., 2017; Huang, 2020; Nilam et al., 2020). In general, a sudden southward or northward turning of the IMF B_z leads to enhancement/weakening of the dawn-to-dusk convection electric field, and it cannot be balanced immediately by the inner magnetosphere shielding layer. This produces eastward/westward PPEF into the dayside low-latitude ionosphere (Rastogi and Patel, 1975; Kelley et al., 1979; Abdu et al., 1995; Kikuchi et al., 2003; Basu et al., 2005; Tulasi Ram et al., 2012; 2016; Bhaskar and Vichare, 2013; Ohtani et al., 2013).

Apart from the effects of the southward/northward turning of IMF B_z, previous studies have also revealed that solar wind dynamic pressure and solar wind density can modify the low latitude ionospheric electrodynamics. For instance, Yuan and Deng (2007) showed that under stable southward IMF B_z conditions on 17 April 1999, an enhancement in solar wind dynamic pressure increased the electric field in the equatorial ionosphere. Huang et al. (2008) indicated that due to the magnetosphere compression by an interplanetary shock, both high-latitude ionospheric convection and equatorial ionospheric electric field simultaneously intensified. Furthermore, a statistical study performed by Nilam et al. (2020) demonstrated that the ionospheric electric field over the equator undergoes eastward/westward disturbances in response to the transient increase/decrease in solar wind density. Wei et al. (2012) investigated the solar wind density effect on PPEF, suggesting that the increment in PPEF arises from the interaction between the solar wind and magnetopause. They also indicated that the mechanism behind PPEF induced by the transient changes in P_dyn mainly due to the magnetopause compression may differ from the mechanism driving PPEF primarily associated with IMF B_z associated with magnetic reconnection.

While previous research has made significant progress in exploring the features and mechanisms of equatorial ionospheric electrodynamics in response to transient changes in solar wind conditions, some outstanding questions remain unresolved. For example, the response time scale of the equatorial ionospheric electrodynamics to solar wind or IMF changes typically does not exceed 1 h (Senior and Blanc, 1984; Kikuchi et al., 2000; Peymirat et al., 2000; Maruyama et al., 2007), but occasionally lasts for several hours (Huang et al., 2005). It is still unknown the statistical patterns of the ionospheric response time characteristics and the penetration efficiency between solar wind electric fields and equatorial ionospheric electric fields. In addition, it is yet to be unknown that the individual impacts of solar wind velocity and density from solar wind dynamic pressure, given the fact that: (1) enhanced solar wind velocity may compress the dayside magnetosphere and produce an electric potential in the ionosphere due to the merging of the solar and geomagnetic fields in the magnetopause (Shue et al., 2002); (2) the enhanced solar wind density may compress both the dayside and nightside magnetosphere (Zhou and Tsurutani, 2001).

The equatorial electrojet (EEJ) (Chapman, 1951) is an enhanced eastward current over the magnetic equator in the ionosphere E region. As a manifestation of equatorial ionospheric electrodynamics, it has been extensively utilized in studies related to PPEF (e.g., Forbes, 1981; Anderson et al., 2002; Fejer et al., 2007; Nilam et al., 2020). In this paper, we statistically investigated the EEJ responses to the transient changes in solar wind velocity, density, dynamic pressure, and IMF B_z, using 21-year observations from the ground-based magnetometers. Statistical morphology allows for a more detailed representation of the magnitude of EEJ response, and the time required for it to react to solar wind variations. This can better our understanding of the effects of transient solar wind changes on equatorial ionospheric electrodynamics and the subsequent configuration of low-latitude ionospheric plasma structure.

2 Data and methods

2.1 EEJ from magnetometers at 79°W

We retrieved the 21-year EEJ strength data at 79°W using the geomagnetic horizontal components H recorded at Jicamarca (11.9°S, 76.8°W, 0.6°N mag. lat) and Piura (5.2°S, 80.6°W, 6.9°N mag. lat). To reveal ionospheric current disturbances, the average H at local midnight is used as a baseline to remove the main magnetic field of the geomagnetic field (Lühr, 2003). We then subtracted the baseline from the data to determine the EEJ strengths. These strengths were calculated as the difference between the H value recorded at the equatorial station and the off-equatorial station (Rastogi and Klobuchar, 1990; Anderson, 2002).

2.2 Identification of transient events: Sharp increase/decrease in solar wind data

The OMNI solar wind data (velocity, density, dynamic pressure, and IMF B_z) at the Earth’s bow shock nose are collected from the Goddard Space Flight Center of NASA. To identify transient events, we selected the events of transient increase/decrease in solar wind velocity, density, dynamic pressure, and IMF B_z using the solar wind data spanning from 2001 to 2021. Subsequently, we compiled the corresponding EEJ data and conducted superposed epoch analyses to elucidate the corresponding EEJ reactions to the transient events. Our analysis was primarily focused on the dayside EEJ responses (i.e., the intervals between 6 and 18 LT at 79°W). This focus on daytime responses was chosen as nighttime EEJ responses to transient changes in solar wind tend to be less pronounced due to the lower ionospheric conductivity on the nightside. These criteria were meticulously designed to ensure an adequate number of valid samples while minimizing noise interference. Finally, we collected a total of 113 (40) events of solar wind velocity increase (decrease), a total of 47 (51) events of solar wind density increase (decrease), a total of 83 (58) events of solar wind dynamic pressure increase (decrease), a total of 31 (29) events of southward (northward) IMF B_z increase for statistics. In the subsequent equations, we use $\overline{x}$ to denote the average value of $x$, $\sum x$ to denote the total value of $x$, and $∆x$ to denote the variation of $x$. The criteria are as follows.

2.2.1 Solar wind velocity

We chose transient increases/decreases of solar wind velocity with the criteria: (1) a sudden increase/decrease in solar wind velocity with an amplitude exceeding 70 km/s throughout the event [i.e., $\left.\left|\sum ∆V\right|>70\text{\hspace{0.17em}km}/\mathrm{s}\right]$ and an average change rate of velocity greater than 5 km/s per minute [i.e., $\left.\left|\sum ∆V/t_{\text{event}}\right|>5\text{\hspace{0.17em}km}/\left(\mathrm{s}\bullet \min \right)\right]$. (2) Total velocity change in the 5 min preceding the event not exceeding 20 km/s in the 5 min before the events [i.e., $\left|\sum ∆V_{5\min \text{pre}}\right|<20\text{\hspace{0.17em}km}/\mathrm{s}$]. (3) An average EEJ change exceeding 2 nT within the first 10 min of the event [i.e., $\left|\overline{∆{\text{EEJ}}_{10\min }}\right|>2\text{\hspace{0.17em}nT}$].

2.2.2 Solar wind density

The criteria for the transient increases/decreases of solar wind density are as follows: (1) a sudden increase/decrease in solar wind density with an amplitude exceeding 8 particles/cm³ throughout the event [i.e., $\left.\left|\sum ∆N\right|>8\text{\hspace{0.17em}particles}/{\text{cm}}^3\right]$ and an average change exceeding 2 particles/(cm³$\bullet$min) [i.e., $\left.\left.\left|\sum ∆N/t_{\text{evnt}}\right|>2\text{\hspace{0.17em}particles}{/(\text{cm}}^3\bullet \min \right)\right]$. (2) Total density changes not exceeding 5 particles/cm³ in the 5-min period before the event [i.e., $\left|\sum ∆N_{5\min \text{pre}}\right|<5\text{\hspace{0.17em}particles}/{\text{cm}}^3$]. (3) Standard deviations of density during the 30 min before and after the event less than 3 particles/cm³. (4) Weakening the effects of other solar wind parameters except density to make sure the results mainly depend on solar wind density. The changes in the solar wind velocity are smaller than 50 km/s during the 10-min period from the onset of density change [i.e., $\sum \left.{\left|∆V\right.}_{10\min }\right|<50\text{\hspace{0.17em}km}/\mathrm{s}$], the changes in the IMF B_y and B_z are smaller than 10 nT during the first 10-min period from the onset of density change [i.e., $\left|\sum ∆B_{\mathrm{y}10\min }\right|<10\text{\hspace{0.17em}nT}$; $\left|\sum ∆B_{\mathrm{z}10\min }\right|<10\text{\hspace{0.17em}nT}$]. (5) An average change in EEJ exceeding 3 nT within the first 10 min of the event [i.e., $\left|\overline{∆{\text{EEJ}}_{10\min }}\right|>3\text{\hspace{0.17em}nT}$].

2.2.3 Solar wind dynamic pressure

We chose transient increases/decreases in solar wind dynamic pressure with the criteria: (1) a sudden increase/decrease in solar wind dynamic pressure with an amplitude exceeding 4 nPa throughout the event [i.e., $\left|\sum ∆P_{\text{dyn}}\right|>4\text{\hspace{0.17em}nPa}$] and an average change exceeding 1 nPa per minute [i.e., $\left|\sum ∆P_{\text{dyn}}/t_{\text{event}}\right|>1\text{\hspace{0.17em}nPa}/\min$]. (2) Total dynamic pressure changes not exceeding 3 nPa in the 5 min before the event [i.e., $\left|\sum ∆P_{\text{dyn}5\min \text{pre}}\right|<3\text{nPa}$]. (3) Standard deviations of solar wind dynamic pressure during the 30 min before and after the event less than 2 nPa. (4) The changes in the IMF B_y and B_z are smaller than 10 nT during the first 10 min from the onset of dynamic pressure change [i.e., $\left|\sum B_{\mathrm{y}10\min }\right|<10\text{\hspace{0.17em}nT}$; $\left|\sum ∆B_{\mathrm{z}10\min }\right|<10\text{\hspace{0.17em}nT}$]. (5) An average change in EEJ exceeding 1 nT within the first 10 min of the event [i.e., $\left|\overline{∆{\text{EEJ}}_{10\min }}\right|>1\text{\hspace{0.17em}nT}$].

2.2.4 IMF B_z

In the superposed epoch analyses, we subtracted the baseline values from the original data to normalize the results, representing the southward or northward trend of IMF B_z.

The criteria for transient increases in southward/northward IMF B_z are: (1) a sudden southward/northward IMF B_z increase with an amplitude exceeding 15 nT throughout the event [i.e., $\left|\sum ∆B_{\mathrm{z}}\right|>15\text{\hspace{0.17em}nT}$] and an average change exceeding 3 nT per minute (i.e., $\left|\sum ∆B_{\mathrm{z}}/t_{\text{event}}\right|>3\text{\hspace{0.17em}nT}/\min )$. (2) Total change in IMF B_z not exceeding 10 nT in the 20-min period before the event [i.e., $\left|\sum ∆B_{\mathrm{z}20\min \text{pre}}\right|<10\text{\hspace{0.17em}nT}$].

3 Results

3.1 EEJ responses to the step-like changes in solar wind dynamic pressure

The EEJ reacts rapidly and positively to transient changes in solar wind dynamic pressure and associated parameters. The solar wind dynamic pressure, denoted as P_dyn, is determined by both solar wind velocity V and density N and can be expressed as $P_{\text{dyn}}=\sum mN{V}^2$, where m is the mass of a single particle (Dendy, 1995). To illustrate the EEJ responses due to variations in solar wind dynamic pressure and associated parameters, we chose three typical events of sharp solar wind velocity, density, and dynamic pressure enhancements as depicted in Figure 1. In the first event (column 1), a sudden increase solely in solar wind velocity occurred during an 11-min period on 06 May 2003, at 1328UT (0812LT), with a magnitude of 85 km/s, while other solar wind parameters including N, IMF B_y, and B_z were quite stable during this interval. Accordingly, the EEJ exhibited a sharp increase of ∼50 nT, peaked in ∼16 min, and returned to its original state at ∼1408UT (0852LT) (Figure 1A₅). In this event, solar wind velocity displayed a sudden and strong increase along with a weak southward turning of IMF B_z with a magnitude of 5 nT. IMF B_z plays a dominant role in magnetosphere-ionosphere coupling (Bhaskar and Vichare, 2013). We cannot rule out the possibility that the variations in EEJ in this event may be influenced by IMF B_z. According to subsequent statistical analysis, the change in IMF B_z in this event is too small to be considered the primary cause of the sudden variation in EEJ, and the main reason for the EEJ’s sudden increase in this event is primarily due to the abrupt increase in solar wind velocity. The second column of Figure 1 shows an event in which only the solar wind density increased rapidly, with an amplitude of 10 particles/cm³ within 4 min at 1551UT (1035LT) on 02 August 2012. Correspondingly, the EEJ exhibited a simultaneous pulse-like enhancement of 67 nT as the solar wind density, peaked in 11 min, and returned to its original state in 37 min. The third column of Figure 1 demonstrates an event on 14 February 2011 characterized by sharp increases in solar wind density (black line), velocity (blue line), and dynamic pressure. The interplanetary shock with dynamic pressure enhancement by 5 nPa within 1 min at 1556UT (1040LT) and triggered a 56 nT growth pulse of EEJ in 20 min. In all three cases, the EEJ exhibited enhancements to the enhancements in solar wind parameters. The EEJ expression is $\text{EEJ}={\sigma }_{\mathrm{c}}E$, where ${\sigma }_{\mathrm{c}}$ is the cowling conductivity, and E is the dawn-to-dusk electric field in the ionosphere (Untiedt, 1967), EEJ depends on both cowling conductivity and the dawn-to-dusk electric field. The increased EEJ responses observed in all three events suggest the presence of eastward electric fields at low latitudes on the dayside.

FIGURE 1

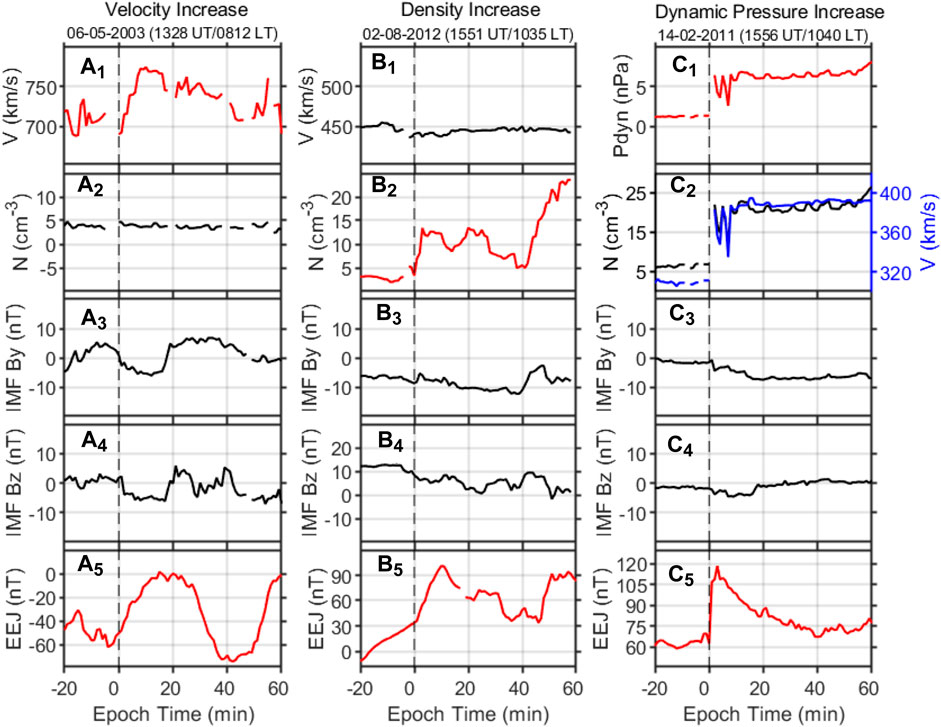
FIGURE 1. Three cases of sharply increased in solar wind (a₁) velocity V, (b₂) density N, (c₁) dynamic pressure P_dyn, and the corresponding increases in equatorial electrojet (EEJ) on the dayside (79°W) as well as the corresponding changes of interplanetary magnetic field (IMF) B_y and B_z. The vertical black dashed lines indicate the beginning time of the enhancement (zero epoch time).

As opposed to the enhancements in solar wind parameters, Figure 2 shows three events of sharply decreased solar wind velocity, density, and dynamic pressure as well as their effects on EEJ. In these cases, the EEJ responses were also positively correlated with the changes, which were decreases in the cases. These findings suggest the presence of westward electric fields on the dayside in response to decreases in solar wind velocity, density, and dynamic pressure. In summary, these observations indicate that the EEJ exhibits high responsiveness to sudden changes in the solar wind dynamic pressure and associated parameters.

FIGURE 2

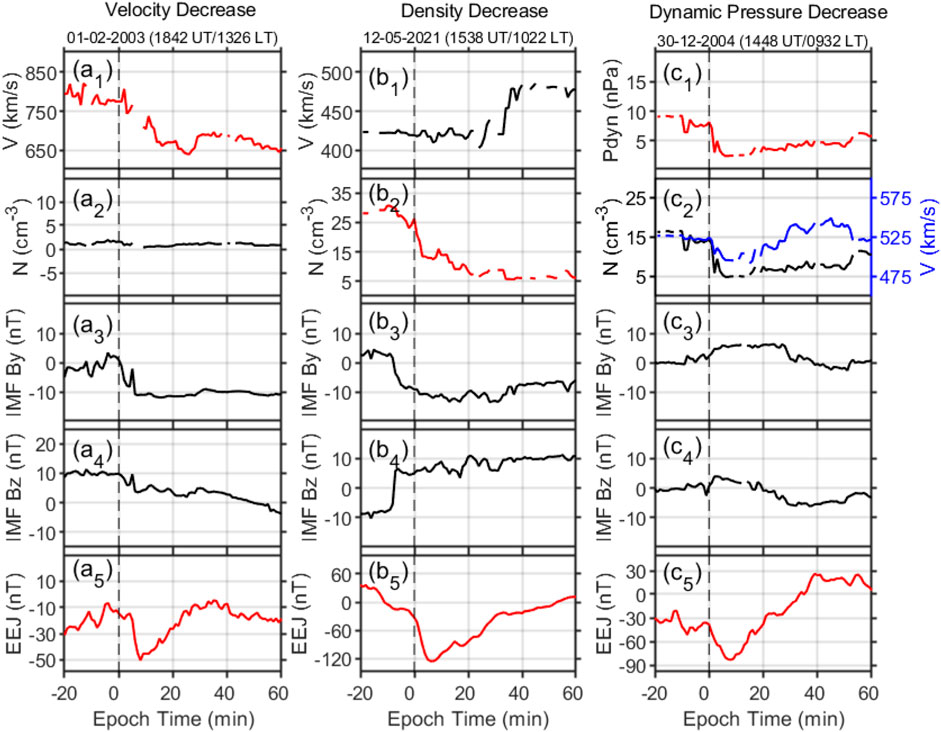
FIGURE 2. Similar to Figure 1 except for the typical cases of a sharp decrease in the solar wind velocity, density, and dynamic pressure.

Compared to individual case studies, conducting a statistical study on how the equatorial electric current responds to changes in solar wind parameters can eliminate randomness and reveal the underlying general principles of the phenomenon. Nilam et al. (2020) conducted a superposed epoch analysis of EEJ response to solar wind density in the India region, which resulted in a positive correlation between the EEJ and the variation in solar wind density. We also conducted a superposed epoch analysis to further investigate the EEJ responses to solar wind disturbances in South America and obtained the same result and extended it from the solar wind density to all the solar wind dynamic pressure associated parameters. Figures 3, 4 present the results of the analysis for transient increases and decreases in the solar wind parameters, respectively. In each figure, the individual events are shown as thin gray curves, while the thick red or black curves represent the average values of all events. The shaded areas in these panels represent the upper and lower quartiles. In Figure 3, the EEJ increased as the solar wind dynamic pressure parameters increased. For the 113 velocity increase events with a mean change of 85 km/s, the average increase in the EEJ is 8 nT. For the 47 density increase events with a mean change of 8 particles/cm³, the average increase in the EEJ is 6 nT, while for the 83 dynamic pressure increase events with a mean change of 3 nPa, the average increase in the EEJ is 6 nT. The statistical results showed that responses of the EEJ to the transient step-like increases in solar wind dynamic pressure parameters were also pulse-like in shape, with delays of ∼5 min and peaks at ∼11 min. To further illuminate our findings, Panel (a₅) of Figure 3 offers a bivariate histogram. This graphical representation illustrates the distribution of event samples across two-dimensional bins of EEJ strength and epoch time. The coloration of each bin serves as a visual cue, indicating the number of events contained within. Conversely, in Figure 4, the EEJ displayed rapid decreases when the solar wind dynamic pressure and associated parameters experienced a sudden drop. Overall, both cases and statistical results indicate that EEJ responses are positively correlated with changes in solar wind velocity, density, and dynamic pressure.

FIGURE 3

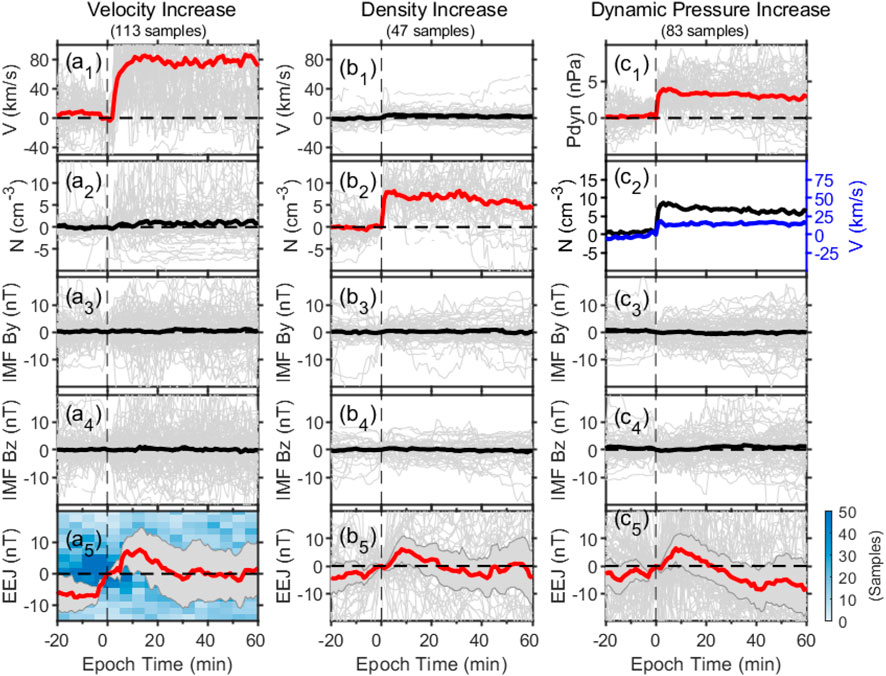
FIGURE 3. Superposed epoch analysis of the sharp increases in solar wind (a₁) velocity V, (b₁) density N, and (c₁) dynamic pressure P_dyn and the corresponding changes in EEJ on the dayside (79°W) as well as the corresponding changes of IMF B_y and B_z. The gray lines represent single cases. The solid black and red lines represent the statistical averages of all cases, and the shaded areas represent the upper and lower quartiles. The vertical black dashed lines indicate the beginning time of the enhancement (zero epoch time).

FIGURE 4

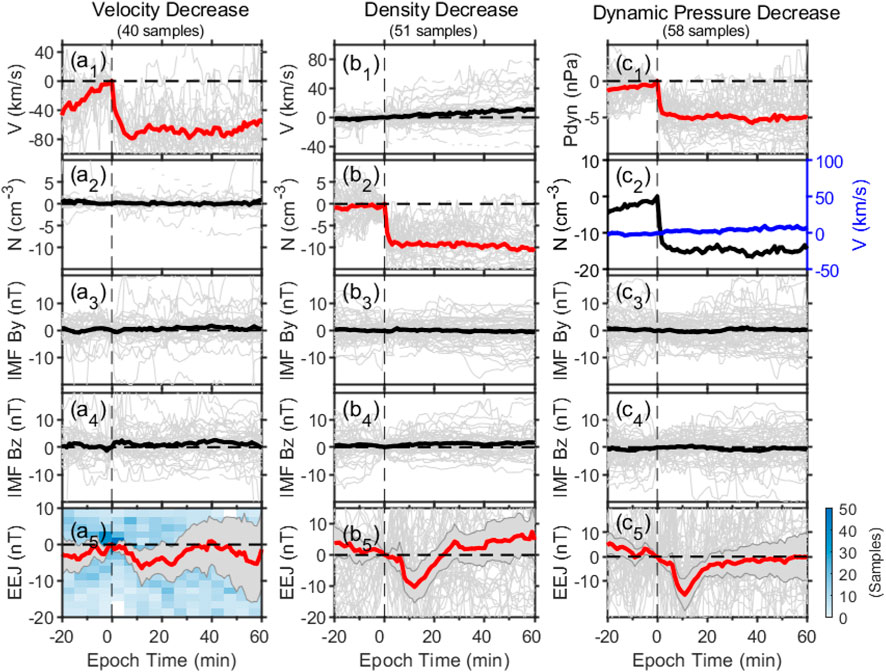
FIGURE 4. Similar to Figure 3 except for the cases of a sharp decrease of the solar wind dynamic pressure parameters.

3.2 EEJ responses due to the transient changes in IMFB_z

IMF B_z also has appreciable effects on the low-latitude ionospheric electrodynamics. Figures 5, 6 show that EEJ tends to increase/decrease when IMF B_z has a sharply southward/northward enhancement. In the first column of Figure 6, on 06 December 2014, IMF B_z underwent a sudden southward turning with a magnitude of 22 nT within 8 min, and EEJ exhibited a sudden increase of 69 nT within 14 min. In contrast, in the second column, on 23 May 2002, IMF B_z exhibited a northward turning with an amplitude of 32 nT within 12 min, leading to a synchronous decrease of 109 nT in EEJ within19 min. For the superposed epoch analysis of IMF B_z, there are totally 31 southward IMF B_z turning increase events and 29 northward IMF B_z turning increase events, with average amplitudes of 23 nT for both. The average responses are 57 nT and 32 nT, as shown in Figure 6. Compared with solar wind dynamic pressure parameters, IMF B_z has a greater influence on EEJ, due to the dominant role of magnetic reconnection in equatorial electric field fluctuations (Rastogi and Patel, 1975; Kelley et al., 1979; Abdu et al., 1995; Kikuchi et al., 2003; Basu et al., 2005; Tulasi Ram et al., 2012; 2016; Bhaskar and Vichare, 2013; Ohtani et al., 2013). On the other hand, we observed a significant asymmetry in the response of the EEJ to increase in southward IMF B_z and northward IMF B_z. The EEJ’s response to northward IMF B_z growth is nearly twice as strong as its response to southward IMF B_z growth.

FIGURE 5

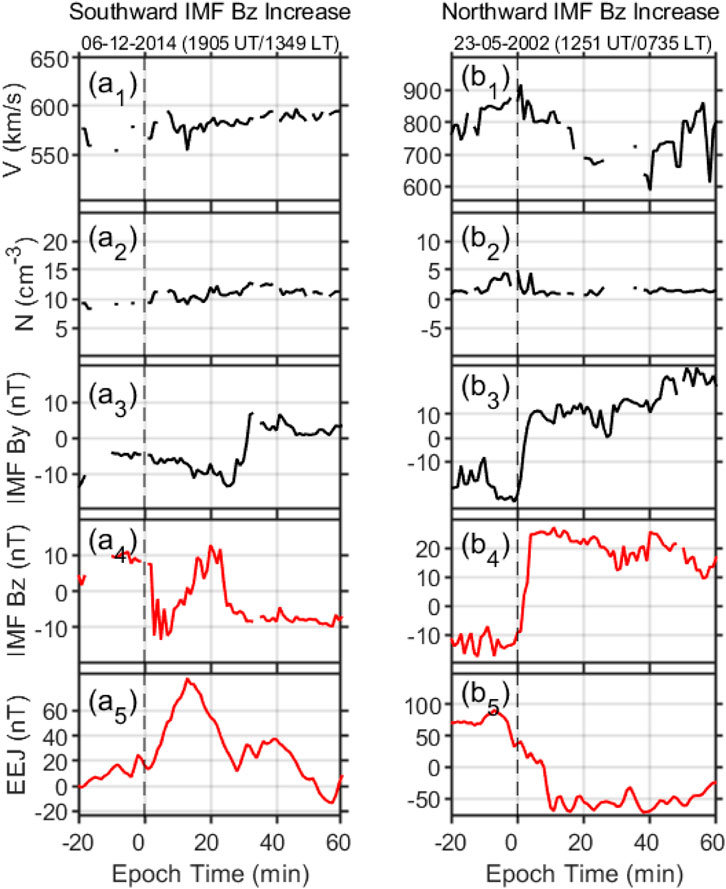
FIGURE 5. Examples of sharp (a₄) southward and (b₄) northward increase in IMF z component B_z and the related changes in EEJ at local daytime (79°W) as well as the corresponding changes of solar wind velocity V, density N, and IMF B_y. The vertical black dashed lines indicate the beginning time of the events (zero epoch time).

FIGURE 6

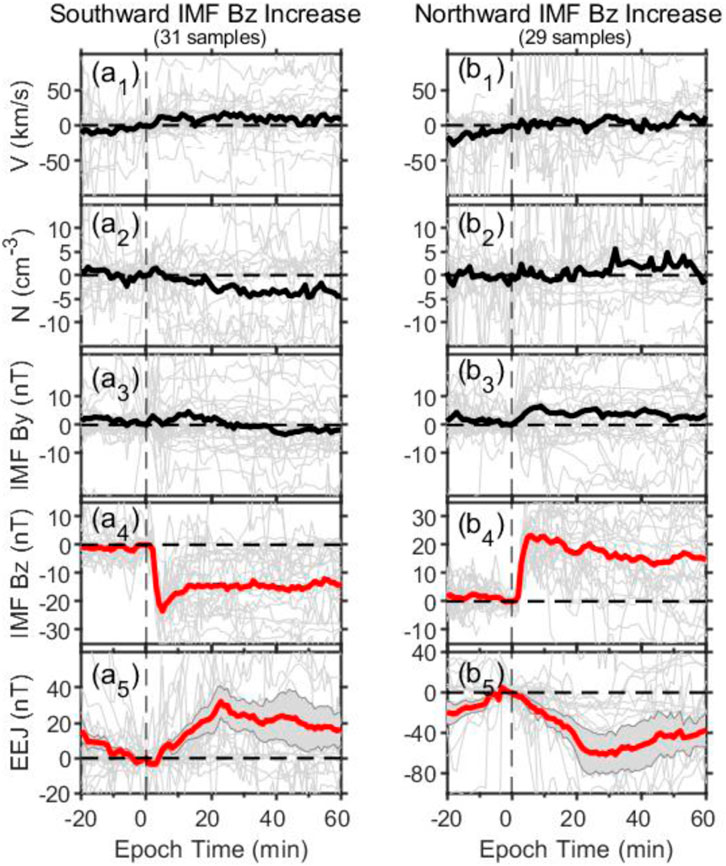
FIGURE 6. Superposed epoch analysis of the sharp (a₄) southward and (b₄) northward increase in the IMF B_z and the related changes in the equatorial electrojet (EEJ) at local daytime (79°W) as well as the corresponding changes in solar wind velocity V, density N and IMF B_y. The shaded areas represent the upper and lower quartiles. The vertical black dashed lines indicate the beginning time of the events (zero epoch time).

3.3 Local time dependence of EEJ responses to changes in solar wind parameters

The changes in EEJ are local time dependent (Bhaskar and Vichare, 2013). The factors influencing the variation of EEJ with local time are numerous. For example, the post-noon eastward ΔEEJ may be indirectly influenced by the upward electric field linked to the SAPS electric field within the SAPS channel, while the pre-noon ΔEEJ could be a direct result of the SAPS-associated polarization electric field penetration (Zhang et al., 2022). To further investigate the local time dependences in EEJ response to solar wind dynamic pressure parameters or IMF B_z changes, Figure 7 shows four distinct categories of increases: solar wind (a) velocity, (b) density, (c) dynamic pressure, (d) northward IMF B_z. Our methodology hinges on capturing the maximum change in EEJ within a 30-min window following the event onset, serving as a representation of the EEJ’s response intensity. Each point represents an event, with the coloration indicating the magnitude of the corresponding solar wind parameters. The horizontal axis represents the local time of the event onset, and the vertical axis represents the response intensity of EEJ in the event.

FIGURE 7

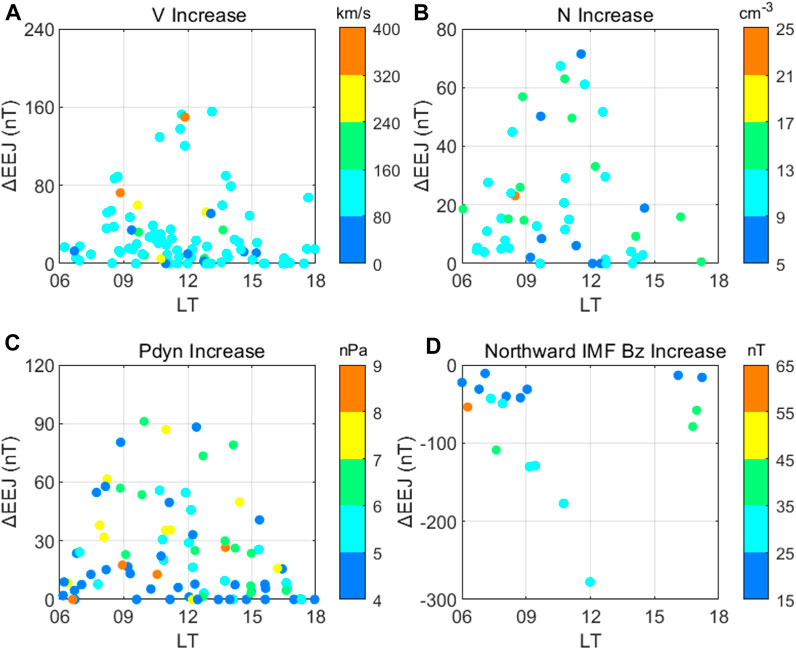
FIGURE 7. The corresponding distributions of local time, intensity changes in EEJ, and solar wind parameters for the transient events of (A) solar wind velocity increase, (B) solar wind density increase, (C) solar wind dynamic pressure increase, (D) northward IMF B_z increase. Each point represents an event, the horizontal axis represents the local time, the vertical axis represents the amplitude of EEJ in this event, and different colors represent the different amplitudes of the studied parameters’ changes, as the standards are shown in the color bar.

The EEJ responses to solar wind variations are most pronounced at local noon. Bhaskar and Vichare (2013) achieved a similar result before, they eliminated the local time dependence by eliminating the conductivity effect, which indicated the dependence is related to daytime conductivity. When solar radiation is enhanced, the ionization rate in the atmosphere increases, electron density and ionospheric conductivities increase. At noon, the conductivity is maximum and EEJ changes are most pronounced, while near sunrise and sunset, the conductivity is small and EEJ changes caused by the disturbance are small. We have not found any explicit relationship between the intensities of solar wind conditions and EEJ responses in our study.

4 Discussion

The EEJ, located between ±2° latitude at an altitude of ∼100–120 km above the ground, serves as a proxy for the equatorial electric field. It mainly arises from the dynamo in the ionosphere. At the height of ∼100–130 km in the E layer, the Pedersen conductivity and Hall conductivity are greatly enhanced, turning the E layer into a conductive layer. The neutral winds and tidal driving force propel charged particles across the geomagnetic field, thereby generating currents and electric fields, which is the neutral wind dynamo process (Baker and Martyn, 1953). Due to the nearly horizontal magnetic field lines over the equator, the Hall effect produces a downward Hall current that polarizes the E region of the ionosphere, giving rise to an upward polarized electric field. This enhances the horizontal current and leads to the formation of the EEJ along the east-west direction (Richmond, 1989).

4.1 Effects of the solar wind dynamic pressure on EEJ

EEJ undergoes an increase/decrease with a ∼5-min delay as solar wind velocity, density, and dynamic pressure increase/decrease. The impacts of these three parameters on EEJ are consistent. The EEJ responses to stepwise changes in the three parameters V, N, and P_dyn, are always impulsive with delays of ∼5 min, and they return to their original state within ∼20–40 min. To compare the strength of the EEJ responses to different solar wind dynamic pressure parameters, we analyzed the amplitude difference of EEJ responses. Over the span of 21 years of data, the average solar wind velocity measures ∼430 km/s, with an average velocity variation of ∼80 km/s (∼18%) during the selected events. This leads to an average EEJ response of ∼7 nT. The average solar wind density is ∼6 particles/cm³ and the density change during the chosen events amounts to ∼9 particles/cm³ (∼150%), resulting in an average EEJ response of ∼8 nT. The average dynamic pressure is estimated at ∼2 nPa, while the mean change in dynamic pressure during the chosen events is ∼4 nPa (∼200%), resulting in an average EEJ response of ∼10 nT.

The EEJ responds to changes in solar wind dynamic pressure possibly due to magnetopause deformation. Magnetopause is the boundary between solar wind pressure and the geomagnetic field pressure. When the solar wind dynamic pressure changes, the magnetopause contracts or expands accordingly. This process causes plasma flow towards the Earth’s magnetosphere through viscous interaction on the dayside, increasing plasma velocity near the magnetopause and magnetosphere flanks (Axford and Hines, 1961). As the plasma flows toward the interior of the magnetosphere, the velocity decreases, creating a flow shear near the magnetospheric flanks called “Transit Cell Convection” (Fujita et al., 2003). This shear enhances the region 1 field-aligned current (Kubota et al., 2015), leading to an imbalance between the region 1 field-aligned current and the region 2 field-aligned current. This imbalance can induce PPEF and increase EEJ. As the plasma flow gradually adapts to the new state, the response decays over ∼30–40 min (Huang et al., 2008). EEJ responses always have a 5-min delay because the solar wind data used is from the bow shock nose, which takes time to propagate into the magnetosphere and affects EEJ. Changes in conductivity may also affect EEJ responses. Li et al. (2021) observed that TEC fluctuations at low latitudes may be due to the impact of the interplanetary shock on the magnetopause, generating cavity mode oscillation in the cavity between the magnetosphere and plasmasphere, causing plasma oscillations (Wright, 1994). The resultant electron density variation due to the impact of interplanetary shock on the magnetopause can change the conductivity and thus EEJ.

The EEJ is most sensitive to changes in velocity and least sensitive to changes in dynamic pressure. Specifically, the different responses of EEJ to solar wind velocity, density, and dynamic pressure may be due to the individual effects of solar wind velocity and density on magnetospheric compression. Since $P_{\text{dyn}}=mN{V}^2$, the dynamic pressure is related to the square of the velocity and linearly related to the density. An increased solar wind electric field would lead to a higher magnetopause reconnection rate and smaller magnetopause standoff distance, due to the higher solar wind velocity (Lee and Lee, 2020). During the compression process, many empirical magnetopause models show that the relationship between solar wind dynamic pressure P_dyn and the magnetopause standoff distance R_sub is $R_{\text{sub}}\sim P_{\text{dyn}}^{-1/K}$ (Beard, 1960; Shue et al., 1998; Lin et al., 2010; Liu et al., 2015), where K is a constant. However, Samsonov et al. (2020) showed a more accurate expression of R_sub using solar wind velocity and density: $R_{sub}\sim N^{-1/X}{V}^{-2/Y}$, where $X\ne Y$ and both X and Y may depend on the sign of IMF B_z. Samsonov et al. (2020) indicated that the changes in R_sub for a velocity increase were greater than those for a density increase for the same P_dyn, indicating a greater magnetopause deformation. A greater compression of the magnetopause will cause stronger EEJ perturbations compared with the deformation caused by changes in solar wind density.

In addition, solar wind density can also affect EEJ through other mechanisms. Nilam and Tulasi Ram (2022) found that a decrease in solar wind density reduced EEJ, which was related to the location of magnetic reconnection. Magnetic reconnection plays a crucial role in controlling PPEF and magnetosphere-ionosphere coupling. Specifically, the reconnection rate at the magnetopause and the energy transfer to the magnetosphere are determined by the IMF B_z in the magnetosheath region (Kataoka et al., 2005). With a sudden decrease in solar wind density, the magnetopause where the dayside magnetic reconnection occurs is expanded, then the magnetosheath IMF B_z reduces and causes a reduction of the dayside reconnection rate at the magnetopause. Then the magnetic reconnection affects the EEJ by influencing the high-latitude convective electric field.

4.2 Effect of the IMF B_z on EEJ

Our results revealed that EEJ tends to increase/decrease when there is sharp southward/northward enhancement of IMF B_z. Specifically, when there were transient southward increases in IMF B_z with an average amplitude of 23 nT, the EEJ experienced an average increase of 32 nT. Conversely, when there were transient northward increases in IMF B_z with an average amplitude of 23 nT, the EEJ experienced an average decrease of 57 nT. These results are consistent with previous findings that electric field perturbations are related to the north-south turning of IMF B_z (Huang et al., 2007), and show that the northward IMF B_z increases have stronger influences on EEJ than southward IMF B_z increases. When IMF B_z has a southward trend, the geomagnetic field and IMF are in opposite directions, then a magnetic reconnection occurs (Dungey, 1961). The solar wind drives large-scale magnetospheric convection through reconnection. The imbalance between region 1 field-aligned currents generated in the low-latitude boundary layer of the magnetosphere and the region 2 field-aligned currents generated in the inner boundary of the plasma sheet (Iijima and Potemra, 1978) leads to the PPEF from high latitude to low latitudes, which is eastward on the dayside and westward on the nightside (Richmond et al., 2003), leading to the enhancement of dayside EEJ. Therefore, EEJ is enhanced when IMF B_z has a southward turning. Conversely, if IMF B_z becomes more northward, the magnetic reconnection rate decreases, weakening the injection of field-aligned current into the ionosphere and decreasing EEJ. Bhaskar and Vichars (2013) found that the variations of ionospheric signatures were mainly controlled by the magnitude of southward IMF B_z, and the magnitude of northward IMF B_z did not influence the ionospheric characteristics. They also observed the asymmetry of the EEJ response to the southward and northward IMF B_z variation and estimated that for southward IMF B_z turnings, $∆\text{EEJ}=4.5\times ∆E_{\text{swy}}+3.19$, for northward turnings, $∆\text{EEJ}=8.23\times ∆E_{\text{swy}}+7.35$, where E_swy is a component of solar wind electric field along the y-axis (eastward) in GSM coordinate system. The response intensity of EEJ during IMF B_z northward is about twice as strong as during IMF B_z northward. This is consistent with our results. The asymmetry is mainly related to the stronger magnetospheric convection during the southward IMF B_z.

In addition to the variations in EEJ caused by solar wind changes investigated in this study, changes in the background ionosphere can also impact the low-latitude ionospheric current and electric field. For instance, during a solar eclipse, higher levels of solar obscuration result in lower electron density and stronger polarization electric field, leading to the appearance of gradient drift wave at higher altitudes with larger amplitude (Sekar et al., 2014). The Sun can not only influence the magnetosphere-ionosphere coupling in the form of solar wind but also create changes in the ionosphere through solar radiation. In this study, we primarily focus on the rapid response of EEJ to changes in solar wind conditions, with a time scale much shorter than the variations in the background ionosphere. When processing the data, we used the relative values of the geomagnetic horizontal components H, from which the background ionosphere has been subtracted, to calculate EEJ. This approach eliminated the influence of the background ionosphere.

5 Conclusion

In this paper, we investigated the response of EEJ to variations in solar wind velocity, density, dynamic pressure, and IMF B_z changes using ground-based magnetometers spanning 21 years. Our results demonstrate that the EEJ responds rapidly to changes in critical solar wind factors such as velocity, density, dynamic pressure, and IMF B_z. These variations can trigger rapid fluctuations in the EEJ within 20–40 min. Among those dynamic solar wind pressure parameters, it is evident that EEJ exhibits the highest sensitivity to changes in solar wind velocity while being relatively less sensitive to variations in dynamic pressure. Regarding IMF B_z, EEJ displays greater sensitivity to northward IMF B_z than to southward IMF B_z. The increases or decreases in EEJ reflect the variations in the electric field from dawn to dusk due to changing solar wind conditions. The generation of the EEJ response is attributed to the PPEF, induced by the deformation of the magnetospheric boundary and magnetic reconnection. Furthermore, our analysis highlights the significant impact of IMF B_z on EEJ. It is noteworthy that a sharp southward enhancement of IMF B_z often leads to an increase in EEJ, with an average magnitude of 32 nT during instances of southward IMF B_z increase. Conversely, when IMF B_z sharply strengthens northward, EEJ, on average, decreases by 57 nT. we have summarized the possible mechanisms driving these EEJ responses. Changes in solar wind dynamic pressure induce deformation of the magnetospheric boundary, playing a crucial role in modulating EEJ. Specifically, variations in solar wind dynamic pressure lead to the expansion or contraction of the magnetospheric boundary, influencing the plasma flow toward the Earth’s magnetosphere. This flow, in turn, affects the region 1 field-aligned currents, ultimately causing disturbances in the EEJ. Additionally, magnetic reconnection also serves as a significant factor influencing EEJ. Changes in the direction of IMF B_z can affect EEJ by influencing the location of magnetic reconnection. Fluctuations in the magnetospheric boundary due to solar wind density fluctuations can alter the daytime magnetic reconnection rate, thereby affecting EEJ through its impact on high-latitude convection electric fields.

Data availability statement

Interplanetary solar wind datasets at the Earth’s bow shock nose are downloaded from http://omniweb.gsfc.nasa.gov. The ground-based magnetometer datasets are downloaded from http://lisn.igp.gob.pe/jdata/database/. The total electron content datasets are downloaded from http://millstonehill.haystack.mit.edu/.

Author contributions

JZ: Data curation, Investigation, Writing–original draft. QL: Methodology, Supervision, Writing–review and editing. SL: Methodology, Supervision, Writing–review and editing. JL: Methodology, Supervision, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China (42122031, 42074188, 42104147, and 42304168); and the Natural Science Foundation of Shandong Province (ZR2022JQ18), the Chinese Meridian Project.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdu, M. A. (1997). Major phenomena of the equatorial ionosphere-thermosphere system under disturbed conditions. J. Atmos. Solar-Terrestrial Phys. 59 (13), 1505–1519. doi:10.1016/S1364-6826(96)00152-6

CrossRef Full Text | Google Scholar

Abdu, M. A., Batista, I. S., Walker, G. O., Sobral, J. H. A., Trivedi, N. B., and Depaula, E. R. (1995). Equatorial ionospheric electric fields during magnetospheric disturbances: local time/longitude dependences from recent EITS campaigns. J. Atmos. Terr. Phys. 57 (10), 1065–1083. doi:10.1016/0021-9169(94)00123-6

CrossRef Full Text | Google Scholar

Anderson, D., Anghel, A., Yumoto, K., Ishitsuka, M., and Kudeki, E. (2002). Estimating daytime vertical ExB drift velocities in the equatorial F-region using ground-based magnetometer observations. Geophys. Res. Lett. 29 (12), 1596. doi:10.1029/2001GL014562

CrossRef Full Text | Google Scholar

Axford, W. I., and Hines, C. O. (1961). A unifying theory of high-latitude geophysical phenomena and geomagnetic storms. Can. J. Phys. 39 (10), 1433–1464. doi:10.1139/p61-172

CrossRef Full Text | Google Scholar

Baker, W. G., and Martyn, D. F. (1953). Electric currents in the ionosphere. I. The conductivity. Philosophical Trans. R. Soc. Lond. Ser. A 246, 281–294. doi:10.1098/rsta.1953.0016

CrossRef Full Text | Google Scholar

Basu, S., Basu, S., Groves, K. M., Mackenzie, E., Keskinen, M. J., and Rich, F. J. (2005). Near-simultaneous plasma structuring in the midlatitude and equatorial ionosphere during magnetic superstorms. Geophys. Res. Lett. 32 (12), L12S05. doi:10.1029/2004GL021678

CrossRef Full Text | Google Scholar

Beard, D. B. (1960). The interaction of the terrestrial magnetic field with the solar corpuscular radiation. J. Geophys. Res. (1896-1977) 65 (11), 3559–3568. doi:10.1029/JZ065i011p03559

CrossRef Full Text | Google Scholar

Bhaskar, A., and Vichare, G. (2013). Characteristics of penetration electric fields to the equatorial ionosphere during southward and northward IMF turnings. J. Geophys. Res. Space Phys. 118 (7), 4696–4709. doi:10.1002/jgra.50436

CrossRef Full Text | Google Scholar

Bruntz, R., Lopez, R. E., Wiltberger, M., and Lyon, J. G. (2012). Investigation of the viscous potential using an MHD simulation. J. Geophys. Res. Space Phys. 117 (A3), A03214. doi:10.1029/2011JA017022

CrossRef Full Text | Google Scholar

Chapman, S. (1951). The equatorial electrojet as detected from the abnormal electric current distribution above huancayo, Peru, and elsewhere. Arch. für Meteorol. Geophys. Bioklimatol. Ser. A 4 (1), 368–390. doi:10.1007/BF02246814

CrossRef Full Text | Google Scholar

Dendy, R. (1995). Plasma Physics: an introductory course. Cambridge, UK: Cambridge University Press.

Google Scholar

Dungey, J. W. (1961). Interplanetary magnetic field and the auroral zones. Phys. Rev. Lett. 6 (2), 47–48. doi:10.1103/PhysRevLett.6.47

CrossRef Full Text | Google Scholar

Ebihara, Y., Tanaka, T., and Kikuchi, T. (2014). Counter equatorial electrojet and overshielding after substorm onset: global MHD simulation study. J. Geophys. Res. Space Phys. 119 (9), 7281–7296. doi:10.1002/2014JA020065

CrossRef Full Text | Google Scholar

Fejer, B. G., Jensen, J. W., Kikuchi, T., Abdu, M. A., and Chau, J. L. (2007). Equatorial ionospheric electric fields during the november 2004 magnetic storm. J. Geophys. Research-Space Phys. 112 (A10), A10304. doi:10.1029/2007JA012376

CrossRef Full Text | Google Scholar

Forbes, J. M. (1981). The equatorial electrojet. Rev. Geophys. 19 (3), 469–504. doi:10.1029/RG019i003p00469

CrossRef Full Text | Google Scholar

Fujita, S., Tanaka, T., Kikuchi, T., Fujimoto, K., and Itonaga, M. (2003). A numerical simulation of the geomagnetic sudden commencement: 1. Generation of the field-aligned current associated with the preliminary impulse. J. Geophys. Res. Space Phys. 108 (A12), 1416. doi:10.1029/2002ja009407

CrossRef Full Text | Google Scholar

Huang, C. S. (2020). Systematical analyses of global ionospheric disturbance current systems caused by multiple processes: penetration electric fields, solar wind pressure impulses, magnetospheric substorms, and ULF waves. J. Geophys. Res. Space Phys. 125 (9), e2020JA027942. doi:10.1029/2020JA027942

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, C. S., Foster, J. C., and Kelley, M. C. (2005). Long-duration penetration of the interplanetary electric field to the low-latitude ionosphere during the main phase of magnetic storms. J. Geophys. Res. Space Phys. 110 (A11), A11309. doi:10.1029/2005JA011202

CrossRef Full Text | Google Scholar

Huang, C. S., Sazykin, S., Chau, J. L., Maruyama, N., and Kelley, M. C. (2007). Penetration electric fields: efficiency and characteristic time scale. J. Atmos. Solar-Terrestrial Phys. 69 (10-11), 1135–1146. doi:10.1016/j.jastp.2006.08.016

CrossRef Full Text | Google Scholar

Huang, C. S., Yumoto, K., Abe, S., and Sofko, G. (2008). Low-latitude ionospheric electric and magnetic field disturbances in response to solar wind pressure enhancements. J. Geophys. Res. Space Phys. 113 (A8), A08314. doi:10.1029/2007JA012940

CrossRef Full Text | Google Scholar

Iijima, T., and Potemra, T. A. (1978). Large-scale characteristics of field-aligned currents associated with substorms. J. Geophys. Res. Space Phys. 83 (A2), 599–615. doi:10.1029/JA083iA02p00599

CrossRef Full Text | Google Scholar

Kataoka, R., Fairfield, D. H., Sibeck, D. G., Rastatter, L., Fok, M. C., Nagatsuma, T., et al. (2005). Magnetosheath variations during the storm main phase on 20 november 2003: evidence for solar wind density control of energy transfer to the magnetosphere. Geophys. Res. Lett. 32 (21), L21108. doi:10.1029/2005GL024495

CrossRef Full Text | Google Scholar

Kelley, M. C., Fejer, B. G., and Gonzales, C. A. (1979). An explanation for anomalous equatorial ionospheric electric fields associated with a northward turning of the interplanetary magnetic field. Geophys. Res. Lett. 6 (4), 301–304. doi:10.1029/GL006i004p00301

CrossRef Full Text | Google Scholar

Kikuchi, T., Hashimoto, K., Kitamura, T. I., Tachihara, H., and Fejer, B. (2003). Equatorial counterelectrojets during substorms. J. Geophys. Res. Space Phys. 108 (A11), 1406. doi:10.1029/2003JA009915

CrossRef Full Text | Google Scholar

Kikuchi, T., Luhr, H., Schlegel, K., Tachihara, H., Shinohara, M., and Kitamura, T. I. (2000). Penetration of auroral electric fields to the equator during a substorm. J. Geophys. Res. Space Phys. 105 (A10), 23251–23261. doi:10.1029/2000JA900016

CrossRef Full Text | Google Scholar

Kubota, Y., Kataoka, R., Den, M., Tanka, T., Nagatsuma, T., and Fujita, S. (2015). Global MHD simulation of magnetospheric response of preliminary impulse to large and sudden enhancement of the solar wind dynamic pressure. Earth, Planets Space 67 (1), 94. doi:10.1186/s40623-015-0270-7

CrossRef Full Text | Google Scholar

Lee, L. C., and Lee, K. H. (2020). Fluid and kinetic aspects of magnetic reconnection and some related magnetospheric phenomena. Rev. Mod. Plasma Phys. 4 (1), 9. doi:10.1007/s41614-020-00045-7

CrossRef Full Text | Google Scholar

Li, X., Chen, X. R., Zong, Q. G., Li, Q. H., and Zhang, D. H. (2021). Observational study of ionosphere TEC fluctuations triggered by interplanetary shock. Sci. Sin. Technol. 51 (8), 948–958. doi:10.1360/SST-2020-0506

CrossRef Full Text | Google Scholar

Lin, R. L., Zhang, X. X., Liu, S. Q., Wang, Y. L., and Gong, J. C. (2010). A three-dimensional asymmetric magnetopause model. J. Geophys. Res. Space Phys. 115 (A4), A04207. doi:10.1029/2009JA014235

CrossRef Full Text | Google Scholar

Liu, Z.-Q., Lu, J. Y., Wang, C., Kabin, K., Zhao, J. S., Wang, M., et al. (2015). A three-dimensional high mach number asymmetric magnetopause model from global MHD simulation. J. Geophys. Res. Space Phys. 120 (7), 5645–5666. doi:10.1002/2014ja020961

CrossRef Full Text | Google Scholar

Lühr, H. (2003). “Night-time ionospheric currents,” in First CHAMP mission results for gravity, magnetic and atmospheric studies (Berlin, Heidelberg: Springer), 328–338. doi:10.1007/978-3-540-38366-6_48

CrossRef Full Text | Google Scholar

Maruyama, N., Sazykin, S., Spiro, R. W., Anderson, D., Anghel, A., Wolf, R. A., et al. (2007). Modeling storm-time electrodynamics of the low-latitude ionosphere-thermo sphere system: can long lasting disturbance electric fields Be accounted for? J. Atmos. Solar-Terrestrial Phys. 69 (10-11), 1182–1199. doi:10.1016/j.jastp.2006.08.020

CrossRef Full Text | Google Scholar

Nilam, B., and Tulasi Ram, S. (2022). Large geomagnetically induced currents at equator caused by an interplanetary magnetic cloud. Space weather 20 (6), e2022SW003111. doi:10.1029/2022SW003111

CrossRef Full Text | Google Scholar

Nilam, B., Tulasi Ram, S., Shiokawa, K., Balan, N., and Zhang, Q. (2020). The solar wind density control on the prompt penetration electric field and equatorial electrojet. J. Geophys. Res. Space Phys. 125 (9), e2020JA027869. doi:10.1029/2020JA027869

CrossRef Full Text | Google Scholar

Nishida, A. (1968). Coherence of geomagnetic DP 2 fluctuations with interplanetary magnetic variations. J. Geophys. Res. (1896-1977) 73 (17), 5549–5559. doi:10.1029/JA073i017p05549

CrossRef Full Text | Google Scholar

Ohtani, S., Uozumi, T., Kawano, H., Yoshikawa, A., Utada, H., Nagatsuma, T., et al. (2013). The response of the dayside equatorial electrojet to step-like changes of IMF B_Z. J. Geophys. Res. Space Phys. 118 (6), 3637–3646. doi:10.1002/jgra.50318

CrossRef Full Text | Google Scholar

Peymirat, C., Richmond, A. D., and Kobea, A. T. (2000). Electrodynamic coupling of high and low latitudes: simulations of shielding/overshielding effects. J. Geophys. Res. Space Phys. 105 (A10), 22991–23003. doi:10.1029/2000JA000057

CrossRef Full Text | Google Scholar

Rastogi, R. G., and Klobuchar, J. A. (1990). Ionospheric electron-content within the equatorial F2 layer anomaly belt. J. Geophys. Res. Space Phys. 95 (A11), 19045–19052. doi:10.1029/JA095iA11p19045

CrossRef Full Text | Google Scholar

Rastogi, R. G., and Patel, V. L. (1975). Effect of interplanetary magnetic field on ionosphere over the magnetic equator. Proc. Indian Acad. Sci. Sect. A 82 (4), 121–141. doi:10.1007/BF03046722

CrossRef Full Text | Google Scholar

Richmond, A. D. (1989). Modeling the ionosphere wind dynamo: a review. Pure Appl. Geophys. 131 (3), 413–435. doi:10.1007/BF00876837

CrossRef Full Text | Google Scholar

Richmond, A. D., Peymirat, C., and Roble, R. G. (2003). Long-lasting disturbances in the equatorial ionospheric electric field simulated with a coupled magnetosphere-ionosphere-thermosphere model. J. Geophys. Res. Space Phys. 108 (A3), 1118. doi:10.1029/2002JA009758

CrossRef Full Text | Google Scholar

Samsonov, A. A., Bogdanova, Y. V., Branduardi-Raymont, G., Sibeck, D. G., and Toth, G. (2020). Is the relation between the solar wind dynamic pressure and the magnetopause standoff distance so straightforward? Geophys. Res. Lett. 47 (8), e2019GL086474. doi:10.1029/2019GL086474

CrossRef Full Text | Google Scholar

Sastri, J. H. (1988). Equatorial electric-fields of ionospheric disturbance dynamo orgin. Ann. Geophysicae-Atmospheres Hydrospheres Space Sci. 6 (6), 635–642.

Google Scholar

Sekar, R., Gupta, S. P., and Chakrabarty, D. (2014). Characteristics of E-region background ionosphere and plasma waves measured over the Dip equator during total solar eclipse Campaign. J. Atmos. Solar-Terrestrial Phys. 114, 58–65. doi:10.1016/j.jastp.2014.04.006

CrossRef Full Text | Google Scholar

Senior, C., and Blanc, M. (1984). On the control of magnetospheric convection by the spatial distribution of ionospheric conductivities. J. Geophys. Res. Space Phys. 89 (A1), 261–284. doi:10.1029/JA089iA01p00261

CrossRef Full Text | Google Scholar

Shue, J.-H., Newell, P. T., Liou, K., and Meng, C.-I. (2002). Solar wind density and velocity control of auroral brightness under normal interplanetary magnetic field conditions. J. Geophys. Res. Space Phys. 107 (A12), SMP 9-1–SMP 9-6. doi:10.1029/2001JA009138

CrossRef Full Text | Google Scholar

Shue, J.-H., Song, P., Russell, C. T., Steinberg, J. T., Chao, J. K., Zastenker, G., et al. (1998). Magnetopause location under extreme solar wind conditions. J. Geophys. Res. Space Phys. 103 (A8), 17691–17700. doi:10.1029/98JA01103

CrossRef Full Text | Google Scholar

Spiro, R. W., Wolf, R. A., and Fejer, B. G. (1988). Penetration of high-latitude-electric-field effects to low latitudes during sundial 1984. Ann. Geophysicae-Atmospheres Hydrospheres Space Sci. 6 (1), 39–49.

Google Scholar

Tulasi Ram, S., Balan, N., Veenadhari, B., Gurubaran, S., Ravindran, S., Tsugawa, T., et al. (2012). First observational evidence for opposite zonal electric fields in equatorial E and F region altitudes during a geomagnetic storm period. J. Geophys. Res. Space Phys. 117 (A9), A09318. doi:10.1029/2012JA018045

CrossRef Full Text | Google Scholar

Tulasi Ram, S., Yokoyama, T., Otsuka, Y., Shiokawa, K., Sripathi, S., Veenadhari, B., et al. (2016). Duskside enhancement of equatorial zonal electric field response to convection electric fields during the st. Patrick’s day storm on 17 march 2015. J. Geophys. Res. Space Phys. 121 (1), 538–548. doi:10.1002/2015JA021932

CrossRef Full Text | Google Scholar

Untiedt, J. (1967). A model of the equatorial electrojet involving meridional currents. J. Geophys. Res. (1896-1977) 72 (23), 5799–5810. doi:10.1029/JZ072i023p05799

CrossRef Full Text | Google Scholar

Venkatesh, K., Tulasi Ram, S., Fagundes, P. R., Seemala, G. K., and Batista, I. S. (2017). Electrodynamic disturbances in the Brazilian equatorial and low-latitude ionosphere on st. Patrick’s day storm of 17 march 2015. J. Geophys. Res. Space Phys. 122 (4), 4553–4570. doi:10.1002/2017JA024009

CrossRef Full Text | Google Scholar

Wei, Y., Wan, W., Zhao, B., Hong, M., Ridley, A., Ren, Z., et al. (2012). Solar wind density controlling penetration electric field at the equatorial ionosphere during a saturation of cross polar cap potential. J. Geophys. Res. Space Phys. 117 (A9), A09308. doi:10.1029/2012JA017597

CrossRef Full Text | Google Scholar

Wright, A. N. (1994). Dispersion and wave coupling in inhomogeneous MHD waveguides. J. Geophys. Res. Space Phys. 99 (A1), 159–167. doi:10.1029/93JA02206

CrossRef Full Text | Google Scholar

Xiong, C., Lühr, H., and Fejer, B. G. (2016). The response of equatorial electrojet, vertical plasma drift, and thermospheric zonal wind to enhanced solar wind input. J. Geophys. Res. Space Phys. 121 (6), 5653–5663. doi:10.1002/2015JA022133

CrossRef Full Text | Google Scholar

Yuan, Z. G., and Deng, X. H. (2007). Effects of continuous solar wind pressure variations on the long-lasting penetration of the interplanetary electric field during southward interplanetary magnetic field. Adv. Space Res. 39 (8), 1342–1346. doi:10.1016/j.asr.2007.02.033

CrossRef Full Text | Google Scholar

Zhang, K. D., Wang, H., and Wang, W. B. (2022). Local time variations of the equatorial electrojet in simultaneous response to subauroral polarization streams during quiet time. Geophys. Res. Lett. 49 (7), e2022GL098623. doi:10.1029/2022GL098623

CrossRef Full Text | Google Scholar

Zhou, X. Y., and Tsurutani, B. T. (2001). Interplanetary shock triggering of nightside geomagnetic activity: substorms, pseudobreakups, and quiescent events. J. Geophys. Res. Space Phys. 106 (A9), 18957–18967. doi:10.1029/2000JA003028

CrossRef Full Text | Google Scholar