Application of collisional analysis to the differential velocity of solar wind ions

Collisional analysis combines the effects of collisional relaxation and large-scale expansion to quantify how solar wind parameters evolve as the plasma expands through the heliosphere. Though previous studies have applied collisional analysis to the temperature ratio between protons (ionized hydrogen) and α-particles (fully ionized helium), this is the first study to explore α-proton differential flow with collisional analysis. First, the mathematical model for the collisional analysis of differential flow was derived. Then, this model was applied to individual in-situ observations from Parker Solar Probe (PSP; r = 0.1–0.27 au) to generate predictions of the α-proton differential flow in the near-Earth solar wind. A comparison of these predicted values with contemporaneous measurements from the Wind spacecraft (r = 1.0 au) shows strong agreement, which may imply that the effects of expansion and Coulomb collisions have a large role in governing the evolution of differential flow through the inner heliosphere.

1 Introduction

The solar wind ions consist of protons (ionized hydrogen), a small but variable percentage (typically $\approx 4\%$ and ≲ 20%; Kasper et al., 2012) of α-particles (fully ionized helium), with trace amounts of heavier ions (Schmelz et al., 2012). Solar wind plasma often shows deviations from local thermal equilibrium (LTE) (Griem, 1963), in which, for example, the ion species exhibit distinct temperatures and bulk speeds (Marsch, 2006; Verscharen et al., 2019). Once generated, these non-LTE features are preserved by the solar wind’s high temperature and low density, which reduces the rate of Coulomb collisions—“soft,” small-angle deflections between charged particles mediated by the electrostatic force. These collisions, which allow the particles to exchange energy and momentum in “collisional relaxation,” serve as the ultimate drivers of thermal equilibrium (Hernández and Marsch, 1985; Livi et al., 1986). The time required for collisions to substantially reduce a given non-LTE feature is the “collisional timescale,” with the process being unique for each parameter and system configuration (e.g., the “slowing-down time” for the difference in bulk speed).

For example, considerable attention has been given to the difference in proton and α-particle temperatures, which can be quantified by the ratio

${\theta }_{\alpha \mathrm{p}}=\frac{T_{\alpha }}{T_{\text{p}}},(1)$

where T_α is the scalar temperature of the α-particles and T_p is the proton scalar temperature. Early studies (Feldman et al., 1974; Neugebauer, 1976; Marsch et al., 1982) found that typically θ_αp ≳ 1 and that θ_αp is strongly anti-correlated with “Coulomb number,” the ratio of the expansion time to the collisional timescale. This finding, which was later confirmed by Kasper et al. (2008), Maruca et al. (2013), and Tracy et al. (2015), was interpreted as indicating that α-particles are preferentially heated relative to the protons in the solar corona and that Coulomb collisions slowly thermalize these two species as the plasma expands.

Though Coulomb number is a useful tool in understanding collisional thermalization, Maruca et al. (2013) introduced “collisional analysis” to provide a more quantitative method for studying θ_αp (Eq. 1). In this technique, basic models for the solar wind’s expansion are incorporated into the equations of collisional relaxation, this generates a prediction for how θ_αp in a given parcel of plasma varies with distance, r, from the Sun. Maruca et al. (2013) applied this technique to individual θ_αp-measurements from the Wind spacecraft (r = 1.0 au) to predict the distribution of θ_αp-values at r = 0.1 au, i.e., near-Sun solar wind. This prediction was confirmed by Johnson et al. (2023), who further validated the collisional analysis technique by showing that it could be applied to θ_αp-measurements from Parker Solar Probe (PSP; r = 0.1–0.27 au) to effectively predict contemporaneous measurements of θ_αp from Wind.

This study extends collisional analysis to model the collisional effects on “differential flow,” which is the difference in the bulk velocities of two ion species:

$\mathrm{\Delta }{\mathbf{v}}_{ij}={\mathbf{v}}_i-{\mathbf{v}}_j,(2)$

where v_i and v_j are the bulk velocities of i- and j-particle species, respectively. Just as α-particles are observed to typically be hotter than protons (T_α > T_p), they are also typically faster than the protons (|v_α| > |v_p|). Likewise, prior studies have shown that |Δv_αp| anti-correlates with Coulomb number just as θ_αp does (Kasper et al., 2008; Alterman et al., 2018). Nevertheless, the extended collisional analysis technique described herein offers a more quantitative examination of collisional slowing of ion species in the solar wind.

Section 2 derives the mathematical model for the collisional analysis of differential flow. In Section 3, this model is applied to measurements from PSP to generate predictions of the near-Earth solar wind that are then compared to contemporaneous Wind observations. Concluding remarks are presented in Section 4.

2 Background

Coulomb number (N_C) was used in earlier studies, such as Neugebauer (1976), Marsch et al. (1982) and Neugebauer and Feldman (1979), to demonstrate that |Δv_αp| → 0 and θ_αp → 1 as N_C increases Verscharen et al. (2019, Fig 13). However, N_C assumes that plasma parameters remain constant and do not scale with distance, yet plasma parameters, such as those of temperature and density, have strong radial trends. To address these issues works by Hernández et al. (1987), Kasper et al. (2017) and Kasper and Klein (2019) use an integral form of the Coulomb number known as the collisional age, which accounts for radial dependencies of plasma parameters. Collisional analysis was introduced by Maruca et al. (2013), combining the effects of expansion and Coulomb collisions on ion temperature ratios in any given parcel of solar wind plasma. A full in-depth review on collisional analysis is presented in Maruca et al. (2013), with Johnson et al. (2023) applying this technique to PSP data for the first time. This section presents a variation of collisional analysis that, for the first time, addresses ion differential flow rather than differences in ion temperature.

The rate at which the differential flow, Δv_ij (Eq. 2), between i- and j-particles is eroded by Coulomb collisions is given by (Richardson, 2019):

$\frac{d\mathrm{\Delta }{\mathbf{v}}_{ij}}{dt}=-{\nu }_{ij}^{\left(\mathrm{s}\right)}\mathrm{\Delta }{\mathbf{v}}_{ij},(3)$

where t is time, and ${\nu }_{ij}^{(\mathrm{s})}$ is the collision frequency for the reduction of differential flow between i- and j-particles. Richardson (2019); Larroche (2021) expresses this as:

${\nu }_{ij}^{\left(\mathrm{s}\right)}=\left(1+\frac{m_i}{m_j}\right)\psi \left(\frac{m_j{v}_i^2}{2k_{\text{B}}{T}_j}\right)\left(\frac{4\pi q_i^2{q}_j^2{n}_j}{m_i^2{v}_i^3}\right){\lambda }_{ij},(4)$

where, for i-particles, m_i is mass, q_i is charge, v_i is the bulk velocity, T_i is scalar temperature, n_i is number density and k_B is the Boltzmann constant. The Coulomb logarithm, λ_ij, for the collision of an i- and j-particle (i.e., mixed ion-ion collisions) is (Richardson, 2019):

${\lambda }_{ij}=23-\ln \left[\frac{Z_i{Z}_j\left({\mu }_i+{\mu }_j\right)}{{\mu }_i{T}_j+{\mu }_j{T}_i}{\left(\frac{n_i{Z}_i^2}{T_i}+\frac{n_j{Z}_j^2}{T_j}\right)}^{1/2}\right],(5)$

with μ_i = m_i/m_p, Z_i = q_i/q_p, where m_p and q_p are the proton mass and charge. The ψ function for any given x-value is defined to be

$\psi \left(x\right)=\frac{2}{\sqrt{\pi }}{\int }_0^x{e}^{-t}\sqrt{t}dt=1-\frac{2\mathrm{\Gamma }\left(3/2,x\right)}{\sqrt{\pi }},(6)$

where Γ denotes the incomplete gamma function (Arfken and Weber, 2011). The derivation directly models the collisional thermalization of two ion species. This is achieved by considering a multi-species plasma with no relative drift or temperature anisotropy (Maruca et al., 2013; Richardson, 2019).

Following the example in Maruca et al. (2013), the collision rate can be converted from a time derivative to one with respect to distance, r. The system is assumed to be in steady state, other deviations from equilibrium are neglected and η_{i j} = n_i/n_j remains constant in any parcel of plasma. Under the assumption that the plasma is radially streaming from the Sun in steady state,

$\frac{d\mathrm{\Delta }{\mathbf{v}}_{ij}}{dr}=\frac{d\mathrm{\Delta }{\mathbf{v}}_{ij}}{dt}\frac{dt}{dr}=\frac{1}{v_{\text{p}}}\frac{d\mathrm{\Delta }{\mathbf{v}}_{ij}}{dt},(7)$

where the solar wind speed is approximated as the proton bulk speed, v_p = |v_p|, i.e., the background particle speed.

In line with Maruca et al. (2013) and for the specific case of α-particles drifting relative to protons, only protons and α-particles were considered: other ion species and electrons were neglected. Equations 3–7 combine to give

$\frac{d\mathrm{\Delta }{\mathbf{v}}_{\alpha \mathrm{p}}}{dr}=-{\nu }_{\alpha \mathrm{p}}^{\left(\mathrm{s}\right)}\frac{\mathrm{\Delta }{\mathbf{v}}_{\alpha \mathrm{p}}}{v_{\text{p}}},(8)$

with the collision rate,

${\nu }_{\alpha \mathrm{p}}^{\left(\mathrm{s}\right)}=\left(1+\frac{m_{\alpha }}{m_{\text{p}}}\right)\left(1-\frac{2\mathrm{\Gamma }\left(\frac{3}{2},\frac{m_{\text{p}}{v}_{\alpha }^2}{2k_{\text{B}}{T}_{\text{p}}}\right)}{\sqrt{\pi }}\right)\left(\frac{4\pi q_{\alpha }^2{q}_{\text{p}}^2{n}_{\text{p}}}{m_{\alpha }^2{v}_{\alpha }^3}\right){\lambda }_{\alpha \mathrm{p}},(9)$

remaining consistent with prior derivations, such as Hernández and Marsch (1985), Eq. 23 and Spitzer (1962).

On its own, Eq. 8 only models the effects of collisions on Δv_αp. Nevertheless, the average effects of expansion can be incorporated by allowing density, bulk speed, and scalar temperature to scale with r. For example, Hellinger et al. (2011) utilized Helios observations to conclude that:

$\begin{array}{c}{n}_{\text{p}}\left(r\right)\propto r^{-1.8},v_{r,\mathrm{p}}\left(r\right)\propto r^{-0.2},\\ T_{\text{p}}\left(r\right)\propto r^{-0.74},\mathrm{a}\mathrm{n}\mathrm{d}B\left(r\right)\propto r^{-1.6}.\end{array}(10)$

Scaling in magnetic-field strength, B, is not explicitly required for Eq. 8, and it is not used in any of the collisional analysis. It is only required to normalize Δv_αp to the Alfvén speed,

$v_{\text{A}}=\frac{B}{\sqrt{{\mu }_0\left(n_{\alpha }{m}_{\alpha }+n_{\text{p}}{m}_{\text{p}}\right)}},(11)$

where μ₀ is the vacuum permeability. These scaling values are used to remain consistent with prior works, such as Maruca et al. (2013) and Johnson et al. (2023). Additionally, the values are not fixed and can be taken from observations or simulations. For example, both Durovcova et al. (2019) and Maruca et al. (2023) provide alternative scaling values, that when implemented produce comparable results when compared to Hellinger et al. (2011).

3 Analysis

The data set used in this study is the same as the one used by Johnson et al. (2023), who provide a detailed discussion of its properties and of the algorithm applied to correct for variations in sampling cadence. The data were derived from ion measurements from the electrostatic analyzer (ESA; Livi et al., 2021) in the SWEAP instrument suite (Kasper et al., 2016) onboard the PSP spacecraft (Fox et al., 2016). Proton and α-particle parameter values were extracted from PSP/SWEAP ESA distribution via a non-linear fitting algorithm. Three distinct ion populations were considered: a proton core, and proton beam, and a single alpha-particle population. Each population was modeled with a bi-Maxwellian VDF. Though the VDF’s were allowed to drift relative to one another, proton beam-core drift was only permitted along the magnetic-field axis (McManus et al., 2022; Mostafavi et al., 2022), the α-particle velocities are not constrained in this way. The final data set consisted of 23,770 total data entries spanning approximately three, 10-day intervals¹; corresponding to three distinct 10-day observation periods from PSP, occurring at three distinct time periods. During those intervals, PSP ranged from r ≈ 0.1 to 0.27 au.

Figure 1 shows the probability distribution of the α-proton differential flow (|Δv_αp|, Eq. 2) for the data set, it also shows this distribution normalized by the Alfvén speed (|Δv_αp|/v_A). The data were sorted among 40 bins spanning Δv_αp = 0–200 km/s and Δv_αp/v_A = 0 to 2.0. The count of data in each bin was divided by the total number of data and the width of the bin to approximate probability density (Maruca et al., 2011). Poisson statistics determined the average uncertainty to be ${\sigma }_{\mathrm{\Delta }{\mathbf{v}}_{\alpha \mathrm{p}}}=7.20\%$.

FIGURE 1

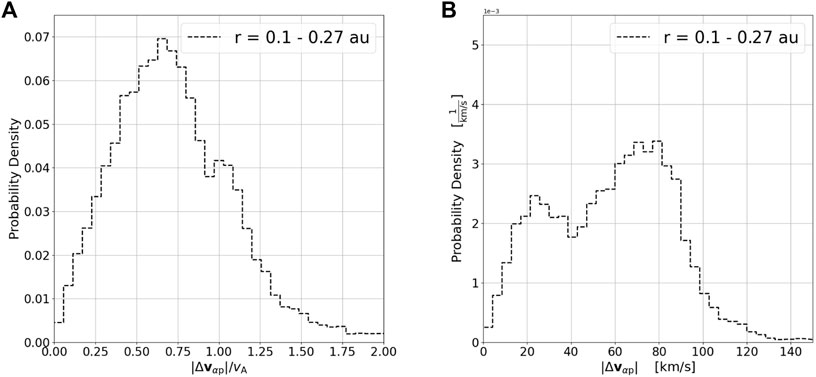
FIGURE 1. Histogram of observed values of α-proton differential flow: (A) normalized |Δv_αp|/v_A and (B) unnormalized |Δv_αp| from the PSP data set (r =0.1 to 0.27 au). Bin counts have been normalized to approximate probability density.

Collisional analysis was applied to the PSP data (r = 0.1–0.27 au) set to predict the values of |Δv_αp| in the near-Earth solar wind (r = 1.0 au). A PSP “datum” from this data set consisted of a set of values for n_α, n_p, T_α, T_p, v_α, v_p and B derived from measurements made a given distance r₀ from the Sun. These are applied as a boundary condition to Eq. 8 and the scaling functions in Eq. 10 are implemented to solve for Δv_αp(r).

Figure 2 shows this collisional analysis applied to seven exemplar data from the PSP data set. Black dots indicate the measured values of differential flow and PSP’s distance from the Sun at the time. The colored curves show the predicted differential flow values farther from the Sun based on the effects of collisions and expansion. The scaling functions come into play not only in Eq. 8 but also in computing the Alfvén speed (v_A; Eq. 11) for the normalized differential flow (|Δv_αp|/v_A). Since v_A almost invariably rapidly decreases with distance from the Sun, all of the curves in Figure 2A monotonically increase. In contrast, Figure 2B shows monotonically decreasing curves, which reveal the gradual erosion of differential flow by Coulomb collisions. Some of the curves in Figure 2B cross due to the wide variation in collision rates (Eq. 9) across the PSP data set.

FIGURE 2

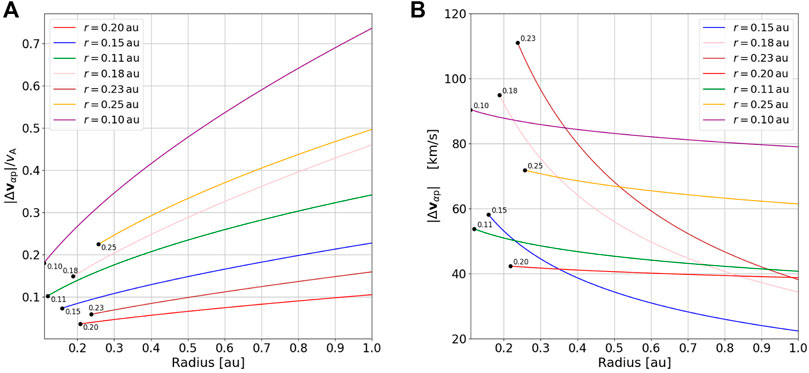
FIGURE 2. Radial evolution of α-proton differential flow: (A) normalized |Δv_αp|/v_A and (B) unnormalized |Δv_αp|. The black dots are observations from PSP, the colors are a prediction of the differential flow based on that observation. Table 1 provides a detailed overview of these parameters.

TABLE 1

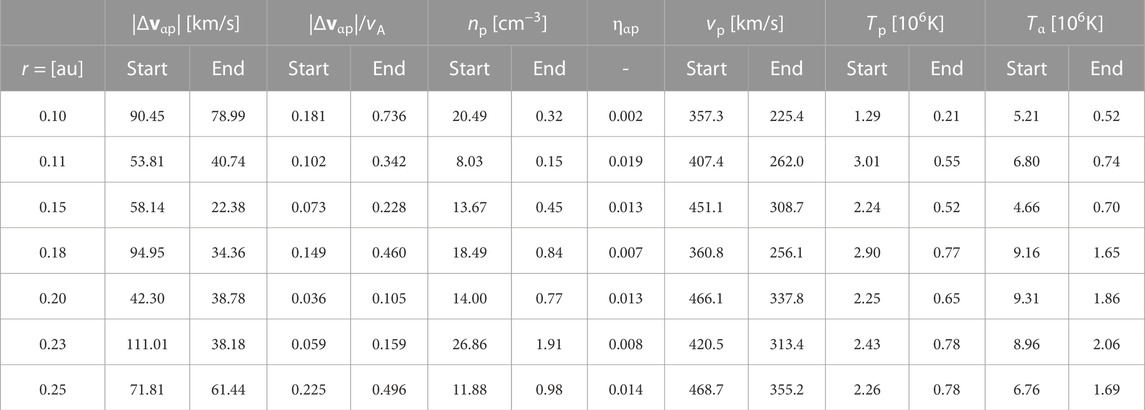
TABLE 1. Differential flow values and additional plasma parameters from Figure 2. Start values are from PSP observations, end values are at r =1.0 au and are calculated from collisional analysis.

This collisional analysis procedure was applied to all data in the PSP data set to generate a prediction of α-proton differential flow for the near-Earth solar wind (r = 1.0 au). Figure 3 shows the observed differential flow in the near-Sun solar wind compared to the predicted near-Earth differential flow from collisional analysis for an exemplar time interval. It can be seen the α-proton differential flow decreases with distance from the corona.

FIGURE 3

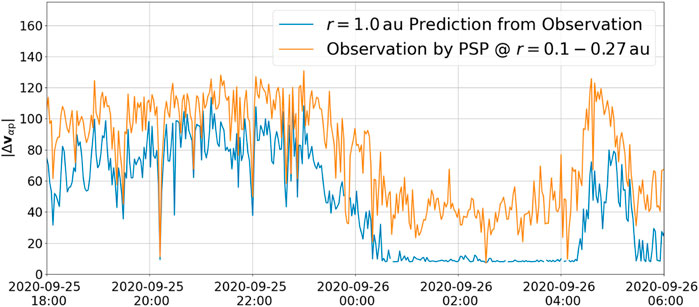
FIGURE 3. Observation from PSP of the α-proton differential flow, prediction from collisional analysis of the near-Earth α-proton differential flow using the observation from PSP.

Figure 4 shows in blue-solid the distribution of these predicted values: (a) normalized to the Alfvén speed and (b) unnormalized. To validate the predicted values, Figure 4 also shows in red-dashed the distribution of α-proton differential flow values measured contemporaneously with the Wind spacecraft (Acuna et al., 1995; Wilson et al., 2021), which orbits in the first Lagrange point (L1) of the Earth-Sun system (r ≈ 1.0 au from the Sun). The Wind ion measurements shown in Figure 4 are specifically from the Faraday cups in the Solar Wind Experiment (SWE; Ogilvie et al., 1995) and were the same data set as used by Johnson et al. (2023).

FIGURE 4

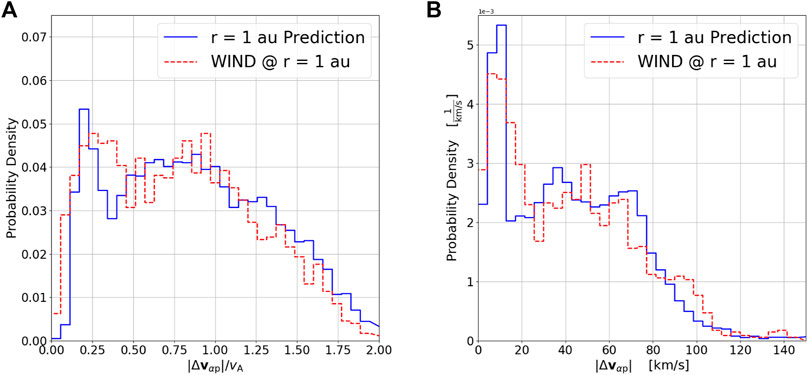
FIGURE 4. Histogram of observed values of α-proton differential flow: (A) normalized |Δv_αp|/v_A and (B) unnormalized |Δv_αp| from the Wind data set at r =1.0 au (red dashed). Histogram of predicted α-proton differential flow values at r =1.0 au from the PSP data set based on collisional analysis (blue solid).

4 Discussion

Both plots in Figure 4 show a remarkable agreement between the distribution of α-proton differential flow observed (red dashed curve) at r = 1 au with Wind and that predicted (solid blue curve) from collisional analysis for r = 1 au from PSP observations (r = 0.1 to 0.27 au). This may imply that the radial evolution of Δv_αp from the outer corona through to the inner heliosphere is governed by the effects of expansion and Coulomb collisions.

In general, collisional analysis was found to produce less dramatic changes in α-proton differential flow (this study) than in relative temperatures (Johnson et al., 2023). Utilizing Poisson statistics, the average uncertainty was calculated as ${\sigma }_{\mathrm{\Delta }{\mathbf{v}}_{\alpha \mathrm{p}}}=8.77\%$. The median predicted percent change in Δv_αp in going from PSP to Wind for the data set in this study was 23%, though the predicted change varied widely across the data set. The 25th- and 75th-percentile values of this percentage were 8% and 50%, indicating that the effect of collisions on Δv_αp was sometimes modest and other time more dramatic.

To date, this is the first study to directly apply the collisional analysis technique to ion differential flow. No preferential heating, acceleration or instabilities were included in the model (Eq. 8). Rather, it was assumed that the only collisions and expansion affect the relative drift between protons and α-particles. The strong agreement between the distributions of predicted and measured 1-au Δv_αp-values suggests that the preferential acceleration of α-particles predominantly occurs closer to the Sun (r ≲ 0.1 au), which is consistent with expectations for preferential heating (e.g., Kasper et al., 2017; Kasper and Klein, 2019).

Ideally, to test collisional analysis data should be taken simultaneously from two different spacecraft in the same steady solar wind stream. The differences in heliographic longitude between Wind and PSP are accounted for by populating the Wind data with measurements from a time period ranging from 10 days before to 10 days after each observation event, roughly the length of one Carrington rotation. Ensuring Wind has the largest possible number of kinetic states for a single solar wind stream and is statistically representative. Additionally, a solar wind stream is never fully steady and no accommodation has been made in this study for any intrinsic error propagating from spacecraft observations. These constraints and the limited coverage make it difficult to generalize about the full role of Coulomb collisions and expansion in the solar wind, thus any conclusion must include these caveats.

The continuation of the PSP mission will allow the data set to grow substantially, which will enable a more comprehensive study whose data set spans a larger number of solar-wind streams (i.e., a wider range of plasma conditions). Additionally, the perihelion of PSP’s orbit is continuing to progress closer to the Sun, which may allow it to probe the region of the heliosphere where the preferential acceleration ions substantially occurs.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

EJ: Conceptualization, Formal Analysis, Investigation, Methodology, Software, Writing–original draft, Writing–review and editing. BAM: Funding acquisition, Resources, Supervision, Writing–review and editing. MMc: Data curation, Writing–review and editing. MS: Writing–review and editing. KGK: Writing–review and editing. PM: Writing–review and editing, Conceptualization.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article. EJ and BAM are partially supported by the NSF Award No. 1931435. This research made use of PlasmaPy, a community-developed open-source Python package for plasma science PlasmaPy (2021).

Acknowledgments

We acknowledge the NASA Parker Solar Probe Mission and Solar Wind Electrons Alphas and Protons (SWEAP) team led by Professor Justin Kasper, NASA contract NNN06AA01C. Thanks to the Integrated Science Investigation of the Sun (ISIS) Science Team (PI: David McComas, Princeton University) (McComas et al., 2014). The authors thank Brandy for assistance and fruitful discussions, this work is dedicated to her loving memory. The following software was utilized in this research: numpy (Harris et al., 2020), astropy (Astropy Collaboration et al., 2022), plasmapy (PlasmaPy, 2021), matplotlib (Hunter, 2007).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹The first three 10-day encounter was comparably slower (v_p) and denser (n_p) than the later two encounters. Encounters are combined to generate a larger data-set that is more statistically significant and is more representative of an average solar wind stream.

References

Acuna, M. H., Ogilvie, K. W., Baker, D. N., Curtis, S. A., Fairfield, D. H., and Mish, W. H. (1995). The global geospace science program and its investigations. Space Sci. Rev. 71, 5–21. doi:10.1007/bf00751323

CrossRef Full Text | Google Scholar

Alterman, B. L., Kasper, J. C., Stevens, M. L., and Koval, A. (2018). A comparison of alpha particle and proton beam differential flows in collisionally young solar wind. Astrophysical J. 864, 112. doi:10.3847/1538-4357/aad23f

CrossRef Full Text | Google Scholar

Arfken, G. B., and Weber, H.-J. (2011). Mathematical methods for physicists. Germany: Elsevier.

Google Scholar

Astropy Collaboration Price-Whelan, A. M., Lim, P. L., Earl, N., Starkman, N., Bradley, L., et al. (2022). The astropy project: sustaining and growing a community-oriented open-source project and the latest major release (v5.0) of the core package. ApJ 935, 167. doi:10.3847/1538-4357/ac7c74

CrossRef Full Text | Google Scholar

Durovcova, T., Nemecek, Z., and Safrankova, J. (2019). Evolution of the alpha-proton differential motion across stream interaction regions. Astrophysical J. 873, 24. doi:10.3847/1538-4357/ab01c8

CrossRef Full Text | Google Scholar

Feldman, W. C., Asbridge, J. R., and Bame, S. J. (1974). The solar wind he2+ to h+ temperature ratio. J. Geophys. Res. 79, 2319–2323. doi:10.1029/JA079i016p02319

CrossRef Full Text | Google Scholar

Fox, N. J., Velli, M. C., Bale, S. D., Decker, R., Driesman, A., Howard, R. A., et al. (2016). The solar probe plus mission: humanity’s first visit to our star. Space Sci. Rev. 204, 7–48. doi:10.1007/s11214-015-0211-6

CrossRef Full Text | Google Scholar

Griem, H. R. (1963). Validity of local thermal equilibrium in plasma spectroscopy. Phys. Rev. 131, 1170–1176. doi:10.1103/PhysRev.131.1170

CrossRef Full Text | Google Scholar

Harris, C. R., Millman, K. J., van der Walt, S. J., Gommers, R., Virtanen, P., Cournapeau, D., et al. (2020). Array programming with NumPy. Nature 585, 357–362. doi:10.1038/s41586-020-2649-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Hellinger, P., Matteini, L., Štverák, v., Trávníček, P. M., and Marsch, E. (2011). Heating and cooling of protons in the fast solar wind between 0.3 and 1 au: helios revisited. J. Geophys. Res. Space Phys. 116. doi:10.1029/2011JA016674

CrossRef Full Text | Google Scholar

Hernández, R., Livi, S., and Marsch, E. (1987). On the he2+ to h+ temperature ratio in slow solar wind. J. Geophys. Res. Space Phys. 92, 7723–7727. doi:10.1029/JA092iA07p07723

CrossRef Full Text | Google Scholar

Hernández, R., and Marsch, E. (1985). Collisional time scales for temperature and velocity exchange between drifting maxwellians. J. Geophys. Res. Space Phys. 90, 11062–11066. doi:10.1029/JA090iA11p11062

CrossRef Full Text | Google Scholar

Hunter, J. D. (2007). Matplotlib: a 2d graphics environment. Comput. Sci. Eng. 9, 90–95. doi:10.1109/MCSE.2007.55

CrossRef Full Text | Google Scholar

Johnson, E., Maruca, B. A., McManus, M., Klein, K. G., Lichko, E. R., Verniero, J., et al. (2023). Anterograde collisional analysis of solar wind ions. Astrophysical J. 950, 51. doi:10.3847/1538-4357/accc32

CrossRef Full Text | Google Scholar

Kasper, J. C., Abiad, R., Austin, G., Balat-Pichelin, M., Bale, S. D., Belcher, J. W., et al. (2016). Solar wind electrons alphas and protons (sweap) investigation: design of the solar wind and coronal plasma instrument suite for solar probe plus. Space Sci. Rev. 204, 131–186. doi:10.1007/s11214-015-0206-3

CrossRef Full Text | Google Scholar

Kasper, J. C., and Klein, K. G. (2019). Strong preferential ion heating is limited to within the solar alfvén surface. Astrophysical J. 877, L35. doi:10.3847/2041-8213/ab1de5

CrossRef Full Text | Google Scholar

Kasper, J. C., Klein, K. G., Weber, T., Maksimovic, M., Zaslavsky, A., Bale, S. D., et al. (2017). A zone of preferential ion heating extends tens of solar radii from the sun. Astrophysical J. 849, 126. doi:10.3847/1538-4357/aa84b1

CrossRef Full Text | Google Scholar

Kasper, J. C., Lazarus, A. J., and Gary, S. P. (2008). Hot solar-wind helium: direct evidence for local heating by alfvén-cyclotron dissipation. Phys. Rev. Lett. 101, 261103. doi:10.1103/PhysRevLett.101.261103

PubMed Abstract | CrossRef Full Text | Google Scholar

Kasper, J. C., Stevens, M. L., Korreck, K. E., Maruca, B. A., Kiefer, K. K., Schwadron, N. A., et al. (2012). Evolution of the relationships between helium abundance, minor ion charge state, and solar wind speed over the solar cycle. Astrophysical J. 745, 162. doi:10.1088/0004-637x/745/2/162

CrossRef Full Text | Google Scholar

Larroche, O. (2021). An extended hydrodynamics model for inertial confinement fusion hohlraums. Eur. Phys. J. D 75, 297. doi:10.1140/epjd/s10053-021-00305-2

CrossRef Full Text | Google Scholar

Livi, R., Larson, D. E., Kasper, J. C., Abiad, R., Case, A. W., Klein, K. G., et al. (2021). The solar probe analyzer -ions on parker solar probe. Earth Space Sci. Open Archive 20. doi:10.1002/essoar.10508651.1

CrossRef Full Text | Google Scholar

Livi, R., Larson, D. E., and Rahmati, A. (2020). Psp solar wind electrons alphas and protons (sweap) span-a proton distribution function, partial moments, instrument frame. level 3 (l3), 7. doi:10.48322/ypyh-s325

CrossRef Full Text | Google Scholar

Livi, S., Marsch, E., and Rosenbauer, H. (1986). Coulomb collisional domains in the solar wind. J. Geophys. Res. 91, 8045–8050. doi:10.1029/ja091ia07p08045

CrossRef Full Text | Google Scholar

Marsch, E. (2006). Kinetic physics of the solar corona and solar wind. Living Rev. Sol. Phys. 3. doi:10.12942/lrsp-2006-1

CrossRef Full Text | Google Scholar

Marsch, E., Mühlhäuser, K.-H., Rosenbauer, H., Schwenn, R., and Neubauer, F. M. (1982). Solar wind helium ions: observations of the helios solar probes between 0.3 and 1 au. J. Geophys. Res. Space Phys. 87, 35–51. doi:10.1029/JA087iA01p00035

CrossRef Full Text | Google Scholar

Maruca, B. A., Bale, S. D., Sorriso-Valvo, L., Kasper, J. C., and Stevens, M. L. (2013). Collisional thermalization of hydrogen and helium in solar-wind plasma. Phys. Rev. Lett. 111, 241101. doi:10.1103/physrevlett.111.241101

PubMed Abstract | CrossRef Full Text | Google Scholar

Maruca, B. A., Kasper, J. C., and Bale, S. D. (2011). What are the relative roles of heating and cooling in generating solar wind temperature anisotropies? Phys. Rev. Lett. 107, 201101. doi:10.1103/PhysRevLett.107.201101

PubMed Abstract | CrossRef Full Text | Google Scholar

Maruca, B. A., Qudsi, R. A., Alterman, B. L., Walsh, B. M., Korreck, K. E., Verscharen, D., et al. (2023). VizieR online data catalog: trans-heliospheric survey. Radial trends (Maruca+, 2023). USA: VizieR Online Data Catalog. J/A+A/675/A196.

Google Scholar

McComas, D. J., Alexander, N., Angold, N., Bale, S., Beebe, C., Birdwell, B., et al. (2014). Integrated science investigation of the sun (isis): design of the energetic particle investigation. Space Sci. Rev. 204, 187–256. doi:10.1007/s11214-014-0059-1

CrossRef Full Text | Google Scholar

McManus, M. D., Verniero, J., Bale, S. D., Bowen, T. A., Larson, D. E., Kasper, J. C., et al. (2022). Density and velocity fluctuations of alpha particles in magnetic switchbacks. Astrophysical J. 933, 43. doi:10.3847/1538-4357/ac6ba3

CrossRef Full Text | Google Scholar

Mostafavi, P., Allen, R. C., McManus, M. D., Ho, G. C., Raouafi, N. E., Larson, D. E., et al. (2022). Alpha–proton differential flow of the young solar wind: parker solar probe observations. Astrophysical J. Lett. 926, L38. doi:10.3847/2041-8213/ac51e1

CrossRef Full Text | Google Scholar

Neugebauer, M. (1976). The role of coulomb collisions in limiting differential flow and temperature differences in the solar wind. J. Geophys. Res. 81, 78–82. doi:10.1029/JA081i001p00078

CrossRef Full Text | Google Scholar

Neugebauer, M. M., and Feldman, W. C. (1979). Relation between superheating and superacceleration of helium in the solar wind. Sol. Phys. 63, 201–205. doi:10.1007/bf00155710

CrossRef Full Text | Google Scholar

Ogilvie, K. W., Chornay, D. J., Fritzenreiter, R. J., Hunsaker, F., Keller, J., Lobell, J., et al. (1995). Swe, a comprehensive plasma instrument for the wind spacecraft. Space Sci. Rev. 71, 55–77. doi:10.1007/bf00751326

CrossRef Full Text | Google Scholar

PlasmaPy, C. (2021). Plasmapy. version 0.6.0 Zenodo.

Google Scholar

Richardson, A. S. (2019). NRL plasma formulary. Washington, DC: Naval Research Laboratory.

Google Scholar

Schmelz, J. T., Reames, D. V., von Steiger, R., and Basu, S. (2012). Composition of the solar corona, solar wind and solar energetic particles. Astrophysical J. 755, 33. doi:10.1088/0004-637x/755/1/33

CrossRef Full Text | Google Scholar

Spitzer, L. (1962). Physics of fully ionized gases. China: Interscience Publishers.

Google Scholar

Tracy, P. J., Kasper, J. C., Zurbuchen, T. H., Raines, J. M., Shearer, P., and Gilbert, J. (2015). Thermalization of heavy ions in the solar wind. Astrophysical J. 812, 170. doi:10.1088/0004-637x/812/2/170

CrossRef Full Text | Google Scholar

Verscharen, D., Klein, K. G., and Maruca, B. A. (2019). The multi-scale nature of the solar wind. Living Rev. Sol. Phys. 16, 5. doi:10.1007/s41116-019-0021-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilson, I., Lynn, B., Brosius, A. L., Gopalswamy, N., Nieves-Chinchilla, T., Szabo, A., et al. (2021). A quarter century of wind spacecraft discoveries. Rev. Geophys. 59, e2020RG000714. doi:10.1029/2020RG000714

CrossRef Full Text | Google Scholar