T. E. Moore
J. L. Burch
D. E. Wendel2- 13rd Rock Research, Annapolis, MD, United States
- 2NASA Goddard SFC, Greenbelt, MD, United States
- 3Southwest Research Institute, San Antonio, TX, United States
A recently published analysis of current sheets has updated the classic Harris 1D static solution by considering multiple classes of charged particle trajectories in a generalized and dynamic current sheet. It uses a 1D PIC simulation to describe dynamic pinching and bifurcation of the current sheet. These 1D results strongly suggest that properties of the inflowing plasma, including the plasma beta, have an important effect on the equilibrium thickness of the pinched current sheet. Since 1D studies cannot describe magnetic reconnection, the time appears right to carry such 1D studies over to 2D or 3D simulations to explore current sheet thickness effects on reconnection. The Magnetospheric Multiscale Mission (MMS), with its well-resolved multipoint measurements of collisionless plasma and fields, has found that collisionless reconnection is accompanied by non-adiabatic motions of electrons that only occur in magnetic structures with a narrow scale comparable to electron inertial lengths (de). The recent 1D studies suggest that a plasma pinch to such scales may only occur for inflowing magnetized plasmas with relatively low plasma beta. We conclude that a parametric exploration of simulated and observed reconnection inflow conditions, particularly plasma beta, should shed light on the enablement of reconnection in collisionless plasmas.
Introduction
Magnetic reconnection is the focus of the Magnetospheric Multiscale Mission (MMS), launched in March 2015 to investigate a process that had been invoked and identified for decades as an important factor in the storage and release of energy in the solar atmosphere and the magnetospheres of planets (Burch et al., 2016). The design of the mission was driven by a belief, based on theoretical efforts, that phenomena on the smallest scales (electron gyro radius and inertial length or skin depth) are crucial to a full understanding collisionless reconnection.
The capabilities of MMS have revealed a cornucopia of small scale phenomena that provide a comprehensive view of the reconnection process in the electron diffusion region where a strong electric field produces the plasma and magnetic flux transport of reconnection (Burch and Phan, 2016). The reconnection process was revealed to be nearly laminar on the smallest scales, in accord with the generalized Ohm’s Law (GOL), without predominant effects corresponding to (Torbert et al., 2018), We adopt the Torbert et al. nomenclature for “laminar” reconnection to distinguish it from reconnection supported by turbulent or anomalous dissipation processes.
This is not to say that fluctuations and turbulence play no important roles in reconnection. Turbulence disrupts laminar current sheets and provides effective collisions and anomalous dissipation in some cases (e.g., Li et al., 2023). However, the dominant factor may often be the tight curvature of the magnetic field in thin current sheets, leading to non-adiabatic motions that enable dissipation “without collisions or noise” (Speiser, 1970). The main point here is that kinetic scale current sheets cannot be regarded as a “given” in space plasmas, and the factors that control current sheet thickness must be relevant to laminar reconnection.
Current sheet thickness is influenced by the phenomenon known as the plasma current pinch effect (Yamada, 2010). Electrical currents self-attract such that tubes of current, if carried by insufficiently strong structures, will collapse those structures. Magnetized plasma systems, like a solar arcade or a magnetosphere, undergo spontaneous dynamical episodes like substorms, involving the onset and-or termination of magnetic reconnection. Reconnection is enabled by dissipative terms of the generalized Ohm’s Law, which in turn are enabled by fluid dynamics, as influenced by forces that compress current sheets to kinetic scales against the pressure of the ambient plasma.
Discussions of magnetotail phenomena, notably substorms, have long invoked variations of the thickness of the cross tail current sheet, which thins, reconnects, and then thickens cyclically. On the other hand, reconnection is observed to be steadier on the dayside magnetopause, albeit subject to relocation in response to the interplanetary magnetic field orientation (Moore et al., 2002; Trattner et al., 2017). The arrival of magnetized plasma at the Earth must in general form a current sheet separating the Earth’s field from the cloud’s magnetic field. A relatively static current sheet must then form, but of what thickness?
Harris current sheet thickness
The classical kinetic description of steady current sheets (Harris, 1962) yields a stable sheet when pressure balance is reached, that is when the peak plasma pressure at the center of the current sheet balances the external magnetic field pressure. The local plasma beta at the sheet center, where the magnetic field vanishes as it reverses (in 1D), is then infinite, but the ratio of this peak plasma pressure to external field pressure is unity in equilibrium. For reasons that will become apparent, we refer to this ratio as the “peak plasma beta” or just the “peak beta.”
The thickness of the Harris sheet ranges up to c/VD times the plasma Debye length (Harris, 1962, Eq. 25), where VD is the magnetization drift speed. If VD in the pressure gradient rises to electron thermal speeds, the Harris current sheet thickness thins to the electron inertial scale or skin depth (de = c/ωpi). Conversely, lower VD implies a current sheet thickness larger than the inertial scale. The magnetization drift speed is determined by the steepness of the pressure gradient and the magnitude of the magnetic field, while the electron thermal speed is an independent parameter. This suggests that low exterior plasma beta and thermal speed give an equilibrium with a thin, kinetic scale current sheet.
The simple Harris model of the static current sheet thus suggests that current sheets that form in disequilibrium will then pinch or thin to an equilibrium that may or may not be sufficiently thin to enable laminar reconnection, depending on the prevailing plasma conditions under which the sheet current forms. A relevant finding (Tageshika et al., 2015) argues that low beta current sheets collapse and increase the “peak beta” (ratio of plasma to external field pressure) as they do so. Similarly, Artemyev (2007) found that current sheets in low beta plasmas collapse at a constant total current until Lcs∼de, and a dissipative reconnection electric field then appears.
Yoon current sheet dynamics
Yoon et al. (2021) studied the formation and dynamic evolution of 1D current sheets under the action of the pinch effect, with a focus on their evolution into bifurcated diamagnetic reconnecting current sheets. Based on their analysis, they suggested that:
“… an initially thick, under-heated current sheet equilibrates to a thin, sub-skin depth bifurcated structure, which then undergoes collisionless reconnection… the equilibrium presented here [seems more likely] than widely-used specific solutions such as the Harris sheet.”
Yoon et al. should be credited with having evolved and improved on the Harris current sheet model by considering the more complex non-adiabatic motions of particles in such current sheets, bringing to bear the work of Speiser (1965, 1970). Apart from their focus on the bifurcation of thin current sheets, they have also opened a path to studies that are needed to better understand where and when collisionless reconnection will be active or inactive in a given magnetized plasma situation. We briefly recap their results below:
They used the Harris solution as a guide, noting that, to be an equilibrium solution of the stationary Vlasov kinetic plasma, the drifting Maxwellian formulation must satisfy two important conditions:
1. The peak plasma pressure must equal the external magnetic field pressure (peak beta = 1)
2. The sheet thickness must equal the Debye length times a factor of c/VD, where VD is the Maxwellian magnetization drift speed
In general, multiple classes of particle orbits take place in a current sheet, depending on its thickness, electric potential structure, and the presence of a guide field. These include non-crossing and crossing double-well potential orbits, partial crossing orbits and meandering orbits that are free of the potential influence. The relative population of the different orbit types is determined by the drift and thermal velocities of particles injected into the sheet, which may or may not satisfy the Harris equilibrium conditions above.
If a set of particles is inserted that is too cold or low beta to satisfy the Harris equilibrium [“under-heated” per Yoon et al. (2021) terminology], a linearized time-dependent Vlasov analysis performed by Yoon et al. (2021), in their Eqs 3, 4, shows that the sheet particles are brought closer to the centre of the sheet and accelerated or heated. This was then simulated in full kinetic detail with consideration of all particle trajectory classes. These results were illustrated in Figure 4 of Yoon et al. (2021), which is reproduced here as Figure 1. The simulation started with a plasma temperature 0.2 of the Harris equilibrium temperature, and the initial thickness was 10di. The sheet was found to pinch and heat up for 30 ion cyclotron periods, after which it settled at an equilibrium thickness of about 10de. During this simulation, the particles were found to develop non-Maxwellian and agyrotropic features reflecting the evolution into different classes of orbit as the sheet pinched.
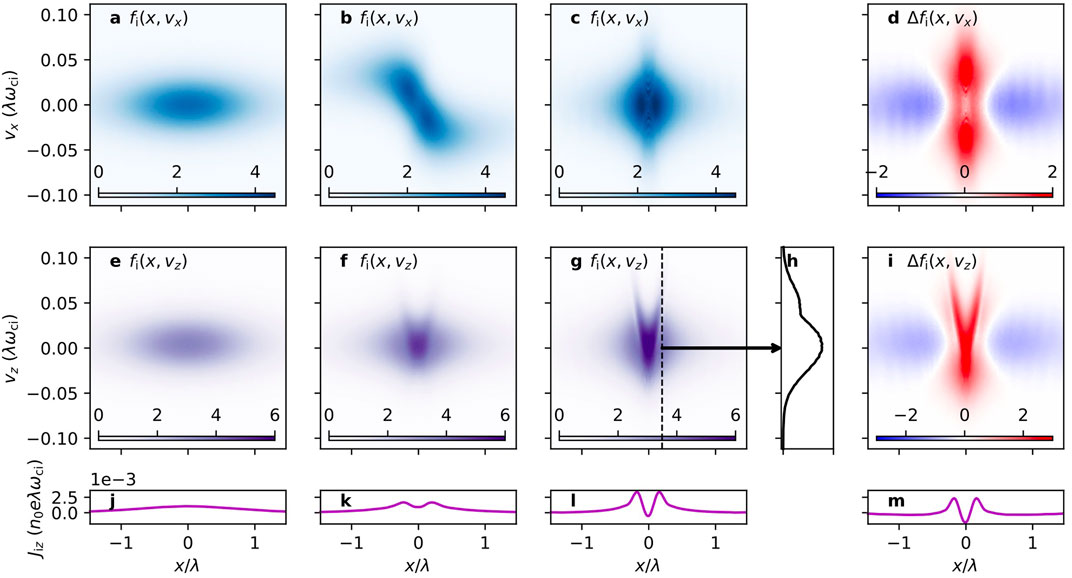
FIGURE 1. Evolution of particle velocity distributions and current density from an initial MHD scale with Maxwellian particles, to a bifurcated electron scale structure with non-Maxwellian features, in tens of ion cyclotron periods. Ion velocity distribution fi(x-vx) and fi(x-vz) space at (A) t = 0 𝛚pi−1, (B) t = 10 𝛚pi−1, and (C) t = 100 𝛚pi−1. Difference (D) between fi at t = 0 𝛚pi−1 and t = 100 𝛚pi−1. (H) is a slice along dotted line in (G). (J–L) are the current density jiz, from (E–G). (M) is the difference between (J,L). [after Yoon et al (2021)].
The final sheet was compared with observations from MMS of 17 June 2017 (Wang et al., 2018):
“The half-width of the simulated sheet pinches down to ∼0.1λ = 1di = 10de (because mi/me = 100 was used in the simulation).… The simulated sheet and the observed sheet are thus similar in that their widths are ∼10de and ≲1di, so their sheet dynamics are mainly controlled by electrons.”
Some differences from the MMS observations were explained as the result of reconnection observed in the MMS case, whereas reconnection could not happen in the simulated current sheet, since it was one dimensional. There was also substantial discussion of the simulated bifurcation of the pinched electron scale current sheet, which has also been observed in a number of cited direct space observations of both reconnecting and non-reconnecting current sheets. Overall, the simulations reflected closely the scenario quoted at the beginning this section, in which an initially thick current sheet thins to an equilibrium that was thin enough for collisionless reconnection to proceed, as observed by MMS.
Relevance to reconnection
As illustrated schematically in Figure 2, the Yoon et al. (2021) results suggest that current sheets often form out of equilibrium at MHD scales and then undergo a pinch until they reach the Harris-like equilibrium of external field and internal plasma pressure balance, but with non-Maxwellian velocity distributions. The final scale is determined by the amount of thinning required to raise the peak beta to unity. The lower the initial plasma beta, the more thinning must occur for this to be achieved. If the initial plasma beta is too high, peak beta of unity will be achieved at scales exceeding kinetic scales, potentially suppressing reconnection, or requiring that anomalous dissipative processes develop to enable it.
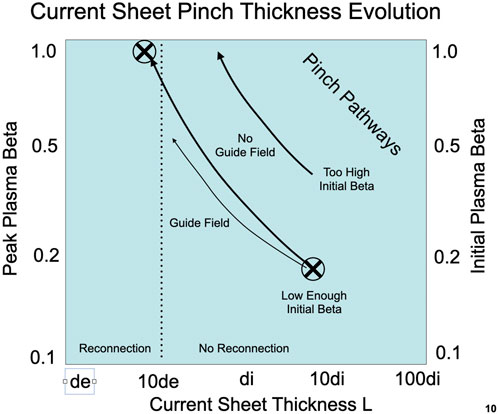
FIGURE 2. Schematic extension of the current sheet study of Yoon et al.9 illustrating pinch effect pathways during thinning and heating of MHD current sheets to kinetic scales, enabling reconnection for paths that reach thicknesses approaching de, and not for paths that terminate, that is, reach peak plasma beta of unity, at greater thickness. Points marked with circled X are those of the Yoon et al. (2021) study.
As also illustrated by Figure 2, it seems reasonable to suggest that laminar reconnection may not occur unless the inflowing plasma beta is sufficiently low to produce pinch thinning that eventually approaches the kinetic scale de. Conversely, a reconnecting sheet in which the peak beta were to be pushed higher than unity would subsequently thicken and potentially disable reconnection. This could give rise to interesting dynamic variations of reconnection in response to inflow conditions.
It would seem to be of great interest to explore the development of current sheets along the lines of the Yoon et al. (2021) study, in 1D, over a broad grid space of initial current sheet and boundary plasma conditions, to determine quantitatively what parameter space of initial and boundary conditions lead to thinning to kinetic scales. If the results confirm the suggested relevance to reconnection, 2D and 3D simulations capable of producing reconnection would then need to be explored over the same parameter space grid to confirm this relevance and determine how the operation of reconnection itself influences the results.
It would also be of great interest to explore how multi-dimensional, reconnecting current sheets react when the inflow conditions vary, using suitable simulations. Presumably, conditions that would not support sufficient thinning and activation of laminar reconnection would cause reconnection to be disabled or to require anomalous dissipation by thickening the current sheet to a new equilibrium. Overshoots and oscillations around equilibrium were not seen by Yoon et al. in their 1D 2021 study, but might appear in more realistic 3D simulations. It is tempting to speculate about magnetospheric circulation of higher and lower pressure plasma populations originating from different sources, and how they might interact with reconnection, but that should be reserved for study using global circulation models with multiple fluids from solar and ionospheric sources, as well as embedded, multi-dimensional kinetic descriptions able to reflect the pinch dynamics of current sheet thickness.
Yoon et al. (2023) have published new results that bear on the application to component or guide field cases. The role of a guide field is considered using the same tools as those described above. A guide field gives rise to the possibility of a mixed Harris and “force-free” equilibrium, in which the plasma pressure and peak plasma beta need not be raised as much by the pinch effect to reach a mixed equilibrium. That leads to less thinning of an initial MHD scale current sheet. Basically, less magnetic field shear means a smaller relevant reconnecting component of the magnetic field, which leads to a smaller amount of thinning. To force a guide field current sheet to reach kinetic scales and reconnect will apparently require lower initial beta plasma than for an antiparallel sheet, as alluded to in Figure 2. This should of course be explored in full multi-dimensional simulations of spontaneous laminar reconnection.
Future needs
The activation or disablement of reconnection (or more generally, the modulation of reconnection rate) is now known to be a fundamental control of energy release and transport in all of Heliophysics. We suggest that the knowledge gained from MMS, used in conjunction with multi-dimensional simulation tools (Hesse et al., 2016; Ji et al., 2022), could more fully explore current sheet formation and evolution and elucidate the as-yet unsolved problem of what boundary conditions produce, accelerate, or disable spontaneous laminar reconnection, leading to large scale system dynamics in reconnecting magnetized plasma situations.
We suggest a program of multidimensional simulations of collisionless reconnection including some or all elements of the following:
1. Uniform unstructured boundary conditions varying across a grid of initial thicknesses (from 1 to 10 di or greater as available computational resources permit) and plasma beta (from perhaps 0.01–1).
2. Avoidance of features known to forcibly drive laminar reconnection.
3. Search for boundary conditions where laminar reconnection is spontaneous.
4. Search for boundary conditions that disable reconnection spontaneity.
5. Separately investigate perturbations that initiate or disable ongoing laminar reconnection.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
TM: Conceptualization, Formal Analysis, Funding acquisition, Visualization, Writing–original draft, Writing–review and editing. JB: Formal Analysis, Funding acquisition, Investigation, Methodology, Resources, Writing–review and editing. DW: Formal Analysis, Investigation, Methodology, Writing–review and editing.
Funding
The authors declare financial support was received for the research, authorship, and/or publication of this article from the NASA Magnetospheric Multiscale Mission Project and Science Team under Contract #80GSFC17C003. Magnetospheric Multiscale Mission Project and Science Team.
Acknowledgments
The authors benefitted from enlightening discussions with Li-Jen Chen, Jan Egedahl, Michael Hesse, Yi-shin Liu, Mikhail Sitnov, Masaaki Yamada and Young Yoon. Figure 1 was reproduced under open access to Nature Communications.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Artemyev, A. R. (2008). Evolution of a Harris current sheet in an electric field. Mosc. Univ. Phys. Bull. 63 (3), 193–196. doi:10.3103/s0027134908030089
Burch, J. L., Moore, T. E., Torbert, R. B., and Giles, B. L. (2016). Magnetospheric multiscale overview and science objectives. Space Sci. Rev. 199, 5–21. doi:10.1007/s11214-015-0164-9
Burch, J. L., and Phan, T. D. (2016). Magnetic reconnection at the dayside magnetopause: advances with MMS. Geophys. Res. Lett. 43, 8327–8338. doi:10.1002/2016GL069787
Harris, E. (1962). On a plasma sheath separating regions of oppositely directed magnetic field. Nuovo Cimento 23, 115–121. doi:10.1007/bf02733547
Hesse, M., Aunai, N., Birn, J., Cassak, P., Denton, R. E., Drake, J. F., et al. (2016). Theory and modeling for the magnetospheric multiscale mission. Space Sci. Rev. 199, 577–630. doi:10.1007/s11214-014-0078-y
Ji, H., Daughton, W., Jara-Almonte, J., Stanier, A., and Yoo, J. (2022). Magnetic reconnection in the era of exascale computing and multiscale experiments. Nat. Rev. Phys. 4, 263–282. doi:10.1038/s42254-021-00419-x
Moore, T. E., Fok, M.-C., and Chandler, M. O. (2002). The dayside reconnection X line. J. Geophys. Res. 107 (A10), 1332. doi:10.1029/2002JA009381
Speiser, T. W. (1965). Particle trajectories in model current sheets: 1. Analytical solutions. J. Geophys. Res. 70, 4219–4226. doi:10.1029/JZ070i017p04219
Speiser, T. W. (1970). Conductivity without collisions or noise. Planet. Space Sci. 18 (4), 613–622. doi:10.1016/0032-0633(70)90136-4
Takeshige, S., Takasao, S., and Shibata, K. (2015). A theoretical model of a thinning current sheet in the low β plasmas. Astrophysical J. 807 (9pp), 159. doi:10.1088/0004-637X/807/2/159
Torbert, R. B., Phan, T. D., Hesse, M., Argall, M. R., Shuster, J., Ergun, R. E., et al. (2018). Electron-scale dynamics of the diffusion region during symmetric magnetic reconnection in space. SCIENCE 362 (6421), 1391–1395. doi:10.1126/science.aat2998
Trattner, K. J., Burch, J. L., Ergun, R., Eriksson, S., Fuselier, S. A., Giles, B. L., et al. (2017). The MMS dayside magnetic reconnection locations during phase 1 and their relation to the predictions of the maximum magnetic shear model. J. Geophys. Res. Space Phys. 122 (11), 991–1012. doi:10.1002/2017JA024488
Wang, R., Lu, Q., Lu, S., Russell, C. T., Burch, J. L., Gershman, D. J., et al. (2020). Physical implication of two types of reconnection electron diffusion regions with and without ion-coupling in the magnetotail current sheet. Geophys. Res. Lett. 47, e2020GL088761. doi:10.1029/2020GL088761
Yoon, Y. D., Wendel, D. E., and Yun, G. S. (2023). Equilibrium selection via current sheet relaxation and guide field amplification. Nat. Commun. 14, 139. doi:10.1038/s41467-023-35821-9
Keywords: reconnection, pinch, current sheet, beta, thinning
Citation: Moore TE, Burch JL and Wendel DE (2023) Reconnection in a pinch. Front. Astron. Space Sci. 10:1283185. doi: 10.3389/fspas.2023.1283185
Received: 25 August 2023; Accepted: 15 November 2023;
Published: 27 November 2023.
Edited by:
Joseph E. Borovsky, Space Science Institute (SSI), United StatesReviewed by:
Xiaocan Li, Dartmouth College, United StatesRongsheng Wang, University of Science and Technology of China, China
Copyright © 2023 Moore, Burch and Wendel. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: T. E. Moore, thomem@iiirdrock.net