Ion kinetic effects linked to magnetic field discontinuities in the slow Alfvénic wind observed by Solar Orbiter in the inner heliosphere

Slow solar wind, sharing magnetic and plasma properties typical of fast wind, the so-called slow Alfvénic wind, has been widely observed in the heliosphere. Here, we report an analysis of the turbulent properties of a slow Alfvénic stream observed by Solar Orbiter at 0.64 AU. This solar wind stream is characterized by well distinguishable regions, namely, a main portion, an intermediate region, and a rarefaction region. Each of those intervals have been studied separately, in order to enhance similarities and differences in their turbulence properties. Coherent structures naturally emerge over different time/spatial scales and their characteristics at ion scales have been investigated. The presence of these intermittent events have been found to be closely related to kinetic features in the ion (both proton and alpha particles) velocity distribution functions, suggesting a fundamental role in the kinetic physical processes that mediate the sub-ion turbulence cascade.

1 Introduction

Turbulence is ubiquitous in ordinary and magnetized fluids. It is characterized by a complex cross-scale coupling of the relevant fields, which induces their energy contained at large-scales to cascade all the way down to small scales. In particular, in collisionless plasmas, small scales are mediated by kinetic processes, where particles interact with electromagnetic fluctuations, giving rise to non-thermal features in the particle velocity distribution functions (VDFs), which appear as distortions and deviations from thermodynamic equilibrium (Marsch et al., 1982a; b). However, how turbulence interacts with particles remains one of the major unsolved problems in plasma physics, with strong implications for space (Bruno and Carbone, 2016; Verscharen et al., 2019), astrophysical (Webb et al., 2018; Verscharen et al., 2021), and laboratory plasmas (White et al., 2019). Since many of these plasmas can be described as turbulent collision-free systems, the heating process related to the irreversible degradation of information due to collisions, is missing (Pezzi et al., 2019; Matthaeus et al., 2020).

The heliosphere represents the best natural laboratory to study plasma turbulence, thanks to in-situ spacecraft measurements. This environment can be described as almost collisionless, magnetized, and quasi-neutral, and can represent a sample for plasma processes that occur also in distant astrophysical plasmas, such as the interstellar medium, plasma in astrophysical jets, or the intra-cluster medium. One example of heliospheric plasmas is the solar wind, a continuous, but highly variable, weakly collisional plasma flow originating at the Sun, which travels at high speed and interacts with the environment of the planets. The solar wind is in a state of fully developed turbulence and is dominated by a broad variety of processes, such as shocks, waves, coherent structures, magnetic reconnection, and particle acceleration (Marsch, 2006; Bruno and Carbone, 2013). This general picture of astrophysical turbulence becomes more complicated because of the multi-component nature of the solar wind. Although protons represent the main solar wind component, it is also made of a finite amount of doubled ionized helium (alpha particles), together with a few percentages of heavier ions, which are observed to be preferentially heated (Marsch et al., 1982a; Marsch et al., 1982b; Kasper et al., 2008).

Turbulent fluctuations of the fields in the solar wind are not homogeneous but are highly space-localized. The degree of non-homogeneity increases as the spatial/time scales decrease. This aspect of the solar wind turbulence is called intermittency and it is due to the emergence of coherent structures towards small scales, which can be described as strong discontinuities in the magnetic field (Retinò et al., 2007; Perri et al., 2012; Greco and Perri, 2014; Perrone et al., 2016; Perrone et al., 2017; Perrone et al., 2020; Perrone et al., 2022) over a broad range of scales (Greco et al., 2016; Lion et al., 2016). Both in-situ observations and numerical experiments have shown that coherent structures are strongly related to the presence of kinetic effects, such as particle energization, temperature anisotropy, and deviation from Maxwellian VDF (Matteini et al., 2010; Osman et al., 2010; Greco et al., 2012; Servidio et al., 2012; Servidio et al., 2015; Servidio et al., 2017; Perrone et al., 2013; Perrone et al., 2014; Wu et al., 2013; Pezzi et al., 2018; Sorriso-Valvo et al., 2018). Understanding the physical mechanisms that generate coherent structures and how these structures contribute to dissipation in collisionless plasma fits into the general problem of solar wind heating.

The bimodal structure of the solar-wind speed distribution (McGregor et al., 2011), characterized at 1 AU by two distinct peaks rather than a smooth transition, indicates that the solar wind can be described by two different types of plasma, namely, slow (∼400 km/s) and fast (∼800 km/s) solar wind, whose characteristics are strongly related to their source regions on the Sun. However, even if the standard classification between fast and slow solar wind is widely accepted, it cannot always explain the observations. Indeed, it is not rare to observe slow wind streams that, apart from the speed, have almost the same characteristics of the fast wind, mainly high degree of correlations between velocity and magnetic field components and low compressibility (i.e., Alfvénicity). This kind of wind, which is statistically relevant, is called slow Alfvénic wind (see D’Amicis et al., 2021b, for a review on this topic) and, recently, it has mostly been observed in the inner heliosphere by the new solar missions Parker Solar Probe (Fox et al., 2016) and Solar Orbiter (Müller et al., 2020).The first observation of a slow Alfvénic interval by Parker Solar Probe was during its first perihelion passage at about 0.17 AU from the Sun. This stream originated from a small equatorial coronal hole (Bale et al., 2019; Badman et al., 2020) and it was characterized by the presence of isolated intermittent velocity enhancements (Kasper et al., 2019; Horbury et al., 2020a) associated with magnetic field deflections, namely, switchbacks (Bale et al., 2019; Dudok de Wit et al., 2020). Then, Parker Solar Probe observed several intervals of slow Alfvénic wind during its initial encounters (see, e.g., Woolley et al., 2021). On the other hand, Solar Orbiter also measured in detail several intervals of slow Alfvénic wind in the inner heliosphere. In particular, the first observation occurred in July 2020 at a heliocentric distance of 0.64 AU (D’Amicis et al., 2021a), when Solar Orbiter was still in its cruise phase. The source region of this stream was identified in a coronal pseudostreamer configuration, whose topology allows the formation and development of twin filament channels (Panasenco et al., 2019), related to an anomalous expansion rate. The speed profile of this interval is very similar to the one typical of the fast wind, consisting in well-defined plasma regions, namely, a compression region (but in this case it is partially missing), a main portion of the stream and a rarefaction region. Moreover, here, another region between the main portion and the rarefaction region has been identified, which is characterized by a spaghetti-like flux-tube texture of the magnetic field with the presence of several large-scale structures (D’Amicis et al., 2021a).

In this paper, we study the nature of the turbulent magnetic fluctuations around proton scales in the interval of slow Alfvénic wind observed by Solar Orbiter in July 2020 (D’Amicis et al., 2021a). In particular, we focus on a 1 h interval of very high Alfvénicity in each well-defined plasma region identified and we statistically investigate the observed coherent structures. Finally, we study the link between coherent events and kinetic effects on the proton and alpha particles VDFs. The paper is organized as follows: in Section 2 Solar Orbiter observations of a slow Alfvénic stream are described along with a computation of the relevant plasma parameters; in Section 3 turbulence properties are studied in the three regions forming the data set; in Section 4 an analysis on the ion scale coherent magnetic structures is presented and the role played by such structures in the kinetic processes is also investigated and discussed; Section 5 shows our conclusions.

2 Alfvénic slow wind interval

In July 2020 Solar Orbiter was embedded in a slow Alfvénic solar wind stream at a radial distance of about 0.64 AU (D’Amicis et al., 2021a). In this paper, we consider three 1 h periods characterized by a very high value of the v-b correlation coefficient, namely,

${\rho }_{vb}=\frac{{\mathrm{\Sigma }}_j\left(V_j-\bar{V}\right)\left(B_j-\bar{B}\right)}{\sqrt{{\mathrm{\Sigma }}_j{\left(V_j-\bar{V}\right)}^2{\left(B_j-\bar{B}\right)}^2}}\simeq -1(1)$

between July 15th and July 18th, where V_j and B_j are the velocity and magnetic field single measurements and $\bar{V}$ and $\bar{B}$ are the velocity and magnetic field averages in a 30 min window (D’Amicis et al., 2021a). In order to fully characterize the turbulence and the related kinetic effects on particles, we focus on the full cadence measurements available for the magnetic field vector (64 Hz) from the fluxgate magnetometer MAG (Horbury et al., 2020b) and reprocessed ion data, sampled at 4 s resolution from the Proton and Alpha particle sensor (PAS) of the Solar Wind Analyser (SWA) suite (Owen et al., 2020). For the latter, an innovative method, based on the statistical technique of clustering, has been applied directly to the full three-dimensional VDFs measured by PAS to separate the proton core, the proton beam, and the alpha particles, and derive their moments (see De Marco et al., 2023, for all the details on the method and validation of the results).

2.1 Interval characterization

Figure 1 shows the plasma properties of the 1 h Alfvénic intervals in the main portion on July 15th (left column), intermediate region on July 16th (middle column), and rarefaction region on July 17th (right column) of the slow Alfvénic wind observed by Solar Orbiter (D’Amicis et al., 2021a). Each column, from top to bottom, displays: the three components in the radial tangential normal (RTN) reference frame (radial in blue, tangential in red, and normal in green) and magnitude (in black) of the magnetic field (panels a–c), and of the velocity field for the proton core, V_c (panels d–f); the cosine of the angle between B and V_c, cos θ_BV (panels g–i); the density for the proton core in green, n_c, proton beam in orange, n_b, and for alpha particles in violet, n_α (panels j–l); and the temperature for the proton core in green, T_c, proton beam in orange, T_b, and for alpha particles in violet, T_α (panels m–o). For an easy comparison, in the latter plots, the alpha particle temperature has been divided by 4. Typical solar wind parameters, averaged within these intervals, can be found inTable 1.

FIGURE 1

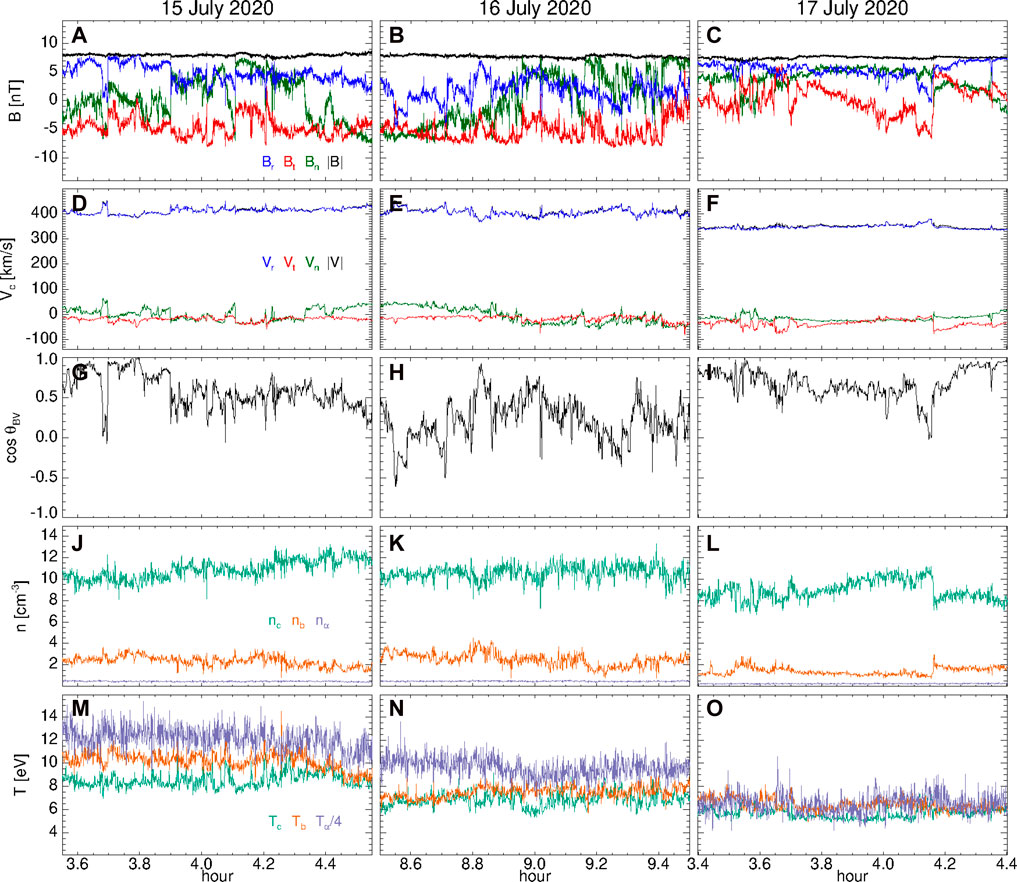
FIGURE 1. Characteristics of 1 h high-Alfvénic intervals in the main portion on July 15th (left column), intermediate region on July 16th (middle column), and rarefaction region on July 17th (right column) of the slow Alfvénic wind observed by Solar Orbiter in 2020. From top to bottom: components in RTN (radial in blue, tangential in red, and normal in green) and magnitude (in black) of the magnetic field vector (A–C); components in RTN and magnitude of the velocity field vector (for the proton core) with the same color legend used for the magnetic field in the first row (D–F); cosine of the angle between the velocity (of the proton core) and magnetic field vectors (G–I); density for the proton core (green) and beam (orange), and for alpha particles (violet) (J–L); and temperature for the proton core (green) and beam (orange), and for alpha particles (violet) (M–O). The alpha particle temperature has been divided by 4 to be easily compared with the proton temperature.

TABLE 1

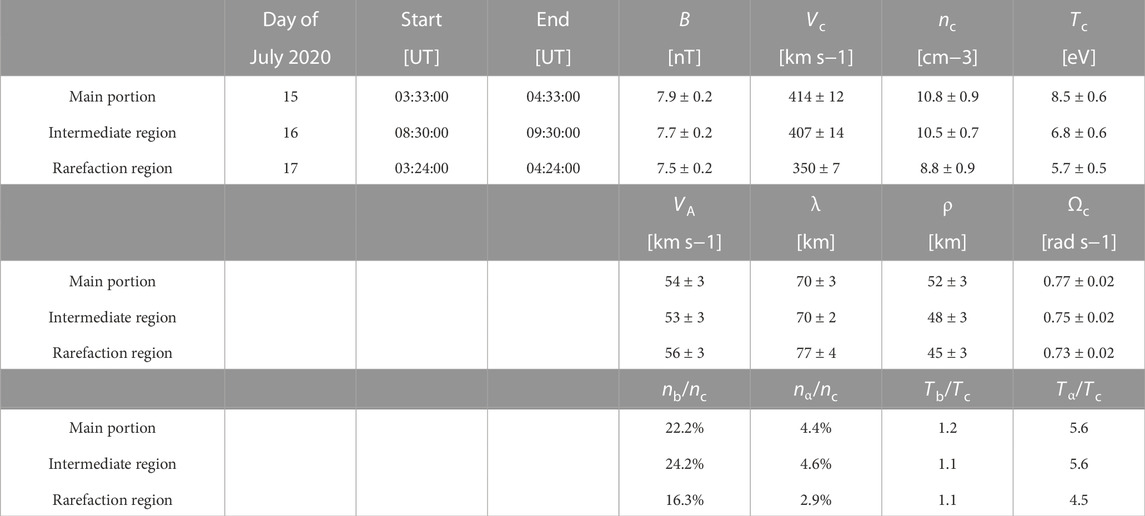
TABLE 1. Solar wind parameters averaged within each 1 h selected period in the slow Alfvénic interval observed by Solar Orbiter at 0.64 AU. We also report the Alfvén speed V_A, the proton inertial length λ, the proton Larmor radius ρ, and the proton cyclotron frequency Ω_c. Only the proton core has been considered for plasma parameters, but ratios between other populations, namely, proton beam and alpha particles, and proton core are given. The errors refer to the standard deviation evaluated in each period.

Each selected 1 h period shows a decrease of speed, as expected since from July 15th to July 17th Solar Orbiter moves from the main portion of the stream to the rarefaction region. However, all the intervals have an almost constant, and similar, magnetic field magnitude, even if the behavior of the magnetic components is quite different. Moreover, several deflections of the radial component B_r (blue line), that is switchbacks, are recovered. These structures are associated with local enhancements in the proton speed and with changes in the cos θ_BV as in the case of the strong deflection at about 3.7 h on July 15th. It is worth pointing out that the presence of switchbacks does not influence the results on coherent structures, since we focus on scales much smaller than the switchback typical time scales. Then, panels (g)-(i) show a different behavior for the three periods and give a first indication on the different turbulence sampled by Solar Orbiter. Indeed, the spacecraft looks at a more parallel turbulence in the rarefaction region than in the intermediate one (see cos θ_BV).

The main differences between the three periods can be seen in the plasma quantities, such as density and temperature, by considering separately the different populations that constitute the solar wind plasma. Although the proton core density (and also the total ion density) is similar in both the main portion and the intermediate region, it does not follow the typical anti-correlation with the flow speed (see, e.g., Elliott et al., 2016). However, this anti-correlation is typically expected when the plasma parameters are averaged over larger time windows than the 4s resolution of the particle data used in the present analysis. In our work, we have considered all the timeseries variations within a 1h time window, thus producing a certain lack of stationarity that could influence the relation between the density and speed. On the other hand, higher proton core temperature is found for higher speed as expected (see, e.g., Perrone et al., 2019). Moreover, the percentage of the proton beam and alpha particles, with respect to the proton core, is very similar in the main portion and in the intermediate region but significantly decreases in the rarefaction region. Finally, the temperature ratio between the proton beam and the core is almost the same in the three periods, but not for the alpha particles. Indeed, T_α/T_c is about 5.6 in the main portion and in the intermediate region, but decreases (∼4.5) in the rarefaction region, meaning that in the first two regions alpha particles experience an anomalous heating while in the rarefaction region the two species have almost equal thermal speeds (Kasper et al., 2008).

3 Turbulence and intermittency

Solar wind measurements have revealed that the plasma is in a state of fully developed turbulence (Bruno and Carbone, 2013). The energy, stored in the electromagnetic and velocity fields, is injected at the Sun into the heliosphere and is channeled towards smaller time/spatial scales through a turbulent cascade until it is eventually dissipated. The magnetic power spectrum typically follows a Kolmogorov-like power law in the so-called inertial range, in analogy with ordinary fluids (Kolmogorov, 1941; Frisch, 1995; Tu and Marsch, 1995). At scales close to the characteristic ion lengths, namely, the ion Larmor radius or the ion skin depth, the spectrum becomes steeper (Alexandrova et al., 2013), the ions become unmagnetized, and the plasma dynamics is governed by kinetic features. Indeed, effects such as wave-particle interactions with strong anisotropies in the particle VDFs dominate the plasma dynamics and the fluid, intermediate scale treatment fails.

Panel (a) of Figure 2 shows the total power spectral density (PSD), namely, the trace of the spectral matrix, of the magnetic field for the 1 h periods in the main portion (green), in the intermediate region (orange), and in the rarefaction region (violet). The magnetic fluctuations show an almost similar power level in the three regions, even if the power is lower in the rarefaction region. To characterize the turbulence, the spectral indices γ and δ have been evaluated in the frequency range f ∈ [0.03, 0.15] Hz for the inertial range, and f ∈ [0.4, 1] Hz for the sub-proton range, respectively. Notice that the best fit performed in the high-frequency range is limited to a narrow range of frequencies because of the decrease of the signal-to-noise ratio. The spectral index values are summarized in Table 2. Although in the main portion and in the intermediate region we observe in the inertial range a power law close to the typical Kolmogorov scaling, the spectrum in the rarefaction region is steeper. Indeed, the angle θ_BV indicates that in this period Solar Orbiter is sampling the solar wind mainly parallel to the local magnetic field, suggesting a slope closer to −2 in the inertial range, as predicted by the critical balance theory (Goldreich and Sridhar, 1995; Horbury et al., 2008). However, the observed deviation from −2 (i.e., γ ≃ − 1.89 ± 0.04, in the rarefaction region) can be explained by different reasons, such as a quasi parallel sampling by the spacecraft (Horbury et al., 2008), the applicability of the critical balance theory to strong turbulence, or the presence of intermittency. Another difference between the rarefaction region and the other two periods is related to the position of the spectral break (indicated by stars in Figure 2A), which has been evaluated by fitting a power law decay on either side of the break and finding the intersection of both curves (Perri et al., 2010; Bruno and Trenchi, 2014). Indeed, in the main portion and in the intermediate region the spectral break frequency is around 0.3 Hz, while in the rarefaction region is around 0.2 Hz. These frequencies are closer to the proton cyclotron resonance frequencies (dashed lines), namely, f_R = V_c*f_c/(V_A + Vth_,c) ≃ 0.5 Hz (Bruno and Trenchi, 2014), being f_c the proton gyrofrequency, than the other proton characteristic frequencies, namely, the timescales corresponding to the proton Larmor radius (dot-dot-dot-dashed lines) and to the proton inertia length (dot-dashed lines), which are located at about 1 Hz.

FIGURE 2

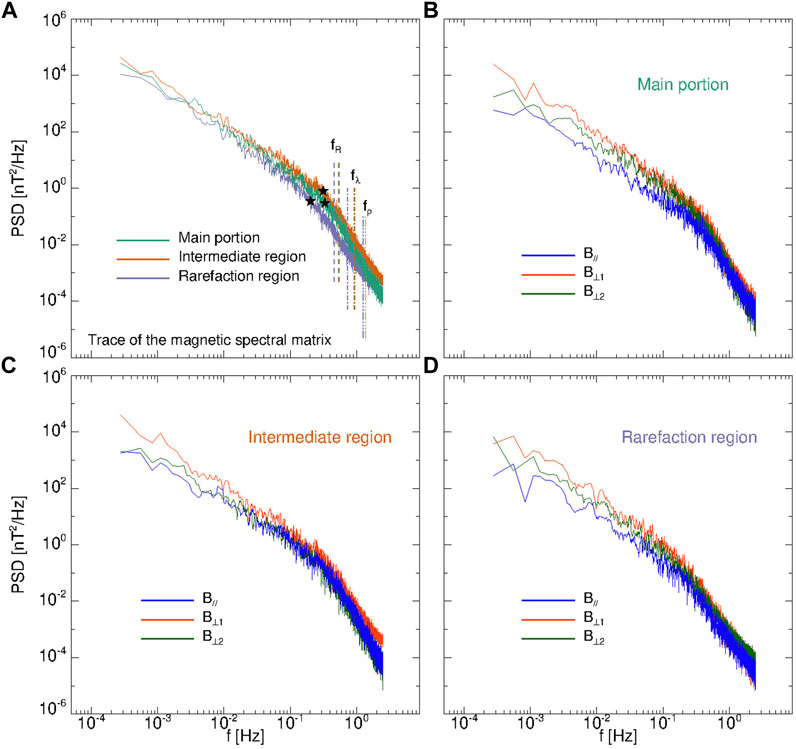
FIGURE 2. Power spectral density (PSD) of the total magnetic field fluctuations (A) for the 1 h intervals in the main portion (green), intermediate region (orange) and rarefaction region (violet). The stars refer to the spectral breaks, while vertical lines refer to the proton characteristic frequencies, namely, the cyclotron resonance frequency, f_R (dashed lines), the frequencies corresponding to the Larmor radius, f_ρ (dot-dot-dot-dashed lines), and to the inertial length, f_λ (dot-dashed lines). PSDs of the components of the magnetic field in the mean magnetic field reference frame (parallel direction in blue) for the main portion (B) intermediate region (C) and rarefaction region (D).

TABLE 2

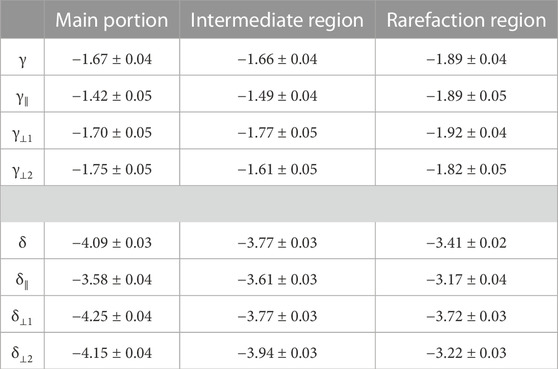
TABLE 2. Spectral indices γ and δ evaluated in the frequency range f ∈[0.03,0.15] Hz for the inertial range and f ∈[0.4,1] Hz for the sub-proton range, respectively, for the turbulent spectra in Figure 2.

To better appreciate the anisotropy of the magnetic field, in panels (b)-(d) we show for each selected interval the PSD of the magnetic field components in the mean field reference frame. Thus, the magnetic field data have been rotated in a reference frame in which the x-axis is aligned with the mean field direction (the average value of B computed over each entire interval), the y-axis is along the V ×B direction, and the z-axis completes the frame. As expected for Alfvénic intervals, in the inertial range the power stored in the fluctuations parallel to the mean field tends to be lower than the power stored in the transverse components (Bruno and Carbone, 2013).

We have also analyzed the degree of intermittency of our samples by computing the kurtosis (Frisch, 1995), namely, the fourth-order moment of the distribution of the magnetic field increments δB (t, τ) = B (t + τ) − B(t) at each time scale τ:

$K_i\left(\tau \right)=\frac{\langle \delta B_i{\left(t,\tau \right)\rangle }_{t_{*}}^4}{{\left(\langle \delta B_i{\left(t,\tau \right)\rangle }_{t_{*}}^2\right)}^2},(2)$

where ${⟨\cdots ⟩}_{t_{*}}$ indicates a time average over a given interval of length t and the index i runs over the magnetic field components. In Figure 3 the kurtosis as a function of the time scale is displayed in log-lin scale, showing for all the three components of B, in the mean magnetic reference frame, a deviation from the Gaussian distribution value of 3 (dashed line) as the time scale reduces. This trend is typical within the inertial range in the solar wind (Marsch and Tu, 1997; Sorriso-Valvo et al., 1999; Bruno and Carbone, 2013). Since the scale broadening of the sub-proton range is very limited in these intervals, owing to the low signal-to-noise ratio at time scales shorter than 1 s, it is not possible to infer a trend of the kurtosis within such a range.

FIGURE 3

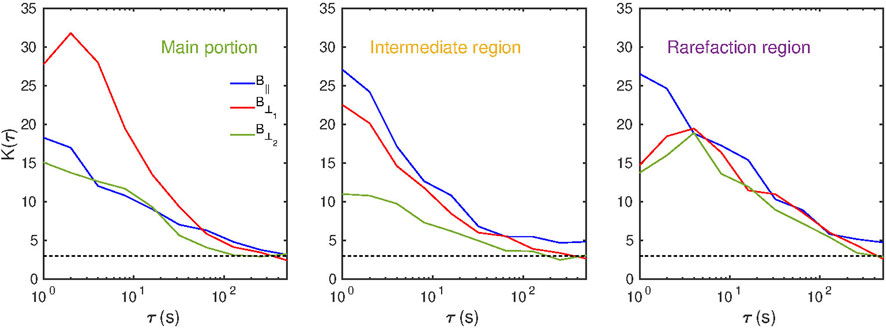
FIGURE 3. Fourth-order moments of the magnetic field fluctuations (kurtosis) as a function of the time scale for the component of B parallel to the mean field direction (blue line) and for the two perpendicular components (red and green lines). The reference value of 3 expected for a Gaussian distribution of magnetic field increments is also shown (dashed line). Each panel refers to the different intervals here analyzed.

4 Coherent events and kinetic effects

Beyond the general information about the global properties of the turbulent activity provided by the magnetic field spectra, here we focus on the details of the turbulence properties and, in particular, we study the distribution in time and frequency of the magnetic field energy by using a local analysis of the fluctuations. Panels (a-c) and (d-f) of Figure 4 show the behaviour of the Local Intermittency Measure (LIM; Farge, 1992) for the parallel and perpendicular magnetic energy, respectively. The LIM is defined as the energy of magnetic fluctuations, as a function of time (t) and timescales (τ), normalized at each time point by a mean spectrum over the whole time interval, namely,

$I_{\Vert ,\perp }\left(\tau ,t\right)=\frac{|{\mathcal{W}}_{\Vert ,\perp }\left(\tau ,t\right){|}^2}{{⟨|{\mathcal{W}}_{\Vert ,\perp }\left(\tau ,t\right){|}^2⟩}_t},(3)$

where the brackets indicate a time average while $|{\mathcal{W}}_{\Vert ,\perp }(\tau ,t){|}^2$ the energy for parallel and perpendicular magnetic field fluctuations. In particular, $|{\mathcal{W}}_{\Vert }(\tau ,t){|}^2=|{\mathcal{W}}_{|B|}(\tau ,t){|}^2$ since the variations of the magnetic field magnitude can be used as a proxy of the parallel (compressive) fluctuations (Perrone et al., 2016), while the energy of the perpendicular (Alfvénic) fluctuations is defined as $|{\mathcal{W}}_{\perp }(\tau ,t){|}^2=|{\mathcal{W}}_{\mathbf{B}}(\tau ,t){|}^2-|{\mathcal{W}}_{\Vert }(\tau ,t){|}^2$, where $|{\mathcal{W}}_{\mathbf{B}}(\tau ,t){|}^2={\sum }_i|{\mathcal{W}}_i(\tau ,t){|}^2$ (with i = r, t, n) is the total energy of the fluctuations. The decomposition in time and scales is done by using the wavelet transform. Indeed, ${\mathcal{W}}_i(\tau ,t)$ are the wavelet coefficients (Torrence and Compo, 1998), i.e., ${\mathcal{W}}_i(\tau ,t)={\sum }_{j=0}^{N-1}{B}_i(t_j)\psi *\left[\left(t_j-t\right)/\tau \right]$, where B_i(t_j) is the ith magnetic field component and ψ* is the conjugate of the wavelet function. Here, the Morlet wavelet is the mother function (Torrence and Compo, 1998), which consists of a plane wave modulated by a Gaussian. LIM, both in the parallel and perpendicular direction, shows a clear non-homogeneity in the distribution of magnetic energy in time. Indeed, time localised energetic events appear covering a certain range of time scales. This is an inherent property of intermittent coherent structures (Farge, 1992). I_∥ and I_⊥ look almost correlated, meaning that at same time magnetic energy goes in both directions, although the most energetic events are found in I_⊥.

FIGURE 4

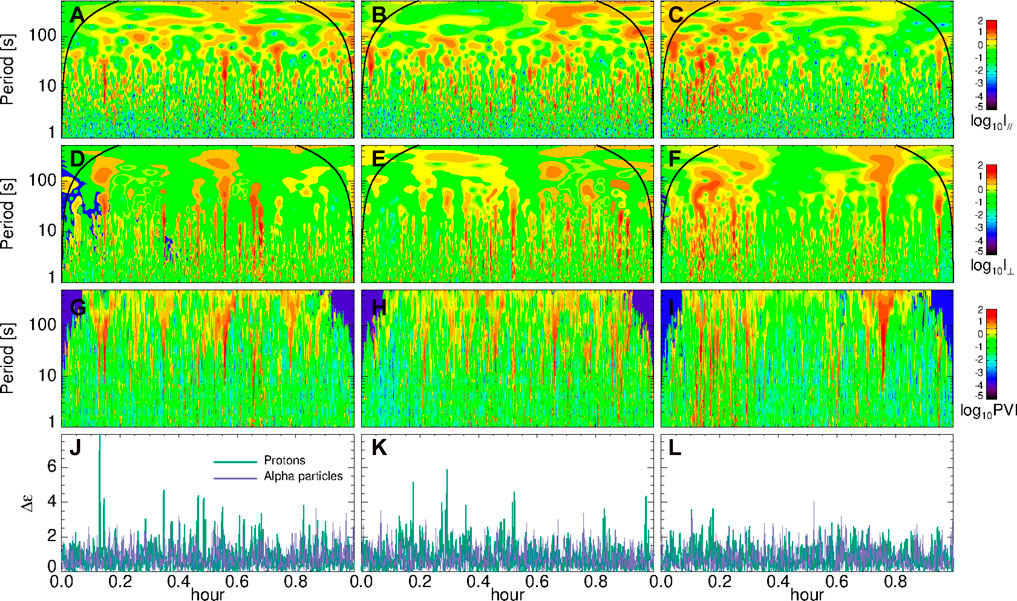
FIGURE 4. Logarithmic contour plots of the local intermittency measure (LIM) of the parallel, I_∥ (A–C), and perpendicular, I_⊥ (D–F), magnetic field fluctuations, where curved lines, at each side of the plots, indicate the cone of influence. Logarithmic contour plots of the magnetic PVI (G–I). Dimensionless proton (green) and alpha particle (violet) increment of non-Maxwellianity parameter, Δϵ (J–L).

Most of the studies of plasma discontinuities are based on the use of the partial variance of increments (PVI) technique (Greco et al., 2008) or Haar wavelet (Veltri and Mangeney, 1999). These methods are oriented to catch planar/slab discontinuities in different regimes of the turbulence cascade. Indeed, they have been found to be efficient in detecting one-dimensional current sheets (Veltri, 1999; Bruno et al., 2001; Osman et al., 2010; Greco et al., 2012; Osman et al., 2012; Perri et al., 2012; Greco and Perri, 2014; Greco et al., 2016). The advantage of using PVI with respect to wavelets is related to its straightforward computation, since it just depends on the magnetic field increments, δB(t, τ), that is the difference between the magnetic field values at two different times separated by a time lag τ, as (Greco et al., 2008)

$\mathrm{P}\mathrm{V}\mathrm{I}\left(t,\tau \right)=\frac{|\delta \mathbf{B}\left(t,\tau \right){|}^2}{⟨|\delta \mathbf{B}\left(t,\tau \right){|}^2⟩},(4)$

being ⟨⋯ ⟩ a time average over the entire dataset. Panels (g-i) of Figure 4 show the scalograms for the magnetic PVI, which look very similar to the panels (a)-(f). Thus, localized (in time) channels of large amplitude PVI and LIM broaden over time scales, implying that within these channels magnetic energy is cascading from large time scales towards small time scales.

In order to enhance how such non-homogeneous (in time) channels influence kinetic physics, we have computed the deviation of the proton and alpha VDF from the thermodynamic equilibrium by means of the parameter ϵ_s, called non-Maxwellianity, defined as (Greco et al., 2012; Valentini et al., 2016)

${ϵ}_s=\frac{1}{n_s}\sqrt{\int {\left(f_s-g_s\right)}^2{d}^{3}v}(5)$

where n_s is the density for a species s, f_s is the measured VDF and g_s is the associated Maxwellian distribution with the same density, temperature and velocity as the observed one. Panels (j-l) show the dimensionless proton (green) and alpha particle (violet) increments of non-Maxwellianity, Δϵ. Indeed, following the PVI technique, we have computed normalised increments for ϵ_s on a time scale of 8 s, which is very close to the spectral break. We observe a clear correspondence, especially in the main portion and intermediate region, between the presence of strong intermittent events and the distortion of both proton and alpha particle VDFs.

4.1 Identification and statistical analysis of coherent events

We focus on the nature of the turbulent magnetic field fluctuations around the spectral break, adopting a bandpass filter based on the wavelet transform (Torrence and Compo, 1998; He et al., 2012; Perrone et al., 2016; Perrone et al., 2017; Perrone et al., 2020; Perrone et al., 2022). We have selected a frequency ranges around proton scales, namely, f ∈ [0.1, 1] Hz to study kinetic effects. Magnetic fluctuations are then defined as

$\delta b_i\left(t\right)=\frac{\delta j\delta t^{1/2}}{C_{\delta }{\psi }_0\left(0\right)}{\displaystyle \sum _{j=j_1}^{j_2}}\frac{\mathcal{R}\left[{\mathcal{W}}_i\left({\tau }_j,t\right)\right]}{{\tau }_j^{1/2}}(6)$

where $\mathcal{R}$ refers to the real-part function, j is the scale index and δj is a constant scale step; ψ₀(0) = π^1/4 and C_δ = 0.776, the latter derived from the reconstruction of a δ function using the Morlet wavelet (Torrence and Compo, 1998). Finally, τ(j₁) = 1 s and τ(j₂) = 10 s (being τ = 1/f).

The presence of large amplitude (in magnetic energy) events, already highlighted by LIM and PVI in Figure 4, has been confirmed by significant non-Gaussian tails in the PDFs of δb_i (not shown here). We decided to study them by selecting only the fluctuations that exceed three standard deviations from the corresponding Gaussian distribution (which includes 99.7% of the Gaussian contribution). More than a hundred intermittent events have been detected by an automated method (see Perrone et al., 2016, for details) for each selected 1 h period. Then, we perform a minimum variance analysis (Sonnerup and Scheible, 1998) around each selected peak in magnetic energy, corresponding to magnetic fluctuations well-localized in time and with a regular profile in a range, Δt′, namely, the width of the event, defined as the time interval between two minima of energy that contains the selected maximum over the threshold. Moreover, we define the characteristic temporal scale of the event, Δt (<Δt′), as the width at half-height of the maximum (Perrone et al., 2016).

Figure 5 shows the results of the statistical analysis on the intermittent events observed in the 1 h intervals in the main portion (green), intermediate region (orange) and rarefaction region (violet). Panel (a) displays the PDFs of the orientation of the eigenvectors, θ, with respect to the local magnetic field, b₀, which has been averaged within each structure, namely, in Δt′. In all the periods, θ_max is perpendicular to b₀, confirming the absence of compressive events due to the high Alfvénicity of the intervals. Indeed, the most peaked distribution around 90° is the one corresponding to the main portion (green line), which is also characterized by the highest Alfvénicity (see Figure 1). On the other hand, the distributions of θ_min are more uniform, with a slight peak at very small angles. A different behavior is observed for the angle between the magnetic and velocity field vectors, θ_BV, within the structures. Indeed, in panel (b), we find three distinct peaks, where 30° < θ_BV < 60° in the rarefaction region (violet line), 50° < θ_BV < 65° in the main portion (green line), and θ_BV ∼ 80° in the intermediate region (orange line). This behavior, which reflects the same behavior observed for the whole three 1 h periods (see panels g–i of Figure 1), suggests that the misalignment of b₀ and v₀ is supported by the presence of large-scale structures, as the spaghetti-like flux-tube texture of the magnetic field observed by D’Amicis et al. (2021b), which produces strong discontinuities. Three distinct peaks are also recovered for the proton plasma beta (panel c). Here, we evaluated a reduced parameter, since in β_p we consider only the proton core population. However, the same physics (the peaks are only shifted to higher values) is found if we take into account the moments of the ion (proton + alpha particles) distribution. As in the case of θ_BV, the distribution of the local β_p, i.e., within Δt′, reflects the global behavior observed for the same parameter in the whole intervals. Finally, to better characterize the compressibility of the structures, we evaluated the local magnetic compressibility, ζ_∥, defined as in Perrone et al. (2016).

${\zeta }_{\Vert }=\sqrt{\frac{\text{max}\left(\delta b_{\Vert }^2\right)}{\text{max}\left(\delta b_{\perp 1}^2+\delta b_{\perp 2}^2\right)}}(7)$

where parallel and perpendicular directions are estimated with respect to b₀ and the maximum of the magnetic components is evaluated within Δt′. Panel (d) in Figure 5 shows a slight shift towards higher values of ζ_∥, even if very small, going from the main portion to the rarefaction region. Indeed, this behavior is expected since the three select intervals are strongly Alfvénic but the amplitude of the Alfvénic fluctuations decreases going towards the rarefaction region.

FIGURE 5

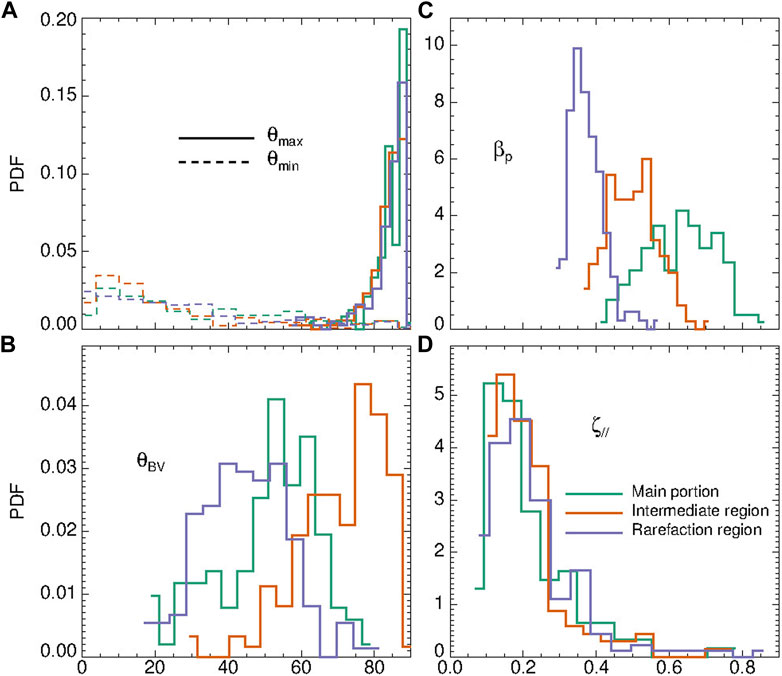
FIGURE 5. Statistical analysis of the observed coherent events for the 1 h intervals in the main portion (green), intermediate region (orange) and rarefaction region (violet). Left panels: PDFs of the angles between the maximum (solid line) and the minimum (dashed line) variance directions and the local magnetic field (A); and θ_BV (B). Right panels: PDFs of the reduced proton plasma beta, β_p (C), evaluated by considering only the proton core, and the local magnetic compressibility, ζ_∥ (D).

4.2 Example of coherent structures: Vortex chain

Looking into the details of each intermittent structure observed in all the selected periods, we can conclude that these events can be described mostly as currents sheets and vortex-like structures. In particular, vortices can be observed as very isolated structures or grouped in chains. The latter are very interesting. Indeed, numerical simulations have shown that turbulence leads to the generation of current sheets and vortices, which evolve in time interacting nonlinearly among each others (see, e.g., Servidio et al., 2012; Perrone et al., 2013;Servidio et al., 2015). Assuming to use a virtual spacecraft in the simulations, which samples magnetic field data along a linear trajectory in the numerical box, it would cross discontinuities and magnetic islands, with the latter appearing as a vortex chain.

An example of a vortex chain crossed by Solar Orbiter is shown in Figure 6. Panel (a) displays the three components of the bandpassed magnetic field fluctuations, defined in Eq. 6, in the local magnetic field reference frame. The yellow box marks the width of the central vortex, Δt′, where the analyses (such as the minimum variance analysis and the local mean parameter estimations) have been performed. Indeed, the minimum variance analysis has highlighted that magnetic fluctuations are characterized by λ_min ≪ λ_int < λ_max and the main variance is in the plane perpendicular to b₀, with very small compressive fluctuations, δb_z ≪ δb_x, δb_y. Moreover, we find that θ_max ∼ 87° and θ_min ∼ 75°, while θ_int ∼ 15°. Finally, its characteristic width is Δr ∼ 1400 km ∼ 18λ_i or ∼ 27ρ_i, assuming that the structure is convected by the wind. The nature of the structure is confirmed by the other panels of Figure 6, which display hodographs of the magnetic field vector (normalized to max (|δb|)) in the plane perpendicular to b₀ (panel b) and in the planes containing δb_z and δb_x (c) or δb_y (d). Indeed, a rotation in the plane perpendicular to the local magnetic field is observed in the central vortex. Moreover, panel (b) suggests that similar structures are present on both sides of the central vortex that the automatic method selects. These two other vortices are also well localized and they are characterized by very small compressive fluctuations (see also panel a).

FIGURE 6

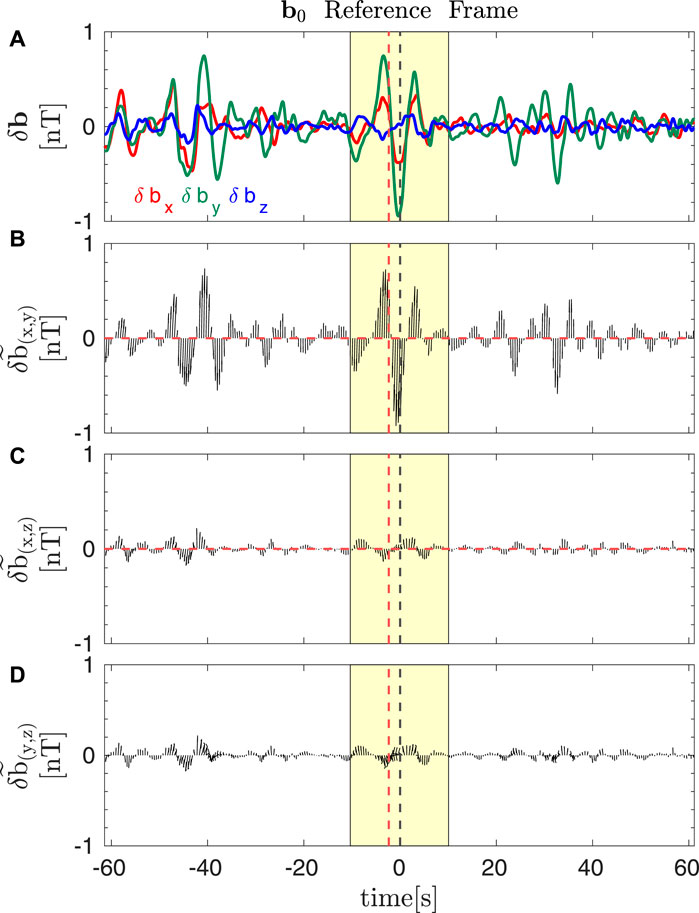
FIGURE 6. Example of a vortex chain centered at 03:27:56.58 UT (black vertical dashed line) on July 17th. From top to bottom: components of the magnetic field fluctuations, defined in Eq. 6, in the local magnetic field reference frame, where b₀ is along the z-direction (A); hodographs of the magnetic field vector (normalized to max (|δb|)) in the plane perpendicular to b₀ (B) and in the planes that contains δb_z and δb_x (C) or δb_y (D). The yellow shadow highlights the extension of the central vortex, Δt′. Finally, the red vertical dashed line marks the time at which the proton and the alpha VDF were taken and showed in Figure 7.

Coherent structures are generally connected to strong distortions in the ion VDFs, such as the presence of a secondary field-aligned beam. Since coherent structures are usually characterized by strong and rapid rotations of the magnetic field direction, the position of the beam could move during the time to collect measurements, thus producing artificial temperature anisotropy. However, stable beams have been observed in both numerical experiments (see, e.g., Valentini et al., 2008; Valentini and Veltri, 2009; Valentini et al., 2010; Valentini et al., 2011) and in-situ observations (see, e.g., Sorriso-Valvo et al., 2019). Here, a first indication of the distortion in the 3D ion VDFs is provided by the increased non-Maxwellianity parameter in correspondence of such intermittent regions and strong discontinuities (see Figure 4). However, in order to investigate this point in more detail, we have directly checked the ion velocity distributions. In particular, in Figure 7, we show an example of 2D contour plots of both proton and alpha particle VDFs at the time 03:27:55.78 UT, close to the center of the main vortex structure (red vertical dashed line in Figure 6), and integrated along the out-plane direction. The VDF of each ion population (protons and alpha particles) is displayed in their respective rest frame. We also point out the different scales of the colorbars for each of the two species which remark the fact that alpha particles are only ∼ 4% of the proton core (see Table 1). From left to right, both proton and alpha particle VDFs are shown in the planes (v_∥, v_⊥,1), (v_∥, v_⊥,2) and (v_⊥,1, v_⊥,2), respectively, where v_∥ represents the direction of the local magnetic field evaluated as an average over 1 s around the time of the considered VDF (which corresponds approximately to the time of acquisition of the 3D VDF by PAS); v_⊥,2 is the direction perpendicular to both the local magnetic field and the local proton bulk velocity, and v_⊥,2 is the cross product v_⊥,2 × v_∥. In the planes containing the magnetic field direction, the proton VDF shows a clear and stable field-aligned beam, panels (a) and (b), while it is gyrotropic in the plane perpendicular to the magnetic field (panel c). Indeed, even after the crossing of the structure, the proton beam is present and stable, showing a timescale longer than the time to collect counts. This suggests that the beam and the related temperature anisotropy are physical features. Moreover, we interestingly find that the alpha particle VDF shows an oblique beam, directed mostly in the negative ⊥, 1 direction (panel d), while it is mostly isotropic in panel (e) and gyrotropic in panel (f). We also point out that the same kinetic features are observed in correspondence of the other two vortex structures detected right before and after the main one. The presence of such a beam in the alpha particle VDFs needs further investigation.

FIGURE 7

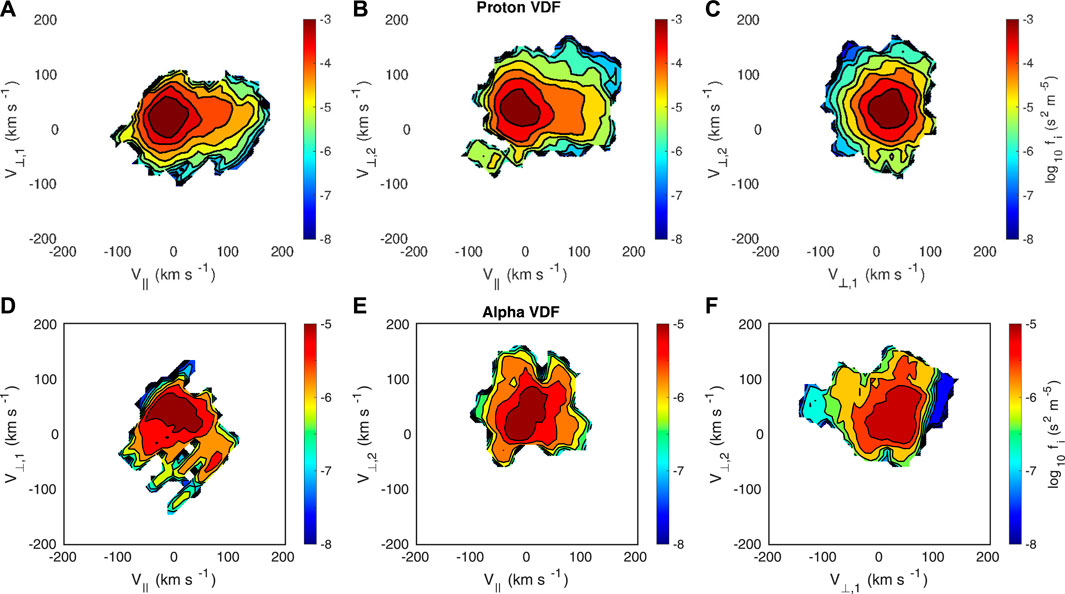
FIGURE 7. 2D contour plots of the reduced velocity distribution functions of protons (A–C) and alpha particles (D–F) plotted in the rest frame coordinate system and at the time 03:27:55.78 UT on July 17th (see red vertical dashed line in Figure 6). From left to right, the distribution functions are showed in the planes determined by the local magnetic field and the bulk velocity: (v_∥, v_⊥,1), (v_∥, v_⊥,2) and (v_⊥,1, v_⊥,2), respectively.

5 Discussion

We have investigated the turbulence properties around a range of time scales (frequencies) where kinetic effects start dominating the plasma dynamics in the slow Alfvénic solar wind interval detected by Solar Orbiter at 0.64 AU. In particular, we have focused on a 1 h interval of very high Alfvénicity (that is the correlation between large amplitude velocity and magnetic field components) in each of the three distinguishable regions, namely, a main portion, an intermediate region and a rarefaction region (D’Amicis et al., 2021b), where the plasma parameters tend to show slight different behaviours. Going from the large scale characteristics of this sample of solar wind, an overview of the characteristics of the magnetic fluctuations from the inertial to sub-proton time scales, ending with the analysis of the ion distribution functions, is given. The main results can be summarized as follows:

• the alignment between the magnetic and the velocity field vectors changes passing from the main portion to the intermediate region and then to the rarefaction region, having an effect on the slope of the magnetic field power spectral densities. Indeed, during the rarefaction region crossing, the radial direction is more aligned to the magnetic field and consequently the slope of the PSD in the inertial range is closer to the predicted limit γ_∥ = −2 (Goldreich and Sridhar, 1995);

• all the three regions are characterized by coherent magnetic structures over a broad range of time scales and highly localized in time. The two techniques used to detect coherent structures, i.e., PVI and LIM, give very similar results. These structures are characterized by a local increase of magnetic energy both along the direction parallel to the mean magnetic field and perpendicular to it. They are responsible for a high level of intermittency through all the three regions;

• interestingly enough, coherent structures tend to be correlated with the presence of gradients in the non-Maxwellianity parameter ϵ_s (both for protons and alpha particles). This parameter, ϵ_s, quantifies the degree of deviation of the VDF of a given species from its associated Maxwellian distribution. It has largely been used both in simulations and in spacecraft observations (Greco et al., 2012; Valentini et al., 2016; Perri et al., 2020);

• most of the detected structures in the three regions (more than 96% of all events, which becomes 99% for the structures in the main region) are almost perpendicular to the local mean field (namely, θ_max > 70°), so that they have a very low level of compressibility. The identified coherent structures are mainly current sheets, isolated vortices or vortex chains. One example of vortex chain is also reported in detail, with a description of the associated distorted VDFs both for protons and alpha particles. Indeed, while for the protons the presence of a typical field aligned beam can be easily recognized (Marsch et al., 1982b; Marsch, 2006), in the alpha particle VDFs an oblique beam with respect to the local direction of the magnetic field is detected. This feature appears also related to the other vortices of this chain and requires a further analysis. The structures here detected share similar characteristics to the ones observed in other types of wind (Greco et al., 2016; Perrone et al., 2016; Perrone et al., 2017; Perrone et al., 2020; Perrone et al., 2022), thus giving indication of common turbulent energy channels through the scales. Thanks to all these observations, we finally start to have a good statistics on structures properties, enabling us to unveil the processes responsible for magnetic energy dissipation and solar wind heating.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://soar.esac.esa.int/soar/.

Author contributions

DP and SP conceived the data analysis. DP wrote the article. SP helped to write the article. AS performed the analysis on the velocity distribution functions with the support of RM, who provided the revised plasma data. RA, AS, and RM contributed to the text writing and helped in improving the analysis and interpreting the data. All authors contributed to the article and approved the submitted version.

Funding

SP is supported by the Italian Space Agency and the National Institute of Astrophysics, in the framework of the CAESAR (Comprehensive spAce wEather Studies for the ASPIS prototype Realization) project, through the ASI-INAF n. 2020-35-HH.0 agreement for the development of the ASPIS (ASI SPace weather InfraStructure) prototype of scientific data centre for Space Weather.

Acknowledgments

Solar Orbiter is a space mission of international collaboration between ESA and NASA, operated by ESA. Solar Orbiter Solar Wind Analyser (SWA) data are derived from scientific sensors which have been designed and created, and are operated under funding provided in numerous contracts from the UK Space Agency (UKSA), the UK Science and Technology Facilities Council (STFC), the Agenzia Spaziale Italiana (ASI), the Centre National d’Etudes SpaDales (CNES, France), the Centre National de la Recherche Scientifique (CNRS, France), the Czech contribution to the ESA PRODEX programme and NASA. DP, SP, and AS would like to acknowledge the International Space Science Institute (ISSI) for its support of the team “Unravelling solar wind microphysics in the inner heliosphere” dedicated in part to the analysis of Solar Orbiter data.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alexandrova, O., Chen, C. H. K., Sorriso-Valvo, L., Horbury, T. S., and Bale, S. D. (2013). Solar wind turbulence and the role of ion instabilities. Space Sci. Rev. 178, 101–139. doi:10.1007/s11214-013-0004-8

CrossRef Full Text | Google Scholar

Badman, S. T., Bale, S. D., Oliveros, J. C. M., Panasenco, O., Velli, M., Stansby, D., et al. (2020). Magnetic connectivity of the ecliptic plane within 0.5 au: potential field source surface modeling of the first parker solar probe encounter. Astrophysical J. Suppl. Ser. 246, 23. doi:10.3847/1538-4365/ab4da7

CrossRef Full Text | Google Scholar

Bale, S. D., Badman, S. T., Bonnell, J. W., Bowen, T. A., Burgess, D., Case, A. W., et al. (2019). Highly structured slow solar wind emerging from an equatorial coronal hole. Nature 576, 237–242. doi:10.1038/s41586-019-1818-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Bruno, R., and Carbone, V. (2013). The solar wind as a turbulence laboratory. Living Rev. Sol. Phys. 10, 2. doi:10.12942/lrsp-2013-2

CrossRef Full Text | Google Scholar

Bruno, R., and Carbone, V. (2016). “Turbulence in the solar wind,” in Lecture notes in physics (Berlin, Germany: Springer). doi:10.1007/978-3-319-43440-7

CrossRef Full Text | Google Scholar

Bruno, R., Carbone, V., Veltri, P., Pietropaolo, E., and Bavassano, B. (2001). Identifying intermittency events in the solar wind. Planet. Space Sci. 49, 1201–1210. doi:10.1016/S0032-0633(01)00061-7

CrossRef Full Text | Google Scholar

Bruno, R., and Trenchi, L. (2014). Radial dependence of the frequency break between fluid and kinetic scales in the solar wind fluctuations. Astrophysical J. Lett. 787, L24. doi:10.1088/2041-8205/787/2/L24

CrossRef Full Text | Google Scholar

D’Amicis, R., Bruno, R., Panasenco, O., Telloni, D., Perrone, D., Marcucci, M. F., et al. (2021a). First Solar Orbiter observation of the Alfvénic slow wind and identification of its solar source. Astronomy Astrophysics 656, A21. doi:10.1051/0004-6361/202140938

CrossRef Full Text | Google Scholar

D’Amicis, R., Perrone, D., Bruno, R., and Velli, M. (2021b). On alfvénic slow wind: A journey from the earth back to the sun. J. Geophys. Res. (Space Phys. 126, e28996. doi:10.1029/2020JA028996

CrossRef Full Text | Google Scholar

De Marco, R., Bruno, R., Jagarlamudi, V. K., D’Amicis, R., Marcucci, M. F., Fortunato, V., et al. (2023). Innovative technique for separating proton core, proton beam, and alpha particles in solar wind 3D velocity distribution functions. Astronomy Astrophysics 669, A108. doi:10.1051/0004-6361/202243719

CrossRef Full Text | Google Scholar

Dudok de Wit, T., Krasnoselskikh, V. V., Bale, S. D., Bonnell, J. W., Bowen, T. A., Chen, C. H. K., et al. (2020). Switchbacks in the near-sun magnetic field: long memory and impact on the turbulence cascade. Astrophysical J. Suppl. Ser. 246, 39. doi:10.3847/1538-4365/ab5853

CrossRef Full Text | Google Scholar

Elliott, H. A., McComas, D. J., and DeForest, C. E. (2016). Long-term trends in the solar wind proton measurements. Astrophysical J. 832, 66. doi:10.3847/0004-637X/832/1/66

CrossRef Full Text | Google Scholar

Farge, M. (1992). Wavelet transforms and their applications to turbulence. Annu. Rev. Fluid Mech. 24, 395–458. doi:10.1146/annurev.fl.24.010192.002143

CrossRef Full Text | Google Scholar

Fox, N. J., Velli, M. C., Bale, S. D., Decker, R., Driesman, A., Howard, R. A., et al. (2016). The solar probe plus mission: humanity’s first visit to our star. Space Sci. Rev. 204, 7–48. doi:10.1007/s11214-015-0211-6

CrossRef Full Text | Google Scholar

Frisch, U. (1995). Turbulence. The legacy of A.N. Kolmogorov.

Google Scholar

Goldreich, P., and Sridhar, S. (1995). Toward a theory of interstellar turbulence. 2: strong alfvenic turbulence. Astrophysical J. 438, 763. doi:10.1086/175121

CrossRef Full Text | Google Scholar

Greco, A., Chuychai, P., Matthaeus, W. H., Servidio, S., and Dmitruk, P. (2008). Intermittent MHD structures and classical discontinuities. Geophys. Res. Lett. 35, L19111. doi:10.1029/2008GL035454

CrossRef Full Text | Google Scholar

Greco, A., and Perri, S. (2014). Identification of high shears and compressive discontinuities in the inner heliosphere. Astrophysical J. 784, 163. doi:10.1088/0004-637X/784/2/163

CrossRef Full Text | Google Scholar

Greco, A., Perri, S., Servidio, S., Yordanova, E., and Veltri, P. (2016). The complex structure of magnetic field discontinuities in the turbulent solar wind. Astrophysical J. Lett. 823, L39. doi:10.3847/2041-8205/823/2/L39

CrossRef Full Text | Google Scholar

Greco, A., Valentini, F., Servidio, S., and Matthaeus, W. H. (2012). Inhomogeneous kinetic effects related to intermittent magnetic discontinuities. Phys. Rev. E 86, 066405. doi:10.1103/PhysRevE.86.066405

PubMed Abstract | CrossRef Full Text | Google Scholar

He, J., Tu, C., Marsch, E., and Yao, S. (2012). Do oblique alfvén/ion-cyclotron or fast-mode/whistler waves dominate the dissipation of solar wind turbulence near the proton inertial length? Astrophysical J. Lett. 745, L8. doi:10.1088/2041-8205/745/1/L8

CrossRef Full Text | Google Scholar

Horbury, T. S., Forman, M., and Oughton, S. (2008). Anisotropic scaling of magnetohydrodynamic turbulence. Phys. Rev. Lett. 101, 175005. doi:10.1103/PhysRevLett.101.175005

PubMed Abstract | CrossRef Full Text | Google Scholar

Horbury, T. S., O’Brien, H., Carrasco Blazquez, I., Bendyk, M., Brown, P., Hudson, R., et al. (2020a). The solar orbiter magnetometer. Astronomy Astrophysics 642, A9. A9, doi:10.1051/0004-6361/201937257

CrossRef Full Text | Google Scholar

Horbury, T. S., Woolley, T., Laker, R., Matteini, L., Eastwood, J., Bale, S. D., et al. (2020b). Sharp alfvénic impulses in the near-sun solar wind. Astrophysical J. Suppl. Ser. 246, 45. doi:10.3847/1538-4365/ab5b15

CrossRef Full Text | Google Scholar

Kasper, J. C., Bale, S. D., Belcher, J. W., Berthomier, M., Case, A. W., Chandran, B. D. G., et al. (2019). Alfvénic velocity spikes and rotational flows in the near-sun solar wind. Nature 576, 228–231. doi:10.1038/s41586-019-1813-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Kasper, J. C., Lazarus, A. J., and Gary, S. P. (2008). Hot solar-wind helium: direct evidence for local heating by alfvén-cyclotron dissipation. Phys. Rev. Lett. 101, 261103. doi:10.1103/PhysRevLett.101.261103

PubMed Abstract | CrossRef Full Text | Google Scholar

Kolmogorov, A. (1941). The local structure of turbulence in incompressible viscous fluid for very large Reynolds’ numbers. Akad. Nauk. SSSR Dokl. 30, 301–305. doi:10.1098/rspa.1991.0075

CrossRef Full Text | Google Scholar

Lion, S., Alexandrova, O., and Zaslavsky, A. (2016). Coherent events and spectral shape at ion kinetic scales in the fast solar wind turbulence. Astrophysical J. 824, 47. doi:10.3847/0004-637X/824/1/47

CrossRef Full Text | Google Scholar

Marsch, E. (2006). Kinetic physics of the solar corona and solar wind. Living Rev. Sol. Phys. 3, 1. doi:10.12942/lrsp-2006-1

CrossRef Full Text | Google Scholar

Marsch, E., Rosenbauer, H., Schwenn, R., Muehlhaeuser, K. H., and Neubauer, F. M. (1982a). Solar wind helium ions: observations of the Helios solar probes between 0.3 and 1 AU. J. Geophys. Res. 87, 35–51. doi:10.1029/JA087iA01p00035

CrossRef Full Text | Google Scholar

Marsch, E., Schwenn, R., Rosenbauer, H., Muehlhaeuser, K. H., Pilipp, W., and Neubauer, F. M. (1982b). Solar wind protons: three-dimensional velocity distributions and derived plasma parameters measured between 0.3 and 1 AU. J. Geophys. Res. 87, 52–72. doi:10.1029/JA087iA01p00052

CrossRef Full Text | Google Scholar

Marsch, E., and Tu, C. Y. (1997). Intermittency, non-Gaussian statistics and fractal scaling of MHD fluctuations in the solar wind. Nonlinear Process. Geophys. 4, 101–124. doi:10.5194/npg-4-101-1997

CrossRef Full Text | Google Scholar

Matteini, L., Landi, S., Velli, M., and Hellinger, P. (2010). Kinetics of parametric instabilities of alfvén waves: evolution of ion distribution functions. J. Geophys. Res. Space Phys. 115. doi:10.1029/2009JA014987

CrossRef Full Text | Google Scholar

Matthaeus, W. H., Yang, Y., Wan, M., Parashar, T. N., Bandyopadhyay, R., Chasapis, A., et al. (2020). Pathways to dissipation in weakly collisional plasmas. Astrophysical J. 891, 101. doi:10.3847/1538-4357/ab6d6a

CrossRef Full Text | Google Scholar

McGregor, S. L., Hughes, W. J., Arge, C. N., Odstrcil, D., and Schwadron, N. A. (2011). The radial evolution of solar wind speeds. J. Geophys. Res. (Space Phys. 116, A03106. doi:10.1029/2010JA016006

CrossRef Full Text | Google Scholar

Müller, D., St Cyr, O. C., Zouganelis, I., Gilbert, H. R., Marsden, R., Nieves-Chinchilla, T., et al. (2020). The Solar Orbiter mission. Science overview. Astronomy Astrophysics 642, A1. doi:10.1051/0004-6361/202038467

CrossRef Full Text | Google Scholar

Osman, K. T., Matthaeus, W. H., Greco, A., and Servidio, S. (2010). Evidence for inhomogeneous heating in the solar wind. Astrophysical J. Lett. 727, L11. doi:10.1088/2041-8205/727/1/L11

CrossRef Full Text | Google Scholar

Osman, K. T., Matthaeus, W. H., Hnat, B., and Chapman, S. C. (2012). Kinetic signatures and intermittent turbulence in the solar wind plasma. Phys. Rev. Lett. 108, 261103. doi:10.1103/PhysRevLett.108.261103

PubMed Abstract | CrossRef Full Text | Google Scholar

Owen, C. J., Bruno, R., Livi, S., Louarn, P., Al Janabi, K., Allegrini, F., et al. (2020). The solar orbiter solar wind analyser (SWA) suite. Astronomy Astrophysics 642, A16. doi:10.1051/0004-6361/201937259

CrossRef Full Text | Google Scholar

Panasenco, O., Velli, M., and Panasenco, A. (2019). Large-scale magnetic funnels in the solar corona. Astrophysical J. 873, 25. doi:10.3847/1538-4357/ab017c

CrossRef Full Text | Google Scholar

Perri, S., Carbone, V., Vecchio, A., Bruno, R., Korth, H., Zurbuchen, T. H., et al. (2012). Phase-synchronization, energy cascade, and intermittency in solar-wind turbulence. Phys. Rev. Lett. 109, 245004. doi:10.1103/PhysRevLett.109.245004

PubMed Abstract | CrossRef Full Text | Google Scholar

Perri, S., Carbone, V., and Veltri, P. (2010). Where does fluid-like turbulence break down in the solar wind? Astrophysical J. Lett. 725, L52–L55. doi:10.1088/2041-8205/725/1/l52

CrossRef Full Text | Google Scholar

Perri, S., Perrone, D., Yordanova, E., Sorriso-Valvo, L., Paterson, W. R., Gershman, D. J., et al. (2020). On the deviation from Maxwellian of the ion velocity distribution functions in the turbulent magnetosheath. J. Plasma Phys. 86, 905860108. doi:10.1017/S0022377820000021

CrossRef Full Text | Google Scholar

Perrone, D., Alexandrova, O., Mangeney, A., Maksimovic, M., Lacombe, C., Rakoto, V., et al. (2016). Compressive coherent structures at ion scales in the slow solar wind. Astrophysical J. 826, 196. doi:10.3847/0004-637X/826/2/196

CrossRef Full Text | Google Scholar

Perrone, D., Alexandrova, O., Roberts, O. W., Lion, S., Lacombe, C., Walsh, A., et al. (2017). Coherent structures at ion scales in fast solar wind: cluster observations. Astrophysical J. 849, 49. doi:10.3847/1538-4357/aa9022

CrossRef Full Text | Google Scholar

Perrone, D., Bruno, R., D’Amicis, R., Telloni, D., De Marco, R., Stangalini, M., et al. (2020). Coherent events at ion scales in the inner heliosphere: parker solar probe observations during the first encounter. Astrophysical J. 905, 142. doi:10.3847/1538-4357/abc480

CrossRef Full Text | Google Scholar

Perrone, D., Perri, S., Bruno, R., Stansby, D., D’Amicis, R., Jagarlamudi, V. K., et al. (2022). Evolution of coronal hole solar wind in the inner heliosphere: combined observations by Solar Orbiter and Parker Solar Probe. Astronomy Astrophysics 668, A189. doi:10.1051/0004-6361/202243989

CrossRef Full Text | Google Scholar

Perrone, D., Stansby, D., Horbury, T. S., and Matteini, L. (2019). Thermodynamics of pure fast solar wind: radial evolution of the temperature-speed relationship in the inner heliosphere. Mon. Notices R. Astronomical Soc. 488, 2380–2386. doi:10.1093/mnras/stz1877

CrossRef Full Text | Google Scholar

Perrone, D., Valentini, F., Servidio, S., Dalena, S., and Veltri, P. (2014). Analysis of intermittent heating in a multi-component turbulent plasma. Eur. Phys. J. D 68, 209. doi:10.1140/epjd/e2014-50152-1

CrossRef Full Text | Google Scholar

Perrone, D., Valentini, F., Servidio, S., Dalena, S., and Veltri, P. (2013). Vlasov simulations of multi-ion plasma turbulence in the solar wind. Astrophysical J. 762, 99. doi:10.1088/0004-637X/762/2/99

CrossRef Full Text | Google Scholar

Pezzi, O., Perrone, D., Servidio, S., Valentini, F., Sorriso-Valvo, L., and Veltri, P. (2019). Proton–proton collisions in the turbulent solar wind: hybrid Boltzmann–maxwell simulations. Astrophysical J. 887, 208. doi:10.3847/1538-4357/ab5285

CrossRef Full Text | Google Scholar

Pezzi, O., Servidio, S., Perrone, D., Valentini, F., Sorriso-Valvo, L., Greco, A., et al. (2018). Velocity-space cascade in magnetized plasmas: numerical simulations. Phys. Plasmas 25, 060704. doi:10.1063/1.5027685

CrossRef Full Text | Google Scholar

Retinò, A., Sundkvist, D., Vaivads, A., Mozer, F., André, M., and Owen, C. J. (2007). In situ evidence of magnetic reconnection in turbulent plasma. Nat. Phys. 3, 235–238. doi:10.1038/nphys574

CrossRef Full Text | Google Scholar

Servidio, S., Chasapis, A., Matthaeus, W. H., Perrone, D., Valentini, F., Parashar, T. N., et al. (2017). Magnetospheric multiscale observation of plasma velocity-space cascade: hermite representation and theory. Phys. Rev. Lett. 119, 205101. doi:10.1103/PhysRevLett.119.205101

PubMed Abstract | CrossRef Full Text | Google Scholar

Servidio, S., Valentini, F., Califano, F., and Veltri, P. (2012). Local kinetic effects in two-dimensional plasma turbulence. Phys. Rev. Lett. 108, 045001. doi:10.1103/PhysRevLett.108.045001

PubMed Abstract | CrossRef Full Text | Google Scholar

Servidio, S., Valentini, F., Perrone, D., Greco, A., Califano, F., Matthaeus, W. H., et al. (2015). A kinetic model of plasma turbulence. J. Plasma Phys. 81, 325810107. doi:10.1017/S0022377814000841

CrossRef Full Text | Google Scholar

Sonnerup, B. U. Ö., and Scheible, M. (1998). Minimum and maximum variance analysis. ISSI Sci. Rep. Ser. 1, 185–220.

Google Scholar

Sorriso-Valvo, L., Carbone, V., Veltri, P., Consolini, G., and Bruno, R. (1999). Intermittency in the solar wind turbulence through probability distribution functions of fluctuations. Geophys. Res. Lett. 26, 1801–1804. doi:10.1029/1999GL900270

CrossRef Full Text | Google Scholar

Sorriso-Valvo, L., Catapano, F., Retinò, A., Le Contel, O., Perrone, D., Roberts, O. W., et al. (2019). Turbulence-driven ion beams in the magnetospheric kelvin-helmholtz instability. Phys. Rev. Lett. 122, 035102. doi:10.1103/PhysRevLett.122.035102

PubMed Abstract | CrossRef Full Text | Google Scholar

Sorriso-Valvo, L., Perrone, D., Pezzi, O., Valentini, F., Servidio, S., Zouganelis, I., et al. (2018). Local energy transfer rate and kinetic processes: the fate of turbulent energy in two-dimensional hybrid vlasov–maxwell numerical simulations. J. Plasma Phys. 84, 725840201. doi:10.1017/S0022377818000302

CrossRef Full Text | Google Scholar

Torrence, C., and Compo, G. P. (1998). A practical guide to wavelet analysis. Bull. Am. Meteorological Soc. 79, 61–78. doi:10.1175/1520-0477(1998)079¡0061:APGTWA¿2.0.CO;2

CrossRef Full Text | Google Scholar

Tu, C. Y., and Marsch, E. (1995). MHD structures, waves and turbulence in the solar wind: observations and theories. Space Sci. Rev. 73, 1–210. doi:10.1007/BF00748891

CrossRef Full Text | Google Scholar

Valentini, F., and Veltri, P. (2009). Electrostatic short-scale termination of solar-wind turbulence. Phys. Rev. Lett. 102, 225001. doi:10.1103/PhysRevLett.102.225001

PubMed Abstract | CrossRef Full Text | Google Scholar

Valentini, F., Califano, F., Perrone, D., Pegoraro, F., and Veltri, P. (2011). New ion-wave path in the energy cascade. Phys. Rev. Lett. 106, 165002. doi:10.1103/PhysRevLett.106.165002

PubMed Abstract | CrossRef Full Text | Google Scholar

Valentini, F., Califano, F., and Veltri, P. (2010). Two-dimensional kinetic turbulence in the solar wind. Phys. Rev. Lett. 104, 205002. doi:10.1103/PhysRevLett.104.205002

PubMed Abstract | CrossRef Full Text | Google Scholar

Valentini, F., Perrone, D., Stabile, S., Pezzi, O., Servidio, S., De Marco, R., et al. (2016). Differential kinetic dynamics and heating of ions in the turbulent solar wind. New J. Phys. 18, 125001. doi:10.1088/1367-2630/18/12/125001

CrossRef Full Text | Google Scholar

Valentini, F., Veltri, P., Califano, F., and Mangeney, A. (2008). Cross-scale effects in solar-wind turbulence. Phys. Rev. Lett. 101, 025006. doi:10.1103/PhysRevLett.101.025006

PubMed Abstract | CrossRef Full Text | Google Scholar

Veltri, P., and Mangeney, A. (1999). “Scaling laws and intermittent structures in solar wind MHD turbulence,” in Solar wind nine. Editors S. R. Habbal, R. Esser, J. V. Hollweg, and P. A. Isenberg (Nantucket: American Institute of Physics), 543–546. doi:10.1063/1.58809

CrossRef Full Text | Google Scholar

Veltri, P. (1999). MHD turbulence in the solar wind: self-similarity, intermittency and coherent structures. Plasma Phys. Control. Fusion 41, A787–A795. doi:10.1088/0741-3335/41/3A/071

CrossRef Full Text | Google Scholar

Verscharen, D., Klein, K. G., and Maruca, B. A. (2019). The multi-scale nature of the solar wind. Living Rev. Sol. Phys. 16, 5. doi:10.1007/s41116-019-0021-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Verscharen, D., Wicks, R. T., Alexandrova, O., Bruno, R., Burgess, D., Chen, C. H. K., et al. (2021). A case for electron-astrophysics. Exp. Astron. 54, 473–519. doi:10.1007/s10686-021-09761-5

CrossRef Full Text | Google Scholar

Webb, G. M., Barghouty, A. F., Hu, Q., and le Roux, J. A. (2018). Particle acceleration due to cosmic-ray viscosity and fluid shear in astrophysical jets. Astrophysical J. 855, 31. doi:10.3847/1538-4357/aaae6c

CrossRef Full Text | Google Scholar

White, T. G., Oliver, M. T., Mabey, P., Kühn-Kauffeldt, M., Bott, A. F. A., Döhl, L. N. K., et al. (2019). Supersonic plasma turbulence in the laboratory. Nat. Commun. 10, 1758. doi:10.1038/s41467-019-09498-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Woolley, T., Matteini, L., McManus, M. D., Berčič, L., Badman, S. T., Woodham, L. D., et al. (2021). Plasma properties, switchback patches, and low α-particle abundance in slow Alfvénic coronal hole wind at 0.13 au. Mon. Notices R. Astronomical Soc. 508, 236–244. doi:10.1093/mnras/stab2281

CrossRef Full Text | Google Scholar

Wu, P., Perri, S., Osman, K., Wan, M., Matthaeus, W. H., Shay, M. A., et al. (2013). Intermittent heating in solar wind and kinetic simulations. Astrophysical J. Lett. 763, L30. doi:10.1088/2041-8205/763/2/L30

CrossRef Full Text | Google Scholar