Solar influences on the Earth’s atmosphere: solved and unsolved questions

The influence of the Sun on the Earth’s atmosphere and climate has been a matter of hot debate for more than two centuries. In spite of the correlations found between the sunspot numbers and various atmospheric parameters, the mechanisms for such influences are not quite clear yet. Though great progress has been recently made, a major problem remains: the correlations are not stable, they may strengthen, weaken, disappear, and even change sign depending on the time period. None of the proposed so far mechanisms explains this temporal variability. The basis of all solar activity is the solar magnetic field which cyclically oscillates between its two components—poloidal and toroidal. We first briefly describe the operation of the solar dynamo transforming the poloidal field into toroidal and back, the evaluated relative variations of these two components, and their geoeffective manifestations. We pay special attention to the reconstruction of the solar irradiance as the key natural driver of climate. We point at some problems in reconstructing the long-term irradiance variations and the implications of the different irradiance composite series on the estimation of the role of the Sun in climate change. We also comment on the recent recalibration of the sunspot number as the only instrumentally measured parameter before 1874, and therefore of crucial importance for reconstructing the solar irradiance variations and their role in climate change. We summarize the main proposed mechanisms of solar influences on the atmosphere, and list some of the modelling and experimental results either confirming or questioning them. Two irradiance-driven mechanisms have been proposed. The “bottom-up” mechanism is based on the enhanced absorption of solar irradiance by the oceans in relatively cloud-free equatorial and subtropical regions, amplified by changes in the temperature gradients, circulation, and cloudiness. The “top-down” mechanism involves absorption by the stratospheric ozone of solar UV radiation whose variability is much greater than that of the visible one, and changes of large-scale circulation patterns like the stratospheric polar vortex and the tropospheric North Atlantic Oscillation. The positive phase of the tropospheric North Atlantic Oscillation indicative of a strong vortex is found to lag by a couple of years the enhanced UV in Smax. It was however shown that this positive response is not due to lagged UV effects but instead to precipitating energetic particles which also peak a couple of years after Smax. The solar wind and its transients modulate the flux of galactic cosmic rays which are the main source of ionization of the Earth’s atmosphere below ∼50 km. This modulation leads to modulation of the production of aerosols which are cloud condensation nuclei, and to modulation of cloudiness. Increased cloudiness decreases the solar irradiance reaching the low atmosphere and the Earth’s surface. Variations of the galactic cosmic rays also lead to variations of the electric currents and the ionospheric potential in the polar caps which may intensify microphysical processes in clouds and thus also cause cloudiness variations. Solar energetic particles are produced during eruptive events at the Sun. They produce reactive odd hydrogen HO_x and nitrogen NO_x which catalytically destroy ozone in the mesosphere and upper stratosphere—“direct effect.” NO_x which are long-lived in the lack of photoionization during the polar night, can descend to lower altitudes and destroy ozone there producing a delayed “indirect effect.” In the absence of sunlight ozone absorbs longwave outgoing radiation emitted by the Earth and atmosphere. Ozone depletion associated with ionization increases leads to cooling of the polar middle atmosphere, enhancing the temperature contrast between polar and midlatitudes and, thus, the strength of the stratospheric polar vortex. Solar energetic particles are powerful but sporadic and rare events. An additional source of energetic particles are the electrons trapped in the Earth’s magnetosphere which during geomagnetic disturbances are accelerated and precipitate into the atmosphere. They are less energetic but are always present. Their effects are the same as that of the solar energetic particles: additional production of reactive HO_x and NO_x which destroy ozone resulting in a stronger vortex and a positive phase of the North Atlantic Oscillation. It has been shown that the reversals of the correlations between solar activity and atmospheric parameters have a periodicity of ∼60 years and are related to the evolution of the main forms of large-scale atmospheric circulation whose occurrence has a similar periodicity. The large-scale circulation forms are in turn influenced by the state of the polar vortex which can affect the troposphere-stratosphere interaction via the propagation of planetary waves. Two solar activity agents are supposed to affect the stratospheric polar vortex: spectral solar irradiance through the “top-down” mechanism, and energetic particles. Increased UV irradiance was found to lead to a negative phase of the North Atlantic Oscillation, while increased energetic particles result in a positive phase. Solar irradiance, like sunspots, is related to the solar toroidal field, and energetic particle precipitation is related to the solar poloidal field. In the course of the solar cycle the irradiance is maximum in sunspot maximum, and particle precipitation peaks strongly in the cycle’s declining phase. The solar poloidal and toroidal fields are the two faces of the solar large-scale magnetic field. They are closely connected, but because they are generated in different domains and because of the randomness involved in the generation of the poloidal field from the toroidal field, on longer time-scales their variations differ. As a result, in some periods poloidal field-related solar drivers prevail, in other periods toroidal field-related drivers prevail. These periods vary cyclically. When the poloidal field-related drivers prevail, the stratospheric polar vortex is stronger, and the correlation between solar activity and atmospheric parameters is positive. When toroidal field-related drivers prevail, the vortex is weaker and the correlations are negative.

1 Introduction

Sun is the main source of energy for the Earth, providing light and heat necessary for life and determining the terrestrial cycles. Many ancient civilizations have worshiped it (Wigington, 2023).

Probably the earliest documented ideas about a connection between the solar appearance and weather date back to about 400 years BC. Meton of Athens, based on more than 20 years of solar observations, concluded that when Sun has spots, the weather tends to be wetter and rainier. These findings were reported in the fourth century BC by Theophrastus (Hoyt and Schatten, 1997).

More than two millennia later, the interest in this subject was revived by the famous paper of sir William Herschel (1801) who noticed a connection between the number of sunspots and the wheat prices at the London stock market since 1650 during five prolonged periods of few sunspots, the prices were high while during five other durations the prices were low. Herschel hypothesized that times of many sunspots “may lead us to expect a copious emission of heat and therefore mild seasons,” and periods of few spots would signal “spare emission of heat” and “severe seasons” which would lead to low yield and high prices.

Herschel was at that time severely ridiculed, however this subject still remains an area of hot discussions. A detailed review of the papers published up to 2013 supporting or rejecting Herschel’s hypothesis is given by Love (2013), who also refuted it. Love repeated Herschel’s analysis on data from two London annual mean wheat price lists covering years 1646–1755 and 1756–1880, respectively, combined with two lists of the monthly mean prices for wheat in United States for the periods 1842–1907 and 1908–2012, respectively. The combined list covers the period from 1646 to 2012, and based on it, Love found that Herschel’s hypothesis is statistically insignificant.

However, as Pustil’nik and Yom Din (2013) pointed out: “to implement the possible effect of space weather on the terrestrial harvests and prices, a simultaneous fulfillment of three conditions is required:

1) sensitivity of local weather to the state of space weather;

2) sensitivity of the area-specific agricultural crops to the weather anomalies;

3) relative isolation of the market.”

Medieval England answered all 3 conditions. Weather there is sensitive to space weather (Chapter 6). Agriculture is sensitive to weather conditions: severe winters, or insufficient irradiance during the growth period would lead to low yields and high prices. (It should be noted that in other regions, e.g., with hot and arid climate, the dependence of the yields on temperature may be opposite). Finally, the wheat market in Medieval England was an isolated market with no import of agricultural goods.

None of these is true about Love’s (2013) data set:

(i) It combines data from widely separated regions (England and US), one of them very big, with different climatic characteristics, different sensitivity of local weather to space weather, different sensitivity of agriculture to local weather;

(ii) During the long period from 1646 until 2012, several reversals of the correlation between solar activity and climate have been reported (Chapter 6);

(iii) During at least its later part international trade has been quite active.

We are paying so much attention to the conclusion about the statistical insignificance of Herschel’s hypothesis because it is an excellent example of a major problem in Sun-climate relations: the relations are not stationary and homogenous, they vary in both time and space.

A new revival of the interest in Sun-climate connections was triggered by the paper by C.P. Smyth in the proceedings of the Royal Society in 1870, in which he reported that the most marked cycle in terrestrial temperature “has a period of 11.1 years, or practically the same as Schwabe’s numbers of new groups of solar spots”. It was followed by dozens of papers relating sunspots to the Earth’s temperature, rainfall and droughts, river flow, cyclones, insect populations, shipwrecks, economic activity, wine vintages, etc.

The next boost was given by Eddy’s seminal 1976 paper “The Maunder Minimum” (Eddy, 1976) in which he announced a period of very low solar activity in the second half of the 17th century and related it to a period of low temperatures.

Many solar-climate studies were summarized by Herman and Goldberg (1978), and later in the comprehensive review by Hoyt and Schatten (1997) who compiled a bibliography of over 2,000 papers and books concerning the Sun’s influence of weather and climate.

Extensive studies of the Sun-climate connection were organized in the framework of SCOSTEP’s (Scientific Committee On Solar TErrestrial Physics) scientific programs Climate and Weather of the Sun-Earth System “CAWSES” (Gray et al., 2010), CAWSES 2 (Seppälä et al., 2014), and VarSITI (Variability of the Sun and Its Terrestrial Impacts), for reviews see Ward et al. (2021) and Shiokawa and Georgieva (2021), and in the ongoing SCOSTEP’s program PRESTO (Predictability of the Variable Solar-Terrestrial Coupling).

The pronounced temporal variability of the correlation links observed between atmospheric parameters and solar activity factors is a major problem in solar influences on the terrestrial atmosphere. The correlations may strengthen, weaken, disappear, and even change sign depending on the time period (e.g., Herman and Goldberg, 1978 and the references therein), moreover they may be different in different regions. If this spatial and temporal variability is not taken into account, the correlations between the manifestations of solar activity and climatic parameters may be estimated to be statistically insignificant, and the hypothesis of solar influences on the atmosphere may be refuted, as in (Love, 2013).

All of the proposed so far mechanisms do not explain this temporal variability. This means that an important aspect of the solar-atmospheric influences is still not understood.

After a brief description of the solar dynamo and the two components of the solar magnetic field, we make an overview of the geoeffective agents of solar activity, and the main proposed so far mechanisms for the influences of these agents on the atmosphere, especially on long-term (climatic) time-scales. We emphasize on the reversals in the sign of correlation between solar activity and atmospheric parameters, and on the finding that the solar influences on the atmosphere depend on the state of the stratospheric polar vortex. Based on the reported relative evolution of the two solar magnetic field components, and on the different effects of their manifestations on the vortex, we suggest that the vortex intensifies/weakens when poloidal/toroidal field-related solar activity agents have stronger impact on the atmosphere, and that the epochs of prevailing poloidal/toroidal field-related agents coincide with epochs of positive/negative correlations between solar activity and atmospheric parameters.

The paper is structured as follows: Chapter 2 gives a brief description of the basics of solar activity and solar dynamo related to the way Sun affects the Earth. Chapter 3 summarizes the geoeffective manifestations of solar activity. Chapter 4 highlights some of the proposed mechanisms for solar influences on climate. Chapter 5 discusses the instability of solar-climate relationship, and proposes a possible explanation. The summary and discussions are in Chapter 6.

Figure 1 summarizes the main topics on the paper.

FIGURE 1

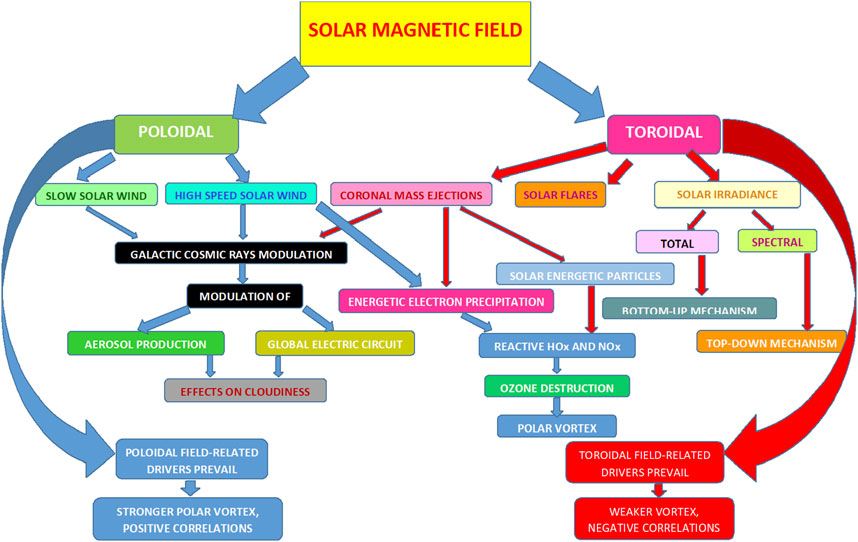
FIGURE 1. Schematics of the solar activity geoeffective drivers and the mechanisms of their influences on the atmosphere. See the text for details.

2 Solar dynamo

The term “solar activity” encompasses all changes in the appearance and energy output of the Sun. The base of all solar activity is the large-scale solar magnetic field which oscillates between its two components, poloidal and toroidal, much like the oscillations between kinetic and potential energies in a simple harmonic oscillator (Parker, 1955).

The driver of solar activity is the solar dynamo mechanism. There are excellent recent reviews highlighting the current understanding and unsolved problems in solar dynamo theory (e.g., Charbonneau, 2020; Karak, 2023). Here we will only briefly explain the general way the solar dynamo is believed to operate, with an emphasis on the features directly related to the way solar activity affects the terrestrial weather and climate.

The large-scale solar magnetic field is poloidal at sunspot minimum. At the tachocline, a thin layer at 0.7 solar radii between the rigidly rotating radiative zone and the differentially rotating convection zones where the angular velocity gradient is greatest, the differential rotation stretches this poloidal North-South magnetic field in East-West direction making it toroidal, and the convection concentrates it in bundles of field lines—magnetic flux tubes. When the magnetic field in a flux tube gets strong enough, the flux tube becomes buoyant and emerges, piercing the solar surface in two spots (sunspots) with opposite polarities. During its rise through the convection zone, the flux tube is subjected to the Coriolis force and rotates with respect to the East-West direction. As a result, the leading (in the direction of solar rotation) sunspots appear at lower heliolatitudes than the trailing sunspots. In each hemisphere the leading sunspots have the polarity of the respective poles which are opposite in the two hemispheres (Parker, 1955).

This part of the solar dynamo, the generation of the toroidal field from the poloidal field, is commonly accepted.

The second part, the regeneration from this toroidal field of a poloidal field with the opposite magnetic polarity, is less clear. The mechanism presently considered as the most promising one was proposed as an idea by Babkock (1961) and mathematically developed by Leighton (1969): In the course of the solar cycle, the sunspots emerge at lower and lower heliolatitudes. The leading spots which are closer to the equator diffuse across the equator and cancel with the opposite polarity leading spots in the opposite hemisphere. The trailing sunspots and the remaining sunspot pairs are carried toward the poles. On their way some of them cancel each other, others merge to form bigger unipolar regions. Because of the cancellation of the leading polarity spots across the equator, there is excess trailing polarity flux, and the net flux reaching the poles has the polarity of the trailing sunspots. There it cancels the polar field of the old ∼11-year sunspot cycle, then accumulates to form the opposite polarity poloidal field of the new cycle.

In the original Leighton’s mathematical model, the trailing polarity flux is carried to the pole by diffusion caused by supergranular convection in the solar outer layers (Leighton, 1964). Wang et al. (1991) proposed an additional mechanism—a large-scale meridional circulation. At the surface it carries the trailing polarity flux to the poles where it accumulates to reverse the old polar fields, sinks to the tachocline, and returns towards the equator like a conveyor belt, on the way transforming the poloidal field into toroidal field which emerges at progressively lower and lower latitudes as the sunspots of the new solar cycle.

In the course of a typical activity cycle, about 10²⁵ Mx of unsigned magnetic flux emerge in active regions (groups of bipolar sunspot pairs). The polar cap magnetic flux reaches 10²² Mx, which is equivalent to the unsigned flux contained in one single large bipolar active region, so the toroidal-to-poloidal flux conversion efficiency required by the Babcock–Leighton mechanism is quite low (Charbonneau, 2020). There is a strong correlation between the solar polar field and the following sunspot cycle amplitude, but there is no correlation between the sunspot cycle amplitude and the following polar field. It was suggested that this is due to the randomness in the production of the poloidal field by the decay of tilted sunspot pairs, because of the scatter in the tilt angles of the bipolar sunspot groups. This is pointed as a possible reason for the sunspot cycle variability (e.g., Stenflo and Kosovichev (2012); Jiang et al. (2014); Karak and Miecsh (2017); Choudhuri (2023) among others).

In summary, the two components of the large-scale solar magnetic field, toroidal and poloidal, are generated in different domains, at the tachocline and in the upper part of the convection zone, respectively. They are phase shifted, and the phase shift is not necessarily constant but depends on the speeds of the meridional circulation in the two domains which are not constant either. Finally, because of the randomness in the generation of the poloidal field from the toroidal field, they may have different long-term variations.

3 Geoeffective manifestations of the two components of the solar magnetic field

3.1 Solar drivers of geomagnetic activity

On 1 September 1859 Carrington, simultaneously with Hodgson, an English amateur astronomer, observed by chance a bright outburst of light in a group of large sunspots, lasting about 5 min. Carrington named it “solar flare.” This first ever observed flare was followed 17 h later by the strongest registered so far geomagnetic storm.

The paradigm that solar flares are drivers of geomagnetic disturbances survived for more than a century, until the paper “The solar flare myth” (Gosling, 1993) which demonstrated that geomagnetic disturbances are caused not by solar flares, but by coronal mass ejections (CME’s) which often accompany them. Both flares and CME’s originate from active regions, sites of strong and turbulent magnetic fields. The sudden release of accumulated magnetic energy in an active region can produce either a solar flare—an intense burst of radiation across the whole electromagnetic spectrum, along with particle acceleration, or a CME—a huge bubble of plasma with embedded magnetic fields ejected from the corona, or often both. With increasing flare intensity, the percentage of flares without observed CME’s decreases (Yashiro et al., 2004).

Both flares and CME’s are manifestations of the solar toroidal field, so their numbers and intensity follow the sunspot cycle. While solar flares alone have no effect on the geomagnetic activity, CME’s interact with the Earth’s magnetosphere and are the drivers of the most intense geomagnetic storms. Therefore, there is a maximum in geomagnetic activity caused by CME’s around sunspot maximum (Smax).

Later in the sunspot cycle, when the leading sunspots have canceled with the leading opposite polarity sunspots of the opposite hemisphere, the trailing polarity spots are carried poleward, and on the way some of them merge to form bigger and bigger unipolar regions (“coronal holes”). As the coronal holes are unipolar regions, their field lines do not close back on the solar surface, and the solar plasma freely flows and accelerates along them into the heliosphere as high speed solar wind streams (HSS’s) which also interact with the Earth’s magnetosphere and cause geomagnetic storms. They are as a rule weaker than CME-driven ones, however much longer and recurrent during the long lifetime of the coronal holes (Borovsky and Denton, 2006). HSS’s are manifestations of the solar poloidal field and are the main drivers of geomagnetic activity in periods when they are maximum in number and intensity (Richardson and Cane, 2012), which is a couple year after Smax (Wang and Sheeley, 1990). Also related to the solar poloidal field is the slow solar wind—the ever expanding solar atmosphere (Parker, 1955).

Therefore, geomagnetic activity and geomagnetic activity and sunspot number are only weekly correlated (Figure 2A). Geomagnetic activity has two maxima in the sunspot cycle: one coinciding with Smax and caused by solar toroidal-field related CME’s, and a second one on the sunspot declining phase caused by poloidal field-related HSS’s (Figure 2B).

FIGURE 2

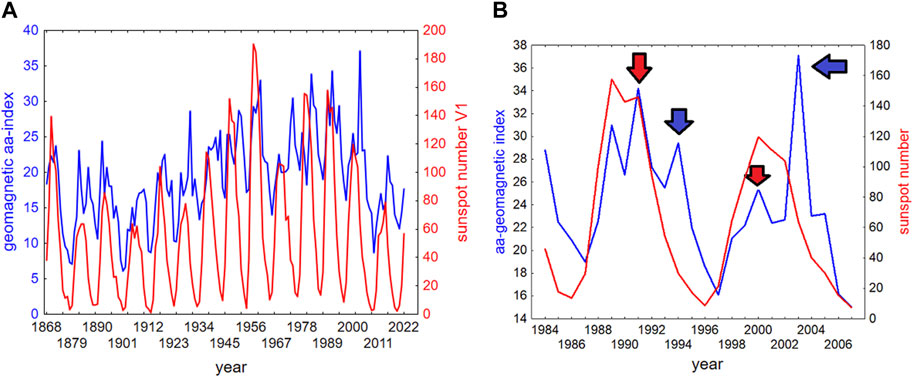
FIGURE 2. (A) Sunspot (red line) and geomagnetic (blue line) activity since 1868. Here and further, the sunspot activity is presented by the International sunspot number (now known as Version V.1), with the values from 2015 onward calculated from the correlation between V1 and V2 during cycles 19 and 20, and the geomagnetic activity is presented by the geomagnetic aa-index. (B) An illustration of the two peaks of the geomagnetic activity in the sunspot cycle: one caused by solar toroidal-field related CME’s, and coinciding with Smax (red arrows), and a second one on the sunspot declining phase caused by solar poloidal field-related HSS’s (blue arrows).

3.2 Solar irradiance

Sun emits electromagnetic radiation at all wavelengths from gamma to infrared. The integrated energy flux is referred to as total solar irradiance (TSI) measured in power per unit area. The spectrally resolved radiative flux (power per unit area and wavelength) is denoted as spectral solar irradiance (SSI). Earlier, TSI was known as “solar constant.” Only after the launch of instruments outside the Earth’s atmosphere, it was proven that the “solar constant” is not constant but varies in phase with the sunspot number (Fröhlich, 2000).

It may seem counterintuitive that TSI increases with increasing number and area of sunspots which are dark features. The explanation is that the brightness of a flux tube is determined by its diameter. The emerging flux tubes range in size from large, sunspot-containing active regions to pores, to faculae, to small bipoles that populate the quiet Sun. In large flux tubes (sunspot and pores) the magnetic field inhibits the convective energy transport within the flux tube and attenuates the heat flux from below; the flux tube is cooled and dark. In small flux tubes (faculae and network), the radiative inflow through the hot walls can significantly heat up the middle and upper parts of the flux tube’s photosphere making these layers hotter and brighter than the quiet Sun (Fligge and Solanki, 2000). The bright faculae and network outnumber and outlast the dark sunspots, so with increasing solar toroidal field/sunspot number the irradiance increases.

Solar irradiance is dominated by radiative output at wavelengths between 400 and 800 nm. Radiation at wavelengths >400 nm (visible and infrared) can reach the troposphere and the Earth’s surface, and directly cause variations in the Earth’s energy balance. Radiation at shorter wavelengths is absorbed higher in the atmosphere and plays key role in chemical-dynamical coupling of the atmospheric layers via interactions with atmospheric ozone.

3.3 Estimation of the long-term variations of the solar magnetic field components and their geoeffective agents

The geoeffective solar activity agents can be divided in two ways:

- by the type of emission: electromagnetic (solar flares and solar irradiance), or corpuscular (CME’s, HSS’s, and slow solar wind

- by their origin: toroidal (solar irradiance, flares, CME’s) or poloidal solar magnetic field (HSS’s, slow solar wind).

We are interested in the long-term variations of the solar activity agents according to their origin.

The most straightforward manifestation of the solar activity effects on the Earth is geomagnetic activity. The geomagnetic activity records are much longer than instrumental solar magnetic field observations and can be used as proxy to estimate the long-term variations of the solar magnetic field and its components.

Feynman (1982) noticed that if a geomagnetic activity index (e.g., aa) is plotted against the sunspot number, all points lie above a straight line such that for any number of sunspots there is some minimum value below which the geomagnetic activity cannot fall (Figure 3). Feynman (1982) defined this minimum value as the sunspot-related geomagnetic activity—the minimum geomagnetic activity aa_R for a given number of sunspots R. We now know that it is due to CME’s whose number and intensity increase with increasing number of sunspots. The points above this minimum line denote non sunspot-related geomagnetic activity aa_I due to HSS’s so that

$\mathit{aa}={\mathit{aa}}_{\mathit{R}}+{\mathit{aa}}_{\mathit{I}}$

where $a{a}_R=a_0+bR$

FIGURE 3

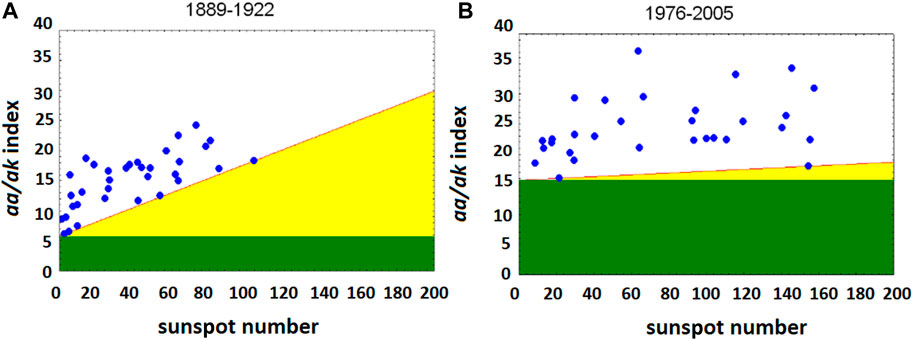
FIGURE 3. Dependence of the geomagnetic activity on the sunspot number in the period (A) 1899–1922 and (B) 1976–2005. Adapted with permission from Figure 4 in Georgieva et al. (2012).

The value of a₀ was chosen as the intercept of the minimal line with the aa-axis and, according to Feynman (1982), has no physical meaning as far as the variations in aa_R and aa_I are concerned.

For the period 1868–1975, Feynman (1982) determined a₀ = 5.38 and b = 0.12. Other authors calculated these coefficients using data covering different periods, and received different values:

$a{a}_R=5.17+0.07*R$ (Ruzmaikin and Feynman, 2001).

$a{a}_R=10.9+0.097*R$ (Hathaway and Wilson, 2006).

$a{a}_R=7.1+0.106*R$ (Georgieva et al., 2007).

This may be due to either different methodology to calculate them, or to real temporal variability.

Kirov et al. (2013) calculated the cycle-to-cycle values of a₀ and b from cycle 9 to 24 using for all cycles the method described by Hathaway and Wilson (2006). Table 1; Figure 3 demonstrates that a₀ and b are indeed different in different periods. They both have physical meanings:

TABLE 1

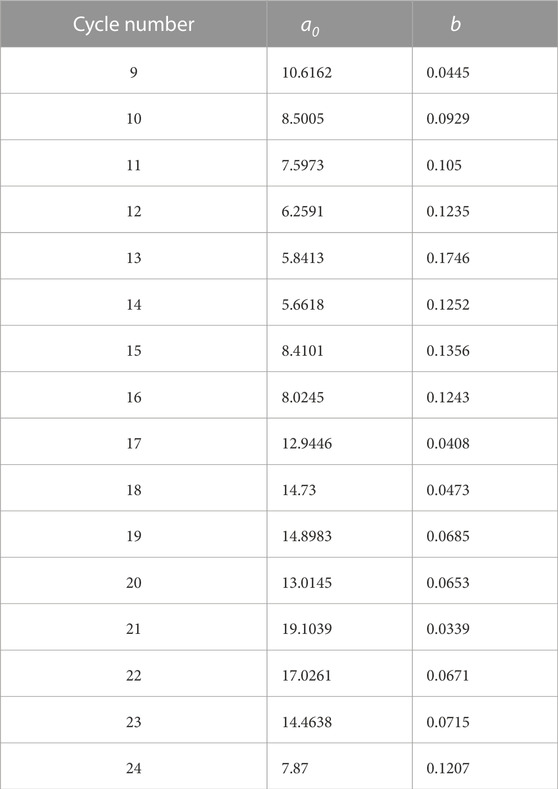
TABLE 1. Values of the coefficients a0 and b in Chapter 4.3 for sunspot cycles from 9 to 24 Kirov et al. (2013).

a₀ named “geomagnetic activity floor” is the level below which geomagnetic activity cannot fall even in the absence of any sunspots and HSS’s. Unlike sunspots, geomagnetic activity never falls to zero in cycle minimum (Figure 2A). This geomagnetic activity floor is due to the slow solar wind, in which Earth is immersed all the time and atop of which CME’s and HSS’s ride (Georgieva, 2013). Kirov et al. (2015) showed that the slow solar wind parameters vary from minimum to minimum. As both the slow solar wind and HSS’s are related to the solar poloidal field, both a₀ and aa_I increase with increasing poloidal field.

b is a measure of the sensitivity of the geomagnetic activity to increasing number of sunspots/CME’s. b was shown to be strongly correlated (r = 0.923 with p = 0.025) with the rate of increase from sunspot minimum to maximum of the magnetic fields in sunspots, respectively, active regions from which CME’s originate (Georgieva et al., 2012). In other words, the faster the magnetic field in active regions increases with increasing SSN, the faster the intensity of CME’s generated there grows, and the faster geomagnetic activity increases.

Figure 4 demonstrates that a₀ and b vary in time with quasi-centennial periodicities which are in antiphase: in some periods the slow solar wind is weakly geoeffective and HSS’s have little impact on the overall geomagnetic activity, which however quickly increases with increasing sunspot number due to the quickly increasing magnetic field in active regions, respectively the geoeffectiveness of CME’s (Figure 3A). In other periods the situation is opposite (Figure 3B).

FIGURE 4

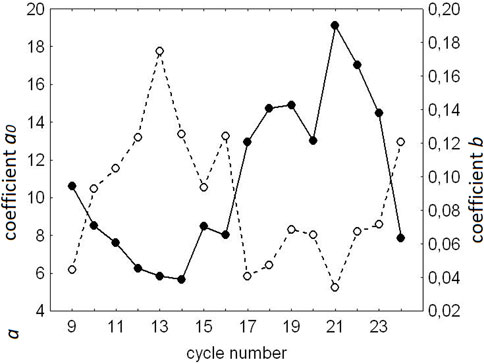
FIGURE 4. Long term variations of the coefficients a0 (solid line) and b (dashed line). Adapted with permission from Figure 2 in Georgieva et al. (2012).

3.4 Estimation of the long-term variations of solar irradiance

Solar irradiance is a key natural driver of climate, so the correct estimation of its variations is crucial for the evaluation of the solar influence on climate change.

Reliable measurement of solar irradiance began when instruments were launched outside the Earth’s atmosphere. The first space-borne instrument was the Hickey–Frieden radiometer (Hickey et al., 1980) aboard the NOAA/NASA mission Nimbus-7 launched in 1978, followed by the ACRIM experiment aboard the Solar Maximum Mission. Since then, TSI has been measured by numerous instruments with partly overlapping periods.

3.4.1 Composite instrumental TSI series

The record of even a single instrument needs a careful calibration because of orbital changes and the sensor’s degradation with time (BenMoussa et al., 2013). Further, mutual calibration is needed to construct a single composite series from several instruments.

The three most popular composite TSI series are ACRIM (e.g., Wilson and Mordvinov, 2003; Wilson, 2017), IRMB4 (Dewitte et al., 2004; Mekaoui and Dewitte, 2008; Dewitte and Nevens, 2016), and PMOD/WRC5 (Fröhlich, 2000; Fröhlich, 2006). They all feature an ∼11-year cycle matching the sunspot cycle, but with different amplitudes and different cycle-to-cycle variations. Figure 5 illustrates their differences: The ACRIM composite shows a general TSI increase during the 1980s and 1990s followed by a slight decline. According to the Royal Meteorological Institute of Belgium (IRMB)’s composite, there are practically no cycle-to cycle TSI variations, while in the Physikalisch-Meteorologisches Observatorium Davos (PMOD) composite a steady decrease is seen.

FIGURE 5

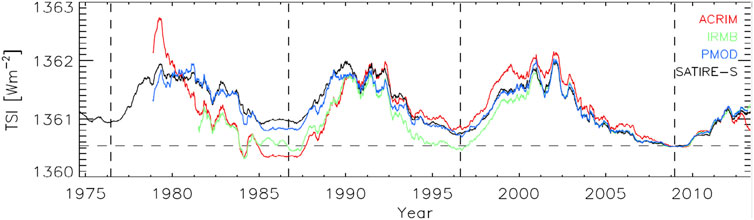
FIGURE 5. The ACRIM (version 11/13), IRMB (version dated 19th December 2013, provided by S. Dewitte) and PMOD (version d41 62 1302) composite records of TSI. Also plotted is the SATIRE-S (Yeo et al., 2014) reconstruction of TSI. The vertical dashed lines mark the position of solar cycle minima. All the time series were normalized to TIM at the 2008 solar cycle minimum (horizontal dashed line) and smoothed with a 181-day boxcar filter. Reproduced with permission from Yeo et al. (2014).

The discrepancies are even bigger for periods before direct satellite measurements when proxies must be used.

3.4.2 Derivation of TSI from proxies

The derivation of TSI from proxies is based on the correlations between the proxies’ values and direct irradiance measurements for periods when they overlap (Chapman et al., 1997). It is assumed that all solar irradiance variations on time scales more than hours are caused by variations of the photospheric magnetism, and are traceable through features like sunspots, faculae, ephemeral regions, network, plus the contribution of the quiet Sun (Solanki et al., 2013). The magnetic flux through each component is best provided by full-disc magnetograms which, however, are only available since 1974. For earlier times, back to 1874, records of sunspot areas are used, based on the correlation between the sunspot’s area and its magnetic field (Nicholson, 1933). Before 1874 the sunspot number is used as a proxy for the sunspot area, based on the high linear correlation between the two (Hathaway, 2010). Facular areas were routinely measured at RGO from 1874 to 1976 and at USAF afterwards. The reconstructions for earlier periods (Solanki et al., 2002) are based on the correlation between the facular and sunspots areas in cycle 22 (Chapman et al., 1997), and on the correlation between the sunspot area and sunspot number after 1874.

The importance of the TSI reconstruction for estimation of the solar irradiative forcing on climate was studied by Connolly et al. (2021). They compiled from literature sixteen different reconstructions of the TSI variations since at least the 19th century, which used different instrumental composites, different functions for the inter-relationships between sunspots, faculae and TSI during the satellite era, and different other proxies like solar microwave emissions, plage areas, cosmogenic isotopes, etc. Half of these reconstructions are “low variability” and half are “high variability” (Figure 6).

FIGURE 6

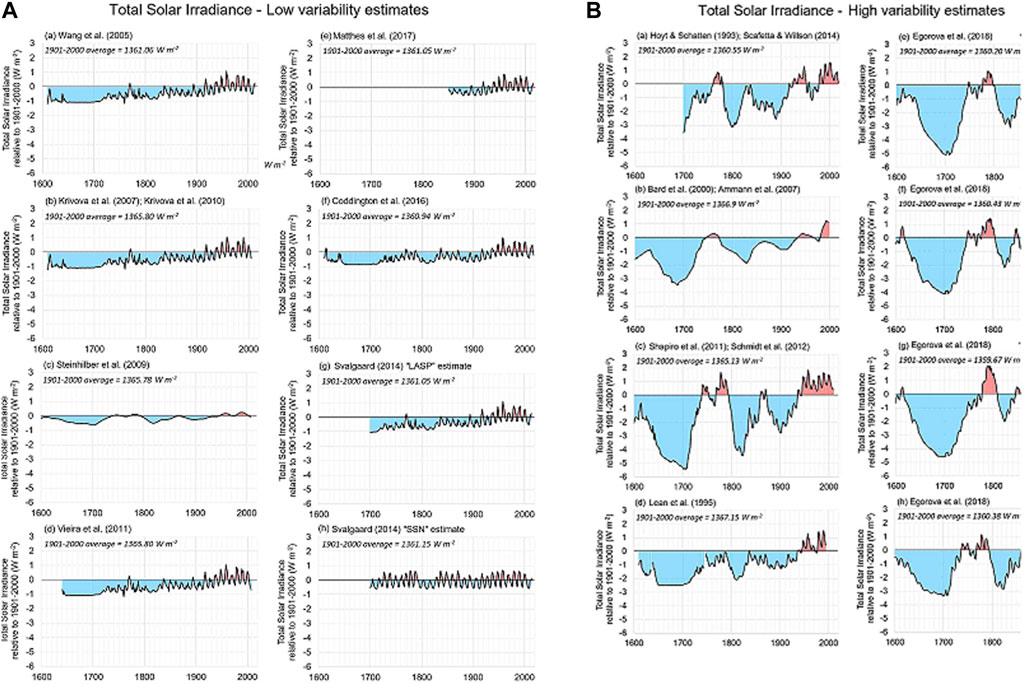
FIGURE 6. (A) Eight low variability estimates of TSI changes relative to the 1901–2000 average; 6 (B) Eight high variability estimates of the TSI changes relative to the 1901–2000 average. Note the y-axis scales are the same in this figures (A,B). Reproduced from Figures 2, 3 in Connolly et al. (2021).

Further, Connolly et al. (2021) based on five independent estimates of the Northern Hemisphere temperature trends, evaluated the contribution from direct solar forcing to temperature trends for all sixteen estimates of TSI. The evaluated solar contributions ranged from 0.00% role of the Sun in recent decades for Svalgaard’s low variability reconstruction (https://leif.org/research/download-data.htm) for all Northerh hemisphere datasets, to 100% for high variability reconstruction of ocean temperatures of Bard et al. (2000) updated by Ammann et al. (2007). Therefore, the TSI reconstructions are crucial for estimating the solar activity contribution to climate change. It should be noted that IPCC only uses low variability reconstructions (Connolly et al., 2021).

3.5 The sunspot series

As explained above, longer TSI reconstructions include progressively less directly measured parameters, and all reconstructions starting before 1874 have the number of sunspots or sunspot groups as the only instrumentally measured parameter. Therefore, the sunspot record is of critical importance for estimating the long-term solar irradiance variations and their impact on climate change.

Until 2015, there were two long sunspot series:

- the original “Zurich International Sunspot Number” or “Wolf Number,” WN, now named “Version 1.” It was defined by Wolf as WN = k(10xGN + SN) where GN is the number of sunspot groups, and SN—the number of individual sunspots (Waldmeier, 1961). This data series covers the period from 1700 to 2015.

- The Group sunspot number WG based on the parameter GN in Wolf’s formula (Hoyt and Schatten, 1998). The number of sunspot groups is determined more reliably than sunspots which allows to include earlier observations and to extend the data series back to 1610. A normalizing factor is used to scale WG to WN which, based on the period 1874–1976, is 12.08, so that WG = 12.08xGN.

WN and WG are highly correlated (r = 0.92) but differ in their long-term trends: much greater in WG (Figure 7, top panel) implying that the second half of the 20th century was a period of unusually high solar activity (“Modern Grand Maximum”), and that there was a substantial increase in the solar irradiance since the Maunder minimum. Thus studies using WG would estimate much higher role of the Sun in climate changes than studies using WN.

FIGURE 7

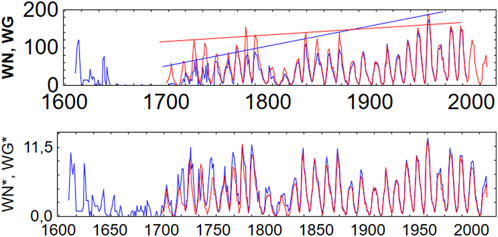
FIGURE 7. Top: The original Wolf sunspot number WN (red) and Group sunspot number WG (blue); bottom: The recalibrated sunspot number WN* known as V2.0 (red), and group sunspot WG* (blue). Adapted from Figure 1 and Figure 2 of Georgieva et al. (2016).

This inspired a group of scientists to “rectify discrepancy between Group and International sunspot number series,” and to publish “a vetted and agreed upon single sunspot number time series” (Cliver et al., 2013; Clette et al., 2014), because “given the importance of the reconstructed time series, the co-existence of two conflicting series is a highly unsatisfactory solution which should be actively addressed” (Cliver et al., 2013). This highly unsatisfactory solution was actively addressed during a series of “Sunspot Number” Workshops, starting 2011. The workshops and the related activities resulted in the creation of new sunspot and group sunspot numbers series (Figure 7, bottom panel). Since 1 July 2015, SILSO (the Sunspot Index and Long-term Solar Observations) center in Brussels which was created in 1980 (then named the Sunspot Index Data Center) as a World Data Center with the task to continue the International Sunspot Number record, terminated this more than 400 years-long data series, and replaced it by the “new entirely revised data series” named Version 2.0.

The new series and its implications were made public at a press briefing during the IAU XXIX General Assembly in Honolulu, Hawaï, United States in 2015 (https://www.iau.org/news/pressreleases/detail/iau1508/):

“The new record has no significant long-term upward trend in solar activity since 1700, as was previously indicated. This suggests that rising global temperatures since the industrial revolution cannot be attributed to increased solar activity. The new correction of the sunspot number, called the Sunspot Number Version 2.0, nullifies the claim that there has been a Modern Grand Maximum. The results, presented at the IAU XXIX General Assembly in Honolulu, Hawaï, make it difficult to explain the observed changes in the climate that started in the 18th century and extended through the industrial revolution to the 20th century as being significantly influenced by natural solar trends.”

Meanwhile, the group sunspot number time series was also recalibrated (Svalgaard and Schatten, 2016) to bring it to closely match the Version 2.0 sunspot time series, and to show no long-term trend (Figure 7, bottom panel). With this, the task “to rectify discrepancies between the two series” was achieved, but not the task “to publish an agreed upon single sunspot number time series,” as this endeavor triggered the creation of multiple new alternative series (Clette, 2016). For the latest achievements in creating the new series see Clette et al. (2023).

Without going into further detail on the various series, we will emphasize on one problem of “rectifying the discrepancies” between WN and WG. The relations between various sunspot related solar parameters are not stable, e.g., between the number of sunspots and their total area, between the sunspot and facular areas, etc. It can be expected that ratio of the sunspots and sunspot group numbers is also variable. Tlatov (2013) showed that the average number of sunspots per group has cyclic variations with a period of about 100 years. Georgieva et al. (2016) demonstrated that the ratio varies both in the course of the sunspot cycle and from cycle to cycle. Figure 8A demonstrates that this ratio has well expressed long-term variations even during the interval 1874–1976 when their normalizing coefficient was calculated.

FIGURE 8

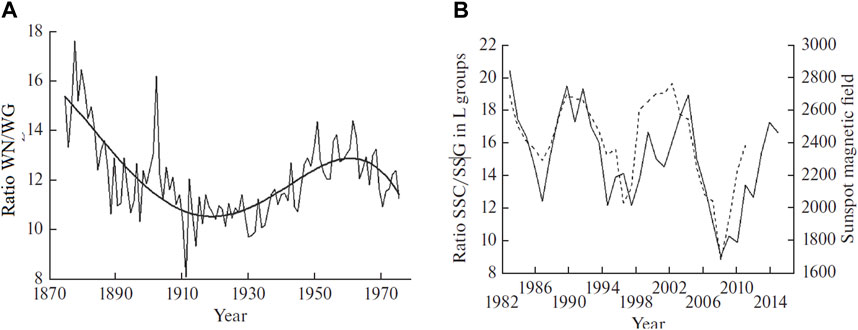
FIGURE 8. (A) Variations in the ratio between the International Zurich sunspot number WN and the number of sunspot groups WG in the period 1874 to 1976 during which the normalization factor 12.08 was determined to make WG identical to WN; (B) Variations of the average number of sunspots in large sunspot groups (solid line) and of the sunspot magnetic fields (dashed line), yearly averages. Adapted from Georgieva et al. (2016).

Sheeley (1966) found that the complexity (number of sunspots) of a sunspot group increases with its magnetic field. In the right panel of Figure 8B the biggest sunspot’s magnetic field (Pevtsov et al., 2011) is compared to the average number of sunspots in large sunspots groups. The correlation is 0.79 with p < 0.001. Therefore, the discrepancies between the two data series are a real feature reflecting variations in the solar magnetic fields, and the attempts to “reconcile” them are not justified. With the new “recalibrated” series important information is lost which can shed light on the long-term evolution of the Sun and solar magnetism. In the same time, modifying the sunspot time series leads to modified TSI and SSI time series, respectively to modified estimations of the impact of solar irradiance variations to climate change.

4 Proposed mechanisms for solar influences on climate

As the solar magnetic field has two components, toroidal and poloidal, two classes of solar activity drivers are expected to affect the terrestrial climate. The toroidal field related ones are solar irradiance, CMEs, and solar flares. The poloidal field-related ones are slow solar wind and HSS’s. CMEs and flares are sporadic and short-lasting events, and though they may have vigorous short-lasting responses, effects on the Earth on time scale of a solar rotation and longer are primarily determined by solar irradiance and poloidal field-related solar activity (Richardson and Cane, 2012).

4.1 Mechanisms related to solar irradiance variability

According to the IPCC (2023), “Estimation of TSI changes since 1900 has further strengthened, and confirms a small (less than about 0.1 Wm^–2) contribution to global climate forcing.”

Two mechanisms have been proposed to amplify this small solar irradiance forcing. One is related to TSI, the other to SSI.

4.1.1 “Bottom-up” mechanism—TSI

Sun emits most of its radiation in visible and infrared which penetrate down to the Earth’s surface and is absorbed by the surface which gets warmer and heats the adjacent air. Therefore, the most straightforward mechanism of solar influence on the surface air temperature can be direct heating.

The bottom-up mechanism is based on the spatially heterogeneous distribution of TSI reaching the surface, and on the amplification by positive feedbacks in the climate system. It involves TSI absorbed by the oceans in cloud-free equatorial and subtropical regions. According to some estimations (e.g., Misios et al., 2019), an additional solar forcing of 0.1 Wm⁻² in Smax as cited in IPCC AR6, can lead to warming in the tropical Pacific by ∼0.4°C.

4.1.1.1 Some basics

Due to the Coriolis force, easterly winds (known as “trade winds”) blow along the equator in the Pacific, pushing moist and warm surface water from South America towards Asia and Australia. It is replaced by colder water upwelling from deeper layers, so the sea surface in the eastern and central equatorial Pacific is relatively cold. The thermocline (boundary between warm surface and cold deep water) is deeper in the west than in the east. The warm water in the west heats the air above which ascends to form cumulus clouds and cause rainfalls. The already dried air at higher altitude travels back eastward, cooling on the way, and subsides there completing an east-west circulation cell known as Walker circulation.

During El Niño events, the trade winds weaken or even reverse leading to less water pushed to the west, weaker upwelling and deeper thermocline, respectively higher sea surface temperature in the eastern and central Pacific. The upward branch of the Walker circulation and the rainfall move eastward. In contrast, during La Niña events the trade winds are stronger, more warm water is pushed westward, the sea surface in the eastern and central Pacific cools even more, upwelling strengthens and the thermocline moves to the surface, the upward branch of the Walker circulation and the rainfall move eastward and intensify. El Niño and La Niña are the two opposite phases of “El Niño/Southern Oscillation” (ENSO).

4.1.1.2 Modeling and observational results

Meehl et al. (2003) performed ensemble experiments with a global coupled climate model and proposed a mechanism in which the solar forcing is amplified by coupled regional feedbacks involving the combination of temperature gradients, circulation regimes, and clouds. Increased TSI over the relatively cloud-free equatorial eastern Pacific increases the heating of the sea surface, respectively the evaporation. The trade winds carry this moisture westward to the precipitation zone to intensify the precipitation there, strengthen the Walker cell and the Hadley cell (meridional circulation between the equator and the tropics), and enhance the trade winds and upwelling, lowering the sea surface temperature in the east. The enhanced subsidence in the eastern Pacific atmosphere further reduces clouds, so even more solar radiation reaches the sea surface, and so on (Meehl et al., 2003; Meehl et al., 2009; Gray et al., 2010).

Meehl et al.’s (2003) model simulations were associated with low-frequency solar forcing in the early 20th century. Later Meehl et al. (2009) demonstrated that this mechanism is also applicable to the tropical climate system response to the 11-year solar cycle.

Meehl et al. (2007), Meehl et al. (2009), using composite observations for Smax for almost 150 years, demonstrated observationally that the increase of solar forcing/TSI is related to cold La Niña-like pattern in the Pacific during December–February, though the two have been shown to be due to different processes (van Loon and Meehl, 2008). Van Loon and Meehl. (2008), based on reanalysis data, also found La Niña-like anomalies in peak sunspot/TSI years. However, other studies show opposite results. White et al. (1997) used two independent datasets and found positive El Niño–like anomalies on decadal and interdecadal time-scales, oscillating almost in phase with the 11-year solar cycle. Meehl and Arblaster (2009) used reconstructed and reanalysis data and found negative La Niña–like anomalies in the eastern Pacific, followed by a transition to higher eastern equatorial sea surface temperatures a couple of years later, and explained them by dynamical air-sea coupling. But Roy and Haigh (2012) found colder temperatures in high solar activity not restricted to years of peak sunspot number, without lagged El Niño–like variation.

There are discrepancies also in the model results (e.g., Misios and Schmidt, 2013; Misios et al., 2019; Hou et al., 2021 among others). As some possible reasons for these discrepancies, the uneven distribution of La Niña and El Niño events has been proposed which may lead to biases in relatively short data series. Longer-term data should remove this problem.

Kirov and Georgieva (2002) used a long time-series: the ENSO reconstruction of Quinn et al. (1987) with the update of Ortlieb (2000), and compared it to the group sunspot numbers since 1610 (Figure 9A). The correlation coefficient is −0.76 with p < 0.01. Therefore, at least on interdecadal to centennial time-scales, increased sunspot numbers/TSI lead to La Niña-like anomalies in the equatorial Pacific, and this relation is stable. Figure 9B presents a superposed method analysis from the same dataset with the year of Smax as the 0 year. A well expressed minimum (La Niña-like event) is observed 1 year before Smax with subsequent recovery, but without El Niño-like event.

FIGURE 9

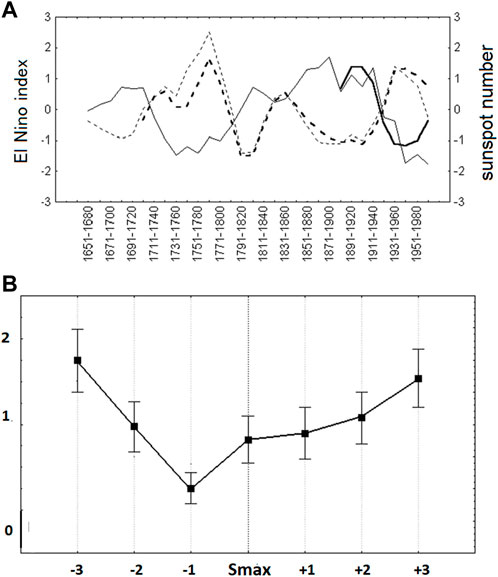
FIGURE 9. (A) Comparison between El Niño and solar activity: Quinn’s El Niño index—thin solid line and its analogue Cold Tongue Index (CTI), the average SST anomalies over 6N-6S, 180-90W (Deser and Wallace, 1987)—thick solid line; the group sunspot numbers WG—thin broken line and international sunspot numbers WN—thick broken line, in units of standard deviations, 30-year averages, detrended; (B) Superposed method analysis of El Niño intensity relative to sunspot maximum in the 11-year solar cycle (dotted vertical line). Adapted from Kirov and Georgieva (2002).

4.1.2 Top-down mechanism—SSI

The solar irradiance variability increases with decreasing wavelength–near 8% at 200 nm compared to 0.1% in TSI (Ermolli et al., 2013). Radiation with different wavelengths is absorbed at different levels in the atmosphere. Extreme UV (10–100 nm) which ionizes O₂ and N₂ and dissociates O₂, does not penetrate below 100 km. UV between 100 and 200 nm dissociates O₂ and NO, and is almost fully absorbed above the mesopause (∼80 km), except Ly-α (121.56 nm) which reaches 70 km and dissociates H₂O, CO₂ and CH₄ (e.g., Pikulina et al., 2022).

The “top-down” mechanism is based on solar UV reaching the stratosphere. UV between 240 and 320 nm is absorbed by stratospheric ozone leading to warming near the tropical stratopause (∼50 km). Increased UV below 242 nm leads to increased production of ozone, therefore more ozone to absorb UV, additionally increasing warming in low latitude mid and upper stratosphere ∼30–50 km (Hood, 2004; Crooks and Gray, 2005; Haigh, 2007). The increased temperature gradient between low and high latitudes drives a circulation pattern called Brewer-Dobson circulation—a large-scale overturning circulation in the stratosphere, in which air is transported from the tropics upward and to the poles where it descends back to the troposphere. Through the thermal wind balance, this results in westerly wind anomalies in the subtropical stratosphere which change the propagation of the planetary waves and the atmospheric wave-mean flow interaction. Consequently, these stratospheric westerly wind anomalies descend poleward to the troposphere and further to the surface, and influence the jet streams and the circulation patterns like the North Atlantic Oscillation (NAO—the pressure difference between Azores High and Icelandic Low), and its hemispheric analogue: Northern Annular Mode (NAM) defined as the pressure difference between high and middle northern latitudes at different levels (e.g., Baldwin and Dunkerton, 1999; Baldwin and Dunkerton, 2001; Baldwin and Dunkerton, 2005; Kodera and Kuroda, 2002; Matthes et al., 2006 among others). NAO/NAM is an indicator of the state of the polar vortex—a large-scale circulation pattern in the stratosphere which develops during polar winter and which can impact the tropospheric circulation patterns including the position and intensity of the jet stream, and weather regimes. It is an area of westerly winds in the high-latitude wintertime stratosphere separating cold polar and warmer lower-latitude air due to the temperature difference between them.

A number of studies (Gray et al., 2013; Scaife et al., 2013; Maliniemi et al., 2019; Kuroda et al., 2022) found that the positive NAO response lags by a couple of years the increased solar UV in Smax. Scaife et al. (2013) proposed a mechanism for this lagged response based on the extended memory of ocean heat content anomalies, and their subsequent feedback onto the atmosphere. It is however possible that the NAO response after Smax may be due not to the lagged effect of increased UV but to the concurrent effect of the increase of solar driven precipitating particles.

4.2 Mechanisms related to energetic particles

The energetic particles are the main source of ionization in the Earth’s atmosphere below 100 km where solar EUV and X-ray are already weakened. These can be galactic cosmic rays (GCRs) originating from outside the Solar system, consisting mostly of protons and some heavier elements, solar energetic particles (SEPs) dominated by protons, auroral and radiation belts electrons (Figure 1 in Mironova et al., 2015).

4.2.1 Galactic cosmic rays

Galactic cosmic rays (GCRs) are the main source of ionization of the Earth’s atmosphere below ∼50 km. Thanks to their high energy (10⁷–10²⁰ eV), colliding with atmospheric particles, they produce a cascade of secondary particles. Earth’s magnetic field shields the magnetosphere against the GCRs, so that for any geomagnetic latitude there is a “cutoff rigidity”—the minimum energy a particle needs to penetrate at this location. The solar wind and embedded magnetic field modulate the GCR flux. Following a powerful solar wind transient, a rapid decrease in the GCR flux is observed—a phenomenon known as a “Forbush decrease” (FD) after the name of Scott Forbush who first described it (Forbush, 1938). Traditionally both the GCR modulation and the FDs have been attributed to the solar toroidal field-related solar agents (CME’s), but recently the impact of the poloidal field has been emphasized (Krainev et al., 2019; Krainev et al., 2021; Vršnak et al., 2021 and the references therein).

Two main mechanisms are suggested for the influences of GCR on the atmosphere: through their effects on cloudiness, and on the global electric circuit.

4.2.1.1 Galactic cosmic rays—cloudiness

Dickinson (1975) reviewed the possible mechanisms of solar influences on climate, and concluded that only significant variations in the absorption of solar radiation or emission of infrared radiation by the lower atmosphere and the Earth’s surface can produce notable changes in the lower atmosphere. Because variations in solar radiation are too small (at that time even not yet detected), he suggested a second possible cause—the distribution of cloudiness as an indirect linkage to solar activity. As the only lower atmosphere process known to have large variations with solar activity he suggested the solar activity modulation of the GCR flux which ionizes the atmosphere (Ney, 1959). This leads to modulation of the production of aerosols which are cloud condensation nuclei, and to modulation of cloudiness. Increased cloudiness decreases the solar irradiance reaching the low atmosphere and the Earth’s surface. Dickinson (1975) estimated that an 8% increase in cloud cover would be equivalent to a 2% decrease in the solar constant.

Svensmark and Friis-Christensen (1997) compared cloud cover data from the International Satellite Cloud Climatology Project (ISCCP) from July 1983 to December 1990 with the GCR intensity from Climax, Colorado, and found a good positive correlation, confirming Dickinson’s (1975) theoretical speculations. This conclusion was criticized because:

- it was based on observations of regional rather than global cloud coverage;

- the actual microphysical explanation of a relationship between the GCR intensity and cloudiness was still lacking;

- the large-scale cloudiness may be influenced by other drivers like ENSO or volcanic eruptions (e.g., Jørgensen and Hansen, 2000);

- the correlation was not valid for all types of clouds (Kernthaler et al., 1999);

- short time series and uncertainties concerning instrument calibrations (Kristjánsson and Kristiansen, 2000);

- the correlation found for this short period does not hold during longer periods (Sun and Bradley, 2002).

On the other hand, this idea was supported by other studies (e.g., Feynman and Ruzmaikin, 1999; Shumilov et al., 2000; Harrison and Aplin, 2001; Todd and Kniveton, 2001; Eichkorn et al., 2002; Tinsley and Fangqun, 2004, among others).

Nowadays, this possible mechanism is still a matter of controversy. Some model studies (e.g., Bondo et al., 2010) found that the optical properties of aerosols show a distinct response to FDs, while others (e.g., Snow-Kropla et al., 2011) found very little response. Svensmark et al. (2012) used observations of the 13 strongest, with regard to ionization changes, FD’s during 2000–2006 from the Moderate Resolution Imaging Spectroradiometer (MODIS) aboard the Terra satellite to examine the response in six cloud microphysical parameters during FD’s rather than in cloudiness alone. The analysis showed that the observed parameters change consistently with each other during a FD, and there appears to exist a correlation between the magnitude of the FD event and its effect. However, Laken et al. (2012) used data from ISCCP and MODIS, and found no evidence in either of them of a solar-cloud link at either long or short timescales. Dunne et al. (2016) built a global model of aerosol formation based on laboratory measurements in the Cosmics Leaving Outdoor Droplets (CLOUD) chamber in Cern, and concluded that variations in cosmic ray intensity do not appreciably affect climate through nucleation in the present-day atmosphere. The conclusion in IPCC (2023) is that “There is high confidence that GCRs contribute a negligible effective radiative forcing over the period 1750–2019.” On the other hand, Svensmark et al. (2021), using CERES satellite observations, found that the 5 strongest week-long FD events coincide with changes in the average net radiative balance of 1.7 W/m², consistent with a link in which atmospheric ionization modulates formation and growth of aerosols which survive to cloud condensation nuclei and ultimately affect cloud formation and thereby temporarily the radiative balance of Earth.

Most of the aforementioned analyses are based on the aerosols’ response to FD’s, and short-term GCR effects on cloudiness. There are relatively few studies on long-term effects. Recently Kumar et al. (2023), based on 42 years of ERA-5 data (1979–2020) rather than on sporadic FD’s, reported that the GCR effects on cloudiness are significant but regional: negative in Eurasia mid-latitudes, positive below 2 km altitude in regional Walker circulations in the tropics, and positive in the free atmosphere (2–6 km) of the intertropical convergence zone.

In summary, the ever increasing number of published contradicting model, experimental, and observational results demonstrate that this possible mechanism of GCR influences on climate is still an open question and worth further research.

4.2.1.2 Galactic cosmic rays—global electric circuit

Electrical currents in the atmosphere are collectively denoted as the Global Electric Circuit (GEC). GEC consists of the highly conductive Earth’s surface and ionosphere, with the thunderstorm and other electrified clouds in-between (e.g., Tinsley, 2008; Lam and Tinsley, 2016). The positive charge in the order of 1A per storm from the ∼1,000 thunderstorms and electrified clouds flowing upward as a conduction current charges the ionosphere to ∼200–300 kV with respect to the ground. The circuit closes by the downward current density J_z.

GEC varies in response to varying solar activity through variations of the conductivity and J_z due to solar modulation of the ionization by GCRs, other energetic particles, and at high latitudes also the solar wind electric field. The lower atmosphere, especially at middle and low latitudes where energetic particles, except for high-energy GCR, do not reach, is mostly ionized by natural ground sources. An important source of ionization near the ground (up to 3 km) which affects GEC is the radioactive isotope radon-222 (Golubenko et al., 2020).

An enhancement of electric currents associated with GCR variations, as well as with changes of the ionospheric potential in the polar caps may intensify microphysical processes in clouds (Tinsley, 2008; Tinsley, 2022). The flow of electric currents through a low-conducting cloud layer contributes to the accumulation of space charge on cloud edges. Charging cloud particles influences microphysical interactions, one of the most important processes being the enhancement of the collection of aerosols by cloud droplets (electro-scavenging). In the case of super-cooled water droplets, electro-scavenging can enhance the contact ice nucleation and ice production in high-level clouds. Changes of cloud cover associated with GCR decreases on a daily time scale were detected by Pudovkin and Veretenenko (1995), Svensmark et al. (2016), Matsumoto et al. (2022). In turn, clouds regulate both the incoming short-wave solar radiation and the outgoing long-wave radiation emitted by the Earth and atmosphere. In the winter polar atmosphere, when the income of solar radiation is decreased, clouds influence mainly longwave radiation, producing a warming in the underlying atmosphere and a cooling above a cloud layer. Thus, cloudiness variations due to GCR effects on conductivity and the density of electric currents may be a plausible factor affecting the thermal-radiative balance and the dynamics of the polar atmosphere.

Observations of various meteorological effects correlating to J_z are summarized by Tinsley (2008) and Lam and Tinsley (2016). However, recently the statistical significance and credibility of some of the observations have been questioned (e.g., Edvartsen et al., 2022; Karagodin et al., 2022, etc.) Tinsley (2022) updated and evaluated correlations of day-to-day cloud opacity and surface pressure at high latitudes with changes in J_z, with suggestions for future work to resolve a number of outstanding issues.

4.2.2 Solar energetic particles

Solar Energetic Particles (SEPs), also known as Solar Cosmic Rays or Solar Proton Events, are produced during eruptive events at the Sun such as solar flares and CME’s (e.g., Reames et al., 2013; Desai and Giacalone, 2016, and references therein). They consist of protons (>90%), electrons and heavy ions with energies ranging from a few tens of keV to tens of GeV. SEP’s occur sporadically during high sunspot activity, and often appear together with FD’s, so the two phenomena partly compensate each other. Only in the polar atmosphere the SPE-induced ionization increase significantly exceeds the FD-induced decrease (Usoskin et al., 2011).

A special subset of SEP’s where charged particles from the Sun have sufficient energy to generate effects measurable at the Earth’s surface are Ground Level Enhancements (GLE’s) first described by Forbush (1938).

Shumilov et al. (1996) studied the 16 February 1984 SEP with a GLE and found an enhancement of stratospheric aerosols after the event. Later, case studies of a possible influence of ionization rate increases on aerosol formation during several GLE’s were carried out in (Mironova et al., 2012; Mironova et al., 2008; Mironova and Usoskin, 2013; Mironova and Usoskin, 2014). However, the results of these studies did not provide strong evidences for this influence. The aerosol responses revealed strong seasonal dependence, being detected only in polar night and pronounced temperature decreases. No effects were detected during other seasons, in spite of big enhancements of ionization in the polar middle atmosphere. The observed effect in (Mironova et al., 2012) is marginally detectable for a severe SEP event and may be undetectable for the majority of weak-moderate events. Thus, the problem of ionization influence of aerosol formation needs further investigation.

SEP’s produce reactive odd hydrogen HO_x (H + OH + HO₂) and nitrogen NO_x (N + NO + NO₂) which catalytically destroy ozone in the mesosphere and upper stratosphere—“direct effect” (e.g., Rusch et al., 1981; Solomon et al., 1981) Ozone depletion was really detected in the mesosphere and upper stratosphere during strong SPEs, e.g., 2003 Halloween events (Seppälä et al., 2004), 15–20 January 2005 (Jackman et al., 2011) etc. HO_x are short-lived and can produce direct destruction of ozone in the course of SPEs in the region of ionization increase. Long-lived NO_x in the absence of UV photodissociation during polar night can survive to descend to lower altitudes and destroy ozone there producing a delayed “indirect effect” (e.g., Brasseur and Solomon, 2005; Mironova et al., 2015). Denton et al. (2018) analyzed ozonesonde data from four sites in relation to 191 SEP’s from 1989 to 2016, and found reduction of ∼5–10% in stratospheric ozone following the SEP’s, lasting for over 30 days with the maximum decrease ∼10–20 days after SEPs, which indicates the role of “indirect” ozone destruction. Veretenenko S. (2021), Veretenenko (2022) showed the “direct” effect on the chemical composition of powerful SEPs in January 2005 when protons reached the stratosphere. Figure 10 illustrates the effects of this strong SEP series in January 2005 on the zonal wind velocity in the Northern hemisphere vortex (50 hPa level). Noticeable vortex intensification observed several days after the series onset seems to indicate a possible influence of ozone destruction caused by strong SEP’s on the middle atmosphere temperature and dynamics.

FIGURE 10

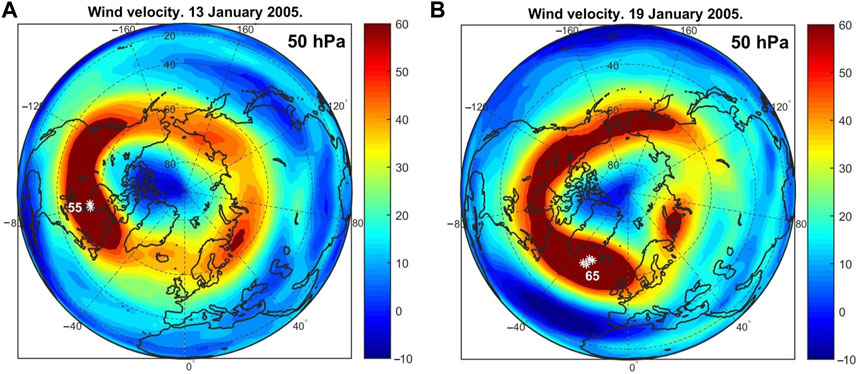
FIGURE 10. Distribution of daily values of zonal wind velocity (in m/s) at the 50 hPa level: (A) before the onset of the SPE series (13 January 2005); (B) after the onset of the SPE series (19 January 2005). The areas covered by western winds with U > 40 m/s are highlighted in dark brown. White asterisks indicate maximal values of zonal wind velocity (Umax). The area of westerly winds with velocity U > 40 m/s which was localized over the northern part of North America before the SPE onset, expanded noticeably, especially to the east, covering the high-latitudinal parts of the North Atlantic. Maximal values of wind velocity in this area (indicated by white asterisks) were also shifted to the east and increased. Adapted from Veretenenko (2022).

Ozone is a radiatively active gas influencing both shortwave and longwave radiation fluxes. Ozone absorbs UV in the broad Hartley band (∼200–320 nm), but also has a number of vibrational-rotational bands in IR, with a maximum at 9.6 μm (Brasseur and Solomon, 2005). In the absence of sunlight ozone absorbs longwave outgoing radiation emitted by the Earth and atmosphere, acting as a greenhouse gas. Ozone depletion associated with ionization increases contributes to cooling of the polar middle atmosphere, enhancing the temperature contrast between polar and midlatitudes and, thus, the strength of the stratospheric polar vortex. Model studies (Baumgaertner et al., 2011) found that ozone depletion by ∼20% in winter polar stratosphere due to NO_x enhancement associated with EEP contributes to a temperature decrease of ∼3 K.

GCR can also contribute to the ozone mechanism of solar influences on the atmosphere together with other ionizing particles. Rozanov et al. (2012) simulated the combined effect of different charged particles (galactic and solar cosmic rays, auroral electrons) on the atmosphere chemistry and climate. It was estimated that the annual ozone depletion associated with these particles may reach ≥10% in the polar mesosphere and ∼3–4% in the upper stratosphere resulting in a decrease of stratosphere temperature (0.5 K) and the polar vortex intensification. These results suggest that the energetic particles are able to affect atmospheric chemical composition, dynamics, and climate.

On the other hand, in Mironova et al. (2021), results of ensemble experiments were presented on the impact of SEP events and FD using the chemistry-climate model SOCOLv2. Despite the 50% decrease in HO_x due to a reduction in ionization rates caused by FD after solar proton events, no statistically significant response in either NO_x or ozone was found. Therefore, the problem remains controversial. An alternative mechanism for GCR influences on the atmosphere with ozone as a mediator was proposed by Kilifarska (2012), Kilifarska (2017).

4.2.3 Energetic electron precipitation (EEP)

SEP’s are powerful but sporadic and rare events. Solar wind provides an additional source of energetic particles, mostly electrons, which are less energetic but are always present. They are trapped in the Earth’s magnetosphere and during geomagnetic disturbances are accelerated and precipitate into the atmosphere.

All precipitating energetic particles like GCR, solar protons, alpha particles, auroral and radiation belt electrons ionize neutral molecules in the Earth’s atmosphere and produce chemically active radicals which can be further transformed by gas phase chemistry. The effects of EEP are considered to be practically the same as of SEP’s: additional production of reactive HO_x and NO_x which can destroy ozone (Mironova et al., 2015 and the references therein). Like SEPs, EEP also have direct effects in the mesosphere (Andersson et al., 2014) and indirect effects in the stratosphere (e.g., Salminen et al., 2020).

Andersson et al. (2014), using ozone observations from three different satellite instruments, found extremely large (up to 90%) direct HO_x-caused effects: short-term (days) ozone depletions in the mesosphere caused by EEP, comparable to those caused by large but much less frequent SEP’s, and up to 34% ozone variations at 70–80 km on solar cycle scales.

As in the case of SEPs, long-lived NO_x during the polar night can descend to stratosphere and destroy ozone there. Baumgaertner et al. (2011) used atmospheric chemistry general circulation model ECHAM5/MESSy and found polar stratospheric ozone loss due to EEP and associated NO_x enhancement, resulting in a stronger vortex and a positive NAM. This is confirmed by other model (e.g., Greer et al., 2015; Peck et al., 2015; Ward et al., 2021 and the references therein) and observational studies (e.g., Lu et al., 2008; Seppala et al., 2014; Salminen et al., 2019). A review of the recent studies is given by Ward et al. (2021).

5 Spatial and temporal variability of solar activity effects on the lower atmosphere

A number of studies (Herman and Golberg, 1978 and the references therein; Georgieva et al., 2007; Georgieva et al., 2012; Veretenenko and Ogurtsov, 2012; Veretenenko and Ogurtsov, 2019, among many others) revealed several changes in the correlation sign between characteristics of the lower atmosphere and sunspot activity. Moreover, these correlations have also regional dependencies.

As an example, Figure 11 demonstrates the spatial distribution of correlation coefficients between tropospheric pressure and GCR intensity for two time intervals, before and after ∼1980, together with the mean long-term (climatic) positions of the main atmospheric fronts (Khromov and Petrociants, 1994). Arctic fronts separate the cold Arctic air from the warmer mid-latitudinal air, whereas Polar fronts separate the mid-latitudinal from tropical air masses. The atmospheric fronts are closely related to the formation and development of mid-latitudinal cyclones. Extratropical cyclones usually arise at Polar fronts and move from West to East declining to higher latitudes and contributing to the movement of the associated frontal systems. Thus, the climatic positions of Polar fronts may be considered as the regions of most frequent formation and passages of cyclones and indicate the main directions of their movement. They also determine the spatial distribution of the correlation coefficients.

FIGURE 11

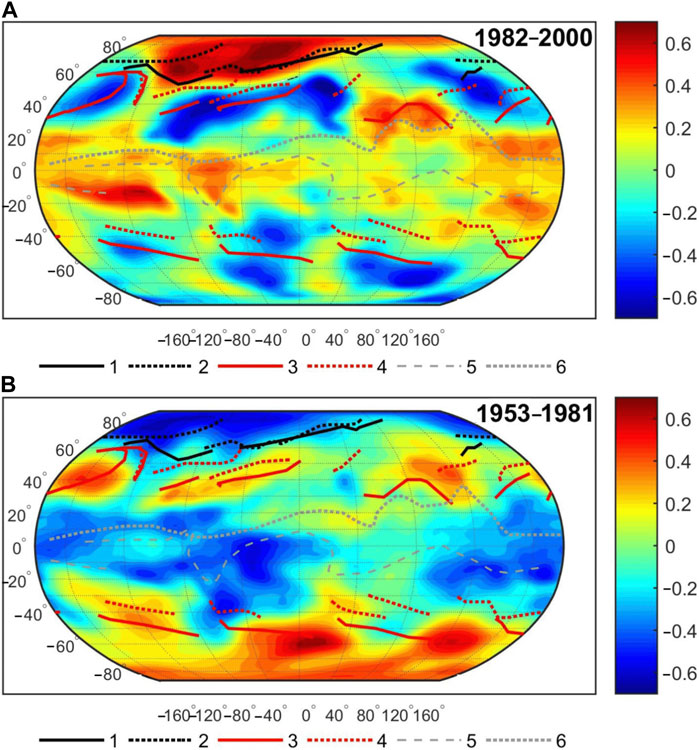
FIGURE 11. Spatial distribution of the correlation coefficients between mean yearly values of troposphere pressure (GPH700) and GCR intensity (NM count rate in Climax) for the periods 1982–2000 (A) and 1953–1981 (B). Curves 1 and 2 show the climatic positions of Arctic fronts in January and July, respectively. Similarly, curves 3 and 4 are the same for Polar fronts; curves 5 and 6 are the same for the equatorial trough axis. Adapted from Veretenenko (2022).

During 1982–2000 the highest pressure-GCR positive correlations of ∼0.6–0.7 are observed at extratropical latitudes in the Northern polar region bounded by the climatic Arctic fronts where high pressure systems (Arctic anticyclones) are usually formed (Figure 11A). Similar correlations, but with the opposite sign are observed in the areas of the climatic Polar fronts of the Northern hemisphere. The correlation coefficients are statistically significant, with confidence level p = 0.95–0.97, according to the random-phase test (Ebisuzaki, 1997). Increased GCR fluxes on decadal time-scales contributed to the intensification of cyclone formation and deepening (pressure decrease) at Polar fronts of mid-latitudes in both hemispheres, resulting in negative GCR-pressure correlation. In the Northern hemisphere the intensification of cyclonic processes at mid-latitudes was accompanied by pressure increase, i.e., the intensification of Arctic anticyclone formation in the polar region, which resulted in positive pressure-GCR correlation. Thus, during this period increases of GCR intensity in minima of the 11-year solar cycle seem to contribute to more intensive formation and development of those baric systems which are typical for the given region.

During the previous period 1953–1981 the correlation signs in the same large areas were opposite to those in 1982–2000, showing weakening of the baric systems typical for the given regions (mid-latitudinal cyclones and Polar anticyclones) with GCR increases (Figure 11B).

Figure 11 shows that cyclonic processes at extratropical latitudes may intensify or weaken with increasing GCR depending on the time period which results in temporal variability of solar activity effects on the lower atmosphere. It also shows that circulation disturbances associated with solar activity/GCR variations cover the entire troposphere which indicates the global character of the solar influences on the Earth’s atmosphere. The analysis of sliding correlations between troposphere pressure in different latitudinal belts and GCR intensity (Veretenenko and Ogurtsov, 2012) showed that the correlation reversal near 1980 occurred almost simultaneously in all studied belts. Therefore, dynamical processes developing in different regions as a response to solar activity are closely interconnected. At the same time, the manifestations of global atmospheric disturbances in particular regions strongly depend on the specific circulation features in these regions.

5.1 Possible reasons for the temporal variability of solar activity influences: the role of the stratospheric polar vortex

Figure 12 shows correlation coefficients between yearly values of sea level pressure (SLP) and SSN for the regions of intense formation of Arctic anticyclones and extratropical cyclones in the Northern hemisphere: Polar region and North Atlantic Polar frontal zone (PFZ), respectively. The correlation coefficients R (SLP, SSN) in the two regions vary in antiphase, in agreement with Figure 11, and reveal several reversals: ∼1890, early 1920s, ∼1950 and early 1980s, suggesting a periodicity of ∼60 years in solar influences on dynamic processes in the troposphere. A similar ∼60-year variability is observed in numerous climatic characteristics [e.g., (Veretenenko and Ogurtsov (2019) and references therein]. The years of reversals are in good agreement with those reported in (Herman and Goldberg, 1978; Sánchez Santillán et al., 2002; Thejll et al., 2003; Lukianova and Alexeev, 2004; Georgieva et al., 2007; Georgieva et al., 2012).

FIGURE 12

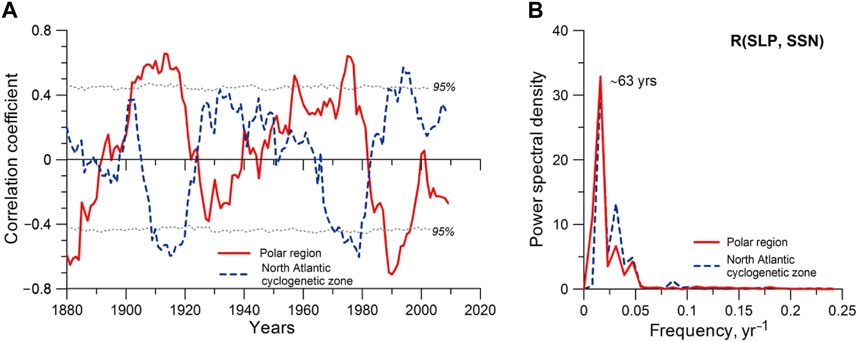
FIGURE 12. (A) Correlation coefficients between yearly values of sea level pressure and sunspot numbers R (SLP, SSN) for the Polar region (solid line) and the North Atlantic cyclogenesis zone (dashed line) for sliding 15-year intervals. Dotted lines show the 95% significance level according to Monte-Carlo tests. (B) Fourier spectra of sliding correlation coefficients R (SLP, SSN) for the Polar region (solid line) and the North Atlantic PZF (dashed line). After Veretenenko (2022).

The temporal variations of pressure-SSN/GCR correlations at extratropical latitudes were compared with the evolution of large-scale circulation forms according to Vangengeim-Girs classification (Veretenenko and Ogurtsov, 2014; Veretenenko and Ogurtsov, 2019). This classification defines three main forms of atmospheric circulation in the Northern hemisphere: W (zonal or westerly), C (meridional), and E (easterly) in the Atlantic-Eurasian sector, and three similar forms: Z, M1 and M2 in the Pacific-American sector (Vangengeim, 1952; Girs, 1964).

It was found that the reversals of correlations were preceded by (or coincided with) the turning points in the evolution of the main forms of large-scale circulation [Figure 3 in (Veretenenko and Ogurtsov, 2019)] and mainly of the meridional forms C and M1. A dominant ∼60-year periodicity close to that observed in the GCR/pressure correlations was shown in the annual occurrences of these forms. Intensification of typical baric systems in the Polar region (polar anticyclones) and in the North Atlantic PZF (extratropical cyclones) with increasing GCR observed in ∼1980–2000 (Figure 12) took place when annual occurrences of C and M1 were increasing. Similar tendency was observed during the increasing occurrences of the meridional forms in ∼1920–1950. In periods of weakening meridional circulation (∼1890–1920 and ∼1950–1980), the SSN/GCR effects on the development of baric systems were opposite. The correlation reversal ∼1980 occurred under almost simultaneous changes in the evolution of all main circulation forms both in the Atlantic-Eurasian and Pacific-American sectors.

The presented data imply that reversals of correlations between surface pressure and SSN/GCR are associated with changes in the epochs of large-scale circulation which in turn are affected by the stratospheric polar vortex, so the changes in circulation epochs may be associated with the changes in the state of the vortex (e.g., Gudkovich et al., 2009; Veretenenko and Ogurtsov, 2014; Veretenenko and Ogurtsov, 2019). The state of the polar vortex can affect the troposphere-stratosphere interaction via planetary waves. If zonal wind velocity in the vortex exceeds a critical value, planetary waves propagating upward can be reflected back to the troposphere (e.g., Avdiushin and Danilov, 2000; Perlwitz and Graf, 2001), so under a strong vortex the stratosphere can influence the troposphere. Under a weak vortex, planetary waves propagate to upper atmospheric levels. Veretenenko and Ogurtsov (2014), Veretenenko and Ogurtsov, (2019) showed that the reversal of correlation between surface pressure and GCR is preceded by the transition of the polar vortex between its strong and weak states. Under a strong vortex, cyclone tracks are shifted northward, so more North Atlantic cyclones arrive into the Polar region, resulting in warming in this region (Gudkovich et al., 2009). Under a weak vortex, cyclone tracks are shifted southward and fewer cyclones arrive to the Polar region, resulting in a cold epoch in the Arctic.

A possible role of the polar vortex in the formation of solar activity effects on the lower atmosphere is discussed in more detail in (Veretenenko, 2022). In particular, the reversal of the correlation between low clouds and GCR intensity near 2000 (Chapter 4.2.1), which caused doubts in the reality of this link, may be explained by a sharp weakening of the vortex resulting in the reversal of GCR effects on extratropical cyclogenesis on a multidecadal time scale.

5.2 Solar influences on the stratospheric polar vortex

The effects of solar activity drivers on the polar vortex state were studied in (Veretenenko and Ogurtsov, 2020; Veretenenko S., 2021; Veretenenko S. V., 2021; Veretenenko, 2022). The obtained results suggest solar activity influence on the polar vortex state on different time scales from daily to multidecadal. Long-term oscillations of storm track latitudes in the North Atlantic (Veretenenko and Dmitriev, 2023) also provide evidence for secular variations of the vortex intensity.

Two solar activity agents are supposed to affect the stratospheric polar vortex: SSI through the “Top-down” mechanism (Chapter 4.1.2), and energetic particles (Chapter 4.2.2). As shown, the positive phase of NAO (a proxy for the intensification of the polar vortex) lags by a few years maximum UV in Smax, while it coincides with EEP maximum which is also a few years after Smax. So the question is whether the intensification of NAO/polar vortex is due to energetic particles alone, or to the combined action of energetic particles and delayed effects of SSI.

The conditions in the high-latitudinal area where the vortex forms are characterized by low geomagnetic cutoff rigidities (≥2–3 GV), therefore it is accessible to cosmic particles which produce atmospheric ionization in a wide energy range (Bazilevskaya et al., 2008): GCR’s, modulated by solar activity, SEP’s accelerated during solar flares in the corona and interplanetary space; auroral zone particles associated with geomagnetic disturbances; precipitating low energy magnetospheric electrons, and relativistic radiation belt electrons. All of them contribute to ionization increases in the high-latitudinal atmosphere and production of reactive nitrogen and hydrogen species which destroy ozone (Chapter 4.2). Ionization increases also affect conductivity and, consequently, density of vertical electric currents which can contribute to cloudiness changes and related changes of the radiation-thermal balance at high latitudes (Chapter 4.2.1.2).

Asikainen and Ruopsa (2016) investigated the solar wind drivers of EEP, and found that HSS contribution nearly always dominates over the other drivers and peaks strongly in the declining solar cycle phase. Maliniemi et al. (2019) assessed the influence of sunspot (irradiance) and geomagnetic (particle precipitation) solar activity on NAO during 1948–2017, without dividing it into subperiods with different sunspot/NAO correlations, and found that the responses in the atmosphere related to geomagnetic/particle and sunspot/irradiance activity evolve differently. Most importantly, geomagnetic/particle response is seen in all months as strengthening of the polar vortex, hardly changing with increasing the lag.

The impact of the two solar activity agents on the polar vortex/NAO were studied by Georgieva et al. (2012). The NAM index (Baldwin and Dunkerton, 2001) was used, and the winters were divided into two groups: high aa-index/low sunspot number (high particle impact/low solar UV), and vice versa. Figure 13 illustrates the difference between them: during high geomagnetic activity/solar poloidal field drivers, the polar vortex is intensified, during high solar UV it is weakened. This is in agreement with an earlier finding (Kirov and Georgieva, 2002) that at sunspot maximum the pressure in the Icelandic Low has a maximum, and in the Azores High a minimum, therefore NAO index which is defined as the pressure difference between the Azores High and Icelandic Low is negative. We can therefore speculate that the “delayed SSI effect” on the polar vortex is in fact the immediate effect of HSS which maximize in the same period.

FIGURE 13

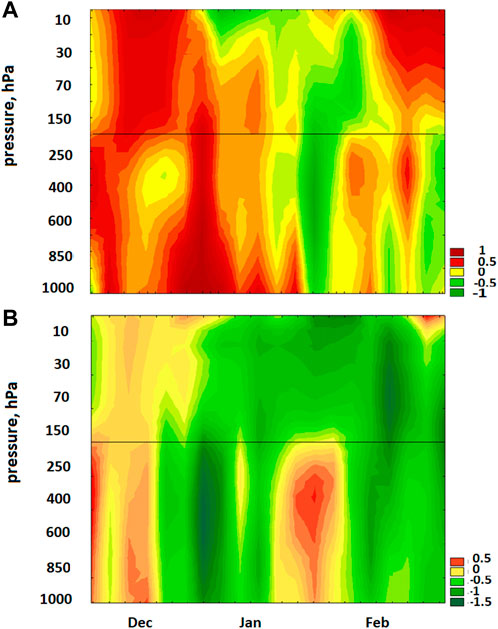
FIGURE 13. Composites of time-height development of the Northern Annular Mode for the 11 winters of high aa-index and low sunspot number and F10.7 (A), and the 9 winters of high sunspot number and F10.7 and low aa-index (B). The horizontal line denotes the approximate altitude of the tropopause. Adapted with permission from Georgieva et al. (2012).

Figure 14 presents the sunspot cycle averages of the winter NAO/polar vortex and sunspot numbers. For comparison, in the bottom panel Figure 4 is reproduced presenting the relative impact of poloidal field activity prevails, the correlation between NAO and solar activity is positive, when the toroidal field related activity prevails, the correlation is negative. We should remind here that the long-term correlation between SSN and ENSO has no sign reversals which means TSI is the main solar activity agent at low latitudes, which is also a confirmation of the Bottom-up mechanism, while the polar vortex/NAO is subjected to both particle precipitation and effects of SSI transferred from lower latitudes.

FIGURE 14

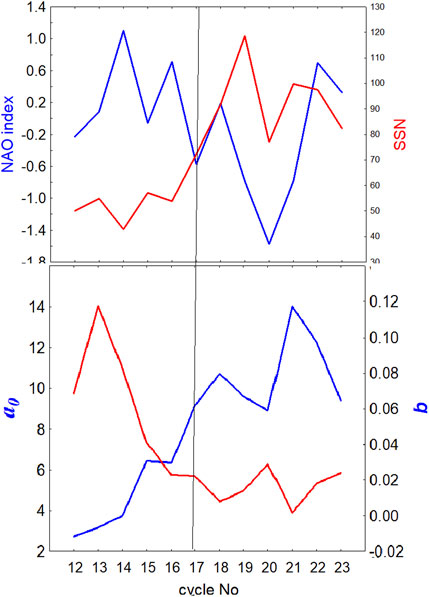
FIGURE 14. Top panel: Blue—NAO winter (DJF) index (Jones et al., 1997); red—sunspot number, both sunspot cycle averages. Bottom panel: cycle-to-cycle evolution of the relative impact of poloidal field-related (solid line) and toroidal field-related (broken line) solar activity (reproduced from Figure 4).

6 Summary and conclusion

The basis of all solar activity is the large-scale solar magnetic field oscillating between its two components, poloidal and toroidal. Geoeffective agents of the solar toroidal field are solar irradiance, solar flares, and CME’s. The manifestations of the solar poloidal field are the slow solar wind, and HSS’s from solar coronal holes.

Numerous studies have found statistically significant correlations between solar activity and atmospheric parameters. However, the variations of the solar forcings are believed to be too small to explain them, so amplification mechanisms have been proposed. Some of them are related to solar poloidal field-related, other to toroidal field-related drivers.

Many studies revealed changes in the correlation sign between characteristics of the lower atmosphere and sunspot activity. None of the mechanisms listed above explains this instability of the solar-atmospheric influences.

Cyclonic processes at extratropical latitudes intensify or weaken with increasing GCR’s with a period of ∼60 years. A similar ∼60-year variability is observed in numerous climatic characteristic, and also in the prevalence of the large-scale circulation forms. The reversals of correlations are around the turning points in the evolution of the main large-scale circulation forms, which are in turn affected by the stratospheric polar vortex. Therefore, the changes in the sign of the correlations and circulation epochs may be associated with the changes in the state of the vortex.

NAO and its hemispheric analogue NAM are proxy for the state of the polar vortex. The vortex is strong in their positive phase which peaks strongly a couple of years after Smax/UV maximum and coincides with EEP maximum, while increased UV in Smax is related to negative NAO/NAM phases and a weak vortex.

The solar poloidal magnetic field and toroidal field are the two faces of the large-scale solar magnetic field, but there is no one-to-one correspondence between them, because they are generated in different domains, and because of the randomness involved in the toroidal-to-poloidal field transformation. They have opposite cyclic long-term variations with a period of ∼60 years. The results cited here imply that when the relative impact of poloidal/toroidal solar magnetic field-related manifestations prevails, NAO is in its positive/negative phase, the polar vortex is strong/weak, and atmospheric parameters positively/negatively correlated with solar activity.

Author contributions

KG mainly contributed to Section 1, Section 2, and Section 3. SV mainly contributed to Section 5. The two authors contributed equally to Section 4. Both authors contributed to the article and approved the submitted version.

Funding

Bulgarian National Science Fund, Grant No. KP-06-N44/2.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ammann, C. M., Joos, F., Schimel, D. S., Otto-Bliesner, B. L., and Tomas, R. A. (2007). Solar influence on climate during the past millennium: results from transient simulations with the NCAR Climate System Model. Model PNAS 104, 3713–3718. doi:10.1073/pnas.0605064103

PubMed Abstract | CrossRef Full Text | Google Scholar

Andersson, M. E., Verronen, P. T., Rodger, C. J., Clilverd, M. A., and Seppälä, A. (2014). Missing driver in the Sun–Earth connection from energetic electron precipitation impacts mesospheric ozone. Nat. Commun. 5, 5197. doi:10.1038/ncomms6197

PubMed Abstract | CrossRef Full Text | Google Scholar

Asikainen, T., and Ruopsa, M. (2016). Solar wind drivers of energetic electron precipitation. J. Geophys. Res. Space Phys. 121, 2209–2225. doi:10.1002/2015ja022215

CrossRef Full Text | Google Scholar

Avdyushin, S. I., and Danilov, A. D. (2000). The Sun, weather, and climate: a present-day view of the problem (review). Geomagn. Aeron. 40, 545–555.

Google Scholar

Babcock, H. W. (1961). The topology of the sun’s magnetic field and the 22-year cycle. Astrophys. J. 133, 572–587. doi:10.1086/147060

CrossRef Full Text | Google Scholar

Baldwin, M. P., and Dunkerton, T. J. (1999). Propagation of the arctic oscillation from the stratosphere to the troposphere. J. Geophys. Res. Atmos. 104 (D24), 937–1030.

Google Scholar

Baldwin, M. P., and Dunkerton, T. J. (2001). Stratospheric harbingers of anomalous weather regimes. Science 294, 581–584. doi:10.1126/science.1063315

PubMed Abstract | CrossRef Full Text | Google Scholar

Baldwin, M. P., and Dunkerton, T. J. (2005). The solar cycle and stratosphere troposphere dynamical coupling. J. Atm. Solar-Terr. Phys. 67 (1-2), 71–82. doi:10.1016/j.jastp.2004.07.018

CrossRef Full Text | Google Scholar

Bard, E., Raisbeck, G., Yiou, F., and Jouzel, J. (2000). Solar irradiance during the last 1200 years based on cosmogenic nuclides. Tellus Series B: Chemical and Physical Meteorology 52, 985. doi:10.3402/tellusb.v52i3.17080

CrossRef Full Text | Google Scholar

Baumgaertner, A. J., Seppälä, A., Jöckel, P., and Clilverd, M. A. (2011). Geomagnetic activity related NOx enhancements and polar surface air temperature variability in a chemistry climate model: modulation of the NAM index. Atmos. Chem. Phys. 11 (9), 4521–4531. doi:10.5194/acp-11-4521-2011

CrossRef Full Text | Google Scholar

Bazilevskaya, G. A., Usoskin, I. G., Flückiger, E. O., Harrison, R. G., Desorgher, L., Bütikofer, R., et al. (2008). Cosmic ray induced ion production in the atmosphere. Space Sci. Rev. 137, 149–173. doi:10.1007/s11214-008-9339-y

CrossRef Full Text | Google Scholar

BenMoussa, A., Gissot, S., Schühle, U., Del Zanna, G., Auchère, F., Mekaoui, S., et al. (2013). On-orbit degradation of solar instruments. Sol. Phys. 288, 389–434. doi:10.1007/s11207-013-0290-z

CrossRef Full Text | Google Scholar

Bondo, T., Enghoff, M. B., and Svensmark, H. (2010). Model of optical response of marine aerosols to Forbush decreases. Atmos. Chem. Phys. 10, 2765–2776. doi:10.5194/acp-10-2765-2010

CrossRef Full Text | Google Scholar

Borovsky, J. E., and Denton, M. H. (2006). Differences between CME-driven storms and CIR-driven storms. J. Geophys. Res. Space Phys. 111 (A7). CiteID A07S08. doi:10.1029/2005ja011447

CrossRef Full Text | Google Scholar

Brasseur, G. P., and Solomon, S. (2005). Aeronomy of the middle atmosphere. Dordrecht, The Netherlands: Springer.

Google Scholar

Chapman, G. A., Cookson, A. M., and Dobias, J. J. (1997). Solar variability and the relation of facular to sunspot areas during solar cycle 22. Astrophys. J. 482, 541–545. doi:10.1086/304138

CrossRef Full Text | Google Scholar

Charbonneau, P. (2020). Dynamo models of the solar cycle. Living Rev. Sol. Phys. 17 (4), 4. doi:10.1007/s41116-020-00025-6

CrossRef Full Text | Google Scholar

Choudhuri, A. R. (2023). The emergence and growth of the flux transport dynamo model of the sunspot cycle. Rev. Mod. Plasma Phys. 7, 18. doi:10.1007/s41614-023-00120-9

CrossRef Full Text | Google Scholar

Clette, F. (2016). The new sunspot number in focus. Available at: http://satdat.oulu.fi/space_climate/meetings/SC6/presentations/session2b/Frederic_Clette_SC6.pdf.

Google Scholar

Clette, F., Lefèvre, L., Chatzistergos, T., Hayakawa, H., Carrasco, V. M. S., Arlt, R., et al. (2023). Recalibration of the sunspot-number: status report. Sol. Phys. 298 (3), 44. article id.44. doi:10.1007/s11207-023-02136-3

CrossRef Full Text | Google Scholar

Clette, F., Svalgaard, L., Vaquero, J. M., and Cliver, E. W. (2014). Revisiting the sunspot number. A 400-year perspective on the solar cycle. Space Sci. Rev. 186 (1-4), 35–103. doi:10.1007/s11214-014-0074-2

CrossRef Full Text | Google Scholar

Cliver, E. W., Clette, F., and Svalgaard, L. (2013). Recalibrating the sunspot number (SSN): the SSN workshops, central europ. Astrophys. Bull. 37, 401–416.

Google Scholar

Connolly, R., Soon, W., Connolly, M., Baliunas, S., Berglund, J., Butler, C. J., et al. (2021). How much has the Sun influenced Northern Hemisphere temperature trends? An ongoing debate. Res. Astron. Astrophys. 21, 131. doi:10.1088/1674-4527/21/6/131

CrossRef Full Text | Google Scholar

Crooks, S. A., and Gray, L. J. (2005). Characterization of the 11-year solar signal using a multiple regression analysis of the ERA-40 dataset. J. Clim. 18 (7), 996–1015. doi:10.1175/jcli-3308.1

CrossRef Full Text | Google Scholar

Denton, M. H., Kivi, R., Ulich, T., Clilverd, M. A., Rodger, C. J., and von der Gathen, P. (2018). Northern hemisphere stratospheric ozone depletion caused by solar proton events: the role of the polar vortex. Geophys. Res. Lett. 45 (4), 2115–2124. doi:10.1002/2017gl075966

CrossRef Full Text | Google Scholar

Desai, M., and Giacalone, J. (2016). Large gradual solar energetic particle events. Living Rev. Sol. Phys. 13, 3. doi:10.1007/s41116-016-0002-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Deser, C., and Wallace, J. M. (1987). El Niño events and their relation to the southern oscillation: 1925–1986. J. Geophys. Res. 92, 14189–14196. doi:10.1029/jc092ic13p14189

CrossRef Full Text | Google Scholar

Dewitte, S., Crommelynck, D., Mekaoui, S., and Joukoff, A. (2004). Measurement and uncertainty of the long-term total solar irradiance trend. Sol. Phys. 224, 209–216. doi:10.1007/s11207-005-5698-7

CrossRef Full Text | Google Scholar

Dewitte, S., and Nevens, S. (2016). The Total Solar Irradiance climate data record. ApJ 830 (1), 25. doi:10.3847/0004-637x/830/1/25

CrossRef Full Text | Google Scholar

Dickinson, R. E. (1975). Solar variability and the lower atmosphere. Bull. Am. Meteor. Soc. 56, 1240–1248. doi:10.1175/1520-0477(1975)056<1240:svatla>2.0.co;2

CrossRef Full Text | Google Scholar

Dunne, E. M., Gordon, H., Kürten, A., Almeida, J., Duplissy, J., Williamson, C., et al. (2016). Global atmospheric particle formation from CERN CLOUD measurements. Science 354 (6316), 1119–1124. doi:10.1126/science.aaf2649

PubMed Abstract | CrossRef Full Text | Google Scholar

Ebisuzaki, W. (1997). A method to estimate the statistical significance of a correlation when the data are serially correlated. J. Clim. 10, 2147–2153. doi:10.1175/1520-0442(1997)010<2147:amtets>2.0.co;2

CrossRef Full Text | Google Scholar

Eddy, J. A. (1976). The maunder minimum. Science 192, 1189–1202. doi:10.1126/science.192.4245.1189

PubMed Abstract | CrossRef Full Text | Google Scholar

Edvartsen, J., Maliniemi, V., Nesse Tyssøy, H., Asikainen, T., and Hatch, S. (2022) The Mansurov effect: statistical significance and the role of autocorrelation. J. Space Weather Space Clim. 12, id.11, doi:10.1051/swsc/2022008

CrossRef Full Text | Google Scholar

Eichkorn, S., Wilhelm, S., Aufmhoff, H., Wohlfrom, K. H., and Arnold, F. (2002). Cosmic ray-induced aerosol-formation: first observational evidence from aircraft-based ion mass spectrometer measurements in the upper troposphere. Geophys. Res. Let. 29 (14), 1698. doi:10.1029/2002gl015044

CrossRef Full Text | Google Scholar

Ermolli, I., Matthes, K., Dudok de Wit, T., Krivova, N. A., Tourpali, K., Weber, M., et al. (2013). Recent variability of the solar spectral irradiance and its impact on climate modelling. Atmos. Chem. Phys. 13, 3945–3977. doi:10.5194/acp-13-3945-2013

CrossRef Full Text | Google Scholar

Feynman, J. (1982). Geomagnetic and solar wind cycles, 1900-1975. J. Geophys. Res. 87, 6153–6162. doi:10.1029/ja087ia08p06153

CrossRef Full Text | Google Scholar

Feynman, J., and Ruzmaikin, A. (1999). Modulation of cosmic ray precipitation related to climate. Geophys. Res. Lett. 26 (14), 2057–2060. doi:10.1029/1999gl900326

CrossRef Full Text | Google Scholar

Fligge, M., and Solanki, S. K. (2000). Properties of flux tubes and the relation with solar irradiance variability. J. Astrophysics Astronomy 21, 275–282. doi:10.1007/bf02702409

CrossRef Full Text | Google Scholar

Forbush, S. E. (1938). On cosmic-ray effects associated with magnetic storms. Terr. Magnetism Atmos. Electr. 43, 203–218. doi:10.1029/te043i003p00203

CrossRef Full Text | Google Scholar

Fröhlich, C. (2000). Observations of irradiance variations. Space Sci. Rev. 94 (1/2), 15–24. doi:10.1023/a:1026765712084

CrossRef Full Text | Google Scholar

Fröhlich, C. (2006). Solar irradiance variability since 1978. Revision of the PMOD composite during solar cycle 21. Space Sci. Rev. 125 (1-4), 53–65. doi:10.1007/s11214-006-9046-5

CrossRef Full Text | Google Scholar

Georgieva, K. (2013). “Space weather and space climate—what the look from the Earth tells us about the Sun,” in The environments of the Sun and the stars. Lecture notes in physics. Editors J. P. Rozelot, and C. Neiner (Berlin Heidelberg: Springer-Verlag).

Google Scholar

Georgieva, K., Kilcik, A., Nagovitsyn, Yu., and Kirov, B. (2016). “About the recalibration of the sunspot record,” in Proceedings of the XX Conference "Solar and solar-terrestrial Physics, St.Petersburg, Pulkovo, 04-10 Oct.2016, 61–66.

Google Scholar

Georgieva, K., Kirov, B., Koucka-Knızova, P., Mosna, Z., Kouba, D., and Asenovska, Y. (2012). Solar influences on atmospheric circulation. J. Atm. Solar-Terr. Phys. 90-91, 15–25. doi:10.1016/j.jastp.2012.05.010

CrossRef Full Text | Google Scholar

Georgieva, K., Kirov, B., Tonev, P., Guineva, V., and Atanasov, D. (2007). Long-term variations in the correlation between NAO and solar activity: the importance of north–south solar activity asymmetry for atmospheric circulation. Adv. Space Res. 40, 1152–1166. doi:10.1016/j.asr.2007.02.091

CrossRef Full Text | Google Scholar

Girs, A. A. (1964). About the creation of a unified classification of the macrosynoptic processes in the Northern hemisphere. Meteorol. i Gidrol. 4, 43–47.

Google Scholar

Golubenko, K., Rozanov, E., Mironova, I., Karagodin, A., and Usoskin, I. (2020). Natural sources of ionization and their impact on atmospheric electricity. Geophys. Res. Lett. 47, e2020GL088619. doi:10.1029/2020gl088619

CrossRef Full Text | Google Scholar

Gosling, J. T. (1993). The solar flare myth. J. Geophys. Res. 98 (A11), 18937–18949. doi:10.1029/93ja01896

CrossRef Full Text | Google Scholar

Gray, L. J., Beer, J., Geller, M., Haigh, J. D., Lockwood, M., Matthes, K., et al. (2010). Solar influences on climate. Rev. Geophys. 48. CiteID RG4001. doi:10.1029/2009rg000282

CrossRef Full Text | Google Scholar

Gray, L. J., Scaife, A. A., Mitchell, D. M., Osprey, S. M., Ineson, S., Hardiman, S., et al. (2013). A lagged response to the 11 year solar cycle in observed winter Atlantic/European weather patterns. J. Geophys. Res. 118 (24), 13405–13420. doi:10.1002/2013jd020062

CrossRef Full Text | Google Scholar

Greer, K. R., Thayer, J. P., Harvey, V. L., and Peck, E. D. (2015). Modeling and mechanisms of polar winter upper stratosphere/lower mesosphere disturbances in WACCM. J. Geophys. Res. Atmos. 120 (15), 7635–7647. doi:10.1002/2015jd023471

CrossRef Full Text | Google Scholar

Gudkovich, Z. M., Karklin, V. P., Smolyanitsky, V. M., and Frolov, I. E. (2009). On the character and causes of the Earth’s climate change. Probl. Arct. Antarct. 81, 15–23.

Google Scholar

Haigh, J. D. (2007). The Sun and the Earth’s climate. Living Rev. Sol. Phys. 4. doi:10.12942/lrsp-2007-2

CrossRef Full Text | Google Scholar

Harrison, R. G., and Aplin, K. L. (2001). Atmospheric condensation nuclei formation and high-energy radiation. J. Atmos. Solar-Terr. Phys. 63 (17), 1811–1819. doi:10.1016/s1364-6826(01)00059-1

CrossRef Full Text | Google Scholar

Hathaway, D. H. (2010). The solar cycle. Living Rev. Sol. Phys. 7 (1), 1. doi:10.12942/lrsp-2010-1

CrossRef Full Text | Google Scholar

Hathaway, D. H., and Wilson, R. M. (2006). Geomagnetic activity indicates large amplitude for sunspot cycle 24. Geophys. Res. Lett. 33 (18). CiteID L18101/. doi:10.1029/2006gl027053

CrossRef Full Text | Google Scholar

Herman, J. R., and Goldberg, R. A. (1978). Sun, weather and climate. Washington, DC, USA: NASA Scientific and Technical Information Branch.

Google Scholar

Herschel, W. (1801). Observations tending to investigate the nature of the Sun, in order to find the causes or symptoms of its variable emission of light and heat; with remarks on the use that may possibly be drawn from solar observations. Phil. Trans. R. Soc. Lond. 91, 265–318.

Google Scholar

Hickey, J. R., Stowe, L. L., Jacobowitz, H., Pellegrino, P., Maschhoff, R. H., House, F., et al. (1980). Initial solar irradiance determinations from Nimbus 7 cavity radiometer measurements. Science 208 (4441), 281–283. doi:10.1126/science.208.4441.281

PubMed Abstract | CrossRef Full Text | Google Scholar

Hood, L. L. (2004). “Effects of solar UV variability on the stratosphere,” in Solar variability and its effects on climate. Geophysical monograph 141. Editors J. M. Pap, P. Fox, C. Frohlich, and H. S. Hudson (Washington, DC, USA: American Geophysical Union), 283.

CrossRef Full Text | Google Scholar

Hou, Z., Li, Ji., and Zuo, B. (2021). Correction of monthly SST forecasts in CFSv2 using the local dynamical analog method. Weather Forecast. 36 (3), 843–858. doi:10.1175/waf-d-20-0123.1

CrossRef Full Text | Google Scholar

Hoyt, D. V., and Schatten, K. H. (1997). The role of the sun in climate change. New York: Oxford University Press.

Google Scholar

Hoyt, D. V., and Schatten, K. H. (1998). Group sunspot numbers: a new solar activity reconstruction. Sol. Phys. 181, 491–512. doi:10.1023/A:1005056326158

CrossRef Full Text | Google Scholar

IPCC (2023). Sixth assessment report. Available at: https://www.ipcc.ch/report/sixth-assessment-report-cycle/.

Google Scholar

Jackman, C. H., Marsh, D. R., Vitt, F. M., Roble, R. G., Randall, C. E., Bernath, P. F., et al. (2011). Northern Hemisphere atmospheric influence of the solar proton events and ground level enhancement in January 2005. Atmos. Chem. Phys. 11, 6153–6166. doi:10.5194/acp-11-6153-2011

CrossRef Full Text | Google Scholar

Jiang, J., Cameron, R. H., and Schüssler, M. (2014). Effects of the scatter in sunspot group tilt angles on the large-scale magnetic field at the solar surface. Ap. J. 791 (1), 5. article id. 5. doi:10.1088/0004-637x/791/1/5

CrossRef Full Text | Google Scholar

Jones, P. D., Jónsson, T., and Wheeler, D. (1997). Extension to the North Atlantic Oscillation using early instrumental pressure observations from Gibraltar and South-West Iceland. Int. J. Climatol. 17, 1433–1450. doi:10.1002/(SICI)1097-0088(19971115)17:13<1433::AID-JOC203>3.0.CO;2-P

CrossRef Full Text | Google Scholar

Jørgensen, T. S., and Hansen, A. W. (2000). Comments on “Variation of cosmic ray flux and global cloud coverage - a missing link in solar-climate relationships” by Henrik Svensmark and Eigil Friis-Christensen. [Journal of Atmospheric and Solar-Terrestrial Physics 59 (1997) 1225-1232]. J. Atm. Solar-Terr. Phys. 62 (1), 73–77. doi:10.1016/s1364-6826(99)00106-6

CrossRef Full Text | Google Scholar

Karagodin, A., Rozanov, E., and Mironova, I. (2022). On the possibility of modeling the IMF by-weather coupling through GEC-related effects on cloud droplet coalescence rate. Atmosphere 13 (6), 881–897. doi:10.3390/atmos13060881

CrossRef Full Text | Google Scholar

Karak, B. B. (2023). Models for the long-term variations of solar activity. Living Rev. Sol. Phys. 20 (1), 3. article id.3. doi:10.1007/s41116-023-00037-y

CrossRef Full Text | Google Scholar

Karak, B. B., and Miesch, M. (2017). Solar cycle variability induced by tilt angle scatter in a babcock-leighton solar dynamo model. Astrophysical J. 847 (1), 69. article id. 69. doi:10.3847/1538-4357/aa8636

CrossRef Full Text | Google Scholar

Kernthaler, S. C., Toumi, R., and Haigh, J. D. (1999). Some doubts concerning a link between cosmic ray fluxes and global cloudiness. Geophys. Res. Lett. 26, 863–865. doi:10.1029/1999gl900121

CrossRef Full Text | Google Scholar

Khromov, S. P., and Petrociants, M. A. (1994). Meteorology and Climatology. Moscow, Russia: Moscow University Press.

Google Scholar

Kilifarska, N. A. (2012). Ozone as a mediator of galactic cosmic rays’ influence on climate. Sun and Geosphere 7 (2), 97–102.

Google Scholar

Kilifarska, N. A. (2017). Hemispherical asymmetry of the lower stratospheric O3 response to galactic cosmic rays forcing. ACS Earth Space Chem 1 (2), 80–88. doi:10.1021/acsearthspacechem.6b00009

CrossRef Full Text | Google Scholar

Kirov, B., Asenovski, S., Georgieva, K., and Obridko, V. N. (2015). What causes geomagnetic activity during sunspot minimum? Geomagnetism Aeronomy 55 (8), 1033–1038. doi:10.1134/s0016793215080149

CrossRef Full Text | Google Scholar

Kirov, B., and Georgieva, K. (2002). Long-term variations and interrelations of ENSO, NAO and solar activity. Phys. Chem. Earth, Parts A/B/C 27 (6-8), 441–448. doi:10.1016/s1474-7065(02)00024-4

CrossRef Full Text | Google Scholar

Kirov, B., Obridko, V. N., Georgieva, K., Nepomnyashtaya, E. V., and Shelting, B. D. (2013). Long-term variations of geomagnetic activity and their solar sources. Geomagnetism Aeronomy 53 (7), 813–817. doi:10.1134/s0016793213070128

CrossRef Full Text | Google Scholar

Kodera, K., and Kuroda, Y. (2002). Dynamical response to the solar cycle. J. Geophys. Res. 107 (D24), 4749. doi:10.1029/2002jd002224

CrossRef Full Text | Google Scholar

Krainev, M., Gvozdevsky, B., Kalinin, M., Aslam, O. P. M., Ngobeni, D., and Potgieter, M. (2021). “On the solar poloidal magnetic field as one of the main factors for maximum GCR intensity for the last five sunspot minima,” in 37th International Cosmic Ray Conference, Berlin, Germany, 12-23 July 2021.

CrossRef Full Text | Google Scholar

Krainev, M. B., Bazilevskaya, G. A., Kalinin, M. S., and Svirzhevsky, N. S. (2019). On contribution of poloidal branch of solar activity to heliosphere and GCR modulation. J. Phys. Conf. Ser. 1181 (Issue 1), 012010. article id. doi:10.1088/1742-6596/1181/1/012010

CrossRef Full Text | Google Scholar

Kristjánsson, J. E., and Kristiansen, J. (2000). Is there a cosmic ray signal in recent variations in global cloudiness and cloud radiative forcing? J. Geophys. Res. 105, 11851–11863. doi:10.1029/2000jd900029

CrossRef Full Text | Google Scholar

Kumar, V., Dhaka, S. K., Hitchman, M. H., and Yoden, S. (2023). The influence of solar-modulated regional circulations and galactic cosmic rays on global cloud distribution. Sci. Rep. 13, 3707. doi:10.1038/s41598-023-30447-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuroda, Y., Kodera, K., Yoshida, K., Yukimoto, S., and Gray, L. (2022). Influence of the solar cycle on the North Atlantic oscillation. J. Geophys. Res. 127 (1), e2021JD035519. doi:10.1029/2021jd035519

CrossRef Full Text | Google Scholar

Laken, B. A., Pallé, E., Čalogović, J., and Dunne, E. M. (2012). A cosmic ray-climate link and cloud observations. J. Space Weather Space Clim. 2, 13. doi:10.1051/swsc/2012018

CrossRef Full Text | Google Scholar

Lam, M. M., and Tinsley, B. A. (2016). Solar wind-atmospheric electricity-cloud microphysics connections to weather and climate. J. Atm. Solar-Terr. Phys. 149, 277–290. doi:10.1016/j.jastp.2015.10.019

CrossRef Full Text | Google Scholar

Leighton, R. B. (1964). Transport of magnetic fields on the sun. Astrophysical J. 140, 1547–1561. doi:10.1086/148058

CrossRef Full Text | Google Scholar

Leighton, R. B. (1969). A magneto-kinematic model of the solar cycle. Astrophysical J. 156, 1–26. doi:10.1086/149943

CrossRef Full Text | Google Scholar

Love, J. J. (2013). On the insignificance of Herschel's sunspot correlation. Geophys. Res. Lett. 40, 4171–4176. doi:10.1002/grl.50846

CrossRef Full Text | Google Scholar

Lu, H., Clilverd, M. A., Seppälä, A., and Hood, L. L. (2008). Geomagnetic perturbations on stratospheric circulation in late winter and spring. J. Geophys. Res. Atmos. 11 3 (D16), D16106. doi:10.1029/2007jd008915

CrossRef Full Text | Google Scholar

Lukianova, R., and Alekseev, G. (2004). Long-term correlation between the NAO and solar activity. Sol. Phys. 224, 445–454. doi:10.1007/s11207-005-4974-x

CrossRef Full Text | Google Scholar

Maliniemi, V., Asikainen, T., Salminen, A., and Mursula, K. (2019). Assessing North Atlantic winter climate response to geomagnetic activity and solar irradiance variability. Q. J. R. Meteorological Soc. 145 (725), 3780–3789. doi:10.1002/qj.3657

CrossRef Full Text | Google Scholar

Matsumoto, H., Svensmark, H., and Enghoff, M. B. (2022). Effects of Forbush decreases on clouds determined from PATMOS-x. J. Atmos. Sol.–Terr. Phys. 230, 105845. doi:10.1016/j.jastp.2022.105845

CrossRef Full Text | Google Scholar

Matthes, K., Kuroda, Y., Kodera, K., and Langematz, U. (2006). Transfer of the solar signal from the stratosphere to the troposphere: northern winter. J. Geophys. Res. 111, 06108. doi:10.1029/2005jd006283

CrossRef Full Text | Google Scholar

Meehl, G. A., and Arblaster, J. M. (2009). A lagged warm event-like response to peaks in solar forcing in the pacific region. J. Clim. 22 (13), 3647–3660. doi:10.1175/2009jcli2619.1

CrossRef Full Text | Google Scholar

Meehl, G. A., Arblaster, J. M., Matthes, K., Sassi, F., and van Loon, H. (2009). Amplifying the pacific climate system response to a small 11-year solar cycle forcing. Science 325, 1114–1118. doi:10.1126/science.1172872

PubMed Abstract | CrossRef Full Text | Google Scholar

Meehl, G. A., Arblaster, J. M., and Tebaldi, C. (2007). Contributions of natural and anthropogenic forcing to changes in temperature extremes over the United States. Geophys. Res. Lett. 34 (19), L19709. doi:10.1029/2007gl030948

CrossRef Full Text | Google Scholar

Meehl, G. A., Washington, W. M., Wigley, T. M. L., Arblaster, J. M., and Dai, A. (2003). Solar and greenhouse gas forcing and climate response in the twentieth century. J. Clim. 16, 426–444. doi:10.1175/1520-0442(2003)016<0426:saggfa>2.0.co;2

CrossRef Full Text | Google Scholar

Mekaoui, S., and Dewitte, S. (2008). Total solar irradiance measurement and modelling during cycle 23. Sol. Phys. 247 (1), 203–216. doi:10.1007/s11207-007-9070-y

CrossRef Full Text | Google Scholar

Mironova, I., Karagodin-Doyennel, A., and Rozanov, E. (2021). The effect of Forbush decreases on the polar-night HOx concentration affecting stratospheric ozone. Front. Earth Sci. 8, 618583. doi:10.3389/feart.2020.618583

CrossRef Full Text | Google Scholar

Mironova, I. A., Aplin, K. L., Arnold, F., Bazilevskaya, G. A., Harrison, R. G., Krivolutsky, A. A., et al. (2015). Energetic particle influence on the Earth's atmosphere. Space Sci. Rev. 194, 1–96. doi:10.1007/s11214-015-0185-4

CrossRef Full Text | Google Scholar

Mironova, I. A., Desorgher, L., Usoskin, I. G., Flückiger, E. O., and Bütikofer, R. (2008). Variations of aerosol optical properties during the extreme solar event in January 2005. Geophys. Res. Lett. 35, L18610. doi:10.1029/2008gl035120

CrossRef Full Text | Google Scholar

Mironova, I. A., and Usoskin, I. G. (2013). Possible effect of extreme solar energetic particle events of September–October 1989 on polar stratospheric aerosols: a case study. Atmos. Chem. Phys. 13, 8543–8550. doi:10.5194/acp-13-8543-2013

CrossRef Full Text | Google Scholar

Mironova, I. A., and Usoskin, I. G. (2014). Possible effect of strong solar energetic particle events on polar stratospheric aerosol: a summary of observational results. Environ. Res. Lett. 9 (Issue 1), 015002. article id. doi:10.1088/1748-9326/9/1/015002

CrossRef Full Text | Google Scholar

Mironova, I. A., Usoskin, I. G., Kovaltsov, G. A., and Petelina, S. V. (2012). Possible effect of extreme solar energetic particle event of 20 January 2005 on polar stratospheric aerosols: direct observational evidence. Atmos. Chem. Phys. 12, 769–778. doi:10.5194/acp-12-769-2012

CrossRef Full Text | Google Scholar

Misios, S., Gray, L. J., Knudsen, M. F., Karoff, C., Schmidt, H., and Haigh, J. D. (2019). Slowdown of the Walker circulation at solar cycle maximum. Proc. Natl. Acad. Sci. 116 (15), 7186–7191. doi:10.1073/pnas.1815060116

PubMed Abstract | CrossRef Full Text | Google Scholar

Misios, S., and Schmidt, H. (2013). The role of the oceans in shaping the tropospheric response to the 11 year solar cycle. Geophys. Res. Lett. 40 (24), 6373–6377. doi:10.1002/2013gl058439

CrossRef Full Text | Google Scholar

Ney, E. P. (1959). Cosmic radiation and the weather. Nature 183 (4659), 451–452. doi:10.1038/183451a0

CrossRef Full Text | Google Scholar

Nicholson, S. B. (1933). The area of a sun-spot and the intensity of its magnetic field. Publ. Astron. Soc. Pac. 45 (263), 51–53. doi:10.1086/124301

CrossRef Full Text | Google Scholar

Ortlieb, L. (2000). “The documented historical record of El Niño events in Peru: an update of the Quinn record (Sixteenth through Nineteenth centuries),” in El Niño and the southern oscillation, multiscale variability and global and regional impacts. Editors H. F. Diaz, and V. Markgraf (Cambridge: Cambridge Univ. Press), 207–295.

Google Scholar

Parker, E. N. (1955). Hydromagnetic dynamo models. Astrophysical J. 122, 293–314. doi:10.1086/146087

CrossRef Full Text | Google Scholar

Peck, E. D., Randall, C. E., Harvey, V. L., and Marsh, D. R. (2015). Simulated solar cycle effects on the middle atmosphere: WACCM3 versus WACCM4. J. Adv. Model. Earth Syst. 7 (2), 806–822. doi:10.1002/2014ms000387

CrossRef Full Text | Google Scholar

Perlwitz, J., and Graf, H.-F. (2001). Troposphere-stratosphere dynamic coupling under strong and weak polar vortex conditions. Geophys. Res. Lett. 28, 271–274. doi:10.1029/2000gl012405

CrossRef Full Text | Google Scholar

Pevtsov, A. A., Nagovitsyn, Yu.A., Tlatov, A. G., and Rybak, A. L. (2011). Long-term trends in sunspot magnetic fields. Astrophys. J. Lett. 742 (2), L36. doi:10.1088/2041-8205/742/2/l36

CrossRef Full Text | Google Scholar

Pikulina, P., Mironova, I., Rozanov, E., and Karagodin, A. (2022). September 2017 solar flares effect on the middle atmosphere. Remote Sens. 14 (11), 2560. doi:10.3390/rs14112560

CrossRef Full Text | Google Scholar

Pudovkin, M. I., and Veretenenko, S. V. (1995). Cloudiness decreases associated with Forbush-decreases of galactic cosmic rays. J. Atmos. Terr. Phys. 57, 1349–1355. doi:10.1016/0021-9169(94)00109-2

CrossRef Full Text | Google Scholar

Pustil'nik, L., and Yom Din, G. (2013). On possible influence of space weather on agricultural markets: necessary conditions and probable scenarios. Astrophys. Bull. 68 (1), 107–124. doi:10.1134/s1990341313010100

CrossRef Full Text | Google Scholar

Quinn, W. H., Neal, V. T., and Antunez de Mayolo, S. E. (1987). El Niño occurrences over the past four and a half centuries. J. Geophys. Res. 92, 14449–14461. doi:10.1029/jc092ic13p14449

CrossRef Full Text | Google Scholar

Reames, D. V., Ng, C. K., and Tylka, A. J. (2013). Spatial distribution of solar energetic particles in the inner heliosphere. Sol. Phys. 285, 233–250. doi:10.1007/s11207-012-0038-1

CrossRef Full Text | Google Scholar

Richardson, I. G., and Cane, H. V. (2012). Near-earth solar wind flows and related geomagnetic activity during more than four solar cycles (1963-2011). J. Space Weather Space Clim. 2, A02. doi:10.1051/swsc/2012003

CrossRef Full Text | Google Scholar

Roy, I., and Haigh, J. D. (2012). Solar cycle signals in the pacific and the issue of timings. J. Atmos. Sci. 69 (4), 1446–1451. doi:10.1175/jas-d-11-0277.1

CrossRef Full Text | Google Scholar

Rozanov, E., Calisto, M., Egorova, T., Peter, T., and Schmutz, W. (2012). Influence of the precipitating energetic particles on atmospheric chemistry and climate. Surv. Geophys. 33, 483–501. doi:10.1007/s10712-012-9192-0

CrossRef Full Text | Google Scholar

Rusch, D. W., Gerard, J.-C., Solomon, S., Crutzen, P. J., and Reid, G. C. (1981). The effect of particle precipitation events on the neutral and ion chemistry of the middle atmosphere I. Odd nitrogen. Planet Space Sci. 29, 767–774. doi:10.1016/0032-0633(81)90048-9

CrossRef Full Text | Google Scholar

Ruzmaikin, A., and Feynman, J. (2001). Strength and phase of the solar dynamo during the last 12 cycles. J. Geophys. Res. 106 (A8), 15783–15789. doi:10.1029/2000ja000287

CrossRef Full Text | Google Scholar

Salminen, A., Asikainen, T., Maliniemi, V., and Mursula, K. (2019). Effect of energetic electron precipitation on the northern polar vortex: explaining the QBO modulation via control of meridional circulation. J. Geophys. Res. Atmos. 124 (11), 5807–5821. doi:10.1029/2018jd029296

CrossRef Full Text | Google Scholar

Salminen, A., Asikainen, T., Maliniemi, V., and Mursula, K. (2020). Comparing the effects of solar-related and terrestrial drivers on the northern polar vortex. J. Space Weather Space Clim. 10, 56. doi:10.1051/swsc/2020058

CrossRef Full Text | Google Scholar

Sánchez Santillán, N., Esquivel Herrera, A., and Sánchez-Trejo, R. (2002). Evidences for a shift in barometric pressure, air temperature and rainfall pattern circa 1920 and its possible relation to solar activity. Hidrobiologica 12, 29–36.

Google Scholar

Scaife, A. A., Ineson, S., Knight, J. R., Gray, L. J., Kodera, K., and Smith, D. M. (2013). A mechanism for lagged North Atlantic climate response to solar variability. Geophys. Res. Lett. 40 (2), 434–439. doi:10.1002/grl.50099

CrossRef Full Text | Google Scholar

Seppälä, A., Matthes, K., Randall, C. E., and Mironova, I. A. (2014). What is the solar influence on climate? Overview of activities during CAWSES-II. Prog. Earth Planet. Sci. 1, 24. doi:10.1186/s40645-014-0024-3

CrossRef Full Text | Google Scholar

Seppälä, A., Verronen, P. T., Kyrölä, E., Hassinen, S., Backman, L., Hauchecorne, A., et al. (2004). Solar proton events of October–November 2003: ozone depletion in the Northern Hemisphere polar winter as seen by GOMOS/Envisat. Res. Lett. 31, L19107. doi:10.1029/2004gl021042

CrossRef Full Text | Google Scholar

Sheeley, N. R. (1966). Measurements of solar magnetic fields. Astrophysical J. 144, 723–732. doi:10.1086/148651

CrossRef Full Text | Google Scholar

Shiokawa, K., and Georgieva, K. (2021). A review of the SCOSTEP's 5-year scientific program VarSITI—variability of the sun and its terrestrial impact. Prog. Earth Planet. Sci. 8 (1), 21. article id.21. doi:10.1186/s40645-021-00410-1

CrossRef Full Text | Google Scholar

Shumilov, O. I., Kasatkina, E. A., Henriksen, K., and Vashenyuk, E. V. (1996). Enhancement of stratospheric aerosols after solar proton event. Ann. Geophys. 14 (11), 1119–1123. doi:10.1007/s00585-996-1119-y

CrossRef Full Text | Google Scholar

Shumilov, O. I., Kasatkina, E. A., Raspopov, O. M., Turunen, E., Jacoby, G., and Morner, N.-A. (2000). “Influence of cosmic ray intensity modulated by solar activity and volcanic eruptions on the climate,” in The solar cycle and terrestrial climate, solar and space weather euroconference (1 : 2000: santa cruz de Tenerife, tenerife, Spain) proceedings of the 1st solar and space weather euroconference, 25-29 september 2000, santa cruz de Tenerife, tenerife, Spain. Editor A. Wilson (Noordwijk, Netherlands: ESA Publications Division), 547–550.

Google Scholar

Snow-Kropla, E. J., Pierce, J. R., Westervelt, D. M., and Trivitayanurak, W. (2011). Cosmic rays, aerosol formation and cloud-condensation nuclei: sensitivities to model uncertainties. Atm. Chem. Phys. 11 (8), 4001–4013. doi:10.5194/acp-11-4001-2011

CrossRef Full Text | Google Scholar

Solanki, S. K., Krivova, N. A., and Haigh, J. D. (2013). Solar irradiance variability and climate. Annu. Rev. Astronomy Astrophysics 51 (1), 311–351. doi:10.1146/annurev-astro-082812-141007

CrossRef Full Text | Google Scholar

Solanki, S. K., Schüssler, M., and Fligge, M. (2002). Secular variation of the Sun's magnetic flux. Astron. Astroph. 383, 706–712. doi:10.1051/0004-6361:20011790

CrossRef Full Text | Google Scholar

Solomon, S., Rusch, D. W., Gerard, J.-C., Reid, G. C., and Crutzen, P. J. (1981). The effect of particle precipitation events on the neutral and ion chemistry of the middle atmosphere: II. Odd hydrogen. Planet Space Sci. 29, 885–893. doi:10.1016/0032-0633(81)90078-7

CrossRef Full Text | Google Scholar

Stenflo, J. O., and Kosovichev, A. G. (2012). Bipolar magnetic regions on the sun: global analysis of the SOHO/MDI data set. Astrophysical J. 745 (2), 129. article id. 129. doi:10.1088/0004-637x/745/2/129

CrossRef Full Text | Google Scholar

Sun, B., and Bradley, R. S. (2002). Solar influences on cosmic rays and cloud formation: a reassessment. J. Geophys. Res. Atmos. 107 (D14). CiteID 4211. doi:10.1029/2001jd000560

CrossRef Full Text | Google Scholar

Svalgaard, L., and Schatten, K. (2016). Reconstruction of the sunspot group number: the backbone method. Sol. Phys. 291 (9-10), 2653–2684. doi:10.1007/s11207-015-0815-8

CrossRef Full Text | Google Scholar

Svensmark, H., and Friis-Christensen, E. (1997). Variation of cosmic ray flux and global cloud coverage-a missing link in solar-climate relationships. J. Atm. Terr. Phys. 59, 1225–1232. doi:10.1016/s1364-6826(97)00001-1

CrossRef Full Text | Google Scholar

Svensmark, H., Svensmark, J., Enghoff, M. B., and Shaviv, N. D. (2021). Atmospheric ionization and cloud radiative forcing. Sci. Rep. 11, 19668. Article number: 19668. doi:10.1038/s41598-021-99033-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Svensmark, J., Enghoff, M. B., Shaviv, N. J., and Svensmark, H. (2016). The response of clouds and aerosols to cosmic ray decreases. J. Geophys. Res. 121, 8152–8181. doi:10.1002/2016ja022689

CrossRef Full Text | Google Scholar

Svensmark, J., Enghoff, M. B., and Svensmark, H. (2012). Effects of cosmic ray decreases on cloud microphysics. Atm. Chem. Phys. Discuss. 12 (2), 3595–3617. doi:10.5194/acpd-12-3595-2012

CrossRef Full Text | Google Scholar

Thejll, P., Christiansen, B., and Gleisner, H. (2003). On correlations between the North Atlantic Oscillation, geopotential heights, and geomagnetic activity. Geophys. Res. Lett. 30, 1347. doi:10.1029/2002gl016598

CrossRef Full Text | Google Scholar

Tinsley, B. A. (2008). The global atmospheric electric circuit and its effects on cloud microphysics. Rep. Prog. Phys. 71, 066801. doi:10.1088/0034-4885/71/6/066801

CrossRef Full Text | Google Scholar

Tinsley, B. A. (2022). Uncertainties in evaluating global electric circuit interactions with atmospheric clouds and aerosols, and consequences for radiation and dynamics. J. Geophys. Res. 127, e2021JD035954. doi:10.1029/2021jd035954

CrossRef Full Text | Google Scholar

Tinsley, B. A., and Fangqun, Yu (2004). “Atmospheric ionization and clouds as links between solar activity and climate,” in Solar variability and its effects on climate. Geophysical monograph 141. Editors J. M. Pap, P. Fox, C. Frohlich, and H. S. Hudson (Washington, DC, USA: American Geophysical Union), 321.

CrossRef Full Text | Google Scholar

Tlatov, A. G. (2013). Long-term variations in sunspot characteristics. Geomagn. Aeron. 53, 953–956. doi:10.1134/s0016793213080264

CrossRef Full Text | Google Scholar

Todd, M. C., and Kniveton, D. R. (2001). Changes in cloud cover associated with Forbush decreases of galactic cosmic rays. J. Geophys. Res. 106 (D23), 32031–32041. doi:10.1029/2001jd000405

CrossRef Full Text | Google Scholar

Usoskin, I. G., Kovaltsov, G. A., Mironova, I. A., Tylka, A. J., and Dietrich, W. F. (2011). Ionization effect of solar particle GLE events in low and middle atmosphere. Atmos. Chem. Phys. 11, 1979–1988. –88. doi:10.5194/acp-11-1979-2011

CrossRef Full Text | Google Scholar

Vangengeim, G. Y. (1952). Principles of the macro-circulation methods of long-term meteorological forecasts for the Arctic. Tr. AANII 34, 11–66.

Google Scholar

van Loon, H., and Meehl, G. A. (2008). The response in the Pacific to the sun's decadal peaks and contrasts to cold events in the Southern Oscillation. J. Atm. Solar-Terr. Phys. 70 (7), 1046–1055. doi:10.1016/j.jastp.2008.01.009

CrossRef Full Text | Google Scholar

Veretenenko, S. (2021a). Effects of solar proton events of january 2005 on the middle atmosphere dynamics in the northern hemisphere. Adv. Space Res. 68, 1814–1824. doi:10.1016/j.asr.2021.04.005

CrossRef Full Text | Google Scholar

Veretenenko, S. (2022). Stratospheric polar vortex as an important link between the lower atmosphere circulation and solar activity. Atmosphere 13 (7), 1132. doi:10.3390/atmos13071132

CrossRef Full Text | Google Scholar

Veretenenko, S., and Dmitriev, P. (2023). Possible influence of solar cyclicity on extratropical cyclone trajectories in the North Atlantic. Atmosphere 14 (9), 1339. doi:10.3390/atmos14091339

CrossRef Full Text | Google Scholar

Veretenenko, S., and Ogurtsov, M. (2012). Regional and temporal variability of solar activity and galactic cosmic ray effects on the lower atmosphere circulation. Adv. Space Res. 49, 770–783. doi:10.1016/j.asr.2011.11.020

CrossRef Full Text | Google Scholar

Veretenenko, S., and Ogurtsov, M. (2014). Stratospheric polar vortex as a possible reason for temporal variations of solar activity and galactic cosmic ray effects on the lower atmosphere circulation. Adv. Space Res. 54 (12), 2467–2477. doi:10.1016/j.asr.2013.09.001

CrossRef Full Text | Google Scholar

Veretenenko, S., and Ogurtsov, M. (2019). Manifestation and possible reasons of ∼60-year oscillations in solar-atmospheric links. Adv. Space Res. 64, 104–116. doi:10.1016/j.asr.2019.03.022

CrossRef Full Text | Google Scholar

Veretenenko, S. V. (2021b). Effects of energetic Solar Proton Events of solar cycle 23 on intensity of the stratospheric polar vortex. Geomagn. Aeron. 61, 985–992. doi:10.1134/s0016793221070227

CrossRef Full Text | Google Scholar

Veretenenko, S. V., and Ogurtsov, M. G. (2020). Influence of solar-geophysical factors on the state of the stratospheric polar vortex. Geomagn. Aeron. 60, 974–981. doi:10.1134/s0016793220070282

CrossRef Full Text | Google Scholar

Vršnak, B., Dumbović, M., Heber, B., and Kirin, A. (2021). Analytic modeling of recurrent Forbush decreases caused by corotating interaction regions. A&A 658, A86. doi:10.1051/0004-6361/202140846

CrossRef Full Text | Google Scholar

Waldmeier, M. (1961). The sunspot-activity in the years 1610-1960. Zürich, Swtzerland: Schulthess & Co., 5.

Google Scholar

Wang, Y.-M., and Sheeley, N. R. (1990). Magnetic flux transport and the sunspot-cycle evolution of coronal holes and their wind streams. Astrophys. J. Part 1 365, 372–386. doi:10.1086/169492

CrossRef Full Text | Google Scholar

Wang, Y.-M., Sheeley, N. R., and Nash, A. G. (1991). A new solar cycle model including meridional circulation. Astrophysical J. 383, 431–441. doi:10.1086/170800

CrossRef Full Text | Google Scholar

Ward, W., Seppälä, A., Yiǧit, E., Nakamura, T., Stolle, C., Laštovička, J., et al. (2021). Role of the Sun and the Middle atmosphere/thermosphere/ionosphere in Climate (ROSMIC): a retrospective and prospective view. Prog. Earth Planet. Sci. 8 (1), 47. article id.47. doi:10.1186/s40645-021-00433-8

CrossRef Full Text | Google Scholar

White, W. B., Lean, J., Cayan, D. R., and Dettinger, M. D. (1997). Response of global upper ocean temperature to changing solar irradiance. J. Geophys. Res. 102 (C2), 3255–3266. doi:10.1029/96jc03549

CrossRef Full Text | Google Scholar

Wigington, P. (2023). Sun worship. Learn religions, apr. 5, 2023. Available at: http://learnreligions.com/history-of-sun-worship-2562246.

Google Scholar

Willson, R. C. (2014). ACRIM3 and the total solar irradiance database. Astrophys. Space Sc.i 352, 341–352. doi:10.1007/s10509-014-1961-4

CrossRef Full Text | Google Scholar

Willson, R. C., and Mordvinov, A. V. (2003). Secular total solar irradiance trend during solar cycles 21-23. Geophys. Res. Lett. 30 (5), 3–1. doi:10.1029/2002gl016038

CrossRef Full Text | Google Scholar

Yashiro, S., Gopalswamy, N., Michalek, G., St. Cyr, O. C., Plunkett, S. P., Rich, N. B., et al. (2004). A catalog of white light coronal mass ejections observed by the SOHO spacecraft. J. Geophys. Res. 109 (A7), A07105. doi:10.1029/2003ja010282

CrossRef Full Text | Google Scholar

Yeo, K. L., Krivova, N. A., and Solanki, S. K. (2014). Solar cycle variation in solar irradiance. Space Sci. Rev. 186, 137–167. doi:10.1007/s11214-014-0061-7

CrossRef Full Text | Google Scholar