Ionosphere-thermosphere coupling via global-scale waves: new insights from two-years of concurrent in situ and remotely-sensed satellite observations

1 Introduction

The generation and propagation of atmospheric waves with different spatiotemporal scales represent the primary mechanism through which energy and momentum are carried from the lower atmosphere to the ionosphere-thermosphere (IT) system. Solar tides are primarily generated by the periodic absorption of solar radiation in longitude and localtime (LT) by tropospheric water vapor, stratospheric ozone, and latent heat release in deep tropical clouds. Planetary waves (PWs), Kelvin waves (KWs), and gravity waves (GWs) are mainly excited by surface topography, unstable shear flows, and convection. The subset of this wave spectrum that can effectively propagate upward grows exponentially with height into the less dense atmosphere. As a result, the waves achieve their largest amplitudes in the dissipative region between about 100 km and 150 km known as the mesosphere-lower-thermosphere (MLT) (e.g., Yiğit and Medvedev, 2015; Liu, 2016; Yiğit et al., 2016). A fraction of the wave spectrum can reach the upper thermosphere and exosphere (e.g., Forbes et al., 2009; Oberheide et al., 2009; Gasperini et al., 2015; 2018; 2020; 2022). As part of their vertical propagation, nonlinear wave-wave interactions can occur that contribute to modifying the interacting waves and generating secondary waves (Palo et al., 1999; Chang et al., 2011; Liu, 2016; Gasperini et al., 2015; 2021; Forbes et al., 2021a; b). The wave-driven IT wind variations can redistribute ionospheric plasma through the electric fields generated via the dynamo mechanism in the MLT or directly by moving plasma along magnetic field lines at higher levels (e.g., Liu, 2016).

The global IT coupling described above occurs primarily at low latitudes $(<30°)$ as a result of the geometry of the magnetic field lines near the equator and is largely driven by waves of tropical tropospheric origin. Two prominent examples of such large-scale waves from the tropical wave spectrum that preferentially propagate into the IT system are the well-known diurnal eastward propagating with zonal wavenumber s = −3 (DE3), and the eastward-propagating ∼2.5–4-day period ultra-fast Kelvin wave (UFKW) with zonal wavenumber s = −1, hereafter UFKW1 (e.g., Forbes et al., 2009; 2020a; b; Oberheide et al., 2009; Gasperini et al., 2015; 2021; 2022; Chang et al., 2011; Gu et al., 2014a; Pedatella and Forbes, 2009; Yamasaki et al., 2020; Liu et al., 2013). As discussed by Gasperini et al. (2022), these so-called ‘ultra-fast tropical waves’ that include DE3 and UFKWs, are known to preferentially propagate into the IT system and significantly alter thermospheric winds (Gasperini et al., 2015; 2020) and ionospheric densities (Pedatella and Forbes, 2009; Chang et al., 2011; He et al., 2011; Gu et al., 2014a; Gasperini et al., 2021). DE3 originates primarily in the tropical troposphere by latent heat release in deep convective clouds (e.g., Hagan, 1996; Lieberman et al., 2007), and its equatorially symmetric mode is the largest component in the lower thermosphere (e.g., Truskowski et al., 2014) and can propagate into the middle thermosphere (e.g., Oberheide et al., 2011; Gasperini et al., 2015; 2018) and ionosphere (e.g., Gasperini et al., 2021) due to its long vertical wavelength of about 56 km. UFKWs are a special kind of GW trapped in equatorial and low-latitude regions, where the Coriolis force is negligible (Salby et al., 1984; Andrews et al., 1987). Similarly to DE3, UFKWs originate primarily from latent heat release in the tropical troposphere and are the largest in the zonal wind component. UFKWs are characterized by the longest vertical wavelength (∼51 km) of all Kelvin waves and thus can penetrate well into the lower and middle thermosphere (e.g., Forbes et al., 2020a; b), with amplitudes of upwards of 30 m/s in the MLT zonal wind (Gu et al., 2014a), and middle thermospheric zonal wind amplitudes exceeding 10 m/s (Gasperini et al., 2015; 2018; 2020). The focus of this study is on diurnal tides and UFKWs, however, semidiurnal tides (and terdiurnal tides) can also play a large role in IT coupling and connections to the lower atmosphere, as recently demonstrated observationally by Forbes et al. (2022).

Using concurrent satellite observations from Ionospheric Connection Explorer (ICON; Immel et al., 2018; Immel et al., 2021) observatory, the Scintillation Observations and Response of The Ionosphere to Electrodynamics (SORTIE; Crowley et al., 2016) CubeSat, and the Thermosphere Ionosphere Mesosphere Energetics Dynamics (TIMED) Sounding of the Atmosphere using Broadband Emission Radiometry (SABER) instrument (Mertens et al., 2001), along with Specified-Dynamics Whole Atmosphere Community Climate Model with thermosphere and ionosphere eXtension (SD/WACCM-X; Liu et al., 2018; Gasperini et al., 2020) modeling, Gasperini et al. (2021) demonstrated a pronounced zonal wavenumber 4 (WN4) structure in the global low-latitude ionosphere due to the DE3 propagating through the lower thermosphere. More recently, Gasperini et al. (2022) revealed a rich spectrum of waves coupling the lower (∼90–105 km) and middle (∼200–270 km) thermosphere with the upper F-region (∼540 and ∼590 km) ionosphere through analyses of simultaneous ICON and Constellation Observing System for Meteorology, Ionosphere and Climate 2 (COSMIC-2) observations. These and other recent studies (e.g., Heelis R. A. et al., 2022; Lieberman et al., 2022; Harding et al., 2022; Yamazaki et al., 2022; Forbes et al., 2021a; b; Immel et al., 2021; Liu et al., 2021; Wautelet et al., 2021), demonstrate the utility of employing a diverse set of contemporaneous satellite observations to characterize and better understand the origin of large-scale variability occurring in the tightly-coupled IT system.

Despite some improved understanding of IT connections involving global-scale waves afforded by recent ICON, Global-scale Observations of the Limb and Disk (GOLD), and COSMIC-2 satellite observations, there are many unresolved questions regarding the variability of the wave spectrum and its impacts on the low-latitude IT system. Availability of simultaneous lower (i.e., ∼90–110 km) and middle (i.e., ∼200–300 km) thermospheric winds and topside F-region (i.e., ∼590 km) ion density from the ICON mission (Immel et al., 2018; 2021), combined with periods of concurrent ionospheric observations from the SORTIE CubeSat (Crowley et al., 2016) near 420 km, during the solar minimum and generally geomagnetic-quiescent period (Kp$>$4 on only about 8.7% of the days) between January 2020 and March 2022 provides a unique opportunity to develop an improved experimental understanding of how global-scale waves couple lower thermospheric variability with IT variability. This study evaluates, for the first time, the simultaneous diurnal tidal spectrum and other high-impact global-scale waves in the lower and middle thermosphere and topside F-region ion density using the most recent version of the data publicly available at the time of writing. This is accomplished through spectral analyses of the recently-released version 5 (v05) of ICON MIGHTI wind data over the height ranges ∼93–106 km and ∼200–270 km, where wind measurements are made during both day and night, and in-situ-measured topside F-region ion density from IVM instruments onboard ICON (v06) and SORTIE (v02).

This paper is organized as follows: Section 2 briefly describes the satellite data, modeling, and methodologies, Section 3 contains the results and related discussions, while Section 4 provides a summary and the main conclusions.

2 Satellite observations, modeling, and methods

This study employs simultaneous ICON MIGHTI horizontal wind, ICON IVM ion density, and SORTIE IVM ion density satellite observations, along with diurnal tidal output from the Climatological Tidal Model of the Thermosphere (CTMT). A brief overview of these observational datasets, CTMT, and the spectral methods herein adopted are provided below. This summary provides the necessary context for the interpretation of the global-scale wave analyses presented in Section 3.

2.1 Satellite data

ICON is a NASA Heliophysics System Observatory (HSO) mission launched on 10 October 2019 on a nearly circular $\sim 27°$ inclination orbit at an altitude near 590 km (Immel et al., 2018). The ICON mission aims to directly measure the processes of ionospheric modification by the dynamics of the neutral atmosphere (Immel et al., 2018; 2021; Immel and Eastes, 2019). As a single satellite, ICON only covers two local solar times (LST) a day, each precessing by about 29.8 min toward earlier LST each day.

This study employs MIGHTI Level 2 Version 5 (V05) green-line vector winds (∼95–106 km) and red-line vector winds (∼200–270 km) that provide coverage during both daytime and nighttime. Dhadly et al. (2021) showed agreement between MIGHTI and Thermosphere, Ionosphere, Mesosphere Energetics and Dynamics Doppler Interferometer (TIMED/TIDI) zonal wind observations, with correlations around 0.6 and root mean square (RMS) differences of ∼56 m/s, and similar large amplitude longitudinal variations. RMS differences between MIGHTI winds and ground-based radars and interferometers are on the order of 20 m/s (Harding et al., 2021; Makela et al., 2021). Characterization of the mean horizontal winds and the associated circulation by ICON/MIGHTI for Northern Hemisphere summer solstice conditions was also studied by Yiğit et al. (2022). While the aforementioned studies employed previous data versions, a new calibration method for the so-called ‘zero wind’ was developed for V05 MIGHTI winds that uses a long-term comparison of the ascending- and descending-orbit data to perform a self-calibration of the zero baselines, which is independent of external data or models (Englert et al., 2023). The estimated accuracy of the V05 wind data is generally 10–25 m/s (Englert et al., 2023). Such uncertainties are negligible in tidal/wave fits when a sufficiently large number of data points are used. Recent work by Yamazaki et al. (2023) shows general agreement between MIGHTI V05 mean winds and Horizontal Wind Model 14 (HWM14) winds.

Along with the MIGHTI thermospheric wind observations described above, this study utilizes ICON IVM-A L2-7 V06 ion densities (Heelis et al., 2017; 2022a; b; Huba et al., 2021; Park et al., 2021a; Park et al., 2021b). The IVM is comprised of two instruments, the Retarding Potential Analyzer (RPA) and the Drift Meter (DM). The IVM data are down-selected by including data only for times where the two ‘RPA’ and ‘DM’ flags are both less than 1. Heelis et al. (2017) reported ICON/IVM ion densities to have an accuracy exceeding 10³cm⁻³ based on mission requirement considerations. Total ion concentrations measured by ICON IVM (primarily O+ and H+) are considered equivalent to electron density and hereafter referred to as ‘Ne’. Gasperini et al. (2021) found strong agreement (r$>$0.8) between nearly-coincident independent Ne observations from IVM instruments onboard ICON and COSMIC-2 during a period of similar LT coverage. Similar results were obtained in the recent study by Choi et al. (2023), wherein comparisons of in situ ion density measurements from IVMs onboard COSMIC-2 and ICON using observations during geomagnetic quiet days at solar minimum showed strong agreement.

SORTIE is a NASA HSO 6U CubeSat mission launched onboard Dragon CRS-19 to the International Space Station, from where it deployed on 19 February 2020 in a nearly circular $\sim 51.6°$ inclination orbit near 420 km (Crowley et al., 2016). SORTIE reentered Earth’s orbit around 8 September 2022. The primary objective of the SORTIE mission is to discover the sources of wave-like plasma perturbations in the F-region ionosphere, including the relative role of dynamo action versus direct mechanical forcing in their formation. The SORTIE sensor suite consists of two components; a micro planar Langmuir probe (μPLP) and an IVM. The temperature, composition, and vector velocity of the ionospheric plasma are measured by the IVM. Gasperini et al. (2021) used concurrent ICON and SORTIE IVM ion density observations to demonstrate coupling from the lower thermosphere to the topside ionosphere from the DE3 tide during a period of similar local time coverage. Azeem et al. (2022) showed the first observation of Traveling Ionospheric Disturbances (TIDs) by SORTIE above a deep convection system over Texas and used model simulation and corroborating satellite and ground-based data to demonstrate their connection to vertically propagating GWs. This study uses the in situ L2 total ion density product from the miniature IVM (day and night) from 27 May 2020–8 October 2020 (i.e., days 148–282) and 8 April 2021–21 October 2021 (i.e., days 464–660).

2.2 Climatological Tidal Model of the thermosphere (CTMT)

The CTMT (Oberheide et al., 2011) characterizes the global behavior of vertically propagating tides in the thermosphere (90–400 km; pole to pole). CTMT is based on tidal temperatures and winds in the mesosphere-lower-thermosphere (MLT) region from the Sounding of the Atmosphere using Broadband Emission Radiometer (SABER) and TIMED Doppler Interferometer (TIDI) instruments onboard the Thermosphere Ionosphere Mesosphere Energetics Dynamics (TIMED) satellite extended into the thermosphere using Hough Mode Extension (HME) modeling.

In brief, HMEs represent global solutions (pole-to-pole, 0- to 400-km altitude) to the linearized dynamical equations of the atmosphere for an oscillation of a given frequency and zonal wavenumber, taking into account dissipative effects (including radiative cooling, eddy and molecular diffusion of heat and momentum) above the forcing region (Lindzen and Hong, 1974; Forbes and Hagan, 1988). These perturbations are computed for a background windless atmosphere characterized by a single climatological height profile of temperature. HMEs can be thought of as a latitude versus height table of self-consistent amplitudes and phases for the velocity, temperature, and density perturbation fields of an oscillation with a particular frequency and zonal wavenumber (e.g., Forbes et al., 1994; 2017; 2022). More details on HMEs and CTMT can be found in the recent study by Forbes et al. (2022), which focuses on the vertical evolution of the non-migrating semidiurnal tidal spectrum and their relationship to viscous dissipation and in situ thermospheric sources.

As detailed in Oberheide et al. (2011), monthly tidal climatologies for CTMT are obtained from averaging about 6 years (2002–2008) of TIMED SABER and TIDI observations. CTMT accounts for contributions from solar radiation absorption in the troposphere and stratosphere, tropospheric latent heat release, and nonlinear wave-wave interactions occurring within and below the MLT and is valid for low-to-medium solar radio flux conditions (F10.7 = 110 SFU). One should keep in mind that thermospheric tidal forcing occurring above the MLT is not accounted for by CTMT. As a result, this model is not able to capture migrating tides forced in situ by the absorption of solar EUV radiation and nonmigrating tides forced in the thermosphere (e.g., Jones et al., 2013).

This study employs zonal and meridional wind diurnal tidal amplitudes from CTMT for comparison with ICON MIGHTI. Given the observationally-based climatological height-latitude tidal information provided by CTMT for solar low-to-medium conditions (F10.7 = 110 SFU), CTMT is an excellent model for the interpretation of the MIGHTI-derived tidal amplitudes during 2020–2021.

2.3 Spectral analyses and nomenclature

As noted in Section 2.1, ICON only covers two LSTs each day which prohibits the reliable extraction of tidal variability on a daily or quasi-daily basis. Cullens et al. (2020) showed that at least 35 days of data have to be combined into a composite day to obtain LST coverage sufficient for tidal diagnostics at all latitudes observed by MIGHTI ($\sim 10°$S to $\sim 40°$N). Similar considerations can be made for ICON IVM. The tidal diagnostics of the composite data is further explained in Forbes et al. (2022) and Gasperini et al. (2022) and follows a similar procedure as that adopted by Gasperini et al. (2015, 2017, 2020) in the analyses of GOCE and CHAMP tidal winds and densities.

Only data collected during the period between 1 January 2020 and 23 March 2022 were used in this study. This period was selected because it occurs near solar minimum and is and generally geomagnetic-quiescent. The daily Kp index reaches Kp ≥ 6 (Kp ≥ 5) only on 4 (17) out of the 813 days examined. Data collected during days with Kp $>$ 5 are excluded from the analysis. Note that during the period under investigation, ∼25.3% of days have Kp$>$3, ∼8.7% of days have Kp$>$4, ∼2.1% of days have Kp$>$5, and ∼0.5% of days have Kp$>$6. It is pertinent to note that recent investigations (e.g., Cai et al., 2020; 2021) elucidate that even modest levels of geomagnetic activity (Kp$<$3) have the potential to generate large IT perturbations, which can penetrate the equatorial regions. Nonetheless, the low-latitude protracted oscillations in IT parameters investigated in this study and the composite 40-day moving means involved in the tidal fitting, are likely to significantly reduce any impact from any underlying fluctuations in geomagnetic activity. The effect of solar and geomagnetic preconditioning in IT coupling via global-scale waves is an important topic of research that will be investigated further in future work.

The green-line winds are given every ∼2.5 km for the height range ∼91–112 km, while the red-line winds are given every ∼10 km between ∼203–301 km. Diurnal tidal fits are performed using 40-day moving windows on winds averaged in 6° latitude, 40° longitude, and 2-h UT bins extending from 10°S to 40°N using the native ∼2.5 km (green-line) and ∼10 km (red-line) altitude sampling. To determine the spatiotemporal evolution of the waves, a linear 2-dimensional least squares fit is performed to waves propagating in time and longitudes. A moving window of 40 days is chosen instead of 35 days to alleviate negative effects associated with the occurrence of occasional gaps, data quality issues, and instrument calibrations. As noted by Forbes et al. (2022), this binning effectively removes the effects of small-scale variations and improves the statistics while also leading to smoother visual depictions. The fits are performed for diurnal (24-h period), semidiurnal (12-h period), terdiurnal (8-h period), and quarterdiurnal (6-h period) tides with zonal wave numbers s = ±4. Note that quarterdiurnal tides were recently demonstrated to play a non-negligible role in the lower thermosphere (Pancheva and mukhtarov, 2023). The primary reason for using the same averaging window for both greenline and redline wind data, despite the different dynamic and electrodynamic processes at play, is consistency in the wave retrieval at the two altitudes, including averaging nearly identical local times, which is a preferred condition for comparing tidal winds between these two different altitude regions. The fitting method allows for robustness in the statistics as the 40-day wave fits are assumed to be valid only when at least 35 days of data are available.

For ICON MIGHTI, only the data that are flagged as ‘Good’ or (Wind Quality = 1) and ‘Caution’ (Wind Quality = 0.5) are used. This data quality selection criterion largely eliminates observations near the South Atlantic Anomaly (SAA) where the retrieval of wind velocities is difficult due to increased radiation, observations with small airglow signals, and observations from the day-night terminators where mode changes of the instrument take place. Their removal primarily eliminates data near 270°–330° longitude in the Southern Hemisphere, which are away from the primary latitude regions of interest for the wind results contained in this study (i.e., 0°–40°N). Occasional data gaps in the V05 MIGHTI winds are largely removed by the 40-day averaging. Data gaps may be a source of uncertainty in the retrieval of wave amplitudes due to incomplete local time sampling, especially during more extensive data gaps in mid-2021. Future data releases that improve coverage are expected to alleviate any potential detrimental effects of missing data. For ICON IVM, the ‘RPA’ and ‘DM’ flags are less than 1 when the data is of the highest quality and greater than 1 when it should be used with caution or rejected (see the data product documentation in the University of California at Berkely (UCB) ICON’s public FTP site provided in the Data Availability Statement for further details). This data quality selection criterion (flags $<$1) is adopted for ICON IVM.

The tidal nomenclature used here is standard (e.g., Hagan et al., 1995; Hagan and Forbes, 2002): DWs or DEs is a westward or eastward propagating diurnal tide, respectively, with zonal wavenumber s. For semidiurnal tides, D is replaced by S. D0 is the zonally symmetric diurnal tide, while S0 is the zonally symmetric semidiurnal tide. Stationary PWs with zonal wavenumber m are denoted ‘SPWm’.

3 Results and discussion

Figure 1A shows the diurnal non-migrating tidal spectrum of ICON IVM Ne near the geomagnetic equator (±5° MLAT) and 590 km altitude covering zonal wavenumbers s = ±4 and extending from 1 January 2020 to 23 March 2022 (days 1–813). The strong day-night Ne difference ‘aliased’ into DW1 is removed to highlight non-migrating diurnal tidal variability. The tidal variations are shown as percentages relative to the zonal mean. The time series of the solar (daily F10.7 solar radio flux) and geomagnetic (3-hourly kp) indices is shown in Figure 1B. This ∼2-year period is characterized by solar flux that increases from about 70 SFU in early 2020 to about 100–130 SFU in early 2022, and by geomagnetic activity that is generally below kp = 6. For the period examined, the daily Kp index exceeded Kp = 5 (Kp = 6) during 17 (4) days. The 17 days with Kp$>$5 were excluded from the analysis. Only 3 days or less occurred in the same 40-day windows, thus their removal generated no significant gaps in the analysis. This method assumes that any deviations related to enhanced geomagnetic activity are averaged out. It is important to keep in mind that due to the 40-day averaging required to derive the full zonal wavenumber tidal spectrum from ICON observations, day-to-day tidal variability is largely absent in the tidal spectra herein presented. Moreover, tidal amplitudes are likely to appear reduced due to the 40-day averaging (see, e.g., related discussions in Forbes et al. (2017); Hausler et al. (2014)).

FIGURE 1

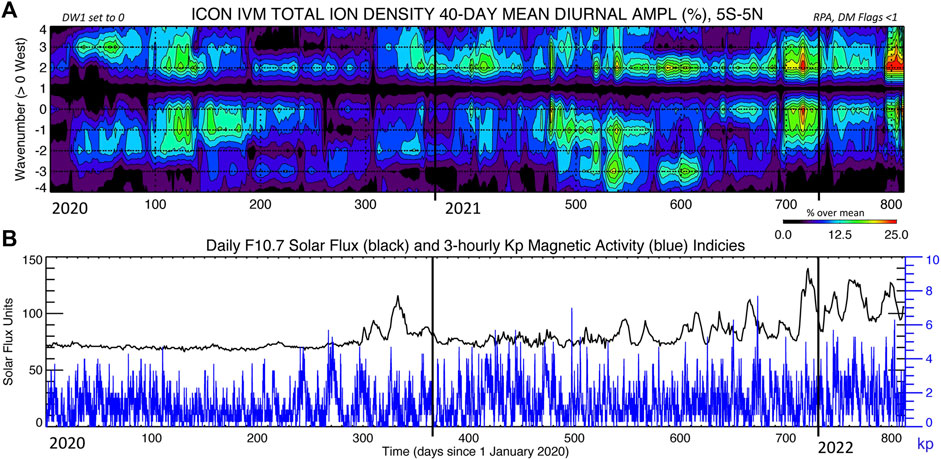
FIGURE 1. (A) Diurnal spectrum of ICON IVM total ion density (i.e., Ne, electron density) during 1 January 2020–23 March 2022 near the geomagnetic equator (±5° MLAT) near 590 km showing zonal wavenumbers ‘s’ (positive for westward propagation) within ±4. The spectrum is obtained by applying 2-dimensional spectral fitting on 40-day moving windows and including only data with RPA and DM flags $<$1 occurring on 3-hourly intervals with kp $<$ 6. DW1 is set to 0. The amplitudes are shown as percentage variations with respect to the zonal mean. Contours are shown from 0% to 25% in 2.5% intervals. (B) Time series of the daily F10.7 solar radio flux (black line) and 3-hourly kp geomagnetic (blue line) indices.

Strong Ne variability associated with DE3 is observed around days 510–630 (i.e., June-September 2021), with amplitudes upward of 20%. Smaller (∼10%–15%) DE3 Ne variability is observed around days 150–280 (i.e., June-September 2020) in agreement with the well-known seasonal and inter-annual variations in the thermospheric DE3. Large D0 and DW2 Ne variability, exceeding 20% is several occasions, is observed throughout the ∼820 days displayed. A close relationship between the temporal variations of D0 and DW2 Ne variations can be seen by a close inspection of Figure 1A. Larger D0 and DW2 can be seen during days 700–820 corresponding to increased solar flux in early 2022. Note also some remarkable correspondence between prominent quasi-27-day solar rotation variations in flux (see the black curve in Figure 1B) and D0 and DW2 Ne variability, further suggesting a connection to solar forcing for these tidal components that will be discussed in further detail below. Shown in Figure 1A are also large (up to 15%–20%) DE1 Ne amplitudes around days ∼100–200 and ∼460–580 and occasionally enhanced DE2 and DW3 (e.g., days ∼20–80) Ne amplitudes.

Next, we examine the concurrent diurnal non-migrating tidal spectrum from ICON MIGHTI zonal winds in the lower (i.e., ∼105 km) and middle (i.e., ∼220 km) thermosphere near the geographic equator and at 10°N-20°N geographic latitude (GLAT), as shown in Figure 2. The lower thermospheric diurnal non-migrating tidal spectrum is dominated by DE3 with amplitude variations upward of 25 m/s during days 180–320 and 540–690 corresponding to early July through mid-November 2020 and 2021, respectively. In the middle thermosphere, DE3 still retains significant amplitudes up to around 15 m/s in agreement with the vertical propagation of this wave component to higher thermospheric altitudes. For both altitudes shown in Figure 2, DE3 attains the largest amplitudes near the geographic equator in accordance with the Kelvin wave equatorially-trapped nature of the dominant thermospheric Hough mode of DE3 with a vertical wavelength of about 56 km (e.g., Gasperini et al., 2015; 2017). Remarkable correspondence is also found between the seasonal variations in the thermospheric zonal wind DE3 and the ionospheric Ne DE3 concurrently measured by ICON IVM and shown in Figure 1A. Given the significantly larger DE3 amplitudes observed in the lower thermosphere, the primary coupling process is likely to be associated with the E-region dynamo. Nonetheless, direct propagation to the middle thermosphere is also likely to constitute a non-negligible source of ionospheric DE3 (e.g., Gasperini et al., 2021). More work needed to be done to understand possible ion-neutral coupling effects in the zonal wind DE3 near 220 km due to the component of DE3 associated with E-region dynamo processes.

FIGURE 2

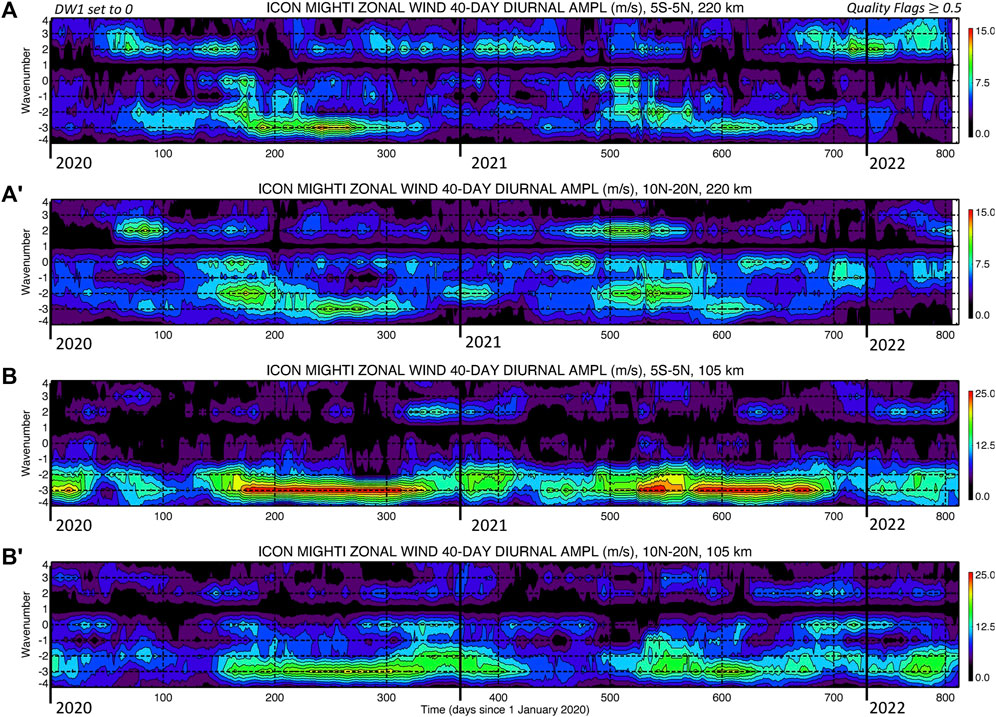
FIGURE 2. (A-A′) Diurnal non-migrating tidal spectrum (s ± 4, positive to the west) of ICON MIGHTI red-line middle thermospheric (∼220 km) zonal winds during 1 January 2020–23 March 2022 near the geographic equator (±5° GLAT) and between 10°N and 20°N GLAT, respectively. (B-B′) same as (A-A′) but in the lower thermosphere near 105 km. The wind tidal amplitudes are shown as m/s, with maxima set to 15 m/s near 220 km and 25 m/s near 105 km. Different color scale ranges are chosen for the lower and middle thermospheric wind spectra to facilitate visual representation. Contours at ∼220 km (∼105 km) are shown from 0 m/s to 15 m/s (25 m/s) in ∼1.7 m/s (∼2.8 m/s) intervals. Quality flags ≥0.5 are adopted. As for Figure 1, the tidal spectrum is obtained by applying 2-dimensional spectral fitting on 40-day moving windows, and DW1 is set equal to 0.

Hagan and Forbes (2002) demonstrated that DE3 and DE2 are mostly forced by latent heat release in persistent large-scale tropical rainfall systems and provide a direct coupling mechanism between tropospheric weather and upper thermospheric variability via upward propagation. These and other nonmigrating tides were also shown to induce a significant longitudinal and local time variation in the low-latitude F-region plasma, as discovered by Sagawa et al. (2005) and Immel et al. (2006), and more recently shown by Gasperini et al. (2021) using concurrent ICON, SORTIE, and TIMED satellite data, along with SD/WACCM-X modeling. An important neutral-plasma coupling process is the longitudinal modulation of E-region dynamo electric fields by nonmigrating zonal wind tides (Hagan et al., 2007; Jin et al., 2008) although F-region meridional tidal winds and thermospheric tidal O/N2 variations also play an important role (England et al., 2010).

Figure 2 also shows large zonal wind DW2, DE2, and D0 amplitudes with maxima near 15–20 m/s and larger amplitudes generally occurring in the middle thermosphere. Closer comparisons between Figures 2A,B near the equator and between Figure 2A′ and Figure 2B′ near 10°N-20°N GLAT reveal that significant middle thermospheric variability associated with DW2, DE2, and D0 is not traceable to lower thermospheric variability. This result is a strong indication of in situ generation in the thermosphere for these wave components. As hypothesized by Oberheide et al. (2011) and later demonstrated by Jones et al. (2013) using Thermosphere-Ionosphere-Mesosphere-Electrodynamics General Circulation Model (TIME-GCM) simulations, D0 and DW2 can originate via nonlinear interaction between the in-situ EUV-generated DW1 and the stationary planetary wave with s = 1 (SPW1) resulting from the geographic and geomagnetic field offset driven by plasma-neutral interactions. Similar D0 and DW2 variability is also observed in Ne measured in situ by ICON IVM near 590 km (see Figure 1A). Using TIME-GCM, Jones et al. (2013) distinguished between diurnal and semidiurnal migrating and non-migrating tidal components generated locally in the thermosphere from those that originate in the troposphere. They found that at low and middle latitudes both migrating and nonmigrating tides can be generated in situ through ion-neutral interactions due to the longitude-dependent ionosphere imposed by the realistic magnetic field configuration. Specifically, Jones et al. (2013) found that during solar maximum, non-migrating diurnal and semidiurnal tides forced by ion-neutral interactions are responsible for the majority of the longitude-dependent tidal structure seen in the low and middle latitude upper thermosphere, with D0 and DW2 arising from hydromagnetic coupling between SPW1 (i.e., modified ionosphere) and DW1 (i.e., idealized wind circulation) that can reach amplitudes of up to 20 m/s near 500 km. More discussion on this important finding and discrepancies with the modeling results by Jones et al. (2013) is provided in the later part of this study.

Note that the geographic coordinate system is the more natural and effective frame for diagnosing the origins of tidal dynamics. Therefore, in the present study, zonal winds near 105 km (typically corresponding to the peak height of the Hall conductivity) and 220 km are ordered in geographic coordinates to diagnose the lower-to-middle thermospheric connection. This allows us to understand what component of the thermospheric DE3 can propagate to the middle thermosphere. A geomagnetic reference frame may be appropriate to study connections between the middle thermospheric wave amplitudes and those observed in the topside F-region ionosphere. A geomagnetic frame will certainly generate some distortions in the structures. This is due to the way that a wind field ordered in geographic coordinates interacts with a magnetic field whose inclination, declination, and magnitude vary with longitude (see, e.g., Maute et al., 2012; Forbes et al., 2021b). However, magnetic coordinates are most appropriate for diagnosing global-scale waves in ionospheric parameters, as shown in many IT wave coupling studies (e.g., see references in Forbes et al., 2021b). A geomagnetic reference frame may be appropriate to study connections to the topside ionosphere DE3, however, the distortions in the structures due to the way that a wind field ordered in geographic coordinates interacts with a magnetic field whose inclination, declination, and magnitude vary with longitude are not the primary focus of this study and will be subject of follow-on work.

We now turn our attention to the diurnal non-migrating tidal spectrum in meridional winds measured by ICON MIGHTI. Figure 3 shows the same spectral depictions of MIGHTI winds as Figure 2 but for the meridional wind component. Clearly, the spectra are dominated by D0 and DW2 variability in both the lower and middle thermosphere with meridional wind amplitudes exceeding 20 m/s on several occasions. In the lower thermosphere (i.e., ∼105 km), particularly striking are the DW2 variations around days 255–415 (i.e., mid-September 2020—mid-February 2021) and 620–780 (i.e., mid-September 2021 - mid-Feruary 2022) and 10°N-20°N GLAT and D0 variations around days 255–450 (i.e., mid-September 2020 - late-March 2021) and 520–780 (i.e., early-June 2021 - mid-February 2022) near the geographic equator and 10°N-20°N GLAT. In the middle thermosphere (i.e., ∼220 km), significant D0 and DW2 variations are observed throughout 2020–2022 with amplitude maxima near 15 m/s a little correspondence with the lower thermospheric D0 and DW2. This finding suggests, similar to what was discussed in the context of Figure 2, that these wave components are likely to be generated in situ likely from the nonlinear interaction between in-situ EUV-generated DW1 and the SPW1. More discussion on this topic is provided below.

FIGURE 3

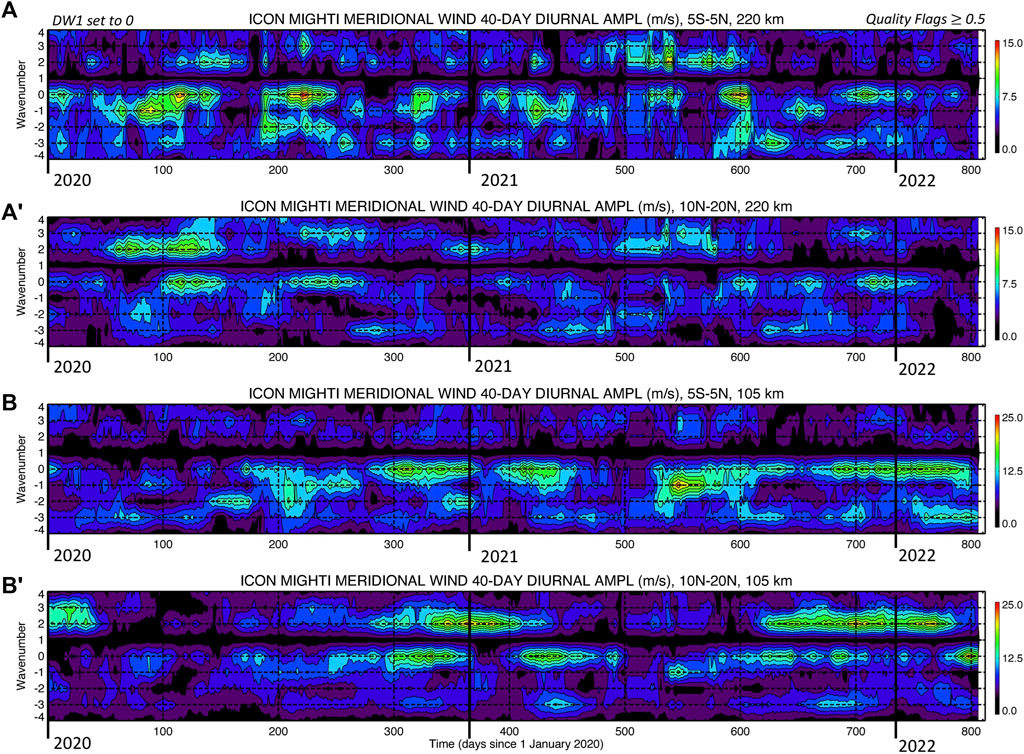
FIGURE 3. Same as Figure 2 (A–B′) but for ICON MIGHTI meridional winds. As for Figure 2, contours at ∼220 km (∼105 km) are shown from 0 m/s to 15 m/s (25 m/s) in ∼1.7 m/s (∼2.8 m/s) intervals.

Next, we compare the ionospheric diurnal tidal spectrum observed at two different ionospheric heights to investigate the persistence of certain features through different altitude regions in the topside F-region ionosphere. For this purpose, we compare tidal results from concurrent IVM measurements onboard the SORTIE CubeSat near 420 km and ICON near 590 km. Due to their different altitudes, SORTIE IVM observes an O + -dominated ionosphere while ICON IVM samples nonnegligible H+ (especially during nighttime). Thus, to best interpret the ionospheric tidal signatures observed concurrently by ICON and SORTIE, Figure 4 compares ICON O+ density with SORTIE total ion density (i.e., Ne). Gasperini et al. (2021) already demonstrated a strong correlation between the WN4 structure seen in SORTIE Ne and ICON O+ density during May 2020, with Pearson correlation coefficients as high as 0.87.

FIGURE 4

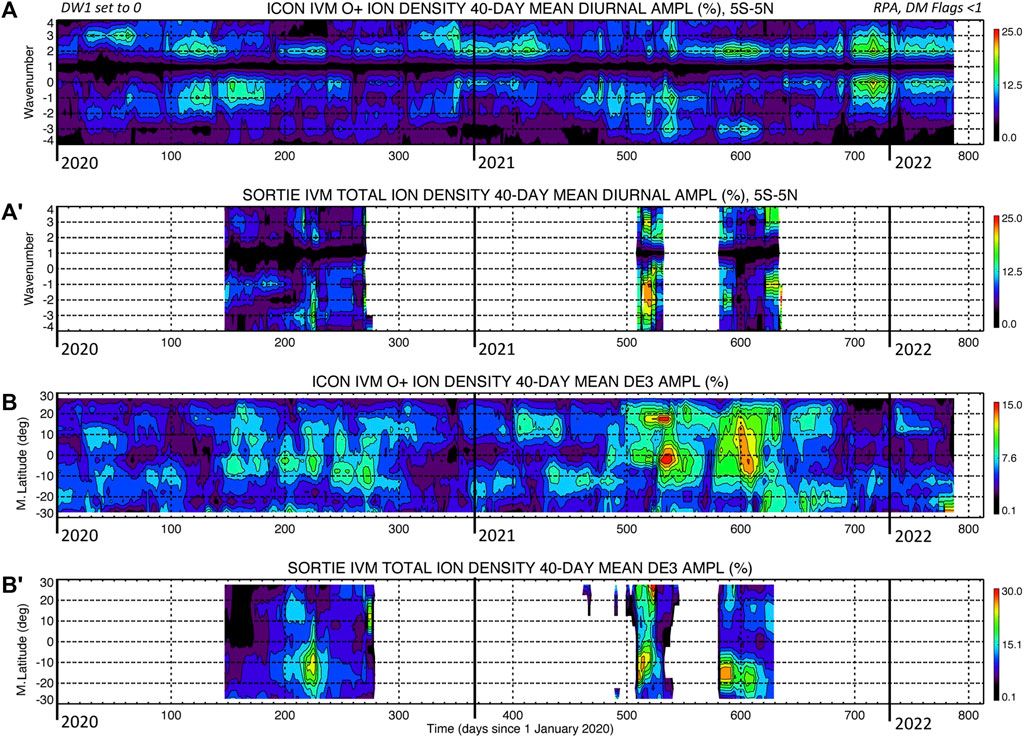
FIGURE 4. (A-A′) Wavenumber-DOY diurnal spectrum of O⁺ ion density near the geomagnetic equator (5°S-5°N MLAT) from ICON IVM near 590 km and SORTIE IVM near 420 km, respectively. (B-B′) MLAT-DOY depiction of ICON IVM and SORTIE IVM DE3 O⁺ amplitudes. The amplitudes (shown as percentages over the zonal mean) are obtained by applying 2-dimensional spectral fitting on 40-day moving windows. Note the different color scales for SORTIE and ICON DE3. SORTIE (ICON) DE3 maxima near 30% (15%). Contours for ICON (SORTIE) are shown from 0% to 15% (25%) in 1.5% (2.5%) intervals.

Figure 4A, A′ show the diurnal nonmigrating tidal spectrum as a function of time near the geomagnetic equator (5°S-5°N MLAT) of ICON IVM O+ density and SORTIE IVM Ne, respectively. For SORTIE, IVM data is sufficiently continuous to allow 40-day spectral fitting during the two periods: 27 May 2020–8 October 2020 (i.e., days 148–282) and 8 April 2021–21 October 2021 (i.e., days 464–660). Comparisons between the diurnal spectra of ICON IVM Ne near 590 km and SORTIE IVM Ne near 420 km suggest the presence of similar wave components, with large DE3, D0, DE2, and DW2 (note that the enhancements are not concurrent for all times and wave components). Near the geomagnetic equator, Ne tidal amplitudes near 420 km are about 40% larger than those observed near 590 km (note the different color scales between Figures 4A,B). This result is evidence that the prominent D0 and DW2 Ne variations previously discussed are not isolated to 590 km but are a common feature throughout the topside ionosphere.

Further, Figure 4B, B′ elucidate the MLAT-temporal structure of DE3 amplitudes (as percentages over the zonal mean) of ICON O+ density and SORTIE Ne, respectively. Effects from the equatorial ionization anomaly (EIA) in DE3 appear evident at both altitudes, although at ∼420 km the peaks occur near ±20° MLAT while at ∼590 km the peaks are near ±10° MLAT. This effect is likely due to SORTIE’s lower mean altitude in accordance with the well-known ionospheric fountain effect (e.g., Andrews et al., 1987). Important equatorial asymmetries exist in DE3 Ne amplitudes near 420 km that are not as clearly present near 590 km.

We now focus on the latitudinal-temporal amplitude structure of a few dominant wave components in the lower and middle thermospheric and topside ionospheric diurnal spectra, specifically DW1, SPW1, D0, and DW2 as shown in Figure 5. Prominent variability in the nonmigrating tidal components is observed in both lower and middle thermospheric zonal winds with amplitudes up to ∼18 m/s. The lower thermospheric DW1 shows little resemblance with the middle thermospheric DW1, as expected since the latter is largely driven in situ in the thermosphere by the absorption of solar EUV radiation. The DW1 Ne appears to be rather equatorially symmetric and shows a closer association with the middle thermospheric DW1 than the lower thermospheric DW1. A closer inspection of Figure 5 reveals strong similarities in the timing and latitude structure of the middle thermospheric zonal wind SPW1 and D0 (particularly in the northern hemisphere around days 150–220 and 480–610), and some correspondence with DW1 and DW2. Similar considerations can be made for the latitudinal-temporal of these 4 wave components in Ne. A more detailed discussion on DW2 and D0 is provided below in the context of previous studies and CTMT results.

FIGURE 5

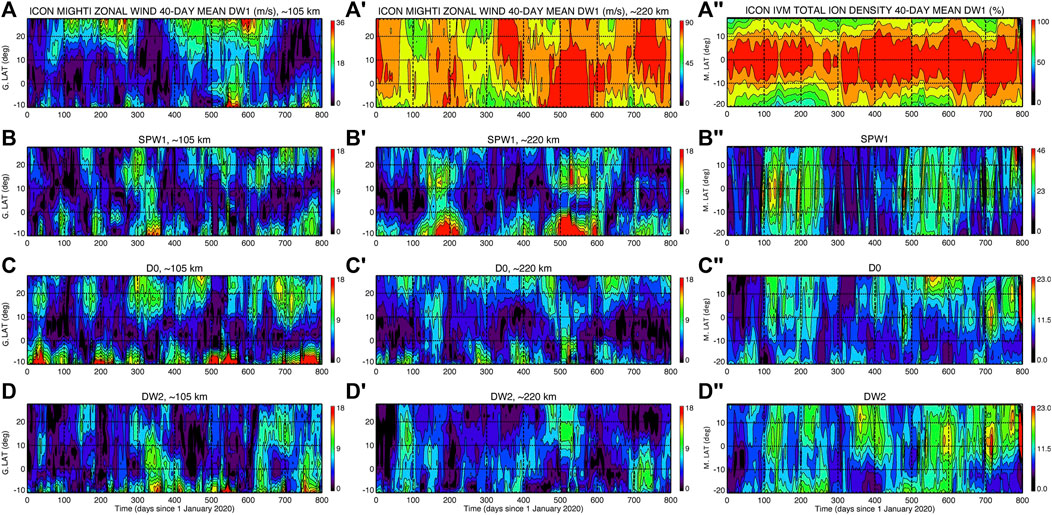
FIGURE 5. Geographic latitude (GLAT) versus DOY structure of ICON MIGHTI zonal wind DW1 (A), SPW1 (B), D0 (C), and DW2 (D) amplitudes in the lower thermosphere near 105 km. (A″–D″) Same as (A–D), but in the middle thermosphere near 220 km. (A″–D″) Same as (A–D), but from ICON IVM Ne near 590 km. All the spectra are obtained by least squares fitting data in 40-day moving windows. Contours for DW1 at ∼105 km, ∼220 km, and ∼590 km are shown up from 0 m/s/% to 36 m/s, 90 m/s, and 100% in ∼3.2 m/s, ∼8.2 m/s, and 9.1% intervals, respectively. Contours for SPW1 at ∼105 km, ∼220 km, and ∼590 km are shown from 0 m/s/% to 18 m/s, 18 m/s, and 46% in ∼1.6 m/s, ∼1.6 m/s, and 4.2% intervals, respectively. Contours for D0 and DW2 at ∼105 km, ∼220 km, and ∼590 km are shown from 0 m/s or 0% to 18 m/s, 18 m/s, and 23% in ∼1.6 m/s, ∼1.6 m/s, and 2.1% intervals, respectively.

Next, we investigate diurnal tidal variability in the zonal winds from the CTMT model. The focus is on latitude-temporal and altitude-temporal structures and comparisons with those observed by MIGHTI. As already discussed in Section 2.2, tidal forcing occurring in situ in the thermosphere is not accounted for in CTMT. In other words, CTMT is not capable of reproducing in-situ-forced migrating tides resulting from EUV forcing (e.g., the middle thermospheric DW1), and in-situ-forced nonmigrating tides in the middle thermosphere due to nonlinear interactions, most notably the diurnal nonmigrating tidal components DW2 and D0. For context, Table 1 contains information on the peak height, peak latitudes, and vertical wavelengths for zonal wind HME1 and HME2 for DW2, DW1, D0, DE1, DE2, and DE3 that are at the basis of CTMT. Also included in Table 1 are HME1 and HME2 of the 3-day UFKW1. HME1 and HME2 correspond to the first symmetric and first antisymmetric Hough modes with symmetric and antisymmetric referring to the relative phasing across the equator. Note that meridional wind HMEs always have the opposite symmetry. As shown in previous studies (e.g., Oberheide and Forbes, 2008; Oberheide et al., 2009; 2011) non-equatorial tidal peaks in the middle/upper thermosphere tend to shift toward higher latitudes due to molecular diffusion. Gasperini et al. (2017) studied the effects of mean winds and dissipation on both DE3 and a 3-day UFKW1 in a general circulation model for solar minimum conditions, reporting that the effects of asymmetric mean winds are to distort the horizontal shapes of these waves and shifting their peaks toward westward wind regimes.

The latitude versus month-of-the-year structure of the major (DW2, DW1, D0, DE2, and DE3) diurnal tidal amplitudes from CTMT near 105 km (220 km) altitude in zonal and meridional winds are contained in Figure 6 (Figure 7). While Figure 8 shows the latitude-height structure of the annual-mean diurnal tidal amplitudes also from CTMT. As already discussed by Oberheide et al. (2011) in the context of comparisons between CTMT and neutral density and wind observations from the Challenging Minisatellite Payload (CHAMP) satellite, the presence of strong middle/upper thermospheric DW2 and D0 and their absence in CTMT suggests the presence of additional forcing mechanisms in the thermosphere. For tides, the time constants of eddy and molecular diffusion are proportional to the square of their vertical wavelengths (e.g., Oberheide et al., 2011). As such, the short vertical wavelength characterizing DW2 (∼33 km) makes it not capable of effectively propagating into higher thermospheric altitudes. As shown in Table 1, for the zonal winds only the antisymmetric HME (HME2) of D0 has a sufficiently long vertical wavelength (∼69 km) to propagate into the thermosphere. Note that for the meridional winds (not shown in Table 1) only the symmetric HME (HME1) of D0 can effectively propagate to the thermosphere. HME2 is responsible for generating prominent antisymmetric signals in the lower (partly shown by Figure 6C) and middle (partly shown in Figure 7C) thermospheric D0 zonal winds, while HME1 is responsible for producing symmetric signals in the lower (Figure 6C′) and middle (Figure 7C′) thermospheric D0 meridional winds. These tidal signatures (and latitude structures) in D0 are also found in the MIGHTI observations (Figure 5 for the zonal wind component), although CTMT underestimates the amplitudes by up to ∼75% in the middle thermosphere (i.e., near 20 m/s in MIGHTI and near 5 m/s in CTMT, depending on latitude and month of the year) due to lack on in situ generation. DW2 meridional and zonal winds are very large below about 100 km (not shown), small near 105 km (Figure 6A, A′, respectively), and nearly absent in the middle thermosphere (Figure 7A, A′, respectively) as the zonal wind component is associated with the first symmetric HME. DW2 zonal wind amplitudes in the lower thermosphere are underestimated by CTMT by up to ∼67%(12 m/s versus 4 m/s), while the strong (15 m/s) middle thermospheric DW2 observed by MIGHTI is nearly absent in CTMT likely due to in situ generation not reproduced by CTMT.

FIGURE 6

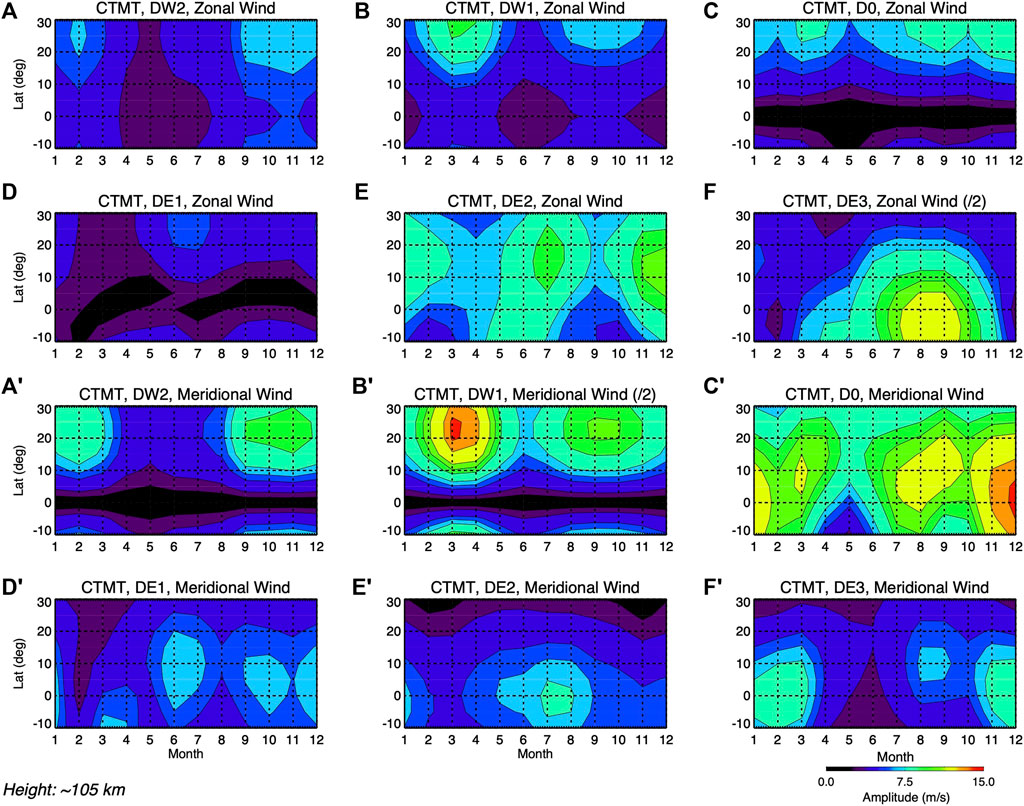
FIGURE 6. Latitude versus month zonal wind amplitude structure of DW2 (A), DW1 (B), D0 (C), DE1 (D), DE2 (E), and DE3 (F) near 105 km altitude from the Climatological Tidal Model of the Thermosphere (CTMT) model. (A′–F′) Same as (A–F), but for the meridional wind component. Contours are shown from 0 m/s to 15 m/s in 1.5 m/s intervals. The zonal (meridional) wind DE3 (DW1) amplitudes are divided in half to facilitate visual representation.

FIGURE 7

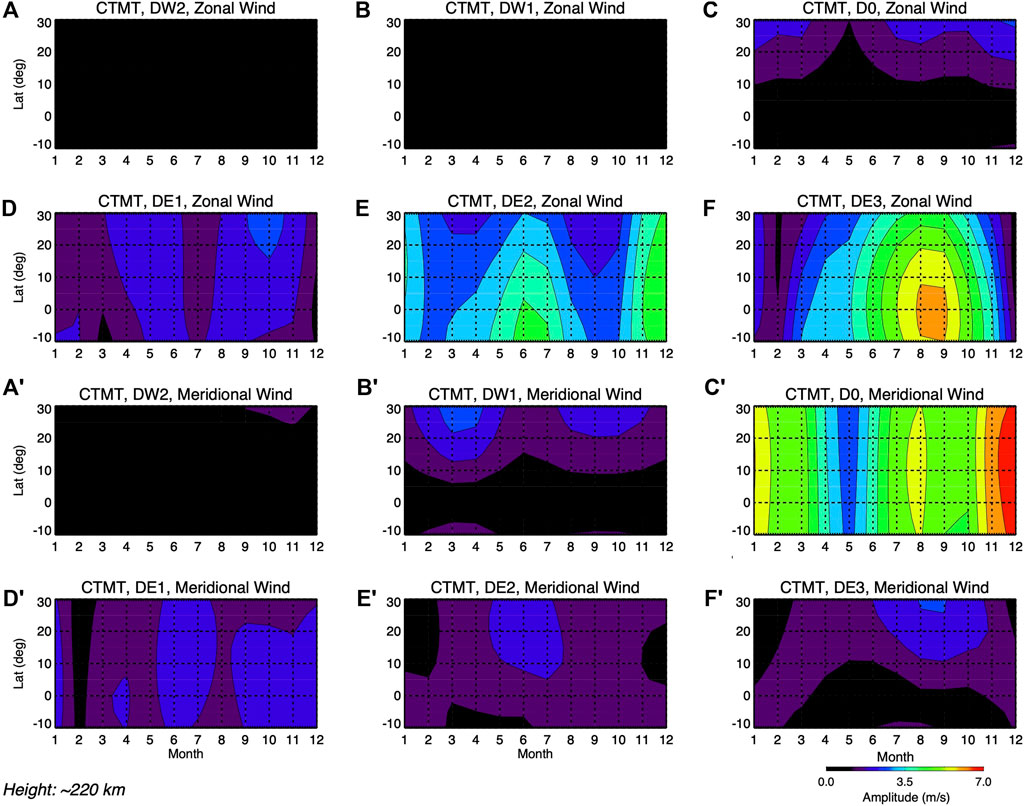
FIGURE 7. Same as Figure 6 (A–F′), but near 220 km altitude. Contours are shown from 0 m/s to 7 m/s in ∼0.7 m/s intervals.

FIGURE 8

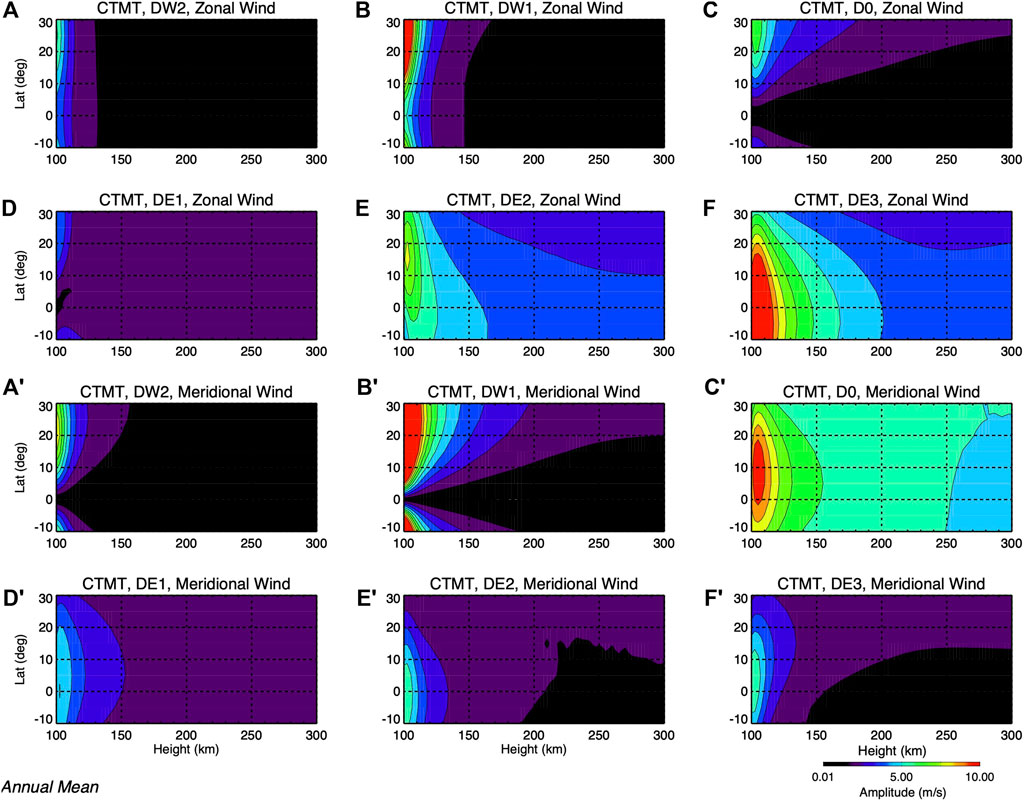
FIGURE 8. Latitude (10°S-40°N, y-axis) versus height (100–300 km, x-axis) zonal wind amplitude structure of DW2 (A), DW1 (B), D0 (C), DE1 (D), DE2 (E), and DE3 (F) as annual means from the CTMT model. (A′–F′) Same as (A–F), but for the meridional wind component. Contours are shown from 0 m/s to 10 m/s in 1 m/s intervals.

TABLE 1

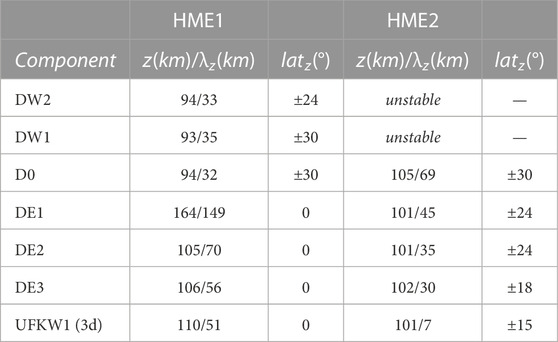
TABLE 1. Zonal wind HMEs for diurnal tides and the 3-day UFKW1. ‘z’ is the altitude of maximum amplitude, $‘{\lambda }_z^{\prime }$ denotes the vertical wavelength between 90 and 120 km for F10.7 = 125, while ‘lat_z’ the latitudes of zonal wind peaks at ‘z’.

To summarize, diagnostics of MIGHTI red-line winds (Figure 5A′–D′) indicate middle thermospheric diurnal tidal amplitudes exceeding 15 m/s with D0, DW2, and SPW1 often the largest nonmigrating diurnal tides present. This finding, already suggested by Oberheide et al. (2011) and confirmed numerically by Jones et al. (2013), demonstrates that the nonmigrating components DW2 and D0 have an upper thermospheric source. This source is most likely associated with the nonlinear interaction occurring in situ in the middle/upper thermosphere of the in-situ-generated DW1 and SPW1, as clearly demonstrated by the close association between the latitude-temporal structure of these 4 wave components (Figure 5). A strong and somewhat prominent finding from Figure 5 that is different than what was modeled by Jones et al. (2013) is the presence of D0 and DW2 with prominent amplitudes even during weak solar flux conditions. Jones et al. (2013) showed that these non-migrating tides were less likely to be strong under solar minimum/maximum conditions, which is not in agreement with the MIGHTI results shown in Figure 5.

The HME2 of DW2 does not play a significant role here since DW2 is fully symmetric below about 100 km altitude. As one can see from Figure 8, the eastward propagating DE2 and DE3 zonal wind tides can propagate directly into the thermosphere without substantial changes to their latitudinal structures as a result of their relatively longer vertical wavelengths (70 km and 56 km, respectively, as shown in Table 1) that correspond to reduced molecular dissipation for their first symmetric modes. In general, the MIGHTI latitude-temporal structures at 220 km are significantly different than those shown by the CTMT. In the case of D0, DW1, and DW2 this is due to the presence of in situ-generated components in the MIGHTI tides which are not included in the CTMT. Comparisons between MIGHTI and CTMT diurnal tides reveal discrepancies connected with differences in tides with longer vertical wavelengths that are more capable of propagating from ∼105 km to ∼220 km. Lower (middle) thermospheric zonal wind DE3 amplitudes from CTMT maximizing near 15 m/s (∼7 m/s) are largely underestimated (by about 50%) compared to those observed by MIGHTI with maxima near 30 ∼ m/s (∼15 m/s). Note that the MIGHTI-observed DE3 zonal wind amplitudes are generally consistent with previous observations (e.g., Gasperini et al., 2015; 2018; 2021). Some model-data differences not ascribed to in situ generation in the thermosphere may be ascribed to lower solar flux in the observations (70–100 SFU for MIGHTI versus ∼110 SFU for CTMT) that favors wave propagation to the middle thermosphere and by the well-known inter-annual variability in the waves (note that CTMT is a ‘climatology’ of the tidal spectrum obtained combining over 6 years of TIMED data).

Seminal theoretical studies (e.g., Lindzen, 1967; Lindzen and Hong, 1974; Volland, 1974; Volland and Mayr, 1977; Forbes and Garrett, 1979; Forbes and Hagan, 1988; Forbes and Vincent, 1989) reported on some basic characteristics of waves propagating into the thermosphere, where the dissipative time scales increase roughly as the inverse of density. Entering the thermosphere, tidal amplitudes generally increase up to a region where dissipation is important and then (case 1) asymptotically approach constant values (with no significant decrease in amplitude with increasing altitude), or can increase up to a region where dissipation is important but then (case 2) decrease considerably before asymptotically reaching a constant value. In previous work, Gasperini et al. (2017) examined the vertical propagation of DE3 (and UFKW1) to the thermosphere using TIME-GCM with the lower boundary based on Modern-Era Retrospective analysis for Research and Applications (MERRA) reanalysis data. This study found that (a) the effect of molecular dissipation is to broaden the latitudinal structures in accord with prior theoretical predictions and satellite observations (e.g., Gasperini et al., 2015); (b) the main effect of background zonal mean winds is to distort the height-latitude structures; (c) the altitude where upward propagating waves maximize is related to the ratio between the timescale for dissipation and the wave’s Doppler-shifted frequency.

Figure 9 contains the vertical structure of CTMT equatorial DE3 zonal wind amplitudes (panel a) and phases (panel b) during September, which shows a behavior largely consistent with a significant reduction in wave amplitudes in the thermosphere. As previously noted, careful analysis of the observational results contained in Figure 2 reveals DE3 zonal wind amplitudes that are reduced by about 50% near 220 km compared to ∼105 km. This result suggests that the MIGHTI-observed DE3 in the middle thermosphere is undergoing dissipation more closely resembling case (2). It is important to note that while the DE3 may still have appreciable amplitudes near 220 km, there is likely only some small phase progression with altitude, i.e., dissipative effects have made its vertical wavelength extremely long. As such, one may argue that the DE3 is no longer propagating vertically.

FIGURE 9

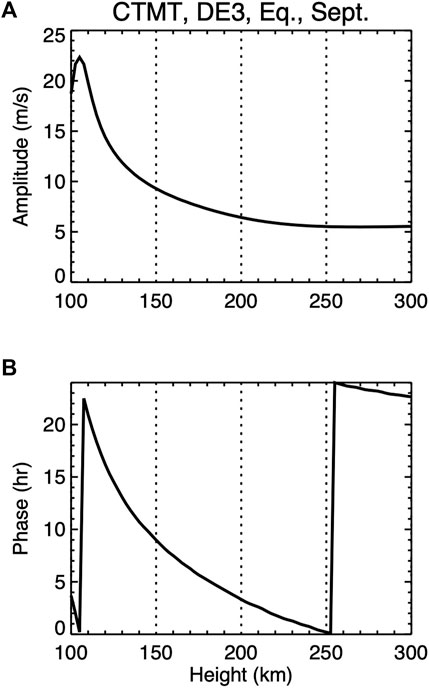
FIGURE 9. Vertical structure (100–300 km, x-axis) of CTMT equatorial DE3 zonal wind amplitudes (A) and phases (B) during September.

Finally, we examine the global-scale wave spectrum extending from 0.5 days to 7 days as revealed by 2-dimensional least-squares fitting of remotely-sensed MIGHTI lower (i.e., 105 km) and middle (i.e., 220 km) thermospheric zonal winds and we compare it with the one inferred by in-situ-measured IVM Ne near 590 km. These spectral results near the equator (10°S-10°N GLAT for the winds and 10°S-10°N MLAT for Ne) that combine over 800 days of data are shown in Figures 10A–C, respectively. The migrating tides are set to 0 to facilitate visual representation. The dominant diurnal tidal periodicities present near 105 km are DE3, DE2, D0, and DW2 (already extensively discussed in Figures 2, 5).

FIGURE 10

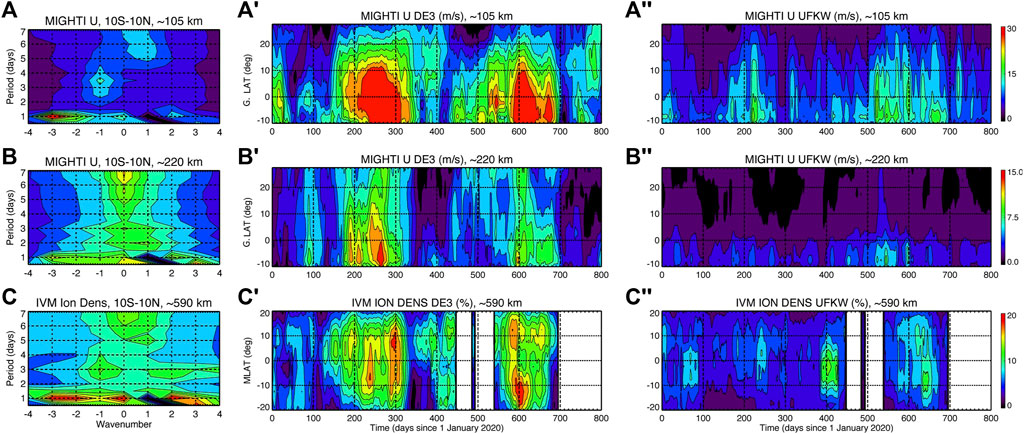
FIGURE 10. (A) Period-wavenumber spectrum of ICON MIGHTI green-line zonal winds near the geographic equator (10°S-10°N GLAT) and 105 km altitude, obtained by combining all data from 1 January 2020 through 23 March 2022. The migrating DW1 and SW2 tidal amplitudes are set to 0. (A′) GLAT-DOY amplitude structure of DE3 zonal winds near 105 km. (A′′) GLAT-DOY amplitude structure of UFKW1 zonal winds near 105 km. (B–B″) Same as (A–A″), but for ICON MIGHTI red-line zonal winds near 220 km. (C–C″) Same as (A–A″), but for ICON IVM Ne near 590 km. Contours are shown from 0 m/s or 0% to 30 m/s, 15 m/s, 20% in 3 m/s, 1.5 m/s, and 2% intervals at ∼105 km, ∼220 km, and ∼590 km, respectively.

Figure 10A reveals the existence of a prominent and persistent ∼3-day UFKW1 in the lower thermosphere, with ∼2-year mean amplitudes near 10 m/s. UFKWs constitute the subset of Kelvin waves with faster horizontal phase speeds (∼150 m/s) enabling their propagation to MLT heights and above (e.g., Salby et al., 1984; Forbes, 2000; Gu et al., 2014; Gasperini et al., 2015; 2018; Forbes et al., 2020). In the MLT the most frequent and longest-lasting UFKW events have s = −1 and ∼2–4-day periods. UFKWs can effectively drive F-region ionospheric variability (Liu et al., 2013; 2015; Gu et al., 2014; Abdu et al., 2015) primarily through the E-region dynamo processes (e.g., Chang et al., 2010) but also in situ via F-region winds and field-aligned drifts (e.g., Forbes et al., 2020).

The lower thermospheric zonal wind wave spectrum in Figure 10A also demonstrates a strong s = +1 ∼6-day variation associated with the westward quasi-6-day planetary wave with zonal wavenumber 1 (Q6DW). The Q6DW is a prominent and recurrent planetary wave in the MLT region (e.g., Talaat et al., 2002; 2001; Lieberman et al., 2003; Riggin et al., 2006; Forbes and Zhang, 2017). A number of recent studies demonstrated impacts on F-region ionospheric variability from Q6DWs (Gan et al., 2016; 2017; Gu et al., 2014b; 2018a; b; Qin et al., 2019; Yamazaki, 2018). As noted by Forbes et al. (2020c), changes in F-region electron densities at Q6DW periods result from transport by ExB drifts, where the electric field E is generated in the ionospheric E-region through dynamo action of Q6DW winds and possibly Q6DW modulation of tides and/or gravity waves. The spatial structure of Q6DW in the MLT region is highly consistent with the theoretical Rossby (1, 1) normal mode (Talaat et al., 2001), with Q6DW amplitudes in the zonal wind maximizing around the equator (e.g., Qin et al., 2019; 2021; Forbes et al., 2020c).

Spectral analyses of MIGHTI middle thermospheric winds indicate significantly reduced amplitudes (by ∼50%–80%) for both the UFKW1 and Q6DW near 220 km (see Figure 10B″ for UFKW1). This result suggests that both these wave components undergo strong dissipation in their propagation between ∼105 km and ∼220 km. It is important to realize that the wave spectra in Figures 10A–C are averages of over 2 years of MIGHTI and IVM observations. However, previous modeling and observational evidence indicate that thermospheric UFKW and Q6DW occur mainly in limited events lasting from about 10 days to 30 days. Hence, the UFKW1 and Q6DW amplitudes in Figures 10A–C are likely to be significantly suppressed by the averaging involved.

Closer examination of the middle thermospheric wave spectrum reveals dominant s = 0 variations with periods of 12 h (i.e., S0, as recently shown by Forbes et al., 2022), 1-day (i.e., D0, previously discussed), and 7 days; and other notable s = 0 variations near 2 and 3 days. Remarkably, along with the expected strong DE3, DE2, D0, and DW2 variations, the Ne wave spectrum (Figure 10C) shows prominent variability near 3 days and s = −1 associated with the lower thermospheric UFKW1 and near 6 days and s = +1 associated with the Q6DW (Figure 10A). Figure 10C also shows strong SW3 variability (similar to that discussed by Forbes et al., 2022), westward propagating 3-day variations, and prominent s = 0 variability near 7 days that closely resembles the variability in zonal winds near 220 km (Figure 10B). These latter two variations have not been reported before in ICON data and will be the subject of future work. Comparison between Figures 10A–C, allowed by contemporaneous MIGHTI and IVM observations, demonstrates how the short-term large-scale variability of ionospheric density is mostly driven by lower and middle thermospheric waves, at least at low latitudes for low solar activity and relatively quiet geomagnetic conditions. The similarities between the ∼2-year-averaged lower thermospheric zonal wind and ionospheric Ne wave spectra in Figures 10A–C are quite remarkable.

Similar to DE3 which is known to be primarily generated in the tropical troposphere by latent heat release in deep convective clouds (e.g., Hagan, 1996; Lieberman et al., 2007), UFKWs also originate primarily from latent heat release in the tropical troposphere and have a predominance of the kinetic energy in the zonal wind component (e.g., Forbes, 2000). As previously discussed, UFKWs are a special kind of gravity waves modified by the Earth’s rotation and trapped in the equatorial and low-latitude regions, where the Coriolis force is negligible (Salby et al., 1984; Andrews et al., 1987), and have a long vertical wavelength ($>$50 km) that allow them to propagate into the lower and middle thermosphere, with zonal wind amplitudes exceeding 30 m/s near 110 km (Gu et al., 2014a) and 10 m/s near 260 km (Gasperini et al., 2015). Using HMEs, Forbes et al. (2023) recently showed that UFKWs with periods shorter than about 4 days can effectively penetrate above the lower thermosphere, and dissipation broadens UFKW latitude structures with increasing height and lengthens vertical wavelengths with increasing latitude, whereas ion drag effectively dampens UFKW amplitudes with increasing efficiency at higher solar activity levels.

Figures 10A–C demonstrate the prominence of the thermospheric DE3 and UFKW1 and their ability to effectively couple into the ionosphere. Next, we focus our attention on their latitude-temporal structures in MIGHTI zonal winds near 105 km (Figure 10A′ and Figure 10A″, respectively) and 220 km (Figure 10B′ and Figure 10B″, respectively) and in IVM Ne near 590 km (Figure 10C′ and Figure 10C″, respectively). After the exact UFKW1 period is determined using spectral analysis, simultaneous least-squares fits are performed on these 40-day windows to derive DE3 and UFKW1 amplitudes and phases. UFKW1 amplitudes are derived using 40-day moving windows for consistency with the tidal diagnostics. As discussed in detail for Figure 2, the lower thermospheric zonal wind DE3 shows prominent amplitudes upward of ∼25 m/s during days 180–320 and 540–690 (early July through mid-November 2020 and 2021), while the middle thermospheric DE3 retains large amplitudes up to about 15 m/s.

The latitude-temporal structure of the DE3 zonal winds is similar between the two heights in agreement with the primarily first symmetric mode of DE3 (with vertical wavelengths of ∼56 km, see Table 1) that dominates at both heights compared to the second antisymmetric mode (with vertical wavelengths of ∼30 km, see Table 1) that peaks near 102 km, and is thus likely to be already mostly dissipated by about 105 km altitude. The UFKW1 shows similar seasonal behavior to DE3 with large amplitudes upward of 18 m/s during days 180–320 and 540–690 corresponding to early July through mid-November 2020 and 2021. While this finding is not surprising considering that both DE3 and UFKWs are known to be generated via similar processes in the lower thermosphere (i.e., latent head in tropical convective systems), various previous studies (e.g., Gasperini et al., 2015; 2018) noted lack of a defined seasonal variation for UFKWs. While it is possible that the 40-day averaging would hide some of the variability, Figure 10A″ suggests that some recurrent seasonal pattern in the lower thermospheric UFKW may be present. This finding may require further verification that will necessitate additional analyses and longer observational datasets. UFKW1 middle thermospheric amplitudes show maxima near 8 m/s, i.e., about 50% less than their corresponding amplitudes near 105 km. Significant latitudinal asymmetry is found in both DE3 and UFKW1 at both thermospheric heights. Using a general circulation model, Gasperini et al. (2017) showed notable effects from mean winds on DE3 and UFKW amplitudes. These effects are significantly more severe for DE3 than for the UFKW despite the fact that they share the same phase speed and that their full latitudinal widths at half-maximum are both near 30° thus making them subject to effectively the same mean winds. Similar conclusions can be made by close inspection of Figure 10. Note that UFKWs are not included in CTMT, hence no comparisons can be made for these wave components.

4 Conclusion

This study evaluates the simultaneous diurnal tidal spectrum and other high-impact waves in the lower and middle thermosphere and topside F-region ion density (i.e., Ne) from ICON and SORTIE. This is accomplished through spectral analyses of recently-released version 5 (v05) ICON MIGHTI wind data over the height ranges ∼93–106 km and ∼200–270 km (with day and night coverage), and in-situ topside F-region ion densities from IVMs onboard ICON (v06) near 590 km and the SORTIE CubeSat (v02) near 420 km. Results are presented during the solar minimum and generally geomagnetic-quiescent period (Kp$>$4 on only about 8.7% of the days) extending from January 2020 to March 2022 which provides a unique opportunity to better understand how a selected group of global-scale waves couple lower thermospheric variability with IT variability. Comparisons with the CTMT tidal model are also presented. These analyses of remotely-sensed horizontal thermospheric winds from ICON MIGHTI and in-situ-measured F-region Ne from ICON and SORTIE IVMs, along with comparisons with tidal output from CTMT, reveal the following.

1. ICON IVM diurnal spectral analyses reveal large D0-and DW2-induced ion density variability, exceeding 20% on several occasions, throughout January 2020 - March 2022. A close relationship between the D0 and DW2 Ne variations is found consistent with strong quasi-27-day variations in the amplitudes during later 2021 likely induced by corresponding solar rotation variations in flux. Strong Ne variability associated with DE3 is observed around July-October 2021 with amplitudes upward of 20%. Smaller (∼10%–15%) DE3 Ne variability is observed around July-October 2020 in agreement with the well-known seasonal and inter-annual variations in the thermospheric DE3.

2. The lower thermospheric diurnal non-migrating tidal spectrum is dominated by DE3 with amplitude variations upward of 25 m/s from early July to mid-November 2020 and 2021. The middle thermospheric DE3 retains significant amplitudes up to around 15 m/s near the equator in agreement with the vertical propagation of this wave component to higher thermospheric altitudes. Remarkable correspondence is also found between the latitude-temporal variations of the lower thermospheric zonal wind DE3 and corresponding variation in the ionospheric DE3, consistent with primary coupling through E-region dynamo processes.

3. Large zonal wind DW2, DE2, and D0 amplitudes with maxima near 15–20 m/s and larger amplitudes generally occur in the middle thermosphere. Significant DW2, DE2, and D0 middle thermospheric variability is not traceable to lower thermospheric variability in these wave components, indicating in situ generation in the thermosphere for these wave components (as hypothesized by Oberheide et al., 2011 and later demonstrated numerically by Jones et al., 2013). Results indicate that D0 and DW2 are likely to originate via nonlinear interaction between in-situ EUV-generated DW1 and the stationary planetary wave with s = 1 (SPW1) resulting from the geographic and geomagnetic field offset, driven by plasma-neutral interactions. Similar D0 and DW2 variability is also observed in Ne near 590 km. An important finding from MIGHTI different than what was modeled by Jones et al. (2013) is the presence of prominent D0 and DW2 even during weak solar flux conditions.

4. The diurnal non-migrating tidal spectrum in meridional winds measured by ICON MIGHTI is dominated by D0 and DW2 variability in both the lower and middle thermosphere with meridional wind amplitudes exceeding 20 m/s on several occasions. In the lower thermosphere particularly striking are the DW2 variations and D0 variations consistent with their in-situ generation from the nonlinear interaction between in-situ EUV-generated DW1 and the SPW1. Detailed diagnostics of MIGHTI red-line winds indicate middle thermospheric diurnal amplitudes exceeding 15 m/s with D0, DW2, and SPW1 often the largest nonmigrating diurnal tides present. This source is most likely associated with the nonlinear interaction occurring in situ in the middle/upper thermosphere of the in-situ-generated DW1 and SPW1, as clearly demonstrated by the close association between the latitude-temporal structure of these 4 wave components. The middle/upper thermospheric DW1 is largely due to in-situ EUV forcing, while SPW1 is the result of the geographic/geomagnetic pole displacement.

5. Comparisons between the diurnal spectra of ICON IVM Ne near 590 km and SORTIE IVM Ne near 420 km suggest the presence of similar wave components, with large DE3, D0, DE2, and DW2 (with enhancements that are not concurrent for all times and wave components). Near the geomagnetic equator, Ne tidal amplitudes near 420 km are about 40% larger than 590 km, indicating that the prominent D0 and DW2 Ne variations previously discussed are a common feature throughout the topside ionosphere and not limited to the altitudes sampled by ICON IVM near 590 km. EIA-induced effects are evident in DE3 with peaks occurring near ±20° MLAT near 420 km while the peaks are near ±10° MLAT near ∼590 km, likely due to SORTIE’s lower mean altitude. Important equatorial asymmetries exist in DE3 Ne amplitudes near 420 km that are not present near 590 km, possibly due to vertically changing mean winds in the 420–590 km region.

6. The latitude-temporal and altitude-temporal diurnal non-migrating tidal structures from the CTMT model are analyzed and compared with MIGHTI observations. The lower thermospheric spectra are in general agreement, while large discrepancies are found in the middle thermosphere due to in situ tidal generation not captured by CTMT. The presence of strong middle thermospheric DW2 and D0 and their absence in CTMT is consistent with the presence of additional forcing mechanisms in the thermosphere. For the zonal winds, only the antisymmetric HME (HME2) of D0 has a sufficiently long vertical wavelength to propagate into the thermosphere; while for the meridional winds only the symmetric HME (HME1) of D0 can effectively propagate to the thermosphere. HME2 is responsible for generating antisymmetric signals in the lower and middle thermospheric D0 zonal winds, while HME1 is responsible for producing symmetric signals in the lower and middle thermospheric D0 meridional winds. The D0 amplitudes in CTMT are underestimated by up to ∼75% near 220 km, and DW2 zonal wind amplitudes in the lower thermosphere are underestimated by CTMT by up to ∼67%, while the strong (∼15 m/s) middle thermospheric DW2 observed by MIGHTI is nearly absent in CTMT due to the lack of in situ generation in CTMT. These results suggest that CTMT (and any tidal model of the thermosphere) would strongly benefit from the assimilation of concurrent satellite measurements, including those from ICON and SORTIE.

7. The MIGHTI lower and middle thermospheric zonal wind wave spectra with periods from 0.5 days to 7 days are analyzed and compared with that of Ne inferred from IVM near 590 km. Prominent and persistent ∼3-day UFKW1 lower thermospheric zonal wind variability with ∼2-year mean amplitudes near 10 m/s is found to be consistent with ionospheric Ne signatures. Given the greatly reduced UFKW1 amplitudes near 220 km, we surmise that the F-region UFKW1 ionospheric Ne variability is primarily driven by E-region dynamo processes, while in situ driving via F-region winds and field-aligned drifts are likely to play a smaller role. The UFKW1 shows similar seasonal behavior to DE3 with large amplitudes upward of 18 m/s during early July through mid-November 2020 and 2021. UFKW1 middle thermospheric amplitudes show maxima near 8 m/s, i.e., about 50% less than their corresponding amplitudes near 105 km. Significant latitudinal asymmetry is found in both DE3 and the UFKW1 at both thermospheric heights, similar to previous modeling studies (e.g., Gasperini et al., 2017). These effects are significantly more severe for DE3 than for the UFKW despite the fact that they share the same phase speed and that their full latitudinal widths at half-maximum are both near 30° thus making them subject to effectively the same mean winds that warrant further investigations.

8. The lower thermospheric zonal wind wave spectrum also reveals marked Q6DW variability during 2020–2021. Spectral analyses of MIGHTI middle thermospheric winds show significantly reduced amplitudes (by ∼50%–80%) for both the UFKW1 and Q6DW near 220 km. This result suggests that both these wave components undergo strong dissipation in their propagation between 105 km and 220 km.

9. The middle thermospheric zonal wind wave spectrum reveals dominant s = +0 variations with periods of 0.5 days (i.e., S0, as recently shown by Forbes et al., 2022), 1-day (i.e., D0, discussed in Section 3), and 7 days; and other notable s = 0 variations near 2 and 3 days. These middle thermospheric s = 0 variations (including large s = 0 IT variability near 9 days not shown or discussed in this article) are reflecting prominent topside F-region ion density variability that will be the subject of follow on work.

Despite improved observational capabilities afforded by recent satellite missions, our ability to attain a comprehensive physical understanding of the relevant processes is significantly impaired by data sparsity in the IT system. This study highlights the importance of simultaneous satellite measurements to provide much-needed day/night wind, temperature, and composition observations throughout the thermosphere and ionosphere that will enable the investigation of wave-mean flow interactions, ion-neutral interactions, and dynamo processes critical for improvided nowcasting and forecasting capabilities of IT phenomena.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author. ICON data were obtained from https://icon.ssl.berkeley.edu/Data/. Post-processed SORTIE IVM Level 2 ion density data can be accessed on Zenodo at https://zenodo.org/record/6811341. The 3-hourly Kp index was obtained from GFZ Potsdam at https://www.gfz-potsdam.de/en/kp-index/, the F10.7 cm radio flux from NASA/GSFC OMNIWeb at https://omniweb.gsfc.nasa.gov/form/dx1.html. We gratefully acknowledge J. Oberheide for making the Climatological Tidal Model of the Thermosphere (CTMT) model freely available at: https://doi.org/10.5281/zenodo.5541913.

Author contributions

FG performed the analyses, made the interpretations, and wrote the manuscript. BH, GC, and TI supported the interpretation and reviewed the draft. GC and TI supported the funding acquisition. All authors contributed to the article and approved the submitted version.

Acknowledgments

FG acknowledges support from NASA grants No. 80NSSC22K0019 and 80NSSC22K1010, AFOSR grant No. FA9550-22-1-0328, and NSF grant No. 2113411. The SORTIE mission is supported by NASA grant No. 80NSSC18K0094. ICON is supported by NASA’s Explorers Program through contracts NNG12FA45C and NNG12FA42I.

Conflict of interest

Authors FG and GC were employed by Orion Space Solutions.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdu, M. A., Brum, C., Batista, P. P., Gurubaran, S., Pancheva, D., Bageston, J. V., et al. (2015). Fast and ultrafast Kelvin wave modulations of the equatorial evening F region vertical drift and spread F development. Earth, Planets Space 67, 1. doi:10.1186/s40623-014-0143-5

CrossRef Full Text | Google Scholar

Andrews, D. G., Holton, J. R., and Leovy, C. B. (1987). Middle atmospheric dynamics. Academic Press, 489.

Google Scholar

Azeem, I., Crowley, G., Wu, W., Randall, C. E., Harvey, V. L., Sharon, S. L., et al. (2022). Travelling ionospheric Disturbances detected by the scintillation observations and response of the ionosphere to electrodynamics (SORTIE) CubeSat at 420 km altitude. Authorea. doi:10.1002/essoar.10511395.1

CrossRef Full Text | Google Scholar

Cai, X., Burns, A. G., Wang, W., Qian, L., Pedatella, N., Coster, A., et al. (2021). Variations in thermosphere composi-tion and ionosphere total electron content under ‘geomagnetically quiet’ conditions at solar-minimum. Geophys Res. Lett. 48, e2021GL093300. doi:10.1029/2021GL093300

CrossRef Full Text | Google Scholar

Cai, X., Burns, A. G., Wang, W., Qian, L., Solomon, S. C., Eastes, R. W., et al. (2020). The two-dimensional evolution of thermospheric O/N2 response to weak geomagnetic activity during solar-minimum observed by GOLD. Geophys Res. Lett. 47, e2020GL088838. doi:10.1029/2020GL088838

CrossRef Full Text | Google Scholar

Chang, L. C., Liu, J. Y., and Palo, S. E. (2011). Propagating planetary wave coupling in SABER MLT temperatures and GPS TEC during the 2005/2006 austral summer. J. Geophys Res. 116, A10324. doi:10.1029/2011JA016687

CrossRef Full Text | Google Scholar

Chang, L. C., Palo, S. E., Liu, H.-L., Fang, T.-W., and Lin, C. S. (2010). Response of the thermosphere and ionosphere to an ultra fast Kelvin wave. J. Geophys. Res. 115, A00G04. doi:10.1029/2010JA015453

CrossRef Full Text | Google Scholar

Choi, J. M., Lin, C. C. H., Panthalingal Krishanunni, R., Park, J., Kwak, Y. S., Chen, S. P., et al. (2023). Comparisons of in situ ionospheric density using ion velocity meters onboard FORMOSAT-7/COSMIC-2 and ICON missions. Earth Planets Space 75, 15. doi:10.1186/s40623-022-01759-3

CrossRef Full Text | Google Scholar

Cullens, C. Y., Immel, T. J., Triplett, C. C., Wu, Y. J., England, S. L., Forbes, J. M., et al. (2020). Sensitivity study for ICON tidal analysis. Prog. Earth Planet Sci. 7, 18. doi:10.1186/s40645-020-00330-6

PubMed Abstract | CrossRef Full Text | Google Scholar

England, S. L., Immel, T. J., Huba, J. D., Hagan, M. E., Maute, A., and DeMajistre, R. (2010). Modeling of multiple effects of atmospheric tides on the ionosphere: an examination of possible coupling mechanisms responsible for the longitudinal structure of the equatorial ionosphere. J. Geophys. Res. 115, A05308. doi:10.1029/2009JA014894

CrossRef Full Text | Google Scholar

Englert, C. R., Harlander, J. M., Marr, K. D., Harding, B. J., Makela, J. J., Fae, T., et al. (2023). Michelson interferometer for global high-resolution thermospheric imaging (MIGHTI) on-orbit wind observations: data analysis and instrument performance. Space Sci. Rev. 219, 27. doi:10.1007/s11214-023-00971-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Forbes, J. M., Bruinsma, S. L., Zhang, X., and Oberheide, J. (2009). Surface-exosphere coupling due to thermal tides. Geophys Res. Lett. 36, L15812. doi:10.1029/2009GL038748

CrossRef Full Text | Google Scholar

Forbes, J. M., He, M., Maute, A., and Zhang, X. (2020a). Ultrafast Kelvin wave variations in the surface magnetic field. J. Geophys Res. Space Phys. 125, e2020JA028488. doi:10.1029/2020JA028488

CrossRef Full Text | Google Scholar

Forbes, J. M., Heelis, R., Zhang, X., Englert, C. R., Harding, B. J., He, M., et al. (2021a). Q2DW-tide and-ionosphere interactions as observed from ICON and ground-based radars. J. Geophys Res. Space Phys. 126, e2021JA029961. doi:10.1029/2021JA029961

PubMed Abstract | CrossRef Full Text | Google Scholar

Forbes, J. M., Manson, A. H., Vincent, R. A., Fraser, G. J., Vial, F., Wand, R., et al. (1994). Semidiurnal tide in the 80-150 km region: an assimilative data analysis. J. Atmos. Terr. Phys. 56, 1237–1249. doi:10.1016/0021-9169(94)90062-0

CrossRef Full Text | Google Scholar

Forbes, J. M., Maute, A., and Zhang, X. (2020b). Dynamics and electrodynamics of an ultra-fast Kelvin wave (UFKW) packet in the ionosphere-thermosphere (IT). J. Geophys Res. Space Phys. 125, e2020JA027856. doi:10.1029/2020JA027856

CrossRef Full Text | Google Scholar

Forbes, J. M., Zhang, X., Heelis, R., Stoneback, R., Englert, C. R., Harlander, J. M., et al. (2021b). Atmosphere-ionosphere (A-I) coupling as viewed by ICON: day-to-day variability due to planetary wave (PW)-tide interactions. J. Geophys Res. Space Phys. 126, e2020JA028927. doi:10.1029/2020JA028927

PubMed Abstract | CrossRef Full Text | Google Scholar

Forbes, J. M., Zhang, X., and Maute, A. (2020c). Planetary wave (PW) generation in the thermosphere driven by the PW-modulated tidal spectrum. J. Geophys Res. Space Phys. 125, e2019JA027704. doi:10.1029/2019JA027704

CrossRef Full Text | Google Scholar

Forbes, J. M., and Garrett, H. B. (1979). Theoretical studies of atmospheric tides. Rev. Geophys. 17 (8), 1951–1981. doi:10.1029/RG017i008p01951

CrossRef Full Text | Google Scholar

Forbes, J. M., and Hagan, M. E. (1988). Diurnal propagating tide in the presence of mean winds and dissipation: a numerical investigation. Space Sci. 36 (6), 579–590. doi:10.1016/0032-0633(88)90027-x

CrossRef Full Text | Google Scholar

Forbes, J. M., Oberheide, J., Zhang, X., Cullens, C., Englert, C. R., Harding, B. J., et al. (2022). Vertical coupling by solar semidiurnal tides in the thermosphere from ICON/MIGHTI measurements. J. Geophys. Res. space Phys. 127, e2022JA030288. doi:10.1029/2022JA030288

CrossRef Full Text | Google Scholar

Forbes, J. M., and Vincent, R. A. (1989). Effects of mean winds and dissipation on the diurnal propagating tide: an analytic approach. Planet. Space Sci. 37, 197–209. doi:10.1016/0032-0633(89)90007-x

CrossRef Full Text | Google Scholar

Forbes, J. M. (2000). Wave coupling between the lower and upper atmosphere: case study of an ultra-fast Kelvin wave. J. Atmos. Solar-Terrestrial Phys. 62, 1603–1621. doi:10.1016/s1364-6826(00)00115-2

CrossRef Full Text | Google Scholar

Forbes, J. M., Zhang, X., Hagan, M. E., England, S. L., Liu, G., and Gasperini, F. (2017). On the specification of upward-propagating tides for ICON science investigations. Space Sci. Rev. 212, 697–713. doi:10.1007/s11214-017-0401-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Forbes, J. M., Zhang, X., and Palo, S. E. (2023b). UFKW propagation in the dissipative thermosphere. J. Geophys. Res. space Phys. 128 (1), e2022JA030921. doi:10.1029/2022JA030921

CrossRef Full Text | Google Scholar

Forbes, J. M., and Zhang, X. (2017). The quasi-6-day wave and its interactions with solar tides. J. Geophys. Res. space Phys. 122, 4764–4776. doi:10.1002/2017JA023954

CrossRef Full Text | Google Scholar

Gan, Q., Oberheide, J., Yue, J., and Wang, W. (2017). Short-term variability in the ionosphere due to the nonlinear interaction between the 6-day wave and migrating tides. J. Geophys. Res. Space Phys. 122, 8831–8846. doi:10.1002/2017JA023947

CrossRef Full Text | Google Scholar

Gan, Q., Wang, W., Yue, J., Liu, H., Chang, L. C., Zhang, S., et al. (2016). Numerical simulation of the 6 day wave effects on the ionosphere: dynamo modulation. J. Geophys. Res. Space Phys. 121 (10), 116. 103–10. doi:10.1002/2016JA022907

CrossRef Full Text | Google Scholar

Gasperini, F., Azeem, I., Crowley, G., Perdue, M., Depew, M., Immel, T., et al. (2021). Dynamical coupling between the low-latitude lower thermosphere and ionosphere via the non-migrating diurnal tide as revealed by concurrent satellite observations and numerical modeling. Geophys Res. Lett. 48, e2021GL093277. doi:10.1029/2021GL093277

CrossRef Full Text | Google Scholar

Gasperini, F., Forbes, J. M., Doornbos, E. N., and Bruinsma, S. L. (2018). Kelvin wave coupling from TIMED and GOCE: inter/intra-annual variability and solar activity effects. J. Atmos. Sol-Terr Phys. 171, 176–187. doi:10.1016/j.jastp.2017.08.034

CrossRef Full Text | Google Scholar

Gasperini, F., Forbes, J. M., Doornbos, E. N., and Bruinsma, S. L. (2015). Wave coupling between the lower and middle thermosphere as viewed from TIMED and GOCE. J. Geophys Res. 120, 5788–5804. doi:10.1002/2015JA021300

CrossRef Full Text | Google Scholar

Gasperini, F., Forbes, J. M., and Hagan, M. E. (2017). Wave coupling from the lower to the middle thermosphere: effects of mean winds and dissipation. J. Geophys Res. 122, 7781–7797. doi:10.1002/2017JA024317

CrossRef Full Text | Google Scholar

Gasperini, F., Liu, H., and McInerney, J. (2020). Preliminary evidence of Madden-Julian oscillation effects on ultra-fast tropical waves in the thermosphere. J. Geophys Res. 125, e2019JA027649. doi:10.1029/2019JA027649

CrossRef Full Text | Google Scholar

Gasperini, F., Crowley, G., Immel, T. J., and Harding, B. J. (2022). Vertical wave coupling in the low-latitude ionosphere-thermosphere as revealed by concurrent ICON and COSMIC-2 observations. Space Sci. Rev. 218, 55. doi:10.1007/s11214-022-00923-1

CrossRef Full Text | Google Scholar

Gu, S-Y., Dou, X., Lei, J., Li, T., Luan, X., Wan, W., et al. (2014a). Ionospheric response to the ultrafast Kelvin wave in the MLT region. J. Geophys Res. Space Phys. 119, 1369–1380. doi:10.1002/2013JA019086

CrossRef Full Text | Google Scholar

Gu, S-Y., Liu, H. L., Li, T., Dou, X. K., Wu, Q., and Russell, J. M. (2014b). Observation of the neutral-ion coupling through 6 day planetary wave. J. Geophys Res. Space Phys. 119, 10376–10383. doi:10.1002/2014JA020530

CrossRef Full Text | Google Scholar

Gu, S.-Y., Dou, X., Lei, J., Li, T., Luan, L., Wan, W., et al. (2014). Ionospheric response to the ultrafast Kelvin wave in the MLT region. J. Geophys. Res. Space Phys. 119, 1369–1380. doi:10.1002/2013JA019086

CrossRef Full Text | Google Scholar

Gu, S.-Y., Liu, H.-L., Dou, X., and Jia, M. (2018a). Ionospheric variability due to tides and quasi-two day wave interactions. J. Geophys. Res. Space Phys. 123, 1554–1565. doi:10.1002/2017JA025105

CrossRef Full Text | Google Scholar

Gu, S.-Y., Ruan, H., Yang, C.-Y., Gan, Q., Dou, X., and Wang, N. (2018b). The morphology of the 6-day wave in both the neutral atmosphere and F region ionosphere under solar minimum conditions. J. Geophys. Res. Space Phys. 123, 4232–4240. doi:10.1029/2018JA025302

CrossRef Full Text | Google Scholar

Hagan, M. E. (1996). Comparative effects of migrating solar sources on tidal signatures in the middle and upper atmosphere. J. Geophys Res. 101, 21213–21222. doi:10.1029/96jd01374

CrossRef Full Text | Google Scholar

Hagan, M. E., and Forbes, J. M. (2002). Migrating and nonmigrating diurnal tides in the middle and upper atmosphere excited by tropospher-ic latent heat release. J. Geophys. Res. 107 (D24), 4754. doi:10.1029/2001JD001236

CrossRef Full Text | Google Scholar

Hagan, M. E., Maute, A., Roble, R. G., Richmond, A. D., Immel, T. J., and England, S. L. (2007). Connections between deep tropical clouds and the Earth’s ionosphere. Geophys. Res. Lett. 34, L20109. doi:10.1029/2007GL030142

CrossRef Full Text | Google Scholar

Hagan, M., Forbes, J., and Vial, F. (1995). On modeling migrating solar tides. Geophys. Res. Lett. 22 (8), 893–896. doi:10.1029/95GL00783

CrossRef Full Text | Google Scholar

Harding, B. J., Chau, J. L., He, M., Englert, C. R., Harlander, J. M., Marr, K. D., et al. (2021). Validation of ICON-MIGHTI thermospheric wind observations: 2. Green-Line comparisons to specular meteor radars. J. Geophys. Res. Space Phys. 126, e2020JA028947. doi:10.1029/2020JA028947

PubMed Abstract | CrossRef Full Text | Google Scholar

Harding, B. J., Wu, Y.-J. J., Alken, P., Yamazaki, Y., Triplett, C. C., Immel, T. J., et al. (2022). Impacts of the january 2022 Tonga volcanic eruption on the ionospheric dynamo: ICON-MIGHTI and swarm observations of extreme neutral winds and currents. Geophys. Res. Lett. 49, e2022GL098577. doi:10.1029/2022GL098577

CrossRef Full Text | Google Scholar

Hausler, K., Hagan, M. E., Baumgaertner, A. J. G., Maute, A., Lu, G., Doornbos, E., et al. (2014). Improved short-term variability in the thermosphere-ionosphere- mesosphere-electrodynamics general circulation model. J. Geophys. Res. Space Phys. 119, 6623–6630. doi:10.1002/2014JA020006

CrossRef Full Text | Google Scholar

He, M., Liu, L., Wan, W., and Wei, Y. (2011). Strong evidence for couplings between the ionospheric wave-4 structure and atmospheric tides. Geophys Res. Lett. 38, L14101. doi:10.1029/2011GL047855

CrossRef Full Text | Google Scholar

Heelis, R. A., Chen, Y.-J., Depew, M. D., Harding, B. J., Immel, T. J., Wu, Y.-J., et al. (2022b). Topside plasma flows in the equatorial ionosphere and their relationships to F-region winds near 250 km. J. Geophys. Res. Space Phys. 127. e2022JA030415. doi:10.1029/2022JA030415

CrossRef Full Text | Google Scholar

Heelis, R. A., Depew, M. D., Chen, Y. J., and Perdue, M. D. (2022a). Ionospheric connections (ICON) ion velocity meter (IVM) observations of the equatorial ionosphere at solar minimum. Space Sci. Rev. 218 (8), 68–16. Public access. doi:10.1007/s11214-022-00936-w

CrossRef Full Text | Google Scholar

Heelis, R. A., Stoneback, R. A., Perdue, M. D., Depew, M. D., Morgan, W. A., Mankey, M. W., et al. (2017). Ion velocity measurements for the ionospheric connections explorer. Space Sci. Rev. 212, 615–629. doi:10.1007/s11214-017-0383-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Huba, J. D., Heelis, R., and Maute, A. (2021). Large-scale O+ depletions observed by ICON in the post-midnight topside ionosphere: data/model comparison. Geophys. Res. Lett. 48, e2020GL092061. doi:10.1029/2020GL092061

CrossRef Full Text | Google Scholar

Immel, T. J., and Eastes, R. W. (2019). New NASA missions focus on terrestrial forc-ing of the space environment. Bull. Am. Meteorol. Soc. 100, 2153–2156. doi:10.1175/BAMS-D-19-0066.1

CrossRef Full Text | Google Scholar

Immel, T. J., England, S. L., Mende, S. B., Heelis, R. A., Englert, C. R., Edelstein, J., et al. (2018). The ionospheric connection explorer mission: mission goals and design. Space Sci. Rev. 214, 13. doi:10.1007/s11214-017-0449-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Immel, T. J., Harding, B. J., Heelis, R. A., Maute, A., Forbes, J. M., England, S. L., et al. (2021). Regulation of ionospheric plasma velocities by thermospheric winds. Nat. Geosci. 14, 893–898. doi:10.1038/s41561-021-00848-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Immel, T. J., Sagawa, E., England, S. L., Henderson, S. B., Hagan, M. E., Mende, S. B., et al. (2006). Control of equatorial ionospheric morphology by atmospheric tides. Geophys. Res. Lett. 33 (15), L15108. doi:10.1029/2006GL026161

CrossRef Full Text | Google Scholar

Jin, H., Miyoshi, Y., Fujiwara, H., and Shinagawa, H. (2008). Electrodynamics of the formation of ionospheric wave number 4 longitudinal structure. J. Geophys. Res. 113, A09307. doi:10.1029/2008JA013301

CrossRef Full Text | Google Scholar

Jones, M., Forbes, J. M., Hagan, M. E., and Maute, A. (2013). Non-migrating tides in the ionosphere-thermosphere: in situ versus tropospheric sources. J. Geophys. Res. Space Phys. 118, 2438–2451. doi:10.1002/jgra.50257

CrossRef Full Text | Google Scholar

Lieberman, R. S., Riggin, D. M., Ortland, D. A., Nesbitt, S. W., and Vincent, R. A. (2007). Variability of mesospheric diurnal tides and tropospheric diurnal heating during 1997-1998. J. Geophys Res. 112, D20110. doi:10.1029/2007JD008578

CrossRef Full Text | Google Scholar

Lieberman, R. S., Harding, B. J., Heelis, R. A., Pedatella, N. M., Forbes, J. M., and Oberheide, J. (2022). Atmospheric lunar tide in the low latitude thermosphere-ionosphere. Geophys. Res. Lett. 49, e2022GL098078. doi:10.1029/2022GL098078

PubMed Abstract | CrossRef Full Text | Google Scholar

Lieberman, R. S., Riggin, D. M., Franke, S. J., Manson, A. H., Meek, C., Nakamura, T., et al. (2003). The 6.5-day wave in the mesosphere and lower thermosphere: evidence for baroclinic/barotropic instability. J. Geophys. Res. 108 (D20), 4640. doi:10.1029/2002JD003349

CrossRef Full Text | Google Scholar

Lindzen, R. S., and Hong, S. S. (1974). Effects of mean winds and horizontal temperature gradients on solar and lunar semidiurnal tides in the atmosphere. J. Atmos. Sci. 31, 1421–1446. doi:10.1175/1520-0469(1974)031<1421:eomwah>2.0.co;2

CrossRef Full Text | Google Scholar

Lindzen, R. S. (1967). Thermally driven diurnal tide in the atmosphere. Q. J. R. Meteorol. Soc. 93, 18–42. doi:10.1002/qj.49709339503

CrossRef Full Text | Google Scholar

Liu, G., England, S. L., Immel, T. J., Frey, H. U., Mannucci, A. J., and Mitchell, N. J. (2015). A comprehensive survey of atmospheric quasi 3-day planetary-scale waves and their impacts on the day-to-day variations of the equatorial ionosphere. J. Geophys. Res. Space Phys. 120, 2979–2992. doi:10.1002/2014JA020805

CrossRef Full Text | Google Scholar

Liu, G., England, S. L., Lin, C. S., Pedatella, N. M., Klenzing, J. H., Englert, C. R., et al. (2021). Evaluation of atmospheric 3-day waves as a source of day-to-day variation of the ionospheric longitudinal structure. Geophys. Res. Lett. 48, e2021GL094877. doi:10.1029/2021GL094877

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, G., Immel, T. J., England, S. L., Frey, H. U., Mende, S. B., Kumar, K. K., et al. (2013). Impacts of atmospheric ultrafast Kelvin waves on radio scintillations in the equatorial ionosphere. J. Geophys. Res. space Phys. 118, 885–891. doi:10.1002/jgra.50139

CrossRef Full Text | Google Scholar

Liu, H-L., Yudin, V. A., and Roble, R. G. (2013). Day-to-day ionospheric variability due to lower atmosphere perturbations. Geophys Res. Lett. 40, 665–670. doi:10.1002/grl.50125

CrossRef Full Text | Google Scholar

Liu, H.-L., Bardeen, C. G., Foster, B. T., Lauritzen, P., Liu, J., Lu, G., et al. (2018). Development and validation of the Whole atmosphere community climate model with thermosphere and ionosphere extension (WACCM-X 2.0). J. Adv. Model. Earth Syst. 10, 381–402. doi:10.1002/2017MS001232

CrossRef Full Text | Google Scholar

Liu, H.-L. (2016). Variability and predictability of the space environment as related to lower atmosphere forcing. Space weather. 14, 634–658. doi:10.1002/2016SW001450

CrossRef Full Text | Google Scholar

Makela, J. J., Baughman, M., Navarro, L. A., Harding, B. J., Englert, C. R., Harlander, J. M., et al. (2021). Validation of ICON-MIGHTI thermospheric wind observations: 1. Nighttime red-line ground-based fabry-perot interferometers. J. Geophys. Res. Space Phys. 126, e2020JA028726. doi:10.1029/2020JA028726

PubMed Abstract | CrossRef Full Text | Google Scholar

Maute, A., Richmond, A. D., and Roble, R. G. (2012). Sources of low-latitude ionospheric E × B drifts and their variability. J. Geophys. Res. 117, A06312. doi:10.1029/2011JA017502

CrossRef Full Text | Google Scholar

Oberheide, J., Forbes, J., Hausler, K., Wu, Q., and Bruinsma, S. L. (2009). Tropospheric tides from 80 to 400 km: propagation, interannual variability, and solar cycle effects. J. Geophys Res. 114. doi:10.1029/2009JD012388

CrossRef Full Text | Google Scholar

Oberheide, J., Forbes, J. M., Zhang, X., and Bruinsma, S. L. (2011). Climatology of upward propagating diurnal and semidiurnal tides in the thermosphere. J. Geophys Res. 116, A11306. doi:10.1029/2011JA016784

CrossRef Full Text | Google Scholar

Oberheide, J., and Forbes, J. M. (2008). Tidal propagation of deep tropical cloud signatures into the thermosphere from TIMED observations. Geophys. Res. Lett. 35, L04816. doi:10.1029/2007GL032397

CrossRef Full Text | Google Scholar

Palo, S. E., Roble, R. G., and Hagan, M. E. (1999). Middle atmosphere effects of the quasi-two-day wave determined from a General Circulation Model. Earth Planets Space 51, 629–647. doi:10.1186/bf03353221

CrossRef Full Text | Google Scholar

Pancheva, D., and Mukhtarov, P. (2023). Climatology and interannual variability of the migrating quarterdiurnal tide (QW4) seen in the SABER/TIMED temperatures (2002–2022). J. Atmos. Solar-Terrestrial Phys. 250, 106111. doi:10.1016/j.jastp.2023.106111

CrossRef Full Text | Google Scholar

Park, J., Evans, J. S., Eastes, R. W., Lumpe, J. D., van den Ijssel, J., Englert, C. R., et al. (2022a). Exospheric temperature measured by NASA-GOLD under low solar activity: comparison with other data sets. J. Geophys. Res. Space Phys. 127, e2021JA030041. doi:10.1029/2021JA030041

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, J., Mende, S. B., Eastes, R. W., and Frey, H. U. (2022b). Climatology of equatorial plasma bubbles in ionospheric connection explorer/far-UltraViolet (ICON/FUV) Limb images. J. Astronomy Space Sci. 39 (3), 87–98. doi:10.5140/JASS.2022.39.3.87

CrossRef Full Text | Google Scholar

Pedatella, N. M., and Forbes, J. M. (2009). Interannual variability in the longitudinal structure of the low-latitude iono-sphere due to the El Niño–southern oscillation. J. Geophys Res. 114, A12316. doi:10.1029/2009JA014494

CrossRef Full Text | Google Scholar

Qin, Y., Gu, S.-Y., Dou, X., Gong, Y., Chen, G., Zhang, S., et al. (2019). Climatology of the quasi-6-day wave in the mesopause region and its modulations on total electron content during 2003–2017. J. Geophys. Res. Space Phys. 124, 573–583. doi:10.1029/2018JA025981

CrossRef Full Text | Google Scholar

Qin, Y., Gu, S-Y., Teng, C-K-M., Dou, X-K., Yu, Y., and Li, N. (2021). Comprehensive study of the climatology of the quasi-6-day wave in the MLT region based on aura/MLS observations and SD-WACCM-X simulations. J. Geophys. Res. Space Phys. 126, e2020JA028454. doi:10.1029/2020JA028454

CrossRef Full Text | Google Scholar

Riggin, D. M., Hays, P. B., Skinner, W. R., Roble, R. G., Russell III, J. M., Mertens, C. J., et al. (2006). Observations of the 5-day wave in the mesosphere and lower thermosphere. J. Atmos. Solar-Terrestrial Phys. 68, 323–339. doi:10.1016/j.jastp.2005.05.010

CrossRef Full Text | Google Scholar

Sagawa, E., Immel, T. J., Frey, H. U., and Mende, S. B. (2005). Longitudinal structure of the equatorial anomaly in the nighttime ionosphere observed by IMAGE/FUV. J. Geophys. Res. 110, A11302. doi:10.1029/2004JA010848

CrossRef Full Text | Google Scholar

Salby, M. L., Hartmann, D. L., Bailey, P. L., and Gille, J. C. (1984). Evidence for equatorial Kelvin modes in nimbus-7 LIMS. J. Atmos. Sci. 41, 220–235. doi:10.1175/1520-0469(1984)041<0220:efekmi>2.0.co;2

CrossRef Full Text | Google Scholar

Stromberg, E., Crowley, G., Azeem, I., Fish, C., Frazier, C., Reynolds, A., et al. (2016). “Scintillation observations and response of the ionosphere to electrodynamics (SORTIE),” in Proceedings of the 30th annual AIAA/USU SmallSat conference. paper: SSC16-VI-3.

Google Scholar

Talaat, E. R., Yee, J.-H., and Zhu, X. (2002). The 6.5-day wave in the tropical stratosphere and mesosphere. J. Geophys. Res. 107 (D12), 4133. doi:10.1029/2001JD000822

CrossRef Full Text | Google Scholar

Talaat, E. R., Yee, J. H., and Zhu, X. (2001). Observations of the 6.5-day wave in the mesosphere and lower thermosphere. J. Geophys. Res. 106, 20,715–20,723. doi:10.1029/2001jd900227

CrossRef Full Text | Google Scholar

Truskowski, A. O., Forbes, J. M., Zhang, X., and Palo, S. E. (2014). New perspectives on thermosphere tides - 1. Lower thermosphere spectra and seasonal-latitudinal structures. Earth Planets Space 66, 136. doi:10.1186/s40623-014-0136-4

CrossRef Full Text | Google Scholar

Volland, H., and Mayr, H. G. (1977). Theoretical aspects of tidal and planetary wave propagation at thermospheric heights. Rev. Geophys. 15 (2), 203–226. doi:10.1029/RG015i002p00203

CrossRef Full Text | Google Scholar

Volland, H., and Mayr, H. G. (1974). Theoretical aspects of tidal and planetary wave propagation at thermospheric heights. J. Atmos. Sol. Terr. Phys. 36, 203–460. doi:10.1029/RG015i002p00203

CrossRef Full Text | Google Scholar

Wautelet, G., Hubert, B., Gérard, J.-C., Immel, T. J., Frey, H. U., Mende, S. B., et al. (2021). First ICON-FUV nighttime NmF2 and hmF2 comparison to ground and space-based measurements. J. Geophys. Res. Space Phys. 126, e2021JA029360. doi:10.1029/2021JA029360

PubMed Abstract | CrossRef Full Text | Google Scholar

Yamazaki, Y., Arras, C., Andoh, S., Miyoshi, Y., Shinagawa, H., Harding, B. J., et al. (2022). Examining the wind shear theory of sporadic E with ICON/MIGHTI winds and COSMIC-2 radio occultation data. Geophys. Res. Lett. 49, e2021GL096202. doi:10.1029/2021GL096202

CrossRef Full Text | Google Scholar

Yamazaki, Y., Harding, B. J., Qiu, L., Stolle, C., Siddiqui, T. A., Miyoshi, Y., et al. (2023). Monthly climatologies of zonal-mean and tidal winds in the thermosphere as observed by ICON/MIGHTI during April 2020-March 2022. Authorea. doi:10.22541/essoar.168056794.43452415/v1

CrossRef Full Text | Google Scholar

Yamazaki, Y., Miyoshi, Y., Xiong, C., Stolle, C., Soares, G., and Yoshikawa, A. (2020). Whole atmosphere model simulations of ultra-fast Kelvin wave effects in the ionosphere and thermosphere. J. Geophys. Res. Space Phys. 125, e2020JA027939. doi:10.1029/2020JA027939

CrossRef Full Text | Google Scholar

Yamazaki, Y. (2018). Quasi-6-day wave effects on the equatorial ionization anomaly over a solar cycle. J. Geophys. Res. Space Phys. 123, 9881–9892. doi:10.1029/2018JA026014

CrossRef Full Text | Google Scholar

Yiğit, E., and Medvedev, A. S. (2015). Internal wave coupling processes in Earth’s atmosphere. Adv. Space Res. 55, 983–1003. doi:10.1016/j.asr.2014.11.020

CrossRef Full Text | Google Scholar

Yiğit, E., Dhadly, M., Medvedev, A. S., Harding, B. J., Englert, C. R., Wu, Q., et al. (2022). Characterization of the thermospheric mean winds and circulation during solstice using ICON/MIGHTI observations. J. Geophys. Res. Space Phys. 127. e2022JA030851. doi:10.1029/2022JA030851

CrossRef Full Text | Google Scholar

Yiğit, E., Knízova, P. K., Georgieva, K., and Ward, W. (2016). A review of vertical coupling in the atmosphere-ionosphere system: effects of waves, sudden stratospheric warmings, space weather, and of solar activity. J. Atmos. Sol. Terr. Phys. 141, 1–12. doi:10.1016/j.jastp.2016.02.011

CrossRef Full Text | Google Scholar