The saturation mechanism of thermal instability

1 Introduction

Thermal instability (TI) is a linear instability of the equations of non-adiabatic gas dynamics that was first identified by Parker (1953). He discussed an application to the solar atmosphere, namely the brightness fluctuations in solar flares and prominences, and there has recently been a resurgence of interest by the solar physics community in understanding the role of TI in prominence formation and the coronal rain phenomenon (e.g., Soler et al., 2012; Antolin, 2020; Claes and Keppens, 2021; Antolin and Froment, 2022; Soler and Ballester, 2022). TI became a topic of importance to the wider astrophysics community with the classic work by Field (1965). In recent years, various review articles on galactic outflows, the circumgalactic medium (CGM) and active galactic nuclei (AGN) have made it clear that ‘multiphase gas dynamics’ has become recognizable as an astrophysical subfield of its own (e.g., Tumlinson et al., 2017; Zhang, 2018; Laha et al., 2020; Veilleux et al., 2020; Choudhury, 2023; Faucher-Giguere and Oh, 2023).

However, the use of the term ‘multiphase’ warrants clarification in any given context. In the original two-phase (Field et al., 1969) and three-phase (McKee and Ostriker, 1977) models of the interstellar medium (ISM), each phase is true to the sense of the word, representing a cold atomic or molecular phase interacting with a warm partially ionized phase. This is the meaning of the term also in observations of molecular outflows from AGN, as well as in galactic winds and other studies related to the ISM/CGM. Outside central cluster galaxies in the intracluster medium, the gas temperatures are nearly virialized and ‘multiphase gas’ refers to a multi-temperature plasma, one in which both ‘phases’ are near collisional ionization equilibrium (CIE) conditions, with the lower temperature plasma undergoing stronger bremsstrahlung cooling and coronal line emission than the fully ionized plasma. This is likewise the sense of the term on subparsec scale regions of AGN, albeit the plasma is much closer to photoionization equilibrium than to CIE due to the presence of an intense ionizing radiation field (e.g., Krolik et al., 1981; Lepp et al., 1985).

In almost all cases where these astrophysical environments are modeled using hydrodynamical simulations that include radiative heating/cooling and multiphase gas appears, its production is attributable to TI reaching the nonlinear regime. The dynamics associated with this regime first involves the saturation of TI, whereby the gas pressure force halts the exponential growth of condensation modes traversing a TI zone—the location in density/temperature parameter space satisfying the generalized stability criteria first derived by Balbus (1986). As we review in Section 2, in addition to the entropy mode, there can be two isochoric condensation modes that are associated with a different TI zone than the entropy mode. There is also the possibility that acoustic modes can become overstable within this isochoric TI zone, but it remains to be demonstrated that this can actually lead to multiphase gas production in global simulations. In this article, we focus on understanding the process by which individual entropy modes saturate in a homogeneous plasma, although the equations used for this purpose apply to inhomogeneous flows and the other modes as well. These equations and our analysis of the saturation process is given in Section 3, where we also discuss several topics that might benefit from a similar analysis. In Section 4, we summarize our results and address a couple of controversial claims in the literature.

2 Summary of (non)linear theory results

In the early literature on TI, emphasis is placed on isobaric and isochoric instability criteria rather than on the linear modes obeying these criteria. Upon considering the full parameter space of TI, it becomes important to draw a distinction between the stability criteria, individual modes, and timescales dictating the type of nonlinear evolution. This understanding aids the presentation of our new results. Here we attempt to clarify these concepts by summarizing our results from Waters and Proga (2019b; hereafter WP19). In that work, we revisited the original analysis of the governing cubic dispersion relationship presented by Field (1965) to identify the nonisobaric regime of TI, and we also showed that at sufficiently long wavelengths, there can be both the fast and slow isochoric condensation modes.

In WP19, we neglected to point out an inconsistency between two approaches for deriving the stability criterion of these isochoric modes under circumstances where the background flow is out of thermal equilibrium (i.e., for $\mathcal{L}\ne 0$ and where $\mathcal{L}$ is the net sum of radiative heating and cooling processes). Reworking Field’s analysis after taking $\mathcal{L}\ne 0$, we found that his original criterion for isochoric instability is recovered, while as shown by Balbus (1986), a different criterion follows from a direct perturbation analysis of the entropy equation. By contrast, the dispersion relationship analysis recovers Balbus’ criterion in the case of the entropy mode. As discussed in Section 2.4, this discrepancy has implications for plasmas in states of thermal non-equilibrium (TNE), as Balbus’ criterion implies the existence of an isochoric TI zone that would otherwise have gone undetected by linear theory.

2.1 Condensation modes

Upon linearizing the equations of non-adiabatic gas dynamics with perturbations of the form exp(ω t + ik ⋅x), where ω = ω_R + iω_I is the complex-valued frequency of a mode with wavenumber k = |k|, two speeds emerge: the phase velocity v_p = ω_I/k that gives the propagation speed of the mode and the ‘condensation velocity’ v_c = ω_R/k that characterizes the speed of the advective flow that grows or damps the amplitude of the density perturbation. Condensation modes are non-propagating (v_p = 0) linear modes with v_c ≠ 0, whereas adiabatic acoustic modes are non-condensating (v_c = 0) with v_p≠ 0 . This statement holds so long as all non-adiabatic source terms aside from a heat flux due to thermal conduction can be written as a volumetric term $\mathcal{L}=\mathcal{L}(\rho ,T)$.

As discussed in detail in Section 2.3, the classifier ‘isochoric’ refers to the type of derivative of $\mathcal{L}/T$ that governs the stability of the isochoric modes; it does not, however, imply evolution that differs from the entropy mode during the linear growth phase. In a homogeneous gas (or when the local approximation holds), all three modes grow or damp according to the analytic solution:

$\begin{array}{cc}\hfill \rho \left(\mathit{x},t\right)& ={\rho }_0+A{\rho }_0{e}^{{\omega }_{R}t}\cos \left(\mathit{k}\cdot \mathit{x}\right)\hfill \\ \hfill v\left(\mathit{x},t\right)& =v_0-A{v}_c{e}^{{\omega }_{R}t}\sin \left(\mathit{k}\cdot \mathit{x}\right)\hfill \\ \hfill p\left(\mathit{x},t\right)& =p_0-A{\rho }_0{v}_c^2{e}^{{\omega }_{R}t}\cos \left(\mathit{k}\cdot \mathit{x}\right),\hfill \end{array}(1)$

where ρ₀, v₀, and p₀ are the density, velocity, and pressure, respectively, of the uniform background flow; A is the perturbation amplitude; and v_c is the solution to the cubic dispersion relation, which can be expressed as

$v_c=-\frac{N_{\rho }}{k{t}_{\text{cool}}}\frac{R_{\lambda }+{\left(v_c/c_{s,0}\right)}^2}{1+{\left(v_c/c_{s,0}\right)}^2}.(2)$

Here, $c_{s,0}=\sqrt{\gamma p_0/{\rho }_0}$ and t_cool is the characteristic cooling time defined as

$t_{\text{cool}}\equiv \frac{{\mathcal{E}}_0}{{\mathrm{\Lambda }}_0},(3)$

where ${\mathcal{E}}_0=c_{\mathrm{v}}{T}_0$ is the gas internal energy and Λ₀ is the cooling rate (in units of erg s⁻¹ g⁻¹) evaluated in the background flow. The quantity R_λ is the ratio

$R_{\lambda }\equiv \frac{N_p}{\gamma N_{\rho }},(4)$

where N_p and N_ρ are dimensionless measures of how the net cooling rate varies with temperature:¹

$N_p=\frac{T_0}{{\mathrm{\Lambda }}_0}{\left[T{\left(\frac{\partial \mathcal{L}/T}{\partial T}\right)}_p\right]}_{T=T_0}+{\left(\frac{{\lambda }_F}{\lambda }\right)}^2,(5)$

$N_{\rho }={\left.\frac{T_0}{{\mathrm{\Lambda }}_0}{\left(\frac{\partial \mathcal{L}}{\partial T}\right)}_{\rho }\right|}_{T=T_0}+{\left(\frac{{\lambda }_F}{\lambda }\right)}^2.(6)$

The subscript on R_λ emphasizes the wavelength dependence of this ratio; in Eq. 5 and Eq. 6, λ_F is the Field length defined as

${\lambda }_F=2\pi \sqrt{\frac{{\kappa }_0{T}_0}{{\rho }_0{\mathrm{\Lambda }}_0}},(7)$

where κ₀ is the (isotropic) thermal conductivity evaluated in the background flow.

Condensation modes can be classified by the solution branch that they occupy when solving Eq. 2. Equivalently, they can be classified by their stability criteria. The stability of the entropy mode is always governed by the sign of N_p. In particular, when thermal conduction is negligible (requiring either λ_F → 0 or λ ≫ λ_F in Eq. 5 and Eq. 6), the stability of the entropy mode depends only on the sign of the isobaric temperature derivative of $\mathcal{L}/T$, i.e., they are unstable if the inequality

${\left(\frac{\partial \mathcal{L}/T}{\partial T}\right)}_p<0,(8)$

known as Balbus’ instability criterion (after Balbus, 1986), is satisfied. Likewise, the stability of the fast/slow isochoric modes is determined by the sign of N_ρ; the instability criterion for them is

${\left(\frac{\partial \mathcal{L}}{\partial T}\right)}_{\rho }<0,(9)$

when neglecting thermal conduction. Note the temperature derivative is not of $\mathcal{L}/T$ in the isochoric case; this is the discrepancy mentioned above that we will examine further in Section 2.4.

Typically, only one of the condensation modes, namely, the entropy mode or the fast isochoric mode, will exist in the plasma for any given value of R≡ R_λ(λ_F= 0), the other two modes being acoustic. The main exception is the long-wavelength regime for a gas with R < 0; there is a critical wavelength λ_crit such that for λ > λ_crit, the acoustic modes transition into the fast and slow isochoric condensation modes, so all three modes can exist simultaneously. This critical wavelength is, to a good approximation,

${\lambda }_{\text{crit}}=\frac{2\pi }{|N_{\rho }|}\sqrt{-\frac{B}{R}}{\lambda }_{\text{cool}},(10)$

where $B=27{(R-1/3)}^2/4-1$ and λ_cool is the so-called cooling length that is defined as

${\lambda }_{\text{cool}}=c_{s,0}{t}_{\text{cool}}.(11)$

For λ < λ_crit, only the entropy mode exists; when the isochoric modes appear at λ > λ_crit, they are stable when the entropy mode is unstable (i.e., when N_p < 0) and vice versa. The R > 0 regime is very different, as the fast isochoric mode takes the place of the entropy mode as the main condensation mode accompanying acoustic modes, and these acoustic modes are also unstable (or to use proper terminology, they are overstable), their stability being governed by the isochoric criterion provided R < 1. Note by Eq. 4 that instability when R > 0 requires N_p < 0 and N_ρ < 0—both the isobaric and isochoric instability criteria are satisfied. For R > 1, the only condensation mode that can exist is the fast isochoric one; the overstability of acoustic modes is no longer determined by the sign of N_ρ but rather by the sign of the isentropic derivative ${(\partial \mathcal{L}/\partial T)}_s$, where s is the specific entropy.

2.2 Isobaric versus nonisobaric regimes

A number of properties can be inferred from Eq. 1 and Eq. 2, making it clear under what circumstances a transition away from isobaric growth rates implies nonisobaric evolution in the nonlinear regime, regardless of which stability criterion is satisfied. Notice that the quantity $A{v}_c{e}^{{\omega }_{R}t}$ is the maximum magnitude of the instantaneous velocity at which plasma is supplied to the slightly cooler gas by the slightly warmer gas to grow the density perturbation with time. At the end of the linear regime when $A{e}^{{\omega }_{R}t}\sim 1$, v_c is the maximum velocity reached. It is therefore the characteristic velocity of advective flows upon entering the saturation phase of nonlinear growth. Stated differently, not only is the quantity v_c the solution to the dispersion relation of the linearized equations of gas dynamics but also its value reveals what type of dynamics to expect in the nonlinear regime of TI.

Our reference point is therefore the isobaric value of v_c that can be derived by taking the limit |v_c| ≪ c_s,0 in Eq. 2, namely, v_c = −N_p/(γt_coolk). Since v_c ≡ ω_R/k, this corresponds to the growth rate ω_R = −N_p/(γt_cool) derived by Field (1965) for the short-wavelength limit (when neglecting thermal conduction) that defines the isobaric regime. Unstable growth requires ω_R > 0, giving N_p < 0 as the instability criterion. This derivation of the maximum growth rate and Balbus’ instability criterion from taking the limit |v_c| ≪ c_s,0 thus reveals the dynamics associated with isobaric evolution; at the end of the linear regime, only tiny pressure gradients are necessary to give rise to flows with |v_c| ≪ c_s,0 that regulate the growth and saturation of entropy modes.

Thus, the nonisobaric regime can be defined as the wavelengths for which solutions to Eq. 2 do not satisfy |v_c| ≪ c_s,0. As mentioned above, the entropy mode is the only condensation mode that can exist for wavelengths λ < λ_crit and R < 0. It occupies the solution branch of Eq. 2 with the property that v_c rises smoothly from 0 in the short-wavelength (k → ∞) limit to $|v_c|=c_{s,0}\sqrt{-R}$ in the long-wavelength (k → 0) limit. Hence, as the wavelength increases, the entropy modes undergo a transition from isobaric to nonisobaric dynamics unless |R| ≪ 1. The two isochoric condensation mode branches only appear for λ > λ_crit and asymptote to $|v_c|=c_{s,0}\sqrt{-R}$ and $|v_c|={(k{t}_{\text{cool}})}^{-1}{N}_{\rho }$ in the k → 0 limit. We named the mode with v_c ∝ k⁻¹ the fast isochoric mode due to this divergent property. Because k can always be chosen small enough to make |v_c| > c_s,0, this mode is associated with an explosive saturation regime at sufficiently long wavelengths, the expected outcome being a self-fragmentation of the cloud after the saturation phase. With $|v_c|/c_{s,0}=\sqrt{-R}$ for both the entropy mode and slow isochoric mode in the k = 0 limit, the advective flows of long enough wavelength modes will become supersonic during saturation provided R ≲ − 1. In WP19, we speculated that this could also lead to self-fragmentation, referring to either instance of saturation leading to self-fragmentation as ‘splattering’. This has since been demonstrated by Gronke and Oh (2020), although they did not specify if the unstable condensation modes in their simulations were fast isochoric ones or entropy modes, and they incorrectly attributed the self-fragmentation seen to the now discredited (see WP19; Das et al., 2021; Farber and Gronke, 2022) ‘shattering’ hypothesis of McCourt et al. (2018) that is discussed below.

2.3 Nonisobaric versus isochoric evolution

The nonisobaric behavior at wavelengths giving |v_c|≳ 0.1c_s,0, but before reaching the splattering regime at |v_c|∼ c_s,0, has been confirmed by other researchers and is the following. The response to the halting of the compression phase once the cooling gas reaches its equilibrium temperature is for the core of the condensation to ‘bounce’ and enter an expansion phase. Jennings and Li (2021) coined the term ‘contraction rebound’ to conceptualize this saturation dynamics. Further compressive/expansive motions recur as damped oscillations, causing the cloud to ‘pulsate’—the descriptor used by Gronke and Oh (2020). If this rich dynamics is studied using a single entropy mode for the initial conditions, the frequency of the pulsations is the linear theory growth rate, ω_R (see WP19).

In the literature on nonlinear TI, there are a number of conflicting claims about the differences between the short- and long-wavelength regimes and their relationships to isobaric and isochoric instability (e.g., Meerson, 1996; Burkert and Lin, 2000; Vázquez-Semadeni et al., 2003; McCourt et al., 2018; Mandelker et al., 2021). The most controversial claim came from McCourt et al. (2018), who presented simulations that appear to show an isochorically cooling background flow containing unstable perturbations spontaneously shatter during the nonlinear saturation phase of TI. Their study was aimed at establishing λ_cool evaluated in the cold phase gas after TI saturates as the more relevant length scale characterizing cloud sizes when compared with the already established value, namely, λ_cool evaluated in the background flow out of which the clouds had condensed (e.g., Perry and Dyson, 1985; Burkert and Lin, 2000). We showed in WP19 that λ_cool in the cold phase gas will generically be smaller than the Field length of the background flow, making McCourt et al. (2018)’s hypothetical ‘cloudlets’ subject to immediate evaporation (see Begelman and McKee, 1990). Additionally, we interpreted their simulations as being a demonstration not of ‘shattering’ but rather of ‘isobaric takeover’, a process described succinctly by Burkert and Lin (2000): “the fluctuations that can first reach non-linearity would dominate the growth of all perturbations with longer wavelengths and homogenize disturbances with smaller wavelengths. Thus, they determine the characteristic size and mass of the cold dense clumps that would emerge from the cooling of an initially nearly homogeneous cloud.” In other words, since McCourt et al. (2018) introduced a spectrum of perturbations into their initial conditions (a pre-existing cloud with a density contrast χ = 10), the short-wavelength condensation modes with the highest growth rates saturated while the ones with the longest wavelengths were still in the linear regime, making it appear as though the cloud as a whole underwent fragmentation. We return to this point in Section 4.1.

To quote again from Burkert and Lin (2000), when discussing the nonisobaric regime, they state: “Because of its long sound-crossing timescale, the perturbation cannot be compressed significantly while cooling; it cools almost isochorically (Parker, 1953).” We view this wording as confusing on account of the fact that as already mentioned, all condensation modes undergo compression according to Eq. 1 during the linear growth phase, regardless of the sound-crossing timescale. To clarify matters, we note that there are two common usages of the word isochoric in the literature on TI: i) a reference to the isochoric instability criterion or to the two condensation modes obeying this criterion and ii) a reference to long timescales for any small-amplitude thermal fluctuations in the background flow (which can be decomposed into a superposition of sinusoidal condensation modes of various wavelengths) to lead to changes in the density, i.e., for t_ρ ≡ |∂ ln ρ/∂t|⁻¹ ≫ t_cool. Because t_ρ can only be as large as the relevant dynamical time—the perturbation sound crossing time, t_cross, in local simulations—usage ii) entails having t_cool ≪ t_cross. This in turn requires distinguishing between the short- and long-wavelength condensation modes, but the concept of ‘long wavelength’ only makes sense when the modes become nonlinear so that they can excite and interact with sound waves to ‘be informed’ of their lengths. Once this interaction occurs, if t_cool ≪ t_cross, the sound waves cannot quickly communicate the pressure changes accompanying the thermal fluctuations. As we demonstrated in WP19, what happens instead of isochoric evolution (the density remaining approximately constant in this nonlinear interaction phase with sound waves) is the characteristic nonisobaric behavior described above: oscillations commence throughout the condensation. Thus, ‘isochoric evolution’ is not a meaningful concept unless the oscillations fully dampen, this mechanical equilibrium state being reached only if the condensation is free of thermal disturbances.

In summary, in the linear phase of TI, the descriptors ‘isobaric’ and ‘isochoric’ only have meaning as classifiers of the instability criteria. When discussing evolution in the nonlinear phase of TI, ‘isobaric’, ‘nonisobaric’, and ‘isochoric’ are associated with t_cross ≲ t_cool, t_cross ≳ t_cool, and t_cross ≫ t_cool, respectively. However, it is clear that the regime t_cross ≫ t_cool represents ‘extreme nonisobaric behavior’ that will not allow t_ρ ∼ t_cross. For this reason, we feel that in studies discussing the long-wavelength regime of TI, phrases such as ‘the evolution should be nearly isochoric’ should be interpreted as ‘the evolution should be highly nonisobaric’.

2.4 TI zones

All of the possibilities for TI can be assessed graphically given the function $\mathcal{L}$. In general, this function can only be computed numerically using, for example, a photoionization code, and so it is impossible to arrive at analytic expressions for the instability thresholds—the zero contours of N_p and N_ρ. Recently, however, in extending the theory of TI to radiation hydrodynamics (RHD), we arrived at a simple function $\mathcal{L}$ that does have analytic expressions for N_p and N_ρ, and the curves defining their zero contours (see Proga et al., 2022). In the Appendix, we take the optically thin limit of these equations to facilitate their use in hydro/MHD codes and to make our results here easily reproducible. In Figure 1, we plot the contour $\mathcal{L}=0$ on a pressure–density phase plane (referred to as just the ‘phase diagram’ hereafter). In textbook presentations of TI, typically only the regions where $\mathcal{L}>0$ and $\mathcal{L}<0$ are marked, masking any connection to nonlinear dynamics. We will see below how overplotting TI zones makes the phase diagram useful for understanding nonisobaric evolution. In Section 3, we employ a combined graphical and analytical analysis to uncover the saturation process.

FIGURE 1

FIGURE 1. Pressure–density phase diagram depicting the equilibrium curve (black line), TI zone (pink region), isochoric TI zone (gray region), and boundary of the TI zone (the Balbus contour, red line). In the bottom panel, we plot an initial unstable equilibrium state (black dot) along with two sets of ‘tracks’ to depict the two limiting ways in which condensation modes begin to evolve in the nonlinear phase of TI, with blue (red) symbols denoting gas being cooled (heated): (i) nearly isobarically along horizontal tracks (diamonds); (ii) highly non-isobarically along tracks following the equilibrium curve (dots). The saturation mechanism begins at the location where the tracks end; it is triggered when the tracks cross the Balbus contour into a region of stability.

We can use the cooling function defined in Eq. A2 in the Appendix to highlight the significance of the discrepancy mentioned at the beginning of Section 2, namely the existence of an isochoric TI zone according to Balbus’ criterion and the lack of unstable parameter space for isochoric modes according to Field’s criterion. Taking the temperature derivative at fixed density of Eq. A2 gives

${\left(\frac{\partial \mathcal{L}}{\partial T}\right)}_{\rho }=\frac{1}{2}c{A}_{\text{ff}}\rho T^{-4.5}\left(a{T}^4+7E_{r,\mathrm{s}}\right)+c{A}_C{E}_r.(12)$

Here, E_r and E_r,s are both constant values of the radiation energy density (see the Appendix) and A_ff and A_C are positive constants. We see that this derivative is always positive and thus cannot satisfy Field’s instability criterion as given by Eq. 9. However, Balbus’ instability criterion for isochoric modes is ${[\partial (\mathcal{L}/T)/\partial T]}_{\rho }<0$, which expands to

${\left(\frac{\partial \mathcal{L}}{\partial T}\right)}_{\rho }<\frac{\mathcal{L}}{T}.(13)$

Substituting Eq. 12 into Eq. 13 yields an expression that can be satisfied, demonstrating how allowing for $\mathcal{L}>0$ increases the parameter space for TI. We define any circumstance where the background flow has $\mathcal{L}\ne 0$ as it being in a state of thermal non-equilibrium (TNE). There has been confusion in the literature regarding the onset of TI in a TNE state, which we address directly in Section 4.2.

At this point, it is useful to recognize that the contour where ${(\partial \mathcal{L}/\partial T)}_{\rho }=\mathcal{L}/T$ is equivalent to the zero contour of the dimensionless quantity

$N_{\rho }^{\prime }=\frac{T_0}{{\mathrm{\Lambda }}_0}{\left[T\left(\frac{\partial \mathcal{L}/T}{\partial T}\right)\right]}_{\rho }.(14)$

The region on the phase diagram satisfying Eq. 13, or equivalently $N_{\rho }^{\prime }<0$, is what we refer to as the isochoric TI zone; the gray region in Figure 1 is therefore where the fast/slow isochoric modes are unstable and where the acoustic modes can be overstable. The TI zone marking where entropy modes are unstable is likewise defined by the zero contour of the quantity:

$N_p^{\prime }=\frac{T_0}{{\mathrm{\Lambda }}_0}{\left[T\left(\frac{\partial \mathcal{L}/T}{\partial T}\right)\right]}_p.(15)$

We avoided terming this the ‘isobaric TI zone’ because the long-wavelength entropy modes that give rise to nonisobaric evolution in the nonlinear regime of TI are still nevertheless governed by the ‘isobaric’ instability criterion $N_p^{\prime }<0$. Note that, upon neglecting thermal conduction, Eq. 15 is identical to Eq. 5 (after evaluating it at a given T₀), whereas Eq. 14 is equivalent to Eq. 6 only for $\mathcal{L}=0$.

From Figure 1, notice that the gray region is a subset of the red region, implying both $N_p^{\prime }<0$ and $N_{\rho }^{\prime }<0$ there; in terms of the discussion from Section 2.1, along the equilibrium curve, this net cooling function lacks parameter space where R_λ < 0 due to N_p > 0 and N_ρ < 0. Again, the only way the isochoric TI zone will be entered is if the gas undergoes cooling with $\mathcal{L}>0$, i.e., if the background flow is in a TNE state.

The bottom panel of Figure 1 illustrates our point about it being necessary to replace the concept of ‘isochoric evolution’ with ‘highly nonisobaric evolution’. The black dot marks an unstable position on the equilibrium curve. If the background flow is assigned the initial conditions at this location, then the linear growth phase of TI takes place on this dot because any noticeable deviation away from the initial conditions implies nonlinear amplitudes. The two sets of ‘tracks’ shown therefore represent the paths that can be taken by an unstable condensation mode once its amplitude becomes nonlinear. The horizontal set corresponds to isobaric evolution. A vertical set would correspond to isochoric evolution. What is shown instead is what actually happens in the long-wavelength regime: a condensation mode follows the equilibrium curve. This was first revealed by numerical simulations (see WP19), but it is clear in hindsight that this is what the nonlinear dynamics requires; when t_cool ≪ t_cross, the gas will be driven to equilibrium as it evolves.²

The red solid line in Figure 1 is the boundary of the TI zone that we refer to as the Balbus contour. We terminate the tracks once they cross this contour to emphasize that this stage of evolution marks the beginning of the saturation process, as we show in the following section.

3 Saturation mechanism

The dynamics of how TI saturates is highly nonlinear, hence most prior work has been based on constructing simplified dynamical models (see Meerson, 1996) or analyzing the results of numerical simulations. In WP19, we associated the temporal event of the cooling gas ‘landing on the equilibrium curve’ with the dynamical response henceforth referred to as ‘contraction rebound’, to adopt the term introduced by Jennings and Li (2021). The sequence of events leading up to contraction rebound is initiated well before the cloud reaches the equilibrium curve. As we show in Section 3.2, the trigger is a change in the sign of $N_p^{\prime }$, i.e., when the gas crosses the boundary of the TI zone and thus switches from being unstable to stable.

3.1 Equations governing nonlinear regime of TI

Our starting point is the evolution equation for the specific entropy (neglecting thermal conduction)

$\frac{Ds}{Dt}=-\frac{\mathcal{L}}{T},(16)$

where D/Dt = ∂/∂t + v ⋅∇ is the advective derivative. It is convenient to make this equation dimensionless. If we introduce the primed variables s′ ≡ s/c_v, t′ ≡ t/t_cool, ${\mathcal{L}}^{\prime }\equiv \mathcal{L}/{\mathrm{\Lambda }}_0$, and T′ ≡ T/T₀, this equation becomes $D{s}^{\prime }/D{t}^{\prime }=-{\mathcal{L}}^{\prime }/T^{\prime }$ for t_cool = c_vT₀/Λ₀ as defined in Eq. 3.³ To proceed without an excessive use of ‘primes’, all equations from here are understood to be written in terms of these primed variables.

As mentioned by Balbus (1986), applying a Lagrangian perturbation operator to Eq. 16 is the key to understanding TI anytime the flow is in a TNE state, having departed from the equilibrium curve. This hints at it being useful to apply a second advective derivative instead, to give

$\frac{D^{2}s}{D{t}^2}=-\frac{\mathrm{D}}{\mathrm{Dt}}\frac{\mathcal{L}}{T}.(17)$

In the Appendix, we show that for net cooling functions of the form $\mathcal{L}=\mathcal{L}(\rho ,T)$, Eq. 17 is equivalent to

$\frac{D^{2}s}{D{t}^2}=N_p^{\prime }\frac{D\ln \rho }{Dt}-N_{\rho }^{\prime }\frac{D\ln p}{Dt},(18)$

where $N_p^{\prime }$ and $N_{\rho }^{\prime }$ are just the quantities from Eq. 14 and Eq. 15 expressed in dimensionless variables:

$\begin{array}{cc}\hfill N_p^{\prime }& =T{\left(\frac{\partial \mathcal{L}/T}{\partial T}\right)}_p;\hfill \\ \hfill N_{\rho }^{\prime }& =T{\left(\frac{\partial \mathcal{L}/T}{\partial T}\right)}_{\rho }.\hfill \end{array}(19)$

Eq. 18 is therefore a dynamical relationship that connects the gas density and pressure gradients with the quantities determining the stability criteria and growth rates of the condensation modes. Whereas in linear theory, N_p and N_ρ are considered constant parameters describing the background flow, here $N_p^{\prime }$ and $N_{\rho }^{\prime }$ are time dependent, and this equation can be applied to the modes themselves to understand their nonlinear evolution. It becomes immediately clear that once the Balbus contour is crossed (i.e., once $N_p^{\prime }$ changes the sign), D ln ρ/Dt and D ln p/Dt must also change, implying that the linear growth regime given by Eq. 1 has ended.

Less elegant versions of Eq. 18 are required for understanding the saturation dynamics of TI in detail. In going from Eq. 17 to Eq. 18, we have already assumed an ideal gas, making Eq. 18 not yet fully simplified. The specific entropy is s = ln(p/ρ^γ) up to an additive constant. Hence, either the left-hand side of Eq. 18 can be written in terms of D²p/Dt² and D²ρ/Dt², or either D ln p/Dt or D ln ρ/Dt can be eliminated in favor of Ds/Dt on the right-hand side. Retaining both forms of the second option is the key to understanding the full saturation mechanism. By analogy with Eq. 4, we define the ratio

$R^{\prime }\equiv \frac{N_p^{\prime }}{\gamma N_{\rho }^{\prime }},(20)$

leading to, after a bit of algebra,

$\begin{array}{cc}\hfill \frac{D^{2}s}{D{t}^2}+\frac{N_p^{\prime }}{\gamma }\frac{Ds}{Dt}& =-N_{\rho }^{\prime }\left(1-R^{\prime }\right)\frac{D\ln p}{Dt};\hfill \\ \hfill \frac{D^{2}s}{D{t}^2}+N_{\rho }^{\prime }\frac{Ds}{Dt}& =-\gamma N_{\rho }^{\prime }\left(1-R^{\prime }\right)\frac{D\ln \rho }{Dt}.\hfill \end{array}(21)$

By eliminating Ds/Dt and D²s/Dt² using Eq. 16 and Eq. 17, respectively, and then solving for D ln p/Dt and D ln ρ/Dt, we arrive at

$\begin{array}{c}\hfill \frac{D\ln p}{Dt}=\frac{1}{N_{\rho }^{\prime }\left(1-R^{\prime }\right)}\left[\frac{D}{Dt}\frac{\mathcal{L}}{T}+\frac{N_p^{\prime }}{\gamma }\frac{\mathcal{L}}{T}\right];\\ \hfill \frac{D\ln \rho }{Dt}=\frac{1}{\gamma N_{\rho }^{\prime }\left(1-R^{\prime }\right)}\left[\frac{D}{Dt}\frac{\mathcal{L}}{T}+N_{\rho }^{\prime }\frac{\mathcal{L}}{T}\right].\end{array}(22)$

The first of these final expressions reveals that the sign changes of D ln p/Dt are determined by the location on the phase diagram (the value of $N_p^{\prime }$, $N_{\rho }^{\prime }$, R′, and $\mathcal{L}/T$), as well as by $D(\mathcal{L}/T)/Dt$, the rate of change of the instantaneous entropy production rate as measured by tracking a fluid element. The latter quantity accounts for the kinematic motion of the fluid element that is determined by the continuity and force equations.

The second expression is interpreted similarly, but it is distinct in that $N_p^{\prime }$ no longer appears in the expression in brackets. As we show in Section 3.3, for the dynamics taking place once the gas lands on the equilibrium curve, sign changes in D ln ρ/Dt are accompanied by sign changes in D ln p/Dt, and this is associated with ‘pulsations’—oscillations in the size of the cloud.

3.2 Crossing the Balbus contour

We now apply Eq. 22 to a single condensation mode in the nonlinear phase of TI to infer the sequence of dynamical events that must take place during saturation. We focus our analysis on the blue horizontal tracks in Figure 1, corresponding to nearly isobaric evolution within a TI zone (where $N_{\rho }^{\prime }>0$, $N_p^{\prime }<0$, and R′ < 0). It is clear from Figure 1 that $N_p^{\prime }=0$ will occur well before the cooling gas reaches the equilibrium curve (at which point n ≈ 9 × 10¹¹ cm⁻³). Evaluating the D ln p/Dt equation at $N_p^{\prime }=0$ gives

$\frac{D\ln p}{Dt}=\frac{1}{N_{\rho }^{\prime }\left(1-R^{\prime }\right)}\frac{D}{Dt}\frac{\mathcal{L}}{T}.(23)$

This equation states that provided R′ < 1, there can be only two possibilities once the density has increased enough to place the cool gas at the Balbus contour: i) the sign of D ln p/Dt is the same as that of $D(\mathcal{L}/T)/Dt$ or ii) both D ln p/Dt and $D(\mathcal{L}/T)/Dt$ are zero. We will henceforth refer to the event of D ln p/Dt passing through zero as a ‘pressure reversal’. The proviso that R′ < 1 is confirmed in Figure 2.

FIGURE 2

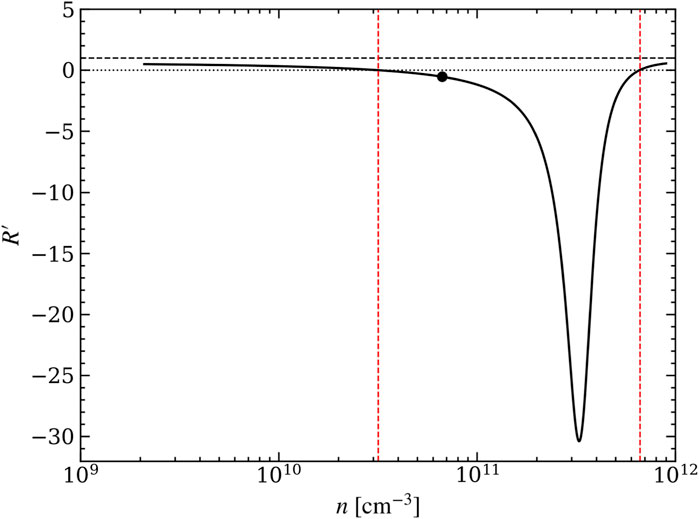
FIGURE 2. Variation of the parameter R′ defined in Eq. 20 during isobaric evolution. The red vertical lines demarcate the TI zone corresponding to the horizontal tracks in Figure 1, with a black dot again marking the initial equilibrium state of the background flow. Once a short-wavelength condensation mode reaches nonlinear amplitudes, it will sample the R′ values given by the black curve. This curve terminates on either end at stable (R′ > 0) points on the equilibrium curve. A dashed horizontal line is drawn at R′ = 1; the property R′ < 1 for isobaric evolution is likely a generic one for astrophysical cooling functions.

Possibility ii) would imply that a pressure reversal accompanies a Balbus crossing and also coincides with the time that $\mathcal{L}/T$ reaches its maximum value. Our claim is that possibility i) would imply that all three events are not simultaneous but that a pressure reversal is nevertheless associated with the event of the gas reaching $N_p^{\prime }=0$. If the evolution were to exactly follow an isobar, then using the chain rule,

$\frac{D}{Dt}\frac{\mathcal{L}}{T}={\left(\frac{\partial \mathcal{L}/T}{\partial T}\right)}_p\frac{DT}{Dt}.(24)$

The Balbus contour is by definition where the first term in parenthesis vanishes, so in this instance, there is only possibility ii) above. Because perfect isobaric evolution is in violation of Eq. 1, we conclude that these events cannot be simultaneous. However, the causal link has been established and we expect the interval between a Balbus crossing and a pressure reversal to be a measure of (non)isobaricity.

To sort out the order in which the events occur, we can follow similar reasoning and express Balbus’ instability criterion from Eq. 8 as

${\left[{\left(\frac{\partial T}{\partial t}\right)}^{-1}\frac{\partial }{\partial t}\frac{\mathcal{L}}{T}\right]}_p<0.(25)$

This expression reveals that unstable cooling gas has $\partial (\mathcal{L}/T)/\partial t>0$ at any fixed position within the overdense region of a condensation mode. It therefore tells us that the sign of $D(\mathcal{L}/T)/Dt$ starts off positive during the linear growth phase. By Eq. 1, D ln p/Dt < 0 in the linear regime—physically, unstable cooling gas loses pressure support because the temperature drops faster than the density can rise. As the Balbus contour is approached, it is possible mathematically for D ln p/Dt to reach 0 before $D(\mathcal{L}/T)/Dt$ does; by Eq. 22, D ln p/Dt = 0 corresponds to

$\frac{D}{Dt}\frac{\mathcal{L}}{T}=-\frac{N_p^{\prime }}{\gamma }\frac{\mathcal{L}}{T}.(26)$

Above the Balbus contour $N_p^{\prime }<0$, giving $D(\mathcal{L}/T)/Dt>0$ as required. However, this order of events implies that a pressure reversal was not preceded by a sign change in $D(\mathcal{L}/T)/Dt$ or a change in stability conditions. On this basis, we can discount this outcome except in instances where the cooling gas passes through the isochoric TI zone (see Section 3.4).

The remaining outcome is the following sequence of events:

1. The cooling rate $\mathcal{L}/T$ reaches its maximum value prior to crossing the Balbus contour, i.e., $D(\mathcal{L}/T)/Dt=0$ in a region where $N_p^{\prime }<0$. After this time, $D(\mathcal{L}/T)/Dt<0$.

2. The cooling gas reaches the Balbus contour. Since $D(\mathcal{L}/T)/Dt<0$ now, D ln p/Dt < 0 according to Eq. 23 i.e., the sign of D ln p/Dt is still that of the linear growth phase.

3. Prior to reaching the equilibrium curve where $\mathcal{L}=0$, a pressure reversal takes place when Eq. 26 is satisfied. Because $N_p^{\prime }>0$ now, $D(\mathcal{L}/T)/Dt<0$ by Eq. 26, consistent with the first event.We conclude that the true trigger for saturation is not crossing the actual Balbus contour corresponding to $N_p^{\prime }=0$ on the phase diagram, but rather the ‘local Balbus contour’ seen by a comoving fluid element, $D(\mathcal{L}/T)/Dt=0$. In practice, however, it is likely that these first two events occur within one thermal time, making the distinction unimportant.

3.3 Landing on the equilibrium curve

Figure 2 shows that R′ < 1 during the entire path traced by the condensation mode as it isobarically approaches the equilibrium curve. This is the expected result based on linear theory (see Section 2.1). The sign changes in D ln p/Dt and D ln ρ/Dt are therefore controlled by the bracketed terms in Eq. 22. We will reserve the phrase ‘pressure reversal’ to apply exclusively to the circumstance that D ln p/Dt changes the sign due to crossing the Balbus contour. Other options for the sign changes will be referred to as ‘zero crossings’.

We have already mentioned that $N_p^{\prime }$ does not appear in the bracketed term of the D ln ρ/Dt equation, and this means that contraction continues during and after a pressure reversal. Because $D(\mathcal{L}/T)/Dt<0$ outside the TI zone after the Balbus contour is crossed, the first time that D ln ρ/Dt can reach 0 is, according to Eq. 22, when

$\frac{D}{Dt}\frac{\mathcal{L}}{T}=-N_{\rho }^{\prime }\frac{\mathcal{L}}{T}.(27)$

This event corresponds to the density reaching its maximum value, thus marking the transition from contraction to expansion. In other words, this marks the beginning of the contraction rebound process.

In an isobaric case, it is likely for Eq. 27 to be satisfied only once—this single contraction rebound event leading directly to the cloud reaching a steady state on the equilibrium curve. For nonisobaric evolution, the pulsations that occur after contraction rebound, as observed in numerical simulations (see WP19; Gronke and Oh, 2020), correspond to cycles between subsequent zero crossings of D ln p/Dt and D ln ρ/Dt, with each zero crossing satisfying Eq. 26 and Eq. 27. Notice that this will involve oscillations about the equilibrium curve $\mathcal{L}=0$. A dedicated study of the D ln ρ/Dt equation in Eq. 22 is necessary to understand what parameters govern the pulsation damping rate.

3.4 Passing through the isochoric TI zone

Notice from Figure 1 that for the net cooling function given in the Appendix, it is possible to enter a regime of isochoric TI during isobaric evolution at just slightly higher pressures than that of the black dot. As mentioned in Section 3.2, this allows for a pressure reversal to occur inside the isochoric TI zone at a location where Eq. 26 can be satisfied. The only new constraint is found by setting $N_{\rho }^{\prime }=0$ in Eq. 22 to give

$\frac{D\ln \rho }{Dt}=-\frac{1}{N_p^{\prime }}\frac{D}{Dt}\frac{\mathcal{L}}{T}.(28)$

This relationship must hold at the boundary of the isochoric TI zone, revealing that if density is to remain monotonically increasing upon both entering and exiting this region (throughout which $N_p^{\prime }<0$), $D(\mathcal{L}/T)/Dt$ must remain positive. Substituting Eq. 28 into the D ln p/Dt equation in Eq. 22 additionally shows that a pressure reversal will occur at this boundary if $D\ln \rho /Dt={\gamma }^{-1}\mathcal{L}/T$ there. The alternative is for $\mathcal{L}/T$ to reach its maximum value at the boundary of this zone, which would correspond to having D ln ρ/Dt = 0, thereby satisfying Eq. 27 also. This would imply that contraction rebound precedes the pressure reversal because $D\ln p/Dt=-\mathcal{L}/T$ by Eq. 22, i.e., the sign of D ln p/Dt is still that of the linear growth phase. The viability of either of these sequences of events has to be verified numerically.

3.5 Other applications of the new identities

Being a general identity of non-adiabatic gas dynamics, Eq. 18 may prove useful in a variety of settings.⁴ In particular, Eqs 18–28 are unchanged in ideal MHD, hence so should be the overall saturation mechanism. However, the thermal evolution can differ in detail because in MHD, the paths traced on the phase diagram depend on the field strength (Bottorff et al., 2000, WP19). The linear theory of TI in MHD has recently been revisited by Claes and Keppens (2019), and it would be interesting to determine the plasma beta at which unstable condensation modes no longer carry out the sequence of events listed in Section 3.2.

Another obvious application is to the connection between TI and convective instability in stratified atmospheres (see Balbus and Soker, 1989; Binney et al., 2009; Balbus and Potter, 2016). To show that Eq. 18 is a generalization of results derived in that context, it is sufficient to examine one of the identities in Eq. 21 in a steady state. Taking D/Dt → v ⋅∇ gives, for the D ln p/Dt equation,

$\mathit{v}\cdot \nabla \left(\mathit{v}\cdot \nabla s\right)+\frac{N_p^{\prime }}{\gamma }\mathit{v}\cdot \nabla s=-N_{\rho }^{\prime }\left(1-R^{\prime }\right)\mathit{v}\cdot \nabla \ln p.(29)$

Noting that $N_{\rho }^{\prime }(1-R^{\prime })=N_{\rho }^{\prime }-N_p^{\prime }/\gamma$ by Eq. 20, we now also assume that the background state of the gas is in thermal equilibrium with $\mathcal{L}=0$. This reduces the quantity $N_{\rho }^{\prime }-N_p^{\prime }/\gamma$ to $T[{(\partial \mathcal{L}/\partial T)}_{\rho }-{\gamma }^{-1}{(\partial \mathcal{L}/\partial T)}_p]$, which is simply related to the quantity ${(\partial \mathcal{L}/\partial T)}_s$ by the thermodynamic identity (e.g., see Balbus, 1995):

$\frac{\gamma -1}{\gamma }{\left(\frac{\partial \mathcal{L}}{\partial T}\right)}_s={\left(\frac{\partial \mathcal{L}}{\partial T}\right)}_{\rho }-\frac{1}{\gamma }{\left(\frac{\partial \mathcal{L}}{\partial T}\right)}_p,(30)$

bringing us to

$\mathit{v}\cdot \left[\nabla \left(\mathit{v}\cdot \nabla s\right)+\frac{1}{\gamma }{\left(\frac{\partial \mathcal{L}}{\partial T}\right)}_p\nabla s+\frac{\gamma -1}{\gamma }{\left(\frac{\partial \mathcal{L}}{\partial T}\right)}_s\nabla \ln p\right]=0.(31)$

If we now apply an Eulerian perturbation operator to this equation, the result is a product rule giving, schematically, δv ⋅ […] + v ⋅ δ[…] = 0. As a last step, we assume the background atmosphere is static and spherically symmetric, leaving just the bracket attached to δv, which simplifies to

${\left(\frac{\partial \mathcal{L}}{\partial T}\right)}_p\frac{\partial s}{\partial r}=-\left(\gamma -1\right){\left(\frac{\partial \mathcal{L}}{\partial T}\right)}_s\frac{\partial \ln p}{\partial r}.(32)$

This equation is identical to Eq. 96 in Balbus and Potter (2016), who obtained it through a more involved Lagrangian perturbation analysis. As they explain, this relationship implies that TI will be accompanied by convective instability in an unstable static atmosphere.

In complicated flows, TI zone boundary crossings are likely common if not inevitable events during thermal evolution. Pressure reversals could therefore also play a role in mediating fragmentation caused by flow interactions. To provide an illustrative example, first note that a pre-existing cloud put in ‘by hand’ as initial conditions in non-adiabatic cloud–wind simulations and the fragments that appear as the cloud’s surface layers are disrupted, all occupy the same parameter space on a phase diagram as the cloud that is formed from TI. Referring to the tracks in Figure 1, as this gas changes its temperature upon interacting with the wind, the cold phase gas may repeatedly enter and exit the TI zone. A less disruptive example where crossing the Balbus contour may initiate the underlying fragmentation process is the ‘tearing’ mechanism identified by Jennings and Li (2021). By following individual fluid elements and applying Eq. 22, it should be possible to decipher the causal relationship between forces and the overall thermal evolution.

Yet, another topic concerns the dynamic role of pulsations in a regime of isochoric TI. Pulsations correspond to a change in the sign of D ln ρ/Dt, as discussed in Section 3.3. We have not yet studied nonisobaric evolution in a regime of isochoric TI using numerical simulations, and it is unclear if other groups have either. It is not standard practice to calculate the value of R_λ in Eq. 4 or R′ in Eq. 20 that characterizes any particular TI regime. This is especially relevant for a recent work on cloud coalescence instability; Gronke and Oh (2022) claim that this instability is aided by overstable acoustic modes, but such modes only exist when the isochoric or isentropic instability criterion is satisfied. Because they do not indicate which instability regime they consider, their claim of unstable acoustic modes being the agent that increases the coalescence rate is questionable. In our work on this instability (Waters and Proga, 2019a), we mentioned that coalescence can potentially be very fast; its rate can reach the rate set by the dynamical timescale provided the flow is continually subject to thermal disturbances, for this (re)excites pulsations and their accompanying advective flows that mediate the entire merger process.

4 Summary and discussion of controversial claims

In previous studies, we have shown that plotting the Balbus contour (the boundary of the TI zone on a phase diagram) is an essential diagnostic for understanding dynamical TI (Barai et al., 2012; Dannen et al., 2020; Waters et al., 2021; Waters et al., 2022), the counterpart to local TI when the background flow gradients are non-zero and the only type of TI encountered in global accretion flow or outflow simulations. Here, we have established that the Balbus contour plays an important dynamical role for local TI also. Specifically, Eq. 22 reveals the mechanism by which TI saturates: whenever this contour is crossed, a sequence of events unfolds that causes Dp/Dt to undergo a change in the sign. This marks the end of the exponential growth phase, i.e., crossing the Balbus contour causes the density, velocity, and pressure profiles to no longer resemble the solution to the linearized equations given in Eq. 1.

The saturation process is initiated in the gas undergoing cooling. The pressure reversal implied by a change in the sign of Dp/Dt indicates that the condensation can start gaining pressure support; at a fixed location within the condensation, −∇p changes from pointing inward to outward and thus begins to halt further contraction. The confining gas, meanwhile, continues to occupy the TI zone and undergoes runaway heating because the hotter gas is less dense and therefore heats up at a lower rate than the rate at which the condensation cools down. This, in turn, means that the confinement pressure continues to rise during and after contraction rebound. Once the hot phase gas rises above the Balbus contour and undergoes a pressure reversal, its pressure switches from increasing to decreasing with time, and the reduction in the confinement pressure aids further expansion of the condensation until, in the isobaric case, a steady state is reached.

In the nonisobaric case, i.e., for wavelengths large enough for the condensation velocity to become a significant fraction of the ambient sound speed, pulsations will set in after contraction rebound. Pressure oscillations first arise through the nonlinear interaction between the condensation and sound waves that become excited when each fluid element undergoes a pressure reversal (which occurs at different times for different locations in the cloud core). To emphasize this last point, we reiterate that in an isobaric case, mechanical equilibrium is closely maintained, whereas in a nonisobaric case, it is temporarily lost. There is a build-up of strong gas pressure forces, so that by the time TI saturates and most of the gas is thermally stable (with the cold gas nearly in thermal equilibrium again), the mechanical state is still far from equilibrium. Therefore, the next phase of the evolution is dominated by pressure waves that eventually bring the system to mechanical equilibrium. The significance of the gas crossing the Balbus contour is in it being associated with the very first qualitative change in the gas behavior, a precursor to a chain of events resulting in a very dynamic evolution of the system to a new thermal and mechanical equilibrium.

4.1 Shattering versus splattering

In Section 2, we did not draw a distinction on ‘nonisobaric evolution’ as it relates to TI and nonisobaric dynamics more generally. The latter is simply the tendency for the gas with t_cool ≲ t_cross to undergo oscillations in response to a thermal disturbance, and the cloud coalescence simulations we presented in Waters and Proga (2019a) provide an example of this. The former refers to the nonisobaric dynamics accompanying the saturation of TI, and as the wavelength of a condensation mode increases, nonisobaric evolution involves increasingly strong pulsations following contraction rebound. Extreme nonisobaric behavior is characterized by ‘splattering’, a term we introduced to indicate a contraction rebound so strong that the cloud undergoes self-fragmentation.

The ‘shattering’ hypothesis by contrast, described by McCourt et al. (2018) as there being a tendency for highly nonisobaric clouds to undergo spontaneous self-fragmentation—as opposed to breakup caused by a dynamical response to contraction—has not held up to scrutiny (Gronke and Oh, 2020; Das et al., 2021; Jennings and Li, 2021; Farber and Gronke, 2022). As we have explained in WP19 and again here in more detail (Section 2.3), McCourt et al.'s (2018) simulations, with the initial conditions of having a spectrum of perturbations, can be understood as a clear example of ‘isobaric takeover’, where short-wavelength perturbations form many isobaric condensations within a much larger pre-existing cloud. In other words, those simulations do not follow self-fragmentation of one entity but rather the evolution of a nonisobaric cloud serving as the background flow within which the shortest wavelength condensation modes (that have the fastest growth rates) can form clouds and interact. Burkert and Lin (2000) described such an outcome, claiming that the end result is indistinguishable from a fragmentation process. While we disagree with this, especially on the grounds that isobaric takeover will lead to coalescence (the opposite of fragmentation), even accepting the claim does not invalidate our takeaway point that ‘splattering’ refers to a definite mechanism leading to self-fragmentation (namely, contraction rebound) while ‘shattering’ does not.

Despite our pointing out in WP19 that McCourt et al.'s (2018) simulations are a demonstration of isobaric takeover, the term ‘shattering’ is still regularly invoked when describing the appearance of small-scale cloud fragments in wind–cloud or shock–cloud interaction simulations that include radiative cooling (e.g., Sparre et al., 2020; Banda-Barragán et al., 2021; Bustard and Gronke, 2022; Jennings et al., 2023). The use of the term here is likely because the size of these fragments appears to be the cooling length evaluated in the cold phase gas, denoted by min(λ_cool), which is the isobaric length scale identified by McCourt et al. (2018). A cloud fragment with a characteristic size d_c has an associated crossing time t_cross = d_c/c_s and can be said to be isobaric if t_cross ≲ t_cool. Equivalently, because λ_cool = c_st_cool is the length scale over which sound waves can effectively communicate thermal disturbances, isobaric cloud sizes satisfy d_c ≲ λ_cool, meaning that opposite sides of the cloud remain in sonic contact. The finding that interactions with the wind cause fragments to reach this length scale is not an unexpected outcome, hence this occurrence should not be confused with the regions of the cloud not interacting with the wind undergoing fragmentation, which is what ‘shattering’ would entail. Moreover, it is crucial to note that in Jennings et al.'s (2023) simulations, these isobaric fragments all evaporated in the runs with thermal conduction, consistent with our result that min(λ_cool) is generically smaller than the Field length (λ_F) evaluated in the warm phase gas (see WP19). Thus, while min(λ_cool) is a characteristic size scale for cloud fragments, it is not a physically relevant one unless thermal conduction is highly suppressed.

While ‘splattering’ refers exclusively to a highly nonisobaric regime of TI, the pulsation behavior it relates to could permit the characteristic size of cloud fragments to significantly exceed the scale min(λ_cool) in non-adiabatic wind–cloud interaction simulations. These fragments are expected to become larger upon increasing the wind temperature (while keeping the wind pressure the same), based on the following reasoning. The descriptors ‘isobaric’ and ‘nonisobaric’ have thus far been used for both the size and behavior of the cold phase gas, but they also apply to the confining warm phase gas. A parcel of the warm phase gas is isobaric on scales d_w < max(λ_cool), where max(λ_cool) denotes evaluating the cooling length at the warm phase temperature. This gas can easily remain isobaric, depending on how much hotter it is compared to the cold phase, and can therefore be effective in dampening the pulsations of nonisobaric clouds when max(λ_cool) ≫ d_c. In other words, two equally sized clouds, with d_c ≫ min(λ_cool) (and with the same pressure) embedded in different temperature environments, will not exhibit the same nonisobaric behavior when subjected to the same thermal disturbance.⁵ The pulsation damping rate is expected to be larger in a higher temperature environment, making that cloud effectively less nonisobaric and therefore less prone to fragmentation when interacting with a shearing flow. Even if this effect is significant, the fragments would still evaporate when they include isotropic thermal conduction because λ_F ∝ T^11/4/p (under Spitzer conductivity and fixed gas pressure p), while max(λ_cool) ∝ T^5/2/p. However, higher wind temperatures might allow larger fragments to survive when thermal conduction is anisotropic.

4.2 Thermal instability versus thermal non-equilibrium

In the solar physics literature, the relationship between TNE and TI is explained with reference to the TNE-TI cycle that describes observed phenomenology (e.g., see Antolin and Froment, 2022), specifically the dynamics taking place in coronal loops (magnetic flux tubes that extend from the chromosphere into the corona but are rooted to the solar surface at both ends). TNE itself has been described as a process that occurs when the heating rate profile in a loop drops off sharply with height and is unchanging with time, while the cooling rate remains a local quantity, making it possible for there to be no ‘nearby’ thermal equilibrium state (in ρ-T phase space) where cooling can reach a balance with heating (Klimchuk, 2019). Both evaporative and bulk flows can occur in response to pressure changes during a TNE cycle.

Klimchuk (2019) claimed that it is meaningless to consider TI occurring under TNE conditions on the (false) premise that diagnosing TI requires the background flow to be in a steady state. We stress that Balbus's (1986) stability criterion supersedes Field’s criterion for the very purpose of applying to TNE conditions. For there to be a consensus on this issue, the concept of TNE as given in the preceding paragraph would have to be generalized to adopt the definition that we have used in Section 2.4, namely, TNE is simply the circumstance that flow departs from the equilibrium curve, meaning $\mathcal{L}\ne 0$. We should furthermore specify that the bulk flow is subjected to $\mathcal{L}\ne 0$ on dynamical timescales to distinguish TNE from thermal misbalance, which simply refers to there being fluctuations about $\mathcal{L}=0$ on very short timescales due to acoustic compression and expansion cycles that result in the damping of MHD waves (Kolotkov et al., 2019; Kolotkov et al., 2021).

It follows that under TNE conditions, the criterion for entropy modes to be thermally unstable is given by Eq. 8, which expands to

${\left(\frac{\partial \mathcal{L}}{\partial T}\right)}_p<\frac{\mathcal{L}}{T}.(33)$

This reduces to the isobaric instability criterion of Field (1965) when the gas reaches thermal equilibrium with $\mathcal{L}=0$. In the astrophysics literature, the canonical example of a plasma that violates either criterion is one with (e.g., McCourt et al., 2012; Mościbrodzka and Proga, 2013; Balbus and Potter, 2016)

$\mathcal{L}=A\rho T^d-B,(34)$

where A, B, and d are constants satisfying A > 0, B ≥ 0, and d < 1. This is, however, the same example used by Klimchuk (2019) in an attempt to illustrate a condensation forming under TNE conditions in the absence of TI.⁶

Because the gas can be in TNE due to a variety of causes, a further distinction has to be drawn between local TI and dynamical TI. The theory of local TI, as summarized in Sections 2.1–2.2, is not confined to a homogeneous gas; it applies whenever the so-called local approximation holds, i.e., on length scales Δx over which Δx ≪ λ_q, where λ_q ≡|∇ ln q|⁻¹ is the scale length for the gradient of the background flow quantity q to be significant. Dynamical TI is the situation when the growth rates predicted by local TI cease to be valid because Δx ∼ λ_q for at least one of the relevant flow variables among q = (ρ, v, p, T).

Given the above considerations, the background flow for local TI can be an initially uniform region that is in an evolving equilibrium state or in a TNE state. As discussed in Section 2.4, the various isochoric instability regimes are associated with the gas starting off in TNE, as the entire isochoric TI zone is far from the equilibrium curve. In Proga et al. (2022), we provided a qualitative example of a column of gas starting off thermally stable but becoming unstable to local TI upon following a time-dependent equilibrium curve. In dynamical TI, by contrast, a flow can attempt to evolve along the equilibrium curve to maintain $\mathcal{L}=0$, but the timescale associated with adiabatic cooling can become shorter than t_cool, thereby causing the flow to tend toward a steady state at some position off the equilibrium curve where $\mathcal{L}\ne 0$.

If the coronal rain observed in coronal loops is attributable to the saturation of condensation modes, then due to the presence of flows and a chromosphere–corona transition region in these loops, the condensations are a clear instance of dynamical TI. Rather than the black dot in Figure 1, which represents a constant density initial condition appropriate for local TI, let us consider instead a possible initial coronal loop TNE state having a density spanning the range n ≈ 10¹¹−10¹² cm⁻³ and a nearly flat pressure profile that places it below the equilibrium curve in a region of net heating (with $\mathcal{L}<0$). The plasma will approach the equilibrium curve with time, but the flow traversing a converging (diverging) portion of the loop will undergo slight adiabatic heating (cooling), making the phase diagram ‘tracks’ of this flow spread vertically at different rates even if the heating rate is uniform. The plasma with n ≳ 1.5 × 10¹¹ cm⁻³ is very close to the stable cold branch of the equilibrium curve and will therefore not be subject to runaway heating. However, the stable equilibrium state of the plasma with n < 1.5 × 10¹¹ cm⁻³ is the hot branch where n ≲ 10¹⁰ cm⁻³. If pressure equilibrium can be closely maintained, the bulk of the coronal region plasma may approach this branch without ever entering the TI zone.

This is, in essence, a TNE runaway heating scenario that leads to a multi-temperature plasma without ever invoking TI. We therefore agree with the overall premise of Klimchuk (2019), but our example above debunks his assertion that “the physics that governs the thermal runaway in a TNE loop is equivalent to the physics that governs the thermal runaway in a [thermally] unstable equilibrium loop”. To examine condensation formation occurring under TNE conditions because of TI, we could alternatively imagine initial conditions that place the gas above the equilibrium curve in Figure 1 in a region of net cooling. Here, we would have to confront both bulk runaway cooling and the saturation of unstable entropy modes, but we have hopefully made it clear that these are distinct processes.

Either coronal loop scenario is complicated by the fact that equilibrium curves are in general time dependent, i.e., the contour $\mathcal{L}=0$ can change with time according to how the radiation field or other background sources of heating evolve. If this evolution occurs on timescales shorter than t_cool, the plasma cannot maintain $\mathcal{L}=0$ even if it can settle on the equilibrium curve and will thus re-enter TNE. The heating and cooling rates used for illustrative purposes in this article allow studying this situation. Namely, the equilibrium curve in Figure 1 models a column of gas being irradiated by both a thermal and non-thermal source of X-rays, and the two parameters T_C,h and f_h (controlling the temperature and flux of the non-thermal photons, respectively) can be made time dependent to vary the effective Compton temperature, which controls the shape of the equilibrium curve (see the Appendix).

We have recently worked on several other applications of dynamical TI that reveal the interplay between TI and TNE. In Waters et al. (2021), we have shown that the multiphase radial outflow solutions discovered in 1D by Dannen et al. (2020) can reach a steady state, permitting a formal stability analysis of an outflow occupying parameter space with $\mathcal{L}\ne 0$. There we also investigated the interconnection between TI and runaway heating in 2D simulations of accretion disk winds driven by external irradiation from X-rays, showing that it is possible to identify the presence of local TI even in a time-dependent, turbulent flow by plotting the ‘tracks’ of individual streamlines on the phase diagram to see if they pass through a TI zone. Finally, in Waters et al. (2022), we have addressed a different point that was raised by Klimchuk (2019). Referring to the stratified flow within a magnetic flux tube, Klimchuk posed the question: “if a perturbation grows, does it have time to reach a substantial amplitude before it is carried to the chromosphere by the flow?” We have shown how to calculate whether or not outflowing entropy modes have time to saturate when they sample a time-dependent growth rate as they ‘fly through’ a TI zone.

Data availability statement

The original contributions presented in the study are included in the article/; further inquiries can be directed to the corresponding author.

Author contributions

TW derived the identities in Section 3 while working as a postdoc in DP’s group at UNLV. TW wrote the first draft of the manuscript after several discussions with DP regarding the recent literature. Together, TW and DP analyzed the new identities to understand the saturation mechanism of TI and finalized the text. Both authors approved the submitted version.

Funding

This research was supported by the National Aeronautics and Space Administration under TCAN grant 80NSSC21K0496.

Acknowledgments

TW acknowledges funding support from Hui Li to attend the conference entitled AGN Santa Fe: where are the objects in AGN disks?, where this work was completed.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, editors, and reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2023.1198135/full#supplementary-material

Footnotes

¹The subscripted ‘T = T₀’ here corrects a notational error in Eq. 6 of WP19; this bracketed term is equal to ${(\partial \mathcal{L}/\partial T)}_p-\mathcal{L}/T$ evaluated at T = T₀.

²To view an animation comparing isobaric and nonisobaric evolution, please refer to the published article data here.

³Whereas in linear theory, the subscript ‘0’ denotes a quantity evaluated in uniform background flow, here it denotes just a fiducial value, as Eq. 16 is a dynamical equation for how the background flow varies.

⁴Note this equation is more general than Eq. 16 because that equation neglects all effects of thermal conduction due to a heat flux vector q, whereas Eq. 17, Eq. 18, and Eq. 21 will still hold in regions where ∇ ⋅q = constant.

⁵An idealized version of this thought experiment is ‘the pulsating sphere’, a well-known problem in acoustics (e.g., Devaud and Hocquet, 2013).

⁶We note that Klimchuk (2019) introduced a (half-wavelength) entropy mode into his initial conditions by the choice of a density profile given by Eq. 1 with A = 0.01.

References

Antolin, P., and Froment, C. (2022). Multi-scale variability of coronal loops set by thermal non-equilibrium and instability as a probe for coronal heating. Front. Astronomy Space Sci. 9. doi:10.3389/fspas.2022.820116

CrossRef Full Text | Google Scholar

Antolin, P. (2020). Thermal instability and non-equilibrium in solar coronal loops: From coronal rain to long-period intensity pulsations. Plasma Phys. Control. Fusion 62, 014016. doi:10.1088/1361-6587/ab5406

CrossRef Full Text | Google Scholar

Balbus, S. A. (1986). Local dynamic thermal instability. ApJL 303, L79. doi:10.1086/184657

CrossRef Full Text | Google Scholar

Balbus, S. A., and Potter, W. J. (2016). Surprises in astrophysical gasdynamics. Rep. Prog. Phys. 79, 066901. doi:10.1088/0034-4885/79/6/066901

PubMed Abstract | CrossRef Full Text | Google Scholar

Balbus, S. A., and Soker, N. (1989). Theory of local thermal instability in spherical systems. ApJ 341, 611. doi:10.1086/167521

CrossRef Full Text | Google Scholar

Balbus, S. A. (1995). “Thermal instability,” in The physics of the interstellar medium and intergalactic medium of astronomical society of the pacific conference series. Editors A. Ferrara, C. F. McKee, C. Heiles, and P. R. Shapiro, 80, 328.

Google Scholar

Banda-Barragán, W. E., Brüggen, M., Heesen, V., Scannapieco, E., Cottle, J., Federrath, C., et al. (2021). Shock-multicloud interactions in galactic outflows - II. Radiative fractal clouds and cold gas thermodynamics. MNRAS 506, 5658–5680. doi:10.1093/mnras/stab1884

CrossRef Full Text | Google Scholar

Barai, P., Proga, D., and Nagamine, K. (2012). Multiphase, non-spherical gas accretion on to a black hole. MNRAS 424, 728–746. doi:10.1111/j.1365-2966.2012.21260.x

CrossRef Full Text | Google Scholar

Begelman, M. C., and McKee, C. F. (1990). Global effects of thermal conduction on two-phase media. ApJ 358, 375. doi:10.1086/168994

CrossRef Full Text | Google Scholar

Binney, J., Nipoti, C., and Fraternali, F. (2009). Do high-velocity clouds form by thermal instability? MNRAS 397, 1804–1815. doi:10.1111/j.1365-2966.2009.15113.x

CrossRef Full Text | Google Scholar

Bottorff, M. C., Korista, K. T., and Shlosman, I. (2000). Dynamics of warm absorbing gas in seyfert galaxies: Ngc 5548. ApJ 537, 134–151. doi:10.1086/309006

CrossRef Full Text | Google Scholar

Burkert, A., and Lin, D. N. C. (2000). Thermal instability and the formation of clumpy gas clouds. ApJ 537, 270–282. doi:10.1086/308989

CrossRef Full Text | Google Scholar

Bustard, C., and Gronke, M. (2022). Radiative turbulent mixing layers and the survival of magellanic debris. ApJ 933, 120. doi:10.3847/1538-4357/ac752b

CrossRef Full Text | Google Scholar

Choudhury, P. P. (2023). Formation of multiphase plasma in galactic haloes and an analogy to solar plasma. Front. Astronomy Space Sci. 10, 1155865. doi:10.3389/fspas.2023.1155865

CrossRef Full Text | Google Scholar

Claes, N., and Keppens, R. (2021). Magnetohydrodynamic spectroscopy of a non-adiabatic solar atmosphere. SoPh 296, 143. doi:10.1007/s11207-021-01894-2

CrossRef Full Text | Google Scholar

Claes, N., and Keppens, R. (2019). Thermal stability of magnetohydrodynamic modes in homogeneous plasmas. A&A 624, A96. doi:10.1051/0004-6361/201834699

CrossRef Full Text | Google Scholar

Dannen, R. C., Proga, D., Waters, T., and Dyda, S. (2020). Clumpy AGN outflows due to thermal instability. ApJL 893, L34. doi:10.3847/2041-8213/ab87a5

CrossRef Full Text | Google Scholar

Das, H. K., Choudhury, P. P., and Sharma, P. (2021). Shatter or not: Role of temperature and metallicity in the evolution of thermal instability. MNRAS 502, 4935–4952. doi:10.1093/mnras/stab382

CrossRef Full Text | Google Scholar

Devaud, M., and Hocquet, T. (2013). Lagrangian sound. hal-00904571.

Google Scholar

Farber, R. J., and Gronke, M. (2022). Molecular shattering. arXiv e-prints, arXiv:2209.13622. doi:10.48550/arXiv.2209.13622

CrossRef Full Text | Google Scholar

Faucher-Giguere, C.-A., and Oh, S. P. (2023). Key physical processes in the circumgalactic medium. arXiv e-prints, arXiv:2301.10253. doi:10.48550/arXiv.2301.10253

CrossRef Full Text | Google Scholar

Field, G. B., Goldsmith, D. W., and Habing, H. J. (1969). Cosmic-ray heating of the interstellar gas. ApJL 155, L149. doi:10.1086/180324

CrossRef Full Text | Google Scholar

Field, G. B. (1965). Thermal instability. ApJ 142, 531. doi:10.1086/148317

CrossRef Full Text | Google Scholar

Gronke, M., and Oh, S. P. (2022). Cooling driven coagulation. arXiv e-prints, arXiv:2209.00732. doi:10.48550/arXiv.2209.00732

CrossRef Full Text | Google Scholar

Gronke, M., and Oh, S. P. (2020). Is multiphase gas cloudy or misty? MNRAS 494, L27–L31. doi:10.1093/mnrasl/slaa033

CrossRef Full Text | Google Scholar

Jennings, F., Beckmann, R. S., Sijacki, D., and Dubois, Y. (2023). Shattering and growth of cold clouds in galaxy clusters: The role of radiative cooling, magnetic fields, and thermal conduction. MNRAS 518, 5215–5235. doi:10.1093/mnras/stac3426

CrossRef Full Text | Google Scholar

Jennings, R. M., and Li, Y. (2021). Thermal instability and multiphase gas in the simulated interstellar medium with conduction, viscosity, and magnetic fields. MNRAS 505, 5238–5252. doi:10.1093/mnras/stab1607

CrossRef Full Text | Google Scholar

Klimchuk, J. A. (2019). The distinction between thermal nonequilibrium and thermal instability. SoPh 294, 173. doi:10.1007/s11207-019-1562-z

CrossRef Full Text | Google Scholar

Kolotkov, D. Y., Nakariakov, V. M., and Zavershinskii, D. I. (2019). Damping of slow magnetoacoustic oscillations by the misbalance between heating and cooling processes in the solar corona. A&A 628 (A133), 6. doi:10.1051/0004-6361/201936072

CrossRef Full Text | Google Scholar

Kolotkov, D. Y., Zavershinskii, D. I., and Nakariakov, V. M. (2021). The solar corona as an active medium for magnetoacoustic waves. Plasma Phys. Control. Fusion 63, 124008. doi:10.1088/1361-6587/ac36a5

CrossRef Full Text | Google Scholar

Krolik, J. H., McKee, C. F., and Tarter, C. B. (1981). Two-phase models of quasar emission line regions. ApJ 249, 422–442. doi:10.1086/159303

CrossRef Full Text | Google Scholar

Laha, S., Reynolds, C. S., Reeves, J., Kriss, G., Guainazzi, M., Smith, R., et al. (2020). Ionized outflows from active galactic nuclei as the essential elements of feedback. Nat. Astron. 5, 13–24. doi:10.1038/s41550-020-01255-2

CrossRef Full Text | Google Scholar

Lepp, S., McCray, R., Shull, J. M., Woods, D. T., and Kallman, T. (1985). Thermal phases of interstellar and quasar gas. ApJ 288, 58–64. doi:10.1086/162763

CrossRef Full Text | Google Scholar

Mandelker, N., van den Bosch, F. C., Springel, V., van de Voort, F., Burchett, J. N., Butsky, I. S., et al. (2021). Thermal instabilities and shattering in the high-redshift WHIM: Convergence criteria and implications for low-metallicity strong H I absorbers. ApJ 923, 115. doi:10.3847/1538-4357/ac2d29

CrossRef Full Text | Google Scholar

McCourt, M., Oh, S. P., O’Leary, R., and Madigan, A.-M. (2018). A characteristic scale for cold gas. MNRAS 473, 5407–5431. doi:10.1093/mnras/stx2687

CrossRef Full Text | Google Scholar

McCourt, M., Sharma, P., Quataert, E., and Parrish, I. J. (2012). Thermal instability in gravitationally stratified plasmas: Implications for multiphase structure in clusters and galaxy haloes. MNRAS 419, 3319–3337. doi:10.1111/j.1365-2966.2011.19972.x

CrossRef Full Text | Google Scholar

McKee, C. F., and Ostriker, J. P. (1977). A theory of the interstellar medium: Three components regulated by supernova explosions in an inhomogeneous substrate. ApJ 218, 148–169. doi:10.1086/155667

CrossRef Full Text | Google Scholar

Meerson, B. (1996). Nonlinear dynamics of radiative condensations in optically thin plasmas. Rev. Mod. Phys. 68, 215–257. doi:10.1103/RevModPhys.68.215

CrossRef Full Text | Google Scholar

Mościbrodzka, M., and Proga, D. (2013). Thermal and dynamical properties of gas accreting onto a supermassive black hole in an active galactic nucleus. ApJ 767, 156. doi:10.1088/0004-637X/767/2/156

CrossRef Full Text | Google Scholar

Parker, E. N. (1953). Instability of thermal fields. ApJ 117, 431. doi:10.1086/145707

CrossRef Full Text | Google Scholar

Perry, J. J., and Dyson, J. E. (1985). Shock formation of the broad emission-line regions in QSOs and active galactic nuclei. MNRAS 213, 665–710. doi:10.1093/mnras/213.3.665

CrossRef Full Text | Google Scholar

Proga, D., Waters, T., Dyda, S., and Zhu, Z. (2022). Thermal instability in radiation hydrodynamics: Instability mechanisms, position-dependent S-curves, and attenuation curves. ApJL 935, L37. doi:10.3847/2041-8213/ac87b0

CrossRef Full Text | Google Scholar

Soler, R., Ballester, J. L., and Parenti, S. (2012). Stability of thermal modes in cool prominence plasmas. A&A 540, A7. doi:10.1051/0004-6361/201118492

CrossRef Full Text | Google Scholar

Soler, R., and Ballester, J. L. (2022). Theory of fluid instabilities in partially ionized plasmas: An overview. Front. Astronomy Space Sci. 9, 789083. doi:10.3389/fspas.2022.789083

CrossRef Full Text | Google Scholar

Sparre, M., Pfrommer, C., and Ehlert, K. (2020). Interaction of a cold cloud with a hot wind: The regimes of cloud growth and destruction and the impact of magnetic fields. MNRAS 499, 4261–4281. doi:10.1093/mnras/staa3177

CrossRef Full Text | Google Scholar

Tumlinson, J., Peeples, M. S., and Werk, J. K. (2017). The circumgalactic medium. ARA&A 55, 389–432. doi:10.1146/annurev-astro-091916-055240

CrossRef Full Text | Google Scholar

Vázquez-Semadeni, E., Gazol, A., Passot, T., et al. (2003). “Thermal instability and magnetic pressure in the turbulent interstellar medium,” in Turbulence and magnetic fields in astrophysics. Editors E. Falgarone, and T. Passot, 614, 213–251. doi:10.48550/arXiv.astro-ph/0201521

CrossRef Full Text | Google Scholar

Veilleux, S., Maiolino, R., Bolatto, A. D., and Aalto, S. (2020). Cool outflows in galaxies and their implications. A&A Rv 28, 2. doi:10.1007/s00159-019-0121-9

CrossRef Full Text | Google Scholar

Waters, T., and Proga, D. (2019a). Cloud coalescence: A dynamical instability affecting multiphase environments. ApJL 876, L3. doi:10.3847/2041-8213/ab12e8

PubMed Abstract | CrossRef Full Text | Google Scholar

Waters, T., Proga, D., Dannen, R., and Dyda, S. (2022). Dynamical thermal instability in highly supersonic outflows. ApJ 931, 134. doi:10.3847/1538-4357/ac6612

CrossRef Full Text | Google Scholar

Waters, T., Proga, D., and Dannen, R. (2021). Multiphase AGN winds from X-ray-irradiated disk atmospheres. ApJ 914, 62. doi:10.3847/1538-4357/abfbe6

CrossRef Full Text | Google Scholar

Waters, T., and Proga, D. (2019b). Nonisobaric thermal instability. ApJ 875, 158. doi:10.3847/1538-4357/ab10e1

CrossRef Full Text | Google Scholar

Zhang, D. (2018). A review of the theory of galactic winds driven by stellar feedback. Galaxies 6, 114. doi:10.3390/galaxies6040114

CrossRef Full Text | Google Scholar