RCM modeling of bubble injections into the inner magnetosphere: geosynchronous orbit and the ionospheric responses

Sadeghzadeh, Sina; Yang, Jian; Toffoletto, Frank; Wolf, Richard; Mousavi, Ameneh; Wang, Chih-Ping

doi:10.3389/fspas.2023.1189298

ORIGINAL RESEARCH article

Front. Astron. Space Sci., 22 May 2023

Sec. Space Physics

Volume 10 - 2023 | https://doi.org/10.3389/fspas.2023.1189298

This article is part of the Research Topic Computational Modelling in Space Physics View all 4 articles

RCM modeling of bubble injections into the inner magnetosphere: geosynchronous orbit and the ionospheric responses

Jian Yang¹*

¹Department of Earth and Space Sciences, Southern University of Science and Technology, Shenzhen, China
²Physics and Astronomy Department, Rice University, Houston, TX, United States
³Department of Atmospheric and Oceanic Sciences, University of California, Los Angeles, CA, United States

Introduction: Accurate characterization of the plasma sheet source population in the ring current region and its outer boundary at geosynchronous orbit is crucial for understanding the dynamics of the Earth’s magnetosphere. The interaction between the ring current and plasma populations from the ionosphere is a focus of extensive research.

Methods: We used the Rice Convection Model (RCM) to simulate the transient meso-scale injections of fast flows or plasma sheet bubbles from the outer boundary into the inner magnetosphere and the associated impacts on the ionosphere. We compared our simulation results of the average properties of bulk plasma access to geosynchronous orbit to a number of empirical models. We also examined the role of plasma sheet bubbles in forming field-aligned currents (FACs).

Results: Our modeling results show that impulsive plasma sheet injections dramatically alter the average distribution of FACs in the ionosphere. We found both quantitative and qualitative agreements and disagreements when comparing our simulation results to empirical models. Furthermore, we demonstrated that several discrete auroral structures can be identified in the nightside ionosphere in accordance with theupward FACs.

Discussion: The significance of plasma sheet bubbles in modifying the averageplasma properties at geosynchronous orbit and FACs in the ionosphere is highlighted by oursimulation findings, offering novel understandings into the dynamics of Earth's magnetosphere,and emphasizing the necessity for further research in this field.

1 Introduction

The transport of particles and energy in the coupled system of solar wind-magnetosphere-ionosphere (SMI) during different geomagnetic conditions is still a debated topic in space science (Borovsky et al., 2020). The transport of hot magnetotail plasma to the central and inner (inside of $10 R_{e}$ ) magnetosphere, in particular, has received much attention (e.g., Eastman et al., 1984; Angelopoulos et al., 1992; Chen and Wolf, 1993; Borovsky et al., 1998; Yang et al., 2015; 2016). Fast-moving magnetic flux tubes with severely depleted entropy can penetrate deep into the inner magnetosphere and reach inside geosynchronous orbit (GEO) (e.g., Dubyagin et al., 2011; Yu et al., 2014; Cramer et al., 2017). These plasma sheet bubbles tend to move earthward due to the interchange instability (Xing and Wolf, 2007), in which dawn-to-dusk electric fields are enhanced inside the bubble, creating shear flows (Pontius and Wolf, 1990). Plasma bubbles are a theoretical interpretation of bursty bulk flows (BBFs), which are often observed during a variety of geomagnetic conditions (Baumjohann et al., 1990). The role of low-entropy bubbles in mediating energy and momentum transport from the tail into the ring current region has been investigated before (e.g., Yang et al., 2010; Gkioulidou et al., 2011). The extent of bubble injections in contributing to the Earth’s ring current buildup and at GEO during geomagnetic storms has been a point of contention. Studies suggest that during periods of heightened geomagnetic activity, bubble injections may account for up to 50% of the total ring current energy, while non-bubble plasma is expected to be the primary contributor during regular periods. Thus, the influence of bubbles and non-bubbles on the ring current energy can vary depending on the level of geomagnetic activity. Although energetic particle injections at GEO were frequently referenced as fundamental substorm signatures, recent multispacecraft analyses show that only a fraction of all flow bursts have the potential to reach the inner magnetosphere and provide a particle injection at GEO (e.g., Ohtani et al., 2006; Sergeev et al., 2012). Specifically, Sergeev et al. (2012) revealed that only one-third of all flow bursts at $8 - 13 R_{e}$ were related to particle injection at GEO, but those injection-associated flows had smaller values of the plasma tube entropy parameter linked to dipolarizations. This further supports a scenario where bursty flows at the inner magnetosphere’s entry infiltrate GEO and contribute to the energetic particle flux increase. Gkioulidou et al. (2014) estimated the contribution of multiple ion injections to the total energy accumulated in the inner magnetosphere during a specific geomagnetic storm using observations from the Van Allen Probe B spacecraft. They found that the direct effect of these injections accounted for roughly 30% of the energy gain in the ring current region, indicating that this mode of particle transport and energization can substantially contribute to the total energy gained throughout a geomagnetic storm. However, the authors noted that other mechanisms could also impact the ring current energy and that further research is necessary to fully understand the dynamics of the Earth’s ring current. Yang et al. (2015) employed a test particle tracing code to identify sources for the ring current within GEO. Their study’s primary finding is that bubbles contribute approximately 61% of the plasma energy inside GEO for storms with Dst smaller than $70 n T$ , while non-bubble-like transport from the plasma sheet and trapped particles contribute only 18% and 21%, respectively, on average. Their analysis supports the notion that plasma sheet bubbles are the primary source of the ring current for moderate and intense storms. Numerous studies have been conducted in order to predict the energetic electron and ion fluxes in the near-Earth region, as their distribution is critical to the protection of satellite operations in harsh environments (e.g., Thomsen et al., 2007; Boynton et al., 2013; Sillanpää et al., 2017; Coleman et al., 2018). As a result, developing an accurate model of the plasma sheet source population for the ring current region is crucially important (e.g., Jordanova et al., 1997; Zaharia et al., 2006). Properties of plasma populations as a function of local time, energy, geomagnetic condition, and solar activity have been extensively studied through observations, models, and simulations, particularly at the outer boundary of the ring current along geosynchronous orbit ( $R \sim 6.6 R_{e}$ ) (e.g., Thomsen et al., 1996; 1999; Korth et al., 1999; Lemon and O’Brien, 2008). Denton et al. (2005) analyzed the local time variability of plasma sheet materials with respect to the Dst and Kp indices using data from 11 years of LANL geosynchronous satellite observations. Different data-driven models for electron and ion fluxes at geosynchronous orbit as a function of local time, energy, solar activity (e.g., F_10.7), and Kp index are also constructed using LANL and Cluster satellites (e.g., Denton et al., 2015; 2016; 2019). Sillanpää et al. (2017) developed an empirical model for electron fluxes at energies of 40, 75, and 150 keV using data from the Geostationary Operational Environmental Satellite (GOES). While these empirical models are very useful, they can only provide highly averaged values and have limitations in providing insights into the physical processes involved. Physics-based simulations, on the other hand, can provide some insight into the physical system but are constrained by the assumptions that are used to develop them. Despite considerable efforts in both simulations and observations, more research is required to better predict the conditions that govern the nature of plasma in the near-Earth region.

Field-aligned currents (FACs) play a key role in exchanging energy and momentum in the coupled magnetosphere-ionosphere system. Under quasi-steady conditions, the density of FACs in the closed magnetic field line region is related to the distribution of the flux tube volume (V) and plasma pressure (P) in the magnetosphere (Vasyliunas, 1970). While plasma distribution is an important factor in determining both region-1 and 2 FACs, its impact is generally considered to be more significant for region-2 FACs, which are primarily driven by the cross-tail electric field and are sensitive to the plasma sheet density and pressure distribution. In the northern hemisphere, the high-latitude region-1 FACs flow downward into the ionosphere at dawn and upward out of it at dusk. Whereas the region-2 FACs flow in the opposite directions equatorward of the region-1 currents (e.g., Zmuda and Armstrong, 1974; Iijima and Potemra, 1976a; 1976b). FAC distribution and intensity are found to be influenced by factors other than the plasma distribution in the magnetosphere, such as interplanetary magnetic field (IMF) orientation (e.g., Milan et al., 2000; Weimer, 2001), solar wind pressure (e.g., Edwards et al., 2017), and ionospheric conductance (Korth et al., 2010). Several studies have been conducted to determine the origins and characteristics of regions 1 and 2 FACs. In most of these studies, magnetic field data from spacecraft are used to calculate FACs at the ionospheric altitude. Observations from the THEMIS mission led Liu et al. (2016) to conclude that the region-1 and 2 Birkeland currents on the nightside have plasma sheet origins, likely related to pressure buildup or flow vortices. Their finding is consistent with the earlier work of Sato and Iijima (1979), who also revealed the source and distribution of region-1 and 2 currents. Apart from large-scale ( $\geq$ 1,000 km) current systems, mesoscale (10 s–100 s km) and small-scale (<10 km) ones have also been found. McGranaghan et al. (2017) presented a comprehensive analysis of the characteristics of these multiscale FACs using data from the Swarm and AMPERE satellites. Significant differences were found between the scales at noon and midnight. Furthermore, and in accordance with the previous studies (e.g., Neubert and Christiansen, 2003; Lühr et al., 2015), they concluded that the current density is inversely proportional to scale, i.e., on the order of $\sim 1 - 2 μ A / m^{2}$ for large-scale FACs and a few (and even tens) of $μ A / m^{2}$ for fine-scale currents. Hasunuma et al. (2008) used Akebono satellite data to examine the intensity, distribution, and key characteristics of dayside meso-scale FACs. Their research reveals that meso-scale FACs are more intense and have different characteristics than their large-scale counterparts. Ochieng et al. (2019) investigated geomagnetic dependence, occurrence, and spatio-temporal variation of meso-scale FACs during geomagnetic storms using CHAllenging Minisatellite Payload (CHAMP) observations. They used a criterion to identify the occurrence of meso-scale FACs (i.e., $\geq 1 μ A {/ m}^{2}$ ) and found that during southward (northward) IMF the intensity of FACs is higher near dawn and dusk (noon and midnight) sectors. The MHD simulations of magnetotail reconnection leading to fast plasma flows reveal another important feature of FACs, which is related to substorm current wedge (SCW) (e.g., Scholer and Otto, 1991; Birn and Hesse, 1991; Kepko et al., 2015 and references therein; Birn et al., 2019). However, few simulations have investigated the morphology of these currents in light of the kinetic drift physics of the inner magnetosphere (e.g., Yang et al., 2012).

Our study focuses on two main topics: 1) particle fluxes and bulk plasma properties at geosynchronous orbit, and 2) the global ionospheric distribution of FACs and auroral morphology. To this end, we employ the inertial version of the Rice Convection Model (Yang et al., 2019) to simulate the average configuration of magnetosphere-ionosphere coupled system that includes the effects of fast plasma flows. In our simulation, sporadic, low-entropy bubble injections are imposed from the high latitude boundary of modeling region to alleviate the so-called “pressure-balance crisis” (Erickson and Wolf, 1980; Pontius and Wolf, 1990). This setup resembles a more realistic magnetospheric condition rather than a purely large-scale convection (Yang et al., 2014a). We used the same time-, local-time-, and energy-dependent boundary conditions as Sadeghzadeh et al. (2021) - henceforth referred to as Paper 1–to model random bubble injections through the nightside boundary. There are three low-entropy plasma flow channels with a width of 0.67 h in magnetic local time (MLT) that are randomly positioned between 21 and 3 h in MLT and operate over three different fixed periods of time (tens of minutes). Table 1 presents a summary of the similarities and differences between the RCM configuration used in this study and the one described in Paper 1. We conducted three separate 2-h runs of the RCM simulation, each with a different profile for the local time and degree of entropy depletion in the plasma flow channels. It is worth noting that there is no advantage of one run over another, but we chose to run the simulations multiple times and average the results to obtain a more accurate statistical picture for comparison with observational data. This decision was motivated by our observation that the mapping gets distorted when $B_{z}$ -minimum drops ahead of the severely depleted bubbles after about 2 hours, leading to code crashes. In this scenario, we needed to inject low-entropy bubbles in shorter timescales to match the number of injections in the longer 6-h run presented in Paper 1 and to ensure compliance with the observational data. Other than the boundary conditions, the initial conditions are carefully adjusted to best capture 1) the probability density functions (PDFs) of $V_{x}$ and $V_{y}$ from THEMIS and Geotail observations, and 2) data-driven models of electron and proton distributions in the central plasma sheet proposed by Dubyagin et al. (2016) (hereafter referred to as DGSR2016) and Tsyganenko and Mukai (2003) (hereafter referred to as TM2003). The rest of this study is organized as follows. Section 2 briefly introduces the simulation setup including the modeling region, initial, and boundary conditions. We will analyze the coupled response of the inner magnetosphere and ionosphere separately in Section 3. Section 4 summarizes the conclusions.

TABLE 1

TABLE 1. RCM setup scheme in Paper 1 and the current paper.

2 Simulation setup

We describe our simulation setup in this section, including the initial and boundary conditions as well as the electron precipitation model. The initial plasma moments are taken from two empirical models, TM2003 and DGSR2016. The TM2003 (DGSR2016) model is based on Geotail (THEMIS) observations and is intended to provide bulk ions (electrons) properties at distances of $10 - 50 R_{e}$ ( $6 - 10 R_{e}$ ) in the equatorial plane on the nightside. The details of the plasma distributions can be found in our previous Paper 1. We have also made several changes to the simulation to improve the agreement with observations and numerical stability, i.e., to prevent the electric potential from becoming noisy and to make FACs pattern smoother. Here, we list these changes as follows:

1. The radial-distance-dependent proton-to-electron temperature ratio (i.e., $T_{p} / T_{e}$ ) is prescribed as the initial condition, whereas in Paper 1 we simply assumed $T_{p} / T_{e} = 1.5$ , independent of the radial distance. In this study, the $T_{p} / T_{e}$ ratio at distances of $20 R_{e} > R > 6 R_{e}$ has a functional form of $3.4 + 1.75 \tan^{- 1} ((R / 1.1) - 10)$ which gives the ratio of $\sim 1$ at geosynchronous orbit and $\sim 2.1$ at $10 R_{e}$ . For the region outside of $10 R_{e}$ , $T_{p} / T_{e}$ gradually increases tailward and reaches $\sim 6$ at $R \sim 20 R_{e}$ . This choice reasonably satisfies 1) the plasma moments (pressure, temperature, and density) from empirical models TM2003 and DGSR2016 at different radial distances, and 2) the spatial distribution of THEMIS measurements described by Wang et al. (2012). Note that $T_{p} / T_{e} = 1.5$ is retained as Paper 1 at $R < 6 R_{e}$ distances.

2. This study uses Orlova et al. (2014) electron loss model. They developed a comprehensive model of electron lifetimes by analyzing wave parameters from Combined Release and Radiation Effects Satellite (CRRES) observations. In contrast, in Paper 1, the electron loss model of Chen and Schulz (2001) was used, which assumed that the scattering rate is less than everywhere strong but is dependent on MLT. We found that using Orlova’s model, we can achieve much better consistency for electron distribution between our simulation results and the DGSR2016 empirical model at distance of $\sim 4 - 6 R_{e}$ .

3. We have also modified the energy-invariant-dependent depletion function ( $Q (λ_{s})$ ) which is used to control the degree of $P V^{5 / 3}$ reduction inside the bubbles. Here, $λ_{s} = W_{s} V^{2 / 3}$ is the energy invariant where $W_{s}$ is energy of particle and $V = \int d s / B$ is flux tube volume per unit magnetic flux. In this study, we specify the flux tube content $η_{s}$ [defined as the number of particles per unit magnetic flux for a specific energy invariant and a specific chemical species ( $s$ )] inside the bubbles on the boundary through $η_{s} (λ_{s}) = η_{s}^{b g} (λ_{s}) Q (λ_{s})$ , where $Q (λ_{s}) = π^{- 1} \tan^{- 1} (λ_{s} λ_{p, e}^{- 1} - 10) (d_{p} - 1) + 0.5 (d_{p} + 1)$ with the threshold values of the electron and proton energy invariants (i.e., $λ_{e}$ and $λ_{p}$ , respectively) of 300 and 4,000 $e V {(R_{e} / n T)}^{2 / 3}$ , respectively. The reason behind the choice of these values is detailed in the Supplementary Data S1 and illustrated in Supplementary Figure S1. In Paper 1, a fixed large value was used to adjust the degree of entropy depletion (i.e., $d_{p} ≫ 50 % -$ where “ $d_{p}$ ” refers to the degree of reduction in entropy within a specific group of flux tubes) for high energy particles, whereas in this paper, we defined a varying depletion for each channel.

4. Because we are comparing findings of RCM simulation of idealized bubble injections to data/observations, we chose to run three RCM simulations—each lasting two hours—with the same setup but different $d_{p}$ factors for this study. A more realistic statistical picture, in our opinion, will be obtained by randomly repeating the RCM simulations and averaging them as opposed to picking just one run. Only the local time and degree of $P V^{5 / 3}$ depletion in channels change from one run to another, and one run has no advantage over another. The averaged outcomes are then contrasted with observations and/or empirical models. Figure 1 shows the entropy-depletion (i.e., $d_{p}$ ) choices in three runs. The histograms show skewed distributions centered on larger $d_{p}$ values. Our experiments show that such a distribution guarantees: 1) enough strong bubble injections to bring the plasma sheet probability density function of velocities in accordance with Geotail and THEMIS observations, and 2) the prevention for numerical instability accumulation in the ionosphere.

FIGURE 1

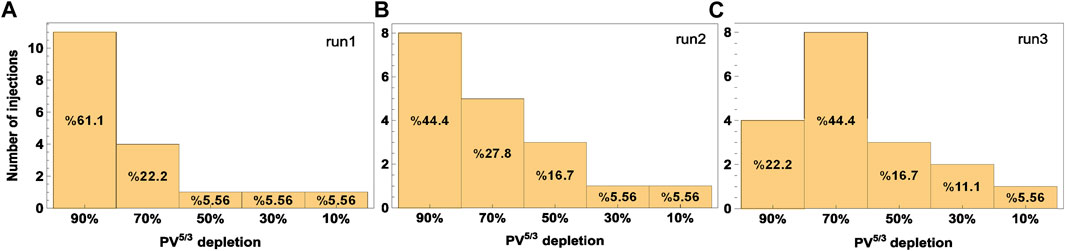
FIGURE 1. The three RCM simulations denoted by labels (A, B), and (C) and based on profiles of PV^5/3 depletions. In panel (A), which represents run1, approximately 61% of all bubble injections had an average entropy parameter depletion (i.e., d_p) of 90%.

It is worth noting that the magnetospheric particle distribution in the RCM modeling region follows the transport equation (i.e., $\partial η / \partial t + v_{D} . \nabla η = - L$ , where $η$ is the flux tube content, $v_{D}$ is the drift velocity, and $L$ represents the loss rate). The remainder of the setup, which is briefly described below, is identical to that in Paper 1. 1) Our modeling area as mapped to the equatorial plane is an ellipse with the midnight boundary at $X = - 22 R_{e}$ , which is earthward of the average boundary of the open-closed magnetic field lines. Accordingly, we exclude ionospheric high latitudes (including the polar cap region) and the distant plasma sheet in the magnetotail. 2) The number of RCM grid points are $300$ and $270$ in the latitude and longitude directions, respectively. 3) A moderate solar wind condition is applied, i.e., IMF $B_{z} = - 2.5 n T$ , solar wind velocity $V_{X} = - 400 k m / s$ , and solar wind proton number density $N_{S W} = 5 {c m}^{- 3}$ . Such conditions might imply Kp values of ∼3. 4) As shown in Figure 2 and Table 2, the initial plasma moments are prescribed using different empirical models in different regions. $T_{p e}$ expresses the proton-to-electron temperature ratio (i.e., $T_{p} / T_{e}$ ). $P_{M H D}$ yields the initial proton pressure in the regions with plus (i.e., “+” inside $R < 6 R_{e}$ ) and cross (i.e., “ $\times$ ” inside $R = 6 - 10 R_{e}$ ) symbols, according to the force-equilibrium configuration computed in an MHD friction equilibrium code (Lemon et al., 2003). At midnight, the proton temperature at $R = 10 R_{e}$ and geosynchronous orbit is $T_{T M 2003 |_{R = 10}} = 6.16 k e V$ and $T_{G E O} = 7.0 k e V$ , respectively (Denton et al., 2005).

FIGURE 2

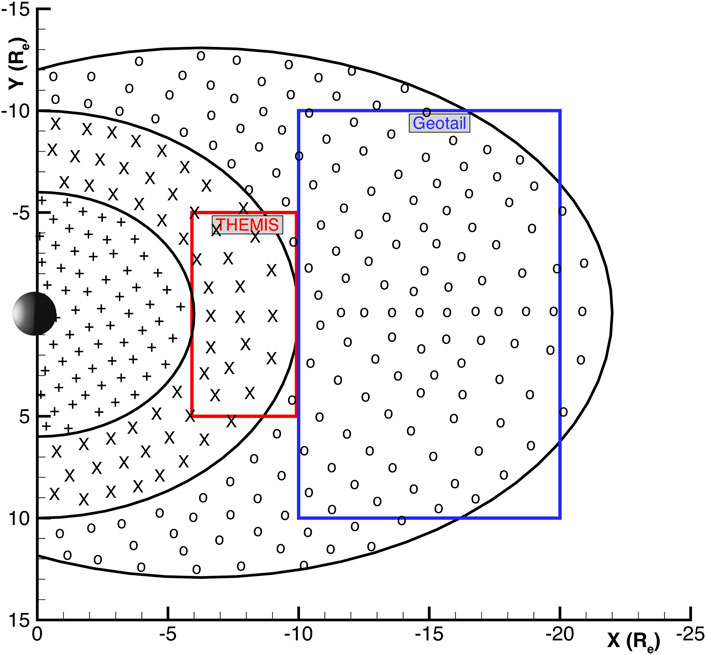
FIGURE 2. Different regions in the equatorial plane, each of which represents a different initial temperature and density distribution. The regions with symbols of circle (i.e., “o” inside $R > 10 R_{e}$ ) and cross (i.e., “ $\times$ ” inside $6 R_{e} \leq R \leq 10 R_{e}$ ) employ TM2003 and DGSR2016 models, respectively. The X-Y domains of the Geotail and THEMIS data used to build the TM2003 and DGSR2016 models, respectively, are represented by blue and red rectangular regions. The Sun is to the left.

TABLE 2

TABLE 2. The initial density and temperature settings inside the RCM modeling region.

3 Results

To demonstrate that our simulation results are consistent with the climatology of the plasma sheet, we compare our obtained results to observational data using two benchmarks. In Section 3.1, we examine the consistency of 1) calculated velocity probability density functions (PDFs) with Geotail and THEMIS observations, and 2) calculated plasma moments with the empirical models DGSR2016 and TM2003. We then analyze geosynchronous plasma moments and fluxes in Section 3.2 and ionospheric FAC distributions in Section 3.3. Note that going forward, all the parameters are averaged twice: once over the course of the 2-h RCM simulation, and then again, over the three RCM runs.

3.1 Constraint validation

Figure 3 compares the simulated PDFs of velocities (within the rectangular-shaped regions in Figure 1) to THEMIS ( $R = 6 - 10 R_{e}$ ) and Geotail ( $R = 10 - 20 R_{e}$ ) observations, using the same selection criteria as in Geotail and THEMIS observations (see Table 2 of Paper 1). Two important characteristics of the RCM calculated velocities are that they are perpendicular to the magnetic field and that they result from the combination of $E \times B$ and diamagnetic drifts. In contrast to the Geotail data, which did not provide perpendicular components of velocities, we compared the RCM calculated velocities with the observed perpendicular components of velocities from THEMIS. Also, it should be noted that the RCM calculated PDFs of velocities are 2-h averages while the data was collected by the Geotail (THEMIS) spacecraft between 1995 and 2005 (2008–2015). The averaged PDFs from three RCM runs make up the final plots that are shown. The boundary conditions were carefully designed to model the fast flows created tailward of the simulation region. The parameters are deliberately tuned in the simulation with BBFs to ensure that 1) the calculated PDFs closely match those from Geotail and THEMIS, and 2) numerical artifacts in the results are minimized. The green curves show that RCM simulations without bubbles cannot reproduce fast flows. Clearly, the integrated effects of plasma bubbles transported from the tail to the central and inner plasma sheet can make PDFs more consistent with the observational data than if no bubble injections are used. The facts that 1) the measurements used to create THEMIS and Geotail observations are taken from actual events, during which AE<100 and Kp<2, respectively, and 2) the RCM simulations are based on highly idealized isolated bubble injections may help to explain some minor differences.

FIGURE 3

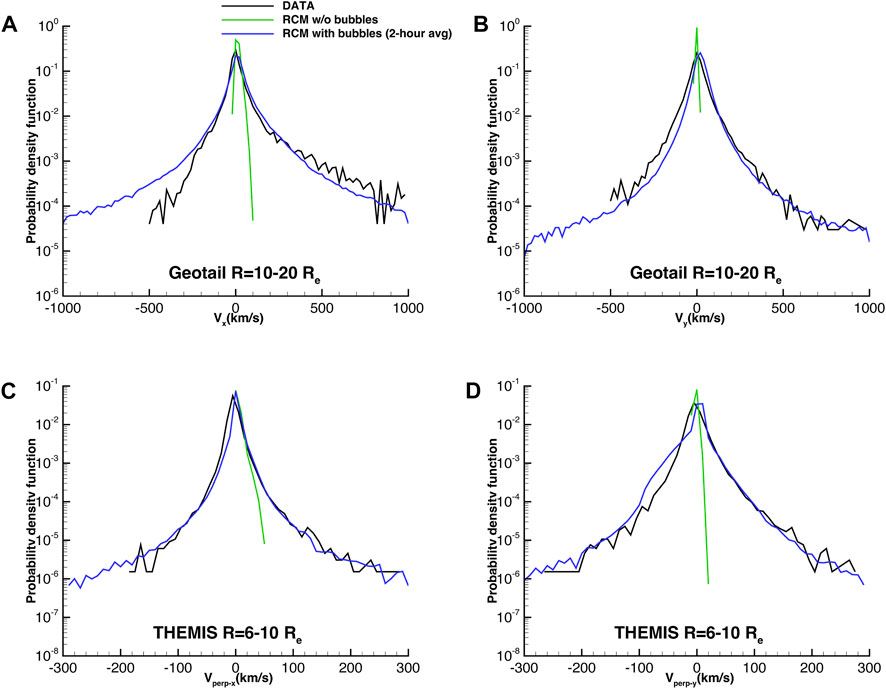
FIGURE 3. The averaged probability density functions (PDFs) of velocities from the RCM simulation with bubbles compared with Geotail observations of (A) $V_{x}$ and (B) $V_{y}$ and THEMIS observations of (C) $V_{⊥ x}$ and (D) $V_{⊥ y}$ . Here, “ $⊥$ ” denotes the velocity perpendicular to the local magnetic field. The green lines show the 2-h average PDFs of the RCM simulation without bubbles.

In Figure 4, we compare the calculated plasma moments to those of the DGSR2016 and TM2003 models along the noon-midnight meridian (i.e., Y = Z = 0) within $- 20 R_{e} \leq X \leq - 5 R_{e}$ . The DGSR2016 model provides the electron moments contributed by particles with energies ranging from 30 eV to 300 keV between $6$ and $10 R_{e}$ . The TM2003 model provides the ion moments contributed by particles with energies ranging from 30 eV to 43 keV between $10$ and $20 R_{e}$ . The RCM results are calculated within these energy and spatial range constraints. It should be highlighted that 1) the RCM was able to capture smooth profiles from the inner magnetosphere to the high latitude boundary, 2) interestingly, under the solar wind conditions characterized by $B_{z} = - 2.5 n T$ , $V_{X} = - 400 k m / s$ , and $N_{S W} = 5 {c m}^{- 3}$ , nearly similar pressure (i.e., ∼0.4 nPa) is predicted at $X \sim - 10 R_{e}$ by the empirical models TM2003 and DGSR2016, 3) the maximum difference between RCM calculated electron and proton moments occurs at $X \sim - 10 R_{e}$ , which are likely a result of energy- and species-dependent gradient/curvature drift, and 4) the RCM generated proton-to-electron temperature ratio ( $T_{p} / T_{e}$ ) at $X = - 10 R_{e}$ is consistent with the THEMIS results (e.g., see Figure 9 of Wang et al., 2020). Although the RCM calculated electron temperature and pressure values are small in comparison to the observed statistics between $\sim 7 - 10 R_{e}$ , our modified initial settings still result in much better agreement between the DGSR2016 model and RCM simulation than Paper 1. One instance where our results show improvement over previous work is in the estimation of temperature, density, and pressure at $X = - 7 R_{e}$ . In Paper1, the RCM calculated values of approximately $4.5 k e V$ , $0.3 c m^{- 3}$ , and $0.25 n P a$ , while we were able to obtain values of $4.2 k e V$ , $0.82 c m^{- 3}$ , and $0.56 n P a$ . These values, when compared to the values of $5.4 k e V$ , $0.95 c m^{- 3}$ , and $0.83 n P a$ from the DGSR2016 empirical model, demonstrate overall better agreement. Our simulation uses an initial condition of a proton-to-electron temperature ratio of 1 at GEO, while the RCM estimates a 2-h average ratio of almost 2 at GEO during moderate solar wind conditions, as seen in Figure 4. While our simulation value is not in perfect agreement with observational results, it does not appear to contradict them. For instance, Wang et al. (2012) observed that the $T_{p} / T_{e}$ ratio varied from around 6–10 during a northward IMF when the plasma sheet was relatively cool to approximately 2–5 during a higher auroral electrojet (AE) value when it was relatively warm, depending on the local time and radial distance from the Earth. Sergeev et al. (2015) used THEMIS data from six tail seasons and found that during periods of BBFs, electrons experience a stronger heating than protons, causing $T_{p} / T_{e}$ to sometimes drop to around 1. Runov et al. (2015) investigated the average thermodynamic properties of the plasma in and around dipolarizing flux bundles (DFB) in the magnetotail using THEMIS data at radial distances between 5 and 25 $R_{e}$ . They discovered that the average $T_{p} / T_{e}$ value was approximately 7 for relatively cold ion populations ( $T_{p}$ < 10 keV), whereas for the hotter ion population and nearer to the Earth (at $R < 12 R_{e}$ ), $T_{p} / T_{e}$ dropped down to around 1.0. It is also worth noting that the “without bubble” profiles were not included in the plots of Figure 4 because we explained in detail how plasma bubbles resolve the pressure-balance crisis in Paper 1. In the absence of bubbles in the inner magnetosphere, the pressure-balance (or more precisely, entropy) crisis occurs when the magnetic field develops a deep $B_{z}$ -minimum with too high plasma pressure compared to observations. Now that the initial and boundary conditions have been successfully implemented, we can present the results of plasma sheet access to geosynchronous orbit and the ionosphere, which are the topics of the following two subsections.

FIGURE 4

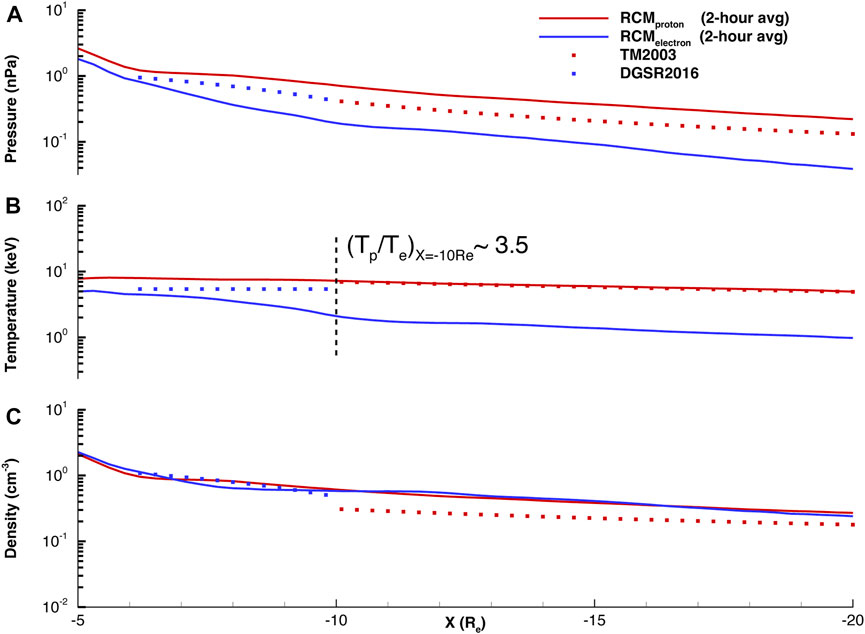
FIGURE 4. The average proton (solid red lines) and electron (solid blue lines) (A) pressure (B) temperature, and (C) density calculated by RCM are compared to the corresponding predictions made by the TM2003 (red dots) and DGSR2016 (blue dots) models. RCM estimates a 2-h average proton-to-electron temperature ratio of ∼3.5 at $X = - 10 R_{e}$ .

3.2 Geosynchronous altitudes

Figure 5 illustrates the average variability of entropy parameter $P V^{5 / 3}$ , total plasma pressure $P$ , magnetic field $B_{z}$ , and moments of protons and electrons with energies ranging from 1 eV to 45 keV near geosynchronous orbit. Because of the gradient and curvature drifts, there are dawn-dusk asymmetries in all of the profiles (except $B_{z}$ ). The MLT location of peaks and valleys in $P V^{5 / 3}$ and $P$ profiles at geosynchronous orbit are typically similar, as shown in Figures 5B, D. Comparing with the initial values (T = 00:00), a continuous plasma bubble injection causes an increase in $P V^{5 / 3}$ and $P$ near midnight. The magnetic field strength is lowest near midnight and increases towards dawn and dusk, indicating a more dipolar magnetic field in those regions. When compared to the initial configuration, the streams of low entropy flux tubes created more stretched field lines near midnight, as illustrated in Figure 5F. The temperature profiles of protons and electrons show maxima around midnight and dawn regions in panels (Figures 5G, H) and (Figures 5M, N), respectively. Note that the proton (electron) temperature exhibits this dawn-dusk symmetry (asymmetry) as a result of the TM2003 (DGSR2016) model’s fundamental assumptions. Figures 5L, R highlight the lack of dawnside (duskside) access for the plasma sheet proton (electron) populations, which is the essence of the magnetic drifts. Based on the product of temperature and density, protons’ (electrons’) pressure profile produces almost similar peak at the dusk (dawn) terminator due to high densities in this region (Figures 5J, P). The distributions of proton and electron moments at geosynchronous orbit are compared with two empirical models derived from observations in the following paragraphs.

FIGURE 5

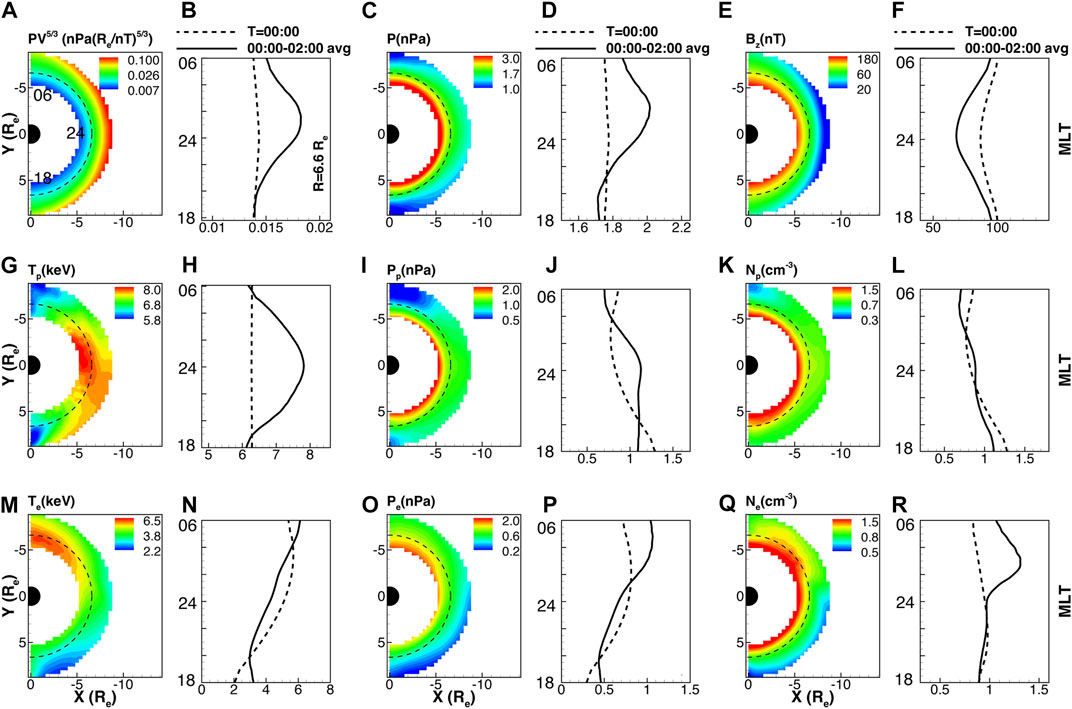
FIGURE 5. Equatorial distribution of RCM calculated (A) entropy parameter $P V^{5 / 3}$ , (C) plasma pressure $P$ , (E) magnetic field $B_{z}$ , and bulk properties (temperature, pressure, and density) of the plasma sheet proton (G,I,K) and electron (M,O,Q) populations. The black dashed line inside the ring-shaped region shows geosynchronous orbit ( $R \sim 6.6 R_{e}$ ). The initial (T = 00:00) and average magnetic local time variation of each parameter along geosynchronous orbit is also shown in separate panels (B,D,F,H,J,L,N,P,R). The Sun is to the left.

Figure 6 compares our Figure 5 results to those from the Magnetospheric Plasma Analyzer (MPA) data onboard the Los Alamos National Laboratory’s (LANL) geosynchronous satellites (Denton et al., 2005). Their analyses include plots of averaged bulk plasma parameters (pressure, number density, and temperature) as a function of Kp and local time. To facilitate comparison, the original plots from Denton et al. (2005) (Figures 6A–F) are adapted and displayed along with RCM results in the smaller windows (labeled with RCM). The RCM’s estimated peak values in hot proton moments are roughly consistent with those measured by the MPA model (Figures 6A, C, E). However, the corresponding MLT locations do not exactly match the observed profiles, nor does a dawn-dusk asymmetry. The RCM calculated proton and electron number densities peak at the dusk and dawn terminators, respectively, whereas the peak proton and electron number densities can be seen around the midnight and midnight-to-post-midnight sectors based on MPA observations. Furthermore, the RCM computed electron temperature and pressure profiles do not satisfactorily fall within the range of the MPA observations. For example, around magnetic midnight, our simulation yields $N_{e} \sim 0.98 c m^{- 3}$ , $T_{e} \sim 4 k e V$ , and $P_{e} \sim 0.65 n P a$ whereas based on Denton et al. (2005) model, $N_{e} \sim 1 c m^{- 3}$ , $T_{e} \sim 2 k e V$ , and $P_{e} \sim 0.3 n P a$ . Factors that may contribute to these differences are: 1) While the RCM provides valuable insights into certain aspects of plasma dynamics, it is not a fully comprehensive model, as it does not account for important phenomena such as diffusion and wave-particle interactions. These processes play a particularly critical role in the inner magnetosphere, where they can induce significant changes in the plasma moments and contribute to dawn-dusk asymmetry (e.g., Thorne, 2010). 2) The MPA data analysis is based on the average of plasma parameters between 1990 and 2001, whereas the RCM calculated profiles are based on the average of 2 hours of simulations, which are oversimplified with initial conditions constructed by empirical models such as DGSR2016, TM2003, and electron and proton loss models. 3) The phases of the solar cycle have been shown to be closely related to overall geomagnetic activity, and as statistical studies have indicated, this may also have an impact on the empirical observational data, potentially contributing to discrepancies with RCM simulation results. 4) The RCM results are in the current sheet, however the MPA observations may be out of the current sheet.

FIGURE 6

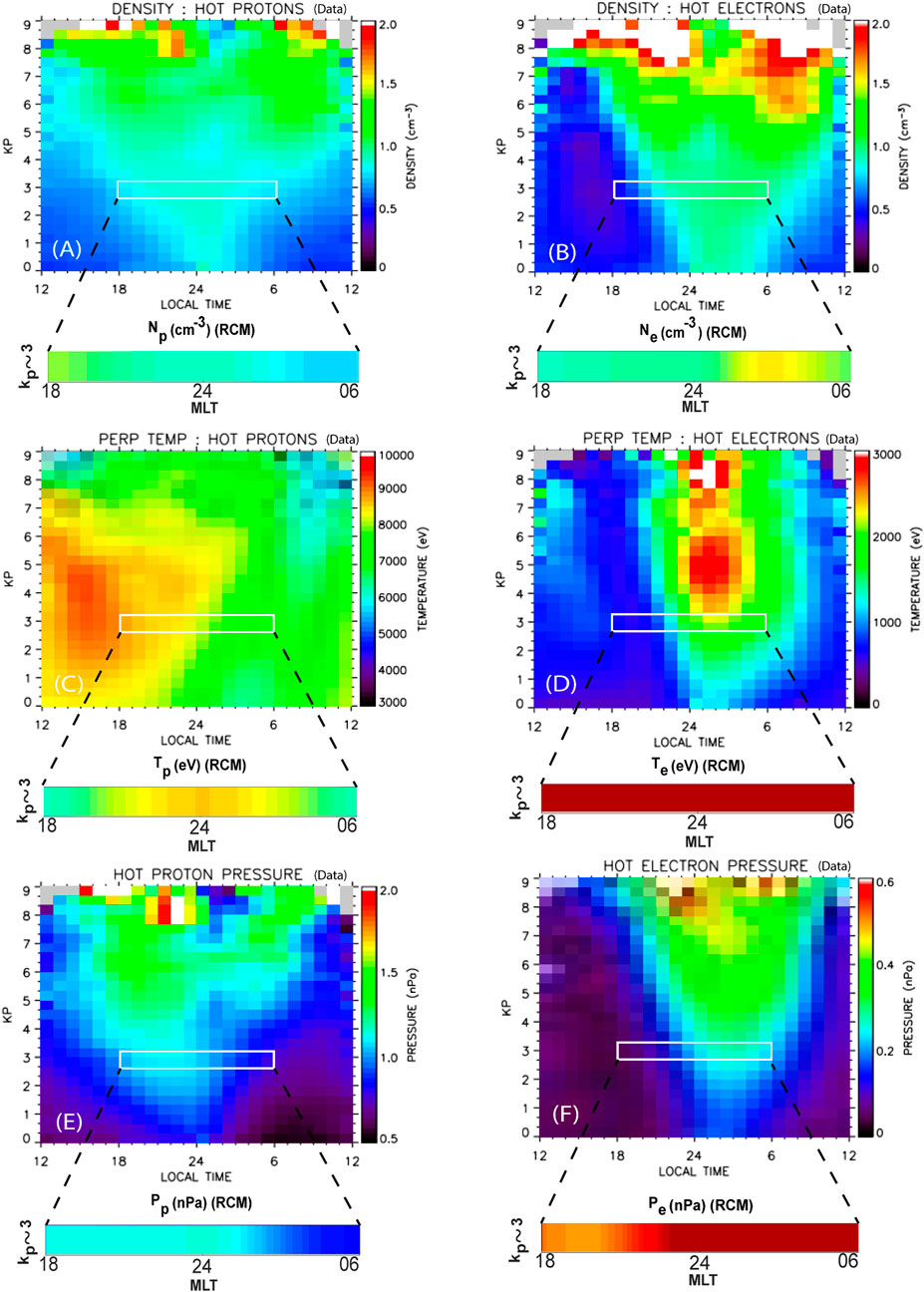
FIGURE 6. The average values of proton and electron (A,B) density (C,D) perpendicular temperature, and (E,F) pressure as a function of Kp index and magnetic local time based on MPA data (Denton et al., 2005) are compared against RCM calculated counterparts. The white box indicates the nightside region (MLT = 18–06) under a moderate geomagnetic condition with Kp∼3. The RCM results are comparable to the data within the white boxes. (A–F) are adapted from Denton et al. (2005).

Lemon and O’Brien (2008) developed an empirical model of bulk plasma properties based on solar wind parameters (e.g., solar wind flow pressure and the interplanetary magnetic field) and MPA data from geosynchronous LANL satellites. The MPA data in their model spans the years 1990–2005, and they have compiled hourly averages of the data during that time. Their model establishes the local time variation of proton and electron densities and temperatures by a user-specified solar wind parameter in the energy range of the MPA instrument, i.e., 1 eV–40 keV. Figure 7 presents the original plots from their model in which data are binned by MLT and IMF $B_{z}$ . The RCM simulation results from Figure 5 are also shown in the smaller windows (labeled with RCM) to facilitate comparisons. Model comparison shows that we could reproduce the protons’ profile, though the electrons’ temperature is still ∼1.5–2 times higher than the observations. Overall, it is far simpler to estimate the moments of protons than the moments of electrons, and the discrepancies that were found could be attributed to modeling issues with plasma sheet electron access to geosynchronous orbit. Another hypothesis is that, when the high energy electrons are abundant, the MPA-based models, which are based on energies up to 40 keV, may underestimate the actual temperature. In addition, the RCM assumes adiabatic electron transport and energization. In this manner, our model does not take into account the interactions between the wave and the particles that are non-adiabatic. Such non-adiabatic processes have been shown to play an important role in altering the electron distribution in several examples (e.g., Horne and Thorne, 1998; Thorne et al., 2010). One other thing worth mentioning is that our RCM simulation is an idealized representation of bubble injection events and might not accurately reflect Kp∼3 characteristics. Additionally, Kp is a 3-hour average parameter, and 3 hours might be very eventful.

FIGURE 7

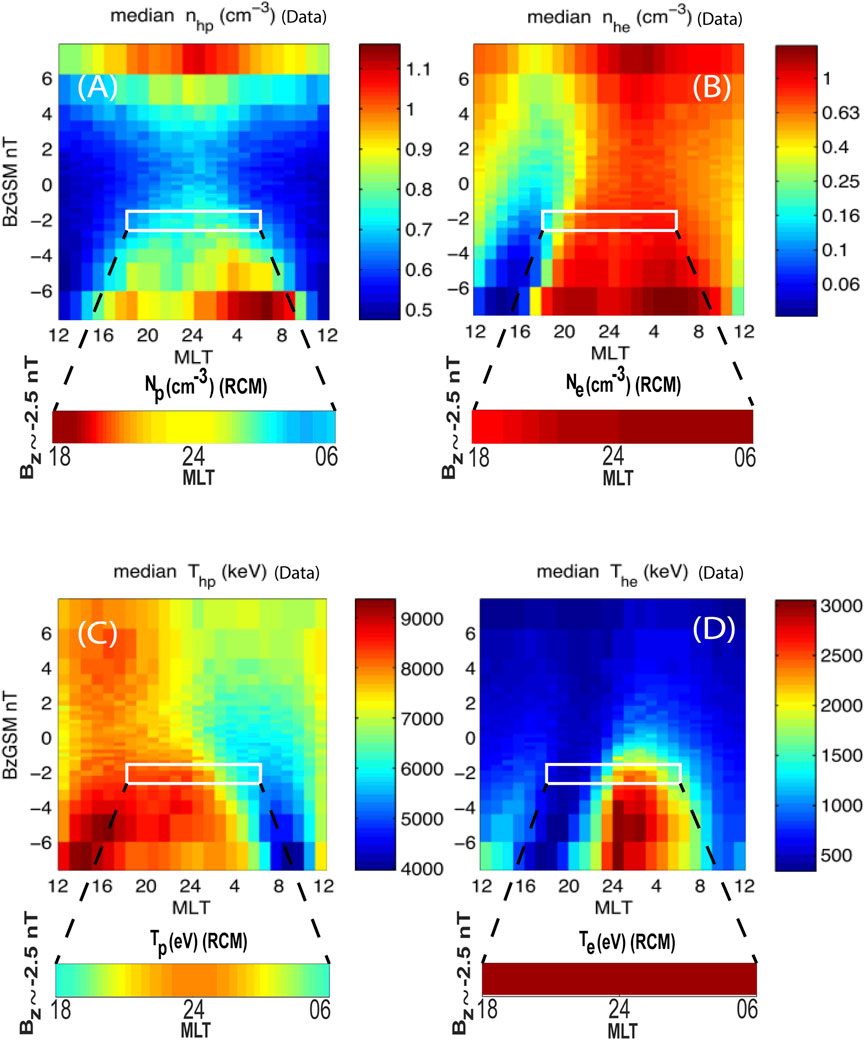
FIGURE 7. The average values of proton and electron (A,B) density and (C,D) temperature as a function of $I M F B_{z}$ and magnetic local time based on MPA data (Lemon and O’Brien, 2008) are compared against RCM calculated counterparts. The white box indicates the nightside region (MLT = 18–06) under the solar wind $I M F B_{z} \sim - 2.5 n T$ . The RCM results are comparable to the data within the white boxes. (A–D) are adapted from Lemon and O'Brien (2008).

Figures 8, 9 show, respectively, the RCM results of averaged differential proton and electron fluxes at different energy channels up to 300 keV near geosynchronous orbit. As with the moment profiles, the dawn-dusk asymmetry in proton and electron differential fluxes persists (e.g., Korth et al., 1999; Jordanova et al., 2006). In general, the energy-dependent proton and electron fluxes tend to be enhanced at dusk and dawn sectors, respectively. The high-energy plasma sheet protons follow gradient/curvature drift paths and can access the dayside through the dusk. However, low energy protons (i.e., 5–10 keV), as shown in Figure 8D, exhibit a dawnside shift in the differential flux profile. In fact, protons with energies ranging from a few eV to several keV $E \times B$ drift dawnward and are frequently observed in the postmidnight and dawn sectors (Yue et al., 2017). Furthermore, high energy protons are less likely to reach geosynchronous orbit than low energy protons; for example, the differential flux of protons around local midnight at energies of 5–10 keV is approximately 4.5 orders of magnitude greater than that of protons at energies of 250–300 keV. This implies that for higher energy plasma sheet particles, geosynchronous orbit lies in the region of closed drift trajectory.

FIGURE 8

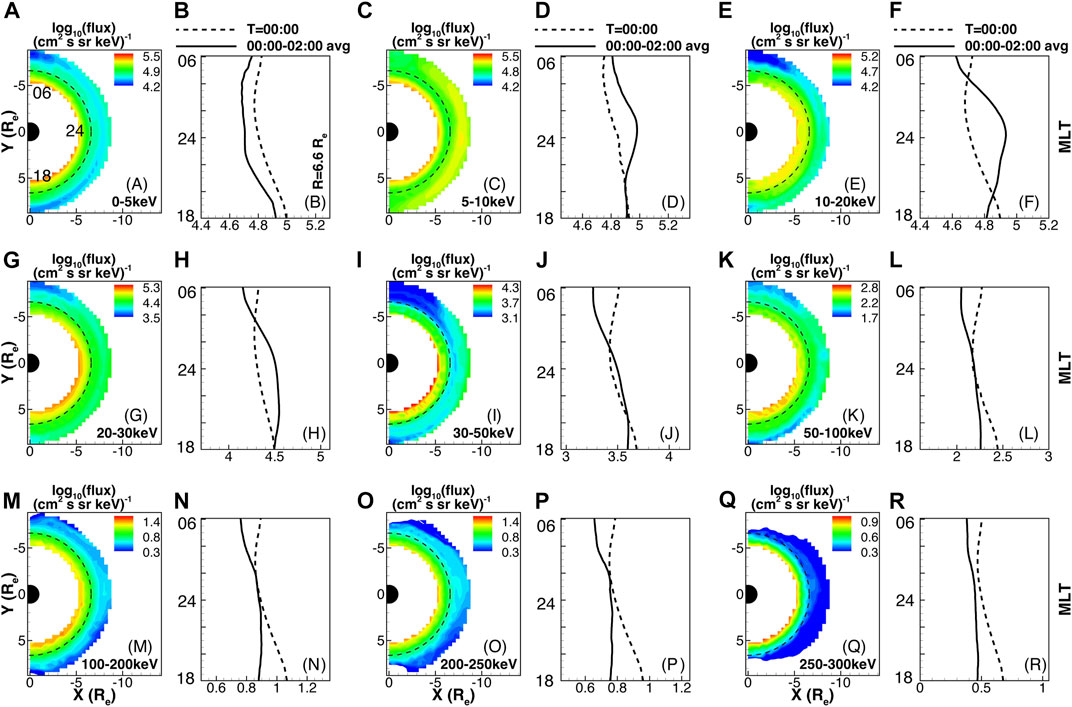
FIGURE 8. The initial (T = 00:00) and average variation of RCM calculated proton differential flux (in $\log_{10}$ scale). The energies are 0–5 (A,B), 5–10 (C,D), 10–20 (E,F), 20–30 (G,H), 30–50 (I,J), 50–100 (K,L), 100–200 (M,N), 200–250 (O,P), and 250–300 keV (Q,R). The magnetic local time variation of each parameter is also shown in separate panels (B,D,F,H,J,L,N,P,R). The black dashed line inside the ring-shaped region shows geosynchronous orbit ( $R \sim 6.6 R_{e}$ ). The Sun is to the left.

FIGURE 9

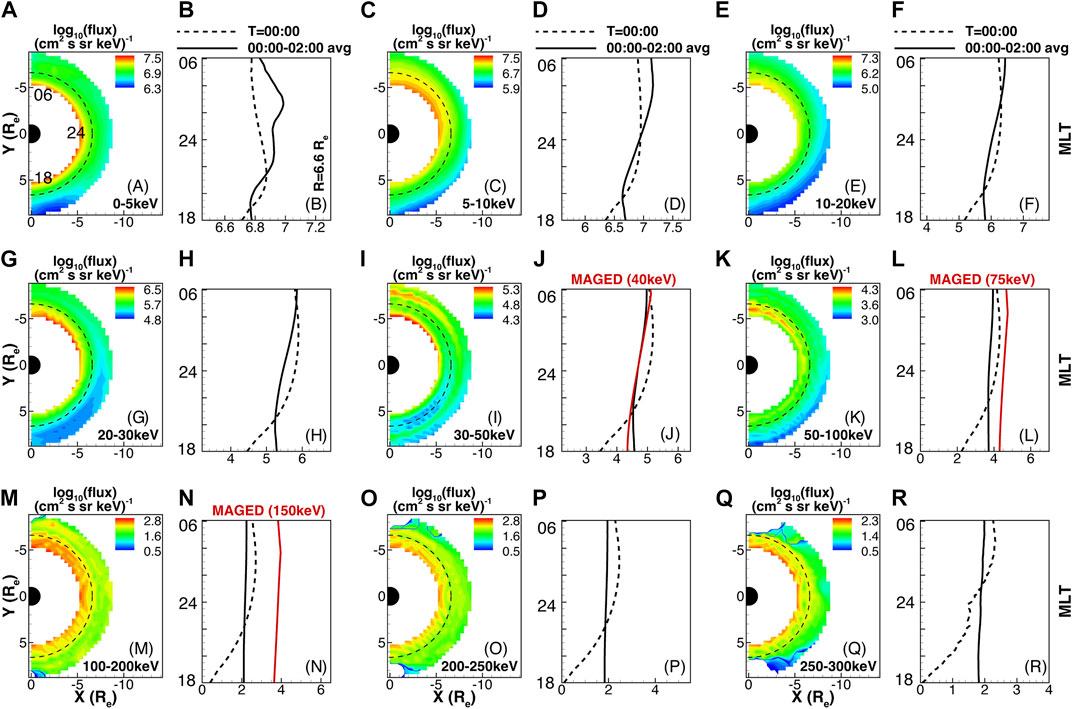
FIGURE 9. Similar to Figure 8, but for electrons. The energy ranges considered are as follows: 0–5 (A, B), 5–10 (C, D), 10–20 (E, F), 20–30 (G, H), 30–50 (I, J), 50–100 (K, L), 100–200 (M, N), 200–250 (O, P), and 250–300 keV (Q, R). The empirical model of electron flux at energies of 40 (J), 75 (L), and 150 keV (N), based on GOES-13 MAGED data are also displayed as red lines using the empirical equation 3 from Sillanpää et al. (2017).

The low energy electrons (i.e., a few keV) are mostly governed by the corotation electric field, resulting in a counterclockwise motion of the electrons around the Earth. Thus, the flux dominated by the lower energy tail of the plasma sheet electrons is elevated near the dawn sector (e.g., Figures 9B, D). On the other hand, the high energy electrons, which are influenced by the gradient/curvature drifts, flow westward along closed drift paths. We also compared the RCM calculated electron differential fluxes at geosynchronous orbit to measurements from the Geostationary Operational Environmental Satellite (GOES-13) MAGnetospheric Electron Detector (MAGED) instrument at three energies of 40, 75, and 150 keV, shown in Figures 9J, L, N (Sillanpää et al., 2017). It should be noted that the MAGED energy values are the midpoints of three energy ranges (i.e., 30–50, 50–100, and 100–200 keV). The RCM computed differential electron flux shows reasonable consistency with those of the empirical flux at the energy channels of 30–50 (Figure 9J) and 50–100 keV (Figure 9L). The simulated flux at energies of 150 keV is lower than that of the MAGED model, most likely due to the exclusion of near-Earth wave-particle interactions. The differential fluxes of electrons at energies of 40, 75, and 150 keV simulated by RCM (measured by MAGED) in $\log_{10}$ scale near geosynchronous region at local midnight (MLT∼24 h) are $\sim$ 4.7 (4.7), 3.75 (4.5), and 2.2 (3.5) ${(c m}^{2} s s r k e V))^{- 1}$ , respectively. The MAGED electron flux empirical model was developed based on quantitative analyses of data over a 5-year period (2011–2015). According to Sillanpää et al. (2017), the highest (∼0.6) and lowest (∼0.4) correlation coefficients between their model and data are found at energies of 40 and 150 keV, respectively.

In addition, as shown in Figure 10, we compared the electron and proton differential fluxes in the RCM simulation to those in the Denton et al. (2015) model along geostationary orbit. Their model which is based on measurements from the LANL/MPA at geosynchronous orbit between 1990 and 2007, provides mean flux of electrons and protons with energies ranging from 1 eV to 40 keV as a function of local time, energy, and geomagnetic activity. Figure 10 shows the original plots adapted from Denton et al. (2015) (Figures 10A, B), as well as the RCM calculated fluxes indicated on the smaller red windows by dashed lines. Comparisons are made through the nightside sector (i.e., 18–06 MLT) and the flux and energy values are expressed in $l o g_{10}$ scale. The MPA-based model and RCM simulation differential energy flux profiles show a dawn-dusk asymmetry, particularly for the high energy plasma sheet electrons that can reach geosynchronous orbit via open drift paths during times of moderate magnetic activity. Overall, the agreement between the LANL-based model and RCM is acceptable, but not perfect. Despite the differences between our results and those of the LANL empirical model, neither has an advantage over the other. According to Denton et al. (2015), their model is more accurate at noon than at midnight in predicting electron fluxes measured by AMC-12/Compact Environmental Anomaly Sensor II (CEASE-II). Note that the RCM simulation does not include the dynamics of very low-energy (i.e., energies of eV) plasma sheet electrons as they are primarily lost through their precipitation along the magnetic field lines into the Earth. Our work has not addressed the spectra of electrons and protons with very low energies.

FIGURE 10

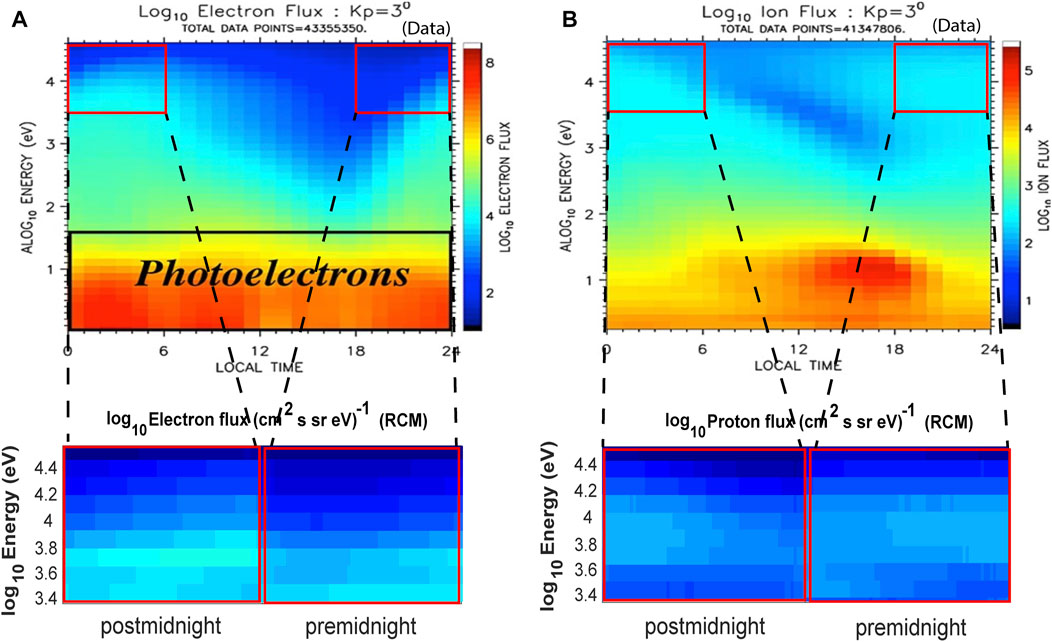
FIGURE 10. The mean (A) electron and (B) ion flux as a function of energy and magnetic local time based on MPA data (1990–2007) are compared against RCM calculated counterparts. The red boxes indicate the nightside region (i.e., premidnight with MLT = 18–24, and postmidnight with MLT = 24–06) with energies between $3 k e V$ and $40 k e V$ ( $\sim 3.5 - 4.5$ in $\log_{10}$ scale). The RCM results are comparable to the data within the red boxes. (A,B) are adapted from Denton et al. (2015).

Denton et al. (2019) used Cluster/RAPID data to develop another empirical model for electron fluxes in the equatorial plane from $6 - 20 R_{e}$ . Their model predicts the electron fluxes in the energy range of ∼45 eV–325 keV as a function of local time, radial distance from the Earth, and Kp index. Figures 11A, B show, respectively, the original electron fluxes adapted from Denton et al. (2019) in the energy channel of 128–244 and 95–128 keV, with the mean energy of ∼185 and 110 keV. The smaller windows on the left show the RCM’s averaged electron flux at radial distances of $\sim 6 - 10 R_{e}$ . The RCM is capable of predicting electron fluxes for the 128–244 and 95–128 keV energy channels up to approximately $3$ and $4 {(c m}^{2} s s r k e V^{)})^{- 1}$ (in $l o g_{10}$ scale), respectively, near GEO and across a wide range of local times. We can therefore conclude that the RCM outputs and their data-driven model near GEO are reasonably similar, but not identical. Furthermore, Figure 11C [also adapted from Denton et al. (2019)] compares the electron flux at an energy of 40 keV at GEO for Kp = 2 using the Cluster/RAPID model (Denton et al., 2019) to the LANL/MPA electron flux model (Denton et al., 2015). The RCM electron flux in the energy range of 35–45 keV (with a median energy of 40 keV) along geosynchronous orbit is also shown in green in this panel. Note that the dayside (i.e., MLT = 06–18) RCM results are not addressed in this work. The comparisons point out that first, there are some differences between Cluster/RAPID and LANL/MPA data-driven models near local midnight, and second, despite the fact that the RCM results are derived from idealized solar wind conditions and data averaging, the quantified electron flux is consistent with LANL/MPA empirical models. It is worth noting that the differences observed between the RCM and Denton’s results in Figure 11C could be attributed to the use of Kp = 2 data in Denton’s plot, whereas the RCM assumed a Kp∼3 solar wind condition. Nevertheless, any potential changes in the parameters due to a shift in Kp from 2 to 3 (or vice versa) are expected to be relatively minor.

FIGURE 11

FIGURE 11. The equatorial distribution of mean electron flux from Cluster/RAPID observations at the energy range of (A) 185 keV, and (B) 110 keV. On the left, the RCM computed average electron flux at the same energy range are shown. The pink region indicates the nightside region (MLT = 18–06) and radial distances of $R = 6 - 10 R_{e}$ . The RCM results are comparable with data lying within this ring-shaped region. (C) The magnetic local time variation of mean electron flux derived from MPA (blue circles) and Cluster/RAPID (red circles) observations versus the RCM computed average electron flux (green line) at $R = 6.6 R_{e}$ . For the Cluster data, the median, upper, and lower quartiles are also shown by dashed/dotted red lines. (A–C) are adapted from Denton et al. (2019).

3.3 Ionospheric response

In the following section, we show the important role of bubbles on the dynamics of the ionosphere, with a particular importance given to the ionospheric FACs, $E \times B$ drift flows, and the electron precipitation energy flux. Understanding the spatio-temporal characteristics of these variables can also provide insight into auroral morphology. Figure 12 depicts the probability density function (PDF) of FAC intensities in the nightside ionosphere between magnetic latitudes $55 ° - 75 °$ . In this paper, we use the terms “moderate” ( $\leq 1 μ A / m^{2}$ ) and “intense” ( $> 1 μ A {/ m}^{2}$ ) to describe the large-scale and meso-scale FACs, respectively. The terminology used here is consistent with the criteria ( $\geq 1 μ A / m^{2}$ ) used by Ochieng et al. (2019) to identify occurrence of meso-scale FACs. The meso-scale structures are believed to be embedded within the much larger scale FACs. These large- and meso-scale FACs developed during a 2-hour simulation of random bubble injections into the inner magnetosphere. If we divide the average RCM modeled FAC uniformly into $80$ bins, each with a width of 0.25 $μ A / m^{2}$ , then about 89% of the FACs are estimated to be upward and downward meso-scale FACs (i.e., |FAC| $> 1 μ A / m^{2}$ ), while only ∼11% of total currents are moderate (i.e., |FAC| $\leq 1 μ A / m^{2}$ ). It is worth mentioning that meso-scale FACs are probably a combination of both meso-scale and large-scale FACs. This is because various factors, including the solar wind, ionospheric conductivity, and the Earth’s magnetic field, can affect meso-scale FACs locally and globally. Consequently, the estimated meso-scale FACs may not only be the result of local influences but also of larger-scale features. Figure 13 further clarifies the local time distribution of FACs in the ionosphere. As can be seen, 1) the meso-scale FACs can reach a strength of $\sim 10 μ A / m^{2}$ in the nightside ionosphere (Figures 13B, D), and 2) the FAC intensities in the dayside ionosphere do not exceed $\sim 5 μ A {/ m}^{2}$ and are primarily attributed to the large-scale counterparts (Figures 13A, C).

FIGURE 12

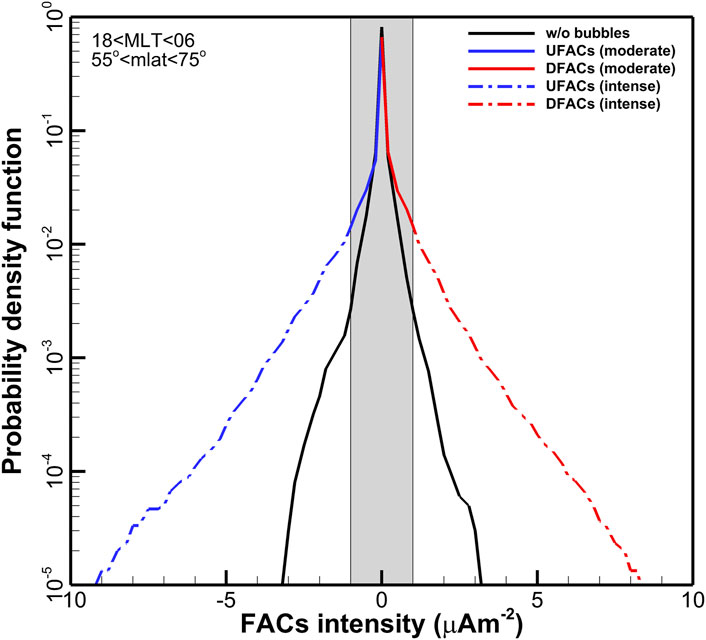
FIGURE 12. The RCM calculated average probability density function of FACs in the nightside ionosphere between $55 °$ and $75 °$ magnetic latitude. The solid (dash-dotted) lines represents large-(meso-) scale FACs. The blue (red) color indicates upward (downward) FACs (labelled UFAC/DFAC). The inside (outside) of the gray rectangular region defines the large-scale (meso-scale) FACs. The solid black curve represents PDF of FACs in the simulation without plasma-sheet bubbles.

FIGURE 13

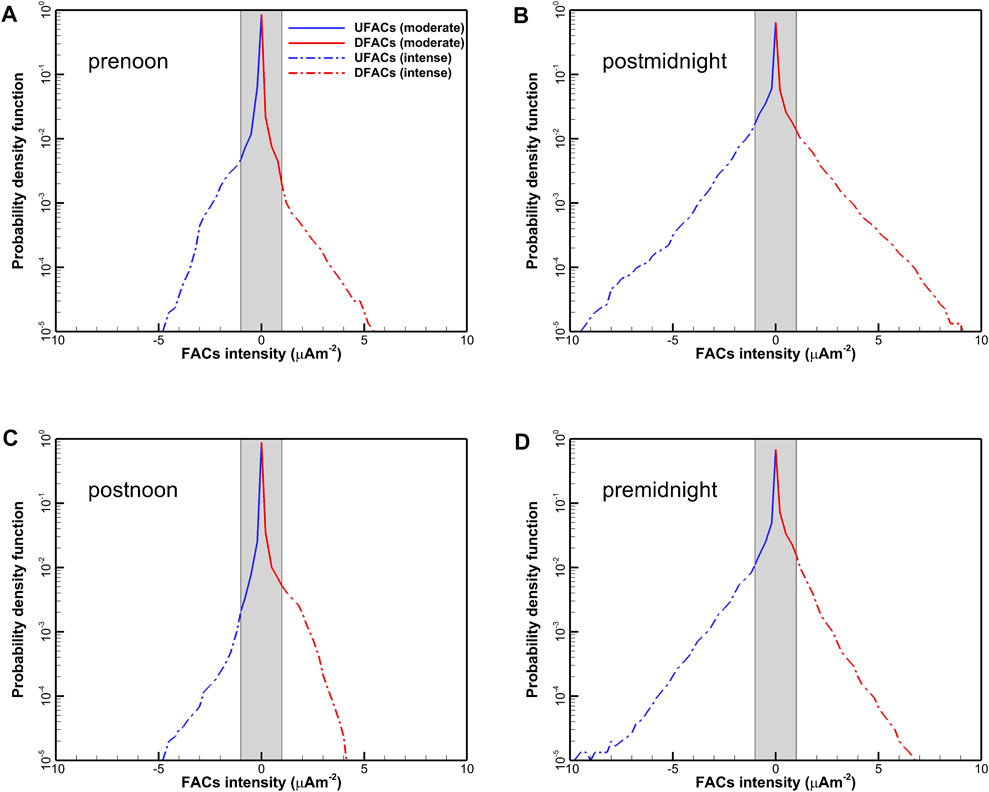
FIGURE 13. The averaged RCM calculated probability density function of FACs in different MLTs of the polar ionosphere; (A) 06–12, (B) 24–06 (C) 12–18, and (D) 18–24 MLT. The solid (dash-dotted) curve represents large-(meso-)scale FACs. The blue (red) color indicates upward (downward) FACs (labelled UFAC/DFAC). The inside (outside) of the gray rectangular region defines the large-scale (meso-scale) FACs features.

Figure 14 shows the average ionospheric $E \times B$ drift velocities, electric field, FAC intensity, and electron precipitation energy flux in the nightside ionosphere. Given that there should be a significant enhancement in FACs within the auroral oval, the equatorward and poleward boundaries of the auroral oval in the midnight sector are approximated to be at $64 °$ and $70 °$ latitudes, respectively, in this study. Highly asymmetric and complex structures are simplified into much smoother FACs and energy flux intensities of $\sim \pm 1 μ A / m^{2}$ and $\sim 8 e r g c m^{- 2} s^{- 1}$ , respectively, through averaging. The eastward and westward ionospheric flows can reach velocities of ∼400 m/s, as indicated by colored arrows in Figure 14A. Figure 14B depicts equatorward (poleward) ionospheric electric field vectors with an average strength of $≲$ 20 mV/m in the dawn (dusk) sector. Figure 14C clearly illustrates that the FAC system produced in the RCM below $70 °$ latitude can be divided into: 1) the equatorward region-2 premidnight downward (postmidnight upward) currents; 2) the poleward region-1 premidnight upward (postmidnight downward) currents. The FACs orientation and latitudinal location in our simulation also appear to be consistent with the classic distribution of FACs. Figure 14D illustrates the average modified precipitation energy flux ( $f_{e n}^{*}$ ) calculated using the postprocessing procedure described in Yang et al. (2012). The nightside is dominated by bright discrete auroral structures associated with large upward FACs. Auroras of this type are frequently observed in the evening sector of the ionosphere and tend to drift to the equator. As shown in Figure 14D the regions of the enhanced $f_{e n}^{*}$ are correlated with those of increased $E \times B$ velocity and intensified electric field. There are several points that highlight the roles and relationships among different input parameters:

FIGURE 14

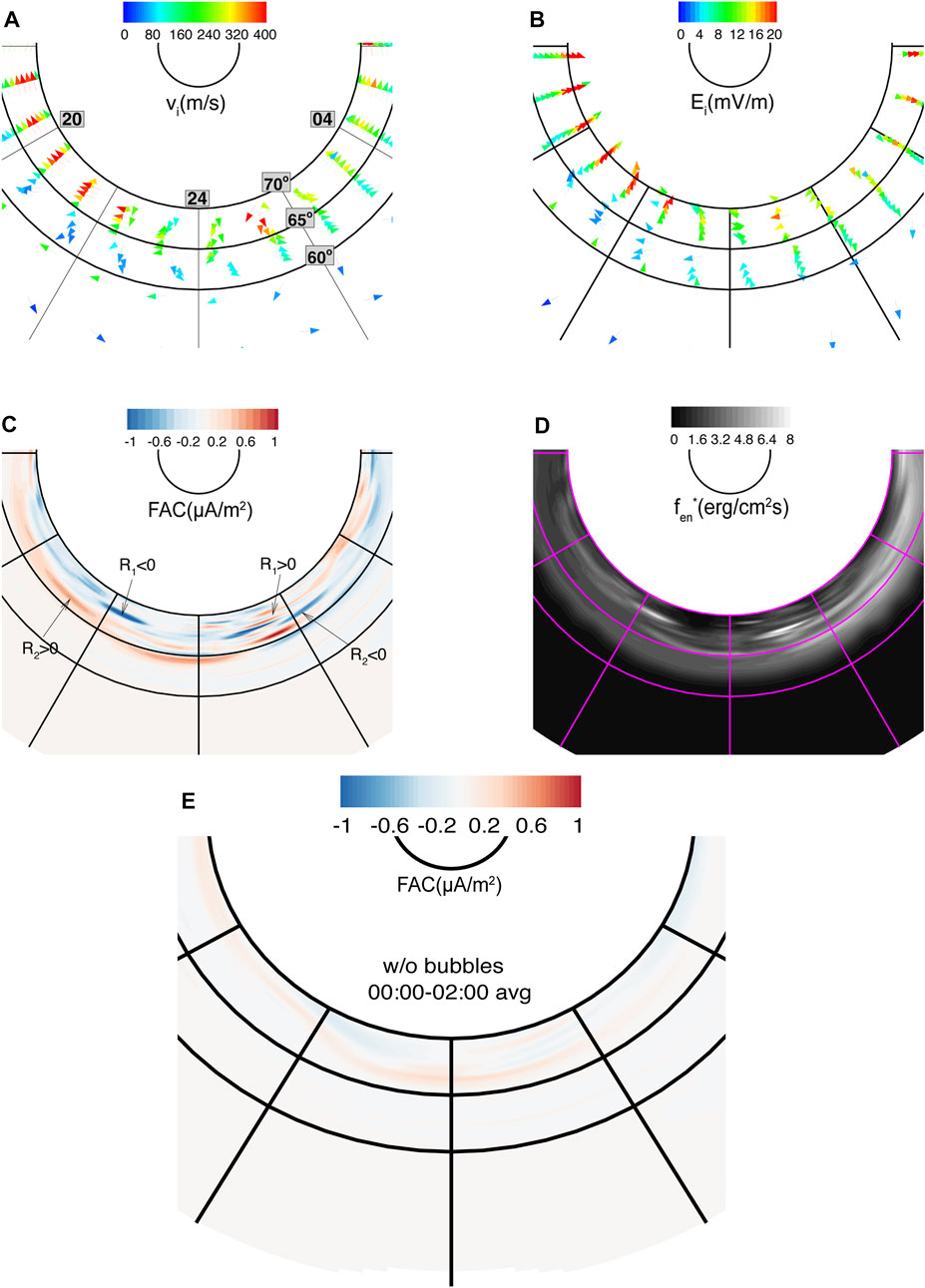
FIGURE 14. The average distribution of ionospheric (A) $E \times B$ drift velocity (B) electric field, (C) FACs with bubbles (D) electron precipitation energy flux, and (E) FACs without bubbles. The solid lines in the magnetic latitude (MLat) and magnetic local time (MLT) directions are spaced at $5 °$ and $2$ hours, respectively. The region-1 and 2 (R1 and R2) sense FACs are also shown in (C). Note that the velocity and electric field vectors are plotted in the corotating frame.

First, when the bubbles are not launched (Figure 14E), the distribution of current systems is smoothed, and we can see the peak intensity of a confined premidnight downward region-2 currents.

Second, when bubbles are imposed through the RCM tailward boundary, they are initially elongated along the Sun-Earth direction due to $E \times B$ drift. As the bubbles approach the transition region, where the azimuthal gradient/curvature drifts become dominant, upward FACs develop associated with gradients of pressure and $P V^{5 / 3}$ .

Third, a depleted bubble can result in two ionospheric manifestations: a streamer at the westward edge of the bubble as it moves earthward in the plasma sheet, and a subsequent thin arc associated with the disruption of the $P V^{5 / 3}$ profile near the plasma sheet inner edge when the bubble reaches the magnetic transition region. This mechanism for creating a thin arc is only effective if the bubble is able to reach the magnetic transition region. We consider it essential to expound on several observational and modeling results that corroborate the existence of thin, elongated arcs aligned in an east-west direction, as observed in our simulation. Prior research (e.g., Henderson et al., 1998) proposed a relationship between auroral streamers and BBFs. Auroral streamers are linked to a BBF in the plasma sheet, with the streamer’s development corresponding to the flow channel’s earthward expansion (e.g., Zesta et al., 2000). The streamer connects to the flow channel through a pair of upward and downward FACs, which were predicted by the bubble model of Chen and Wolf (1993). Zesta et al. (2002) discussed poleward boundary intensifications (PBIs) and the emergence of north-south or east-west-oriented structures propagating equatorward. They observed that east-west events consist of a series of narrow east-west arcs formed near the separatrix that move equatorward. Nishimura et al. (2010) presented a large statistical set of both north-south and east-west auroral streamers, where north-south-oriented streamers transformed into east-west arcs in many cases when nearing the growth phase arc. Mende et al. (2011) concluded that a group of east-west oriented thin arcs appear before substorm onset. Yang et al. (2014b) observed the formation of bright thin aurora arcs in RCM-E simulations, consistent with observational studies in Yao et al. (2013). They demonstrated that a single bubble injection could result in a north-south-aligned auroral streamer followed by a thin arc. Another aspect to consider is that adding a current loop to the substorm current wedge can bring about substantial changes in the magnetosphere-ionosphere mapping. While the twisting of magnetic field lines around upward and downward currents is responsible for some of the azimuthal deflection of auroral streamers that approach diffuse auroras, true flow deflection in the azimuthal direction could also contribute to this effect. This has been discussed in previous studies such as Nikolaev et al. (2015) and related references.

We hypothesized that a high number of bubble injections could hinder the formation of streamers. The injection of bubbles into the plasma sheet can cause disturbances that affect the conditions required for streamer formation. Moreover, subsequent bubble injections might increase the brightness of preexisting thin arcs aligned in the east-west direction or trigger the formation of new ones. In our simulation, the ionospheric footprints of deformed bubbles are observed as only thin arcs that propagate in the east-west direction, and we do not observe the streamer-arc sequence. Despite the fact that a significant fraction (at least 50%) of bubble injections in our simulation exhibit a high degree of depletion (70% and more), the lack of a streamer propagating towards the equator (associated with the first bubble) and the presence of thin arcs extending in the azimuthal direction could also be attributed to inadequate depletion within that particular bubble and weak dipolarization.

Fourth, our method for calculating the energy flux of precipitating electrons is relatively simple and may result in the production of artificially bright synthetic aurora patches in areas where the upward FAC is strong. It is important to note, however, that a strong FAC does not always correspond to a strong energy flux in the ionosphere. The global configuration of the FACs, including the presence of field-aligned potential drops (FAPDs), can play a significant role. During the substorm expansion phase, for example, strong FAPDs can cause the FACs to become stronger, even if the energy flux is not particularly high. The Supplementary Material contains Supplementary Video S1 illustrating the evolution of plasma sheet entropy, pressure, current system, and synthetic aurora in run3 over a period of 2 hours.

4 Discussion and conclusion

This paper presents a data-model comparison of average bulk plasma properties near geosynchronous orbit and simulation of FACs in the ionosphere. The RCM model is used to study how the transport of transient meso-scale structures interacts with large-scale convection in the formation and electrodynamics of magnetosphere-ionosphere (M-I) coupling. We utilized the Inertialized version of the RCM (Yang et al., 2019) to examine the effects of MLT-dependent sporadic plasma bubble injections on the average configuration of the M-I coupled system. We believe that the current simulation results are much more realistic in this regard than previous RCM studies because the boundary conditions have been improved and, more importantly, time-dependent inertial effects due to bubble injections have been included. However, some major discrepancies between RCM simulated moments and fluxes and statistical models derived from MPA and MAGED data need to be discussed further. First, Figures 6, 7, 9 demonstrated that our RCM simulation could only produce acceptable quantitative average values. Second, the RCM-generated results could not reflect the observed general dawn-dusk asymmetry. Third, the RCM simulation yields an electron population temperature at GEO that was substantially different from the MPA data-driven model. Comparing Figures 6D, 7D, it is also interesting to see that even two MPA-based empirical models for electron temperature [i.e., T_e (MLT, Kp) and T_e (MLT, $B_{z}$ )] produced different outcomes within the white rectangular at MLT ∼24–04. The origins of the aforementioned discrepancies are not obscure and can be related to the following processes:

1. There are cold plasma components coming from the flanks that we are missing (Wang et al., 2010). These populations may enter the magnetosphere via Kelvin-Helmholtz (KH) instability or diffusion, contributing to lower T_e and some dawn-dusk asymmetry. Wang et al. (2010) showed that diffusive transport caused by flow fluctuations is a decisive factor in changing plasma number density and temperature. We did not include diffusive transport in our simulation. Wang et al. (2001) also discussed the contribution of cooler plasma components entering from the low latitude boundary layer.

2. In the RCM simulations, we assume that particles are subjected to strong elastic collisions to maintain the isotropy of the distribution function without changing their energies. But the electrons are not isotropic in the inner magnetosphere, and different kinds of wave-particle interactions are also MLT dependent (e.g., see Figure 1 of Thorne, 2010).

3. There have been reports of microinjection clusters from dusk to midnight (e.g., Fennell et al., 2016). These injections are not isotropic and are frequently observed in the presence of fluctuating magnetic fields. While they may contribute to the difference in electron temperature and dawn-dusk asymmetry, the RCM is not capable of modeling them.

4. The current RCM simulation excludes ion outflows from the ionosphere (Dandouras, 2021). However, even during quiet periods, a large number of cold plasma outflows may affect the magnetosphere.

Having said that, and having made it clear that considerable improvements are still needed to accomplish satisfactory simulations, here is a quick summary of the most important findings from this study:

1. Comparisons of RCM-computed average pressure, temperature, and density with observation-based empirical models TM2003 and DGSR2016 show that the properties of the plasma sheet populations with access to the inner magnetosphere and GEO derived in this work are more consistent with previous empirical models than those in Paper 1. The electron loss model developed by Orlova et al. (2014) delivers much better agreement between the RCM and the DGSR2016 model, though it is not perfect. Nonetheless, the imperfections are most likely due to our simulation’s inability to account for complex processes, such as wave-particle/wave interactions, diffusion, ion outflows, etc. The moment profiles of protons along GEO agree with two empirical models (Denton et al., 2005; Lemon and O’Brien, 2008) built upon the LANL MPA data, supporting our RCM simulation. However, the RCM calculated moment profiles of electrons along GEO differ from those obtained through the empirical models because the dynamics of high energy electrons in the near-Earth plasma sheet cannot be determined precisely by RCM physics alone, indicating the need for more comprehensive models and initialization.

2. As computed by RCM, the average differential fluxes of particles at different energy levels for both ions and electrons partially match those derived from MPA, Cluster, and MAGED models. RCM results of differential fluxes differ most from observations when compared qualitatively. This is due to our use of a highly idealized simulation, whereas the satellite-based models analyze their statistics using realistic settings and over the years. The access of the average plasma sheet to geostationary orbit is highly dependent on particle species, energy, and geomagnetic activity. During a moderate geomagnetic activity (e.g., Kp∼3), the Alfvén boundary moves closer to the Earth, exposing GEO to the plasma sheet particles almost at all local times (LT). The LT distribution of electrons across all energy channels is similar, whereas low (high) energy protons are more likely to be inclined at dawn (dusk). This is because the electric and magnetic fields cause the electrons to drift in the same direction, whereas the electric (magnetic) field controls the transport of low (high) energy protons from the tail.

3. In the ionosphere, the intensity and distribution of the FACs as simulated by the RCM resemble the classic description of the Iijima-Potemra current system. Furthermore, the inclusion of multiple bubble injections during the 2-hour simulation has resulted in region-1 and 2 sense FACs covering a broader latitude range, in contrast to the narrow FAC structures observed in a simulation without bubbles. When it comes to the average pattern and strength of the eastward/westward plasma flows ( $E \times B$ ) and the poleward/equatorward electric fields in the ionosphere, observations and simulations are somewhat consistent. The probability density function (PDF) of FACs indicates the presence of more intense and structured FACs associated with bubble injections. However, the probability density of FACs in the ionosphere resulting from RCM needs further investigation. Applying statistical analyses to the magnetic field data measured by, for instance Defense Meteorological Satellite Project (DMSP) satellites would be one way to evaluate the probability of occurrence of ionospheric FAC in RCM and improve our data-model comparison. There are several theories regarding the generation of FAPDs (Borovsky, 1993). One theory proposes that FAPDs help to maintain the continuity of auroral FACs against the mirror force exerted on the energetic electrons. Theories have been developed to examine the relationship between upward FACs and FAPDs (Lyons et al., 1979; Fridman and Lemaire, 1980; Khazanov et al., 1998). According to Lyons et al. (1979), auroral observations made from rocket flights have shown that the energy flux of precipitating electrons usually changes depending on the electric potential difference, with FACs typically being proportional to the corresponding FAPDs. However, some observational evidence shows disagreement between the observed FACs and Knight’s model current (Knight, 1973). This discrepancy is attributed to the contribution of low-energy electrons to the current, which is not considered in Knight’s model that only takes into account the interaction of high-energy electrons (e.g., see Morooka et al., 2004 and references therein). Another group of theories attributes the presence of parallel electric fields to the appearance of anomalous resistivity in intense FACs and that unstable FACs are the origin of FAPDs (Haerendel, 1994). In summary, it is crucial to exercise caution when modeling ionospheric FACs realistically, given the ongoing research to comprehend the cause-effect relationship between FAPDs and FACs.

It is worth mentioning that the differences that arose between RCM simulation and either of the empirical models do not necessarily raise doubts about their validity, as the values extracted from each data-driven empirical model are highly averaged and are model-dependent. Another important point is that even data-driven models can only provide a crude description of reality and can differ from one another. Checking the differential flux of 40 keV electrons along GEO using RAPID, MPA, and MAGED models, for example, reveals that they do not produce unique quantitative and qualitative results. As another example, the average plasma moments based on (1991–2001) and (1990–2005) MPA datasets show that the electron temperature at midnight can reach up to ∼2 and ∼3 keV, respectively (Figures 6D, 7D).

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://doi.org/10.5281/zenodo.7478369.

Author contributions

Like a symphony, the collaborative efforts of this team produced a magnificent composition. SS composed the code and conducted the simulations with precision, while JY harmonized with the team in analyzing the simulation results and refining the manuscript. FT, RW, and C-PW contributed their technical expertise and artistic flair during stimulating discussions, inspiring new and innovative ideas. And finally, AM contributed her scientific prowess, conducting thoughtful and insightful discussions that elevated the quality of the work to new heights. All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

The work at SUSTech was supported by grants 41974187 and 42174197 of the National Natural Science Foundation of China (NSFC), the Stable Support Plan Program of Shenzhen Natural Science Fund (Grant No. 20200925153644003), and grant XDB41000000 of the Strategic Priority Research Program of Chinese Academy of Sciences. Work at Rice is supported by NASA HSR grant 80NSSC18K1226 and NASA TMS grant 80NSSC20K1276.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2023.1189298/full#supplementary-material

References

Angelopoulos, V., Baumjohann, W., Kennel, C. F., Coroniti, F. V., Kivelson, M. G., Pellat, R., et al. (1992). Bursty bulk flows in the inner central plasma sheet. J. Geophys. Res. 97 (4), 4027–4039. doi:10.1029/91JA02701