Next-decade needs for 3-D ionosphere imaging

1 Introduction

Accurate specification and modeling of the 3-D spatial variation together with the temporal evolution of Earth’s ionosphere has always been a strong need but a challenging task for the space weather community, as the ionosphere is a highly complicated geospace environment that exhibits not only remarkable climatological variation but also significant weather disturbances. Dynamic ionospheric spatial-temporal variations are ultimately dependent on solar extreme ultraviolet radiation, geomagnetic disturbances, and lower atmospheric waves. These variations can significantly affect radio wave propagation and impose detrimental effects on many modern technological systems, such as shortwave communication, satellite navigation, positioning and timing services, Wide Area Augmentation System (WAAS), and over-the-horizon radars (e.g., Jakowski et al., 2012; Zhang et al., 2017). In an effort to better investigate the dynamic spatial-temporal variation of the ionosphere as well as to mitigate ionospheric error and detriments on civilian and commercial systems, it is important to provide accurate and reliable ionospheric specification and nowcasting, eventually leading to forecast quality products, especially in the 3-D domain. 3-D ionospheric imaging will also help boost the scientific discovery potential to advance the current understanding of cross-scale coupling and modes of response to solar windtransients.

Recent decades have witnessed tremendous steps forward in implementing ionospheric imaging, with the rapid growth of ionospheric data availability from multiple ground-based and space-borne sources. In particular, the growing availability of ionospheric total electron content (TEC) data derived from dense ground-based Global Navigation Satellite Systems (GNSS) receivers has been playing a crucial role in specifying the dynamic features of the ionosphere. The approach also greatly promotes the development of different global and regional ionospheric 2-D imaging maps (e.g., Mannucci et al., 1998; Hernández-Pajares et al., 1999; Schaer, 1999; Fuller-Rowell et al., 2006). However, the substantial variability of the ionosphere can be seen in the vertical domain as well. The altitude variation of the ionosphere is actually an essential feature of any ionospheric structure, and provides important, unique information on ionospheric dynamics (e.g., plasma motion) and thermal configuration (the topside plasma scale height). Scientific understanding of multi-scale ionospheric structures and phenomena, such as the equatorial ionization anomaly (Balan et al., 2018), storm-enhanced density (Foster, 1993), tongue-of-ionization (Foster et al., 2005), polar cap patches (Weber et al., 1984), and the main ionospheric trough (Rodger, 2008), will be significantly advanced through 3-D imaging beyond what is currently known from 2-D TEC information. Moreover, the electron density is certainly the most important parameter from the application perspective since it governs all of the effects on radio signals (Bust and Mitchell, 2008), and the 3-D time-evolving electron density distribution is the most desirable parameter for the above-mentioned radio system applications. In reality, with the continuous increase of multi-instrument ionospheric measurements from diverse sources, such as ground-based GNSS TEC, radio occultation data from low-Earth orbit satellites, global digisonde profiles, incoherent scatter radar (ISR) measurements, in situN_e measurements, and ultraviolet airglow data, recent results have highlighted that 3-D dynamic variations in the ionosphere could be specified through data-based imaging technique, such as ionospheric data assimilation and tomography, to reconstruct 3-D electron density distributions (e.g., Zhai et al., 2020; Aa et al., 2022).

2 Ionospheric imaging approaches

2.1 Ionospheric data assimilation

Data assimilation is intrinsically an optimal state estimation technique, which incorporates a myriad of observations into an existing physical model to obtain a better state estimation (Daley, 1993). Some of the typical optimization methods of data assimilation include recursive estimation techniques, such as Kalman filter and its different derivatives (Kalman, 1960; Kalman and Bucy, 1961; Evensen, 1994), as well as variational techniques such as 3-D/4-D variational algorithms (Barker et al., 2004). Although the data assimilation technique has been traditionally implemented more often in meteorology and oceanography, a great number of data assimilation models have also been developed recently by the ionospheric research community to meet the needs of ionospheric specification (e.g., Bust et al., 2004; Schunk et al., 2004; Yue et al., 2012). For example, the Assimilative Mapping of Ionospheric Electrodynamics (AMIE, Richmond (1992)) is the original physics-based assimilative model that is widely used to study high-latitude ionospheric science. Ionospheric data assimilation can be categorized with respect to different types of background models. These include: 1) Data assimilation on the basis of theoretical ionospheric models. Examples are the Global Assimilation of Ionospheric Measurements built by Utah State University (USU-GAIM) (Scherliess et al., 2004; 2006; Schunk et al., 2004) and the Global Assimilative Ionospheric Model collectively developed by the University of Southern California and NASA’s Jet Propulsion Laboratory (USC/JPL-GAIM) (Pi et al., 2003; Wang et al., 2004; Komjathy et al., 2010). Theoretical models have the advantage of providing physics-based simulation and prediction, yet may be somewhat restricted by the accuracy and reliability of drivers and boundary specification (Jee et al., 2007). 2) Data assimilation on the basis of coupled ionosphere-thermosphere models. Examples include the Coupled Thermosphere Ionosphere Plasmasphere and Electrodynamics (CTIPe) (Codrescu et al., 2018), and the Thermosphere-Ionosphere-Electrodynamics General Circulation Model (TIEGCM, Richmond et al. (1992)) as implemented in the Data Assimilation Research Testbed (DART, Anderson et al. (2009)) (e.g., Lee et al., 2012; Matsuo et al., 2013; Hsu et al., 2014; Hsu et al., 2018; Chartier et al., 2016; Chen et al., 2017; Sutton, 2018; He et al., 2019). It is known that the ionosphere can be strongly adjusted by certain thermospheric parameters, such as neutral winds, temperature, and composition (Buonsanto, 1999). Thus, one major merit of utilizing the coupled thermosphere-ionosphere model to implement data assimilation though with high computation cost is that the updated thermospheric conditions can effectively contribute to a longer timescale of ionospheric state prediction, since the relaxation time of neutral conditions is much slower than that of ionosphere Matsuo and Araujo-Pradere (2011); Pedatella et al. (2020). 3) Data assimilation on the basis of empirical ionospheric models. Examples include the Ionospheric Data Assimilation Three/Four-Dimensional (IDA3D/4D, Bust et al. (2004; 2007); Datta-Barua et al. (2011)), the United States TEC and North American TEC (Spencer et al., 2004; Fuller-Rowell et al., 2006), the Ionosphere Real-time Assimilative Model (Galkin et al., 2012; Galkin et al., 2015), as well as other global and regional assimilation models based on the widely-used International Reference Ionosphere or NeQuick models (e.g., Aa et al., 2015; Aa et al., 2016; Aa et al., 2018; Forsythe et al., 2020a; Forsythe et al., 2020b; Lin et al., 2017; Mengist et al., 2019; Nava et al., 2005; Ssessanga et al., 2019; Yue et al., 2012; 2014). Empirical model-based data assimilation can be readily utilized for ionospheric specification and even operational nowcasting services due to its modest computational cost, yet is limited by insufficient forecast abilities. Therefore, the above-mentioned advantages and challenges continue to drive the ionospheric and space weather community to upgrade data assimilation techniques for better ionospheric imaging.

2.2 Ionospheric tomography

Similar to ionospheric data assimilation, computerized ionospheric tomography is intrinsically an inversion method that allows the 3-D imaging of ionospheric electron density, which is usually based on TEC observations along the line-of-sight rays from ground-based GNSS receivers and low-Earth orbiting (LEO) satellite occultation observations (Austen et al., 1988; Yao et al., 2014). To date, various tomography algorithms have been provided to resolve the ill-posed ionospheric inversion problem due to the insufficient viewing angle of TEC rays and sparse receiver distribution. These algorithms can be generally classified into the following two types: 1) Iterative algorithm. It refers to an image reconstruction that starts from an initial assumption by using a background model, and compares it to measurements while making constant adjustments until the two are in agreement. The commonly used iterative algorithms include the algebraic reconstruction technique (ART, Austen et al. (1986)), multiplicative algebraic reconstruction technique (MART, Raymund et al. (1990)), simultaneous iteration reconstruction technique (SIRT, Pryse et al. (1993)), as well as other revised methods based on these three techniques. 2) Non-iterative algorithms, within which the inversion quality is independent of the initial assumption but relies on some regularization methods, such as singular value decomposition and its modifications (Zhou et al., 1999), empirical orthogonal decomposition (Sutton and Na, 1994), etc. In short, tomography techniques have been used to reconstruct the ionospheric electron density distribution and ionospheric dynamic variations, such as ionospheric storm-time characteristics (Prol et al., 2021), storm-enhanced density (Zhai et al., 2020), main ionospheric trough (Yizengaw and Moldwin, 2005), and equatorial plasma depletions (Comberiate et al., 2006).

3 Discussion of challenges and future needs

Remarkable progress has been made through previous ionospheric data assimilation and tomography studies over the past decades. We have identified the following future research areas for 3-D ionosphere imaging that are potentially important but challenging: 1) high-resolution and high-precision regional ionospheric imaging to specify important dynamical structures that have space weather impact; 2) Improved capability of error covariance specification and uncertainty quantification; 3) Estimation of physical drivers from reanalyzed ionospheric imaging data; 4) Serving space weather application that needs comprehensive and efficient nowcast and forecasts; 5) Sustained efforts to increase data coverage and availability.

3.1 High-resolution and high-precision regional ionospheric imaging to specify important dynamical structures that have space weather impact

Resolution and precision are mutual constraints in ionospheric imaging. The current algorithms for providing 3-D ionospheric electron density imaging are relatively mature and well-validated, but research on improving imaging resolution and precision has always been linked to the issue of solving the ill-conditioned inversion problem due to insufficient data coverage. Moreover, most current ionospheric data assimilation models have been built to run on a global scale that may not always have an optimal performance in representing local mesoscale ionosphere morphology, especially for those important dynamical structures that have space weather impact, such as storm-enhanced density (SED). Thus, developing high-fidelity regional ionospheric imaging products with a high spatial-temporal resolution to specify localized smaller-scale plasma structuring is of great importance from both scientific and applicational perspectives. In particular, some regions have consistently been an active research target of growing scientific interest (e.g., North American and European sectors), not only because of significant ionospheric density gradients seen in these regions associated with important space weather impact due to complicated ionospheric dynamics and electrodynamics therein that are worth in-depth exploration; but also due to the availability of dense networks of ground-based GNSS receivers and other powerful instruments such as ISRs over this area. Moreover, the subauroral and high-latitude ionosphere presents an immense opportunity for 4-D ionospheric imaging for both applied and discovery science, with an ever-expanding network of sensors/models in place, such as the Canadian High Arctic Ionospheric Network (CHAIN) and empirical/assimilative models (E-CHAIM/A-CHAIM, Themens et al. (2021); Reid et al. (2023)), EISCAT-3D, PFISR, RISR, Millstone Hill ISR, SuperDARN, and other optical networks, as well as a burgeoning need for assimilative modeling and GNSS accuracy with the opening of arctic navigation. Thus, the combination of strong science/application merit and relatively abundant data availability collectively drive the need to specify the 3-D time-evolving (actually 4-D) electron density variation in certain key areas with high spatial-temporal resolution sufficient to characterize and help understand fine and regional ionospheric dynamics, variability and weather. Figure 1 shows an example of high-resolution 3-D ionospheric imaging over the continental US and adjacent regions during the 17 March 2015 severe geomagnetic storm, given by a new TEC-based Ionospheric Data Assimilation System (TIDAS; Aa et al. (2022)) with a spatial-temporal resolution of 1° (latitude) × 1° (longitude) × 20 km (altitude) × 5 min. Fine structures of mid-latitude SED plume and associated density gradients are clearly demonstrated in the reanalyzed data assimilation result.

FIGURE 1

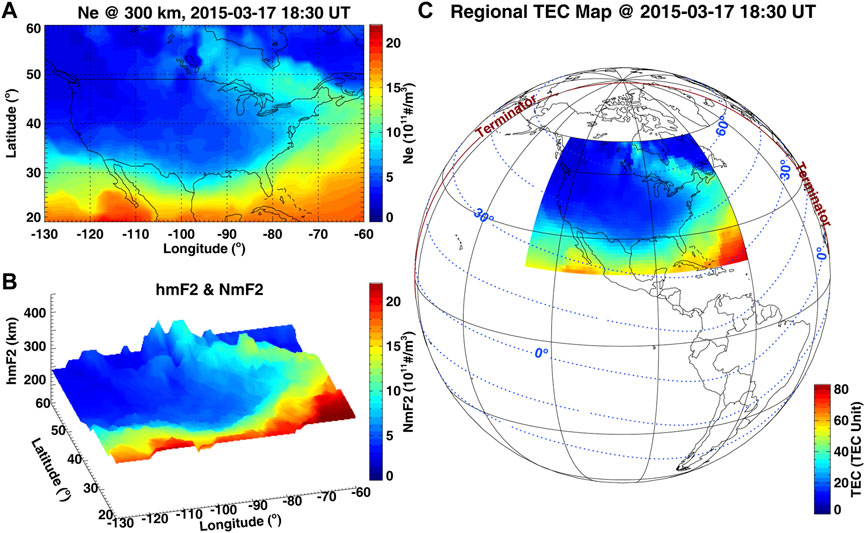
FIGURE 1. An example of 3-D ionospheric imaging with storm-enhanced density plume during the 17 March 2015 severe geomagnetic storm given by TIDAS data assimilation system (Aa et al., 2022): (A) electron density at 300 km; (B) ionospheric F2 layer peak height (hmF2) and peak density (NmF2, color-coded) distribution; (C) reanalyzed regional TEC with the terminator (red line) and certain geomagnetic latitude lines being marked.

Recommendation: An important goal of 3-D ionospheric imaging in the next decade targeted research areas (e.g., American and European sectors, Arctic region) is to achieve a horizontal resolution of 0.5° in longitude/latitude and vertical resolution of 10 km, to serve the need for advancing scientific understanding of important multi-scale ionospheric dynamical structures that have space weather impact. Observations providing vertical electron density profile information are necessary to improve model representation of the ionosphere and are critically needed.

3.2 Improving capability of error covariance specification and uncertainty quantification

A major challenge in developing an accurate and reliable data assimilation system is the proper construction of the background error covariance, which determines the contribution weights and information transition from the data-driven to model-driven regions in the assimilation algorithms (Forsythe et al., 2020a). However, it is almost impossible to obtain a realistic specification of this covariance matrix, due to lacking true state values and real errors at each grid point as well as insufficient knowledge of the spatial distribution of ionospheric correlations. There are typically two methods to deal with this difficulty. The first one is to use the ensemble Kalman Filter algorithm, which uses sample statistics from short-term ensemble forecast of background model to calculate the error covariance Evensen (1994). This method has been widely implemented in many theoretical model-based data assimilation attempts (e.g., Hsu et al., 2014; Chartier et al., 2016; Pedatella et al., 2018; He et al., 2019). However, the proper ensemble size, huge computational cost, and appropriate covariance localization scheme are some issues that have not been fully addressed. The second method is to use a modeled covariance matrix with functioned ionospheric correlation description on the basis of certain mathematical assumptions (e.g., Bust et al., 2004; Yue et al., 2007; Yue et al., 2011; Aa et al., 2015; Aa et al., 2016; Forsythe et al., 2020b). In reality, however, the ionospheric correlation distance may not always be well represented by some simplified expressions, especially among geospace storm intervals with large spatial inhomogeneity. Recently, some studies built global distribution of ionospheric spatial correlation distances and developed novel background covariance models based on scale tests of long-term observations and model runs (e.g., Forsythe et al., 2020a; Forsythe et al., 2020b; Forsythe et al., 2021a; Forsythe et al., 2021b).

Figure 2A provides an example of the horizontal correlation lengths for the covariance matrix modeling. According to the distribution of the correlations between the model errors (calculated using vertical TEC from the International Reference Ionosphere (IRI-2016) (Bilitza et al., 2017) and the vertical TEC from the Global Ionospheric Maps (GIM)), there exists horizontal anisotropy, where the zonal (meridional) correlation lengths L₂ and L₄ (L₁ and L₃) are not equal in length. Moreover, even for the regional grid, these lengths vary significantly with the location, as can be seen in Figure 2B. Perhaps even more importantly, the variation of the vertical correlation lengths (calculated using ISR data) with height, shown in Figure 2C, has particular characteristics that actually preserve the layered shape of the vertical density distribution, unlike the typically used monotonically increased ionospheric scale height (shown with a white line in Figure 2C) (Forsythe et al., 2021b). These routes provide a useful step toward improving the modeling of background error covariance.

FIGURE 2

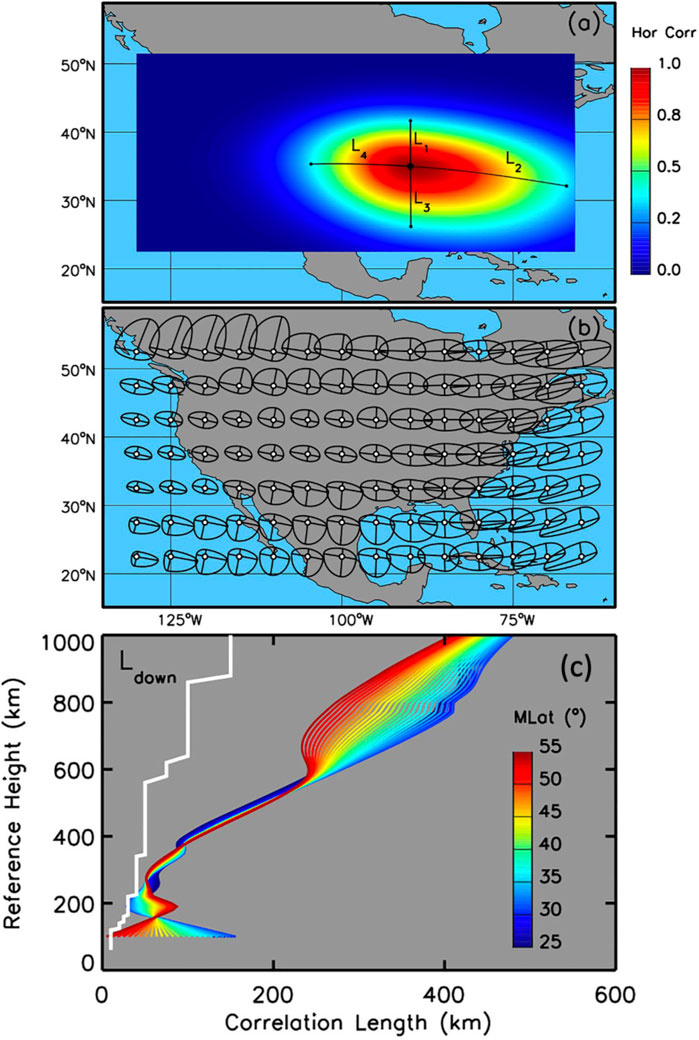
FIGURE 2. An example of the horizontal correlation length (Forsythe et al., 2021a) (A, B) modeled using IRI-2016 and GIM, and vertical correlation length (C) modeled using IRI-2016 with ISR data (Forsythe et al., 2021b).

Uncertainty quantification consists of the uncertainty propagation from the input to the output and inverse problems that result from the calibration of models against measurements. Uncertainty quantification in theoretical model-based data assimilation often faces two key challenges: high dimensionality and high computational cost. Such a background model often involves the presence of a large number of uncertainty parameters and uncertainty in the initial and boundary conditions. Exploiting such high-dimensional spaces typically relies on the utilization of a large number of computational samples, such as those implemented in the Ensemble Kalman Filtering technique. Increasing ensemble size would cause extremely high computational costs that may not always be a feasible solution to meet the space weather requirements of near-real-time nowcasting and forecasting.

Recommendation: Continuous advance in improving the capability of background error covariance specification as well as uncertainty quantification in ionospheric imaging.

3.3 Estimation of physical drivers from reanalyzed ionospheric imaging data

The background physical model is typically an indispensable part of ionospheric 3-D imaging in both data assimilation and tomography, which plays an important role in providing an a priori state estimation used for measurements update, and sometimes, especially in data assimilation, being used as a state transition (forward) operator to make the forecast based on a posteriori reanalyzed results for recursive state update (Wang et al., 2004). In particular, ionospheric theoretical models can assimilate a diverse set of data sources and have the merits of providing physics-based nowcasting and forecasting, yet are somewhat restricted by lacking reliable drivers and boundary conditions. The combination of the physical model and ionospheric imaging can be considered a powerful tool that not only yields 3-D time-evolving ionospheric electron density reconstruction but also provides appropriate input values of physical drivers in the model. The time-evolving electron density distribution can be used to retrieve the driver inputs as well as provide an updated condition to restart the physical model so that the time-evolving variation of the drivers could be continuously updated. Considering the complexity of the forward module in theoretical models, making an accurate estimation of the input drivers in terms of the reanalyzed imaging data is still a challenging problem but would be with strong needs in the next decade.

Recommendation: The community should implement approaches to utilize the reanalyzed electron density imaging data to retrieve quantitative information on the input physical drivers (e.g., electric fields, neutral winds) that cause the electron density variations in three dimensions, based on state-of-the-art ionosphere-thermosphere theoretical models.

3.4 Serving space weather application that needs comprehensive and efficient nowcast and forecasts

In addition to advancing the current scientific understanding of ionospheric dynamic structures, characterization of the 3-D electron density distribution via ionospheric imaging is useful for a number of space weather applications, such as communications, navigation, and surveillance. According to the “National Space Weather Strategy and Action Plan”, one important objective is to develop and disseminate accurate and timely space Weather characterization and forecasts (Spann et al., 2019). Thus, the ultimate interest of ionospheric imaging should be to develop operational capabilities to serve space weather applications for robust, accurate, and timely ionospheric nowcast and forecast to help quantitatively evaluate ionospheric weather effects due to geospace disturbances, such as those related to positioning, navigation, and timing.

Recommendation: Enhanced near-real-time accessibility with wide spatial coverage and sharing of observational data across the geospace and other communities are essential for the success of ionospheric imaging and related nowcast and forecast. Information of ionospheric electron density profiles from ground-based ISRs, ionosonde, and next-generation bottomside ionospheric sounding networks in conjugation with space-based radio occultation data, in addition to all kinds of GNSS observations, are fundamental and indispensable data resources. The community should push the boundaries of observational data availability toward near real-time.

3.5 Sustained effort to improve data coverage and availability

Despite that the algorithm development for ionospheric imaging is important, there still exists a critical issue of lacking data for global 3-D imaging. This fundamental problem should be addressed by effectively filling the critical data gaps beside the widely-used ground-based GNSS network and LEO radio occultation data. This includes the deployment of incoherent scatter radar and affordable digisondes and the increase of radio occultation data coverage. In particular, the powerful incoherent scatter radars, such as EISCAT-3D, Poker Flat ISR, Resolute Bay ISR, Millstone Hill ISR, Jicamarca ISR, etc., will provide important altitude structural information on electron densities, as well as plasma drift velocities, electron and ion temperatures, etc., over the E/F region and topside ionosphere for high-precision 3-D ionospheric imaging (Stamm et al., 2021). Significant data can also be supplied from in-situ density observations from LEO satellites such as NASA’s Ionospheric Connection Explorer (ICON), as well as from remote sensing data observed by ultraviolet imager onboard GEO satellites such as the Global-scale Observations of the Limb and Disk (GOLD). In addition to ionospheric electron density that is used to generate ionospheric imaging, both space and ground-based observations of global neutral parameters as well as ionospheric electric fields and drifts, are highly desired to constrain and assess physics-based models, validate the retrieved drivers, as well as to help fill the data gaps. For example, the Super Dual Auroral Radar Network (SuperDARN) can be used for imaging the flow field, which is critical to analyze 4-D ionospheric dynamics. Current observations of these parameters are not adequate but this problem should be addressed in the next decade. Moreover, data gaps also exist in the vertical domain. In particular, the lower ionosphere of the D/E region is very important for the trans-ionosphere and/or waveguide propagation of low-frequency electromagnetic waves. This region is not only controlled by solar extreme ultraviolet radiation, but also influenced by solar flares, lower atmospheric waves, and other space weather events, yet the knowledge of this region is still inadequate due to the limitation of observation means. The incoherent scatter radar and LEO-satellite radio occultation measurements can partially cover this region. Moreover, the medium-frequency radar and the very low-frequency measurements can be used to derive the variation characteristics of the D region. Accurately imaging the lower ionosphere requires further expanding the observations to include more measurements covering this region into data assimilation.

Recommendation: Continuous investment across agencies and joint effort through the community in support of utilizing more sensors of measurements, deployment of new ionospheric radar infrastructure, designing of new satellite missions with various measurements, as well as the development and update physics-based ionosphere-thermosphere numerical models.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

EA and VF were responsible for preparing the manuscript draft. All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

We acknowledge NSF awards AGS-1952737, AGS-2033787, AGS-2149698, and PHY-2028125, NASA support 80NSSC22K0171, 80NSSC21K1310, 80NSSC21K1775, 80NSSC19K0834, 80GSFC22CA011, 80GSFC18C0061, and 80NSSC22M0163, AFOSR MURI Project FA9559-16-1-0364, and ONR Grant N00014-17-1-2186 and N00014-22-1-2284. VF is supported by the Office of Naval Research.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aa, E., Huang, W., Yu, S., Liu, S., Shi, L., Gong, J., et al. (2015). A regional ionospheric TEC mapping technique over China and adjacent areas on the basis of data assimilation. J. Geophys. Res. Space Phys.120, 5049–5061. doi:10.1002/2015JA021140

CrossRef Full Text | Google Scholar

Aa, E., Liu, S., Huang, W., Shi, L., Gong, J., Chen, Y., et al. (2016). Regional 3-D ionospheric electron density specification on the basis of data assimilation of ground-based GNSS and radio occultation data. Space weather.14, 433–448. doi:10.1002/2016SW001363

CrossRef Full Text | Google Scholar

Aa, E., Ridley, A., Huang, W., Zou, S., Liu, S., Coster, A. J., et al. (2018). An ionosphere specification technique based on data ingestion algorithm and empirical orthogonal function analysis method. Space weather.16, 1410–1423. doi:10.1029/2018SW001987

CrossRef Full Text | Google Scholar

Aa, E., Zhang, S.-R., Erickson, P. J., Wang, W., Coster, A. J., and Rideout, W. (2022). 3-D regional ionosphere imaging and SED reconstruction with a new TEC-based ionospheric data assimilation system (TIDAS). Space weather.20, e03055. doi:10.1029/2022SW003055

CrossRef Full Text | Google Scholar

Anderson, J., Hoar, T., Raeder, K., Liu, H., Collins, N., Torn, R., et al. (2009). The data assimilation research testbed: A community facility. Bull. Am. Meteorological Soc.90, 1283–1296. doi:10.1175/2009BAMS2618.1

CrossRef Full Text | Google Scholar

Austen, J. R., Franke, S. J., and Liu, C. H. (1988). Ionospheric imaging using computerized tomography. Radio Sci.23, 299–307. doi:10.1029/RS023i003p00299

CrossRef Full Text | Google Scholar

Austen, J. R., Franke, S. J., Liu, C. H., and Yeh, K. C. (1986). “Application of computerized tomography techniques to ionospheric research,” in International beacon satellite symposium on radio beacon contribution to the study of ionization and dynamics of the ionosphere and to corrections to geodesy and technical workshop, 25–35.

Google Scholar

Balan, N., Liu, L., and Le, H. (2018). A brief review of equatorial ionization anomaly and ionospheric irregularities. Earth Planet. Phys.2, 1–19. doi:10.26464/epp2018025

CrossRef Full Text | Google Scholar

Barker, D. M., Huang, W., Guo, Y. R., Bourgeois, A. J., and Xiao, Q. N. (2004). A three-dimensional variational data assimilation system for MM5: Implementation and initial results. Mon. Weather Rev.132, 897. doi:10.1175/1520-0493(2004)132¡0897:ATVDAS¿2.0.CO;2

CrossRef Full Text | Google Scholar

Bilitza, D., Altadill, D., Truhlik, V., Shubin, V., Galkin, I., Reinisch, B., et al. (2017). International reference ionosphere 2016: From ionospheric climate to real-time weather predictions. Space weather.15, 418–429. doi:10.1002/2016sw001593

CrossRef Full Text | Google Scholar

Buonsanto, M. J. (1999). Ionospheric storms — a review. Space Sci. Rev.88, 563–601. doi:10.1023/A:1005107532631

CrossRef Full Text | Google Scholar

Bust, G. S., Crowley, G., Garner, T. W., Gaussiran, T. L., Meggs, R. W., Mitchell, C. N., et al. (2007). Four-dimensional GPS imaging of space weather storms. Space weather.5, 02003. doi:10.1029/2006SW000237

CrossRef Full Text | Google Scholar

Bust, G. S., Garner, T. W., and Gaussiran, T. L. (2004). Ionospheric data assimilation three-dimensional (IDA3D): A global, multisensor, electron density specification algorithm. J. Geophys. Res. Space Phys.109, A11312. doi:10.1029/2003JA010234

CrossRef Full Text | Google Scholar

Bust, G. S., and Mitchell, C. N. (2008). History, current state, and future directions of ionospheric imaging. Rev. Geophys.46, RG1003. doi:10.1029/2006RG000212

CrossRef Full Text | Google Scholar

Chartier, A. T., Matsuo, T., Anderson, J. L., Collins, N., Hoar, T. J., Lu, G., et al. (2016). Ionospheric data assimilation and forecasting during storms. J. Geophys. Res. Space Phys.121, 764–778. doi:10.1002/2014JA020799

CrossRef Full Text | Google Scholar

Chen, C.-H., Lin, C., Chen, W.-H., and Matsuo, T. (2017). Modeling the ionospheric prereversal enhancement by using coupled thermosphere-ionosphere data assimilation. Geophys. Res. Lett.44, 1652–1659. doi:10.1002/2016GL071812

CrossRef Full Text | Google Scholar

Codrescu, S. M., Codrescu, M. V., and Fedrizzi, M. (2018). An ensemble kalman filter for the thermosphere-ionosphere. Space weather.16, 57–68. doi:10.1002/2017SW001752

CrossRef Full Text | Google Scholar

Comberiate, J. M., Kamalabadi, F., and Paxton, L. (2006). Tomographic imaging of equatorial plasma bubbles. Geophys. Res. Lett.33, L15805. doi:10.1029/2006GL025820

CrossRef Full Text | Google Scholar

Daley, R. (1993). Atmospheric data analysis. Cambridge University Press.

Google Scholar

Datta-Barua, S., Bust, G. S., and Crowley, G. (2011). Deducing storm time F region ionospheric dynamics from 3-D time-varying imaging. J. Geophys. Res. Space Phys.116, A05324. doi:10.1029/2010JA016304

CrossRef Full Text | Google Scholar

Evensen, G. (1994). Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res.99, 10143. doi:10.1029/94JC00572

CrossRef Full Text | Google Scholar

Forsythe, V. V., Azeem, I., Blay, R., Crowley, G., Gasperini, F., Hughes, J., et al. (2021a). Evaluation of the new background covariance model for the ionospheric data assimilation. Radio Sci.56, e07286. doi:10.1029/2021RS007286

CrossRef Full Text | Google Scholar

Forsythe, V. V., Azeem, I., and Crowley, G. (2020a). Ionospheric horizontal correlation distances: Estimation, analysis, and implications for ionospheric data assimilation. Radio Sci.55, e07159. doi:10.1029/2020RS007159

CrossRef Full Text | Google Scholar

Forsythe, V. V., Azeem, I., Crowley, G., Makarevich, R. A., and Wang, C. (2020b). The global analysis of the ionospheric correlation time and its implications for ionospheric data assimilation. Radio Sci.55, e2020RS007181. doi:10.1029/2020RS007181

CrossRef Full Text | Google Scholar

Forsythe, V. V., Azeem, I., Crowley, G., and Themens, D. R. (2021b). Ionospheric vertical correlation distances: Estimation from ISR data, analysis, and implications for ionospheric data assimilation. Radio Sci.56, e2020RS007177. doi:10.1029/2020RS007177

CrossRef Full Text | Google Scholar

Foster, J. C., Coster, A. J., Erickson, P. J., Holt, J. M., Lind, F. D., Rideout, W., et al. (2005). Multiradar observations of the polar tongue of ionization. J. Geophys. Res. Space Phys.110, A09S31. doi:10.1029/2004JA010928

CrossRef Full Text | Google Scholar

Foster, J. C. (1993). Storm time plasma transport at middle and high latitudes. J. Geophys. Res.98, 1675–1689. doi:10.1029/92JA02032

CrossRef Full Text | Google Scholar

Fuller-Rowell, T., Araujo-Pradere, E., Minter, C., Codrescu, M., Spencer, P., Robertson, D., et al. (2006). US-TEC: A new data assimilation product from the space environment center characterizing the ionospheric total electron content using real-time gps data. Radio Sci.41, RS6003. doi:10.1029/2005RS003393

CrossRef Full Text | Google Scholar

Galkin, I. A., Reinisch, B. W., Huang, X., and Bilitza, D. (2012). Assimilation of GIRO data into a real-time IRI. Radio Sci.47, RS0L07. doi:10.1029/2011RS004952

CrossRef Full Text | Google Scholar

Galkin, I. A., Vesnin, A. M., Kozlov, A. V., Huang, X., and Reinisch, B. W. (2015). “Gambit database and explorer,” in In 2015 1st URSI atlantic radio science conference (URSI AT-RASC), 1. doi:10.1109/URSI-AT-RASC.2015.7303116

CrossRef Full Text | Google Scholar

He, J., Yue, X., Wang, W., and Wan, W. (2019). EnKF ionosphere and thermosphere data assimilation algorithm through a sparse matrix method. J. Geophys. Res. Space Phys.124, 7356–7365. doi:10.1029/2019JA026554

CrossRef Full Text | Google Scholar

Hernández-Pajares, M., Juan, J. M., and Sanz, J. (1999). New approaches in global ionospheric determination using ground GPS data. J. Atmos. Sol-Terr. Phys.61, 1237–1247. doi:10.1016/S1364-6826(99)00054-1

CrossRef Full Text | Google Scholar

Hsu, C.-T., Matsuo, T., Wang, W., and Liu, J.-Y. (2014). Effects of inferring unobserved thermospheric and ionospheric state variables by using an Ensemble Kalman Filter on global ionospheric specification and forecasting. J. Geophys. Res. Space Phys.119, 9256–9267. doi:10.1002/2014JA020390

CrossRef Full Text | Google Scholar

Hsu, C. T., Matsuo, T., Yue, X., Fang, T. W., Fuller-Rowell, T., Ide, K., et al. (2018). Assessment of the impact of FORMOSAT-7/COSMIC-2 GNSS RO observations on midlatitude and low-latitude ionosphere specification: Observing system simulation experiments using ensemble square root filter. J. Geophys. Res. Space Phys.123, 2296–2314. doi:10.1002/2017JA025109

CrossRef Full Text | Google Scholar

Jakowski, N., Béniguel, Y., De Franceschi, G., Hernandez Pajares, M., Jacobsen, K. S., Stanislawska, I., et al. (2012). Monitoring, tracking and forecasting ionospheric perturbations using GNSS techniques. J. Space Weather Space Clim.2, A22. doi:10.1051/swsc/2012022

CrossRef Full Text | Google Scholar

Jee, G., Burns, A. G., Wang, W., Solomon, S. C., Schunk, R. W., Scherliess, L., et al. (2007). Duration of an ionospheric data assimilation initialization of a coupled thermosphere-ionosphere model. Space weather.5, 01004. doi:10.1029/2006SW000250

CrossRef Full Text | Google Scholar

Kalman, R. E. (1960). A new approach to linear filtering and prediction problems. J. Basic Eng.82, 35–45. doi:10.1115/1.3662552

CrossRef Full Text | Google Scholar

Kalman, R. E., and Bucy, R. (1961). New results in linear filtering and prediction theory. J. Basic Eng.83, 95–108. doi:10.1115/1.3658902

CrossRef Full Text | Google Scholar

Komjathy, A., Wilson, B., Pi, X., Akopian, V., Dumett, M., Iijima, B., et al. (2010). JPL/USC gaim: On the impact of using COSMIC and ground-based GPS measurements to estimate ionospheric parameters. J. Geophys. Res. Space Phys.115, A02307. doi:10.1029/2009JA014420

CrossRef Full Text | Google Scholar

Lee, I. T., Matsuo, T., Richmond, A. D., Liu, J. Y., Wang, W., Lin, C. H., et al. (2012). Assimilation of FORMOSAT-3/COSMIC electron density profiles into a coupled thermosphere/ionosphere model using ensemble Kalman filtering. J. Geophys. Res. Space Phys.117, A10318. doi:10.1029/2012JA017700

CrossRef Full Text | Google Scholar

Lin, C. Y., Matsuo, T., Liu, J. Y., Lin, C. H., Huba, J. D., Tsai, H. F., et al. (2017). Data assimilation of ground-based GPS and radio occultation total electron content for global ionospheric specification. J. Geophys. Res. Space Phys.122, 10,876–10,886. doi:10.1002/2017JA024185

CrossRef Full Text | Google Scholar

Mannucci, A. J., Wilson, B. D., Yuan, D. N., Ho, C. H., Lindqwister, U. J., and Runge, T. F. (1998). A global mapping technique for GPS-derived ionospheric total electron content measurements. Radio Sci.33, 565–582. doi:10.1029/97RS02707

CrossRef Full Text | Google Scholar

Matsuo, T., and Araujo-Pradere, E. A. (2011). Role of thermosphere-ionosphere coupling in a global ionospheric specification. Radio Sci.46, RS0D23. doi:10.1029/2010RS004576

CrossRef Full Text | Google Scholar

Matsuo, T., Lee, I. T., and Anderson, J. L. (2013). Thermospheric mass density specification using an ensemble Kalman filter. J. Geophys. Res. Space Phys.118, 1339–1350. doi:10.1002/jgra.50162

CrossRef Full Text | Google Scholar

Mengist, C. K., Ssessanga, N., Jeong, S.-H., Kim, J.-H., Kim, Y. H., and Kwak, Y.-S. (2019). Assimilation of multiple data types to a regional ionosphere model with a 3D-var algorithm (IDA4D). Space weather.17, 1018–1039. doi:10.1029/2019SW002159

CrossRef Full Text | Google Scholar

Nava, B., Coïsson, P., Miró Amarante, G., Azpilicueta, F., and Radicella, S. M. (2005). A model assisted ionospheric electron density reconstruction method based on vertical tec data ingestion. Ann. Geophys.48. doi:10.4401/ag-3203

CrossRef Full Text | Google Scholar

Pedatella, N. M., Anderson, J. L., Chen, C. H., Raeder, K., Liu, J., Liu, H. L., et al. (2020). Assimilation of ionosphere observations in the whole atmosphere community climate model with thermosphere-ionosphere EXtension (WACCMX). J. Geophys. Res. Space Phys.125, e28251. doi:10.1029/2020JA028251

CrossRef Full Text | Google Scholar

Pedatella, N. M., Liu, H. L., Marsh, D. R., Raeder, K., Anderson, J. L., Chau, J. L., et al. (2018). Analysis and hindcast experiments of the 2009 sudden stratospheric warming in WACCMX+DART. J. Geophys. Res. Space Phys.123, 3131–3153. doi:10.1002/2017JA025107

CrossRef Full Text | Google Scholar

Pi, X., Wang, C., Hajj, G. A., Rosen, G., Wilson, B. D., and Bailey, G. J. (2003). Estimation of E × B drift using a global assimilative ionospheric model: An observation system simulation experiment. J. Geophys. Res. Space Phys.108, 1075. doi:10.1029/2001JA009235

CrossRef Full Text | Google Scholar

Prol, F. S., Kodikara, T., Hoque, M. M., and Borries, C. (2021). Global-scale ionospheric tomography during the March 17, 2015 geomagnetic storm. Space weather.19, e02889. doi:10.1029/2021SW002889

CrossRef Full Text | Google Scholar

Pryse, S. E., Kersley, L., Rice, D. L., Russell, C. D., and Walker, I. K. (1993). Tomographic imaging of the ionospheric mid-latitude trough. Ann. Geophys.11, 144–149.

Google Scholar

Raymund, T. D., Franke, S. J., Liu, C. H., Austen, J. R., Klobuchar, J. A., and Stalker, J. (1990). Application of computerized tomography to the investigation of ionospheric structures. Radio Sci.25, 771–789. doi:10.1029/RS025i005p00771

CrossRef Full Text | Google Scholar

Reid, B., Themens, D. R., McCaffrey, A., Jayachandran, P. T., Johnsen, M. G., and Ulich, T. (2023). A-CHAIM: Near-Real-Time data assimilation of the high latitude ionosphere with a particle filter. Space weather.21, e2022SW003185. doi:10.1029/2022SW003185

CrossRef Full Text | Google Scholar

Richmond, A. D. (1992). Assimilative mapping of ionospheric electrodynamics. Adv. Space Res.12, 59–68. doi:10.1016/0273-1177(92)90040-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Richmond, A. D., Ridley, E. C., and Roble, R. G. (1992). A thermosphere/ionosphere general circulation model with coupled electrodynamics. Geophys. Res. Lett.19, 601–604. doi:10.1029/92GL00401

CrossRef Full Text | Google Scholar

Rodger, A. (2008). “The mid-latitude trough—revisited,” in Washington DC American geophysical union geophysical monograph series, 181, 25–33. doi:10.1029/181GM04

CrossRef Full Text | Google Scholar

Schaer, S. (1999). Mapping and predicting the Earth’s ionosphere using the global positioning system. Geod.-Geophys. Arb. Schweiz59.

Google Scholar

Scherliess, L., Schunk, R. W., Sojka, J. J., and Thompson, D. C. (2004). Development of a physics-based reduced state Kalman filter for the ionosphere. Radio Sci.39, RS1S04. doi:10.1029/2002RS002797

CrossRef Full Text | Google Scholar

Scherliess, L., Schunk, R. W., Sojka, J. J., Thompson, D. C., and Zhu, L. (2006). Utah state university global assimilation of ionospheric measurements gauss-markov kalman filter model of the ionosphere: Model description and validation. J. Geophys. Res. Space Phys.111, A11315. doi:10.1029/2006JA011712

CrossRef Full Text | Google Scholar

Schunk, R. W., Scherliess, L., Sojka, J. J., Thompson, D. C., Anderson, D. N., Codrescu, M., et al. (2004). Global assimilation of ionospheric measurements (GAIM). Radio Sci.39, RS1S02. doi:10.1029/2002RS002794

CrossRef Full Text | Google Scholar

Spann, J. F., Talaat, E. R., Keshian, J., Bonadonna, L. C. M. F., Murtagh, W. J., Blunt, K., et al. (2019). “National space weather Strategy and action plan - implications for space weather observations and applications,” in AGU fall meeting abstracts, 2019, IN51B–07.

Google Scholar

Spencer, P. S. J., Robertson, D. S., and Mader, G. L. (2004). “Ionospheric data assimilation methods for geodetic applications,” in PLANS 2004. Position location and navigation symposium (IEEE Cat), 510–517. No.04CH37556. doi:10.1109/PLANS.2004.1309036

CrossRef Full Text | Google Scholar

Ssessanga, N., Kim, Y. H., Habarulema, J. B., and Kwak, Y.-S. (2019). On imaging South African regional ionosphere using 4D-var technique. Space weather.17, 1584–1604. doi:10.1029/2019SW002321

CrossRef Full Text | Google Scholar

Stamm, J., Vierinen, J., Urco, J. M., Gustavsson, B., and Chau, J. L. (2021). Radar imaging with EISCAT 3D. Ann. Geophys.39, 119–134. doi:10.5194/angeo-39-119-2021

CrossRef Full Text | Google Scholar

Sutton, E. K. (2018). A new method of physics-based data assimilation for the quiet and disturbed thermosphere. Space weather.16, 736–753. doi:10.1002/2017SW001785

CrossRef Full Text | Google Scholar

Sutton, E., and Na, H. (1994). Orthogonal decomposition framework for ionospheric tomography algorithms. Int. J. Imaging Syst. Technol.5, 106–111. doi:10.1002/ima.1850050207

CrossRef Full Text | Google Scholar

Themens, D. R., Reid, B., Jayachandran, P. T., Larson, B., Koustov, A. V., Elvidge, S., et al. (2021). E-CHAIM as a model of total electron content: Performance and diagnostics. Space weather.19, e02872. doi:10.1029/2021SW002872

CrossRef Full Text | Google Scholar

Wang, C., Hajj, G., Pi, X., Rosen, I. G., and Wilson, B. (2004). Development of the global assimilative ionospheric model. Radio Sci.39, RS1S06. doi:10.1029/2002RS002854

CrossRef Full Text | Google Scholar

Weber, E. J., Buchau, J., Moore, J. G., Sharber, J. R., Livingston, R. C., Winningham, J. D., et al. (1984). Flayer ionization patches in the polar cap. J. Geophys. Res.89, 1683–1696. doi:10.1029/JA089iA03p01683

CrossRef Full Text | Google Scholar

Yao, Y., Tang, J., Chen, P., Zhang, S., and Chen, J. (2014). An improved iterative algorithm for 3-D ionospheric tomography reconstruction. IEEE Trans. Geoscience Remote Sens.52, 4696–4706. doi:10.1109/TGRS.2013.2283736

CrossRef Full Text | Google Scholar

Yizengaw, E., and Moldwin, M. B. (2005). The altitude extension of the mid-latitude trough and its correlation with plasmapause position. Geophys. Res. Lett.32, L09105. doi:10.1029/2005GL022854

CrossRef Full Text | Google Scholar

Yue, X., Schreiner, W. S., Kuo, Y.-H., Braun, J. J., Lin, Y.-C., and Wan, W. (2014). Observing system simulation experiment study on imaging the ionosphere by assimilating observations from ground GNSS, LEO-based radio occultation and ocean reflection, and cross link. IEEE Trans. Geoscience Remote Sens.52, 3759–3773. doi:10.1109/TGRS.2013.2275753

CrossRef Full Text | Google Scholar

Yue, X., Schreiner, W. S., Kuo, Y.-H., Hunt, D. C., Wang, W., Solomon, S. C., et al. (2012). Global 3-D ionospheric electron density reanalysis based on multisource data assimilation. J. Geophys. Res. Space Phys.117, A09325. doi:10.1029/2012JA017968

CrossRef Full Text | Google Scholar

Yue, X., Schreiner, W. S., Lin, Y.-C., Rocken, C., Kuo, Y.-H., and Zhao, B. (2011). Data assimilation retrieval of electron density profiles from radio occultation measurements. J. Geophys. Res. Space Phys.116, A03317. doi:10.1029/2010JA015980

CrossRef Full Text | Google Scholar

Yue, X., Wan, W., Liu, L., Zheng, F., Lei, J., Zhao, B., et al. (2007). Data assimilation of incoherent scatter radar observation into a one-dimensional midlatitude ionospheric model by applying ensemble Kalman filter. Radio Sci.42, RS6006. doi:10.1029/2007RS003631

CrossRef Full Text | Google Scholar

Zhai, C., Lu, G., Yao, Y., Wang, W., Zhang, S., Liu, J., et al. (2020). 3-D tomographic reconstruction of SED plume during 17 March 2013 storm. J. Geophys. Res. Space Phys.125, e28257. doi:10.1029/2020JA028257

CrossRef Full Text | Google Scholar

Zhang, S.-R., Zhang, Y., Wang, W., and Verkhoglyadova, O. P. (2017). Geospace system responses to the St. Patrick’s Day storms in 2013 and 2015. J. Geophys. Res. Space Phys.122, 6901–6906. doi:10.1002/2017JA024232

CrossRef Full Text | Google Scholar

Zhou, C., Fremouw, E. J., and Sahr, J. D. (1999). Optimal truncation criterion for application of singular value decomposition to ionospheric tomography. Radio Sci.34, 155–166. doi:10.1029/1998RS900015

CrossRef Full Text | Google Scholar