Exact solution to the problem of slow oscillations in coronal loops and its diagnostic applications

1 Introduction

Nowadays, the processes in the solar atmosphere are actively studied with spaceborne and ground-based instruments. The accuracy of instruments has made it possible to detect signals from individual structural elements of the solar atmosphere like coronal loops, spicules, etc. The observed periodic or quasi-periodic signals can be readily associated with the magnetoacoustic (MA) waves evolving in these structures (see Nakariakov and Kolotkov (2020) for a recent review). Developed MHD theories and amount of observed events allow us to use MA waves as a diagnostic tool for the coronal plasma, giving birth to such a research field as coronal seismology. Speaking of some applications, the observations of fast MA waves are used for estimations of the density stratification (Andries et al., 2005), corona loop parameters (Chen et al., 2015), etc. For the most recent reviews, we refer the reader to the works of Nakariakov et al. (2021); Li et al. (2020); Banerjee et al. (2021). In turn, the slow MA waves are used to seismologically infer coronal temperature (Marsh and Walsh, 2009), transport coefficients (Wang et al., 2015), adiabatic index (Krishna Prasad et al., 2018), magnetic field strength and local Alfvens speed (Jess et al., 2016; Cho et al., 2017), or even to introduce some constraints on enigmatic coronal heating function (Kolotkov et al., 2020). Prospects for the application of slow waves for coronal plasma diagnostics are discussed in detail in a recent review by Wang et al. (2021). The diagnostics of plasma parameters requires a sufficiently reliable MHD model and accurate observational data analysis. In this paper, we will be focused on the former, i.e., developing an advanced exact analytical model of slow waves in the corona.

The use of MA waves as a seismological tool involves taking into account the primary processes, which determine the dispersion properties of waves. For magnetoacoustic waves (fast and slow), it is important to correctly take into account the influence of magnetic structuring on wave properties. For such needs, one can apply the classical approach from pioneering works by Zaitsev and Stepanov (1975; 1982); Edwin and Roberts (1983), representing the coronal loop as a straight plasma cylinder. Despite the generality of the given description, this approach is quite complicated even under the assumption of ideal adiabatic plasma. In this regard, to describe MA waves, one often uses the thin flux tube approximation (Zhugzhda, 1996). This approach allows us to easily analytically show the wave-guiding dispersion of slow waves, which, in particular, is manifested as the variation of the slow-wave phase speed from the usual sound speed for short periods to the so-called tube speed in the long period limit. The latter speed is frequently used for the estimation of loop magnetic field (Wang et al., 2007; Jess et al., 2016) and other loop parameters. However, if the plasma β is sufficiently low, the mentioned dispersion effect on slow waves becomes rather weak. In this case, the modelling can be further simplified for the slow waves propagating along the magnetic field lines. This approach is known as an infinite magnetic field approximation (see, e.g., Zavershinskii et al. (2019); Kolotkov et al. (2019); Reale et al. (2018) for details).

Thus, one may show that in a highly magnetized plasma, the main dispersion sources for slow waves become thermal conduction and non-adiabatic processes. It has been shown in Zavershinskii et al. (2019); Kolotkov et al. (2019), using the infinite magnetic field approximation, that the long-period limit of the slow-wave phase velocity is highly affected by the coronal heating and cooling rates. Moreover, this statement is valid for any plasma β less than unity. It has been confirmed within the thin flux tube approximation (Belov et al., 2021) and using slab geometry (Agapova et al., 2022). Additionally, plasma heating/cooling can lead to the amplification/attenuation of slow waves depending on the form of non-adiabatic functions. The mentioned damping can support the dissipation by thermal conduction and can be used to introduce constraints for the coronal heating function (Kolotkov et al., 2020; 2023). In turn, the amplification by non-adiabatic processes may lead to suppressed damping or even the growth of slow waves. Combination of dispersion effects and amplification can lead to the formation of quasi-periodic patterns (see Zavershinskii et al. (2019) for details). If the amplification is not balanced by the thermal conduction damping, then it will be limited by non-linear processes allowing autowave-shock structures to exist (Chin et al., 2010; Zavershinskii et al., 2020; Molevich and Riashchikov, 2021). In addition, non-adiabatic processes introduce the phase-shift between perturbation of different parameters (e.g., temperature and density), which also depends on the form of heat-loss functions (Zavershinskii et al., 2021). The problem of heating/cooling influence on the phase shift of propagating slow waves has been investigated by Prasad et al. (2021); Molevich et al. (2022) and by Prasad et al. (2022) for standing modes. It should be noted, that heating/cooling affects not only slow waves but also entropy waves (Somov et al., 2007). The latter waves can be amplified separately, with or without slow waves. The increase of entropy waves is often considered as a possible trigger of coronal rain Antolin (2020); Antolin and Froment (2022). More details about the mixed properties of entropy and slow waves can be found in Zavershinskii et al. (2021). The set of discussed effects is known as a thermal misbalance effect, directly linked to the physics of thermal instabilities traditionally considered in heliospheric and interstellar plasma communities Field (1965). The recent review on the thermal misbalance in application to the coronal plasma can be found in Kolotkov et al. (2021). Special attention deserves a modern look at the frequency-dependent damping of slow waves through the prism of the thermal misbalance Kolotkov and Nakariakov (2022). It is shown that the thermodynamic activity modifies the relationship between the damping time and oscillation period, and it becomes a non-power-law function.

The thermal conduction also leads to the dispersion of the slow-wave phase velocity. In this case, the phase speed tends to the isothermal sound speed in the short period limit. The damping associated with thermal conduction also has a dependence on the wave period, namely, the higher harmonics decay faster. Furthermore, it also introduces the phase shift between the perturbations of plasma parameters. In fact, damping time and phase shifts can be expressed using the thermal conductivity coefficient. Usually, this coefficient is taken equal to the value proposed by Spitzer (Spitzer, 1965). However, a series of studies by Ofman and Wang (2002); Wang et al. (2015); Krishna Prasad et al. (2019); Ofman and Wang (2022) dedicated to the seismological determination of plasma transport coefficients propose the suppression of this coefficient. These seismological estimations are based on the assumption that the observed oscillation can be associated with the dynamics of the slow wave and application of the relationship between the thermal conduction coefficient and wave parameters. In order to analyze the thermal conduction influence on the properties of slow waves and obtain required relationships, one can apply some simplifying approximations. In particular, the assumptions of weak (Owen et al., 2009; Van Doorsselaere et al., 2011; Wang et al., 2015; Krishna Prasad et al., 2018; Prasad et al., 2022) or strong (Krishna Prasad et al., 2014; Duckenfield et al., 2021) impact of thermal conduction are frequently used for this purpose. However, the results presented in Kolotkov (2022) show that by assuming that the thermal conductivity satisfies the value proposed by Spitzer, the dynamics of the fundamental slow-wave harmonic can be described with neither strong nor weak thermal conductivity limits (see Figure 2 in Kolotkov (2022) for details). In this case, the general description without limitation on the thermal conduction coefficient is required. The latter can be obtained using, for example, the numerical solution of model equations.

The current research aims to contribute to the problem of coronal seismology by non-adiabatic slow and entropy waves in coronal loops. In particular, we aim to derive explicit analytical conditions under which observed compression perturbations should be associated with the dynamics of slow waves, entropy waves, or their linear superposition. For this reason, we will obtain not a particular (for slow or entropy mode separately), but a full exact solution (for a combination of slow and entropy modes) to the evolutionary equation. Furthermore, using the obtained solution, we will introduce some relationships between the thermal conduction coefficient and wave parameters, which can be applied to coronal seismology needs. Both these issues will be conducted without setting any restriction on the thermal conduction coefficient.

Our manuscript is organized in the following way. In Section 2, we introduce the analyzed MHD model, discuss the made assumptions, and indicate the main control parameter. Further, in Section 3, we briefly demonstrate the methodology used to derive the exact solution and show the difference between the cases of only thermal misbalance and only thermal conduction effect on wave dynamics. The description of the obtained exact solution for perturbations of various plasma parameters can be found in Section 4. We apply our theoretical results using the solar corona parameters in Section 5. Finally, we summarize our results and introduce the main conclusions in Section 6.

2 Model and basic equations

Further, we will analyze the linear evolution of slow MA and entropy waves. We assume that waves propagate along magnetic field lines and apply the infinite magnetic field approximation. The compression viscosity is neglected. Thus, the evolutionary equation has the form shown below (Zavershinskii et al., 2019):

$\frac{{\partial }^3{a}_1}{\partial t^3}-c_{\mathrm{S}}^2\frac{{\partial }^3{a}_1}{\partial t\partial z^2}=\frac{\kappa }{{\rho }_0{C}_V}\left(,\frac{{\partial }^4{a}_1}{\partial z^2\partial t^2}-c_{\text{Si}}^2\frac{{\partial }^4{a}_1}{\partial z^4},\right)-\frac{1}{{\tau }_{\mathrm{V}}}\left(\frac{{\partial }^2{a}_1}{\partial t^2}-c_{\mathrm{S}Q}^2\frac{{\partial }^2{a}_1}{\partial z^2}\right).(1)$

Here, a means any variable (density ρ, temperature T, pressure P, or velocity u) describing the state of plasma. Hereafter, index “0” means the stationary value of the parameter, and index “1” indicates that the quantity is of the first order of smallness (i.e., ρ₁/ρ₀ ∼ T₁/T₀ ∼ P₁/P₀ ∼ u₁/c_S ∼ϵ≪ 1). The first term on the right-hand side (RHS) describes the influence of the field-aligned thermal conduction with the coefficient κ. In turn, the second term on the RHS describes the effect of thermal misbalance on the wave dynamics. The characteristic timescales of the misbalance can be written as follows:

${\tau }_{\mathrm{V}}=\frac{C_{\mathrm{V}}}{{\left(\partial Q/\partial T\right)}_{\rho }},{\tau }_{\mathrm{P}}=\frac{C_{\mathrm{P}}}{{\left(\partial Q/\partial T\right)}_{\rho }-\left({\rho }_0/T_0\right){\left(\partial Q/\partial \rho \right)}_T},(2)$

where, C_V and C_P are specific heat capacities at constant volume and pressure, respectively. The timescales τ_V, τ_P (τ₂, τ₁ in terms used in Zavershinskii et al. (2019)) are written using the derivatives of heat [H] and loss [L] function:

$Q\left(\rho ,T\right)=L\left(\rho ,T\right)-H\left(\rho ,T\right).(3)$

In Eq. 1, we also use characteristic speed:

$c_{\mathrm{S}}=\sqrt{\frac{\gamma {\mathrm{k}}_{\mathrm{B}}{T}_0}{m}},c_{\mathrm{S}i}=\sqrt{\frac{{\mathrm{k}}_{\mathrm{B}}{T}_0}{m}},c_{\mathrm{S}Q}=\sqrt{\frac{{\gamma }_Q{\mathrm{k}}_{\mathrm{B}}{T}_0}{m}},(4)$

where k_B is the Boltzmann constant, m is the mean particle mass. The standard adiabatic (with the adiabatic index γ = 5/3) and isothermal sound speeds are c_S and c_Si, respectively. The speed c_SQ is the sound speed of wave propagation in the regime of strong thermal misbalance, prescribed by effective polytropic index γ_Q = γτ_V/τ_P (Heyvaerts, 1974; Molevich et al., 1988).

In the general case, when the characteristic timescales of the thermal misbalance and thermal conduction are of the same order, one has to solve Eq. 1 to give an exact description of the dynamics of some arbitrary linear perturbation. In Zavershinskii et al. (2021), we considered the case of strong thermal misbalance and weak thermal conduction, i.e., neglected the first term on the RHS of Eq. 1 by assuming that τ_V and τ_P are much shorter than the characteristic time of thermal conduction. However, previous estimations of τ_V and τ_P showed that they vary in the fairly broad range, from a few minutes to a few hundred minutes, for typical combinations of coronal plasma parameters (see, e.g., Kolotkov et al., 2020; Figure 2). Hence, in the current study, the opposite problem is addressed. Namely, we consider the case of weak thermal misbalance and strong impact of thermal conduction. In other words, we will assume that the second term on the RHS of Eq. 1 can be neglected.

Thus, governing evolutionary equation for slow MA and entropy waves in the plasma with strong impact of thermal conduction (strong in relation to thermal misbalance) can be written in the following dimensionless form:

$\frac{{\partial }^3{\tilde{a}}_j}{\partial {\tilde{t}}^3}-\gamma \frac{{\partial }^3{\tilde{a}}_j}{\partial \tilde{t}\partial {\tilde{z}}^2}=\tilde{d}\left(\frac{{\partial }^4{\tilde{a}}_j}{\partial {\tilde{t}}^2\partial {\tilde{z}}^2}-\frac{{\partial }^4{\tilde{a}}_j}{\partial {\tilde{z}}^4}\right).(5)$

Here, we have introduced the dimensionless perturbation of plasma parameter ${\tilde{a}}_j$. The index j defines the parameter under study, i.e., it is used for symbols ρ, P, T, and u. In other words, we use the following values $[{\tilde{a}}_{\rho }={\rho }_1/{\rho }_0]$ for density perturbation, $[{\tilde{a}}_P=P_1/P_0]$ for pressure perturbation, $[{\tilde{a}}_T=T_1/T_0]$ for temperature perturbation, and $[{\tilde{a}}_u=u_1/c_{\mathrm{S}i}]$ for velocity perturbation. We also use dimensionless coordinate $[\tilde{z}=z/L]$, and time $[\tilde{t}=t/t_L,t_L=c_{\mathrm{S}i}/L]$. Here, L is the characteristic spatial scale.

Special attention should be paid to the dimensionless parameter $\tilde{d}$:

$\tilde{d}=\frac{1}{{\tilde{\tau }}_{\text{cond}}}=\frac{t_L}{{\tau }_{\text{cond}}},{\tau }_{\text{cond}}=\frac{L^2{C}_{\mathrm{V}}{\rho }_0}{\kappa },(6)$

which is the reciprocal dimensionless characteristic timescale ${\tilde{\tau }}_{\text{cond}}$ attributed to the thermal conduction. It can be seen that $\tilde{d}$ is the main control parameter that determines the spatiotemporal evolution of the perturbation. For clarity, we should mention that the timescale τ_cond has a similar form as in De Moortel and Hood (2003). In turn, the introduced $\tilde{d}$ is greater than value d in De Moortel and Hood (2003) by γ^3/2 times.

Further, we will obtain the exact solution of Eq. 5. In what follows, we will work in dimensionless units, so the tilde sign above the quantities will be omitted. The only exception will be made for $\tilde{d}$, in order to distinguish it with respect to the differentiation operation.

3 Behaviour of the individual Fourier harmonics

In order to obtain the exact analytical solution for Eq. 5, we will follow the approach we used before in (Zavershinskii et al., 2021). According to this approach, we will search for the solution for Eq. 5, using the Fourier method. In other words, we will use the substitution $a\left(z,t\right)=\phi \left(z\right)\psi \left(t\right)$. It allows us to split Eq. 5 into two equations. The first one is the equation describing the dependence of the full solution on the coordinate, $\phi \left(z\right)$:

$\frac{d^2\phi }{d{z}^2}+k^2\phi =0,(7)$

This equation has to be solved using appropriate boundary conditions. In the current research, we will use reflecting conditions which, in general, allows for the formation of standing slow waves. It means that one should apply Dirichlet boundary conditions $(\phi \left(0\right)=\phi \left(l\right)=0)$ for velocity equation and Neumann boundary conditions $(d\phi \left(0\right)/dz=d\phi \left(l\right)/dz=0)$ for density, pressure and temperature equations. In both cases, we obtain the set of eigenvalues k defined by the harmonic number n as:

$k=\frac{\pi n}{l},n=\mathrm{1,2,3},(8)$

Here, l is the length of the medium normalised to the characteristic length scale L. For definiteness, let us assume that L is the loop length.

In turn, the equation describing the dependence of the full solution on time $\psi \left(t\right)$ can be written in the form shown below:

$\frac{d^3\psi }{d{t}^3}+k^2\left(n\right)\tilde{d}\frac{d^2\psi }{d{t}^2}+k^2\left(n\right)\gamma \frac{d\psi }{dt}+k^4\left(n\right)\tilde{d}\psi =0.(9)$

The solution to Eq. 9 can be found using the corresponding cubic equation. This cubic equation can be obtained by writing d/d t → iω:

${\omega }^3-\mathrm{i}{k}^2\left(n\right)\tilde{d}{\omega }^2-k^2\left(n\right)\gamma \omega +\mathrm{i}{k}^4\left(n\right)\tilde{d}=0,(10)$

The cubic equation with complex coefficients (Eq. 10) coincides with the general dispersion relation for slow and entropy modes in the plasma affected by thermal conduction only (see e.g., De Moortel and Hood, 2003). Similar to the case of the thermal misbalance influence only (Zavershinskii et al., 2021), one can consider the roots of Eq. 10 as complex frequencies ω_1,2,3 of entropy and slow MA harmonics, which corresponds to real wavenumbers k.

To describe the roots, let us introduce the discriminant Δ of Eq. 10:

$\mathrm{\Delta }=-108\left(R^3+U^2\right),(11)$

where R and U are real coefficients defined by wavenumbers and characteristic dimensionless parameters of plasma:

$R=k^2\frac{3\gamma -k^2{\tilde{d}}^2}{9},U=k^4\tilde{d}\frac{2k^2{\tilde{d}}^2-9\left(\gamma -3\right)}{54}.$

Thus, the roots of the dispersion relation (Eq. 10) according to Cardano’s formula take the form shown below:

$\begin{array}{ll}\hfill & {\omega }_1=\mathrm{i}\left(-\frac{k^2\tilde{d}}{3}+A+B\right),\hfill \\ \hfill & {\omega }_2=\frac{A-B}{2}\sqrt{3}-\mathrm{i}\left(\frac{k^2\tilde{d}}{3}+\frac{A+B}{2}\right),\hfill \\ \hfill & {\omega }_3=-\frac{A-B}{2}\sqrt{3}-\mathrm{i}\left(\frac{k^2\tilde{d}}{3}+\frac{A+B}{2}\right),\hfill \end{array}(12)$

where

$A=\sqrt[3]{-U+\sqrt{-\mathrm{\Delta }/108}},B=-R/A.$

Analyzing Eq. 11 one can show that for any k and $\tilde{d}$ the discriminant is negatively defined Δ < 0. This means that regardless of plasma parameters, the dispersion relation (Eq. 10) always has one purely imaginary root and two complex conjugate roots.

The purely imaginary root can be associated with the decrement of the entropy mode harmonics:

${\omega }_{\text{EI}}=-\frac{k^2\tilde{d}}{3}+A+B.(13)$

In turn, the complex conjugate roots ω_2,3 = ±ω_AR − iω_AI can be associated with two oppositely propagating decaying slow waves. The imaginary part ω_AI (i.e., decrement of slow waves) and real part ω_AR are as follows:

${\omega }_{\text{AI}}=\frac{k^2\tilde{d}}{3}+\frac{A+B}{2},{\omega }_{\text{AR}}=\frac{A-B}{2}\sqrt{3}.(14)$

This is significantly different from the case of misbalance only considered by (Zavershinskii et al., 2021), in which the properties of slow and entropy waves can be mixed. In other words, when some harmonics of slow waves can become non-propagating and evolve in a similar way to entropy mode harmonics. In the plasma with the strong impact of thermal conduction, there is no such possibility. The entropy modes are always decaying and non-propagating and two slow waves are always propagating and decaying.

4 Exact solution

As we have mentioned before, the solution for Eq. 5 can be written as the sum of harmonics of entropy and slow modes. Let us describe the solution for the case of Neumann reflecting boundary conditions (i.e., for density, pressure, or temperature perturbations). For definiteness, we will consider density perturbation. Then, the solution for the nth harmonic can be written as follows:

$\begin{array}{ll}{a}_{\rho n}\left(z,t\right)=\hfill & C_{1\rho n}{\mathrm{e}}^{{\omega }_{\text{EI}}t}\cos \left(kz\right)\hfill \\ \hfill & +C_{0\rho n}{\mathrm{e}}^{{\omega }_{\text{AI}}t}\left[\cos \left({\omega }_{\text{AR}}t+kz-{\varphi }_{\rho n}\right)+\cos \left({\omega }_{\text{AR}}t-kz-{\varphi }_{\rho n}\right)\right],\hfill & \hfill \end{array}(15)$

where

$C_{0\rho n}=\frac{\sqrt{C_{2\rho n}^2+C_{3\rho n}^2}}{2},{\varphi }_{\rho n}=\arctan \left(\frac{C_{3\rho n}}{C_{2\rho n}}\right).(16)$

The first and second terms in Eq. 15 correspond to non-propagating entropy-mode harmonic and two slow-mode harmonics propagating in opposite directions. To define the magnitudes of entropy-mode C_1ρn and slow-mode C_0ρn harmonics, one has to solve the following set of linear equations,

$\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill {\omega }_{\text{EI}}\hfill & \hfill -{\omega }_{\text{AI}}\hfill & \hfill {\omega }_{\text{AR}}\hfill \\ \hfill {\omega }_{\text{EI}}^2\hfill & \hfill \left({\omega }_{\text{AI}}^2-{\omega }_{\text{AR}}^2\right)\hfill & \hfill -2{\omega }_{\text{AR}}{\omega }_{\text{AI}}\hfill \end{array}\right)\left(\begin{array}{c}\hfill C_{1\rho n}\hfill \\ \hfill C_{2\rho n}\hfill \\ \hfill C_{3\rho n}\hfill \end{array}\right)=\left(\begin{array}{c}\hfill I_{1n}\hfill \\ \hfill I_{2n}\hfill \\ \hfill I_{3n}\hfill \end{array}\right).(17)$

The integrals in the right-hand side I_1n, I_2n, and I_3n are prescribed by the initial perturbation ρ_in (z, 0) and the derivatives ${\left.(\partial \rho (z,t)/\partial t)\right|}_{t=0}$, and ${\left.({\partial }^2\rho (z,t)/\partial t^2)\right|}_{t=0}$ as

$\begin{array}{ll}\hfill & I_{1n}=\frac{2}{l}{\int }_0^l{\rho }_{\text{in}}\left(z,0\right)\cos \left(kz\right)\mathrm{d}z,\hfill \\ \hfill & I_{2n}=\frac{2}{l}{\int }_0^l{\left.\frac{\partial \rho \left(z,t\right)}{\partial t}\right|}_{t=0}\cos \left(kz\right)\mathrm{d}z,\hfill \\ \hfill & I_{3n}=\frac{2}{l}{\int }_0^l{\left.\frac{{\partial }^2\rho \left(z,t\right)}{\partial t^2}\right|}_{t=0}\cos \left(kz\right)\mathrm{d}z.\hfill \end{array}(18)$

The non-oscillating and non-propagating background is defined by the expression shown below:

$a_{\rho 0}\left(z,t\right)=I_{10}=\frac{1}{l}{\int }_0^l{\rho }_{\text{in}}\left(z,0\right)\mathrm{d}z.(19)$

To construct the exact solution of Eq. 5, one should apply the superposition principle. This means, that the full compressive perturbation can be described by the sum of non-oscillating and non-propagating background (Kolotkov et al., 2023) and all harmonics from n = 1 to infinity, using Eq. 15:

$a_{\rho }\left(z,t\right)=a_{\rho 0}\left(z,t\right)+\sum _{n=1}^{\infty }{a}_{\rho n}\left(z,t\right).(20)$

The solution for velocity perturbation, which requires Dirichlet boundary condition, can be constructed in a similar way. There are two main differences in solutions. First, the cosine function in Eqs 15, 18 must be replaced by sine. Second, the background is zero as we assume that the plasma under consideration is non-propagating.

5 Applications of the exact solution

The obtained exact solution Eq. (20) has a number of applications for analyzing the properties and evolution of compression perturbations in plasma. As we have mentioned previously, it allows us not only to follow the dynamics of the full solution but also to monitor the evolution of the eigenmodes that determine it. Moreover, we also can analyze how any harmonics of slow and entropy modes evolve. Further, in this section, we will apply the obtained exact solution to illustrate some evolution ways of the localised initial perturbation and discuss some results revealed by means of it.

5.1 Spatio-temporal evolution of entropy and slow MA modes

First, in order to analyze the spatio-temporal evolution, we have to define the initial perturbation. In this work, we will follow the way we applied in (Zavershinskii et al., 2021), to enable the reader to compare results. In other words, we will consider some Gaussian pulse, which perturbs plasma density, pressure, and temperature:

$\begin{array}{ll}\hfill & a_{\rho ,in}\left(z,0\right)=A_{\rho }\exp \left[-{\left(z-z_0\right)}^2/w\right],\hfill \\ \hfill & a_{P,in}\left(z,0\right)=A_P\exp \left[-{\left(z-z_0\right)}^2/w\right],\hfill \\ \hfill & a_{T,in}\left(z,0\right)=a_{P,in}\left(z,0\right)-a_{P,in}\left(z,0\right),\hfill \\ \hfill & a_{u,in}\left(z,0\right)=0.\hfill \end{array}(21)$

Here, A_ρ and A_P are dimensionless magnitudes of the density and pressure variations; w and z₀ are the effective width and position of the perturbing pulse, respectively.

Secondly, the ranges of control parameters should be specified. The main control parameter in this work is the characteristic timescale attributed to the thermal conduction τ_cond or its reciprocal $\tilde{d}$. To estimate the range of τ_cond, we use typical coronal loop parameters from Table 1 of Reale (2014). Our estimations of the characteristic timescale τ_cond calculated for various coronal loop parameters are shown in Table 1. One may notice that the timescale τ_cond also vary in the fairly broad range. The dimensional characteristic time (Eq. 6), can be an order of magnitude or several orders of magnitude greater or less than the characteristic travel time of isothermal sound, even for loops belonging to the same type. The latter applies to loops in active region and bright points. Under coronal temperatures, the increase in characteristic thermal conduction time is primarily determined by an increase in loop length and density.

TABLE 1

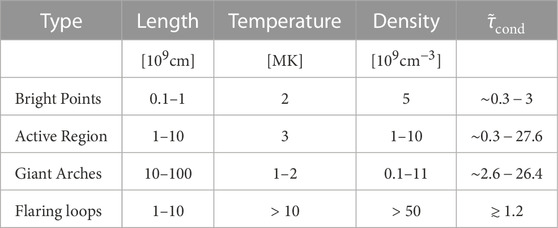
TABLE 1. Estimations of the characteristic timescale ${\tilde{\tau }}_{\text{cond}}$ (Eq. 6) calculated for typical coronal loop parameters taken from Reale (2014).

As we have mentioned above, in this manuscript, we would like to draw attention to the fact, that in the solar corona, the initiated compression perturbation should not always be associated with the slow wave only. In the general case, the initiated perturbation is polytropic. In other words, the ratio of pressure and density magnitudes A_P/A_ρ is not necessarily equal to γ = 5/3 like in the slow mode perturbation and depends on the initiating mechanism. It is quite intuitive that the distribution of energy between the entropy mode and slow modes should be defined by the form and type of initial condition. To illustrate this fact, we use the initial perturbation (Eq. 21) and consider three different values 1.5, 1 and 0.5 of ratio A_P/A_ρ. It can be seen in Figure 1A that an increase in the difference with respect to γ = 5/3 (i.e., decrease in the perturbation adiabaticity) increases the contribution of the entropy mode to the full solution (blue lines). One may also notice the asymmetry of slow mode perturbation growing in time, this is a result of slow wave dispersion caused by thermal conduction. Longer harmonics propagate faster towards the long wavelength limit c_S (adiabatic sound speed) than shorter harmonics tending to c_Si (isothermal sound speed) (Eq. 4).

However, our analysis also revealed a very interesting result, namely, that the distribution of energy between modes depends on the value of thermal conduction and the coronal loop parameters (i.e., on τ_cond). We show the temporal evolution of Gaussian pulse in the plasma with low τ_cond in Figure 1. For illustration, we choose the isothermal initial condition (A_P/A_ρ = 1). The calculations revealed that in the plasma with low τ_cond, the initiating mechanism becomes insignificant and the full solution is defined primarily by the slow mode.

FIGURE 1

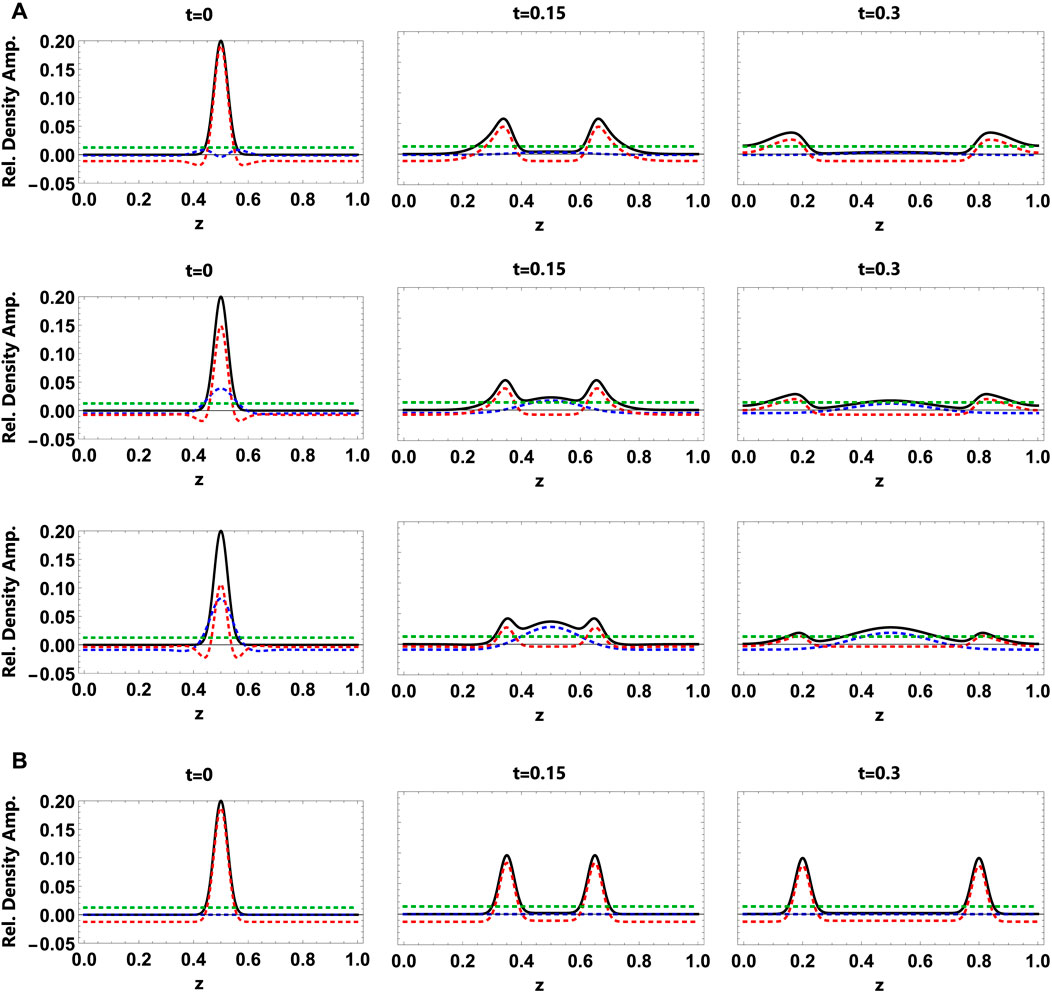
FIGURE 1. (A) Evolution of the initial Gaussian perturbation with width w = l/40 situated at z₀= l/2. The characteristic time is set to τ_cond =25. The top, middle and bottom rows correspond to the ratio of magnitudes A_P/A_ρ equals 1.5,1 and 0.5, respectively. Left, middle, and right columns indicate the solutions at t =0, t =0.15, and t =0.3 of the computational time, respectively. The black solid line corresponds to the full solution (sum of solutions for one entropy and two slow MA modes). The red and blue dashed lines indicate the sum of two slow MA modes and one entropy mode, respectively. The green dashed line corresponds to the non-oscillating and non-propagating background. (B) Evolution of the initial Gaussian perturbation with width w = l/40 situated at z₀= l/2. The characteristic time is set to τ_cond =1. Calculations are made for the ratio of magnitudes A_P/A_ρ equal to 1.

In order to verify the obtained exact solution Eq. 20, we compare it with the numerical solution of Eq. 5. The animation, which shows the construction of an exact solution by summation of harmonics can be found in the Supplementary material. In practice, accounting for the first $\sim 50$ harmonics in Eq. 20 allows for the reproduction of the considered full solution with sufficient accuracy.

5.2 Partition of energy between entropy and slow MA modes

In this Section, we will discuss the issues, when taking into consideration the influence of the entropy mode (even at the stage of perturbation initialization) becomes highly important. In order to answer this question, we aim to calculate the partition of the total (i.e., integrated over all harmonics) initial energy between the modes. For this purpose, we apply the formulation used before in (Zavershinskii et al., 2021) and estimate the ratio of the total initial energies gained by the entropy and slow MA modes, respectively, from the initial Gaussian pulse as

$\mathcal{R}=\sum _{n=1}^{\infty }{C}_{1n}^2/\sum _{n=1}^{\infty }4C_{0n}^2=\frac{Es}{As}.(22)$

In our calculations, we consider how the ratio $\mathcal{R}$ depends on the characteristic timescale τ_cond and the type of initial perturbation, defined by ratio A_P/A_ρ. The results of our estimations are shown in Figure 2. One may notice the two main features, which have been proposed using the analysis of the spatio-temporal evolution of complete perturbation.

FIGURE 2

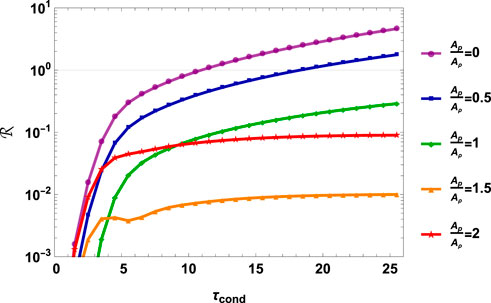
FIGURE 2. Dependence of the ratio $\mathcal{R}$ (Eq. 22) on dimensionless characteristic timescale τ_cond (Eq. 6) calculated for different values magnitude ratio A_P/A_ρ.

The first one concerns the relation between the initiation mechanism of the original signal and the energy distribution. It is seen from Figure 2, that the slow mode tends to be the dominant part of the full solution, when the initial perturbation tends to be adiabatic (A_P/A_ρ → γ = 5/3). The closest to this condition shown in Figure 2 is the orange curve, corresponding to A_P/A_ρ = 1.5. It is seen, that for any τ_cond, the impact of entropy mode is negligible in this case, for illustration we refer to previously shown results in the top row in Figure 1A. The greater the difference of magnitude ratio A_P/A_ρ from value 1.66, the greater impact of entropy mode in the full solution. It can be seen using Figure 2 by comparing the behavior of orange (A_P/A_ρ = 1.5) and green and red curves (A_P/A_ρ = 1 and A_P/A_ρ = 2, respectively). For an illustration of this effect, we refer to Figure 1A, namely, the middle and bottom rows.

The second feature concerns the relation between the energy distribution and the characteristic timescale τ_cond. It is clearly seen that the entropy mode becomes more important for the greater value of τ_cond and that the dependence of $\mathcal{R}$ on τ_cond is highly non-linear. One can notice that for some initialization mechanisms, the entropy mode can become not only comparable to the slow mode but the dominant part of the full solution (see, for example, purple and blue curves in Figure 2). For an illustration of the mentioned feature, we recommend to compare the results in Figures 1A,B. A similar sensitivity of the apparent entropy mode excitation to both the perturbation type and characteristic value of thermal conduction has been demonstrated numerically by Kolotkov (2022).

Further, using the obtained results and estimations of characteristic time τ_cond (see Table 1), we propose, when taking into consideration the influence of the entropy mode becomes important. In particular, an analysis of the compression perturbations in the bright points can be carried out under the assumption that the perturbation is a slow wave with sufficiently high accuracy. The same conclusion can be applied to the perturbation in rarefied and short coronal loops in the active region, for giant arches and flaring loops. In turn, in the longer and denser coronal loops, the influence of the entropy mode becomes more and more significant or even becomes the main feature of the perturbation evolution. And one of these specific cases, will be discussed in the following subsection.

5.3 Phase shifts

In this subsection, we introduce the expressions for phase shifts between perturbations of various plasma parameters.

In order to derive the relationships for the phase shifts in the slow mode, we derive the full exact solution for all considered plasma parameters, namely, for density, temperature, pressuse and velocity perturbation. Using obtained solutions, we introduce the phase shift between temperature and density by calculating the following difference:

${\varphi }_{\rho T}={\varphi }_{\rho n}-{\varphi }_{Tn}=\arctan \left(\frac{\left({\omega }_{\text{AI}}^2+{\omega }_{\text{AR}}^2\right)\sin 2{\varphi }_{\mathrm{\rho }\mathrm{u}}}{\left({\omega }_{\text{AI}}^2+{\omega }_{\text{AR}}^2\right)\cos 2{\varphi }_{\mathrm{\rho }\mathrm{u}}+k^2}\right).(23)$

where n is the harmonic number. Here, we use the following notation

${\varphi }_{\rho u}={\varphi }_{\rho n}-{\varphi }_{un}=\arctan \left(\frac{-{\omega }_{\text{AR}}}{{\omega }_{\text{AI}}}\right),(24)$

which is the phase shift between density and velocity perturbation in the slow wave. In order to estimate the phase shifts, the real ω_AR and imaginary ω_AI parts of the slow wave frequencies have to be calculated. For this purpose, one can use previously introduced analytical expressions (Eq. 14) following from dispersion relation (Eq. 10) or the numerical solution of the dispersion relation (Eq. 10).

It should be noted that obtained relationships (Eq. 23) and (Eq. 24) are valid not only for the fundamental harmonic but can be applied for the estimation of the phase shift of any arbitrary harmonic. Since these expressions follow directly from the exact solution, they also have no restrictions on the value of the thermal conduction coefficient. Thus, the expressions (Eq. 23) and (Eq. 24) are generalisations of the previously obtained relationship for the fundamental harmonic (see, e.g., Wang et al., 2021; (Eq. 51)).

Let us analyze the dependence of the phase shift between temperature and density perturbations for the first three harmonics on characteristic timescale τ_cond. Our calculations are shown in Figure 3. One can notice, that regardless of the number of harmonics, the phase shift ϕ_ρT (Eq. 23) tends to 90° as τ_cond → 0 and tends to 0° as τ_cond → ∞. However, an increase in the harmonic number leads to an increase in the phase shift compared to the fundamental harmonic. Here, we also compare our results with the well-known expression for the phase shift of fundamental harmonic obtained using assumptions of the weak impact of thermal conduction (see, e.g., (Owen et al., 2009)), which is shown by the dashed curve in Figure 3 and can be written as $\arctan \left(\pi /{\tau }_{\text{cond}}\sqrt{\gamma }\right)$ using introduced dimensionless units. The approximate solution works well in the area of its applicability, however, with a strong effect of thermal conductivity, differences appear.

FIGURE 3

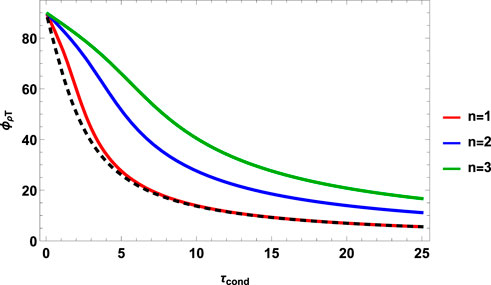
FIGURE 3. The phase shifts ϕ_ρT (Eq. 23) between density and temperature perturbations as a function of dimensionless characteristic timescale τ_cond (Eq. 6). The red, blue, and green colors are for the first (fundamental), second, and third harmonic, respectively. The dashed line indicates the dependence described by the expression for the phase shift of fundamental harmonic obtained using assumptions of the weak impact of thermal conduction (see, e.g., Owen et al., 2009).

For example, Kupriyanova et al. (2019) observed the event of quasi-periodic pulsations (QPP) which has been associated with the second harmonic of a standing slow MA wave in a flaring loop. The oscillations with period p ≈ 74 −80 s have been detected in the loop with length L ≈ 17 −22 Mm, temperature T ≈ 1.1 −1.6 MK. The estimated plasma density is N ≈ 1.2 −1.5 × 10¹¹ cm⁻³ and assumed magnetic field is B ≈ 100 −150 G. The phase shift observed between temperature and density perturbations has been estimated to equal ϕ_ρT ≈ 180°. It follows, from the result shown in Figure 3, that such a large value of the phase shift cannot be described by the thermal conduction, even for the second harmonic of a slow wave. However, for the given loop parameters the estimated dimensionless characteristic timescale τ_cond ≈ 220 (Eq. 6). According to the results shown in Figure 2, this value of τ_cond implies the significant impact of entropy mode in the perturbation evolution. In this case, the observed compression perturbation cannot be unambiguously associated with the slow mode. In other words, the use of the expressions for slow mode phase shifts (Eq. 23) and (Eq. 24) for the interpretation of observations may not be justified.

6 Summary and conclusion

The obtained exact solution (Eq. 20) presents the effect of thermal conduction on the evolution of the compression perturbation in the non-adiabatic plasma of the hot solar corona. This solution gives us comprehensive information about the spatio-temporal dynamics of some initiated variations of plasma parameters. Moreover, it allows us not only to follow the dynamics of the full solution but also to analyze the eigenmodes that determine it, namely, entropy and slow mode. In particular, we can check how justified the association of the observed oscillations with the evolution of only slow waves is. Further, we summarise results, which have been revealed using the exact solution obtained.

• The theory presented is developed for any values of the characteristic timescale τ_cond associated with thermal conduction. Thus, the performed quantitative analysis extends the predictions made using assumptions of weak (Owen et al., 2009; Van Doorsselaere et al., 2011; Wang et al., 2015; Krishna Prasad et al., 2018; Prasad et al., 2022) or strong (Krishna Prasad et al., 2014; Duckenfield et al., 2021) impact of thermal conduction. It also generalises the phase-shift theory constructed earlier with no constraints on thermal conduction (see e.g., Wang et al., 2021) for the fundamental harmonic to the case of an arbitrary harmonic number.

• Analyzing the behaviour of individual Fourier harmonic, we solve the general dispersion relation (Eq. 10) for slow and entropy modes in the plasma affected by thermal conduction only (see e.g., De Moortel and Hood (2003). Our analysis of its solution (Eq. 12) reveals that in contrast to the thermal misbalance (Zavershinskii et al., 2021), the thermal conduction gives no possibility for properties of entropy mode and slow mode to be mixed. The slow waves are always propagating and decaying and entropy modes are always decaying and non-propagating for any value of thermal conduction and harmonic number.

• In this manuscript, we analyze some possible evolution ways of Gaussian compression perturbation (see Figures 1A, B). It has been shown, that the energy fraction attributable to the slow wave in the full solution can vary not only due to a change in the initialization mechanism but also due to a change in the characteristic timescale τ_cond attributed to the thermal conduction and loop parameters. Our estimations of the ratio of the total initial energies gained by the entropy and slow MA modes in an initial Gaussian pulse are shown in Figure 2. In order to propose for the oscillations in which coronal loops it is important to take into account the entropy mode on a par with the slow wave, we estimated the characteristic time τ_cond for typical coronal loop parameters (Reale, 2014). It follows that in the bright points, the compression perturbation is totally defined by the slow mode only. However, for the long and dense loops in the active region, flaring loops, and giant arches the entropy mode can become not only comparable but the dominant part of perturbation.

• The obtained exact solution allows us to derive the expressions (Eq. 23) and (Eq. 24) for the phase shifts between perturbations of various plasma parameters, without limitation on the harmonic number and thermal conduction impact. The phase shift between temperature and density ϕ_ρT (Eq. 23) calculated for the first three harmonics and various values of characteristic timescale τ_cond is shown in Figure 3. It is seen that for any values of thermal conduction and harmonic number, the phase shift is between 90° and 0°. Such a conclusion is in agreement with the results obtained using assumptions of the weak impact of thermal conduction for the fundamental harmonic only (see e.g;, Owen et al., 2009). Using our analytical results, we show that the approximate solution for ϕ_ρT works well in the area of its applicability, however, with a strong effect of thermal conductivity, differences appear. An increase in the harmonic number leads to an increase in the phase shift compared to the fundamental harmonic. Comparing our estimations of the second harmonic phase shift and observations presented by Kupriyanova et al. (2019), we should admit that the observed value ϕ_ρT ≈ 180° are out of range of values prescribed by thermal conduction effect. However, our estimation of characteristic thermal conduction timescale for the given loop parameters gives value τ_cond ≈ 220. According to the results shown in Figure 2, this means that observed compression perturbation may not be unambiguously associated with the slow mode. Thus, the use of the expressions for slow mode phase shifts in their pure form (Eq. 23), and Eq. 24 may not be justified.

As we have mentioned previously, the main limitation of the conducted research is the neglecting of the thermal misbalance effect. In our future work, we plan to consider the combined effect of thermal conduction and thermal misbalance. In other words, we are aiming for derivation of exact solution of Eq. 1. The solution of such a general problem will improve the accuracy of the determination coronal heating function using compression perturbation. Nevertheless, in our opinion for the regions where the effect of thermal misbalance is weak, the presented solution (Eq. 20) and expression following from it are a good help for coronal seismology problems.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

The study was supported in part by the Ministry of Science and Higher Education of Russian Federation under State assignment to educational and research institutions under Project No. FSSS-2023-0009 and No. 0023-2019-0003. CHIANTI is a collaborative project involving George Mason University, the University of Michigan (US), University of Cambridge (UK), and NASA Goddard Space Flight Center (US).

Acknowledgments

The authors would like to thank members of the International Online Team “Effects of Coronal Heating/Cooling on MHD Waves” for inspiring and constructively discussing the research findings.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor DK declared a past co-authorship with the author(s) NM, DZ, and DR.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2023.1167781/full#supplementary-material

References

Agapova, D. V., Belov, S. A., Molevich, N. E., and Zavershinskii, D. I. (2022). Dynamics of fast and slow magnetoacoustic waves in plasma slabs with thermal misbalance. Mon. Notices R. Astronomical Soc. 514, 5941–5951. doi:10.1093/mnras/stac1612

CrossRef Full Text | Google Scholar

Andries, J., Arregui, I., and Goossens, M. (2005). Determination of the coronal density stratification from the observation of harmonic coronal loop oscillations. Astrophysical J. Lett. 624, L57–L60. doi:10.1086/430347

CrossRef Full Text | Google Scholar

Antolin, P., and Froment, C. (2022). Multi-scale variability of coronal loops set by thermal non-equilibrium and instability as a probe for coronal heating. Front. Astronomy Space Sci. 9, 820116. doi:10.3389/fspas.2022.820116

CrossRef Full Text | Google Scholar

Antolin, P. (2020). Thermal instability and non-equilibrium in solar coronal loops: From coronal rain to long-period intensity pulsations. Plasma Phys. Control. Fusion 62, 014016. doi:10.1088/1361-6587/ab5406

CrossRef Full Text | Google Scholar

Banerjee, D., Krishna Prasad, S., Pant, V., McLaughlin, J. A., Antolin, P., Magyar, N., et al. (2021). Magnetohydrodynamic waves in open coronal structures. Space Sci. Rev. 217, 76. doi:10.1007/s11214-021-00849-0

CrossRef Full Text | Google Scholar

Belov, S. A., Molevich, N. E., and Zavershinskii, D. I. (2021). Dispersion of slow magnetoacoustic waves in the active region fan loops introduced by thermal misbalance. Sol. Phys. 296, 122. doi:10.1007/s11207-021-01868-4

CrossRef Full Text | Google Scholar

Chen, S.-X., Li, B., Xiong, M., Yu, H., and Guo, M.-Z. (2015). Standing sausage modes in nonuniform magnetic tubes: An inversion scheme for inferring flare loop parameters. Astrophysical J. 812, 22. doi:10.1088/0004-637x/812/1/22

CrossRef Full Text | Google Scholar

Chin, R., Verwichte, E., Rowlands, G., and Nakariakov, V. M. (2010). Self-organization of magnetoacoustic waves in a thermally unstable environment. Phys. Plasmas 17, 032107. doi:10.1063/1.3314721

CrossRef Full Text | Google Scholar

Cho, I. H., Cho, K. S., Bong, S. C., Moon, Y. J., Nakariakov, V. M., Park, J., et al. (2017). Determination of the alfvén speed and plasma-beta using the seismology of sunspot Umbra. Astrophysical J. Lett. 837, L11. doi:10.3847/2041-8213/aa611b

CrossRef Full Text | Google Scholar

De Moortel, I., and Hood, A. W. (2003). The damping of slow MHD waves in solar coronal magnetic fields. Astronomy Astrophysics 408, 755–765. doi:10.1051/0004-6361:20030984

CrossRef Full Text | Google Scholar

Duckenfield, T. J., Kolotkov, D. Y., and Nakariakov, V. M. (2021). The effect of the magnetic field on the damping of slow waves in the solar corona. Astronomy Astrophysics 646, A155. doi:10.1051/0004-6361/202039791

CrossRef Full Text | Google Scholar

Edwin, P. M., and Roberts, B. (1983). Wave propagation in a magnetic cylinder. Sol. Phys. 88, 179–191. doi:10.1007/bf00196186

CrossRef Full Text | Google Scholar

Field, G. B. (1965). Thermal instability. Astrophysical J. 142, 531. doi:10.1086/148317

CrossRef Full Text | Google Scholar

Heyvaerts, J. (1974). The thermal instability in a magnetohydrodynamic medium. Astronomy Astrophysics 37, 65–73 .37.

Google Scholar

Jess, D. B., Reznikova, V. E., Ryans, R. S. I., Christian, D. J., Keys, P. H., Mathioudakis, M., et al. (2016). Solar coronal magnetic fields derived using seismology techniques applied to omnipresent sunspot waves. Nat. Phys. 12, 179–185. doi:10.1038/nphys3544

CrossRef Full Text | Google Scholar

Kolotkov, D. Y. (2022). Coronal seismology by slow waves in non-adiabatic conditions. Front. Astronomy Space Sci. 9, 1073664. doi:10.3389/fspas.2022.1073664

CrossRef Full Text | Google Scholar

Kolotkov, D. Y., Duckenfield, T. J., and Nakariakov, V. M. (2020). Seismological constraints on the solar coronal heating function. Astronomy Astrophysics 644, A33. doi:10.1051/0004-6361/202039095

CrossRef Full Text | Google Scholar

Kolotkov, D. Y., and Nakariakov, V. M. (2022). A new look at the frequency-dependent damping of slow-mode waves in the solar corona. Mon. Notices R. Astronomical Soc. 514, L51–L55. doi:10.1093/mnrasl/slac054

CrossRef Full Text | Google Scholar

Kolotkov, D. Y., Nakariakov, V. M., and Fihosy, J. B. (2023). Stability of slow magnetoacoustic and entropy waves in the solar coronal plasma with thermal misbalance. arXiv e-prints , arXiv:2301.09012. doi:10.48550/arXiv.2301.09012

CrossRef Full Text | Google Scholar

Kolotkov, D. Y., Nakariakov, V. M., and Zavershinskii, D. I. (2019). Damping of slow magnetoacoustic oscillations by the misbalance between heating and cooling processes in the solar corona. Astronomy Astrophysics 628, A133. doi:10.1051/0004-6361/201936072

CrossRef Full Text | Google Scholar

Kolotkov, D. Y., Zavershinskii, D. I., and Nakariakov, V. M. (2021). The solar corona as an active medium for magnetoacoustic waves. Plasma Phys. Control. Fusion 63, 124008. doi:10.1088/1361-6587/ac36a5

CrossRef Full Text | Google Scholar

Krishna Prasad, S., Banerjee, D., and Van Doorsselaere, T. (2014). Frequency-dependent damping in propagating slow magneto-acoustic waves. Astrophysical J. 789, 118. doi:10.1088/0004-637x/789/2/118

CrossRef Full Text | Google Scholar

Krishna Prasad, S., Jess, D. B., and Van Doorsselaere, T. (2019). The temperature-dependent damping of propagating slow magnetoacoustic waves. Front. Astronomy Space Sci. 6, 57. doi:10.3389/fspas.2019.00057

CrossRef Full Text | Google Scholar

Krishna Prasad, S., Raes, J. O., Van Doorsselaere, T., Magyar, N., and Jess, D. B. (2018). The polytropic index of solar coronal plasma in sunspot fan loops and its temperature dependence. Astrophysical J. 868, 149. doi:10.3847/1538-4357/aae9f5

CrossRef Full Text | Google Scholar

Kupriyanova, E. G., Kashapova, L. K., Van Doorsselaere, T., Chowdhury, P., Srivastava, A. K., and Moon, Y.-J. (2019). Quasi-periodic pulsations in a solar flare with an unusual phase shift. Mon. Notices R. Astronomical Soc. 483, 5499–5507. doi:10.1093/mnras/sty3480

CrossRef Full Text | Google Scholar

Li, B., Antolin, P., Guo, M. Z., Kuznetsov, A. A., Pascoe, D. J., Van Doorsselaere, T., et al. (2020). Magnetohydrodynamic fast sausage waves in the solar corona. Space Sci. Rev. 216, 136. doi:10.1007/s11214-020-00761-z

CrossRef Full Text | Google Scholar

Marsh, M. S., and Walsh, R. W. (2009). Using HINODE/Extreme-Ultraviolet imaging spectrometer to confirm a seismologically inferred coronal temperature. Astrophysical J. Lett. 706, L76–L79. doi:10.1088/0004-637x/706/1/l76

CrossRef Full Text | Google Scholar

Molevich, N. E., and Oraevskii, A. N. (1988). Second viscosity in thermodynamically nonequilibrium media. J. Exp. Theor. Phys. 67, 504.

Google Scholar

Molevich, N. E., Riashchikov, D. S., Zavershinskii, D. I., and Belov, S. A. (2022). Phase shift between temperature, pressure, and density perturbations in a heat-releasing medium. Bull. Lebedev Phys. Inst. 49, 282–287. doi:10.3103/s1068335622090056

CrossRef Full Text | Google Scholar

Molevich, N., and Riashchikov, D. (2021). Shock wave structures in an isentropically unstable heat-releasing gas. Phys. Fluids 33, 076110. doi:10.1063/5.0053394

CrossRef Full Text | Google Scholar

Nakariakov, V. M., Anfinogentov, S. A., Antolin, P., Jain, R., Kolotkov, D. Y., Kupriyanova, E. G., et al. (2021). Kink oscillations of coronal loops. Space Sci. Rev. 217, 73. doi:10.1007/s11214-021-00847-2

CrossRef Full Text | Google Scholar

Nakariakov, V. M., and Kolotkov, D. Y. (2020). Magnetohydrodynamic waves in the solar corona. Annu. Rev. Astronomy Astrophysics 58, 441–481. doi:10.1146/annurev-astro-032320-042940

CrossRef Full Text | Google Scholar

Ofman, L., and Wang, T. (2022). Excitation and damping of slow magnetosonic waves in flaring hot coronal loops: Effects of compressive viscosity. Astrophysical J. 926, 64. doi:10.3847/1538-4357/ac4090

CrossRef Full Text | Google Scholar

Ofman, L., and Wang, T. (2002). Hot coronal loop oscillations observed by SUMER: Slow magnetosonic wave damping by thermal conduction. Astrophysical J. Lett. 580, L85–L88. doi:10.1086/345548

CrossRef Full Text | Google Scholar

Owen, N. R., De Moortel, I., and Hood, A. W. (2009). Forward modelling to determine the observational signatures of propagating slow waves for TRACE, SoHO/CDS, and Hinode/EIS. Astronomy Astrophysics 494, 339–353. doi:10.1051/0004-6361:200810828

CrossRef Full Text | Google Scholar

Prasad, A., Srivastava, A. K., and Wang, T. J. (2021). Role of compressive viscosity and thermal conductivity on the damping of slow waves in coronal loops with and without heating-cooling imbalance. Sol. Phys. 296, 20. doi:10.1007/s11207-021-01764-x

CrossRef Full Text | Google Scholar

Prasad, A., Srivastava, A. K., Wang, T., and Sangal, K. (2022). Role of non-ideal dissipation with heating-cooling misbalance on the phase shifts of standing slow magnetohydrodynamic waves. Sol. Phys. 297, 5. doi:10.1007/s11207-021-01940-z

CrossRef Full Text | Google Scholar

Reale, F. (2014). Coronal loops: Observations and modeling of confined plasma. Living Rev. Sol. Phys. 11, 4. doi:10.12942/lrsp-2014-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Reale, F., Lopez-Santiago, J., Flaccomio, E., Petralia, A., and Sciortino, S. (2018). X-ray flare oscillations track plasma sloshing along star-disk magnetic tubes in the orion star-forming region. Astrophysical J. 856, 51. doi:10.3847/1538-4357/aaaf1f

CrossRef Full Text | Google Scholar

Somov, B. V., Dzhalilov, N. S., and Staude, J. (2007). Peculiarities of entropy and magnetosonic waves in optically thin cosmic plasma. Astron. Lett. 33, 309–318. doi:10.1134/s1063773707050040

CrossRef Full Text | Google Scholar

Spitzer, L. (1965). Physics of fully ionized gases.

Google Scholar

Van Doorsselaere, T., Wardle, N., Del Zanna, G., Jansari, K., Verwichte, E., and Nakariakov, V. M. (2011). The first measurement of the adiabatic index in the solar corona using time-dependent spectroscopy of hinode/EIS observations. Astrophysical J. Lett. 727, L32. doi:10.1088/2041-8205/727/2/l32

CrossRef Full Text | Google Scholar

Wang, T., Innes, D. E., and Qiu, J. (2007). Determination of the coronal magnetic field from hot-loop oscillations observed by SUMER and SXT. Astrophysical J. 656, 598–609. doi:10.1086/510424

CrossRef Full Text | Google Scholar

Wang, T., Ofman, L., Sun, X., Provornikova, E., and Davila, J. M. (2015). Evidence of thermal conduction suppression in a solar flaring loop by coronal seismology of slow-mode waves. Astrophysical J. Lett. 811, L13. doi:10.1088/2041-8205/811/1/l13

CrossRef Full Text | Google Scholar

Wang, T., Ofman, L., Yuan, D., Reale, F., Kolotkov, D. Y., and Srivastava, A. K. (2021). Slow-mode magnetoacoustic waves in coronal loops. Space Sci. Rev. 217, 34. doi:10.1007/s11214-021-00811-0

CrossRef Full Text | Google Scholar

Zaitsev, V. V., and Stepanov, A. V. (1975). On the origin of pulsations of type IV solar radio emission. Plasma cylinder oscillations (I). Issled. Geomagn. Aeron. i Fiz. Solntsa 37, 3–10. 3Z.

Google Scholar

Zaitsev, V. V., and Stepanov, A. V. (1982). On the origin of the hard X-ray pulsations during solar flares. Sov. Astron Lett. 8, 132–134.

Google Scholar

Zavershinskii, D. I., Kolotkov, D. Y., Nakariakov, V. M., Molevich, N. E., and Ryashchikov, D. S. (2019). Formation of quasi-periodic slow magnetoacoustic wave trains by the heating/cooling misbalance. Phys. Plasmas 26, 082113. doi:10.1063/1.5115224

CrossRef Full Text | Google Scholar

Zavershinskii, D. I., Molevich, N. E., Riashchikov, D. S., and Belov, S. A. (2020). Nonlinear magnetoacoustic waves in plasma with isentropic thermal instability. Phys. Rev. E 101, 043204. doi:10.1103/PhysRevE.101.043204

PubMed Abstract | CrossRef Full Text | Google Scholar

Zavershinskii, D., Kolotkov, D., Riashchikov, D., and Molevich, N. (2021). Mixed properties of slow magnetoacoustic and entropy waves in a plasma with heating/cooling misbalance. Sol. Phys. 296, 96. doi:10.1007/s11207-021-01841-1

CrossRef Full Text | Google Scholar

Zhugzhda, Y. D. (1996). Force-free thin flux tubes: Basic equations and stability. Phys. Plasmas 3, 10–21. doi:10.1063/1.871836

CrossRef Full Text | Google Scholar