Dimensionally-dependent uncertainty relations, or why we (probably) won’t see micro-black holes at the LHC, even if large extra dimensions exist

We present a simple gedanken experiment in which a compact object traverses a spacetime with three macroscopic spatial dimensions and n compact dimensions. The compactification radius is allowed to vary, as a function of the object’s position in the four-dimensional space, and we show that the conservation of gravitational self-energy implies the dimensional dependence of the mass-radius relation. In spacetimes with extra dimensions that are compactified at the Planck scale, no deviation from the four-dimensional result is found, but, in spacetimes with extra dimensions that are much larger than the Planck length, energy conservation implies a deviation from the normal Compton wavelength formula. The new relation restores the symmetry between the Compton wavelength and Schwarzschild radius lines on the mass-radius diagram and precludes the formation of black holes at TeV scales, even if large extra dimensions exist. We show how this follows, intuitively, as a direct consequence of the increased gravitational field strength at distances below the compactification scale. Combining these results with the heuristic identification between the Compton wavelength and the minimum value of the position uncertainty, due to the Heisenberg uncertainty principle, suggests the existence of generalised, higher-dimensional uncertainty relations. These relations may be expected to hold for self-gravitating quantum wave packets, in higher-dimensional spacetimes, with interesting implications for particle physics and cosmology in extra-dimensional scenarios.

1 Introduction

For over 40 years, models with compact extra dimensions have attracted a great deal of attention in the theoretical physics literature. Much of this interest was motivated by superstring theory, which is only consistent in ten spacetime dimensions (Green et al., 1988a; Green et al., 1988b), requiring six space-like dimensions to be curled up on scales that make them inaccessible to current high-energy experiments. Theoretically, the compactification scale may be as low as the Planck length, placing it forever beyond the reach of terrestrial particle physics, but models with effective compactification scales as high a millimetre have also been proposed (Antoniadis et al., 1998; Arkani-Hamed et al., 1998). Prior to the start-up of the Large Hadron Collider (LHC), in 2010, interest in the phenomenology of higher dimensional models reached an all-time high. It peaked again following beam upgrades in 2015, but, since then, has been in decline.

In the heady days of the late nineteen-nineties and the first 2 decades of the 21th century, it was hoped, and, indeed, argued persuasively in the scientific literature, that the TeV scale experiments soon to be conducted at CERN would enable the direct detection of compact dimensions with length scales down to $\sim 10^{-19}$ m. It was claimed that these, so-called ‘large’ extra dimensions, could induce the formation of microscopic black holes (Arkani-Hamed et al., 1999; Bleicher et al., 2011; Khachatryan et al., 2011; Kiritsis and Taliotis, 2011; Bellagamba et al., 2012; Mureika et al., 2012; Park, 2012; Alberghi et al., 2013; Nicolini et al., 2013; Taliotis, 2013; Torres et al., 2013; Winstanley, 2013; Belyaev and Calmet, 2015; Hou et al., 2015; Sokolov and Pshirkov, 2017), also known as primordial black holes (PBH), in reference to their cosmic cousins (Carr, 2005; Carr and Kuhnel, 2020; Carr et al., 2021; Green and Kavanagh, 2021; Escrivà et al., 2022; Friedlander et al., 2022). These claims even attracted considerable attention in the popular press (American Physical Society, 2008; NASA, 2008; New York Times, 2008; BBC, 2013; Huffington Post, 2014; Forbes, 2016).

The argument behind this assertion was straightforward and reasonable. It is well known that the radius of an uncharged and non-spinning (Schwarzschild) black hole depends, not only on its mass, but also on the dimensionality it of the spacetime it inhabits. The higher-dimensional Schwarzschild radius varies as ${\mathcal{R}}_{\text{S}}\propto M^{\frac{1}{1+n}}$, where n is the number of space-like extra dimensions, over and above the three Hubble scale dimensions that make up the macroscopic Universe (Weinberg, 2008). Thus, assuming that the usual mass-dependence of the Compton wavelength, R_C ∝ M⁻¹, remains unchanged in the presence of the compact space, the intersection between ${\mathcal{R}}_{\text{S}}$ and R_C occurs close to the critical values

$R_{\text{crit}}={\left(\frac{\hslash G_{4+n}}{c^3}\right)}^{\frac{1}{2+n}},M_{\text{crit}}={\left(\frac{{\hslash }^{1+n}{c}^{1-n}}{G_{4+n}}\right)}^{\frac{1}{2+n}}.(1)$

For n ≥ 0, these expressions serve as the definitions of the Planck length, and mass, respectively (Horowitz, 2012). Since, in spacetimes with n compact dimensions, the four-dimensional Newton’s constant is related to its higher-dimensional counterpart, and to the compactification radius R_E, via (Maartens and Koyama, 2010)

$G_{4+n}=G_4{R}_{\text{E}}^n,(2)$

it follows that, for sufficiently large R_E, the mass-energy needed to create a black hole may be brought within the TeV range of the LHC.

More recently, new phenomenological models have been proposed, in which the possible dimensional dependence of the Compton wavelength has been explored (Lake and Carr, 2016; Carrr, 2018; Lake and Carr, 2018; Carr, 2022), via so-called black hole–uncertainty principle (BHUP) correspondence, which is also referred to as the Compton–Schwarzschild correspondence in the literature (Carr et al., 2011; Carr et al., 2015; Carr, 2016; Lake and Carr, 2015; Singh, 2017; Singh, 2018; da Silva and Silva, 2022). This modification alters the intersection with the Schwarzschild radius, and is capable of restoring complete symmetry to the (M, R) diagram, pushing the threshold for black hole formation back up to the four-dimensional Planck mass, $M_{\text{Pl}}=\sqrt{\hslash c/G_4}$. However, despite the various arguments used to justify these models (Lake and Carr, 2016; Carrr, 2018; Lake and Carr, 2018; Carr, 2022), the proposed dimensional dependence lacks a clear physical motivation. In this work, we motivate them in a more direct way, by outlining a clear physical mechanism that is capable of altering the mass-radius relation of any compact object, including that of fundamental particles.

The structure of this paper is as follows. In the main body of the work, Sec. II, we present a simple gedanken experiment in a hypothetical Universe with three macroscopic spatial dimensions and n compact extra dimensions. The compactification radius is allowed to vary as a function of position in the four-dimensional subspace, which is divided into three regions. In the first region, the extra dimensions are compactified at the four-dimensional Planck-scale, $R_{\text{Pl}}=\sqrt{\hslash G/c^3}$, while in the third they are compactified at a much larger radius, R_E > R_Pl. The second region, in which the compactification scale grows monotonically, interpolates smoothly between the other two. We then consider a compact object, which passes from region 1 to region 3, and impose the conservation of gravitational self-energy. Roughly speaking, since gravity becomes stronger on scales R_Pl < R < R_E, as we move through region 2, the radius of the object must increase, in order to keep its gravitational self-energy constant. Furthermore, since rest mass is conserved during this transition, it follows that the mass-radius relation must be modified.

In this study, we perform explicit calculations by assuming that the gravitational potential of the object can be approximated by the weak field (Newtonian) limit. However, despite this, our analysis correctly reproduces well-known results for strongly-gravitating objects, such as higher-dimensional black holes and neutron stars, up to numerical factors of order unity, which is consistent with the non-relativistic approximation. This gives us confidence in the method, which we then extend to the study of fundamental particles, for which the non-relativistic approximation is undoubtedly valid.

We verify that, beginning with an effectively four-dimensional black hole in region 1, we obtain the correct (order of magnitude) expression for the higher-dimensional Schwarzschild radius in region 3. This gives us confidence in our procedure, which we note is agnostic to the initial mass-radius relation of the object. We then consider a fundamental particle, by beginning instead with the standard formula for the Compton wavelength, and obtain an effective, higher-dimensional Compton radius, in the third region. Its implications for the (non-) formation of black holes at the LHC, as well as for the quantum mechanical uncertainty relations of self-gravitating wave packets in higher-dimensional spacetimes, are briefly discussed. We summarise our conclusions, and consider the prospects for future work on this model, in Sec. III.

2 The gedanken experiment

Let us assume, for simplicity, that the compact object we consider is spherically symmetric. In region 1, its internal energy is, therefore

$E=M{c}^2-{\alpha }_4\frac{G_4{M}^2}{R},(3)$

where α₄ is a numerical constant determined by the mass profile of the sphere, M(r). For example, α₄ = 3/5 for a sphere of uniform density and should be of order unity for all non-pathological profiles (Weisstein et al., 1973). Here, R denotes the effective macrosopic radius of the object and Eq. 3 holds for all R ≳ R_E = R_Pl. We note that distances below this scale cannot be probed directly, by either black holes or fundamental particles, due to the intersection of the Compton wavelength and Schwarzschild radius lines near the Planck point on the (M, R) diagram (Lake and Carr, 2015; Carr, 2016).

Requiring E ≤ 0, which implies a bound state, yields

$R\le {\alpha }_4\frac{G_{4}M}{c^2}.(4)$

For α₄ = 2, we then recover the condition

$R\le R_{\text{S}}\left(M\right)=\frac{2G_{4}M}{c^2},(5)$

where R_S is the four-dimensional Schwarzschild radius. Thus, if Eq. 5 is satisfied, the object is a black hole in the first region. For α₄ = 9/4, an analogous condition implies violation of the Buchdahl inequality (Buchdahl, 1959) and the sphere may be viewed as a compact star undergoing collapse. Conversely, for E > 0, R > (9/4)G₄M/c², the object is stable against its own self-gravity.

Setting R = R_C, where

$R_{\text{C}}\left(M\right)=\frac{\hslash }{Mc}(6)$

is the standard Compton radius (Rae and Napolitano, 2015), Eq. 3 implies that a fundamental particle is stable against gravitational collapse (E > 0) when

$M\lesssim M_{\text{Pl}},R_{\text{C}}\left(M\right)\gtrsim R_{\text{Pl}},(7)$

where

$R_{\text{Pl}}=\sqrt{\frac{\hslash G_4}{c^3}}\simeq 10^{-35}\mathrm{m},M_{\text{Pl}}=\sqrt{\frac{\hslash c}{G_4}}\simeq 10^{-8}\mathrm{k}\mathrm{g}.(8)$

Equation 7 justifies our previous assertion that Eq. 3 holds, for R ≳ R_Pl, when the extra dimensions are compactified at the (four-dimensional) Planck scale. For fundamental particles, this corresponds to the region M ≲ M_Pl, whereas, for black holes, it corresponds to

$M\gtrsim M_{\text{Pl}},R_{\text{S}}\left(M\right)\gtrsim R_{\text{Pl}}.(9)$

The intersection of the standard Compton line and the four-dimensional Schwarzschild line near the Planck point then precludes the existence of any fundamental object with R(M) ≲ R_Pl.

In the third region, the internal energy of the object is given by Eq. 3, for R > R_E, where R_E > R_Pl is the compactification radius, but by

$E=M{c}^2-{\alpha }_{4+n}\frac{G_{4+n}{M}^2}{{\mathcal{R}}^{1+n}}(10)$

for $R_{\text{Pl}}\le \mathcal{R}\le R_{\text{E}}$. Here, $\mathcal{R}$ denotes the (4 + n)-dimensional radius in region 3 and α_4+n is a numerical constant determined by the mass profile of the object in the higher-dimensional space. For simplicity, we assume that all n extra dimensions are compactified on the same scale. The relation between G₄ and the higher-dimensional Newton’s constant, G_4+n, is given by Eq. 2 (Maartens and Koyama, 2010).

By choosing appropriate values of α_4+n, we may recover the (4 + n)-dimensional analogues of the Buchdahl bound (Burikham et al., 2015; Burikham et al., 2016) and the Schwarzschild radius (Horowitz, 2012), from the energy conditions E < (>) 0. In any number of dimensions, the Buchdahl radius is proportional to the Schwarzschild radius, and, neglecting numerical factors of order unity, the latter may be written as

${\mathcal{R}}_{\text{S}}\left(M\right)\simeq {\left(\frac{G_{4+n}M}{c^2}\right)}^{\frac{1}{1+n}}\simeq {\left(R_{\text{S}}\left(M\right)R_{\text{E}}^n\right)}^{\frac{1}{1+n}}.(11)$

where R_S(M) again denotes the four-dimensional Schwarzschild radius, as in Eq. 5.

Let us now consider a non-relativistic, self-gravitating sphere, with arbitrary mass-radius relation, passing from region 1 to region 3. Furthermore, let us assume that, whatever its mass-radius relation in the four-dimensional space of the first region, the sphere remains small enough to be effectively (4 + n)-dimensional in the third. Thus, in region 1, its radius in the three macroscopic spatial dimensions is R(M) ≳ R_Pl and, in region 3, its higher-dimensional radius satisfies $R_{\text{Pl}}\lesssim \mathcal{R}(M)\lesssim R_{\text{E}}$. If its internal energy remains unchanged, energy conservation then implies

$\mathcal{R}\left(M\right)\simeq {\left(R\left(M\right)R_{\text{E}}^n\right)}^{\frac{1}{1+n}}.(12)$

again ignoring numerical factors of order unity, which is consistent with the non-relativistic approximation. Note that we again use the calligraphic font, $\mathcal{R}$, to denote radii in (4 + n) dimensions, and the normal font R to denote four-dimensional radii.

Substituting R(M) ≃ R_S(M) 5) into (12), we recover the correct expression for the higher-dimensional Schwarzschild radius, ${\mathcal{R}}_{\text{S}}(M)$ (11). Next, we note that, if $R_{\text{Pl}}<{\mathcal{R}}_{\text{S}}(M)<R_{\text{E}}$, then R_Pl < R_S(M) < R_E. It follows, immediately, that ${\mathcal{R}}_{\text{S}}(M)>R_{\text{S}}(M)$. This result can be understood intuitively as follows. Since, in the third region, the gravitational force is stronger than in the first on scales $\mathcal{R}<R_{\text{E}}$, the radius of the black hole can neither decrease, nor remain the constant, without increasing its internal energy. If this energy is conserved, the black hole must increase in size and the (4 + n)-dimensional Schwarzschild radius, ${\mathcal{R}}_{\text{S}}(M)$, must be larger than the four-dimensional radius, R_S(M). The relation between the two is fixed, by energy conservation, according to Eq. 11,

Clearly, we may repeat a similar argument for stable compact objects obeying the four-dimensional Buchdahl bound in region 1. The same compact spheres then obey the higher-dimensional Buchdahl bound in region 3. Hence, although the argument presented above is simple and heuristic, it allows us to recover the same relations (to within an order of magnitude) as those obtained by exactly solving the gravitational field equations in (4 + n)-dimensional spacetime (Horowitz, 2012; Burikham et al., 2015; Burikham et al., 2016).

However, its greatest advantage is that is agnostic to the mass-radius relation of the compact object. We may therefore apply it to fundamental particles, as well as to black holes and conventional fluid spheres. Thus, substituting R(M) = R_C(M) ∝ M⁻¹ 6) into Eq. 12, we obtain the higher-dimensional Compton wavelength,

${\mathcal{R}}_{\text{C}}\left(M\right)\simeq {\left(R_{\text{C}}\left(M\right)R_{\text{E}}^n\right)}^{\frac{1}{1+n}}\simeq R_{*}{\left(\frac{M_{\text{Pl}}}{M}\right)}^{\frac{1}{1+n}}.(13)$

where

$R_{*}={\left(R_{\text{Pl}}{R}_{\text{E}}^n\right)}^{\frac{1}{1+n}},(14)$

so that R_Pl < R_* < R_E. It may be verified that the (4 + n)-dimensional Compton and Schwarzschild lines intersect at the point (M, R) ≃ (M_Pl, R_*), so that the production of PBHs still requires energies of the order of the Planck energy (Lake and Carr, 2016; Carrr, 2018; Lake and Carr, 2018; Carr, 2022).

This result also be understood, intuitively, in the same way as our heuristic derivation of the higher-dimensional Schwarzschild radius. Namely, if the rest mass of the particle remains constant as it traverses the path from region 1 to region 3, its radius cannot remain constant, or decrease, without increasing its gravitational binding energy. Therefore, if its total internal energy remains constant, its radius must expand as it enters the higher-dimensional region, in which gravity is stronger, on scales $\mathcal{R}<R_{\text{E}}$, than in four-dimensional space. Clearly, this relation must also hold for particles that were always confined to region 3.

To aid visualisation, a schematic representation of the gedanken experiment set up is given in Figure 1. In Figure 2A, the key length and mass scales of the standard scenario, corresponding to Eq. 1, are depicted on the (M, R) diagram, while the key scales for our scenario are depicted in Figure 2B. The important difference between the two scenarios is that the former does not account for the self-gravitational energy of the particle, whereas the latter does, to within the accuracy permitted by the non-relativistic, weak-field approximation, which we also apply to micro-black holes. Maintaining this approximation, we may apply the usual, heuristic identification between the Compton wavelength formula and the limiting values of the Heisenberg uncertainty principle (HUP),

${\left(\mathrm{\Delta }X\right)}_{\text{min}}\simeq {\mathcal{R}}_{\text{C}}\left(M\right),{\left(\mathrm{\Delta }P\right)}_{\text{max}}\simeq Mc,(15)$

giving

$\mathrm{\Delta }X\gtrsim R_{*}{\left(\frac{M_{\text{Pl}}c}{\mathrm{\Delta }P}\right)}^{\frac{1}{1+n}}.(16)$

We recall that, for ΔP ≳ Mc, fundamental particles have sufficient energy to undergo pair-production, in interactions that conserve the relevant quantum numbers (Peskin and Schroeder, 1995; Donoghue et al., 2014), yielding the limits in Eq. 15. These, in turn, correspond to the dimensionally-dependent uncertainty relation, Eq. 16.

FIGURE 1

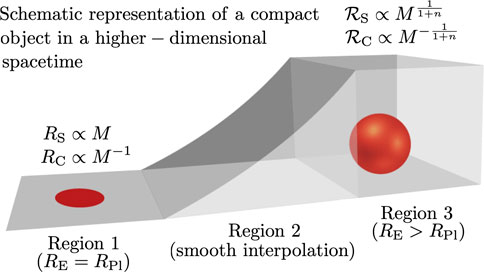
FIGURE 1. Schematic illustration of the three-part universe in our gedanken experiment. To enable the schematic representation of (3+ n)-dimensional space, neglecting the time dimension of the (4+ n)-dimensional spacetime, the three large dimensions are depicted as a two-dimensional plane and the n compact directions are depicted as a single extra dimension, extending into the z-direction of the diagram. Furthermore, since Planck-sized extra dimensions do not contribute correction terms, either to the higher-dimensional Schwarzschild radius, or to the Compton wavelength, we neglect them in this illustration. Hence, the region on the far left-hand side represents (3+ n)-dimensional space, with n dimensions compactified at the Planck scale, while the region on the far right-hand side represents a space with three large dimensions and n extra dimensions, compactified on some scale R_E > R_Pl. The central region interpolates smoothly between the two, so that the gravitational radius of the compact body changes, according to the following scheme: In region 1 (left), the extra dimensions are compactified at the (four-dimensional) Planck scale and both black holes and fundamental particles are effectively four-dimensional, even in the presence of the higher-dimensional space. In region 3 (right), the compactification radius is much larger than the Planck length and all objects are effectively (4+ n)-dimensional, on scales smaller than the compactification radius. Conservation of energy implies that, whatever the mass-radius relation of the object in the first region, R(M), its radius in the third region, $\mathcal{R}(M)$, must be larger: $\mathcal{R}(M)>R(M)$. This is due to the increased strength of the gravitational field in higher dimensions. For black holes, R_S ∝ M in region 1 and ${\mathcal{R}}_{\text{S}}\propto M^{\frac{1}{1+n}}$ in region 3. Applying the same logic to the gravitational radius of fundamental particles, R_C ∝ M⁻¹ in region 1, yielding ${\mathcal{R}}_{\text{C}}\propto M^{-\frac{1}{1+n}}$ in region 3, due to the conservation of gravitational self-energy.

FIGURE 2

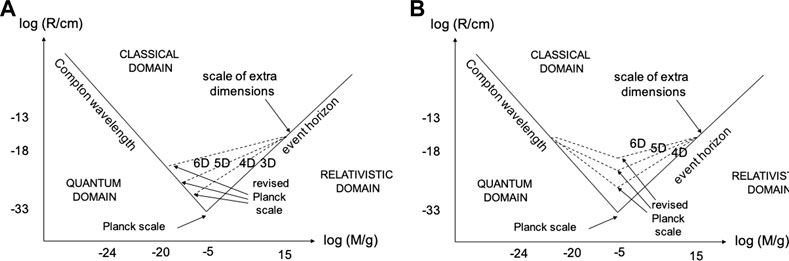
FIGURE 2. Figure 2A (left panel) shows the standard Compton line, R_C ∝ M⁻¹, and the Schwarzschild radius lines for n =0, n =1, n =2 and n =3. These lines intersect near the higher-dimensional Planck point, $(M,R)=({(M_{\text{Pl}}^2{M}_{\text{E}}^n)}^{\frac{1}{2+n}},{(R_{\text{Pl}}^2{R}_{\text{E}}^n)}^{\frac{1}{2+n}})\left.\right)$, where R_Pl and M_Pl denote the four-dimensional Planck scales, R_E > R_Pl is the compactification radius, and M_E = ℏ/(R_Ec)< M_Pl is the associated mass scale. The points of intersection are equivalent to the critical scales shown in Eq. 1, due to Eq. 2; Figure 2B (right panel) shows the modified scenario, in which we account for the increased self-gravity of the quantum particle in the presence of the extra dimensions, yielding ${\mathcal{R}}_{\text{C}}\propto M^{-\frac{1}{1+n}}$. The Compton and Scwarzschild lines now intersect at the point (M, R)=(M_Pl, R_*), where R_* is defined in Eq. 14. The restored symmetry of the mass-radius diagram precludes the formation of black holes at TeV scales, even if large extra dimensions exist. These figures are reproduced from (Lake and Carr, 2018), with permission.

Equation 16 may be expected to hold for self-gravitating wave packets, on scales $\mathcal{R}<R_{\text{E}}$, in spacetimes with compact extra dimensions. By contrast, on scales $\mathcal{R}>R_{\text{E}}$, or when R_E ≃ R_Pl, the standard HUP,

$\mathrm{\Delta }X\gtrsim \frac{R_{\text{Pl}}{M}_{\text{Pl}}c}{\mathrm{\Delta }P},(17)$

still holds, where we have rewritten ℏ = R_PlM_Plc.

Finally, before concluding this section, we note that, although Eq. 16 represents a form of generalised uncertainty principle, which is valid for self-gravitating objects in higher-dimensional spacetimes, this is not the same as the ‘generalised uncertainty principle’ (GUP), commonly referred to in the quantum gravity literature (see, for example (Adler et al., 2001; Maziashvili, 2006; Xiang and Wen, 2009; Lake et al., 2019; Sakalli and Kanzi, 2022; Lake et al., 2023), and references therein). In fact, the derivation of Eq. 16 is based on two fundamental assumptions, namely, a) that the gravitational self-energy of the quantum wave packet is conserved in the presence of extra dimensions, and b) that the standard HUP holds in their absence.

By contrast, the usual GUP is derived, via a gedanken experiment in four-dimensional spacetime, by considering the gravitational interaction between a measured particle and a probing photon. This gives rise to a correction term, to the position uncertainty Δx, which is proportional to the effective four-dimensional Schwarzschild radius of the wave packet, R_S ≃ G₄Δp/c³, yielding

$\mathrm{\Delta }x\gtrsim \frac{\hslash }{2\mathrm{\Delta }p}+\frac{2G_4}{c^3}\mathrm{\Delta }p,(18)$

where α again denotes a numerical constant of order unity. Assuming, instead, that the GUP (18) holds in a four-dimensional Universe, in place of the HUP (17), we may expect a unification of the Compton and Schwarzschild lines, of the form

$R_{\text{C/S}}\simeq \frac{\hslash }{2Mc}+\frac{2G_4}{c^2}Mc,(19)$

as predicted by the so-called BHUP correspondence, mentioned in the Introduction (Carrr, 2018; Lake and Carr, 2018; Carr, 2022; Lake and Carr, 2016; Carr et al., 2011; Carr et al., 2015; Carr, 2016; Lake and Carr, 2015; Singh, 2017; Singh, 2018; da Silva and Silva, 2022). Combing these expressions with the arguments presented above yields even richer phenomenology: rather than simply restoring symmetry to the (M, R) diagram higher dimensions, it may provide a way to unify the Compton and Schwarzschild lines, even in higher-dimensional spacetimes. Such an analysis lies outside the scope of the present, preliminary study, and is left to a future work.

3 Discussion

We have presented a simple gedanken experiment in a hypothetical spacetime with three macroscopic spatial dimensions and n compact extra dimensions. The compactification radius was allowed to vary as a function of spatial position, in the four-dimensional submanifold, which is divided into three regions. In the first region, the extra dimensions are Planck-scale, while in the third they are compactified at a much larger radius. The second region, in which the compactification scale grows monotonically, interpolates smoothly between the other two. We considered a spherical compact object that traverses a path from region 1 to region 3, and imposed the conservation of gravitational self-energy.

If the object is a black hole in the first region, with R ∝ M, energy conservation alone yields the correct expression for the higher-dimensional Schwarzschild radius, $R\propto M^{\frac{1}{1+n}}$, in the third. However, this procedure is agnostic to the mass-radius relation of the object. Hence, considering a fundamental particle instead of a black hole, we instead imposed the standard formula for the Compton wavelength, R ∝ M⁻¹, in the first region. Conservation of energy then implies the existence of a higher-dimensional Compton wavelength, $R\propto M^{-\frac{1}{1+n}}$, in the third region. Clearly, this relation must also hold for particles that have always been confined to region 3.

The new relation restores the symmetry between the Compton and Schwarzschild lines on the mass-radius diagram, in higher-dimensional spacetimes, and precludes the formation of black holes at TeV scales, even if large extra dimensions exist. We have shown how this follows, intuitively, as a direct consequence of the increased gravitational field strength at distances below the compactification scale. Combining these results with the usual, heuristic identification between the Compton wavelength and the minimum position uncertainty allowed by the Heisenberg uncertainty principle, ΔX ≳ R_C (ΔP ≲ Mc), suggests the existence of generalised, higher-dimensional uncertainty relations.

Indeed, the possible dependence of the uncertainty relations on the dimensionality of the spacetime has already been explored in the literature, in the context of the so-called black hole-uncertainty principle (BHUP) correspondence (Lake and Carr, 2016; Carrr, 2018; Lake and Carr, 2018; Carr, 2022). If the usual uncertainty relation-Compton wavelength correspondence is still required to hold, in a higher-dimensional context, then the dimensional-dependence of the Compton wavelength is also (theoretically) necessary.

The difference between this and previous work is that, here, we present a clear physical argument for why this change should occur, and show, explicitly, that the effects of self-gravitation on quantum wave packets are precisely those required to maintain the, up to now conjectured, higher-dimensional BHUP correspondence. This is also known as the Compton-Schwarzschild correspondence, in some of the previous literature (Carr et al., 2011; Carr et al., 2015; Carr, 2016; Lake and Carr, 2015; Singh, 2017; Singh, 2018; da Silva and Silva, 2022).

In the present, preliminary analysis, we assumed throughout that the gravitational potential of the compact sphere can be well approximated by the Newtonian regime. Though this is undoubtedly a limitation of the current work, we were still able to recover, to within numerical factors of order unity, the well-known expressions for relativistic objects, such as higher-dimensional black holes and neutron stars (Burikham et al., 2015; Burikham et al., 2016). This strongly suggests that the dimensionally-dimensional uncertainty relations, which we derive for self-gravitating wave packets, are robust, since the weak field approximation is undoubtedly valid for fundamental particles.

As extensions of the current analysis, we should consider relativistic corrections, as well as the incorporation of modified uncertainty principles, obtained from the quantum gravity literature, such as the generalised uncertainty principle (GUP) (Adler et al., 2001; Maziashvili, 2006; Xiang and Wen, 2009; Lake et al., 2019; Sakalli and Kanzi, 2022; Lake et al., 2023), extended uncertainty principle (EUP), and extended generalised uncertainty principle (EGUP) (Bolen and Cavaglia, 2005; Bambi and Urban, 2008; Park, 2008). Furthermore, in order to consistently incorporate the latter, we must also consider the conditions for the formation of gravitational bound states, in higher dimensions, in the presence of a positive cosmological constant (Burikham et al., 2015; Burikham et al., 2016).

Previous studies suggest that these modifications may give rise to a unified description of the Compton and Schwarzschild radii, linking the properties of black holes and fundamental particles in higher-dimensional scenarios (Lake and Carr, 2016; Carrr, 2018; Lake and Carr, 2018; Carr, 2022). The present work represents a small, preliminary step towards understanding the physical mechanism behind this potentially important correspondence, which may have important phenomenological implications for black holes, cosmology, and high-energy particle physics, beyond the non-production of PBH at TeV scales.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the Natural Science Foundation of Guangdong Province, grant no. 008120251030 (ML) and by the Grant of Scientific and Technological Projection of Guangdong province, no. 2021A1515010036 (SDL). AW acknowledges partial support from the Center of Excellence in Quantum Technology, Faculty of Engineering, Chiang Mai University, and the NSRF via the Program Management Unit for Human Resources and Institutional Development, Research and Innovation (grant number B05F640218), National Higher Education Science Research and Innovation Policy Council.

Acknowledgments

Grateful thanks to Wansuree Massagram, for the artful rendering of Figure 1, and Bernard Carr, for permission to reproduce Figure 2, and for helpful discussions and suggestions during the preparation of the manuscript. ML acknowledges the Department of Physics and Materials Science, Faculty of Science, Chiang Mai University, for providing research facilities. AW would like to acknowledge partial support from the Center of Excellence in Quantum Technology, Faculty of Engineering, Chiang Mai University, and the NSRF via the Program Management Unit for Human Resources and Institutional Development, Research and Innovation (grant number B05F640218), National Higher Education Science Research and Innovation Policy Council. This work was supported by the Natural Science Foundation of Guangdong Province, grant no. 008120251030 (ML) and by the Grant of Scientific and Technological Projection of Guangdong province, no. 2021A1515010036 (SDL).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adler, R. J., Chen, P., and Santiago, D. I. (2001). The Generalized uncertainty principle and black hole remnants. Gen. Rel. Grav. 33, 2101–2108. doi:10.1023/a:1015281430411

CrossRef Full Text | Google Scholar

Alberghi, G. L., Bellagamba, L., Calmet, X., Casadio, R., and Micu, O. (2013). Charged black hole remnants at the LHC. Eur. Phys. J. C 73 (6), 2448. doi:10.1140/epjc/s10052-013-2448-0

CrossRef Full Text | Google Scholar

American Physical Society (2008). The end of the world at the large Hadron collider? Available at: https://physics.aps.org/articles/v1/14.

Google Scholar

Antoniadis, I., Arkani-Hamed, N., Dimopoulos, S., and Dvali, G. R. (1998). New dimensions at a millimeter to a Fermi and superstrings at a TeV. Phys. Lett. B 436, 257–263. doi:10.1016/s0370-2693(98)00860-0

CrossRef Full Text | Google Scholar

Arkani-Hamed, N., Dimopoulos, S., and Dvali, G. R. (1999). Phenomenology, astrophysics and cosmology of theories with submillimeter dimensions and TeV scale quantum gravity. Phys. Rev. D. 59, 086004. doi:10.1103/physrevd.59.086004

CrossRef Full Text | Google Scholar

Arkani-Hamed, N., Dimopoulos, S., and Dvali, G. R. (1998). The Hierarchy problem and new dimensions at a millimeter. Phys. Lett. B 429, 263–272. doi:10.1016/s0370-2693(98)00466-3

CrossRef Full Text | Google Scholar

Bambi, C., and Urban, F. R. (2008). Natural extension of the generalized uncertainty principle. Quant. Grav. 25, 095006. doi:10.1088/0264-9381/25/9/095006

CrossRef Full Text | Google Scholar

BBC (2013). Will we ever create a black hole in the laboratory? Available at: https://www.bbc.com/future/article/20130716-will-we-ever-create-a-black-hole.

Google Scholar

Bellagamba, L., Casadio, R., Di Sipio, R., and Viventi, V. (2012). Black hole remnants at the LHC. Eur. Phys. J. C 72, 1957. doi:10.1140/epjc/s10052-012-1957-6

CrossRef Full Text | Google Scholar

Belyaev, A., and Calmet, X. (2015). Quantum black holes and their lepton signatures at the LHC with CalCHEP. J. High. Energy Phys. 08, 139. doi:10.1007/jhep08(2015)139

CrossRef Full Text | Google Scholar

Bolen, B., and Cavaglia, M. (2005). (Anti-)de Sitter black hole thermodynamics and the generalized uncertainty principle. Gen. Rel. Grav. 37, 1255–1262. doi:10.1007/s10714-005-0108-x

CrossRef Full Text | Google Scholar

Buchdahl, H. A. (1959). General relativistic fluid spheres. Phys. Rev. 116, 1027–1034. doi:10.1103/physrev.116.1027

CrossRef Full Text | Google Scholar

Burikham, P., Cheamsawat, K., Harko, T., and Lake, M. J. (2016). The minimum mass of a charged spherically symmetric object in D dimensions, its implications for fundamental particles, and holography. Eur. Phys. J. C 76 (3), 106. doi:10.1140/epjc/s10052-016-3948-5

CrossRef Full Text | Google Scholar

Burikham, P., Cheamsawat, K., Harko, T., and Lake, M. J. (2015). The minimum mass of a spherically symmetric object in D-dimensions, and its implications for the mass hierarchy problem. Eur. Phys. J. C 75 (9), 442. doi:10.1140/epjc/s10052-015-3673-5

CrossRef Full Text | Google Scholar

Carr, B. J., Mureika, J., and Nicolini, P. (2015). Sub-planckian black holes and the generalized uncertainty principle. J. High. Energy Phys. 07, 052.

CrossRef Full Text | Google Scholar

Carr, B. J. (2005). Primordial black holes: Do they exist and are they useful? Ithaca, New York: Cornell University. arXiv:astro-ph/0511743 [astro-ph].

Google Scholar

Carr, B. J. (2016). The black hole uncertainty principle correspondence. Springer Proc. Phys. 170, 159–167.

CrossRef Full Text | Google Scholar

Carr, B. J. (2022). The Generalized Uncertainty Principle and higher dimensions: Linking black holes and elementary particles. Front. Astron. Space Sci. 9, 1008221. doi:10.3389/fspas.2022.1008221

CrossRef Full Text | Google Scholar

Carr, B., Kohri, K., Sendouda, Y., and Yokoyama, J. (2021). Constraints on primordial black holes. Rept. Prog. Phys. 84 (11), 116902. doi:10.1088/1361-6633/ac1e31

CrossRef Full Text | Google Scholar

Carr, B., and Kuhnel, F. (2020). Primordial black holes as dark matter: Recent developments. Ann. Rev. Nucl. Part. Sci. 70, 355–394. doi:10.1146/annurev-nucl-050520-125911

CrossRef Full Text | Google Scholar

Carr, B., Modesto, L., and Premont-Schwarz, I. (2011). Generalized uncertainty principle and self-dual black holes. Ithaca, New York: Cornell University. arXiv:1107.0708 [gr-qc].

Google Scholar

Carrr, B. J. (2018). Quantum black holes as the link between microphysics and macrophysics. Springer Proc. Phys. 208, 85–94.

CrossRef Full Text | Google Scholar

da Silva, M. F., and Silva, C. A. S. (2022). The Compton/Schwarzschild duality, black hole entropy and quantum information. Ithaca, New York: Cornell University. arXiv:2205.09502 [gr-qc].

Google Scholar

Donoghue, J. F., Golowich, E., and Holstein, B. R. (2014). Dynamics of the standard model. Cambridge, U.K. Cambridge University Press.

Google Scholar

Escrivà, A., Kuhnel, F., and Tada, Y. (2022). Primordial black holes. Ithaca, New York: Cornell University. arXiv:2211.05767 [astro-ph.CO].

Google Scholar

Forbes, (2016). Could the large Hadron collider make an earth-killing black hole? https://www.forbes.com/sites/startswithabang/2016/03/11/could-the-lhc-make-an-earth-killing-black-hole/?sh =19ea834d2ed5.

Google Scholar

Friedlander, A., Mack, K. J., Schon, S., Song, N., and Vincent, A. C. (2022). Primordial black hole dark matter in the context of extra dimensions. Phys. Rev. D. 105 (10), 103508. doi:10.1103/physrevd.105.103508

CrossRef Full Text | Google Scholar

Green, A. M., and Kavanagh, B. J. (2021). Primordial Black Holes as a dark matter candidate. J. Phys. G. 48 (4), 043001. doi:10.1088/1361-6471/abc534

CrossRef Full Text | Google Scholar

Green, M. B., Schwarz, J. H., and Witten, E. (1988). Superstring theory vol. 1: Introduction. Cambridge, U.K.: Cambridge University Press. ISBN 978-0-521-35752-4.

Google Scholar

Green, M. B., Schwarz, J. H., and Witten, E. (1988). Superstring theory vol. 2: Loop amplitudes, anomalies and phenomenology. Cambridge, U.K.: Cambridge University Press. ISBN 978-0-521-35753-1.

Google Scholar

Horowitz, G. T. (2012). Black holes in higher dimensions. Cambridge, U.K.: Cambridge University Press. ISBN 978-1-107-01345-2.

Google Scholar

Hou, S., Harms, B., and Cavaglia, M. (2015). Bounds on large extra dimensions from the simulation of black hole events at the LHC. J. High. Energy Phys. 11, 185. doi:10.1007/jhep11(2015)185

CrossRef Full Text | Google Scholar

Huffington Post (2014). Large Hadron collider hasn’t created any black holes, despite early fears. Available at: https://www.huffpost.com/entry/lhc-black-hole_n__5249511.

Google Scholar

Khachatryan, V., Sirunyan, A. M., Tumasyan, A., Adam, W., Bergauer, T., and Dragicevic, M. (2011). Search for microscopic black hole signatures at the large Hadron collider. Phys. Lett. B 697, 434–453. doi:10.1016/j.physletb.2011.02.032

CrossRef Full Text | Google Scholar

Kiritsis, E., and Taliotis, A. (2011). Mini-black-hole production at RHIC and LHC. Ithaca, New York: Cornell University. PoS EPS-HEP2011.

Google Scholar

Lake, M. J., and Carr, B. (2018). Does Compton–Schwarzschild duality in higher dimensions exclude TeV quantum gravity? Int. J. Mod. Phys. D. 27 (16), 1930001. doi:10.1142/s0218271819300015

CrossRef Full Text | Google Scholar

Lake, M. J., and Carr, B. (2015). The Compton-Schwarzschild correspondence from extended de Broglie relations. J. High. Energy Phys. 11, 105. doi:10.1007/jhep11(2015)105

CrossRef Full Text | Google Scholar

Lake, M. J., and Carr, B. (2016). The Compton-Schwarzschild relations in higher dimensions. Ithaca, New York: Cornell University. arXiv:1611.01913 [gr-qc].

Google Scholar

Lake, M. J., Miller, M., Ganardi, R. F., Liu, Z., Liang, S. D., and Paterek, T. (2019). Generalised uncertainty relations from superpositions of geometries. Cl. Quant. Grav. 36 (15), 155012. doi:10.1088/1361-6382/ab2160

CrossRef Full Text | Google Scholar

Lake, M. J., Miller, M., Ganardi, R., and Paterek, T. (2023). ıtGeneralised uncertainty relations from finite-accuracy measurements. Front. Astron. Space Sci. 10, 1087724.

CrossRef Full Text | Google Scholar

Maartens, R., and Koyama, K. (2010). Brane-World gravity. Living Rev. rel. 13, 5. doi:10.12942/lrr-2010-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Maziashvili, M. (2006). Black hole remnants due to GUP or quantum gravity? Phys. Lett. B 635, 232–234. doi:10.1016/j.physletb.2006.03.009

CrossRef Full Text | Google Scholar

Bleicher, M., Nicolini, P., Sprenger, M., and Winstanley, E. (2011). Micro black holes in the laboratory. Int. J. Mod. Phys. E 20, 7–14. doi:10.1142/s0218301311040529

CrossRef Full Text | Google Scholar

Mureika, J., Nicolini, P., and Spallucci, E. (2012). Could any black holes be produced at the LHC? Phys. Rev. D. 85, 106007. doi:10.1103/physrevd.85.106007

CrossRef Full Text | Google Scholar

NASA (2008). The day the world didn’t end. Available at: https://science.nasa.gov/science-news/science-at-nasa/2008/10oct_lhc.

Google Scholar

New York Times (2008). Large Hadron collider - risk of a black hole. Available at: https://www.nytimes.com/2008/04/15/science/15risk.html.

Google Scholar

Nicolini, P., Mureika, J., Spallucci, E., Winstanley, E., and Bleicher, M. (2013). Production and evaporation of Planck scale black holes at the LHC. Ithaca, New York: Cornell University. arXiv:1302.2640 [hep-th].

Google Scholar

Park, M. i. (2008). The generalized uncertainty principle in (A)dS space and the modification of hawking temperature from the minimal length. Phys. Lett. B 659, 698–702. doi:10.1016/j.physletb.2007.11.090

CrossRef Full Text | Google Scholar

Park, S. C. (2012). Black holes and the LHC: A review. Prog. Part. Nucl. Phys. 67, 617–650. doi:10.1016/j.ppnp.2012.03.004

CrossRef Full Text | Google Scholar

Peskin, M. E., and Schroeder, D. V. (1995). An Introduction to quantum field theory. Boca Raton, U.S.A.: Taylor and Francis. ISBN 978-0-201-50397-5.

Google Scholar

Rae, A. I. M., and Napolitano, J. (2015). Quantum mechanics. Sixth Edition. Abingdon, U.K.: Taylor and Francis. ISBN 1482299186, 9781482299182.

Google Scholar

Sakalli, İ., and Kanzi, S. (2022). Topical review: Greybody factors and quasinormal modes for black holes in various theories - fingerprints of invisibles. Turk. J. Phys. 46 (2), 51–103. doi:10.55730/1300-0101.2691

CrossRef Full Text | Google Scholar

Singh, T. P. (2017). A new length scale for quantum gravity: A resolution of the black hole information loss paradox. Int. J. Mod. Phys. 26, 1743015. doi:10.1142/s0218271817430155

CrossRef Full Text | Google Scholar

Singh, T. P. (2018). A new length scale, and modified Einstein–Cartan–Dirac equations for a point mass. Int. J. Mod. Phys. D. 27 (08), 1850077. doi:10.1142/s0218271818500773

CrossRef Full Text | Google Scholar

Sokolov, A. V., and Pshirkov, M. S. (2017). Possibility of hypothetical stable micro black hole production at future 100 TeV collider. Eur. Phys. J. C 77 (12), 908. doi:10.1140/epjc/s10052-017-5464-7

CrossRef Full Text | Google Scholar

Taliotis, A. (2013). Extra dimensions, black holes and fireballs at the LHC. J. High. Energy Phys. 05, 034.

CrossRef Full Text | Google Scholar

Torres, R., Fayos, F., and Lorente-Espín, O. (2013). The mechanism why colliders could create quasi-stable black holes. Int. J. Mod. Phys. D. 22 (14), 1350086. doi:10.1142/s0218271813500867

CrossRef Full Text | Google Scholar

Winstanley, E. (2013). Black holes, TeV-scale gravity and the LHC. Ithaca, New York: Cornell University. arXiv:1306.5409 [hep-th].

Google Scholar

Weinberg, S. (2008). Cosmology. Oxford, U.K.: Oxford University Press. ISBN 978-0-191-52360-1.

Google Scholar

Weisstein, E. W. (1973). “Sphere gravitational potential energy, Mathworld, Wolfram (1996-2007),” in Mechanics. Editors C. Kittel, W. D. Knight, and M. A Ruderman. 2nd ed. (New York, USA: McGraw-Hill), 268–269.

Google Scholar

Xiang, L., and Wen, X. Q. (2009). A heuristic analysis of black hole thermodynamics with generalized uncertainty principle. J. High. Energy Phys. 10, 046. doi:10.1088/1126-6708/2009/10/046

CrossRef Full Text | Google Scholar