Cosmic ray propagation in turbulent magnetic fields

Propagation of cosmic rays (CRs) in turbulent and magnetized astrophysical media is a long-standing problem that requires both understanding of the properties of turbulent magnetic fields and their interaction with energetic particles. This review focuses on selected recent theoretical findings made based on the progress in understanding and simulating magnetohydrodynamic (MHD) turbulence. In particular, we address the problem of perpendicular and parallel propagation of CRs and identify the conditions when the perpendicular propagation is superdiffusive and diffusive. For the parallel diffusion, we discuss the problems of the traditionally used diffusion mechanism arising from pitch angle scattering and the possible solutions provided by the recently identified “mirror diffusion” in the presence of turbulent magnetic mirrors.

1 Introduction

Nature demonstrates unique abilities to accelerate energetic particles. In astrophysical literature, such particles with energies ranging from 10⁷ eV to 10²⁰ eV are usually termed cosmic rays (CRs). The processes of acceleration include systematic First Order Fermi and stochastic Second Order Fermi acceleration mechanisms (Melrose, 1969), and shocks, magnetic reconnection, and turbulence are involved in the acceleration processes (Longair, 2011). CRs in the Galaxy have energy density and pressure comparable to those arising from interstellar turbulence and magnetic fields (Parker, 1966). Therefore, they are dynamically important.

The observed CR flux and (an) isotropy in their arrival directions depends on both their acceleration and propagation from their sources to the Earth (Ginzburg and Syrovatskii, 1964; Schlickeiser, 2002). This review focuses on selected recent theoretical findings on CR propagation in turbulent magnetic fields, which are ubiquitous in space and astrophysical environments. CR propagation has numerous implications on various processes in the solar wind, heliosphere, interstellar media, and intracluster media (see monograph by Longair (2011) and references therein). It is a crucial part of CR acceleration process (e.g., Jokipii, 1982; Perri and Zimbardo, 2009; Lazarian and Yan, 2014; Demidem et al., 2020; Marcowith et al., 2020; Xu and Lazarian, 2022). The diffusion in the vicinity of CR acceleration sites, e.g., supernova remnants, and pulsar wind nebulae, is important for understanding gamma-ray observations (Di Mauro et al., 2020; Xu, 2021). Other implications include the solar modulation of Galactic CRs, space weather forecasting (Parker, 1965; Jokipii, 1971; Singer et al., 2001), the origin and chemical composition of CRs, ionization in molecular gas and circumstellar discs (e.g., Schlickeiser et al., 2016; Padovani et al., 2018), Fermi Bubble emission (Anjos and Catalani, 2020), galactic winds (e.g., Ipavich, 1975; Holguin et al., 2019; Hopkins et al., 2020; Quataert et al., 2022), feedback heating in clusters of galaxies (e.g., Guo and Oh, 2008; Brunetti and Jones, 2014), modeling the synchrotron foreground emission for cosmic microwave background (CMB) radiation and redshifted 21 cm radiation (e.g., Cho and Lazarian, 2002b; Cho et al., 2012).

In the propagation process, CRs interact with the pre-existing magnetohydrodynamic (MHD) fluctuations and the magnetic fluctuations created by themselves. The most notable example for the latter is the perturbations created by the streaming instability (see Kulsrud and Pearce, 1969). The suppression of streaming instability by various damping effects in the multi-phase interstellar medium (Plotnikov et al., 2021; Xu and Lazarian, 2022; Sampson et al., 2023) and by MHD turbulence (Yan and Lazarian, 2002; Farmer and Goldreich, 2004; Lazarian, 2016) is an important effect that modifies the CR propagation (see Krumholz et al., 2020 and review by Lazarian and Xu, 2022). Below we discuss the CR propagation in the pre-existing MHD turbulence.

The interaction of CRs with magnetic turbulence has been investigated for decades (Jokipii, 1966; Kulsrud and Pearce, 1969; Schlickeiser and Miller, 1998; Giacalone and Jokipii, 1999), mostly with ad hoc models of MHD turbulence, including superposition of MHD waves (Giacalone and Jokipii, 1999), isotropic MHD turbulence (see Schlickeiser, 2002 and references therein), and 2D + slab superposition model for solar wind turbulence (Matthaeus et al., 1990; Zank et al., 2017). More recently, both MHD simulations with driven turbulence (Cho and Vishniac, 2000; Maron and Goldreich, 2001; Cho et al., 2002; Cho and Lazarian, 2003; Kowal and Lazarian, 2010; Beresnyak, 2014) and solar wind observations (e.g., Horbury et al., 2008; Luo and Wu, 2010; Forman et al., 2011) show evidence for the statistical properties of MHD turbulence corresponding to theoretical expectations (Goldreich and Sridhar, 1995; Lazarian and Vishniac, 1999, see also Beresnyak and Lazarian, 2019 and references therein). As we discuss in the review, the progress in the understanding of MHD turbulence brings significant changes in understanding CR propagation¹.

In what follows, in §2 we briefly discuss the basic properties and scaling relations of turbulent magnetic fields. §3 deals with CR superdiffusion and diffusion in the direction perpendicular to the mean magnetic field that arise from the perpendicular superdiffusion and diffusion of turbulent magnetic fields. In §4, we discuss different mechanisms leading to the parallel diffusion of CRs, including a recently identified new mechanism, the mirror diffusion, that can significantly suppress the CR diffusion in the vicinity of CR sources. A summary is provided in §5.

2 Properties of MHD turbulence that affect CR propagation

2.1 Compressible MHD turbulence and fast modes

We consider turbulence as a result of non-linear interactions inducing the energy cascade from large to small scales. Therefore, other types of excitations, including the streaming instability (see Kulsrud and Pearce, 1969; Farmer and Goldreich, 2004; Lazarian, 2016), gyro-resonance instabilities (see Lazarian and Beresnyak, 2006), are not classified as turbulence. The changes in plasma conditions affect MHD turbulence and, through this, the CR propagation. For instance, partial ionization of astrophysical media can significantly affect the dynamics of CRs (Xu et al., 2016).

The turbulence in magnetized media in typical astrophysical settings is injected at a large scale L, i.e., the injection scale, with the injected turbulent velocity at L equal to V_L. The values of L and V_L depend on the driving mechanism of turbulence. For instance, for the interstellar turbulence driven by supernova explosions, the typical values of L and V_L are $\sim 100$ pc and $\sim 10$ km s⁻¹ (Chamandy and Shukurov, 2020). We note that, unlike the bulk fluid velocity, the turbulent velocity is the averaged velocity difference between two points in space separated by a given length scale. For MHD turbulence, if the injection of turbulence happens with V_L > V_A, where V_A is the Alfvén speed, this is the case of super-Alfvénic turbulence². If V_L < V_A, the turbulence is sub-Alfvénic. The ratio M_A = V_L/V_A is the Alfvén Mach number, which is an important parameter characterizing the properties of MHD turbulence. The special case with M_A = 1 corresponds to the trans-Alfvénic turbulence, with energy equipartition between turbulence and magnetic fields at L. The trans-Alfvénic turbulence was originally studied in Goldreich and Sridhar (1995). Other turbulence regimes were covered in Lazarian and Vishniac (1999). Figure 1 illustrates the different magnetic field structures in sub- and super-Alfvénic turbulence. The turbulent energy then cascades down to a small scale l_d that in most cases is determined by microphysical processes. The range of scales between L and l_d is the inertial range, and it is usually a very extended range in typical astrophysical settings. For instance, Figure 2 illustrates the Galactic electron density spectrum (Chepurnov and Lazarian, 2010) induced by the interstellar turbulence in the warm ionized medium, and the velocity spectrum towards Taurus molecular cloud (Yuen et al., 2022). The properties of turbulence over the inertial range are the most relevant for the CR physics that we deal with in this review. All the scaling relations that we will discuss are within the inertial range of turbulence.

FIGURE 1

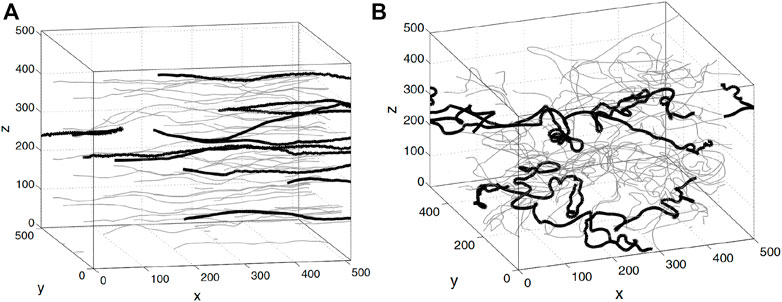
FIGURE 1. Magnetic field lines (thin lines) and trajectories of CRs (thick lines) in (A) sub-Alfvénic turbulence with M_A = 0.3 and (B) super-Alfvénic turbulence with M_A = 1.5. From Xu and Yan (2013).

FIGURE 2

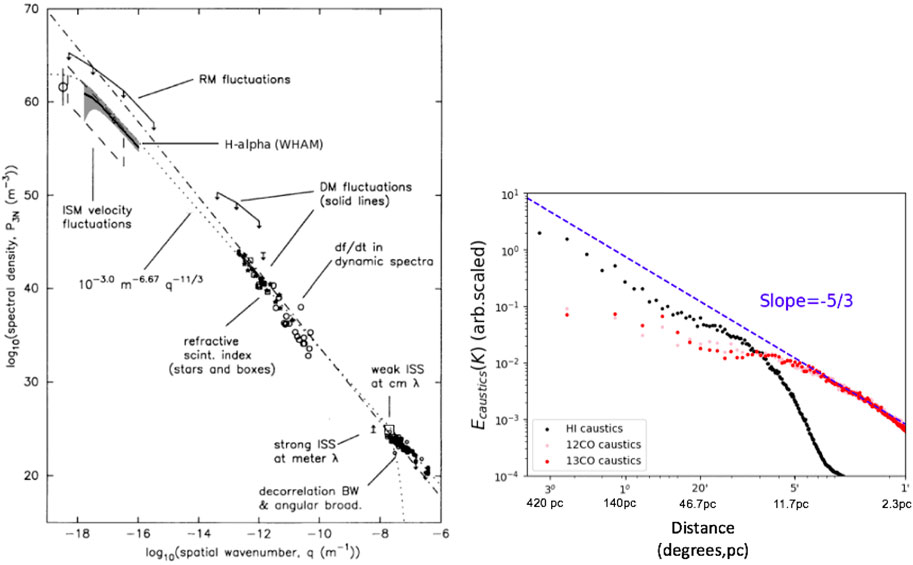
FIGURE 2. Left panel: “Extended Big Power Law in the Sky” of Galactic electron density fluctuations obtained by combining the scattering measurements of nearby pulsars in Armstrong et al. (1995) and H_α measurements from WHAM data in Chepurnov and Lazarian (2010). Right panel: Power law of velocity fluctuations measured toward the Taurus molecular cloud. The horizontal axis corresponds to log₁₀ (spatial wavenumber) and the slope in the right panel is consistent with that in the left panel. From Yuen et al. (2022).

The current understanding of MHD turbulence differs significantly from the earlier models adopted for CR studies in the literature (e.g., Matthaeus et al., 1990; Kóta and Jokipii, 2000; Qin et al., 2002). MHD turbulence in a compressible medium (see Beresnyak and Lazarian, 2019) can be approximated as a superposition of three cascades of fundamental modes, i.e., Alfvén, slow, and fast modes. The Alfvén modes play a dominant role in regulating the dynamics of MHD turbulence and shaping turbulence anisotropy. Unlike long-lived wave oscillations about a fixed equilibrium point in space, the reconnection diffusion of turbulent magnetic fields enables their turbulent motions in the direction perpendicular to the local magnetic field (Lazarian and Vishniac, 1999), with a limited lifetime determined by the turbulent eddy turnover time in the strong MHD turbulence regime. Therefore, we use the term “modes” rather than “waves” for describing MHD turbulence. Another important property of MHD turbulence is its scale-dependent anisotropy. Matthaeus et al. (1996) reported the anisotropy being greater for smaller wavenumber. By contrast, larger anisotropy toward smaller length scales (larger wavenumber) is seen in MHD turbulence simulations in the reference frame with respect to the local magnetic field (Cho and Vishniac, 2000; Cho and Lazarian, 2002a; Cho and Lazarian, 2003). The latter is well expected by the MHD turbulence theory (Goldreich and Sridhar, 1995; henceforth GS95) based on the critical balance relation of Alfvén modes³.

The numerical decomposition of MHD turbulence into different modes has demonstrated that the interaction between fast modes and other modes, i.e., Alfvén and slow modes, is relatively weak for sub-Alfvénic non-relativistic MHD turbulence (Cho and Lazarian, 2002a). Therefore, the cascade of fast modes can be assumed independent of the cascades of Alfvén and slow modes. The cascade of fast modes is similar to the acoustic one in a high β medium, where β is the ratio of the plasma to magnetic pressure. In this regime, fast modes are mostly compressions of plasmas that propagate with the sound speed c_s. It is also shown by Cho and Lazarian (2002a) that in the opposite limit of a low β medium, fast modes are expected to form a cascade similar to the acoustic one, even though the fluctuations are compressions of magnetic fields that propagate with ∼ V_A. The numerical simulations by Cho and Lazarian (2002a), Cho and Lazarian (2003) support that the cascade of fast modes is very similar to the acoustic cascade for various values of β.

The acoustic turbulence in non-magnetized gas has the energy spectrum E_s(k) ∼ k^−3/2 for low-amplitude perturbations. The spectrum tends to steepen with E_s(k) ∼ k⁻² as the amplitude of perturbations increases. For fast modes in a high β medium, the perturbation amplitude increases with increasing sonic Mach number M_s = V_L/c_s. For fast modes in a low-β medium, it increases with the increase of M_A. The numerical results in Cho and Lazarian (2003) are consistent with E_f ∼ k^−3/2, while those in Kowal and Lazarian (2010); Hu et al. (2022b) are better fitted by E_f ∼ k⁻² (see Figure 3). The difference may be accounted for by appealing to the analogy with the acoustic turbulent cascade mentioned above. However, the issue has not been settled. In any case, similar to the acoustic cascade, fast modes have isotropic energy distribution.

FIGURE 3

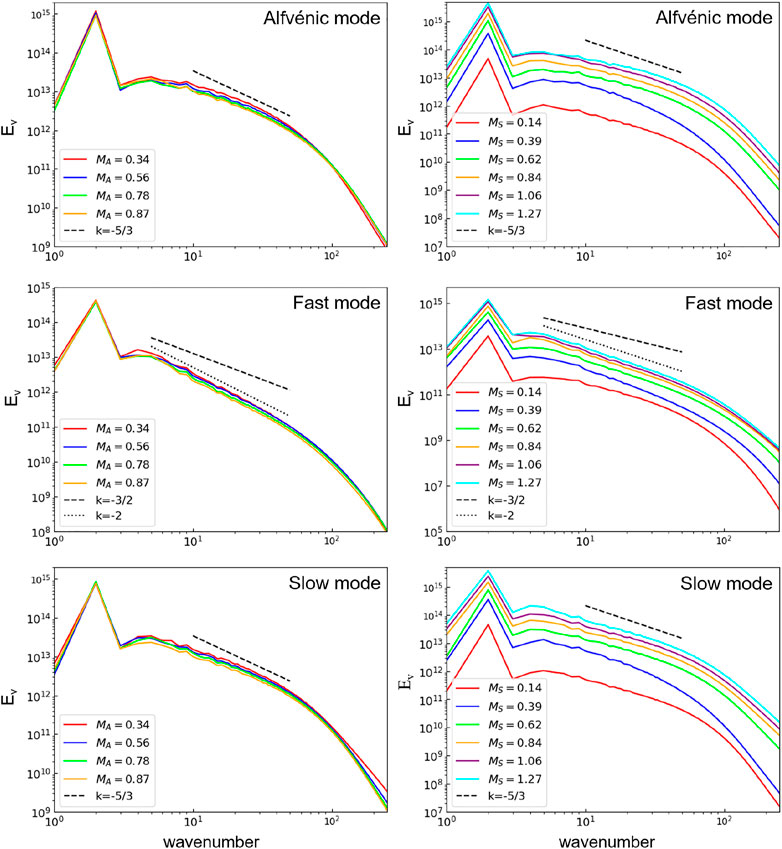
FIGURE 3. Left: The turbulent kinetic energy spectra for Alfvén (top), fast (middle), and slow (bottom) modes for various M_A values and M_s ≈ 0.6. Right: Same as left panels but for various M_s values and M_A ≈ 0.5. From Hu et al. (2022b).

2.2 Properties of Alfvén and slow modes

Slow modes are cascaded by Alfvén modes, and their anisotropy is imposed by that of Alfvén modes (Goldreich and Sridhar, 1995; Lithwick and Goldreich, 2001; Cho and Lazarian, 2002a; Cho and Lazarian, 2003). Figure 3 shows the numerically measured turbulent kinetic energy spectra of decomposed MHD modes. As expected, the spectral scalings of Alfvén and slow modes in both compressible and incompressible media are similar (Cho and Lazarian, 2003). This allows appealing to high-resolution simulations of incompressible MHD turbulence (Beresnyak, 2014) to test their spectral scalings.

The turbulent motions, rather than wave oscillations, of magnetic fields in Alfvén modes are enabled by the turbulent reconnection of magnetic fields (Lazarian and Vishniac, 1999) (henceforth LV99), which is an intrinsic part of MHD turbulence. The LV99 theory treats Alfvén modes as a collection of turbulent eddies whose axes of rotation are aligned with the local magnetic field surrounding them. Due to turbulent reconnection, the fluid turbulent motions perpendicular to the local magnetic field are not constrained. As a result, an eddy with scale l_⊥ perpendicular to the local magnetic field induces Alfvénic perturbation of scale l_‖ that propagates along the magnetic field with speed V_A. The timescale of this perturbation l_‖/V_A should be equal to the eddy turnover time l_⊥/v_l. The corresponding relation between the parallel and perpendicular sizes of the eddy:

$\frac{l_{\Vert }}{V_A}\approx \frac{l_{\perp }}{v_l},(1)$

constitutes the modern understanding of the critical balance for Alfvénic turbulence (GS95). It follows that the GS95 theory is only valid in the so-called local system of reference defined by the local mean magnetic field of the eddies. This fact is confirmed by numerical simulations (Cho and Vishniac, 2000; Maron and Goldreich, 2001; Cho et al., 2002). The direction of the local magnetic field at a given length scale can differ significantly from the global mean magnetic field direction resulting from the large-scale averaging. For CR propagation, it is important that the local small-scale magnetic field is the magnetic field sampled by CRs. This justifies the perturbative approach for describing the propagation of low-energy CRs, even though the large-scale variations of the magnetic field can be significant.

As the turbulent reconnection allows the turbulent cascade in the direction perpendicular to the local magnetic field, this cascade is not affected by the back-reaction of the magnetic field and remains Kolmogorov-like. For trans-Alfvénic turbulence with V_L = V_A, this means that:

$v_l\approx V_A{\left(\frac{l_{\perp }}{L}\right)}^{1/3},(2)$

where v_l is the turbulent velocity at l_⊥, and l_⊥ is the perpendicular size of a turbulent eddy. By combining Eqs 1, 2, it is easy to obtain the scale-dependent anisotropy of trans-Alfvénic turbulence in the local system of reference:

$l_{\Vert }\approx L{\left(\frac{l_{\perp }}{L}\right)}^{2/3}.(3)$

From Eq. 3, it is evident that smaller eddies are more elongated along the local magnetic field. We note, however, that Eqs 2, 3 should be understood in the statistical sense. They represent the scaling relations between the most probable values of the quantities involved rather than the properties of individual eddies. The eddies have a distribution of scales. Using MHD turbulence simulations, Cho et al. (2002) provided an analytical fit to the probability distribution function of l_⊥ at a given l_‖. This distribution was adopted later in Yan and Lazarian (2002), Yan and Lazarian (2004) as well as the subsequent studies on CR scattering.

In super-Alfvénic turbulence, the magnetic field is of marginal importance at scales near L. Therefore, super-Alfvénic turbulence has an isotropic Kolmogorov energy spectrum at large scales. However, as the turbulent velocity decreases along the energy cascade, i.e., v_l ∼ V_L (l/L)^1/3, the effect of the magnetic field becomes more and more manifested. At the Alfvénic scale (Lazarian, 2006)

$l_A=L{M}_A^{-3},(4)$

v_l becomes equal to V_A, and the turbulence becomes fully magnetohydrodynamic. Its properties at scales smaller than l_A can be described by trans-Alfvénic scaling, provided that L in Eqs 2, 3 is replaced by l_A.

In sub-Alfvénic turbulence, it was shown in LV99 that below L, there is a range of scales where the cascade is in the weak turbulence regime. In this regime, the parallel scale of wave packets remains unchanged, i.e., l_‖ = L, and oppositely directed wave packets have to interact multiple times to get cascaded. The scaling obtained in LV99 for the weak turbulence⁴ under the assumption of the isotropic turbulence driving at L is

$v_l\approx V_L{\left(\frac{l_{\perp }}{L}\right)}^{1/2},(5)$

and this result was supported by the subsequent analytical study by Galtier et al. (2000). With the decrease of l_⊥, the intensity of interactions of Alfvénic perturbations increases despite the decrease in the turbulence amplitude. It was shown in LV99 that at the transition scale

$l_{\text{tran}}\approx L{M}_A^2,(6)$

where M_A < 1, the turbulence gets into the strong turbulence regime. For the sub-Alfvénic turbulence at l < l_tran, there are

$v_l\approx V_L{\left(\frac{l_{\perp }}{L}\right)}^{1/3}{M}_A^{1/3},(7)$

and:

$l_{\Vert }\approx L{\left(\frac{l_{\perp }}{L}\right)}^{2/3}{M}_A^{-4/3}.(8)$

The above relations derived in LV99 differ from Eqs 2, 3 for trans-Alfvénic turbulence by the additional dependence on M_A.

To unify the formalism of scalings of super- and sub-Alfvénic turbulence, Lazarian and Xu (2021) (henceforth LX21) proposed to introduce an effective injection scale:

$L_{\text{eff}}=L{M}_A^{-4}.(9)$

Using L_eff, Eqs 7, 8 can be rewritten as:

$v_l\approx V_A{\left(\frac{l_{\perp }}{L_{\text{eff}}}\right)}^{1/3},(10)$

and:

$l_{\Vert }\approx L_{\text{eff}}{\left(\frac{l_{\perp }}{L_{\text{eff}}}\right)}^{2/3},(11)$

which take the same forms as Eqs 2, 3 with L replaced by L_eff. We note that unlike l_A for super-Alfvénic turbulence, L_eff does not have a particular physical meaning. LX21 introduced L_eff to present the turbulent scaling on scales less than l_tran for sub-Alfvénic turbulence in a more convenient way.

2.3 Interactions of CRs with MHD turbulence

Without magnetic fields, CRs would propagate ballistically and easily escape from cosmic accelerators and diffuse astrophysical media. It is MHD turbulence that induces pitch-angle scattering, stochastic acceleration, and spatial diffusion of CRs along the magnetic field (e.g., Chandran, 2000b; Yan and Lazarian, 2002; Yan and Lazarian, 2004; Brunetti and Lazarian, 2007; Strong et al., 2007; Yan and Lazarian, 2008; Blasi and Amato, 2012; Lynn et al., 2012; Xu and Yan, 2013; Xu and Lazarian, 2018; Lemoine and Malkov, 2020; Sioulas et al., 2020; Kempski and Quataert, 2022), as well as superdiffusion and diffusion perpendicular to the mean magnetic field (Yan and Lazarian, 2008; Xu and Yan, 2013; Lazarian and Yan, 2014; Hu et al., 2022b; Maiti et al., 2022).

Traditionally, the transport of CRs is separated in two categories, the transport along a magnetic field and the transport perpendicular to the magnetic field. In general, parallel and perpendicular transport take place simultaneously. Magnetic fluctuations are assumed to be small and therefore the magnetic field direction approximately coincides with that of the mean magnetic field. This is a very idealized presentation of the actual CR propagation in realistic astrophysical environments. In reality, the magnetic fluctuations are comparable to the mean magnetic field for trans-Alfvénic turbulence and are larger than the mean field for super-Alfvénic turbulence. Moreover, LX21 demonstrated that the processes of parallel and perpendicular diffusion can be interdependent.

The field line wandering causes the diffusion of CRs perpendicular to the mean magnetic field. This effect was discussed extensively in the literature (Jokipii, 1966). However, perpendicular diffusion only applies on scales larger than L. On scales less than L, LV99 showed that the magnetic field lines are superdiffusive and exhibit fast dispersion, which is also numerically demonstrated by Lazarian et al. (2004); Beresnyak (2013). This fast separation of magnetic field lines induces superdiffusive transport of CRs perpendicular to the mean magnetic field direction (Lazarian and Yan, 2014). As we will discuss further, the superdiffusion of CRs is an essential but frequently ignored aspect of CR propagation.

As CRs move along magnetic field lines, they interact with magnetic fluctuations, including resonant (e.g., scattering, transit-time damping) and non-resonant (e.g., mirroring) interactions. These interactions affect the parallel transport of CRs. The well-known interaction of CRs with magnetic fluctuations is gyroresonant scattering (i.e., pitch-angle scattering). It occurs as magnetic fluctuations induce fluctuations of the electric field in the reference frame of CRs with a frequency equal to the Larmor frequency of CRs. All MHD modes induce pitch angle scattering. In addition, a special type of interaction is related to compressible fluctuations, i.e., slow and fast modes, and is termed Transit-time Damping (TTD) interaction (Schlickeiser, 2002; Xu and Lazarian, 2018). This sort of interaction is associated with the surfing of CRs on the front of an oblique compressible wave. It changes the CR momentum parallel to the local magnetic field.

In super-Alfvénic turbulence, when the parallel mean free path of CRs is larger than l_A, the tangling of field lines acts to confine CRs, with an effective mean free path equal to l_A (Brunetti and Lazarian, 2007), and the CR diffusion becomes isotropic. Super-Alfvénic turbulence in molecular clouds and starburst galaxies plays an important role in determining the diffusion of CRs (Krumholz et al., 2020; Xu, 2021).

The new understanding of the statistics and dynamics of turbulent magnetic fields can shed light on some long-standing problems and observational puzzles (e.g., Palmer, 1982; Evoli and Yan, 2014; López-Barquero et al., 2016; Krumholz et al., 2020; Xu, 2021). It was found that the numerically tested model of MHD turbulence, rather than isotropic Kolmogorov turbulence, can satisfactorily interpret the high-precision AMS-02 measurements of CRs (Fornieri et al., 2021). Updated multifrequency observations and direct CR measurements (e.g., Nava and Gabici, 2013; Orlando, 2018; Gabici et al., 2019; Amato and Casanova, 2021) request improved understanding on interactions of CRs with MHD turbulence, as well as measurements on the properties of astrophysical turbulent magnetic fields (Lazarian et al., 2018; Hu et al., 2021; Hu et al., 2022a; Xu and Hu, 2021).

3 CR propagation perpendicular to the mean magnetic field

The perpendicular (super) diffusion of CRs arises from that of turbulent magnetic fields. In the direction perpendicular to the mean magnetic field, the mean squared displacement ⟨y²⟩ of CRs is proportional to s^α, where s is the distance traveled by CRs along the magnetic field. α = 1 corresponds to normal diffusion, α > 1 corresponds to superdiffusion, and α < 1 corresponds to subdiffusion. Subdiffusion, i.e., compound diffusion, was proposed in, e.g., Kóta and Jokipii (2000) under the assumption that CRs are able to retrace the same magnetic field line. This is not possible due to the stochasticity of turbulent magnetic fields (Yan and Lazarian, 2008; Lazarian and Yan, 2014; Lazarian and Xu, 2021). Subdiffusion of CRs is not observed in MHD turbulence simulations (Xu and Yan, 2013; Hu et al., 2022b).

3.1 Perpendicular superdiffusion of CRs

Based on the kinetic theory, a CR particle is approximately shifted one Larmor radius perpendicular to the magnetic field during one scattering mean free path λ_‖ (Jokipii, 1987). The resulting perpendicular diffusion is usually negligible with r_L ≪ λ_‖, where r_L is the Larmor radius. Even in the limited case of strong scattering, i.e., in the case of the so-called Bohm diffusion, the perpendicular diffusion coefficient does not exceed r_Lc, where c is the speed of light. When the scattering is less efficient, CRs follow magnetic field lines during the time between the scattering events. As a result, the CR dynamics are very much affected by the stochasticity and (super) diffusion of turbulent magnetic fields. On scales smaller than L, the superdiffusion of magnetic fields was identified in LV99, which is a natural consequence of turbulent energy cascade and reconnection diffusion of magnetic fields (Lazarian, 2014).

The LV99 scaling for magnetic field superdiffusion can be obtained by considering the energy cascade of Alfvén modes. It is natural to assume that when one follows the magnetic field line over the parallel size l_‖ of a turbulent eddy, the magnetic field line undergoes perpendicular displacement equal to the transverse size l_⊥ of the eddy. The displacement l_⊥ can be either positive or negative, and therefore the dispersion ⟨y²⟩ of magnetic field lines increases in a random-walk manner with

$d⟨y^2⟩\approx l_{\perp }^2\frac{ds}{l_{\Vert }},(12)$

where ds is the distance measured along the magnetic field line, and the ⟨…⟩ denotes an ensemble average. Using the above relation and the scaling relation between l_‖ and l_⊥ for sub-Alfvénic turbulence given by Eq. 8 and associating $l_{\perp }^2$ with ⟨y²⟩, one gets (LV99):

$d\langle y^2\rangle \approx {\langle y^2\rangle }^{2/3}{M}_A^{4/3}{L}^{-1/3}ds,(13)$

which indicates an accelerated separation of field lines. Superdiffusion of magnetic fields in MHD turbulence is analogous to Richardson dispersion (Richardson, 1926) in hydrodynamic turbulence. Numerically, the superdiffusion of turbulent magnetic fields was demonstrated in Lazarian et al. (2004); Beresnyak (2013). The accelerated separation of magnetic field lines manifests that the “frozen-in” condition is grossly violated in turbulent media. More discussion on the relation between superdiffusion and flux-freezing breakdown can be found in Eyink et al. (2011). The latter has been numerically confirmed by Eyink et al. (2013).

The essence of superdiffusion is easy to understand. As one follows neighboring magnetic field lines over the distance s, the divergence rate of field lines increases as larger and larger turbulent eddies contribute to the dispersion of field line separations. In terms of CRs dynamics, Eq. 13 also applies to the dispersion of separations of CRs that move ballistically along magnetic field lines. The resulting perpendicular divergence of CR trajectories was studied in Yan and Lazarian (2008); Lazarian and Yan (2014), with the analytical predictions numerically confirmed in Xu and Yan (2013). The dispersion of CR separations in the direction perpendicular to the mean magnetic field in sub-Alfvénic turbulence is:

$⟨y_{cr}^2⟩\approx \frac{s^3}{L}{M}_A^4,M_A<1,s<{\lambda }_{\Vert },s<L,(14)$

where s is the distance traveled by CRs along the magnetic field line, and λ_‖ is the CR parallel mean free path. In super-Alfvénic turbulence, there is

$⟨y_{cr}^2⟩\approx \frac{s^3}{L}{M}_A^3,M_A>1,s<{\lambda }_{\Vert },s<l_A.(15)$

In the case with efficient scattering, the arguments above can be generalized to describe the perpendicular superdiffusion of CRs while they propagate diffusively along the field lines. We have

$s^2\approx D_{\Vert }t\approx {\lambda }_{\Vert }{v}_{cr}t,(16)$

where v_cr is the CR velocity, and D_‖ is the parallel diffusion coefficient. The average angle of a given magnetic field line with respect to the mean magnetic field is approximately

$\alpha \left(s\right)\approx \frac{{⟨y^2\left(s\right)⟩}^{1/2}}{s}\approx \frac{s^{1/2}}{L^{1/2}}{M}_A^2,(17)$

where Eq. 14 is used. It is easy to see that in the system of reference with respect to the mean magnetic field, the perpendicular displacement of CRs is λ_cr,⊥ ≈ α(s)λ_‖ as they move over λ_‖ along the mean magnetic field. The perpendicular to the mean magnetic field component of CR velocity is v_cr,⊥ ≈ α(s)v_cr,‖, where v_cr,‖ is the CR velocity along the mean magnetic field. The perpendicular propagation is a random walk with the step size λ_cr,⊥ and the velocity v_cr,⊥ that increase with s. Therefore, for a given s the perpendicular diffusion coefficient is ∼ v_cr,⊥λ_cr,⊥∼ α² (s) D_‖. The motion of CRs perpendicular to the mean magnetic field can be described as

$⟨y_{cr}^2⟩\approx {\alpha }^2{D}_{\Vert }t\approx \frac{s^3}{L}{M}_A^4,M_A<1,{\lambda }_{\Vert }\ll s,(18)$

It shows a similar superdiffusion as the case of inefficient scattering (Eq. 14).

We note that the concept of perpendicular superdiffusion of CRs contradicts some existing theories on small-scale CR transport, e.g., the Non-Linear Guiding Center Theory (NLGC) (Matthaeus et al., 2003). There it is assumed that in both parallel and perpendicular directions with respect to the mean magnetic field, the propagation of CRs is diffusive. However, test particle simulations in MHD turbulence support perpendicular superdiffusion of CRs on scales less than L in both cases with ballistic and diffusive motions of CRs along magnetic field lines (Xu and Yan, 2013; Hu et al., 2022b).

3.2 Perpendicular diffusion of CRs

The perpendicular diffusion of magnetic field lines in MHD turbulence takes place on scales larger than l_A for super-Alfvénic turbulence and l_tran for sub-Alfvénic turbulence (see Table 1 in Lazarian and Yan, 2019). For the former, magnetic field lines get entangled on the scale l_A and this induces the random walk with the step l_A, i.e.,:

$⟨y^2⟩\approx l_A^2\frac{s}{l_A}=s{l}_A=sL{M}_A^{-3},M_A>1,s\gg l_A.(19)$

For sub-Alfvénic turbulence, when perpendicular scales are larger than l_tran, turbulence is in the weak turbulence regime, and the growth of magnetic field separation is diffusive with the step in the perpendicular direction $L{M}_A^2$ for every transposition along the magnetic field by L. Thus for s ≫ L, there is

$⟨y^2⟩\approx {\left(L{M}_A^2\right)}^2\frac{s}{L}=sL{M}_A^4,M_A<1,s\gg L.(20)$

For the CRs moving ballistically along magnetic field lines with s < λ_‖, the perpendicular diffusion of CRs is also given by Eqs 19, 20. If the CR propagation along the magnetic field is diffusive with s ≫ λ_‖, the perpendicular diffusion has dependence on the parallel diffusion.

In super-Alfvénic turbulence at scales s ≫ l_A, the CR diffusion is isotropic. The characteristic diffusion coefficient is

$D\approx v_{cr}X,X=min\left[{\lambda }_{\Vert },l_A\right].(21)$

In sub-Alfvénic turbulence, if L ≪ s < λ_‖, Eq. 20 leads to the perpendicular diffusion coefficient of CRs (Yan and Lazarian, 2008)

$D_{\perp }\approx v_{cr}L{M}_A^4.(22)$

If λ_‖ ≪ L ≪ s, CRs propagate diffusively over L along the magnetic field line. Below, we reproduce the derivation of the diffusion coefficient in Lazarian (2006)⁵. According to Eq. 20 the magnetic field lines that guide the perpendicular diffusion undergo a random walk. As the magnetic field line is traced over L, its perpendicular transposition is $L{M}_A^2$. To cover the distance ${⟨y_{cr}^2⟩}^{1/2}$ with the step size $L{M}_A^2$, it requires $N={({⟨y_{cr}^2⟩}^{1/2}/L{M}_A^2)}^2$ steps. The time required for each step is δt_step ≈ L²/D_‖, and the total time is δt ≈ Nδt_step. Substituting this into the expression for the diffusion coefficient one gets

$D_{\perp }\approx \frac{⟨y_{cr}^2⟩}{\delta t}\approx D_{\Vert }{M}_A^4.(23)$

This agrees with the CR perpendicular diffusion coefficient in (Yan and Lazarian, 2008). This diffusion coefficient differs from that in the literature (see Jokipii, 1966) by having a dependence on $M_A^4$ rather than $M_A^2$. The $M_A^4$ dependence was numerically confirmed in Xu and Yan (2013).

4 Propagation of CRs along the magnetic field

4.1 Gyroresonance scattering

Gyroresonance scattering, i.e., pitch angle scattering, requires that the Doppler-shifted wave frequency is equal to the gyrofrequency of the particle or its harmonics. Through the gyroresonant interaction with magnetic fluctuations, CRs experience diffusion in their pitch angles (the angle between the particle velocity and magnetic field direction) while moving along the local magnetic field. The distance that CRs travel along the magnetic field corresponding to the change of pitch angles by 90° is λ_‖.

For theoretical studies, the Quasilinear Theory (QLT) (Jokipii, 1966) is frequently adopted in the literature. In QLT, particles are assumed to propagate along the magnetic field with infinitesimal fluctuations. Given r_L ≪ L and the turbulent energy cascade, the magnetic fluctuations that satisfy the gyroresonance condition can be sufficiently small for the above assumption to be valid. However, the QLT faces the so-called 90° problem, with vanishing scattering close to 90° and thus infinitely large λ_‖. The resonance broadening induced by, e.g., magnetic fluctuations, can help alleviate but not fully resolve the problem (Xu and Lazarian, 2018).

A remarkable consequence of the modern MHD turbulence theory is the inefficiency of gyroresonance scattering of CR with r_L ≪ L by Alfvén and slow modes. This effect was studied by Chandran (2000b); Yan and Lazarian (2002, 2003). Yan and Lazarian (2002, 2003) identified fast modes as the main scattering agent of CRs with r_L ≪ L in MHD turbulence. Yan and Lazarian (2002), Yan and Lazarian (2003), Xu and Lazarian (2020) adopted the anisotropic distribution of magnetic fluctuations measured from MHD turbulence simulations (Cho et al., 2002). This significantly shifted the paradigm of CR propagation and turbulent acceleration, as in earlier studies, Alfvén modes were mostly considered as the source of gyroresonance scattering.

The inefficiency of gyroresonance scattering by Alfvén and slow modes for CRs with r_L ≪ L arises from the scale-dependent anisotropy. The gyroresonance condition requires that r_L is comparable to l_‖. However, with scale-dependent anisotropy, there is l_⊥≪ l_‖ for small-scale magnetic fluctuations. As a result, a CR with r_L ∼ l_‖ samples many uncorrelated turbulent eddies within one gyro-orbit. In addition, the energy cascade of Alfvén and slow modes is mainly in the direction perpendicular to the local magnetic field. With a steep parallel energy spectrum $E(k_{\Vert })\sim k_{\Vert }^{-2}$ (Beresnyak, 2015), the power that induces the gyroresonance scattering falls relatively fast with the decrease of r_L. Both effects cause the inefficiency of gyroresonance scattering by Alfvén and slow modes (Chandran, 2000b; Yan and Lazarian, 2002; Yan and Lazarian, 2003; Xu and Lazarian, 2020).

As suggested by numerical simulations (Cho and Lazarian, 2003), fast modes have isotropic energy distribution. As a result, their interaction with CRs is not reduced due to geometrical factors. However, compared with Alfvén and slow modes, fast modes are more subject to damping effects because of their slower cascading rate. The anisotropic nature of collisionless damping induces the preferential suppression of the modes with wavevectors perpendicular to the magnetic field, creating mostly slab-type structures of scattering fluctuations (Yan and Lazarian, 2003; Beresnyak and Lazarian, 2007). This mitigates the supression of scattering by fast modes in the presence of significant damping (Yan and Lazarian, 2003). In a weakly ionized medium, fast modes are severely damped due to ion-neutral collisional damping (Xu et al., 2016). Only CRs with r_L larger than the damping scale can be efficiently scattered.

4.2 Transit-time damping (TTD) interaction

TTD interaction in plasma physics is usually associated with the damping of waves in collisionless plasmas. For CR studies, the TTD is the process of stochastically accelerating CRs by compressible MHD waves (Schlickeiser, 2002). The process is easy to understand if one considers compressible waves oblique to the magnetic field direction. If the phase speed of waves is v_ph, and the angle between the wavefront and the magnetic field is α, then the intersection point between the wavefront and the magnetic field moves with the speed v_inter = v_ph/sin α ≫ v_ph if α is small. If a CR moves along the magnetic field in the same direction with the speed close to v_inter, it can surf the wave, gaining or losing energy. With a linear resonance function, the limitation of the process is that only waves in the limited range of oblique angles can interact with fast-moving CRs. Due to magnetic fluctuations and nonlinear decorrelation of turbulence, the resonance broadening effects in MHD turbulence plays an important role in determining the TTD efficiency by slow and fast modes beyond the threshold of the linear resonance (Xu and Lazarian, 2018).

The change of pitch angles caused by TTD is due to the particle acceleration. TTD interaction increases the parallel component of CR momentum in a stochastic manner. Compared with gyroresonance scattering, the advantage of TTD is that it is much less subject to damping effects that cut off the turbulent energy cascade. Thus the process can act in settings where the gyroresonance scattering is inefficient (Yan and Lazarian, 2003; Beresnyak and Lazarian, 2007; Xu et al., 2016).

4.3 Mirror diffusion of CRs

In addition to the pitch-angle scattering, it has long been known that CR propagation can also be affected by magnetic mirror reflection (Fermi, 1949; Noerdlinger, 1968; Cesarsky and Kulsrud, 1973; Klepach and Ptuskin, 1995; Chandran, 2000a). In particular, the magnetic mirroring effect was explored to resolve the 90° problem that arises in the QLT describing the pitch-angle scattering (see Section 4.1). In these studies, the mirroring effect was invoked for trapping CRs that bounce back and forth between two mirror points. On the basis of improved understanding of MHD turbulence theory, Lazarian and Xu (2021) identified a new effect associated with CRs interacting stochastically with different mirrors, which is termed mirror diffusion. It serves as a new diffusion mechanism that can effectively confine CRs. In MHD turbulence, compressions of magnetic fields, which arise from slow and fast modes in a compressible medium and pseudo Alfvén modes in an incompressible medium, naturally, induce the mirroring effect over a range of length scales. The properties of the magnetic mirrors are determined by the scaling properties of slow (pseudo Alfvén) and fast modes. Combined with the intrinsic perpendicular superdiffusion of turbulent magnetic fields arising from Alfvénic modes (Lazarian and Vishniac, 1999; Eyink et al., 2013; Lazarian and Yan, 2014), this results in mirror diffusion of CRs along magnetic field lines. In other words, CRs are not trapped between mirrors, but exhibit a new type of diffusive propagation.

Magnetic compressions arising from slow and fast modes create magnetic mirrors that result in the reflecting of CRs. The mirroring effect caused by static magnetic bottles has been well studied in plasma physics (e.g., Post, 1958; Budker, 1959; Noerdlinger, 1968; Kulsrud and Pearce, 1969). A CR with r_L smaller than the variation scale of the magnetic field preserves its first adiabatic invariant, i.e., $p_{\perp }^2/B=$const. Therefore, as a particle moves along the magnetic field with the field strength increasing from B₀ to B₀ + δb, its perpendicular momentum p_⊥ increases. It implies that with pitch angle cosine μ

$\mu <{\mu }_{lc}=\sqrt{\frac{\delta b}{B_0+\delta b}},(24)$

the particle can be reflected at the mirror point, while particles with larger μ’s, i.e., smaller pitch angles, can escape from the mirror. Earlier studies considered that the magnetic mirrors trap the CRs until the gyroresonance scattering allows the particles to escape the mirrors (Cesarsky and Kulsrud, 1973). CRs with μ < μ_lc were considered “trapped” in magnetic bottles and thus unable to diffuse. However, in Lazarian and Xu (2021) it was shown that this is not true in realistic MHD turbulence. During the perpendicular superdiffusion, CRs cannot trace back the same magnetic field line. Instead, after each mirroring interaction, they always encounter a different mirror, leading to their diffusion along magnetic field lines (see Figure 4).

FIGURE 4

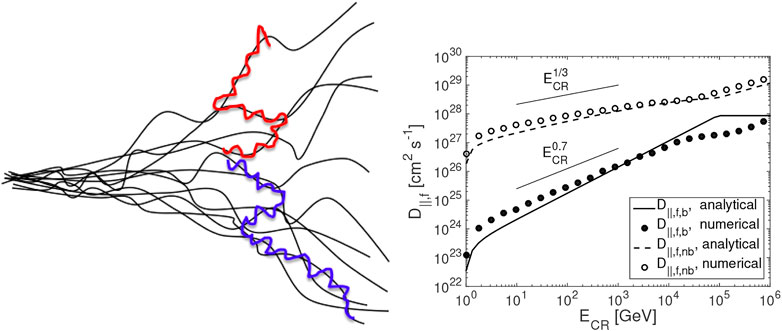
FIGURE 4. Left: Illustration of mirror diffusion. Thin lines represent turbulent magnetic field lines. Thick lines represent the trajectories of two CR particles whose initial separation is small. Right: Parallel diffusion coefficients D_‖,f,b of mirror diffusion and D_‖,f,nb of scattering diffusion induced by fast modes. From LX21.

For mirroring interaction with fast modes, the corresponding parallel diffusion coefficient is (LX21).

$D_{\Vert ,b}(\mu )=\left\{\begin{array}{c}v\mu k^{-1}=vL{\left(\frac{\delta B_f}{B_0}\right)}^{-4}{\mu }^9,{\mu }_{\text{min,f}}<\mu <{\mu }_c,\hfill \\ v\mu r_L,\mu <{\mu }_{\text{min,f}},\hfill \end{array}\right.(25)$

Where

${\mu }_c\approx {\left[\frac{14}{\pi }\frac{\delta B_f^2}{B_0^2}{\left(\frac{v}{L\mathrm{\Omega }}\right)}^{\frac{1}{2}}\right]}^{\frac{2}{11}}(26)$

is the critical μ at the balance between pitch-angle scattering and mirroring,

${\mu }_{\text{min,f}}=\sqrt{\frac{\delta B_f}{B_0}}{\left(\frac{r_L}{L}\right)}^{\frac{1}{8}},(27)$

v is the particle velocity, Ω is the gyrofrequency, B₀ is the mean magnetic field strength, and δB_f is the magnetic fluctuation of fast modes at L. For μ > μ_c the diffusion is determined by scattering, and the scattering diffusion coefficient is typically much larger than that of mirror diffusion (see Figure 4). In the vicinity of CR sources, e.g., supernova remnants, the mirror diffusion of CRs with μ < μ_c can prevent fast escape of CRs (Xu, 2021). With pitch angle change by pitch-angle scattering, CRs undergo periods of slow mirror diffusion separated by periods of fast scattering diffusion, showing a Lévy-flight-like characteristic.

5 Summary

The progress in understanding CR propagation was hindered for decades due to an inadequate understanding of MHD turbulence. Recent development in MHD turbulence theories, MHD turbulence simulations, as well as new observational techniques in measuring turbulence and magnetic fields, bring us new physical insight into the interaction of CRs with MHD turbulence and CR diffusion. The perpendicular (super) diffusion of CRs arises from that of turbulent magnetic fields regulated by Alfvén modes of MHD turbulence. The highly tangled magnetic field lines in super-Alfvénic turbulence provide additional confinement of CRs with an effective mean free path determined by the Alfvénic scale l_A. For parallel diffusion, the widely-used gyroresonance scattering, i.e., pitch-angle scattering, is inefficient in scattering CRs with large pitch angles and low-energy CRs in the presence of severe damping of fast modes, e.g., in a weakly ionized medium. With resonance broadening effects in MHD turbulence taken into account, the transit-time damping interaction can efficiently cause the change of pitch angles via stochastic particle acceleration. With both magnetic compressions and superdiffusion of magnetic field lines in MHD turbulence, CRs interacting with turbulent magnetic mirrors undergo mirror diffusion. It results in a slow diffusion of CRs in the vicinity of their sources and a Lévy-flight-like propagation of CRs.

The perpendicular (super) diffusion and parallel diffusion of CRs strongly depend on the regime and properties of MHD turbulence. Combining the updated theoretical understanding of CR propagation and new observational techniques for mapping the characteristic parameters, e.g., M_A, in diverse astrophysical conditions (e.g., Lazarian et al., 2018; Hu et al., 2019; Hu et al., 2020; Zhang et al., 2019; Xu and Hu, 2021; Hu et al., 2022a) holds a great promise in realistic modeling of CR propagation and solving long-standing observational puzzles related to CRs.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

The research of AL and YH is supported by NASA ATP AAH7546. SX acknowledges the support for this work provided by NASA through the NASA Hubble Fellowship grant # HST-HF2-51473.001-A awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Incorporated, under NASA contract NAS5-26555. YH is supported by NASA through award 09_0231 issued by the Universities Space Research Association, Inc. (USRA).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹For the sake of simplicity, we discuss only the so-called “balanced” MHD turbulence, i.e., MHD turbulence with equal fluxes of Alfvén energy in opposite directions. This is not the case for Solar wind over distances less than 1 AU. However, the turbulence gets balanced at larger scales. The theory of imbalanced MHD turbulence is described in the book by Beresnyak and Lazarian 2019.

²Super-Alfvénic turbulence should be distinguished from super-Alfvénic (e.g., solar wind) flow. In super-Alfvénic turbulence, it is the averaged relative velocity at L, rather than the bulk flow velocity, that exceeds V_A.

³However, in the global reference frame with respect to the mean magnetic field adopted in Goldreich and Sridhar (1995), the scale-dependent anisotropy is not expected. The local reference frame, i.e., the only reference frame for one to see the scale-dependent anisotropy, was introduced in Lazarian and Vishniac (1999).

⁴Weak turbulence is weak in terms of the non-linear interactions of oppositely directed wave packets.

⁵The initial derivation was performed for the problem of thermal electron diffusion in clusters of galaxies. However, the physics of the diffusion of non-relativistic and relativistic particles are identical.

References

Amato, E., and Casanova, S. (2021). On particle acceleration and transport in plasmas in the galaxy: Theory and observations. J. Plasma Phys. 87, 845870101. doi:10.1017/S0022377821000064

CrossRef Full Text | Google Scholar

Anjos, R. C., and Catalani, F. (2020). Galactic Center as an efficient source of cosmic rays. Phys. Rev. D. 101, 123015. doi:10.1103/PhysRevD.101.123015

CrossRef Full Text | Google Scholar

Armstrong, J. W., Rickett, B. J., and Spangler, S. R. (1995). Electron density power spectrum in the local interstellar medium. ApJ 443, 209–221. doi:10.1086/175515

CrossRef Full Text | Google Scholar

Beresnyak, A. (2013). Asymmetric diffusion of magnetic field lines. ApJ 767, L39. doi:10.1088/2041-8205/767/2/L39

CrossRef Full Text | Google Scholar

Beresnyak, A., and Lazarian, A. (2007). Strong imbalanced turbulence. B3: AGU Fall Meeting Abstracts.

Google Scholar

Beresnyak, A., and Lazarian, A. (2019). Turbulence in magnetohydrodynamics.

Google Scholar

Beresnyak, A. (2015). On the parallel spectrum in magnetohydrodynamic turbulence. ApJ 801, L9. doi:10.1088/2041-8205/801/1/L9

CrossRef Full Text | Google Scholar

Beresnyak, A. (2014). Spectra of strong magnetohydrodynamic turbulence from high-resolution simulations. ApJ 784, L20. doi:10.1088/2041-8205/784/2/L20

CrossRef Full Text | Google Scholar

Blasi, P., and Amato, E. (2012). Diffusive propagation of cosmic rays from supernova remnants in the galaxy. I: Spectrum and chemical composition. J. Cosmol. Astropart. Phys. 2012, 010. doi:10.1088/1475-7516/2012/01/010

CrossRef Full Text | Google Scholar

Brunetti, G., and Jones, T. W. (2014). Cosmic rays in galaxy clusters and their nonthermal emission. Int. J. Mod. Phys. D 23, 1430007–1430098. doi:10.1142/S0218271814300079

CrossRef Full Text | Google Scholar

Brunetti, G., and Lazarian, A. (2007). Compressible turbulence in galaxy clusters: Physics and stochastic particle re-acceleration. MNRAS 378, 245–275. doi:10.1111/j.1365-2966.2007.11771.x

CrossRef Full Text | Google Scholar

Budker, G. I. (1959). in Plasma physics and the problem of controlled thermonuclear reactions, Ed. by M. A. Leontovich (Pergamon, New York), Vol. 1

Google Scholar

Cesarsky, C. J., and Kulsrud, R. M. (1973). Role of hydromagnetic waves in cosmic-ray confinement in the disk. Theory of behavior in general wave spectra. ApJ 185, 153. doi:10.1086/152405

CrossRef Full Text | Google Scholar

Chamandy, L., and Shukurov, A. (2020). Parameters of the supernova-driven interstellar turbulence. Galaxies 8, 56. doi:10.3390/galaxies8030056

CrossRef Full Text | Google Scholar

Chandran, B. D. G. (2000a). Confinement and isotropization of galactic cosmic rays by molecular-cloud magnetic mirrors when turbulent scattering is weak. ApJ 529, 513–535. doi:10.1086/308232

CrossRef Full Text | Google Scholar

Chandran, B. D. G. (2000b). Scattering of energetic particles by anisotropic magnetohydrodynamic turbulence with a goldreich-sridhar power spectrum. Phys. Rev. Lett. 85, 4656–4659. doi:10.1103/PhysRevLett.85.4656

PubMed Abstract | CrossRef Full Text | Google Scholar

Chepurnov, A., and Lazarian, A. (2010). Extending the Big power law in the Sky with turbulence spectra from Wisconsin Hα mapper data. ApJ 710, 853–858. doi:10.1088/0004-637X/710/1/853

CrossRef Full Text | Google Scholar

Cho, J., and Lazarian, A. (2003). Compressible magnetohydrodynamic turbulence: Mode coupling, scaling relations, anisotropy, viscosity-damped regime and astrophysical implications. MNRAS 345, 325–339. doi:10.1046/j.1365-8711.2003.06941.x

CrossRef Full Text | Google Scholar

Cho, J., and Lazarian, A. (2002a). Compressible sub-alfvénic MHD turbulence in low- β plasmas. Phys. Rev. Lett. 88, 245001. doi:10.1103/PhysRevLett.88.245001

PubMed Abstract | CrossRef Full Text | Google Scholar

Cho, J., and Lazarian, A. (2002b). Magnetohydrodynamic turbulence as a foreground for cosmic microwave background studies. ApJ 575, L63–L66. doi:10.1086/342722

CrossRef Full Text | Google Scholar

Cho, J., Lazarian, A., and Timbie, P. T. (2012). A technique for foreground subtraction in redshifted 21 cm observations. ApJ 749, 164. doi:10.1088/0004-637X/749/2/164

CrossRef Full Text | Google Scholar

Cho, J., Lazarian, A., and Vishniac, E. T. (2002). Simulations of magnetohydrodynamic turbulence in a strongly magnetized medium. ApJ 564, 291–301. doi:10.1086/324186

CrossRef Full Text | Google Scholar

Cho, J., and Vishniac, E. T. (2000). The anisotropy of magnetohydrodynamic alfvénic turbulence. ApJ 539, 273–282. doi:10.1086/309213

CrossRef Full Text | Google Scholar

Demidem, C., Lemoine, M., and Casse, F. (2020). Particle acceleration in relativistic turbulence: A theoretical appraisal. Phys. Rev. D. 102, 023003. doi:10.1103/PhysRevD.102.023003

CrossRef Full Text | Google Scholar

Di Mauro, M., Manconi, S., and Donato, F. (2020). Evidences of low-diffusion bubbles around Galactic pulsars. Phys. Rev. D. 101, 103035. doi:10.1103/PhysRevD.101.103035

CrossRef Full Text | Google Scholar

Evoli, C., and Yan, H. (2014). Cosmic ray propagation in galactic turbulence. ApJ 782, 36. doi:10.1088/0004-637X/782/1/36

CrossRef Full Text | Google Scholar

Eyink, G. L., Lazarian, A., and Vishniac, E. T. (2011). Fast magnetic reconnection and spontaneous stochasticity. ApJ 743, 51. doi:10.1088/0004-637X/743/1/51

CrossRef Full Text | Google Scholar

Eyink, G., Vishniac, E., Lalescu, C., Aluie, H., Kanov, K., Bürger, K., et al. (2013). Flux-freezing breakdown in high-conductivity magnetohydrodynamic turbulence. Nature 497, 466–469. doi:10.1038/nature12128

PubMed Abstract | CrossRef Full Text | Google Scholar

Farmer, A. J., and Goldreich, P. (2004). Wave damping by magnetohydrodynamic turbulence and its effect on cosmic-ray propagation in the interstellar medium. ApJ 604, 671–674. doi:10.1086/382040

CrossRef Full Text | Google Scholar

Fermi, E. (1949). On the origin of the cosmic radiation. Phys. Rev. 75, 1169–1174. doi:10.1103/PhysRev.75.1169

CrossRef Full Text | Google Scholar

Forman, M. A., Wicks, R. T., and Horbury, T. S. (2011). Detailed fit of “critical balance” theory to solar wind turbulence measurements. ApJ 733, 76. doi:10.1088/0004-637X/733/2/76

CrossRef Full Text | Google Scholar

Fornieri, O., Gaggero, D., Cerri, S. S., De La Torre Luque, P., and Gabici, S. (2021). The theory of cosmic ray scattering on pre-existing MHD modes meets data. MNRAS 502, 5821–5838. doi:10.1093/mnras/stab355

CrossRef Full Text | Google Scholar

Gabici, S., Evoli, C., Gaggero, D., Lipari, P., Mertsch, P., Orlando, E., et al. (2019). The origin of galactic cosmic rays: Challenges to the standard paradigm. arXiv e-prints , arXiv:1903.11584.

Google Scholar

Galtier, S., Nazarenko, S. V., Newell, A. C., and Pouquet, A. (2000). A weak turbulence theory for incompressible magnetohydrodynamics. J. Plasma Phys. 63, 447–488. doi:10.1017/S0022377899008284

CrossRef Full Text | Google Scholar

Giacalone, J., and Jokipii, J. R. (1999). The transport of cosmic rays across a turbulent magnetic field. ApJ 520, 204–214. doi:10.1086/307452

CrossRef Full Text | Google Scholar

Ginzburg, V. L., and Syrovatskii, S. I. (1964). The origin of cosmic rays.

Google Scholar

Goldreich, P., and Sridhar, S. (1995). Toward a theory of interstellar turbulence. 2: Strong alfvenic turbulence. ApJ 438, 763–775. doi:10.1086/175121

CrossRef Full Text | Google Scholar

Guo, F., and Oh, S. P. (2008). Feedback heating by cosmic rays in clusters of galaxies. MNRAS 384, 251–266. doi:10.1111/j.1365-2966.2007.12692.x

CrossRef Full Text | Google Scholar

Holguin, F., Ruszkowski, M., Lazarian, A., Farber, R., and Yang, H. Y. K. (2019). Role of cosmic-ray streaming and turbulent damping in driving galactic winds. MNRAS 490, 1271–1282. doi:10.1093/mnras/stz2568

CrossRef Full Text | Google Scholar

Hopkins, P. F., Chan, T. K., Garrison-Kimmel, S., Ji, S., Su, K.-Y., Hummels, C. B., et al. (2020). But what about.: Cosmic rays, magnetic fields, conduction, and viscosity in galaxy formation. MNRAS 492, 3465–3498. doi:10.1093/mnras/stz3321

CrossRef Full Text | Google Scholar

Horbury, T. S., Forman, M., and Oughton, S. (2008). Anisotropic scaling of magnetohydrodynamic turbulence. Phys. Rev. Lett. 101, 175005. doi:10.1103/PhysRevLett.101.175005

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, Y., Lazarian, A., Beck, R., and Xu, S. (2022a). Role of magnetic fields in fueling seyfert nuclei. ApJ 941, 92. doi:10.3847/1538-4357/ac9df0

CrossRef Full Text | Google Scholar

Hu, Y., Lazarian, A., Li, Y., Zhuravleva, I., and Gendron-Marsolais, M.-L. (2020). Probing magnetic field morphology in galaxy clusters with the gradient technique. ApJ 901, 162. doi:10.3847/1538-4357/abb1c3

CrossRef Full Text | Google Scholar

Hu, Y., Lazarian, A., and Xu, S. (2022b). Superdiffusion of cosmic rays in compressible magnetized turbulence. MNRAS 512, 2111–2124. doi:10.1093/mnras/stac319

CrossRef Full Text | Google Scholar

Hu, Y., Xu, S., and Lazarian, A. (2021). Anisotropies in compressible MHD turbulence: Probing magnetic fields and measuring magnetization. ApJ 911, 37. doi:10.3847/1538-4357/abea18

CrossRef Full Text | Google Scholar

Hu, Y., Yuen, K. H., Lazarian, V., Ho, K. W., Benjamin, R. A., Hill, A. S., et al. (2019). Magnetic field morphology in interstellar clouds with the velocity gradient technique. Nat. Astron. 3, 776–782. doi:10.1038/s41550-019-0769-0

CrossRef Full Text | Google Scholar

Ipavich, F. M. (1975). Galactic winds driven by cosmic rays. ApJ 196, 107–120. doi:10.1086/153397

CrossRef Full Text | Google Scholar

Jokipii, J. R. (1966). Cosmic-ray propagation. I. Charged particles in a random magnetic field. ApJ 146, 480. doi:10.1086/148912

CrossRef Full Text | Google Scholar

Jokipii, J. R. (1982). Particle drift, diffusion, and acceleration at shocks. ApJ 255, 716–720. doi:10.1086/159870

CrossRef Full Text | Google Scholar

Jokipii, J. R. (1971). Propagation of cosmic rays in the solar wind. Rev. Geophys. Space Phys. 9, 27–87. doi:10.1029/RG009i001p00027

CrossRef Full Text | Google Scholar

Jokipii, J. R. (1987). Rate of energy gain and maximum energy in diffusive shock acceleration. ApJ 313, 842. doi:10.1086/165022

CrossRef Full Text | Google Scholar

Kempski, P., and Quataert, E. (2022). Reconciling cosmic ray transport theory with phenomenological models motivated by Milky-Way data. MNRAS 514, 657–674. doi:10.1093/mnras/stac1240

CrossRef Full Text | Google Scholar

Klepach, E. G., and Ptuskin, V. S. (1995). Propagation of cosmic rays in a medium with magnetic traps. Astron. Lett. 21, 411–417.

Google Scholar

Kóta, J., and Jokipii, J. R. (2000). Velocity correlation and the spatial diffusion coefficients of cosmic rays: Compound diffusion. ApJ 531, 1067–1070. doi:10.1086/308492

CrossRef Full Text | Google Scholar

Kowal, G., and Lazarian, A. (2010). Velocity field of compressible magnetohydrodynamic turbulence: Wavelet decomposition and mode scalings. ApJ 720, 742–756. doi:10.1088/0004-637X/720/1/742

CrossRef Full Text | Google Scholar

Krumholz, M. R., Crocker, R. M., Xu, S., Lazarian, A., Rosevear, M. T., and Bedwell-Wilson, J. (2020). Cosmic ray transport in starburst galaxies. MNRAS 493, 2817–2833. doi:10.1093/mnras/staa493

CrossRef Full Text | Google Scholar

Kulsrud, R., and Pearce, W. P. (1969). The effect of wave-particle interactions on the propagation of cosmic rays. ApJ 156, 445. doi:10.1086/149981

CrossRef Full Text | Google Scholar

Lazarian, A., and Beresnyak, A. (2006). Cosmic ray scattering in compressible turbulence. MNRAS 373, 1195–1202. doi:10.1111/j.1365-2966.2006.11093.x

CrossRef Full Text | Google Scholar

Lazarian, A. (2016). Damping of Alfvén waves by turbulence and its consequences: From cosmic-ray streaming to launching winds. ApJ 833, 131. doi:10.3847/1538-4357/833/2/131

CrossRef Full Text | Google Scholar

Lazarian, A. (2006). Enhancement and suppression of heat transfer by MHD turbulence. ApJ 645, L25–L28. doi:10.1086/505796

CrossRef Full Text | Google Scholar

Lazarian, A. (2014). Reconnection diffusion in turbulent fluids and its implications for star formation. Space Sci. Rev. 181, 1–59. doi:10.1007/s11214-013-0031-5

CrossRef Full Text | Google Scholar

Lazarian, A., Vishniac, E. T., and Cho, J. (2004). Magnetic field structure and stochastic reconnection in a partially ionized gas. ApJ 603, 180–197. doi:10.1086/381383

CrossRef Full Text | Google Scholar

Lazarian, A., and Vishniac, E. T. (1999). Reconnection in a weakly stochastic field. ApJ 517, 700–718. doi:10.1086/307233

CrossRef Full Text | Google Scholar

Lazarian, A., and Xu, S. (2022). Damping of Alfvén waves in MHD turbulence and implications for cosmic ray streaming instability and galactic winds. Front. Phys. 10, 702799. doi:10.3389/fphy.2022.702799

CrossRef Full Text | Google Scholar

Lazarian, A., and Xu, S. (2021). Diffusion of cosmic rays in MHD turbulence with magnetic mirrors. ApJ 923, 53. doi:10.3847/1538-4357/ac2de9

CrossRef Full Text | Google Scholar

Lazarian, A., and Yan, H. (2019). Erratum: “Superdiffusion of cosmic rays: Implications for cosmic ray acceleration”. ApJ 885, 170. doi:10.3847/1538-4357/ab50ba

CrossRef Full Text | Google Scholar

Lazarian, A., and Yan, H. (2014). Superdiffusion of cosmic rays: Implications for cosmic ray acceleration. ApJ 784, 38. doi:10.1088/0004-637X/784/1/38

CrossRef Full Text | Google Scholar

Lazarian, A., Yuen, K. H., Ho, K. W., Chen, J., Lazarian, V., Lu, Z., et al. (2018). Distribution of velocity gradient orientations: Mapping magnetization with the velocity gradient technique. ApJ 865, 46. doi:10.3847/1538-4357/aad7ff

CrossRef Full Text | Google Scholar

Lemoine, M., and Malkov, M. A. (2020). Power-law spectra from stochastic acceleration. MNRAS 499, 4972–4983. doi:10.1093/mnras/staa3131

CrossRef Full Text | Google Scholar

Lithwick, Y., and Goldreich, P. (2001). Compressible magnetohydrodynamic turbulence in interstellar plasmas. ApJ 562, 279–296. doi:10.1086/323470

CrossRef Full Text | Google Scholar

Longair, M. S. (2011). High energy astrophysics.

Google Scholar

López-Barquero, V., Farber, R., Xu, S., Desiati, P., and Lazarian, A. (2016). Cosmic-ray small-scale anisotropies and local turbulent magnetic fields. ApJ 830, 19. doi:10.3847/0004-637X/830/1/19

CrossRef Full Text | Google Scholar

Luo, Q. Y., and Wu, D. J. (2010). Observations of anisotropic scaling of solar wind turbulence. ApJ 714, L138–L141. doi:10.1088/2041-8205/714/1/L138

CrossRef Full Text | Google Scholar

Lynn, J. W., Parrish, I. J., Quataert, E., and Chandran, B. D. G. (2012). Resonance broadening and heating of charged particles in magnetohydrodynamic turbulence. ApJ 758, 78. doi:10.1088/0004-637X/758/2/78

CrossRef Full Text | Google Scholar

Maiti, S., Makwana, K., Zhang, H., and Yan, H. (2022). Cosmic-ray transport in magnetohydrodynamic turbulence. ApJ 926, 94. doi:10.3847/1538-4357/ac46c8

CrossRef Full Text | Google Scholar

Marcowith, A., Ferrand, G., Grech, M., Meliani, Z., Plotnikov, I., and Walder, R. (2020). Multi-scale simulations of particle acceleration in astrophysical systems. Living Rev. Comput. Astrophysics 6, 1. doi:10.1007/s41115-020-0007-6

CrossRef Full Text | Google Scholar

Maron, J., and Goldreich, P. (2001). Simulations of incompressible magnetohydrodynamic turbulence. ApJ 554, 1175–1196. doi:10.1086/321413

CrossRef Full Text | Google Scholar

Matthaeus, W. H., Ghosh, S., Oughton, S., and Roberts, D. A. (1996). Anisotropic three-dimensional MHD turbulence. J. Geophys. Res. 101, 7619–7629. doi:10.1029/95JA03830

CrossRef Full Text | Google Scholar

Matthaeus, W. H., Goldstein, M. L., and Roberts, D. A. (1990). Evidence for the presence of quasi-two-dimensional nearly incompressible fluctuations in the solar wind. J. Geophys. Res. 95, 20673–20683. doi:10.1029/JA095iA12p20673

CrossRef Full Text | Google Scholar

Matthaeus, W. H., Qin, G., Bieber, J. W., and Zank, G. P. (2003). Nonlinear collisionless perpendicular diffusion of charged particles. ApJ 590, L53–L56. doi:10.1086/376613

CrossRef Full Text | Google Scholar

Melrose, D. B. (1969). On the formation of energy spectra in synchrotron sources. Ap&SS 5, 131–149. doi:10.1007/BF00650288

CrossRef Full Text | Google Scholar

Nava, L., and Gabici, S. (2013). Anisotropic cosmic ray diffusion and gamma-ray production close to supernova remnants, with an application to W28. MNRAS 429, 1643–1651. doi:10.1093/mnras/sts450

CrossRef Full Text | Google Scholar

Noerdlinger, P. D. (1968). An improved model for cosmic-ray propagation. Phys. Rev. Lett. 20, 1513–1516. doi:10.1103/PhysRevLett.20.1513

CrossRef Full Text | Google Scholar

Orlando, E. (2018). Imprints of cosmic rays in multifrequency observations of the interstellar emission. MNRAS 475, 2724–2742. doi:10.1093/mnras/stx3280

CrossRef Full Text | Google Scholar

Post, R. F. (1958). “Proc. Of Second U.N,” in Int. Conf. on Peaceful Uses of Atomic Energy, 1 September- 13 September (Geneva, 245–265. Paper A/Conf. 15/P/377.32

PubMed Abstract | Google Scholar

Padovani, M., Ivlev, A. V., Galli, D., and Caselli, P. (2018). Cosmic-ray ionisation in circumstellar discs. A&A 614, A111. doi:10.1051/0004-6361/201732202

CrossRef Full Text | Google Scholar

Palmer, I. D. (1982). Transport coefficients of low-energy cosmic rays in interplanetary space. Rev. Geophys. Space Phys. 20, 335–351. doi:10.1029/RG020i002p00335

CrossRef Full Text | Google Scholar

Parker, E. N. (1966). The kinetic properties of the galactic cosmic-ray gas. ApJ 144, 916. doi:10.1086/148689

CrossRef Full Text | Google Scholar

Parker, E. N. (1965). The passage of energetic charged particles through interplanetary space. Planet. Space Sci. 13, 9–49. doi:10.1016/0032-0633(65)90131-5

CrossRef Full Text | Google Scholar

Perri, S., and Zimbardo, G. (2009). Ion superdiffusion at the solar wind termination shock. ApJ 693, L118–L121. doi:10.1088/0004-637X/693/2/L118

CrossRef Full Text | Google Scholar

Plotnikov, I., Ostriker, E. C., and Bai, X.-N. (2021). Influence of ion-neutral damping on the cosmic-ray streaming instability: Magnetohydrodynamic particle-in-cell simulations. ApJ 914, 3. doi:10.3847/1538-4357/abf7b3

CrossRef Full Text | Google Scholar

Qin, G., Matthaeus, W. H., and Bieber, J. W. (2002). Perpendicular transport of charged particles in composite model turbulence: Recovery of diffusion. ApJ 578, L117–L120. doi:10.1086/344687

CrossRef Full Text | Google Scholar

Quataert, E., Thompson, T. A., and Jiang, Y.-F. (2022). The physics of galactic winds driven by cosmic rays I: Diffusion. MNRAS 510, 1184–1203. doi:10.1093/mnras/stab3273

CrossRef Full Text | Google Scholar

Richardson, L. F. (1926). Atmospheric diffusion shown on a distance-neighbour graph. Proc. R. Soc. Lond. Ser. A 110, 709–737. doi:10.1098/rspa.1926.0043

CrossRef Full Text | Google Scholar

Sampson, M. L., Beattie, J. R., Krumholz, M. R., Crocker, R. M., Federrath, C., and Seta, A. (2023). Turbulent diffusion of streaming cosmic rays in compressible, partially ionized plasma. MNRAS 519, 1503–1525. doi:10.1093/mnras/stac3207

CrossRef Full Text | Google Scholar

Schlickeiser, R., Caglar, M., and Lazarian, A. (2016). Cosmic rays and MHD turbulence generation in interstellar giant molecular clouds. ApJ 824, 89. doi:10.3847/0004-637X/824/2/89

CrossRef Full Text | Google Scholar

Schlickeiser, R. (2002). Cosmic ray astrophysics.

Google Scholar

Schlickeiser, R., and Miller, J. A. (1998). Quasi-linear theory of cosmic-ray transport and acceleration: The role of oblique magnetohydrodynamic waves and transit-time damping. ApJ 492, 352–378. doi:10.1086/305023

CrossRef Full Text | Google Scholar

Singer, H. J., Heckman, G. R., and Hirman, J. W. (2001). “Space weather forecasting: A grand challenge,” in Geophysical monograph series (Washington DC: American Geophysical Union), 125, 23–29. doi:10.1029/GM125p0023

CrossRef Full Text | Google Scholar

Sioulas, N., Isliker, H., Vlahos, L., Koumtzis, A., and Pisokas, T. (2020). Superdiffusive stochastic Fermi acceleration in space and energy. MNRAS 491, 3860–3869. doi:10.1093/mnras/stz3259

CrossRef Full Text | Google Scholar

Strong, A. W., Moskalenko, I. V., and Ptuskin, V. S. (2007). Cosmic-ray propagation and interactions in the galaxy. Annu. Rev. Nucl. Part. Sci. 57, 285–327. doi:10.1146/annurev.nucl.57.090506.123011

CrossRef Full Text | Google Scholar

Xu, S., and Hu, Y. (2021). Measuring magnetization with rotation measures and velocity centroids in supersonic MHD turbulence. ApJ 910, 88. doi:10.3847/1538-4357/abe403

CrossRef Full Text | Google Scholar

Xu, S., and Lazarian, A. (2018). Resonance-broadened transit time damping of particles in MHD turbulence. ApJ 868, 36. doi:10.3847/1538-4357/aae840

CrossRef Full Text | Google Scholar

Xu, S., and Lazarian, A. (2022). Shock acceleration with oblique and turbulent magnetic fields. ApJ 925, 48. doi:10.3847/1538-4357/ac3824

CrossRef Full Text | Google Scholar

Xu, S., and Lazarian, A. (2020). Trapping of cosmic rays in MHD turbulence. ApJ 894, 63. doi:10.3847/1538-4357/ab8465

CrossRef Full Text | Google Scholar

Xu, S. (2021). Mirror diffusion of cosmic rays in highly compressible turbulence near supernova remnants. Astrophysical J. 922. doi:10.3847/1538-4357/ac2d8f

CrossRef Full Text | Google Scholar

Xu, S., and Yan, H. (2013). Cosmic-ray parallel and perpendicular transport in turbulent magnetic fields. ApJ 779, 140. doi:10.1088/0004-637X/779/2/140

CrossRef Full Text | Google Scholar

Xu, S., Yan, H., and Lazarian, A. (2016). Damping of magnetohydrodynamic turbulence in partially ionized plasma: Implications for cosmic ray propagation. ApJ 826, 166. doi:10.3847/0004-637X/826/2/166

CrossRef Full Text | Google Scholar

Yan, H., and Lazarian, A. (2008). Cosmic-ray propagation: Nonlinear diffusion parallel and perpendicular to mean magnetic field. ApJ 673, 942–953. doi:10.1086/524771

CrossRef Full Text | Google Scholar

Yan, H., and Lazarian, A. (2004). Cosmic-ray scattering and streaming in compressible magnetohydrodynamic turbulence. ApJ 614, 757–769. doi:10.1086/423733

CrossRef Full Text | Google Scholar

Yan, H., and Lazarian, A. (2003). Grain acceleration by magnetohydrodynamic turbulence: Gyroresonance mechanism. ApJ 592, L33–L36. doi:10.1086/377487

CrossRef Full Text | Google Scholar

Yan, H., and Lazarian, A. (2002). Scattering of cosmic rays by magnetohydrodynamic interstellar turbulence. Phys. Rev. Lett. 89, 281102. doi:10.1103/PhysRevLett.89.281102

PubMed Abstract | CrossRef Full Text | Google Scholar

Yuen, K. H., Ho, K. W., Law, C. Y., Chen, A., and Lazarian, A. (2022). Turbulent universal galactic Kolmogorov velocity cascade over 6 decades. arXiv:2204.13760.

Google Scholar

Zank, G. P., Adhikari, L., Hunana, P., Shiota, D., Bruno, R., and Telloni, D. (2017). Theory and transport of nearly incompressible magnetohydrodynamic turbulence. ApJ 835, 147. doi:10.3847/1538-4357/835/2/147

CrossRef Full Text | Google Scholar

Zhang, J.-F., Liu, Q., and Lazarian, A. (2019). Tracing magnetic fields by the synergies of synchrotron emission gradients. ApJ 886, 63. doi:10.3847/1538-4357/ab4b4a

CrossRef Full Text | Google Scholar