Kelvin-Helmholtz instability-driven magnetopause dynamics as turbulent pathway for the solar wind-magnetosphere coupling and the flank-central plasma sheet communication

1 Introduction

Since Dungey (1961) and Axford and Hines (1961) proposed different models of the solar wind (SW)-magnetosphere interaction, two most important physical processes in the SW-Earth’s magnetosphere coupling are thought to be magnetic reconnection and the Kelvin-Helmholtz instability (KHI). The former is based on the concept of dayside magnetic reconnection under large magnetic field shear. The latter is on quasi-viscous interaction in the flank-side boundary layer powered by large flow velocity shear. Understanding the former has been advanced via the recently-launched MMS spacecraft (Burch et al., 2016) with its high-resolution measurements, while the latter still leaves room for enhanced understanding. In particular, Kelvin-Helmholtz vortices (KHVs), i.e., the non-linearly-developed form of Kelvin-Helmholtz waves (KHWs) grow in size along the flank magnetopause down the tail. Thus, the impact of the latter could become important at the mid-tail X-line or beyond (X $\le$ −20 R_E, where R_E is the earth radii), where neither previous nor exiting spacecraft have often or routinely visited.

The KHI condition in the ideal MHD (magneto-hydro-dynamics) regime predicts that the condition becomes easily satisfied at the dawn flank than the dusk flank under typical Parker-Spiral IMF (interplanetary magnetic field) (Hasegawa, 1975; Nykyri, 2013). Under the same IMF condition, the kinetic physics also predicts the dawn-side magnetosheath to be more turbulent since enhanced fluctuations in the foreshock propagate downstream of the bow shock (Yordanova et al., 2020). These fluctuations or turbulence in the magnetosheath can act as seeds for KHI or lead to a stronger growth of KHI on the dawn side than the dusk side (Omidi et al., 2009; Nykyri et al., 2017; Nakamura et al., 2020). The observed dawn-favored asymmetry of the ion mixing layer containing cold magnetosheath-origin plasmas (Hasegawa et al., 2003; Wing et al., 2005; Moore et al., 2016; 2017) may evidence the role of KHWs in the solar wind entry. Yet, the importance and effectiveness of KHWs for plasma transport, in comparison to dayside subsolar and cusp reconnection, remain elusive. A case study for a certain IMF condition has been made in the near-Earth (X = −10 R_E) tail flank magnetopause (e.g., Phan et al., 2006). It is, however, crucial to understand the roles of mid-tail flank KHWs in terms of various solar wind conditions.

KHWs/KHVs provide a place for not only solar wind transport into the magnetosphere but also energetic (>30 keV) particle transport, being an efficient channel for “two-way transport”. Sorathia et al. (2017) showed that energetic particles originated from the central plasma sheet can be entrained in the tailward KHWs at dawn/dusk flanks. These particles can penetrate the magnetosheath depending on their energy and species. Furthermore, dayside reconnection leads to the formation of cusp diamagnetic cavities (Adamson et al., 2011; Adamson et al., 2012; Nykyri et al., 2011a; Nykyri et al., 2011b), which can be filled with energetic particles via local acceleration. These trapped particles can leak out via either IMF orientation changes or high-latitude KHWs (Hwang et al., 2012; Ma et al., 2016). Thus, KHWs can play roles in the leakage of energetic particles into the magnetosheath or their transport within the KHVs from the dayside magnetosphere to the tail flanks and further inside the magnetosphere. We lack the observational framework to determine the importance and efficiency of magnetopause KHWs in such roles.

Another unsolved mystery is how, where, and when KHWs/KHVs drive the global magnetosphere via “flank-central (near-midnight) magnetotail communication”. Recent simulations and observations (Merkin et al., 2013; Wang et al., 2017; Ling et al., 2018; Nishino et al., 2022) showed that the magnetic fluctuations and plasma density/flow perturbations associated with flank-side KHWs can penetrate inward as deep as the near-midnight central plasma sheet. Such KHW-engaged disturbances may serve as an onset trigger of the marginally stable current sheet in the magnetotail. The KHWs are, in turn, regulated by the midnight-origin instabilities and waves, such as the current sheet flapping that often propagates from the midnight meridian to the dawn/dusk flank. These studies indicate a possible causal relationship between flank-side KHWs/KHVs and central current sheet behavior, which has been never explored.

In the following sections we detail unsolved science questions in these three aspects (Sections 2–4) and how observational and numerical approaches as well as their incorporation would advance our understanding in this less explored area of the Heliophysics (Section 5). Summary follows in Section 6.

2 Roles and importance of flank dynamics in the solar wind transport

Multiple mechanisms have been proposed to explain the KHW-induced transfer of the SW plasma into the magnetosphere. While these mechanisms are inter-correlated to some extents, we divide them into three categories: 1) diffusive transport via finite gyroradius effects (as KHWs/KHVs lead to a thinning of the boundary layer) and/or through the turbulent decay of KHVs or coalescence of neighboring KHVs (Matsumoto and Hoshino, 2004; Faganello et al., 2008; Cowee et al., 2010; Matsumoto and Seki, 2010); 2) in-plane and/or mid-latitude vortex-induced reconnection (Nykyri and Otto, 2001; Faganello et al., 2012; Eriksson et al., 2016; Vernisse et al., 2016; Nakamura et al., 2017; Hwang et al., 2020; Hwang et al., 2021); 3) mode conversion from KHWs to kinetic Alfvén waves (Chaston et al., 2007) or anomalous transport driven by ion gyro-radius scale waves (Yao et al., 2011).

Regarding 1), in the MHD limit magnetic reconnection is required while in the hybrid or fully-kinetic regime both reconnection and diffusive transport due to large gyroradius effects can operate (Delamere et al., 2021). In particular, during the KHI growth the non-linear vortex flow rapidly compresses any initially-thick layer down to electron scales (Nakamura et al., 2008; Nakamura et al., 2011), which facilitates both diffusive transport and KHV-driven reconnection, leading to 2). Previous simulations (Nykyri and Otto, 2001; Nakamura and Daughton, 2014; Ma et al., 2017; Ma et al., 2019) showed that KHWs cause efficient transport with a diffusion coefficient of 10⁹⁻¹⁰ m²/s. This rate is sufficient in generating the cold-dense-plasma sheet in 1–2 h during the strongly northward IMF. A pre-existing LLBL (low-latitude boundary layer) can form via high-latitude cusp reconnection during northward IMF and promote the diffusion with the coefficient of 10¹⁰⁻¹¹ m²/s (Nakamura et al., 2017). In particular, vortex-induced reconnection and/or secondary tearing/KH/RT (Rayleigh-Taylor) instabilities can occur along the KHV boundary. Nakamura and Daughton (2014) showed that vortex-induced reconnection causes a rapid mixing while the secondary KHI and RTI cause a gradual transport deeper into the magnetosphere (Figure 1A).

FIGURE 1

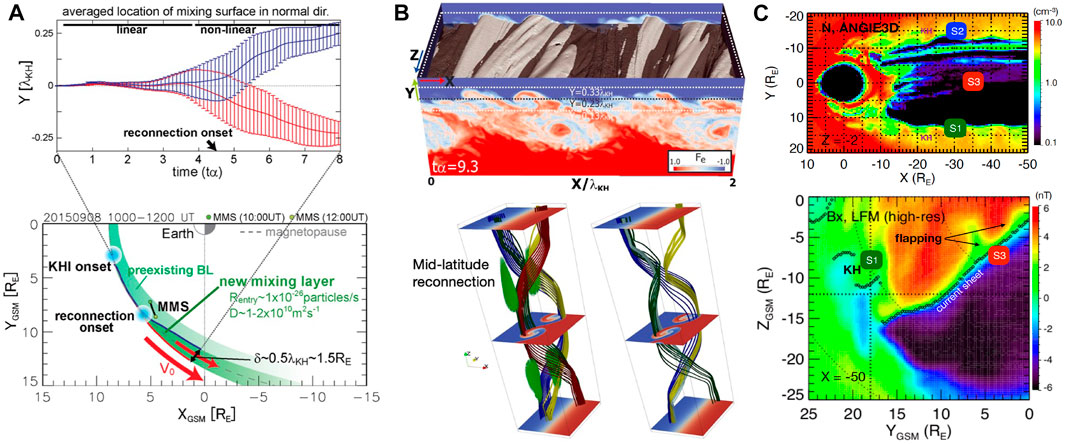
FIGURE 1. Solar wind plasma transport into the magnetosphere induced by KHWs via diffusive transport (A) upper: time evolution of the plasma mixing, lower: the locations of the mixing layer shown in the upper plot projected onto the modeled magnetopause together with particle entry rate and diffusion coefficient near the MMS location marked by the dumbell-like symbol). Vortex-induced “in-plane” reconnection occurs along the KHV boundary generating a series of flux ropes ((B), upper). KHVs also facilitate mid-latitude reconnection ((B), lower) north/south of the velocity shear plane near the equatorial region from Faganello et al. (2012). Illustration of KHWs externally driving current sheet fluctuations as predicted in a global hybrid simulation using ANGIE3D code ((C), upper panel; Lin et al., 2014; Lin et al., 2017) and global MHD (LFM) simulation (lower panel, Merkin et al., 2013). Under the development of KHVs (marked by S1 and S2 in the upper panel), inward-propagating KHW-associated fluctuations drive a north-to-south asymmetry in the central current sheet, which causes current sheet flapping (S3; (C)). This perturbation may play a role in the magnetotail reconnection onset or serve triggers of the marginally stable current sheet. The KHWs are, in turn, affected by the current sheet flapping that often propagates from midnight to dawn/dusk flanks. Simultaneous observations of the KH activity at the dawn/dusk flank and the current sheet thickness and behavior at a location deep inside the magnetopause provide an important causal relationship between the flank and midnight current sheet dynamics.

Reconnection can also occur out of the shear plane as a consequence of the relative flow shears at the low-latitude and high-latitude locations, which results in a 3-D twist of magnetospheric and magnetosheath magnetic fields induced by KHVs (Figure 1B). The same 3-D twisted magnetic topologies can generate field-aligned currents contributing to Region-1 currents (Johnson and Wing, 2015; Johnson et al., 2021; Hwang et al., 2022; Petrinec et al., 2022), indicating roles of magnetopause KHVs in the coupled SW-magnetosphere-ionosphere system. How vortex-induced in-plane or mid-latitude reconnection influences the large-scale system is unknown.

Another question concerning macroscopic impact of KHI-driven dynamics is whether or not KHWs/KHVs result in significant entry of shocked plasmas beyond the boundary layer or they rather simply form a mixing layer immediately inside the magnetopause. Recently Nishino et al. (2022) traced the source region of cold and dense ion beams observed by MMS located in the duskward plasma sheet to be further (∼5 R_E) duskward and tailward location. This suggests large-scale transport of KHI-driven shocked solar wind entry across the magnetopause and mixing low-latitude boundary layer.

Which processes among 1 to 3 is dominant in which evolution phase/location of the flank dynamics under which external conditions is an open question. How deep into the magnetosphere KHWs can transport mixed plasmas is important in quantifying the efficiency of KHW-driven SW-magnetosphere coupling. We specify the following science questions and relevant sub-questions:

Q1. What are the roles and importance of flank dynamics in the solar wind transport?

Q1.1: How importantly do flank dynamics transfer the solar wind plasma into the magnetosphere?

• In particular, how important and efficient are their roles in the solar wind transfer compared to dayside subsolar and/or cusp reconnection?

• How does the efficiency change in terms of external conditions including varying IMF orientation and the dawn vs. dusk sectors?

• How does flank dynamics influence solar wind-magnetosphere-ionosphere coupling?

Q1.2: How deeply do flank dynamics transport solar wind or mixed plasmas into the magnetosphere beyond the boundary layer?

• What are the transport paths and mechanisms (e.g., interchange instability) from the flank magnetopause to the central magnetosphere?

• Is there a dawn-dusk asymmetry?

Answering these questions enables us to resolve the long-standing Axford-Hines/Dungey dichotomy. This will ultimately bring crucial breakthroughs in the physics of the coupled SW-magnetosphere system by overcoming the long-standing lack of determining the roles and impact of flank dynamics.

3 Roles of KHWs/KHVs in the energetic particle transport or escape

KHWs/KHVs also act as a channel for energetic (>30 keV) particle transport. The simulation by Sorathia et al. (2017) showed that the propagation and evolution of energetic particles (H⁺, O⁺, and electrons) that are originated from the central magnetosphere are separated into two streams: one moving inward toward trapped drift orbits and the other moving along the magnetopause flanks. The higher-energy particles with larger gyroradii preferentially escape to the duskward magnetosheath. Depth of the magnetosheath penetration was larger for O⁺ than H⁺. Electrons whose equatorial crossings were within KHWs were entrained in the tailward propagation of KHWs. KHWs/KHVs thus play a role in the energetic particle transport and/or escape.

Furthermore, KHWs can promote the transport of high-energy particles generated in association with diamagnetic cavities at the high-latitude (∼8–10 R_E) magnetosphere. For any given IMF orientation, the IMF and geomagnetic field can be anti-parallel in the vicinity of the northern and southern high-altitude cusps, leading to the formation of cusp diamagnetic cavities (Adamson et al., 2011; Adamson et al., 2012; Nykyri et al., 2011a; Nykyri et al., 2011b). Cluster spacecraft observations showed 90°-pitch angle high-energy (37.3–127.5 keV) electrons in the northern high-altitude cusp cavity, with their fluxes dropping as a function of distance from the cavity, strongly suggestive of local acceleration mechanisms (Nykyri et al., 2012). Once the IMF orientation changes, these trapped particles in the cavity can end up in the loss cone depending on the local changes to the draping geometry and leak out of the cavity (Nykyri et al., 2021a).

In addition to the IMF orientation change, high-latitude KHWs in the dawn and dusk sectors of the northern and southern cusps where the geomagnetic field is mostly perpendicular to magnetosheath flow (Hwang et al., 2012; Ma et al., 2016) can help release the energetic particles from the cavity. The propagation of high-latitude KHWs toward the tailward and equatorward flanks may play a role in particle leakage into the magnetosheath or transport into the plasma sheet via KHV-driven diffusion. Recently, four MMS spacecraft discovered KHVs at southern-hemispheric high-latitude cusps (Figure 2; Nykyri et al., 2021b; Michael et al., 2021). The KHW structures trapped 90°-pitch angle, high-energy electrons, as well as energetic ions. Such ions, being less adiabatic, occasionally leaked out from the wave structures.

FIGURE 2

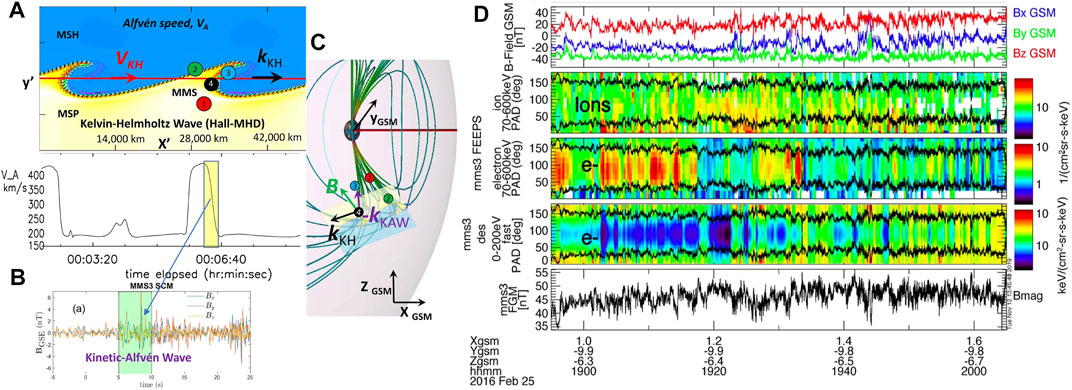
FIGURE 2. Example of MMS observations of KHWs at the vicinity of the southern exterior cusp ((C); Nykyri et al., 2021b). When MMS travels through strong Alfvén speed gradients (A), kinetic Alfvén waves (KAW) were observed (B). The KAWs carry energy into the ionosphere and were responsible for partial parallel heating of cold electrons. The stack plot (D) shows magnetic field (top), pitch-angle distributions of energetic ions and electrons (second and third panels), pitch-angle distributions of low energy electrons (fourth panel), and magnetic field strength (bottom panel). The low-energy electrons are in the loss cone (outside the black envelope which is the local trapping angle), while the high-energy (70–600 keV) electrons are trapped. The high-energy ions are less adiabatic and can stream out. The origin of these high-energy particles within KHWs is currently not known but may be related to the previously-formed diamagnetic cavities and/or local acceleration within KHI.

KHWs can host ample wave modes since mixed magnetic field topology and plasmas as well as multiple kinetic layers coexist within the wave structures, readily providing a free energy source to generate waves, such as kinetic Alfvén waves (KAWs), ion acoustic waves, and lower-hybrid waves (Johnson and Cheng, 2001; Chaston et al., 2007; Yao et al., 2011; Wilder et al., 2016; Dokgo et al., 2021). How these waves affect particle energization and/or transport remains elusive.

These studies suggest the roles played by KHWs/KHVs in energetic particle transport over the entire surface of the magnetopause or outside/inside the magnetosphere. The observational framework about the roles and impact of KHWs in such roles is in a primeval state. We list the following science questions and relevant sub-questions regarding this aspect:

Q2. What roles do magnetopause KHWs/KHVs play in the energetic particle transport and/or escape?

Q2.1: How far and how effectively do flankside and high-latitude KHWs transport energetic particles?

• What are the transport paths and mechanisms from the high-latitude diamagnetic cavities or inner magnetosphere to the flanks or into the magnetosheath?

• How does the KHW-driven energetic particle transport depend on hemispheres, IMF orientations, and varying external conditions?

Q2.2: Which particle species in what energy ranges are effectively transported/escape or generated via KHWs at flanks and high-latitude magnetopause?

• How do energetic particle species and their typical energies vary in terms of the dawn vs. dusk sectors?

• How do the local waves generated within KHWs affect particle energization and/or transport?

Answering these questions, when combined with Q1, will complete our understanding of the roles and impact of the magnetopause KHWs as a channel for two-way transport.

4 Causality between flank dynamics and central current sheet behavior

KHWs/KHVs can drive the global magnetosphere via “flank-central (near-midnight) magnetotail communication”. Simulations and observations (Li et al., 2012; Merkin et al., 2013; Wang et al., 2017; Ling et al., 2018) have indicated that as KHWs propagate down the tail beyond X = −20 R_E, the wavelength of the KHVs grows larger to ∼10 R_E, the north-south width of KHVs expands with a certain k _z component, and the plasma flow and magnetic fluctuations associated with KHWs penetrate inward to as deep as the midnight region (Figure 1C). As the magnetospheric magnetic fields become weaker with increasing downtail distances, the tail current sheet at X ≤ −20 R_E can be easily disturbed by such KHW-engaged fluctuations.

Two-point observations by ARTEMIS together with MHD simulations (Wang et al., 2017) suggest that the inward-propagating fluctuations caused by the magnetopause KHWs drive an asymmetry in the central (near-midnight) current sheet between above and below the current sheet, which causes current sheet flapping in both the kink and sausage modes (in a time scale of a few minutes with a Y-scale of ∼2–3 R_E). The localized thinning or thickening of the current sheet associated with the sausage mode may play a role in controlling the onset of magnetotail reconnection. This KHWs/KHVs driving is different from other mechanisms proposed for the current sheet flapping, such as double gradients (Erkaev et al., 2008), ion drift-kink instability (Daughton, 1998), ballooning/interchange instability (Golovchanskaya and Maltsev, 2005), firehose instability (Wang et al., 2020), and non-adiabatic ions (Wei et al., 2015). It is also different from the current sheet flapping externally driven by the SW (IMF) perturbations (Forsyth et al., 2009; Wang et al., 2019).

On the other hand, the evolution of KHWs is modulated by the width of the KH-unstable band due to the stabilization effect of the lobe magnetic field (Hashimoto and Fujimoto, 2006). Moreover, the current sheet flapping that is excited internally and propagates from the midnight region toward flanks may potentially disturb the existing KHWs/KHVs. The temporal and spatial scales and propagation of the current sheet flapping associated with different drivers/mechanisms can be different. These studies indicate causality between flank-side KHWs/KHVs and central current sheet behavior, which has been never explored. We outline the following science questions and sub-questions:

Q3. Is there a causal relationship between flank dynamics and central current sheet dynamics?

Q3.1: Can flank dynamics/conditions serve triggers of the marginally stable current sheet in the central plasma sheet?

• How do flank dynamics drive the current sheet into an unstable state? E.g., via KHW-driven SW entry, modifying tail reconnection inflow conditions and/or current sheet thickness/orientation?

• Is there any regulation by external (SW/IMF) conditions?

Q3.2: Whether or not and how does the current sheet behavior affect the flank dynamics?

• What are the intermediaries from the central current sheet to the flanks? E.g., current-sheet flapping or any dawn/dusk-ward large-scale waves, expansion or relocation of the magnetotail reconnection X-line?

• Where in the magnetotail and what evolutionary phases of KHWs communicate with the central plasma sheet?

Answering Q3 will impact our understanding of the drivers of the unstable central current sheet and its self-consistent behavior via communications with flank dynamics, which potentially bring paradigm-shifting advancement in magnetospheric and planetary physics.

5 Anticipated approach and methodology

We have described missing links in the magnetospheric research associated with KHI, thus leaving important science questions Q1-3 unanswered for decades, in Sections 2–4. We now discuss how we could fill these gaps in the near future using in-situ observations and state-of-the-art numerical techniques.

Q1, regarding the roles and importance of flank dynamics in the SW transport, can be answered by simultaneous measurements of dayside subsolar/cusp reconnection and flank-side KHWs/KHVs for a variety of external conditions. Identification of the activity of reconnection and KHW/KHV and their characteristics and quantifying reconnection rate, particle entry rate, and diffusion coefficient under such driving conditions will bring us an important clue in answering Q1. Polar-orbiting satellites skimming the dayside magnetopause and equator-orbiting spacecraft traversing the mid-tail flank magnetopause will constitute a complete suite to tackle Q1. Polar orbiters conjunctive to the flank-side satellites will provide subsolar and (dual) poleward-of-the-cusp reconnection observation for a range of IMF conditions, revealing the roles of flankside KHWs compared to dayside reconnection in a quantitative manner.

The local reconnection rate calculated from in-situ measurements (e.g., Genestreti et al., 2018) needs to be combined with the global reconnection rate to answer Q1. The total reconnection rate can be constraint by analyzing the global all-sky image of the auroral morphology along the open-closed boundary (i.e., the total auroral precipitation power that represents the energy released from the reconnection site) or SuperDARN observations of the global convection pattern (i.e., cross-polar cap potential or the ionospheric convection electron field, which indicates the total reconnection electric field) (Matar et al., 2020). Particle entry rate or diffusion coefficients can be estimated using the method described by Izutsu and Fujimoto, (2012). In principle, this method requires the measurements by closely-spaced multiple spacecraft. However, when the time dependence of the boundary layer thickness is determined statistically for similar external conditions, the local time (spatial) distribution can be converted to the time evolution of the boundary layer thickness, which enables the diffusion coefficient estimate.

Thus, coordination of multiple in-situ observations with ground-based measurements and/or low Earth-orbit satellites will shed a new light on the coupled SW-magnetosphere-ionosphere system regulated by KHWs/KHVs.

The same spacecraft constellation will enable us to answer Q2, concerning the roles played by KHWs/KHVs in the energetic particle escape or transport. Such configuration of the multi-spacecraft mission promotes detecting the high-latitude dayside KHWs and cusp diamagnetic cavities as well as flank-magnetopause KHWs, simultaneously, that may have propagated from the high-latitude region.

Answering Q3, pertaining to causality between flank dynamics and central current sheet behavior, requires co-located observations of dawn/dusk flank-side and near-midnight current sheet dynamics. These three-point measurements will provide the temporal and spatial variations of the KHW activity and the central current sheet thickness and flapping as well as detect the occurrence of reconnection jets. Two equatorial-orbiting satellites at dawn and dusk flanks, respectively, and a third equatorial orbiter probing the near-midnight plasma sheet will optimize conjunctive measurements to reveal unexplored sequential links or correlations between the midnight current sheet and flank dynamics.

All five spacecraft need to be equipped with the same minimum suite of instruments: the fluxgate magnetometer (MAG), the ion and electron electrostatic analyzer (ESA), and the solid state telescope (SST) to measure the magnetic field, thermal plasma, and energetic particles, respectively. In-situ data of the magnetic field configuration and thermal plasma features enable the identification of reconnecting current sheets and KHWs/KHVs (Q1-3) (Eriksson et al., 2016; Haaland et al., 2020; Hwang et al., 2020; Settino et al., 2021). The energetic particle detector is required to achieve answering Q2. The measurement requirements can be adopted from previous missions (e.g., MMS and THEMIS): 25,000 nT range and >32 Hz sampling rate for MAG; 10 eV to 30 keV range and 1 sample per 4 s (fast mode) and per ∼100 ms (burst mode) for ESA; 25 keV to 0.5 MeV range and the same frequency to ESA for SST.

In-situ multi-spacecraft observations are integrated with global to kinetic models. These models include global MHD, global hybrid (kinetic ions and fluid electrons), and fully kinetic PIC (particle-in-cell) simulations. Systematical comparisons between MHD/Hall-MHD with test particle simulation, hybrid simulation, and fully kinetic PIC simulation advance our understanding of the major transport and energization mechanisms that are dominant at certain scales. Quantitative comparison of in-situ data with these models then provides the interpolation of the globally-scattered multi-spacecraft data. Global MHD/Hall-MHD simulations are performed with various steady and varying driver conditions such as the IMF, solar wind velocity, and density. This will place the spacecraft observation into the context of large-scale magnetic topology and dynamics as well as giving information on the shape, location, and thickness of magnetospheric boundaries. Corresponding to these macroscale variations, the observation from each spacecraft establishes the local conditions, which are used as inputs for meso- and micro-scale simulations.

Challenges in using this integrated approach may include how well the models describe realistic particle, momentum, and energy transfer through the boundary between two different schemes (e.g., Daldorff et al., 2014 for MHD and PIC coupling) and how well they predict the coupled magnetosphere-ionosphere system (e.g., Sugiyama et al., 2006). The coupling of the global modeling with a PIC simulation is the present-day progress/effort. In the near-term future the global hybrid code with an ionosphere/thermosphere model down to kinetic scales is expected. This will support the data interpretation on the roles of flank dynamics in the solar wind-magnetosphere-ionosphere coupling. Furthermore, the next-generation peta-to-exa scale resources will allow us to perform PIC simulations with a few hundreds d _i (ion inertial length) domain, which corresponds to the scale sizes describing KHI and reconnection.

These numerical efforts will eventually enable the coupling of realistic global magnetosphere-ionosphere modeling with a local PIC simulation for fully ion and electron kinetics. Ultimately, we will construct a complete picture of KHI-driven multiscale coupling across all different scales to determine the importance of the different roles of KHI described in Q1-3.

6 Summary

In this paper we discuss an important missing element in the Heliophysics System Observatory’s view: the flank magnetosphere and magnetopause dynamics associated with KHI, is one of the most fundamental physical processes in the heliosphere and the Universe. The roles and importance of this element in the solar wind-magnetosphere coupling (Q1), transport and escape of energetic particles (Q2), and the onset of the central magnetotail plasma sheet dynamics (Q3) have remained elusive.

While compilation and comparison with the data obtained from the previous and existing near-Earth (Cluster, THEMIS, MMS) and distant-tail (ARTEMIS) missions can give us an important indication of the flank dynamics in terms of the evolutionary phases of KHWs, we lack simultaneous observations of the dayside and flank magnetopause and/or the flank and central magnetotail requisite to address Q1-3. In particular, to answer these questions the orbit of multiple spacecraft needs to encompass the region within/around −27 R_E ≤ X ≤ −55 R_E, where multiple current sheet activities in the midnight region and KHWs/KHVs at dawn/dusk flanks occur, and neither previous nor existing spacecraft have routinely traversed up to date.

The multi-spacecraft mission suggested in Section 5 will greatly enhance the missing gaps highlighted in this paper by overcoming the difficulty through providing comprehensive simultaneous measurements of dayside reconnection (two or more polar-orbiting satellites) and flank-side diffusive process (two equator-orbiting satellites at dawn and dusk flanks, respectively). The coordinated in-situ data will enable us to 1) resolve the long-standing Dungey vs. Axford-Hines dichotomy, 2) trace the trajectory of energetic particles, and 3) explore the unprecedented area of causality between flank dynamics and central tail current sheet dynamics. This mission concept combined with cutting-edge numerical simulations is, thus, poised for fundamental breakthroughs in magnetospheric physics, which applies widely to planetary environments.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: http://lasp.colorado.edu/mms/sdc/public/.

Author contributions

All authors contributed to developing perspectives on the subject. K-JH wrote the overall paper. KN, C-PW, TM, YL, and XW contributed/provided figures. MT and HH contributed to spacecraft mission orbits.

Funding

This study was supported, in part, by NASA’s MMS project at SwRI, NASA 80NSSC18K0570, 80NSSC18K0693, 80NSSC18K1534, and 80NSSC23K0417. The data from MMS used for the present study are accessible through the public links http://lasp.colorado.edu/mms/sdc/public/, https://cdaweb.gsfc.nasa.gov/.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adamson, E., Otto, A., and Nykyri, K. (2011). 3-D mesoscale MHD simulations of a cusp-like magnetic configuration: Method and first results. Ann. Geophys. 29, 759–770. doi:10.5194/angeo-29-759-2011

CrossRef Full Text | Google Scholar

Adamson, E., Otto, A., and Nykyri, K. (2012). 3-D mesoscale MHD simulations of magnetospheric cusp-like configurations: Cusp diamagnetic cavities and boundary structure. Ann. Geophys. 30, 325–341. doi:10.5194/angeo-30-325-2012

CrossRef Full Text | Google Scholar

Axford, W. I., and Hines, C. O. (1961). A unifying theory of high-latitude geophysical phenomena and geomagnetic storms. Can. J. Phys. 39, 1433–1464. doi:10.1139/p61-172

CrossRef Full Text | Google Scholar

Burch, J. L., Moore, T. E., Torbert, R. B., and Giles, B. L. (2016). Magnetospheric multiscale overview and science objectives. Space Sci. Rev. 199, 5–21. doi:10.1007/s11214-015-0164-9

CrossRef Full Text | Google Scholar

Chaston, C. C., Wilber, M., Mozer, F. S., Fujimoto, M., Goldstein, M. L., Acuna, M., et al. (2007). Mode conversion and anomalous transport in kelvin-helmholtz vortices and kinetic Alfvén waves at the Earth’s magnetopause. Phys. Rev. Lett. 99, 175004. doi:10.1103/physrevlett.99.175004

PubMed Abstract | CrossRef Full Text | Google Scholar

Cowee, M. M., Winske, D., and Gary, S. P. (2010). Hybrid simulations of plasma transport by Kelvin-Helmholtz instability at the magnetopause: Density variations and magnetic shear. J. Geophys. Res. 115, A06214. doi:10.1029/2009JA015011

CrossRef Full Text | Google Scholar

Daldorff, L. K. S., Toth, G., Gombosi, T. I., Lapenta, G., Amaya, J., Markidis, S., et al. (2014). Two-way coupling of a global Hall magnetohydrodynamics model with a local implicit particle-in-cell model. J. Comput. Phys. 268, 236–254. doi:10.1016/j.jcp.2014.03.009

CrossRef Full Text | Google Scholar

Daughton, W. (1998). Kinetic theory of the drift kink instability in a current sheet. J. Geophys. Res. 103 (12), 29429–29443. doi:10.1029/1998JA900028

CrossRef Full Text | Google Scholar

Delamere, P. A., Barnes, N. P., Ma, X., and Johnson, J. R. (2021). The kelvin-helmholtz instability from the perspective of hybrid simulations. Front. Astron. Space Sci. 8, 801824. doi:10.3389/fspas.2021.801824

CrossRef Full Text | Google Scholar

Dokgo, K., Hwang, K.-J., Burch, J. L., and Yoon, P. H. (2021). Waves generated by electron beam in a crater-shaped flux rope. Front. Phys. 9, 734437. doi:10.3389/fphy.2021.734437

CrossRef Full Text | Google Scholar

Dungey, J. W. (1961). Interplanetary magnetic field and the auroral zones. Phys. Rev. Lett. 6, 47–48. doi:10.1103/PhysRevLett.6.47

CrossRef Full Text | Google Scholar

Eriksson, S., Lavraud, B., Wilder, F. D., Stawarz, J. E., Giles, B. L., Burch, J. L., et al. (2016). Magnetospheric Multiscale observations of magnetic reconnection associated with Kelvin-Helmholtz waves. Geophys. Res. Lett. 43, 5606–5615. doi:10.1002/2016GL068783

CrossRef Full Text | Google Scholar

Erkaev, N. V., Semenov, V. S., and Biernat, H. K. (2008). Magnetic double gradient mechanism for flapping oscillations of a current sheet. Geophys. Res. Lett. 35, L02111. doi:10.1029/2007GL032277

CrossRef Full Text | Google Scholar

Faganello, M., Califano, F., Pegoraro, F., and Andreussi, T. (2012). Double mid-latitude dynamical reconnection at the magnetopause: An efficient mechanism allowing solar wind to enter the Earth's magnetosphere. Europhys. Lett. 100 (6), 69001. doi:10.1209/0295-5075/100/69001

CrossRef Full Text | Google Scholar

Faganello, M., Califano, F., and Pegoraro, F. (2008). Numerical evidence of undriven, fast reconnection in the solar-wind interaction with Earth’s magnetosphere: Formation of electromagnetic coherent structures. Phys. Rev. Lett. 101, 105001. doi:10.1103/PhysRevLett.101.105001

PubMed Abstract | CrossRef Full Text | Google Scholar

Forsyth, C., Lester, M., Fear, R. C., Lucek, E., Dandouras, I., Fazakerley, A. N., et al. (2009). Solar wind and substorm excitation of the wavy current sheet. Ann. Geophys. 27 (6), 2457–2474. doi:10.5194/angeo-27-2457-2009

CrossRef Full Text | Google Scholar

Genestreti, K. J., Nakamura, T. K. M., Nakamura, R., Denton, R. E., Torbert, R. B., Burch, J. L., et al. (2018). How accurately can we measure the reconnection rate EM for the MMS diffusion region eventof 11 July 2017? J. Geophys. Res. Space Phys. 123, 9130–9149. doi:10.1029/2018JA025711

PubMed Abstract | CrossRef Full Text | Google Scholar

Golovchanskaya, I., and Maltsev, Y. (2005). On the identification of plasma sheet flapping waves observed by cluster. Geophys. Res. Lett. 32, L02102. doi:10.1029/2004GL021552

CrossRef Full Text | Google Scholar

Haaland, S., Paschmann, G., Øieroset, M., Phan, T., Hasegawa, H., Fuselier, S., et al. (2020). Characteristics of the flank magnetopause: MMS results. J. Geophys. Res. Space Phys. 125, e2019JA027623. doi:10.1029/2019JA027623

CrossRef Full Text | Google Scholar

Hasegawa, A. (1975). Plasma instabilities and non-linear effects. New York: Springer-Verlag.

Google Scholar

Hasegawa, H., Fujimoto, M., Maezawa, K., Saito, Y., and Mukai, T. (2003). Geotail observations of the dayside outer boundary region: Interplanetary magnetic field control and dawn-dusk asymmetry. J. Geophys. Res. 108 (A4), 1163. doi:10.1029/2002JA009667

CrossRef Full Text | Google Scholar

Hashimoto, C., and Fujimoto, M. (2006). Kelvin-Helmholtz instability in an unstable layer of finite thickness. Adv. Space Res. 37, 527–531. doi:10.1016/j.asr.2005.06.020

CrossRef Full Text | Google Scholar

Hwang, K.-J., Burch, J. L., Russell, C. T., Choi, E., Dokgo, K., Fear, R. C., et al. (2021). Microscale processes determining macroscale evolution of magnetic flux tubes along Earth’s magnetopause. Astrophys. J. 914, 26. doi:10.3847/1538-4357/abf8b1

CrossRef Full Text | Google Scholar

Hwang, K.-J., Dokgo, K., Choi, E., Burch, J. L., Sibeck, D. G., Giles, B. L., et al. (2020). Magnetic reconnection inside a flux rope induced by Kelvin-Helmholtz vortices. J. Geophys. Res. Space Phys. 125, e2019JA027665. doi:10.1029/2019JA027665

PubMed Abstract | CrossRef Full Text | Google Scholar

Hwang, K.-J., Goldstein, M. L., Kuznetsova, M. M., Wang, Y., Viñas, A. F., and Sibeck, D. G. (2012). The first in situ observation of kelvin-helmholtz waves at high-latitude magnetopause during strongly dawnward interplanetary magnetic field conditions. J. Geophys. Res. Space Phys. 117 (A8), a08233. doi:10.1029/2011JA017256

CrossRef Full Text | Google Scholar

Hwang, K.-J., Weygand, J. M., Sibeck, D. G., Burch, J. L., Goldstein, M. L., Escoubet, C. P., et al. (2022). Kelvin-Helmholtz vortices as an interplay of magnetosphere-ionosphere coupling. Front. Astron. Space Sci. 9, 895514. doi:10.3389/fspas.2022.895514

CrossRef Full Text | Google Scholar

Izutsu, T., and Fujimoto, M. (2012). THEMIS observations of plasma transport via eddy diffusion. Ann. Geophys. 30, 1703–1707. doi:10.5194/angeo-30-1703-2012

CrossRef Full Text | Google Scholar

Johnson, J. R., and Cheng, C. Z. (2001). Stochastic ion heating at the magnetopause due to kinetic Alfven waves. Geophys. Res. Lett. 28, 4421–4424. doi:10.1029/2001GL013509

CrossRef Full Text | Google Scholar

Johnson, J. R., Wing, S., Delamere, P., Petrinec, S., and Kavosi, S. (2021). Field-aligned currents in auroral vortices. J. Geophys. Res. Sp. Phys. 126, 1–15. doi:10.1029/2020JA028583

CrossRef Full Text | Google Scholar

Johnson, J. R., and Wing, S. (2015). The dependence of the strength and thickness of field-aligned currents on solar wind and ionospheric parameters. J. Geophys. Res. Sp. Phys. 120, 3987–4008. doi:10.1002/2014JA020312

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, W. Y., Guo, X. C., and Wang, C. (2012). Spatial distribution of Kelvin-Helmholtz instability at low-latitude boundary layer under different solar wind speed conditions. J. Geophys. Res. 117, A08230. doi:10.1029/2012JA017780

CrossRef Full Text | Google Scholar

Lin, Y., Wang, X. Y., Lu, S., Perez, J. D., and Lu, Q. (2014). Investigation of storm time magnetotail and ion injection using three-dimensional global hybrid simulation. J. Geophys. Res. Space Phys. 119, 7413–7432. doi:10.1002/2014JA020005

CrossRef Full Text | Google Scholar

Lin, Y., Wing, S., Johnson, J. R., Wang, X. Y., Perez, J. D., and Cheng, L. (2017). Formation and transport of entropy structures in the magnetotail simulated with a 3-D global hybrid code. Geophys. Res. Lett. 44, 5892–5899. doi:10.1002/2017GL073957

CrossRef Full Text | Google Scholar

Ling, Y., Shi, Q., Shen, X.-C., Tian, A., Li, W., Tang, B., et al. (2018). Observations of Kelvin-Helmholtz waves in the Earth’s magnetotail near the lunar orbit. J. Geophys. Res. Space Phys. 123, 3836–3847. doi:10.1029/2018JA025183

CrossRef Full Text | Google Scholar

Ma, X., Delamere, P. A., Nykyri, K., Burkholder, B., Neupane, B., and Rice, R. C. (2019). Comparison between fluid simulation with test particles and hybrid simulation for the Kelvin-Helmholtz instability. J. Geophys. Res. Space Phys. 124, 6654–6668. doi:10.1029/2019JA026890

CrossRef Full Text | Google Scholar

Ma, X., Delamere, P., Otto, A., and Burkholder, B. (2017). Plasma transport driven by the three-dimensional kelvin-helmholtz instability. J. Geophys. Res. Space Phys. 122 (10). doi:10.1002/2017JA024394

CrossRef Full Text | Google Scholar

Ma, X., Otto, A., Delamere, P. A., and Zhang, H. (2016). Interaction between reconnection and kelvin-helmholtz at the high-latitude magnetopause. Adv. Space Res. 58 (2), 231–239. doi:10.1016/j.asr.2016.02.025

CrossRef Full Text | Google Scholar

Matar, J., Hubert, B., Yao, Z., Guo, R., Cowley, S. W. H., Milan, S. E., et al. (2020). Concurrent observations of magnetic reconnection from cluster, image and SuperDARN: A comparison of reconnection rates and energy conversion. J. Geophys. Res. Space Phys. 125, e2019JA027264. doi:10.1029/2019JA027264

CrossRef Full Text | Google Scholar

Matsumoto, Y., and Hoshino, M. (2004). Onset of turbulence induced by a Kelvin-Helmholtz vortex. Geophys. Res. Lett. 31, L02807. doi:10.1029/2003GL018195

CrossRef Full Text | Google Scholar

Matsumoto, Y., and Seki, K. (2010). Formation of a broad plasma turbulent layer by forward and inverse energy cascades of the Kelvin-Helmholtz instability. J. Geophys. Res. 115, A10231. doi:10.1029/2009JA014637

CrossRef Full Text | Google Scholar

Merkin, V. G., Lyon, J. G., and Claudepierre, S. G. (2013). Kelvin-Helmholtz instability of the magnetospheric bound-ary in a three-dimensional global MHD simulation during northward IMF conditions. J. Geophys. Res. Space Phys. 118, 5478–5496. doi:10.1002/jgra.50520

CrossRef Full Text | Google Scholar

Michael, A. T., Sorathia, K. A., Merkin, V. G., Nykyri, K., Burkholder, B., Ma, X., et al. (2021). Modeling Kelvin-Helmholtz instability at the high-latitude boundary layer in a global magnetosphere simulation. Geophys. Res. Lett. 48, e2021GL094002. doi:10.1029/2021GL094002

PubMed Abstract | CrossRef Full Text | Google Scholar

Moore, T. W., Nykyri, K., and Dimmock, A. P. (2016). Cross-scale energy transport in space plasmas. Nat. Phys. 12, 1164–1169. doi:10.1038/nphys3869

CrossRef Full Text | Google Scholar

Moore, T. W., Nykyri, K., and Dimmock, A. P. (2017). Ion-scale wave properties and enhanced ion heating across the low-latitude boundary layer during kelvin-helmholtz instability. J. Geophys. Res. 122. doi:10.1002/2017JA024591

CrossRef Full Text | Google Scholar

Nakamura, T. K. M., and Daughton, W. (2014). Turbulent plasma transport across the Earth’s low-latitude boundary layer. Geophys. Res. Lett. 41, 8704–8712. doi:10.1002/2014GL061952

CrossRef Full Text | Google Scholar

Nakamura, T. K. M., Fujimoto, M., and Otto, A. (2008). Structure of an MHD-scale Kelvin-Helmholtz vortex: Two-dimensional two-fluid simulations including finite electron inertial effects. J. Geophys. Res. 113, A09204. doi:10.1029/2007JA012803

CrossRef Full Text | Google Scholar

Nakamura, T. K. M., Hasegawa, H., Daughton, W., Eriksson, S., Li, W. Y., and Nakamura, R. (2017). Turbulent mass transfer caused by vortex induced reconnection in collisionless magnetospheric plasmas. Nat. Commun. 8, 1582. doi:10.1038/s41467-017-01579-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakamura, T. K. M., Hasegawa, H., Shinohara, I., and Fujimoto, M. (2011). Evolution of an MHD-scale Kelvin–Helmholtz vortex accompanied by magnetic reconnection: Two-dimensional particle simulations. J. Geophys. Res. 116, A03227. doi:10.1029/2010JA016046

CrossRef Full Text | Google Scholar

Nakamura, T. K. M., Stawarz, J. E., Hasegawa, H., Narita, Y., Franci, L., Wilder, F. D., et al. (2020). Effects of fluctuating magnetic field on the growth of the Kelvin-Helmholtz instability at the Earth's magnetopause. J. Geophys. Res. Space Phys. 125, e2019JA027515. doi:10.1029/2019JA027515

CrossRef Full Text | Google Scholar

Nishino, M. N., Hasegawa, H., Saito, Y., Kitamura, N., Miyashita, Y., Nagai, T., et al. (2022). Transport path of cold-dense plasmas in the dusk magnetotail plasma sheet: MMS observations. J. Geophys. Res. Space Phys. 126, e2021JA029747. doi:10.1029/2021JA029747

CrossRef Full Text | Google Scholar

Nykyri, K. (2013). Impact of MHD shock physics on magnetosheath asymmetry and Kelvin-Helmholtz instability. J. Geophys. Res. Space Phys. 118, 5068–5081. doi:10.1002/jgra.50499

CrossRef Full Text | Google Scholar

Nykyri, K., Johnson, J., Kronberg, E., Turner, D., Wing, S., Cohen, I., et al. (2021a). Magnetospheric multiscale observations of the source region of energetic electron microinjections along the duskside, high-latitude magnetopause boundary layer. Geophys. Res. Lett. 48, e2021GL092466. doi:10.1029/2021GL092466

CrossRef Full Text | Google Scholar

Nykyri, K., Ma, X., Burkholder, B., Rice, R., Johnson, J. R., Kim, E.-K., et al. (2021b). MMS observations of the multiscale wave structures and parallel electron heating in the vicinity of the southern exterior cusp. J. Geophys. Res. Space Phys. 126, e2019JA027698. doi:10.1029/2019JA027698

CrossRef Full Text | Google Scholar

Nykyri, K., Ma, X., Dimmock, A., Foullon, C., Otto, A., and Osmane, A. (2017). Influence of velocity fluctuations on the Kelvin-Helmholtz instability and its associated mass transport. J. Geophys. Res. Space Phys. 122, 9489–9512. doi:10.1002/2017JA024374

CrossRef Full Text | Google Scholar

Nykyri, K., Otto, A., Adamson, E., Dougal, E., and Mumme, J. (2011a). Cluster observations of a cusp diamagnetic cavity: Structure, size, and dynamics. J. Geophys. Res. (Space Phys. 116, A03228. doi:10.1029/2010JA015897

CrossRef Full Text | Google Scholar

Nykyri, K., Otto, A., Adamson, E., Kronberg, E., and Daly, P. (2012). On the origin of high-energy particles in the cusp diamagnetic cavity. J. Atmos. Solar-Terrestrial Phys. 87, 70–81. doi:10.1016/j.jastp.2011.08.012

CrossRef Full Text | Google Scholar

Nykyri, K., Otto, A., Adamson, E., and Tjulin, A. (2011b). On the origin of fluctuations in the cusp diamagnetic cavity. J. Geophys. Res. (Space Phys. 116, A06208. doi:10.1029/2010JA015888

CrossRef Full Text | Google Scholar

Nykyri, K., and Otto, A. (2001). Plasma transport at the magnetospheric boundary due to reconnection in Kelvin-Helmholtz vortices. Geophys. Res. Lett. 28, 3565–3568. doi:10.1029/2001gl013239

CrossRef Full Text | Google Scholar

Omidi, N., Sibeck, D. G., and Blanco-Cano, X. (2009). Foreshock compressional boundary. J. Geophys. Res. 114, A08205. doi:10.1029/2008JA013950

CrossRef Full Text | Google Scholar

Petrinec, S. M., Wing, S., Johnson, J. R., and Zhang, Y. (2022). Multi-spacecraft observations of fluctuations occurring along the dusk flank magnetopause, and testing the connection to an observed ionospheric bead. Front. Astron. Space Sci. 9, 827612. doi:10.3389/fspas.2022.827612

CrossRef Full Text | Google Scholar

Phan, T. D., Hasegawa, H., Fujimoto, M., Oieroset, M., Mukai, T., Lin, R. P., et al. (2006). Simultaneous Geotail and Wind observations of reconnection at the subsolar and tail flank magnetopause. Geophys. Res. Lett. 33, L09104. doi:10.1029/2006GL025756

CrossRef Full Text | Google Scholar

Settino, A., Perrone, D., Khotyaintsev, Yu. V., Graham, D. B., and Valentini, F. (2021). Kinetic features for the identification of kelvin–helmholtz vortices in in situ observations. Astrophys. J. 912, 154. doi:10.3847/1538-4357/abf1f5

CrossRef Full Text | Google Scholar

Sorathia, K. A., Merkin, V. G., Ukhorskiy, A. Y., Mauk, B. H., and Sibeck, D. G. (2017). Energetic particle loss through the magnetopause: A combined global MHD and test-particle study. J. Geophys. Res. Space Phys. 122, 9329–9343. doi:10.1002/2017JA024268

CrossRef Full Text | Google Scholar

Sugiyama, T., Kusano, K., Hirose, S., and Kageyama, A. (2006). MHD–PIC connection model in a magnetosphere–ionosphere coupling system. J. Plasma Phys. 72 (6), 945–948. doi:10.1017/S0022377806005356

CrossRef Full Text | Google Scholar

Vernisse, Y., Lavraud, B., Eriksson, S., Gershman, D. J., Dorelli, J., Pollock, C., et al. (2016). Signatures of complex magnetic topologies from multiple reconnection sites induced by Kelvin-Helmholtz instability. J. Geophys. Res. Space Phys. 121, 9926–9939. doi:10.1002/2016JA023051

CrossRef Full Text | Google Scholar

Wang, C.-P., Merkin, V. G., and Angelopoulos, V. (2017). Mesoscale perturbations in midtail lobe/mantle during steady northward IMF: ARTEMIS observation and MHD simulation. J. Geophys. Res. Space Phys. 122, 6430–6441. doi:10.1002/2017JA024305

CrossRef Full Text | Google Scholar

Wang, C.-P., Liu, Y.-H., Xing, X., Runov, A., Artemyev, A., and Zhang, X. (2020). An event study of simultaneous earthward and tailward reconnection exhaust flows in the Earth's midtail. J. Geophys. Res. Space Phys. 125, e2019JA027406. doi:10.1029/2019JA027406

CrossRef Full Text | Google Scholar

Wang, G. Q., Zhang, T. L., Wu, M. Y., Schmid, D., Cao, J. B., and Volwerk, M. (2019). Solar wind directional change triggering flapping motions of the current sheet: MMS observations. Geophys. Res. Lett. 46, 64–70. doi:10.1029/2018GL080023

CrossRef Full Text | Google Scholar

Wei, X. H., Cai, C. L., Cao, J. B., Rème, H., Dandouras, I., and Parks, G. K. (2015). Flapping motions of the magnetotail current sheet excited by nonadiabatic ions. Geophys. Res. Lett. 42, 4731–4735. doi:10.1002/2015GL064459

CrossRef Full Text | Google Scholar

Wilder, F. D., Ergun, R. E., Schwartz, S. J., Newman, D. L., Eriksson, S., Stawarz, J. E., et al. (2016). Observations of large-amplitude, parallel, electrostatic waves associated with the kelvin-helmholtz instability by the magnetospheric multiscale mission. Geophys. Res. Lett. 43, 8859–8866. doi:10.1002/2016GL070404

CrossRef Full Text | Google Scholar

Wing, S., Johnson, J. R., Newell, P. T., and Meng, C.-I. (2005). Dawn-dusk asymmetries, ion spectra, and sources in the northward interplanetary magnetic field plasma sheet. J. Geophys. Res. 110, A08205. doi:10.1029/2005JA011086

CrossRef Full Text | Google Scholar

Yao, Y., Chaston, C. C., Glassmeier, K.-H., and Angelopoulos, V. (2011). Electromagnetic waves on ion gyro-radii scales across the magne-topause. Geophys. Res. Lett. 38, L09102. doi:10.1029/2011GL047328

CrossRef Full Text | Google Scholar

Yordanova, E., Vörös, Z., Raptis, S., and Karlsson, T. (2020). Current sheet statistics in the magnetosheath. Front. Astronomy Space Sci. 7, 1–11. doi:10.3389/fspas.2020.00002

CrossRef Full Text | Google Scholar