- Department of Physics and Astronomy, Rutgers University, Piscataway, NJ, United States
Exploratory missions have found that regolith on interplanetary bodies can be loosely packed and freely flowing—a state that strongly affects mission plans and that may also influence the large-scale shapes of these bodies. We investigate here whether notable circumferential ridges seen on Saturn’s moons may be a byproduct of free flow of loosely packed regolith. Such ridges and other features likely record the history of the moons, and we find that if surface grains are freely flowing, then the combined gravity of Saturn itself and its tenuous ring generate similar circumferential features. Moreover, analysis of these features reveals the possibility of previously unreported morphologies, for example, a stationary torus around a non-rotating satellite. Some of these features persist even for a very low density and distant disk, which raises the prospect that nonlinear analysis of interactions from disks to moons and back again may lead to new insights.
Introduction
International exploratory missions have visited interplanetary bodies and have found their regolith to be loosely packed and freely flowing (Thomas et al., 2015; Lauretta et al., 2017). These findings concur with both modeling (Meakin et al., 1986) and terrestrial experiments (Shinbrot et al., 2004; Shinbrot et al., 2017) intended to investigate how the processes of fine scale regolith accretion produce larger scale morphogenesis. Nowhere is this morphogenesis more striking than on Saturn’s moons, which exhibit remarkable equatorial features, some of which are shown in Figure 1. Pan and Atlas (Figures 1A,B) have such prominent equatorial ridges that the moons resemble ravioli, with aspect ratios around ½. Iapetus (Figure 1C) is much larger and is nearly spherical, but has a sharp, 20 km high, ridge over most of its circumference. By contrast, the asteroid Vesta (Figure 1D) is scoured by multiple, 2 km deep, troughs extending along much of its equator.
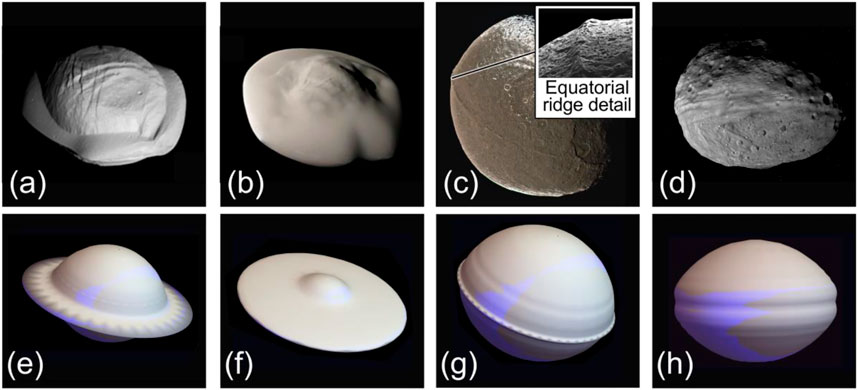
FIGURE 1. (A–D) Saturn’s moons Pan, Atlas and Iapetus, and the asteroid Vesta (credit NASA/JPL-Caltech/SSI) compared with simulations (E–H) of morphology expected for freely flowing grains on a spheroidal mass influenced by a thin, weakly gravitational plane. Simulation parameters (defined in text): (E)
The origins of these features are unknown. Theories for the formation of equatorial ridges include collisions between matched pairs of bodies (Leleu et al., 2018), viscous deformation of ring material (Charnoz et al., 2011), and accretion of material from a flat ring onto a central satellite (Charnoz et al., 2007; Porco et al., 2007). No existing theory predicts equatorial troughs. We show here that troughs as well as ridges arise naturally if freely flowing grains follow equipotentials of a massive spheroid in a massive plane, as shown in Figures 1E–H). This possibility does not appear to have been examined previously.
The binary collision theory produces veridical equatorial ridges (Leleu et al., 2018), but requires that the two bodies have nearly identical masses, and deform rather than fragment. Additionally, constraints on the collision impact parameter are stringent, both so that the bodies aren’t torn apart by centrifugal forces and because any nonzero impact parameter would produce rotation perpendicular to the moons’ equators—opposite of their current orientations. Moreover Pan and Atlas, and possibly Pandora and Daphnis as well, are quite similar in shape, making for an impressive coincidence of remarkable events.
The theories of ridge formation from ring material, on the other hand, involve highly probable mechanisms such as viscous spreading early in a moon’s evolution (Charnoz et al., 2011) and deposition of ring material onto a satellite later (Charnoz et al., 2007; Porco et al., 2007). The deposition model is supported by data from close fly-bys indicating that Pan, Atlas and other smaller moons are likely composed of a high density core surrounded by much lower density accreted material (Buratti et al., 2019). To date, however, deposition models have not reproduced the curious shapes shown in Figure 1.
Gravitational equipotentials
Both types of theory are based on the presumption that equatorial features require a secondary morphogenetic process—collision, viscous spreading, or accretion—because equatorial features are not predicted from simple gravitational and inertial considerations. That is, as shown in cross section in Figure 2A, equipotentials of a rotating spheroid are themselves nearly spheroidal (for example, in the blue cross section shown), and lack equatorial ridges or grooves. On the other hand, equipotentials for the same rotating spheroid embedded in a thin stationary planar disk can exhibit both a ridge (red) and a groove (green) shown in Figure 2B, and enlarged in Figure 2D. This means that either a ridge or a groove could form depending on the history of material deposition (discussed shortly).
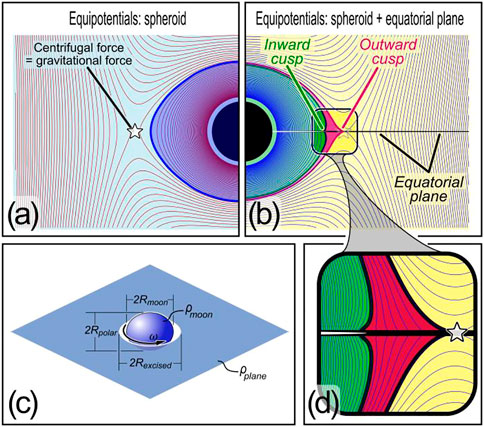
FIGURE 2. Gravitational equipotentials. (A) Equipotentials of central sphere (black) rotating with speed
All equipotentials shown are based on a solution to Laplace’s equation for a uniform massive ellipsoid that has been known since 1840 (Chasles, 1840). Details of the solution appear elsewhere (Moritz, 1990), and we provide an annotated numerical code for its analysis in Supplementary Materials S1 accompanying this article. The essence of the solution is to break the gravitational geopotential into three parts: a net mass and a quadrupole term that define gravity outside of an ellipsoid of uniform density, and a centrifugal term that accounts for steady rotation. All terms are 3D, but we take the ellipsoid to have azimuthal symmetry—hence we show 2D cross sections in Figures 2A,B and elsewhere. Surfaces of revolution are included to aid visualization in Figures 1, 5.
In this work we calculate equipotentials of a central spheroid embedded in a planar mass using the geometry sketched in Figure 2C, and we determine shapes of resulting surfaces assuming that deposited mass flows freely with minimal friction. For generality, our analysis defines the central mass rotating at constant angular speed
We define both the plane and the excised mass using the same 1840 ellipsoidal model as for the central spheroid, but we approximate a planar geometry by using very thin spheroids, with polar radii
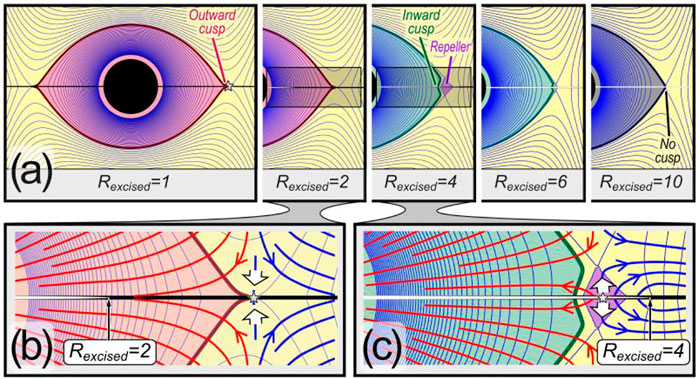
FIGURE 3. Mechanism of bifurcation between outward and inward cusp. (A) Progression of cusp shapes as distance,
To summarize, we calculate the gravitational potential,
where
The gravitational potential of a single spheroid has been calculated previously (Hofmeister et al., 2018), but compares unfavorably with shapes of Saturn’s moons. The equipotentials shown in Figure 2A are typical, and use
To examine the effect of a surrounding planar mass, we begin with a first, simplest, example: we consider a central sphere
The same solution superimposed on a flattened spheroidal plane as we have described is shown in Figure 2B. Parameters for this example are defined in the figure caption; in short, all parameters for the central spheroidal moon are as in Figure 2A, and the surrounding plane has density half that of the moon:
Two related remarks concerning the equipotentials shown must be stressed before continuing. First, it is important to make clear the meaning of equipotentials. An equipotential is by no means the only possible shape of a satellite: equipotentials are surfaces free of tangential stress, so they are the shapes that would be adopted if surficial material (e.g., freely flowing grains) fully relaxes in response to gravitational and centrifugal forces. Future investigations of accretion history as well as visco-elastic effects, are clearly merited: the intent here is to present shapes that would develop in the freely-flowing limit. Figure 2 shows multiple equipotentials; the choice of which is adopted depends on the amount of mass present. The equipotentials identified in green and red in Figure 2 are chosen to define surfaces with the most pronounced inward or outward cusp respectively. If more material were deposited onto the green surface and allowed to relax freely, the cusp would diminish its curvature, whereas if material were added to the red surface and again allowed to relax freely, it would be stripped away by centrifugal acceleration.
Second, the solutions entirely neglect gravitational interactions between the body and freely flowing material being accreted. These interactions would change the gravitational shape of the body, which in turn would change the shape of the equipotentials, but this fully nonlinear problem is non-integrable, and a complete solution is neither unique nor generally obtainable. We do discuss gravitational influences of a parent body (here, Saturn) at the conclusion of this paper, but we emphasize that the satellite shapes that we display – either with or without Saturn’s gravity—are idealized.
With this in mind, to understand the mechanism underlying cusp formation, we observe that cusps emerge as the plane approaches the central spheroid. That is, as
Figure 3A and the enlargement of Figure 3B show that a nearby concentric plane,
Putting details of the bifurcation aside for a moment, the coarse-grained outcome is that if a massive plane is near a satellite, it will tend to produce an outward cusp, and as the planar mass moves away from the moon, the outward cusp will give way to an inward one. As mass recedes still further from the moon, its effect will diminish until equipotentials are indistinguishable from those with no plane at all, shown to the right of Figure 3A at
The mechanism underlying cusp formation can be further exposed by examination of the enlargements of Figures 3B–C. If a massive plane is near the moon, shown in Figure 3B, all nearby mass is drawn equatorward, as the streamlines indicate. This either brings nearby mass toward the moon (red arrows) producing an outward cusp, or brings it away (blue arrows), to augment the surrounding plane. When the plane recedes past the unstable point indicated by the star, a bifurcation reverses mass flow near the starred point. This can be seen by comparing the flow directions shown by the white arrows in Figures 3B,C. This bifurcation arises when the planar mass moves from inside the region identified by the red equipotential in Figures 3A,B (drawing mass inward, toward the moon) to outside that region (drawing mass outward, toward the surrounding plane). Between these two extremes, both states can co-exist, as shown in Figure 2B.
Dynamically speaking, the violet region surrounds what would be the Lagrange point, L1, if there were a single orbiting mass rather than mass within a plane. In our case, for small
In Figure 3 we held
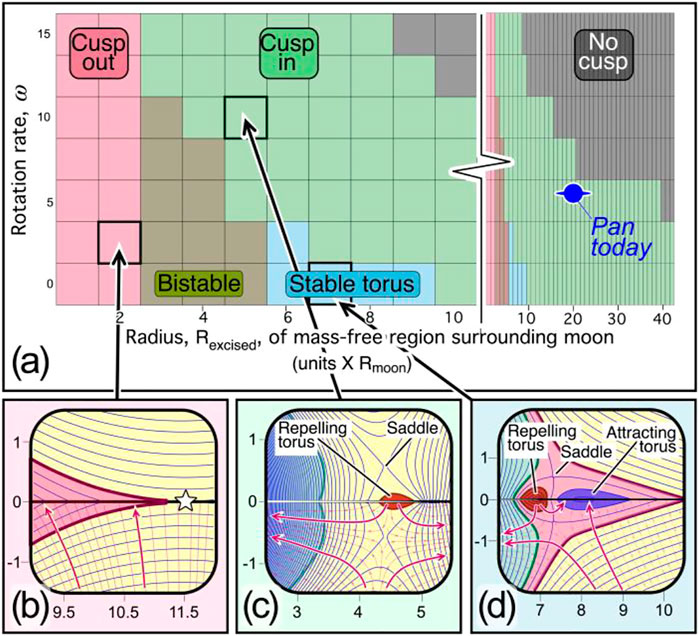
FIGURE 4. Phase diagram of equatorial features of freely flowing material. (A) Five distinct states identified as rotation rate
Bearing these caveats in mind, Figure 4 reveals the presence of five distinct states of freely flowing regolith subject to gravitational equipotentials for satellites embedded in a massive plane. For small
As
Finally, a new, fifth, state is predicted by this model, shown in Figure 4D: for small rotational speeds and for a massive plane around
We reiterate that all of these states form for free surface flow under linear and steady-state conditions. History dependence, self-gravitation, and viscoelastic behavior of satellite material are neglected. Processes that generated cusps on Saturn’s moons doubtless occurred long ago, and so
Nevertheless, we can orient ourselves on Figure 4 using current data, as indicated by the “Pan today” marking in Figure 4A. We have mentioned that units in that panel are dimensionless, and are obtained for a central sphere of unit radius and mass, and a time scale set by choosing the gravitational constant (we use
In Figure 5A, we also plot the stable torus’ location for the conditions shown in Figure 4D:
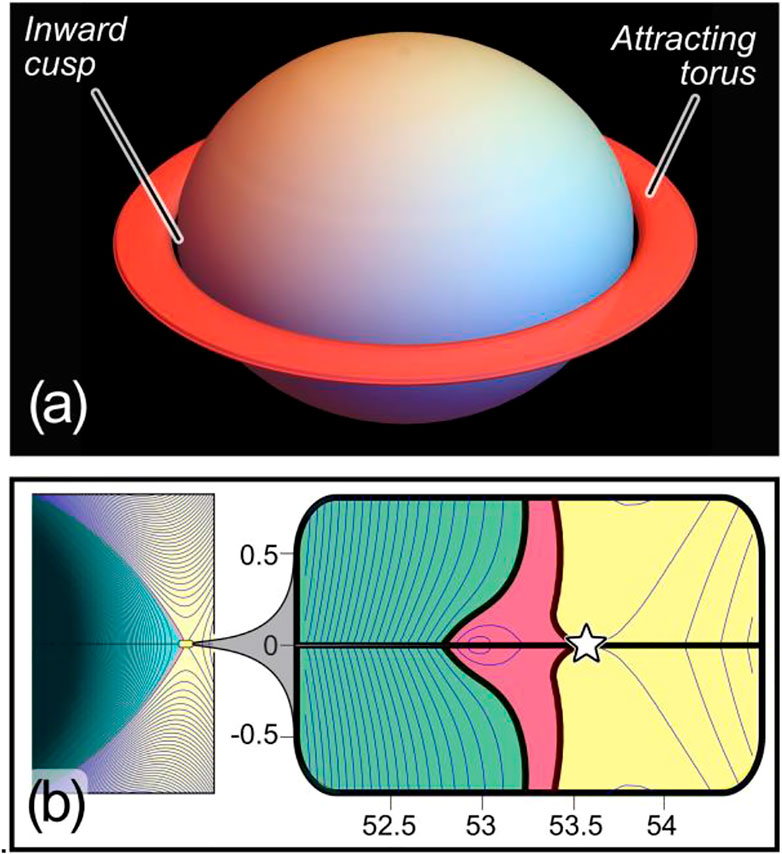
FIGURE 5. Extremes in cusp behavior. (A) 3D rendition of attracting torus from Figure 4D. The torus shown is at the outer extreme of the attractive region, and mass would gravitate toward a central torus within. (B) Equipotential cusps for very low planar density:
Two final, practical, issues remain. First, arguably the mass of Saturn’s disk material could seem to be too small to produce significant gravitational effects on its moons, and second, effects of Saturn’s gravity (mentioned earlier) are yet to be discussed. We consider these two issues next.
Saturn’s disk mass
With respect to the mass of Saturn’s disk material, two facts suggest that this mass could be sufficient to produce the satellite shapes that we have displayed. First, the density of Saturn’s rings was almost certainly higher during the evolution of its moons than it is today (Charnoz et al., 2007). Indeed, prior work (Salmon and Canup, 2017) has estimated the ratio of the mass of rings to moons to have been as high as 1:3. By the same token, satellites (e.g., Iapetus) or asteroids (e.g., Vesta) that are currently far from disk material may have been embedded in such material earlier during their formation. Second, we can quantify how large the density of a surrounding plane must be to produce equatorial cusps, and we will next show that cusps arise even for extremely small planar densities.
To evaluate effects of planar density,
From this exercise, we find that cusps persist at least down to
It remains uncertain how dense the rings once were, but comparison with the 1/10,000 figure that produces cusps suggests that sufficient ring density may be present, even currently, to affect satellite geomorphology. Moreover as we have mentioned, the observation that a interplanetary body is currently far from a planar mass does not imply that the body was not influenced by such a mass earlier in its history. Since it is not possible to determine complete histories of these bodies in retrospect, we propose that their current morphologies can be used to provide evidence of that history a posteriori. That is, on mathematical grounds, we find that circumferential ridges and grooves on celestial bodies may be indications that the bodies at one time were embedded in a planar mass and covered with freely flowing regolith.
Saturn’s gravity
This brings us to the final practical issue: effects of Saturn’s gravity. Here we note that Saturn’s gravity at the current locations of Pan and Atlas is 3 orders of magnitude stronger than their surface gravities. From that perspective, the relevance of analyzing gravitational equipotentials needs justification.
Pan and Atlas are currently about
where
This is the maximum acceleration responsible for tides (Chandrasekhar, 1989), and is readily evaluated. For the four examples shown in Figure 1, from right to left, Vesta is not in Saturn’s orbit, and both
Focusing on these two moons that are most strongly influenced by Saturn’s gravity, Atlas’ rotation rate is not known, but Pan is in synchronous rotation with the same side always facing Saturn, so tidal forcing on its surface is static and its perturbation to the equipotential due to Saturn is bounded by the following term:
where
In Figure 6, we plot a polar photograph of Pan alongside orthographic views of the deformation that one would naïvely obtain from Eq. 4. The superimposed dashed line in the polar view is a simple circular outline, as would be expected without a perturbing gravitational potential. The solid line shows an ellipse with semi-minor axis of the circle and semi-major axis obtained by adding the perturbation of Eq. 4. The arrow indicates Pan’s orientation with respect to Saturn, and the orthographic views give respective cross-sections that one would expect perpendicular to (i.e., uninfluenced by) Saturn’s field, and parallel to Saturn’s gravity.
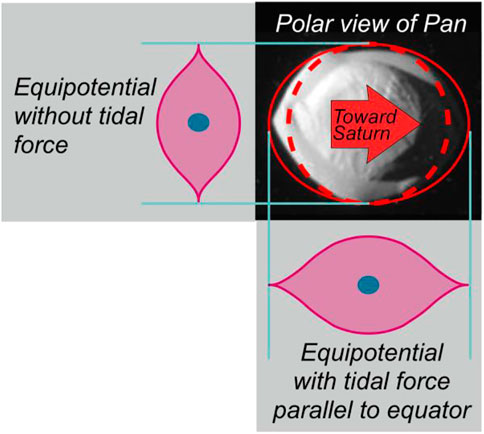
FIGURE 6. Pan and orthographic depictions of distortion of gravitational equipotentials by tidal force from distant planet. Upper right shows polar view of Pan with superimposed circle (dashed curve) and ellipse (solid). The ellipse’s semi-minor axis is obtained from the maximum radius of potential (Thomas et al., 2015); cross-section shown in upper left. The ellipse’s semi-major axis is obtained by adding the potential (Shinbrot et al., 2004) with
This is again only an idealized analysis and is far simpler than the complete problem—for example, both the temporal reshaping due to long periods of tidal damping and important nonlinear interactions are overlooked. Likewise, continuing the spirit of the rest of our analysis, we neglect changes to equipotentials due to redistribution of mass, here from the orbital direction to the Saturn-moon direction. The merit of Eq. 1 and Eq. 4 is that they permit us to calculate equipotentials, which give the lowest order stress-free state of a satellite’s surface that could be expected to be adopted by a linear analysis of individual and sedately settling particles.
Conclusion
It is well recognized that Saturn’s moons affect its rings (Pollack, 1975), for example, producing wakes, gaps and resonances that dominate ring morphology (Showalter et al., 1986). Effects that rings have on moons are less well studied (Charnoz et al., 2007), and gravitational potentials of satellites are assumed to be insensitive to influences of rings. Contrary to this assumption, we have found that distinctive features of Saturn’s moons, including equatorial cusps and even a predicted stable circumferential torus, arise naturally by including the influence of rings in the simplest possible gravitational model of a central satellite surrounded by a massive equatorial plane. Remarkably, equatorial cusps endure even for distant and low mass rings. It is important to emphasize that these results are purely linear: like the effect that moons have on rings, we neglect nonlinear feedback between rings and moons. It is likely—especially since ring densities several orders of magnitude smaller than moon density have significant gravitational effects—that this feedback is important, and indeed the model presented here does not yet consider how accreted mass affects a satellite’s gravitational potential. A fully nonlinear model continues to be an important challenge. Likewise, as we have mentioned, results here apply in the limit of entirely freely flowing grains: effects of accretion history and of friction, viscosity, and elasticity also remain for future investigation.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
This material is based on support from NSF CBET, Award No. 1804286.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2023.1146705/full#supplementary-material
References
Buratti, B. J., Thomas, P. C., Roussos, E., Howett, C., Seiss, M., Hendrix, A. R., et al. (2019). Close cassini flybys of Saturn’s ring moons Pan, Daphnis, Atlas, Pandora, and epimetheus. Science 364, eaat2349. doi:10.1126/science.aat2349
Chandrasekhar, S. (1989). The equilibrium and the stability of the roche ellipsoids: lasma physics, hydrodynamic and hydromagnetic stability, and applications of the tensor-virial theorem. Sel. Pap. 4, 430.
Charnoz, S., Brahic, A., Thomas, P. C., and Porco, C. C. (2007). The equatorial ridges of Pan and Atlas: Terminal accretionary ornaments? Science 318 (5856), 1622–1624. doi:10.1126/science.1148631
Charnoz, S., Crida, A., Castillo-Rogez, J. C., Lainey, V., Dones, L., Karatekin Ö, Tobie G., et al. (2011). Accretion of Saturn’s mid-sized moons during the viscous spreading of young massive rings: Solving the paradox of silicate-poor rings versus silicate-rich moons. Icarus 216 (2), 535–550. doi:10.1016/j.icarus.2011.09.017
Chasles, M. (1840). “Solution nouvelle du problème de l’attraction d’un ellipsoïde hétérogène sur un point exterieur,” Jour. Liouville 5, 465–488.
Hofmeister, A. M., Criss, R. E., and Criss, E. M. (2018). Verified solutions for the gravitational attraction to an oblate spheroid: Implications for planet mass and satellite orbits. Planet. Space Sci. 152, 68–81. doi:10.1016/j.pss.2018.01.005
Iess, L., Militzer, B., Kaspi, Y., Nicholson, P., Durante, D., Racioppa, P., et al. (2019). Measurement and implications of Saturn’s gravity field and ring mass. Science 364, eaat2965. doi:10.1126/science.aat2965
Lauretta, D. S., Balram-Knutson, S. S., Beshore, E., Boynton, W. V., Drouet d’Aubigny, C., DellaGiustina, D. N., et al. (2017). OSIRIS-REx: Sample return from asteroid (101955) bennu. Bennu. Space Sci. Rev. 212 (1), 925–984. doi:10.1007/s11214-017-0405-1
Leleu, A., Jutzi, M., and Rubin, M. (2018). The peculiar shapes of Saturn’s small inner moons as evidence of mergers of similar-sized moonlets. Nat. Astron. 2 (7), 555–561. doi:10.1038/s41550-018-0471-7
Meakin, P., Ramanlal, P., Sander, L. M., and Ball, R. C. (1986). Ballistic deposition on surfaces. Phys. Rev. A 34 (6), 5091–5103. doi:10.1103/physreva.34.5091
Moritz, H. (1990). The figure of the earth: Theoretical geodesy and the earth's interior. Karlsr. Wichmann, pp.126–60.
Porco, C. C., Thomas, P. C., Weiss, J. W., and Richardson, D. C. (2007). Saturn's small inner satellites: Clues to their origins. science 318 (5856), 1602–1607. doi:10.1126/science.1143977
Salmon, J., and Canup, R. M. (2017). Accretion of Saturn’s inner mid-sized moons from a massive primordial ice ring. Astrophysical J. 836 (1), 109. doi:10.3847/1538-4357/836/1/109
Shinbrot, T., Duong, N. H., Kwan, L., and Alvarez, M. M. (2004). Dry granular flows can generate surface features resembling those seen in Martian gullies. Proc. Natl. Acad. Sci. 101 (23), 8542–8546. doi:10.1073/pnas.0308251101
Shinbrot, T., Sabuwala, T., Siu, T., Lazo, M. V., and Chakraborty, P. (2017). Size sorting on the rubble-pile asteroid Itokawa. Phys. Rev. Lett. 118 (11), 111101. doi:10.1103/physrevlett.118.111101
Showalter, M. R., Cuzzi, J. N., Marouf, E. A., and Esposito, L. W. (1986). Satellite “wakes” and the orbit of the Encke Gap moonlet. Icarus 66 (2), 297–323. doi:10.1016/0019-1035(86)90160-0
Keywords: Saturn, moons in the Solar system, gravitational model, granular flow, nonlinear analysis
Citation: Shinbrot T (2023) Gravitational influence of Saturn’s rings on its moons: a case for free granular flow. Front. Astron. Space Sci. 10:1146705. doi: 10.3389/fspas.2023.1146705
Received: 17 January 2023; Accepted: 17 April 2023;
Published: 11 May 2023.
Edited by:
Sergei M. Kopeikin, University of Missouri, United StatesReviewed by:
Louis Neal Irwin, The University of Texas at El Paso, United StatesAntonio Genova, Sapienza University of Rome, Italy
Copyright © 2023 Shinbrot. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Troy Shinbrot, c2hpbmJyb3RAcnV0Z2Vycy5lZHU=
 Troy Shinbrot
Troy Shinbrot