Protonation of apolar species: From Cl2H+ to (E)-NCCHCHCNH+ through computational investigations

Radioastronomy is a powerful tool for the discovery of molecules in space but it requires molecular species to be polar. The observation of apolar species can be however enabled by protonation, which occurs from reaction with the abundant ${{\text{H}}_3}^{+}$ ion whenever the proton affinity of the species under consideration is greater than that of H₂. This property can be easily investigated by computational chemistry and, in this work, it has been used to asses the potential protonation of simple homo diatomics, such as Cl₂, P₂, and Si₂, as well as apolar species containing two equivalent CN moieties, such as diisocyanogen (CNNC) and (E)-1,2-dicyanoethene. Quantum chemistry has also been exploited to investigate the mechanisms of three protonation reactions of ${{\text{H}}_3}^{+}$ with Cl₂, P₂, and CNNC. To support laboratory measurements and astronomical observations of the resulting transient species, their rotational spectroscopic parameters were accurately computed together with fundamental vibrational frequencies. For this purpose, we have employed CCSD(T)-based computational methodologies, which provide equilibrium structures with errors smaller than 0.001 Å and 0.1° for bond distances and angles, respectively. Such an accuracy is expected to lead to rotational constants predicted, in relative terms, with uncertainties better than 0.2%. Instead, the expected accuracy on vibrational frequencies is ∼10 cm⁻¹, thus being well suited to guide band assignments.

1 Introduction

The overwhelming majority of chemical species in the interstellar medium (ISM) have been discovered via radioastronomy, which exploits their rotational signatures. However, the observation of new astronomical species comes to a setback when the species of interest are weakly polar or apolar (Yamamoto, 2017). In the former case, a possible way out is offered by the line stacking technique (Yen et al., 2016), while for apolar molecules, one has to rely on the observation of the so-called molecular proxies. These are polar systems whose presence in the astronomical object under consideration can be directly related to non-observable species. Molecular proxies can be obtained in several ways, with some of them being well established in the literature.

A first possibility is to claim the presence of an apolar species based on the observation of its cyano-derivatives, which usually have a significant electric dipole moment. Indeed, the high abundance of the CN radical together with its highly reactive nature leads to species containing the CN moiety through formation pathways that are usually accessible even in the conditions of the ISM. A significant example is provided by the observation of benzonitrile (C₆H₅CN) (McGuire et al., 2018), whose detection in the ISM has been undoubtedly related to the presence of benzene in the same environment. Indeed, different experiments have demonstrated the effectiveness of the reaction between the CN radical and benzene C₆H₆ (Lee et al., 2019; Cooke et al., 2020). Similarly, the observation of cyanonaphthalene towards TMC-1 (McGuire et al., 2021) suggests the presence of naphthalene in this cold core. Other than the CN radical, proxies can also be formed by the CCH radical. However, the observation of its derivatives is more challenging because the ethynyl group leads to molecular proxies with a smaller electric dipole moment when compared to the CN-containing counterpart (Cernicharo, J. et al., 2021; McCarthy et al., 2021).

Another important way to observe apolar species is to consider their protonated form. Protonation in the ISM occurs owing to the presence of ${{\text{H}}_3}^{+}$, which in turn is obtained from the reaction between H₂ and ${{\text{H}}_2}^{+}$, with the latter being formed via cosmic ray ionization (Yamamoto, 2017). The ${{\text{H}}_3}^{+}$ initiates the protonation via this general mechanism:

${{\text{H}}_3}^{+}+\text{A}\to {\text{AH}}^{+}+{\text{H}}_2,(1)$

which proceeds only if the proton affinity (PA) of the generic species A is greater than that of H₂. Based on the PA values reported by Yamamoto (2017), ${{\text{H}}_3}^{+}$ is the primary source of N₂H⁺ and HCO⁺/HOC⁺, but it does not lead to the formation of O₂H⁺ because O₂ has a smaller PA than H₂.

In the present paper, we propose the use of protonated species as suitable proxy for the radio-observation of apolar species of astrochemical interest. To this end, their computed rotational spectra are reported here for the first time. This study will involve simple diatomic molecules, such as P₂, Si₂, and Cl₂, a linear centrosymmetric species, i.e., CNNC, and a C_2h species, the (E) isomer of NC − CH = CH − CN. The first three are simple diatomic molecules that can be considered as reservoirs of atomic P, Si, and Cl, respectively. This is particularly interesting because the chemistry of third-row atoms in astronomical environments is still in early stages, with only a few species containing P, Si, or Cl being detected so far (McGuire, 2022). Since both vibrational (infrared) and rotational spectra of homonuclear diatomics cannot be observed, the only way-out for their detection (if avoiding electronic spectroscopy) is offered by their protonated forms. As an example, the N₂H⁺ molecule–observed for the first time in 1974 by Turner (1974)—is considered a good tracer of N₂, which is otherwise not observable at radio frequencies. For this reason, the study of the simple ${{\text{HP}}_2}^{+}$, ${{\text{HSi}}_2}^{+}$, and Cl₂H⁺ ions can potentially provide useful data to guide laboratory and/or astronomical observations. While the P₂ and Si₂ precursors might be considered somewhat exotic, Cl₂ is a simple species stable under Earth conditions. To assess the accuracy of our work, the N₂H⁺ and HCO⁺ ions will be used as references to test our computational strategy.

Another interesting molecule is the linear species diisocyanogen (CNNC) because two isomers of its family, namely CNCN and NCCN, have already been detected in the ISM. While the former was observed directly via its rotational transitions (Agúndez et al., 2018), the presence of NCCN was inferred thanks to the observation of its protonated counterpart, i.e NCCNH⁺ (Agúndez et al., 2015). Thus, the computational spectroscopic characterization of CNNCH⁺ surely represents a preliminary step toward its astronomical detection. In this case, the well-characterized NCCNH⁺ species will be used as reference to understand the uncertainties associated with our methodology.

The last molecule considered is the (E) isomer of 1,2-dicyanoethene, which is the main product of the reaction between the CN radical and vinyl cyanide (CH₂ = CH − CN, Marchione et al. (2022)), also known as acrylonitrile. While the (Z) isomer of 1,2-dicyanoethene, being a polar molecule, might be detected directly, without the use of any molecular proxy, the (E) form lacks of a permanent electric dipole moment. Thus, we aim at providing good estimates for the rotational parameters of its counterpart, i.e. (E)-NC − CH = CH − CNH⁺.

This work will also report the fundamental vibrational frequencies and intensities of all the species mentioned above. These data could provide reliable starting points for experimental measurements of their vibrational spectra as well as will be benchmark references for future computations.

The manuscript is organized as follows. In the next Section 2, we detail the computational strategy adopted to describe the protonated species, with specific focus on the computation of proton affinity and formation routes as well as spectroscopic parameters. Then, the results are reported in Section 3 where they are discussed together with those of chemically related species. After briefly addressing the PA values, the formation routes for the species considered are detailed, and then the computational spectroscopic characterization is discussed. The last Section 4 will draw the main conclusions of the present study.

2 Computational details

For most of the species considered in this work, experimental and computational data are missing, thus a preliminary study using density functional theory (DFT) was carried out to understand their stable form. For this purpose, the double-hybrid rev-DSD-PBEP86 functional (Santra et al., 2019), combined with the GD3BJ empirical dispersion (Grimme et al., 2011; 2010), was used in conjunction with the jun-cc-pVTZ basis set (Dunning Jr, 1989; Papajak and Truhlar, 2011). Overall, this level of theory is shortly denoted as revDSD/junTZ. Noted is that, for third-row elements, the d-augmented jun-cc-pV(T+d)Z set has been employed (Dunning et al., 2001). The revDSD/junTZ level has been employed to derive preliminary values for equilibrium geometries, electronic energies and (harmonic) zero-point energy corrections (ZPEs) of the protonated species here considered.

2.1 Proton affinity and formation routes

To understand if a protonated molecule can be formed in the ISM starting from ${{\text{H}}_3}^{+}$, its PA value has to be considered in comparison with that of the H₂ molecule. The PA at T = 0 K is computed as (McNaught and Wilkinson, 1997; Marino et al., 2000):

$\mathrm{P}\mathrm{A}=\mathrm{\Delta }{H}_0^{\text{neutral}}-\mathrm{\Delta }{H}_0^{\text{protonated}}(2)$

where, in this study, both ΔH₀ values are obtained by combining the electronic energy obtained using the jun-Cheap composite scheme (hereafter junChS) (Alessandrini et al., 2019) with anharmonic ZPE. The latter correction was computed at the ae-CCSD(T)/cc-pwCVQZ for protonated diatomics, while the cc-pwCVTZ basis set was used for NCCNH⁺ and CNNCH⁺. For protonated 1,2-dicyanoethene, the ZPE was evaluated at the revDSD/junTZ level. Here, ae-CCSD(T) stands for the coupled-cluster (CC) method including a full treatment of single and double excitations and a perturbative estimate of triples (Raghavachari et al., 1989), with all electrons (ae) correlated. Anharmonic computations were carried out at the corresponding reference geometry, on top of which junChS energy evaluations were also performed. Within the junChS approach, the electronic energy, E(junChS), is obtained as follows (Alessandrini et al., 2019):

$E\left(\text{junChS}\right)=E\left(\text{CCSD}\left(\text{T}\right)/\text{junTZ}\right)+\mathrm{\Delta }{E}_{\text{MP}2}^{\infty }+\mathrm{\Delta }{E}_{\text{MP}2}^{\text{CV}}.(3)$

Here, the first term on the right-hand side is the fc-CCSD(T)/jun-cc-pVTZ energy (with jun-cc-pV(T+d)Z being used for third-row elements), where fc indicates that the frozen-core approximation is employed. The second term accounts for the extrapolation to the complete basis set (CBS) limit at the MP2 level, with MP2 denoting Møller-Plesset perturbation theory to the second order (Møller and Plesset, 1934). This extrapolation exploits the n⁻³ formula by Helgaker et al. (1997), and requires energy computations with two consecutive members of a hierarchical family of basis sets. In this case, the jun-cc-pV(T+d)Z and jun-cc-pV(Q+d)Z sets were used. The third term in Eq. 3 is the core-valence (CV) correction and incorporates the effect of the correlation of inner-shell electrons, which is not included in the previous computations. This term is computed as the difference between all-electron and frozen-core calculations, both with the cc-pwCVTZ basis set (Peterson and Dunning Jr, 2002).

For three species, namely Cl₂H⁺, ${{\text{HP}}_2}^{+}$, and CNNCH⁺, the formation route was also investigated. To this end, the revDSD/junTZ level of theory was employed to locate minima (MINs) and transition states (TSs) on reactive potential energy surface (PES). The correct assignment of two MINs to the connecting TS was assured by exploiting the intrinsic reaction coordinate (IRC) analysis (Fukui, 1981), performed at the same level of theory. To refine the electronic energy of each stationary point, the junChS approach was employed, while the harmonic ZPE was evaluated at the revDSD/junTZ level.

2.2 Spectroscopic characterization

Focusing on rotational spectroscopy, the main parameters influencing the spectrum are the rotational constants (Barone et al., 2021). For a given inertia axis (γ = a, b, or c), in the framework of vibrational perturbation theory to second order (VPT2) (Mills, 1972), the rotational constant of the vibrational ground state ($B_0^{\gamma }$, corresponding to A₀ for γ = a, B₀ for γ = b, and C₀ for γ = c), can be written as:

$B_0^{\gamma }=B_e^{\gamma }-\sum _r\frac{d_r}{2}{\alpha }_r^{\gamma }.(4)$

The first term on the right-hand side of Eq. 4 is the equilibrium rotational constant, which entirely depends on the isotopic composition of the molecule and equilibrium structure. Thus, $B_e^{\gamma }$ is straightforwardly obtained from a geometry optimization and accounts for about 99% of the value of $B_0^{\gamma }$ (Puzzarini et al., 2008; 2010; Alessandrini et al., 2018). The second term on the right-hand side of Eq. 4 is the vibrational contribution to the rotational constant which is obtained as the sum over all r vibrational modes of the vibration-rotation interaction constants $({\alpha }_r^{\gamma })$. In Eq. 4, d_r denotes the degeneracy of the rth vibrational mode. The vibrational correction represents a minor contribution to $B_0^{\gamma }$, but its consideration is crucial to reach accurate computational results, comparable with experimental ones (Puzzarini et al., 2008; 2010; Alessandrini et al., 2018).

Since $B_e^{\gamma }$ is the major contribution to $B_0^{\gamma }$, it should be computed at the highest possible level of theory when aiming at high accuracy. For this reason, for Cl₂H⁺, ${{\text{HP}}_2}^{+}$, ${{\text{HSi}}_2}^{+}$, and CNNCH⁺, the equilibrium geometry was obtained by exploiting a composite scheme entirely based on coupled-cluster (CC) theory (Heckert et al., 2005; 2006), which requires the minimization of the following energy gradient:

$\begin{array}{ll}\hfill \frac{d{E}_{\text{CBS}+\text{CV}+\text{fT}+\text{fQ}}}{dx}& =\frac{d{E}^{\infty }(\mathrm{H}\mathrm{F}-\mathrm{S}\mathrm{C}\mathrm{F})}{dx}+\frac{d\mathrm{\Delta }{E}^{\infty }(\mathrm{C}\mathrm{C}\mathrm{S}\mathrm{D}(\mathrm{T}))}{dx}\hfill \\ \hfill & +\frac{d\mathrm{\Delta }E\left(\mathrm{C}\mathrm{V}\right)}{dx}+\frac{d\mathrm{\Delta }E\left(\mathrm{f}\mathrm{T}\right)}{dx}+\frac{d\mathrm{\Delta }E\left(\mathrm{f}\mathrm{Q}\right)}{dx}.\hfill \end{array}(5)$

This composite scheme is denoted as “CBS+CV+fT+fQ” and it consists of 5 different terms.

• The extrapolation to the CBS limit, which is obtained by the sum of the HF-SCF and fc-CCSD(T) extrapolated gradients, i.e. $\frac{d{E}^{\infty }(\mathrm{H}\mathrm{F}-\mathrm{S}\mathrm{C}\mathrm{F})}{dx}$ and $\frac{d\mathrm{\Delta }{E}^{\infty }(\mathrm{C}\mathrm{C}\mathrm{S}\mathrm{D}(\mathrm{T}))}{dx}$, respectively. The former is evaluated using the three-point formula by Feller (1993) and the cc-pVTnZ basis sets, with n = T,Q,5. For the CCSD(T) correlation energy, ΔE (CCSD(T)), gradient the n⁻³ formula (Helgaker et al., 1997) is exploited in conjunction with the cc-pVTZ and cc-pVQZ basis sets.

• The CV contribution, which is obtained as difference between ae- and fc-CCSD(T)/cc-pwCVTZ computations.

• The fT term, which accounts for the full treatment of triples. This is obtained as difference between two computations carried out with the cc-pVTZ basis set, the first employing the CCSDT (Noga and Bartlett, 1987; Scuseria and Schaefer, 1988) method (the acronym standing for CC singles, doubles and triples) and the second one with CCSD(T), both within the fc approximation.

• The fQ term, which is the contribution due to quadruple excitations. This is computed as difference between CCSDTQ (CC singles, doubles, triples and quadruples; Kállay and Gauss (2008); Kucharski and Bartlett (1991)) and CCSDT calculations, both with the cc-pVDZ basis set and within the fc approximation.

The CBS+CV+fT+fQ equilibrium rotational constants were then corrected for the vibrational contribution. The evaluation of vibration-rotation interaction constants requires a full cubic force field (Puzzarini et al., 2010), which was computed at the ae-CCSD(T)/cc-pwCVQZ level. For the CNNCH⁺ ion, a smaller basis set, cc-pwCVTZ, was instead employed. For the (E)-NC − CH = CH − CNH⁺ species, the computational approach was slightly different because of its size. The equilibrium rotational constants were obtained from the minimization of the “CBS+CV” energy gradient, thus retaining only the first three terms on the right-hand side of Eq. 5 in conjunction with the same basis sets mentioned above. In addition, the anharmonic computation required for the vibrational corrections was carried out at the revDSD/junTZ level of theory.

For all the species considered, the VPT2 calculations performed on the computed anharmonic force field allowed for obtaining other spectroscopic parameters, such as quartic centrifugal distortion constants of the S-reduced Watson Hamiltonian (D_J, D_JK, D_K, d₁, d₂) (Papousek and Aliev, 1982) and fundamental vibrational frequencies (ν). These latter can be obtained because the computations of the cubic force constants give access, without any other additional cost, to the semi-diagonal quartic force constants. For protonated 1,2-dicyanoethene, quartic centrifugal distortion constants were computed at a different level of theory than the vibrational corrections to rotational constants, indeed considering the harmonic force field at the fc-CCSD(T)/jun-cc-pVTZ level.

On top of the best geometry, the electric dipole moment (μ) and the nuclear quadrupole-coupling constants (NQCCs, χ_ii, with i = a, b, c), which are both first-order properties, were obtained. While the electric dipole moment is required to predict the type and intensity of rotational transitions, the NQCCs shape the rotational spectrum (hyperfine structure). NQC is the interaction between the quadrupole moment of a nucleus and the electric gradient at the same nucleus. This determines a splitting of the rotational energy levels, thus causing a splitting of the rotational transitions, i.e. the so-called hypefine structure. Noted is that a nucleus with I > 1/2 has a non-zero quadrupole moment. The hyperfine structure can be useful for the assignment and analysis of rotational lines in the laboratory and in astronomical observations (Turner, 1974; Puzzarini et al., 2010; Melosso et al., 2021); thus, spectral simulations strongly benefit from the introduction of such interaction terms. Both NQCCs and electric dipole moment components were obtained at the ae-CCSD(T)/aug-cc-pwCVQZ level for protonated diatomics, while for CNNCH⁺ the aug-cc-pwCVTZ basis set was used. For protonated (E)-1,2-dicyanoethene, the fc-CCSD(T)/jun-cc-pVTZ level of theory was employed. Additionally, the vibrational corrections to the NQCCs and the electric dipole moment were also considered and obtained from the anharmonic treatment mentioned above.

The computational strategy outlined above was also employed to describe three molecules that are experimentally well-characterized in the literature. These are N₂H⁺ and HCO⁺, which offer a good reference for the new protonated diatomics, and NCCNH⁺ for the direct comparison with CNNCH⁺.

All DFT and MP2 computations were carried out using the Gaussian16 suite of programs (Frisch et al., 2016), while the CFour quantum-chemistry program (Stanton et al., 2016; Matthews et al., 2020) was used for all computations based on the CC theory. Concerning VPT2 calculations, its generalized version (GVPT2) (Schiff, 1955; Piccardo et al., 2015) was employed whenever using the Gaussian16 package.

3 Results

As starting point, the work investigated the stable form of Cl₂H⁺, ${{\text{HP}}_2}^{+}$, and ${{\text{HSi}}_2}^{+}$. For this purpose, equilibrium structures ranging from linear to cyclic were considered and the most stable forms of each species are shown in Figure 1, where their electronic state is also reported. The same figure also provides the equilibrium structure of CNNCH⁺ and (E)-NC − CH = CH − CNH⁺, which were somewhat more straightforward to derive since bent structures would be very unstable.

FIGURE 1

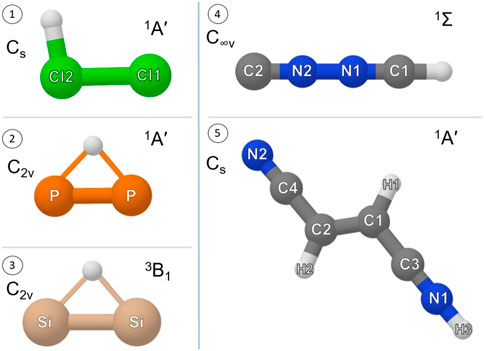
FIGURE 1. Equilibrium structure, point group symmetry and electronic ground state of (1) Cl₂H⁺, (2) ${{\text{HP}}_2}^{+}$, (3) ${{\text{HSi}}_2}^{+}$, (4) CNNCH⁺, and (5) protonated (E)-1,2-dicyanoethene.

The main molecule driving protonation in the ISM being ${{\text{H}}_3}^{+}$, the first mandatory step is to investigate whether the species considered in this work can be produced by reaction 1. The first screening is based on PA. If PA of P₂, Si₂, Cl₂, CNNC, and NCCHCHCN is greater than that of H₂, the protonation occurs and the reaction proceeds at the Langevin rate (Yamamoto, 2017). The latter is typically around 10^–9 cm³s⁻¹ and is rather independent from the temperature. The data required for this comparison are reported in Table 1, which also includes the data for N₂, CO, and NCCN, whose protonated forms have already been observed in the ISM.

TABLE 1

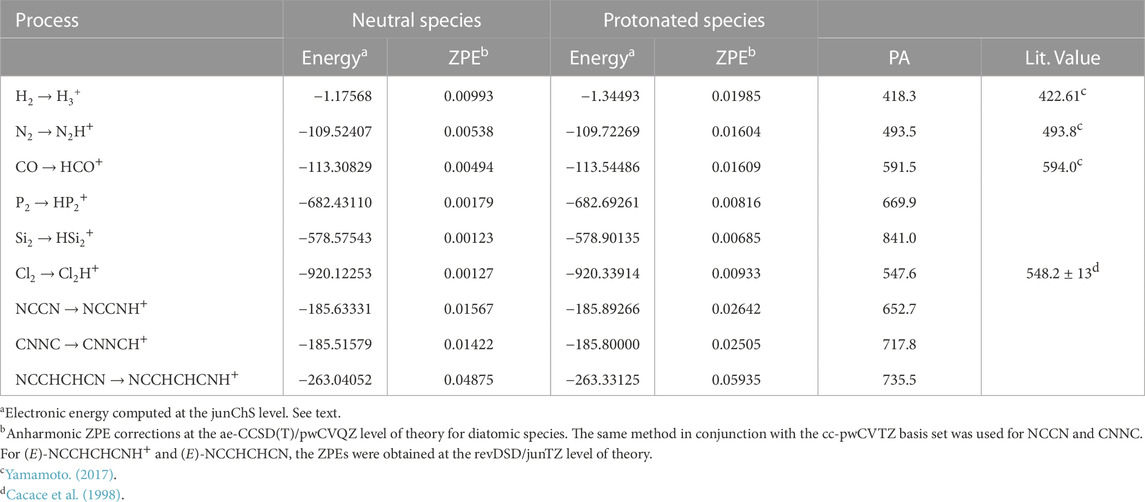
TABLE 1. Computed proton affinities (kJ mol⁻¹) for the molecules considered in this work. Electronic energies and ZPE are in Hartrees.

Table 1 indicates a PA value of 418 kJ⋅mol⁻¹ for H₂, in good agreement with what reported by Yamamoto (2017) and Hunter and Lias (1998), i.e. 422.61 kJ⋅mol⁻¹. A similar agreement is noted for N₂ and CO, with values of 493.5 kJ⋅mol⁻¹ and 591.1 kJ⋅mol⁻¹, respectively, to be compared with 493.8 kJ⋅mol⁻¹ and 594 kJ⋅mol⁻¹ given in Yamamoto (2017). The PA values reported in this work refer to 0 K and are more accurate than those available in the literature. The differences noted can be ascribed to the (small) thermal correction, the literature values referring to a temperature of 298.15 K.

From Table 1, it is noted that a PA value greater than that of H₂ has been obtained for Cl₂, thus suggesting the possible formation of Cl₂H⁺ in the ISM. A further support to this is provided by the fact that PA(Cl₂) is intermediate between PA(N₂) and PA(CO), with both N₂H⁺ and HCO⁺ detected in the ISM. In particular, our PA(Cl₂) value of 547.6 kJ⋅mol⁻¹ is in good agreement with that established experimentally by Cacace et al. (1998), i.e. 548.1 ± 13 kJ⋅mol⁻¹.

The PA value of P₂ is 669.9 kJ⋅mol⁻¹ and it is very close to that of NCCN, i.e., 652.7 kJ⋅mol⁻¹, thus confirming the plausible formation of the protonated form of P₂. Finally, large PA values have been obtained for CNNC, (E)-NCCHCHCN, and Si₂. For the first two species, the PA values are 717.8 kJ⋅mol⁻¹ and 735.5 kJ⋅mol⁻¹, respectively, which are comparable with those of molecules like H₂O, H₂S, and H₂CO (Yamamoto, 2017). The Si₂ species shows the largest PA, 841.0 kJ⋅mol⁻¹, this result being likely due to its triplet electronic ground state. Indeed, a similar value (869 kJ⋅mol⁻¹) is obtained for the CCS radical in the same electronic state (Yamamoto, 2017). Notably, HCCS⁺ as well as H₃O⁺ and H₂COH⁺ have already been observed in the ISM (Cabezas, C. et al., 2022; Wootten et al., 1991; Bacmann et al., 2016; Ohishi et al., 1996)

3.1 Formation routes

While the discussion above on PA values suggests that all the species under consideration could be formed in the ISM, the next step is the investigation of their formation routes. For this purpose, three test cases have been chosen: Cl₂H⁺, ${{\text{HP}}_2}^{+}$, and NCCNH⁺. According to the literature (Klippenstein et al., 2010; Zhu et al., 2019), the reaction between any molecule and ${{\text{H}}_3}^{+}$ is barrierless and proceeds through the formation of a stable intermediate characterized by a weak interaction between the protonated species and the H₂ molecule. This also applies to the reactive PESs considered in this work, which are shown in Figure 2. While a full account on their energetics is provided in the Supporting Material (SM), in the following, only the junChS+ZPE energies will be considered for our discussion.

FIGURE 2

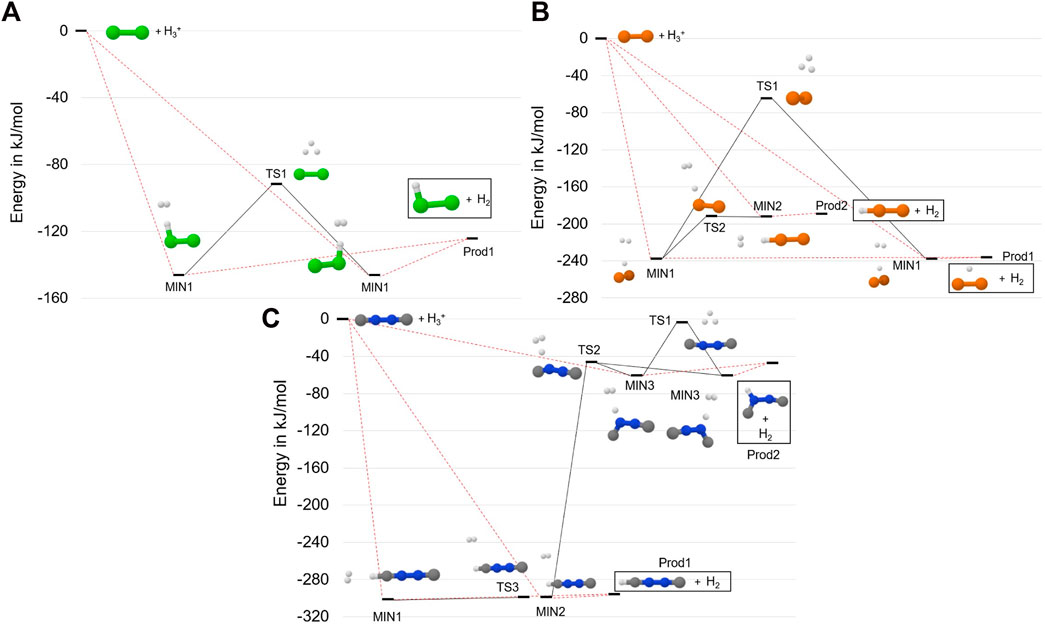
FIGURE 2. Reactive PES for: the Cl₂ + ${{\text{H}}_3}^{+}$ reaction (panel A), the P₂ + ${{\text{H}}_3}^{+}$ reaction (panel B), and the CNNC + ${{\text{H}}_3}^{+}$ reaction (panel C). The full list of stationary-point energies is reported in the SM.

Let us start by considering the formation of Cl₂H⁺ from the reaction between ${{\text{H}}_3}^{+}$ and Cl₂ (panel A in Figure 2). The first intermediate formed, denoted as MIN1, is located at −143.2 kJ⋅mol⁻¹ with respect to the energy of the reactants. This minimum can interconvert to its spatial equivalent structure via TS1 (−85.7 kJ⋅mol⁻¹) and form Cl₂H⁺ and H₂ without any exiting barrier. A similar reaction mechanism is also observed for P₂, panel B of Figure 2. However, two different products can be formed in this case. Starting from the reactants the open routes are: a barrierless approach to MIN1 (−237.7 kJ⋅mol⁻¹) and a barrierless approach to MIN2 (−192.4 kJ⋅mol⁻¹). These two intermediates are connected by the transition state TS2, located at −191.8 kJ⋅ mol⁻¹. In addition, MIN1 can also form its spatial equivalent structure through TS1. MIN1 leads to product Prod1 without any exiting barrier, with Prod1 being the most stable stationary point of the ${{\text{HP}}_2}^{+}$ + H₂ reactive PES. Instead, MIN2 forms Prod2, i.e. the linear isomer of ${{\text{HP}}_2}^{+}$, which might be potentially present in the ISM, even though it lies ∼50 kJ⋅mol⁻¹ higher in energy than the cyclic form.

The last panel of Figure 2 (panel C) shows the reaction mechanism for the protonation of CNNC. In this case, there are three open barrierless approaches that lead to the formation of MIN1, MIN2 and MIN3. The first two intermediates are very close in energy: MIN1 lies at −305.5 kJ⋅mol⁻¹ and MIN2 at −301.8 kJ⋅mol⁻¹. They can interconvert through TS3, which differs from MIN2 for the orientation of the H₂ moiety with respect to the linear backbone. The motion of H₂ is a large amplitude one, TS3 being indeed characterized by an imaginary frequency of only 14 cm⁻¹. Consequently, the two structures are very close in energy, i.e. they differ by 0.1 kJ⋅mol⁻¹ at both the revDSD/junTZ and junChS levels of theory augmented by corresponding ZPEs. From Figure 2, it is noted that both MIN1 and MIN2 can form–without going through any barrier–Prod1, i.e. linear CNNCH⁺ and H₂. TS2, lying at −46.4 kJ⋅mol⁻¹, represents the barrier to be overcome for distorting the linear chain and forming MIN3, which can then interconvert with its equivalent structure via TS1 or form Prod2, i.e. a bent form of CNNCH⁺ + H₂.

The three protonation reactions of Figure 2 demonstrate that Cl₂H⁺, ${{\text{HP}}_2}^{+}$ and CNNCH⁺ can be formed in the ISM. The energetic characterization there reported is expected to have an accuracy of 1–5 kJ⋅mol⁻¹ (Alessandrini et al., 2019; 2021b) and can thus be used to guide the kinetic analysis of these reactions. While there are no doubts about the isomeric form produced in the reaction between Cl₂ and ${{\text{H}}_3}^{+}$, for the other two reactions, two possible products are present. However, the stability of MIN1 and the small energy difference between MIN1 and Prod1 should favor the formation of cyclic ${{\text{HP}}_2}^{+}$ and linear CNNCH⁺. Therefore, only these forms have been considered in the following spectroscopic characterization.

3.2 Spectroscopic characterization

To enable the experimental detection of the protonated species considered in this work, a computational spectroscopic characterization involving fundamental vibrational frequencies and rotational spectroscopy parameters has been carried out. In the following, the results are presented according to the class of species they belong: (i) protonated diatomics, where the experimental reference is offered by N₂H⁺ and HCO⁺; (ii) the linear CNNCH⁺ cation compared with the NCCNH⁺ counterpart; (iii) the protonated form of (E)-1,2-dicyanoethene. These species, with the only exception of the linear CNNCH⁺ molecule, are planar asymmetric rotors. Their planarity leads to a null dipole moment component along the c axis (μ_c = 0, with ab thus being the molecular plane). For ${{\text{HP}}_2}^{+}$ and ${{\text{HSi}}_2}^{+}$, the μ_a component is equal to zero as well because of symmetry reasons. For the linear rotor CNNCH⁺, the only non-null dipole moment component is that along the molecular axis, and it is simply denoted as μ.

3.2.1 Protonated diatomics

The rotational parameters of Cl₂H⁺, ${{\text{HP}}_2}^{+}$, and HSi₂⁺ are reported in Table 2, while those of N₂H⁺ and HCO⁺ are provided in the SM. It should be pointed out that protonated CO and N₂ are linear rotors, and thus they are characterized by a single rotational constant and one quartic centrifugal distortion term. Differently, Cl₂H⁺, ${{\text{HP}}_2}^{+}$ and ${{\text{HSi}}_2}^{+}$ are asymmetric rotors, very close to the prolate limit (i.e., Ray’s asymmetry parameter, κ, being 0.999). Therefore, these species have three rotational constants and five quartic centrifugal distortion parameters.

TABLE 2

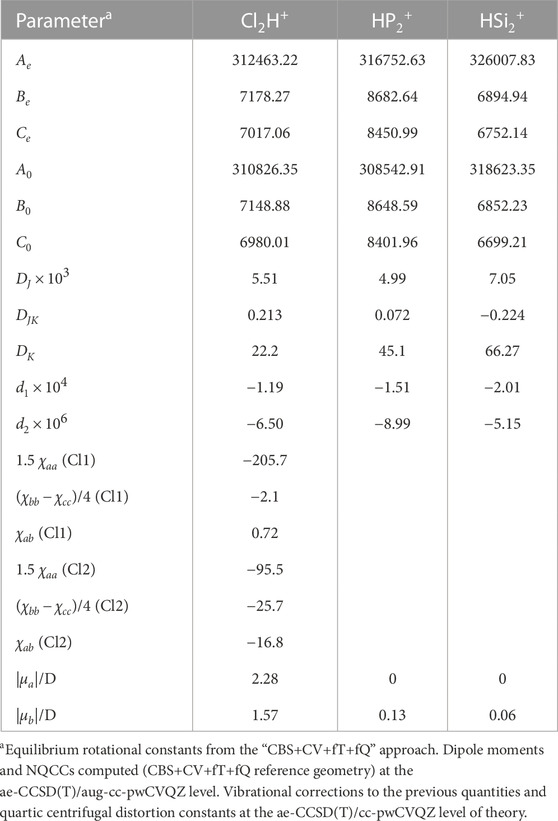
TABLE 2. Rotational parameters (in MHz) of Watson’s S reduced Hamiltonian (I^r representation) for Cl₂H⁺, ${{\text{HP}}_2}^{+}$, and ${{\text{HSi}}_2}^{+}$. Dipole moment components (in debye) are also reported.

The “CBS+CV+fT+fQ” level of theory augmented by vibrational corrections at the ae-CCSD(T)/cc-pwCVQZ level of theory, provides the rotational constant for N₂H⁺ with an error as low as 0.01%, as shown in Table S1. For HCO⁺, the error is slightly larger, this being 0.07%. However, both values are within the uncertainty predicted by benchmark studies for the “CBS+CV+fT+fQ” approach (Puzzarini et al., 2008). Even though N₂H⁺ and HCO⁺ are linear molecules, the accuracy reached for such species should hold also for the rotational constants of the bent Cl₂H⁺ cation and the cyclic ${{\text{HP}}_2}^{+}$ and ${{\text{HSi}}_2}^{+}$ species, at least when the mean error of the three rotational constants is considered.

To accurately simulate rotational spectra, other parameters are required. These are the NQCCs of the N and Cl atoms together with quartic centrifugal distortion constants for all species. As mentioned in Computational details section, the latter parameters have been computed at the ae-CCSD(T)/cc-pwCVQZ level of theory, while NQCCs have been obtained, on top of the “CBS+CV+fT+fQ” geometry, by computing the electric-field gradient at the quadrupolar nuclei at the ae-CCSD(T)/aug-cc-pwCVQZ level. The NQCCs have also been corrected for the vibrational contribution evaluated at the ae-CCSD(T)/cc-pwCVQZ level.

For N₂H⁺, the experimental D_J quartic centrifugal distortion constant is reproduced with a discrepancy of about 3%, while for HCO⁺ the error is 2%. Similar uncertainties are expected for the quartic centrifugal distortion constants of the protonated species of Table 2. Moving to NQCCs, for N₂H⁺, the discrepancy with respect to experiment is on average 1% and, thus, a similar accuracy is expected for the constants of Cl₂H⁺, as found in other works in the literature (Cazzoli et al., 2006; Puzzarini et al., 2010).

Finally, to simulate the rotational spectrum, the electric dipole moment components were computed at the same level of theory as NQCCs. The obtained values indicate that ${{\text{HP}}_2}^{+}$ and ${{\text{HSi}}_2}^{+}$ have a (very) weak b-type rotational spectrum, the only non-null dipole moment component (μ_b) being equal to 0.06 D for ${{\text{HSi}}_2}^{+}$ and to 0.13 for HP₂. In the case of ${{\text{HP}}_2}^{+}$, the intensity of the rotational lines is also affected by spin statistics. Indeed, ³¹P has a nuclear spin I of 1/2 (fermion) and the total wave function has to be anti-symmetric with respect to the exchange of the two equivalent P nuclei. The electronic and vibrational ground states being total symmetric, the overall symmetry of the total wave function is determined by the rotational and nuclear terms. Three ortho (symmetric) and one para (anti-symmetric) states arise for the nuclear wave function. Instead, the symmetry of the rotational contribution is determined by the K_a + K_c sum¹ because the nuclei exchange occurs by rotation around the b axis. As a consequence, the rotational transitions associated with odd K_a + K_c values are three times more intense than those with even K_a + K_c values.

The Cl₂H⁺ species has both a-type and b-type spectra, the corresponding dipole moment components being 2.28 D and 1.57 D, respectively. Thus, a-type transitions should have an intensity comparable to that of N₂H⁺ and HCO⁺, while b-type transitions are expected to be weaker. An example is shown in Figure 3, where the blue spectrum reports a μ_a transition of Cl₂H⁺ at around 98307 MHz and a weaker μ_b transition predicted at 98352 MHz. These are compared with the J = 1 ← 0 transition of N₂H⁺, for which both the theoretical simulation (this work, in red) and the experimental data (Cazzoli et al. (2012), in black) are considered. The experimental transition occurs at 93173 MHz and the theoretical simulation lies close in frequency, indeed being centered at 93181 MHz. In relative terms, this discrepancy should also apply to the simulation of Cl₂H⁺. Conservatively, based on benchmark studies (Alessandrini et al., 2018), an uncertainty of 0.1% can be expected for each rotational constant of Cl₂H⁺. This would locate the $J_{K_a,K_c}=7_{\mathrm{1,7}}\leftarrow 6_{\mathrm{1,6}}$ transition of Figure 3 in the range 98307.6 ± 18 MHz (3σ deviation). Lastly, the two insets of Figure 3 show the hyperfine splittings based on the computed NQCCs. For N₂H⁺, the structure reproduces very well the experimental one in terms of both intensity and shift with respect to the unperturbed frequency. The same should apply to Cl₂H⁺.

FIGURE 3

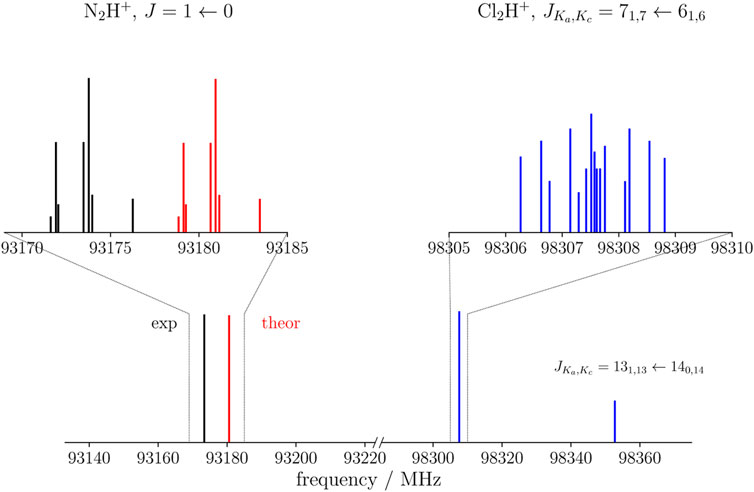
FIGURE 3. Theoretical (red) and experimental (black) J =1←0 transition of N₂H⁺ compared with the simulated spectrum of Cl₂H⁺ (blue) in the nearby frequency region. For the latter, both a-type $(J_{K_a,K_c}=7_{\mathrm{1,7}}\leftarrow 6_{\mathrm{1,6}})$ and b-type $(J_{K_a,K_c}=13_{\mathrm{1,13}}\leftarrow 14_{\mathrm{0,14}})$ transitions are visible. The two insets show the hyperfine structures due to nitrogen and chlorine nuclei for N₂H⁺ and Cl₂H⁺, respectively.

For Cl₂H⁺, ${{\text{HP}}_2}^{+}$, and ${{\text{HSi}}_2}^{+}$, vibrational frequencies have been obtained at the ae-CCSD(T)/cc-pwCVQZ level. The results are reported in Table 3, while those of N₂H⁺ and HCO⁺ are provided in the SM, where they are also compared with the experimental counterparts. To understand the accuracy of the predictions for the protonated species addressed in this work, we start by analyzing the results for N₂H⁺ and HCO⁺. For the former cation, the lowest fundamental frequency is due to the bending mode. This is predicted at 700.94 cm⁻¹ within the harmonic approximation and about 9 cm⁻¹ lower in energy at the anharmonic level. The experiment locates this band at 698.6353 (14) cm⁻¹ (Foster and McKellar, 1984). The other two bands of N₂H⁺ were observed at 3233.96085 cm⁻¹ (Nakanaga et al., 1990) and 2257.8667 (13) cm⁻¹ (Owrutsky et al., 1986). Both of them are well predicted by the VPT2 treatment, with an error of only 8 cm⁻¹. For HCO⁺, the fundamental bands are predicted (incorporating anharmonicity) to lie at ν₁ = 3090.31 cm⁻¹, ν₂ = 2187.67 cm⁻¹, and ν₃ = 830.05 cm⁻¹. These are in good agreement with the experimental data, with discrepancies of about 2–4 cm⁻¹. In fact, the experimental observed frequencies are: ν₁ = 3088.7951 (31) cm⁻¹ (Amano, 1983), ν₂ = 2183.9496 (6) cm⁻¹ (Foster and McKellar, 1984), and ν₃ = 828.2305 (9) cm⁻¹ (Kawaguchi et al., 1985).

TABLE 3

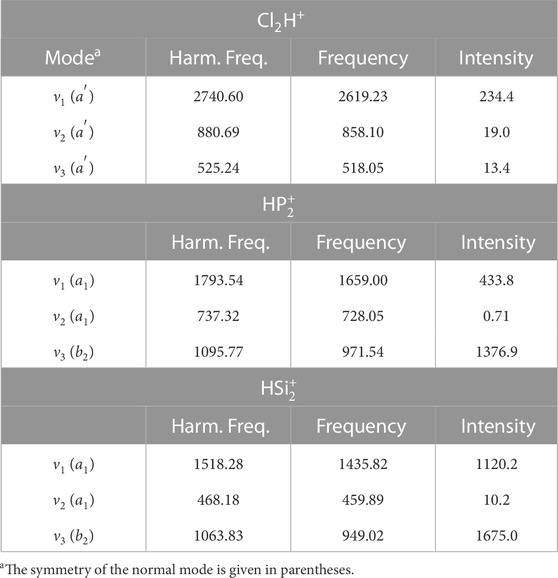
TABLE 3. Harmonic and anharmonic vibrational frequencies (cm⁻¹) for Cl₂H⁺, ${{\text{HP}}_2}^{+}$, and ${{\text{HSi}}_2}^{+}$. Anharmonic intensities in km mol⁻¹. All quantities are at the ae-CCSD(T)/cc-pwCVQZ level of theory.

A similar accuracy is expected for the other protonated diatomics. The lowest fundamental band is observed for the stretching involving third-row atoms (ν₂ band for ${{\text{HP}}_2}^{+}$ and ${{\text{HSi}}_2}^{+}$, ν₃ band for Cl₂H⁺). This vibrational mode lies at 518.0 cm⁻¹ for Cl₂H⁺, 728.05 cm⁻¹ for ${{\text{HP}}_2}^{+}$, and 459.89 cm⁻¹ for ${{\text{HSi}}_2}^{+}$. The ν₃ band for ${{\text{HP}}_2}^{+}$ and ${{\text{HSi}}_2}^{+}$, and the ν₂ band for Cl₂H⁺ correspond to the asymmetric stretching involving the H atom, which is predicted at 949.02 cm⁻¹, 971.54 cm⁻¹, and 858.1 cm⁻¹ for ${{\text{HSi}}_2}^{+}$, ${{\text{HP}}_2}^{+}$, and Cl₂H⁺, respectively. The fundamental frequencies for symmetric stretching (ν₁) are, in the same order as before, 1435.82 cm⁻¹, 1659.00 cm⁻¹, and 2619.23 cm⁻¹. For the Cl₂H⁺ species, the most intense band is ν₁, while for ${{\text{HP}}_2}^{+}$ and ${{\text{HSi}}_2}^{+}$ it is ν₃. In conclusion, in view of their accuracy (Puzzarini et al., 2019; Barone et al., 2021)—which is conservatively expected to be better than 10 cm⁻¹—the data obtained in this work can allow the investigation of the vibrational spectrum of these species as well as the ro-vibrational ones².

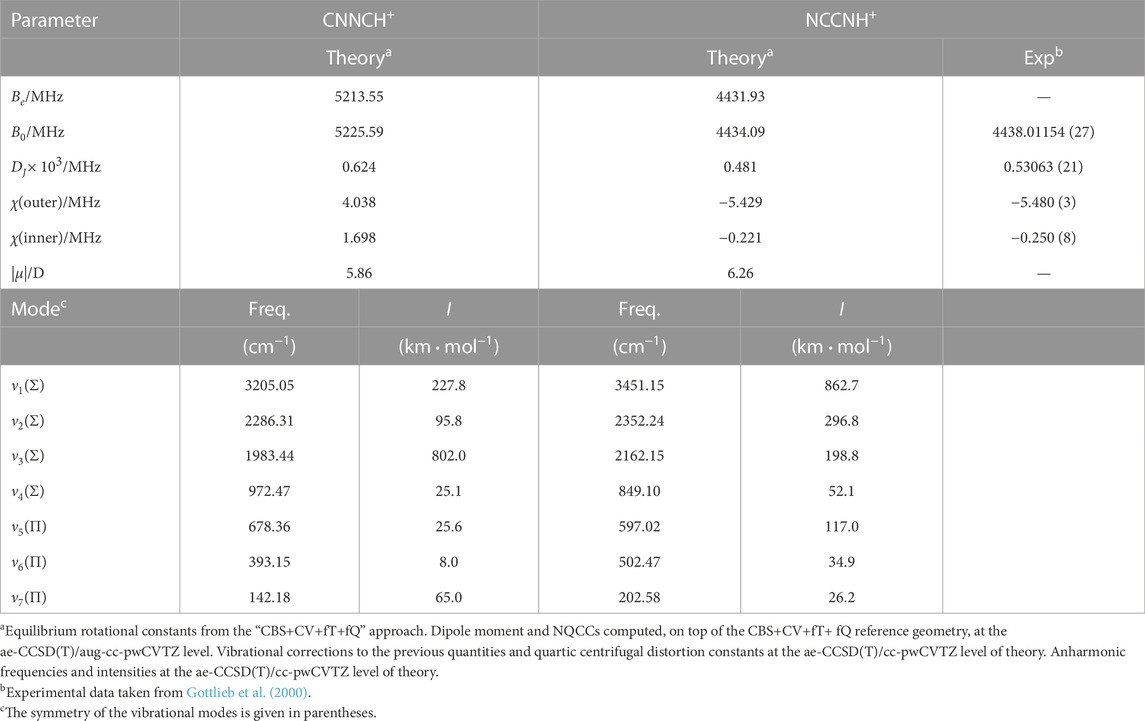
3.2.2 CNNCH⁺ and NCCNH⁺

The rotational parameters of CNNCH⁺ are compared with those of NCCNH⁺ in Table 4. The error associated with our computational strategy can be derived by considering the experimental values of NCCNH⁺ (Gottlieb et al., 2000). For B₀ of NCCNH⁺, the discrepancy between experiment and theory is about 4 MHz, which means 0.09% in relative terms; thus, the value of the rotational constant of CNNCH⁺ lies within the interval 5225.59 MHz ± 4.7 MHz. For D_J of NCCNH⁺, the deviation of the computed value (0.480 × 10⁻³ MHz) from experiment is 9.3% and the same confidence range is expected to apply to CNNCH⁺. Moving to NQCCs, in both molecules, we have two nitrogen atoms which are denoted as the outer N and the inner N; while such denotation is rather straightforward for NCCNH⁺, in the case of CNNCH⁺, the outer N is the furthest from H, i.e., N2 in Figure 1. In NCCNH⁺, the NQCC of the outer N is well reproduced, the error being 0.2%, while a discrepancy of about 12% is noted for the inner NQCC, the experimental value being 0.250 MHz and the computed one 0.221 MHz. However, it has to be noted that the absolute discrepancy is nearly the same: ∼50 kHz for χ(outer) and ∼30 kHz for χ(inner). Therefore, the hyperfine splittings are well reproduced as shown in the left inset in Figure 4, where the experimental and theoretical hyperfine structures of the J = 3 ← 2 transition of NCCNH⁺ are depicted. Focusing on the unperturbed transition, the experimental frequency of NCCNH⁺ is 24 MHz lower than the simulated one. This deviation can be considered as the uncertainty affecting the J = 3 ← 2 transition of CNNCH⁺, which is shown in Figure 4 together with its hyperfine structure. Concerning the latter, an analogous accuracy to that observed for NCCNH⁺ is expected. Indeed, in absolute terms, the uncertainty affecting NQCCs should be of the order of 50 kHz. Since the dipole moment of CNNCH⁺ is large (about 6 D) and only 0.4 D smaller than that of NCCNH⁺, the detection of this new protonated form is reasonable and future works will benefit from the present data.

TABLE 4

TABLE 4. Rotational parameters and fundamental vibrational frequencies of CNNCH⁺ and NCCNH⁺.

FIGURE 4

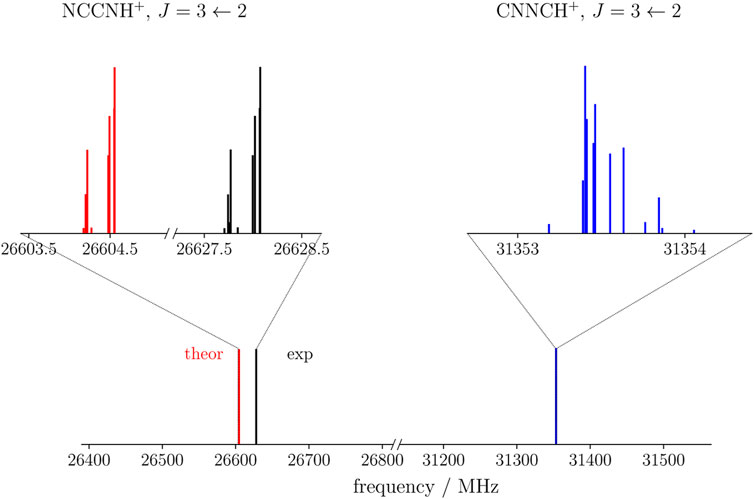
FIGURE 4. Theoretical (red) and experimental (black) J =3←2 transition of NCCNH⁺ compared with the simulation of the same transition of CNNCH⁺ (blue). The insets show in detail the corresponding hyperfine structures.

Table 4 also reports the fundamental frequencies and intensities of the vibrational modes for both NCCNH⁺ and CNNCH⁺. In this case, no experimental reference is available in the literature, but vibrational frequencies computed at the ae-CCSD(T)/cc-pwCVTZ level are sufficiently accurate to guide the assignment of the (ro-)vibrational spectrum for both species (Puzzarini et al., 2019; Barone et al., 2021). The most intense vibrational band is ν₃ for CNNCH⁺ and ν₁ for NCCNH+.

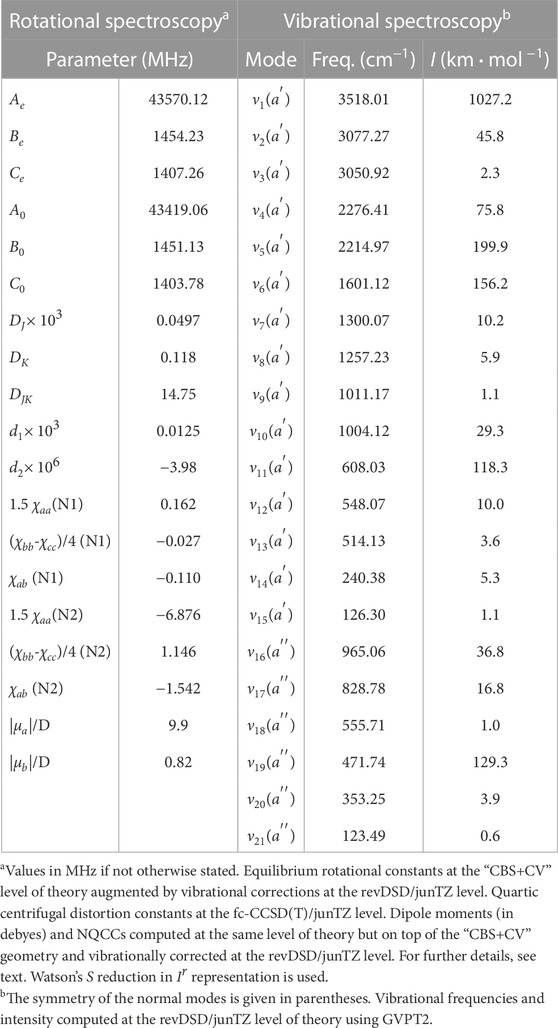
3.2.3 NCCHCHCNH⁺

The last molecule considered in this work is the E isomer of NCCHCHCNH⁺. According to the computed electric dipole moment components, a-type transitions are the most prominent features of the rotational spectrum because the associated dipole component is as large as 10.1 D. Based on the literature on this topic (Puzzarini et al., 2008; Puzzarini, 2016), in relative terms, the uncertainty affecting the equilibrium “CBS+CV” rotational constants is expected to be 0.6%, which drastically reduces to about 0.1% when vibrational corrections are incorporated. Actually, this uncertainty can be as small as 0.05%, as demonstrated, for example, by Melosso et al. (2022); Alessandrini et al. (2021a). For an accurate simulation of the rotational spectrum of this species, the NQCCs of both nitrogen atoms have been computed, on top of the “CBS+CV” geometry, at the fc-CCSD(T)/jun-cc-pVTZ level. Quartic centrifugal distortion constants have been obtained from a harmonic force field at the same level of theory. All these data, collected in Table 5, can guide future experimental measurements as well as astronomical search of this molecule in view of its large dipole moment (in particular that associated with a-type transitions) and the small uncertainties affecting our spectroscopic parameters. Notably, the observation of this species in the ISM would indirectly confirm the feasibility of the reaction between the CN radical and vinyl cyanide, as suggested in Marchione et al. (2022).

TABLE 5

TABLE 5. Computed spectroscopic parameters of (E)-NCCHCHCNH⁺.

In Table 5, the vibrational fundamental frequencies of (E)-NCCHCHCNH⁺ are reported. It is noted that the strongest band is the one associated with the stretching of the terminal H atom. The weakest band has an intensity of 0.6 km⋅mol⁻¹ and it is the out-of-plane bending of the CN and CNH terminal groups. According to the literature on this topic (Barone et al., 2015), double-hybrid functionals should reproduce the experimental fundamental frequencies with a mean error of about 10.4 cm⁻¹.

4 Conclusion

In the ISM conditions, protonation can occur easily thanks to the abundance of ${{\text{H}}_3}^{+}$. For this reason, protonated forms of “invisible” (to rotational spectroscopy and thus to radioastronomy) apolar species are considered tracers of the latter and can be used to derive an estimate of their abundance. In this work, we suggest the use of the protonated species ${{\text{HP}}_2}^{+}$, Cl₂H⁺, ${{\text{HSi}}_2}^{+}$, CNNCH⁺, and (E)-NCCHCHCNH⁺ as proxies for the corresponding apolar form (P₂, Cl₂, Si₂, CNNC, NCCHCHCN). The most stable structures of these species have been preliminary investigated at the revDSD/junTZ level of theory. This pointed out that Cl₂H⁺ has a bent structure, while ${{\text{HP}}_2}^{+}$ (in contrast with N₂H⁺ which is linear) and ${{\text{HSi}}_2}^{+}$ have a cyclic structure. CNNCH⁺ is linear in analogy to the NCCNH⁺ isomer, which has already been characterized and detected in the ISM. Finally, a planar structure has been found for (E)-NCCHCHCNH⁺.

State-of-the-art computational methodologies have been used to assess the PA values of Cl₂, P₂, Si₂, CNNC, and (E)-NCCHCHCN to be compared with that of H₂. Indeed, a PA greater than that of H₂ implies that protonation due to ${{\text{H}}_3}^{+}$ is favored. This is the case for all the species considered in this study, and the computed PA values have been found in good agreement with experimental and previous theoretical estimates available in the literature.

To provide more details on the protonation mechanisms, the formation routes leading to Cl₂H⁺, ${{\text{HP}}_2}^{+}$, and CNNCH⁺ have been explored. The junChS+ZPE energies, evaluated on top of revDSD/junTZ geometries, pointed out the presence of simple reaction paths starting from the corresponding apolar species and ${{\text{H}}_3}^{+}$. All these mechanisms are dominated by a barrierless step from reactants to adducts, but also from these latter to products. In all the three cases, the minimum energy path leads to the most stable protonated forms, namely bent Cl₂H⁺, cyclic ${{\text{HP}}_2}^{+}$, and linear CNNCH⁺. The first two formation routes are similar to those producing N₂H⁺ and HCO⁺; therefore, it can be safely assumed that a similar mechanism leads to ${{\text{HSi}}_2}^{+}$. We also expect that the formation of (E)-NCCHCHCNH⁺ presents similarity with that of CNNCH⁺.

Since the investigated protonated species are potentially present in the ISM, an accurate computational spectroscopic characterization has also been carried out. For protonated diatomics, the rotational constants are expected to reproduce the experimental counterparts with an error of 0.1%, or even smaller as in the case of HCO⁺ and N₂H⁺. For CNNCH⁺ and (E)-NCCHCHCNH⁺, because of the reduction in the level of theory employed, a larger uncertainty has been obtained, but still on the order of 0.1%. For all the species investigated, a full set of rotational parameters, also including quartic centrifugal distortion constants and NQCCs, has been obtained and used to estimate low-J rotational transitions. For CNNCH⁺, the J = 3 ← 2 rotational transition is predicted to be centered at around 30353.5 MHz with an uncertainty of about 24 MHz. The spectroscopic characterization of (E)-NCCHCHCNH⁺ is of particular interest because it results from protonation of the E isomer of 1,2-dicyanoethene, which in turn is the main product of the reaction between the CN radical and acrylonitrile (Marchione et al., 2022). This reaction is of great astrochemical relevance, but the only possible option for detecting (E)-NCCHCHCN is via its protonated proxy. This work reports–for the first time–the rotational constants of this species and points out that protonation leads to a large dipole moment of about 10 D, which further suggests the detectability of (E)-NCCHCHCNH⁺. Therefore, our simulations will be useful to support and complement experimental measurements as well as to guide possible radioastronomical observation.

For all the aforementioned molecules, the fundamental vibrational frequencies have accurately been obtained by exploiting a methodology that incorporates the effects of anharmonicity. Therefore, the expected accuracy of our predictions is 10 cm⁻¹ or even better, which is largely sufficient for the assignment of experimental infrared bands.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

SA worked on conceptualization of the work as well as investigation. SA, LB, and MM carried out the formal analysis and wrote a first draft of the manuscript. SA and CP reviewed the manuscript and provided the funding. Final editing was carried out by CP, LB, MM, and SA.

Funding

This work has been supported by MIUR (PRIN Grant Number 202082CE3T) and by the University of Bologna (RFO funds). The COST Action CA21101 “COSY—Confined molecular systems: from a new generation of materials to the stars” is also acknowledged. This work was partially supported by the Open Access Publishing Fund of the Scuola Normale Superiore.

Acknowledgments

The SMART@SNS Laboratory (http://smart.sns.it) is acknowledged for providing high-performance computing facilities.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2023.1128896/full#supplementary-material

Footnotes

¹The asymmetric rotor energy levels are labeled using (in addition to the J quantum number) two “pseudo” quantum numbers: K_a and K_c, which correspond to the K values of the two limiting prolate (referred to the a symmetry axis) and oblate (referred to the c symmetry axis) cases of the symmetric rotor, respectively.

²For those interested in the prediction of the rotational constants of vibrational excited states, the required ${\alpha }_r^{\gamma }$ values are available in Supplementary Table S2.

References

Agúndez, M., Cernicharo, J., De Vicente, P., Marcelino, N., Roueff, E., Fuente, A., et al. (2015). Probing non-polar interstellar molecules through their protonated form: Detection of protonated cyanogen (NCCNH⁺). Astron. Astrophys. 579, L10. doi:10.1051/0004-6361/201526650

PubMed Abstract | CrossRef Full Text | Google Scholar

Agúndez, M., Marcelino, N., and Cernicharo, J. (2018). Discovery of interstellar isocyanogen (CNCN): Further evidence that dicyanopolyynes are abundant in space. Astrophys. J. Lett. 861, L22. doi:10.3847/2041-8213/aad089

PubMed Abstract | CrossRef Full Text | Google Scholar

Alessandrini, S., Barone, V., and Puzzarini, C. (2019). Extension of the “cheap” composite approach to noncovalent interactions: The jun-chs scheme. J. Chem. Theory Comput. 16, 988–1006. doi:10.1021/acs.jctc.9b01037

CrossRef Full Text | Google Scholar

Alessandrini, S., Gauss, J., and Puzzarini, C. (2018). Accuracy of rotational parameters predicted by high-level quantum-chemical calculations: Case study of sulfur-containing molecules of astrochemical interest. J. Chem. Theory Comput. 14, 5360–5371. doi:10.1021/acs.jctc.8b00695

PubMed Abstract | CrossRef Full Text | Google Scholar

Alessandrini, S., Melosso, M., Jiang, N., Bizzocchi, L., Dore, L., and Puzzarini, C. (2021a). Conformational stability of cyclopropanecarboxaldehyde is ruled by vibrational effects. Mol. Phys. 119, e1955988. doi:10.1080/00268976.2021.1955988

CrossRef Full Text | Google Scholar

Alessandrini, S., Tonolo, F., and Puzzarini, C. (2021b). In search of phosphorus in astronomical environments: The reaction between the cp radical (X²Σ⁺) and methanimine. J. Chem. Phys. 154, 054306. doi:10.1063/5.0038072

PubMed Abstract | CrossRef Full Text | Google Scholar

Amano, T. (1983). The ν₁ fundamental band of HCO⁺ by difference frequency laser spectroscopy. J. Chem. Phys. 79, 3595. doi:10.1063/1.446216

CrossRef Full Text | Google Scholar

Bacmann, A., García-García, E., and Faure, A. (2016). Detection of protonated formaldehyde in the prestellar core L1689B. Astron. Astrophys. 588, L8. doi:10.1051/0004-6361/201628280

CrossRef Full Text | Google Scholar

Barone, V., Alessandrini, S., Biczysko, M., Cheeseman, J. R., Clary, D. C., McCoy, A. B., et al. (2021). Computational molecular spectroscopy. Nat. Rev. Methods Prim. 1, 38–27. doi:10.1038/s43586-021-00034-1

CrossRef Full Text | Google Scholar

Barone, V., Biczysko, M., Bloino, J., Cimino, P., Penocchio, E., and Puzzarini, C. (2015). Cc/dft route toward accurate structures and spectroscopic features for observed and elusive conformers of flexible molecules: Pyruvic acid as a case study. J. Chem. Theory Comput. 11, 4342–4363. doi:10.1021/acs.jctc.5b00580

PubMed Abstract | CrossRef Full Text | Google Scholar

Cabezas, C., Agúndez, M., Marcelino, N., Tercero, B., Endo, Y., Fuentetaja, R., et al. (2022). Discovery of the elusive thioketenylium, HCCS⁺, in TMC-1. Astron. Astrophys. 657, L4. doi:10.1051/0004-6361/202142815

CrossRef Full Text | Google Scholar

Cacace, F., de Petris, G., Pepi, F., Rosi, M., and Sgamellotti, A. (1998). Elemental chlorine and chlorine fluoride: Theoretical and experimental proton affinity and the gas phase chemistry of Cl₂H⁺ and FClH⁺ ions. J. Phys. Chem. A 102, 10560–10567. doi:10.1021/jp9831379

CrossRef Full Text | Google Scholar

Cazzoli, G., Cludi, L., Buffa, G., and Puzzarini, C. (2012). Precise thz measurements of HCO⁺, N₂H⁺, and CF⁺ for astrophysical observations. Astrophys. J. Suppl. Ser. 203, 11. doi:10.1088/0067-0049/203/1/11

CrossRef Full Text | Google Scholar

Cazzoli, G., Puzzarini, C., Gambi, A., and Gauss, J. (2006). Rotational spectra of 1-chloro-2-fluoroethylene. i. main isotopologues and deuterated species of the trans isomer. J. Chem. Phys. 125, 054313. doi:10.1063/1.2217372

PubMed Abstract | CrossRef Full Text | Google Scholar

Cernicharo, J., Agúndez, M., Kaiser, R. I., Cabezas, C., Tercero, B., Marcelino, N., et al. (2021). Discovery of two isomers of ethynyl cyclopentadiene in TMC-1: Abundances of CCH and CN derivatives of hydrocarbon cycles. Astron. and Astrophys 655, L1. doi:10.1051/0004-6361/202142226

CrossRef Full Text | Google Scholar

Cooke, I. R., Gupta, D., Messinger, J. P., and Sims, I. R. (2020). Benzonitrile as a proxy for benzene in the cold ism: Low-temperature rate coefficients for CN + C₆H₆. Astrophys. J. Lett. 891, L41. doi:10.3847/2041-8213/ab7a9c

CrossRef Full Text | Google Scholar

Dunning, T. H., (1989). Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 90, 1007–1023. doi:10.1063/1.456153

CrossRef Full Text | Google Scholar

Dunning, T. H., Peterson, K. A., and Wilson, A. K. (2001). Gaussian basis sets for use in correlated molecular calculations. x. the atoms aluminum through argon revisited. J. Chem. Phys. 114, 9244–9253. doi:10.1063/1.1367373

CrossRef Full Text | Google Scholar

Feller, D. (1993). The use of systematic sequences of wave functions for estimating the complete basis set, full configuration interaction limit in water. J. Phys. Chem. 98, 7059–7071. doi:10.1063/1.464749

CrossRef Full Text | Google Scholar

Foster, S., and McKellar, A. (1984). The ν₃ fundamental bands of, and DCO+. J. Chem. Phys. 81, 3424–3428. doi:10.1063/1.448066

CrossRef Full Text | Google Scholar

Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2016). Gaussian16 revision C.01. Wallingford CT: Gaussian Inc.

Google Scholar

Fukui, K. (1981). The path of chemical reactions - the IRC approach. Acc. Chem. Res. 14, 363–368. doi:10.1021/ar00072a001

CrossRef Full Text | Google Scholar

Gottlieb, C., Apponi, A., McCarthy, M., Thaddeus, P., and Linnartz, H. (2000). The rotational spectra of the HCCCNH⁺, NCCNH⁺, and CH₃CNH⁺ ions. J. Chem. Phys. 113, 1910–1915. doi:10.1063/1.481994

CrossRef Full Text | Google Scholar

Grimme, S., Antony, J., Ehrlich, S., and Krieg, H. (2010). A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132, 154104. doi:10.1063/1.3382344

PubMed Abstract | CrossRef Full Text | Google Scholar

Grimme, S., Ehrlich, S., and Goerigk, L. (2011). Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 32, 1456–1465. doi:10.1002/jcc.21759

PubMed Abstract | CrossRef Full Text | Google Scholar

Heckert, M., Kállay, M., and Gauss, J. (2005). Molecular equilibrium geometries based on coupled-cluster calculations including quadruple excitations. Mol. Phys. 103, 2109–2115. doi:10.1080/00268970500083416

CrossRef Full Text | Google Scholar

Heckert, M., Kállay, M., Tew, D. P., Klopper, W., and Gauss, J. (2006). Basis-set extrapolation techniques for the accurate calculation of molecular equilibrium geometries using coupled-cluster theory. J. Chem. Phys. 125, 044108. doi:10.1063/1.2217732

CrossRef Full Text | Google Scholar

Helgaker, T., Klopper, W., Koch, H., and Noga, J. (1997). Basis-set convergence of correlated calculations on Water. J. Chem. Phys. 106, 9639–9646. doi:10.1063/1.473863

CrossRef Full Text | Google Scholar

Hunter, E. P., and Lias, S. G. (1998). Evaluated gas phase basicities and proton affinities of molecules: An update. J. Phys. Chem. Ref. Data 27, 413–656. doi:10.1063/1.556018

CrossRef Full Text | Google Scholar

Kállay, M., and Gauss, J. (2008). Approximate treatment of higher excitations in coupled-cluster theory. II. Extension to general single-determinant reference functions and improved approaches for the canonical Hartree–Fock case. J. Chem. Phys. 129, 144101. doi:10.1063/1.2988052

PubMed Abstract | CrossRef Full Text | Google Scholar

Kawaguchi, K., Yamada, C., Saito, S., and Hirota, E. (1985). Magnetic field modulated infrared laser spectroscopy of molecular ions: The ν₂ band of HCO⁺. J. Chem. Phys. 82, 1750–1755. doi:10.1063/1.448407

CrossRef Full Text | Google Scholar

Klippenstein, S. J., Georgievskii, Y., and McCall, B. J. (2010). Temperature dependence of two key interstellar reactions of H₃⁺: O(³P) + H₃⁺ and CO + H₃ + H₃⁺. J. Phys. Chem. A 114, 278–290. doi:10.1021/jp908500h

PubMed Abstract | CrossRef Full Text | Google Scholar

Kucharski, S. A., and Bartlett, R. J. (1991). Recursive intermediate factorization and complete computational linearization of the coupled-cluster single, double, triple, and quadruple excitation equations. Theor. Chim. Acta 80, 387–405. doi:10.1007/bf01117419

CrossRef Full Text | Google Scholar

Lee, K. L. K., McGuire, B. A., and McCarthy, M. C. (2019). Gas-phase synthetic pathways to benzene and benzonitrile: A combined microwave and thermochemical investigation. Phys. Chem. Chem. Phys. 21, 2946–2956. doi:10.1039/c8cp06070c

PubMed Abstract | CrossRef Full Text | Google Scholar

Marchione, D., Mancini, L., Liang, P., Vanuzzo, G., Pirani, F., Skouteris, D., et al. (2022). Unsaturated dinitriles formation routes in extraterrestrial environments: A combined experimental and theoretical investigation of the reaction between cyano radicals and cyanoethene (C₂H₃CN). J. Phys. Chem. A 126, 3569–3582. doi:10.1021/acs.jpca.2c01802

PubMed Abstract | CrossRef Full Text | Google Scholar

Marino, T., Russo, N., Sicilia, E., Toscano, M., and Mineva, T. (2000). “Density functional computations and mass spectrometric measurements. can this coupling enlarge the knowledge of gas-phase chemistry?,” in Advances in quantum chemistry (Netherlands: Elsevier), 36, 93–120.

CrossRef Full Text | Google Scholar

Matthews, D. A., Cheng, L., Harding, M. E., Lipparini, F., Stopkowicz, S., Jagau, T.-C., et al. (2020). Coupled-cluster techniques for computational chemistry: The CFOUR program package. J. Chem. Phys. 152, 214108. doi:10.1063/5.0004837

PubMed Abstract | CrossRef Full Text | Google Scholar

McCarthy, M. C., Lee, K. L. K., Loomis, R. A., Burkhardt, A. M., Shingledecker, C. N., Charnley, S. B., et al. (2021). Interstellar detection of the highly polar five-membered ring cyanocyclopentadiene. Nat. Astron. 5, 176–180. doi:10.1038/s41550-020-01213-y

CrossRef Full Text | Google Scholar

McGuire, B. A. (2022). 2021 census of interstellar, circumstellar, extragalactic, protoplanetary disk, and exoplanetary molecules. Astrophys. J. Suppl. Ser. 259, 30. doi:10.3847/1538-4365/ac2a48

CrossRef Full Text | Google Scholar

McGuire, B. A., Burkhardt, A. M., Kalenskii, S., Shingledecker, C. N., Remijan, A. J., Herbst, E., et al. (2018). Detection of the aromatic molecule benzonitrile (c-C₆H₅CN) in the interstellar medium. Science 359, 202–205. doi:10.1126/science.aao4890

PubMed Abstract | CrossRef Full Text | Google Scholar

McGuire, B. A., Loomis, R. A., Burkhardt, A. M., Lee, K. L. K., Shingledecker, C. N., Charnley, S. B., et al. (2021). Detection of two interstellar polycyclic aromatic hydrocarbons via spectral matched filtering. Science 371, 1265–1269. doi:10.1126/science.abb7535

PubMed Abstract | CrossRef Full Text | Google Scholar

McNaught, A. D., and Wilkinson, A. (1997). “IUPAC compendium of chemical terminology,”in Gold Book. 2nd edn. Oxford: Blackwell Science. doi:10.1351/goldbook

CrossRef Full Text | Google Scholar

Melosso, M., Bizzocchi, L., Dore, L., Kisiel, Z., Jiang, N., Spezzano, S., et al. (2021). Improved centrifugal and hyperfine analysis of ND₂H and NH₂D and its application to the spectral line survey of L1544. J. Mol. Spectrosc. 377, 111431. doi:10.1016/j.jms.2021.111431

CrossRef Full Text | Google Scholar

Melosso, M., Bizzocchi, L., Gazzeh, H., Tonolo, F., Guillemin, J.-C., Alessandrini, S., et al. (2022). Gas-phase identification of (Z)-1,2-ethenediol, a key prebiotic intermediate in the formose reaction. Chem. Comm. 58, 2750–2753. doi:10.1039/d1cc06919e

PubMed Abstract | CrossRef Full Text | Google Scholar

Mills, I. M. (1972). Molecular spectroscopy: Modern research. Editors K. N. Rao, and C. W. Mathews (New York: Academic Press), Chapt. 3.2, 115–140.

CrossRef Full Text

Møller, C., and Plesset, M. S. (1934). Note on an approximation treatment for many-electron systems. Phys. Rev. 46, 618–622. doi:10.1103/physrev.46.618

CrossRef Full Text | Google Scholar

Nakanaga, T., Ito, F., Sugawara, K., Takeo, H., and Matsumura, C. (1990). Observation of infrared absorption spectra of molecular ions, H3+ and HN2+, by FTIR spectroscopy and, by FTIR spectroscopy. Chem. Phys. Lett. 169, 269–273. doi:10.1016/0009-2614(90)85199-m

CrossRef Full Text | Google Scholar

Noga, J., and Bartlett, R. J. (1987). The full CCSDT model for molecular electronic structure. J. Chem. Phys. 86, 7041–7050. doi:10.1063/1.452353

CrossRef Full Text | Google Scholar

Ohishi, M., Ishikawa, S.-i., Amano, T., Oka, H., Irvine, W. M., Dickens, J. E., et al. (1996). Detection of a new interstellar molecular ion, H₂COH⁺ (protonated formaldehyde). Astrophys. J. 471, L61–L64. doi:10.1086/310325

PubMed Abstract | CrossRef Full Text | Google Scholar

Owrutsky, J., Gudeman, C., Martner, C., Tack, L., Rosenbaum, N., and Saykally, R. (1986). Determination of the equilibrium structure of protonated nitrogen by high resolution infrared laser spectroscopy. J. Chem. Phys. 84, 605–617. doi:10.1063/1.450607

CrossRef Full Text | Google Scholar

Papajak, E., and Truhlar, D. G. (2011). Convergent partially augmented basis sets for post-Hartree-Fock calculations of molecular properties and reaction barrier heights. J. Chem. Theory Comput. 7, 10–18. doi:10.1021/ct1005533

PubMed Abstract | CrossRef Full Text | Google Scholar

Papousek, D., and Aliev, M. R. (1982). Molecular vibrational-rotational spectra. Amsterdam: Elsevier Scientific Publishing Company.

Google Scholar

Peterson, K. A., and Dunning, T. H., (2002). Accurate correlation consistent basis sets for molecular core-valence correlation effects: The second row atoms Al-Ar, and the first row atoms B-Ne revisited. J. Chem. Phys. 117, 10548–10560. doi:10.1063/1.1520138

CrossRef Full Text | Google Scholar

Piccardo, M., Bloino, J., and Barone, V. (2015). Generalized vibrational perturbation theory for rotovibrational energies of linear, symmetric and asymmetric tops: Theory, approximations, and automated approaches to deal with medium-to-large molecular systems. Int. J. Quantum Chem. 115, 948–982. doi:10.1002/qua.24931

PubMed Abstract | CrossRef Full Text | Google Scholar

Puzzarini, C. (2016). Accurate molecular structures of small-and medium-sized molecules. Int. J. Quantum Chem. 116, 1513–1519. doi:10.1002/qua.25202

CrossRef Full Text | Google Scholar

Puzzarini, C., Bloino, J., Tasinato, N., and Barone, V. (2019). Accuracy and interpretability: The devil and the holy grail. new routes across old boundaries in computational spectroscopy. Chem. Rev. 119, 8131–8191. doi:10.1021/acs.chemrev.9b00007

PubMed Abstract | CrossRef Full Text | Google Scholar

Puzzarini, C., Heckert, J., and Gauss, J. (2008). The accuracy of rotational constants predicted by high-level quantum-chemical calculations. I. Molecules containing first-row atoms. J. Chem. Phys. 128, 194108. doi:10.1063/1.2912941

PubMed Abstract | CrossRef Full Text | Google Scholar

Puzzarini, C., Stanton, J. F., and Gauss, J. (2010). Quantum-chemical calculation of spectroscopic parameters for rotational spectroscopy. Int. Rev. Phys. Chem. 29, 273–367. doi:10.1080/01442351003643401

CrossRef Full Text | Google Scholar

Raghavachari, K., Trucks, G. W., Pople, J. A., and Head-Gordon, M. (1989). A fifth-order perturbation comparison of electron correlation theories. Chem. Phys. Lett. 157, 479–483. doi:10.1016/s0009-2614(89)87395-6

CrossRef Full Text | Google Scholar

Santra, G., Sylvetsky, N., and Martin, J. M. L. (2019). Minimally empirical double-hybrid functionals trained against the GMTKN55 database: revDSD-PBEP86-D4, revDOD-PBE-D4, and DOD-SCAN-D4. J. Phys. Chem. A 123, 5129–5143. doi:10.1021/acs.jpca.9b03157

PubMed Abstract | CrossRef Full Text | Google Scholar

Schiff, L. I. (1955). Quantum mechanics. New York City: McGraw-Hill.

Google Scholar

Scuseria, G. E., and Schaefer, H. F. (1988). A new implementation of the full CCSDT model for molecular electronic structure. Chem. Phys. Lett. 152, 382–386. doi:10.1016/0009-2614(88)80110-6

CrossRef Full Text | Google Scholar

Stanton, J. F., Gauss, J., Cheng, L., Harding, M. E., Matthews, D. A., and Szalay, P. G. (2016). CFOUR, Coupled-Cluster techniques for Computational Chemistry, a quantum-chemical program package with contributions from A. Available at: http://www.cfour.de.

Google Scholar

Turner, B. (1974). U93.174-a new interstellar line with quadrupole hyperfine splitting. Astrophys. J. 193, L83–L87. doi:10.1086/181638

CrossRef Full Text | Google Scholar

Wootten, A., Mangum, J. G., Turner, B. E., Bogey, M., Boulanger, F., Combes, F., et al. (1991). Detection of interstellar H₃O⁺: A confirming line. Astrophys. J. Lett. 380, L79. doi:10.1086/186178

CrossRef Full Text | Google Scholar

Yamamoto, S. (2017). Introduction to astrochemistry. Editorial: Springer.

Google Scholar

Yen, H.-W., Koch, P. M., Liu, H. B., Puspitaningrum, E., Hirano, N., Lee, C.-F., et al. (2016). Stacking spectra in protoplanetary disks: Detecting intensity profiles from hidden molecular lines in HD 163296. Astrophys. J. 832, 204. doi:10.3847/0004-637x/832/2/204

CrossRef Full Text | Google Scholar

Zhu, Y., Tian, L., Song, H., and Yang, M. (2019). Kinetic and dynamic studies of the H₃⁺+ CO → H₂+ HCO⁺/HOC⁺reaction on a high-levelab initiopotential energy surface + CO → H₂ + HCO⁺/HOC⁺ reaction on a high-level ab initio potential energy surface. J. Chem. Phys. 151, 054311. doi:10.1063/1.5110934

CrossRef Full Text | Google Scholar