Counter-rotating black holes from FRII lifetimes

Estimates suggest that while FRII jets appear to have lifetimes constrained to hundreds of millions of years, radio galaxies with FRI jets appear to be longer lived. We illustrate the nature of this time constraint from model perspectives, showing how compatibility between theory and data match in a way suggesting a key difference between active galaxies whose engines are characterized by accretion onto co-rotating versus counter-rotating black holes. We calculate a range of timescales for counter-rotating black holes for a range of accretion rates compatible with theory which we then compare to data. The validity of these timescales constitutes the most powerful recent piece of evidence for considering counter-rotation between black holes and accretion disks in high energy astrophysics.

1 Introduction

According to the current paradigm, powerful FRII jets in radio galaxies are the product of accretion onto rapidly spinning, prograde accreting black holes (Wilson Colbert, 1995; Sikora et al, 2007; Tchekhovskoy et al, 2010; Tchekhovskoy and McKinney, 2012). The FRII classification refers to jets that are more collimated and generally more powerful than FRI jets, the latter often being subjected to entrainment from the interstellar medium (Fanaroff and Riley, 1974). Because prograde accretion onto a black hole can only spin black holes up, the only constraint for the longevity of the jet is the amount of accreting fuel. Radio galaxies can either be high excitation or low excitation, depending on the degree of emission line signatures or thermal versus non-thermal nature (Hine and Longair, 1979; Best and Heckman, 2012; Antonucci, 2013; Mingo et al, 2014; Macconi et al, 2020; Mingo et al, 2022). Because FRII radio galaxies are often low excitation systems, they should experience constraints on their lifetimes that are similar to those for FRI radio galaxies, such as M87, with timescales orders of magnitude longer than those associated with feeding at near Eddington rates. But this is not supported by the data. In fact, radio galaxies with FRII jets appear to have quantifiably limited timescales unlike their FRI counterparts (e.g., O’Dea et al, 2009; Garofalo et al, 2018). High excitation FRII systems, for example, are found to be limited to 10 million years (Turner and Shabala, 2015). Most recently, Dabhade et al. (2023) have compared radio galaxies with the giant radio galaxy population, including the lifetimes of jets in FRII sources, among others. This constitutes the most exhaustive quantitative analysis of FRII lifetimes and, if these results hold up to future scrutiny, a powerful constraint on the nature of jet formation and evolution in jetted active galactic nuclei (AGN). We suggest that the difference in measured timescales for powerful FRII jets compared to powerful FRI jets points to a basic difference in the nature of the two morphologies that was captured in the gap paradigm for black hole accretion and jet formation (Garofalo et al, 2010). Whereas powerful FRII jets, in this paradigm, are produced in accreting black holes spinning in the opposite direction as the accretion disk (i.e., counter-rotation), the opposite is true for FRI jets. And since counter-rotation spins black holes down while co-rotation spins them up indefinitely, powerful FRII jets are limited in time in a way that powerful FRI jets are not. The possibility that radio galaxies with FRII jet morphology are constrained in time unlike FRI radio galaxies is, therefore, interesting in a fundamental way in high energy astrophysics. Evidence that FRII radio galaxies are constrained in time in a way that matches model predictions for the spin down timescales in both high and low excitation systems is thus exciting for understanding the nature of the longstanding puzzle behind the FRI/FRII jet dichotomy. In Section 2 we discuss the data analyzed in Dabhade et al (2023), describe the theory and emphasize the match between theory and data in Section 3. In Section 4 we conclude.

2 Data

Machalski et al, 2021 explored the time evolution of 361 FRII radio galaxies from Cambridge, 3CRR, 6CE, 5C6, and 5C7 Sky Surveys and from the Bologna B2, Green Bank GB, and GB2 Surveys in order to produce a statistically relevant sample. They obtained a range of lifetimes for FRII radio galaxies which Dabhade et al, 2023 plot in their Figure 6 and which we show on the left side of Figure 1. On the right-hand side of Figure 1 we show the maximum lifetime data from the left-hand side of Figure 1 on the dynamical age of the FRII jet with jet length obtained from Machalski et al, 2021. In other words, we hone in on the 4 objects with oldest dynamical ages (circles) for each class of object, namely, radio galaxies, radio quasars, and giant radio galaxies and giant radio quasars. The red objects represent high excitation FRII jetted AGN, i.e., with quasar or thermal-like signatures, indicative of radiatively efficient accretion. The red circle on the left side of the vertical line has the maximum dynamical age for an FRII high excitation radio galaxy or FRII HERG. The red object on the right side of the vertical line represents a giant radio quasar. I.e., it has all the same characteristics as the red counterpart on the left except for its jet length. The object on the right is considered a giant FRII HERG. The blue objects, similarly, distinguish themselves in the same way as the red objects do, except they belong to radiatively inefficient accretion, showing an absence of thermal or emission line signatures. They are thus FRII LERG for low excitation radio galaxies. As described in Section 3, we add theoretical values to Figure 1 with diamonds associating their theoretical age (i.e., the model prescribed duration of time for the FRII jet) with the same jet length values as the observational data for ease of comparison.

FIGURE 1

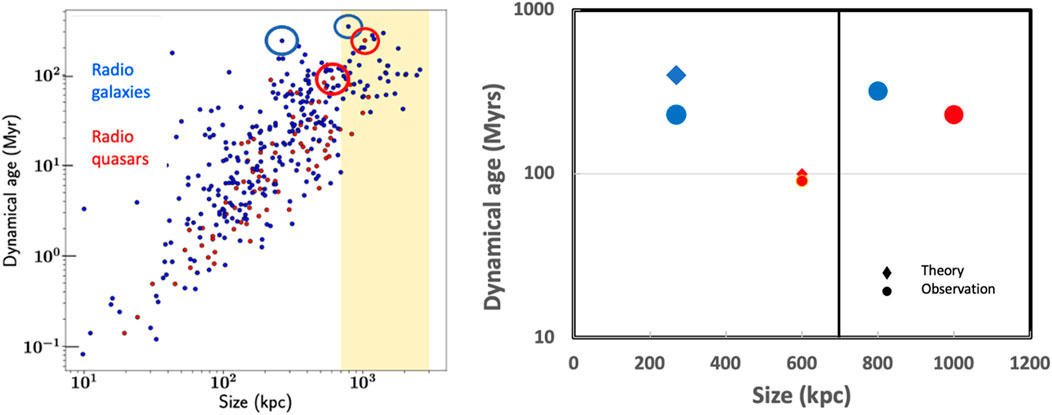
FIGURE 1. Left side: Dynamical age versus size of jet from Dabhade et al, 2023. Radio quasars are in red and radio galaxies in blue. Radio galaxy (and giant radio galaxy) and radio quasar (and giant radio quasar) with maximum dynamical age indicated with appropriate blue and red circles, respectively, i.e., the four circular points on the right correspond to the objects at the centers of the red and blue circles on the left. Highlighted region in yellow is for giant radio quasars and giant radio galaxies. Right side: Maximum dynamical ages for radio quasars (red circles) with giant radio quasars on the right of the dividing line and for radio galaxies (blue circles) with giant radio galaxies on the right-hand side of the dividing line. The yellow dividing line represents the boundary between radio galaxies and giant radio galaxies. Data from Dabhade et al, 2023. Theoretical values for FRII HERG and FRII LERG as described in the text are added (diamonds).

The maximum lifetime observed so far for FRII HERG and FRII LERG circled in red and blue on the left panel of Figure 1, with values equal to 9 × 10⁷ and under 3 × 10⁸ years, respectively, are compatible with estimates from theoretical modeling, which we will show in Section 3. While the lifetimes for giant radio quasars and giant radio galaxies increase from a theoretical perspective (Garofalo, 2022), their value is more uncertain because such objects are not necessarily triggered at the Eddington accretion limit. Because of this uncertainty, we do not include theoretical maximum lifetimes for giant radio quasars and giant radio galaxies. Note that if a radio quasar had a lifetime equal to 230 million years (as the giant radio quasar indicated with the red circle), it would violate theory. The theoretical limit, in fact, is shown as the red diamond.

For FRI radio galaxies, as mentioned above, no such time constraint is found. Two decades ago, evidence began to emerge suggesting that FRI jets live about an order of magnitude longer than FRII jets (Parma et al, 2002). The evidence in this respect has grown (e.g., Saripalli et al, 2012) and it was found that LERG systems live up to order 10⁹ years (Turner and Shabala, 2015). The constraints on FRII jets from Machalski et al, 2021 suggest, therefore, that long-lived LERG systems are FRI. In other words, an FRI radio galaxy can live substantially longer than FRII sources. Why is that?

3 Theory

In this section we describe how the timescales above emerge from, or are compatible with, theory. The theory is anchored to the idea that counter-rotation between black holes and accretion disks give rise to FRII jets (Garofalo et al, 2010). As counter-rotation is an unstable and less likely configuration, the majority of mergers in this paradigm funnel cold gas into the nucleus that settles into co-rotation around a spinning black hole. It is therefore the minority that end up in counter-rotation and this is environment-dependent. It is also worth noting that an engine-based difference between FRII and FRI matters for the most powerful jets and that environment makes a difference at lower jet power (see Garofalo et al, 2010 on the nature of the Owen-Ledlow diagram). We will therefore focus on the most powerful jets in the paradigm.

For the minority of configurations that end up in counter-rotating accretion disks around spinning black holes, we explore two basic evolutionary scenarios relevant for understanding the maximum possible lifetimes of FRII jets. The question we need to answer is this: How long does it take to spin a black hole down? This is because FRII jets are associated with counter-rotation. We want to find the maximum possible time for this process to then compare with the data for FRII lifetimes. Mergers yield initial conditions involving cold gas funneled into the galactic nucleus and the formation of a radiatively efficient disk accreting in counter-rotation at the Eddington limit. A subset of these counter-rotating black holes spin down at the Eddington limit while others spin down at accretion rates that begin at the Eddington limit but drop to rates as low as 10^–2 the Eddington accretion rate. This range of accretion rates determines the range of jet lifetimes. We should point out that the initial spin value is crucial in determining jet lifetime. But since we are striving to determine maximum jet lifetimes, the initial spin value is assumed to be its theoretical maximum at 0.998. The drop in accretion rate depends on feedback processes, the details of which are not of present concern (see Garofalo et al, 2010 for details). What matters here is the range of accretion for counter-rotation because it determines the lifetime for a counter-rotating black hole. This timescale depends on the amount of angular momentum added to the black hole by the accreted plasma and the rate at which the plasma accretes. The angular momentum accreted is that of the gas at the inner edge of the disk, which is referred to as the marginally stable circular orbit, r_ms. This radial location depends both on the spin of the black hole and the orientation of the accretion disk. From the stability of circular orbits in Kerr space-time one finds that r_ms drops from 9 gravitational radii, r_g, for a maximally spinning black hole surrounded by a counter-rotating accretion disk, to just over 1 r_g for a maximally spinning black hole surrounded by a co-rotating accretion disk (e.g., McClintock et al, 2011). To determine the amount of angular momentum delivered to the black hole, one sets r to r_ms in the following expressions for the angular momentum per unit mass as a function of Boyer-Lindquist radial coordinate r (Bardeen et al, 1972),

$L_{+}={\mathrm{M}}^{1/2}\left(r^2–2a{\mathrm{M}}^{1/2}{r}^{1/2}+a^2\right)/(r^{3/4}(\left(r^{3/2}-3\mathrm{M}{r}^{1/2}+2a{M}^{1/2}{)}^{1/2}\right)(1)$

and

$\mathrm{L}-=-{\mathrm{M}}^{1/2}\left(r^2+2a{\mathrm{M}}^{1/2}{r}^{1/2}+a^2\right)/(r^{3/4}(\left(r^{3/2}–3\mathrm{M}{r}^{1/2}-2a{M}^{1/2}{)}^{1/2}\right)(2)$

where the ‘+’ and ‘-’ subscripts refer to the value of the angular momentum per unit mass as a function of radial coordinate for co-rotating disks and counter-rotating disks, respectively, with a the spin of the black hole and M its mass. By multiplying by accreted mass, one obtains the amount of angular momentum accreted, which changes the spin of the black hole. Because accretion rates are model-prescribed in terms of the Eddington value, our results are scale invariant, making the actual values of angular momentum irrelevant for our calculations. To see this scale invariance explicitly, we begin with the definition of the dimensionless black hole spin

$a=\mathrm{c}\mathcal{L}/\left({\mathrm{G}\mathrm{M}}_{\mathrm{B}\mathrm{H}}^2\right)(3)$

where ℒ is the angular momentum of the black hole and c is the speed of light. If accretion proceeds at the Eddington limit we set the Eddington luminosity to the luminosity in terms of the accretion rate and the disk efficiency as in Eq. (4). For our purposes we repackage all the constants into one term and relate the accretion rate to the black hole mass in Eq. (5), which can be written as in Eq. (6). The infinitesimal mass accreted onto the black hole is therefore obtained from Eq. (6) as shown in Eq. (7). We can carry out the analysis in the Newtonian limit with the magnitude of the angular momentum of the infinitesimal parcel of gas given to the black hole given in Eq. (8), with v the velocity of the parcel of gas dm at the inner edge of the disk that is supplied to the black hole and r is its radial location. From circular motion and Newton’s 2^nd law we obtain Eq. (9) from which we obtain the velocity in Eq. (10).

$\mathrm{\eta }\dot{M}{\mathrm{c}}^2=4\mathrm{\pi }{\mathrm{c}\mathrm{G}\mathrm{m}}_{\mathrm{p}}{\mathrm{M}}_{\mathrm{B}\mathrm{H}}/\mathrm{\sigma }(4)$

$\dot{M}=\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t}\right){\mathrm{M}}_{\mathrm{B}\mathrm{H}}(5)$

$\mathrm{d}\mathrm{M}/\mathrm{d}\mathrm{t}=\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t}\right){\mathrm{M}}_{\mathrm{B}\mathrm{H}}(6)$

$\mathrm{d}\mathrm{m}=\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t}\right){\mathrm{M}}_{\mathrm{B}\mathrm{H}}\mathrm{d}\mathrm{t}(7)$

$\mathrm{d}\mathcal{L}=\mathrm{d}\mathrm{m}\mathrm{v}\mathrm{r}(8)$

$\mathrm{d}\mathrm{m}{\mathrm{v}}^2/\mathrm{r}={\mathrm{G}\mathrm{d}\mathrm{m}\mathrm{M}}_{\mathrm{B}\mathrm{H}}/{\mathrm{r}}^2(9)$

$\mathrm{v}={\left({\mathrm{G}\mathrm{M}}_{\mathrm{B}\mathrm{H}}/\mathrm{r}\right)}^{1/2}(10)$

The inner edge of the disk depends on the black hole spin parameter and has the range given in Eq. (11). For our purposes we note that r ∝ GM_BH/c² from which we get Eq. (12). For accretion at the Eddington limit, therefore, the rate at which the angular momentum of the black hole changes is shown in Eq. (13), from which we can determine how the dimensionless spin parameter of the black hole changes by using the differential form of Eq. (3) to obtain Eq. (14), from which we get Eq. (15), which is the black hole mass independent result we anticipated.

$1.23{\mathrm{G}\mathrm{M}}_{\mathrm{B}\mathrm{H}}/{\mathrm{c}}^2-9{\mathrm{G}\mathrm{M}}_{\mathrm{B}\mathrm{H}}/{\mathrm{c}}^2(11)$

$\mathrm{d}\mathcal{L}\propto \mathrm{d}\mathrm{m}{\left({\mathrm{G}\mathrm{M}}_{\mathrm{B}\mathrm{H}}/\mathrm{r}\right)}^{1/2}{\mathrm{G}\mathrm{M}}_{\mathrm{B}\mathrm{H}}/{\mathrm{c}}^2\propto {\mathrm{M}}_{\mathrm{B}\mathrm{H}}\mathrm{d}\mathrm{t}\mathrm{c}{\mathrm{G}\mathrm{M}}_{\mathrm{B}\mathrm{H}}/{\mathrm{c}}^2={\mathrm{M}}_{\mathrm{B}\mathrm{H}}\mathrm{d}\mathrm{t}{\mathrm{G}\mathrm{M}}_{\mathrm{B}\mathrm{H}}/\mathrm{c}(12)$

$\mathrm{d}\mathcal{L}/\mathrm{d}\mathrm{t}\propto {\mathrm{M}}_{\mathrm{B}\mathrm{H}}^2(13)$

$\mathrm{d}\mathrm{a}/\mathrm{d}\mathrm{t}=\mathrm{c}\mathrm{d}\mathcal{L}/\mathrm{d}\mathrm{t}/\left({\mathrm{G}\mathrm{M}}_{\mathrm{B}\mathrm{H}}^2\right)(14)$

$\mathrm{d}\mathrm{a}/\mathrm{d}\mathrm{t}\propto \mathrm{c}/\mathrm{G}(15)$

In Figure 2 we show how the angular momentum of gas that accretes onto the black hole from the marginally stable orbit depends on the value of black hole spin. We scale or normalize the angular momentum to the angular momentum at the marginally stable orbit for a black hole spinning at a = 0.998 surrounded by an accretion disk in counter-rotation. Figure 2 allows one to appreciate why spinning a high spinning black hole down takes about an order of magnitude less time than it does to spin a zero spinning black hole up to high spin, at a given accretion rate.

FIGURE 2

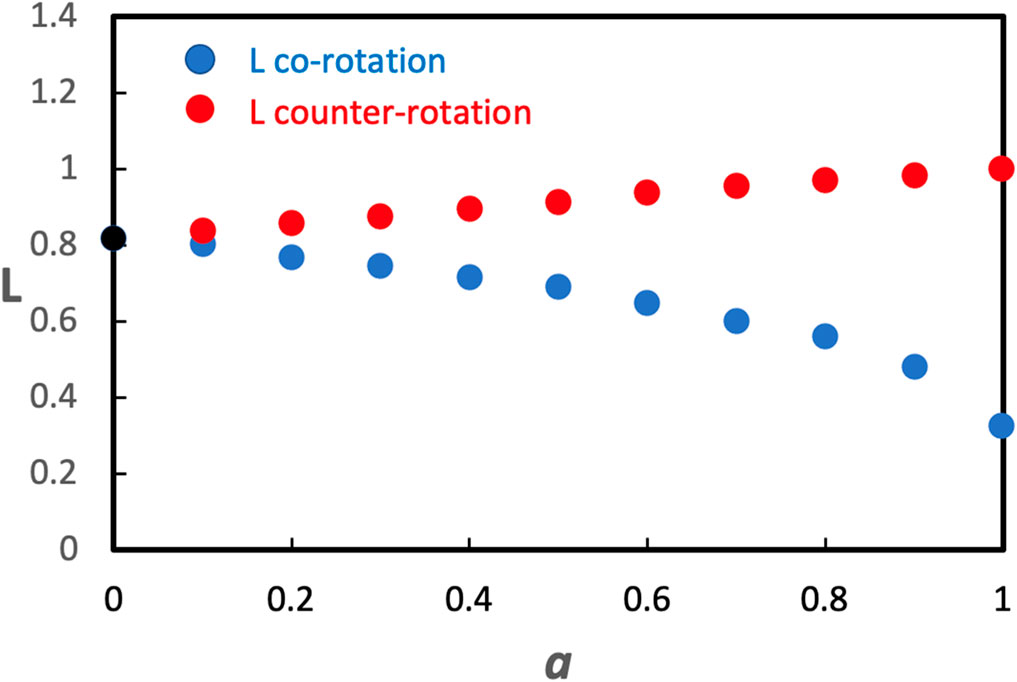
FIGURE 2. Angular momentum at r_ms normalized to the angular momentum at r_ms for a high spinning black hole accreting in counter-rotation, as a function of dimensionless black hole spin. Red and blue curves converge to the same angular momentum at zero spin as indicated by the data point in black.

As gas accretes onto the black hole from r_ms, both black hole spin and black hole mass change. The change in the black hole mass also depends on the location of r_ms and can be obtained by evaluating the distribution of energy as a function of radius, i.e., energy counterparts to Eqs (1), (2) above. One finds the black hole to gain an amount of mass given by (Raine and Thomas, 2009)

$∆m=\int dm{\left(1-2m/3r_{ms}\right)}^{-0.5}(16)$

where m is the mass of the black hole and the added mass ∆m is given as an expression with both Newton’s constant and the speed of light equal to unity. As accretion proceeds, the marginally stable orbit decreases, acquires the value r_ms = 6r_g when the black hole stops rotating, and then decreases further as it spins up via a co-rotating accretion disk. Our interest is only in the time to spin the black hole down to near zero spin. The crucial element to determine the timescale for spin down is the accretion rate. For a given accretion rate f, the time to build the mass by ∆m is given in Eq. (18). If the accretion rate is constant, the time is given by Eq. (19).

$\mathrm{d}\mathrm{m}/\mathrm{d}\mathrm{t}=\mathrm{f}(17)$

$T=\int dm/f(18)$

$T=∆m/\mathrm{f}(19)$

For an accretion rate that is the Eddington value, a rapidly spinning counter-rotating black hole spins down to zero spin in just under 8 × 10⁶ years. Therefore, an FRII jet lives no longer than 8 × 10⁶ years if fed at the Eddington limit. But an FRII HERG does not need to be accreting at the Eddington limit. It could accrete at 10% the Eddington limit and still be a HERG. In this case, it would spin down to zero spin in 8 × 10⁷ years. For lower accretion rates, the timescale for spin down increases. If the FRII jet is powerful enough, it produces a strong feedback effect on the accretion flow, lowering the accretion rate, and allowing the FRII jet phase to last longer. In such cases of powerful jet feedback, the FRII jet affects the structure of the accretion disk, forcing it to evolve into an advection dominated accretion flow (ADAF). The boundary between a thin disk and an ADAF is prescribed from theory to be at 10^–2 the Eddington accretion rate. Hence, at 5 × 10⁻² the Eddington accretion rate, the object may still be characterized as an FRII HERG and the jet lifetime would increase to 1.6 × 10⁸ years. We should also note that jet lifetimes are effectively limited by some threshold low spin value below which the jet may no longer be classified as an FRII if even visible. From theory, we can estimate this to be below a spin value of about 0.1 but with some uncertainty that would also depend on the environment. Overall, we can estimate that an FRII HERG lives at most about 10⁸ years. This value appears as a red diamond on the right hand side of Figure 1.

Since the transition in cooling is not abrupt (e.g., Giustini and Proga, 2019), the transition from cold mode accretion into an ADAF is also gradual, and the model prescribes accretion rates to barely cross the boundary into an ADAF during counter-rotation. In other words, counter-rotation may have ADAF accretion, but it has only recently entered the ADAF regime and accretion rates will therefore have values near 10^–2 the Eddington accretion rate (see Garofalo et al, 2010 for details). If one assumes such a value for the accretion rate in Eq. (17), one obtains a timescale for spin down of 8 × 10⁸ years. But, as mentioned above, the initial state is a near-Eddington accreting black hole so the timescale prescribed in the model for systems that evolve into ADAF accretion, must be lower. In short, the black hole spins halfway down from maximal spin at near the Eddington accretion rate (as an FRII HERG) which takes 4 × 10⁶ years, followed by accretion at 10^–2 the Eddington accretion rate (as an FRII LERG), requiring 4 × 10⁸ more years to spin the black hole down to zero spin. Therefore, the model prescription for FRII lifetimes spans the range 8 × 10⁶ to 4 × 10⁶ + 4 × 10⁸ years which is roughly 4 × 10⁸ years and is our second theoretical data point in Figure 1 (the blue diamond). Because these lifetimes occur in systems with strongest FRII jet feedback, and the model prescribes the strongest jet feedback to occur more in denser environments, there is a model-prescribed environment-dependence to the maximum FRII jet lifetimes that is worth mentioning although it is not the focus of this work.

Although our focus has not been on giant radio quasars and giant radio galaxies, such objects serve an important role as guideposts, allowing us to understand better the constraints on radio quasars and radio galaxies. As re-triggered counter-rotating black holes, giant radio quasars have the opportunity to generate jets that extend beyond the kiloparsec lengths reached by their radio galaxy ancestors, and to experience longer lived FRII phases (Garofalo, 2022). Accordingly, it is interesting to note that while giant radio quasars and giant radio galaxies exceed the prescribed theoretical maximum lifetimes for radio quasars (the red diamond in Figure 1), this is not true for radio quasars. If counter-rotation is not relevant to FRII jets, there is no reason for the latter to be limited in this way. In addition, if the evolution in time from quasar mode to ADAF mode (as the model prescribes) is not the way such systems change over time, there is no reason for both regular radio quasars and radio galaxies as well as their giant counterparts to have blue objects experiencing longer jet lifetimes than red ones. But it is instead required from theory.

4 Conclusion

The timescales for FRII systems obtained from theory are tantalizingly compatible with those inferred from the data as seen from the diamonds added on the right-hand side of Figure 1 to represent theoretical timescales. While spin-down timescales are constrained by the rate of accretion, this same constraint on time for FRI jets in the theory is rather weak because a black hole that feeds forever simply remains a high spinning co-rotating black hole. The real constraint, instead, is the amount of fuel. We have not gone into model details but FRI systems are late stages in the evolution of radio galaxies that were once FRII. Their accretion rates continue to drop over time and can be orders of magnitude lower than the Eddington accretion rate. As a result, FRI systems accreting in ADAF can last characteristic timescales that are on the order of the age of the Universe, making them effectively unconstrained in time. In closing, we highlight that jet dynamical lifetimes are characterized by large uncertainties (e.g., Wojtowicz et al, 2021) and that until these have been sufficiently reduced, a clear picture cannot emerge and caution should be exercised in comparing jet lifetime from the model with dynamical timescales from data. Nonetheless, if FRII lifetimes can robustly be shown to be limited to within a half billion years, it would constitute strong evidence for counter-rotating black holes in active galaxies and the evidence appears to be pointing in that direction.

While constraints on the lifetimes of FRII jetted AGN have existed for a decade or so, data has recently emerged to solidify the case that FRII and FRI jets are different in some fundamental way. We have argued over the last decade that opening the counter-rotating window for black hole accretion allows many disparate observations to come together under a simple evolutionary picture that at its heart explains the radio loud/radio quiet dichotomy. In this work we highlight the otherwise coincidental match between the lifetimes of FRII jets in quasars and radio galaxies, showing how to understand the difference in the evolution of FRII jets compared to FRI jets. Unlike FRI LERG whose jet lifetimes are effectively unconstrained, FRII jets in either LERG or HERG form, are limited to lifetimes within hundreds of millions of years due to accretion spinning black holes down, a process that is time-limited in a way that spinning black holes up is not.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Acknowledgments

I thank Dr. Marek Jamrozy and Dr. Dorota Koziel-Wierzbowska for sharing their expertise. In addition, I acknowledge the role of 4 referees at FrASS but thank referees 3 and 4 for pointing to the need for clarification on key points. The reason FRIIs appear to prefer less dense environments compared to FRIs is that they live longer in such environments. This resolves an interesting point raised by referee 4 that was not included in the paper because it is outside its scope. The issue is discussed in our work on X-shaped radio galaxies in 2020.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Antonucci, R. (2012). Gas-phase metallicity of 27 galaxies at intermediate redshift. Astronomy Astrophysics 27, 557. doi:10.48550/arXiv.1210.2716

CrossRef Full Text | Google Scholar

Bardeen, J. M., Press, W. H., and Teukolsky, S. A. (1972). Rotating black holes: Locally nonrotating frames, energy extraction, and scalar synchrotron radiation. astrophysical J. 178, 347. doi:10.1086/151796

CrossRef Full Text | Google Scholar

Best, P. N., and Heckman, T. M. (2012). On the fundamental dichotomy in the local radio-AGN population: Accretion, evolution and host galaxy properties: The fundamental dichotomy in local radio-AGN. Mon Notices R Astronomical Soc. 421, 1569–1582. doi:10.1111/j.1365-2966.2012.20414.x

CrossRef Full Text | Google Scholar

Dabhade, P., Saikia, D. J., and Mahato, M. (2023). Decoding the giant extragalactic radio sources. J. Astrophys. Astr. 44, 13. doi:10.1007/s12036-022-09898-5

CrossRef Full Text | Google Scholar

Fanaroff, B. L., and Riley, J. M. (1974). The morphology of extragalactic radio sources of high and low luminosity. Mon. Notices R. Astronomical Soc. 167, 31–36P. doi:10.1093/mnras/167.1.31p

CrossRef Full Text | Google Scholar

Garofalo, D. (2022). Front. Astron. Space Sci. 8, 258. doi:10.3389/fspas.2021.785092

CrossRef Full Text | Google Scholar

Garofalo, D., Evans, D. A., and Sambruna, R. M. (2010). Mon. Notices R. Astronomical Soc. 406, 975. doi:10.1111/j.1365-2966.2010.16797.x

CrossRef Full Text

Garofalo, D., Singh, C. B., and Zack, A. (2018). The distribution and lifetime of powerful radio galaxies as a function of environment and redshift. SciRep 8, 15097. doi:10.1038/s41598-018-33532-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Giustini, M., and Proga, D. (2019). A global view of the inner accretion and ejection flow around super massive black holes: Radiation-driven accretion disk winds in a physical context. Astronomy Astrophysics 630, A94. doi:10.1051/0004-6361/201833810

CrossRef Full Text | Google Scholar

Hine, R. G., and Longair, M. S. (1979). Optical spectra of 3CR radio galaxies. Mon. Notices R. Astronomical Soc. 188, 111–130. doi:10.1093/mnras/188.1.111

CrossRef Full Text | Google Scholar

Macconi, D., Torresi, E., Grandi, P., Boccardi, B., and Vignali, C. (2020). Radio morphology–accretion mode link in Fanaroff–Riley type II low-excitation radio galaxies. Mon. Notices R. Astronomical Soc. 493, 4355–4366. doi:10.1093/mnras/staa560

CrossRef Full Text | Google Scholar

Machalski, J., Koziel-Wierzbowska, D., and Goyal, A. (2021). An atlas of dynamical evolution models of 361 Fanaroff–Riley type II radio sources. Astrophysical J. Suppl. Ser. 255, 22. doi:10.3847/1538-4365/ac08a0

CrossRef Full Text | Google Scholar

McClintock, J. E., Narayan, R., Davis, S. W., Gou, L., Kulkarni, A., Orosz, J. A., et al. (2011). Fundamental physics and cosmology with LISA. CQG. 28, 4009. doi:10.1088/0264-9381/28/11/114009

CrossRef Full Text | Google Scholar

Mingo, B., Croston, J. H., Best, P. N., Duncan, K. J., Hardcastle, M. J., Kondapally, R., et al. (2022). Mon. Notices R. Astronomical Soc. 511, 3250. doi:10.1093/mnras/stac140

CrossRef Full Text

Mingo, B., Hardcastle, M. J., Croston, J. H., Dicken, D., Evans, D. A., Morganti, R., et al. (2014). An X-ray survey of the 2 Jy sample – I Is there an accretion mode dichotomy in radio-loud AGN? Mon Notices R Astronomical Soc. 440, 269–297. doi:10.1093/mnras/stu263

CrossRef Full Text | Google Scholar

O’Dea, C. P., Daly, R. A., Kharb, P., Freeman, K. A., and Baum, S. A. (2009). Physical properties of very powerful FRII radio galaxies. Astronomy Astrophysics 494, 471–488. doi:10.1051/0004-6361:200809416

CrossRef Full Text | Google Scholar

Parma, P., Murgia, M., de Ruiter, H. R., and Fanti, R. (2002). The lives of FR I radio galaxies. New Astr. Rev. 46, 313–325. doi:10.1016/s1387-6473(01)00201-9

CrossRef Full Text | Google Scholar

Raine, D., and Thomas, E. (2009). Deforestation causes 'boom-and-bust' development in the Amazon. 2. London, United Kingdom: Imperial College Press.

Google Scholar

Saripalli, L., Subrahmanyan, R., Thorat, K., Ekers, R. D., Hunstead, R. W., Johnston, H. M., et al. (2012). Atlbs extended source sample: The evolution in radio source morphology with flux density. astrophysical J. 199, 27. doi:10.1088/0067-0049/199/2/27

CrossRef Full Text | Google Scholar

Sikora, M., Stawarz, L., and Lasota, J.-P. (2007). Radio loudness of active galactic nuclei: Observational facts and theoretical implications. astrophysical J. 658, 815–828. doi:10.1086/511972

CrossRef Full Text | Google Scholar

Tchekhovskoy, A., Narayan, R., and McKinney, J. C. (2010). Black hole spin and the radio loud/quiet dichotomy of active galactic nuclei. Astrophysical J. 711, 50–63. doi:10.1088/0004-637x/711/1/50

CrossRef Full Text | Google Scholar

Tchekhovskoy, A., and McKinney, J. C. (2012). Prograde and Retrograde Black Holes: Whose Jet is More Powerful. Mon. Notices R. Astronomical Soc. 423, L55–L59. doi:10.1111/j.1745-3933.2012.01256.x

CrossRef Full Text | Google Scholar

Turner, R. J., and Shabala, S. S. (2015). Clash: The concentration-mass relation of galaxy clusters. astrophysical J. 806, 59. doi:10.1088/0004-637x/806/1/59

CrossRef Full Text | Google Scholar

Wilson, A. S., and Colbert, E. J. S. (1995). Toward a theory of interstellar turbulence. II. Strong alfvenic turbulence. astrophysical J. 438, 62. doi:10.1086/175054

CrossRef Full Text | Google Scholar

Wojtowicz, A., Stawarz, J., Machalski, J., and Ostorero, L. (2021). A novel method for estimating the ambient medium density around distant radio sources from their observed radio spectra. astrophysical J. 922, 197. doi:10.3847/1538-4357/ac116c

CrossRef Full Text | Google Scholar