
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Astron. Space Sci. , 17 February 2023
Sec. Space Physics
Volume 10 - 2023 | https://doi.org/10.3389/fspas.2023.1094282
This article is part of the Research Topic Reviews in Astronomy and Space Sciences View all 27 articles
 Marius Echim1,2,3
Marius Echim1,2,3 Mirela Voiculescu4*
Mirela Voiculescu4* Costel Munteanu1
Costel Munteanu1 Eliza Teodorescu1
Eliza Teodorescu1 Gabriel Voitcu1
Gabriel Voitcu1 Cătălin Negrea1
Cătălin Negrea1 Simona Condurache-Bota4
Simona Condurache-Bota4 Emilian Bujor Dănilă4
Emilian Bujor Dănilă4Introduction: During recent years magnetosheath plasma structures called “jets” are identified in spacecraft data as localized regions in the magnetosheath where the dynamic pressure is enhanced compared to the background. Although the nomenclature and detection algorithms vary from author to author, magnetosheath jets are part of a larger class of phenomena which can be globally called magnetosheath irregularities. In this review we focus on elements of jets phenomenology less discussed in the literature, though sustained by theoretical models for solar wind magnetosphere interaction, numerical studies based on Vlasov equilibrium models or kinetic numerical simulations.
Methods: The self-consistency of magnetosheath jets and the preservation of their physical identity (shape and physical properties), implicitly assumed in many recent experimental studies, is discussed in modelling and simulations studies and results as a consequence of kinetic processes at the edges of the jets. These studies provide evidence for the fundamental role played by a polarization electric field sustaining the forward motion of the jet with respect to the background plasma. Another natural consequence is the backward motion of surrounding magnetosheath plasma at the edges of jets. The conservation of magnetic moment of ions leads to a decrease of jets forward speed when it moves into increasing magnetic field. Our review is complemented by an analysis of magnetosheath data recorded by Cluster in 2007 and 2008. We applied an algorithm to detect jets based on searching localized enhancements of the dynamic pressure.
Results: This algorithm identifies a number of 960 magnetosheath jets (354 events in 2007 versus 606 events in 2008). A statistical analysis of jet plasma properties reveals an asymmetric distribution of the number of jets as well as a dawn-dusk asymmetry of jets temperature and density. The perturbative effects of jets on the background magnetosheath density/temperature are stronger in the dusk/dawn flank. We also found evidence for deceleration and perpendicular heating of jets with decreasing distance to the Earth. The braking of jets is correlated with the variation of the magnetic field intensity: the stronger the magnetic field gradient, the more efficient is the jet breaking.
Models of solar wind—magnetosphere interaction postulate the key role of solar wind and magnetosheath irregularities, characterized by an excess of their dynamic pressure and/or momentum with respect to the background magnetosheath plasma state, in transferring the mass, momentum and energy from the solar wind to the magnetosphere (Lemaire, 1977; Lemaire and Roth, 1978; Lemaire and Roth, 1981). In these early models it is argued that such plasma irregularities propagate as self-sustained structures through the entire magnetosheath and finally collide with the magnetopause. Due to their excess of momentum/dynamic pressure compared to the magnetosheath average, they can move across the magnetopause and enter into the magnetosphere (Lemaire, 1977). In these models the magnetopause is viewed as a three dimensional surface defined as the locus of total (dynamic + magnetic) pressure equilibrium between the magnetosheath and magnetospheric plasma, and where the magnetic field experiences rather rapid variations.
Magnetosheath irregularities are investigated theoretically and with in-situ experimental data. They are described in the literature under various names, like magnetosheath plasma blobs or plasmoids (Lemaire, 1985; Echim and Lemaire, 2000; Karlsson et al., 2012; Karlsson et al., 2015), magnetosheath transient flux enhancements (Nemecek et al., 1998), plasma clouds or plasma transfer events (Lundin et al., 2003), magnetosheath pressure pulses (Archer et al., 2012), plasma jets (Echim and Lemaire, 2005; Savin et al., 2008; Hietala et al., 2009; Amata et al., 2011), plasma filaments (Lyatsky et al., 2016a; Lyatsky et al., 2016b) (see also Table 1 in Plaschke et al., 2018).
Some authors use the term “jet” for magnetosheath structures characterized by an excess of dynamic pressure, pdyn = ρV2 (e.g., Plaschke et al., 2013), while the term “plasmoid” is used for magnetosheath irregularities with an excess of density, ρ (e.g., Karlsson et al., 2012), or momentum, p = ρV (Lemaire, 1977; Lemaire, 1985). Note also that the term “plasmoid” was first used by Bostick (1956) to define self-organized plasma elements created in laboratory experiments and characterized by i) a measurable translation (bulk) speed, ii) a transverse electric field, iii) a measurable magnetic moment, and iv) a measurable size (see also Roth, 1995). The term “fast plasmoids” is used for plasmoids characterized by a “pure” excess of velocity, V, with respect to the background magnetosheath (Karlsson et al., 2012, 2015; Goncharov et al., 2020). Plashke et al. (2018) and Goncharov et al. (2020) attempt a classification of various magnetosheath irregularities based on their dynamical properties (see also Preisser et al., 2020). In the following we will use the term “magnetosheath jet” (MSHJ) for the magnetosheath plasma structures characterized by an excess of the dynamics pressure compared to a background value. Studies of magnetosheath jets benefit from high resolution, multi-point measurements provided by spacecraft like Cluster, THEMIS and MMS during the minimum and/or maximum phase of the solar cycle (Shue et al., 2009; Archer et al., 2012; Plaschke et al., 2013; Plaschke et al., 2016; Plaschke et al., 2020; Plaschke et al., 2018; Karlsson et al., 2018; Raptis et al., 2019; Raptis et al., 2020; Vuorinen et al., 2019; Goncharov et al., 2020; Escoubet et al., 2020; Dmitriev et al., 2021; Koller et al., 2022, see Plaschke et al., 2018 for a review). High resolution data allow for a better sampling of plasma parameters and a better statistics for jet detection.
Dynamical properties of magnetosheath irregularities are derived from statistical analyses of data provided by various spacecraft, such as Cluster (e.g., Karlsson et al., 2012; Karlsson et al., 2015), THEMIS (e.g., Shue et al., 2009; Archer et al., 2012; Plaschke et al., 2016; Plaschke et al., 2018; Vuorinen et al., 2019), MMS or a combination between these (e.g., Raptis et al., 2019; Escoubet et al., 2020; Goncharov et al., 2020; Plaschke et al., 2020; Raptis et al., 2020). A review of jet observations is given by Plaschke et al. (2018). In terms of scales, it is found that the structures characterized by an excess of density have spatial scales of the order of one to several Earth radii (Karlsson et al., 2012). The structures characterized by an excess of dynamic pressures span a larger range, skewed however towards smaller scales, with a peak at roughly one RE (Plaschke et al., 2013; Plaschke et al., 2016), revised later to 0.1 RE (Plaschke et al., 2020). A tendency of jets to expand while moving away from the bow-shock is reported by Goncharov et al. (2020) based on MMS data.
In terms of their speed, one study based on THEMIS data reports than 98% jets are super-Alfvénic; however, this finding is based on the analysis of the velocity component in the anti-sunward direction (Plaschke et al., 2013). A superposed epoch analysis of the angle between magnetic field and ion velocity vectors as a function of normalized times suggests that the angles are changing only by about 10° (Plaschke et al., 2020). Liu et al. (2020) show that approximately 13% of high speed magnetosheath jets have a bow wave ahead of them with Mach number typically larger than 1.1, and that for such jets the electron energy flux is enhanced on average by a factor of 2 as compared to both those without bow waves and the ambient magnetosheath. A statistical analysis of jets detected by MMS suggest their speed tends to decrease with the distance from the bow-shock (Goncharov et al., 2020).
Jets are omnipresent in the magnetosheath. Vuorinen et al. (2019) estimate, in a study based on 3 years of THEMIS observations, that “jets larger than >2.0 RE hit the magnetopause around 9.4 times per hour during quasi-radial IMF, around 4.1 times per hour during oblique IMF and around 0.85 times per hour during high cone angle IMF.” According to the same study, smaller sized jets (0.5–2.0 RE) impact almost continuously the magnetopause, at a rate between 3.3 and 0.31 jets per minute, depending on the IMF orientation.
In our view, all variants of magnetosheath jets/plasmoids/ion flux enhancements reported in the literature from various spacecraft observations pertain to the same general class of magnetosheath phenomena, which can be named “multiscale dynamical irregularities of the background magnetosheath plasma state.” It is a paradigm which covers the broad range of spatio-temporal structures formed in the magnetosheath and contributing to the observed variability; these structures manifest themselves as local perturbations of plasma parameters and/or field, spanning a large range of spatio-temporal scales. They represent an experimental confirmation of the early ideas advocated by Lemaire (1977), Lemaire (1985), Lemaire and Roth (1978), and Lemaire and Roth (1981) who emphasized the key role of isolated magnetosheath plasma structures for the physics of solar wind—magnetosphere interaction. The magnetosheath irregularities are most likely three-dimensional plasma structures, fulfilling the “plasmoid” definition given by Bostick (1956), see also Roth (1995). Indeed, the points i) and iv) of Bostick’s definition introduced above are confirmed by observations in the magnetosheath (see, e.g., Plaschke et al., 2017; Karlsson et al., 2018).
The formation of magnetosheath jets irregularities is considered the effect of several possible physical mechanisms acting in the solar wind and/or at the terrestrial bow shock. There is no consensus on the dominant one(s). Lemaire (1977) and Lemaire (1985) suggests the magnetosheath irregularities impacting the terrestrial magnetopause are linked to the inherent multiscale and omnipresent non-homogeneity of the solar wind. In a study based on Cluster data; Karlsson et al. (2015) finds evidence for solar wind irregularities with properties very similar to magnetosheath jets and argues that “diamagnetic magnetosheath plasmoids originate from the solar wind plasmoids that cross the bow shock and convect downtail in the magnetosheath;” Parkhomov et al. (2021) considers that magnetosheath plasmoids are closely related to a class of solar wind irregularities which they called “diamagnetic structures (DS).’
Nemecek et al. (1998) argues that an interplanetary magnetic field (IMF) discontinuity interacting with the bow shock is at the origin of the plasma flux enhancements observed in the magnetosheath. In Savin et al. (2008) an argument is given that the high kinetic energy jets observed by INTERBALL are formed due to local processes mainly linked to a transition from a metastable plasma state with super-Alfvénic velocity to a stable state with Alfvénic or sub-Alfvénic flows. The induced “magnetic stress balance” leads to the observed high kinetic energy fluxes. Hietala et al. (2009) suggest that the local bow shock ripples occurring when the IMF is radial and the solar wind Mach number is large (MA > 10) could be the source of super magnetosonic magnetosheath jets. This mechanism is also evidenced in hybrid simulations (Preisser et al., 2020). Simulations also suggest antiparallel reconnection observed at the quasi-parallel bow-shock can lead to the formation of diamagnetic irregularities/plasmoids (Preisser et al., 2020). Escoubet et al. (2020) consider the solar wind nanodust clouds (Lai and Russell, 2018) could be added in the list of possible sources for magnetosheath jets. A recent study (Raptis et al., 2020) discusses the shock reformation as an additional mechanism possibly contributing to the formation of magnetosheath jets. Voros et al. (2019) discuss small scale magnetosheath dynamical (coherent) structures as a local manifestation of the non-linear turbulent processes developing in the magnetosheath (for a recent review on magnetosheath turbulence see Echim et al., 2021). Larger scale structures observed in the vicinity of the magnetopause, close to the equatorial plane, can be linked to the formation of Kelvin-Helmholtz vortices (Hasegawa et al., 2004). The non-linear stage of the Kelvin-Helmholtz instability (Nykiri. 2013), may lead to detachment of rolled-up vortices which may interact with the magnetopause and lead to transport into the magnetosphere (Nykiri and Otto, 2001). In the close vicinity of the magnetopause such vortices can be detected as local irregularities of the magnetosheath plasma.
Lemaire (1985) discusses the physical properties of magnetosheath plasmoids from a theoretical (kinetic) point of view. It is argued that magnetosheath plasmoids dynamics in a background plasma and field is characterized by several key aspects like: a) a high plasma dielectric constant, b) the decoupling from the background plasma and field due to electric fields confined in the plasmoid’s boundary layers, c) the formation of a self-polarization electric field allowing the forward motion of the plasmoid, d) the breaking of the plasmoid when moving in increased magnetic field due to a conversion of the bulk forward motion into gyration, similar to the physics of mirroring particles. This process, called adiabatic breaking, was probed in laboratory (e.g., Burgess and Scholer, 2013) and by numerical simulations (Voitcu and Echim, 2016).
Echim et al. (2005) describe a Vlasov equilibrium model for a plasma slab, defined as a localized plasma structure in motion with respect to the background plasma and field and which is characterized by an excess of the dynamic pressure compared to the background. The Vlasov model emphasizes dynamical features of the plasma slab which seem similar to properties of magnetosheath jets reported from observations by, for instance, Plaschke et al. (2017) or Karlsson et al. (2018). Indeed, counterstreaming of the background plasma at the edges of the magnetosheath slab/jet, as well as the formation of asymmetries at jet’s edges are observed both in observations and model.
Interestingly, the vast majority of statistical analysis of jets properties based on experimental data implicitly assume the jets are self-sustained plasma structures which preserve their coherence, or self-identity, during their propagation in the magnetosheath, from the bow-shock to the magnetopause (e.g., Archer and Horbury, 2013; Dmitriev and Suvorova, 2015; Karlsson et al., 2015; Raptis et al., 2020). The physical mechanisms allowing for the self-existence and organization of such structures are less discussed in the observational reports. Nevertheless, the theoretical model proposed by Lemaire (1985) to describe the dynamics of magnetosheath plasmoids argues that kinetic processes at plasmoid’s boundary layers contribute to an electric self-polarization (Schmidt, 1960) which allows the plasma irregularity to preserve its shape and dynamics.
Echim and Lemaire (2005) compute local Vlasov equilibrium solutions tailored for the boundary layers of plasma jets and demonstrate qualitatively and quantitatively that the jet is decoupled from the background plasma and field by a combination of Schmidt-like polarization electric field and weak-double-layers. The weak parallel electric fields/perpendicular polarization electric field ensures jet’s decoupling in the direction parallel/perpendicular to the background magnetic field. At the origin of these electric field components stay plasma bulk velocity shears with a non-vanishing component in the direction parallel and perpendicular to the background magnetic field.
Three-dimensional kinetic simulations of jets injected into non-uniform distribution of the magnetic field (Voitcu and Echim, 2016; Voitcu and Echim, 2017) confirm the electric self-polarization of jets is a key physical process. These simulations evidence the self-formation of space charge layers at the edges of the moving jet sustaining a Schmidt-like polarization electric field. The jet maintains its self-coherence during the transport through the region of non-uniform field with a strong gradient, similar to the magnetosheath region in the vicinity of the magnetopause. A diffusion of jets mass is observed in the direction parallel to the magnetic field. However, in these numerical simulations the contribution of the background plasma is neglected and therefore the weak double-layers predicted theoretically cannot be simulated and their confining/decoupling effect is not simulated.
Data from magnetospheric spacecraft collected during the last decades confirm that dynamical irregularities populate the entire magnetosheath, for a broad range of solar wind input conditions. They carry a significant amount of mass and momentum towards the magnetopause, at virtually all local times and latitudes. A large fraction of these irregularities reaches the magnetopause and interacts with it locally. The emerging picture is that of quasi-permanent localized perturbations of the magnetopause driven by magnetosheath dynamical irregularities, as advocated by Lemaire (1977) and Lemaire and Roth (1978).
The effects of magnetosheath irregularities/jets on the dynamics and electrodynamics of the terrestrial magnetosphere and ionosphere are under study. Based on first order kinetic plasma physics arguments, Lemaire 1977 and Lemaire 1985 argues that i) the magnetosheath irregularities are effectively decoupled from the background plasma and field, ii) they traverse the magnetopause and iii) they entry into the magnetosphere where they become local plasma perturbations. It is also postulated that intruding magnetosheath plasma jets are braked and eventually stopped in the magnetosphere by adiabatic and/or irreversible processes (e.g., coupling with the conducting ionosphere, see also Echim and Lemaire, 2000; Echim and Lemaire, 2002; Wing et al., 2014). The conditions for magnetopause traversal are investigated with 3D electromagnetic Particle-in-Cell numerical simulations (Voitcu and Echim, 2016; Voitcu and Echim, 2017; Voitcu and Echim, 2018). Magnetospheric observations of fully penetrated magnetosheath plasma elements are reported by studies based on data from magnetospheric missions like Prognoz-7 (Lundin and Aparicio, 1982; Lundin and Dubinin, 1984; Lundin, 1988), INTERBALL (Vaisberg et al., 1998), Cluster (Lundin et al., 2003; Gunell et al., 2012; Lyatsky et al., 2016a; Lyatsky et al., 2016b), THEMIS (Dmitriev and Suvorova, 2015).
Lundin et al. (2003) report Cluster observations of 134 magnetosheath jets detected, between January—March 2001, inside the magnetosphere, at high latitudes (they call these structures plasma transfer events—PTE). The authors discuss local magnetospheric effects like plasma drifts and energization, electric fields and currents occurring in response to the interaction of the background magnetospheric plasma with the penetrating magnetosheath jets/PTEs. “Evanescent” PTEs are magnetosheath plasma structures which no longer propagates in the magnetosphere but are stagnant and form static pressure irregularities. Lundin et al. (2003) also argue that the most likely mechanism leading to the occurrence of PTEs observed by Cluster is the transport of magnetosheath irregularities with an excess of dynamic pressure at the magnetopause and their impulsive penetration inside the magnetosphere. A more recent analysis of Cluster data recorded between 2007 and 2008 close to the equatorial regions, within a maximum cone angle range of 30°, finds evidence for more than 200 magnetosheath-like plasma structures, called plasma filaments, inside the magnetosphere (Lyatsky et al., 2016a; Lyatsky et al., 2016b). Generally, these plasma filaments show a strong stable earthward component of the plasma bulk velocity. This study also argues that a majority of the observed filaments are detached from the magnetopause. In a study of 642 large scale magnetosheath jets detected by THEMIS, Dmitriev and Suvorova (2015) find that more than 60% of jets move across the magnetopause, into the magnetosphere. The penetrating jets are generally characterized by velocities higher than 200 km/s and a large beta.
Recently, Parkhomov et al. (2021) and Parkhomov et al. (2022) analyze the magnetospheric effects of solar wind irregularities which they call “diamagnetic structures” (DS) based on the anticorrelation between the solar wind plasma density, which increases, and the magnetic field intensity, which decreases. The authors consider that DS move from the solar wind in the magnetosheath and in the magnetosphere and show evidence for global magnetic field perturbations linked to the interaction of DSs with the Earth’s magnetosphere. One prominent feature is the occurrence of bursts of irregular magnetic field pulsations PI1-2 recorded on ground for a broad range of local times. Parkhomov et al., 2021; Parkhomov et al., 2022) argue that the pulsations observed by ground observatories have properties similar to the pulsations detected in-situ in the vicinity of magnetosheath jets (Katsavriasi et al., 2021). It is argued that the propagation of the pulsations to the ground, along closed magnetic field lines, proves the irregularities, which are the source of pulsations, moved impulsively from the magnetosheath into the magnetosphere, across the magnetopause (Echim and Lemaire, 2000).
Inside the magnetosphere, the propagating jets lead to the formation of sheared plasma flows layers at the interface with the background plasma (see, e.g., Lundin et al., 2003; Gunnell et al., 2012). It was shown that the coupling of sheared flow plasma layers with the conducting ionosphere leads to auroral effects sustained by a magnetospheric generator formed in the sheared flow region (Roth., 1995; Echim et al., 2007; Génot et al., 2021). Indeed, such generators sustain field aligned potential drops leading to accelerated precipitating electrons and auroral arcs in regions like the Low Latitude Boundary Layer, the Plasma Sheet Boundary Layer or the polar cap (Echim et al., 2008; Echim et al., 2009; Balogh et al., 1997; Johnson and Wing, 2015, see also the review by Borovsky et al., 2020). The sheared flows formed at the interface between magnetosheath jets propagating inside the magnetosphere and the background magnetospheric plasma can be at the origin of throat auroras reported in the polar caps by Han et al. (2017), Han et al. (2018), Wang et al. (2018), and Raptis et al. (2019).
Other magnetospheric effects of magnetosheath jets are discussed by Hietala et al. (2009) who argue that high speed jets provide a “source for magnetopause waves during steady solar wind conditions,” which can have an impact on the magnetosphere-ionosphere coupling. Plaschke et al. (2016) present a series of possible consequences of high speed magnetosheath jets such as: ionospheric flow enhancements, magnetic field variations observed on the ground, local magnetopause reconnection, inner magnetospheric and boundary surface waves, drop outs and other variations in radiation belt electron populations. Archer et al. (2019) evidence magnetopause perturbative effects of jets in terms of eigenmodes propagating tangentially to the magnetopause. Liu et al. (2020) argue that a magnetosheath jet compresses the ambient plasma such that a bow wave or shock can form ahead of the jet, which accelerates particles, and thus, contributes to magnetosheath heating and particle acceleration in the extended environment of the Earth’s bow shock.
In order to probe some of the theoretical predictions less investigated in the past and outlined in the previous section, like, e.g., the formation of space charge layers at the edges of magnetosheath jets, enabling their self-consistent forward motion in the background magnetosheath, the adiabatic breaking and the correlation between local jet perpendicular component of the bulk velocity and the local magnetic field intensity, the correlation between the local jet perpendicular temperature and the local magnetic field intensity, we performed an analysis of magnetosheath data collected by Cluster 3 (Escoubet et al., 1997) between 2007 and 2008. We applied a procedure to identify magnetosheath jets which follows the algorithm proposed by Archer and Horbury (2013) based on searching for local enhancements of the magnetosheath ion dynamic pressure with respect to a background reference value estimated from a running window average. In the following we discuss the observed dynamical properties of jets and how the possible links with the phenomenology presented in the previous section.
There is no general consensus on which methodology to be applied for detecting magnetosheath jets (MSHJ) from in-situ spacecraft observations. Different data selection criteria focus on different plasma parameters, such as dynamical pressure, density, bulk velocity. An earlier study identified “ion flux enhancements” (Nemecek et al., 1998), precursors of what we call today magnetosheath jets, from combined observations of plasma density and plasma velocity. Savin et al. (2008) consider a jet is defined by an increase of the ion kinetic energy well above the corresponding solar wind value. Hietala et al. (2009) used a combination of criteria to define the magnetosheath jets: the ion velocity takes values larger than 500 km/s, the jet shows a dominant sunward magnetic field component BX and the angle between the flow direction and the magnetic field is less than 20°. Archer et al. (2012) defined jets as “magnetosheath pressure pulses” based on dynamic pressure enhancements above a background magnetosheath value. Karlsson et al. (2012) identified jets as “plasmoids” when the plasma density was larger than the background level. Plaschke et al. (2013) used the term “high speed jets” for magnetosheath structures satisfying several conditions, like an anti-sunward dynamic pressure of the jet be higher than half of the solar wind (SW) dynamic pressure.
Recent reports use the term “magnetosheath jets” (Raptis et al., 2020) for events characterized by a magnetosheath dynamic pressure higher than the corresponding 20 min average of SW dynamic pressure. In Plaschke et al. (2020), Liu et al. (2020) and Escoubet et al. (2020), “magnetosheath jets” are defined as events for which the dynamic pressure in the anti-sunward direction, in the GSE system, is larger than half of the SW dynamic pressure, while their duration is defined as the time interval for which the magnetosheath dynamic pressure is larger than a quarter of the SW corresponding magnitude.
In this study we analyze magnetosheath data provided by Cluster 3. The time intervals when the spacecraft 3 was in the magnetosheath are extracted from the FP7 STORM database built for an analysis of magnetosheath turbulence (http://www.storm-fp7.eu). Cluster’s highly eccentric orbit allows for a seasonal sweeping of the magnetosheath between January and May of each year. All magnetosheath time intervals selected for this study were verified by a visual inspection of data summary plots provided by the Cluster UK database (http://www.cluster.rl.ac.uk) to ensure there is no mixing with the foreshock and/or solar wind.
The procedure we adopt here to identify the magnetosheath jets follows the method proposed by Archer and Horbury (2013) based on searching an excess of the dynamic pressure with respect to a background value, estimated from a running average with a time window of fixed length. The jet detection algorithm proceeds in two steps. First, the signal is divided in contiguous windows of equal time length, Δt. An automatic survey is performed to select those time windows within which at least one local value of the ion dynamic pressure, pdyn, is N times larger than the background value. The latter is estimated from an average of pdyn computed over all values included in the respective time window. We tested several variants of this approach, for various values adopted for N (N = 1.3, N = 1.5, N = 2), and for Δt (Δt = 10, 15 or 20 min). After verification of all results, we adopted a combination of parameters with Ns = 1.3 and Δts = 20 min. For larger values of Ns some smaller amplitude jets were missed; for smaller values of Δts the procedure required more time and some of the medium sized jets were missed. In the second step, the data for each time interval are inspected visually in order to select the time of start and time of end for each individual jet. In Figure 1 we illustrate an example of Cluster-3 which shows two jets identified in 22 January 2007. The two stars indicate the maximum of the dynamic pressure for each of the two jets. In the analyses included in this study for various plasma parameters (Figures 4–7, 9–13) we consider one value of each variable per jet, precisely the one corresponding to the peak value of the dynamic pressure, exemplified by the two stars in Figure 1.
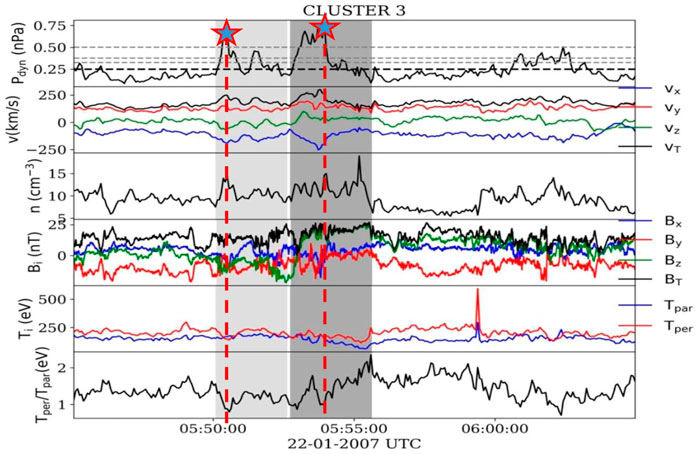
FIGURE 1. An example of Cluster 3 data illustrating two jets detected with the procedure described in the text. The panels show, from top to bottom, the dynamical pressure, pdyn, the three components of the ion bulk velocity and the total speed, the number density, n, the three components of the magnetic field and the magnetic field intensity, the parallel and perpendicular temperature, the temperature anisotropy. The shaded areas indicate the two jets detected at 05:50:00 UT and 05:53:10 UT, respectively. The thin dashed lines represent the average value of the dynamic pressure computed over the 20 min of data showed in the figure and multiplied by N = 1.3, N = 1.5, N = 1.7, N = 2.The thick dashed line indicate the average value of the dynamic pressure. The two stars mark the maximum of the dynamic pressure and the vertical red dashed lines mark the time when this maximum is detected.
The method was applied on data from Cluster Ion Spectrometer (CIS, Reme, 1997) on board Cluster 3 and resulted in the detection of 960 events of which 354 jets in 2007 and 606 jets in 2008. Figure 2 illustrates the dynamical characteristics of the entire ensemble of jets; in this figure we show only one measurement per jet, namely, the measurement taken when the jet dynamic pressure reaches its maximum. One notes a significant variability of jets properties. The density, the antisunward velocity, the total magnetic field and the ion temperature at maximum dynamic pressure span a large range of values. A discussion on these variations is provided in the section below.
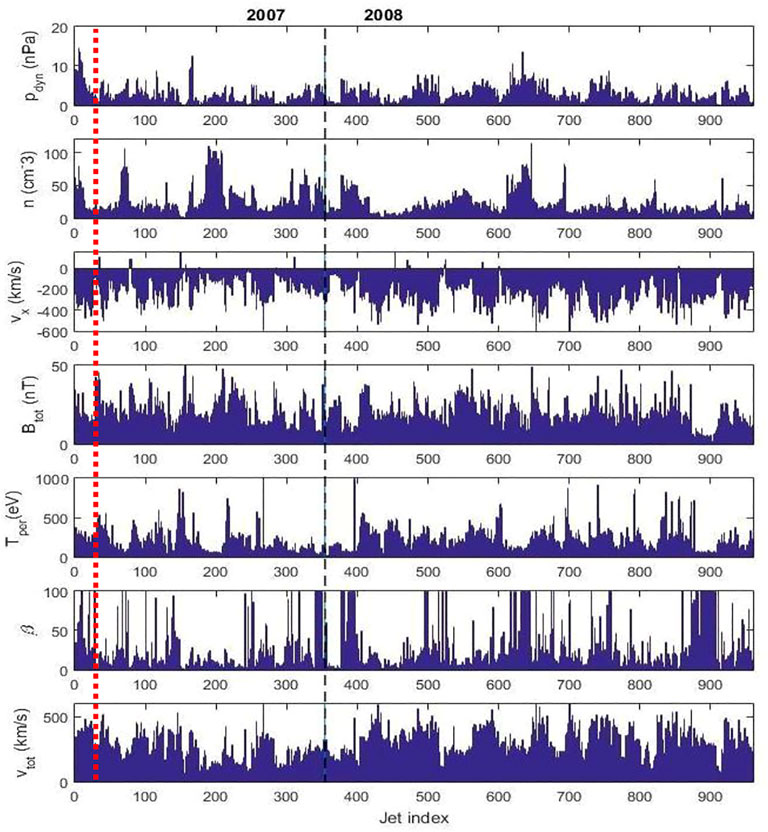
FIGURE 2. A summary of jets’ properties included in this study. The panels show from top to bottom: the dynamic pressure, pdyn, the plasma density, n, the component of the jet’s velocity in GSE x direction, vx, the magnetic field intensity, Btot, the perpendicular ion temperature, Tperp, the total plasma beta, β, and the bulk speed, vtot. Only one measurement per jet is shown, the one at the moment when the jet’s dynamic pressure is maximum. The red dashed red line indicates the two jets presented in detail in Figure 1.
For each jet we also compute the position of a model magnetopause (using the approach by Shue et al., 1997) and of a model bow-shock (using the model Farris and Russel, 1994). The two models are initialized with solar wind data provided by OMNI database (https://omniweb.gsfc.nasa.gov/html/HROdocum.html). Thus, for each jet, we estimate model curves for:
a) the magnetopause (Shue et al., 1997):
where α = 0.5 is the tail flaring, and r0 is the standoff distance and depends on the dynamical pressure, Dp, and the Oz component of the IMF, Bz (taken from the OMNI data) as:
b) for the bow shock (Farris and Russell, 1994):
where RBS is the bow-shock (BS) radial distance, θ is the solar zenith angle in aberrated coordinates, ε = 0.81 is the eccentricity, and
For each jet we also calculate an estimation for the distance to the model magnetopause (denoted DMP) as well as to the model bow shock (denoted DBS). The two distances are estimated in the direction normal to the model magnetopause (MP) and bow-shock (BS), from jet’s position, as illustrated in Figure 3A. Other approaches considered mapping to the bow-shock along magnetosheath streamlines (Karlson et al., 2018). More details on the procedure applied to determine the normal direction to the model bow shock and model magnetopause can be found in Teodorescu et al. (2021). Note that the data needed to compute DMP and DBS were available for a subset of 850 jets, illustrated in Figure 3 where we show their positions in the (X,RYZ)GSE plane, where
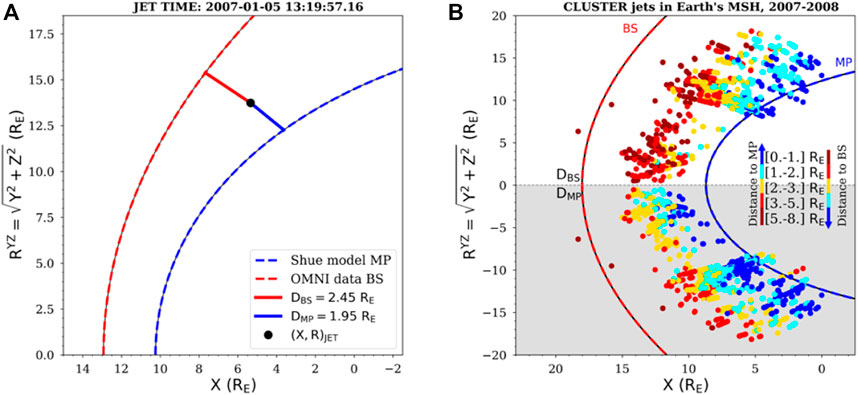
FIGURE 3. (A) Example of the estimated distance from the jet to the magnetopause (blue-curve) and to the bow shock (red-curve), (B) Overview of all jets locations in the (X, RYZ) GSE plane: Positive R plane shows distances with respect to the bow shock; negative R plane (gray shaded area) shows distances with respect to the magnetopause. The blue and red curves indicate the innermost magnetopause and the outermost bow shock within the entire set.
The model magnetopause and bow shock profiles shown in Figure 3B correspond to the innermost model magnetopause and outermost model bow shock of the ensemble of all model magnetopauses and bow-shocks computed for the entire set of jets. For a compact and symmetric view, we plot the distances to the magnetopause (highlighted by the gray shaded area) in a “mirrored” view, by artificially changing the values of the coordinate RYZ from positive to negative. We defined five bins for the estimated distances: [0.,1.] RE, [1.,2.] RE, [2.,3.] RE, [3.,5.] RE and [5.,8.] RE, where RE is the Earth’s radius; these bins are illustrated with different colors, as indicated in the figure.
During the first 4 months of 2007 and 2008 the Earth’s magnetosphere was impacted by a sequence of recurrent high-speed streams (HSS) and Corotating Interaction Regions (CIRs), whose dynamical characteristics (maximum speed, maximum density) were different in 2007 compared to 2008 (see, e.g., Munteanu et al., 2019). The differences in driver’s properties for 2007 compared to 2008 motivated us to analyze separately each of the 2 years. Koller et al. (2022) recently pointed out, from an analysis of THEMIS data, that the number of jets increases by 50% during HSS and CIR events A thorough analysis of the correlation between the interplanetary parameters and the properties of jets included in our database is the subject of another forthcoming study.
A set of dynamical properties (density, bulk velocity, magnetic field, temperature and dynamic pressure) of jets observed by Cluster 3 in 2007 and 2008 is illustrated in Figures 4, 6 as a function of jet position projected in the (XGSE, YGSE) plane. In addition to the dynamical properties of jets, we plot in Figures 5, 7 the perturbation of the background magnetosheath produced by the jets, for the same set of physical variables as in Figures 4, 6. The perturbation of a physical parameter Q is estimated in Figures 5, 7 from the ration,
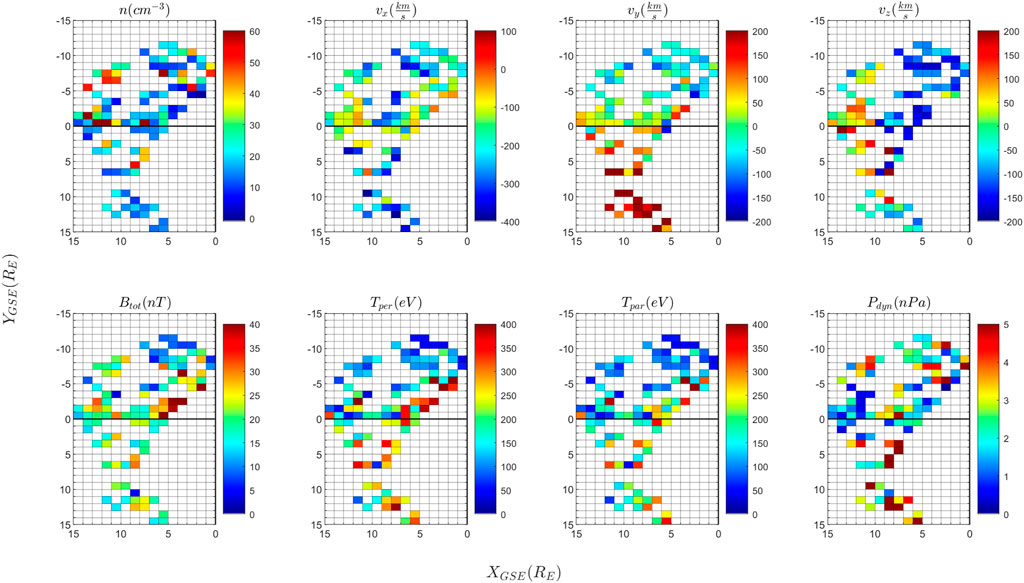
FIGURE 4. Summary of dynamical properties of magnetosheath jets observed by Cluster 3 between January and April 2007. The panels show the plasma density (n), the three components of the plasma bulk velocity (vx,vy,vz), the magnetic field intensity (Btot), the parallel and perpendicular temperature (Tper, Tpar), the dynamic pressure (Pdyn). The value of the parameters is color coded as shown in the tables next to the panels; the values in each spatial bin are estimated as the median of the respective parameter for the ensemble of all jets detected in the respective bin. Only one value per jet is considered, namely, the one measured at the time when the dynamic pressure is maximum (indicated with stars in Figure 1).
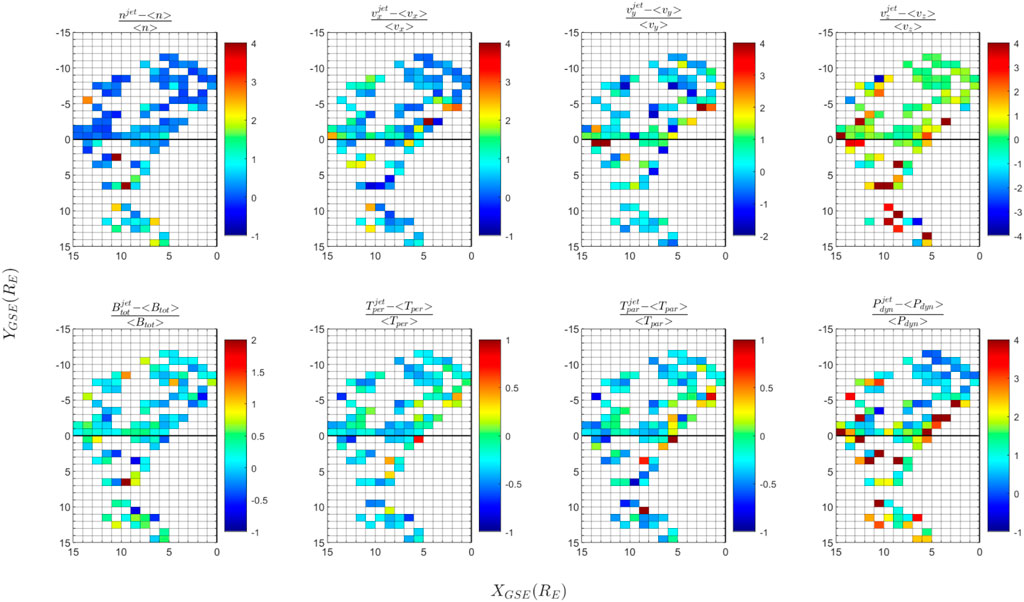
FIGURE 5. Relative perturbation of the background magnetosheath state produced by jets, for data recorded in 2007. We illustrate the same set of plasma variables as in Figure 4. The value of the relative perturbation is color coded as shown in the tables next to the panels. The perturbation of the variable Q is estimated as the ration
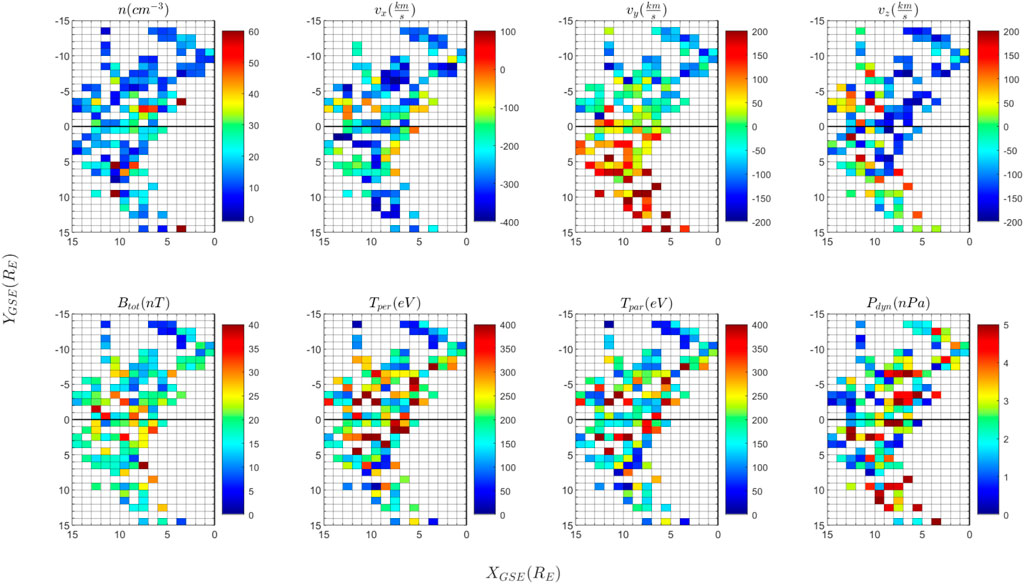
FIGURE 6. Summary of dynamical properties of magnetosheath jets observed by Cluster 3 in January–April 2008. Same format as Figure 4.
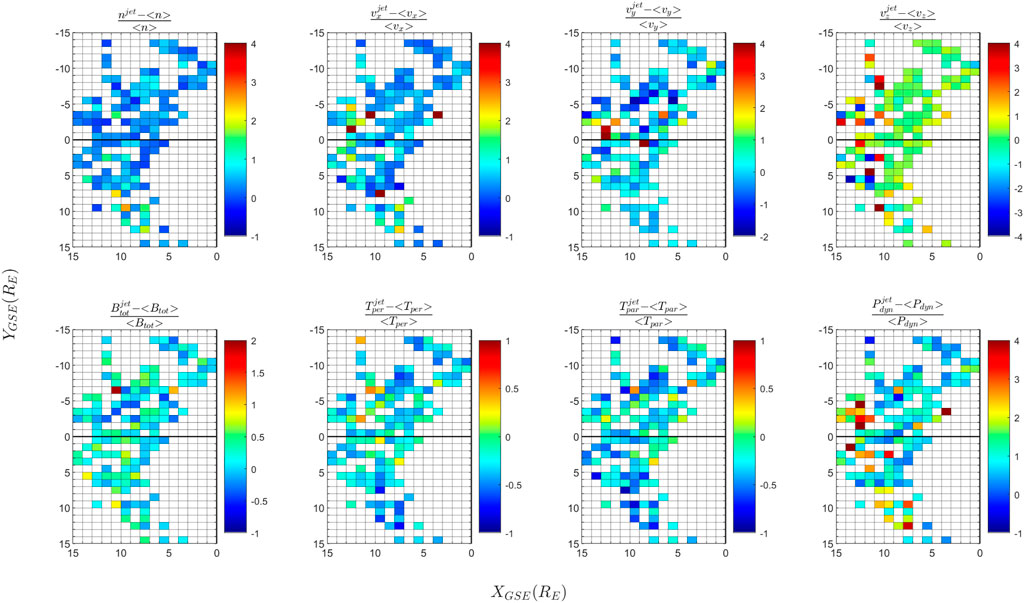
FIGURE 7. Relative perturbation of the background magnetosheath state produced by jets, illustrated for each physical quantity included in Figure 6, for data recorded in 2008. Same format as Figure 5.
The results are shown in Figures 4–7 on a uniform spatial grid formed of squared bins of one Earth radius size. In each spatial bin we plot, color coded, the median value of the respective variable estimated for the ensemble of jets (Figures 4, 6) and of the background magnetosheath perturbation (Figures 5, 7) detected in the respective bin. Only one value per jet is considered, namely, the value recorded at the maximum of the dynamic pressure; the perturbation value is estimated as a time average, as described above.
The number of jets detected by Cluster-3 in the dawn flank is larger than at dusk. This asymmetry persists for the 2 years, 2007 and 2008. Nevertheless, the total number of observed jets is larger in 2008 than in 2007. The predominance of jets in the dawn flank is partly due to Cluster orbit, which intersects for slightly longer times the dawn magnetosheath flank during the time interval targeted by this study. However, in a recent study, Vuorinen et al. (2019) argue that a dawn-dusk asymmetry of the number of detected jets (with more jets detected in the dawn flank) should mostly be observed for oblique IMF. This effect is linked, according to Vuorinen et al. (2019), to a predominance of the quasi-parallel geometry in the dawn flank for oblique IMF. Radial and perpendicular orientation of the IMF seem to inhibit this relative asymmetry.
The distribution of the cone angle for our entire jets dataset is shown in Figure 8. One notes that in 2007 the distribution is skewed towards values larger than 60°. This effect is less present in 2008. Indeed, the cone angles in 2008 are more “ordered,” their distribution is closer to the normal. This is probably due to the recurrent interaction with the high-speed streams and the corotating interaction regions observed in 2008 and which are characterized by a more “ordered” structure of the interplanetary magnetic field. In a recent study, Munteanu et al. (2019) showed that two systems of CIRs and HSS whose origin stayed stable on the Sun (same group of coronal holes) for several months in 2008, impacted the Earth, including for the time period investigated in this study (see, also, Negrea et al., 2021). While in 2007 the Earth was also impacted by HSS and CIRs their origin was more dynamic and their properties were therefore much more variable compared to 2008. A discussion of the driver properties for the jets included in this study is the topic of another paper, in preparation.
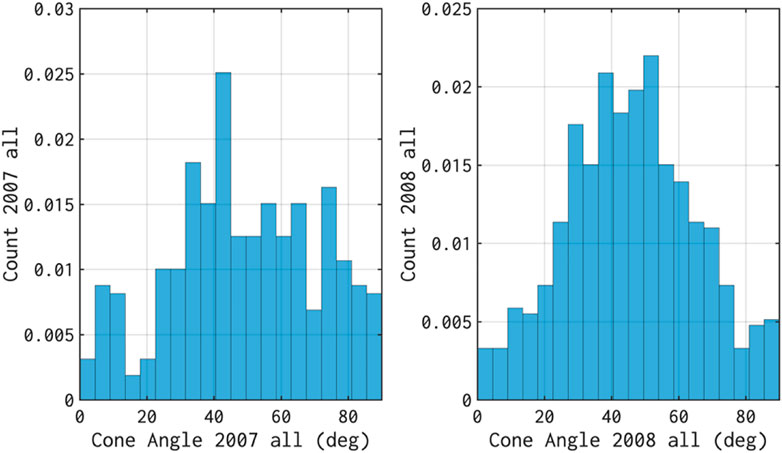
FIGURE 8. Normalized histograms of the IMF cone angle computed from OMNI data for time intervals when the jets were detected; left/right panels show results for 2007/2008.
Figures 4, 6 also reveal asymmetries and spatial trends of jets plasma variables. The anti-sunward component of jet plasma bulk velocity, vX, decreases when jets get closer to the magnetopause, for both years in the subsolar magnetosheath, for
The properties of the background magnetosheath show similar asymmetries, although the pattern is slightly different compared to jets. Figures 5, 7 illustrate the relative perturbation produced by jets on the background magnetosheath state. We conclude these perturbations give a measure of the jet impact on the magnetosheath and also on the intrinsic jet asymmetries, not linked to the background magnetosheath asymmetric trends. We note the recurrence of increased density perturbations by jets is higher in the dusk than in the dawn, this tendency being more evident for data recorded in 2007. Following the plasmoid definition by Karlson et al. (2012), this asymmetry could mean that plasmoids are more likely encountered in the dusk sector. We also note that the density of jets tends to be larger in the dawn flank, however, the jet perturbation of the background magnetosheath density tends to be stronger in the dusk flank.
The strongest perturbation of the background magnetosheath temperature is observed in spatial bins located mostly in the dawn flank. However, one cannot assign a clear general dawn-dusk asymmetry for temperature perturbations. One notes that in 2007 the strongest perturbations of the temperature are observed at shorter distances from the Earth; this trend is not retrieved for 2008. The perturbation of the magnetosheath dynamic pressure by jets is asymmetric: the jet perturbations are stronger in the dusk flank (more visible in 2007 than in 2008).
A quantitative estimation of the asymmetries observed for jets temperature and density is provided by the probability density functions (normalized histograms) shown in Figure 9. We define three ad hoc temperature ranges: a) “cold,” from 50 eV to 200 eV; b) “warm,” from 200 eV to 400 eV and c) “hot,” for more than 400 eV. The probabilities calculated for data measured in 2007 in the “cold” range are higher in the dawn than in the dusk flank; the probabilities calculated for the “warm” range are higher for the dusk flank. In the “hot” range the events for temperatures higher than 600 eV are detected only in the dawn flank but their statistic is poor. This trend in temperature asymmetry is not retrieved for 2008 data, except for a contracted “warm” range, between 375 eV and 475 eV, where the probabilities in the dusk flank are higher.
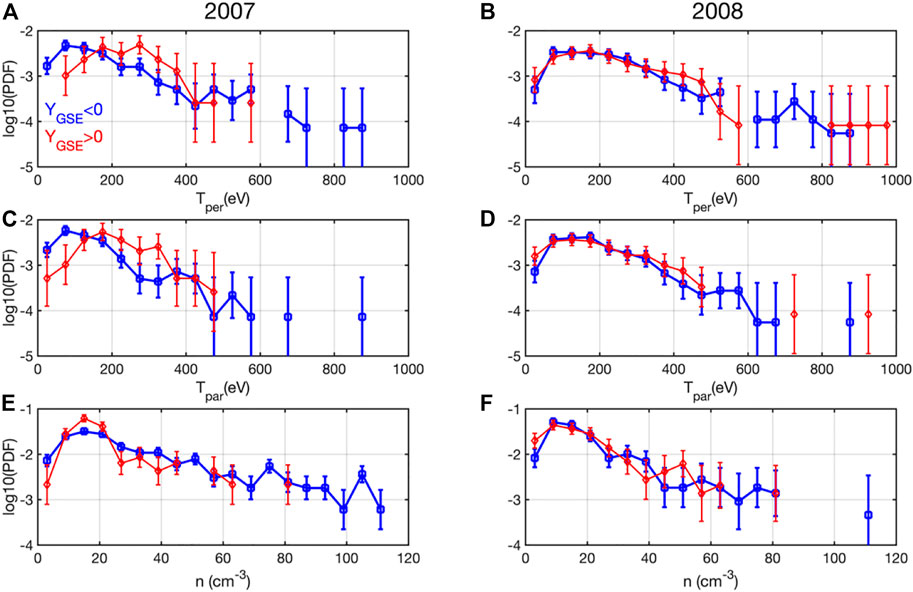
FIGURE 9. Histogram of the ion perpendicular [upper panels, (A, B)], parallel [lower panels, (C, D)] temperature and plasma density [lower panels, (E, F)] for 2007 (left) and 2008 (right). Blue/red profiles correspond to dawn (Y < 0)/dusk (Y > 0) flanks, respectively.
We also define three ad hoc density ranges for the probabilities computed in Figure 9: a) between 5 cm−3 and 20 cm−3, b) between 25 cm−3 and 42 cm−3 and c) for densities higher than 50 cm−3. In 2007 the probabilities for the lowest density range are slightly higher in the dusk than in the dawn flank. The probabilities in the intermediate density range are higher in the dawn than in the dusk. For densities higher than 50 cm−3 we do not see a significant dawn-dusk asymmetry. This trend is not retrieved in 2008, except for a contracted range between 45 and 55 cm−3 where the probabilities in the dusk are higher than in the dawn.
Thus, the jet properties recorded in 2007 suggest the jet inflow was denser and colder in the dawn than in the dusk flank. In 2008 this asymmetry is only partially retrieved, with jets being a bit warmer in the dusk side where they also show a slightly increased probability for higher densities. Interestingly, this asymmetry is partially consistent with the properties of the cold population of the cold dense plasma sheet, as reported by Wing et al. (2005), or Wing et al. (2014). Nevertheless, the formation of the cold dense plasma sheet is considered a signature of prolonged Northward IMF driving. Different mechanisms are believed to be involved in its formation (e.g., Kelvin-Helmholtz vortices in the flanks, Hasegawa et al., 2004). From an analysis of THEMIS magnetosheath data recorded between 2009 and 2015, Dimmock et al. (2016) find that the magnetosheath ion density shows a dawn-dusk asymmetry, with larger values at the dawn-side. The asymmetry detected for jets density is consistent with the trend found by Dimmock et al. (2016) and also the trends found in our background magnetosheath datasets.
The maps shown in Figure 10 illustrate the distribution of jet speed (normalized to the solar wind speed) and magnetic field intensity as a function of the distance from the magnetopause and the perpendicular temperature of ions. The data suggest that the closer to the magnetopause is the jet, the more likely is that the jet speed decreases while the jet perpendicular temperature increases. This effect can be linked to an adiabatic breaking of the jet while it moves towards the magnetopause, in an increasing magnetic field.
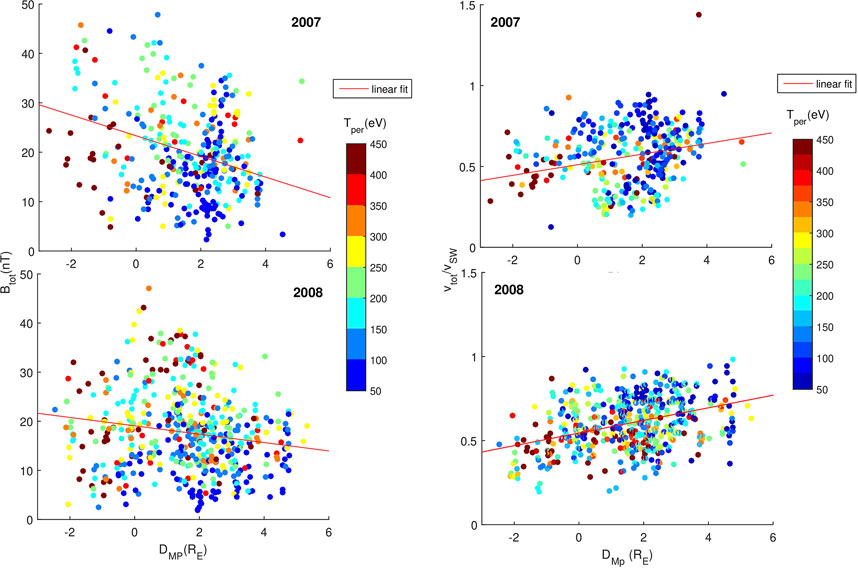
FIGURE 10. Distribution of ratio between jets speed and solar wind speed (vtot/VSW, right column) and magnetic field (Btot, left column) as a function of the distance to the magnetopause (DISTMP), for 2007 (top row), and 2008 (bottom row). The symbols identify the position of each individual jet, the color assigned to each symbol is a measure of the perpendicular temperature. DistMP is the distance from the jet position to the magnetopause, estimated using the Shue et al. (1997) model (see text for details); negative values indicate the jet is detected downstream the model magnetopause. The red lines trace a linear regression over the ensemble of data in each set.
Indeed, when the gradient of the magnetic field is smooth and the Alfven conditions are satisfied, the magnetic moment of ions is conserved leading to an increase of the kinetic perpendicular velocity, thus of the perpendicular temperature, while the jet ions move into an increasing magnetic field. On the other hand, collective effects linked to the electric polarization of the jet itself (Lemaire, 1985; Borovsky, 2021, see also Voitcu and Echim, 2016) lead to a conservation of the sum between the bulk forward energy and the thermal energy:
where
To further investigate a possible signature for the perpendicular heating of jets, we compute the variation of the jet ion temperature anisotropy, the ratio between parallel and perpendicular temperature,
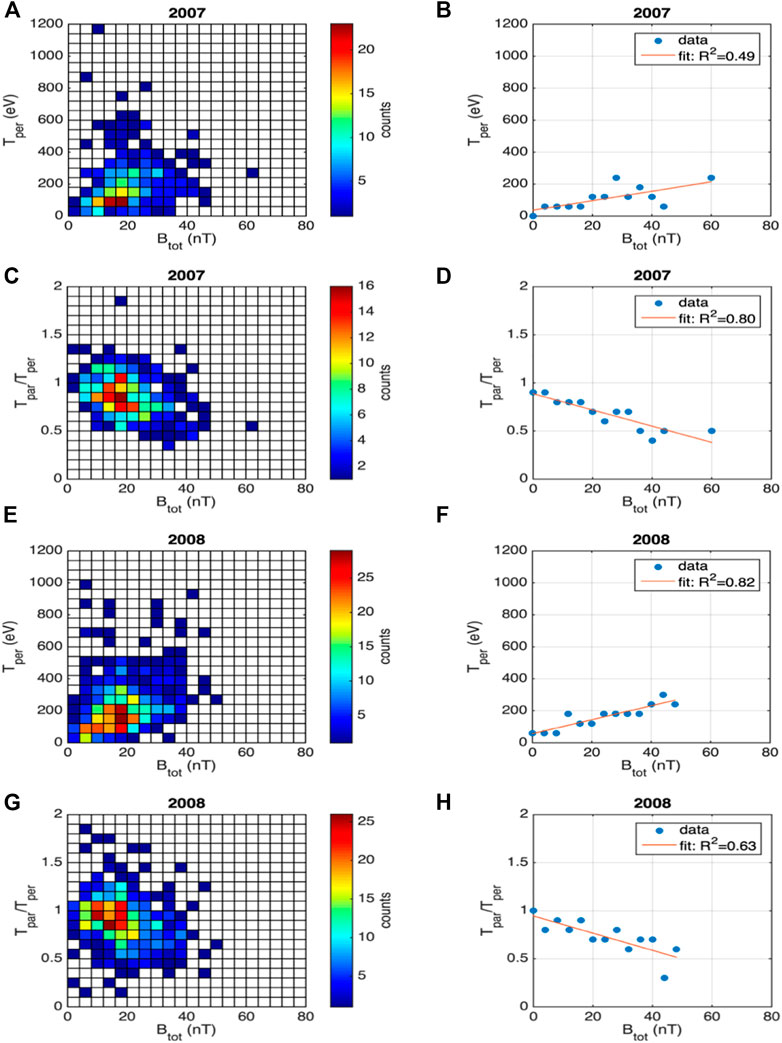
FIGURE 11. Left column: Histograms computed in the two-dimensional space defined by jet’s perpendicular ion temperature, Tper, and magnetic field intensity, Btot, (A) for 2007, and (E) for 2008 and by the jet’s ion temperature anisotropy (Tpar/Tper) and magnetic field in the jet (C, G). Only one value per jet is considered, the one at maximum of the dynamic pressure (see Figure 1). Panels in the right column (B, D, F, H) show linear fits of the respective quantities as a function of the local value of the jet magnetic field intensity.
The observed correlation between the perpendicular temperature of jet ions with the jet magnetic field intensity, suggested by the results shown in Figure 11, can be a local effect, possibly linked to the adiabatic breaking of jets while advancing in an increasing magnetic field, or it can be imprinted in the solar wind and preserved during jet propagation in the magnetosheath. The latter scenario was investigated by assessing the correlation between the solar wind ion temperature and the solar wind magnetic field intensity, at the moment of jet detection. However, ACE, the solar wind monitoring spacecraft, provides measurement of the total ion temperature and not of the temperature anisotropy. Thus, we evaluated the correlation between the solar wind ion total temperature and the solar wind magnetic field intensity, for those time intervals when Cluster detected jets in the magnetosheath. In order to be consistent with the analysis performed for solar wind ion temperature data, we recomputed the correlation between the jet total ion temperature versus jet total magnetic field. These results are presented in Figure 12.
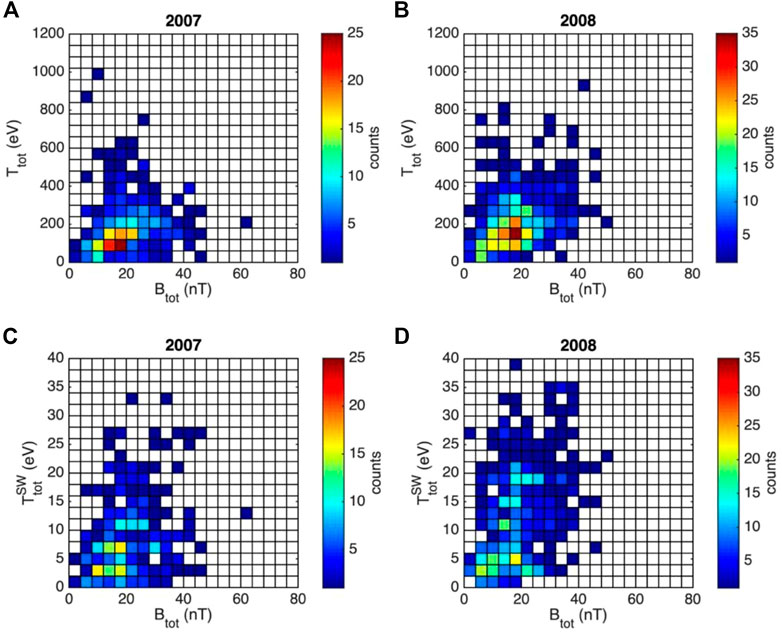
FIGURE 12. Upper row: 2D histograms in the space defined by the jet ion total temperature computed as
The two-dimensional histogram of jet total ion temperature versus jet total magnetic field intensity suggests that the number of observations of jets with higher ion temperatures increases with the magnetic field intensity. However, the histogram computed for solar wind ion temperature shows a larger spreading of data and the trend observed for jets is not retrieved. We consider that the increase of ion temperature with the magnetic field is a result of a local process in the magnetosheath and not inherited from the solar wind origin of jets.
A measure of the jet adiabatic breaking is given by ΔV, the amount of speed the jet loses while it advances in a magnetic field which increases by ΔB. This measure is, however, difficult to estimate experimentally as the spacecraft intersects the jet at a given position and time, with no access to jet’s history, i.e., its speed at the origin, close to the bow-shock. In this study we use a proxy to estimate the jet deceleration taking place between the moment when the jet enters the magnetosheath (assumed to be at the bow-shock) and the moment when the jet is detected by Cluster. We estimate the difference between the jet velocity observed by Cluster in the magnetosheath and its initial perpendicular speed. The latter is not known of course, we approximate it by the value of the solar wind velocity at the bow shock (from OMNI database) at the time when the jet is detected.
Since only the perpendicular component is affected by the adiabatic braking (Lemaire, 1985; Voitcu and Echim, 2017), a measure of the braking/deceleration is given by ΔV =Vjet–VSW, where Vjet, VSW denote the perpendicular component of the jet and solar wind plasma bulk velocity, respectively. Larger negative values of ΔV correspond to a stronger jet braking. Similarly, the increase in magnetic field is computed as the difference, ΔB =Bjet–BSW, between the magnetic field intensity measured in jet, at the moment of maximum dynamic pressure, and the magnetic field intensity measured in the solar wind at the moment of jet detection.
The two-dimensional histograms shown in Figure 13 illustrate the distribution of jets in the (ΔV, ΔB) plane, where ΔV is the variation of the perpendicular velocity estimated as the difference between the jet’s perpendicular velocity when the jet dynamic pressure is maximum and the solar wind perpendicular speed at the moment of jet detection. The number of jets with large negative values of ΔV, corresponding to a strong deceleration/braking, increases with stronger magnetic field gradients, ΔB, for both years, 2007 and 2008. This correlation is consistent with the adiabatic breaking scenario. In other words, we observe that the jet perpendicular velocity decreases in an increasing magnetic field. This effect is consistent with the mechanism described in Eq. 4 leading to gradual transfer of jet’s bulk speed into ion gyromotion and perpendicular heating.
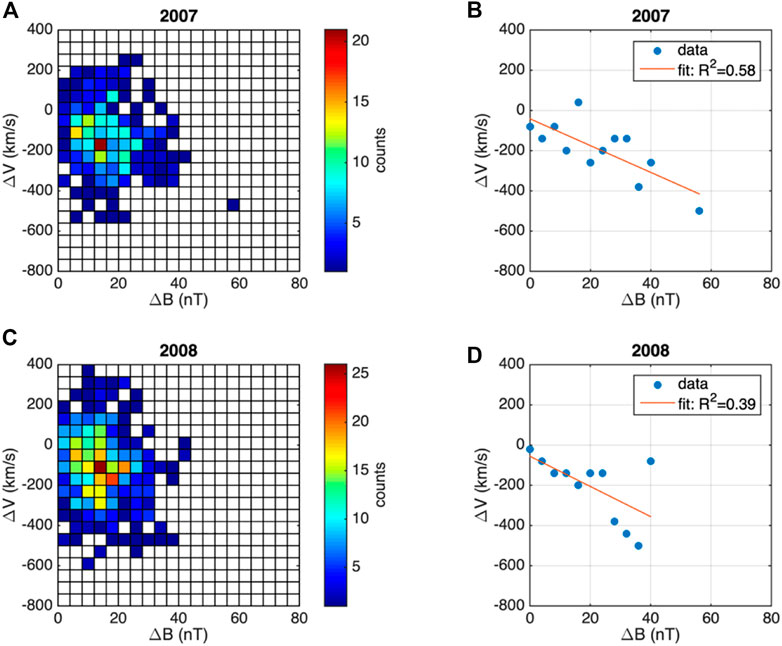
FIGURE 13. Left column: 2D histograms in the space defined by the jet perpendicular velocity breaking, quantified by the difference between the perpendicular jet speed at maximum dynamic pressure and the solar wind perpendicular speed, and total magnetic variation, ΔB, estimated as the difference between the jet magnetic field and the solar wind magnetic field, for 2007 (A) and 2008 (C). Right column: Linear fit of ΔV function of ΔB, where ΔV is computed from the average over all bins in ΔV corresponding to each ΔB value in the 2D histogram at left for 2007 (B) and 2008 (D). The results are obtained for a subset of jets in the subsolar magnetosheath
One could question the contribution of the background magnetosheath on the dynamical properties of jets and braking revealed in Figures 11–13. There is certainly a breaking of the magnetosheath plasma, from the bow-shock to the magnetopause, which is a result of the general (magnetohydrodynamic) circulation flow of the shocked solar wind plasma surrounding the magnetospheric obstacle. The background magnetosheath plasma has a bulk velocity equal to zero at the magnetopause. However, this is not necessarily true for jets. A recent study based on MHD simulations and experimental data (Sibeck et al., 2022) suggests the anti-sunward component of the magnetosheath plasma bulk velocity decreases linearly from a quarter of the solar wind speed, at the bow-shock, to zero, at the magnetopause.
In Figure 14 we illustrate a 2D histogram of the background magnetosheath data in the (ΔV,ΔB) space, similar to Figure 13. The perpendicular velocity braking ΔV and maximum magnetic field variation, ΔB, are defined as for the jets. Generally, the distribution in (ΔV, ΔB) space look different for the background magnetosheath compared to the jets. Nevertheless, the linear regression shows better fitting parameters. Thus, one can argue that signatures of braking and correlation with magnetic gradient are retrieved also in the background magnetosheath. In a future study we will attempt to characterize in detail the magnetosheath braking and check against existing models, like, e.g., Sibeck et al. (2022), describing the decrease of background magnetosheath speed, from the bow-shock to the magnetopause.
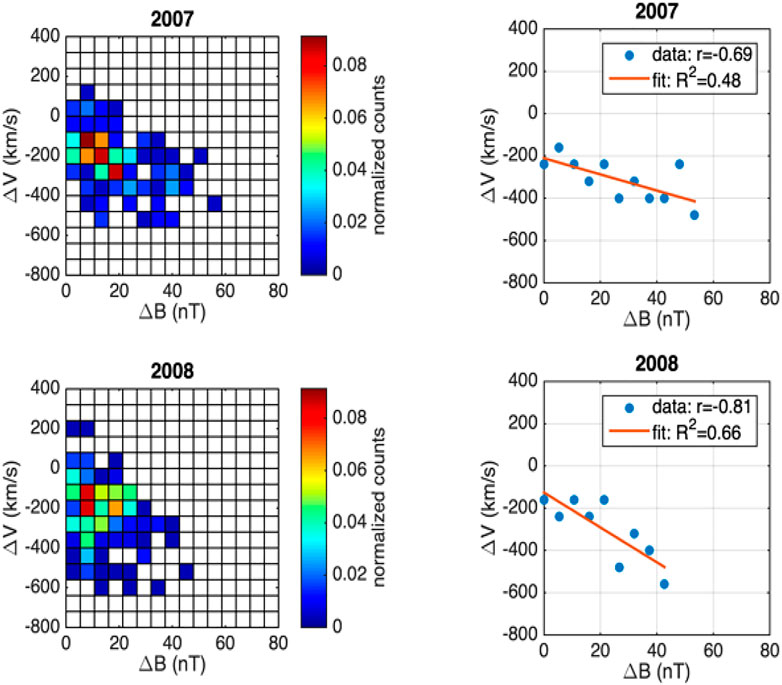
FIGURE 14. Same as Figure 13 but for the background magnetosheath data.
We discuss the dynamical properties of magnetosheath jets from the perspective of a phenomenology less considered in past studies devoted to this topic and supported by theory, numerical simulations and previous observational data, briefly reviewed in the introductory part of the manuscript. In-situ observations by fleet of spacecraft confirm that magnetosheath irregularities represent a quasi-permanent feature of the Earth’s magnetosheath. Advocated in the past by theoretical models for the solar wind—magnetosphere interactions, magnetosheath irregularities/jets have an effective impact on the magnetopause and magnetosphere, like magnetic perturbations on ground, activation of auroral emissions, ionospheric effects.
Numerical simulations and models reveal that kinetic effects, like the electric self-polarization, have a role in the self-consistence of jets, implicitly assumed in many statistical studies based on in-situ observations. Collective plasma effects can also lead to a decoupling of jets from the background plasma and field, can foster the transport across the magnetopause, inside the magnetosphere. Such effects can also contribute to the deceleration of the jet bulk motion across an increasing magnetic field, like is the case in the vicinity of the magnetopause and/or inside the magnetosphere. The conservation of the adiabatic moment, the electric self-polarization of the jet, enable a decrease of the bulk motional energy perpendicular to the magnetic field, when the jet moves in and increasing magnetic field. The bulk motional energy is transferred into gyration energy. The jet forward motion stops where the magnetic field intensity is high enough such that the bulk motional energy is exhausted and fully transferred into gyration. In-situ jets observations by Cluster and THEMIS demonstrate the transport across the magnetopause, and the propagation well inside the magnetosphere (Dmitriev and Suvorova, 2015; Lyatsky et al., 2016b). Some of these penetrating jets loose completely their momentum inside the magnetosphere, become stagnant structures forming magnetospheric irregularities/cloud populated by magnetosheath plasma.
In this study we analyze observations of jets in the magnetosheath by Cluster 3 in 2007 and 2008, respectively. A number of 960 magnetosheath jets were identified by a searching procedure which detects the excess of the local dynamic pressure with respect to the background magnetosheath state. The latter is estimated from a running window average. The analysis provides insight on jet dynamical properties, relevant for the phenomenology discussed in first part of the manuscript. We find that:
1. The jet density, ion parallel and perpendicular temperature show a dawn-dusk asymmetry with a tendency of jet plasma being denser and colder in the dawn flank. This trend is found for data recorded in 2007 and is less clear for 2008. Nevertheless, the data analyzed for 2008 indicate a limited range of higher jet densities, 45–55 cm−3, which has slightly higher probabilities in the dusk flank. The perturbation produced by jets on the background state is also asymmetric. The density perturbations produced by jets are stronger in the dusk than in the dawn flank, this tendency being more evident for data recorded in 2007. The strongest perturbations of the background magnetosheath temperature are detected in the dawn flank, generally closer to the magnetopause. However, one cannot assign a clear asymmetric trend for temperature perturbations produced by jets. The perturbations of the dynamical pressure are stronger in the dusk flank.
2. The jet speed decreases the closer the jets are detected to the Earth, in the subsolar magnetosheath. We find a correlation between jets perpendicular velocity decrease and the gradient of the magnetic field intensity, with a tendency of the perpendicular speed braking to increase with increasing magnetic field gradient. Such a behavior may be hallmark of an adiabatic breaking process.
3. The jet perpendicular ion temperature shows a tendency to increase with decreasing distance to the Earth. Data also show a correlation between jet perpendicular temperature and the local value of the magnetic field intensity, a possible signature of an adiabatic kinetic process converting forward bulk motion into perpendicular heating.
The tendencies described in conclusion 2 and 3 above are partially retrieved in background magnetosheath data. Future analyses on the same dataset will help us further discriminate between features pertaining exclusively to the dynamics of jets themselves and the background magnetosheath.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
ME: Conceptualization, data analysis, manuscript writing, project management MV: Conceptualization, data analysis, manuscript writing, project management CM: Conceptualization, data analysis, manuscript writing SC-B: Data analysis, manuscript writing ET: Conceptualization, data analysis, manuscript writing, project management ED: Conceptualization, data analysis GV: Conceptualization, data analysis, manuscript writing, project management CN: data analysis, manuscript writing.
The VESS project PN-III-P1-1.2-PCCDI-2017 0371, 18PCCDI/2018, funded by the Romanian Ministry of Research and Innovation, CCCDI-UEFISCDI, the PRODEX projects PEA4000134960 (MISION) and PEA4000130552 (CON-CLUSTER-III) funded by the European Space Agency, the project BRAIN-BE 2.0 B2//223/P1/PLATINUM funded by the Belgian Office for Research (BELSPO) are acknowledged for supporting this research. Partial funding was provided by the Romanian Ministry of Research, Innovation and Digitalization under Romanian National Core Program LAPLAS VII – contract no. 30N/2023 and the Belgian Solar Terrestrial Center of Excellence. CM, GV, ET, and CN acknowledge support from the PRODEX project MISION PEA. ME acknowledges support from the PRODEX project CLUSTER PEA and the Belgian Solar Terrestrial Center of Excellence (STCE).
The AMDA database, the ESA Cluster mission, the UK Cluster Data Centre and the SILS database are deeply thanked for their efforts and progress in science and technology and extended data provided. We used the OMNI definitive 1-min IMF and plasma data time-shifted to the nose of the Earth’s bow shock (https://omniweb.gsfc.nasa.gov/html/HROdocum.html), downloaded from https://cdaweb.gsfc.nasa.gov. The European FP7 project STORM (http://www.storm-fp7.eu) is acknowledged for providing the time intervals when Cluster 3 crossed the magnetosheath.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Amata, E., Savin, S. P., Ambrosino, D., Bogdanova, Y. V., Marcucci, M. F., Romanov, S., et al. (2011). High kinetic energy density jets in the Earth’s magnetosheath: A case study. Planet. Space Sci. 59, 482–494. ISSN 0032-0633. doi:10.1016/j.pss.2010.07.021
Archer, M. O., Hietala, H., Hartinger, M. D., Plaschke, F., and Angelopoulos, V. (2019). Direct observations of a surface eigenmode of the dayside magnetopause. Nat. Commun. 10, 615. doi:10.1038/s41467-018-08134-5
Archer, M. O., Horbury, T. S., and Eastwood, J. P. (2012). Magnetosheath pressure pulses: Generation downstream of the bow shock from solar wind discontinuities. J. Geophys. Res. 117, A05228. doi:10.1029/2011ja017468
Archer, M. O., and Horbury, T. S. (2013). Magnetosheath dynamic pressure enhancements: Occurrence and typical properties. Ann. Geophys. 31, 319–331. doi:10.5194/angeo-31-319-2013
Balogh, A., Dunlop, M. W., Cowley, S. W. H., Southwood, D. J., Thomlinson, J. G., Glassmeier, K. H., et al. (1997). The cluster magnetic field investigation. Space Sci. Rev. 79 (1/2), 65–91. doi:10.1023/a:1004970907748
Borovsky, J. E., Birn, J., Echim, M. M., Fujita, S., Lysak, R. L., Knudsen, D. J., et al. (2020). Quiescent discrete auroral arcs: A review of magnetospheric generator mechanisms. Space Sci. Rev. 216, 1. doi:10.1007/s11214-019-0619-5
Borovsky, J. E. (2021). “Is our understanding of solar-wind/magnetosphere coupling satisfactory ?,” in Frontiers in Astronomy and space sciences 8, 634073. doi:10.3389/fspas.2021.634073
Bostick, W. H. (1956). Experimental study of ionized matter projected across a magnetic field. Phys. Rev. 104, 292–299. doi:10.1103/physrev.104.292
Burgess, D., and Scholer, M. (2013). Microphysics of quasi-parallel shocks in collisionless plasmas. Space Sci. Rev. 178 (2-4), 513–533. doi:10.1007/s11214-013-9969-6
Dimmock, A. P., Pulkkinen, T. I., Osmane, A., and Nykyri, K. (2016). The dawn–dusk asymmetry of ion density in the dayside magnetosheath and its annual variability measured by THEMIS. Ann. Geophys. 34, 511–528. doi:10.5194/angeo-34-511-2016
Dmitriev, A. V., Lalchand, B., and Ghosh, S. (2021). Mechanisms and evolution of geoeffective large-scale plasma jets in the magnetosheath. Universe 7, 152. doi:10.3390/universe7050152
Dmitriev, A. V., and Suvorova, A. V. (2015). Large-scale jets in the magnetosheath and plasma penetration across the magnetopause: THEMIS observations. J. Geophys. Res. Space Phys 120, 4423–4437. doi:10.1002/2014JA020953
Echim, M., Chang, T., Kovacs, P., Wawrzaszek, A., Yordanova, E., Narita, Y., et al. (2021). “Turbulence and complexity of magnetospheric plasmas,” in Magnetospheres in the solar system. Editors R. Maggiolo, N. André, H. Hasegawa, D. T. Welling, Y. Zhang, and L. J. Paxton Hoboken, NJ: Wiley-American Geophysical Union doi:10.1002/9781119815624
Echim, M., Lemaire, J. F., and Roth, M. (2005). Self-consistent solution for a collisionless plasma slab in motion across a magnetic field. Phys. Plasmas 12, 072904. doi:10.1063/1.1943848
Echim, M., and Lemaire, J. (2000). Laboratory and numerical simulations of the impulsive penetration mechanism. Space Sci. Rev. 92, 565–601. doi:10.1023/a:1005264212972
Echim, M., and Lemaire, J. (2002). Positive density gradients at the magnetopause: Interpretation in the framework of the impulsive penetration mechanism. J. Atmos. Solar-Terrestrial Phys. 64 (18), 2019–2028. doi:10.1016/s1364-6826(02)00229-8
Echim, M., and Lemaire, J. (2005). Two-dimensional Vlasov solution for a collisionless plasma jet across transverse magnetic field lines with a sheared bulk velocity. Phys. Rev. E 72, 036405. doi:10.1103/physreve.72.036405
Echim, M. M., Maggiolo, R., Roth, M., and De Keyser, J. (2009). A magnetospheric generator driving ion and electron acceleration and electric currents in a discrete auroral arc observed by Cluster and DMSP. Geophys. Res. Lett. 36, L12111. doi:10.1029/2009GL038343
Echim, M. M., Roth, M., and De Keyser, J. (2008). Ionospheric feedback effects on the quasi-stationary coupling between LLBL and postnoon/evening discrete auroral arcs. Ann. Geophys. 26, 913–928. doi:10.5194/angeo-26-913-2008
Echim, M. M., Roth, M., and De Keyser, J. (2007). Sheared magnetospheric plasma flows and discrete auroral arcs: A quasi-static coupling model. Ann. Geophys. 25, 317–330. doi:10.5194/angeo-25-317-2007
Escoubet, C. P., Hwang, K-J., Toledo-Redondo, S., Turc, L., Haaland, S. E., Aunai, N., et al. (2020). Cluster and MMS simultaneous observations of magnetosheath high speed jets and their impact on the magnetopause. Front. Astron. Space Sci. 6, 78. doi:10.3389/fspas.2019.00078
Escoubet, C. P., Schmidt, R., and Goldstein, M. (1997). Cluster - science and mission Overview. Space Sci. Rev. 79, 11–32. doi:10.1023/A:1004923124586
Farris, M. H., and Russell, C. T. (1994). Determining the standoff distance of the bow shock: Mach number dependence and use of models. J. Geophys. Res. 99 (A9), 17681–17689. doi:10.1029/94JA01020
Génot, V., Budnik, E., Jacquey, C., Bouchemit, M., Renard, B., Dufourg, N., et al. (2021). Automated Multi-Dataset Analysis (AMDA): An on-line database and analysis tool Automated Multi-Dataset Analysis (AMDA): An on-line database and analysis tool for heliospheric and planetary plasma data for heliospheric and planetary plasma data. Planet. Space Sci. 201, 105214. doi:10.1016/j.pss.2021.105214
Goncharov, O., Gunell, H., Hamrin, M., and Chong, S. (2020). Evolution of high-speed jets and plasmoids downstream of the quasi-perpendicular bow shock. J. Geophys. Res. Space Phys. 125, e2019JA027667. doi:10.1029/2019JA027667
Gunell, H., Nilsson, H., Stenberg, G., Hamrin, M., Karlsson, T., Maggiolo, R., et al. (2012). Plasma penetration of the dayside magnetopause. Phys. Plasmas 19 (072), 072906. doi:10.1063/1.4739446
Gustafsson, G., Bostrom, R., Holback, B., Holmgren, G., Lundgren, A., Stasiewicz, K., et al. (1997). The electric field and wave experiment for the cluster mission. Space Sci. Rev. 79 (1/2), 137–156. doi:10.1023/a:1004975108657
Han, D.-S., Hietala, H., Chen, X.-C., Nishimura, Y., Lyons, L. R., Liu, J.-J., et al. (2017). Observational properties of dayside throat aurora and implications on the possible generation mechanisms. J. Geophys. Res. Space Phys. 122, 1853–1870. doi:10.1002/2016ja023394
Han, D.-S., Liu, J.-J., Chen, X.-C., Xu, T., Li, B., Hu, Z.-J., et al. (2018). Direct evidence for throat aurora being the ionospheric signature of magnetopause transient and reflecting localized magnetopause indentations. J. Geophys. Res. Space Phys. 123, 2658–2667. doi:10.1002/2017JA024945
Hasegawa, H., Fujimoto, M., Phan, T.-D., Reme, H., Balogh, A., Dunlop, M. W., et al. (2004). Transport of solar wind into Earth’s, magnetosphere through rolled-up, Kelvin–Helmholtz vortices. NATURE 430, 755–758. doi:10.1038/nature02799
Hietala, H., Laitinen, T. V., Andréeová, K., Vainio, R., Vaivads, A., Palmroth, M., et al. (2009). Supermagnetosonic jets behind a collisionless quasiparallel shock. Phys. Rev. Lett. 103, 245001. doi:10.1103/physrevlett.103.245001
Hietala, H., Partamies, N., Laitinen, T. V., Clausen, L. B. N., Facskó, G., Vaivads, A., et al. (2012). Supermagnetosonic subsolar magnetosheath jets and their effects: From the solar wind to the ionospheric convection. Ann. Geophys. 30, 33–48. doi:10.5194/angeo-30-33-2012
Johnson, J. R., and Wing, S. (2015). The dependence of the strength and thickness of field-aligned currents on solar wind and ionospheric parameters. J. Geophys. Res. Space Phys. 120, 3987–4008. doi:10.1002/2014JA020312
Karlsson, T., Brenning, N., Nilsson, H., Trotignon, J.-G., Vallières, X., and Facsko, G. (2012). Localized density enhancements in the magnetosheath: Three-dimensional morphology and possible importance for impulsive penetration. J. Geophys. Res. 117, A03227. doi:10.1029/2011JA017059
Karlsson, T., Kullen, A., Liljeblad, E., Brenning, N., Nilsson, H., Gunell, H., et al. (2015). On the origin of magnetosheath plasmoids and their relation to magnetosheath jets. J. Geophys. Res. Space Phys. 120, 7390–7403. doi:10.1002/2015JA021487
Karlsson, T., Plaschke, F., Hietala, H., Archer, M., Blanco-Cano, X., Kajdič, P., et al. (2018). Investigating the anatomy of magnetosheath jets – MMS observations. Ann. Geophys. 36, 655–677. doi:10.5194/angeo-36-655-2018
Katsavriasi, C., Raptis, S., Daglis, L. A., Karlsson, T., Georgiou, M., and Balasis, G. (2021). On the generation of Pi2 pulsations due to plasma flow patterns around magnetosheath jets. Geophys. Res. Lett. 48, e2021GL093611. doi:10.1029/2021GL093611
Koller, F., Temmer, M., Preisser, L., Plaschke, F., Geyer, P., Jian, L. K., et al. (2022). Magnetosheath jet occurrence rate in relation to CMEs and SIRs. J. Geophys. Res. Space Phys. 127, e2021JA030124. doi:10.1029/2021JA030124
Lai, H. R., and Russell, C. T. (2018). Nanodust released in interplanetary collisions. Planet. Space Sci. 156, 2–6. doi:10.1016/j.pss.2017.10.003
Lemaire, J. (1977). Impulsive penetration of filamentary plasma elements into the magnetospheres of the Earth and Jupiter. Planet. Space Sci. 25, 887–890. doi:10.1016/0032-0633(77)90042-3
Lemaire, J. (1985). Plasmoid motion across a tangential discontinuity - with application to the magnetopause. J. Plasma Phys. 33, 425–436. doi:10.1017/s0022377800002592
Lemaire, J., and Roth, M. (1981). Differences between solar wind plasmoids and ideal magnetohydrodynamic filaments. Planet. Space Sci. 29, 843–849. doi:10.1016/0032-0633(81)90075-1
Lemaire, J., and Roth, M. (1978). Penetration of solar wind plasma elements into the magnetosphere. J. Atmos. Terr. Phys. 40, 331–335. doi:10.1016/0021-9169(78)90049-1
Liu, T. Z., Hietala, H., Angelopoulos, V., Omelchenko, Y., Vainio, R., and Plaschke, F. (2020). Statistical study of magnetosheath jet-driven bow waves. J. Geophys. Res. Space Phys. 125, e2019JA027710. doi:10.1029/2019JA027710
Lundin, R., and Aparicio, B. (1982). Observations of penetrated solar wind plasma elements in the plasma mantle. Planet. Space Sci. 30, 81–91. doi:10.1016/0032-0633(82)90075-7
Lundin, R., and Dubinin, E. (1984). Solar wind energy transfer regions inside the dayside magnetopause. I - evidence for magnetosheath plasma penetration. Planet. Space Sci. 32, 745–755. doi:10.1016/0032-0633(84)90098-9
Lundin, R. (1988). On the magnetospheric boundary layer and solar wind energy transfer into the magnetosphere. Space Sci. Rev. (ISSN 0038-6308 48 (3-4), 263–320. doi:10.1007/bf00226010
Lundin, R., Sauvaud, J.-A., Rème, H., Balogh, A., Dandouras, I., Bosqued, J. M., et al. (2003). Evidence for impulsive solar wind plasma penetration through the dayside magnetopause. Ann. Geophys. 21, 457–472. doi:10.5194/angeo-21-457-2003
Lyatsky, W., Pollock, C., Goldstein, M. L., Lyatskaya, S., and Avanov, L. (2016a). Penetration of magnetosheath plasma into dayside magnetosphere: 1. Density, velocity, and rotation. J. Geophys. Res. Space Phys. 121, 7699–7712. doi:10.1002/2015JA022119
Lyatsky, W., Pollock, C., Goldstein, M. L., Lyatskaya, S., and Avanov, L. (2016b). Penetration of magnetosheath plasma into dayside magnetosphere: 2. Magnetic field in plasma filaments. J. Geophys. Res. Space Phys. 121, 7713–7727. doi:10.1002/2015JA022120
Munteanu, C., Hamada, A., and Mursula, K. (2019). High-speed solar wind streams in 2007-2008: Turning on the Russell-McPherron effect. J. Geophys. Res. Space Phys. 124, 8913–8927. doi:10.1029/2019JA026846
Negrea, C., Munteanu, C., and Echim, M. M. (2021). Global ionospheric response to a periodic sequence of HSS/CIR events during the 2007–2008 solar minimum. J. Geophys. Res. Space Phys. 126, e2020JA029071. doi:10.1029/2020JA029071
Nemecek, Z., Šafránková, J. M., Prech, L., Sibeck, D. G., Kokubun, S., Mukai, T., et al. (1998). Transient flux enhancements in the magnetosheath. Geophys. Res. Lett. 25, 1273–1276. doi:10.1029/98GL50873
Nykyri, K. (2013). Impact of MHD shock physics on magnetosheath asymmetry and Kelvin-Helmholtz instability. J. Geophys. Res. Space Phys. 118 (8), 5068–5081. doi:10.1002/jgra.50499
Nykyri, K., and Otto, A. (2001). Plasma transport at the magnetospheric boundary due to reconnection in Kelvin-Helmholtz vortices. Geophys. Res. Lett. 28, 3565–3568. doi:10.1029/2001GL013239
Parkhomov, V. A., Eselevich, V. G., Eselevich, M. V., Dmitriev, A. V., Suvorova, A. V., Khomutov, S. Yu., et al. (2021). Magnetospheric response to the interaction with the sporadic solar wind diamagnetic structure. Solar-Terr. Phys. 7 (3), 11–28. doi:10.12737/stp-73202102
Parkhomov, V. A., Eselevich, V. G., Eselevich, M. V., Tsegmed, B., Khomutov, S. Yu., Raita, T., et al. (2022). Correspondence of a global isolated substorm to the McPherron statistical model. Solar-Terrestrial Phys. 8 (1), 37–46. doi:10.12737/stp-82202206
Plaschke, F., Hietala, H., and Angelopoulos, V. (2013). Anti-sunward high-speed jets in the subsolar magnetosheath. Ann. Geophys. 31 (10), 1877–1889. doi:10.5194/angeo-31-1877-2013
Plaschke, F., Hietala, H., Angelopoulos, V., and Nakamura, R. (2016). Geoeffective jets impacting the magnetopause are very common. J. Geophys. Res. Space Phys. 121, 3240–3253. doi:10.1002/2016JA022534
Plaschke, F., Hietala, H., Archer, M., Blanco-Cano, X., Kajdiˇc, P., Karlsson, T., et al. (2018). Jets downstream of collisionless shocks. Space Sci. Rev. 214, 81. doi:10.1007/s11214-018-0516-3
Plaschke, F., Jernej, M., Hietala, H., and Vuorinen, L. (2020). On the alignment of velocity and magnetic fields within magnetosheath jets. Ann. Geophys. 38, 287–296. doi:10.5194/angeo-38-287-2020
Plaschke, F., Karlsson, T., Hietala, H., Archer, M., Voros, Z., Nakamura, R., et al. (2017). Magnetosheath high-speed jets: Internal structure and interaction with ambient plasma. J. Geophys. Res. Space Phys. 122 (10), 175. 157–10. doi:10.1002/2017JA024471
Preisser, L. (2020). Magnetosheath jets and plasmoids: Characteristics and formation mechanisms from hybrid simulations. Astrophysical J. Lett. 900, abad2b. doi:10.3847/2041-8213/abad2b
Raptis, S., Aminalragia-Giamini, S., Karlsson, T., and Lindberg, M. (2020). Classification of magnetosheath jets using neural networks and high resolution OMNI(HRO) data. Front. Astronomy Space Sci. 7, 24. doi:10.3389/fspas.2020.00024
Raptis, S., Karlsson, T., Plaschke, F., Kullen, A., and Lindqvist, P.-A. L. (2019). Classifying magnetosheath jets using MMS - statistical properties. ESSOAr. doi:10.1002/essoar.10501493.2
Reme, H. (1997). “The cluster ion spectrometry (CIS) experiment,” in The cluster and phoenix missions. Editors C. P. Escoubet, C. T. Russell, and R. Schmidt (Dordrecht: Springer). doi:10.1007/978-94-011-5666-012
Roth, M. (1995). “Impulsive transport of solar wind into the magnetosphere in Physics of the magnetopause,” in Geophysical monograph. Editors P. Song, B. U. Ö. Sonnerup, and M. F. Thomsen (Washington, D. C: AGU), 90, 343–348.
Savin, S., Amata, E., Zelenyi, L., Budaev, V., Consolini, G., Treumann, R., et al. (2008). High energy jets in the Earth’s magnetosheath: Implications for plasma dynamics and anomalous transport. JETP Lett. 87, 593–599. doi:10.1134/S0021364008110015
Schmidt, G. (1960). Plasma motion across magnetic fields. Phys. Fluids 3, 961–965. doi:10.1063/1.1706163
Shue, J.-H., Chao, J.-K., Song, P., McFadden, J. P., Suvorova, A., Angelopoulos, V., et al. (2009). Anomalous magnetosheath flows and distorted subsolar magnetopause for radial interplanetary magnetic fields. Geophys. Res. Lett. 36, L18112. doi:10.1029/2009GL039842
Shue, J.-H., Chao, J. K., Fu, H. C., Russell, C. T., Song, P., Khurana, K. K., et al. (1997). A new functional form to study the solar wind control of the magnetopause size and shape. J. Geophys. Res. 102 (A5), 9497–9511. doi:10.1029/97JA00196
Sibeck, D. G., Silveira, M. V. D., and Collier, M. R. (2022). Tracking the Subsolar Bow Shock and Magnetopause. Journal of Geophysical Research: Space Physics 127 (9), e30704. doi:10.1029/2022JA030704
Teodorescu, E., Echim, M., and Voitcu, G. (2021). A perspective on the scaling of magnetosheath turbulence and effects of bow shock properties. Astrophysical J. 910, 13. doi:10.3847/1538-4357/abe12d
Vaisberg, O. L., Smirnov, V. N., Avanov, L. A., Waite, J. H., Burch, J. L., Russell, C. T., et al. (1998). Observation of isolated structures of the low latitude boundary layer with the INTERBALL/tail probe. Geophys. Res. Lett. 25 (23), 4305–4308. doi:10.1029/1998GL900167
Voitcu, G., and Echim, M. (2018). Crescent-shaped electron velocity distribution functions formed at the edges of plasma jets interacting with a tangential discontinuity. Ann. Geophys. 36, 1521–1535. doi:10.5194/angeo-36-1521-2018
Voitcu, G., and Echim, M. (2017). Tangential deflection and formation of counterstreaming flows at the impact of a plasma jet on a tangential discontinuity. Geophys. Res. Lett. 44, 5920–5927. doi:10.1002/2017GL073763
Voitcu, G., and Echim, M. (2016). Transport and entry of plasma clouds/jets across transverse magnetic discontinuities: Three-dimensional electromagnetic particle-in-cell simulations. J. Geophys. Res. Space Phys. 121, 4343–4361. doi:10.1002/2015JA021973
Vörös, Z., Yordanova, E., Echim, M., Consolini, G., and Narita, Y., TURBULENCE-GENERATED proton-scale structures in the terrestrial magnetosheath, Astrophysical J. Lett., 819 L15, doi:10.3847/2041-8205/819/1/L152019
Vuorinen, L., Hietala, H., and Plaschke, F. (2019). Jets in the magnetosheath: IMF control of where they occur. Ann. Geophys. 37, 689–697. doi:10.5194/angeo-37-689-2019
Wang, B., Nishimura, Y., Hietala, H., Lyons, L., Angelopoulos, V., Plaschke, F., et al. (2018). Impacts of magnetosheath high-speed jets on the magnetosphere and ionosphere measured by optical imaging and satellite observations. J. Geophys. Res.-Space 123, 4879–4894. doi:10.1029/2017JA024954
Wing, S., Johnson, J. R., Chaston, C. C., Echim, M., Escoubet, C. P., Lavraud, B., et al. (2014). Review of solar wind entry into and transport within the plasma sheet. Space Sci. Rev. 184, 33–86. doi:10.1007/s11214-014-0108-9
Keywords: magnetosheath, plasma jets, magnetosphere, Cluster, solar wind-magnetosphere coupling, dawn-dusk asymmetries, adiabatic breaking
Citation: Echim M, Voiculescu M, Munteanu C, Teodorescu E, Voitcu G, Negrea C, Condurache-Bota S and Dănilă EB (2023) On the phenomenology of magnetosheath jets with insight from theory, modelling, numerical simulations and observations by Cluster spacecraft. Front. Astron. Space Sci. 10:1094282. doi: 10.3389/fspas.2023.1094282
Received: 09 November 2022; Accepted: 02 February 2023;
Published: 17 February 2023.
Edited by:
Olga V. Khabarova, Tel Aviv University, IsraelReviewed by:
Terry Zixu Liu, University of California, Los Angeles, United StatesCopyright © 2023 Echim, Voiculescu, Munteanu, Teodorescu, Voitcu, Negrea, Condurache-Bota and Dănilă. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mirela Voiculescu, TWlyZWxhLlZvaWN1bGVzY3VAdWdhbC5ybw==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.