Seismology of active regions: Current status and perspectives

Tripathy, Sushanta

doi:10.3389/fspas.2023.1091777

REVIEW article

Front. Astron. Space Sci., 20 March 2023

Sec. Stellar and Solar Physics

Volume 10 - 2023 | https://doi.org/10.3389/fspas.2023.1091777

This article is part of the Research Topic Connecting Solar Flows and Fields to Understand Surface Magnetism View all 6 articles

Seismology of active regions: Current status and perspectives

Sushanta Tripathy*

National Solar Observatory, Boulder, CO, United States

The goal of helioseismology is to provide accurate information about the Sun’s interior from the observations of the wave field at its surface. In the last three decades, both global and local helioseismology studies have made significant advances and breakthroughs in solar physics. However, 3-d mapping of the structure and dynamics of sunspots and active regions below the surface has been a challenging task and is among the long standing and intriguing puzzles in solar physics due to the complexity of the turbulent and dynamic nature of magnetized regions. In this review, I present some of the recent results relevant for helioseismology of sunspots and active regions obtained from high resolution observations, forward modeling and numerical simulations.

1 Introduction

Magnetic fields on the Sun exist in various forms and exhibit a large variety of phenomena. Its key elements are sunspots and active regions (ARs) which control most of the solar dynamics and evolution. Although the formation and stability of sunspots are one of the richest subjects of study in solar physics, the topology of the magnetic field above and beneath the Sun’s surface is poorly understood. In particular, knowledge of the magnetic field in the interior presents theoretical and observational challenges since direct measurements are not possible. The only way it could be probed is through the framework of helioseismology which analyzes the acoustic waves of the Sun. Prior to the development of local helioseismic techniques, the dynamics and structure of sunspots were studied from high-resolution observations of the solar surface. Local helioseismic techniques such as time-distance (TD; Duvall et al., 1993), helioseismic holography (HH; Lindsey and Braun, 1997) and ring-diagram (RD; Hill, 1988) have presented new opportunities to probe the subsurface structure and dynamics of sunspots and active regions (for previous reviews see Gizon and Birch, 2005; Kosovichev, 2012).

Despite the abundance of clues from observations at the solar surface and application of these helioseismic techniques, theories about formation, subsurface structure, thermal properties and topology of active regions are still being debated. As demonstrated by Gizon et al., 2009, Gizon et al., 2010), wave speed perturbations beneath the sunspot in Active Region 9787 obtained from time-distance inversions are different from ring-diagram inversions and disagree with the results from semi-empirical models or radiative magnetohydrodynamic (MHD) simulations. Moradi et al. (2010) reanalyzed this active region and the result is presented in Figure 1 which shows the wave speed perturbations from different models as well as the wave-speed inversions from both ring-diagram analysis and time-distance helioseismology. As evident, three out of four curves shown in Figure 1 are consistent with a strong, positive wave-speed perturbation extending about 2–3 Mm below the surface. Below this depth, the helioseismic inversions showconsiderably stronger deep wave-speed perturbations than the other methods. This is commonly referred to as the two-layer structure with a negative variation of the sound speed in a shallow subsurface layer and a positive variation in the deep interior. However, the two local helioseismic inversions give subsurface wave-speed profiles with opposite signs and different amplitudes. Although the papers cited above discuss a number of factors which could contribute to such a disagreement; Moradi et al. (2010) recommend that the structure of the sunspot in AR 9787 is probably associated with a shallow, positive wave-speed perturbation instead of the two-layer model. It is also plausible that the helioseismic inversions for sound speed beneath the sunspots are contaminated by surface effects associated with the sunspot magnetic field (Couvidat and Rajaguru, 2007). In order to further understand the discrepancy, Kosovichev (2012) combined the sound speed differences that have been previously inferred by various authors and the results are shown in Figure 2. It is clearly seen that the sound speed differences between different helioseismic techniques provide better qualitative agreement; an enhancement in the deep interior (2–10 Mm) and a decrease in the subsurface layers, i.e., a two layer model. The TD results show a shallow negative variation while the acoustic imaging inversion lacks it. The results of RD inversions show the structure qualitatively similar to the TD results but the negative variation is spread deeper than in the TD profiles. A similar result was also reported by Baldner et al. (2009). For comparison, the figure also shows the sound speed perturbation published by (Gizon et al. 2009; Gizon et al. 2010) using the ring-diagram analysis and as discussed previously, the behaviour is remarkably different from other curves obtained by the same technique.

FIGURE 1

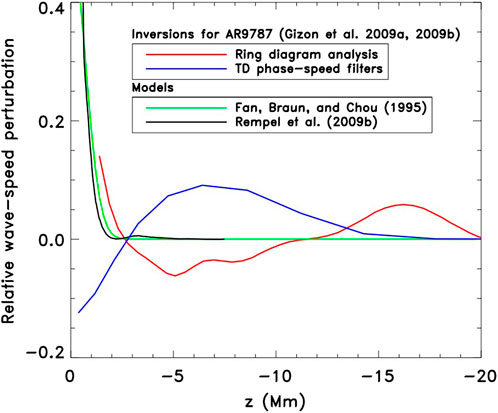
FIGURE 1. Comparison of different helioseismic methods used to infer wave-speed perturbations below the sunspot in Active Region 9787. The red and blue curves show the ring-diagram and phase-speed filtered time-distance results, respectively, as displayed in Gizon et al. (2009, 2010). The time—distance result is shown along the axis of the sunspot; the ring-diagram results have been scaled by a factor of ten. The black curve indicates the fast-mode speed perturbation from the radiative MHD simulations of Rempel et al. (2009b). The green line represents the on-axis wave-speed perturbations deduced from the phenomenological model of Fan et al. (1995). Figure from Moradi et al. (2010).

FIGURE 2

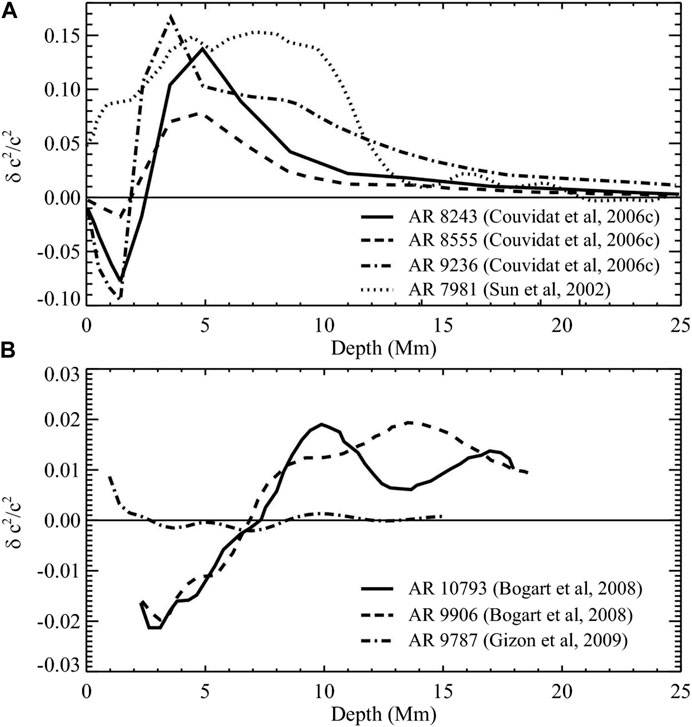
FIGURE 2. Sound speed beneath various sunspots obtained by different local helioseismology methods: (A) solid, dashed, and dot-dashed curves are obtained by using time-distance helioseismology technique (Couvidat et al., 2006), the dotted curve is derived by applying the technique of acoustic imaging (Sun et al., 2002); (B) solid and dashed curves are from Bogart et al. (2008) and dot-dashed curve is from Gizon et al. (2009); both the curves are derived through the ring-diagram method. Figure from Kosovichev (2012).

In addition, there are several other observed phenomena associated with active regions that are yet to be fully understood in terms of coherent physical mechanisms. For example, power absorption in sunspots and enhanced acoustic power surrounding active regions, known as acoustic halos and acoustic glories are yet to be fully explained. It has also been noticed that when a sunspot is located near the limb, the phase shift of the acoustic waves vary in a sunspot penumbra relative to the direction of the disk center. This effect termed as “Shower-glass” effect was first reported by Schunker et al. (2005) and later confirmed by Zhao and Kosovichev (2006) and is believed to be produced by surface phase perturbations. Certainly, an understanding of these phenomena are important for the development of realistic sunspot models.

The primary reasons for the failure of local helioseismic techniques to interpret the surface features and internal properties below the sunspots and active regions arise from the lack of understanding the complex interaction between solar oscillations and the magnetic field. Recent forward modeling (Cally, 2007) and numerical simulations (Cally and Moradi, 2013, and references therein) suggest that active regions open a window from the interior into the solar atmosphere and that the seismic waves leak through this window. Multi-spectral helioseismic observations with the Magneto-Optical filters at Two Heights (MOTH) instrument which was operated in Antarctica for a limited time indicated the existence of “magnetic portals” through which acoustic energy could leak into the chromosphere (Jefferies et al., 2006). These leaked acoustic waves, under certain conditions, are converted into additional fast and slow magneto-acoustic waves. The converted fast wave continues upwards to be reflected where its horizontal phase speed matches the local Alfvén speed. After it reflects, the fast wave re-enter the interior to rejoin the confined seismic wave field altering the original acoustic signal with signatures of the atmosphere. Additionally the fast wave may partially mode convert to upward and downward propagating Alfvén waves, depending on the magnetic field inclination relative to the wave vector (see Figure 1 of Khomenko and Cally, 2012), thereby removing energy from the seismic field and potentially altering its phase. Thus, further advancements in helioseismic inferences below the active region require a precise understanding of interaction between the acoustic waves and the strong inclined magnetic field as a function of height in the solar atmosphere in addition to improvement in helioseismic techniques. In this review, I briefly highlight some of the recent progress achieved in our understanding of the acoustic modes in the presence of magnetic field as well as future directions.

2 Power absorption and acoustic emissions

There is considerable observational evidence that sunspots have large effects on the amplitude of solar p-modes as measured by Doppler velocity. Measuring the power of an annular region surrounding a sunspot Braun et al. (1987) found that sunspots absorb up to 50% of the incoming acoustic power and shift the phase of incoming waves (Braun et al., 1988, 1992). The study used Hankel decomposition where the incoming wave power is analyzed in terms of the incoming and outgoing waves (for details see Gizon and Birch, 2005). Later studies found that the suppression is frequency and radial order dependent (Brown et al., 1992). These phenomena have also been studied with other techniques, e.g., acoustic holography (Chang et al., 1997), ring-diagrams (Rajaguru et al., 2001; Howe et al., 2004; Jain et al., 2008) and time-distance methodology (Ilonidis and Zhao, 2011). Several possible mechanisms exist that may explain the observed suppression but the most favorable one is the partial conversion of the incoming waves into slow magnetoacoustic waves that propagate downward, channelled by the magnetic field (Cally et al., 2003, and references therein).

Another observational phenomena associated with active regions are the existence of acoustic halos which are manifested as power enhancements around active regions (Figure 3). The acoustic halos were first observed in Dopplergrams at frequencies between 5.5 and 7.5 mHz which is higher than the cutoff frequency (Brown et al., 1992). These regions with excess power are characterized by a patchy structure at spatial scales of a few arcseconds having substantial magnetic field strength. These enhanced emissions were subsequently confirmed extending up to chromospheric heights (Braun et al., 1992; Toner and Labonte, 1993) but were absent in measurements of the continuum intensity (Hindman and Brown, 1998; Jain and Haber, 2002). With the availability of multi-height observations from Solar Dynamics Observatory (SDO; Pesnell et al., 2012), several studies showed the presence of intensity halos in different spectral lines but at higher heights (Moretti et al., 2007; Schunker and Braun, 2011; Howe et al., 2012; Tripathy et al., 2012; Rajaguru et al., 2013; Tripathy et al., 2018). Figure 3 shows the power maps for AR 11092 in different frequency bands and at different heights of the solar atmosphere corresponding to different observables (Tripathy et al., 2012). The power in Helioseismic and Magnetic Imager (HMI) Doppler (V) observations beyond 5 mHz is found to be enhanced in a narrow zone seen as a ring around the sunspot. As reported earlier no halos were seen in the HMI continuum intensity observations. In case of HMI line core (L_c, difference between I_c and line depth) and the Atmospheric Imaging Assembly (AIA) 1600 Å and 1700 Å bands, both power suppression and halos can be seen in the extended region around the sunspot. The studies mentioned earlier revealed new features, e.g., presence of halos up to 10 mHz and are found to be strong functions of magnetic field and their inclination angle. Numerous theories have been suggested as possible mechanisms for the halo phenomenon. Kuridze et al. (2008) proposed that high-order azimuthal modes may become trapped under field free magnetic canopy regions thus enhancing higher frequency wave power. By conducting radiative simulations, Jacoutot et al. (2008) showed that high-frequency turbulent convective motions, in the presence of moderate magnetic fields, may enhance the local acoustic emission. Hanasoge (2009) further advocated that the halo is a consequence of a MHD mode mixing due to scattering from the magnetic flux tube. On the other hand, Khomenko and Collados (2009) suggested that the refraction of fast waves in the higher atmosphere could deposit additional energy into photospheric regions where the process of mode conversion describes the intrinsic physics. This study also put forward several potentially observable properties of halos, derived from their model of fast magneto-acoustic wave refraction.

FIGURE 3

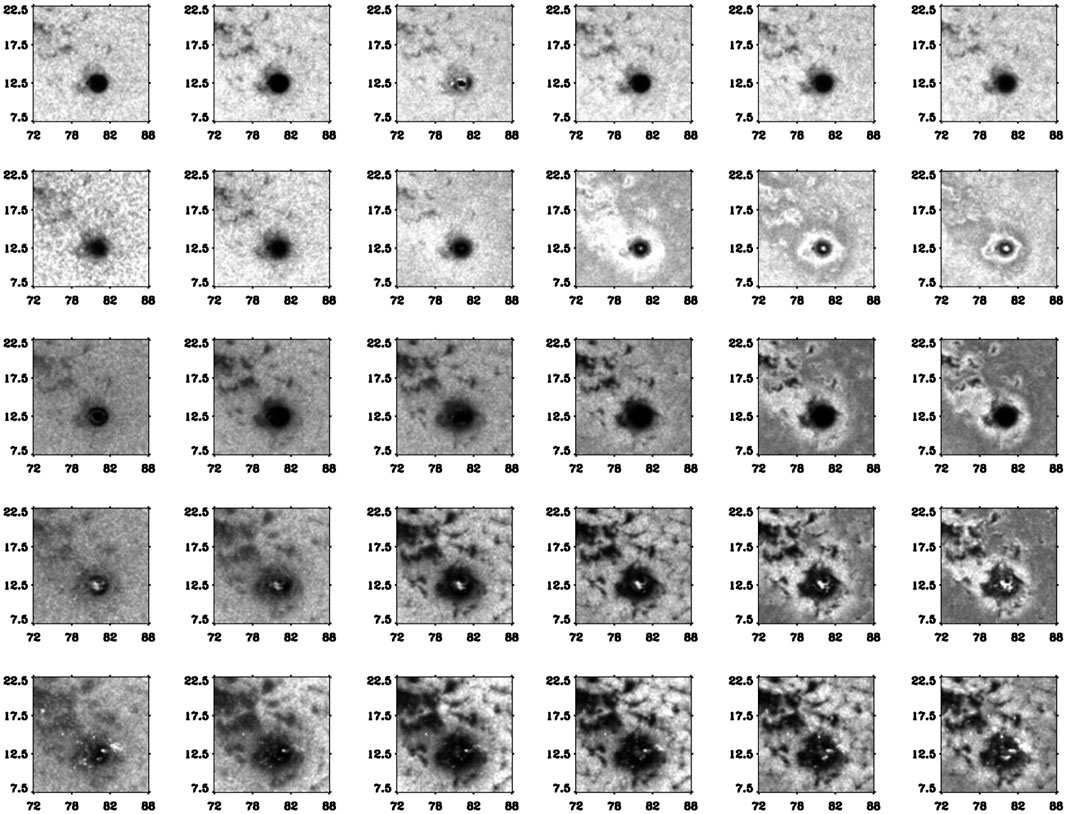
FIGURE 3. Two-dimensional power maps of AR 11092 on 2010 August 3. The vertical columns from left to right represents power in 3–8 mHz in 1-mhz bands. The rows from top to bottom represent HMI continuum intensity (I_c), HMI Doppler (V), HMI line core (L_c), AIA 1700 Å and AIA 1600 Å respectively, i.e., in order of the increasing height from about 20 to 450 km. The x-axis and y-axis in each panel represents longitude and latitude, respectively. Figure from Tripathy et al. (2012).

Recent numerical simulations of Rijs et al. (2016) provided further evidence that the halo is solely produced by the return of the reflected fast magneto-acoustic waves. In this simulation, the high-chromosphere Alfvén speed was artificially limited thereby preventing fast wave reflection. As illustrated in Figure 4, the halos were reduced for smaller Alfvén velocity and was completely suppressed when the velocity was about 12 km/s, dramatically illustrating that the atmosphere can indeed shape the observed surface seismology. However, why these reflected fast waves are at a higher frequency than the cutoff frequency is still unclear. Also, the power enhancements above the cutoff frequency around the active regions are accompanied by power suppression below the cutoff frequency within the same active regions (Jain and Haber, 2002) and the magnitude of such power suppression increases with height just above the surface (Jain et al., 2014). The variation of acoustic power in active regions may have significant effects on inferences of subsurface flows, because the suppression of acoustic sources in magnetized regions causes anisotropy in wave propagation properties. Recent preliminary studies also indicate that power halos seen in different active regions behave differently (Tripathy et al., 2020). This warrants a statistical analysis of many active regions as a function of height along with vector magnetic field measurements since both strength and inclination angle of the magnetic field plays major role in the formation of acoustic halos.

FIGURE 4

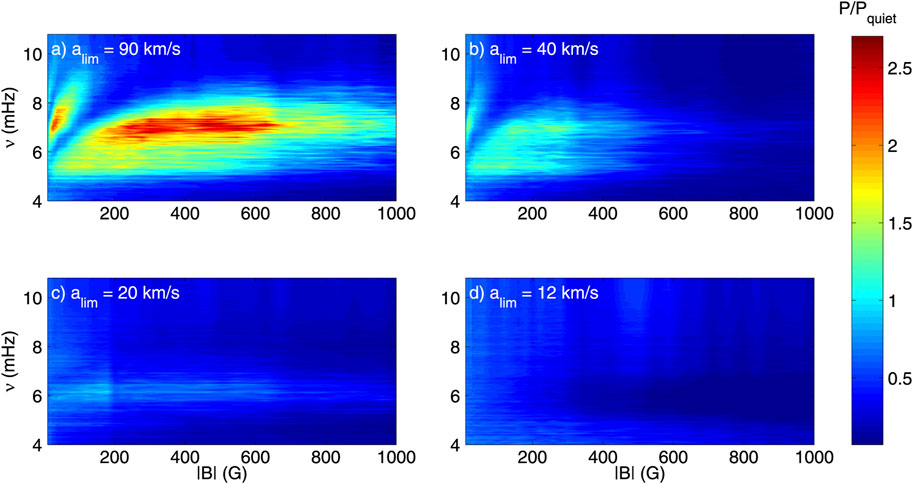
FIGURE 4. Signature of power halos for different Alfvén velocity seen in numerical simulation of Rijs et al. (2016). Note that in this simulation the maximum value of Alfvén speed limiter (a_lim) as described in Rempel et al. (2009b) is set at 90 km/s (panel a) which yields a time step of around 0.2 s in the simulation. Panels (b-d) shows the same power halos with progressively lower values of a_lim. As the Alfvén velocity is reduced, the halos disappear since it limits the space for fast waves to return. Figure from Rijs et al. (2016) and is reproduced by permission of the AAS.

In addition to the acoustic halos, active regions also show enhanced high-frequency acoustic emission in egression power maps when the active region is analyzed using the technique of helioseismic holography (Braun and Lindsey, 1999) or Hankel-Fourier analysis (Couvidat, 2013). Since these appear as discrete regions of sustained acoustic power within the emission halos, these are known as acoustic glories. Since both acoustic halos and glories are associated with enhanced emissions, it is important to make a distinction between these two phenomena. Donea et al. (2000) pointed out that the localized enhancement of the surface disturbance that registers the arrival of an underlying wave generally gives rise to the acoustic power halos while the enhanced seismic emission that characterizes acoustic glories are largely comprised of small, discrete seismic emitters that tend to cluster in strings in low-magnetic field regions (Donea and Newington, 2011). A comparison of traditional halo maps with emission maps generated using holography indicate that the two maps have similar properties with respect to the magnetic field but lack spatial correlation when the highest-power regions are examined (Hanson et al., 2015). It may also be noted that isolated sunspots do not normally show acoustic glories. The most promising mechanisms to explain these phenomena are interaction of waves with the horizontal field of a canopy structure (Muglach et al., 2005), mode conversion (Khomenko and Collados, 2009) and the trapping of waves under the canopy (Kuridze et al., 2008). Once again this is not a well understood phenomena and requires further observational studies and numerical simulations to comprehend the nature of the wave interaction in the presence of magnetic field.

3 Wave propagation in magnetized regions

In order to comprehend the seismic signal and associated phenomena observed on the surface of the Sun, it is critical to model the propagation of acoustic waves through a magnetized region. However from a theoretical point of view, the influence of magnetic fields on incident acoustic waves is a complex phenomenon. Although there is insufficient understanding of the processes involved, rapid progress is being made due to the synergy between numerical simulations and multi-height observations. Considering a simplified simulation of wave propagation (Figure 5) in which a helioseismic ray from below approached a magnetized region, Cally (2007) inferred that in the presence of strong magnetic field the acoustic waves split into fast and slow magnetoacoustic waves near the a = c equipartition depth and shortens the skip time of fast rays by up to several minutes. Under certain conditions, the fast waves are reflected back to the interior and in this process, it is believed that the phase of the acoustic waves (corresponding to travel times) is altered (Cally and Moradi, 2013). Further it has been demonstrated that scattering and mode mixing by the magnetic field causes modifications to the acoustic wave field (Hindman and Jain, 2012) which manifest as a redistribution of power between different acoustic waves in the vicinity of a magnetized region. Thus, the separation of scattered and reflected waves from different heights is also important for understanding the inhomogeneity in magnetic field regions above the surface. In the next section, we will discuss some of the recent progress made in this field especially in the field of numerical simulations of wave propagation in magnetized plasma to provide better insight of the wave interaction with the magnetic field.

FIGURE 5

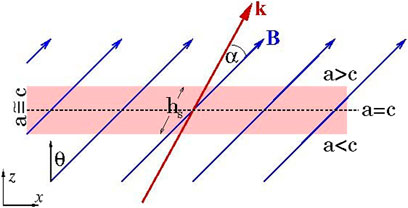
FIGURE 5. Schematic diagram illustrating the propagation of a wave with wave vector k approaching a magnetic region from below. Here c is the sound speed, a is the Alfvén velocity, θ is the field inclination from the vertical, α, the attack angle, is the angle between k and magnetic field B, h_s is the thickness of the a ≈ c layer. Figure from Cally (2007).

3.1 Forward modeling and numerical simulations

The generation of artificial data through numerical modeling and its analysis through various local helioseismic techniques have highlighted the issues associated with wave propagation in strong magnetized regions. For example, Braun et al. (2012) compared helioseismic travel-time shifts measured from a realistic magnetoconvective sunspot simulation and observed sunspots. The numerical sunspot model used were based on the methods described in Rempel et al. (2009a,b) while the mature spots were selected from the active regions AR10615 and AR11092. The travel time maps were measured following the general procedures for surface-focused helioseismic holography (Braun and Birch, 2008) and time-distance methods. The study found similarities in the travel-time shifts measured by both the techniques for the simulated sunspots. Figure 6 shows quantitative comparisons of the average travel-time shifts over the umbra between the HH measurements made for the simulated sunspot and the two observed ones for four different phase speed filters TD1 through TD4 corresponding to the mean annulus radius of 6.2, 8.7, 11.6, and 16.95 Mm, respectively (the phase speed increases from 12.8 to 24.8 km/s). It is evident that there is remarkable agreement for most of the filter combinations below 4.5 mHz but significant differences above it and mostly for the phase-speed filters TD1 and TD4 which represent lowest and highest phase speeds. In the center of the sunspots, the travel-time shifts of the real sunspots is found to be positive (longer travel times) while the corresponding shifts in the simulated spot are negative (shorter travel times). It should also be noted that there were significant differences between the two real sunspots for some phase-speed filter and frequency combinations once again emphasizing the need for statistical analysis of many active regions with different magnetic and topological characteristics.

FIGURE 6

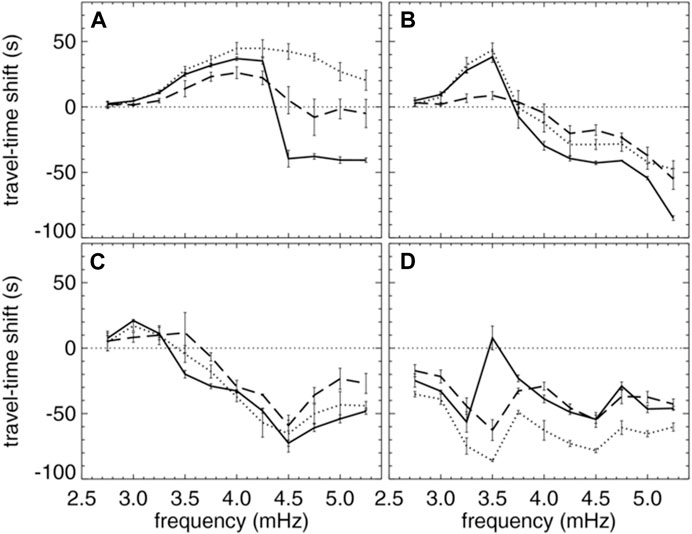
FIGURE 6. Averages of the mean travel-time shifts over the umbra of the sunspot in the magnetoconvective simulation (solid lines) and AR11092 (dotted line) and AR10615 (dashed line) as a function of the central frequency of the bandpass filter measured through the technique of helioseismic holography. The error bars represent the total spread in values. The (A–D) show the results for four different phase-speed filters TD1-TD4. Figure from Braun et al. (2012) and is reproduced by permission of the AAS.

In order to comprehend the role of the magnetic field in the seismology of the active regions through wave propagation and conversion, Cally and Moradi (2013) introduced a directionally filtered TD approach sensitive to magnetic field orientation to simulated data in a simple translationally invariant atmosphere. The study found substantial wave travel time discrepancies of several tens of seconds depending on the field strength, frequency and wave number (for example, 40 s in 1 KG magnetic field) and indicated that processes occurring in higher up in the atmosphere strongly influence the signal used in helioseismic studies. The approach was further extended to include a realistic sunspot model atmosphere spanning the sub-photosphere to the chromosphere to analyze the sensitivity of directional helioseismology measurements to changes in the photospheric and subsurface structure of sunspot models (Moradi et al., 2015). Figure 7 shows contour plots of time-distance phase travel-time perturbations (δτ) with respect to the quiet Sun model as a function of field inclination from vertical (θ) and azimuthal angle (ϕ) for different wave travel distances from the source (Δ) derived from sunspot models with surface field strength of 1.5 KG. The left and right column shows the results for 3 and 5 mHz frequency bands, respectively. The figure clearly shows manifestations of the acoustic cutoff at θ = 30°–40° for 5 mHz and θ = 50°–60° at 3 mHz. Below these inclinations, δτ is small and typically positive. At larger inclinations, negative travel time shifts are seen (slower travel time, faster speed) which are interpreted as manifestation of the wave properties. At larger field inclinations, the atmosphere is open to wave propagation and mode conversion. This results in negative δτ for these θ and particularly at small ϕ (around 0° and 180°), the fast magnetically dominated waves emerging from the layer where sound speed equals the Alfvén velocity return to the surface after reflection near the cutoff frequency with a different phase compared to that of the simply reflecting acoustic waves in the quiet Sun. However, away from ϕ = 0° or 180°, the fast waves lose energy as they are partially converted to the Alfvén waves, and further suffer a phase retardation that may be interpreted as partially cancelling the underlying negative travel time perturbation. Overall, these results illustrate that the seismic waves that leak through the active regions can directly affect the wave travel times that form the basis to infer the subsurface structure and dynamics below active regions.

FIGURE 7

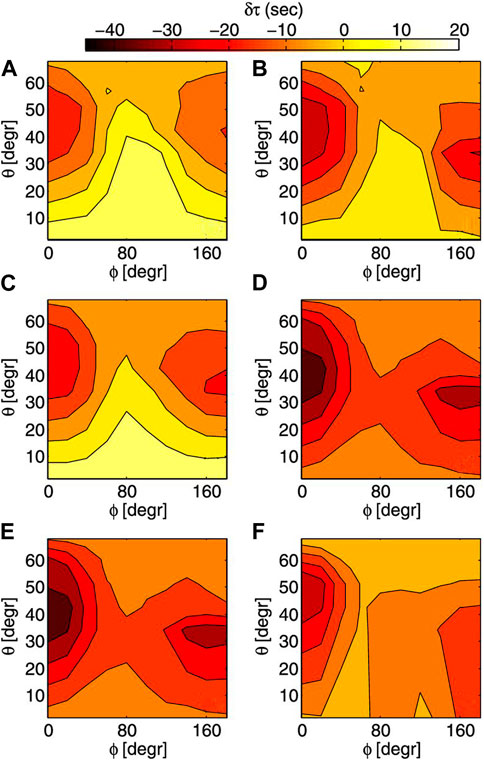
FIGURE 7. Phase travel-time perturbations derived from the 1.5 KG sunspot model simulation as a function of field inclination (θ) from the vertical, and azimuthal angle (ϕ) for wave travel distances of Δ = 6.2 (A,B), 8.7 (C,D) and 11.6 Mm (E,F). Left hand column represent 3 mHz and right-hand column 5 mHz band. Figure from Moradi et al. (2015).

Several different numerical simulations of wave propagation through magneto-hydrostatic (MHS) sunspot models were carried out by Felipe et al. (2016) to assess the contributions of thermal and magnetic effects. In the thermal only simulation, the atmospheric model’s magnetic field was set to zero while in the magnetic only sunspot simulation, the thermal variation was neglected but the direct effect of the magnetic field was included. In addition a full simulation retaining both the effects were also carried out. The measured mean travel time (average of the incoming and outgoing travel time shifts relative to the quiet Sun) for all three simulations in different frequency bands and phase speed filters are shown in Figure 8. Travel-time shifts for the full simulation ranges between −20 and −30 s for most of the combinations of phase speed and frequency filters that present a negative travel-time which are similar but smaller in magnitude than those found in realistic magnetoconvective simulations (Braun et al., 2012). It is conjectured that the difference could be due to the different properties of the sunspot model used in those studies. It is further evident that in some ranges of horizontal phase speed and frequency, there is agreement between the travel times measured in the full model and the thermal model but major disagreement with the magnetic model which shows mostly positive travel time-shifts. Since the fast magnetoacoustic waves propagates faster in the regions where the Alfvén speed is higher, one expected shorter travel times or negative shifts in the magnetic only simulation. This result is consistent with Cally (2009) who evaluated the travel-time perturbation produced by an uniform magnetic field added to the model of the quiet Sun. Thus, it appears that the travel time-shifts which is related to the phase changes could have been caused by the interaction of the waves with the magnetic field through variety of processes, e.g., mode conversion, transmission or reflection of the fast waves. (Felipe et al., 2016) also used the ray approximation to show that the travel-time shifts in the thermal sunspot model are primarily produced by the changes in the wave path due to the Wilson depression rather than the variations in the wave speed suggesting that inversions for the subsurface structure of sunspots must account for local changes in the density. These results were subsequently confirmed by performing a parametric study of the sensitivity of the travel-time shifts measured from sunspot models with different Wilson depression and magnetic field strengths (Felipe et al., 2017). This study further confirmed the frequency-dependent directional behavior, consistent with the signature of magneto-hydrodynamic mode conversion regardless of the sunspot field strength or depth of its Wilson depression. In a previous study, Schunker et al. (2013) had also explored the sensitivity of the travel times to Wilson depression and magnetic field and had concluded that the numerical modeling of MHD wave propagation is an essential tool for interpreting the effects of sunspots on seismic waveforms. Recently, Duvall et al. (2018) measured travel times for waves reflecting on the bottom side of an active region and compared this with theoretical calculations of travel times through a sunspot model and found that the travel times averaged over the umbra is significantly different from the quiet Sun. They also performed numerical experiments on the model sunspot of Przybylski et al. (2015) using standard magnetohydrodynamic ray theory to calculate the travel times and confirmed that the thermal rather than magnetic structure of the spot is responsible for the travel time delays.

FIGURE 8

FIGURE 8. Mean travel-time shifts measured from the full sunspot simulation (top left), thermal-only sunspot simulation (top right) and magnetic-only sunspot simulation (bottom) using phase speed and frequency bandpass filters. Columns correspond to the different phase speed filters used, with the name of the filter and its phase speed at the top of each figure. Each row shows a frequency filter, with the central frequency indicated at the left side. The frequency bandpass width is equal to 0.5 mHz. Figure adapted from Felipe et al. (2016) and is reproduced by permission of the AAS.

Since in TD inversions, travel time shifts are commonly represented as resulting from the changes in the local sound speed (Kosovichev et al., 1997), Braun et al. (2012) computed the travel times from the actual perturbation to the sound speed in the simulated sunspot. The study, however, found a major disagreement between the model and measured travel-time shifts. Since an earlier hare and hound analysis of simulated data containing only pure sound speed perturbation had shown remarkable agreement between the model and measured shifts (Birch et al., 2011), it is believed that the inclusion of the magnetic field in the sunspot simulation has caused the disagreement in the travel-time shifts. Thus, it is conjectured that the inversion methods which incorporate direct effects of the magnetic field (Crouch et al., 2011), including mode conversion are required to make further progress. Developing an inversion method which can account for the complicated influence of the strong magnetic fields on travel-time shifts remains a challenge for sunspot seismology. All these investigations clearly point to the importance of understanding the wave interactions in the immediate vicinity of strong and inclined magnetic field especially at the height where the magnetic field dominates the plasma motion.

4 Future directions

Theory of linear propagation of the waves in strong and inclined magnetic field regions suggests that the incident fast acoustic wave from below the surface leaks into the higher atmosphere through the magnetized regions and under certain conditions these waves are converted into additional MHD waves. Numerical simulations of wave propagation in magnetized regions further demonstrate the mode conversion process and the implications of the returning fast and Alfvén waves for the seismology of the photosphere. However at the present time the critical missing data are simultaneous vector magnetic field and high-cadence, full disk Doppler observations at multiple heights. Such observations are crucial for improving the understanding of acoustic wave propagation in the presence of magnetic field and decoding the structure and dynamics of sunspot and active regions in the subsurface layers that are crucial to determine how and why the Sun varies. In addition, high spatial, spectral, and temporal resolution observations over small areas will also provide information on the unresolved small-scale processes that may be important. The required observations can be obtained from both ground-based and space-borne observatories. In addition, observing active regions from different angles (multi-vantage and polar observations) will also help to understand the coupling of different waves. From a theoretical point of view, the next big step in the interpretation of the helioseismic signals will be to perform and analyze wave propagation through full magneto-hydrodynamic instead of magneto-hydrostatic simulations.

Author contributions

The author (ST) planned and prepared the manuscript.

Funding

This work is partially funded by NASA grant 80NSSC22M0162 to Stanford University. This work is supported by the National Solar Observatory’s Integrated Synoptic Program. The National Solar Observatory is the national center for ground-based solar physics in the United States and is operated by the Association of Universities for Research in Astronomy under a cooperative agreement with the National Science Foundation Division of Astronomical Sciences.

Acknowledgments

I thank the reviewers for their suggestions.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Baldner, C. S., Bogart, R. S., Basu, S., and Antia, H. M. (2009). “The evolution of the sub-surface structure of long-lived active regions,” in Solar-stellar dynamos as revealed by helio- and asteroseismology: Gong 2008/SOHO 21. Editors M. Dikpati, T. Arentoft, I. González Hernández, C. Lindsey, and F. Hill (Astronomical Society of the Pacific Conference Series, San Francisco), 416, 119.

Google Scholar

Birch, A. C., Parchevsky, K. V., Braun, D. C., and Kosovichev, A. G. (2011). “Hare and hounds” tests of helioseismic holography. Sol. Phys. 272, 11–28. doi:10.1007/s11207-011-9799-1